当前位置：文档之家 › 用重叠卡诺图法化简各种表达式的逻辑函数

用重叠卡诺图法化简各种表达式的逻辑函数

  • 格式：pdf
  • 大小：84.97 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

03第二章-2 卡诺图化简逻辑函数

03第二章-2 卡诺图化简逻辑函数
注意：卡诺图水平方向同一行首尾，同一列 首尾也为逻辑相邻相。
m0 与 m1 、 m2 逻辑相邻。
三变量卡诺图
四变量卡诺图
圆柱面
m0 与 m1 m2 m4 m1 与 m0 m3 m5
球面
均为逻辑相邻 均为逻辑相邻
m0 与 m1 m2 m4 m8 均为逻辑相邻 m1 与 m0 m3 m5 m9 均为逻辑相邻
(1) 在卡诺图构成过程中，变量的 取值按格雷码的顺序排列。 二变量卡诺图
格雷码：相邻两个代码之间只有一位发生变化
B0 A
1
0 m0 m1
1 m2 m3
平面表格
(2) 卡诺图两侧标注的数值代表 的二进制数对应的十进制数即为 格中对应的最小项编号。 (3) 几何位置相邻的最小项也是 逻辑相邻项。 (4) 卡诺图是上下、左右闭合的 图形。
二、用卡诺图表示逻辑函数
由于任何一个逻辑函数都能表示为若干最小 项之和的形式，所以自然也就可以用卡诺图表示 逻辑函数了。 1、逻辑函数→卡诺图 (1) 最小项法 ① 将逻辑函数化为最小项表达式； ② 在卡诺图上与这些最小项对应的位 置上填入1，在其余位置填入0或不填。 这样就得到了表示该逻辑函数的卡诺图。
例1：
Y = ABC + ABC ′ + AB′ = AB(C + C ′) + AB′ = AB + AB′ = A
例2
ABC + A′ + B′ + C ′ ′ = ABC + ( ABC ) = 1 A′BC ′ + AC ′ + B′C ′
例3
= A′BC ′ + ( A + B′)C ′ ′ = A′BC ′ + ( A′B ) C ′ = C ′

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数

1.4 用卡诺图化简逻辑函数本次重点内容1、卡诺图的画法与性质2、用卡诺图化简函数 教学过程 应用卡诺图化简 一、卡诺图逻辑函数可以用卡诺图表示。

所谓卡诺图，就是逻辑函数的一种图形表示。

对n 个变量的卡诺图来说，有2n 个小方格组成，每一小方格代表一个最小项。

在卡诺图中，几何位置相邻（包括边缘、四角）的小方格在逻辑上也是相邻的。

二、最小项的定义及基本性质： 1、最小项的定义在n 个变量的逻辑函数中，如乘积项中包含了全部变量，并且每个变量在该乘积项中或以原变量或以反变量的形式但只出现一次，则该乘积项就定义为该逻辑函数的最小项。

通常用m 表示最小项，其下标为最小项的编号。

编号的方法是：最小项的原变量取1，反变量取0，则最小项取值为一组二进制数，其对应的十进制数便为该最小项的编号。

如最小项C B A 对应的变量取值为000，它对应十进制数为0。

因此，最小项C B A 的编号为m 0，如最小项C B A 的编号为m 4，其余最小项的编号以此类推。

2、最小项的基本性质：（1）对于任意一个最小项，只有一组变量取值使它的值为1，而其余各种变量取值均使它的值为0。

（2）不同的最小项，使它的值为1的那组变量取值也不同。

（3）对于变量的任一组取值，全体最小项的和为1。

图1.4.1分别为二变量、三变量和四变量卡诺图。

在卡诺图的行和列分别标出变量及其状态。

变量状态的次序是00，01，11，10，而不是二进制递增的次序00，01，10，11。

这样排列是为了使任意两个相邻最小项之间只有一个变量改变（即满足相邻性）。

小方格也可用二进制数对应于十进制数编号，如图中的四变量卡诺图，也就是变量的最小项可用m 0, m １,m ２,……来编号。

1010001111001A BCAB CD B A 0001111000011110m m m m m mmmm m m m 012300112233m m m m m m m m m m m m m m m m 456789101112131415图1.4.1 卡诺图二、应用卡诺图表示逻辑函数应用卡诺图化简逻辑函数时，先将逻辑式中的最小项(或逻辑状态表中取值为1的最小项)分别用1填入相应的小方格内，其它的则填0或空着不填。

逻辑函数的卡诺图法化简

逻辑函数的卡诺图法化简

精品课件
26
输入变量ABC取值为001、010、100时，
逻辑函数Y有确定的值，根据题意，有任一命令（正 转、反转和停止）时为1，否则为0。
反变 函换 数为
CD BD
CD
AB
00 01 11 10
Y AB AC BD CD AB
00 1
0
1
1
01 1
0
0
1
11 0
0
0
0
10 0
0
1
1
AC
精品课件
13
4、卡诺图的性质
（1）任何两个（21个）标1的相邻最小项，可以合并为一项， 并消去一个变量（消去互为反变量的因子，保留公因子）。
AB C
但是，若 F= ABCD+ABC+BC+ABC ，显然，该函数式
难于找到相邻项。
精品课件
1
2.4.2 逻辑函数的标准式——最小项表达 式
问题的提出：逻辑函数 F= ABC+ABC ，之所以易于看出它们 的乘积项是逻辑相邻项，是因为它们的每一个乘积项中都包 含了所有的变量。而F= ABCD+ABC+BC+ABC，每个乘积项没有 包含所有的变量，所以逻辑相邻关系不直观。于是引入了最 小项的概念。
15
AB CD
00 01 11 10
00 0
1
1
0
01 1 0 0 1
11 1
0
0
1 ＡＤ
10 0 1 1 0
ＢＤ
AB CD
00 01 11 10
00 1
0
0
1
01 0
1
1
0
11 0

数字电子电路 卡诺图法化简

数字电子电路 卡诺图法化简

A
BC
B
Y A BC BD
D
例1-11 化简图示逻辑函数。
解：
1
2
多余
的圈
4
3
Y ACD ABC ACD ABC
1
2
3
4
圈组技巧(防止多圈组的方法)：
① 先圈孤立的1； ② 再圈只有一种圈法的1； ③ 最后圈大圈； ④ 检查：每个圈中至少有一个1未被其它圈圈 过。
5、 具有无关项的逻辑函数及其化简 无关项的概念：
2. OC门的应用举例
OC门的输出端并联，实现线与功能。
RL为外接负载电阻。
Y1 =AB Y2 = CD
Y1 Y2 Y 0 00 0 10 1 00 1 11
Y 图2Y-210•YOC2门的A输B出•端C并D联实A现B线与C功D能
五、三态输出门电路（TS门）
返回
三态门电路的输出有三种可能出现的状态：高电平、
与
Y=A·B
全1出1 见0出0
或
Y=A+B
全0出0 见1出1
非
YA
见0出1 见1出0
四、集电极开路门（OC门） 1．集电极开路门的电路结构
(1)电路结构：输出级是集电极开路的。
(2)逻辑符号：用“◇”表示集电极开路。 集电极 开路
集电极开路的TTL与非门 （a）电路 （b）逻辑符号
注意： OC门电路必须外接电源和负载电阻， 才能提供高电平输出信号。
6. 波形图(又一种表示逻辑功能的方法）
7. 逻辑表达式
F＝A B
图3 二极管与门 （a）电路 （b）逻辑符号 （c）波形图
二、二极管或门电路
1. 电路
返回
2. 工作原理

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数

1
ABC 11 1 1 1
ACD
10
11
F = ABC + ACD + ABD + BC
12
电子工程学院
卡诺图化简法举例3
化简逻辑函数 F(A,B,C,D)=Σm(2,3,4,6,10,11,12,13,15)
解：
最简式不唯一，但最 简式中的项数和每一 项的因子数是固定的
BC
CD AB
00
01
11
ABD 01
(2) 画包围圈合并最小 BC
11
项，得到最简与-或
111 11
CD
表达式
10
1
1
ABCD
F = ABCD + ABD + ABD + BC + CD
10
电子工程学院
卡诺图化简法举例2
化简 F(A,B,C,D)=Σm(3,4,5,7,9,13,14,15)为最简与或式
解：
CD AB
00
10
00
11
ABD 01 1
1
ABC 11 1 1 1
ABD
10
11
F = ABC + ABD + ABD + BC
13
电子工程学院
卡诺图化简法举例4
化简逻辑函数 F(A,B,C,D)=Σm(0~3,5~7,8~11,13~15)
圈1：
CD AB
00
01
11
10
B 00 1 1 1 1
圈0：
CD AB
ABCD + ABCD = ABD ABCD + ABCD = ABD ABD + ABD = AD ABD + ABD = AD

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数

1.4 用卡诺图化简逻辑函数本次重点内容1、卡诺图的画法与性质2、用卡诺图化简函数 教学过程 应用卡诺图化简 一、卡诺图逻辑函数可以用卡诺图表示。

所谓卡诺图，就是逻辑函数的一种图形表示。

对n 个变量的卡诺图来说，有2n 个小方格组成，每一小方格代表一个最小项。

在卡诺图中，几何位置相邻（包括边缘、四角）的小方格在逻辑上也是相邻的。

二、最小项的定义及基本性质： 1、最小项的定义在n 个变量的逻辑函数中，如乘积项中包含了全部变量，并且每个变量在该乘积项中或以原变量或以反变量的形式但只出现一次，则该乘积项就定义为该逻辑函数的最小项。

通常用m 表示最小项，其下标为最小项的编号。

编号的方法是：最小项的原变量取1，反变量取0，则最小项取值为一组二进制数，其对应的十进制数便为该最小项的编号。

如最小项C B A 对应的变量取值为000，它对应十进制数为0。

因此，最小项C B A 的编号为m 0，如最小项C B A 的编号为m 4，其余最小项的编号以此类推。

2、最小项的基本性质：（1）对于任意一个最小项，只有一组变量取值使它的值为1，而其余各种变量取值均使它的值为0。

（2）不同的最小项，使它的值为1的那组变量取值也不同。

（3）对于变量的任一组取值，全体最小项的和为1。

图1.4.1分别为二变量、三变量和四变量卡诺图。

在卡诺图的行和列分别标出变量及其状态。

变量状态的次序是00，01，11，10，而不是二进制递增的次序00，01，10，11。

这样排列是为了使任意两个相邻最小项之间只有一个变量改变（即满足相邻性）。

小方格也可用二进制数对应于十进制数编号，如图中的四变量卡诺图，也就是变量的最小项可用m0, m１,m２,……来编号。

01 0100011110 01ABCABCDBA0001111000011110m m m mm m m mm mm m01230112233mmmmmmmmmmmmmmmm456789101112131415图1.4.1 卡诺图二、应用卡诺图表示逻辑函数应用卡诺图化简逻辑函数时，先将逻辑式中的最小项(或逻辑状态表中取值为1的最小项)分别用1填入相应的小方格内，其它的则填0或空着不填。

逻辑函数的卡诺图化简法

逻辑函数的卡诺图化简法

逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法由前面的学习得知，利用代数法可以使逻辑函数变成较简单的形式。

但要求熟练掌握逻辑代数的基本定律，而且需要一些技巧，特别是经化简后得到的逻辑表达式是否是最简式较难确定。

运用卡诺图法可以较简便的方法得到最简表达式。

但首先需要了解最小项的概念。

一、最小项的定义及其性质1.最小项的基本概念由A、B、C三个逻辑变量构成的许多乘积项中有八个被称为A、B、C的最小项的乘积项，它们的特点是1. 每项都只有三个因子2. 每个变量都是它的一个因子3. 每一变量或以原变量(Ａ、Ｂ、Ｃ)的形式出现，或以反（非）变量(Ａ、Ｂ、Ｃ)的形式出现，各出现一次一般情况下，对ｎ个变量来说，最小项共有2n个，如n ＝3时，最小项有23＝8个2.最小项的性质为了分析最小项的性质，以下列出３个变量的所有最小项的真值表。

由此可见，最小项具有下列性质：（1）对于任意一个最小项，只有一组变量取值使得它的值为1，而在变量取其他各组值时，这个最小项的值都是0。

（2）不同的最小项，使它的值为1的那一组变量取值也不同。

（3）对于变量的任一组取值，任意两个最小项的乘积为0。

（4）对于变量的任一组取值，全体最小项之和为1。

3.最小项的编号最小项通常用mi表示，下标i即最小项编号，用十进制数表示。

以ABC为例，因为它和011相对应，所以就称ABC是和变量取值011相对应的最小项，而011相当于十进制中的3，所以把ABC记为m3按此原则，3个变量的最小项二、逻辑函数的最小项表达式利用逻辑代数的基本公式，可以把任一个逻辑函数化成一种典型的表达式，这种典型的表达式是一组最小项之和，称为最小项表达式。

下面举例说明把逻辑表达式展开为最小项表达式的方法。

例如，要将化成最小项表达式,这时可利用的基本运算关系,将逻辑函数中的每一项都化成包含所有变量A、B、C的项，然后再用最小项下标编号来代表最小项，即又如，要将化成最小项表达式，可经下列几步：（1）多次利用摩根定律去掉非号，直至最后得到一个只在单个变量上有非号的表达式；（2）利用分配律除去括号，直至得到一个与或表达式；（3）在以上第5个等式中，有一项AB不是最小项（缺少变量C），可用乘此项，正如第6个等式所示。

代数法化简逻辑函数

代数法化简逻辑函数
另外，也可运用第三项公式 AB AC AB AC BC
2.1 逻辑代数
例1：证明 AB AB A AB B AB
证明： AB AB AB AA AB BB A A B B A B
A AB B AB A AB B AB
A AB B AB
（2）用与非门实现L。
应将表达式转换成与非—与非表达式：
L AB BC AC
L AB BC AC
AB BC AC
AB BC AC
（3）用非门、或非门实现L。
L AB BC AC
ABBC AC
ABBC AC
2.1 逻辑代数
例7化简： L AB BC BC AB
2.1 逻辑代数
例3化简： L AB AC BC CB BD DB ADE(F G) L ABC BC CB BD DB ADE(F G) （利用摩根律 ）
A BC CB BD DB ADE(F G)（利用 AAB AB ）
A BC CB BD DB （利用A+AB=A）
第二章 逻辑代数
2.1 逻辑代数 2.2 逻辑函数的卡诺图化简法
2.1 逻辑代数
二.基本定律和恒等式
1.பைடு நூலகம்基本公式 （公理）
与运算： 0۰0=0 或运算： 0+0=0
0۰1=0 0+1=1
1۰0=0 1+0=1
非运算： 0 1 1 0
2. 定律
常量与变量 运算律：
互补律：
重叠律： A+A=A
A۰ A=A
双重否定律： A A
1۰1=1 1+1=1
2.1 逻辑代数
结合律 (A+B)+C=A+(B+C) ; (AB)·C=A·(BC)

卡诺图化简逻辑表达式

卡诺图化简逻辑表达式
对于包含多个非门或多个连续的与或 非门的逻辑表达式，卡诺图化简可能 无法得到最简结果。
卡诺图对于大规模逻辑电路的优化效果有限
随着逻辑电路规模的增大，卡诺图的化简过程变得复杂且耗时，难以在实际工程 中应用。
对于大规模逻辑电路，可能需要采用其他优化方法，如布尔代数、门级优化等， 以获得更好的优化效果。
THANKS
感谢观看
卡诺图化简逻辑表达式
• 卡诺图简介 • 卡诺图化简逻辑表达式的方法 • 卡诺图化简逻辑表达式的实例 • 卡诺图与其他化简方法的比较 • 卡诺图的局限性
01
卡诺图简介
卡诺图的定义
• 定义：卡诺图是一种用于表示二进制逻辑函数关系的图形表示 法，通过将逻辑函数输入变量的所有可能取值组合在网格中表 示出来，可以直观地观察到函数的最简形式。
卡诺图与布尔代数化简的比较
布尔代数化简
通过使用逻辑运算（与、或、非）的代数性质，如吸收律、分配律等，对逻辑表达式进 行简化。这种方法需要一定的数学基础，但在处理复杂逻辑表达式时可能较为繁琐。
卡诺图化简
利用图形直观地表示输入变量的所有可能组合，通过排除法简化逻辑表达式。卡诺图化 简简单易懂，不需要复杂的数学运算，特别适合初学者和解决多变量逻辑表达式的化简
问题。
卡诺图与公式化简的比较
公式化简
通过逻辑运算的公式和定理，对逻辑表达式 进行简化。这种方法需要熟练掌握各种逻辑 公式和定理，对于初学者有一定的难度。
卡诺图化简
利用图形化的方式表示输入变量的所有可能 组合，通过排除法简化逻辑表达式。卡诺图 化简直观、易于操作，不需要复杂的公式和 定理，特别适合初学者和解决多变量逻辑表 达式的化简问题。
05
卡诺图的局限性
卡诺图适用范围有限

逻辑函数的化简方法

逻辑函数的化简方法

逻辑函数的化简方法逻辑函数的化简是数理逻辑中的一个重要概念，它指的是将复杂的逻辑函数表示形式简化为更为简洁的形式。

逻辑函数化简的目的是为了方便逻辑分析、简化逻辑电路的设计和优化等。

在进行逻辑函数的化简时，可以使用多种方法，包括真值表、卡诺图、代数法等。

下面我将介绍一些常用的逻辑函数化简方法。

1. 真值表法：真值表法是一种直观的方法，适用于简单的逻辑函数。

它通过列出逻辑函数的所有可能输入和对应的输出，通过观察输入和输出之间的关系，找出逻辑函数的简化形式。

2. 卡诺图法：卡诺图法是一种图形化的方法，适用于中等规模的逻辑函数。

它将逻辑函数的输入和输出用二进制位表示，并用一个方格来表示逻辑函数的真值。

通过观察方格的分布情况，将含有相同输出的方格组合起来，得到逻辑函数的简化形式。

3. 代数法：代数法是一种基于代数运算的方法，适用于任意规模的逻辑函数。

它利用逻辑函数的布尔代数性质，通过运用逻辑运算规则和化简规则，将逻辑函数逐步化简为最简形式。

逻辑函数的化简过程一般包括以下几个步骤：1. 将逻辑函数的输入和输出用适当的变量表示。

例如，对于一个三输入的逻辑函数，可以用A、B、C来表示输入变量，用F表示输出变量。

2. 根据逻辑函数的真值表或卡诺图，观察输入变量与输出变量之间的关系，找出可能的化简形式。

这一步可以根据特定的方法进行，如真值表中可以用观察方式寻找具有相同输出的输入组合，卡诺图中可以利用方格分布情况找到可以合并的项等。

3. 利用逻辑运算规则和化简规则，将逻辑函数逐步化简。

逻辑运算规则包括与、或、非、异或、与非、或非等运算规则，化简规则包括吸收律、分配律、德摩根定理等。

4. 不断重复第3步，直到无法再进行化简为止。

最终得到逻辑函数的最简形式。

需要注意的是，逻辑函数的化简目标是找到最简形式，而不一定是最简单形式。

最简形式是指逻辑函数无法再进行化简，而最简单形式是指逻辑函数中只包含最少的逻辑门。

总的来说，逻辑函数的化简方法包括真值表法、卡诺图法和代数法等。

物联网理论与技术第3章：逻辑函数运算规则及化简

物联网理论与技术第3章：逻辑函数运算规则及化简
开为最大项之积的形式。
解：F ABC ABC ABC ABC m 1, 4,5, 7
ABC ABC ABC ABC ABC ABC ABC ABC
( A B C)( A B C)( A B C)( A B C) M 1, 4,5, 7
【例3-12】 将 F ( A B)( A B C) 写成标准或与表达式。 解：F (A B)(A B C) (A B CC)(A B C) ( A B C)(A B C)(A B C) M (0, 2,3)
以上各定律均可用公理来证明，方法是将逻辑变量分别用0和1 代入，所得的表达式符合公理2至公理5。
3.2.2 逻辑代数的基本定律
（8）分配律： A（ B C） AB AC ； A （B C）（A B）（ A C）
加（逻辑或）对乘（逻辑与）的分配律证明如下：
A (B C) A(1 B C) BC A AB AC BC AA AB AC BC A(A B) C(A B) ( A B)(A C)
1
3.3.4 卡诺图表述
(a) 2变量卡诺图
(b) 3变量卡诺图
(c) 4变量卡诺图
图3-2 2、3、4变量的卡诺图
CDE AB
00 01 11 10
000 001 011 010 110 111 101 100
m0
m1
m3
m2
m6
m7
m5
m4
m8
m9
m11
m10
m14
m15
m13
m12
m24
m25
【例3-6】 证明函数 F ( A C)B A(B C) 是一自对偶函数。
证明：
F* (AC B)(A BC) (A B)(C B)(A B)(A C) (A B)(B C)(A C) A(B C)(A C) B(B C)(A C) (B C)(A AC) (B BC)(A C) A(B C) B(A C) F

用卡诺图化简逻辑函数合并最小项的规则

用卡诺图化简逻辑函数合并最小项的规则

上页 下页 返回
24
2020/3/4
第五节 逻辑函数的化简
[例2.5.17]：用卡诺图将下式化简为最简与-或逻辑
函数式。
Y ABC ABD CD ABC ACD ACD
解： Y CD
AB 00 01 11 10
D
00 1 0 0 1
01 1 0 0 1
11 1 1 1 1
第五节 逻辑函数的化简
A A 1
可在逻辑函数式中的某一项乘 ( A A)，
然后拆成两项分别与其他项合并。
[例2.5.13]：Y BC AC AB
( A A)BC AC AB
ABC ABC AC AB
AB AC
上页 下页 返回
则可合并为一项并消去一对因子。 2. 若四个最小项相邻且排列成一个矩形组，
则可合并为一项并消去两对因子。 3. 若八个最小项相邻且排列成一个矩形组，
则可合并为一项并消去三对因子。
上页 下页 返回
20
2020/3/4
第五节 逻辑函数的化简
合并两个相邻最小项的情况：

BC A 00 01 11 10
01 1 0 1
B
上页 下页 返回
23
2020/3/4
第五节 逻辑函数的化简
卡诺图化简的步骤：
1. 将函数化为最小项之和的形式。
2. 画出表示该逻辑函数的卡诺图。
3. 找出可以合并的最小项。
4. 选取化简后的乘积项。
选取乘积项的原则： 1. 这些乘积项应包含函数式中所有的最小项。 2. 所用的乘积项数目最少。 3. 每个乘积项包含的因子最少。
12
2020/3/4

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数

用卡诺图化简逻辑函数
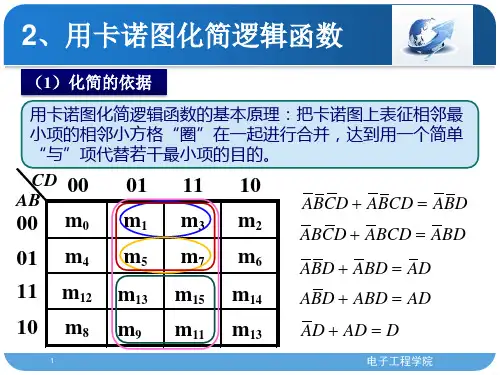
在填好卡诺图后，首先，圈相邻的最小项，只能两项、四项和八项一圈，要保证圈的项最多，且每个圈中包含有未圈过的项；然后，提取每个圈中各项的公因子作为一个乘积项，这就是每个圈中最小项的化简结果，两个相邻最小项合并可消去一个变量，四个相邻最小项合并可消去二个变量，而八个相邻最小项合并，则可消去三个变量；最后，将各个圈中化简的乘积项加起来就得到了最简的与或式。

图1、图2、图3分别画出了两个相邻最小项、四个相邻最小项和八个相邻最小项合并为一项的例子。

[例1] 利用卡诺图化简Y = B CD + B C+A C D + A B C 解：(1) 画出函数Y的卡诺图。

B CD包含了两个最小项Y
11 = A B CD和Y
3
= A B CD。

B C包含了四个最小项Y
14 = ABC D，Y
12
= AB C D，Y
5
=A B C D，Y
4
=A B C
D。

A C D包含了两个最小项Y
5 =A B C D，Y
1
= A B C D。

A B C包含了两个最小项Y
11 = A B CD，Y
10
= A B C D。

(2) 合并最小项
把可以合并的相邻最小项用环分别圈起来，如图4所示。

(3) 根据圈定的各个环，写出的与或式就是最简与或式。

Y = A B D + A B C + B C
可是，用卡诺图合并最小项，实质上就是反复运用AB + A B来合并相邻最小项，从而去多余因子，得到最简的与或式。

逻辑函数的运算和卡诺图

逻辑函数的运算和卡诺图
逻辑函数的最小项表示法，它们具有惟一性。而逻辑表达式和逻辑图 都不是惟一的。使用这些方法时，应当根据具体情况选择最适合的一 种方法表示所研究的逻辑函数。
当前您浏览到是第二十四页，共二十五页。
本章小结
本章介绍了两种逻辑函数化简法。公式化简法是利用逻辑
代数的公式和规则，经过运算，对逻辑表达式进行化简。它的优点是 不受变量个数的限制，但是否能够得到最简的结果，不仅需要熟练地
普通代数结 果如何？
（3）与普通代数相似的定理
交换律 A·B = B·A
A+B=B+A
结合律 A·（B·C）=（A·B）·C A +(B+C)=(A+B)+C
分配律 A·（B+C）=A·B + A·C A+(BC)=(A+B)(A+C)
当前您浏览到是第四页，共二十五页。
（4）特殊的定理
反演律：P14注意
若规定：代表一个最小项的小方格叫做“0”维块。
“0”维块： 表示四个变量一个也没有被消去。
将相邻“0”维块相加，可以将两项合 AB
并为一项，并消去一对因子。
CD 00 01 11 10
相邻项
“0”维块相加“1”维块“2”维“块3”维块00ABmC0D
ABC D
m4
ABCDABC
m12 m8
D
m0+m1 ABC D ABCD ABC
m2 m6 m14 m10
二个“0”维块相加，可合并为一项，并消去一对有 0，1变化因子。 四个“0”维块相加，可合并为一项，并消去二对有 0，1变化因子。
八个“0”维块相加，可合并为一项，并消去三对有 0，1变化因子。
当前您浏览到是第十七页，共二十五页。

卡诺图化简法

卡诺图化简法

浅谈卡诺图法化简逻辑函数摘要：逻辑函数是逻辑电路设计的依据和基础，化简逻辑函数更是为节省器件，降低成本，提高效率作出了巨大贡献，而卡诺图法是化简逻辑函数最常用也是最简单的方法。

关键词：卡诺图；逻辑函数；逻辑电路；逻辑是指事物因果之间所遵循的规律。

为了避免用冗繁的文字来描述逻辑问题，逻辑代数将事物发生的原因（条件）和结果分别用逻辑函数来描述。

逻辑代数的变量和常量取值只有两种，即逻辑0和逻辑1，因而称为二值逻辑。

当然这里的0和1仅代表事物矛盾双方的两种状态，即两种对立的逻辑状态，而不是，它们可以代表事物的真表示数量的大小。

例如，它们可以代表事物的真，伪；开关的开，关；电平的高,低等。

逻辑函数可以用很多方法描述。

例如，代数法，卡诺图法，真值表法，波形图法等。

每一种描述方法都可以示电路的表逻辑功能。

但作为分析和设计逻辑电路的教学工具，节省器件，降低成本，提高工作的可靠性成为了逻辑函数至关重要的基础。

所以，化简逻辑函数便成了提高电路性能和效率必要的一步。

本文我们主要介绍的是卡诺图化简法。

一．卡诺图法的特点及化简步骤卡诺图的特点是：可以从图形上直观、清晰地反映了最小项的相邻关系，被化简函数为“与—或“形式，方法单一,易掌握，且其形式简单明了，能得到最简结果。

例如，化简函数：∑F=)7,6,4,0(m化简步骤：1.填卡诺图，即用卡诺图表示逻辑函数。

12. 画卡诺图合并相邻位置最小项郑芸莹（1989-），女，四川绵阳人，云南大学旅游文化学院信科系，研究方向：电子信息工程3.写出最简函数式。

AB C B F +=从上述的例子中看出卡诺图最小项合并的一些规律：（1）卡诺圈中小方格的个数必须为m 2个，m 2为小于或等于n 的整数。

（2）在满足规律（1）的前提下卡诺圈越大，消去的变量数越多，也就是说卡诺圈数应该尽可能的少而且要尽可能的大（但必须满足m 2个方格）。

二．卡诺图法的优缺点卡诺图的优点是简单，直观。

但当变量数超过6个时，相邻项不直观，不易找。

浅析逻辑函数的卡诺图化简法

浅析逻辑函数的卡诺图化简法

浅析逻辑函数的卡诺图化简法
许斌
【期刊名称】《河北能源职业技术学院学报》
【年(卷),期】2004(000)004
【摘要】本文介绍了用卡诺图化简逻辑函数的一般方法,说明了化简过程中需要注意的问题.
【总页数】3页(P82-84)
【作者】许斌
【作者单位】河北能源职业技术学院,河北,唐山,063004
【正文语种】中文
【中图分类】O14
【相关文献】
1.五～八变量逻辑函数卡诺图化简法研究 [J], 岂云开;杨淑敏
2.卡诺图法化简六变量逻辑函数 [J], 李碧芬
3.用重叠卡诺图法化简各种表达式的逻辑函数 [J], 吴恒玉;王平均;黄果
4.逻辑函数的卡诺图化简法 [J], 陈小芳
5.由与或式逻辑函数直接填写卡诺图化简逻辑函数算法分析 [J], 席红旗;金志伟因版权原因，仅展示原文概要，查看原文内容请购买。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

重 叠 卡 诺 圈
Ｆ的卡诺 圈
３ 重叠卡 诺圈法的应用
（Ｉ）
００ ０１ ００ ０１
１１
１０
—
１
—
１
＼ （Ｉ）
昭＼
００
０１
０１ １１ １０
Ｔ一
ｌ１
ｌ１
１０
１０
面 西 变 量卡诺图
＋ＡＢＣ＋Ｘｏ ＋ＣＤ 变 量 卡 诺 圈
００ ０１ ｌ１ １０
重叠卡诺 图中 ，有偶 数个 “１”时就 取 “１”（“０”算为 偶数 ）， 得 到同或式的卡诺图 。例如 Ｆ＝Ａ０Ｂ。
左式变量 Ａ的卡诺 图 左 式变量 Ａ￣Ｂ的卡诺 图
变量 Ａ的卡诺圈
变 量 Ｂ的卡诺 圈
左 式 重 叠 卡 诺 图
左式卡诺 图
右式的重变叠！ 卡诺叟图Ａ ｃ
右式卡诺图
维普资讯
２００７ 年 ６ 月
第 ８卷 第 ２期 总 第 ３０期
太 原 大 学 学 报 Ｊｏｕｒｎａｌ Ｏｆ Ｔａｉｙｕａｎ Ｕｎｉｖｅｒｓｉｔｙ
文 章编 号 ：１６７１—５９７７（２００７）０２—７５—０２
Ｖｏ１．８Ｎｏ 简 各 种 表 达 式 的逻 辑 函数
据异或卡诺 图的表 示法 ，得 函数卡诺 图。最后 化简 成最
简与或式 。根据卡诺 图化 简后 得 Ｆ＝ＡＣＤ＋ＡＤ。
３．２ 用重叠卡诺 图法证 明逻辑 函数
重叠卡诺 圈
Ｆ的卡诺 图
例如 ：证 明：Ａ（Ｂ０ Ｃ）＝ＡＢ０ ＡＣ。证明过程如下 ：
２．５ “同或 ”式 的卡诺 图表示法
在“同或”式的 卡诺 图表示 法 中 ，首先 作 出各 变量 的 卡诺 图【１－２］，然后将 各变 量 的卡诺 图进 行重 叠 ，表示 在一
变 量 Ａ 的 卡诺 图
变 量 Ｂ的 卡 诺 图
简 ，对 于其它 的表达 式一般都变成 “与或”式后 ，再变 成与
或最小项表达式 ，然 后利用卡诺 图化简 ，本文 给出一 种不
用变 为最小项与或式可直接 利用卡诺 图化简 各种表 达式
的 新 方 法 。
２ 各种表 达式的逻辑函数的卡诺 图表 示法 ２．１ “与 ”式 的卡诺 图表示法 在“与 ”式 的卡 诺 图表示 法 中 ，首先 作 出各变 量 的卡 诺 图Ｌｔ－２］，然后将各变 量 的卡诺 图进行 重 叠 ，表示 在 一重
３．１ 用重叠卡诺法化简逻辑 函数
例如 ：将 逻辑 函数 Ｆ＝（ＡＤ＋ＣＤ＋ＣＤ）０ （ＡＣＤ ＋
ＡＢＣ＋ＡＤ＋ＣＤ）化 简为最简与或式 解 ：先将ＡＤ＋ＣＤ ＋
变量 Ａ的卡诺圈
变量 Ｂ的卡诺 圈
ＣＤ作 为 一 变量 ，Ａ ＣＤ ＋ＡＢＣ＋ＡＤ＋ＣＤ 作 为 另一 变 量 ，根据 前面介绍 的方法 分别 作 出两 变量 的卡 诺 图｝１－２］， 在将两变量 的卡诺 图进 行重叠 ，得异或 式重 叠卡诺 图 ，根
的新方法 ，即“重叠卡诺 图法”，并举例加 以说明。
关键 词 ：重叠卡诺图 ；逻 辑函数 ；化 简 中图分类号 ：Ｏ１
文 献标 识码 ：Ａ
１ 引言
叠卡诺 图中 ，有 …１’时就取“１”，得 到或 式 的卡诺 图。例 如
逻辑 函数 的化 简一般 有 两种 方法 ：一是 公式 法 Ｊ， Ｆ ＝Ａ ＋ Ｂ。
吴 恒 玉 ，王 平 均 ，黄 果
（海南软件职业技 术学 院 ，海南 琼海 ５７１４００）
摘 要 ：用卡诺 图化 简逻 辑函数一般都指的是化 简“与或”最小项表 达式 ，对 于其 它的表达 式一般 都 变成
“与或”式后 ，再 变成 与或 最小项表达式 ，然后 利用卡诺 图化 简，这里给 出一种利 用卡诺 图直接化 简各种表达 式
此法不仅 要熟 记公 式 ，而且 还要 灵活 应 用公 式及 简化 技
巧 ，才能得到最 简式 ，而对初学者 来说很 难判 断最后 的式 子是否是最简 。二是卡诺 图法 【３＿５］，用卡诺 图化简逻辑 函
数一 般都 指的是 化简 “与或 ”最 小项表 达式 ，此法 比较 直
观 、简单 、且 易掌握 ，而且 得 出 的结果 较 易判 断是 否为 最
重叠卡诺 图中 ，在重叠卡诺 图 中有奇数 个“１”时就 取“１”， 得到异或式 的卡诺 图 。例如 Ｆ＝Ａ０Ｂ。
收稿 日期 ：２００６—１０．１９ 作者简 介：吴恒 玉（１９６５一），男，辽 宁抚顺 人 ，海 南软件职 业技 术学院 高级讲 师，在读硕士研 究生 。
· ７５ ·
维普资讯
重 叠 卡 诺 图
Ｆ的 卡诺 图
２．３ “非”式 的卡诺图表示法
在“非 ”式 的卡诺 图表 示法 中 ，“Ｏ”变 “１”，“１”变 “０”， 即可得到非式 的卡诺 图。例 如 Ｆ＝一ＡＢ。
叠卡诺图 中，全 为“１”时取 “１”，得到 与式 的卡诺 图。例如
Ｆ ＝ ＡＢ
变量 Ａ 的 卡 诺 图
变 量 Ｂ的 卡 诺 图
ＡＢ 重 叠 卡诺 图
ＡＢ 的 卡 诺 图
重 叠 卡诺 图
Ｆ 的卡 诺 图
２．２ “或 ”式的卡诺 图表示法
在“或”式的卡诺图表示法中，首先作出各变量 的卡
诺 图［１＿２］，然后将各 变量 的卡诺 图 进行 重叠 ，表 示 在一 重
Ｆ的卡 诺 图 ２．４ “异或 ”式的卡诺 图表示法 在“异或”式 的卡诺 图表示 法 中 ，首先 作 出各变 量 的 卡诺 图［１－２］，然后将 各变 量 的卡诺 图进行 重 叠 ，表示 在 一
北方学 院学报 ，２００７（１）：１－３．
［２］吴恒玉 ，唐 民丽．函数子 卡诺 图及 其在 逻辑 设 计 中的
应用 ［Ｊ］．华 北科技术学院学报 ，２００５（２）：８４—８５．
１０
—
１
——
１
—
１１
—
１１
Ｆ的重叠卡诺圈
Ｆ的卡诺圈
从卡诺 图可以看出等式左边 与右边相 同故证 明之。
４ 结束语
可见 ，采用重 叠卡诺 图法可 以使 逻辑 函数 的化 简 和
证 明更直 观 、更简单 ，且更易掌握 。
参考 文献 ：
［１］吴恒玉 ．引入变 量卡诺图 （Ⅵ Ｍ）的作 图方法 ［Ｊ］．河 北