全等难题——倍长中线法
- 格式:doc
- 大小:1.32 MB
- 文档页数:12
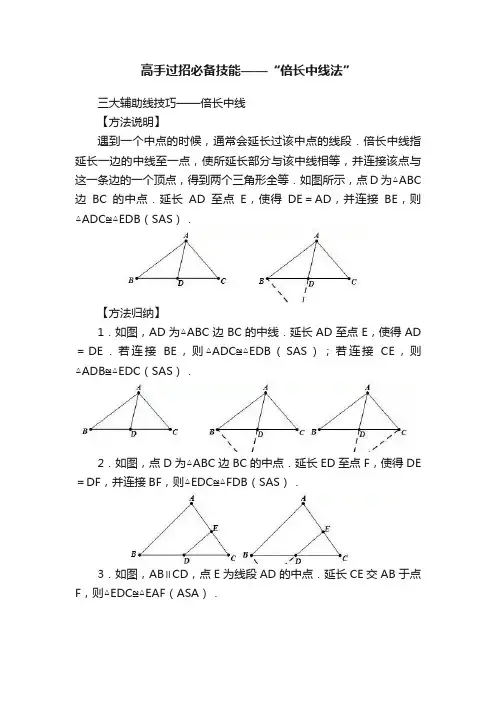
高手过招必备技能——“倍长中线法”三大辅助线技巧——倍长中线【方法说明】遇到一个中点的时候,通常会延长过该中点的线段.倍长中线指延长一边的中线至一点,使所延长部分与该中线相等,并连接该点与这一条边的一个顶点,得到两个三角形全等.如图所示,点D为△ABC 边BC的中点.延长AD至点E,使得DE=AD,并连接BE,则△ADC≌△EDB(SAS).【方法归纳】1.如图,AD为△ABC边BC的中线.延长AD至点E,使得AD =DE.若连接BE,则△ADC≌△EDB(SAS);若连接CE,则△ADB≌△EDC(SAS).2.如图,点D为△ABC边BC的中点.延长ED至点F,使得DE =DF,并连接BF,则△EDC≌△FDB(SAS).3.如图,AB∥CD,点E为线段AD的中点.延长CE交AB于点F,则△EDC≌△EAF(ASA).【典型例题】1.(09莱芜)已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF 中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).【思路点拨】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG =EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF 的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.还知道EG⊥CG.【解题过程】解:(1)∵四边形ABCD是正方形,∴∠DCF=90°,在Rt△FCD中,∵G为DF的中点,∴CG=1/2FD,同理,在Rt△DEF中,EG=1/2FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.【方法一】连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG;∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM 是矩形,在矩形AENM中,AM=EN,在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.【方法二】延长CG至M,使MG=CG,连接MF,ME,EC,在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG.∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC,EF=BE,∴△MFE≌△CBE,∴∠MEF=∠CEB.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1/2MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F 作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC,∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形,∵G为CM中点,∴EG=CG,EG⊥CG.。

倍长中线法构造全等三角形例题《倍长中线法构造全等三角形》一、引言在数学中,全等三角形是非常重要的概念,它们具有相同的三边和三角角度,但形状和位置可能有所不同。
而倍长中线法是构造全等三角形的一种重要方法。
本文将深入探讨倍长中线法的原理和应用,通过具体的例题来演示构造全等三角形的过程。
二、倍长中线法的原理1. 什么是倍长中线法?倍长中线法是指通过将三角形中的两条边分别延长相等的长度,然后连接延长后的两条边的中点,得到一个边长为原来中线的两倍的新三角形的方法。
2. 倍长中线法的原理当我们通过倍长中线法构造全等三角形时,我们实际上是借助了中线的性质。
在三角形中,连接一个顶点和对边中点的线段就是该对边的中线,中线的定义是连接三角形的一个顶点和边对面中点的线段。
对于一个三角形ABC来说,若D为AB的中点,那么有AD = BD,这就是中线的性质之一。
而倍长中线法利用了中线的这一性质,通过延长两条边相等的长度,再连接延长后的两条边的中点,可以构造出一条新的中线,新中线的长度是原中线的两倍。
这样就得到了一个边长为原三角形中线长度两倍的全等三角形。
三、倍长中线法构造全等三角形的例题现在,让我们通过具体的例题来演示倍长中线法对全等三角形的构造过程。
例题1:已知△ABC中,AB = 6cm, AC = 4cm,以AC为底边做三角形ACD,且AD = 6cm,BD = 4cm,连接BC并延长到E,使得CE = AB。
连接DE并延长到F,使得DF = AB。
证明△ADF≌△ABC。
解题步骤:1. 延长BC和DE我们根据题目要求,延长BC和DE,使得CE = AB,DF = AB。
2. 连接CD接下来,连接CD,得到三角形ACD。
3. 寻找AD和DB的中点我们在AD和DB上分别寻找其中点,分别记为G和H。
4. 连接GH连接GH,得到新的中线GH。
5. 观察三角形ADF和三角形ABC我们可以观察到,三角形ADF和三角形ABC中,AD = AB,DG = BH。
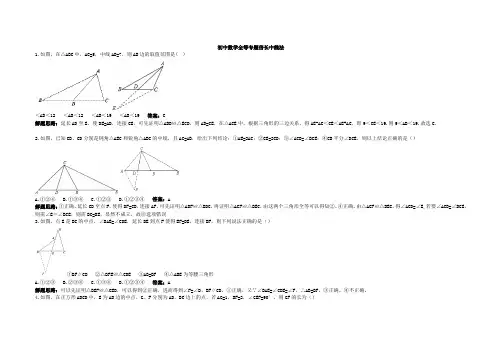
初中数学全等专题倍长中线法1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )<AB<12 <AB<12 <AB<19 <AB<19 答案:C解题思路:延长AD至E,使DE=AD,连接CE,可先证明△ABD≌△ECD,则AB=CE,在△ACE中,根据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19.故选C.2.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④B.①③④C.①②③D.①②③④ 答案:A解题思路:①正确,延长CD至点F,使得DF=CD,连接AF,可先证明△ADF≌△BDC,再证明△ACF≌△BEC,由这两个三角形全等可以得知②、④正确。
由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项错误3.如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF,则下列说法正确的是()①BF∥CD ②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形A.①②③B.②③④C.①③④D.①②③④ 答案:A解题思路:可以先证明△BEF≌△CED,可以得到②正确,进而得到∠F=∠D,BF∥CD,①正确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③正确。
④不正确。
4.如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()答案:C解题思路:延长FE交DA的延长线于点M,则可证△AEM≌△BEF,再证明△GEM≌△GEF,可以得到GF=GM=GA+BF=3,答案选C5.如图,在△ABC中,点D、E为边BC的三等分点,则下列说法正确的有()①BD=DE=EC ②AB+AE>2AD ③AD+AC>2AE ④AB+AC>AD+AE 个个个个答案:D解题思路:点D、E为边BC的三等分点,∴BD=DE=CE延长AD至点M,AE至点N,使得DM=AD,EN=AE,连接EM、CN,则可证明△ABD≌△MED,进而可得AB+AE>2AD,再证明△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可得到AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均正确。


全等三角形辅助线之倍长中线法(总20页)-本页仅作为预览文档封面,使用时请删除本页-全等三角形辅助线之倍长中线法倍长中线法:遇中线,要倍长,倍长之后有全等.当倍长后,连接方式不一样,可以产生更多结论如下:与倍长中线法类似的辅助线作法M ABCDEMD E MD=DE CE BDM CDE BM CE∆≅∆延长至,使,连接可证,AD ABC ∆为的中线DC BAEAD E AD=DE CE BE CE ABEC 延长至,使,当连接时,结论相似; 当连接、,则为平行四边形AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AC BE∆∆∠∠∆≅∆延长至使,连接在和中,,故与此相关的重要结论AD ABC ∆为的中线D CB AE举例:如图,在△ABC 中,AD 为BC 边上的中D CB AEAD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AB-BE AE AB+BE AE <AD<∆∆∠∠∆≅∆<<<<延长至使,连接在和中,,故即2814FE G FE=GE EGC ()EFD ∆≅∆延长至,使可证平行线夹中点F EDCBA G如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE=AC ,BE 的延长线交AC 于点F .求证:∠AEF=∠EAF.F EDCBA 321MA BCD EF1.如图,在△ABC中,AD为BC边上的中线.(1)按要求作图:延长AD到点E,使DE=AD;连接BE.(2)求证:△ACD≌△EBD.(3)求证:AB+AC >2AD.(4)若AB=5,AC=3,求AD的取值范围.2.如图,在△ABC中,AD平分∠BAC,且BD=CD.求证:AB=AC.3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE =AC ,BE的延长线交AC 于点F . 求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交AB于点G ,BG =CF .求证:AD 为△ABC 的角平分线.6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,已知AD =,AE =BE =5,求CE 的长.GFE DB AE D CB AF EDBAGFE DB AGDAFE DCB A7. 如图,在正方形ABCD 中,CD =BC ,∠DCB =90°,点E 在CB 的延长线上,过点E 作EF ⊥BE ,且EF=BE .连接BF ,FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .【参考答案】课前预习1. (1)相等,SSS ;夹角,SAS ;夹边,ASA ;对边,AAS ;直角,HL(2)全等,三,边 2. (1)证明:如图∵O 是AB 的中点 ∴AO =BO在△AOC 和△BOD 中AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD (SAS ) (2)证明:如图 ∵O 是AB 的中点 ∴AO =BO ∵AC ∥BD ∴∠A =∠B在△AOC 和△BOD 中A B AO BOAOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOC ≌△BOD (ASA ) 典型题型 1. 解:(1)如图,(2)证明:如图, ∵AD 为BC 边上的中线 ∴BD =CD21BCDA在△BDE 和△CDA 中12BD CD ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) (3)证明:如图, ∵△BDE ≌△CDA ∴BE =AC ∵DE =AD ∴AE =2 AD在△ABE 中,AB +BE >AE ∴AB +AC >2AD (4)在△ABE 中,AB BE <AE <AB +BE由(3)得 AE =2AD ,BE =AC ∵AC =3,AB =5 ∴53<AE <5+3∴2<2AD <8 ∴1<AD <42. 证明:如图,延长AD 到E ,使DE =AD ,连接BE在△ADC 和△EDB 中CD BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS ) ∴AC =EB ,∠2=∠E ∵AD 平分∠BAC21EDCBA∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC3. 证明:如图,延长CD 到F ,使DF =CD ,连接BF∴CF =2CD∵CD 是△ABC 的中线∴BD =AD在△BDF 和△ADC 中BD AD ADC BDF DF DC =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC (SAS ) ∴BF =AC ,∠1=∠F ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =BF ∵∠1=∠F ∴BF ∥AC∴∠1+∠2+∠5+∠6=180° 又∵AC =AB ∴∠1+∠2=∠5 又∵∠4+∠5=180° ∴∠4=∠5+∠6 即∠CBE =∠CBF 在△CBE 和△CBF 中CB CB CBE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△CBE ≌△CBF (SAS ) ∴CE =CF ,∠2=∠3 ∴CE =2CDCB 平分∠DCE4. 证明:如图,延长AD 到M ,使DM =AD ,连接BM∵D 是BC 边的中点∴BD =CD在△ADC 和△MDB 中CD BD ADC MDB AD MD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△MDB (SAS ) ∴∠1=∠M ,AC =MB ∵BE =AC ∴BE =MB ∴∠M =∠3 ∴∠1=∠3 ∵∠3=∠2 ∴∠1=∠2 即∠AEF =∠EAF5. 证明:如图,延长FE 到M ,使EM =EF ,连接BM∵点E 是BC 的中点∴BE =CE在△CFE 和△BME 中321AFG 321MABCDEFFE ME CEF BEM CE BE =⎧⎪∠=∠⎨⎪=⎩∴△CFE ≌△BME (SAS ) ∴CF =BM ,∠F =∠M ∵BG =CF ∴BG =BM ∴∠1=∠M ∴∠1=∠F ∵AD ∥EF∴∠3=∠F ,∠1=∠2 ∴∠2=∠3即AD 为△ABC 的角平分线6. 解:如图,延长AF 交BC 的延长线于点G∵AD ∥BC ∴∠3=∠G∵点F 是CD 的中点∴DF =CF在△ADF 和△GCF 中3G AFD GFC DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△GCF (AAS )∴AD =CG ∵AD =∴∠1=∠B ∵AB ⊥AF ∴∠1+∠2=90° ∠B +∠G =90° ∴∠2=∠G ∴EG =AE =5 ∴CE =EG CG=5 =7. 证明:如图,延长EG 交CD 的延长线于点M由题意,∠FEB =90°,∠DCB =90°∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 的中点 ∴FG =DG在△FGE 和△DGM 中1M FGE DGM FG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FGE ≌△DGM (AAS ) ∴EF =MD ,EG =MG∵△FEB 是等腰直角三角形M2134GFDA在正方形ABCD 中,BC =CD ∴BE +BC =MD +CD 即EC =MC∴△ECM 是等腰直角三角形 ∵EG =MG∴EG ⊥CG ,∠3=∠4=45° ∴∠2=∠3=45° ∴EG =CG三角形全等之倍长中线(实战演练)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是_______________. 思路分析:①画出草图,标注条件:②根据题目条件,见_________,考虑_____________;添加辅助线是______________________________________;③倍长之后证全等:__________≌___________( ),证全等转移边:______=_______; ④全等转移条件后,利用三角形三边关系可以得到AB 的取值范围.2. 如图,在正方形ABCD 中,AD ∥BC ,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,且AG =1,BF =2.若GE ⊥EF ,则GF 的长为多少G FEAD BC【参考答案】1. 3<AB <13①图略②中线AD 倍长中线 延长AD 到点E ,使DE =AD ,连接CE ③△ADC △EDB SAS AC EB ④略2. AD ∥BC ,E 为AB 边的中点,平行夹中点;AG =BH ,GE =HE ;到线段两端点的距离相等,FH ,AG +BF 解:如图,延长GE 交CB 的延长线于点H ∵AD ∥BC ∴∠GAE =∠HBE ∵E 为AB 边的中点 ∴AE =BE在△AGE 和△BHE 中,AEG BEH AE BEGAE HBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AGE ≌△BHE (ASA ) ∴BH =AG ,HE =GE ∵GE ⊥EF ∴GF =HF ∵BF =2,AG =1 ∴GF =HF =BF +BH =BF +AG =2+1 =3三角形全等之倍长中线(作业)例题示范例1:已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC .求证:AE 平分∠BAC .【思路分析】读题标注:见中线,要倍长,倍长之后证全等.结合此题,DE =EC ,点E 是DC 的中点,考虑倍长,有两种考虑方法: ①考虑倍长FE ,如图所示: ②考虑倍长AE ,如图所示:(这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF ≌△CEG ,由全等转移边和角,重新组织条件证明即可. 【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG .在△DEF 和△CEG 中,ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS ) ∴DF =CG ,∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAEA D CEFA B DCE F??GG??FECDBA ??FE CD B A A B DCE F??G∴∠BAE =∠CAE ∴AE 平分∠BAC巩固练习1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.2. 已知:如图,BD 平分∠ABC 交AC 于D ,点E 为CD 上一点,且AD =DE ,EF ∥BC 交BD 于F .求证:AB =EF .3. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形,AB =AE ,AC =AF ,∠BAE =∠CAF =90°. 求证:EF =2AD .4. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G . 求证:BF =CG .5. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CDD CBAF E DCBAFEB AG FED CBADA的中点,连接AF ,EF ,AE ,若∠DAF =∠EAF ,求证:AF ⊥EF .思考小结1. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .比较下列两种不同的证明方法,并回答问题. 方法1:如图,延长AD 到E ,使DE =AD ,连接BE 在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴AC =BE ,∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS ) ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC21ECDB A 21ECDB A DBA相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等. 不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等. 2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt △ABC 中,∠BCA =90°,CD 是斜边AB 的中线.求证:CD 12AB .【参考答案】巩固练习 1. 22. 证明略(提示:延长FD 到点G ,使得DG =DF ,连接AG ,证明△ADG ≌△EDF ,转角证明AB =EF )3. 证明略(提示:延长AD 到点G ,使得GD =AD ,连接CG ,证明△ABD ≌△GCD ,△EAF ≌△GCA )4. 证明略(提示:延长FE 到点H ,使得EH =FE ,连接CH ,证明△BFE ≌△CHE ,转角证明BF =CG )5. 证明略(提示:延长AF 交BC 的延长线于点G ,证明△ADF ≌△GCF ,转角证明AF ⊥EF ) 思考小结 1. 倍长中线 SAS AAS角2. 证明略DCB A。

完整版)倍长中线法(经典例题)
倍长中线法是解决几何问题中常用的方法之一。
在利用中线解决问题时,我们可以通过添加辅助线,采用倍长中线法来构造全等三角形,从而运用全等三角形的知识来解决问题。
具体来说,倍长中线法的过程是:延长某一中线一倍,使其构造出全等三角形,然后利用全等三角形的有关知识来解决问题。
在构造全等三角形时,我们可以采用两种常用的方法:一是将中线延长到某一点,使其等于另一条中线,然后利用对顶角的SAS证明全等;二是通过间接倍长的方法,利用垂线和平行线构造出全等三角形。
倍长中线法最重要的一点是延长中线一倍,完成SAS全等三角形模型的构造。
我们可以通过经典例题来练这种方法,例如求中线的取值范围、证明BD等于CE、证明AF等于EF 等问题。
自检自测题也是巩固这种方法的好办法。
例如证明AD平分∠BAE、探究线段AB与AF、CF之间的数量关系、证明BE+CF>EF等问题都可以通过倍长中线法来解决。

全等模型—倍长中线模型知识点管理归类探究夯实双基,稳中求进倍长中线模型三角形的中线:三角形的顶点和对边中点的连线三角形边长的不等关系:在三角形中,两边之和大于第三边,两边只差小于第三边倍长中线定义:“倍长中线”是指加倍延长中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则对应角对应边都对应相等。
常用于构造全等三角形。
中线倍长法多用于构造全等三角形和证明边之间的关系(通常用“SAS ”证明)(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
题型一:求三角形中线取值范围【例1】(2021·重庆市暨华中学校八年级月考)在ABC 中,5AC =,中线7AD =,则AB 边的取值范围()A .212AB <<B .412AB <<C .919AB <<D .1019AB <<【答案】C 【分析】延长AD 至E ,使DE =AD ,然后利用“边角边”证明△ABD 和△ECD 全等,根据全等三角形对应边相等可得AB =CE ,再利用三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出CE 的取值范围,即为AB 的取值范围.【详解】解:如图,延长AD 至E ,使DE =AD ,∵AD 是△ABC 的中线,∴BD =CD ,在△ABD 和△ECD 中,BD CD ADB EDC AD DE ⎪∠⎪⎩∠⎧⎨===,∴△ABD ≌△ECD (SAS ),∴AB =CE ,∵AD =7,∴AE =7+7=14,∵14+5=19,14-5=9,∴9<CE <19,即9<AB <19.故选:C .【点睛】本题考查了全等三角形的判定与性质,三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.变式训练【变式1-1】(2021·全国)如图,AD 是ABC 的边BC 上的中线,7,5AB AD ==,则AC 的取值范围为()A .515AC <<B .315AC <<C .317AC <<D .517AC <<【答案】C 【分析】延长AD 至点E ,使5DE AD ==,连接CE ,证明ABD ECD ≌,可得7CE AB ==,然后运用三角形三边关系可得结果.【详解】如图,延长AD 至点E ,使5DE AD ==,连接CE.∵AD 为ABC 的BC 边上的中线,∴BD CD =,在ABD △和ECD 中,,,,AD ED ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABD ECD ≌,∴7CE AB ==.在ACE 中,AE EC AC AE CE -<<+,即557557AC +-<<++,∴317AC <<,故选:C .【点睛】本题考查了全等三角形的判定与性质,三角形三边关系,根据中点倍长法构造全等三角形是解题的关键.【变式1-2】(2021·武汉一初慧泉中学八年级月考)已知AD 是△ABC 的中线,AD =6,CA =5,则边AB 的取值范围是______.【答案】7<AB <17【分析】作出图形,延长AD 至E ,使DE =AD ,然后利用“边角边”证明△ABD 和△ECD 全等,根据全等三角形对应边相等可得AB =CE ,再利用三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出CE 的取值范围,即为AB 的取值范围.【详解】解:如图,延长AD 至E ,使DE =AD,∵AD 是△ABC 的中线,∴BD =CD ,在△ABD 和△ECD 中,BD CD ADB EDC AD DE ⎧⎪∠∠⎨⎪⎩===,∴△ABD ≌△ECD (SAS ),∴AB =CE ,∵AD =6,∴AE =6+6=12,∵12+5=17,12-5=7,∴7<CE <17,即7<AB <17.故答案为:7<AB <17.【点睛】本题考查了全等三角形的判定与性质,三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.【变式1-3】(2021·全国)△ABC 中,AB =8,AC =6,AD 是BC 边上的中线,则AD 长度的范围是__________.【答案】1<AD <7【分析】延长AD 至E ,使DE =AD ,连接CE .根据SAS 证明△ABD ≌△ECD ,得CE =AB ,再根据三角形的三边关系即可求解.【详解】解:延长AD 至E ,使DE =AD ,连接CE.在△ABD 和△ECD 中,DE AD ADB CDE DB DC =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ECD (SAS ),∴CE =AB .在△ACE 中,CE -AC <AE <CE +AC ,即2<2AD <14,故1<AD <7.故答数为:1<AD <7.【点睛】本题主要考查了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.【变式1-4】(2021·陕西城固·七年级期末)如图,在ABC 中,AD 是BC 边上的中线,过C 作AB 的平行线交AD 的延长线于E 点.若6AB =,2AC =,试求AE的取值范围.【答案】4<AE <8【分析】证明△ABD ≌△ECD (AAS ),得到AB =EC =6,AD =ED ,再由三角形的三边关系即可得出答案.【详解】解:∵AD 是BC 边上的中线,∴BD =C D .∵AB ∥CE ,∴∠BAD =∠E ,在△ABD 和△ECD 中,BAD E BDA CDE BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ECD (AAS ),∴AB =EC =6,∴AD =DE ,在△ACE 中,CE -AC <AE <CE +AC ,即6-2<AE <6+2,∴4<AE <8.【点睛】本题考查了全等三角形的判定与性质、平行线的性质、三角形的三边关系等知识;熟练掌握三角形的三边关系,证明三角形全等是解题的关键.题型二:利用倍长中线证明线段、角相等【例题2】(2021·全国八年级课时练习)如图,CE 、CB 分别是ABC 与ADC 的中线,且∠=∠ACB ABC ,AC AB =.求证:2CD CE =.【答案】见解析【详解】解析:过点B 作//BF AC 交CE 的延长线于点F ,由点E 为AB 中点,得到AE EB =,再由BF 与AC 平行,得到两对内错角相等,利用AAS 得到ACE 与BFE △全等,利用全等三角形的对应边相等得到CE EF =,AC BF =,即2CF CE =,再由AC AB =,根据点B 为AD 中点,得到AC AB BD BF ===,利用外角性质及等量代换得到DBC FBC ∠=∠,利用SAS 得到CBD 与CBF V 全等,利用全等三角形对应边相等得到CD CF =,等量代换即可得证.答案:证明:如图,过点B 作//BF AC 交CE 的延长线于点F.∵CE 是ABC 的中线,//BF AC ,∴AE BE =,A ABF ∠=∠,ACE F ∠=∠,在ACE 和BFE △中,∵,,,A ABF ACE F AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACE BFE ≌(AAS ),∴CE EF =,AC BF =,∴2CF CE =,又∵AC AB =,CB 是ADC 的中线,∴AC AB BD BF ===,∵DBC A ACB ABF ABC ∠=∠+∠=∠+∠,∵∠=∠ACB ABC ,∴DBC FBC ∠=∠,在DBC △和FBC 中,∵,,,DB FB DBC FBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴DBC FBC ≌(SAS ),∴2DC CF CE ==.易错:证明:在ACE 和BFE △中,,,,A ABF AE BE ACE F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ACE BFE ≌(ASA ).错因:写错证明方法.满分备考:遇到三角形的中线,可通过倍长中线,使延长线段与原中线长相等,构造全等三角形解决问题.变式训练【变式2-1】(2019·呼和浩特市实验中学八年级期中)(1)AD 是ABC ∆的中线,8AB =,6AC =则AD 的取值范围是__________.(2)在(1)问的启发下,解决下列问题:如图,AD 是ABC ∆的中线,BE 交AC 于E ,交AD 于F ,且AE EF =,求证:AC BF =.【答案】(1)17AD <<(2)见解析【分析】(1)根据倍长中线法将AD 延长一倍,再证△ADC ≌△GDB ,根据三角形的三边关系即可求出AG 的取值范围,从而求出AD 的取值范围;(2)由(1)中结论:△ADC ≌△GDB ,即可得到:AC=BG ,∠CAD=∠G ,再根据等腰三角形的性质和判定即可得到BG=BF=AC.【详解】(1)将AD 延长至G ,使AD=DG ,连接BG,如下图所示:在△ADC 和△GDB 中CD BD ADC GDB AD DG =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△GDB∴AC=BG=6在△ABG 中AB BG AG AB BG-<<+∴86286AD -<<+∴17AD <<(2)将AD 延长至G ,使AD=DG ,连接BG,如下图所示:由(1)中结论:△ADC ≌△GDB∴AC=BG ,∠CAD=∠G又∵AE EF =,∴AFE EAF ∠=∠,∴AFE G∠=∠∵AFE BFG∠=∠∴G BFG∠=∠∴BG=BF=AC【点睛】此题考查的是全等三角形的判定及等腰三角形的判定及性质,掌握用倍长中线法构造全等三角形是解决此题的关键.【变式2-2】(2020·湖南长沙市·月考)如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =、【分析】利用中线类倍长的基本模型进行证明,结合等腰三角形的性质进行论证.【详解】延长AD 到G ,使DG AD =,连结BG∵BD CD =,BDG CDA ∠=∠,AD GD=∴ADC GDB ∆∆≌.∴AC GB =.G EAF∠=∠又∵BE AC =,∴BE BG=∴G BED ∠=∠,而BED AEF∠=∠∴AEF FAE ∠=∠,故FA FE =.【点睛】此题考查的是全等三角形的判定及等腰三角形的判定及性质,掌握用倍长中线法构造全等三角形是解决此题的关键.【变式1-3】(2021·陕西碑林·交大附中分校七年级期中)问题背景:课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC 中,若AB =4,AC =3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到点E ,使DE =AD ,则得到△ADC ≌△EDB ,小明证明△BED ≌△CAD 用到的判定定理是:(用字母表示);问题解决:小明发现:解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.请写出小明解决问题的完整过程;拓展应用:以△ABC 的边AB ,AC 为边向外作△ABE 和△ACD ,AB =AE ,AC =AD ,∠BAE =∠CAD =90°,M 是BC 中点,连接AM ,DE .当AM =3时,求DE 的长.【答案】问题背景:SAS ;问题解决:完整过程见解析;拓展应用:DE =6.【分析】问题背景:先判断出BD =CD ,由对顶角相等∠BDE =∠CDA ,进而得出△ADC ≌△EDB (SAS );问题解决:先证明△ADC ≌△EDB (SAS ),得出BE =AC =3,最后用三角形三边关系即可得出结论;拓展应用:如图2,延长AM 到N ,使得MN =AM ,连接BN ,同(1)的方法得出△BMN ≌△CMA (SAS ),则BN =AC ,进而判断出∠ABN =∠EAD ,进而判断出△ABN ≌△EAD ,得出AN =ED ,即可求解.【详解】问题背景:如图1,延长AD 到点E ,使DE =AD ,连接BE,∵AD 是△ABC 的中线,∴BD =CD ,在△ADC 和△EDB 中,AD ED CDA BDE CD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ),故答案为:SAS ;问题解决:如图1,延长AD 到点E ,使DE =AD ,连接BE ,∵AD 是△ABC 的中线,∴BD =CD ,在△ADC ≌△EDB 中,AD ED CDA BDE CD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ),∴BE =AC ,在△ABE 中,AB ﹣BE <AE <AB +BE ,∵AB =4,AC =3,∴4﹣3<AE <4+3,即1<AE <7,∵DE =AD ,∴AD =12AE ,∴12<AD <72;拓展应用:如图2,延长AM 到N ,使得MN =AM ,连接BN,由问题背景知,△BMN ≌△CMA (SAS ),∴BN =AC ,∠CAM =∠BNM ,∴AC //BN ,∵AC =AD ,∴BN =AD ,∵AC //BN ,∴∠BAC +∠ABN =180°,∵∠BAE =∠CAD =90°,∴∠BAC +∠EAD =180°,∴∠ABN =∠EAD ,在△ABN 和△EAD 中,AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABN ≌△EAD (SAS ),∴AN =DE ,∵MN =AM ,∴DE =AN =2AM ,∵AM =3,∴DE =6.【点睛】此题考查了全等三角形的判定和性质,平行线的判定与性质,补角的性质,掌握倍长中线法,构造全等三角形是解本题的关键.类倍长中线模型【例题3】(2020·宜春市宜阳学校八年级月考)阅读理解:(1)如图1,在ABC 中,若10AB =,6AC =,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E ,使得AD DE =,再连接BE ,把AB ,AC ,2AD 集中在ABE △中,利用三角形三边关系即可判断中线AD 的取值范围是______.(2)解决问题:如图2,在ABC 中,D 是BC 边上的中点,DE DF ⊥,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:BE CF EF +>.【答案】(1)28AD <<;(2)见解析;【分析】(1)如图1延长AD 到点E ,使得AD DE =,再连接BE ,由AD 为中线,推出BD=CD ,可证△ACD ≌△EBD (SAS )得AC=EB ,在ABE △中,由三边关系4<2AD<16即可,(2)如图2延长FD 到G ,使DG=FD ,连结BG ,EG 由D 为BC 中点,BD=CD 可证△FCD ≌△GBD (SAS )得FC=GB ,由DE DF ⊥,DF=DG 得EF=EG ,在△BEG 中由三边关系,【详解】(1)如图1延长AD 到点E ,使得AD DE =,再连接BE ,∵AD 为中线,∴BD=CD ,在△ADC 和△EDB 中,∵CD=BD ,∠ADC=∠EDB ,AD=ED ,∴△ACD ≌△EBD (SAS ),∴AC=EB=6,ABE △,∵AB-BE<AE<AB+BE ,∴4<2AD<16,∴2<AD<8,(2)如图2延长FD 到G ,使DG=FD ,连结BG ,EG ,由D 为BC 中点,BD=CD ,在△FDC 和△GDB 中,∵CD=BD ,∠FDC=∠GDB ,FD=GD ,∴△FCD ≌△GBD (SAS ),∴FC=GB ,∵DE DF ⊥,DF=DG ,∴EF=EG ,在△BEG 中EG<EB+BG ,即BE CF EF +>,【点睛】本题考查中线加倍,三角形全等,三边关系,垂直平分线,等腰三角形,掌握中线加倍构造三角形,用三角形全等转化等量关系,用三边关系求取值范围,用垂直平分线转化线段,用等腰三角形证角是解题关键,变式训练【变式3-1】(2021·广东广州市·月考)如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交AB 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.【分析】通过补长EG ,转换成倍长中线模型【详解】延长FE 到点H ,使得EF EH =,连结BH∵E 是BC 的中点∴BE CE=在EFC ∆和EHB ∆中,CE BE CEF BEHEF EH =⎧⎪∠=∠⎨⎪=⎩∴EFC ∆≌EHB∆∴FC BH =,F H∠=∠∵BG CF=∴BH BG=∴H BGH∠=∠∴F BGH∠=∠∵EF AD∥∴,F CAD BGH BAD∠=∠∠=∠∴CAD BAD∠=∠∴AD 为ABC ∆的角平分线.【变式3-2】(2021·湖北随州市·八年级期末)在通过构造全等三角形解决的问题中,有一种典型的方法是倍延中线.如图3,在四边形ABCD 中,//AD BC ,点E 是AB 的中点,连接CE ,ED 且CE DE ⊥,试猜想线段,,BC CD AD 之间满足的数量关系,并予以证明.【分析】延长CE 到F ,使EF EC =,连接AF ,即可证明AEF BEC ∆≅∆,则可得EAF B AF BC ∠=∠=,,由//AD BC ,以及角度关系即可证明点,,F A D 在一条直线上,通过证明Rt DEF △≌DEC Rt △,即可得到FD CD =,进而通过线段的和差关系得到CD BC AD =+.【详解】(3)CD BC AD =+,延长CE 到F ,使EF EC =,连接AF,AE BE AEF BEC =∠=∠ ,,AEF BEC ∴∆≅∆,EAF B AF BC ∴∠=∠=,,//AD BC ,180BAD B ∴∠+∠=︒,180EAF BAD ∴∠+∠=︒,∴点,,F A D 在一条直线上,CE ED ⊥ ,∴90DEF DEC ==︒∠∠,∴在Rt DEF △和DEC Rt △中,EF EC =,DEF DEC ∠=∠,DE DE =,∴Rt DEF △≌DEC Rt △,FD CD ∴=,∵FD AD AF AD BC =+=+,CD BC AD ∴=+.【点睛】本题考查了三角形中线、全等三角形的证明和性质、三角形的三边关系、等腰三角形的性质、平行线的性质、平角的概念、线段的和差关系等,正确的作出辅助线以及综合运用以上知识是解答本题的关键.【变式3-3】(江苏省南京玄武外国语学校、十三中科利华集团校2019-2020学年八年级下学期期中数学试题)课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC 中,若AB =5,AC =3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E ,使得DE =AD ,再连接BE (或将△ACD 绕点D 逆时针旋转180°得到△EBD ),把AB 、AC 、2AD 集中在△ABE 中,利用三角形的三边关系可得2<AE <8,则1<AD <4.(感悟)解题时,条件中若出现中点、中线字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.(解决问题)受到(1)的启发,请你证明下列命题:如图2,在△ABC 中,D 是BC 边上的中点,DE ⊥DF ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF .求证:BE +CF >EF ,【答案】(1)见解析;(2)222=BE CF EF +,见解析【分析】延长FD 到G ,使得DG=DF ,连接BG 、EG .(或把△CFD 绕点D 逆时针旋转180°得到△BGD ),利用三角形的三边关系即可解决问题;【详解】解:延长FD 到G ,使得DG=DF ,连接BG 、EG .(或把△CFD 绕点D 逆时针旋转180°得到△BGD ),∴CF=BG ,DF=DG ,∵DE ⊥DF ,∴EF=EG .在△BEG 中,BE+BG >EG ,即BE+CF >EF .【点睛】本题考查了旋转的性质、全等三角形的判定和性质、三角形的三边关系、三角形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.综合提升变式练一、填空题1.(2022·安徽亳州·八年级期末)如图,在△ABC 中,AD 为中线,6AB .(1)若4AC =,AD 长度为a ,则a 的取值范围为________;(2)若AD AC ⊥,30BAD ∠=︒,则AC 的长度为________.【答案】15a <<3【分析】(1)延长中线AD 到E ,使DE AD =,可证△ACD ≌△EBD (SAS ),得AC BE =,根据三角形的三边关系可得64264a -<<+,求解即可;(2)延长AD ,使AD DF =,连接CF ,可证△ABD ≌△FCD (SAS ),得BAD CFD ∠=∠,AB FC =,在Rt △AFC 中,根据30°所对的直角边等于斜边的一半可得12AC FC =,从而可求.【详解】解:(1)如图1,延长中线AD 到E ,使DE AD =,∵AD 是三角形的中线,∴BD CD =,在△ACD 和△EBD 中,CD BD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△EBD (SAS ),∴AC BE =,∵4BE AC ==,6AB =,第三边上的中线为a ,∴64264a -<<+,即2210a <<,∴15a <<.故答案为:15a <<.(2)如图2,延长AD ,使AD DF =,连接CF,∵AD 为中线,∴BD CD =,在△ABD 和△FCD 中,AD FD ADB FDC BD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△FCD (SAS ),∴BAD CFD ∠=∠,AB FC =,∵30BAD ∠=︒,∴30CFD ∠=︒,∵AD AC ⊥,∴90CAD ∠=︒,∴12AC FC =,∵6AB =,∴132AC AB ==.【点睛】本题考查了延长中线构成全等三角形,及全等三角形的判定与性质,直角三角形的性质,解题的关键是延长中线作辅助线构造全等三角形.2.(2021·江苏·徐州市第二十六中学八年级阶段练习)如图,AD 是△ABC 中BC 边上的中线,若AB =6,AC =8,则AD 的取值范围是________________.【答案】1<AD <7【分析】延长AD 到E ,使DE =AD ,然后利用“边角边”证明△ABD 和△ECD 全等,根据全等三角形对应边相等可得CE =AB ,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE 的取值范围,然后即可得解.【详解】解:如图,延长AD 到E ,使DE =AD ,∵AD 是BC 边上的中线,∴BD =CD ,在△ABD 和△ECD 中,BD CD ADB EDC AD ED =⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△ECD(SAS),∴CE=AB,∵AB=6,AC=8,∴8-6<AE<8+6,即2<2AD<14,∴1<AD<7,故答案为:1<AD<7.【点睛】本题考查了三角形的三边关系,全等三角形的判定与性质,遇中点加倍延,作辅助线构造出全等三角形是解题的关键.3.(2021·河北·廊坊市第四中学八年级阶段练习)在△ABC中,AB=9,AC=5,AD是△ABC 的中线,则AD的取值范围是_____.【答案】2<AD<7【分析】延长中线利用全等,使AD与已知两边满足三角形的三边关系.【详解】解:延长AD到E,使AD=DE,连接BE,∵AD 是△ABC 的中线,∴BD =CD ,在△ADC 和△EDB 中,CD BD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ),∴EB =AC ,根据三角形的三边关系定理:9﹣5<AE <9+5,∴2<AD <7,故答案为:2<AD <7.【点睛】本题考查三角形的中线,全等三角形的判定(SAS ),三角形的三边长度关系;延长三角形的中线证明全等是常用的解题方法,要熟练掌握.二、解答题4.(2022·贵州毕节·二模)课外兴趣小组活动时,老师提出了如下问题:(1)如图1,△ABC 中,若AB =5,AC =3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到点E ,使DE =AD ,请根据小明的方法思考帮小明完成解答过程.(2)如图2,AD 是△ABC 的中线,BE 交AC 干E ,交AD 于F ,且AE =EF .请判昕AC 与BF 的数量关系,并说明理由.【答案】(1)见解析(2)AC =BF ,理由见解析(1)解:如图,延长AD 到点E ,使DE =AD ,连接BE ,在△ADC 和△EDB 中∵AD DE ADC EDB CD DB =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ).∴BE =AC =3.∵AB -BE <AE <AB +BE∵2<AE <8.∵AE =2AD∴1<AD <4.(2)AC =BF ,理由如下:延长AD 至点G ,使GD =AD ,连接BG,在△ADC 和△GDB 中,AD DG ADC GDB BD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△GDB (SAS ).∴BG =AC ,∠G =∠DAC ..∵AE =EF∴∠AFE =∠FAE .∴∠DAC =∠AFE =∠BFG∴∠G =∠BFG∴BG =BF∴AC =BF .【点睛】本题考查全等三角形判定与性质,三角形三边的关系,作辅助线:延长AD 到点E ,使DE =AD ,构造全等三角形是解题的关键.5.(2022·广西贵港·九年级期末)如图,在平行四边形ABCD 中,点E 、F 分别在边BC ,CD 上,AE 与BF 相交于点O ,AE AD =,AE 平分BF ,AF 平分∠DAE .(1)求证:OA OE BE =+;(2)求证:22BE OE AE =⋅.【答案】(1)见解析(2)见解析【分析】(1)如图1,过点F 作FP BC ∥,FP 与AE 交于点P ,先证明,,PF BE OP OE ==再证明,AP PF =从而可得结论;(2)如图2,过点F 作FP BC ∥,FP 与AE 交于点P ,连接EF ,PB ,证明BPE ABE ∠=∠,结合BEP AEB ∠=∠,证明△BEP ∽△AEB ,可得BE AE PE BE=,从而可得结论.(1)证明:如图1,过点F 作FP BC ∥,FP 与AE 交于点P ,∴FPO BEO ∠=∠,∵AE 平分BF ,即FO BO =,又FOP BOE ∠=∠,∴△POF ≌△EOB ,∴OP OE =,PF EB =,又∵四边形ABCD 是平行四边形,∴PF BC AD ∥∥,∴PFA DAF ∠=∠,∵AF 平分∠DAE ,∴PFA DAF PAF ∠=∠=∠,∴PA PF BE ==,∴OA OP PA OE BE =+=+.(2)如图2,过点F 作FP BC ∥,FP 与AE 交于点P ,连接EF ,PB .∵AE AD =,AF 平分∠DAE ,AF AF =,∴△AEF ≌△ADF ,∴AEF D ∠=∠,又在ABCD 中,ABE D ∠=∠,又由(1)知:△POF ≌△EOB ,,,PF BE FPO BEO ∴=∠=∠,PF BE ∴ ∴四边形BEFP 是平行四边形,∴BPE AEF D ∠=∠=∠,∴BPE ABE ∠=∠,又BEP AEB ∠=∠,∴△BEP ∽△AEB ,∴BE AE PE BE=,∴2BE PE AE =⋅,又2PE OE =,∴22BE OE AE =⋅.【点睛】本题考查的是平行四边形的性质,全等三角形的判定与性质,相似三角形的判定与性质,“熟练运用以上知识,作出适当的辅助线”是解本题的关键.6.(2022·湖南长沙·八年级阶段练习)已知:如图,Rt △ABC 中,AC >BC ,∠ACB =90,CD 是△ABC 的中线,点E 在CD 上,且∠AED =∠B .求证:AE =BC.【答案】见解析【分析】先通过延长CD 到F 使DF =CD ,连接AF ,构造出△BCD 的全等三角形△AFD ,由全等三角形性质可得∠F =∠BCD ,BC =AF ,又根据直角三角形斜边的中线等于斜边的一半得到CD =BD ,∠B =∠BCD ,由等量代换和等角对等边就可推出AE =BC .【详解】证明:延长CD 到F 使DF =CD ,连接AF,如图∵CD 是△ABC 的中线,∴AD =BD ,在△ADF 与△BCD 中,AD BD ADF BDC DF DC =⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△BDC (SAS ),∴∠F =∠BCD ,BC =AF ,∵∠ACB =90°,CD 是△ABC 的中线,∴CD =BD ,∴∠B =∠BCD ,又∵∠AED =∠B∴∠AED =∠BCD ,∵△ADF ≌△BDC ,∴∠F =∠BCD ,∴∠AED =∠F ,∴AE =AF ,∵BC =AF ,∴AE =BC .【点睛】本题主要考查了全等三角形的性质和判定,能正确构造出全等三角形是做出本题的重点.7.(2020·海南·海口市第七中学八年级期中)某数学兴趣小组在活动时,老师提出了这样一个问题:如图,在ABC 中,AB =6,AC =8,D 是BC 的中点,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E ,使DE =AD ,请补充完整证明“△ABD ≌△ECD ”的推理过程.(1)求证:△ABD ≌△ECD证明:延长AD 到点E ,使DE =AD在△ABD 和△ECD 中∵AD =ED (已作)∠ADB =∠EDC ()CD =(中点定义)∴△ABD ≌△ECD ()(2)由(1)的结论,根据AD 与AE 之间的关系,探究得出AD 的取值范围是;(3)【感悟】解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】如下图,ABC 中,90B ∠=︒,2AB =,AD 是ABC 的中线,CE BC ⊥,4CE =,且90ADE ∠=︒,求AE 的长.【答案】(1)对顶角相等;BD ;SAS(2)17AD <<(3)6【分析】(1)延长AD 到点E ,使DE =AD ,根据SAS 定理证明△ABD ≌△ECD ;(2)根据全等三角形的性质、三角形的三边关系计算;(3)延长AD 交EC 的延长线于F ,证明△ABD ≌△FCD ,△ADE ≌△FDE ,根据全等三角形的性质解答.(1)延长AD 到点E ,使DE =AD在△ABD 和△ECD 中∵AD =ED (已作)∠ADB =∠EDC (对顶角相等)CD =BD (中点定义)∴△ABD ≌△ECD (SAS )故答案为:对顶角相等;BD ;SAS(2)∵△ABD ≌△ECD ,AB =6,AC =8,6CE AB ∴==,8686AE -<<+,1AD 7∴<<,故答案为1AD 7<<;(3)延长AD 交EC 的延长线于F ,AB BC ⊥ ,EF BC ⊥,ABD FCD ∴∠=∠,在ABD △和FCD 中,ABD FCD BD CD ADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩,ABD ∴ ≌FCD ,2CF AB ∴==,AD DF =,又∵∠FDE =∠ADE =90°ED =ED∴△ADE ≌△FDEAE EF ∴=,426EF CE CF CE AB =+=+=+= ,6AE ∴=.【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定,解题关键是熟记全等三角形的判定条件.8.(2022·全国·一模)如图,在△ABC 中,∠ACB =90°,BC >AC ,CD ⊥AB 于点D ,点E 是AB 的中点,连接CE.(1)若AC =3,BC =4,求CD 的长;(2)求证:BC 2﹣AC 2=2DE •AB ;(3)求证:CE =12AB .【答案】(1)125(2)见解析(3)见解析【分析】(1)根据勾股定理求出AB ,根据三角形的面积公式计算,求出CD ;(2)根据题意得到BD ﹣AD =2DE ,根据勾股定理计算即可证明;(3)延长CE 至点F ,使EF =CE ,连结AF ,证明△AEF ≌△BEC (SAS ),根据全等三角形的性质得到∠B =∠EAF ,AF =BC ,再证明△ACF ≌△CAB ,得到CF =AB ,证明结论.(1)解:在△ABC 中,∠ACB =90°,AC =3,BC =4,由勾股定理得:AB5,∵∠ACB =90°,CD ⊥AB ,∴S △ABC =12AC •BC =12AB •DE ,即12×3×4=12×5×CD ,解得:CD =125;(2)证明:∵点E 是AB 的中点,∴AE =BE ,∴BD ﹣AD =(BE +DE )﹣(AE ﹣DE )=BE ﹣AE +2DE =2DE ,∵CD ⊥AB ,∴BC 2=BD 2+CD 2,AC 2=AD 2+CD 2,∴BC 2﹣AC 2=(BD 2+CD 2)﹣(AD 2+CD 2)=BD 2﹣AD 2=(BD +AD )(BD ﹣AD )=AB •2DE =2DE •AB ;(3)证明:延长CE 至点F ,使EF =CE ,连结AF,在△AEF 和△BEC 中,AE BE AEF BEC EF EC =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△BEC (SAS ),∴∠B =∠EAF ,AF =BC ,∵∠ACB =90°,∴∠B +∠CAB =∠EAF +∠CAB =90°,∴∠CAF =∠ACB =90°,∵AC =CA ,∴△ACF ≌△CAB (SAS ),∴CF =AB ,∵CF =2CE ,∴CE =12AB .【点睛】本题考查的是全等三角形的判定和性质、三角形的面积计算、勾股定理的应用,掌握全等三角形的判定定理和性质定理是解题的关键.9.(2022·辽宁葫芦岛·八年级期末)已知:多项式x 2+4x +5可以写成(x ﹣1)2+a (x ﹣1)+b 的形式.(1)求a ,b 的值;(2)△ABC 的两边BC ,AC 的长分别是a ,b ,求第三边AB 上的中线CD 的取值范围.【答案】(1)6a =,10b =(2)2<CD <8【分析】(1)把()()211x a x b -+-+展开,然后根据多项式x 2+4x +5可以写成(x ﹣1)2+a(x ﹣1)+b 的形式,可得2415a a b -=⎧⎨-+=⎩,即可求解;(2)延长CD 至点H ,使CD =DH ,连接AH ,可得△CDB ≌△HAD ,从而得到BC =AH =a =6,再根据三角形的三边关系,即可求解.(1)解:∵()()211x a x b-+-+221x x ax a b =-++-+()221x a x a b =+-+-+,根据题意得:x 2+4x +5=(x ﹣1)2+a (x ﹣1)+b∴2415a a b -=⎧⎨-+=⎩,解得:610a b =⎧⎨=⎩;(2)解:如图,延长CD 至点H ,使CD =DH ,连接AH ,∵CD 是AB 边上的中线,∴BD =AD ,在△CDB 和△HDA 中,∵CD =DH ,∠CDB =∠ADH ,BD =DA ,∴△CDB ≌△HDA (SAS ),∴BC =AH =a =6,在△ACH 中,AC -AH <CH <AC +AH ,∴10-6<2CD <10+6,∴2<CD <8.【点睛】本题主要考查了全等三角形的判定和性质,整式乘法和二元一次方程组的应用,三角形的三边关系,熟练掌握全等三角形的判定和性质,整式乘法法则,三角形的三边关系是解题的关键.10.(2022·新疆·乌鲁木齐市第四中学八年级期末)如图,在△ABC 中,AD 为BC 边上的中线,E 为AC 上的一点,BE 交AD 于点F ,已知AE =EF .求证:AC =BF.【答案】见解析【分析】延长AD 到G ,使得DG =AD ,连接BG ,证明△ADC ≌△GDB (SAS )得到AC =BG 且∠CAD =∠G ,再由等腰三角形的性质得到AE =EF ,继而证明BG =BF ,据此解题.【详解】证明:延长AD 到G ,使得DG =AD ,连接BG,在△ADC 和△GDB 中AD GD ADC GDB CD BD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△GDB (SAS )∴AC =BG 且∠CAD =∠G∵AE =EF∴∠EFA =∠EAF∴∠G =∠EFA∵∠EFA =∠BFG∴∠G =∠BFG∴BG =BF∵AC =BG∴BF =AC【点睛】本题考查全等三角形的判定与性质、等边对等角、等角对等边等知识,是重要考点,难度一般,掌握相关知识是解题关键.11.(2021·山东威海·七年级期中)数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在ABC 中,6AB =,10AC =,D 是BC 的中点,求BC 边上的中线AD 的取值范围.【阅读理解】小明在组内经过合作交流,得到了如下的解决方法:(1)如图1,延长AD 到E 点,使DE AD =,连接BE .根据______可以判定ADC ≌△______,得出AC =______.这样就能把线段AB 、AC 、2AD 集中在ABE △中.利用三角形三边的关系,即可得出中线AD 的取值范围是.【方法感悟】当条件中出现“中点”、“中线”等条件时,可以考虑做“辅助线”——把中线延长一倍,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中,这种做辅助线的方法称为“中线加倍”法.【问题解决】(2)如图2,在ABC 中,90A ∠= ,D 是BC 边的中点,90EDF = ∠,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:222BE CF EF +=.【问题拓展】(3)如图3,ABC 中,90B = ∠,3AB =,AD 是ABC 的中线,CE BC ⊥,5CE =,且90ADE ∠= .直接写出AE 的长=______.【答案】(1)SAS ;EDB △;BE ;2<<8AD ;(2)见解析;(3)8.【分析】(1)根据三角形全等的判定方法和全等三角形的性质以及三角形三边的关系求解即可;(2)延长ED 使DG =ED ,连接FG ,GC ,根据垂直平分线的性质得到EF GF =,然后利用SAS 证明BDE CDG ≌,得到BE CG =,B DCG ∠=∠,进而得到18090ACG A ∠=︒-∠=︒,最后根据勾股定理证明即可;(3)延长AD 交EC 的延长线于点F ,根据ASA 证明ABD FCD ∆∆≌,然后根据垂直平分线的性质得到AE CF =,最后根据全等三角形的性质求解即可.【详解】解:(1)在ADC 和EDB △中,AD ED ADC EDB CD BD =⎧⎪∠=∠⎨⎪=⎩∴()ADC EDB SAS ≌△△,∴10AC BE ==.∵6AB =,∴<<BE AB AE BE AB -+,即106<<106AE -+,∴4<<16AE ,∴4<2<16AD ,解得:2<<8AD ;故答案为:SAS ;EDB △;BE ;2<<8AD ;(2)如图所示,延长ED 使DG =ED ,连接FG ,GC,∵90EDF = ∠,∴EF GF =,在BDE 和CDG 中,BD CD BDE CDG DE GD =⎧⎪∠=∠⎨⎪=⎩∴()BDE CDG SAS ≌△△,∴BE CG =,B DCG ∠=∠,∴AB CG ∥,∴18090ACG A ∠=︒-∠=︒,∴在Rt FGC △中,222CG FC FG +=,∴222BE CF EF +=;(3)如图所示,延长AD 交EC 的延长线于点F,∵,AB BC EF BC ⊥⊥,ABD FCD ∴∠=∠,在ABD △和FCD 中,ABD FCD BD CD ADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABD FCD ASA ∴∆∆≌,∴3CF AB ==,AD DF =,∵90ADE ∠= ,∴AE EF =,∵538EF CE AB =+=+=,∴8AE =.【点睛】此题考查了全等三角形的性质和判定方法,三角形的三边关系,“中线加倍”法的运用,解题的关键是根据题意作出辅助线构造全等三角形.12.(2020·北京·八年级单元测试)阅读下面材料:数学课上,老师给出了如下问题:如图,AD 为△ABC 中线,点E 在AC 上,BE 交AD 于点F ,AE =EF .求证:AC =BF.经过讨论,同学们得到以下两种思路:完成下面问题:(1)①思路一的辅助线的作法是:;②思路二的辅助线的作法是:.(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).【答案】(1)①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)见解析【分析】(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论;②作BG=BF交AD的延长线于点G,利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论;(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.【详解】解:(1)①如图①,延长AD至点G,使DG=AD,连接BG,∵AD为△ABC中线,∴BD=CD,在△ADC和△GDB中,∵AD=GD,∠ADC=∠GDB,CD=BD,∴△ADC≌△GDB(SAS),∴AC=BG,∵AE=EF,∴∠CAD=∠EFA,∵∠BFG=∠G,∠G=∠CAD,∴∠G=∠BFG,∴BG=BF,∴AC=BF;②如图②,作BG=BF交AD的延长线于点G,∵BG=BF,∴∠G=∠BFG,∵AE=EF,∴∠EAF=∠EFA,∵∠EFA=∠BFG,∴∠G=∠EAF,在△ADC和△GDB中,∵∠CAD=∠G,∠ADC=∠GDB,CD=BD,∴△ADC≌△GDB(AAS),。

几何模型02——倍长中线法当线段出现一个中点时,特别是三角形中,常常采用“倍长中线法”添加辅助线.倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法. 倍长中线法:△ABC 中AD 是BC 边中线方式1: 延长AD 到E , 使DE=AD ,连接BE例1.已知:如图,AD 是△ABC 的中线,求证:AB +AC >2AD .证明:延长AD 到M ,使DM =AD ,连接BM ,CM ,∵AD 是△ABC 的中线,∴BD =DC ,∵AD =DM ,∴四边形ABMC 是平行四边形,∴BM =AC ,在△ABM 中,AB +BM >AM ,即AB +AC >2AD .例2.已知,如图△ABC 中,AB =5,AC =3,则中线AD 的取值范围是 . 解:延长AD 到点E ,使AD =ED ,连接CE ,∵AD 是△ABC 的中线,∴BD =CD ,在△ABD 和△ECD 中∴△ABD ≌△ECD (SAS ),∴AB =EC ,在△AEC 中,AC +EC >AE , 且EC ﹣AC <AE ,即AB +AC >2AD ,AB ﹣AC <2AD ,∴2<2AD <8,∴1<AD <4,故答案为:1<AD <4.E D A B C练习1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是.例3.如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.解:延长FD至点G,使得DG=DF,连接BG,EG,∵在△CDF和△BDG中,,∴△CDF≌△BDG(SAS),∴BG=CF=4,∠C=∠DBG,∵∠C+∠ABC=90°,∴∠DBG+∠ABC=90°,即∠ABG=90°,∵DE⊥FG,DF=DG,∴EF=EG==5.练习2.如图,已知AD为△ABC的中线,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F.求证:BE+CF>EF.练习3.如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,求GF的长.练习4.如图,在梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD 的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6.求CE的长.例4.如图,在△ABC中,AB=AC,E是AB中点,延长AB到D,使BD=BA,延长CE至F,使得EF=CE.求证:CD=2CE.证明:方法一:如右图1,取AC的中点H,连接BH,∵BD=BA,∴BH是△ACD的中位线,∴CD=2BH,又∵E是AB的中点,AB=AC,∴AE=AH=AB,在△ABH和△ACE中,,∴△ABH≌△ACE(SAS),∴CE=BH,∴CD=2CE.方法二:∵点E为AB的中点,∴BE=AE,在△BEF和△AEC中,,∴△BEF≌△AEC(SAS),∴BF=AC,∠EBF=∠A,∵AB=AC=BD,∴∠ACB=∠ABC,BF=BD,∵∠CBD=∠A+∠ACB,∠CBF=∠ABC+∠EBF,∴∠CBD=∠CBF,在△CBD和△CBF中,,∴△CBD≌△CBF(SAS),∴CD=CF,∵CF=CE+EF,CE=EF,∴CF=2CE,∴CD=2CE.练习5.已知:如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点.求证:CD=2CE练习6.已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE.练习7.如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AD是∠EAC的平分线.例5.如图,在△ABC中,AD平分∠BAC,E为BC的中点,过点E作EF∥AD 交AB于点G,交CA的延长线于点F.求证:BG=CF.证明:作CM∥AB交FE的延长线于M.∵BG∥CM,∴∠B=∠MCE,∵E是BC中点,∴BE=EC,在△BEG和△CEM中,,∴△BEG≌△CEM,∴BG=CM,∵AD∥EF,∴∠1=∠FGA,∠2=∠F,∵∠1=∠2,∴∠F=∠FGA,∵AB∥CM,∴∠FGA=∠M,∴∠F=∠M,∴CF=CM,∴BG=CF.练习8.已知:如图,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,过D 作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.例6.已知在△ABC中,AD是BC边上的中线,分别以AB边、AC边为直角边各向外作等腰直角三角形,如图,求证:EF=2AD.证明:延长AD至点G,使得AD=DG,连接BG,CG,∵AD=DG,BD=CD,∴四边形ABGC是平行四边形,∴AC=AF=BG,AB=AE=CG,∠BAC+∠ABG=180°,∵∠EAF+∠BAC=180°,∴∠EAF=∠ABG,在△EAF和△BAG中,,∴△EAF≌△BAG(SAS),∴EF=AG,∵AG=2AD,∴EF=2AD.练习9.如图,两个正方形ABDE和ACGF,点P为BC中点,连接P A交EF于点Q,试探究AP与EF的数量和位置关系,并证明你的结论.方式2:间接倍长作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN例7.如图,△ABC 中,AB =AC ,点D 在AB 上,点E 在AC 的延长线上,DE 交BC 于F ,且DF =EF ,求证:BD =CE .证明:如图,过点D 作DG ∥AE ,交BC 于点G ;则△DGF ≌△ECF ,∴DG =CE ;∵AB =AC ,∴∠B =∠ACB ;∵DG ∥AE ,∴∠DGB =∠ACB ,∴∠DBG =∠DGB ,∴DG =BD ,∴BD =CE .练习9.如图,△ABC 中,点D 在AB 上,E 是AC 延长线上一点,BD =CE ,DE 交BC 于点F ,DF =EF ,DP ∥AE 交BC 于点P ,求证:AB =AC .F E D C B A N D C B A M课后练习1、如图1已知:AD为△ABC的中线,易证AB+AC>2AD.(1)如图2,在△ABC中,AC=5,AB=13,D为BC的中点,DA⊥AC.求△ABC的面积.(2)问题2:如图3,在△ABC中,AD是三角形的中线.点F在中线AD上,且BF=AC,连接并延长BF交AC于点E.求证AE=EF.2.已知:如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并说明理由.3.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,求证:(1)AE平分∠DAB;(2)AB+CD=AD.4.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证EG=CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°,如图(2),证明:EG=CG且EG⊥CG.(2)如图(3)将△BEF绕点B逆时针旋转180°,证明:EG=CG且EG⊥CG.5.如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作FM∥AD交AC于F,求FC的长.6.如图所示,∠BAC=∠DAE=90°,M是BE的中点,AB=AC,AD=AE,求证:AM⊥CD.7.已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.。

初中数学全等专题倍长中线法(含答案)
得到AD+AC>2AE,故②、③正确。
由于
∠BAE=∠CDE,故ABE和CDE相似,因此XXX,所以
AB+AC>AD+AE,即AB+AC>AD+AD,即AB+AC>2AD,故④正确。
故选项D全部正确。
根据题意可知,AD+AC>2AE,将两式相加可得到XXX
>2AD+2AE,即AB+AC>AD+AE。
因此,可以得出
①②③④均正确的结论。
首先,根据题目要求,需要删除明显有问题的段落。
因此,可以删除最后一段话,因为它没有任何意义。
其次,需要修正文章中的格式错误。
可以将每个式子单独成行,以突出重点。
同时,可以使用符号“=”、“>”等来表示
不同的关系,使文章更加清晰明了。
最后,需要对每段话进行小幅度的改写,以使其更加流畅自然。
例如,可以使用更加简洁的语言,避免重复和冗长,同时保持逻辑严密。
综上所述,修正后的文章如下:
根据题意可知,有AD+AC>2AE。
将两式相加可得到XXX>2AD+2AE,即AB+AC>AD+AE。
因此,可以得出
①②③④均正确的结论。
首先,由题目可知BF∥CD。
其次,根据题意,可以得出△XXX≌△XXX。
因此,可以得出AB=BF。
最后,由题目可知△ABE为等腰三角形。

全等三角形倍长中线法的经典例题示例文章篇一:嘿,同学们!今天我要跟你们讲讲全等三角形倍长中线法,这可太有趣啦!先来说说啥是倍长中线法。
就好像我们搭积木,找到了关键的那块积木,整个造型就稳啦!倍长中线法就像是那个关键的“积木”,能帮我们解决好多全等三角形的难题呢。
比如说有这样一道题:在三角形ABC 中,AD 是中线。
那我们就延长AD 到点E,让AD = DE 。
这时候,连接BE ,哇塞,神奇的事情发生啦!“小明,你说说这时候能发现啥?”我问同桌小明。
小明挠挠头说:“好像能得到一些相等的边和角。
”“对呀!”我兴奋地说,“你看,因为AD 是中线,BD = DC ,又因为我们延长AD ,让AD = DE ,再加上对顶角相等,这不就可以证明三角形ADC 和三角形EDB 全等嘛!”再看这道题,三角形ABC 中,AD 是中线,AB = 5 ,AC = 3 ,求中线AD 的取值范围。
这可难倒了不少同学,可咱们用倍长中线法,不就轻松多啦?我跟后桌的小红一起讨论,我说:“小红,你想想,倍长中线之后,是不是能把条件都联系起来啦?”小红眼睛一亮:“对呀,这样就能构造出全等三角形,然后就能找到边的关系啦!”哎呀,这不就像我们找宝藏,倍长中线法就是那把能打开宝藏大门的钥匙嘛!通过这些例题,咱们是不是发现,倍长中线法简直就是解决全等三角形问题的神器呀!只要我们灵活运用,那些难题就都不在话下啦!我觉得呀,数学就像一个大宝藏,而这些解题方法就是我们挖掘宝藏的工具,只要我们用心去寻找,就能发现无数的惊喜!示例文章篇二:哎呀呀,同学们,今天咱们来聊聊全等三角形里倍长中线法的那些经典例题!先来说说啥是倍长中线法吧。
就好像我们走路遇到一条河,直接过去太困难,但是如果修一座桥,是不是就轻松多啦?倍长中线法就像是那座桥,能让我们在解全等三角形的难题时,一下子找到出路!比如说有这么一道题:在三角形ABC 中,AD 是中线。
延长AD 到E,使DE = AD。

全等三角形辅助线方法------倍长中线一、知,为行之始1.三角形中线的定义2.三角形中线的性质定理3.倍长中线法的核心为“中点”两字二、行,为知之成1.倍长中线辅助线方法一:向中线作垂线构造全等(间接倍长)作法:作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E ,证明△CFD ≌△BED FED C BA【例】已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF.F ED AB C2.倍长中线辅助线方法二:延长或作平行线构造全等(间接倍长)作法:延长MD 到N 使DN=MD ,连接CN 或者过C 作CN ∥AB 交MD 的延长线与点N N DCB AM【例】在四边形ABCD 中,//AD BC ,点E 是AB 的中点,连接CE ,ED 且CE DE ,试猜想线段,,BC CD AD之间满足的数量关系,并予以证明.3.倍长中线辅助线方法三:直接倍长中线构造全等作法:延长AD 到E ,使DE=AD ,连接BE 或者CE ,证明△ACD ≌△EBD ED AB C【例】如图,在△ABC 中,D 是BC 边上的中点.(1)求证:AB+AC >2AD ;(2)若AB=5,AC=7,求AD 的取值范围.三、知行合一1.已知△ABC中,AB=5,AC=7,则BC边上的中线a的取值范围是()A.1<a<6B.5<a<7C.2<a<12D.10<a<14的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则2.如图,AD是ABCEF=().A.2.5B.2C.1.5D.13.如图所示,在△ABC中,AB=6,AC=4,AD是△ABC的中线,若AD的长为偶数,则AD=_____.4.在△ABC中,AC=8,中线AD=5,那么边AB的取值范围为____.5.如图,△ABC中,BC边上的中线AD将∠BAC分成了两角∠BAD、∠DAC分别为70°和40°,若中线AD长为2.4cm,则AC长为________cm.6.如图,AD是△ABC的中线,点E在BC的延长线上,CE=AB,∠BAC=∠BCA,求证:AE=2AD。
三角形中线的定义:三角形顶点和对边中点的连线 中线中位线相关问题(涉及中点的问题)见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见.版块一 倍长中线【例1】 (2002年通化市中考题)在△ABC 中,9,5==AC AB ,则BC 边上的中线AD 的长的取值范围是什么?【补充】已知:ABC ∆中,AM 是中线.求证:1()2AM AB AC <+.重点:主要掌握中线的处理方法,遇见中线考虑中线倍长法难点:全等三角形的综合运用重、难点知识点睛例题精讲专题讲座全等三角形与 中点问题MCBA【例2】 如图,ABC ∆中,<AB AC ,AD 是中线.求证:<DAC DAB ∠∠.GFEDCBA【例3】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FEDC BA【例4】 如图所示,在ABC ∆和A B C '''∆中,AD 、A D ''分别是BC 、B C ''上的中线,且AB AB''=,AC A C ''=,AD A D ''=,求证ABC A B C '''∆∆≌.EDCABB'A'C'D'【例5】 已知AD 为ABC ∆的中线,ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>.FE AB D C版块二、中位线的应用【例10】 AD 是ABC ∆的中线,F 是AD 的中点,BF 的延长线交AC 于E .求证:13AE AC =.FA DE CB【例11】 如图所示,在ABC ∆中,AB AC =,延长AB 到D ,使BD AB =,E 为AB 的中点,连接CE 、CD ,求证2CD EC =.ECB A【例12】 已知,如图四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点. 求证:AME BNE ∠=∠.A CDM FE NB【习题1】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,AF 与EF 相等吗?为什么?FED CBA【习题2】 如右下图,在ABC ∆中,若2B C ∠=∠,AD BC ⊥,E 为BC 边的中点.求证:2AB DE =.。
第13讲 全等三角形中“倍长中线”模型((核心考点讲与练)【基础知识】三角形一边的中线(与中点有关的线段),或中点,通常考虑倍长中线或类中线,构造全等三角形.把该中线延长一倍,证明三角形全等,从而运用全等三角形的有关知识来解决问题的方法.主要思路:倍长中线(线段)造全等在△ABC 中 AD 是BC 边中线延长AD 到E , 使DE=AD ,连接BE作CF ⊥AD 于F , 作BE ⊥AD 的延长线于E连接BE延长MD 到N , 使DN=MD ,连接CD【考点剖析】1、如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .方法1:如图,延长AD 到E ,使DE =AD ,连接BE在△BDE 和△CDA 中BD CD BDE CDADE DA =ìïÐ=Ðíï=î∴△BDE ≌△CDA (SAS )∴A C =BE ,∠E =∠2∵AD 平分∠BACCD B A21ECD B A∴∠1=∠2∴∠1=∠E∴AB =BE∴AB =AC方法2:如图,过点B 作BE ∥AC ,交A D 的延长线于点E∵BE ∥AC∴∠E =∠2在△BDE 和△CDA 中2E BDE CDABD CD Ð=ÐìïÐ=Ðíï=î∴△BDE ≌△CDA (AAS )∴BE =AC∵AD 平分∠BAC∴∠1=∠2∴∠1=∠E∴AB =BE∴AB =AC2、如图1,已知ABC D 中,AD 是BC 边上的中线.21ECD B A求证:2AB AC AD +>.证明:如图2,延长AD 至E ,使DE AD =,∵AD 是BC 边上的中线∴BD CD=在BDE D 和CDA D 中BD CD BDE CDADE DA =ìïÐ=Ðíï=î∴BDE CDA D D ≌∴BE CA=在ABE D 中,AB BE AE+>∴2AB AC AD +>.3.如图,在△ABC 中,AD 为BC 边上的中线.(1)按要求作图:延长AD 到点E ,使DE =AD ;连接BE .(2)求证:△ACD ≌△EBD .(3)求证:AB +AC >2AD .(4)若AB =5,AC =3,求AD 的取值范围.解:(1)如图,D CBA(2)证明:如图,∵AD 为BC 边上的中线∴BD =CD在△BDE 和△CDA 中12BD CD ED AD =ìïÐ=Ðíï=î∴△BDE ≌△CDA (SAS )(3)证明:如图,∵△BDE ≌△CDA∴BE =AC∵DE =AD∴AE =2 AD在△ABE 中,AB +BE >AE∴AB +AC >2AD(4)在△ABE 中,AB -BE <AE <AB +BE由(3)得 AE =2AD ,BE =AC∵AC =3,AB =5∴5-3<AE <5+3∴2<2AD <8∴1<AD <44.如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .21EB CD A证明:如图,延长AD 到E ,使DE =AD ,连接BE在△ADC 和△EDB 中CD BD ADC EDBAD ED =ìïÐ=Ðíï=î∴△ADC ≌△EDB (SAS )∴AC =EB ,∠2=∠E∵AD 平分∠BAC∴∠1=∠2∴∠1=∠E∴AB =BE∴AB =AC5.如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .求证:①CE =2CD ;②CB 平分∠DCE .证明:如图,延长CD 到F ,使DF =CD ,连接BFD CB A21ED CB AE D CB A∴CF =2CD∵CD 是△ABC 的中线∴BD =AD在△BDF 和△ADC 中BD AD ADC BDFDF DC =ìïÐ=Ðíï=î∴△BDF ≌△ADC (SAS )∴BF =AC ,∠1=∠F∵CB 是△AEC 的中线∴BE =AB∵AC =AB∴BE =BF∵∠1=∠F∴BF ∥AC∴∠1+∠2+∠5+∠6=180°又∵AC =AB∴∠1+∠2=∠5又∵∠4+∠5=180°∴∠4=∠5+∠6即∠CBE =∠CBF在△CBE 和△CBF 中CB CB CBE CBFBE BF =ìïÐ=Ðíï=î∴△CBE ≌△CBF (SAS )∴CE =CF ,∠2=∠3∴CE =2CDCB 平分∠DCE6.如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F .求证:∠AEF =∠EAF .证明:如图,延长AD 到M ,使DM =AD ,连接BM∵D 是BC 边的中点∴BD =CD在△ADC 和△MDB 中CD BD ADC MDBAD MD =ìïÐ=Ðíï=î∴△ADC ≌△MDB (SAS )∴∠1=∠M ,AC =MB∵BE =AC∴BE =MB∴∠M =∠3∴∠1=∠3∵∠3=∠2∴∠1=∠2即∠AEF =∠EAF7.如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,BG =CF .FED CB A321MAB CD EF求证:AD 为△ABC 的角平分线.证明:如图,延长FE 到M ,使EM =EF ,连接BM∵点E 是BC 的中点∴BE =CE在△CFE 和△BME 中FE ME CEF BEMCE BE =ìïÐ=Ðíï=î∴△CFE ≌△BME (SAS )∴CF =BM ,∠F =∠M∵BG =CF∴BG =BM∴∠1=∠M∴∠1=∠F∵AD ∥EF∴∠3=∠F ,∠1=∠2∴∠2=∠3即AD 为△ABC 的角平分线GFE D CB A321MAB CD E FG【过关检测】一.选择题(共6小题)1.(2020秋•沈丘县期中)已知△ABC中AD为中线,且AB=5、AC=7,则AD的取值范围为( )A.2<AD<12B.5<AD<7C.1<AD<6D.2<AD<10【分析】先作辅助线,延长AD至点E,使DE=AD,连接EC,先证明△ABD≌△ECD,在△AEC中,由三角形的三边关系定理得出答案.【解答】解:延长AD至点E,使DE=AD,连接EC,在△ADB和△EDC中∴△ADB≌△EDC(SAS),∴CE=AB,∵AB=5,AC=7,∴CE=5,设AD=x,则AE=2x,∴7﹣5<2x<7+5,∴1<x<6,故选:C.【点评】本题考查了三角形的三边关系定理和全等三角形的判定和性质的应用,注意:三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边.2.(2021秋•新城区校级期中)已知AD是△ABC的边BC上的中线,AB=12,AC=8,则中线AD的取值范围是( )A.2<AD<10B.4<AD<20C.1<AD<4D.以上都不对【分析】延长AD至点E,使AD=DE,得出△ACD≌△EBD,进而在△ABE中利用三角形三边关系求解.【解答】解:如图,延长AD至点E,使AD=DE,连接BE,∵AD是△ABC的边BC上的中线,∴BD=CD,又∠ADC=∠BDE,AD=DE∴△ACD≌△EBD,∴BE=AC,在△ABE中,AB﹣BE<AE<AB+BE,即AB﹣AC<AE<AB+AC,12﹣8<AE<12+8,∴4<AE<20,∴2<AD<10.故选:A.【点评】本题主要考查了全等三角形的判定及性质以及三角形的三边关系,添加恰当辅助线构造全等三角形是解题的关键.3.(2020秋•广州校级月考)如图,在△ABC中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是( )A.3<AD<13B.1.5<AD<6.5C.2.5<AD<7.5D.10<AD<16【分析】延长AD到E,使AD=DE,连接BE,证明△ADC≌△EDB,推出EB=AC,根据三角形的三边关系定理求出即可.【解答】解:延长AD到E,使AD=DE,连接BE,∵AD是△ABC的中线,∴BD=CD,在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),∴EB=AC,根据三角形的三边关系定理:8﹣5<AE<8+5,∴1.5<AD<6.5,故选:B.【点评】本题主要考查对全等三角形的性质和判定,三角形的三边关系定理,倍长中线等知识点的理解和掌握,能推出8﹣5<2AD<8+5是解此题的关键.4.(2020秋•江岸区校级月考)在△ABC中,AB=4,AC=6,则BC边上的中线AD的取值范围是( )A.1<AD<5B.4<AD<6C.2<AD<10D.3<AD<6【分析】延长AD至点E,使得DE=AD,可证△ABD≌△CDE,可得AB=CE,AD=DE,在△ACE中,根据三角形三边关系即可求得AE的取值范围,即可解题.【解答】解:延长AD至点E,使得DE=AD,∵在△ABD和△CDE中,,∴△ABD≌△CDE(SAS),∴AB=CE,AD=DE∵△ACE中,AC﹣AB<AE<AC+AB,∴2<AE<10,∴1<AD<5.故选:A.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△CDE是解题的关键.5.(2021秋•肥西县期末)一个三角形的两边长分别为5和9,设第三边上的中线长为x,则x的取值范围是( )A.x>5B.x<7C.4<x<14D.2<x<7【分析】延长AD到E,使AD=DE,连接BE,CE,利用SAS证明ADC≌△EDB,得BE=AC=9,由AD=x,得AE=2x,在△ABE中利用三角形三边关系可得答案.【解答】解:如图,AB=5,AC=9,AD为BC边的中线,延长AD到E,使AD=DE,连接BE,CE,∵AD=x,∴AE=2x,在△BDE与△CDA中,,∴△ADC≌△EDB(SAS),∴BE=AC=9,在△ABE中,AB+BE>AE,BE﹣AB<AE,即5+9>2x,9﹣5<2x,∴2<x<7,故选:D.【点评】本题主要考查了全等三角形的判定与性质,三角形的三边关系等知识,作辅助线构造三角形全等是解题的关键.6.(2020秋•平舆县期中)如图,已知AD是△ABC中BC边上的中线,AB=5,AC=3,则AD的取值范围是( )A.2<AD<8B.1<AD<4C.2<AD<5D.4≤AD≤8【分析】延长AD到E,使DE=AD,连接CE,先证△ABD≌△ECD,得CE=AB,再由三角形任意两边之和大于第三边,两边之差小于第三边求出AE的取值范围,然后即可得解.【解答】解:如图,延长AD到E,使DE=AD,连接CE,∵AD是BC边上的中线,∴BD=CD,在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴CE=AB=5,在△ACE中,由三角形的三边关系得:CE﹣AC<AE<CE+AC,∴5﹣3<AE<5+3,即2<2AD<8,∴1<AD<4,故选:B.【点评】本题考查了三角形的三边关系,全等三角形的判定与性质等知识;遇中点加倍延,作辅助线构造出全等三角形是解题的关键,属于中考常考题型.二.填空题(共5小题)7.(2021秋•九台区期末)如图,△ABC中,AB=6,AC=4,D是BC的中点,AD的取值范围为 1<AD<5 .【分析】延长AD到E,使DE=AD,连接BE,证明△BDE≌△CDA,得出AC=BE,再根据三角形的三边关系得到结论.【解答】解:延长AD到E,使DE=AD,连接BE,在△ACD与△EBD中,,∴△BDE≌△CDA(SAS),∴BE=AC,∵AB=6,AC=4,∴2<AE<10,∴1<AD<5.故答案为:1<AD<5.【点评】本题考查了全等三角形的判定与性质,三角形的三边关系,理解倍长中线法,证明△BDE≌△CDA是解题的关键.8.(2021秋•东莞市期中)在△ABC中,已知AB=3,AC=5,AD是BC边上的中线,则AD取值范围是 1<AD<4 .【分析】如图,首先倍长中线AD至E,连接CE,因此可以得到△ABD≌△ECD,这样就有CE=AB,然后在△ACE中利用三角形的三边的关系即可求解.【解答】解:如图,延长AD至E,使DE=AD,连接CE,∵AD是BC边上的中线,∴BD=CD,∠ADB=∠CDE,∴△ABD≌△ECD,∴CE=AB,在△ACE中,AC﹣CE<AE<AC+CE,而AB=3,AC=5,∴5﹣3<AE<5+3,∴2<2AD<8,即1<AD<4.【点评】此题既考查了全等三角形的性质与判定,也考查了三角形的三边的关系,解题的关键是利用已知条件构造全等三角形,然后利用三角形的三边的关系解决问题.9.(2020秋•荣昌区校级期中)在△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是 2<AD<4 .【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系即可求解.【解答】解:延长AD至E,使DE=AD,连接CE.在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴CE=AB.在△ACE中,CE﹣AC<AE<CE+AC,即4<2AD<8,2<AD<4.故答案为:2<AD<4.【点评】此题综合运用了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.10.(2021秋•木兰县期末)如图,在△ABC中,∠ABC=45°,AM⊥BC于点M,点D在AM上,且DM =CM,F是BC的中点,连接FD并延长,在FD的延长线上有一点E,连接CE,且CE=CA,∠BDF=36°,则∠E= 36° .【分析】先证明△AMC≌△BMD,延长EF到点G,使得FG=EF,连接BG.再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠CEF.【解答】解:∵∠ABM=45°,AM⊥BM,∴∠BMD=∠AMC,BM=AM,在△BMD和△AMC中,,∴△BMD≌△AMC(SAS),延长EF到点G,使得FG=EF,连接BG.如图所示:∵△BMD≌△AMC∴BD=AC,又∵CE=AC,∴BD=CE,在△BFG和△CFE中,,∴△BFG≌△CFE(SAS),∴BG=CE,∠G=∠CEF,∴BD=CE=BG,∴∠BDF=∠G=∠CEF.∴∠BDF=∠CEF,∴∠E=36°.故答案为:36°.【点评】本题考查全等三角形的判定和性质,等腰三角形的性质,解题的关键是熟悉“倍长中线”模型添加辅助线,构造全等三角形.11.(2021秋•淅川县期中)AD是△ABC的边BC上的中线,AB=6,AC=4,则中线AD的取值范围是 1<AD<5 .【分析】如图,延长AD至E,使DE=AD,连接BE,可证得△BDE≌△CDA(SAS),再运用三角形三边关系即可求得答案.【解答】解:如图,延长AD至E,使DE=AD,连接BE,∵AD是△ABC的中线,∴BD=CD,在△BDE和△CDA中,,∴△BDE≌△CDA(SAS),∴BE=AC=4,在△ABE中,AB﹣BE<AE<AB+BE,∴6﹣4<2AD<6+4,∴1<AD<5;故答案为:1<AD<5.【点评】本题考查了全等三角形的判定和性质,三角形的三边关系.解题关键是通过倍延中线构造全等三角形.三.解答题(共5小题)12.(2021秋•南充期末)如图,AD是△ABC的中线,F为AD上一点,E为AD延长线上一点,且DF=DE.求证:BE∥CF.【分析】证明△BDE≌△CDF(SAS),由全等三角形的性质得出∠BED=∠CFD,由平行线的判定可得出结论.【解答】证明:∵AD是△ABC的中线,∴BD=CD,在△BDE和△CDF中,,∴△BDE≌△CDF(SAS),∴∠BED=∠CFD,∴BE∥CF.【点评】本题考查了平行线的判定,全等三角形的判定与性质,证明△BDE≌△CDF是解题的关键.13.(2020秋•津南区期末)(1)如图1,在△ABC中,∠B=60°,∠C=80°,AD平分∠BAC.求证:AD=AC;(2)如图2,在△ABC中,点E在BC边上,中线BD与AE相交于点P,AP=BC.求证:PE=BE.【分析】(1)求∠BAC=180°﹣60°﹣80°=40°,∠BAD BAC=20°,再求∠ADC=∠B+∠BAD =60°+20°=80°,得∠C=∠ADC,即可证明;(2)过点A作AF∥BC交BD的延长线于点F,先证明△ADF≌△CDB,得AF=BC,得AP=AF,证出∠APF=∠F,再得∠BPE=∠PBE,即可证明.【解答】证明:(1)在△ABC中,∠B=60°,∠C=80°,∴∠BAC=180°﹣60°﹣80°=40°,∵AD平分∠BAC,∴∠BAD BAC=20°,∴∠ADC=∠B+∠BAD=60°+20°=80°,∵∠C=80°,∴∠C=∠ADC,∴AD=AC;(2)过点A作AF∥BC交BD的延长线于点F,∴∠F=∠DBC,∠FAD=∠C,∵AD=CD,∴△ADF≌△CDB(AAS),∴AF=BC,∵AP=BC,∴AP=AF,∴∠APF=∠F,∵∠APF=∠BPE,∠F=∠DBC,∴∠BPE=∠PBE,∴PE=BE.【点评】本题考查了等腰三角形的性质和判定,全等三角形的性质与判定,平行线的性质,解题关键是利用倍长中线构造全等三角形.14.(2020秋•田家庵区期末)(1)如图1,在△ABC中,AB=4,AC=6,AD是BC边上的中线,延长AD到点E使DE=AD,连接CE,使得AB、AC、2AD集中在△ACE中,利用三角形三边关系可得AD 的取值范围是 1<AD<5 ;(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF.求证:BE+CF>EF.【分析】(1)证明△CDE≌△BDA(SAS),推出CE=AB=4,在△ACE中,利用三角形的三边关系解决问题即可.(2)如图2中,延长ED到H,使得DH=DE,连接DH,FH.证明△BDE≌△CDH(SAS),推出BE =CH,再证明EF=FH,利用三角形的三边关系即可解决问题.【解答】(1)解:如图1中,∵CD=BD,AD=DE,∠CDE=∠ADB,∴△CDE≌△BDA(SAS),∴EC=AB=4,∵6﹣4<AE<6+4,∴2<2AD<10,∴1<AD<5,故答案为1<AD<5.(2)证明:如图2中,延长ED到H,使得DH=DE,连接DH,FH.∵BD=DC,∠BDE=∠CDH,DE=DH,∴△BDE≌△CDH(SAS),∴BE=CH,∵FD⊥EH.DE=DH,∴EF=FH,在△CFH中,CH+CF>FH,∵CH=BE,FH=EF,∴BE+CF>EF.【点评】本题属于综合题,考查了全等三角形的判定和性质,三角形的中线的性质,三角形的三边关系等知识,解题的关键是学会倍长中线,构造全等三角形解决问题,属于常考题型.15.(2020秋•饶平县校级期中)(1)如图,AD是△ABC的中线,AB=8,AC=6则AD的取值范围是 C A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7(2)在(1)问的启发下,解决下列问题:如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.【分析】(1)延长AD到点M,使DM=AD,连接BM,易证明△ADC≌△BDM,得到BM=AC;在△ABM中,根据三角形三边关系定理,得2<AM<14,即2<2AD<14,即可得出AD的范围;(2)利用(1)中△ADC≌△BDM,得出∠M=∠CAD,BM=AC,进而得出∠BMF=∠BFM即可得出答案.【解答】解:(1)延长AD到点M,使DM=AD,连接BM,∵AD=DM,BD=CD,∠ADC=∠MDB,∴△ADC≌△BDM,∴BM=AC,在△ABM中,根据三角形三边关系定理,得2<AM<14,即2<2AD<14,所以AD的范围是1<AD<7.故选:C.(2)∵△ADC≌△MDB,∴∠M=∠CAD,BM=AC,∵AE=EF,∴∠CAD=∠AFE,∵∠MFB=∠AFE,∴∠BMF=∠BFM,∴BM=BF,∴AC=BF.【点评】此题考查了三角形全等的判定方法;注意此题中的辅助线的作法.能够根据全等三角形的性质,把要求的线段和已知的线段转换到一该三角形,根据三角形的三边关系进行求解.16.(2020秋•岫岩县期中)阅读下面的题目及分析过程,并按要求进行证明.已知:如图,点E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等,因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.(1)现给出如下两种添加辅助线的方法,请任意选出其中一种,对原题进行证明.①如图1,延长DE到点F,使EF=DE,连接BF;②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G.(2)请你在图3中添加不同于上述的辅助线,并对原题进行证明.【分析】(1)①如图1,延长DE到点F,使EF=DE,连接BF,先判断出BE=CE,进而判断出△BEF≌△CED,得出BF=CD,∠F=∠CDE,再判断出AB=BF,即可得出结论;②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G,先判断出BE=CE,进而判断出△BEF≌△CEG,得出BF=CG,再判断出△BAF≌△CDG,即可得出结论;(2)如图3,过C点作CM∥AB,交DE的延长线于点M,先判断出BE=CE,进而判断出△BAE≌△CME(AAS),得出CM=AB,∠BAE=∠M,即可得出结论.【解答】证明:(1)①如图1,延长DE到点F,使EF=DE,连接BF,∵点E是BC的中点,∴BE=CE,在△BEF和△CED中,,∴△BEF≌△CED(SAS),∴BF=CD,∠F=∠CDE,∵∠BAE=∠CDE,∴∠BAE=∠F,∴AB=BF,∴AB=CD;②如图2,分别过点B、C作BF⊥DE,CG⊥DE,垂足分别为点F,G,∴∠F=∠CGE=∠CGD=90°,∵点E是BC的中点,∴BE=CE,在△BEF和△CEG中,,∴△BEF≌△CEG(AAS),∴BF=CG,在△BAF和△CDG中,,∴△BAF≌△CDG(AAS),∴AB=CD;(2)如图3,过C点作CM∥AB,交DE的延长线于点M,则∠BAE=∠EMC,∵E是BC中点,∴BE=CE,在△BAE和△CME中,,∴△BAE≌△CME(AAS),∴CM=AB,∠BAE=∠M,∵∠BAE=∠EDC,∴∠M=∠EDC,∴CM=CD,∴AB=CD.【点评】此题是三角形综合题,主要考查了全等三角形的判定和性质,对顶角相等,平行线的性质,构造出全等三角形是解本题的关键.。
三角形中线的定义:三角形顶点和对边中点的连线三角形中线的相关定理: 直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.中线中位线相关问题(涉及中点的问题)见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见.版块一 倍长中线【例1】 (2002年通化市中考题)在△ABC 中,9,5==AC AB ,则BC 边上的中线AD 的长的取值范围是什重点:主要掌握中线的处理方法,遇见中线考虑中线倍长法难点:全等三角形的综合运用重、难点知识点睛例题精讲中考要求第二讲全等三角形与中点问题么?【补充】已知:ABC ∆中,AM 是中线.求证:1()2AM AB AC <+. 【例2】 (2008年巴中市高中阶段教育学校招生考试)已知:如图,梯形ABCD 中,AD BC ∥,点E 是CD 的中点,BE 的延长线与AD 的延长线相交于点F .求证:BCE FDE ∆∆≌.【例3】 (浙江省2008年初中毕业生学业考试(湖州市)数学试卷)如图,在ABC ∆中,D 是BC 边的中点,F ,E 分别是AD 及其延长线上的点,CF BE ∥.求证:BDE CDF ∆∆≌.【例4】 如图,ABC ∆中,<AB AC ,AD 是中线.求证:<DAC DAB ∠∠.【例5】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.【例6】 如图所示,在ABC ∆和A B C '''∆中,AD 、A D ''分别是BC 、B C ''上的中线,且AB A B ''=,AC A C ''=,AD A D ''=,求证ABC A B C '''∆∆≌.【例7】 如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交EF 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.【例8】 已知AD 为ABC ∆的中线,ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>. 【例9】 在Rt ABC ∆中,90A ∠=︒,点D 为BC 的中点,点E 、F 分别为AB 、AC 上的点,且ED FD ⊥.以线段BE 、EF 、FC 为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形?【例10】 如图所示,在ABC ∆中,D 是BC 的中点,DM 垂直于DN ,如果2222BM CN DM DN +=+,求证()22214AD AB AC =+. 【例10】 (2008年四川省初中数学联赛复赛·初二组)在Rt ABC ∆中,F 是斜边AB 的中点,D 、E 分别在边CA 、CB 上,满足90DFE ∠=︒.若3AD =,4BE =,则线段DE 的长度为_________.【例11】 如图所示,90BAC DAE ∠=∠=︒,M 是BE 的中点,AB AC =,AD AE =,求证AM CD ⊥. 版块二、中位线的应用【例12】 AD 是ABC ∆的中线,F 是AD 的中点,BF 的延长线交AC 于E .求证:13AE AC =. 【例13】 如图所示,在ABC ∆中,AB AC =,延长AB 到D ,使BD AB =,E 为AB 的中点,连接CE 、CD ,求证2CD EC =.【例14】 已知:ABCD 是凸四边形,且AC <BD . E 、F 分别是AD 、BC 的中点,EF 交AC 于M ;EF 交BD 于N ,AC 和BD 交于G 点. 求证:∠GMN >∠GNM .【例15】 在ABC ∆中,90ACB ∠=︒,12AC BC =,以BC 为底作等腰直角BCD ∆,E 是CD 的中点,求证:AE EB ⊥且AE BE =.【例16】 如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.【例17】 (“祖冲之杯”数学竞赛试题,中国国家集训队试题)如图所示,P 是ABC ∆内的一点,PAC PBC ∠=∠,过P 作PM AC ⊥于M ,PL BC ⊥于L ,D 为AB 的中点,求证DM DL =.【例18】 (全国数学联合竞赛试题) 如图所示,在ABC ∆中,D 为AB 的中点,分别延长CA 、CB 到点E 、F ,使DE DF =.过E 、F 分别作直线CA 、CB 的垂线,相交于点P ,设线段PA 、PB 的中点分别为M 、N .求证:(1) DEM FDN ∆∆≌;(2) PAE PBF ∠=∠.【例19】 已知,如图四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点. 求证:AME BNE ∠=∠.【例20】 (2009年大兴安岭地区初中毕业学业考试)已知:在ABC ∆中,BC AC >,动点D 绕ABC ∆ 的顶点A 逆时针旋转,且AD BC =,连结DC .过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N .⑴ 如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、HF ,根据三角形中位线定理和平行线的性质,可得结论AMF BNE ∠=∠(不需证明).⑵ 当点D 旋转到图2或图3中的位置时,AMF ∠与BNE ∠有何数量关系?请分别写出猜想,并任选一种情况证明. 【例21】 如图,AE ⊥AB ,BC ⊥CD ,且AE =AB ,BC =CD ,F 为DE 的中点,FM ⊥AC .证明:FM =12AC . 【例22】 (1991年泉州市初二数学双基赛题)已知:在△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形ABM ,和CAN ,P 是边BC 的中点.求证:PM =PN【习题1】 如图,在等腰ABC ∆中,AB AC =,D 是BC 的中点,过A 作AE DE ⊥,AF DF ⊥,且AE AF =.求证:EDB FDC ∠=∠.【习题2】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,AF 与EF 相等吗?为什么?【习题3】 如右下图,在ABC ∆中,若2B C ∠=∠,AD BC ⊥,E 为BC 边的中点.求证:2AB DE =.【备选1】如图,已知AB =DC ,AD =BC ,O 是BD 中点,过O 点的直线分别交DA 、BC 的延长线于E ,F .求证:∠E =∠F【备选2】如图,ABC ∆中,AB AC =,90BAC ∠=︒,D 是BC 中点,ED FD ⊥,ED 与AB 交于E ,FD 与AC交于F .求证:BE AF =,AE CF =. 月测备选 家庭作业。
初中数学全等专题倍长中线法1。
如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是()A。
2<AB<12 B。
4<AB<12 C。
9<AB<19 D.10<AB<19 答案:C解题思路:延长AD至E,使DE=AD,连接CE,可先证明△ABD≌△ECD,则AB=CE,在△ACE 中,根据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19。
故选C.2.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④ B。
①③④ C。
①②③ D。
①②③④ 答案:A解题思路:①正确,延长CD至点F,使得DF=CD,连接AF,可先证明△ADF≌△BDC,再证明△ACF≌△BEC,由这两个三角形全等可以得知②、④正确.由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项错误3.如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF,则下列说法正确的是()①BF∥CD ②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形A.①②③ B.②③④ C.①③④ D。
①②③④ 答案:A解题思路:可以先证明△BEF≌△CED,可以得到②正确,进而得到∠F=∠D,BF∥CD,①正确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③正确.④不正确。
4。
如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()A。
1 B。
2 C。
3 D.4 答案:C解题思路:延长FE交DA的延长线于点M,则可证△AEM≌△BEF,再证明△GEM≌△GEF,可以得到GF=GM=GA+BF=3,答案选C5.如图,在△ABC中,点D、E为边BC的三等分点,则下列说法正确的有()①BD=DE=EC ②AB+AE>2AD ③AD+AC>2AE ④AB+AC>AD+AE A。
第二讲
全等三角形与
中点问题
中考要求
知识点睛
三角形中线的定义:三角形顶点和对边中点的连线
三角形中线的相关定理:直角三角形斜边的中线等于斜边的一半
等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)
三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.
中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.
中线中位线相关问题(涉及中点的问题)
见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见.
版块一 倍长中线
【例1】 (2002年通化市中考题)在△ABC 中,9,5==AC AB ,则BC 边上的中线AD 的长的取值范围是
什么?
【补充】已知:ABC ∆中,AM 是中线.求证:1
()2
AM AB AC <+.
M
C
B
A
【例2】 (2008年巴中市高中阶段教育学校招生考试)已知:如图,梯形ABCD 中,AD BC ∥,点E 是CD 的
中点,BE 的延长线与AD 的延长线相交于点F .求证:BCE FDE ∆∆≌.
重点:主要掌握中线的处理方法,遇见中线考虑中线倍长法
重、难点
例题精讲
D
F
E
C
B
A
【例3】 (浙江省2008年初中毕业生学业考试(湖州市)数学试卷)如图,在ABC ∆中,D 是BC 边的中点,F ,
E 分别是AD 及其延长线上的点,C
F BE ∥.求证:BDE CDF ∆∆≌.
F
E
D
C
B
A
【例4】 如图,ABC ∆中,<AB AC ,AD 是中线.求证:<DAC DAB ∠∠.
G
F
E
D
C
B
A
【例5】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,
求证:AC BE =.
F
E
D
C B
A
【例6】 如图所示,在ABC ∆和A B C '''∆中,AD 、A D ''分别是BC 、B C ''上的中线,且AB AB
''=,AC A C ''=,AD A D ''=,求证ABC A B C '''∆∆≌.
E
D
C
A
B
B'
A'
C'
D'
E'
【例7】 如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交EF
于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.
F G
E D
C
B
A
【例8】 已知AD 为ABC ∆的中线,ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F .求证:
BE CF EF +>.
F
E A
B D C
【例9】 在Rt ABC ∆中,90A ∠=︒,点D 为BC 的中点,点E 、F 分别为AB 、AC 上的点,且ED FD ⊥.以
线段BE 、EF 、FC 为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形?
F E
D
C
B
A
【例10】 如图所示,在ABC ∆中,D 是BC 的中点,DM 垂直于DN ,如果2222BM CN DM DN +=+,求证
()2221
4
AD AB AC =+.
N
M
D
C
B
A
【例10】(2008年四川省初中数学联赛复赛·初二组)在Rt ABC
∆中,F是斜边AB的中点,D、E分别在边CA、CB上,满足90
DFE
∠=︒.若3
AD=,4
BE=,则线段DE的长度为_________.
【例11】如图所示,90
BAC DAE
∠=∠=︒,M是BE的中点,AB AC
=,AD AE
=,求证AM CD
⊥.
M
E C
B
A 版块二、中位线的应用
【例12】AD是ABC
∆的中线,F是AD的中点,BF的延长线交AC于E.求证:
1
3
AE AC
=.
F
A D
E C
B
【例13】 如图所示,在ABC ∆中,AB AC =,延长AB 到D ,使BD AB =,E 为AB 的中点,连接CE 、CD ,
求证2CD EC =.
E
D
C
B A
【例14】 已知:ABCD 是凸四边形,且AC <BD . E 、F 分别是AD 、BC 的中点,EF 交AC 于M ;EF 交BD
于N ,AC 和BD 交于G 点. 求证:∠GMN >∠GNM .
H
A
B
G N
M F
E
D
C B
A
【例15】 在ABC ∆中,90ACB ∠=︒,1
2
AC BC =
,以BC 为底作等腰直角BCD ∆,E 是CD 的中点,求证:AE EB ⊥且AE BE =.
E
D
C
B
A
【例16】 如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.
E
D
F
C
B
A
【例17】 (“祖冲之杯”数学竞赛试题,中国国家集训队试题)如图所示,P 是ABC ∆内的一点,
PAC PBC ∠=∠,过P 作PM AC ⊥于M ,PL BC ⊥于L ,D 为AB 的中点,求证D M D L =.
L
P
M
D C
B
A
【例18】(全国数学联合竞赛试题) 如图所示,在ABC
∆中,D为AB的中点,分别延长CA、CB到点E、F,使DE DF
=.过E、F分别作直线CA、CB的垂线,相交于点P,设线段PA、PB的中点分别为M、N.求证:
(1) DEM FDN
∆∆
≌;
(2) PAE PBF
∠=∠.
P F
E
D
C
B A
【例19】已知,如图四边形ABCD中,AD BC
=,E、F分别是AB和CD的中点,AD、EF、BC的延长线分别交于M、N两点.求证:AME BNE
∠=∠.
A
C D
M
F
E
N
B
【例20】(2009年大兴安岭地区初中毕业学业考试)已知:在ABC
∆中,BC AC
>,动点D绕ABC
∆的顶点A逆时针旋转,且AD BC
=,连结DC.过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N.
F
图3
图2
图1
F N M
D
C
E B A
N
M
D
C
E B
A
H
F (N )D
M C E B
A
⑴ 如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、
HF ,根据三角形中位线定理和平行线的性质,可得结论AMF BNE ∠=∠(不需证明).
⑵ 当点D 旋转到图2或图3中的位置时,AMF ∠与BNE ∠有何数量关系?请分别写出猜想,并任选一种情况证明.
【例21】 如图,AE ⊥AB ,BC ⊥CD ,且AE =AB ,BC =CD ,F 为DE 的中点,FM ⊥AC .证明:FM =
1
2
AC . H
A
E
M
F
E
D
C B
A
【例22】 (1991年泉州市初二数学双基赛题)已知:在△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形
ABM ,和CAN ,P 是边BC 的中点.求证:PM =PN
N
M
P
B
A
【习题1】 如图,在等腰ABC ∆中,AB AC =,D 是BC 的中点,过A 作AE DE ⊥,AF DF ⊥,且AE AF =.
求证:EDB FDC ∠=∠.
D
F
E
C
B
A
【习题2】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于
F ,AF 与EF 相等吗?为什么?
F
E
D C
B
A
【习题3】 如右下图,在ABC ∆中,若2B C ∠=∠,AD BC ⊥,E 为BC 边的中点.求证:2AB DE =.
家庭作业
【备选1】如图,已知AB =DC ,AD =BC ,O 是BD 中点,过O 点的直线分别交DA 、BC 的延长线于E ,F .
求证:∠E =∠F
【备选2】如图,ABC ∆中,AB AC =,90BAC ∠=︒,D 是BC 中点,ED FD ⊥,ED 与AB 交于E ,FD 与
AC 交于F .求证:BE AF =,AE CF =.
A
B
C
D
E F
月测备选。