求值域经典例题

函数值域的求法在函数概念的三要素中，定义域和对应法则是最基本的，值域是由定义域和对应法则所确定，因此，研究值域仍应注重函数对应法则的作用和定义域对值域的制约，以下试举例说明常用方法.[例1]：求下列函数的值域 (1)y ＝1－2x （x ∈R ） (2)y ＝｜x ｜－1 x ∈{－2，－1，0，1，2} (3)y ＝x 2＋4x ＋3 （－3≤x ≤1） (4)y ＝｜x ＋1｜－｜x －2｜(5)y ＝2x －3＋134-x(6)y ＝2224)1(5+++x x x(7)y ＝521+-x x(8)y ＝1223222++--x x x x(9)y ＝3－2x －x 2x ∈[－3，1](10)y ＝21322+-x x分析：求函数的值域应确定相应的定义域后再根据函数的具体形式及运算确定其值域. 对于(1)(2)可用“直接法”根据它们的定义域及对应法则得到(1)(2)的值域. 对于(3)(4)可借助数形结合思想利用它们的图象得到值域，即“图象法”. 对于(5)(6)可借用整体思想利用“换元法”求得值域.对于(7)可将其分离出一个常数，即利用“分离常数法”求得它的值域. 对于(8)可通过对“Δ”的分析，即利用“判别式”法求得其值域.对于(9)(10)可“通过中间函数的值域去求所求函数的值域”这一方法即“中间媒介法”求得其值域.解：(1)y ∈R(2)y ∈{1，0，－1}(3)画出y ＝x 2＋4x ＋3（－3≤x ≤1）的图象，如图所示，当x ∈[－3，1]时，得y ∈[－1，8](4)对于y ＝｜x ＋1｜－｜x －2｜的理解，从几何意义入手，即利用绝对值的几何意义可知，｜x ＋1｜表示在数轴上表示x 的点到点－1的距离，｜x －2｜表示在数轴上表示x 的点到点2的距离，在数轴上任取三个点x A ≤－1，－1＜x B ＜2，x C ≥c ，如图所示，可以看出｜x A ＋1｜－｜x A －2｜＝－3－3＜｜x B ＋1｜－｜x B －2｜＜3，｜x C ＋1｜－｜x C －2｜＝3，由此可知，对于任意实数x ，都有－3≤｜x ＋1｜－｜x －2｜≤3所以函数y ＝｜x ＋1｜－｜x －2｜的值域为y ∈[－3，3](5)对于没有给定自变量的函数，应先考查函数的定义域，再求其值域.∵4x －13≥0 ∴x ∈[413，＋∞)令t ＝134-x 则得：x ＝4132+t∴y ＝21t 2＋t ＋27∴y ＝21（t ＋1）2＋3∵x ≥413∴t ≥0根据二次函数图象可得y ∈[27，＋∞)(6)∵函数定义域为x ∈R 由原函数可化得：y ＝22222224)1(5)1()1(5+++=+++x x x x x x＝2222222222)1(11)1(5)1()1(5+-+++=+++x x x x x x ＝111)1(5222++-+x x 令t ＝112+x∵x ∈R ∴t ∈(0，1] ∴y ＝5t 2－t ＋1＝5（t －101）2＋2019根据二次函数的图象得当t ＝101时y min ＝2019当t ＝1时，y max ＝5 ∴函数的值域为y ∈[2019，5](7)∵y ＝－21＋5227+x∵5227+x ≠0 ∴y ≠－21∴函数y 的值域为y ∈（－∞，－21）∪（－21，＋∞） (8)由y ＝1223222++--x x x x 得x ∈R 且可化为：（2y －1）x 2＋2（y ＋1）x ＋（y ＋3）＝0 ∴当y ≠21时，Δ＝[2（y ＋1）]2－4（2y －1）（y ＋3）≥0 ∴y 2＋3y －4≤0 ∴－4≤y ≤1且y ≠21 又当y ＝21时，2（1＋21）x ＋（21＋3）＝0 得：x ＝－67，满足条件∴函数的值域为y ∈[－4，1] (9)∵－3≤x ≤1 ∴－2≤x ＋1≤2∴｜x ＋1｜≤2即（x ＋1）2≤4∴y ＝3－2x －x 2＝－（x ＋1）2＋4∈[0，4] ∴函数值域为y ∈[0，4](10)由y ＝21322+-x x 可知，x ∈R 且yx 2＋2y ＝3x 2－1即（3－y ）x 2＝2y ＋1若y ＝3时，则有0＝7，这是不可能的. ∴y ≠3 得：x 2＝y y -+312 ∵x 2≥0 ∴yy -+312≥0 解得：－21≤y ＜3 ∴函数值域为y ∈[－21，3) 评述：（1）求函数的值域是一个相当复杂的问题，它没有现成的方法可套用，要结合函数表达式的特征，以及与所学知识联系，灵活地选择恰当的方法.（2）对于以上例题也可以采取不同的方法求解每一个值域，请读者不妨试一试.（3）除以上介绍的方法求函数值域外，随着学生的继续学习，我们今后还会有“反函数”法、“单调性”法、“三角换元”法、“不等式”法及“导数法”等.二、二次函数（含参数）在区间上的值域问题 [例2]、求下列函数的值域 （1）]1,0(1222∈-++=x a ax x y（2）]1,[142+∈++=t t x x x y三、含参数的其他值域问题［例3］已知函数f (x )=xax x ++22,x ∈［1,+∞)(1)当a =21时，求函数f (x )的最小值.(2)若对任意x ∈［1,+∞),f (x )>0恒成立，试求实数a 的取值范围.知识依托：本题主要通过求f (x )的最值问题来求a 的取值范围，体现了转化的思想与分类讨论的思想.错解分析：考生不易考虑把求a 的取值范围的问题转化为函数的最值问题来解决.技巧与方法：解法一运用转化思想把f (x )>0转化为关于x 的二次不等式；解法二运用分类讨论思想解得.(1)解：当a =21时，f (x )=x +x21+2∵f (x )在区间［1，+∞)上为增函数，∴f (x )在区间［1，+∞)上的最小值为f (1)=27.(2)解法一：在区间［1，+∞)上，f (x )=xax x ++22 >0恒成立⇔x 2+2x +a >0恒成立.设y =x 2+2x +a ,x ∈［1,+∞)∵y =x 2+2x +a =(x +1)2+a －1递增，∴当x =1时，y min =3+a ,当且仅当y min =3+a >0时，函数f (x )>0恒成立，故a >－3.解法二：f (x )=x +xa+2,x ∈［1,+∞)当a ≥0时，函数f (x )的值恒为正；当a <0时，函数f (x )递增，故当x =1时，f (x )min =3+a ,当且仅当f (x )min =3+a >0时，函数f (x )>0恒成立，故a >－3.练习一、选择题1.函数y =x 2+x1(x ≤－21)的值域是( )A.(－∞,－47]B.［－47,+∞)C.［2233,+∞)D.(－∞,－3223］2.函数y =x +x 21-的值域是( )A.(－∞,1] B.(－∞,－1]C.RD.［1,+∞)一、1.解析：∵m 1=x 2在(－∞,－21）上是减函数，m 2=x1在(－∞,－21）上是减函数， ∴y =x 2+x1在x ∈(－∞,－21)上为减函数,∴y =x 2+x1(x ≤－21)的值域为［－47，+∞).答案：B2.解析：令x 21-=t (t ≥0),则x =212t -.∵y =212t -+t =－21 (t －1)2+1≤1∴值域为(－∞,1].。

函数值域1基本初等函数的值域(1)y=kx+b(k≠0)的值域是R.；当a<0时，值域为(2)y=ax2+bx+c(a≠0)的值域是：当a>0时，值域为y y≥4ac−b24a．y y≤4ac−b24a.(3)y=k x(k≠0)的值域是y y≠0(4)y=a x(a>0且a≠1)的值域是(0，+∞).(5)y=log a x(a>0且a≠1)的值域是R.2函数值域的求解方法方法归纳观察法根据最基本函数值域(如x2≥0,a x>0及函数的图像、性质、简单的计算、推理，凭观察能直接得到些简单的复合函数的值域.方法归纳配方法对于形如y=ax2+bx+c a≠0的值域问题可充分利用二次函数可配方的特点，结合二次函数的定义城求出函数的值域.方法归纳图像法(数形结合)根据所给数学式子的特征，构造合适的几何模型.方法归纳基本不等式法注意使用基本不等式的条件，即一正、二定、三相等.方法归纳换元法(代数换元与三角换元)分为三角换元法与代数换元法，对于形y=ax+b+cx+d的值城，可通过换元将原函数转化为二次型函数.方法归纳分离常数法对某些齐次分式型的函数进行常数化处理，使函数解析式简化内便于分析.方法归纳判别式法把函数解析式化为关于x的-元二次方程，利用一元二次方程的判别式求值域，一般地，形如y=Ax+博观而约取 厚积而薄发B ，ax 2+bx +c 或y =ax 2+bx +cd x 2+ex +f的函数值域问题可运用判别式法(注意x 的取值范围必须为实数集R ).方法归纳单调性法先确定函数在定义域(或它的子集)内的单调性，再求出值域.对于形如y =ax +b +cx +d 或y =ax +b +cx +d 的函数，当ac >0时可利用单调性法.方法归纳有界性法充分利用三角函数或一些代数表达式的有界性，求出值域.因为常出现反解出y 的表达式的过程，故又常称此为反解有界性法.方法归纳导数法先利用导数求出函数的极大值和极小值，再确定最大(小)值，从而求出函数的值域.1.例题精讲题型一:观察法1函数y =1x +1-1的值域是( )A.-∞,-1B.+1,+∞C.-∞,-1 ∪-1,+∞D.-∞,+∞2下列函数中，值域为0,+∞ 的是( )A.y =x 2B.y =2xC.y =2xD.y =log 2x3下列函数中，函数值域为(0,+∞)的是( )A.y =(x +1)2,x ∈(0,+∞) B.y =log 2x ,x ∈(1,+∞)C.y =2x -1D.y =2x -1题型二:配方法1函数的y =-x 2-6x -5值域为()A.0,+∞B.0,2C.2,+∞D.2,+∞2函数y =f x 的图象是如图所示的折线段OAB ，其中A 1,2 ，B 3,0 ，函数g x =x ⋅f x ，那么函数g x 的值域为()Ox y 213ABA.0,2B.0,94C.0，32D.0,43已知正实数a ，b ，c 满足2a +b =1，abc +1=2c ，则c 的最大值为()A.12B.23C.815D.2题型三:图像法(数形结合)数形结合：即作出函数的图像，通过观察曲线所覆盖函数值的区域确定值域，以下函数常会考虑进行数形结合(1)分段函数：尽管分段函数可以通过求出每段解析式的范围再取并集的方式解得值域，但对于一些便于作图的分段函数，数形结合也可很方便的计算值域。

一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(根据算术平方根的性质，先求出√(2－3x) 的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√知域为. 点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=( y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函或y&gt;1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4] ∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2] 点评：关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=案:值域为{y∣y≤3})四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法函数y=(2x2－2x+3)/(x2－x+1)的值域。

点拨：将原函数转化为自变量的二次方程，应用二次方程根的判别式解：将上式化为（y－2）x2－(y－2)x+(y-3)=0 （＊）当y≠2时,由Δ=(y－2)2－4（＜x≤10/3当y=2时,方程(＊)无解。

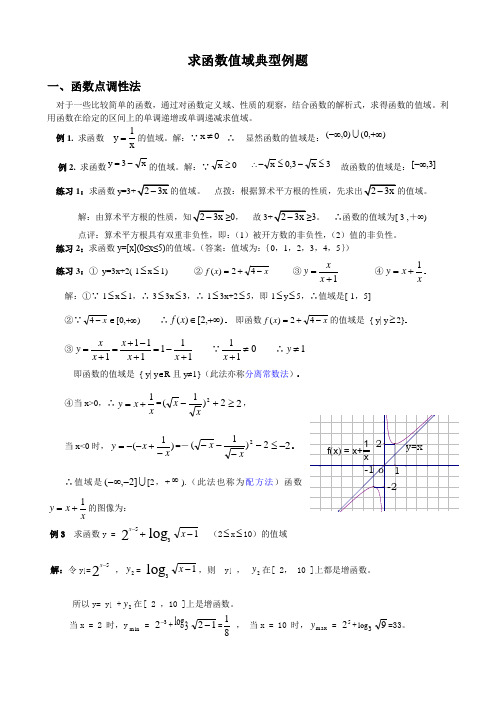
求函数值域典型例题一、函数点调性法对于一些比较简单的函数，通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

利用函数在给定的区间上的单调递增或单调递减求值域。

例1. 求函数1y x=的值域。

解：∵0x ≠ ∴ 显然函数的值域是：),0()0,(+∞-∞例2. 求函数x 3y -=的值域。

解：∵0x ≥ 3x 3,0x ≤-≤-∴ 故函数的值域是：]3,[-∞ 练习1：求函数， 故。

∴函数的值域为[ 3 ,＋∞) 点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

练习2：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝） 练习3：① y=3x+2(-1≤x ≤1) ②x x f -+=42)( ③1+=x x y ④xx y += 解：①∵-1≤x ≤1，∴-3≤3x ≤3，∴-1≤3x+2≤5，即-1≤y ≤5，∴值域是[-1，5]②∵),0[4+∞∈-x ∴,2[)(+∞∈x f 即函数x x f -+=42)(的值域是 { y| y ≥2}③1111111+-=+-+=+=x x x x x y ∵011≠+x ∴1≠y即函数的值域是 { y| y ∈R 且y ≠1}（此法亦称分离常数法） ④当x>0，∴x x y 1+==2)1(2+-xx 2≥， 当x<0时，)1(x x y -+--==－2)1(2----xx -≤ ∴值域是 ]2,(--∞[2，+∞).（此法也称为配方法）函数xx y 1+=的图像为：例3 求函数y =+-25x log31-x （2≤x ≤10）的值域解：令y 1=25-x ，2y =log31-x ，则 y 1 ， 2y 在[ 2， 10 ]上都是增函数。

所以y= y 1 +2y 在[ 2 ，10 ]上是增函数。

当x = 2 时，y m in = 32-+log 312-=81， 当x = 10 时，m ax y = 52+log 39=33。

之袁州冬雪创作高中函数值域和定义域的大小,是高中数学常考的一个知识点,本文先容了函数求值域最常常使用的九种方法和例题讲解.一．观察法通过对函数定义域、性质的观察，连系函数的解析式，求得函数的值域. 例1求函数y=3+√(2－3x)的值域.点拨：根据算术平方根的性质，先求出√(2－3x)的值域.解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3.∴函数的知域为.点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性.本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷了然，不失为一种巧法.操练：求函数y=[x](0≤x≤5)的值域.（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域.例2求函数y=(x+1)/(x+2)的值域.点拨：先求出原函数的反函数，再求出其定义域.解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝.点评：操纵反函数法求原函数的定义域的前提条件是原函数存在反函数.这种方法体现逆向思维的思想，是数学解题的重要方法之一.操练：求函数y=(10x+10-x)/(10x－10-x)的值域.（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以操纵配方法求函数值域例3：求函数y=√(－x2+x+2)的值域.点拨：将被开方数配方成完全平方数，操纵二次函数的最值求.解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2].此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不单要重视对应关系的应用,而且要特别注意定义域对值域的制约作用.配方法是数学的一种重要的思想方法.操练：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四．辨别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用辨别式法求函数的值域.例4求函数y=(2x2－2x+3)/(x2－x+1)的值域.点拨：将原函数转化为自变量的二次方程，应用二次方程根的辨别式，从而确定出原函数的值域.解：将上式化为（y－2）x2－(y－2)x+(y-3)=0（＊）当y≠2时,由Δ=(y－2)2－4（y－2）x+(y－3)≥0，解得：2＜x≤10/3当y=2时,方程(＊)无解.∴函数的值域为2＜y≤10/3.点评：把函数关系化为二次方程F(x,y)=0，由于方程有实数解，故其辨别式为非负数，可求得函数的值域.常适应于形如y=(ax2+bx+c)/(dx2+ex+f)及y=ax+b±√(cx2+dx+e)的函数.操练：求函数y=1/(2x2－3x+1)的值域.（答案：值域为y≤－8或y>0）.五．最值法对于闭区间[a,b]上的持续函数y=f(x),可求出y=f(x)在区间[a,b]内的极值,并与鸿沟值f(a).f(b)作比较,求出函数的最值,可得到函数y的值域.例5已知(2x2-x-3)/(3x2+x+1)≤0,且知足x+y=1,求函数z=xy+3x的值域.点拨：根据已知条件求出自变量x的取值范围，将方针函数消元、配方，可求出函数的值域.解：∵3x2+x+1＞0，上述分式不等式与不等式2x2-x-3≤0同解，解之得－1≤x≤3/2，又x+y=1，将y=1-x 代入z=xy+3x中，得z=-x2+4x(-1≤x≤3/2),∴z=-(x-2)2+4且x∈[-1,3/2],函数z在区间[-1,3/2]上持续，故只需比较鸿沟的大小.当x=-1时，z=－5；当x=3/2时，z=15/4.∴函数z的值域为｛z∣－5≤z≤15/4｝.点评：本题是将函数的值域问题转化为函数的最值.对开区间，若存在最值，也可通过求出最值而获得函数的值域.操练：若√x为实数，则函数y=x2+3x-5的值域为（）A．（－∞，＋∞）B．[－7，＋∞]C．[0，＋∞）D．[－5，＋∞）（答案：D）.六．图象法通过观察函数的图象，运用数形连系的方法得到函数的值域.例6求函数y=∣x+1∣+√(x-2)2的值域.点拨：根据相对值的意义，去掉符号后转化为分段函数，作出其图象.解：原函数化为－2x+1(x≤1)y=3(-1<x≤2)2x-1(x>2)它的图象如图所示.显然函数值y≥3,所以，函数值域[3，＋∞].点评：分段函数应注意函数的端点.操纵函数的图象求函数的值域，体现数形连系的思想.是处理问题的重要方法.求函数值域的方法较多，还适应通过不等式法、函数的单调性、换元法等方法求函数的值域七．单调法操纵函数在给定的区间上的单调递增或单调递减求值域.例1求函数y=4x－√1-3x(x≤1/3)的值域.点拨：由已知的函数是复合函数，即g(x)=－√1-3x,y=f(x)+g(x)，其定义域为x≤1/3，在此区间内分别讨论函数的增减性，从而确定函数的值域.解：设f(x)=4x,g(x)=－√1-3x,(x≤1/3),易知它们在定义域内为增函数，从而y=f(x)+g(x)=4x－√1-3x 在定义域为x≤1/3上也为增函数，而且y≤f(1/3)+g(1/3)=4/3,因此，所求的函数值域为｛y|y≤4/3｝.点评：操纵单调性求函数的值域，是在函数给定的区间上，或求出函数隐含的区间，连系函数的增减性，求出其函数在区间端点的函数值，进而可确定函数的值域.操练：求函数y=3+√4-x的值域.(答案：｛y|y≥3｝)八．换元法以新变量代替函数式中的某些量，使函数转化为以新变量为自变量的函数形式，进而求出值域.例2求函数y=x-3+√2x+1的值域.点拨：通过换元将原函数转化为某个变量的二次函数，操纵二次函数的最值，确定原函数的值域.解：设t=√2x+1（t≥0）,则x=1/2(t2-1).于是y=1/2(t2-1)-3+t=1/2(t+1)2-4≥1/2-4=-7/2.所以，原函数的值域为｛y|y≥－7/2｝.点评：将无理函数或二次型的函数转化为二次函数，通过求出二次函数的最值，从而确定出原函数的值域.这种解题的方法体现换元、化归的思想方法.它的应用十分广泛.操练：求函数y=√x-1–x的值域.（答案：｛y|y≤－3/4｝九．构造法根据函数的布局特征，赋予几何图形，数形连系.例3求函数y=√x2+4x+5+√x2-4x+8的值域.点拨：将原函数变形，构造平面图形，由几何知识，确定出函数的值域.解：原函数变形为f(x)=√(x+2)2+1+√(2-x)2+22作一个长为4、宽为3的矩形ABCD，再切割成12个单位正方形.设HK=x,则ek=2-x,KF=2+x,AK=√(2-x)2+22,KC=√(x+2)2+1.由三角形三边关系知，AK+KC≥AC=5.当A、K、C三点共线时取等号.∴原函数的知域为｛y|y≥5｝.点评：对于形如函数y=√x2+a±√(c-x)2+b(a,b,c 均为正数)，都可通过构造几何图形，由几何的性质，直观了然、方便简捷.这是数形连系思想的体现.操练：求函数y=√x2+9+√(5-x)2+4的值域.（答案：｛y|y≥5√2｝）以上九种是函数求值域最常常使用的方法,下面先容三种特殊情况下求值域的几种方法.十．比例法对于一类含条件的函数的值域的求法，可将条件转化为比例式，代入方针函数，进而求出原函数的值域.例4已知x,y∈R，且3x-4y-5=0,求函数z=x2+y2的值域.点拨：将条件方程3x-4y-5=0转化为比例式，设置参数，代入原函数.解：由3x-4y-5=0变形得，(x3)/4=(y-1)/3=k(k为参数)∴x=3+4k,y=1+3k,∴z=x2+y2=(3+4k)2+(14+3k)2=(5k+3)2+1.当k=－3/5时，x=3/5,y=－4/5时，zmin=1函数的值域为｛z|z≥1｝.点评：本题是多元函数关系，一般含有约束条件，将条件转化为比例式，通过设参数，可将原函数转化为单函数的形式，这种解题方法体现诸多思想方法，具有一定的创新意识.操练：已知x,y∈R，且知足4x-y=0,求函数f(x,y)=2x2-y的值域.（答案：｛f(x,y)|f(x,y)≥1｝）十一．操纵多项式的除法例5求函数y=(3x+2)/(x+1)的值域.点拨：将原分式函数，操纵长除法转化为一个整式与一个分式之和.解：y=(3x+2)/(x+1)=3－1/(x+1).∵1/(x+1)≠0，故y≠3.∴函数y的值域为y≠3的一切实数.点评：对于形如y=(ax+b)/(cx+d)的形式的函数都可操纵这种方法.操练：求函数y=(x2-1)/(x-1)(x≠1)的值域.（答案：y≠2）十二．不等式法例6求函数Y=3x/(3x+1)的值域.点拨：先求出原函数的反函数，根据自变量的取值范围，构造不等式.解：易求得原函数的反函数为y=log3[x/(1-x)],由对数函数的定义知x/(1-x)＞01-x≠0解得，0＜x<1.∴函数的值域（0，1）.点评：考察函数自变量的取值范围构造不等式（组）或构造重要不等式，求出函数定义域，进而求值域.不等式法是重要的解题工具，它的应用非常广泛.是数学解题的方法之一.。

通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x)的值域。

点拨：根据算术平方根的性质，先求出√(2－3x)的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为.点评：算术xx具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－）2＋∈[0，∴0≤√－x2+x+2≤函数的值域是点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

12一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x) 的值域。

点拨：根据算术平方根的性质，先求出√(2－3x) 的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为.点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

专题13：函数的定义域与值域求法典型例题（解析版）函数定义域的常见其一、已知函数解析式型即给出函数的解析式的定义域求法，其解法是由解析式有意义列出关于自变量的不等式或不等式组，解此不等式（或组）即得原函数的定义域。

例1、求函数yx 2 2x 15的定义域。

x 3 82 x 5或x3 x 2x 15 0解：要使函数有意义，则必须满足即 x 5且x 11 x 3 8 0解得x 5或x 3且x 11即函数的定义域为x x 5或x 3且x 11 。

二、抽象函数型抽象函数是指没有给出解析式的函数，不能用常规方法求解，一般表示为已知一个抽象函数的定义域求另一个抽象函数的定义域，一般有两种情况。

（一）已知f (x )的定义域，求f g (x ) 的定义域。

其解法是：已知f (x )的定义域是[a ,b ]求f g (x ) 的定义域是解a g (x ) b ，即为所求的定义域。

例2、已知f (x )的定义域为[ 2,2]，求f (x 1)的定义域。

2解： 2 x 2， 2 x 1 2，解得 3 x 23即函数f (x 1)的定义域为x 3 x 3（二）已知fg (x ) 的定义域，求f (x )的定义域。

2其解法是：已知f g (x ) 的定义域是[a ,b ]求f (x )的定义域的方法是：a x b ，求g (x )的值域，即所求f (x )的定义域。

例3、已知f (2x 1)的定义域为[1,2]，求f (x )的定义域。

解： 1 x 2， 2 2x 4， 3 2x 1 5。

即函数f (x )的定义域是x |3 x 5 。

三、逆向思维型即已知所给函数的定义域求解析式中参数的取值范围。

特别是对于已知定义域为R ,求参数的范围问题通常是转化为恒成立问题来解决。

例4、已知函数ymx 2 6mx m 8的定义域为R 求实数m 的取值范围。

22分析：函数的定义域为R ，表明mx 6mx m 8 0，使一切x R 都成立，由x 项的系数是m ，所以应分m 0或m 0进行讨论。

一．观察法:通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域.例1:求函数)+=的值域.y-3x32(点拨：根据算术平方根的性质，先求出)-的值域.32(x解：由算术平方根的性质，知)2(x-≥3。

∴函数的值域为)3-≥0，故3+)2(x3,3[+∞ .点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法:当函数的反函数存在时，则其反函数的定义域就是原函数的值域.例2:求函数y=(x+1)/(x+2)的值域.点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数, 故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法:当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域. 例3：求函数y=√(－x2+x+2)的值域.点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四.判别式法:若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

函数值域的求法(精选例题)函数值域的求法1.观察法1) 求函数 $y_1=\dfrac{1}{x^2+1}$ 的值域为 $(0,1]$。

2) 求函数 $y_1=2-x$ 的值域为 $(-\infty,2]$。

2.配方法1) 求函数 $y=x^2-2x+5$，其中 $x\in[-1,2]$ 的值域为$[4,8]$。

2) 求函数 $y=-x^2-6x-5$ 的值域为 $[-\dfrac{23}{4},2]$。

3) 已知 $x,y$ 是关于 $m$ 的方程 $m^2-2am+a+6=0$ 的根，则 $(x-1)^2+(y-1)^2$ 的最小值为 $-\dfrac{12}{4}$。

3.换元法1) 求函数 $y=2x+1+\dfrac{1}{x-1}$ 的值域为 $[3,+\infty)$。

2) 求函数 $y=\dfrac{x+2}{x+3}$ 的值域为 $[1,2)$。

3) 求函数 $y=x^3-x$ 的值域为 $[0,+\infty)$。

4) 求函数 $y=x+1-x$ 的值域为 $(-\infty,+\infty)$。

5) 求函数 $y=\dfrac{x^3-x}{x^4+2x^2+1}$ 的值域为$[0,1]$。

4.分离常数法1) 求函数 $y=\dfrac{x-1}{x+2}$，其中 $x\geq -4$，的值域为 $(-\infty,1]\cup[\dfrac{5}{2},+\infty)$。

2) 求函数 $y=\dfrac{x^2-x+1}{x^2+1}$ 的值域为 $[-\dfrac{1}{3},1]$。

5.判别式法1) 求函数 $y=\dfrac{2x^2-x+2}{x^2+x+1}$ 的值域为$[1,5]$。

2) 求函数 $y=\dfrac{2x^2+4x-7}{x^2+2x-9}$ 的值域为 $[-\dfrac{9}{32},2)$。

3) 已知函数$f(x)=\dfrac{x+a}{x^2+1}$ 的值域为$[1,3]$，求实数 $a,b$ 的值，其中 $a=2$ 或 $a=-2$，$b=6$。

通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x) 的值域。

点拨：根据算术平方根的性质，先求出√(2－3x) 的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为 .点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

函数求值域最常用的九种方法和例题讲解.一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x)的值域。

点拨：根据算术平方根的性质，先求出√(2－3x)的值域。

解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。

∴函数的知域为.点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。

（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。

这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。

（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。

此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。

配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

求值域方法常用求值域方法（1）、直接观察法：利用已有的基本函数的值域观察直接得出所求函数的值域对于一些比较简单的函数，如正比例,反比例,一次函数,指数函数,对数函数,等等, 其值域可通过观察直接得到。

例1、求函数1,[1,2]y x x =∈的值域。

例2、 求函数x 3y -=的值域。

【同步练习1】函数221xy +=的值域.（2）、配方法：二次函数或可转化为形如c x bf x f a x F ++=)()]([)(2类的函数的值域问题，均可用配方法，而后一情况要注意)(x f 的范围；配方法是求二次函数值域最基本的方法之一。

例1、求函数225,y x x x R =-+∈的值域。

例2、求函数]2,1[x ,5x 2x y 2-∈+-=的值域。

例3、求()()22log 26log 62log 222222-+=++=x x x y 。

（配方法、换元法）例4、设02x ≤≤，求函数1()4321x x f x +=-+的值域．例5、求函数13432-+-=x x y 的值域。

（配方法、换元法）例6、求函数x x y 422+--=的值域。

（配方法） 【同步练习2】1、求二次函数242y x x =-+-（[]1,4x ∈）的值域.2、求函数342-+-=x x e y 的值域.3、求函数421,[3,2]xx y x --=-+∈-的最大值与最小值.4、求函数])8,1[(4log 2log 22∈⋅=x xx y 的最大值和最小值. 5、已知[]0,2x ∈，求函数12()4325x x f x -=-⋅+的值域.6、若,42=+y x 0,0>>y x ,试求y x lg lg +的最大值。

（3）、换元法：（三角换元法）有时候为了沟通已知与未知的联系，我们常常引进一个（几个）新的量来代替原来的量，实行这种“变量代换”往往可以暴露已知与未知之间被表面形式掩盖着的实质，发现解题方向，这就是换元法．在求值域时，我们可以通过换元将所给函数化成值域容易确定的另一函数，从而求得原函数的值域．例1、求()f x x =+【同步练习3】求函数x x y 21--=的值域。

求值域的五种方法及例题求值域的五种方法如下：1. 集合法：将函数的所有可能输出值组成一个集合。

例题：对于函数 f(x) = x^2，求其值域。

解答：可以发现，x^2 的结果只能是大于等于 0 的数，因此值域为[0, +∞)。

2. 平移法：通过将函数的图像在纵轴方向上进行平移来确定值域。

例题：对于函数 f(x) = x^2 + 1，求其值域。

解答：函数 x^2 + 1 的图像是一个向上开口的抛物线，平移后的抛物线的顶点就是值域的最小值，因此值域为[1, +∞)。

3. 导数法：通过求函数的导数，判断其单调性，进而找到值域的最大值和最小值。

例题：对于函数 f(x) = x^3，求其值域。

解答：f'(x) = 3x^2，可以看出当 x > 0 时，f'(x) > 0，即函数是单调递增的。

当 x < 0 时，f'(x) < 0，即函数是单调递减的。

因此，最小值为负无穷，最大值为正无穷，值域为 (-∞, +∞)。

4. 逢边法：对于有界区间上的函数，将端点的函数值作为值域的边界。

例题：对于函数 f(x) = sin(x)，求其在区间[0, π] 上的值域。

解答：f(0) = 0，f(π) = sin(π) = 0，在区间[0, π] 上，sin(x) 的最小值和最大值都为 0，因此值域为 [0, 0]，即 {0}。

5. 图像法：通过观察函数的图像来确定其值域。

例题：对于函数f(x) = √x，求其值域。

解答：可以发现，√x 的结果只能是大于等于 0 的数，因此值域为[0, +∞)。

这些方法提供了不同的途径来求解函数的值域，根据具体情况选择合适的方法。

三道关于值域的经典例题例1.设函数/(幻=2-衣B和函数g(x) = or + a-1,若对任意xe[0,yo)都有天£ (- s,l]使得/(XJ =鼠天),则实数〃的取值范围是__________ .解析本题难度较高，应充分理解题目所给的条件，弄清两个函数的值域之间的关系是解决问题的关键.当x e [0,口)时,2x+4 N4,，J2x + 4 22, A- j2x + 4 W — 2.・・・2 — j2x + 4 WO,即函数/(x) ( A- e [O,-KZ)))的值域为(-s,O],设该值域为4 设函数g(x)( X£(-8,l])的值域为艮:对任意演e[0,*o)都有& e (-8,1]使得/(须)=g(xj①当a = 0时,g(x) = -l、B = {-1},显然不符合题意,舍去；②当”0时，函数g(x)的值域为(-即8 = (-00,2"1].•・• Aq 8, J 2a-\20,解之得:a 2 上；- 2③当，，v 0时，函数g(x)的值域为[21 -1,—)，即B = [2。

-1,一)，不符合题意. 综上所述，实数。

的取值范围是1+ooj.例2.已知函数产x +工有如下性质:如果常数f>0,那么该函数在(0,，]上是减X函数，在[不,一)上是增函数.(1)已知/(x) = ±£±^,xe[0』,利用上述性质，求函数f(x)的单调区间和2x + l 值域；(2)对于(1)中的函数/㈤和函数g(x) = r-2a,若对于任意的西e[O,l],总存在七e [0』,使得g(x2) = fM成立,求实数〃的值.分析：对/(x)进行变形,使函数解析式中出现x +二形式的结构.设 4x 2 - 12x - 3 = (2x + I)2 + m(2x +1) + 〃，则有: (2m + 4)x + m + 〃 + 1 = -12x - 32〃？ + 4 = —12 . n 、zrl,c ，解之得：《 m + 〃 + 1 = -3••• 4/ - 12x - 3 = (2x +- 8(2x + 1) + 4解：(1) /3 = j — T2.1 = (2八+ 1) — 8(1)+ 4 = 2. +1 + _8 2x + l 2x + l 2x + l 4 设 2x +1 = f ，则 y = r + - — 8. tVxe[0,l],r.re[l,3].由题意可知:函数y =，+ ±-8的单调递减区间为/£[1,2],即xe 0」；单调递增区 f. 2- 间为,£[2,3],即) [ 4；•当 x = 3 时,/ We =2x^ + 1 + --- -- - 8 = -4.2 2 2x- + l2• ・・ /(0) = -3,/(l) = -H• ・・/(x)皿=/(0) = —3• ・・函数f(x)的值域为[-4,-3];(2)当 x e [0,1]时，函数g(x) = -X-2a 的值域为[-1 -2a-2a]，设为 B. 由(1)知函数/(x)的值域为[-4,-3],设为4m = -8〃 =4二 /(x)= 4/一12工一3 (2X +1)2-8(2X + 1) + 42x + l =2x +1 H --- — —8.•・,对于任意的须e [0,1],总存在W田0吐使得以斗)= /($)成立-\-2a<-4<，解之得:- 2a > -3例3.若函数f［.x) =*也的值域为［-1,4］，求实数出〃的值.r+1分析：这是利用逆向思维求函数中参数的值或取值范围的问题.先设),=色二？，然后将该函数整理为关于X的方程，对方程进行分类讨论,当该方厂+1程为一元二次方程且方程有实数根时，对应的根的判别式△力0,这样可以求出y 的取值范围，即原函数的值域.解：设y = + 〃，则＞£ - ax + y - /? = 0.广+1分为两种情况：①当y = 0时，显然y的值在其值域［-14］内，符合题意;②当y X 0时,•「x wR,•••关于x的方程冲2 -ax +y-b = 0有实数根.A = (- a\ - 4y(y - Z?) N0.整理得:4y? -4Z?y-《J <0.丁y e [-1,4]，，一 1 W y W4..♦ ,关于y的方程分j……，即…y-9』的两个实数根为T4.小根与系数的关系定理可得:力=一1 + 41 , I /，解之得：, = -1x44。