全加器实验报告

数电实验报告半加全加器实验目的：掌握半加器和全加器的原理和应用，了解半加器和全加器的构造和工作原理。

实验器材：逻辑电路实验箱、7400四与非门、7402四与非门、7408四与门、7432四或门、7447数码显示器、开关、电源、跳线等。

实验原理：半加器和全加器是数字电路中常用的基本逻辑电路，用于对二进制进行加法运算，主要用于数字电路中的算术逻辑单元(ALU)。

1.半加器实验原理：半加器是一种能够对两个二进制位进行加法运算的电路。

半加器有两个输入端和两个输出端，输入端分别为A和B，输出端分别为S和C。

其中，A和B分别为要加的两个二进制数位，S为运算结果的个位，并且用S=A⊕B表示；C为运算结果的十位（进位），C=A·B表示。

半加器的真值表和逻辑符号表达式如下：```A，B，S，C0，0，0，00，1，1，01，0，1，01，1，0，1```2.全加器实验原理：全加器是一种能够对两个二进制位和一个进位信号进行加法运算的电路。

全加器有三个输入端和两个输出端，输入端分别为A、B和Cin，输出端分别为S和Cout。

其中，A和B分别为要加的两个二进制数位，Cin 为上一位的进位信号，S为运算结果的个位，并且用S=A ⊕ B ⊕ Cin表示；Cout为运算结果的十位（进位），Cout=(A·B) + (A·Cin) + (B·Cin)表示。

全加器的真值表和逻辑符号表达式如下：```A ，B ， Cin ， S ， Cout0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1```实验步骤：1.首先，按照实验原理连接逻辑门实验箱中的电路。

将7400四与非门的1、2号引脚分别连接到开关1、2上，将开关3连接到7400的3号引脚，将开关4连接到7400的5号引脚，将7400的6号引脚连接到LED1上，表示半加器的进位输出。

一位全加器实验报告实验报告：全加器的原理与实验一、实验目的本实验旨在探究全加器的原理及其在数字电路中的应用，通过实际操作加深对全加器的理解，并掌握其工作原理和性能特点。

二、实验器材1. 74LS86集成电路芯片2. 电源3. 示波器4. 逻辑分析仪5. 连接线6. 示波器探头三、实验原理全加器是数字电路中常用的逻辑运算器件，用于实现三个二进制数的相加运算。

全加器由两个半加器和一个进位输入组成，能够实现三个二进制数的相加运算，并输出相应的和与进位。

全加器的工作原理是基于二进制加法的逻辑运算规则，通过逻辑门的组合实现。

四、实验步骤1. 将74LS86集成电路芯片插入实验板中，并连接电源。

2. 将输入端A、B、Cin分别与电源接通，观察输出端Sum和Cout的变化。

3. 使用逻辑分析仪和示波器对输入端和输出端进行观测和分析，记录实验数据。

4. 分别改变输入端A、B、Cin的状态，观察输出端Sum和Cout的变化，记录实验数据。

5. 对实验数据进行分析和总结，验证全加器的工作原理和性能特点。

五、实验结果通过实验观测和数据分析，得出以下结论：1. 全加器能够实现三个二进制数的相加运算，并输出相应的和与进位。

2. 输入端A、B、Cin的状态改变会影响输出端Sum和Cout的变化，符合二进制加法的逻辑运算规则。

3. 74LS86集成电路芯片的性能稳定，能够满足数字电路的应用要求。

六、实验总结本实验通过实际操作加深了对全加器的理解，掌握了全加器的工作原理和性能特点。

全加器作为数字电路中常用的逻辑运算器件，具有重要的应用价值，能够实现二进制加法运算，广泛应用于计算机、通信等领域。

通过本实验的学习，对数字电路和逻辑运算有了更深入的理解，为今后的学习和工作打下了坚实的基础。

七、实验建议在实验过程中，应注意安全操作，避免短路和电路损坏。

同时，对实验数据进行仔细分析和总结，加深对全加器的理解，为今后的学习和应用提供有力支持。

实验二半加/减器与全加/减器一、实验目的：（1）掌握全加器和半加器的逻辑功能。

（2）熟悉集成加法器的使用方法。

（3）了解算术运算电路的结构。

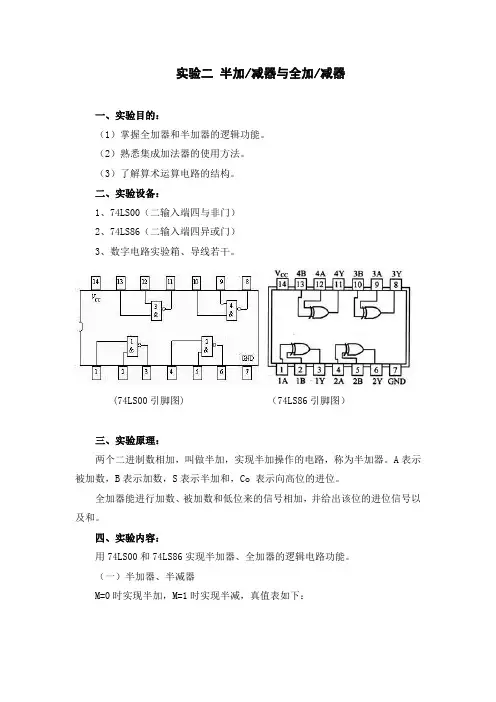
二、实验设备：1、74LS00（二输入端四与非门）2、74LS86（二输入端四异或门）3、数字电路实验箱、导线若干。

(74LS00引脚图) （74LS86引脚图）三、实验原理：两个二进制数相加，叫做半加，实现半加操作的电路，称为半加器。

A表示被加数，B表示加数，S表示半加和，Co 表示向高位的进位。

全加器能进行加数、被加数和低位来的信号相加，并给出该位的进位信号以及和。

四、实验内容：用74LS00和74LS86实现半加器、全加器的逻辑电路功能。

（一）半加器、半减器M=0时实现半加，M=1时实现半减，真值表如下：功能M A B S C半加0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1半减1 0 0 0 0 1 0 1 1 1 1 1 0 1 0 1 1 1 0 0(半加器图形符号)2、MAB00 01 11 100 0 1 1 01 1 0 0 1BABABAS⊕=+=MAB00 01 11 100 0 0 0 01 0 1 0 1)(MABC⊕=（二）全加器、全减器M A B 1-i CS i C0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 1 1 1 0 0 0 0 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 0 1 0 1 1 0 1 0 1 1 1 1 0 0 1 1 111 111-i C B A S ⊕⊕=))((1-i C B A M BC C i ⊕⊕•=五、实验结果半加器：B A B A B A S ⊕=+= )(M A B C ⊕=全加器：1-i C B A S ⊕⊕=M C M C C i 21+=其中11()i C A B C AB -=⊕+，21()i C A B C AB -=+为了方便，以下1i C -用C 表示()()(()()()I C AB AB CM AB AB CM ABM ABM ABCM ABCM ABCM ABCM ABM ABMABCM ABCM ABCM ABCM ABCM ABCM ABCM ABCM BC ABCM ABCM ABCM ABCM M A B C BC =+++++=+++++=+++++++=++++=⊕⊕ 则))((1-i C B A M BC C i ⊕⊕•=六、心得体会本次实验做的是半加/减器和全加/减器两个电路，比上次实验复杂很多，因此充满了挑战性。

eda实验报告全加器EDA实验报告：全加器一、引言在数字电路设计中，全加器是一种基本的组合逻辑电路，用于实现两个二进制数的加法运算。

全加器的设计和性能对于数字电路的正确性和效率至关重要。

本实验报告将介绍全加器的原理、设计方法以及实验结果。

二、全加器的原理全加器是由两个半加器和一个额外的输入引脚组成的。

它可以实现三个二进制输入数的相加运算，并输出相应的和与进位。

1. 半加器半加器是一个简单的组合逻辑电路，用于实现两个二进制数的相加运算。

它有两个输入引脚A和B，分别代表两个二进制数的对应位，一个和输出引脚S和一个进位输出引脚C。

半加器的真值表如下所示：A B S C0 0 0 00 1 1 01 0 1 01 1 0 1可以看出，和输出引脚S等于A和B的异或运算结果，进位输出引脚C等于A 和B的与运算结果。

2. 全加器全加器是由两个半加器和一个额外的输入引脚组成的。

它有三个输入引脚A、B 和Cin，分别代表两个二进制数的对应位以及上一位的进位，两个输出引脚S 和Cout，分别代表相加结果的和以及当前位的进位。

全加器的真值表如下所示：A B Cin S Cout0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1可以看出，和输出引脚S等于A、B和Cin的异或运算结果，进位输出引脚Cout等于A、B和Cin的与运算结果与A和B的或运算结果的与运算结果。

三、全加器的设计方法全加器的设计可以使用逻辑门电路实现。

常用的逻辑门包括与门、或门、非门和异或门。

根据全加器的真值表，可以使用这些逻辑门组合来实现全加器。

1. 使用逻辑门实现半加器半加器可以使用异或门和与门来实现。

异或门用于计算和输出引脚S，与门用于计算和输出引脚C。

2. 使用逻辑门实现全加器全加器可以使用两个半加器和一个或门来实现。

两个半加器分别用于计算和输出引脚S和C1，或门用于计算和输出引脚Cout。

一位全加器的实验报告实验报告：全加器的实验摘要：本实验旨在通过实际操作，了解全加器的原理和工作方式。

通过搭建全加器电路，观察其输入输出关系，验证全加器的功能和性能。

实验结果表明，全加器能够正确地实现三个输入位的加法运算，并且输出结果符合预期。

引言：全加器是数字电路中常用的逻辑电路之一，用于实现多位数的加法运算。

它能够接受三个输入位（A、B、Cin），并输出两个输出位（Sum、Cout）。

全加器的设计和实现对于理解数字电路和计算机原理具有重要意义。

实验步骤：1. 准备实验所需的电子元件和工具，包括逻辑门、电阻、LED灯等。

2. 根据全加器的逻辑电路图，搭建实验电路。

3. 将输入位（A、B、Cin）和电源连接，观察LED灯的亮灭情况。

4. 调整输入位的数值，记录LED灯的亮灭情况。

5. 分析实验结果，验证全加器的功能和性能。

实验结果：经过实验操作和数据记录，我们得出以下结论：1. 当输入位（A、B、Cin）为000时，LED灯均熄灭。

2. 当输入位（A、B、Cin）为001时，LED灯中的某些亮起，表明输出位（Sum、Cout）的数值。

3. 当输入位（A、B、Cin）为111时，LED灯均亮起。

结论：通过本次实验，我们成功地搭建了全加器电路，并验证了其正确的工作方式。

全加器能够实现三个输入位的加法运算，并输出符合预期的结果。

这对于我们理解数字电路和计算机原理具有重要的意义。

展望：在今后的学习和实践中，我们将进一步深入研究数字电路和逻辑电路的原理，不断提高自己的实验操作能力和理论水平，为将来的科研和工程实践做好充分的准备。

一、实验目的1. 理解全加器的原理和结构。

2. 掌握全加器的逻辑功能及其实现方法。

3. 学习全加器在实际电路中的应用。

二、实验原理全加器是一种组合逻辑电路，用于实现两个二进制数相加，同时考虑来自低位的进位信号。

全加器由三个输入端和两个输出端组成，输入端分别为两个加数位（A、B）和来自低位的进位信号（Cin），输出端分别为和位（S）和进位输出信号（Cout）。

全加器的逻辑功能如下：- 当A、B和Cin都为0时，S为0，Cout为0；- 当A、B和Cin中有一个为1时，S为1，Cout为0；- 当A、B和Cin中有两个为1时，S为0，Cout为1；- 当A、B和Cin都为1时，S为1，Cout为1。

全加器可以通过半加器（HAdder）和与门（AND）来实现。

半加器实现两个一位二进制数相加的功能，而与门用于实现进位信号的产生。

三、实验器材1. 74LS系列集成电路芯片（如74LS00、74LS86等）；2. 实验箱；3. 电源；4. 导线；5. 万用表；6. 示波器。

四、实验步骤1. 根据全加器的逻辑功能，设计全加器的原理图，包括半加器和与门；2. 将设计好的原理图连接到实验箱上，包括输入端（A、B、Cin）和输出端（S、Cout）；3. 使用万用表检测各个芯片的引脚电压，确保电路连接正确；4. 使用示波器观察输入信号和输出信号的变化，验证全加器的逻辑功能；5. 改变输入信号，观察全加器的输出信号，进一步验证其逻辑功能；6. 将全加器应用于实际电路，如实现多位加法器等。

五、实验结果与分析1. 实验结果表明，全加器能够实现两个二进制数相加，同时考虑来自低位的进位信号；2. 通过示波器观察，发现全加器的输出信号与输入信号符合逻辑功能；3. 将全加器应用于实际电路，如实现多位加法器，实验结果表明电路能够正常工作。

六、实验心得1. 全加器是一种重要的组合逻辑电路，在数字电路中具有广泛的应用；2. 在实验过程中，需要掌握全加器的原理和结构，熟悉各个芯片的功能和引脚连接；3. 实验过程中，要注意电路的连接和信号的观察，确保实验结果的准确性；4. 通过本次实验，加深了对全加器的理解，为以后的学习和工作打下了基础。

全加器实验报告全加器设计实验报告姓名：班级：学号：实验⽬的：1.熟悉QuartusⅡ原理图设计流程,学习简单电路的设计⽅法、输⼊步骤、层次化步骤。

2.掌握QuartusII的⽂本输⼊⽅式的设计过程，理解VHDL语⾔的结构级描述⽅法，学习元件例化语句的设计⽅法。

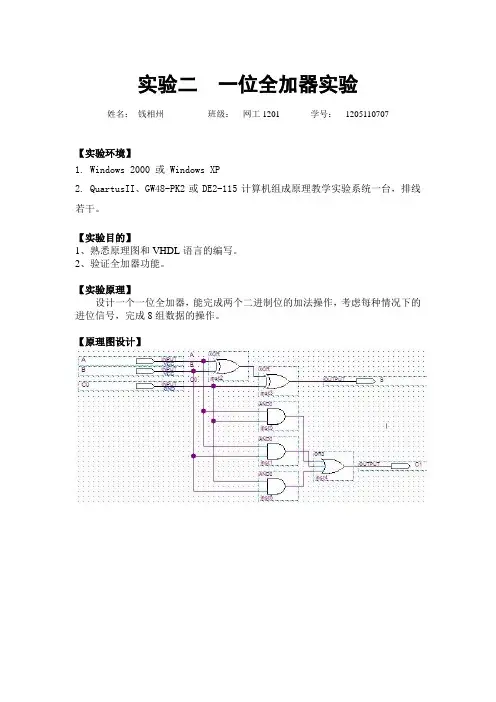
实验原理：⼀位全加器可以⽤两个半加器及⼀个或门连接⽽成。

要求使⽤原理图输⼊的⽅法先进⾏底层半加器设计，再建⽴上层全加器设计⽂件，调⽤半加器和或门符号，连线完成原理图设计。

全加器可以⽤两个半加器和⼀个或门连接⽽成，在半加器描述的基础上，采⽤COMPONENT语句和PORT MAP语句就可以很容易地编写出描述全加器的程序。

⼀.原理图1.半加器实验步骤1.打开Quartus Ⅱ软件，选择新建命令，在新建对话框中选择原理图⽂件编辑输⼊项，完成新建进⼊原理图编辑窗⼝。

2.在原理图编辑窗⼝任意位置右击⿏标，将出现快捷菜单，选择其中的输⼊元件项insert symbol，按照所设计的电路，放置器件，排版，连线，完成设计后选择另存为命令，命名为h_adder存放在指定⽂件夹中。

3.完成半加器的设计后，重复新建命令，开始进⾏全加器设计，在新建的原理图中，双击⿏标，在弹出的窗⼝中选择project选项，将之前存⼊的h_adder元件，放⼊原理图中。

2.全加器实验步骤1.新建⼯程，在新建的⼯程中建⽴VHDL语⾔编辑⽂件，在编辑窗⼝处，输⼊设计的半加器全加器程序。

2.将设计好程序进⾏编译，没有错误之后定义全加器五个引脚所对应⽿朵硬件电路的引脚号。

3.烧录程序，调试，验证程序是否合理。

⼆.程序三.实验波形图：1.半加器2.全加器四.寄存器。

一、实验目的1. 理解全加器的逻辑功能和工作原理。

2. 掌握全加器的组成和电路结构。

3. 学习全加器在实际电路中的应用。

4. 培养动手实践能力和分析问题、解决问题的能力。

二、实验原理全加器是一种能够实现二进制加法运算的数字电路，它由半加器和与门组成。

全加器有三个输入端：两个加数输入端A和B，以及一个进位输入端Cin；三个输出端：进位输出端Cout，和输出端Sum，以及一个进位输入端Cin。

全加器的逻辑功能如下：- 当Cin为0时，全加器相当于一个半加器，即A和B相加，进位输出Cout为0，和输出Sum为A+B。

- 当Cin为1时，全加器将A、B和Cin相加，进位输出Cout为1，和输出Sum为A+B+Cin。

三、实验仪器与设备1. 数字电路实验箱2. 集成芯片（如74LS00、74LS86等）3. 导线4. 逻辑分析仪或示波器5. 实验指导书四、实验步骤1. 搭建全加器电路(1) 使用74LS86芯片搭建半加器电路，连接A、B和Sum端。

(2) 使用74LS00芯片搭建与门电路，连接Sum和Cin端，输出为Cout。

(3) 将半加器和与门电路连接起来，形成全加器电路。

2. 验证全加器功能(1) 将A、B和Cin端分别接入逻辑电平开关。

(2) 通过逻辑电平开关改变A、B和Cin端的电平，观察Cout和Sum端的输出。

(3) 将实验结果与理论计算结果进行对比，验证全加器的功能。

3. 全加器在实际电路中的应用(1) 使用全加器搭建一个4位加法器电路。

(2) 将A、B和Cin端分别接入4位二进制数输入端。

(3) 观察Cout和Sum端的输出，验证4位加法器电路的功能。

五、实验结果与分析1. 全加器功能验证通过实验验证，全加器能够实现二进制加法运算，其逻辑功能与理论计算结果一致。

2. 全加器在实际电路中的应用通过实验验证，全加器可以应用于4位加法器电路，实现多位二进制数的加法运算。

六、实验总结1. 全加器是一种能够实现二进制加法运算的数字电路，具有广泛的应用。

全加器实验报告实验心得
一、实验目的
全加器实验是计算机组成原理课程中的一项重要实验，旨在让我们通过实际操作理解全加器的原理和实现过程，加深对二进制加法运算和计算机内部运算的理解。

二、实验原理
全加器是一种对两个二进制数进行加法运算的逻辑电路，可以处理两个一位的进位输入和一个总的和输出。

全加器的每个输入位都有三个输入端：A、B和C，分别表示被加数、加数和进位输入。

输出端有两个：S和Cout，分别表示和以及是否产生进位。

三、实验步骤
1.准备工具和材料：准备好实验用的导线、电阻、开关、
LED灯等材料，并搭建全加器的电路模型。

2.连接电路：按照全加器的电路图连接各个输入输出端，确
保连接正确无误。

3.输入数据：通过开关给被加数和加数输入二进制数，观察
LED灯的显示，确认输入数据正确。

4.观察结果：在特定的输入下，观察全加器的输出结果，验
证其是否符合预期。

5.重复实验：尝试不同的输入数据，观察全加器的输出结果，
总结规律。

四、实验结果与分析
通过实验，我们发现全加器的输出结果符合预期，能够正确地实现二进制数的加法运算。

在实验过程中，我们深入理解了全加器的工作原理和实现过程，对二进制加法运算和计算机内部运算有了更深入的理解。

五、实验心得
通过这次全加器实验，我深刻体会到了计算机组成原理课程的重要性。

只有通过实际操作，才能真正理解并掌握课程知识。

同时，实验也锻炼了我的动手能力和解决问题的能力。

在未来的学习和工作中，我会继续保持这种学习的热情和态度，不断提高自己的技能和能力。

数字电路实验报告——全加器一、实验目的1.了解全加器的工作原理和应用。

2.掌握全加器的逻辑电路。

3.能够实现全加器的电路。

二、实验原理1.全加器的概念全加器是将三个二进制数相加的电路，其中两个输入用于加，另一个输入用于进位。

目前计算机中都采用二进制数系，因此采用全加器电路可以将二进制数计算的加、减、乘、除等运算转化为逻辑电路控制。

2.全加器电路原理全加器一般包括两个半加器，也就是相邻的两位之间的进/退位。

全加器的三个输入：A、B：相邻位的输入。

Cin：低一级的进位数。

输出：S：相邻位的和。

Cout：进位输出。

半加器（HA）是组成全加器的基本单元，其有两个输入和两个输出。

半加器的输出只考虑了A、B两个输入相加的进位情况，而对于进位需要从低一位的进位来考虑是否产生进位。

因此，需要将半加器和前一位的进位一起运算才能得到正确结果。

三、实验装置1.数字实验箱。

2.全加器IC 7483。

3.数字示波器。

四、实验步骤1. 将全加器IC 7483插在数字实验箱的插孔上。

2. 根据全加器的逻辑关系，接线如下图所示。

3. 输入逻辑信号，并观察全加器的输出结果。

4. 将输出结果接入数字示波器中，观察波形。

五、实验结果及分析本次实验使用全加器IC 7483进行数字电路的设计与实现，由于全加器具有计算机中常见的二进制数加法功能，因此在缺少专业计算机设备或软件的情况下，可以使用数字逻辑电路来进行二进制数的计算。

在实验中，传入的逻辑信号为001和010，分别作为相邻位的数字输入A、B，Cin输入为0，代表即不需要进位。

从输出结果中可以看出，在全加器电路的输出端正确得到了二进制数001和010的相加结果，即为011。

通过实验，可以发现全加器的工作原理和应用，掌握全加器的逻辑电路，并能够实现全加器电路。

六、实验结论1.全加器是一个能够将三个二进制数相加的电路。

2.全加器由两个半加器组成，每个半加器有两个输入和两个输出。

3.在计算机中常用全加器电路进行二进制数的计算。

一、实验目的1. 理解全加器的原理和组成。

2. 掌握半加器、与门、或门等基本逻辑门电路的原理和特性。

3. 学习利用基本逻辑门电路构建全加器。

4. 通过实验加深对数字电路设计和实现过程的理解。

二、实验原理全加器是一种基本的数字电路，用于实现两个二进制数的加法运算。

它由两个半加器和两个与门、一个或门组成。

当两个加数位相加时，全加器可以产生一个和以及一个进位输出。

半加器（hadder）是全加器的基础单元，它由一个异或门（XOR）和一个与门（AND）组成。

异或门负责产生和输出，与门负责产生进位输出。

全加器的原理如下：- 当两个加数位相加时，若两者均为0，则输出和为0，进位为0。

- 若一个加数位为0，另一个为1，则输出和为1，进位为0。

- 若两者均为1，则输出和为0，进位为1。

三、实验设备及器材1. 数字电路实验箱2. 集成芯片（74LS00、74LS10、74LS54、74LS86）3. 导线4. 示波器5. 电源四、实验步骤1. 准备实验器材，搭建半加器电路。

（1）将74LS86（异或门）和74LS00（与门）插入实验箱。

（2）按照图1所示连接半加器电路。

（3）将A、B分别接入电平开关，Y、Z接入发光二极管显示。

（4）通电，观察Y、Z的亮灭情况，验证半加器的逻辑功能。

2. 构建全加器电路。

（1）按照图2所示连接全加器电路。

（2）将A、B、C分别接入电平开关，Y、Z接入发光二极管显示。

（3）通电，观察Y、Z的亮灭情况，验证全加器的逻辑功能。

3. 使用示波器观察全加器的输出波形。

（1）将示波器的探头分别连接到全加器的和输出端和进位输出端。

（2）改变A、B、C的输入值，观察示波器上的波形，分析全加器的逻辑功能。

五、实验结果与分析1. 半加器实验结果：当A、B的输入分别为0、1或1、0时，Y为1，Z为0；当A、B的输入均为0或均为1时，Y为0，Z为0。

验证了半加器的逻辑功能。

2. 全加器实验结果：当A、B、C的输入分别为0、0、0时，Y为0，Z为0；当A、B、C的输入分别为0、0、1时，Y为1，Z为0；当A、B、C的输入分别为0、1、0时，Y为1，Z为0；当A、B、C的输入分别为0、1、1时，Y为0，Z为1；当A、B、C的输入分别为1、0、0时，Y为1，Z为0；当A、B、C的输入分别为1、0、1时，Y为0，Z为1；当A、B、C的输入分别为1、1、0时，Y为0，Z为1；当A、B、C的输入分别为1、1、1时，Y为1，Z为1。

全加器（Full Adder）是数字电路中常用的逻辑门电路，用于将两个二进制位和一个进位位相加，产生一个和位和一个进位位的输出。

下面是一个全加器的构成和测试实验报告的示例。

实验名称：全加器的构成和测试1. 实验目的：了解全加器的工作原理和逻辑。

设计并测试一个全加器电路。

2. 实验材料和设备：74LS86 XOR 门IC芯片（用于实现异或操作）74LS08 AND 门IC芯片（用于实现与操作）面包板连线电源3. 实验原理：一个全加器有三个输入和两个输出。

输入包括两个待相加的二进制位（A和B），以及一个来自上一级的进位位（Cin）。

输出包括一个和位（Sum）和一个输出进位位（Cout）。

全加器的逻辑表达式如下：Sum = A XOR B XOR CinCout = (A AND B) OR (Cin AND (A XOR B))4. 实验步骤：将74LS86和74LS08 IC芯片插入面包板中，确保引脚正确连接。

连接电源到面包板，确保电源电压正确。

使用连线连接74LS86和74LS08的引脚，以构建全加器电路。

按照逻辑表达式中的连接方式。

输入A、B和Cin值，通过开关或信号发生器设置输入。

使用示波器或LED等指示器检查Sum和Cout输出。

5. 实验结果和观察：输入A=0，B=0，Cin=0，Sum=0，Cout=0输入A=0，B=1，Cin=0，Sum=1，Cout=0输入A=1，B=0，Cin=0，Sum=1，Cout=0输入A=1，B=1，Cin=0，Sum=0，Cout=1输入A=0，B=0，Cin=1，Sum=1，Cout=0输入A=0，B=1，Cin=1，Sum=0，Cout=1输入A=1，B=0，Cin=1，Sum=0，Cout=1输入A=1，B=1，Cin=1，Sum=1，Cout=16. 结论：全加器是一个常见的数字逻辑门电路，用于将两个二进制位和一个进位位相加，产生一个和位和一个进位位的输出。

一、实验目的1. 理解全加器和全减器的工作原理。

2. 掌握全加器和全减器的电路设计方法。

3. 通过实验验证全加器和全减器的功能。

二、实验原理全加器（Full Adder）是一种能够处理两个二进制位以及一个来自低位的进位输入的加法器。

全减器（Full Subtractor）则是一种能够处理两个二进制位以及一个来自低位的借位输入的减法器。

它们是数字电路中常用的基本单元。

三、实验器材1. 实验箱2. 逻辑门芯片3. 连接线4. 计算器四、实验步骤1. 全加器设计1.1 根据全加器的真值表，设计全加器的逻辑电路图。

1.2 利用与门、或门、非门和异或门等逻辑门，实现全加器的逻辑功能。

1.3 将设计好的电路图连接到实验箱上，进行测试。

1.4 测试全加器的功能，验证其是否能正确实现加法运算。

2. 全减器设计2.1 根据全减器的真值表，设计全减器的逻辑电路图。

2.2 利用与门、或门、非门和异或门等逻辑门，实现全减器的逻辑功能。

2.3 将设计好的电路图连接到实验箱上，进行测试。

2.4 测试全减器的功能，验证其是否能正确实现减法运算。

五、实验结果与分析1. 全加器测试结果1.1 当输入A、B和进位C(N)均为0时，输出Sum为0，进位C(N1)为0。

1.2 当输入A、B和进位C(N)均为1时，输出Sum为0，进位C(N1)为1。

1.3 当输入A为0，B为1，进位C(N)为0时，输出Sum为1，进位C(N1)为0。

1.4 当输入A为1，B为0，进位C(N)为0时，输出Sum为1，进位C(N1)为0。

1.5 当输入A为1，B为1，进位C(N)为0时，输出Sum为0，进位C(N1)为1。

1.6 当输入A为0，B为0，进位C(N)为1时，输出Sum为1，进位C(N1)为1。

1.7 当输入A为1，B为1，进位C(N)为1时，输出Sum为1，进位C(N1)为1。

通过测试结果可以看出，全加器能够正确实现加法运算。

2. 全减器测试结果2.1 当输入A、B和借位B(N)均为0时，输出差D为A，借位B(N1)为0。

全加器实验报告
目录
1. 实验目的
1.1 实验原理
1.1.1 全加器的定义
1.1.2 全加器的结构
1.2 实验器材
1.3 实验步骤
1.4 数据处理与分析
1.5 实验结论
实验目的
本实验旨在通过实验操作，加深对全加器的理解，掌握全加器的工作原理及实际应用。

实验原理
全加器的定义
全加器是一种加法电路，用于实现两个二进制数的相加操作。

它能够接受两个输入信号和一个进位信号，输出一个和以及一个进位信号。

全加器的结构
全加器由两个半加器和一个OR门组成。

半加器用于处理两个输入位的和，另一个输入位用于进位。

OR门用于将两个半加器的结果进行最终相加。

实验器材
- 电源
- 逻辑门集成电路
- 连接线
- 示波器
实验步骤
1. 按照电路图连接逻辑门集成电路和电源。

2. 设定输入信号的值，观察输出信号的变化。

3. 调节进位信号，观察输出信号的变化。

4. 记录实验数据。

数据处理与分析
通过实验数据的记录和分析，我们可以验证全加器的工作原理，理解其逻辑运算过程，进一步加深对加法电路的理解。

实验结论
通过本次实验，我们成功实现了全加器的搭建并观察了其工作原理。

加深了我们对加法电路的理解，为进一步学习数字电路奠定了基础。

一、实验目的1. 理解全加器的概念和组成原理。

2. 掌握全加器的逻辑功能及其在数字电路中的应用。

3. 通过实验，验证全加器的逻辑功能，加深对全加器电路的理解。

二、实验原理全加器是一种能够实现两个二进制数相加，同时考虑来自低位进位信号的加法器。

它由两个半加器和一个与门组成。

其中，两个半加器分别用于实现两个加数的加法运算，与门用于处理来自低位的进位信号。

全加器的逻辑表达式如下：S = A ⊕ B ⊕ CinCout = (A ∧ B) ∨ (B ∧ Cin) ∨ (Cin ∧ A)其中，S为全加器的和输出，Cout为进位输出，A和B为两个加数，Cin为进位输入。

三、实验器材1. 数字电路实验箱2. 集成芯片：74LS86（异或门）、74LS08（与门）、74LS32（或门）3. 导线四、实验步骤1. 搭建全加器电路（1）根据实验原理图，在实验箱上连接两个半加器和两个与门。

（2）将A、B、Cin分别接入相应的电平开关，将S和Cout分别接入发光二极管。

（3）检查电路连接是否正确。

2. 测试全加器功能（1）设置A、B、Cin的不同电平组合，观察发光二极管显示的S和Cout状态。

（2）记录实验数据，验证全加器的逻辑功能。

3. 比较实验结果与理论值（1）根据实验数据，分析全加器的逻辑功能是否与理论值相符。

（2）对实验过程中出现的问题进行分析和总结。

五、实验结果与分析1. 实验数据| A | B | Cin | S | Cout ||---|---|-----|---|-------|| 0 | 0 | 0 | 0 | 0 || 0 | 0 | 1 | 1 | 0 || 0 | 1 | 0 | 1 | 0 || 0 | 1 | 1 | 0 | 1 || 1 | 0 | 0 | 1 | 0 || 1 | 0 | 1 | 0 | 1 || 1 | 1 | 0 | 0 | 1 || 1 | 1 | 1 | 1 | 1 |2. 分析通过实验数据可以看出，全加器的逻辑功能与理论值相符。

全加器实验总结引言：全加器是数字电路中的基本组件之一，它用来实现二进制加法运算。

全加器通过对输入信号进行逻辑运算，将两个二进制数字相加，并输出相应的结果。

在本次实验中，我们通过搭建一个全加器电路，对其进行了测试和验证，掌握了全加器的工作原理和应用。

一、实验目的本次实验的主要目的是研究全加器的工作原理，理解其逻辑运算和加法运算的过程。

通过设计和搭建全加器电路，掌握其实际应用和功能。

二、实验设备和材料1. 电路板2. 电子元器件（包括逻辑门、开关等）3. 示波器4. 电源供应器三、实验步骤1. 检查电路板和电子元器件的连接是否正确，确保没有短路或接触不良的问题。

2. 根据课程设计要求，选择适当的逻辑门和开关进行连接，并进行必要的调试。

3. 打开电源供应器，给电路板提供所需的工作电压。

4. 分别输入不同的二进制数字，观察输出端的信号变化。

5. 借助示波器，对输入和输出信号进行波形分析和判断，并与理论结果进行对比。

四、实验结果和分析在实验过程中，我们成功搭建了一个全加器电路，并进行了测试。

通过输入不同的二进制数字，我们观察到了输出端的相应变化。

当输入为0和0时，输出结果为0；当输入为0和1，或者1和0时，输出结果为1；当输入为1和1时，输出结果为10，其中的0作为当前位的输出，而1作为进位。

根据实验结果，我们可以得出以下结论：1. 全加器的逻辑运算符合二进制数的加法运算规则，能够正确地实现数字的相加。

2. 全加器的输出结果为两位二进制数，其中的低位作为当前位的输出，而高位作为进位输出。

3. 全加器的工作原理是通过逻辑门的组合，将输入信号进行逻辑运算，并得到相应的结果输出。

五、实验总结本次实验对于全加器的实际应用和工作原理有了更深入的了解。

通过自己动手搭建电路并进行测试，我们对全加器的逻辑运算和加法运算有了更深刻的认识。

通过本次实验，我还意识到了以下几个方面的问题和改进措施：1. 在实验过程中，应更加仔细地检查电路板和元器件的连接，以避免引发不必要的错误。

一、实验目的1. 掌握全加器的基本原理和设计方法。

2. 熟悉Quartus II软件的使用，包括原理图输入、编译、仿真和编程下载等操作。

3. 培养动手实践能力和团队合作精神。

二、实验原理全加器是一种能够处理两个二进制数相加，并考虑来自低位进位信号的组合逻辑电路。

一个n位全加器可以由n个1位全加器级联而成。

本实验设计一个1位全加器，其原理如下：1. 半加器：半加器是全加器的基础，它只考虑两个一位二进制数的相加，不考虑来自低位进位数的运算电路。

半加器的输出包括一个和位S和一个进位位C。

2. 全加器：全加器由两个半加器和一个或门组成。

当输入两个一位二进制数A和B以及一个来自低位的进位信号Cin时，全加器的输出包括一个和位S和一个进位位Cout。

全加器的逻辑表达式如下：S = A ⊕ B ⊕ CinCout = (A ∧ B) ∨ (B ∧ Cin) ∨ (A ∧ Cin)三、实验内容和步骤1. 创建工程：在Quartus II中创建一个新工程，命名为“全加器设计”。

2. 设计原理图：在原理图编辑窗口中，从元件库中分别选取两个半加器（HAdder）和一个或门（Or），并按照全加器的逻辑表达式连接起来。

3. 编译工程：完成原理图设计后，进行编译操作。

Quartus II将对原理图进行综合、实现和编程下载等步骤。

4. 仿真：在仿真环境中，通过输入不同的A、B和Cin值，观察全加器的输出S和Cout是否符合预期。

5. 下载编程：将编译好的程序下载到FPGA开发板上，通过硬件测试验证全加器的功能。

四、实验结果与分析1. 仿真结果：在仿真环境中，我们分别输入以下值进行测试：A B Cin0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1仿真结果显示，全加器的输出S和Cout与预期逻辑表达式相符。

2. 硬件测试结果：将编译好的程序下载到FPGA开发板上，通过硬件测试验证全加器的功能。

测试结果与仿真结果一致，说明全加器设计正确。

全加器构成及测试实验报告一、引言全加器是计算机中常用的关键电路之一，用于实现二进制数的加法运算。

本实验旨在深入了解全加器的构成原理，并通过实验测试其功能和性能。

二、全加器的构成原理全加器包括三个输入端A、B和Cin，以及两个输出端Sum和Cout。

其中，A和B分别是要相加的两个二进制位，Cin是上一级进位的输入，Sum是和的输出，Cout是进位的输出。

全加器的构成可以使用简单逻辑门来实现。

常见的实现方式有两种：基于逻辑门的实现和基于逻辑表达式的实现。

1. 基于逻辑门的实现全加器的基本逻辑门实现是使用两个半加器和一个或门。

半加器用于计算每个位的和和进位。

具体电路连接如下：- 第一个半加器：输入为A和B，输出为Sum1和Cout1；- 第二个半加器：输入为Sum1和Cin，输出为Sum和Cout。

通过组合以上电路，即可得到全加器的实现。

2. 基于逻辑表达式的实现全加器的实现还可以使用逻辑表达式来表示和计算。

假设输入为A、B和Cin，输出为Sum和Cout，则逻辑表达式如下：Sum = A ⊕ B ⊕ CinCout = (A ∧ B) ∨ (Cin ∧ (A ⊕ B))通过实际计算逻辑表达式，可以得到全加器的输出结果。

三、实验步骤1. 确定实验所需材料：电路板、电阻、继电器、开关等。

2. 搭建全加器电路，根据实验要求进行连接。

3. 使用电源连接电路板，确保电路无误。

4. 根据设定的输入值，观察并记录输出结果。

5. 观察全加器的进位和和的输出情况，并进行比对和验证。

四、实验结果与分析在实验中，我们根据设定的输入值进行了多次测试，并观察了全加器的进位和和的输出情况。

通过比对实验结果和预期输出，验证了全加器的正确性。

在多次测试中，我们发现当A和B为0时，Sum等于Cin；当A和B同时为1时，Sum等于Cin的反；当A和B中有一个为1，另一个为0，Sum等于Cin。

同时，通过观察进位的输出情况，我们发现当A和B都为1时，Cout为1；在其他情况下，Cout为0。