最值宝典第十四讲瓜豆原理类问题

最值系列之瓜豆原理在辅助圆问题中，我们了解了求关于动点最值问题的方式之一——求出动点轨迹，即可求出关于动点的最值．本文继续讨论另一类动点引发的最值问题，在此类题目中，题目或许先描述的是动点P，但最终问题问的可以是另一点Q，当然P、Q之间存在某种联系，从P点出发探讨Q点运动轨迹并求出最值，为常规思路．一、轨迹之圆篇引例1：如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．考虑：当点P在圆O上运动时，Q点轨迹是？【分析】观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．【小结】确定Q点轨迹圆即确定其圆心与半径，由A、Q、P始终共线可得：A、M、O三点共线，由Q为AP中点可得：AM=1/2AO．Q点轨迹相当于是P点轨迹成比例缩放．根据动点之间的相对位置关系分析圆心的相对位置关系；根据动点之间的数量关系分析轨迹圆半径数量关系．引例2：如图，P是圆O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．考虑：当点P在圆O上运动时，Q点轨迹是？Q【分析】Q点轨迹是个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P 点轨迹都是圆．接下来确定圆心与半径．考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．即可确定圆M位置，任意时刻均有△APO≌△AQM．引例3：如图，△APQ是直角三角形，∠P AQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？【分析】考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1．即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．【模型总结】为了便于区分动点P、Q，可称点P为“主动点”，点Q为“从动点”．此类问题的必要条件：两个定量主动点、从动点与定点连线的夹角是定量（∠P AQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．Q【结论】（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：∠P AQ=∠OAM；（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比：AP:AQ=AO:AM，也等于两圆半径之比．按以上两点即可确定从动点轨迹圆，Q与P的关系相当于旋转+伸缩．古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．【思考1】：如图，P是圆O上一个动点，A为定点，连接AP，以AP为一边作等边△APQ．考虑：当点P在圆O上运动时，Q点轨迹是？【分析】Q点满足（1）∠P AQ=60°；（2）AP=AQ，故Q点轨迹是个圆：考虑∠P AQ=60°，可得Q点轨迹圆圆心M满足∠MAO=60°；考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．即可确定圆M位置，任意时刻均有△APO≌△AQM．【小结】可以理解AQ由AP旋转得来，故圆M亦由圆O旋转得来，旋转角度与缩放比例均等于AP与AQ的位置和数量关系．【思考2】如图，P是圆O上一个动点，A为定点，连接AP，以AP为斜边作等腰直角△APQ．考虑：当点P在圆O上运动时，如何作出Q点轨迹？【分析】Q点满足（1）∠P AQ=45°；（2）AP:AQ1，故Q点轨迹是个圆．连接AO，构造∠OAM=45°且AO:AM：1．M点即为Q点轨迹圆圆心，此时任意时刻均有△AOP∽△AMQ．即可确定点Q的轨迹圆．【练习】如图，点P（3,4），圆P半径为2，A（2.8,0），B（5.6,0），点M是圆P上的动点，点C是MB的中点，则AC的最小值是_______．【分析】M点为主动点，C点为从动点，B点为定点．考虑C是BM中点，可知C点轨迹：取BP中点O，以O为圆心，OC为半径作圆，即为点C轨迹．当A、C、O三点共线且点C在线段OA上时，AC取到最小值，根据B、P坐标求O，利用两点间距离公式求得OA，再减去OC即可．【2016武汉中考】如图，在等腰Rt △ABC 中，AC =BC=P 在以斜边AB 为直径的半圆上，M 为PC 的中点，当半圆从点A 运动至点B 时，点M 运动的路径长为________．【分析】考虑C 、M 、P 共线及M 是CP 中点，可确定M 点轨迹：取AB 中点O ，连接CO 取CO 中点D ，以D 为圆心，DM 为半径作圆D 分别交AC 、BC 于E 、F 两点，则弧EF 即为M 点轨迹．当然，若能理解M 点与P 点轨迹关系，可直接得到M点的轨迹长为P 点轨迹长一半，即可解决问题．【2018南通中考】如图，正方形ABCD 中，AB O 是BC 边的中点，点E 是正方形内一动点，OE =2，连接DE ，将线段DE 绕点D 逆时针旋转90°得DF ，连接AE 、CF ．求线段OF 长的最小值．OABCDE F【分析】E 是主动点，F 是从动点，D 是定点，E 点满足EO =2，故E 点轨迹是以O 为圆心，2为半径的圆．F考虑DE⊥DF且DE=DF，故作DM⊥DO且DM=DO，F点轨迹是以点M为圆心，2为半径的圆．直接连接OM，与圆M交点即为F点，此时OF最小．可构造三垂直全等求线段长，再利用勾股定理求得OM，减去MF即可得到OF的最小值．【练习】△ABC 中，AB =4，AC =2，以BC 为边在△ABC 外作正方形BCDE ，BD 、CE 交于点O ，则线段AO 的最大值为_____________．AB CDE O【分析】考虑到AB 、AC 均为定值，可以固定其中一个，比如固定AB ，将AC 看成动线段，由此引发正方形BCED 的变化，求得线段AO 的最大值．根据AC =2，可得C 点轨迹是以点A 为圆心，2为半径的圆．OEDCBA接下来题目求AO 的最大值，所以确定O 点轨迹即可，观察△BOC 是等腰直角三角形，锐角顶点C 的轨迹是以点A 为圆心，2为半径的圆，所以O 点轨迹也是圆，以AB 为斜边构造等腰直角三角形，直角顶点M 即为点O 轨迹圆圆心．连接AM 并延长与圆M 交点即为所求的点O ，此时AO 最大，根据AB 先求AM ，再根据BC 与BO 的比值可得圆M 的半径与圆A 半径的比值，得到MO ，相加即得AO ．此题方法也不止这一种，比如可以如下构造旋转，当A 、C 、A ’共线时，可得AO最大值．A'或者直接利用托勒密定理可得最大值．二、轨迹之线段篇引例：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？【分析】当P点轨迹是直线时，Q点轨迹也是一条直线．可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．【引例】如图，△APQ是等腰直角三角形，∠P AQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q 点的起始位置和终点位置，连接即得Q点轨迹线段．Q2AB CQ1【模型总结】 必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP :AQ 是定值）． 结论：P 、Q 两点轨迹所在直线的夹角等于∠P AQ （当∠P AQ ≤90°时，∠P AQ 等于MN 与BC 夹角）P 、Q 两点轨迹长度之比等于AP :AQ （由△ABC ∽△AMN ，可得AP :AQ =BC :MN ）【2017姑苏区二模】如图，在等边△ABC 中，AB =10，BD =4，BE =2，点P 从点E 出发沿EA 方向运动，连结PD ，以PD 为边，在PD 的右侧按如图所示的方式作等边△DPF ，当点P 从点E 运动到点A 时，点F 运动的路径长是________．A【分析】根据△DPF 是等边三角形，所以可知F 点运动路径长与P 点相同，P 从E 点运动到A 点路径长为8，故此题答案为8．【2013湖州中考】如图，已知点A是第一象限内横坐标为AC⊥x轴于点M，交直线y=-x于点N，若点P是线段ON上的一个动点，∠APB=30°，BA⊥P A，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O 运动到点N时，点B运动的路径长是________．【分析】根据∠P AB=90°，∠APB=30°可得：AP:AB，故B点轨迹也是线段，且P点轨迹路径长与B，P点轨迹长ON为B点轨迹长为【练习】如图，在平面直角坐标系中，A（-3,0），点B是y轴正半轴上一动点，点C、D在x正半轴上，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．【分析】求OP是等边三角形且B点在直线上运动，故可知P点轨迹也是直线．取两特殊时刻：（1）当点B与点O重合时，作出P点位置P1；（2）当点B在x轴上方且AB与x轴夹角为60°时，作出P点位置P2．连接P1P2，即为P点轨迹．根据∠ABP =60°可知：12P P 与y 轴夹角为60°，作OP ⊥12P P ，所得OP 长度即为最小值，OP 2=OA =3，所以OP =32．【2019宿迁中考】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE =1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在1G 位置，最终G 点在2G 位置（2G 不一定在CD 边），12G G 即为G 点运动轨迹．G 2CG 最小值即当CG ⊥12G G 的时候取到，作CH ⊥12G G 于点H ，CH 即为所求的最小值．GABCDEF根据模型可知：12G G 与AB 夹角为60°，故12G G ⊥1EG ．过点E 作EF ⊥CH 于点F ，则HF =1G E =1，CF =1322CE =，所以CH =52，因此CG 的最小值为52．G 2三、轨迹之其他图形篇所谓“瓜豆原理”，就是主动点的轨迹与从动点的轨迹是相似性，根据主、从动点与定点连线形成的夹角以及主、从动点到定点的距离之比，可确定从动点的轨迹，而当主动点轨迹是其他图形时，从动点轨迹必然也是．【2016乐山中考】如图，在反比例函数2y x=-的图像上有一个动点A ，连接AO 并延长交图像的另一支于点B ，在第一象限内有一点C ，满足AC =BC ，当点A 运动时，点C 始终在函数ky x=的图像上运动，若tan ∠CAB =2，则k的值为（ ）A ．2B ．4C ．6D ．8【分析】∠AOC=90°且AO:OC=1:2，显然点C的轨迹也是一条双曲线，分别作AM、CN垂直x轴，垂足分别为M、N，连接OC，易证△AMO∽△ONC，∴CN=2OM，ON=2AM，∴ON·CN=4AM·OM，故k=4×2=8．【思考】若将条件“tan∠CAB=2”改为“△ABC是等边三角形”，k会是多少？【练习】如图，A（-1,1），B（-1,4），C（-5,4），点P是△ABC边上一动点，连接OP，以OP为斜边在OP的右上方作等腰直角△OPQ，当点P在△ABC边上运动一周时，点Q的轨迹形成的封闭图形面积为________．【分析】根据△OPQ是等腰直角三角形可得：Q点运动轨迹与P点轨迹形状相同，根据OP:OQ，可得P点轨迹图形与Q，故面积比为2:1，△ABC面积为1/2×3×4=6，故Q点轨迹形成的封闭图形面积为3．【小结】根据瓜豆原理，类似这种求从动点轨迹长或者轨迹图形面积，根据主动点轨迹推导即可，甚至无需作图．【练习】如图所示，AB =4，AC =2，以BC 为底边向上构造等腰直角三角形BCD ，连接AD 并延长至点P ，使AD =PD ，则PB 的取值范围为___________．ABCDP【分析】固定AB 不变，AC =2，则C 点轨迹是以A 为圆心，2为半径的圆，以BC 为斜边作等腰直角三角形BCD ，则D 点轨迹是以点M考虑到AP =2AD ，故P 点轨迹是以N 为圆心，即可求出PB 的取值范围．。

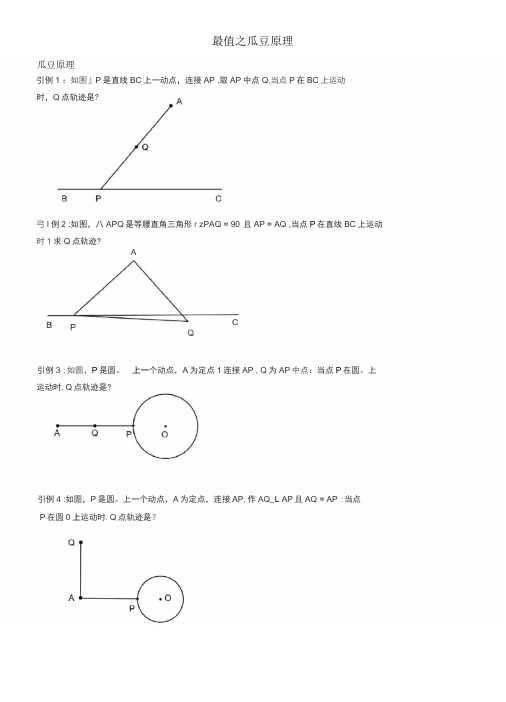
最值之瓜豆原理瓜豆原理引例1 ：如图」P是直线BC上一动点，连接AP ,取AP中点Q,当点P在BC上运动时，Q点轨迹是?弓I例2 :如图，八APQ是等腰直角三角形r zPAQ = 90°且AP = AQ ,当点P在直线BC上运动时1求Q点轨迹?A引例3 :如圄，P是圆。

上一个动点，A为定点1连接AP , Q为AP中点：当点P在圆。

上运动时.Q点轨迹是?引例4 :如圄，P是圆。

上一个动点，A为定点，连接AP,作AQ_L AP且AQ = AP :当点P在圆0上运动时.Q点轨迹是？称点P为“主动点"点Q为"从动点二此类问题的必要条件：两个足量：(1 )主动点、从动点与定点连线的夹角是定量(/PAQ是定值)(2 )主动点、从动点到定点的距离之比是定量(AP:AQ是定值)按以上两点即可确定从动点轨迹圆，。

与P的关系相当于旋转+伸能.古人云：种瓜得瓜,种豆得豆，“种’圆得圆「种”线得线」称之‘瓜豆原理’N如圄，P是圆O上一个动点.A为定点，连接AP ,以AP为斜边作等腰直角&APQ 当点P在圆0上运动时，如何作出Q点轨迹？3 .如图「已知AB=2」点D是等腰Rt .ABC斜边AC上的一动点」以BD为一边向右下方作等边心BDE1当动点D由点A运动到点C时，求动点E运动的轨迹长.变式1如图11，已知AB=2 ,点D是等腰R3ABC斜边AC上的一动点『以BD为一边向右下方作以ZE为直角的等膜Rt'SDE」当动点口由点A运动到点C时，求动点E运动的轨迹长.变式2.如图2 ,已知AB = 2,点口是等腰R6ABC斜边AC上的一动点，以BD为一边向右下方作以zBDE为直角的等暧Rt^BDE ,当动点D由点A运动到点C时，求动点E运动的轨迹长变式3.如图1 ,已知AB=2 ,点D是等腰Rt^ABC斜边AC上的一动点，以BD为一边向右下方作正方形BDEF ,当动点D由点A运动到点C时，求动点E运动的轨迹长.变式4.如图2 r已知AB=2 ,点D是等腰R3ABC斜边AC上的一动点，以BD为一边向右下方作等腰A BDE ,且顶角ZBDE = 120。

最值系列之瓜豆原理轨迹之线段篇引例：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q 点轨迹是？【分析】当P点轨迹是直线时，Q点轨迹也是一条直线．可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．【引例】如图，△APQ是等腰直角三角形，∠P AQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q点的起始位置和终点位置，连接即得Q点轨迹线段．Q2AB CQ1【模型总结】必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．结论：P、Q两点轨迹所在直线的夹角等于∠P AQ（当∠P AQ≤90°时，∠P AQ等于MN与BC夹角）P、Q两点轨迹长度之比等于AP:AQ（由△ABC∽△AMN，可得AP:AQ=BC:MN）【2017姑苏区二模】如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连结PD，以PD为边，在PD的右侧按如图所示的方式作等边△DPF，当点P从点E运动到点A时，点F运动的路径长是________．A【分析】根据△DPF是等边三角形，所以可知F点运动路径长与P点相同，P从E点运动到A点路径长为8，故此题答案为8．【2013湖州中考】如图，已知点A是第一象限内横坐标为AC⊥x轴于点M，交直线y=-x于点N，若点P是线段ON上的一个动点，∠APB=30°，BA⊥P A，则点P 在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是________．【分析】根据∠P AB=90°，∠APB=30°可得：AP:AB，故B点轨迹也是线段，且P点轨迹路径长与B，P点轨迹长ON为B点轨迹长为【练习】如图，在平面直角坐标系中，A（-3,0），点B是y轴正半轴上一动点，点C、D在x正半轴上，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．【分析】求OP 最小值需先作出P 点轨迹，根据△ABP 是等边三角形且B 点在直线上运动，故可知P 点轨迹也是直线．取两特殊时刻：（1）当点B 与点O 重合时，作出P 点位置P 1；（2）当点B 在x 轴上方且AB 与x 轴夹角为60°时，作出P 点位置P 2．连接P 1P 2，即为P 点轨迹．根据∠ABP =60°可知：12P P 与y 轴夹角为60°，作OP ⊥12P P ，所得OP 长度即为最小值，OP 2=OA =3，所以OP =32．【2019宿迁中考】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE =1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在1G 位置，最终G 点在2G 位置（2G 不一定在CD 边），12G G 即为G 点运动轨迹．GABCDEFG 2CG 最小值即当CG ⊥12G G 的时候取到，作CH ⊥12G G 于点H ，CH 即为所求的最小值． 根据模型可知：12G G 与AB 夹角为60°，故12G G ⊥1EG ．过点E 作EF ⊥CH 于点F ，则HF =1G E =1，CF =1322CE ，所以CH =52，因此CG 的最小值为52．G 2。

瓜豆原理---主从联动（放缩旋转）
首先这个题目很有意思，出自成语“种瓜得瓜，种豆得豆”。

它实质上反映了事物的内在联系和必然性。

在这里，我们类比的是，在一类动点问题中，一个动点随另一个动点的运动而运动，我们把它们分别叫做主动点和从动点，主动点怎么动，从动点就跟着怎么动，即所谓的“种瓜得瓜，种豆得豆”。

今天我们就来研究这类双动点问题。

瓜豆原理实质就是双动点运动轨迹问题，主动点是瓜，从动点是豆，瓜在直线上运动，豆的运动轨迹就是直线，瓜在圆周上运动，豆的运动轨迹就是圆。

瓜豆原理的条件是，主动点、从动点与定点连线的夹角为定量，主动点和从动点到定点的距离之比为定量。

瓜豆原理将几何中最难的双动点问题，用通俗易懂成语描述出来，让我们不仅产生了浓厚的研究兴趣，而且将找动点轨迹这一有难度的问题成功的化解，用旋转加位似来解决，从而帮我们建立起解决问题的模型。

瓜豆原理就是几何最值问题中的一朵奇葩。

瓜豆瓜豆，主从联动；
种瓜得瓜，种豆得豆；
瓜圆豆圆，瓜线豆线；
定角定比，放缩旋转。

中考专题 ----- 路径之瓜豆原理知识必备一、旋转及性质1.旋转的定义:一个图形绕点沿定方向旋转定的角度；2.旋转三要素:①旋转中心（绕哪个点转）；②旋转方向（顺时针或逆时针）；③旋转角度；3.旋转的性质:①旋转不改变图形的大小与形状，只改变图形的位置，即旋转前后图形全等;②对应点与旋转中心所连线段间的夹角等于旋转角.二、位似及性质1.位似的定义:若两个图形F和F的点之间可以建立一对应关系,并且满足:①每组对应点的连线所在的直线都经过同一点O；②每组对应点都在点O的同侧或异侧;③对每组对应点A 和OAA',有4 k（k为常数），则称图形F和F位似,k叫位似比；OA2.位似三要素:①位似中心（关于哪个点位似）；②位似方向（同侧或异侧）；③位似比（等于相似比）；3.位似的性质:成位似的两个图形必相似：把一个几何图形变换成与之位似的图形,叫做位似变换；利用位似变换可把一个图形放大或缩小，若位似比大于1，则通过位似变换把原图形放大；若位似比小于1.则通过位似变换把原图形缩小。

方法提炼一.旋转作图问题1：在平面内有两点A.B.请将点B绕点人按顺时针方向旋转40°.二、位似作图1问题2：如图:.已知线段AB，请以点A为位似中心1为位似比，在同侧将线段AB进行位似3变换。

「三、模型建立1 / 13(一)旋转变换问题3:(1)如图14-2-5,已知等腰Rt^APQ.其中A为定点，根据旋转作图的经验，请你说说: 点Q可以看作点P经过怎样的变换得到？(2)如图14-2-6.若改为等边AAPQ呢？⑶如图1-27.若改为任意等腰4APQ(其顶角为o)呢？问题4:在问题3中，若点P在一条定直线l上运动，其他条件不变如图14-2-8至图14-2-10 所示，请问：点Q的运动路径是什么？它可以看作点P的路径如何而来？问题5:在问题4中，若将“定直线1”改为“定。

0〃 .其他条件不变，结果如何?反思：这里是“圆生圆”；注意:点Q所在的轨迹圆圆心0’也是原来的圆心0定点A经过相应的旋转而来;2 / 13总结：这里仅牵扯到“旋转变换”不妨称P 为主动点。

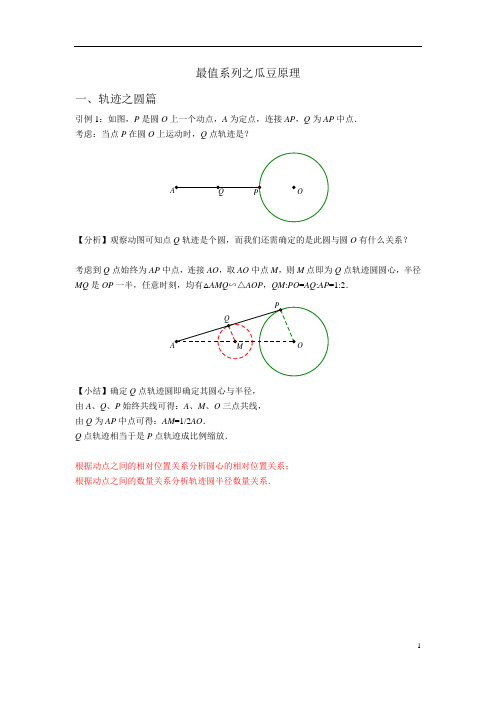
最值系列之瓜豆原理一、轨迹之圆篇引例1：如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．考虑：当点P在圆O上运动时，Q点轨迹是？【分析】观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．【小结】确定Q点轨迹圆即确定其圆心与半径，由A、Q、P始终共线可得：A、M、O三点共线，由Q为AP中点可得：AM=1/2AO．Q点轨迹相当于是P点轨迹成比例缩放．根据动点之间的相对位置关系分析圆心的相对位置关系；根据动点之间的数量关系分析轨迹圆半径数量关系．引例2：如图，P是圆O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．考虑：当点P在圆O上运动时，Q点轨迹是？Q【分析】Q点轨迹是个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P 点轨迹都是圆．接下来确定圆心与半径．考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．即可确定圆M位置，任意时刻均有△APO≌△AQM．引例3：如图，△APQ是直角三角形，∠P AQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？【分析】考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1．即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．【模型总结】为了便于区分动点P、Q，可称点P为“主动点”，点Q为“从动点”．此类问题的必要条件：两个定量主动点、从动点与定点连线的夹角是定量（∠P AQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．Q【结论】（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：∠P AQ=∠OAM；（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比：AP:AQ=AO:AM，也等于两圆半径之比．按以上两点即可确定从动点轨迹圆，Q与P的关系相当于旋转+伸缩．古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．【思考1】：如图，P是圆O上一个动点，A为定点，连接AP，以AP为一边作等边△APQ．考虑：当点P在圆O上运动时，Q点轨迹是？【分析】Q点满足（1）∠P AQ=60°；（2）AP=AQ，故Q点轨迹是个圆：考虑∠P AQ=60°，可得Q点轨迹圆圆心M满足∠MAO=60°；考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．即可确定圆M位置，任意时刻均有△APO≌△AQM．【小结】可以理解AQ由AP旋转得来，故圆M亦由圆O旋转得来，旋转角度与缩放比例均等于AP与AQ的位置和数量关系．【思考2】如图，P是圆O上一个动点，A为定点，连接AP，以AP为斜边作等腰直角△APQ．考虑：当点P在圆O上运动时，如何作出Q点轨迹？【分析】Q点满足（1）∠P AQ=45°；（2）AP:AQ1，故Q点轨迹是个圆．连接AO，构造∠OAM=45°且AO:AM：1．M点即为Q点轨迹圆圆心，此时任意时刻均有△AOP∽△AMQ．即可确定点Q的轨迹圆．【练习】如图，点P（3,4），圆P半径为2，A（2.8,0），B（5.6,0），点M是圆P上的动点，点C是MB的中点，则AC的最小值是_______．【分析】M点为主动点，C点为从动点，B点为定点．考虑C是BM中点，可知C点轨迹：取BP中点O，以O为圆心，OC为半径作圆，即为点C轨迹．当A、C、O三点共线且点C在线段OA上时，AC取到最小值，根据B、P坐标求O，利用两点间距离公式求得OA，再减去OC即可．【2016武汉中考】如图，在等腰Rt △ABC 中，AC =BC=P 在以斜边AB 为直径的半圆上，M 为PC 的中点，当半圆从点A 运动至点B 时，点M 运动的路径长为________．【分析】考虑C 、M 、P 共线及M 是CP 中点，可确定M 点轨迹：取AB 中点O ，连接CO 取CO 中点D ，以D 为圆心，DM 为半径作圆D 分别交AC 、BC 于E 、F 两点，则弧EF 即为M 点轨迹．当然，若能理解M 点与P 点轨迹关系，可直接得到M点的轨迹长为P 点轨迹长一半，即可解决问题．【2018南通中考】如图，正方形ABCD 中，AB O 是BC 边的中点，点E 是正方形内一动点，OE =2，连接DE ，将线段DE 绕点D 逆时针旋转90°得DF ，连接AE 、CF ．求线段OF 长的最小值．OABCDE F【分析】E 是主动点，F 是从动点，D 是定点，E 点满足EO =2，故E 点轨迹是以O 为圆心，2为半径的圆．F考虑DE⊥DF且DE=DF，故作DM⊥DO且DM=DO，F点轨迹是以点M为圆心，2为半径的圆．直接连接OM，与圆M交点即为F点，此时OF最小．可构造三垂直全等求线段长，再利用勾股定理求得OM，减去MF即可得到OF的最小值．【练习】△ABC 中，AB =4，AC =2，以BC 为边在△ABC 外作正方形BCDE ，BD 、CE 交于点O ，则线段AO 的最大值为_____________．AB CDE O【分析】考虑到AB 、AC 均为定值，可以固定其中一个，比如固定AB ，将AC 看成动线段，由此引发正方形BCED 的变化，求得线段AO 的最大值．根据AC =2，可得C 点轨迹是以点A 为圆心，2为半径的圆．OEDCBA接下来题目求AO 的最大值，所以确定O 点轨迹即可，观察△BOC 是等腰直角三角形，锐角顶点C 的轨迹是以点A 为圆心，2为半径的圆，所以O 点轨迹也是圆，以AB 为斜边构造等腰直角三角形，直角顶点M 即为点O 轨迹圆圆心．连接AM 并延长与圆M 交点即为所求的点O ，此时AO 最大，根据AB 先求AM ，再根据BC 与BO 的比值可得圆M 的半径与圆A 半径的比值，得到MO ，相加即得AO ．此题方法也不止这一种，比如可以如下构造旋转，当A 、C 、A ’共线时，可得AO最大值．A'或者直接利用托勒密定理可得最大值．二、轨迹之线段篇引例：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？【分析】当P点轨迹是直线时，Q点轨迹也是一条直线．可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．【引例】如图，△APQ是等腰直角三角形，∠P AQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q 点的起始位置和终点位置，连接即得Q点轨迹线段．Q2AB CQ1【模型总结】 必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP :AQ 是定值）． 结论：P 、Q 两点轨迹所在直线的夹角等于∠P AQ （当∠P AQ ≤90°时，∠P AQ 等于MN 与BC 夹角）P 、Q 两点轨迹长度之比等于AP :AQ （由△ABC ∽△AMN ，可得AP :AQ =BC :MN ）【2017姑苏区二模】如图，在等边△ABC 中，AB =10，BD =4，BE =2，点P 从点E 出发沿EA 方向运动，连结PD ，以PD 为边，在PD 的右侧按如图所示的方式作等边△DPF ，当点P 从点E 运动到点A 时，点F 运动的路径长是________．A【分析】根据△DPF 是等边三角形，所以可知F 点运动路径长与P 点相同，P 从E 点运动到A 点路径长为8，故此题答案为8．【2013湖州中考】如图，已知点A是第一象限内横坐标为AC⊥x轴于点M，交直线y=-x于点N，若点P是线段ON上的一个动点，∠APB=30°，BA⊥P A，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O 运动到点N时，点B运动的路径长是________．【分析】根据∠P AB=90°，∠APB=30°可得：AP:AB，故B点轨迹也是线段，且P点轨迹路径长与B，P点轨迹长ON为B点轨迹长为【练习】如图，在平面直角坐标系中，A（-3,0），点B是y轴正半轴上一动点，点C、D在x正半轴上，以AB为边在AB的下方作等边△ABP，点B在y轴上运动时，求OP的最小值．【分析】求OP是等边三角形且B点在直线上运动，故可知P点轨迹也是直线．取两特殊时刻：（1）当点B与点O重合时，作出P点位置P1；（2）当点B在x轴上方且AB与x轴夹角为60°时，作出P点位置P2．连接P1P2，即为P点轨迹．根据∠ABP =60°可知：12P P 与y 轴夹角为60°，作OP ⊥12P P ，所得OP 长度即为最小值，OP 2=OA =3，所以OP =32．【2019宿迁中考】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE =1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．GABCDEF【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在1G 位置，最终G 点在2G 位置（2G 不一定在CD 边），12G G 即为G 点运动轨迹．G 2CG 最小值即当CG ⊥12G G 的时候取到，作CH ⊥12G G 于点H ，CH 即为所求的最小值．根据模型可知：12G G 与AB 夹角为60°，故12G G ⊥1EG ．过点E 作EF ⊥CH 于点F ，则HF =1G E =1，CF =1322CE =，所以CH =52，因此CG 的最小值为52．G 2三、轨迹之其他图形篇所谓“瓜豆原理”，就是主动点的轨迹与从动点的轨迹是相似性，根据主、从动点与定点连线形成的夹角以及主、从动点到定点的距离之比，可确定从动点的轨迹，而当主动点轨迹是其他图形时，从动点轨迹必然也是．【2016乐山中考】如图，在反比例函数2y x=-的图像上有一个动点A ，连接AO 并延长交图像的另一支于点B ，在第一象限内有一点C ，满足AC =BC ，当点A 运动时，点C 始终在函数ky x=的图像上运动，若tan ∠CAB =2，则k的值为（ ）A ．2B ．4C ．6D ．8【分析】∠AOC=90°且AO:OC=1:2，显然点C的轨迹也是一条双曲线，分别作AM、CN垂直x轴，垂足分别为M、N，连接OC，易证△AMO∽△ONC，∴CN=2OM，ON=2AM，∴ON·CN=4AM·OM，故k=4×2=8．【思考】若将条件“tan∠CAB=2”改为“△ABC是等边三角形”，k会是多少？【练习】如图，A（-1,1），B（-1,4），C（-5,4），点P是△ABC边上一动点，连接OP，以OP为斜边在OP的右上方作等腰直角△OPQ，当点P在△ABC边上运动一周时，点Q的轨迹形成的封闭图形面积为________．【分析】根据△OPQ是等腰直角三角形可得：Q点运动轨迹与P点轨迹形状相同，根据OP:OQ，可得P点轨迹图形与Q，故面积比为2:1，△ABC面积为1/2×3×4=6，故Q点轨迹形成的封闭图形面积为3．【小结】根据瓜豆原理，类似这种求从动点轨迹长或者轨迹图形面积，根据主动点轨迹推导即可，甚至无需作图．【练习】如图所示，AB =4，AC =2，以BC 为底边向上构造等腰直角三角形BCD ，连接AD 并延长至点P ，使AD =PD ，则PB 的取值范围为___________．ABCDP【分析】固定AB 不变，AC =2，则C 点轨迹是以A 为圆心，2为半径的圆，以BC 为斜边作等腰直角三角形BCD ，则D 点轨迹是以点M考虑到AP =2AD ，故P 点轨迹是以N 为圆心，即可求出PB 的取值范围．。

瓜豆原理原理概述俗语云“种瓜得瓜，种豆得豆”，数学上有“种线得线，种圆得圆”：平面内，动点Q 随着动点P 的运动而运动，我们把点P 叫做主动点，点Q 叫做从动点；当这两个动点与某个定点连线的夹角一定，且与该定点距离之比一定时（简记为“定角、定比”），易判断两个动点与定点构成的三角形形状一定，大小可能变，此时两个动点的轨迹形状相同,瓜豆问题的本质是旋转、相似（包含全等）变换，往往与共点旋转（手拉手）模型相结合，考查类型有：（1）确定动点轨迹；（2）求运动路程；（3）求线段最值、面积最值等.基本模型一、种直线得直线（主动点与从动点的轨迹都是直线或直线上一部分）1.图1图2如图1，已知l 为定直线，O 为直线外一定点，P 为直线l 上一动点，连接OP，若Q 为直线OP 上一点（一般在线段OP 上），且Q 点到O 点的距离与P 点到O 点的距离之比为定值k（k＞0且k≠1），即k OP OQ =，此时我们可认为Q、P 两点与定点O 连线的夹角一定（夹角为0°），符合瓜豆原理“定角、定比”的条件，因而Q 点的运动轨迹也是直线；如图2，另取一组对应的点P’、Q’,则k OP OQ P O Q O ==''，因而△OQ’Q∽△OP’P，相似比为k，可知从动点Q 在平行于l 的直线m 上运动.易判断点O 到直线m 和l 的距离之比也等于k.2.图1图2如图1，已知l 为定直线，O 为直线外一定点，P 为直线l 上一动点，将射线OP 绕着点O 按确定的方向（如顺时针）旋转一个确定的角度α（0＜α＜180°），得到射线OM，在射线OM 上取一点Q，使k OP OQ=（k 为大于0的定值），此时符合瓜豆原理“定角、定比”的条件，因而Q 点的运动轨迹也是直线；如图2，另取一组对应的点P’、Q’,则Q 点的运动轨迹即为直线QQ’，∵∠POQ=∠P’OQ’=α，∴∠POP’=∠QOQ’，又∵k P O Q O OP OQ ==''，∴△OPP’∽△OQQ’.特别的，当k=1时，△OPP’≌△OQQ’.k≠1时，△OQQ’可看做由△OPP’绕着O 点旋转并放缩（0＜k＜1时缩小，k＞1时放大）而来.直线QQ’可看做由直线l 绕着点O 顺时针旋转α角而来，0＜α＜90°时，两直线的夹角即为α.典型例题1-1如图，在平面直角坐标系中，A（4,0），B 为y 轴正半轴上一动点，以AB 为一边向下作等边△ABC，连接OC，则线段OC 的最小值为_________.【分析】B 为主动点，C 为从动点；方法一：与从动点有关的线段最值，优先转化为与主动点有关的线段最值，将线段OA绕着点A 顺时针旋转60°，得到线段O’A，构造全等三角形可实现线段的转化；方法二：两动点与定点A 连线的夹角为定值（60°），到点A 的距离之比为定值1（即CA:BA=1），符合瓜豆原理“定角、定比”的特征，主动点B 的轨迹为射线，则从动点C 的轨迹也为射线，确定其轨迹后，依据“垂线段最短”求OC 得最小值.【解答】方法一：如图1，将线段OA 绕着点A 顺时针旋转60°，得到线段O’A；连接O’B，易证△AO’B≌△AOC，则OC=O’B，即求O’B 的最小值；由于O’为定点，点B 在y 轴正半轴上运动，如图2，由垂线段最短，知O’B ⊥y 轴时，O’B 最小，连接OO’，则△AOO’为等边三角形，作O’H⊥OA 于H，此时O’B=OH=21OA=2，即OC 的最小值为2.图1图2方法二：如图3，当点B 位于原点时，对应的点C 位于1C （2，-23）处，当点B 位于2B （0，334）时，对应的点C 位于2C （0，-334）处，则点C 的运动轨迹为射线21C C ，当OC’⊥21C C 时，OC’最小；易证△O AB 2≌△12C AC ，∴∠12C AC =∠O AB 2=60°，则∠C OC '2=60°，∴OC’=223OC =2，即OC 的最小值为2.【小结】1.动点引起的最值问题，经常需要确定动点轨迹；图32.两种方法中，均有两个等边三角形构成“共点旋转（手拉手）”模型，会伴随产生一组全等三角形；3.方法二中，由于从动点的轨迹为射线，因而先确定其端点，再找一组特殊位置的主动点和从动点（目的是便于计算），即可确定从动点的轨迹；4.严格来说，y 轴的正半轴不包括原点，因此C 点的轨迹不包括点1C .典型例题1-2如图，正方形ABCD 的边长为4，动点E 从A 点出发，沿着AB边向终点B 作无折返运动，连接DE，以DE 为边向右上方作正方形DEFG，则点E 在整个运动过程中，点F 经过的路径长为______.【分析】E 为主动点，F 为从动点，依据正方形的性质，两动点与定点A 的连线夹角恒为45°，且始终有DF ：DE=2，符合瓜豆原理“定角、定比”的特征，故F 点的运动轨迹为线段，由临界情况确定该线段的两个端点，结合“共点旋转（手拉手）”相似模型，运用相似比计算该线段长.【解答】如图1，连接BF、BD 和DF，由正方形的性质知DE DF DA DB =2,图1∠BDA=∠FDE=45°，则∠ADE=∠BDF，∴△DAE∽△DBF，∴BF=2AE，当E 点位于A 点处时，F 点位于B 点处，当E 点位于B 点处时，F 点的位置如图2，则F 点的运动轨迹即为图2中的线段BF，BF=2AB=42，即点F 经过的路径长为42.图2【小结】1.图1中，△DAB 与△DEF 构成“共点旋转（手拉手）”模型，伴随产生一组相似三角形（△DAE 和△DBD）；2.瓜豆题型的突破口在于找到从动点、主动点和某定点之间的“定角、定比”关系.变式训练1-1如图，△ABC 为等边三角形，AB=4，AD 为高，E 为直线AD 上一动点，连接CE 并以CE 为边向下作等边△CEF ，连接DF ；则点E 在运动的过程中，线段DF 的最小值为_________.变式训练1-2（原创）如图，在△ABC 中，∠A=105°，∠ABC=30°，AC=2，动点D 从A 点出发，沿着AC 边向终点C 作无折返运动，以BD为边向上作△BDE ，使∠BDE=∠A ，且∠E=45°，则点D 运动的整个过程中，点E 运动的路径长为________；F 为直线CE上一动点，连接BF ，则线段BF 的最小值为_______.变式训练1-3（多种方法）如图，已知AB=12，点C 在线段AB 上，且AC=4，以AC 为一边向上作等边△ACD ，再以CD 为直角边向右作Rt △DCE ，使∠DCE=90°，F 为斜边DE 的中点，连接DF ，随着CE 边长的变化，BF 长也在改变，则BF 长的最小值为_________.二、种曲线得曲线（主动点与从动点的轨迹都是双曲线或双曲线一部分）其原理与模型一类似，不再赘述，直接看例题：典型例题2-1如图，点A 是双曲线x y 4=在第一象限上的一动点，连接AO并延长，交双曲线的另一支于点B，以AB 为斜边作等腰Rt△ABC，点C 落在第二象限内，随着点A 的运动，点C 的位置也在不断变化，但始终在同一函数图像上，则该函数解析式为___________.【分析】A 为主动点，C 为从动点；方法一：根据点C 坐标判断，连接CO 过点C 向x 轴作垂线段，构建“三垂直”模型，设点A 坐标，表示出点C 坐标，观察其坐标符合的函数解析式；方法二：根据反比例函数k 的几何意义判断；方法三：动点A 、C 与定点O 符合瓜豆原理“定角、定比”的特征，因而点C 的轨迹是双曲线的一支，任意的点C 均可看做对应的点A 绕着点O 逆时针旋转90°而来，因而点C 的轨迹可看做由原双曲线第一象限的一支绕点O 逆时针旋转得到.【解答】方法一：连接OC，作CD⊥x 轴于点D，AE⊥x 轴于点E，由双曲线的对称性知OA=OB，又∵△ABC 为等腰直角三角形，∴CO⊥OA，CO=OA，则易证△COD≌△OAE，设A（a,a 4）,则C（-a 4，a），易判断点C 在反比例函数y=-x 4（x＜0）上，故答案为：y=-x 4（x＜0）.方法二：辅助线同方法一，由反比例函数k 的几何意义知COD AOE S S ∆∆==2，易判断点C 在反比例函数y=-x 4（x＜0）上.方法三：点C 的轨迹可看做由原双曲线第一象限的一支绕点O 逆时针旋转得到，因而新反比例函数的k 与原函数k 互为相反数，故点C 在反比例函数y=-x 4（x＜0）上.变式训练2-1如图，Rt△ABO 中，∠AOB=90°，点A 在第一象限、点B 在第四象限，且AO：BO=1：，若点A（x 0，y 0）的坐标x 0，y 0满足y 0=，则点B（x，y）的坐标x，y 所满足的关系式为．三、种圆得圆（主动点与从动点的轨迹都是圆或圆弧）1.图1图2如图1，已知点P 为⊙M 上一动点，O 为定点（一般在圆外），Q 为直线OP 上一点（一般在线段OP 上），若OP OQ =k （k＞0且k≠1），则主动点P、从动点Q 与定点O 符合“定角（0°）、定比”特征，因而Q 点的轨迹也是圆，如何确定该圆的圆心和半径呢？如图2，连接MP、MO，作QN∥PM，交MO 于点N，则△OQN∽△OPM，从而有MP NQ OP OQ OM ON ===k,由于M、O 为定点，k 为定值，∴N 为定点，设⊙M 半径为R，⊙N 半径为r，∵NQ=kMP=kR,∴NQ 长为定值，由圆的定义知，点Q 在以N 为圆心，kR 长为半径的圆上运动,即Q 点的轨迹是以N 为圆心，kR 长为半径的圆.2.图1图2如图1，已知点P 为⊙M 上一动点，O 为定点（一般在圆外），将射线OP 绕着点O 按确定的方向（如顺时针）旋转一个确定的角度α（0＜α＜180°），得到射线OT，在射线OT 上有一点Q，满足OP OQ =k（k 为大于0的常数），则主动点P、从动点Q 与定点O 符合“定角、定比”的特征，因而Q 点的轨迹也是圆，如何确定该圆的圆心和半径呢？如图2，连接MP、MO，将射线OM 绕点O 顺时针旋转α角，得到射线OS，在射线OS 上取一点N，使OM ON =k,则N 为定点，易证△OQN∽OPM，则OP OQ PM QN =k，∴QN=kPM=kR,则QN 为定值，由圆的定义知，点Q 在以N 为圆心，kR 长为半径的圆上运动,即Q 点的轨迹是以N 为圆心，kR 长为半径的圆.特别的，当k=1时，△OQN≌OPM，⊙N 和⊙M 为等圆，⊙N 可看做由⊙M 绕着点O 顺时针旋转α角而来；当k≠1时，⊙N 可看做由⊙M 绕点O 顺时针旋转α角，且半径放缩k 倍（0＜k＜1时缩小，k＞1时放大）而来.典型例题3-1如图，在Rt△ABC 中，∠ACB=90°，AC=8，BC=6，点D 是以点A 为圆心4为半径的圆上一动点，连接BD，点M 为BD 中点，线段CM 长度的最大值为________．【分析】方法一：关联三角形法，取AB 的中点E，连接EC、EM 和AD，放到△CEM 中求解CM 的范围，三点共线时取最大值；方法二：辅助圆法，从动点相关的线段优先转化为主动点相关的线段，将线段BC 加倍延长，借助中位线构造出2CM，即求2CM 的最大值；方法三：符合瓜豆原理基本模型，确定从动点M 的轨迹圆，进而求CM 的最大值.【解答】方法一：如图1，取AB 的中点E，连接EC、EM 和AD，∵M 为BD 的中点，∴EM 为△BAD 的中位线，∴EM=21AD=2；∵∠ACB=90°，∴CE=21AB=5，CM≤CE+EM，即CM≤7，当且仅当C、E、M 共线时（如图2），CM 取得最大值7.图1图2方法二：如图3，延长BC 至点F，使CF=BC，则F 为定点，连接DF，则CM 为△BDF 的中位线，∴FD=2CM，当FD 最大时，CM 最大；如图4，连接FA 并延长，与⊙A 交于点D，此时FD 最大，易知AF=AB=10，则此时FD=14，对应CM 的最大值即为7.图3图4方法三：主动点D、从动点M 与定点B 符合“定角（0°）、定比”特征，因而点M 的轨迹为圆；如图5，连接AD，∵M 为BD 的中点，∴取AB 得中点E，连接EM，可知E 为定点且EM=21AD=2，根据圆的定义知，点M 的轨迹为以E 为圆心，2为半径的圆；如图6，∵C 为⊙E 外一定点，∴连接CE 并延长，与⊙E 交于点M，此时CM 最大，此时CM=CE+EM=7.图5图6【小结】以上方法中，辅助线均有一举多得之妙，我们可总结出一些常见的辅助线作法：①出现直角三角形：常作斜边的中线；②出现直角三角形：常倍长直角边，构造等腰三角形；③出现线段中点：常取另一线段的中点，构造中位线；④出现线段中点：常倍长另一线段，构造中位线.典型例题3-2（改编）如图，△ABC 中，AB=3，AC=2，以BC 为斜边作等腰Rt △BCD （与△ABC分布在直线BC 的两侧），连接AD ，则线段AD 的最大值为___________.【分析】方法一：∵△BCD 为等腰直角三角形，∴以AB 为斜边向下作等腰直角三角形，与△BCD 构成“共点旋转（手拉手）”模型，伴随产生一组相似三角形，用“关联三角形”法求出AD 的最大值.方法二：不妨固定AB 边，则主动点C 在以A 为圆心，2为半径的一段圆弧上运动，它与从动点D 、定点B 符合“定角、定比”特征，借助模型确定D 点的轨迹圆弧，求出AD 的最大值.【解答】方法一:如图1，以AB 为斜边向下作等腰Rt△BAE，连接DE，则△BAE ∽△BCD，从而易证△BAC∽△BED，∴21==AB BE AC DE ，∴DE=2AC =2，又AE=2232=AB ，∴AD≤AE+DE，即AD≤225，如图2，当且仅当A、E、D 三点共线时，AD 取得最大值，最大值为225.图1图2方法二：如图3，假定AB 边固定，则主动点C 在半圆（不包括端点G、H）上运动，从动点D 可看作由主动点C 绕着点B 顺时针旋转45°，且到点B 的距离缩至22倍而来，则将主动圆心A 按照相同的操作可得到从动圆心F，从动圆的半径缩小至主动圆半径的22（即构造△BDF∽△BCA，与构造“手拉手”模型本质相同），D 点在如图所示的半圆（不包括端点I、J）上运动，A 为⊙F 外一定点，∴当A、F、D 共线时，AD最大，最大值为AF+DF=225.图3【小结】1.方法一与方法二实质相同，只是方法二多了确定主动点轨迹、从动点轨迹的过程；2.由图2可知，当AD 取得最大值时，∠BAC=∠BDE=90°，∠BAD=∠CAD=45°，因而可以变换多种问法，如当AD取得最大值时，求∠BAD、∠BAC的大小，求BC长、BD长等；3.本题可稍稍加大难度，将“求AD得最大值”改为“求△ABD面积的最大值”（答案为4269 ，方法见视频讲解）；4.许多同学误将主动点和从动点的轨迹判断为完整的圆，虽不影响结论，但不够严谨.5.共点旋转与瓜豆可谓形影相伴模型，很多题往往用两种方法均可解答；变式训练3-1如图，一次函数y＝2x与反比例函数y＝x k（k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，连接AP，Q是AP的中点，连接OQ，已知OQ长的最大值为23，则k的值为______；BQ的最大值为________.变式训练3-2（原创）如图，在平面直角坐标系中，圆心在x轴正半轴上的⊙M交x轴的负半轴于点A（-1,0），交y轴正半轴于点B（0，3），交y轴负半轴于点C，动点P从点B出发，沿着⊙M顺时针向终点C做无折返运动，D（-2,0），在点P运动过程中，连接DP，Q为线段DP上一点且始终满足PQ=2DQ，则在整个运动过程中，点Q经过的路径长为_______；线段DQ扫过的区域面积为________.变式训练3-3（原创）如图，在平面直角坐标系中，A（2,0），B（-1,0），以OA为直径的圆上有两个动点C、D，连接BC，并以BC为直角边向逆时针方向作Rt△BCE，使∠CBE=90°，∠BEC=30°，连接CD、ED和BD，则C、D两点的位置在变化的过程中，△BCE面积的最大值与最小值之差为_______；线段DE的最小值为_________；当∠EBD最大时，线段BE和CD的数量关系是_____________.中考真题6在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰1.如图，点A是双曲线y=-xk上△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=x运动，则k的值为（）A.1B.2C.3D.42.如图，抛物线y＝x2﹣4与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ．则线段OQ的最大值是（）A．3B．C．D．43.如图，在矩形ABCD中，AB＝4，∠DCA＝30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE＝30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是．4.如图，矩形ABCD 中，AB ＝4，AD ＝2，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是（）A．2B．4C．D．5.如图，在等腰Rt△ABC 中，AC=BC=22，点P 在以斜边AB 为直径的半圆上，M 为PC 的中点，当点P 沿着半圆从点A 运动到点B 时，点M 运动的路径长为．6.如图，在矩形ABCD 中，AB ＝，AD ＝3，点P 是AD 边上的一个动点，连接BP ，作点A 关于直线BP 的对称点A 1，连接A 1C ，设A 1C 的中点为Q ，当点P 从点A 出发，沿边AD 运动到点D 时停止运动，点Q 的运动路径长为．7.如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE ＝1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为．8．如图，正方形ABCD中，AB=2，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D 逆时针旋转90°得DF，连接AE，CF．（1）求证：AE=CF；（2）若A，E，O三点共线，连接OF，求线段OF的长．（3）求线段OF长的最小值．参考答案变式训练1-11.变式训练1-2262+；2622+.变式训练1-36.变式训练2-1y=-x 2.变式训练3-12532，1051452+.变式训练3-298π；27839π+.变式训练3-343；3-3；BE=3CD.中考真题1.B2.C3.3344.D5.π6.33π7.258.（1）证明：如图1，由题意知：∠EDF=90°，ED=DF，∵四边形ABCD 是正方形，∴∠ADC=90°，AD=CD，∴∠ADC=∠EDF，即∠ADE+∠EDC=∠EDC+∠CDF，∴∠ADE=∠CDF，在△ADE 和△DCF 中，∵，∴△ADE≌△DCF，∴AE=CF；（2）如图2，过F 作OC 的垂线，交BC 的延长线于P，∵O 是BC 的中点，且AB=BC=2，∵A，E，O 三点共线，∴OB=，由勾股定理得：AO=5，∵OE=2，∴AE=5﹣2=3，由（1）知△ADE≌△DCF，∴∠DAE=∠DCF，CF=AE=3，∵∠BAD=∠DCP，∴∠OAB=∠PCF，∵∠ABO=∠P=90°，∴△ABO∽△CPF，∴==2，∴CP=2PF，设PF=x，则CP=2x，由勾股定理得：32=x 2+（2x）2，x=或﹣（舍去），∴FP=，OP=+=，由勾股定理得：OF==，（3）方法一：如图3，由于OE=2，所以E 点可以看作是以O 为圆心，2为半径的半圆上运动，延长BA 到P 点，使得AP=OC，连接PE，∵AE=CF，∠PAE=∠OCF，∴△PAE≌△OCF，∴PE=OF，当PE 最小时，为O、E、P 三点共线，OP===5，∴PE=OF=OP﹣OE=5﹣2，∴OF 的最小值是5﹣2．方法二：如图4，连接OD，将△ODE 绕点D 逆时针旋转90°得到△IDF，连接OI、OF，在Rt△OCD 中，OD=22CD OC +=5，在Rt△ODI 中，OI=22ID OD +=52，∵OF≥OI-FI，而FI=OE=2，∴OF≥52-2，即OF 的最小值是5﹣2．。

中考数学最值——瓜豆原理问题【问题背景】古人云：“种瓜得瓜，种豆得豆”。

因此引申出“种圆得圆，种线得线”称之为瓜豆原理。

【知识储备】①相似；②三角形的两边之和大于第三边；③点到直线之间的距离垂线段最短；④点到圆上点共线有最值。

【模型分析】①条件：○O外有一定点A，P为圆上一动点，连接AP，Q为线段AP的中点。

②问题：P在何处时，QP的值最小。

③方法：第一步：找主动点的轨迹；第二步：找从动点与主动点的关系；第三步：找主动点的起点和终点；第四步：通过相似确定从动点的轨迹；第五步：根据轨迹确定点线、点圆最值。

轨迹总结：常见的是线段和圆。

【经典例题】如图，点P（3，4），⊙P的半径为2，A（2.8，0），B（5.6，0），M是⊙P 上的动点，C是MB的中点，则AC的最小值是。

【巩固训练】类型一：轨迹是圆的最值问题练习1：如图,在等腰Rt△ABC中,AC=BC=2√2,点P在以斜边AB为直径的半圆上,M为PC的中点。

当点P沿半圆从点A运动至点B时,点M运动的路径长是( )A.√2πB.πC.2√2D.2练习2：如图，正方形ABCD中，AB=2√5，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得到DF，连接AE，CF。

求线段OF长的最小值。

练习3：△ABC中， AB=4，AC=2，以BC为边在三角形外做正方形BCDE，连接BD，CE交于点O，则线段AO的最大值为。

练习4：如图，在平面直角坐标系中，已知A（2，0），B（5，0），点P为线段AB外一动点，且PA=2，以PB为边作等边△PBM，则线段AM的最大值为（）A.3B.5C.7D.√21练习5：如图，已知△ABC中，∠ACB=90°，BC=4，AC=8，点D在AC上，且AD=6，将线段AD绕点A旋转至AD’，F为BD’的中点，连结CF，则线段CF的取值范围。

类型二：轨迹是线段的最值问题练习6：如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连结PD，以PD为边，在PD的右侧按如图所示的方式作等边△DPF，当点P从点E运动到点A 时，点F运动的路径长是_ __。

最值系列之瓜豆原理在辅助圆问题中，我们了解了求关于动点最值问题的方式之一——求出动点轨迹，即可求出关于动点的最值．本文继续讨论另一类动点引发的最值问题，在此类题目中，题目或许先描述的是动点P，但最终问题问的可以是另一点Q，当然P、Q之间存在某种联系，从P点出发探讨Q点运动轨迹并求出最值，为常规思路．一、轨迹之圆篇引例1：如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．考虑：当点P在圆O上运动时，Q点轨迹是？A OQP【分析】观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．PQA MO【小结】确定Q点轨迹圆即确定其圆心与半径，由A、Q、P始终共线可得：A、M、O三点共线，由Q为AP中点可得：AM=1/2AO．Q点轨迹相当于是P点轨迹成比例缩放．根据动点之间的相对位置关系分析圆心的相对位置关系；根据动点之间的数量关系分析轨迹圆半径数量关系．引例2：如图，P 是圆O 上一个动点，A 为定点，连接AP ，作AQ ⊥AP 且AQ =AP ． 考虑：当点P 在圆O 上运动时，Q 点轨迹是？OP QA【分析】Q 点轨迹是个圆，可理解为将AP 绕点A 逆时针旋转90°得AQ ，故Q 点轨迹与P点轨迹都是圆．接下来确定圆心与半径．考虑AP ⊥AQ ，可得Q 点轨迹圆圆心M 满足AM ⊥AO ；考虑AP =AQ ，可得Q 点轨迹圆圆心M 满足AM =AO ，且可得半径MQ =PO ． 即可确定圆M 位置，任意时刻均有△APO ≌△AQM ．MA QPO引例3：如图，△APQ 是直角三角形，∠P AQ =90°且AP =2AQ ，当P 在圆O 运动时，Q 点轨迹是？OPQA【分析】考虑AP ⊥AQ ，可得Q 点轨迹圆圆心M 满足AM ⊥AO ； 考虑AP :AQ =2:1，可得Q 点轨迹圆圆心M 满足AO :AM =2:1． 即可确定圆M 位置，任意时刻均有△APO ∽△AQM ，且相似比为2．OPQM A【模型总结】为了便于区分动点P 、Q ，可称点P 为“主动点”，点Q 为“从动点”．此类问题的必要条件：两个定量主动点、从动点与定点连线的夹角是定量（∠P AQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP :AQ 是定值）．αA QPOααOPQMA【结论】（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角： ∠P AQ =∠OAM ；（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比： AP :AQ =AO :AM ，也等于两圆半径之比．按以上两点即可确定从动点轨迹圆，Q 与P 的关系相当于旋转+伸缩．古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．【思考1】：如图，P 是圆O 上一个动点，A 为定点，连接AP ，以AP 为一边作等边△APQ ． 考虑：当点P 在圆O 上运动时，Q 点轨迹是？OPA Q【分析】Q 点满足（1）∠P AQ =60°；（2）AP =AQ ，故Q 点轨迹是个圆： 考虑∠P AQ =60°，可得Q 点轨迹圆圆心M 满足∠MAO =60°；考虑AP =AQ ，可得Q 点轨迹圆圆心M 满足AM =AO ，且可得半径MQ =PO ． 即可确定圆M 位置，任意时刻均有△APO ≌△AQM ．60°MQAPO【小结】可以理解AQ 由AP 旋转得来，故圆M 亦由圆O 旋转得来，旋转角度与缩放比例均等于AP 与AQ 的位置和数量关系．【思考2】如图，P 是圆O 上一个动点，A 为定点，连接AP ，以AP 为斜边作等腰直角△APQ ． 考虑：当点P 在圆O 上运动时，如何作出Q 点轨迹？OPQA【分析】Q 点满足（1）∠P AQ =45°；（2）AP :AQ ：1，故Q点轨迹是个圆．连接AO ，构造∠OAM =45°且AO :AM 1．M 点即为Q 点轨迹圆圆心，此时任意时刻均有△AOP ∽△AMQ ．即可确定点Q 的轨迹圆．MOPQA【练习】如图，点P （3,4），圆P 半径为2，A （2.8,0），B （5.6,0），点M 是圆P 上的动点，点C 是MB 的中点，则AC 的最小值是_______．OyxA B CM P【分析】M 点为主动点，C 点为从动点，B 点为定点．考虑C 是BM 中点，可知C 点轨迹：取BP 中点O ，以O 为圆心，OC 为半径作圆，即为点C 轨迹．OOyxABC M P当A 、C 、O 三点共线且点C 在线段OA 上时，AC 取到最小值，根据B 、P 坐标求O ，利用两点间距离公式求得OA ，再减去OC 即可．OPMCBAxyO【2016武汉中考】如图，在等腰Rt △ABC 中，AC =BC=P 在以斜边AB 为直径的半圆上，M 为PC 的中点，当半圆从点A 运动至点B 时，点M 运动的路径长为________．A BC MP【分析】考虑C 、M 、P 共线及M 是CP 中点，可确定M 点轨迹：取AB 中点O ，连接CO 取CO 中点D ，以D 为圆心，DM 为半径作圆D 分别交AC 、BC 于E 、F 两点，则弧EF 即为M 点轨迹．DEFOABCM P当然，若能理解M 点与P 点轨迹关系，可直接得到M 点的轨迹长为P 点轨迹长一半，即可解决问题．【2018南通中考】如图，正方形ABCD 中，AB O 是BC 边的中点，点E 是正方形内一动点，OE =2，连接DE ，将线段DE 绕点D 逆时针旋转90°得DF ，连接AE 、CF ．求线段OF 长的最小值．OABCDE F【分析】E 是主动点，F 是从动点，D 是定点，E 点满足EO =2，故E 点轨迹是以O 为圆心，2为半径的圆．FE DCBAO考虑DE ⊥DF 且DE =DF ，故作DM ⊥DO 且DM =DO ，F 点轨迹是以点M 为圆心，2为半径的圆．OABCDEFM直接连接OM ，与圆M 交点即为F 点，此时OF 最小．可构造三垂直全等求线段长，再利用勾股定理求得OM ，减去MF 即可得到OF 的最小值．OABCDE FM【练习】△ABC 中，AB =4，AC =2，以BC 为边在△ABC 外作正方形BCDE ，BD 、CE 交于点O ，则线段AO 的最大值为_____________．AB CDE O【分析】考虑到AB 、AC 均为定值，可以固定其中一个，比如固定AB ，将AC 看成动线段，由此引发正方形BCED 的变化，求得线段AO 的最大值．根据AC =2，可得C 点轨迹是以点A 为圆心，2为半径的圆．OEDCBA接下来题目求AO 的最大值，所以确定O 点轨迹即可，观察△BOC 是等腰直角三角形，锐角顶点C 的轨迹是以点A 为圆心，2为半径的圆，所以O 点轨迹也是圆，以AB 为斜边构造等腰直角三角形，直角顶点M 即为点O 轨迹圆圆心．E DM ABCO连接AM 并延长与圆M 交点即为所求的点O ，此时AO 最大，根据AB 先求AM ，再根据BC 与BO 的比值可得圆M 的半径与圆A 半径的比值，得到MO ，相加即得AO ．OCBAM DE此题方法也不止这一种，比如可以如下构造旋转，当A 、C 、A ’共线时，可得AO 最大值．AB CDEOA'或者直接利用托勒密定理可得最大值．二、轨迹之线段篇引例：如图，P 是直线BC 上一动点，连接AP ，取AP 中点Q ，当点P 在BC 上运动时，Q 点轨迹是？PQABC【分析】当P 点轨迹是直线时，Q 点轨迹也是一条直线．可以这样理解：分别过A 、Q 向BC 作垂线，垂足分别为M 、N ，在运动过程中，因为AP =2AQ ，所以QN 始终为AM 的一半，即Q 点到BC 的距离是定值，故Q 点轨迹是一条直线．N CBAQP M【引例】如图，△APQ 是等腰直角三角形，∠P AQ =90°且AP =AQ ，当点P 在直线BC 上运动时，求Q 点轨迹？CBAQP【分析】当AP 与AQ 夹角固定且AP :AQ 为定值的话，P 、Q 轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q 点的位置，连线即可，比如Q 点的起始位置和终点位置，连接即得Q 点轨迹线段．Q 2Q 1ABC【模型总结】 必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ 是定值）； 主动点、从动点到定点的距离之比是定量（AP :AQ 是定值）． 结论：P 、Q 两点轨迹所在直线的夹角等于∠P AQ （当∠P AQ ≤90°时，∠P AQ 等于MN 与BC 夹角）MNααPQ A BCP 、Q 两点轨迹长度之比等于AP :AQ （由△ABC ∽△AMN ，可得AP :AQ =BC :MN ）M NααA BC【2017姑苏区二模】如图，在等边△ABC 中，AB =10，BD =4，BE =2，点P 从点E 出发沿EA 方向运动，连结PD ，以PD 为边，在PD 的右侧按如图所示的方式作等边△DPF ，当点P 从点E 运动到点A 时，点F 运动的路径长是________．ABCDE FP【分析】根据△DPF 是等边三角形，所以可知F 点运动路径长与P 点相同，P 从E 点运动到A 点路径长为8，故此题答案为8．【2013湖州中考】如图，已知点A是第一象限内横坐标为的一个定点，AC ⊥x 轴于点M ，交直线y =-x 于点N ，若点P 是线段ON 上的一个动点，∠APB =30°，BA ⊥P A ，则点P 在线段ON 上运动时，A 点不变，B 点随之运动．求当点P 从点O 运动到点N 时，点B 运动的路径长是________．yxN MPACBO【分析】根据∠P AB =90°，∠APB =30°可得：AP :AB，故B 点轨迹也是线段，且P 点轨迹路径长与B，P 点轨迹长ON为B点轨迹长为【练习】如图，在平面直角坐标系中，A （-3,0），点B 是y 轴正半轴上一动点，点C 、D 在x 正半轴上，以AB 为边在AB 的下方作等边△ABP ，点B 在y 轴上运动时，求OP 的最小值．POABxy【分析】求OP 最小值需先作出P 点轨迹，根据△ABP 是等边三角形且B 点在直线上运动，故可知P 点轨迹也是直线．取两特殊时刻：（1）当点B 与点O 重合时，作出P 点位置P 1；（2）当点B 在x 轴上方且AB 与x 轴夹角为60°时，作出P 点位置P 2．连接P 1P 2，即为P 点轨迹．P 2P 1y xBAO根据∠ABP =60°可知：12PP 与y 轴夹角为60°，作OP ⊥12PP ，所得OP 长度即为最小值，OP 2=OA =3，所以OP =32． PP 2P 1y xBAO【2019宿迁中考】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE =1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．GABCDEF【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在1G 位置，最终G 点在2G 位置（2G 不一定在CD 边），12G G 即为G 点运动轨迹．G 2G 1ED CBACG 最小值即当CG ⊥12G G 的时候取到，作CH ⊥12G G 于点H ，CH 即为所求的最小值．根据模型可知：12G G 与AB 夹角为60°，故12G G ⊥1EG ． 过点E 作EF ⊥CH 于点F ，则HF =1G E =1，CF =1322CE =，所以CH =52，因此CG 的最小值为52． FHG 2G 1ED CBA三、轨迹之其他图形篇所谓“瓜豆原理”，就是主动点的轨迹与从动点的轨迹是相似性，根据主、从动点与定点连线形成的夹角以及主、从动点到定点的距离之比，可确定从动点的轨迹，而当主动点轨迹是其他图形时，从动点轨迹必然也是．【2016乐山中考】如图，在反比例函数2y x=-的图像上有一个动点A ，连接AO 并延长交图像的另一支于点B ，在第一象限内有一点C ，满足AC =BC ，当点A 运动时，点C 始终在函数ky x=的图像上运动，若tan ∠CAB =2，则k 的值为（ ） CBAOyxA ．2B ．4C ．6D ．8【分析】∠AOC =90°且AO :OC =1:2，显然点C 的轨迹也是一条双曲线，分别作AM 、CN 垂直x 轴，垂足分别为M 、N ，连接OC ，易证△AMO ∽△ONC ，∴CN =2OM ，ON =2AM ，∴ON ·CN =4AM ·OM ，故k =4×2=8．NM xyOABC【思考】若将条件“tan ∠CAB =2”改为“△ABC 是等边三角形”，k 会是多少？【练习】如图，A （-1,1），B （-1,4），C （-5,4），点P 是△ABC 边上一动点，连接OP ，以OP 为斜边在OP 的右上方作等腰直角△OPQ ，当点P 在△ABC 边上运动一周时，点Q 的轨迹形成的封闭图形面积为________．QCxyOA B P【分析】根据△OPQ 是等腰直角三角形可得：Q 点运动轨迹与P 点轨迹形状相同，根据OP :OQ，可得P 点轨迹图形与Q，故面积比为2:1，△ABC 面积为1/2×3×4=6，故Q 点轨迹形成的封闭图形面积为3．【小结】根据瓜豆原理，类似这种求从动点轨迹长或者轨迹图形面积，根据主动点轨迹推导即可，甚至无需作图．【练习】如图所示，AB =4，AC =2，以BC 为底边向上构造等腰直角三角形BCD ，连接AD 并延长至点P ，使AD =PD ，则PB 的取值范围为___________．ABCDP【分析】固定AB 不变，AC =2，则C 点轨迹是以A 为圆心，2为半径的圆，以BC 为斜边作等腰直角三角形BCD ，则D 点轨迹是以点M为半径的圆EMPD CBA考虑到AP =2AD ，故P 点轨迹是以N 为圆心，即可求出PB 的取值范围．NEA BCD PM。