二次函数平移规律
- 格式:doc
- 大小:111.00 KB
- 文档页数:4

初中阶段关于二次函数的平移变换问题初中阶段二次函数的平移大致分为两类,即为上下平移和左右平移。
(1) 上下平移若原函数为c bx ax y ++=2⎩⎨⎧-++=+++=m c bx ax y m m c bx ax y m 22为个单位,则平移后函数向下平移为个单位,则平移后函数向上平移 注:①其中m 均为正数,若m 为负数则将对应的加(减)号改为(减)加号即可。
②通常上述变换称为上加下减,或者上正下负。
(2) 左右平移若原函数为c bx ax y ++=2,左右平移一般第一步先将函数的一般式化为顶点式k h x a y +-=2)(然后再进行相应的变形⎩⎨⎧+--=++-=k n h x a y n k n h x a y n 22)()(数为个单位,则平移后的函若向右平移了数为个单位,则平移后的函若向左平移了 注:①其中n 均为正数,若n 为负数则将对应的加(减)号改为(减)加号即可。
②通常上述变换称为左加右减,或者左正右负。
例:(2010年兰州)13. 抛物线c bx x y ++=2图像向右平移2个单位再向下平移3个单位,所得图像的解析式为322--=x x y ,则b 、c 的值为 ( )A . b=2,c=2 B. b=2,c=0 C . b= -2,c=-1 D. b= -3,c=2 分析,已知函数是从原函数经过向右和向下平移得来,所以原本函数可以从已知函数向左再向上平移求出,或者向上再向左平移求出,平移没有先后顺序的要求。
解:将函数 322--=x x y 先向上平移3个单位为:3322+--=x x y ,即x x y 22-=;再向左平移两个单位,向将函数化为顶点式1)1(2--=x y 然后x x y x y 2,1)21(22+=-+-=整理得,即b=2,c=0,选择B 选项。

二次函数的平移问题我们从两个方面进行了一些探讨,概括出二次函数平移后其解析式的变化规律.一.当解析式为一般式y=ax2+bx+c(a≠0)时1.向上或向下平移时,二次函数解析式的变化规律.将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=ax2+bx+c+n 将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=ax2+bx+c-n 两式比较:可得抛物线向上平移n个单位,常数项上加n,即解析式由y=ax2+bx+c 变为y=ax2+bx+c+n;同理可推出抛物线向下平移n个单位,常数项上减去n,即解析式由y=ax2+bx+c变为y=ax2+bx+c-n2.向左或向右平移时,解析式的变化规律.将抛物线向左平移m个单位长度后,得到的新抛物线的解析式为y=a(x+m)2+b(x+m)+c将抛物线向右平移m个单位长度后,得到的新抛物线的解析式为y=a(x-m)2+b(x-m)+c两式比较,可得出抛物线向左平移m个单位,自变量上减去m,即解析式由y=ax2+bx+c变为y=a(x+m)2+b(x+m)+c;同理可推出抛物线向右平移m个单位,自变量上加上m,即解析式由y=ax2+bx+c变为y=a(x-m)2+b(x-m)+c3.将抛物线向左平移m个单位长度后,再将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=a(x+m)2+b(x+m)+c+n将抛物线向左平移m个单位长度后,再将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=a(x+m)2+b(x+m)+c-n将抛物线向右平移m个单位长度后,再将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=a(x-m)2+b(x-m)+c+n将抛物线向右平移m个单位长度后,再将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=a(x-m)2+b(x-m)+c-n二.当解析式为顶点式y=a(x-h)2+k(a≠0)时1.向上或向下平移时,解析式的变化规律.将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=a(x-h)2+k+n 将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=a(x-h)2+k-n 将抛物线向上平移n个单位,有点的平移规律可知,顶点坐标由(h,k)变为(h,k+n)所以抛物线的解析式由y=a(x-h)2+k变为y=a(x-h)2+k+n 将抛物线向下平移n个单位,有点的平移规律可知,顶点坐标由(h,k)变为(h,k-n)所以抛物线的解析式由y=a(x-h)2+k变为y=a(x-h)2+k-n 比较两个解析式可得出向上平移n个单位,括号外加n,同理可推出向下平移n 个单位括号外减去n.即抛物线解析式由y=a(x-h)2+k变为y=a(x+m-h)2+k-n2.向右或向左平移时,解析式的变化规律.将抛物线向左平移m个单位长度后,得到的新抛物线的解析式为y=a(x-h+m)2+k 将抛物线向右平移m个单位长度后,得到的新抛物线的解析式为y=a(x-h-m)2+k将抛物线向左平移m 个单位,由点的平移规律可知,顶点坐标由(h,k)变为(h-m,k),所以抛物线解析式由y=a(x-h)2+k 变为y=a[x-(h-m)]2+k=a (x-h+m)2+k将抛物线向右平移m 个单位,由点的平移规律可知,顶点坐标由(h,k)变为(h+m,k),所以抛物线解析式由y=a(x-h)2+k 变为y=a[x-(h+m)]2+k=a (x-h-m)2+k两解析式比较可得出图像向左平移m 个单位,括号内加上m ,即抛物线解析式由y=a(x-h)2+k 变为y=a (x-h+m)2+k ;同理可推出向右平移m 个单位括号内减去m ,即抛物线解析式由y=a(x-h)2+k 变为y=a (x-h-m)2+k综上所述,当解析式为顶点式时,解析式的变化规律为上加下减括号外,左加右减括号内;解析式为一般式时,解析式的变化规律为左加右减自变量,上加下减常数项3.将抛物线向左平移m 个单位长度后,再将抛物线向上平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h+m)2+k+n将抛物线向左平移m 个单位长度后,再将抛物线向下平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h+m)2+k-n将抛物线向右平移m 个单位长度后,再将抛物线向上平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h-m)2+k+n将抛物线向右平移m 个单位长度后,再将抛物线向下平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h-m)2+k-n二次函数的平移练习题1.把抛物线y=-x 2向左平移一个单位,然后向上平移3个单位,则平移后抛物线的表达式为()A.y=-(x-1)2+3B.y=-(x+1)2+3C.y=-(x-1)2-3D.y=-(x+1)2-32.抛物线y=x 2+bx+c 图像向右平移2个单位再向下平移3个单位,所得图像的解析式为y=x 2-2x-3,则b 、c 的值为()A.b=2,c=2B.b=2,c=0C.b=-2,c=-1D.b=-3,c=23.将函数y=x 2+x 的图像向右平移a (a >0)个单位,得到函数y=x 2-3x+2的图像,则a 的值为()A.1B.2C.3D.44.已知二次函数y=x 2-bx+1(-1≤b ≤1),当b 从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是()A.先往左上方移动,再往右下方移动B.先往左下方移动,再往左上方移动B.先往右上方移动,再往右下方移动D.先往右下方移动,再往右上方移动5.已知抛物线C :y=x 2+3x-10,将抛物线C 平移得到抛物线C ′.若两条抛物线C 、C ′关于直线x=1对称,则下列平移方法正确的是()A.将抛物线C 向右平移2.5个单位B.将抛物线C 向右平移3个单位C.将抛物线C 向右平移5个单位D.将抛物线C 向右平移6个单位6.把二次函数y=-41x 2-x+3用配方法化成y=a(x-h)2+k 的形式 A.y=-41(x-2)2+2B.y=41(x-2)2+4C.y=-41(x+2)2+4D.y=(21x-21)2+3 7.在平面直角坐标系中,将二次函数y=2x 2的图象向上平移2个单位,所得图象的解析式为A .y=2x 2-2B .y=2x 2+2C .y=2(x-2)2D .y=2(x+2)28.将抛物线y=2x 2向下平移1个单位,得到的抛物线是( )A .y=2(x+1)2B .y=2(x-1)2C .y=2x 2+1D .y=2x 2-19.将函数y=x 2+x 的图象向右平移a(a >0)个单位,得到函数y=x 2-x+2的图象,则a 的值为()A .1B .2C .3D .410.把抛物线y=-2x 2向右平移2个单位,然后向上平移5个单位,则平移后抛物线的解析式为()A.y=-2(x-2)2+5B.y=-2(x+2)2+5C.y=-2(x-2)2-5D.y=-2(x+2)2-511.在平面直角坐标系中,先将抛物线y=x 2+x-2关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为()A .y=-x 2-x+2B .y=-x 2+x-2 C.y=-x 2+x+2 D .y=x 2+x+212.在平面直角坐标系中,将抛物线y=x 2+2x+3绕着它与y 轴的交点旋转1800,所得抛物线的解析式是()A .y=-(x+1)2+2B .y=-(x-1)2+4C .y=-(x-1)2+2D .y=-(x+1)2+413.要得到二次函数y=-x 2+2x-2的图象,需将y=-x 2的图象().A .向左平移2个单位,再向下平移2个单位B .向右平移2个单位,再向上平移2个单位C .向左平移1个单位,再向上平移1个单位D .向右平移1个单位,再向下平移1个单位14.若二次函数y=(x-m)2-1,当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是()A .m =1B .m >1C .m ≥1D .m ≤115.如图,点A ,B 的坐标分别为(1,4)和(4,4),抛物线y=a (x-m )2+n 的顶点在线段AB 上运动,与x 轴交于C 、D 两点(C 在D 的左侧),点C 的横坐标最小值为-3,则点D 的横坐标最大值为( )A .13B .7C .5D .816.抛物线y=ax 2向左平移5个单位,再向下移动2个单位得到抛物线17.二次函数y=-2(x+3)2-1由y=-2(x-1)2+1向_____平移______个单位,再向_____平移______个单位得到18.抛物线y=3(x+2)2-3可由抛物线y=3(x+2)2+2向平移个单位得到19.将抛物线y=53(x-3)2+5向右平移3个单位,再向上平移2个单位,得到的抛物线是 20.把抛物线y=-(x-1)2-2是由抛物线y=-(x+2)2-3向平移个单位,再向_____平移_____个单位得到21.把抛物线y =ax 2+bx+c 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y =x 2-3x+5,则a+b+c=__________22.抛物线y =x 2-5x+4的图像向右平移三个单位,在向下平移三个单位的解析式23.已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是y 轴,向下平移1个单位后与x 轴只有一个交点,则此二次函数的解析式为 24.已知a+b+c=0,a ≠0,把抛物线y=ax 2+bx+c 向下平移1个单位,再向左平移5个单位所得到的新抛物线的顶点是(-2,0),求原抛物线的解析式 25.已知二次函数y =-x 2-4x-5.①指出这个二次函数图象的开口方向、对称轴和顶点坐标;②把这个二次函数的图象上、下平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式;③把这个二次函数的图象左、右平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式。

二次函数图像的变化规律及应用引言:二次函数是高中数学中的重要内容之一,它的图像呈现出一种独特的形态,具有丰富的变化规律和广泛的应用。
本文将从图像的变化规律和应用两个方面,对二次函数进行深入的探讨。
一、图像的变化规律1. 平移变换二次函数的图像可以通过平移变换而得到不同的形态。
平移变换是指在坐标平面上将图像整体向左、右、上、下平移的操作。
对于二次函数y=ax^2+bx+c,当平移向右时,a保持不变,b不变,c减小;当平移向左时,a保持不变,b不变,c增大;当平移向上时,a增大,b不变,c增大;当平移向下时,a减小,b不变,c减小。
通过平移变换,我们可以观察到二次函数图像在平面上的移动轨迹,进而掌握其变化规律。
2. 缩放变换缩放变换是指在坐标平面上将图像整体放大或缩小的操作。
对于二次函数y=ax^2+bx+c,当缩放因子为k时,a不变,b不变,c增大(或减小)k倍。
缩放变换可以改变二次函数图像的大小和形状,通过观察不同缩放因子下的图像,我们可以总结出二次函数图像的缩放规律。
3. 翻折变换翻折变换是指在坐标平面上将图像关于某一直线进行对称的操作。
对于二次函数y=ax^2+bx+c,当翻折轴为x轴时,a不变,b变号,c不变;当翻折轴为y轴时,a变号,b不变,c不变;当翻折轴为直线x=k时,a不变,b变号,c变号。
翻折变换可以改变二次函数图像的位置和形状,通过观察不同翻折轴下的图像,我们可以总结出二次函数图像的翻折规律。
二、图像的应用1. 最值问题二次函数的图像呈现出一个开口朝上或朝下的抛物线形态,通过观察图像的顶点,我们可以得出二次函数的最值。
当抛物线开口朝上时,顶点为最小值;当抛物线开口朝下时,顶点为最大值。
最值问题在实际应用中有广泛的应用,例如在物理学中,我们可以通过最值问题求解物体的最高点或最低点。
2. 零点问题二次函数的图像与x轴的交点称为零点,也叫根或解。
通过观察图像与x轴的交点,我们可以求解二次函数的零点。

二次函数的平移张尚军在考试中,有些题目是求二次函数平移后的解析式,学生做起来很不方便,普遍感到求平移后的解析式比较困难.就此,我从两个方面进行了一些探讨,概括出二次函数平移后其解析式的变化规律.一.当解析式为顶点式y=a(x-h)2+k (a ≠0)时1.向右或向左平移时,解析式的变化规律.将抛物线向右平移m 个单位,由点的平移规律可知,顶点坐标由(h,k)变为(h+m,k),所以抛物线解析式由y=a(x-h)²+k 变为y=a[x-(h+m)]2+k=a (x-m-h)2+k两解析式比较可得出图像向右平移m 个单位,括号内减去m ,同理可推出向左平移m 个单位括号内加上m ,即抛物线解析式由y=a(x-h)2+k 变为y=a (x+m-h)2+k.2.向上或向下平移时,解析式的变化规律.将抛物线向上平移n 个单位,有点的平移规律可知,顶点坐标由(h ,k )变为(h ,k+n )所以抛物线的解析式由y=a(x-h)2²+k 变为y=a(x-h)2+k+n. 比较两个解析式可得出向上平移n 个单位,括号外加n ,同理可推出向下平移n 个单位括号外减去n.即抛物线解析式由y=a(x-h)2+k 变为y=a (x+m-h)2+k-n.二.当解析式为一般式y=ax 2+bx+c (a ≠0)时1.向右或向左平移时,解析式的变化规律.将抛物线向右平移m 个单位.因为y=ax 2+bx+c=a (x+a 2b )2+ab 4-ac 42 有前面的规律可知。
y=a(x+a 2b -m)2+ab 4-ac 42 =ax 2+a 4b 2+am ²+bx-2amx-bm+c-a 4b 2=ax 2-2amx+am ²+bx-bx+c=a(x-m)2+b(x-m)+c两式比较,可得出抛物线向右平移m 个单位,自变量上减去m;同理可推出抛物线向左平移m 个单位,自变量上加上m,即解析式由y=ax 2+bx+c 变为y=a(x+m)2+b(x+m)+c2.向上或向下平移时,解析式的变化规律.将抛物线向上平移n 个单位,因为y=ax 2+bx+c=a(x+ a 2b )2+ab 4-ac 42 由前面的规律可知 y=a(x+a 2b )2+ab 4-ac 42+n =ax 2+bx+c+n两式比较:可得抛物线向上平移n 个单位,常数项上加n;同理可推出抛物线向下平移n 个单位,自变量上减去n ,即解析式由y=ax 2+bx+c 变为y=ax 2+bx+c -n. 综上所述,当解析式为顶点式时,解析式的变化规律为上加下减括号外,左加右减括号内;解析式为一般式时,解析式的变化规律为左加右减自变量,上加下减常数项.当解析式为交点式y=a(x-1x )(x-2x )时,解析式的变化规律,请读者自己完成.应用这一规律,不但便于教师授课,而且更有利于学生掌握应用,解起题来更加方便快捷.发表于2012.08下旬总第132期《新课程学习》。
二次函数的平移
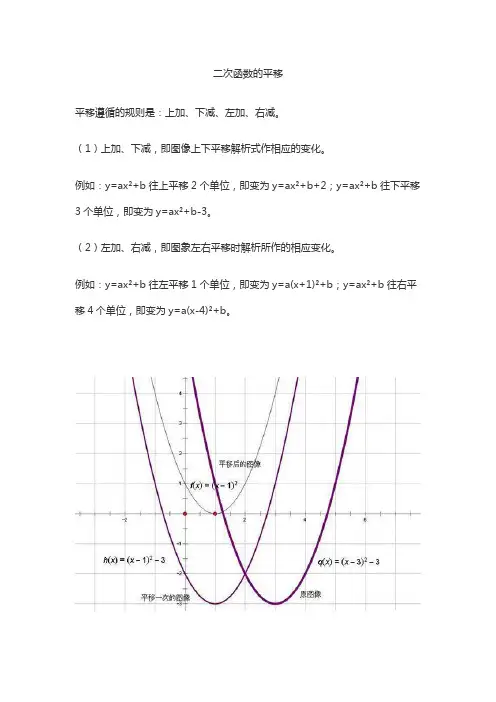
平移遵循的规则是:上加、下减、左加、右减。
(1)上加、下减,即图像上下平移解析式作相应的变化。
例如:y=ax²+b往上平移2个单位,即变为y=ax²+b+2;y=ax²+b往下平移3个单位,即变为y=ax²+b-3。
(2)左加、右减,即图象左右平移时解析所作的相应变化。
例如:y=ax²+b往左平移1个单位,即变为y=a(x+1)²+b;y=ax²+b往右平移4个单位,即变为y=a(x-4)²+b。
扩展资料
二次函数的性质
二次函数(以下称函数)y=ax²+bx+c(a≠0),当y=0时,二次函数为关于x 的一元二次方程(以下称方程),即ax²+bx+c=0(a≠0)。
此时,函数图像与x 轴有无交点即方程有无实数根,函数与x轴交点的横坐标即为方程的根。
a、b、c值与图像关系:
a>0时,抛物线开口向上;a<0时,抛物线开口向下。
当抛物线对称轴在y轴左侧时a,b同号,当抛物线对称轴在y轴右侧时a,b 异号。
c>0时,抛物线与y轴交点在x轴上方;c<0时,抛物线与y轴交点在x轴下方。
a=0时,此图像为一次函数。
b=0时,抛物线顶点在y轴上。
c=0时,抛物线在x轴上。
当抛物线对称轴在y轴左侧时a,b同号,当抛物线对称轴在y轴右侧时a,b 异号。

二次函数的平移问题关于二次函数的平移变换问题二次函数的平移变换可以分为上下平移和左右平移两种情况。
1.上下平移对于原函数y=ax²+bx+c,若要进行上下平移,可以进行以下变换:向上平移m个单位,得到平移后的函数y=ax²+bx+c+m;向下平移m个单位,得到平移后的函数y=ax²+bx+c-m。
需要注意的是,m为正数,若m为负数,则对应的加(减)号需要改为减(加)号。
一般称这种变换为上加下减或上正下负。
2.左右平移对于原函数y=ax²+bx+c,若要进行左右平移,可以进行以下变换:先将函数化为顶点式y=a(x-h)²+k;向左平移n个单位,得到平移后的函数y=a(x-h+n)²+k;向右平移n个单位,得到平移后的函数y=a(x-h-n)²+k。
需要注意的是,n为正数,若n为负数,则对应的加(减)号需要改为减(加)号。
一般称这种变换为左加右减或左正右负。
例题:1.将抛物线y=-x²向左平移一个单位,再向上平移三个单位,平移后的表达式为()A。
y=-(x-1)²+3B。
y=-(x+1)²+3C。
y=-(x-1)²-3D。
y=-(x+1)²-32.抛物线y=x²+bx+c向右平移两个单位,再向下平移三个单位,得到的抛物线表达式为y=x²-2x-3,则b、c的值分别为()A。
b=2,c=2B。
b=2,c=0C。
b=-2,c=-1D。
b=-3,c=23.将函数y=x²+x的图像向右平移a(a>0)个单位,得到函数y=x²-3x+2的图像,则a的值为()A。
1B。
2C。
3D。
44.已知二次函数y=x²-bx+1(-1≤b≤1),当b从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动。
下列关于抛物线移动方向的描述中,正确的是()A。
二次函数专题(3)——函数图像的平移我们知道图像的平移,图像本身不会发生改变,只是图像的位置发生改变。
函数图像的平移也是遵循这样原理,只是我们在平移过程中函数的解析式也发生改变,这节专题主要就是探讨函数平移与解析式的计算。
1. 基础情境:点坐标平移①水平平移:纵坐标不变横坐标加减我们以A(1,2)为例,把A往右平移2个单位到A’,很明显A’的纵坐标不变,但是横坐标变为了1+2=3,即A’(3,2);同理把A往左平移2个单位到A’’(-1,2)②竖直平移:横坐标不变,纵坐标加减我们以A(1,2)为例,把A往上平移三个单位到A’,很明显A’的横坐标不变,但是纵坐标变为了2+3=5,即A’(1,5);同理把A往下平移三个单位到A’’(1,-1),如下图:2. 函数平移:一次函数图像平移①水平平移问题:我们以y=2x+2为例,把它向右平移2个单位,那么新的图像函数解析式为何?分析:由于平移过后仍然是条直线,两点决定一条直线,所以我们选取两个特殊点就可以算出新的函数表达式。
解答:选取原一次函数上两点(0,2)、(-1,0),经过平移后这两点坐标变为(2,2)和(1,0),计算得y=2x-2.观察:平移后,一次函数的系数k(2)不变,b减小了两倍(由2变为-2)推广:对于所有一次函数y=kx+b,向右平移2个单位的函数解析式怎么求?分析:可以按照上面的思路,取特殊点求取新的一次函数解析式解答:方法一:坐标法取两个特殊点(0,b)、(1,k+b),经过平移后这两点坐标变为(2,b)和(3,k+b),计算函数表达式得y=kx+b-2k。
这个式子我们还可以改写成这样y=(k-2)x+b。
反思:解析法特殊点法虽然可以帮助我们解决问题,但是需要计算,有没有更加快速的计算一次函数解析式方法?有!我们回到最初函数的定义,比如坐标系中有一个点A(x,y),其中y=kx+b 代表是x与y之间的等量关系。
如果把A(x,y)向右平移2单位变成A’(m,y),此时m=x+2。
二次函数平移左加右减原理1 什么是二次函数?二次函数是一种函数,它的形式通常是 $y = ax^2 + bx + c$。
其中,$a,b,c$ 是三个常数,$x,y$ 是变量。
二次函数的图像通常是一个开口向上或向下的平滑曲线。
如果$a>0$,则曲线开口向上,如果 $a<0$,则开口向下。
$a$ 控制曲线的斜率和开口的大小,$b$ 控制曲线的水平位置,$c$ 控制曲线的竖直位置。
2 什么是平移?平移是指将一个点或一条曲线在平面上向左、向右、向上或向下移动一定的距离。
平移可以用矩阵的乘法来表示,也可以用坐标公式来表示。
3 左加右减原理左加右减原理是指,如果要将一个函数沿着 $x$ 轴向左移动$a$ 个单位,则需要将函数中 $x$ 的值都加上 $a$;如果要将函数沿着 $x$ 轴向右移动 $a$ 个单位,则需要将函数中 $x$ 的值都减去$a$。
如果函数中有其他参数(如 $a,b,c$),则平移也会影响这些参数。
具体来说,如果要将函数沿着 $x$ 轴向左移动 $a$ 个单位,则需要将 $b$ 的值减去 $2a$,将 $c$ 的值加上 $a^2$;如果要将函数沿着 $x$ 轴向右移动 $a$ 个单位,则需要将 $b$ 的值加上 $2a$,将 $c$ 的值减去 $a^2$。
4 举例说明假设有一个二次函数 $y = 2x^2 + 4x - 1$,现在要将它沿着$x$ 轴向左移动 $3$ 个单位。
根据左加右减原理,将函数中 $x$ 的值都加上 $3$,得到 $y = 2(x+3)^2 + 4(x+3) - 1$。
将式子展开,得到 $y = 2x^2 + 22x + 29$,这就是将原函数沿着 $x$ 轴向左移动 $3$ 个单位后的函数。
同样地,如果要将原函数沿着 $x$ 轴向右移动 $3$ 个单位,根据左加右减原理,需要将函数中 $x$ 的值都减去 $3$,并将 $b$ 的值加上 $2\times3=6$,$c$ 的值减去 $3^2=9$。
二次函数平移平移是二次函数中的常考点,大多以选择题、填空题出现,在判断平移时,首先我们要判断平移类型,再结合口诀“上加下减,左加右减”来解题,拿不准的题目就画图,虽然花费时间较多,但是准确率较高。
1、 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:2、平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”。
方法二:⑴ 2y ax bx c =++ 沿y 轴平移:向上(下)平移m 个单位,2y ax bx c =++ 变成2y ax bx c m =+++(或2y ax bx c m =++- )⑵2y ax bx c =++沿轴平移:向左(右)平移m 个单位,2y ax bx c =++变成2()()y a x m b x m c =++++(或2()()y a x m b x m c =-+-+)3、二次函数2()y a x h k =-+与2y ax bx c =++ 的比较从解析式上看,2()y a x h k =-+与2y ax bx c =++ 是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a -=-=,。
注:我们把2()y a x h k =-+直接就可以看出顶点是:(h ,k ),所以也称为顶点式。
这个函【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位数的关系式还能直接看出此二次函数的对称轴是2bh a=-: 例1:将二次函数y=x 2的图象向下平移一个单位,则平移以后的二次函数的解析式为线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( )A .y=-x 2-x+2B .y=-x 2+x-2 C. y=-x 2+x+2 D .y=x 2+x+2例4. 如图所示,已知抛物线C 0的解析式为x x y22-=,则抛物线C 0的顶点坐标 ;将抛物线C 0每次向右平移2个单位,平移n 次,依次得到抛物线C 1、C 2、C 3、…、C n (n 为正整数),则抛物线C n 的解析式为 .例5.如图,在平面直角坐标系xOy 中,抛物线1C 的顶点为⎪⎭⎫ ⎝⎛--29 3,P ,且过点()0 0,O .⑴ 写出抛物线1C 与x 轴的另一个交点A 的坐标;⑵ 将抛物线1C 向右平移3个单位、再向上平移54.个单位得抛物线2C ,求抛物线2C 的解析式;⑶ 直接写出阴影部分的面积S .练习一、选择题1.把抛物线y=-x 2向左平移一个单位,然后向上平移3个单位,则平移后抛物线的表达式为( )A. y=-(x-1)2+3B. y=-(x+1)2+3C. y=-(x-1)2-3D. y=-(x+1)2-32.抛物线y=x 2+bx+c 图像向右平移2个单位再向下平移3个单位,所得图像的解析式为y=x 2-2x-3,则b 、c 的值为( )A . b=2,c=2 B. b=2,c=0 C . b= -2,c=-1 D. b= -3,c=23.将函数y=x 2+x 的图像向右平移a (a >0)个单位,得到函数y=x 2-3x+2的图像,则a 的值为( )A. 1B. 2C. 3D. 44.已知二次函数y=x 2-bx+1(-1≤b ≤1),当b 从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( ) A. 先往左上方移动,再往右下方移动 B.先往左下方移动,再往左上方移动 B.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动5.已知抛物线C :y=x 2+3x-10,将抛物线C 平移得到抛物线C ′.若两条抛物线C 、C ′关于直线x=1对称,则下列平移方法正确的是( )A. 将抛物线C 向右平移 2.5个单位B.将抛物线C 向右平移3个单位C.将抛物线C 向右平移5个单位D.将抛物线C 向右平移6个单位 6.把二次函数y=-41x 2-x+3用配方法化成y=a(x-h)2+k 的形式A. y=-41(x-2)2+2B. y=41(x-2)2+4C. y=-41(x+2)2+4 D. y= (21x-21)2+37.在平面直角坐标系中,将二次函数y=2x 2的图象向上平移2个单位,所得图象的解析式为A .y=2x 2-2B .y=2x 2+2C .y=2(x-2)2D .y=2(x+2)28.将抛物线y=2x 2向下平移1个单位,得到的抛物线是( )A .y=2(x+1)2B .y=2(x-1)2C .y=2x 2+1D .y=2x 2-19.将函数y=x 2+x 的图象向右平移a(a >0)个单位,得到函数y=x 2-x+2的图象,则a 的值为( ) A .1 B .2 C .3 D .410.把抛物线y=-2x 2向右平移2个单位,然后向上平移5个单位,则平移后抛物线的解析式为( )A. y=-2(x-2)2+5B. y=-2(x+2)2+5C. y=-2(x-2)2-5D. y=-2(x+2)2-511.要得到二次函数y=-x 2+2x-2的图象,需将y=-x 2的图象( ).A .向左平移2个单位,再向下平移2个单位B .向右平移2个单位,再向上平移2个单位C .向左平移1个单位,再向上平移1个单位D .向右平移1个单位,再向下平移1个单位12.若二次函数y=(x-m)2-1,当≤l 时,y 随x 的增大而减小,则m 的取值范围是( ) A .m =1 B .m >1 C .m ≥1 D .m ≤1 二、填空题1.抛物线y=ax 2向左平移5个单位,再向下移动2个单位得到抛物线2.二次函数y=-2(x+3)2-1由y=-2(x-1)2+1向_____平移______个单位,再向_____平移______个单位得到3.抛物线y=3(x+2)2-3可由抛物线y=3(x+2)2+2向 平移 个单位得到 4.将抛物线y=53(x-3)2+5向右平移3个单位,再向上平移2个单位,得到的抛物线是 5.把抛物线y=-(x-1)2-2是由抛物线y=-(x+2)2-3向 平移 个单位,再向_____平移_____个单位得到6.把抛物线y =ax 2+bx+c 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y =x 2-3x+5,则a+b+c=__________7.抛物线y =x 2-5x+4的图像向右平移三个单位,在向下平移三个单位的解析式 8.已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是y 轴,向下平移1个单位后与x 轴只有一个交点,则此二次函数的解析式为 三、解答题1.已知a+b+c=0,a ≠0,把抛物线y=ax 2+bx+c 向下平移1个单位,再向左平移5个单位所得到的新抛物线的顶点是(-2,0),求原抛物线的解析式2.已知二次函数y =-x 2-4x-5.①指出这个二次函数图象的开口方向、对称轴和顶点坐标;②把这个二次函数的图象上、下平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式;③把这个二次函数的图象左、右平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式。
二次函数平移专项练习题
平移规律:针对顶点式抛物线的解析式是“左加右减(括号内),上加下减” 要注意如果知道了顶点坐标在移动时是“左减右加”
|a |的大小决定抛物线开口的大小,|a |越大,抛物线的开口越小.
a>0时 抛物线开口向上,反之向上
c>0时 抛物线交y 轴于正半轴,反之在负半轴
a 、
b 同号时 对称轴在y 轴左侧,异号时在右侧
抛物线平移时只有二次项系数a 是不变的
1、 把抛物线2y x =-向左平移一个单位,然后向上平移3个单位,则平移后抛
物线的表达式为( )
A. 2(1)3y x =--+
B. 2(1)3y x =-++
C. 2(1)3y x =---
D. 2(1)3y x =-+-
根据左加右减、上加下减可得:B. 2(1)3y x =-++
2、将函数2y x x =+的图像向右平移(0)a a >个单位,得到函数232y x x =-+的图
像,则a 的值为( )
A. 1
B. 2
C. 3
D. 4
由:2y x x =+=-(x+
21)2-41 232y x x =-+=(x-23)2-41 得:a=21-(-2
3)=2 ,所以选B 3、抛物线2y x bx c =++的图像向右平移2个单位长度,再向下平移3个单位长度,所得图像的函数解析式为y=x 2
-2x-3,则b 、c 的值为( )
A.b=2,c=3
B.b=2,c=0
C.b=-2.,c=-1
D.b=-3,c=2
由y=x 2-2x-3=(x-1)2
-4,
再根据左加右减、上加下减可得平移前的解析式为:
y=(x+2-1)2-4+3=x 2+2x 所以:b=2 c=0
4、要从抛物线y=-2x 2的图象得到y=-2x 2-1的图象,则抛物线y=-2x 2必须 [ ]
A .向上平移1个单位;
B .向下平移1个单位;
C .向左平移1个单位;
D .向右平移1个单位.
根据上加下减可得:B
5、将抛物线y=-3x 2的图象向右平移1个单位,再向下平移两个单位后,则所得抛
物线解析式为 [ ]
A .y=-3(x-1)2-2;
B .y=-3(x-1)2+2;
C .y=-3(x+1)2-2;
D .y=-3(x+1)2+2.
根据左加右减、上加下减可得:A .y=-3(x-1)2-2;
6、要从抛物线212y x =-得到21(1)32y x =-+-的图像,则抛物线y=-21x 2必须[ ]
A .向左平移1个单位,再向上平移3个单位;
B .向左平移1个单位,再向下平移3个单位;
C .向右平移1个单位,再向上平移3个单位;
D .向右平移1个单位,再向下平移3个单位.
根据左加右减、上加下减可得:B .向左平移1个单位,再向下平移3个单位
7. 把二次函数2x y -=的图象先向右平移2个单位,再向上平移5个单位后得到
一个新图象,则新图象所表示的二次函数的解析式是 ( )
A. ()522+--=x y
B. ()522
++-=x y C. ()522---=x y D. ()522
-+-=x y
根据左加右减、上加下减可得:A :()522
+--=x y 8、将抛物线21(3)22
y x =+-向右平移3个单位,再向上平移2个单位,则所得抛物线解析式为y=x 212 9.抛物线232y x =-向左平移1个单位得到抛物线解析式为y=-23(x-1)2
10、已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是y 轴,
向下平移1个单位后与x 轴只有一个交点,则此二次函数的解析式
为 。
解: 由图像向左平移2个单位后的对称轴是y 轴,向下平移1个单位后与x 轴
只有一个交点可知此二次函数的顶点坐标是(2、1)
故设次抛物线的解析式为:y=a(x-2)2
+1
∵次抛物线过点(0、3)
∴4a+1=3 a=2
1 ∴y=2
1(x-2)2+1
11、已知0=++c b a ,a ≠0,把抛物线c bx ax y ++=2向下平移1个单位,再向左平移
5个单位所得到的新抛物线的顶点是(-2,0),求原抛物线的解析式。
解:由抛物线c bx ax y ++=2
向下平移1个单位,再向左平移5个单位所得到的新抛物
线的顶点是(-2,0),得原抛物线的顶点坐标是(3、1) ∴-32=a b
b=-6 a
a b ac 442
-=1 c=9a+1
把b 、c 的值代入a+b+c=0
得 a-6a+9a+1=0 a=-41
b=23
c=-45 ∴原抛物线的解析式为:y=-41
x 2+23x-4
5。