超经典二次函数图象的平移和对称变换总结

专题05二次函数中的平移、旋转、对称（五大题型）通用的解题思路：1.二次函数的平移变换平移方式（n＞0)一般式y=ax2+bx+c顶点式y＝a(x–h)2＋k平移口诀向左平移n个单位y=a(x+n)2+b(x+n)+c y=a(x-h+n)2+k左加向右平移n个单位y=a(x-n)2+b(x-n)+c y=a(x-h-n)2+k右减向上平移n个单位y=ax2+bx+c+n y=a(x-h)2+k+n上加向下平移n个单位y=ax2+bx+c-n y=a(x-h)2+k-n下减2.平移与增加性变化如果平移后对称轴不发生变化，则不影响增减性，但会改变函数最大(小)值.只对二次函数上下平移，不改变增减性，改变最值.只对二次函数左右平移，改变增减性，不改变最值.3.二次函数的翻转问题的解题思路：①根据二次函数上特殊点的坐标值求得二次函数的表达式；②根据翻转后抛物线与原抛物线的图像关系，确定新抛物线的表达式；③在直角坐标系中画出原抛物线及翻转后抛物线的简易图，根据图像来判断题目中需要求解的量的各种可能性；④根据图像及相关函数表达式进行计算，求得题目中需要求解的值。

4.二次函数图象的翻折与旋转y=a(x-h)²+k绕原点旋转180°y=-a(x+h)²-k a、h、k 均变号沿x 轴翻折y=-a(x-h)²-k a、k 变号，h 不变沿y 轴翻折y=a(x+h)²+ka、h 不变，h 变号题型一：二次函数中的平移问题1．（2024•牡丹区校级一模）如图，在平面直角坐标系xOy 中，抛物线21(0)y ax bx a a=+-<与y 轴交于点A ，将点A 向右平移2个单位长度，得到点B ，点B 在抛物线上．（1）求点B 的坐标（用含a 的式子表示）．（2）当B 的纵坐标为3时，求a 的值；（3）已知点11(,2P a-，(2,2)Q ，若抛物线与线段PQ 恰有一个公共点，请结合函数图象求出a 的取值范围．【分析】（1）令0x =，求出点A 坐标根据平移得出结论；（2）将B 的纵坐标为3代入求出即可；（3）由对称轴为直线1x =得出212y ax ax a =--，当2y =时，解得1|1|a a x a ++=，2|1|a a x a-+=，结合图象得出结论；【解答】解：（1）在21(0)y ax bx a a =+-<中，令0x =，则1y a =-，∴1(0,)A a-，将点A 向右平移2个单位长度，得到点B ，则1(2,)B a-．（2）B 的纵坐标为3，∴13a-=，∴13a =-．（3）由题意得：抛物线的对称轴为直线1x =，2b a ∴=-，∴212y ax ax a=--，当2y =时，2122ax ax a=--，解得1|1|a a x a ++=，2|1|a a x a-+=，当|1|2a a a -+≤时，结合函数图象可得12a ≤-，抛物线与PQ 恰有一个公共点，综上所述，a 的取值范围为12a ≤-．【点评】本题考查二次函数的图象及性质；熟练掌握二次函数图象上点的特征，数形结合讨论交点是解题的关键．2．（2024•平原县模拟）已知抛物线212:23C y ax ax a =++-．（1）写出抛物线1C 的对称轴：．（2）将抛物线1C 平移，使其顶点是坐标原点O ，得到抛物线2C ，且抛物线2C 经过点(2,2)A --和点B （点B 在点A 的左侧），若ABO ∆的面积为4，求点B 的坐标．（3）在（2）的条件下，直线1:2l y kx =-与抛物线2C 交于点M ，N ，分别过点M ，N 的两条直线2l ，3l 交于点P ，且2l ，3l 与y 轴不平行，当直线2l ，3l 与抛物线2C 均只有一个公共点时，请说明点P 在一条定直线上．【分析】（1）根据抛物线的对称轴公式直接可得出答案．（2）根据抛物线2C 的顶点坐标在原点上可设其解析式为2y ax =，然后将点A 的坐标代入求得2C 的解析式，于是可设B 的坐标为21(,)2t t -且(2)t <-，过点A 、B 分别作x 轴的垂线，利用4ABO OBN OAM ABNM S S S S ∆∆∆=--=梯形可求得t 的值，于是可求得点B 的坐标．（3）设1(M x ，1)y ，2(N x ，2)y ，联立抛物线与直线1l 的方程可得出12x x k +=-，124x x =-．再利用直线2l 、直线3l 分别与抛物线相切可求得直线2l 、直线3l 的解析式，再联立组成方程组可求得交点P 的纵坐标为一定值，于是可说明点P 在一条定直线上．【解答】解：（1）抛物线1C 的对称轴为：212ax a=-=-．故答案为：1x =-．故答案为：1x =-．（2） 抛物线1C 平移到顶点是坐标原点O ，得到抛物线2C ，∴可设抛物线2C 的解析式为：2y ax = 点(2,2)A --有抛物线2C 上，22(2)a ∴-=⋅-，解得：12a =-．∴抛物线2C 的解析式为：212y x =-．点B 在抛物线2C 上，且在点A 的左侧，∴设点B 的坐标为21(,)2t t -且(2)t <-，如图，过点A 、B 分别作x 轴的垂线，垂足为点M 、N ．ABO OBN OAM ABNMS S S S ∆∆∆=-- 梯形2211111()()22(2)(2)22222t t t t =⨯-⨯-⨯⨯-⨯+⨯--32311122424t t t t =--++++212t t =+，又4ABO S ∆=，∴2142t t +=，解得：13t +=±，4(2t t ∴=-=不合题意，舍去），则2211(4)822t -=-⨯-=-，(4,8)B ∴--．（3）设1(M x ，1)y ，2(N x ，2)y ，联立方程组：2122y xy kx ⎧=-⎪⎨⎪=-⎩，整理得：2240x kx +-=，122x x k ∴+=-，124x x =-．设过点M 的直线解析式为y mx n =+，联立得方程组212y xy mx n⎧=-⎪⎨⎪=+⎩，整理得2220x mx n ++=．①过点M 的直线与抛物线只有一个公共点，∴△2480m n =-=，∴212n m =．∴由①式可得：221112202x mx m ++⨯=，解得：1m x =-．∴2112n x =．∴过M 点的直线2l 的解析式为21112y x x x =-+．用以上同样的方法可以求得：过N 点的直线3l 的解析式为22212y x x x =-+，联立上两式可得方程组2112221212y x x x y x x x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，解得1212212x x x y x x +⎧=⎪⎪⎨⎪=-⎪⎩，12x x k +=- ，124x x =-．∴(,2)2k P -∴点P 在定直线2y =上．（如图）【点评】本题考查了抛物线的对称轴、求二次函数的解析式、解一元二次方程、一元二次方程的根的情况、求直线交点坐标等知识点，解题的关键是利用所画图形帮助探索解法思路．3．（2024•和平区一模）已知抛物线21(y ax bx a =+-，b 为常数．0)a ≠经过(2,3)，(1,0)两个点．（Ⅰ）求抛物线的解析式；（Ⅱ）抛物线的顶点为；（Ⅲ）将抛物线向右平移1个单位长度，向下平移2个单位长度，就得到抛物线．【分析】（Ⅰ）利用待定系数法即可求解；（Ⅱ）根据抛物线的顶点式即可求得；（Ⅲ）利用平移的规律即可求得．【解答】解：（1） 抛物线21y ax bx =+-经过(2,3)，(1,0)两个点，∴421310a b a b +-=⎧⎨+-=⎩，解得10a b =⎧⎨=⎩，∴抛物线的解析式为21y x =-；（Ⅱ） 抛物线21y x =-，∴抛物线的顶点为(0,1)-，故答案为：(0,1)-；（Ⅲ）将抛物线向右平移1个单位长度，向下平移2个单位长度，就得到抛物线2(1)12y x =---，即2(1)3y x =--．故答案为：2(1)3y x =--．【点评】本题考查了待定系数法求二次函数的解析式，二次函数的性质，二次函数图象与几何变换，熟练掌握待定系数法是解题的关键．4．（2024•礼县模拟）如图，在平面直角坐标系中，抛物线23y ax bx =++交y 轴于点A ，且过点(1,2)B -，(3,0)C ．（1）求抛物线的函数解析式；（2）求ABC ∆的面积；（3）将抛物线向左平移(0)m m >个单位，当抛物线经过点B 时，求m的值．【分析】（1）用待定系数法求函数解析式即可；（2）先求出点A 的坐标，然后切成直线BC 的解析式，求出点D 的坐标，再根据ABC ABD ACD S S S ∆∆∆=+求出ABC ∆的面积；（3）由（1）解析式求出对称轴，再求出点B 关于对称轴的对称点B '，求出BB '的长度即可；【解答】解：（1）把(1,2)B -，(3,0)C 代入23y ax bx =++，则933032a b a b ++=⎧⎨-+=⎩，解得1212a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线的函数解析式为211322y x x =-++；（2） 抛物线23y ax bx =++交y 轴于点A ，(0,3)A ∴，设直线BC 的解析式为y kx n =+，把(1,2)B -，(3,0)C 代入y kx n =+得230k n k n -+=⎧⎨+=⎩，解得1232k n ⎧=-⎪⎪⎨⎪=⎪⎩，∴直线BC 的解析式为1322y x =-+，设BC 交y 于点D，如图：则点D 的坐标为3(0,)2，33322AD ∴=-=，113()(31)3222ABC ABD ACD C B S S S AD x x ∆∆∆∴=+=-=⨯⨯+=，（3）211322y x x =-++ ，∴对称轴为直线122b x a =-=，令B 点关于对称轴的对称点为B '，(2,2)B ∴'，3BB ∴'=，抛物线向左平移(0)m m >个单位经过点B ，3m ∴=．【点评】本题主要考查待定系数法求二次函数的解析式，二次函数图象与几何变换、二次函数的性质、三角形面积等知识，关键是掌握二次函数的性质和平移的性质．5．（2024•珠海校级一模）已知抛物线223y x x =+-．（1）求抛物线的顶点坐标；（2）将该抛物线向右平移(0)m m >个单位长度，平移后所得新抛物线经过坐标原点，求m 的值．【分析】（1）化成顶点是即可求解；（2）根据平移的规律得到2(1)4y x m =-+-+，把原点代入即可求得m 的值．【解答】解：（1）2223(1)4y x x x =+-=+- ，∴抛物线的顶点坐标为(1,4)--．（2）该抛物线向右平移(0)m m >个单位长度，得到的新抛物线对应的函数表达式为2(1)4y x m =+--， 新抛物线经过原点，20(01)4m ∴=+--，解得3m =或1m =-（舍去），3m ∴=，故m 的值为3．【点评】本题考查了二次函数的性质，二次函数图象与几何变换，二次函数图象上点的坐标特征，求得平移后的抛物线的解析式是解题的关键．6．（2024•关岭县一模）如图，二次函数212y x bx c =++与x 轴有两个交点，其中一个交点为(1,0)A -，且图象过点(1,2)B ，过A ，B 两点作直线AB ．（1）求该二次函数的表达式，并用顶点式来表示；（2）将二次函数212y x bx c =++向左平移1个单位，得函数2y =；函数2y 与坐标轴的交点坐标为；（3）在（2）的条件下，将直线AB 向下平移(0)n n >个单位后与函数2y 的图象有唯一交点，求n 的值．【分析】（1）将点(1,0)A -，点(1,2)B 坐标代入抛物线解析式即可求出b 、c 值，再转化为顶点式即可；（2）根据抛物线平移规则“左加右减”得到2y 解析式，令20y =求出与x 轴的交点坐标即可；（3）利用待定系数法求出直线AB 解析式，再根据直线平移法则“上加下减”得到直线平移后解析式，联立消去y ，根据判别式为0解出n 值即可．【解答】解：（1）将点(1,0)A -，点(1,2)B 坐标代入抛物线解析式得：2022b c b c -+=⎧⎨++=⎩，解得11b c =⎧⎨=-⎩，∴抛物线解析式为2219212()48y x x x =+-=+-．∴抛物线解析式为：21192()48y x =+-．（2）将二次函数1y 向左平移1个单位，得函数22592()48y x =+-，令20y =，则2592(048x +-=，解得112x =-，22x =-，∴平移后的抛物线与x 轴的交点坐标为1(2-，0)(2-，0)．故答案为：22592()48y x =+-，1(2-，0)(2-，0)．（3）设直线AB 的解析式为y kx b =+，将(1,0)A -，点(1,2)B 代入得：02k b k b -+=⎧⎨+=⎩，解得11k b =⎧⎨=⎩，∴直线AB 解析式为：1y x =+．将直线AB 向下平移(0)n n >个单位后的解析式为1y x n =+-，与函数2y 联立消去y 得：2592(148x x n +-=+-，整理得：22410x x n +++=，直线AB 与抛物线有唯一交点，△1642(1))0n =-⨯+=，解得1n =．【点评】本题考查了二次函数的图象与几何变换，熟练掌握函数的平移法则是解答本题的关键．7．（2024•温州模拟）如图，直线122y x =-+分别交x 轴、y 轴于点A ，B ，抛物线2y x mx =-+经过点A ．（1）求点B 的坐标和抛物线的函数表达式．（2）若抛物线向左平移n 个单位后经过点B ，求n 的值．【分析】（1）由题意可得点A 、B 的坐标，利用待定系数法求解二次函数的表达式即可解答；（2）根据二次函数图象平移规律“左加右减，上加下减”得到平移后的抛物线的表达式，再代入B 的坐标求解即可．【解答】解：（1）令0x =，则1222y x =-+=，(0,2)B ∴，令0y =，则1202y x =-+=，解得4x =，(4,0)A ∴，抛物线2y x mx =-+经过点A ，1640m ∴-+=，解得4m =，∴二次函数的表达式为24y x x =-+；（2）224(2)4y x x x =-+=--+ ，∴抛物线向左平移n 个单位后得到2(2)4y x n =--++，经过点(0,2)B ，22(2)4n ∴=--++，解得2n =±，故n 的值为2-2+【点评】本题考查待定系数法求二次函数解析式、一次函数图象上点的坐标特征、二次函数的图象与几何变换，二次函数图象上点的坐标特征等知识，熟练掌握待定系数法求二次函数解析式是解答的关键．8．（2024•巴东县模拟）已知二次函数2y ax bx c =++图象经过(2,3)A ，(3,6)B 、(1,6)C -三点．（1）求该二次函数解析式；（2）将该二次函数2y ax bx c =++图象平移使其经过点(5,0)D ，且对称轴为直线4x =，求平移后的二次函数的解析式．【分析】（1）运用待定系数法即可求得抛物线解析式；（2）利用平移的规律求得平移后的二次函数的解析式．【解答】解：（1）把(2,3)A ，(3,6)B 、(1,6)C -代入2y ax bx c =++，得：4239366a b c a b c a b c ++=⎧⎪++=⎨⎪-+=⎩，解得：123a b c =⎧⎪=-⎨⎪=⎩，∴该二次函数的解析式为223y x x =-+；（2）若将该二次函数2y ax bx c =++图象平移后经过点(5,0)D ，且对称轴为直线4x =，设平移后的二次函数的解析式为2(4)y x k =-+，将点(5,0)D 代入2(4)y x k =-+，得2(54)0k -+=，解得，1k =-．∴将二次函数的图象平移后的二次函数的解析式为22(4)1815y x x x =--=-+．【点评】本题考查了待定系数法求解析式，抛物线的性质，熟知待定系数法和平移的规律是解题的关键．9．（2024•郑州模拟）在平面直角坐标系中，抛物线2y x bx c =-++经过点(1,2)A ，(2,1)B ．（1）求抛物线的解析式；（2）直线y x m =+经过点A ，判断点B 是否在直线y x m =+上，并说明理由；（3）平移抛物线2y x bx c =-++使其顶点仍在直线y x m =+上，若平移后抛物线与y 轴交点的纵坐标为n ，求n 的取值范围．【分析】（1）利用待定系数法即可求解；（2）利用待定系数法求得直线y x m =+的解析式，然后代入点B 判断即可；（3）设平移后的抛物线为2()1y x p q =--++，其顶点坐标为(,1)p q +，根据题意得出2221511()24n p q p p p =-++=-++=-++，得出n 的最大值．【解答】解：（1） 抛物线2y x bx c =-++经过点(1,2)A ，(2,1)B ，∴12421b c b c -++=⎧⎨-++=⎩，解得21b c =⎧⎨=⎩，∴抛物线的解析式为：221y x x =-++；（2）点B 不在直线y x m =+上，理由：直线y x m =+经过点A ，12m ∴+=，1m ∴=，1y x ∴=+，把2x =代入1y x =+得，3y =，∴点(2,1)B 不在直线y x m =+上；（3）∴平移抛物线221y x x =-++，使其顶点仍在直线1y x =+上，设平移后的抛物线的解析式为2()1y x p q =--++，其顶点坐标为(,1)p q +， 顶点仍在直线1y x =+上，11p q ∴+=+，p q ∴=，抛物线2()1y x p q =--++与y 轴的交点的纵坐标为21n p q =-++，2221511(24n p q p p p ∴=-++=-++=-++，∴当12p =-时，n 有最大值为54．54n ∴ ．【点评】本题考查了待定系数法求一次函数的解析式和二次函数的解析式，二次函数的图象与几何变换，二次函数的性质，题目有一定难度．10．（2024•鞍山模拟）已知抛物线2246y x x =+-．（1）求抛物线的顶点坐标；（2）将该抛物线向右平移(0)m m >个单位长度，平移后所得新抛物线经过坐标原点，求m 的值．【分析】（1）将二次函数的解析式改写成顶点式即可．（2）将抛物线与x 轴的交点平移到原点即可解决问题．【解答】解：（1）由题知，2222462(21)82(1)8y x x x x x =+-=++-=+-，所以抛物线的顶点坐标为(1,8)--．（2）令0y =得，22460x x +-=，解得11x =，23x =-．又因为将该抛物线向右平移(0)m m >个单位长度，平移后所得新抛物线经过坐标原点，所以30m -+=，解得3m =．故m 的值为3．【点评】本题考查二次函数的图象与性质，熟知利用配方法求二次函数解析式的顶点式及二次函数的图象与性质是解题的关键．11．（2023•原平市模拟）（1）计算：3211()(5)|2|3--+---⨯-；（2）观察表格，完成相应任务：x3-2-1-012221A x x =+-21-2-1-①72(1)2(1)1B x x =-+--721-2-②2任务一：补全表格；任务二：观察表格不难发现，当x m =时代数式A 的值与当1x m =+时代数式B 的值相等，我们称这种现象为代数式B 参照代数式A 取值延后，相应的延后值为1：换个角度来看，将代数式A ，B 变形，得到(A =③2)2-，22B x =-将A 与B 看成二次函数，则将A 的图象④（描述平移方式），可得到B 的图象．若代数式P 参照代数式A 取值延后，延后值为3，则代数式P =⑤．【分析】（1）先算乘方，负整数指数幂，绝对值，再算乘法，最后算加减法即可求解；（2）①把1x =分别代入代数式A ，B 即可求得；②根据代数式B 参照代数式A 取值延后，相应的延后值为1，即可得出二次函数A 、B 平移的规律是向右平移1个单位，据此即可得出代数式P 参照代数式A 取值延后，延后值为3的P 的代数式．【解答】解：（1）原式19(5)2=-+--⨯19(10)=-+--1910=-++18=；（2）任务一：将1x =代入2212A x x =+-=；代入2(1)2(1)11B x x =-+--=-，故答案为：①2，②1-；任务二：将代数式A ，B 变形，得到2(1)2A x =+-，22B x =-将A 与B 看成二次函数，则将A 的图象向右平移1个单位（描述平移方式），可得到B 的图象．若代数式P 参照代数式A 取值延后，延后值为3，则代数式22(13)2(2)2P x x =+--=--．故答案为：①2；②1-；③1x +；④向右平移1个单位；⑤2(2)2P x =--．【点评】本题考查二次函数图象与几何变换，二次函数图象上点的坐标特征，理解题意，能够准确地列出解析式，并进行求解即可．12．（2024•南山区校级模拟）数形结合是解决数学问题的重要方法．小明同学学习二次函数后，对函数2(||1)y x =--进行了探究．在经历列表、描点、连线步骤后，得到如图的函数图象．请根据函数图象，回答下列问题：【观察探究】：方程2(||1)1x --=-的解为：；【问题解决】：若方程2(||1)x a --=有四个实数根，分别为1x 、2x 、3x 、4x ．①a 的取值范围是；②计算1234x x x x +++=；【拓展延伸】：①将函数2(||1)y x =--的图象经过怎样的平移可得到函数21(|2|1)3y x =---+的图象？画出平移后的图象并写出平移过程；②观察平移后的图象，当123y时，直接写出自变量x 的取值范围．【分析】（1）根据图象即可求得；（2）根据“上加下减”的平移规律，画出函数21(|21)3y x =---+的图象，根据图象即可得到结论．【解答】解：（1）观察探究：①由图象可知，当函数值为1-时，直线1y =-与图象交点的横坐标就是方程2(||1)1x --=-的解．故答案为：2x =-或0x =或2x =．（2）问题解决：①若方程2(|1)x a --=有四个实数根，由图象可知a 的取值范围是10a -<<．故答案为：10a -<<．②由图象可知：四个根是两对互为相反数．所以12340x x x x +++=．故答案为：0．（3）拓展延伸：①将函数2(||1)y x =--的图象向右平移2个单位，向上平移3个单位可得到函数21(|2|1)3y x =---+的图象，②当123y 时，自变量x 的取值范围是04x ．故答案为：04x．【点评】本题主要考查了二次函数图象与几何变换，二次函数图象和性质，数形结合是解题的关键．13．（2023•花山区一模）已知抛物线2y x ax b =++的顶点坐标为(1,2)．（1）求a ，b 的值；（2）将抛物线2y x ax b =++向下平移m 个单位得到抛物线1C ，存在点(,1)c 在1C 上，求m 的取值范围；（3）抛物线22:(3)C y x k =-+经过点(1,2)，直线(2)y n n =>与抛物线2y x ax b =++相交于A 、B （点A 在点B 的左侧），与2C 相交于点C 、D （点C 在点D 的左侧），求AD BC -的值．【分析】（1）根据对称轴公式以及当1x =时2y =，用待定系数法求函数解析式；（2）根据（1）可知抛物线2223(1)2y x x x =-+=-+，再由平移性质得出抛物线1C 解析式，然后把点(,1)c 代入抛物线1C ，再根据方程有解得出m 的取值范围；（3）先求出抛物线2C 解析式，再求出A ，B ，C ，D 坐标，然后求值即可．【解答】解：（1）由题意得，1212aa b ⎧-=⎪⎨⎪++=⎩，解得23a b =-⎧⎨=⎩；（2）由（1）知，抛物线2223(1)2y x x x =-+=-+，将其向下平移m 个单位得到抛物线1C ，∴抛物线1C 的解析式为2(1)2y x m =-+-，存在点(,1)c 在1C 上，2(1)21c m ∴-+-=，即2(1)1c m -=-有实数根，10m ∴- ，解得1m，m ∴的取值范围为1m；（3） 抛物线22:(3)C y x k =-+经过点(1,2)，2(13)2k ∴-+=，解得2k =-，∴抛物线2C 的解析式为2(3)2y x =--，把(2)y n n =>代入到2(1)2y x =-+中，得2(1)2n x =-+，解得1x =1x =(1A ∴-，)n ，(1B +)n ，把(2)y n n =>代入到2(3)2y x =--中，得2(3)2n x =--，解得3x =或3x =+(3C ∴)n ，(3D +，)n ，(3(12AD ∴=+--=+，(1(32BC =+--=-+，(2(24AD BC ∴-=+--+=．【点评】本题考查二次函数的几何变换，二次函数的性质以及待定系数法求函数解析式，直线和抛物线交点，关键对平移性质的应用．14．（2023•环翠区一模）已知抛物线2y x bx c =++经过点(1,0)和点(0,3)．（1）求此抛物线的解析式；（2）当自变量x 满足13x -时，求函数值y 的取值范围；（3）将此抛物线沿x 轴平移m 个单位长度后，当自变量x 满足15x时，y 的最小值为5，求m 的值．【分析】（1）利用待定系数法求解；（2）先求出1x =-及3x =时的函数值，结合函数的性质得到答案；（3）设此抛物线沿x 轴向右平移m 个单位后抛物线解析式为(2)2y x m l =---，利用二次函数的性质，当25m +>，此时5x =时，5y =，即(52)215m ---=，设此抛物线沿x 轴向左平移m 个单位后抛物线解析式为(2)21y x m =-+-，利用二次函数的性质得到2m l -<，此时1x =时，5y =，即(12)215m ---=，然后分别解关于m 的方程即可．【解答】解：（1） 抛物线2y x bx c =++经过点(1,0)和点(0,3)，∴103b c c ++=⎧⎨=⎩，解得43b c =-⎧⎨=⎩，∴此抛物线的解析式为243y x x =-+；（2）当1x =-时，1438y =++=，当3x =时，91230y =-+=，2243(2)1y x x x =-+=-- ，∴函数图象的顶点坐标为(2,1)-，∴当13x -时，y 的取值范围是18y - ；（3）设此抛物线x 轴向右平移m 个单位后抛物线解析式为(2)y x m =--21-，当自变量x 满足15x时，y 的最小值为5，25m ∴+>，即3m >，此时5x =时，5y =，即(52)m --215-=，解得13m =+，23m =-（舍去）；设此抛物线沿x 轴向左平移m 个单位后抛物线解析式为(2)y x m =-+21-，当自变量x 满足15x时，y 的最小值为5，21m ∴-<，即1m >，此时1x =时，5y =，即2(12)15m ---=，解得11m =-+，21m =--（舍去），综上所述，m 的值为3+1+【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a 不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式，也考查了二次函数的性质．15．（2023•南宁一模）如图1，抛物线21y x c =-+的图象经过(1,3)．（1）求c 的值及抛物线1y 的顶点坐标；（2）当132x - 时，求1y 的最大值与最小值的和；（3）如图2，将抛物线1y 向右平移m 个单位(0)m >，再向上平移2m 个单位得到新的抛物线2y ，点N 为抛物线1y 与2y 的交点．设点N 到x 轴的距离为n ，求n 关于m 的函数关系式，并直接写出当n 随m 的增大而减小时，m 的取值范围．【分析】（1）把(1,3)代入抛物线解析式求得c 的值；根据抛物线解析式可以直接得到顶点坐标；（2）根据抛物线的性质知：当0x =时，1y 有最大值为4，当3x =-时，1y 有最小值为5-．然后求1y 的最大值与最小值的和；（3）根据平移的性质“左加右减，上加下减”即可得出抛物线2y 的函数解析式；然后根据抛物线的性质分两种情况进行解答：当06m < 时，0y ，2211(2)4344n m m m =--+=-++．当6m >时，0y <，2211(2)4344n y m m m =-=--=--．【解答】解：（1）抛物线21y x c =-+的图象经过(1,3)，∴当0x =时，2113y c =-+=，解得4c =．∴214y x =-+．顶点坐标为(0,4)；（2）10-< ，∴抛物线开口向下．当0x =时，1y 有最大值为4．当3x =-时，21(3)45y =--+=-．当12x =时，21115()424y =-+=．∴当3x =-时，1y 有最小值为5-．∴最大值与最小值的和为4(5)1+-=-；（3）由题意知，新抛物线2y 的顶点为(,42)m m +，∴22()42y x m m =--++．当12y y =时，22()424x m m x --++=-+，化简得：2220mx m m -+=．又0m > ，∴112x m =-．∴2211(1)4(2)424y m m =--+=--+．当21(2)404m --+=时，解得12m =-；26m =， 104-<，∴抛物线开口向下．当06m < 时，0y ，2211(2)4344n m m m =--+=-++．当6m >时，0y <，2211(2)4344n y m m m =-=--=--．∴综上所述2213,06413,64m m m n m m m ⎧-++<⎪⎪=⎨⎪-->⎪⎩ （或21|(2)4|)4n m =--+．当26m <<时，n 随m 的增大而减小．【点评】本题属于二次函数综合题，主要考查了二次函数图象上点的坐标特征，二次函数图象与几何变换，二次函数的图象与性质以及二次函数最值的求法．难度偏大．16．（2023•奉贤区一模）如图，在平面直角坐标系xOy 中，抛物线23y ax bx =++的对称轴为直线2x =，顶点为A ，与x 轴分别交于点B 和点C （点B 在点C 的左边），与y 轴交于点D ，其中点C 的坐标为(3,0)．（1）求抛物线的表达式；（2）将抛物线向左或向右平移，将平移后抛物线的顶点记为E ，联结DE ．①如果//DE AC ，求四边形ACDE 的面积；②如果点E 在直线DC 上，点Q 在平移后抛物线的对称轴上，当DQE CDQ ∠=∠时，求点Q的坐标．【分析】（1）利用待定系数法解答即可；（2）①依据题意画出图形，利用A ，C ，D 的坐标，等腰直角三角形的判定与性质和平行线的性质求得点E ，F 坐标，再利用四边形ACDE 的面积DFC EFCA S S ∆=+平行四边形解答即可；②依据题意画出图形，利用A ，C ，D 的坐标，等腰直角三角形的判定与性质，勾股定理求得点E 坐标和线段DE ，再利用等腰三角形的判定与性质求得线段FQ ，则结论可求．【解答】解：（1） 抛物线23y ax bx =++的对称轴为直线2x =，经过点(3,0)C ，∴229330b a a b ⎧-=⎪⎨⎪++=⎩，解得：14a b =⎧⎨=-⎩，∴抛物线的表达式为243y x x =-+；（2）①2243(2)1y x x x =-+=-- ，(2,1)A ∴-．设抛物线的对称轴交x 轴于点G ，1AG ∴=．令0x =，则3y =，(0,3)D ∴，3OD ∴=．令0y =，则2430x x -+=，解得：1x =或3x =，(1,0)B ∴．如果//DE AC ，需将抛物线向左平移，设DE 交x 轴于点F ，平移后的抛物线对称轴交x 轴于点H ，如图， 点C 的坐标为(3,0)，3OC ∴=．由题意：45ACB ∠=︒，//DE AC ，45DFC ACB ∴∠=∠=︒．3OF OD ∴==，(3,0)F ∴-，由题意：1EH =，1FH EH ∴==，(4,1)E ∴--．//AE x 轴，//DE AC ，∴四边形EFCA 为平行四边形，2(4)6AE =--= ，616EFCA S ∴=⨯=平行四边形．1163922DFC S FC OD ∆=⨯⋅=⨯⨯= ，∴四边形ACDE 的面积6915DFC EFCA S S ∆=+=+=平行四边形；②如果点E 在直线DC 上，点Q 在平移后抛物线的对称轴上，DQE CDQ ∠=∠，如图，当点Q 在x 轴的下方时，设平移后的抛物线的对称轴交x 轴于F ，由题意：1EF =．3OD OC == ，45ODC OCD ∴∠=∠=︒，45FCE OCD ∴∠=∠=︒，1CF EF ∴==，(4,1)E ∴-．CD ==，CE ==DE CD CE ∴=+=DQE CDQ ∠=∠ ，EQ DE ∴==1QF EF EQ ∴=+=，(4,1)Q ∴-；当点Q 在x 轴的上方时，此时为点Q '，DQ E CDQ ∠'=∠' ，EQ DE ∴'==，1Q F EQ EF ∴'='-=，(4Q ∴'，1)-．综上，当DQE CDQ ∠=∠时，点Q 的坐标为(4,1)--或(4，1)-．【点评】本题是二次函数综合题，考查了二次函数图象和性质，待定系数法，三角形面积，直角三角形性质，勾股定理，相似三角形判定和性质等，解题的关键是熟练运用分类讨论思想和方程的思想解决问题．17．（2023•下城区校级模拟）如图已知二次函数2(y x bx c b =++，c 为常数）的图象经过点(3,1)A -，点(0,4)C -，顶点为点M ，过点A 作//AB x 轴，交y 轴于点D ，交二次函数2y x bx c =++的图象于点B ，连接BC ．（1）求该二次函数的表达式及点M 的坐标：（2）若将该二次函数图象向上平移(0)m m >个单位，使平移后得到的二次函数图象的顶点落在ABC ∆的内部（不包括ABC ∆的边界），求m 的取值范围；（3）若E 为y 轴上且位于点C 下方的一点，P 为直线AC 上一点，在第四象限的抛物线上是否存在一点Q ，使以C 、E 、P 、Q 为顶点的四边形是菱形？若存在，请求出点Q的横坐标：若不存在，请说明理由．【分析】（1）将点(3,1)A -，点(0,4)C -代入2y x bx c =++，即可求解；（2）求出平移后的抛物线的顶点(1,5)m -，再求出直线AC 的解析式4y x =-，当顶点在直线AC 上时，2m =，当M 点在AB 上时，4m =，则24m <<；（3）设(0,)E t ，(,4)P p p -，2(,24)Q q q q --，分三种情况讨论：当CE 为菱形对角线时，CP CQ =，22222342(2)p q t q q q q q q =-⎧⎪=--⎨⎪=+-⎩，Q 点横坐标为1；②当CP 为对角线时，CE CQ =，22222824(4)(2)p q p t q q t q q q =⎧⎪-=+--⎨⎪+=+-⎩，Q 点横坐标为2；③当CQ 为菱形对角线时，CE CP =，222284(4)2p q q q t p t q =⎧⎪--=+-⎨⎪+=⎩，Q点横坐标为3【解答】解：（1）将点(3,1)A -，点(0,4)C -代入2y x bx c =++，∴4931c b c =-⎧⎨++=-⎩，解得24b c =-⎧⎨=-⎩，224y x x ∴=--，2224(1)5y x x x =--=-- ，∴顶点(1,5)M -；（2）由题可得平移后的函数解析式为2(1)5y x m =--+，∴抛物线的顶点为(1,5)m -，设直线AC 的解析式为y kx b =+，∴431b k b =-⎧⎨+=-⎩，解得14k b =⎧⎨=-⎩，4y x ∴=-，当顶点在直线AC 上时，53m -=-，2m ∴=，//AB x 轴，(1,1)B ∴--，当M 点在AB 上时，51m -=-，4m ∴=，24m ∴<<；（3）存在一点Q ，使以C 、E 、P 、Q 为顶点的四边形是菱形，理由如下：设(0,)E t ，(,4)P p p -，2(,24)Q q q q --，点E 在点C 下方，4t ∴<-，Q点在第四象限，01q ∴<<，①当CE 为菱形对角线时，CP CQ =，∴22222342(2)p q t q q q q q q =-⎧⎪=--⎨⎪=+-⎩，解得334q p t =⎧⎪=-⎨⎪=-⎩（舍)或116p q t =-⎧⎪=⎨⎪=-⎩，Q ∴点横坐标为1；②当CP 为对角线时，CE CQ =，∴22222824(4)(2)p q p t q q t q q q =⎧⎪-=+--⎨⎪+=+-⎩，解得222q p t =⎧⎪=⎨⎪=-⎩，Q ∴点横坐标为2，不符合题意；③当CQ 为菱形对角线时，CE CP =，∴222284(4)2p q q q t p t q =⎧⎪--=+-⎨⎪+=⎩，解得332p q t ⎧=⎪⎪=⎨⎪=-+⎪⎩（舍)或332p q t ⎧=-⎪⎪=-⎨⎪=--⎪⎩，Q ∴点横坐标为3-综上所述：Q 点横坐标为1或3-【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，函数图象平移的性质，菱形的性质，分类讨论是解题的关键．18．（2023•即墨区一模）如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少一个条件而无法解答，经查询结果发现，该二次函数的解析式为243y x x =-+．已知二次函数2y ax bx c =++的图象经过点(0,3)A ，(1,0)B ，．求该二次函数的解析式．（1）请根据已有信息添加一个适当的条件：(2,1)C -（答案不唯一）；（2）当函数值6y <时，自变量x 的取值范围：；（3）如图1，将函数243(0)y x x x =-+<的图象向右平移4个单位长度，与243(4)y x x x =-+ 的图象组成一个新的函数图象，记为L ．若点(3,)P m 在L 上，求m 的值；（4）如图2，在（3）的条件下，点A 的坐标为(2,0)，在L 上是否存在点Q ，使得9OAQ S ∆=．若存在，求出所有满足条件的点Q 的坐标；若不存在，请说明理由．【分析】（1）只需填一个在抛物线图象上的点的坐标即可；（2）求出6y =时，对应的x 值，再结合图象写出x 的取值范围即可；（3）求出抛物线向右平移4个单位后的解析式为2(6)3y x =--，根据题意可知3x =时，P 点在抛物线2(6)3y x =--的部分上，再求m 的值即可；（4）分两种情况讨论：当Q 点在抛物线2(6)3y x =--的部分上时，设2(,1233)Q t t t -+，由212(1233)92OAQ S t t ∆=⨯⨯-+=，求出Q 点坐标即可；当Q 点在抛物线243y x x =-+的部分上时，设2(,41)Q m m m -+，由212(41)92OAQ S m m ∆=⨯⨯-+=，求出Q 点坐标即可．【解答】解：（1）(2,1)C -，故答案为：(2,1)C -（答案不唯一）；（2）243y x x =-+ ，∴当2436x x -+=时，解得2x =2x =-∴当6y <时，22x <<+，故答案为：22x -<<+；（3）2243(2)1y x x x =-+=-- ，∴抛物线向右平移4个单位后的解析式为2(6)1y x =--，当3x =时，点P 在抛物线2(6)1y x =--的部分上，8m ∴=；（4）存在点Q ，使得9OAQ S ∆=，理由如下：当Q 点在抛物线2(6)1y x =--的部分上时，设2(,1235)Q t t t -+，212(1235)92OAQ S t t ∆∴=⨯⨯-+=，解得6t =+6t =，4t ∴<，6t ∴=-(6Q ∴-，9)；当Q 点在抛物线243y x x =-+的部分上时，设2(,43)Q m m m -+，212(43)92OAQ S m m ∆∴=⨯⨯-+=，解得2m =+或2m =-4m ，2m ∴=+，2Q ∴，9)；综上所述：Q 点坐标为(6，9)或2+，9)．【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，函数图象平移的性质，数形结合解题是关键．19．（2023•武侯区模拟）定义：将二次函数l 的图象沿x 轴向右平移t ，再沿x 轴翻折，得到新函数l '的图象，则称函数l '是函数l 的“t 值衍生抛物线”．已知2:23l y x x =--．（1）当2t =-时，①求衍生抛物线l '的函数解析式；②如图1，函数l 与l '的图象交于(M ，)n ，(,N m -两点，连接MN ．点P 为抛物线l '上一点，且位于线段MN 上方，过点P 作//PQ y 轴，交MN 于点Q ，交抛物线l 于点G ，求QNG S ∆与PNG S ∆存在的数量关系．（2）当2t =时，如图2，函数l 与x 轴交于A ，B 两点，与y 轴交于点C ，连接AC ．函数l '与x 轴交于D ，E 两点，与y 轴交于点F ．点K 在抛物线l '上，且EFK OCA ∠=∠．请直接写出点K 的横坐标．【分析】（1）①利用抛物线的性质和衍生抛物线的定义解答即可；②利用待定系数法求得直线MN 的解析式，设2(,23)P m m m --+，则得到(,2)Q m m -，2(,23)G m m m --，利用m 的代数式分别表示出PQ ，QG 的长，再利用同高的三角形的面积比等于底的比即可得出结论；（2）利用函数解析式求得点A ，B ，C ，D ，E ，F 的坐标，进而得出线段OA ，OC ，OD ，OE ，AC ，OF 的长，设直线FK 的解析式为5y kx =-，设直线FK 交x 轴于点M ，过点M 作MN EF ⊥于点N ，用k 的代数式表示出线段OM ．FM ，ME 的长，利用EFK OCA ∠=∠，得到sin sin EFK OCA ∠=∠，列出关于k 的方程，解方程求得k 值，将直线FK 的解析式与衍生抛物线l '的函数解析式联立即可得出结论．。

【数学知识点】二次函数的性质和平移规律一般地，把形如y=ax²+bx+c（a≠0）（a、b、c是常数）的函数叫做二次函数，下面总结了二次函数的性质和平移规律，供大家参考。

1.二次函数的图像是抛物线，抛物线是轴对称图形。

对称轴为直线x=-b/2a。

2.二次项系数a决定抛物线的开口方向和大小。

3.一次项系数b和二次项系数a共同决定对称轴的位置。

4.常数项c决定抛物线与y轴交点。

抛物线与y轴交于(0,c)。

当c>0时，图像与y轴正半轴相交。

当c<0时，图像与y轴负半轴相交。

上加下减，左加右减y=a(x+b)²+c，是将y=ax²的二次函数图像按以下规律平移(1)c>0时，图像向上平移c个单位(上加上)。

(2)c<0时，图像向下平移c个单位(下减)。

(3)b>0时，图像向左平移b个单位(左加)。

(4)b<0时，图像向右平移b个单位(右减)。

一般地，如果y=ax2+bx+c（a，b，c是常数，a≠0），那么y叫做x的二次函数。

①所谓二次函数就是说自变量最高次数是2;②二次函数y=ax2+bx+c（a≠0）中x、y是变量，a，b，c是常数，自变量x的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为a=0时，y=ax2+bx+c变为y=bx+c若b≠0,则y=bx+c是一次函数，若b=0，则y=c是一个常数函数。

③二次函数y=ax2+bx+c（a≠0）与一元二次方程y=ax2+bx+c（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。

感谢您的阅读，祝您生活愉快。

二次函数图像的变换第一环节 【知识储备】一、二次函数图象的平移变换（1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其顶点平移到(,)h k .具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---； 2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++； 3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-；()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-；4. 关于顶点对称 2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-； ()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+． 5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．第二环节 【新知探究】【问题一】 平移变换求把二次函数y ＝x 2－4x ＋3的图象经过下列平移变换后得到的图象所对应的函数解析式：（1）向右平移2个单位，向下平移1个单位；（2）向上平移3个单位，向左平移2个单位。

二次函数图像的转化与性质二次函数是初中数学中的重要内容，它的图像具有独特的特点和性质。

在学习二次函数时，我们不仅需要了解它的基本形式和图像特点，还需要学习如何进行图像的转化。

本文将介绍二次函数图像的转化方法以及转化后的性质，帮助中学生更好地理解和应用二次函数。

一、平移变换平移变换是指将二次函数的图像沿着横轴或纵轴方向移动一定的单位长度。

平移变换可以改变二次函数图像的位置，但不改变其形状。

常见的平移变换有水平平移和垂直平移两种。

1. 水平平移水平平移是指将二次函数的图像沿着横轴方向移动。

具体操作是，在二次函数的自变量x中加上一个常数h，即可实现水平平移。

例如，对于二次函数y=x^2，若要将其向右平移2个单位，则可得到新的函数y=(x-2)^2。

这样，二次函数的图像将整体向右平移2个单位。

2. 垂直平移垂直平移是指将二次函数的图像沿着纵轴方向移动。

具体操作是，在二次函数的因变量y中加上一个常数k，即可实现垂直平移。

例如，对于二次函数y=x^2，若要将其向上平移3个单位，则可得到新的函数y=x^2+3。

这样，二次函数的图像将整体向上平移3个单位。

二、翻折变换翻折变换是指将二次函数的图像沿着横轴或纵轴方向翻折。

翻折变换可以改变二次函数图像的形状，但不改变其位置。

常见的翻折变换有关于x轴翻折和关于y 轴翻折两种。

1. 关于x轴翻折关于x轴翻折是指将二次函数的图像沿着x轴翻折。

具体操作是，将二次函数的因变量y取相反数，即可实现关于x轴翻折。

例如，对于二次函数y=x^2，若要将其关于x轴翻折，则可得到新的函数y=-x^2。

这样，二次函数的图像将关于x 轴对称。

2. 关于y轴翻折关于y轴翻折是指将二次函数的图像沿着y轴翻折。

具体操作是，将二次函数的自变量x取相反数，即可实现关于y轴翻折。

例如，对于二次函数y=x^2，若要将其关于y轴翻折，则可得到新的函数y=(-x)^2。

这样，二次函数的图像将关于y 轴对称。

三、性质分析通过平移变换和翻折变换，我们可以改变二次函数图像的位置和形状，从而得到新的二次函数。

二次函数的变换与对称轴二次函数是高中数学中的一个重要内容，它在各个学科领域都有广泛的应用。

在学习二次函数时，我们会遇到一个重要概念——二次函数的变换与对称轴。

本文将围绕这一主题展开讨论。

一、二次函数的一般形式二次函数的一般形式为：$y = ax^2 + bx + c$，其中a、b、c为常数，a不等于0。

其中，a决定了二次函数的开口方向：当a大于0时，开口向上；当a小于0时，开口向下。

二、平移变换平移变换是指通过改变二次函数的横坐标和纵坐标的值，使得曲线发生平移。

平移变换有两种类型：水平平移和垂直平移。

1. 水平平移水平平移是指改变二次函数的横坐标的值，使得曲线在平面内左右移动。

若原二次函数为$y = ax^2 + bx + c$，则水平平移后的函数为$y= a(x-h)^2 + b(x-h) + c$，其中h为平移距离。

当h大于0时，曲线向右平移；当h小于0时，曲线向左平移。

2. 垂直平移垂直平移是指改变二次函数的纵坐标的值，使得曲线在平面内上下移动。

若原二次函数为$y = ax^2 + bx + c$，则垂直平移后的函数为$y= a(x-h)^2 + b(x-h) + k$，其中k为平移距离。

当k大于0时，曲线向上平移；当k小于0时，曲线向下平移。

三、对称轴对称轴是指二次函数的图像关于某一直线对称。

对称轴是二次函数的一个重要特征，可以通过一些变换得到。

1. 水平对称轴水平对称轴是指二次函数的图像关于y轴对称。

对于一般形式的二次函数$y = ax^2 + bx + c$，它的对称轴方程为$x = -\frac{b}{2a}$。

2. 垂直对称轴垂直对称轴是指二次函数的图像关于某一条直线对称，该直线垂直于y轴。

对于一般形式的二次函数$y = ax^2 + bx + c$，它的对称轴方程为$x = \frac{-b}{2a}$。

四、应用举例二次函数的变换与对称轴在实际问题中有广泛的应用。

以下举例说明：例1：某个物体的高度与时间的关系可以用二次函数表示。

二次函数的平移与伸缩二次函数是一种常见的数学函数，在数学和物理等领域有广泛的应用。

平移和伸缩是二次函数的重要性质，它们可以改变函数图像的位置和形状。

本文将详细介绍二次函数的平移和伸缩的概念、性质及其在图像变化中的应用。

一、平移的概念与性质平移是指将函数图像沿着坐标轴的方向上下或左右移动，而不改变函数的形状。

对于二次函数 f(x) = ax^2 + bx + c，平移的一般形式可以表示为 f(x - h) + k，其中 (h, k) 表示平移的距离和方向。

1. 水平平移：当 h > 0 时，函数图像向右平移 h 个单位；当 h < 0 时，函数图像向左平移 |h| 个单位。

2. 垂直平移：当 k > 0 时，函数图像向上平移 k 个单位；当 k < 0 时，函数图像向下平移 |k| 个单位。

平移的性质：平移后的函数图像与原函数图像相似，但位置发生了变化。

平移不改变二次函数的对称轴和开口方向。

二、伸缩的概念与性质伸缩是指将函数图像在坐标轴的方向上拉长或压缩，通过改变函数的系数实现。

对于二次函数 f(x) = ax^2 + bx + c，伸缩的一般形式可以表示为 f(px) = a(p·x)^2 + b(p·x) + c，其中 p 表示伸缩的比例。

1. 水平伸缩：当 p > 1 时，函数图像在 x 轴方向上被压缩；当 0 < p < 1 时，函数图像在 x 轴方向上被拉长。

2. 垂直伸缩：当 a > 1 时，函数图像在 y 轴方向上被拉伸；当 0 < a< 1 时，函数图像在 y 轴方向上被压缩。

伸缩的性质：伸缩后的函数图像与原函数图像相似，但形状和大小发生了改变。

伸缩改变了二次函数的开口程度，但不改变二次函数的对称轴。

三、平移与伸缩的应用1. 位置调整：通过平移可以将函数图像移动到坐标系中合适的位置，使得图像与实际问题相符合。

二次函数专题（3）——函数图像的平移我们知道图像的平移，图像本身不会发生改变，只是图像的位置发生改变。

函数图像的平移也是遵循这样原理，只是我们在平移过程中函数的解析式也发生改变，这节专题主要就是探讨函数平移与解析式的计算。

1. 基础情境：点坐标平移①水平平移：纵坐标不变横坐标加减我们以A（1,2）为例，把A往右平移2个单位到A’，很明显A’的纵坐标不变，但是横坐标变为了1+2=3，即A’（3,2）；同理把A往左平移2个单位到A’’（-1，2）②竖直平移：横坐标不变，纵坐标加减我们以A（1,2）为例，把A往上平移三个单位到A’，很明显A’的横坐标不变，但是纵坐标变为了2+3=5，即A’（1,5）；同理把A往下平移三个单位到A’’（1，-1）,如下图：2. 函数平移：一次函数图像平移①水平平移问题：我们以y=2x+2为例，把它向右平移2个单位，那么新的图像函数解析式为何？分析：由于平移过后仍然是条直线，两点决定一条直线，所以我们选取两个特殊点就可以算出新的函数表达式。

解答：选取原一次函数上两点（0,2）、（-1,0），经过平移后这两点坐标变为（2,2）和（1,0），计算得y=2x-2.观察：平移后，一次函数的系数k（2）不变，b减小了两倍（由2变为-2）推广：对于所有一次函数y=kx+b，向右平移2个单位的函数解析式怎么求？分析：可以按照上面的思路，取特殊点求取新的一次函数解析式解答：方法一：坐标法取两个特殊点（0，b）、（1，k+b），经过平移后这两点坐标变为（2,b）和（3,k+b），计算函数表达式得y=kx+b-2k。

这个式子我们还可以改写成这样y=（k-2）x+b。

反思：解析法特殊点法虽然可以帮助我们解决问题，但是需要计算，有没有更加快速的计算一次函数解析式方法？有！我们回到最初函数的定义，比如坐标系中有一个点A（x,y）,其中y=kx+b 代表是x与y之间的等量关系。

如果把A（x,y）向右平移2单位变成A’（m,y），此时m=x+2。

二次函数的平移翻折与缩放二次函数的平移、翻折与缩放是数学中常见的概念，它们描述了二次函数图像相对于原点的位置、方向和大小的变化。

在本文中，我将详细介绍二次函数的平移、翻折与缩放的概念和公式，并通过实例来说明其应用。

一、平移平移是指二次函数图像在平面上沿着坐标轴的平行方向上移动一定的距离。

对于二次函数y = a(x-h)² + k，其中(h, k)表示原点O到新的位置的平移向量。

横向平移：当平移向量为(h, 0)时，图像将沿x轴方向移动h个单位。

若h>0，图像向右移动；若h<0，图像向左移动。

纵向平移：当平移向量为(0, k)时，图像将沿y轴方向移动k个单位。

若k>0，图像向上移动；若k<0，图像向下移动。

通过改变平移向量的值，我们可以观察到二次函数图像在平面上不同位置的变化。

例如，考虑二次函数y = x²，若将其向右平移3个单位，则新的函数为y = (x-3)²。

图像向右移动了3个单位，其形状保持不变。

二、翻折翻折是指二次函数图像关于坐标轴进行对称。

分为横向翻折和纵向翻折两种情况。

横向翻折：当翻折轴为x轴时，二次函数图像关于x轴进行对称。

对于二次函数y = a(x-h)² + k，进行横向翻折后，新的函数为y = -a(x-h)² + k。

此时，形状不变，但图像位于原来位置的上方。

纵向翻折：当翻折轴为y轴时，二次函数图像关于y轴进行对称。

对于二次函数y = a(x-h)² + k，进行纵向翻折后，新的函数为y = a(-x-h)² + k。

此时，形状不变，但图像位于原来位置的左侧。

通过翻折操作，我们可以将二次函数图像在平面上不同位置进行对称变换。

例如，考虑二次函数y = x²，若将其关于x轴翻折，则新的函数为y = -x²。

图像关于x轴对称，形状保持不变。

三、缩放缩放是指二次函数图像在平面上根据比例因子进行拉伸或压缩。

二次函数专题训练（平移、旋转、轴对称变换）一、二次函数图象的平移、旋转（只研究中心对称）、轴对称变换 1、抛物线的平移变换：一般都是在顶点式的情况下进行的。

y=a(x-h)²+k y=a(x-h)²+k ±my=a(x-h)² y=a(x-h ±m)²+k 练习：（1）函数图象沿y 轴向下平移2个单位，再沿x 轴向右平移3个单位，得到函数__________________的图象。

（2）抛物线225y x x =-+向左平移3个单位，再向下平移6个单位，所得抛物线的解析式是 。

2、抛物线的旋转变换（只研究中心对称）：一般都是在顶点式的情况下进行的。

（1）将抛物线绕其顶点旋转180︒（即两条抛物线关于其顶点成中心对称） ()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+。

（2）将抛物线绕原点旋转180︒（即两条抛物线关于原点成中心对称）()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-。

练习：（1）抛物线2246y x x =-+绕其顶点旋转180︒后，所得抛物线的解析式是 （2）将抛物线y ＝x 2＋1绕原点O 旋转180°，则旋转后抛物线的解析式为( ) A ．y ＝－x 2 B ．y ＝－x 2＋1 C ．y ＝x 2－1 D ．y ＝－x 2－1 3、抛物线的轴对称变换： 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---； ()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+； ()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；练习：已知抛物线C 1：2(2)3y x =-+（1）抛物线C 2与抛物线C 1关于y 轴对称，则抛物线C 2的解析式为 （2）抛物线C 3与抛物线C 1关于x 轴对称，则抛物线C 3的解析式为 总结：根据平移、旋转、轴对称的性质，显然无论作何种变换，抛物线的形状一定不会发生变化，因此a 永远不变。

一、二次函数图象的平移变换（1）具体步骤：先利用配方式把二次函数化成2()y a x h k =-+的形式，确信其极点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其极点平移到(,)h k .具体平移方式如下图：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一样有五种情形，能够用一样式或极点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，取得的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，取得的解析式是()2y a x h k =---； 2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，取得的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，取得的解析式是()2y a x h k =++； 3. 关于原点对称2y ax bx c =++关于原点对称后，取得的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，取得的解析式是()2y a x h k =-+-； 4. 关于极点对称2y ax bx c =++关于极点对称后，取得的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于极点对称后，取得的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，取得的解析式是()222y a x h m n k =-+-+- 依照对称的性质，显然不管作何种对称变换，抛物线的形状必然可不能发生转变，因此a 永久不变．求抛物线的对称抛物线的表达式时，能够依据题意或方便运算的原那么，选择适合的形式，适应上是先确信原抛物线（或表达式已知的抛物线）的极点坐标及开口方向，再确信其对称抛物线的极点坐标及开口方向，然后再写出其对称抛物线的表达式．知识点拨二次函数图象的几何变换一、二次函数图象的平移变换【例1】 函数23(2)1y x =+-的图象可由函数23y x =的图象平移取得，那么平移的步骤是：（ ）A. 右移两个单位，下移一个单位B. 右移两个单位，上移一个单位C. 左移两个单位，下移一个单位D. 左移两个单位，上移一个单位【例2】 函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移取得，那么平移的步骤是（ ）A. 右移三个单位，下移四个单位B. 右移三个单位，上移四个单位C. 左移三个单位，下移四个单位D. 左移四个单位，上移四个单位【例3】 二次函数2241y x x =-++的图象如何移动就取得22y x =-的图象（ ）A. 向左移动1个单位，向上移动3个单位.B. 向右移动1个单位，向上移动3个单位.C. 向左移动1个单位，向下移动3个单位.D. 向右移动1个单位，向下移动3个单位.【例4】 将函数2y x x =+的图象向右平移()0a a >个单位，取得函数232y x x =-+的图象，那么a 的值为（ ）A ．1B ．2C ．3D ．4【例5】 把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，那么a b c ++=________________．【例6】 关于每一个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，那么112220092009A B A B A B +++…的值是（ ）A ． 20092008B ．20082009C ．20102009D ．20092010【例7】 把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，那么平移后抛物线的解析式为A ．()213y x =--- B ．()213y x =-+- C ．()213y x =--+D ．()213y x =-++【例8】 将抛物线22y x =向下平移1个单位，取得的抛物线是（ ）A ．()221y x =+B ．()221y x =-C ．221y x =+D ．221y x =-【例9】 将抛物线23y x =向上平移2个单位，取得抛物线的解析式是（ ）A. 232y x =-B. 23y x =C. 23(2)y x =+D. 232y x =+【例10】 一抛物线向右平移3个单位，再向下平移2个单位后得抛物线224y x x =-+，那么平移前抛物线的解析式为________________．【例11】 已知二次函数5632+-=x x y ，求知足以下条件的二次函数的解析式：（1）图象关于x 轴对称；（2）图象关于y 轴对称；（3）图象关于通过其极点且平行于x 轴的直线对称例题精讲【例12】 如图，ABCD 中，4AB =，点D 的坐标是(0，8)，以点C 为极点的抛物线2y ax bx c =++通过x 轴上的点A ，B ．⑴ 求点A ，B ，C 的坐标．⑵ 假设抛物线向上平移后恰好通过点D ，求平移后抛物线的解析式．【例13】 抛物线254y ax x a =-+与x 轴相交于点A B 、，且过点()54C ，． ⑴ 求a 的值和该抛物线极点P 的坐标．⑵ 请你设计一种平移的方式，使平移后抛物线的极点落要第二象限，并写出平移后抛物线的解析式．二、二次函数图象的对称变换【例14】 函数2y x =与2y x =-的图象关于______________对称，也能够以为2y x =是函数2y x =-的图象绕__________旋转取得．【例15】 已知二次函数221y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式；⑶关于原点对称的二次函数解析式．【例16】 在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为 A ．22y x x =--+ B ．22y x x =-+- C ．22y x x =-++ D ．22y x x =++【例17】 已知二次函数2441y ax ax a =++-的图象是1c ．⑴ 求1c 关于()10R ，成中心对称的图象2c 的函数解析式； ⑵ 设曲线12c c 、与y 轴的交点别离为A B ，，当18AB =时，求a 的值．【例18】 已知抛物线265y x x =-+，求⑴ 关于y 轴对称的抛物线的表达式；⑵ 关于x 轴对称的抛物线的表达式； ⑶ 关于原点对称的抛物线的表达式．【例19】 设曲线C 为函数()20y ax bx c a =++≠的图象，C 关于y 轴对称的曲线为1C ，1C关于x 轴对称的曲线为2C ，那么曲线2C 的函数解析式为________________．【例20】 关于任意两个二次函数：()2211112222120y a x b x c y a x b x c a a =++=++≠，，当12a a =时，咱们称这两个二次函数的图象为全等抛物线，现有ABM ∆，()()1010A B -，，，，记过三点的二次函数抛物线为“C”（“□□□”中填写相应三个点的字母）．⑴ 假设已知()01M ，，ABM ABN ∆∆≌（图1），请通过计算判定ABM C 与ABN C 是不是为全等抛物线；⑵ 在图2中，以A B M 、、三点为极点，画出平行四边形． ① 假设已知()0M n ，，求抛物线ABM C 的解析式，并直接写出所有过平行四边形中三个极点且能与ABM C 全等的抛物线解析式．② 假设已知()M m n ，，当m n 、知足什么条件时，存在抛物线ABM C ？依照以上的探讨结果，判定是不是存在过平行四边形中三个极点且能与ABM C 全等的抛物线．假设存在，请写出所有知足条件的抛物线“C”；假设不存在，请说明理由．【例21】 已知：抛物线2:(2)5f y x =--+． 试写出把抛物线f 向左平行移动2个单位后，所得的新抛物线1f 的解析式；和f 关于x 轴对称的曲线2f 的解析式．画出1f 和2f 的略图， 并求：⑴ x 的值什么范围，抛物线1f 和2f 都是下降的；⑵ x 的值在什么范围，曲线1f 和2f 围成一个封锁图形；⑶ 求在1f 和2f 围成封锁图形上，平行于y 轴的线段的长度的最大值．。

函数的平移与对称变换“三系列”之三：练悟试卷二次函数的平移与对称变换一、复习回顾（小巧同学总结的口诀）1、函数解析式“平移变换”的口诀是：上 、下 ；左 、右 ；2、函数解析式“对称变换”的口诀是：叉 、y 、原 ；二、运用口诀1、函数14x y 2++-=x 的图像向上平移2个单位后所得新函数的表达式为： ；2、函数14x y 2++-=x 的图像向右平移3个单位后所得新函数的表达式为： ；3、函数14x y 2++-=x 的图像先向左平移3个单位，再向下平移2个单位，所得新函数的表达式为： ；4、函数()52y 2+--=x 的图像先向左平移3个单位，再向下平移2个单位，所得新函数的表达式为： ；5、函数14x y 2++-=x 关于原点呈中心对称关系的新函数的表达式为： ；6、函数()52y 2+--=x 关于原点呈中心对称关系的新函数的表达式为： ；三、体验过程，理解模仿1、函数14x y 2++-=x 的图像先向左平移3个单位，再向下平移2个单位，求所得新函数的表达式。

﹤小巧同学的分析﹥：由平移口诀“上加、下减；左加、右减”知：向下平移2个单位，只需在原表 达式的“尾巴后面”2-，而向左平移3个单位，则要用“3+x ”去代替原表达式中的“x ”。

﹤小巧同学的解法﹥：新表达式为：()()2221343x y 22+--=⇒-++++-=x x y x﹤小王同学的分析﹥：设点P ()y x ，是所求新函数图像上的任意一点，则把点P “先向右平移3个单位”，“再向上平移2个单位”后所得点Q ()2y 3x ++，必在旧函数的图像上，把点Q 的坐标代入旧函数的表达式即可求出y 与x 之间的函数关系。

﹤小王同学的解法﹥：设点P ()y x ，是所求新函数图像上的任意一点，则点Q ()2y 3x ++，必在旧函数的图像上，把点Q 的坐标代入旧函数的表达式得：()()221343x 2y 22+--=⇒++++-=+x x y x2、函数x x -=22y 的图像先向右平移2个单位，再向上平移5个单位，求所得新函数的表达式。

二次函数图象的几何变换（1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其顶点平移到(,)h k .具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图象的平移变换练习1、函数23(2)1y x =+-的图象可由函数23y x =的图象平移得到，那么平移的步骤是：（ ）A. 右移两个单位，下移一个单位B. 右移两个单位，上移一个单位C. 左移两个单位，下移一个单位D. 左移两个单位，上移一个单位2、函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移得到，那么平移的步骤是（ ）A. 右移三个单位，下移四个单位B. 右移三个单位，上移四个单位C. 左移三个单位，下移四个单位D. 左移四个单位，上移四个单位3、二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象（ ）A. 向左移动1个单位，向上移动3个单位.B. 向右移动1个单位，向上移动3个单位.C. 向左移动1个单位，向下移动3个单位.D. 向右移动1个单位，向下移动3个单位.4、将函数2y x x =+的图象向右平移()0a a >个单位，得到函数232y x x =-+的图象，则a 的值为（ ）A ． 1B ．2C ．3D ．45、把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，则a b c ++=________________． 6、对于每个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，则112220092009A B A B A B +++…的值是（ ）A ．B ．20082009C ．20102009 D ．200920107、把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为A ．()213y x =--- B ．()213y x =-+- C ．()213y x =--+D ．()213y x =-++200920088、将抛物线22y x =向下平移1个单位，得到的抛物线是（ ）A ．B ．C ．221y x =+D ．221y x =-9、将抛物线23y x =向上平移2个单位，得到抛物线的解析式是（ ）A. 232y x =-B. 23y x =C. 23(2)y x =+D. 232y x =+10、一抛物线向右平移3个单位，再向下平移2个单位后得抛物线224y x x =-+，则平移前抛物线的解析式为________________． 11、如图，ABCD 中，4AB =，点D 的坐标是(0，8)，以点C 为顶点的抛物线2y ax bx c =++经过x 轴上的点A ，B ． ⑴ 求点A ，B ，C 的坐标． ⑵ 若抛物线向上平移后恰好经过点D ，求平移后抛物线的解析式．12、已知二次函数221y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式；⑶关于原点对称的二次函数解析式．13、函数2y x =与2y x =-的图象关于______________对称，也可以认为2y x =是函数2y x =-的图象绕__________旋转得到．14、在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y 轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为A ．22y x x =--+B ．22y x x =-+-C ．22y x x =-++D ．22y x x =++()221y x =+()221y x =-。

2二次函数图象的平移、旋转、轴对称专题有关图象的变换一般可采用两种基本的方法，其一是利用特殊点进行变换，其二是利用坐标变换的规律进行变换。

所谓利用特殊点进行变换，即选取原图象上一些特殊的点，把这些点按指定的要求进行变换，再把变换后的点代入到新的解析式中，从而求出变换后的解析式，利用特殊点进行变换，又可以从一般形式入手，选取图象上的三个特殊的点进行变换，也可以把一般形式化为顶点式，选取顶点作为特殊点，然后进行变换。

利用坐标变换的方法，根据题目的要求，利用坐标变换的规律，从而进行变换。

下面由具体的例子进行说明。

一 、 平 移 。

例1、 把抛物线 y=x -4x+6 向左平移 3 个单位，再向下平移 4 个单位后，求其图象的解析式。

法（一）选取图象上三个特殊的点，如（0， 6），（ 1， 3），（ 2，2）【选取使运算最简单的点】，然后把这三个点按要求向左平移3 个单位，再向下平移4 个单位后得到三个新点（ -3 ， 2），（ -2 ， -1 ），（-1 ，-2 ），把这三个新点代入到新的函数关 系式的一般形式 y=ax 2+bx+c 中，求出各项系数即可。

例 2、已知抛物线 y=2x 位，求其解析式。

法（二）2-8x+5, 求其向上平移 4 个单位，再向右平移 3 个单先利用配方法把二次函数化成y a( x h)2 k 的形式，确定其顶点（ 2，-3 ），然后把顶点（ 2， -3 ）向上平移 4 个单位，再向右平移 3 个单位后得到新抛物线的顶点为（ 5， 1），因为是抛物线的平移，因此平移前后 a 的值应该相等，这样我们就得到新的抛物线的解析式中 a=2，且顶点为（ 5， 1），就可以求出其解析式了。

22222【平移规律：在原有函数的基础上“左加右减、上加下减”】 .法（三）根据平移规律进行平移，不论哪种抛物线的形式，平移规律为 “左右平移即把解析式中自变量 x 改为 x 加上或减去一个常数，左加右减，上下平移即把整个解析式加上或减去一个常数，上加下减。

二次函数知识点归纳总结二次函数是高中数学中的一个重要内容，也是数学建模和解几何问题的重要工具。

下面是关于二次函数的知识点的归纳总结。

一、基本概念1. 二次函数的定义：二次函数是形如f(x) = ax^2 + bx + c (a ≠ 0) 的函数，其中 a、b、c 是常数。

2.二次函数的图象：二次函数的图象是一个抛物线，开口方向取决于a的正负性，顶点坐标为(-b/2a,f(-b/2a))。

3.对称轴：二次函数的对称轴是与图象关于x轴对称的直线，其方程为x=-b/2a。

4. 零点：二次函数的零点是函数图象与 x 轴的交点，可以通过求解二次方程 ax^2 + bx + c =0 来得到。

5.最值：二次函数的最值取决于a的正负性，当a>0时，函数取最小值；当a<0时，函数取最大值。

二、二次函数的变形与性质1.平移变换：二次函数可以通过平移变换来改变其图象的位置。

平移变换的一般形式是f(x)→f(x-h)+k，其中h和k是任意实数。

2.缩放变换：二次函数可以通过缩放变换来改变其图象的形状。

缩放变换的一般形式是f(x)→af(x)，其中a是非零实数。

3.纵坐标平移：二次函数可以通过纵坐标平移来改变其图象的位置。

纵坐标平移的一般形式是f(x)→f(x)+k，其中k是任意实数。

4.二次函数的奇偶性：如果a是偶数，则二次函数是偶函数；如果a是奇数，则二次函数是奇函数。

5.顶点坐标的性质：顶点坐标(-b/2a,f(-b/2a))是二次函数的最值点，当a>0时是最小值，当a<0时是最大值。

三、二次函数的方程与不等式1. 二次方程的解：二次方程 ax^2 + bx + c =0 的解可以通过求根公式 x = (-b ± √(b^2 - 4ac))/(2a) 来得到。

2. 解的判别式：二次方程 ax^2 + bx + c =0 的解的判别式是 D =b^2 - 4ac，根据判别式的值可以判断方程有几个实数解。

二次函数专题训练（平移、旋转、轴对称变换）一、二次函数图象的平移、旋转（只研究中心对称）、轴对称变换1、抛物线的平移变换：一般都是在顶点式的情况下进行的。

抛物线的上下平移：________________________y=a(x-h)²+k y=a(x-h)²+k ±m抛物线的左右平移：________________________y=a(x-h)²+k y=a(x-h ±m)²+k练习：（1）函数图象沿y 轴向下平移2个单位，再沿x 轴向右平移3个单位，得到函数__________________的图象。

（2）抛物线225y x x =-+向左平移3个单位，再向下平移6个单位，所得抛物线的解析式是 。

2、抛物线的旋转变换（只研究中心对称）：一般都是在顶点式的情况下进行的。

（1）将抛物线绕其顶点旋转180︒（即两条抛物线关于其顶点成中心对称）()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+。

（2）将抛物线绕原点旋转180︒（即两条抛物线关于原点成中心对称）()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-。

练习：（1）抛物线2246y x x =-+绕其顶点旋转180︒后，所得抛物线的解析式是（2）将抛物线y ＝x 2＋1绕原点O 旋转180°，则旋转后抛物线的解析式为( )A ．y ＝－x 2B ．y ＝－x 2＋1C ．y ＝x 2－1D ．y ＝－x 2－13、抛物线的轴对称变换：关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---； 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++； 练习：已知抛物线C 1：2(2)3y x =-+（1）抛物线C 2与抛物线C 1关于y 轴对称，则抛物线C 2的解析式为（2）抛物线C 3与抛物线C 1关于x 轴对称，则抛物线C 3的解析式为总结：根据平移、旋转、轴对称的性质，显然无论作何种变换，抛物线的形状一定不会发生变化，因此a 永远不变。

二次函数中的平移、翻折、对称、旋转、折叠问题目录题型01二次函数平移问题题型02二次函数翻折问题题型03二次函数对称问题题型04二次函数旋转问题题型05二次函数折叠问题题型01二次函数平移问题1. 二次函数的平移变换平移方式(n>0)一般式y=ax2+bx+c顶点式y=a(x-h)2+k平移口诀向左平移n个单位y=a(x+n)2+b(x+n)+c y=a(x-h+n)2+k左加向右平移n个单位y=a(x-n)2+b(x-n)+c y=a(x-h-n)2+k右减向上平移n个单位y=ax2+bx+c+n y=a(x-h)2+k+n上加向下平移n个单位y=ax2+bx+c-n y=a(x-h)2+k-n下减2.平移与增加性变化如果平移后对称轴不发生变化，则不影响增减性，但会改变函数最大(小)值.只对二次函数上下平移，不改变增减性，改变最值.只对二次函数左右平移，改变增减性，不改变最值.1(2023·上海杨浦·统考一模)已知在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a≠0与x轴交于点A、点B(点A在点B的左侧)，与y轴交于点C，抛物线的顶点为D，且AB=4．(1)求抛物线的表达式；(2)点P 是线段BC 上一点，如果∠PAC =45°，求点P 的坐标；(3)在第(2)小题的条件下，将该抛物线向左平移，点D 平移至点E 处，过点E 作EF ⊥直线AP ，垂足为点F ，如果tan ∠PEF =12，求平移后抛物线的表达式．【答案】(1)y =x 2-2x -3(2)P 53,-43(3)y =x +1792-4【分析】(1)设点A 的横坐标为x A ，点B 的横坐标为x B ，根据对称轴，AB =4，列式x A +x B2=1,x B -x A =4，利用根与系数关系计算确定a 值即可．(2)过点C 作AC ⊥MN 于点C ，交AC 右侧的AP 的延长线于点M ，交AC 左侧的AP 的延长线于点N ，利用三角形全等，确定坐标，后根据解析式交点确定所求坐标即可．(3)设抛物线向左平移了t 个单位，则点E 1-t ,-4 ，过点F 作x 轴的平行线交过点P 和y 轴的平行线于点H ，交过点E 和y 轴的平行线于点G ，证明Rt △FGE ∽Rt △PHF ，根据相似三角形的性质得出GEHF=GF HP =EF FP =1tan ∠PEF =2即可求解．【详解】(1)解：∵抛物线y =ax 2-2ax -3a ≠0 与x 轴交于点A 、点B (点A 在点B 的左侧)，与y 轴交于点C ，抛物线的顶点为D ，且AB =4，∴x A +x B 2=1,x B -x A =4，解得x B =3,x A =-1，∴-3a=3×-1 ，解得a=1，故抛物线的解析式为y =x 2-2x -3．(2)过点C 作AC ⊥MN 于点C ，交AC 右侧的AP 的延长线于点M ，∵∠PAC =45°，∴AC =CM ，过点M 作MT ⊥y 轴于点T ，∴∠ACO =90°-∠ECM =∠CMT ∵∠ACO =∠CMT ∠AOC =∠CTM AC =CM，∴△AOC ≌△CTM AAS ，∴AO =CT ,OC =EM ，∵抛物线的解析式为y =x 2-2x -3，x B =3,x A =-1，∴AO =CT =1,OC =TM =3，A -1,0 ,C 0,-3 ,B 3,0 ，∴OE =2,TM =3∴M 3,-2 ，设AM 的解析式为y =kx +b ，BC 的解析式为y =px +q ∴-k +b =03k +b =-2 ,3p +q =0q =-3 ，解得k =-12b =-12,p =1q =-3 ∴AM 的解析式为y =-12x -12，BC 的解析式为y =x -3，∴y =x -3y =-12x -12 ，解得x =53y =-43，故P 53,-43；(3)∵y =x 2-2x -3=x -1 2-4，点D 1,-4 ,设抛物线向左平移了t 个单位，则点E 1-t ,-4 ，过点F 作x 轴的平行线交过点P 和y 轴的平行线于点H ，交过点E 和y 轴的平行线于点G ，由(2)知，直线AP 的表达式为：y =-12x -12，P 53,-43设F m ,-12m -12 ∵∠EFP =90°，∴∠GFE +∠HFP =90°，∵∠GFE +∠GEF =90°，∴∠GEF =∠HFP ，∴Rt △FGE ∽Rt △PHF ，∴GE HF =GF HP =EF FP =1tan ∠PEF=2，∵GE =y F -y E =-12m -12+4，HF =x P -x F =53-m ，GF =x F -x G =m -1-t ，HP=y F -y P =-12m-12+43，∴-12m -12+453-m =m -1-t -12m -12+43=2，解得：t =269，∴y =x -1+269 2-4=x +179 2-4．【点睛】本题为考查了二次函数综合运用，三角形全等和相似、解直角三角形、图象平移等，正确作辅助线是解题的关键．2(2023·广东湛江·校考一模)如图1，抛物线y =36x 2+433x +23与x 轴交于点A ，B (A 在B 左边)，与y 轴交于点C ，连AC ，点D 与点C 关于抛物线的对称轴对称，过点D 作DE ∥AC 交抛物线于点E ，交y 轴于点P．(1)点F 是直线AC 下方抛物线上点一动点，连DF 交AC 于点G ，连EG ，当△EFG 的面积的最大值时，直线DE 上有一动点M ，直线AC 上有一动点N ，满足MN ⊥AC ，连GM ，NO ，求GM +MN +NO 的最小值；(2)如图2，在(1)的条件下，过点F 作FH ⊥x 轴于点H 交AC 于点L ，将△AHL 沿着射线AC 平移到点A 与点C 重合，从而得到△A H L (点A ，H ，L 分别对应点A ，H ，L )，再将△A H L 绕点H 逆时针旋转α(0°<α<180°)，旋转过程中，边A L 所在直线交直线DE 于Q ，交y 轴于点R ，求当△PQR 为等腰三角形时，直接写出PR 的长．【答案】(1)4+23975(2)1733-3或833【分析】(1)作FH ∥y 轴交DE 于H ．设F m ,36m 2+433m +23 ，求出直线DE 的解析式，联立方程得到x =-3时，FH 的值最大，求出答案；作点G 关于DE 的对称点T ，TG 交DE 于R ，连接OR 交AC 于N ，作NM ⊥DE 于M ，连接TM ，GM ，此时GM +MN +NO 的值最小，求出答案即可；(2)当△PQR 是等腰三角形时，易知∠QPR =120°，易知直线RQ 与x 轴的夹角为60°，得到直线RQ 的解析式为y =3x +3-3，进而求出答案，当△QPR 是等腰三角形，同理求出答案．【详解】(1)如图1中，作FH ∥y 轴交DE 于H ．设F m ,36m 2+433m +23 ．由题意可知A (-6,0)，B (-2,0)，C (0,23)，∵抛物线的对称轴x =-4，C ，D 关于直线x =-4对称，∴D (-8,23)，∴直线AC 的解析式为y =33x +23，∵DE ∥AC ，∴直线DE 的解析式为y =33x +1433，由y =33x +23y =33x +1433，解得x =8y=23 或x =2y =1633，∴E 2,1633 ，H m ,33m +1433，∵S △DEF =S △DEG +S △EFG ，△DEG 的面积为定值，∴△DEG 的面积最大时，△EFG 的面积最大，∵FH 的值最大时，△DEF 的面积最大，∵FH 的值最大时，△EFG 的面积最大，∵FH =-36m 2-3m +833，∵a <0．开口向下，∴x =-3时，FH 的值最大，此时F -3,-32．如图2中，作点G 关于DE 的对称点T ，TG 交DE 于R ，连接OR 交AC 于N ，作NM ⊥DE 于M ，连接TM ，GM ，此时GM +MN +NO 的值最小．∵直线DF 的解析式为：y =-32x -23，由y =-32x -23y =33x +23，解得x =-245y =235，∴G -245,232 ，∵TG ⊥AC ，∴直线GR 的解析式为y =-3x -2235，由y =33x +1433y =-3x -2235 ，解得x =-345y =1235，∴R -345,1235，∴RG =4,OR =23975，∵GM =TM =RN ，∴GM +MN +ON =RN +ON +RG =RG +ON =4+23975．∴GM +MN +NO 的最小值为4+23975．(2)如图3中，如图当△PQR 是等腰三角形时，易知∠QPR =120°，PQ =PR易知直线RQ 与x 轴的夹角为60°，L 3-32,23+32，直线RQ 的解析式为y =3x +3-3，∴R (0,3-3)，∴PR =1433-(3-3)=1733-3．如图4中，当△QPR 是等腰三角形，∵∠QPR =60°，∴△QPR 是等边三角形，同法可得R (0,23)，∴PR =OP -OC =1433-23=833综上所述，满足条件的PR 的值为1733-3或833．【点睛】本题属于二次函数证明题，考查了二次函数的性质，一次函数的应用，解题的关键是学会构建二次函数解决最值问题，学会分类讨论的思想思考问题．3(2023·广东潮州·校考一模)如图，在平面直角坐标系中，抛物线y =-12x 2+bx +c 与x 轴交于A (-2,0),B (4,0)两点(点A 在点B 的左侧)，与y 轴交于点C ，连接AC 、BC ，点P 为直线BC 上方抛物线上一动点，连接OP 交BC 于点Q ．(1)求抛物线的函数表达式；(2)当PQ OQ 的值最大时，求点P 的坐标和PQ OQ的最大值；(3)把抛物线y =-12x 2+bx +c 沿射线AC 方向平移5个单位得新抛物线y ，M 是新抛物线上一点，N 是新抛物线对称轴上一点，当以M 、N 、B 、C 为顶点的四边形是平行四边形时，直接写出N 点的坐标，并把求其中一个N 点坐标的过程写出来．【答案】(1)抛物线的函数表达式为y =-12x 2+x +4(2)当m =2时，PQ OQ取得最大值12，此时，P (2,4)(3)N 点的坐标为N 12,52 ,N 22,-112 ,N 32,-52.其中一个N 点坐标的解答过程见解析【分析】(1)运用待定系数法即可求得答案；(2)运用待定系数法求得直线BC 的解析式为y =-x +4，如图1，过点P 作PD ∥y 轴交BC 于点D ，设P m ,-12m 2+m +4 ，则D (m ,-m +4)，证明△PDQ ∽△OCQ ，得出：PQ OQ =PD OC=-12m 2+2m 4=-18(m -2)2+12，运用求二次函数最值方法即可得出答案；(3)设M t -12t 2+2t +92,N (2,s )，分三种情况：当BC 为▱BCN 1M 1的边时；当BC 为▱BCM 2N 2的边时；当BC 为▱BM 3CN 3的对角线时，运用平行四边形性质即可求得答案．【详解】(1)∵抛物线y =-12x 2+bx +c 与x 轴交于A (-2,0),B (4,0)两点(点A 在点B 的左侧)，∴-12×(-2)2-2b +c =0-12×42+4b +c =0,解得：b =1c =4 ，∴抛物线的函数表达式为y =-12x 2+x +4；(2)∵抛物线y =-12x 2+x +4与y 轴交于点C ，∴C (0,4)，∴OC =4，设直线BC 的解析式为y =kx +d ，把B (4,0),C (0,4)代入，得：4k +d =0,d =4 解得：k =-1d =4 ，∴直线BC 的解析式为y =-x +4，如图1，过点P 作PD ∥y 轴交BC 于点D ，设P m ,-12m 2+m +4 ，则D (m ,-m +4)，∴PD =-12m 2+2m ，∵PD ∥OC ，∴△PDQ ∽△OCQ ，∴PQ OQ =PD OC=-12m 2+2m 4=-18(m -2)2+12,∴当m =2时，PQ OQ取得最大值12，此时，P (2,4)．(3)如图2，沿射线AC 方向平移5个单位，即向右平移1个单位，向上平移2个单位，∴新的物线解析式为y =-12(x -2)2+132=-12x 2+2x +92，对称轴为直线x =2，设M t ,-12t 2+2t +92,N (2,s )，当BC 为▱BCN 1M 1的边时，则BC ∥MN ,BC =MN ，∴t -2=4s =-12t 2+2t +92+4解得：t =6s =52，∴N 12,52;当BC 为▱BCM 2N 2的边时，则BC ∥MN ,BC =MN ，∴t -2=-4s =-12t 2+2t +92-4 ,解得：t =-2s =-112，∴N 22,-112;当BC 为▱BM 3CN 3的对角线时，则t +2=4-12t 2+2t +92+s =4，解得：t =2s =-52，∴N 32,-52;综上所述，N 点的坐标为：N 12,52 ,N 22,-112 ,N 32,-52.【点睛】本题是二次函数综合题，考查了待定系数法，二次函数的图象和性质，抛物线的平移，平行四边形的性质，相似三角形的判定和性质，熟练掌握铅锤法、中点坐标公式，运用数形结合思想、分类讨论思想是解题关键．4(2023·湖北襄阳·校联考模拟预测)坐标综合：(1)平面直角坐标系中，抛物线C 1：y 1=x 2+bx +c 的对称轴为直线x =3，且经过点6,3 ，求抛物线C 1的解析式，并写出其顶点坐标；(2)将抛物线C 1在平面直角坐标系内作某种平移，得到一条新的抛物线C 2：y 2=x 2-2mx +m 2-1，①如图1，设自变量x 在1≤x ≤2的范围内取值时，函数y 2的最小值始终等于-1．此时，若y 2的最大值比最小值大12m ，求m 的值；②如图2，直线l ：y =-12x +n n >0 与x 轴、y 轴分别交于A 、C 两点.过点A 、点C 分别作两坐标轴的平行线，两平行线在第一象限内交于点B ．设抛物线C 2与x 轴交于E 、F 两点(点E 在左边)．现将图中的△CBA 沿直线l 折叠，折叠后的BC 边与x 轴交于点M ．当8≤n ≤12时，若要使点M 始终能够落在线段EF (包括两端点)上，请通过计算加以说明：抛物线C 1在向抛物线C 2平移时，沿x 轴的方向上需要向左还是向右平移？最少要平移几个单位？最多能平移几个单位？【答案】(1)抛物线C 1的解析式为y 1=x 2-6x +3，抛物线C 1的顶点坐标为3,-6(2)①m 的值为2或9-154；②抛物线C 1在向抛物线C 2平移时，沿x 轴的方向上需要向右平移，最少平移2个单位，最多平移7个单位【分析】(1)根据对称轴为直线x =3，可得b =-6，再把把6,3 代入，即可求解；(2)①根据配方可得当x =m 时，函数有最小值-1，再由自变量x 在1≤x ≤2的范围内取值时，函数y 2的最小值始终等于-1，可得1≤m ≤2，然后两种情况讨论，即可求解；②先求出点A ，C 的坐标，可得点B 的坐标，再根据图形折叠的性质可得CM =AM ，在Rt △COM 中，根据勾股定理可得CM =54n ，从而得到点M 的坐标，继而得到n 的取值范围，然后根据点M 始终能够落在线段EF (包括两端点)上，可得m 取值范围，即可求解．【详解】(1)解：∵y 1=x 2+bx +c 的对称轴为直线x =3，∴-b2=3，解得：b =-6，把6,3 代入y 1=x 2-6x +c ，得3=62-6×6+c ，解得：c =3，∴抛物线C 1的解析式为y 1=x 2-6x +3，当x =3时，y 1=32-6×3+3=-6，∴抛物线C 1的顶点坐标为3,-6 ；(2)解：①∵y 2=x 2-2mx +m 2-1=x -m 2-1，∴抛物线C 2的对称轴为直线x =m ，当x =m 时，函数有最小值-1，∵在1≤x ≤2的范围内取值时，函数y 2的最小值始终等于-1，∴1≤m ≤2，当1≤m ≤32时，x =2时y 2有最大值为m 2-4m +3，∴m 2-4m +3+1=12m ，解得m =9±154，∴m =9-154；当32≤m ≤2时，x =1时y 2有最大值为m 2-2m ，∴m 2-2m +1=12m ，解得m =2或m =12(舍)，综上所述：m 的值为2或9-154；②直线l ：y =-12x +n 与x 轴的交点A 2n ,0 ，与y 轴的交点C 0,n ，∴B 2n ,n ，∵△CBA 沿直线l 折叠，∴∠BCA =∠ACM ，∵∠BCA =∠CAM ，∴∠ACM =∠MAC ，∴CM =AM ，在Rt △COM 中，CM 2=CO 2+OM 2，即CM 2=n 2+2n -CM 2，解得CM =54n ，∴OM =34n ，∴M 34n ,0 ，∵8≤n ≤12，∴6≤34n ≤9，当x 2-2mx +m 2-1=0时，解得：x =m +1或x =m -1，∴E m -1,0 ，F m +1,0 ，∵点M 始终能够落在线段EF 上，∴m +1≥6，m -1≤9，∴5≤m ≤10，∵y 1=x 2-6x +3=x -3 2-6，y 2=x -m 2-1，当m =5时，抛物线C 1沿x 轴向右平移2个单位，向上平移5个单位，当m =10时，抛物线C 1沿x 轴向右平移7个单位，向上平移5个单位，∴抛物线C 1在向抛物线C 2平移时，沿x 轴的方向上需要向右平移，最少平移2个单位，最多平移7个单位．【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，函数图象平移的性质，轴对称图形的性质，勾股定理的应用是解题的关键．5(2023·浙江湖州·统考中考真题)如图1，在平面直角坐标系xOy 中，二次函数y =x 2-4x +c 的图象与y 轴的交点坐标为0,5 ，图象的顶点为M ．矩形ABCD 的顶点D 与原点O 重合，顶点A ，C 分别在x 轴，y 轴上，顶点B 的坐标为1,5 ．(1)求c 的值及顶点M 的坐标，(2)如图2，将矩形ABCD 沿x 轴正方向平移t 个单位0<t <3 得到对应的矩形A B C D ．已知边C D ，A B 分别与函数y =x 2-4x +c 的图象交于点P ，Q ，连接PQ ，过点P 作PG ⊥A B 于点G ．①当t =2时，求QG 的长；②当点G 与点Q 不重合时，是否存在这样的t ，使得△PGQ 的面积为1？若存在，求出此时t 的值；若不存在，请说明理由．【答案】(1)c =5，顶点M 的坐标是2,1(2)①1；②存在，t =12或52【分析】(1)把0,5 代入抛物线的解析式即可求出c ，把抛物线转化为顶点式即可求出顶点坐标；(2)①先判断当t =2时，D ，A 的坐标分别是2,0 ，3,0 ，再求出x =3，x =2时点Q 的纵坐标与点P 的纵坐标，进而求解；②先求出QG =2，易得P ，Q 的坐标分别是t ,t 2-4t +5 ，t +1,t 2-2t +2 ，然后分点G 在点Q 的上方与点G 在点Q 的下方两种情况，结合函数图象求解即可．【详解】(1)∵二次函数y =x 2-4x +c 的图象与y 轴的交点坐标为0,5 ，∴c =5， ∴y =x 2-4x +5=x -2 2+1，∴顶点M 的坐标是2,1 ．(2)①∵A 在x 轴上，B 的坐标为1,5 ，∴点A 的坐标是1,0 ．当t =2时，D ，A 的坐标分别是2,0 ，3,0 ．当x =3时，y =3-2 2+1=2，即点Q 的纵坐标是2，当x =2时，y =2-2 2+1=1，即点P 的纵坐标是1．∵PG ⊥A B ，∴点G 的纵坐标是1， ∴QG =2-1=1． ②存在．理由如下：∵△PGQ 的面积为1，PG =1，∴QG =2．根据题意，得P ，Q 的坐标分别是t ,t 2-4t +5 ，t +1,t 2-2t +2 ．如图1，当点G 在点Q 的上方时，QG =t 2-4t +5-t 2-2t +2 =3-2t =2，此时t =12(在0<t <3的范围内)，如图2，当点G 在点Q 的下方时，QG =t 2-2t +2-t 2-4t +5 =2t -3=2，此时t =52(在0<t <3的范围内)．∴t =12或52．【点睛】本题考查了二次函数图象上点的坐标特点、矩形的性质以及三角形的面积等知识，熟练掌握二次函数的图象与性质、灵活应用数形结合思想是解题的关键．6(2023·江苏·统考中考真题)如图，二次函数y =12x 2+bx -4的图像与x 轴相交于点A (-2,0)、B ，其顶点是C ．(1)b =；(2)D 是第三象限抛物线上的一点，连接OD ，tan ∠AOD =52；将原抛物线向左平移，使得平移后的抛物线经过点D ，过点(k ,0)作x 轴的垂线l ．已知在l 的左侧，平移前后的两条抛物线都下降，求k 的取值范围；(3)将原抛物线平移，平移后的抛物线与原抛物线的对称轴相交于点Q ，且其顶点P 落在原抛物线上，连接PC 、QC 、PQ ．已知△PCQ 是直角三角形，求点P 的坐标．【答案】(1)-1；(2)k ≤-3；(3)3,-52 或-1,-52 ．【分析】(1)把A (-2,0)代入y =12x 2+bx -4即可求解；(2)过点D 作DM ⊥OA 于点M ，设D m ,12m 2-m -4 ，由tan ∠AOD =DM OM=-12m 2+m +4-m =52，解得D -1,-52，进而求得平移后得抛物线，平移后得抛物线为y =12x +3 2-92，根据二次函数得性质即可得解；(3)先设出平移后顶点为P p ,12p 2-p -4 ，根据原抛物线y =12x -1 2-92，求得原抛物线的顶点C 1,-92 ，对称轴为x =1，进而得Q 1,p 2-2p -72，再根据勾股定理构造方程即可得解．【详解】(1)解：把A (-2,0)代入y =12x 2+bx -4得，0=12×-2 2+b ×-2 -4，解得b =-1，故答案为-1；(2)解：过点D 作DM ⊥OA 于点M ，∵b =-1，∴二次函数的解析式为y =12x 2-x -4设D m ,12m 2-m -4 ，∵D 是第三象限抛物线上的一点，连接OD ，tan ∠AOD =52，∴tan ∠AOD =DM OM=-12m 2+m +4-m =52，解得m =-1或m =8(舍去)，当m =-1时，12m 2-m -4=12+1-4=-52，∴D -1,-52，∵y =12x 2-x -4=12x -1 2-92，∴设将原抛物线向左平移后的抛物线为y =12x +a 2-92，把D -1,-52 代入y =12x +a 2-92得-52=12-1+a 2-92，解得a =3或a =-1(舍去)，∴平移后得抛物线为y =12x +3 2-92∵过点(k ,0)作x 轴的垂线l ．已知在l 的左侧，平移前后的两条抛物线都下降，在y =12x +3 2-92的对称轴x =-3的左侧，y 随x 的增大而减小，此时原抛物线也是y 随x 的增大而减小，∴k ≤-3；(3)解：由y =12x -1 2-92，设平移后的抛物线为y =12x -p 2+q ，则顶点为P p ,q ，∵顶点为P p ,q 在y =12x -1 2-92上，∴q =12p -1 2-92=12p 2-p -4，∴平移后的抛物线为y =12x -p 2+12p 2-p -4，顶点为P p ,12p 2-p -4 ，∵原抛物线y =12x -1 2-92，∴原抛物线的顶点C 1,-92，对称轴为x =1，∵平移后的抛物线与原抛物线的对称轴相交于点Q ，∴Q 1,p 2-2p -72，∵点Q 、C 在直线x =1上，平移后的抛物线顶点P 在原抛物线顶点C 的上方，两抛物线的交点Q 在顶点P 的上方，∴∠PCQ 与∠CQP 都是锐角，∵△PCQ 是直角三角形，∴∠CPQ =90°，∴QC 2=PC 2+PQ 2，∴p 2-2p -72+92 2=p -1 2+12p 2-p -4+922+p -1 2+12p 2-p -4-p 2+2p +722化简得p -1 2p -3 p +1 =0，∴p =1(舍去)，或p =3或p =-1，当p =3时，12p 2-p -4=12×32-3-4=-52，当p =-1时，12×-1 2+1-4=-52，∴点P 坐标为3,-52 或-1,-52．【点睛】本题考查了二次函数的图像及性质，勾股定理，解直角三角形以及待定系数法求二次函数的解析式，熟练掌握二次函数的图像及性质是解题的关键．7(2023·湖北宜昌·统考模拟预测)如图，过原点的抛物线y 1=ax (x -2n )(a ≠0,a ,n 为常数)与x 轴交于另一点A ，B 是线段OA 的中点，B -4,0 ，点M (-3,3)在抛物线y 1上．(1)点A 的坐标为；(2)C 为x 轴正半轴上一点，且CM =CB ．①求线段BC 的长；②线段CM 与抛物线y 1相交于另一点D ，求点D 的坐标；(3)将抛物线y 1向右平移(4-t )个单位长度，再向下平移165个单位长度得到抛物线y 2，P ，Q 是抛物线y 2上两点，T 是抛物线y 2的顶点．对于每一个确定的t 值，求证：矩形TPNQ 的对角线PQ 必过一定点R ，并求出此时线段TR 的长．【答案】(1)-8,0(2)①BC =5；②D -54,2716 (3)证明见解析，RT =5【分析】(1)根据中点公式求C 点坐标即可；(2)①设C x ,0 ，根据CM =CB ，建立方程(x +3)2+9=x +4，求出C 点坐标即可求BC ；②求出直线CM 的解析式为y =-34x +34，将A -8,0 代入y 1=ax (x -2n )，求出n =-4，将M 点代入y 1=ax (x +8)，求出a =-15，从而求出抛物线y 1=-15x (x +8)，直线CM 与抛物线的交点即为点D -54,2716；(3)根据平移的性质可求y 2=-15(x +t )2，则T (-t ,0)，设直线PQ 的解析式为y =kx +b ，P m ,-15(m +t )2 ，Q n ,15(n +t )2 当kx +b =-15(x +t )2时，整理得x 2+(2t +5k )x +5b +t 2=0，由根与系数的关系可得m +n =-2t -5k ，mn =5b +t 2，过点P 作PF ⊥x 轴交于F 点，过Q 点作QE ⊥x 轴交于E 点，证明△FPT ∽△ETQ ，则PF TE =FT EQ ，即15(m +t )2n +t =-t -m 15(n +t )2，整理得，(m +t )(n +t )=-25，求出b =kt -5，所以直线PQ 的解析式为y =kx +kt -5=k (x +t )-5，对于每一个确定的t 值，直线PQ 必经过定点R (-t ,-5)，RT =5．【详解】(1)∵B 是线段OA 的中点，B -4,0 ，∴OA =8，∴A -8,0 ，故答案为：-8,0 ；(2)①设C x ,0 ，∵CM =CB ，∴(x +3)2+9=x +4，解得x =1，∴BC =5；②设直线CM 的解析式为y =k 'x +b '，∴k '+b '=0-3k '+b '=3 ，解得k '=-34b '=34，∴直线CM 的解析式为y =-34x +34，将A -8,0 代入y 1=ax (x -2n )，∴-8a (-8-2n )=0，∵a ≠0，∴-8-2n =0，解得n =-4，∴y 1=ax (x +8)，将M 点代入y 1=ax (x +8)，∴-3a (-3+8)=3，解得a =-15，∴抛物线y 1=-15x (x +8)，当-34x +34=-15x (x +8)时，解得x =-3或x =-54，∴D -54,2716；(3)证明：∵y 1=-15x (x +8)=-15(x +4)2+165，∴y 2=-15(x +t )2，∴T (-t ,0)，设直线PQ 的解析式为y =kx +b ，P m ,-15(m +t )2 ，Q n ,15(n +t )2 ，当kx +b =-15(x +t )2时，整理得x 2+(2t +5k )x +5b +t 2=0，∴m +n =-2t -5k ，mn =5b +t 2，过点P 作PF ⊥x 轴交于F 点，过Q 点作QE ⊥x 轴交于E 点，∵四边形TPNQ 是矩形，∴∠PTQ =90°，∴∠FTP +∠ETQ =90°，∵∠FTP +∠TPF =90°，∴∠ETQ =∠TPF ，∴△FPT ∽△ETQ ，∴PF TE =FTEQ，即15(m +t )2n +t=-t -m15(n +t )2，整理得，(m +t )(n +t )=-25，∴mn +t (m +n )+t 2=-25，∴b -kt =-5，即b =kt -5，∴直线PQ 的解析式为y =kx +kt -5=k (x +t )-5，∴对于每一个确定的t 值，直线PQ 必经过定点R (-t ,-5)，∴RT =5．【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，三角形相似的判定及性质，一元二次方程根与系数的关系，题型02二次函数翻折问题二次函数的翻转问题的解题思路：①根据二次函数上特殊点的坐标值求得二次函数的表达式；②根据翻转后抛物线与原抛物线的图像关系，确定新抛物线的表达式；③在直角坐标系中画出原抛物线及翻转后抛物线的简易图，根据图像来判断题目中需要求解的量的各种可能性；④根据图像及相关函数表达式进行计算，求得题目中需要求解的值。

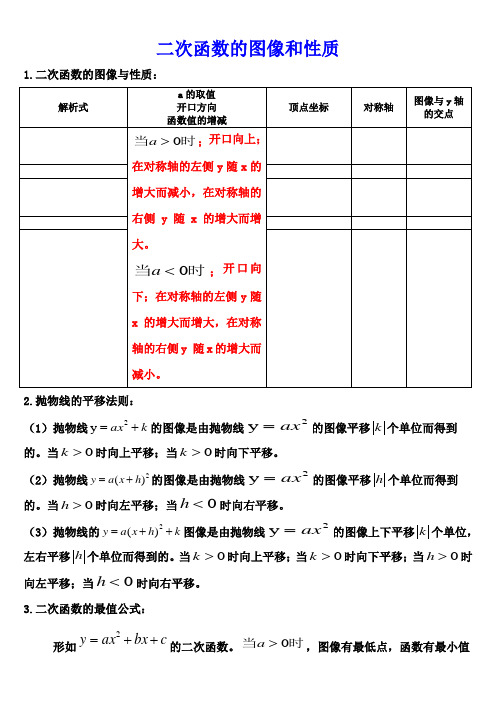
二次函数的图像和性质1.二次函数的图像与性质：解析式a 的取值 开口方向 函数值的增减顶点坐标对称轴图像与y 轴的交点时当0>a ；开口向上；在对称轴的左侧y 随x 的增大而减小，在对称轴的右侧y 随x 的增大而增大。

时当0<a ；开口向下；在对称轴的左侧y 随x 的增大而增大，在对称轴的右侧y 随x 的增大而减小。

2.抛物线的平移法则：（1）抛物线k ax +=2y 的图像是由抛物线2y ax =的图像平移k 个单位而得到的。

当0>k 时向上平移；当0>k 时向下平移。

（2）抛物线2)(h x a y +=的图像是由抛物线2y ax =的图像平移h 个单位而得到的。

当0>h 时向左平移；当0<h 时向右平移。

（3）抛物线的k h x a y ++=2)(图像是由抛物线2y ax =的图像上下平移k 个单位，左右平移h 个单位而得到的。

当0>k 时向上平移；当0>k 时向下平移；当0>h 时向左平移；当0<h 时向右平移。

3.二次函数的最值公式：形如c bx ax y ++=2的二次函数。

时当0>a ，图像有最低点，函数有最小值a b ac y 442-=最小值；时当0<a，图像有最高点，函数有最大值，a b ac y 442-=最大值；4.抛物线c bx ax y ++=2与y 轴的交点坐标是（0，c ）5.抛物线的开口大小是由a 决定的，a 越大开口越小。

6.二次函数c bx ax y ++=2的最值问题：（1）自变量的取值范围是一切实数时求最值的方法有配方法、公式法、判别式法。

（2）自变量的取值范围不是一切实数：自变量的取值范围不是一切实数时，应当抓住对称轴abx 2-=,把他与取值范围相比较，再进行求最值。

6.二次函数与一元二次方程的关系：(1)抛物线c bx ax y ++=2与x 轴的交点坐标的横坐标方程02=++c bx ax 的两根。

初二数学二次函数与图形变换知识点图形变换包含平移、轴对称、旋转、位似四种变换，那么二次函数的图像在其图形改变(平移、轴对称、旋转)的'过程中，如何完成解析式的确定呢？解决此类问题的方法许多，关键在于解决问题的着眼点。

笔者认为最好的方法是用顶点式的方法。

因此解题时，先将二次函数解析式化为顶点式，确定其顶点坐标，再依据详细图形变换的特点，确定改变后新的顶点坐标及a值。

1、平移：二次函数图像经过平移变换不会转变图形的外形和开口方向，因此a值不变。

顶点位置将会随着整个图像的平移而改变，因此只要根据点的移动规律，求出新的顶点坐标即可确定其解析式。

例1.将二次函数y=*2-2*-3的图像向上平移2个单位，再向右平移1个单位，得到的新的图像解析式为_____分析：将y=*2-2*-3化为顶点式y=(*-1)2-4，a值为1，顶点坐标为(1，-4)，将其图像向上平移2个单位，再向右平移1个单位，那么顶点也会相应移动，其坐标为(2，-2),由于平移不转变二次函数的图像的外形和开口方向，因此a值不变，故平移后的解析式为y=(*-2)2-2。

2、轴对称：此图形变换包括*轴对称和关于y轴对称两种方式。

二次函数图像关于*轴对称的图像，其外形不变，但开口方向相反，因此a值为原来的相反数。

顶点位置转变，只要依据关于*轴对称的点的坐标特征求出新的顶点坐标，即可确定其解析式。

二次函数图像关于y轴对称的图像，其外形和开口方向都不变，因此a值不变。

但是顶点位置会转变，只要依据关于y轴对称的点的坐标特征求出新的顶点坐标，即可确定其解析式。

例2.求抛物线y=*2-2*-3关于*轴以及y轴对称的抛物线的解析式。

分析：y=*2-2*-3=(*-1)2-4，a值为1，其顶点坐标为(1，-4)，假设关于*轴对称，a值为-1，新的顶点坐标为(1，4)，故解析式为y=-(*-1)2+4；假设关于y轴对称，a值仍为1，新的顶点坐标为(-1，-4)，因此解析式为y=(*+1)2-4。

二次函数平移规律口诀
一般地，把形如y=ax²+bx+c（a≠0）（a，b，c是常数）的函数叫做二次函数。

二次函数的平移规律口诀是加左减右，加上减下。

二次函数的平移规律口诀
加左减右，加上减下。

意思就是当二次函数写成下面这个样子时：
y=a(x+b)²+c，只要将y=ax²的函数图像按以下规律平移。

(1)b>0时，图像向左平移b个单位(加左)。

(2)b<0时，图像向右平移b个单位(减右)。

(3)c>0时，图像向上平移c个单位(加上)。

(4)c<0时，图像向下平移c个单位(减下)。

二次函数基本定义
一般地，把形如y=ax²+bx+c（a≠0）（a，b，c是常数）的函数叫做二次函数，其中a称为二次项系数，b为一次项系数，c为常数项。

x为自变量，y为因变量。

等号右边自变量的最高次数是2。

注意：“变量”不同于“未知数”，不能说“二次函数是指未知数的最高次数为二次的多项式函数”。

“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在一定范围内任意取值。

在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。

从函数的定义也可看出二者的差别。