九年级数学上册第23章图形的相似23.1成比例线段23.1.1成比例线段_8
- 格式:pdf
- 大小:2.24 MB
- 文档页数:26


23.1 成比例线段1.成比例线段【知识与技能】1.了解成比例线段的意义,会判断四条线段是否成比例.2.会利用比例的性质,求出未知线段的长.【过程与方法】培养学生灵活解题及合作探究的能力.【情感态度】感受数学逻辑推理的魅力.【教学重点】成比例线段的定义;比例的基本性质及直接运用.【教学难点】比例的基本性质的灵活运用,探索比例的其他性质.一、情境导入,初步认识挂上两张照片,问:1.这两个图形有什么联系?它们都是平面图形,它们的形状相同,大小不相同,是相似图形.2.这两个图形是相似图形,为什么有些图形是相似的,而有的图形看起来相像又不会相似呢?相似的两个图形有什么主要特征呢?为了探究相似图形的特征,本节课先学习线段的成比例.二、思考探究,获取新知1.两条线段的比(1)回忆什么叫两个数的比,怎样度量线段的长度,怎样比较两线段的大小.如果选用同一个长度单位量得两条线段AB 、CD 的长度分别是m 、n ,那么就说这两条线段的比AB ∶CD=m ∶n ,或写成ABCD=nm ,其中,线段AB 、CD 分别叫做这两个线段比的前项和后项.如果把n m 表示成比值k ,则CDAB =k 或AB=k ·CD. 注意:在量线段时要选用同一个长度单位.(2)做一做量出数学书的长和宽(精确到0.1cm ),并求出长和宽的比.改用m 作单位,则长为0.211m,宽为0.148m,长与宽的比为0.211∶0.148=211∶148. 只要是选用同一单位测量线段,不管采用什么单位,它们的比值不变.(3)求两条线段的比时要注意的问题①两条线段的长度必须用同一长度单位表示,如果单位长度不同,应先化成同一单位,再求它们的比;②两条线段的比没有长度单位,它与所采用的长度单位无关;③两条线段的长度都是正数,所以两条线段的比值总是正数.问:两条线段长度的比与所采用的长度单位有没有关系?(学生讨论)(答:线段的长度比与所采用的长度单位无关).2.成比例线段的定义四条线段a 、b 、c 、d 中,如果其中两条线段的长度之比等于另外两条线段的长度之比,如d c b a =,那么这四条线段a 、b 、c 、d 叫做成比例线段,简称比例线段.3.比例的基本性质两条线段的比实际上就是两个数的比.如果a 、b 、c 、d 四个数满足dc b a =,那么ad=bc 吗?反过来,如果说ad=bc ,那么d c b a =吗?与同伴交流. 如果dc b a =,那么ad=bc. 若ad=bc(a 、b 、c 、d 都不等于0),那么dc b a =. 例1 在某市城区地图(比例尺1∶9000)上,新安大街的图上长度与光华大街的图上长度分别是16cm 、10cm.(1)新安大街与光华大街的实际长度各是多少米?(2)新安大街与光华大街的图上长度之比是多少?它们的实际长度之比呢? 解:(1)1440米,900米. (2)8∶5,8∶5.例2如图,已知d c b a ==3,求b b a +和dd c +;解:b b a +=4, dd c +=4.三、运用新知,深化理解【教学说明】分组讨论完成并展示.四、师生互动,课堂小结1.注意点:(1)两线段的比值总是正数;(2)讨论线段的比时,不指明长度单位;(3)对两条线段的长度一定要用同一长度单位表示.2.比例尺:图上长度与实际长度的比.3.熟记成比例线段的定义.4.掌握比例的基本性质,并能灵活运用.1.布置作业:从教材相应练习和“习题23.1”中选取.2.完成练习册中本课时练习的“课时作业”部分.本课时从生活实例情境引入线段的比及成比例线段的概念,并引导学生探究比例的基本性质及其应用,通过互动交流加强对知识的理解,培养学生的合作意识.。

第23章 图形的相似23.1 成比例线段23.1.1 成比例线段1.__形状__相同,__大小__不一定相同的图形叫做相似图形.2.对于给定的四条线段a ,b ,c ,d ,如果其中两条线段的长度之比等于另外两条线段的长度之比,如a b =c d(或a ∶b =c ∶d ),那么,这四条线段叫做__成比例线段__,简称比例线段.此时也称这四条线段__成比例__.3.判断四条线段是否为比例线段要注意两点:(1)单位要__统一__;(2)线段长度的大小要__排序__.4.四条线段a ,b ,c ,d ,如果a b =c d,那么__ad =bc __;如果ad =bc (a ,b ,c ,d 都不等于0),那么__a b =c d__.知识点1:线段的比1.延长线段AB 到C ,使得BC =12AB ,则AC ∶AB =( C ) A .2∶1 B .3∶1 C .3∶2 D .4∶32.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm ,下半身长x 与身高l 的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( C )A .4 cmB .6 cmC .8 cmD .10 cm3.已知一个矩形的一边长a =15 cm ,另一边长b =6 dm ,则a b =__14__. 知识点2:成比例线段4.下列各组线段(单位:cm)中,是成比例线段的是( C )A .3,5,7,9B .2,5,6,8C .3,6,9,18D .1,3,4,75.已知线段a ,b ,c ,d 成比例,a ∶b =c ∶d ,且a =3 cm ,b =12 cm ,d =18 cm ,则c =__92__cm. 知识点3:比例的基本性质6.已知ad =bc ,那么下列比例式不成立的是( C )A.a b =c dB.a c =b dC.a d =c bD.b a =d c7.已知5x =4y ,则下列比例式成立的是( C )A.x 5=4yB.x 5=y 4C.x 4=y 5D.x y =548.(1)已知x y =83,则x -y y =__53__,x +y y =__113__,x -y x +y=__511__; (2)已知a b =b c,且a =4 cm ,c =3 cm ,则b =3_cm __. 9.如图,已知AD DB =AE EC,AD =3 cm ,DB =5 cm ,EC =7.5 cm ,求AC 的长.解:∵AD DB =AE EC ,AD =3 cm ,DB =5 cm ,EC =7.5 cm ,∴35=AE 7.5,∴AE =3×7.55=4.5(cm ),∴AC =AE +EC =4.5+7.5=12(cm )。



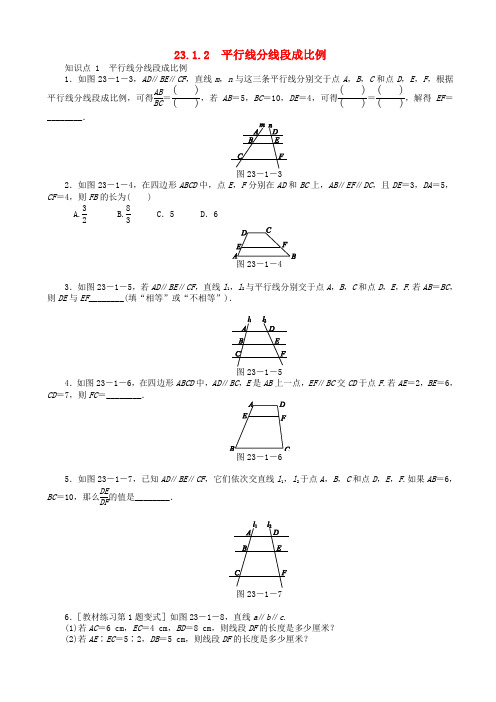
23.1.2 平行线分线段成比例知识点 1 平行线分线段成比例1.如图23-1-3,AD ∥BE ∥CF ,直线m ,n 与这三条平行线分别交于点A ,B ,C 和点D ,E ,F ,根据平行线分线段成比例,可得AB BC =()() ,若AB =5,BC =10,DE =4,可得() () =() (),解得EF =________.2.如图23-1-4,在四边形ABCD 中,点E ,F 分别在AD 和BC 上,AB ∥EF ∥DC ,且DE =3,DA =5,CF =4,则FB 的长为( )A.32B.83C .5D .63.如图23-1-5,若AD ∥BE ∥CF ,直线l 1,l 2与平行线分别交于点A ,B ,C 和点D ,E ,F .若AB =BC ,则DE 与EF ________(填“相等”或“不相等”).4.如图23-1-6,在四边形ABCD 中,AD ∥BC ,E 是AB 上一点,EF ∥BC 交CD 于点F .若AE =2,BE =6,CD =7,则FC =________.5.如图23-1-7,已知AD ∥BE ∥CF ,它们依次交直线l 1,l 2于点A ,B ,C 和点D ,E ,F .如果AB =6,BC =10,那么DEDF的值是________.图23-1-76.[教材练习第1题变式]如图23-1-8,直线a ∥b ∥c .(1)若AC =6 cm ,EC =4 cm ,BD =8 cm ,则线段DF 的长度是多少厘米? (2)若AE ∶EC =5∶2,DB =5 cm ,则线段DF 的长度是多少厘米?知识点 2 平行线分线段成比例的推论7.[2016·兰州改编]如图23-1-9,在△ABC 中,因为DE ∥BC ,所以AD BD =( )( ).若AD BD =23,则ADBD=( )( )=________.8.如图23-1-10,直线l 1∥l 2∥l 3,直线AC 与l 1,l 2,l 3分别交于点A ,B ,C ,直线DF 与l 1,l 2,l 3分别交于点D ,E ,F ,AC 与DF 相交于点G ,且AG =2,GB =1,BC =5,则DEEF的值为( )A. 12 B .2 C. 25 D. 359.如图23-1-11,在△ABC 中,DE ∥BC ,且分别交AB ,AC 于点D ,E ,则下列比例式不正确的是( )A.AB AD =AC AEB.AB AC =ADAEC.AD BD =AE ECD.AB DE =AC EC图23-1-1110.如图23-1-12,若AB ∥DC ,AC ,BD 相交于点E ,且AE =2,EC =3,BD =10,则ED =________.11.如图23-1-13,在△ABC 中,DE ∥5,AC =10,求AE 的长.12.如图23-1-14,已知AB ∥CD ∥EF ,=10,那么BC 的长为________.13.如图23-1-15,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A ,B ,C 都在横格线上.若线段AB =4 cm ,则线段BC =________cm.图23-1-1514. 如图23-1-16,AD 为△ABC 的中线,E 为AD 的中点,连结BE 并延长交AC 于点F ,则CFAF=__________.15.如图23-1-17,在△ABC 中,DF ∥AC ,DE ∥BC ,AE =4,EC =2,BC =8,求CF 的长.16.如图23-1-18,BE 平分∠ABC ,DE =8,AB =9,CE =4,求DE 的长.17.对于平行线,我们有这样的结论:如图23-1-19①,AB∥CD,AD,BC交于点O,则AODO=BOCO.请你利用该结论解答下列问题:如图②,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.图23-1-19教师详答1.DE EF 5 10 4 EF 8 2.B [解析] ∵AB ∥EF ∥DC ,∴DE DA =CF CB .∵DE =3,DA =5,CF =4,∴35=4CB ,∴CB =203,∴FB =CB -CF =203-4=83.故选B.3.相等 [解析] 因为AD ∥BE ∥CF ,所以AB BC =DEEF.因为AB =BC ,所以DE =EF . 4. 214 [解析] 因为AD ∥EF ∥BC ,所以AE EB =DF FC .因为AE =2,BE =6,CD =7,所以26=7-FC FC,所以FC=214. 5 . 38 [解析] ∵AD ∥BE ∥FC ,∴AB BC =DE EF.又∵AB =6,BC =10,∴DE EF =35,∴DE DF =38.6.解:(1)∵a ∥b ∥c ,∴BD DF =ACEC,即8DF =64,解得DF =163(cm). 故线段DF 的长度是163cm.(2)∵a ∥b ∥c ,∴BF DF =AE EC =52,即5+DF DF =52,解得DF =103(cm).故线段DF 的长度是103 cm.7.AE EC AE EC 238.D [解析] ∵AG =2,GB =1,∴AB =AG +GB =3.∵直线l 1∥l 2∥l 3,∴DE EF =AB BC =35.故选D.9.D 10.611.解:∵DE ∥BC ,∴AB DB =ACEC,∴5AE =1010-AE ,∴AE =103. 12. [解析] ∵AB ∥CD ∥EF , ∴BC BE =AD AF ,即BC 10=35,解得BC =6.13. 12 [解析] 如图,过点A 作AE ⊥CE 于点,交于点D .∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,∴AB BC =AD DE ,即4BC =26,∴BC =12(cm).14. 2 [解析] 如图,过点D 作DG ∥BF 则AF FG =AE ED ,FG GC =BD DC. 又∵E 为AD 的中点,AD 为△ABC 的中线, ∴AE =ED ,BD =DC , ∴AF FG =AE ED =1,FG GC =BDDC =1, ∴AF =FG ,FG =GC ,∴CF =2AF ,∴CFAF=2.15.解:∵DE ∥BC , ∴AD AB =AE AC =46=23. ∵DF ∥AC ,∴AD AB =CF BC =23,∴CF 8=23,∴CF =163.16.解:∵DE ∥BC , ∴AB DB =AC CE, ∴9DB =84,∴DB =92. ∵BE 平分∠ABC ,∴∠ABE =∠CBE . ∵DE ∥BC ,∴∠CBE =∠DEB ,∴∠ABE =∠DEB ,∴DE =DB =92.17.解:过点C 作CE ∥AB 交AD 的延长线于点E,则 BD DC =AD DE. 又∵BD =2DC ,AD =2, ∴DE =1. ∵CE ∥AB ,∴∠AEC =∠BAD =75°. 又∵∠CAD =30°,∴∠ACE =75°, ∴AC =AE =AD +DE =3.。

