郑州大学2019年力学硕士研究生入学考试大纲

郑州大学2019 考研专业课参考书目013【物理工程学院】郑大考研小堂学长给大家汇总了，郑大考研专业课各专业的参考书目，希望对大家能够有所帮助。

013【物理工程学院】1.考试专业科目及代码：650 量子力学+901 普通物理（一）（力学、电磁学、光学）专业代码及方向：070201理论物理、07020汝▲粒子物理与原子核物理、070205^★▲凝聚态物理、070207光学、071011生物物理学（物理类考生）初试教材：①《量子力学教程》周世勋高等教育出版社（2009年6月第二版）②《普通物理学》程守洙，高等教育出版社（2006年12月第六版）2. 考试专业科目及代码：651 生物化学（一）+902 遗传学专业代码及方向：071011 生物物理学（生物学、农学类考生）初试教材：①《生物化学》（上、下）沈同人民教育出版社②《遗传学》王亚馥高等教育出版社3. 考试专业科目及代码：901 普通物理（一）（力学、电磁学、光学）或907 材料科学基础（三）专业代码及方向：080501*材料物理与化学选考:901 普通物理（一）（力学、电磁学、光学）初试教材：①《量子力学教程》周世勋高等教育出版社（2009年6月第二版）②《普通物理学》程守洙，高等教育出版社（2006年12月第六版）选考:907 材料科学基础（三）初试教材：①《材料科学基础》曹茂盛哈工大出版社4. 考试专业科目及代码：901普通物理（一）（力学、电磁学、光学）或905 电子技术（含模拟电子、数字电子技术）专业代码及方向：082703核技术及应用初试教材：①《量子力学教程》周世勋高等教育出版社（2009年6月第二版）②《普通物理学》程守洙，高等教育出版社（2006年12月第六版）5. 考试专业科目及代码：904微机原理或905电子技术（含模拟电子、数字电子技术）/906半导体物理专业代码及方向：085203仪器仪表工程初试教材：选考905:①《模拟电子技术基础》童诗白，高等教育出版社（2015年7月第五版）②《数字电子技术基础》阎石，高教出版社（2006年5月第五版）选考906半导体物理：爱人者，人恒爱之；敬人者，人恒敬之；宽以济猛，猛以济宽，政是以和。

郑州大学力学与工程科学学院安全科学与工程专业硕士研究生入学考试《安全工程基础》考试大纲课程名称：955 安全工程基础考试时间：3小时考试形式：闭卷、笔试试卷结构：安全学原理占50%，安全系统工程占50%，满分150分。

试题类型：填空、名词解释、简答题、计算题、问答题、论述题。

考试范围及要求：安全学原理部分安全的基本概念，安全的特征、发展历程、学科体系、研究内容、研究目的、研究方法；人的属性与安全属性的相关性，安全的本质，进行安全本质的分析。

安全的自然与社会属性的耦合关系及规律。

安全科学的指导思想、安全的价值、价值观念，掌握安全的基本规律、价值功能和科学大安全观的内容。

安全与事故；事故的基本特征及事故预防；事故模式；本质安全化方法；人机匹配法；生产安全管理一体化方法；文化与安全文化的定义、层次结构、组成；大众安全文化的重点和公共安全文化；企业安全文化建设。

围绕以上内容，考察相关概念、涵义及理论和方法的具体应用等。

安全系统工程部分安全系统工程概论；安全检查表分析；事件树分析；事故树分析；故障类型和影响与影响分析；预先危险性分析；可靠性分析；原因后果分析；危险指数法；危险和可操作性研究；系统预测方法；系统安全评价；系统危险控制；安全系统工程典型应用实例等。

围绕以上内容，考察相关概念、涵义及理论和方法的具体应用等。

安全系统工程考试参考书目《安全系统工程》，林柏泉、张景林，中国劳动社会保障出版社，2007年。

安全学原理考试参考书目《安全学原理》，张景林，林柏泉，中国劳动社会保障出版社，2009年。

《力学》考试大纲课程名称：956 力学考试时间：3小时考试形式：闭卷、笔试试卷结构：理论力学占50%，材料力学占50%，满分150分。

试题类型：均为计算题与作图题。

考试范围及要求：理论力学部分一、静力学：静力学公理，约束，约束力，物体受力分析和受力图。

汇交力系的合成与平衡，力对点的矩，力对轴的矩，力偶及其特性，力偶系的合成与平衡。

2019年硕士研究生招生考试大纲002信息科学与工程学院目录初试考试大纲 (1)610高等数学 (1)638 量子力学 (1)953 声学基础 (3)806 普通物理 (5)807数据结构 (7)808地理信息系统 (8)810数字电子技术 (10)910高级程序设计 (11)911软件工程 (13)912数据结构和软件工程 (15)940 计算机网络与安全 (18)946 信号与系统 (20)954计算机基础综合 (21)341农业知识综合三 (25)930程序设计基础 (26)复试考试大纲 (29)现代物理基础 (29)科技英语(光学、凝聚态物理) (31)现代光学基础 (31)电子技术基础 (33)科技英语（光学工程专业（学术型080300和专业型085202） 35 电子技术A (35)通信原理 (36)计算机系统结构 (39)面向对象的程序设计 (40)数据库系统 (42)程序设计实践 (44)保密概论 (46)安全程序设计实践 (48)农业工程与信息技术概论 (50)数字信号处理 (53)C++语言编程 (54)科技英语（地图学与地理信息系统、测绘工程） (57)光学电磁学 (57)信号与系统 (60)数字电子技术 (61)科技英语（海洋探测技术、摄影测量与遥感） (62)同等学力加试科目考试大纲 (64)数据结构 (64)软件工程 (65)初试考试大纲610高等数学一、考试性质高等数学是理、工科专业硕士研究生入学考试的专业基础课程。

高等数学入学考试是为招收理、工科专业硕士研究生而实施的具有选拔功能的水平考试，它的指导思想是既要为国家选拔具有较强分析问题与解决问题能力的高层次人才，又要有利于促进高等学校高等数学课程教学质量的提高。

二、考察目标要求考生能系统理解高等数学的基本概念和基本原理，掌握高等数学的基本思想与方法，具有较好的逻辑推理能力、空间想象能力、计算能力以及运用所学知识分析问题和解决问题的能力。

《材料力学》考试大纲(硕士)一、轴向拉伸与压缩（1）基本要求1．运用截面法求轴力，绘轴力图2．轴向拉、压杆的强度计算3．轴向拉、压时的虎克定律及变形、位移计算4．弹性模量E、横向变形系数μ、轴向拉、压时的变形能U5．材料力学性能的主要指标6．一次静不定杆的求解（2）熟练运用的公式σ=N/A, σmax=(N/A)max≤[σ], ε’= －με,σ=Eε, Δl=N l / EA, U=N2 l / 2EA二、圆轴扭转（1）基本要求1．运用截面法求圆轴的扭矩，绘扭矩图2．纯剪应力状态的概念，剪应力互等定理，剪切虎克定律3．圆轴扭转时的强度计算4．圆轴扭转时的变形计算5．圆轴扭转静不定问题的求解（一次静不定）（2）熟练运用的公式τmax = T R / I P = T / W t ≤[τ], φ= Tl / G I P, θ=T / GI PI P = πD4 / 32, W t = πD3 / 16 (实心圆轴)I P =πD4 (1-α4) / 32, W t = πD3 (1-α4) / 16 (空心圆轴)U = T2 l / 2 G I P三、梁的弯曲弯曲内力基本要求1．面法求指定截面上的剪力Q、弯矩M2．列Q、M方程，绘荷载较简单的梁的剪力、弯矩图弯曲应力（1）基本要求1．梁的弯曲强度计算：弯曲正应力计算，弯曲剪应力计算，掌握强度计算的一般步骤2．几个重要的概念：纯弯曲、横力弯曲；中性层、中性轴；抗弯截面模量W、抗弯刚度EI Z3．截面的几何性质：静矩、惯性矩、极惯性矩的定义和概念；主轴、形心主轴和主惯性矩的概念；平行移轴公式4．弯曲变形能的计算（2）熟练运用的公式σ= M y / I Z, σmax = M max y max / I Z = M max / W Z ≤[σ]τmax = Q max S*Z / I Z b ≤[τ]U = m 2 l / 2 E I截面惯性矩计算：矩形截面，T 型截面，圆截面，空心圆截面；S *Z 的计算 弯曲变形(1) 基本要求1． 曲线近似微分方程的建立2． 掌握计算位移的积分法、叠加法；梁的刚度计算3． 掌握简单静不定梁的解法(2) 熟练运用的公式1/ρ= M / EI, EIv’’ = Mf = m l 2 / EI, f = Pl 3 / 3EI, f = q l 4 / 8EI （悬臂梁）f = Pl 3 / 48EI, f = 5ql 4 / 384EI （简支梁）四、 应力状态与强度理论（1） 基本要求1． 明确应力状态的概念及其研究方法2． 掌握平面应力状态下，解析法和图解法求任意斜截面上的应力；熟练掌握主应力和最大剪应力的计算3． 几个重要的概念：一点应力状态，平面应力状态，主平面，主单元体，主应力4． 广义虎克定律. 重点掌握平面应力状态下的广义虎克定律5． 强度理论：第一、第三和第四强度理论6． 运用强度理论对复杂受力构件进行强度校核（2） 熟练运用的公式)],([1Z y x x Eσσμσε+-=(三向应力状态) ),1/()(;],[12μμεεσμσσε-+=-=y x x y x x E E （平面应力状态） ][])()()[(21],[],[213232221311σσσσσσσσσσσσ≤-+-+-≤-≤ 五、 组合变形（1） 基本要求1． 掌握构件组合变形时强度计算的基本原理，叠加原理2． 正确判定构件在组合变形时的危险截面、危险点及危险点处应力值的计算组合变形：拉伸或压缩与弯曲的组合；偏心压缩；扭转与弯曲的组合（无扭转的组合变形，危险点处于单向应力状态；凡有扭转的组合变形，危险点处于复杂应力状态）3．根据危险点处的应力状态，正确选择并建立强度条件，掌握构件组合变形强度计算的一般步骤（2） 熟练运用的公式][1],[)4],[22231σστσσσσ≤+≤+≤-T M W][3],[])()()[(2122213232221στσσσσσσσσ≤+≤-+-+-][75.0122σ≤+T M W六、 能量方法（1） 基本要求1． 掌握杆件变形能的计算：轴向拉压、圆轴扭转、梁的弯曲2． 运用卡氏定理和单位载荷法（莫尔定理）计算结构指定点的位移3． 用力法求解静不定结构（一次静不定问题）（2） 熟练运用的公式⎰⎰⎰++=lP l l GI dx x T EI dx x M EA dx x N U 2)(2)(2)(222 七、 压杆稳定（1） 基本要求1． 理解失稳、临界力、临界应力、长度系数、柔度等基本概念2． 计算细长杆临界力、临界应力的欧拉公式3． 欧拉公式的适用范围，临界应力总图4． 压杆稳定的实用计算；稳定条件；稳定计算（2） 熟练运用的公式A I i E i lE l EI P p cr cr /,/,,/,)/(212222=====σπλμλλπσμπμ值：μ＝1（两端铰支）；μ＝0.5（两端固定）；μ＝2（一端固定，另一端自由）；μ≈0.7（一端固定，另一端铰支）。

2019年硕士研究生招生考试大纲考试科目名称：普通物理（力学、电磁学各占50%）考试科目代码：[613]力学部分一、考试要求1.基本概念质点，位矢，运动学方程，轨道方程，速度，加速度，位移，伽利略时空观；惯性质量，动量，主动力，被动力，非惯性系和惯性力，冲量，质点系，质心系；能量，机械能，动能，势能，功和功率，保守力，非保守力；质点和质点系对参考点或轴的角动量，力矩，守恒量和对称性，经典力学的适用范围；万有引力，引力质量，引力常数；刚体，平动和转动，角速度和角加速度，质心和重心，转动惯量，刚体的动量，转动动能，平面运动，刚体的平衡；简谐振动的运动学和动力学特征，简谐振动的运动学方程，简谐振动的合成，阻尼振动，受迫振动，位移共振；波的基本概念，平面简谐波方程，波动方程和波速，平均能流密度，半波损失，波的叠加和干涉，驻波，多普勒效应。

2.基本定理、定律牛顿运动定律，动量定理，动能定理，角动量定理，动量守恒定律，角动量守恒定律，机械能守恒定律，质心运动定理，功能原理，克尼希定理，开普勒定律和万有引力定律，刚体的质心运动定理，刚体定轴转动的角动量定理和转动定理，刚体定轴转动的动能定理。

3.基本方法利用加速度（或速度）和初始条件求解的质点的运动规律，利用运动学方程求解平面直角坐标系、自然坐标及极坐标系中质点的速度和加速度问题；利用牛顿运动定律求解基本的动力学问题，利用动量和动量守恒定律求解动力学基本问题；利用元功求解变力做功问题，利用动能定理和机械能守恒定律求解动力学问题，求解碰撞的问题；利用角动量和力矩的定义计算质点对轴和参考点的角动量和力矩，利用角动量定理和守恒定律解决基本的动力学问题；利用转动惯量定义计算刚体的转动惯量，利用刚体的运动学方程求解刚体的运动学问题，利用转动定理和角量与线量的关系求解刚体的动力学问题，利用刚体的动能定理求解刚体的动力学问题；根据简谐振动知识求解简谐振动方程、振动速度和振动加速度，利用简谐振动的运动学特征和动力学特征判断一个振动是否是简谐振动，会求解振动的合成问题；由振动方程求解平面简谐波波方程。

2019年硕士研究生入学统一考试大纲考试科目：流体力学一、试卷满分及考试时间试卷满分为100分，考试时间为180分钟。

二、答题方式答题方式为闭卷、笔试。

三、试卷内容结构流体力学100%流体力学一、流体的力学性质考试内容流体与固体、液体与气体的主要区别流体的连续介质假设作用于流体上的力的分类流体的主要力学性质牛顿内摩擦定律流体的分类流体力学研究的内容和方法。

考试要求1．掌握流体与固体的主要区别，掌握液体与气体的主要区别。

2．掌握流体的连续介质假设，包括其内容、依据、意义及其适用范围等。

3．掌握作用于流体上的力的分类，掌握质量力、表面力等概念。

4．掌握流体的密度与重度、膨胀性与压缩性、粘性等主要力学性质，掌握流体的密度、重度、体积膨胀系数、体积压缩系数、体积弹性模量等概念，掌握流体的粘度随温度的变化规律，掌握流体的动力粘度、运动粘度、相对粘度及其相互间的关系，掌握流体粘度的测量方法等。

5．掌握牛顿内摩擦定律及其适用条件，掌握牛顿内摩擦定律的应用。

6．掌握正压流体与斜压流体、可压缩流体与不可压缩流体、牛顿流体与非牛顿流体、理想流体与实际流体等概念。

7．了解流体力学研究的内容和方法。

二．流体静力学考试内容流体静压强欧拉平衡微分方程流体静力学基本方程帕斯卡原理流体的相对平衡平衡液体作用于固体壁面上的总压力及压力中心物体的浮沉理论。

考试要求1．掌握流体静压强的概念、流体静压强的特性、流体静压强的不同单位及其换算、流体静压强的特性等，掌握绝对压强、相对压强、表压强、真空等概念及其相互之间的关系。

2．掌握欧拉平衡微分方程及其意义与应用，掌握流体平衡的几个重要性质。

3．掌握流体静力学基本方程及其几何意义与能量意义，掌握流体静力学基本方程的应用，掌握帕斯卡原理，掌握液柱式测压计的原理及应用。

4．掌握流体相对平衡时的分析与计算。

5．掌握平衡液体作用于固体壁面上的总压力及压力中心的分析与计算。

6．掌握阿基米德原理，掌握浮体与潜体的平衡分析。

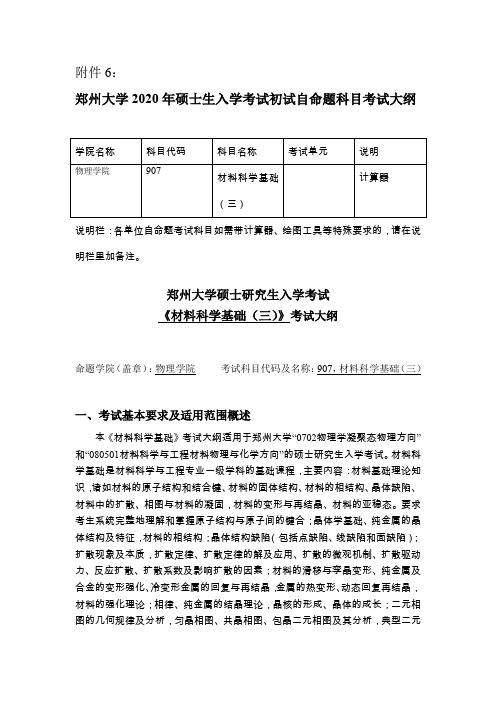
附件6：郑州大学2020年硕士生入学考试初试自命题科目考试大纲说明栏：各单位自命题考试科目如需带计算器、绘图工具等特殊要求的，请在说明栏里加备注。

郑州大学硕士研究生入学考试《材料科学基础（三）》考试大纲命题学院（盖章）：物理学院考试科目代码及名称：907，材料科学基础（三）一、考试基本要求及适用范围概述本《材料科学基础》考试大纲适用于郑州大学“0702物理学凝聚态物理方向”和“080501材料科学与工程材料物理与化学方向”的硕士研究生入学考试。

材料科学基础是材料科学与工程专业一级学科的基础课程，主要内容：材料基础理论知识，诸如材料的原子结构和结合键、材料的固体结构、材料的相结构、晶体缺陷、材料中的扩散、相图与材料的凝固，材料的变形与再结晶、材料的亚稳态。

要求考生系统完整地理解和掌握原子结构与原子间的键合；晶体学基础、纯金属的晶体结构及特征，材料的相结构；晶体结构缺陷（包括点缺陷、线缺陷和面缺陷）；扩散现象及本质，扩散定律、扩散定律的解及应用、扩散的微观机制、扩散驱动力、反应扩散、扩散系数及影响扩散的因素；材料的滑移与孪晶变形、纯金属及合金的变形强化、冷变形金属的回复与再结晶，金属的热变形、动态回复再结晶，材料的强化理论；相律、纯金属的结晶理论，晶核的形成、晶体的成长；二元相图的几何规律及分析，匀晶相图、共晶相图、包晶二元相图及其分析，典型二元相图分析；固溶体的凝固理论、共晶合金的凝固理论等。

了解材料科学的最新进展，能综合运用所学的知识分析问题和解决问题。

二、考试形式硕士研究生入学《材料科学基础》（三）考试为闭卷，笔试，考试时间为180分钟，本试卷满分为150分。

试卷结构（题型）：名词解释、单项选择题、判断题、简答题、问答题及综合应用题三、考试内容1.材料中原子的排列考试内容1）原子的键合特点（金属键、离子键、共价键、范德华力、氢键）。

比较金属材料、陶瓷材料、高分子材料、复合材料在结合键上的差别。

2021年硕士研究生招生测验大纲011 数学科学学院目录初试测验大纲 (1)617 数学阐发 (1)856 高等代数 (6)432 统计学 (8)复试测验大纲 (12)综合测验12概率论与数理统计(统计学) (17)概率论与数理统计〔应用统计〕 (18)初试测验大纲617 数学阐发一、测验性质数学阐发是数学相关专业硕士入学初试测验的专业根底课程。

二、考察目标本测验大纲制定的依据是按照教育部颁布的《数学阐发》教学大纲的根本要求，力求反映与数学相关的硕士专业学位的特点，客不雅、准确、真实地测评考生对数学阐发的掌握和运用情况，为国家培养具有良好数学根底本质和应用能力、具有较强阐发问题与解决问题能力的高层次、复合型的数学专业人才。

本测验旨在测试考生对一元函数微积分学、多元函数微积分学、级数理论等常识掌握的程度和运用能力。

要求考生系统地舆解数学阐发的根本概念和根本理论；掌握数学阐发的根本论证方法和常用结论；具备较熟练的演算技能和较强的逻辑推理能力及初步的应用能力。

三、测验形式本测验为闭卷测验，总分值为150分，测验时间为180分钟。

试卷布局：一元函数微积分学、多元函数微积分学、级数理论及其他〔隐函数理论、场论等〕查核的比例均约为1/3，分值均约为50分。

四、测验内容(一) 变量与函数1、实数：实数的概念、性质，区间，邻域；2、函数：变量，函数的定义，函数的暗示法，几何特征〔有界函数、单调函数、奇偶函数、周期函数〕，运算〔四那么运算、复合函数、反函数〕，根本初等函数，初等函数。

(二) 极限与持续1、数列极限：定义〔ε-N语言〕，性质〔独一性，有界性，保号性，不等式性、迫敛性〕，数列极限的运算，数列极限存在的条件〔单调有界准那么〔重要的数列极限〕，迫敛性法那么，柯西收敛准那么〕；2、无穷小量与无穷大量：定义，性质，运算，阶的比拟；3、函数极限：概念〔在一点的极限，单侧极限，在无限远处的极限，函数值趋于无穷大的情形〔ε-δ, ε-X语言〕〕；性质〔独一性，局部有界性，局部保号性，不等式性，迫敛性〕；函数极限存在的条件〔迫敛性法那么，归结原那么〔Heine定理〕，柯西收敛准那么〕；运算；4、两个常用不等式和两个重要函数极限〔，〕；5、持续函数：概念〔在一点持续，单侧持续，在区间持续〕，不持续点及其分类；持续函数的性质与运算〔局部性质及运算，闭区间上持续函数的性质〔有界性、最值性、零点存在性，介值性、一致持续性〕，复合函数的持续性，反函数的持续性〕；初等函数的持续性。

年硕士研究生入学考试大纲考试科目名称：土木工程专业综合（含材料力学与土力学及混凝土结构综合）考试时间：分钟，满分：分一、考试要求：. 要求考生全面掌握材料力学中的基本概念、基本理论和基本方法，并具有一定的综合应用能力，该部分内容占分；土力学要求考生掌握相关概念、公式、曲线、简单计算和重要结论等内容，并能对所学知识融会贯通，具备进一步分析、推理解决问题的能力，该部分内容占分；要求理解混凝土结构的基本概念、原理和方法，应初步具备运用所学知识分析和处理问题的能力，能够进行受弯构件的设计、偏心受力构件的设计、弯剪扭构件的设计，计算题中相关公式考生应熟练掌握，该部分内容占分。

. 考试时携带必要书写工具之外，须携带计算器。

二、考试内容：．材料力学部分（）：绪论: 材料力学任务；:可变性的固体的基本假设；:杆件变形的基本形式。

（）：拉伸与压缩:轴向直杆的内力、应力计算及强度条件；:单向应力状态的虎克定律，应变能密度；:轴向拉伸、压缩直杆的变形计算及抗拉、压刚度；:简单桁架的节点位移计算；拉伸、压缩静不定问题，装配应力及温度应力；:低碳钢及铸铁等材料的机械性质，应力应变曲线，材料的强度指标及塑性指标（）：剪切: 联接件剪切、挤压使用强度计算；:切应力互等定理，剪切虎克定律，剪切应变能密度能。

（）：扭转:扭转外力偶矩的计算，扭矩与扭矩图；:圆轴扭转时的应力和强度条件，变形和刚度条件；:简单扭转静步定问题。

（）：弯曲内力: 弯曲内力计算及剪力图、弯矩图；:分布载荷集度、剪力、弯矩间的微分关系。

（）：弯曲强度: 平面弯曲梁的正应力计算及强度条件；:弯曲切应力计算及强度条件；:提高弯曲强度的措施。

（）：弯曲变形: 绕曲线近似微分方程;:积分法求弯曲变形，刚度条件；:叠加法求弯曲变形；:提高弯曲刚度的措施；:变形比较法求解静不定梁。

（）：应力状态理论和强度理论:应力状态概念，主应力，主平面及主单元体；:二向应力状态分析的解读法，图解法——应力圆；:三向应力状态的应力圆；:广义虎克定律及其应用；:各向同性材料的三个弹性常数、、之间的关系；:复杂应力状态下的应变能密度能；:强度理论概念，常用的四个强度理论及其应用。

2019年硕士研究生招生考试大纲009 工程学院目录初试考试大纲 (1)841热工学（工程热力学与传热学） (1)842自动控制理论 (5)845水力学 (8)848运筹学 (8)915机械设计（含机械原理） (11)959 结构力学A (16)960 结构力学B (18)复试考试大纲 (19)机械工程综合 (19)动力工程专业综合 (20)电子技术综合 (25)土木工程综合考试 (29)管理信息系统 (31)理论力学 (33)船舶结构力学 (34)初试考试大纲841热工学（工程热力学与传热学）一、考试性质热工学（工程热力学与传热学）是动力工程专业硕士研究生入学考试的专业理论课程。

作为选拔性考试，具有较高的信度、效度、必要的区分度和适当的难度。

二、考察目标重点考核学生对工程热力学和传热学基本定律和基本原理的掌握，常用工质的热物理性质的了解，有关图表及计算公式的综合运用。

对典型热力工程和热力循环的计算和分析能力，对热量传递的工程问题的分析能力和热量传递工程计算方法。

能源合理利用及其高效转换的基本观念的掌握。

三、考试形式本考试为闭卷考试，满分为150分，考试时间为180分钟。

试卷结构：选择20%，计算题80%四、考试内容（一）基本概念1、主要内容：（1）热力系。

（2）热力状态和平衡状态。

（3）工质的状态参数。

状态方程。

热力参数坐标图。

（4）功和热量。

热力过程，可逆过程和不可逆过程。

热力循环。

2、具体要求：理解热力系、理想气体、平衡状态和可逆过程的基本概念。

掌握工质基本状态参数和热效率的计算、理想气体状态方程的应用。

了解热力系的分类和特点、工质状态参数性质。

（二）热力学第一定律1、主要内容：（1）热力学第一定律的实质。

（2）内能。

（3）热力学第一定律表达式。

（4）焓和稳定流动能量方程。

2、具体要求：了解热力学第一定律的来源和本质。

掌握热力学第一定律在不同热力系的表达方程、应用特点和工程计算方法、热与功的计算。