MSDC.初中数学.中考冲刺.第09讲.教师版
- 格式:doc
- 大小:2.30 MB
- 文档页数:22

几何综合7分.几何综合题主要包含三角形(全等、相似)、四边形、锐角三角函数、圆等知识,主要研究图形中的数量关系、位置关系、几何计算以及图形的运动、变换等规律.求解几何综合题时,关键是抓住“基本图形”,能在复杂的几何图形中辨认、分解出基本图形,或通过添加辅助线补全、构造基本图形,或运用图形变换的思想将分散的条件集中起来,从而产生基本图形,再根据基本图形的性质,合理运用方程、三角函数的运算等进行推理与计算.接AP ,平移△ADP ,使点D 移动到点C ,得到△BCQ ,过点Q 作QH ⊥BD 于点H ,连接AH ,PH . (1)若点P 在线段CD 上,如图Z9-1(a ). ①依题意补全图(a );②判断AH 与PH 的数量关系与位置关系,并加以证明.(2)若点P 在线段CD 的延长线上,且∠AHQ =152°,正方形ABCD 的边长为1,请写出求DP 长的思图Z92.[2014·北京] 在正方形ABCD 外侧作直线AP ,点B 关于直线AP 的对称点为E ,连接BE ,DE ,其中DE 交直线AP 于点F . (1)依题意补全图Z9-2①;(2)若∠PAB =20°,求∠ADF 的度数;(3)如图②,若45°<∠PAB <90°,用等式表示线段AB ,FE ,FD 之间的数量关系,并证明.图Z93.[2013·北京] 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段B D.(1)如图Z9-3①,直接写出∠ABD的大小(用含α的式子表示);(2)如图②,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.图 34.[2012·北京] 在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.(1)若α=60°且点P与点M重合(如图Z9-4①),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数;(2)在图②中,点P不与点B,M重合,线段CQ的延长线与射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ 的延长线与射线BM交于点D,且PQ=DQ,请直接写出α的范围.图Z95.[2011·北京] 在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图Z9-5①中证明CE=CF;(2)若∠ABC=90°,G是EF的中点(如图②),直接写出∠BDG的度数;(3)若∠ABC=120=CE,分别连接DB,DG(如图③),求∠BDG的度数.图Z9-] ,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E.(1)依题意补全图Z9-6①;(2)若∠PAB=30°,求∠ACE的度数;(3)如图②,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角2.[2015·朝阳一模] 在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B,C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.(1)如图Z9-7(a),点D在BC边上.①依题意补全图(a);②作DF⊥BC交AB于点F,若AC=8,DF=3,求BE的长.(2)如图(b),点D在BC边的延长线上,用等式表示线段AB,BD,BE之间的数量关系(直接写出结论).图Z93.[2015·海淀一模] 在菱形ABCD中,∠ADC=120°,点E是对角线AC上一点,连接DE,∠DEC =50°,将线段BC绕点B逆时针旋转50°并延长得到射线BF,交ED的延长线于点G.(1)依题意补全图形;(2)求证:EG=BC;________.图Z9-84.[2015·海淀二模] 如图Z9-9①,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD 为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.(1)直接写出∠ADE的度数(用含α的式子表示).(2)以AB,AE为边作平行四边形ABFE.①如图②,若点F恰好落在DE上,求证:BD=CD;②如图③,若点F恰好落在BC上,求证:BD=CF.图Z95.[2015·西城一模] 在△ABC中,AB=AC,取BC边的中点D,作DE⊥AC于点E,取DE的中点F,连接BE,AF交于点H.(1)如图Z9-10①,如果∠BAC=90°,那么∠AHB=________°,AFBE=________;(2)如图②,如果∠BAC=60°,猜想∠AHB的度数和AFBE的值,并证明你的结论;(3)如果∠BAC=α,那么AFBE=________.(用含α的代数式表示)图Z9-6.[2015·丰台一模] 在△ABC中,CA=CB,CD为AB边上的中线,点P是线段AC上任意一点(不与点C重合),过点P作PE交CD于点E,使∠CPE=12∠CAB,过点C作CF⊥PE交PE的延长线于点F,交AB于点G. (1)如果∠ACB=90°,①如图Z9-11(a),当点P与点A重合时,依题意补全图形,并指出与△CDG全等的一个三角形;②如图(b),当点P不与点A重合时,求CFPE的值.(2)如果∠CAB=a,如图(c),请直接写出CFPE的值.(用含a的式子表示)7.[2015·海淀] 将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD.(1)连接BD,①如图Z9-12(a),若α=80°,则∠BDC的度数为________.②在第二次旋转过程中,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数;若改变,请说明理由.(2)如图(b),以AB为斜边作直角三角形ABE,使得∠B=∠ACD,连接CE,DE.若∠CED=90°,求图Z98.[2015·西城二模] 正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.(1)如图Z9-13①,若点E是DC的中点,CH与AB之间的数量关系是________.(2)如图②,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由.(3)如图③,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.图Z9参考答案1.. 证明:连接CH ,由条件易得:△DHQ 为等腰直角三角形, 又∵DP =CQ ,∴△HDP ≌△HQC , ∴PH =CH ,∠HPC =∠HCP .∵BD 为正方形ABCD 的对称轴, ∴AH =CH ,∠DAH =∠HCP , ∴AH =PH ,∠DAH =∠HPC ,∴∠AHP =180°-∠ADP =90°,.过点H 作HR ⊥PC 于点R , ∵∠AHQ =152°, ∴∠AHB =62°, ∴∠DAH =17°,∴∠DCH =17°.设DP =x ,则DR =HR =RQ =1-x2.由tan17°=HRCR 得1-x 21+x2=tan17°,∴x =1-tan17°1+tan17°.(2)AE ,则∠PAB =∠PAE =20°,AE =AB. ∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD , ∴∠EAD =130°,AE =AD. ∴∠ADF =25°.(3)如图②,连接AE ,BF ,BD.EF =BF ,AE =AB =AD ,∠ABF =∠AEF =∠ADF , ∴∠BFD =∠BAD =90°.∴BF 2+FD 2=BD 2.∴EF 2+FD 2=2AB 2.3.解:(1)∵AB =AC ,∠A =α,∴∠ABC =∠ACB =12(180°-∠A )=90°-12α.∵∠ABD =∠ABC -∠DBC ,∠DBC =60°,∴∠ABD =30°-12α.(2)△ABE 是等边三角形. 证明:连接AD ,CD ,ED ,∵线段BC 绕点B 逆时针旋转60°得到线段BD , 则BC =BD ,∠DBC =60°. ∴△BCD 为等边三角形. ∴BD =CD.∵∠ABE =60°,∴∠ABD =60°-∠DBE =∠EBC =30°-12α.在△ABD 与△ACD 中, ⎩⎪⎨⎪⎧AB =AC ,AD =AD ,BD =CD ,∴△ABD ≌△ACD ,∴∠BAD =∠CAD =12∠BAC =12α.∵∠BCE =150°,∴∠BEC =180°-(30°-12α)-150°=12α=∠BAD.在△ABD 和△EBC 中, ⎩⎪⎨⎪⎧∠BEC =∠BAD ,∠EBC =∠ABD ,BC =BD ,∴△ABD ≌△EBC , ∴AB =BE .又∵∠ABE =60°,∴△ABE 是等边三角形.°,∠BCE =150°, ∴∠DCE =150°-60°=90°. ∵∠DEC =45°,∴△DEC 为等腰直角三角形, ∴DC =CE =BC. ∵∠BCE =150°.∴∠EBC =12(180°-150°)=15°.∵∠EBC =30°-12α=15°,∴α=30°.4.解:(1)如图①,∵BA =BC ,∠BAC =60°,M 是AC 的中点, ∴BM ⊥AC ,AM =MC.∵将线段PA 绕点P 顺时针旋转2α得到线段PQ , ∴AM =MQ ,∠AMQ =120°, ∴CM =MQ ,∠ CMQ =60°, ∴△CMQ 是等边三角形, ∴∠ACQ =60°, ∴∠CDB =30°. (2)连接PC ,AD ,∵AB =BC ,M 是AC 的中点, ∴BM ⊥AC ,∴AD =CD ,AP =PC. 在△APD 与△CPD 中, ∵⎩⎪⎨⎪⎧AD =CD ,PD =PD ,PA =PC ,∴△APD ≌△CPD ,∴∠ADB =∠CDB ,∠PAD =∠PCD , ∴∠ADC =2∠CDB. 又∵PQ =PA ,∴PQ =PC ,∴∠PQC =∠PCD =∠PAD , ∴∠PAD +∠PQD =∠PQC +∠PQD =180°,∴∠APQ +∠ADC =360°-(∠PAD +∠PQD )=180°, ∴∠ADC =180°-∠APQ =180°-2α, ∴2∠CDB =180°-2α, ∴∠CDB =90°-α.(3)∵∠CDB =90°-α,且PQ =QD ,∴∠PAD =∠PCQ =∠PQC =2∠CDB =180°-2α. ∵点P 不与点B ,M 重合, ∴∠BAD >∠PAD >∠MAD , ∴2α>180°-2α>α,∴45°<α<60°.5AF 平分∠BAD ∴∠BAF =∠DAF .∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,∴∠DAF =∠CEF ,∠BAF =∠F .∴∠CEF =∠F .(3)如图,分别连接GB ,GE ,GC ,∵AD ∥BC ,AB ∥CD ,∠ABC =120°,∴∠ECF =∠ABC =120°.∵FG ∥CE 且FG =CE ,∴四边形CEGF 是平行四边形.由(1)得CE =CF .∴四边形CEGF 是菱形,∴GE =EC ,①∠GCF =∠GCE =12∠ECF =60°, ∴△ECG 与△FCG 是等边三角形,∴∠GEC =∠FCG ,∴∠BEG =∠DCG ,②由AD ∥BC 及AF 平分∠BAD 可得∠BAE =∠AEB ,∴AB =BE .在▱ABCD 中,AB =DC ,∴BE =D C.③由①②③得△BEG ≌△DCG ,∴BG =DG ,∠1=∠2,∴∠BGD =∠1+∠3=∠2+∠3=∠EGC =60°,∴∠BDG =180°-∠BGD =60°.1.解:(1)(2)连接AD ,如图①.∵点D 与点B 关于直线AP 对称,∴AD =AB ,∠DAP =∠BAP =30°, ∵AB =AC ,∠BAC =60°,∴AD =AC ,∠DAC =120°,∴2∠ACE +120°=180°.∴∠ACE =30°.(3)AB,CE,ED可以构成一个含有60°角的三角形.AP对称,∴AD=AB,DE=BE,可证得∠EDA=∠EB A.∵AB=AC,AB=AD,∴AD=AC,∴∠ADE=∠ACE,∴∠ABE=∠ACE.设AC,BE交于点F,∵∠AFB=∠CFE,∴∠BAC=∠BEC=60°,∴线段AB,CE,ED可以构成一个含有60°角的三角形.(a)所示.),由题意可知AD=DE,∠ADE=90°.∵DF⊥BC,∴∠FDB=90°.∴∠ADF=∠ED B.∵∠C=90°,AC=BC,∴∠ABC=∠DFB=45°.∴DB=DF.∴△ADF≌△EDB.∴AF=EB.∵AC DF=3,∴AB=8 2,BF=3 2.AF=AB-BF=5 2,即BE=5 2,(2)2BD=BE+AB.3.解:(1)补全图形,如图①所示.(2)BE∵四边形ABCD 是菱形,∴AD ∥BC.∵∠ADC =120°,∴∠DCB =60°.∵AC ]是菱形ABCD 的对角线,∴∠DCA =12∠DCB =30°. ∴∠EDC =180°-∠DEC -∠DCA =100°.由菱形的对称性可知,∠BEC =∠DEC =50°,∠EBC =∠EDC =100°, ∴∠GEB =∠DEC +∠BEC =100°.∴∠GEB =∠CBE .∵∠FBC =50°,∴∠EBG =∠EBC -∠FBC =50°.∴∠EBG =∠BEC.在△GEB 与△CBE 中,⎩⎪⎨⎪⎧∠GEB =∠CBE ,BE =EB ,∠EBG =∠BEC ,∴△GEB ≌△CBE .∴EG =BC .方法二:证明:连接BE ,设BG 与EC 交于点H ,如图②.∵四边形ABCD 是菱形,∴AD ∥BC.∵∠ADC =120°,∴∠DCB =60°.∵AC 是菱形ABCD 的对角线,∴∠DCA =12∠DCB =30°. ∴∠EDC =180°-∠DEC -∠DCA =100°.由菱形的对称性可知,∠BEC =∠DEC =50°,∠EBC =∠EDC =100°, ∵∠FBC =50°,∴∠EBG =∠EBC -∠FBC =50°=∠BEC .∴BH =EH .在△GEH 与△CBH 中,⎩⎪⎨⎪⎧∠GEH =∠CBH ,EH =BH ,∠EHG =∠B HC ,∴△GEH ≌△CBH .∴EG =BC .(3)AE +BG =3EG .4.解:(1)∠ADE =90°-α.(2)①证明:∵四边形ABFE是平行四边形,∴AB∥EF.∴∠EDC=∠ABC=α.由(1)知∠ADE=90°-α,∴∠ADC=∠ADE+∠EDC=90°.∴AD⊥BC.∵AB=AC,∴BD=CD.②证明:∵AB=AC,∠ABC=α,∴∠C=α.∵四边形ABFE是平行四边形,∴AE∥BF,AE=BF.∴∠EAC=∠C=α.由(1)知∠DAE=180°-2∠ADE=180°-2(90°-α)=2α,∴∠DAC=α.∴∠DAC=∠C.∴AD=CD.∵AD=AE=BF,∴BF=CD.∴BD=CF.5.解:(1)90 1 2(2)结论:∠AHB=90°,AFBE=32..°,∴△ABC是等边三角形.∵D为BC的中点,∴AD⊥BC.∴∠1+∠2=90°.又∵DE⊥AC,∴∠DEC=90°.∴∠2+∠C=90°.∴∠1=∠C=60°.设AB=BC=k(k>0),则CE=12CD=k4,DE=34k.∵F为DE的中点,∴DF=12DE=38k,AD=32AB=32k.∴ADBC =32,DFCE=32.∴AD BC =DF CE. 又∵∠1=∠C ,∴△ADF ∽△BCE .∴AF BE =AD BC =32, ∠3=∠4.又∵∠4+∠5=90°,∠5=∠6,∴∠3+∠6=90°.∴∠AHB =90°. (3)12tan(90°-α2). 6.解:(1)①作图.交CG 于点N ,交CD 于点M ,∵∠CPE =12∠CAB , ∴∠CPE =12∠CPN .∴∠CPE =∠FPN . ∵PF ⊥CG ,∴∠PFC =∠PFN =90°.∵PF =PF ,∴△PFC ≌△PFN .∴CF =FN .由①得:△PME ≌△CMN .∴PE =CN .∴CF PE =CF CN =12. (2)12tan α. 7.解:(1)①30°.②不改变,∠BDC 的度数为30°.方法一:由题意知AB =AC =A D. ∴点B ,C ,D 在以点A 为圆心,AB 为半径的圆上.∴∠BDC =12∠BAC =30°. 方法二:由题意知AB =AC =A D.∵AC =AD ,∠CAD =α,∴∠ADC =∠ABD =180°-α2=90°-12α. ∵AB =AD ,∠BAD =60°+α,∴∠ADB =∠ABD =180°-()60°+α2=120°-α2=60°-12α.∴∠BDC =∠ADC -∠ADB =(90°-12α)-(60°-12α)=30°. (2)过点A 作AM ⊥CD 于点M ,连接EM .在△AEB 与△AMC 中,⎩⎪⎨⎪⎧∠AEB =∠AMC ,∠B =∠ACD ,AB =AC ,∴△AEB ≌△AMC.∴AE =AM ,∠BAE =∠CAM .∴∠EAM =∠EAC +∠CAM =∠EAC +∠BAE =∠BAC =60°. ∴△AEM 是等边三角形.∴EM =AM =AE .∵AC =AD ,AM ⊥CD ,∴CM =DM .又∵∠DEC =90°,∴EM =CM =DM .∴AM =CM =DM .∴点A ,C ,D 在以M 为圆心,MC 为半径的圆上.∴α=∠CAD =90°.8.解:(1)CH =AB(2)结论成立.证明:如图,连接BE .AB =BC =CD =AD ,∠A =∠BCD =∠ABC =90°.∵DE =DF ,∴AF =CE .在△ABF 和△CBE 中,⎩⎪⎨⎪⎧AB =CB ,∠A =∠BCE ,AF =CE ,∴△ABF ≌△CBE .∴∠1=∠2.∵EH ⊥BF ,∠BCE =90°,∴H ,C 两点都在以BE 为直径的圆上.∴∠3=∠2.∴∠3=∠1.∵∠3+∠4=90°,∠1+∠HBC =90°,∴∠4=∠HB C.∴CH=CB.∴CH=AB. (3)3 2+3.。

无论在中考还是平时的各种考试,涉及最后的一道几何压轴题,基本上考察的内容是与旋转有关的题型是最多的,其他是翻折(轴对称),最少的是与平移有关的题型,而且有的时候某些题型会涉及到旋转和对称有关的知识,因此熟练掌握一些常见的题型与解决方法由为重要。
题型一:轴对称与作图题型说明:此类问题多数会在题干中,给出解决问题的基本思路,因此审题成为解决此类问题的关键。
【例1】 小贝遇到一个有趣的问题:在矩形ABCD 中,8AD =cm ,6AB =cm 。
现有一动点P 按下列方式在矩形内运动:它从A 点出发,沿着AB 边夹角为45︒的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45︒的方向作直线运动,并且它一直按照这种方式不停地运动,即当P 点碰到BC 边,沿着BC 边夹角为45︒的方向作直线运动,当P 点碰到CD 边,再沿着与CD 边夹角为45︒的方向作直线运动,…,如图1所示,问P 点第一次与D 点重合前与边相碰几次,P 点第一次与D 点重合时所经过的路线的总长是多少。
小贝的思考是这样开始的:如图2,将矩形ABCD 沿直线CD 折迭,得到矩形11A B CD ,由轴对称的知识,发现232P P P E =,11P A PE =。
请你参考小贝的思路解决下列问题:⑴P 点第一次与D 点重合前与边相碰 次;P 点从A 点出发到第一次与D 点重合时所经过的路径的总长是 cm ;⑵近一步探究:改变矩形ABCD 中AD 、AB 的长,且满足AD AB >,动点P 从A 点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上。
若P 点第一次与B 点重合前与边相碰7次,则:AB AD 的值为 。
例题精讲翻折与几何探究【答案】⑴5;⑵解题思路示意图:【例2】 如图①,在ABC ∆中,已知45BAC ∠=︒,AD BC ⊥于D ,2BD =,3DC =,求AD 的长小萍同学灵活运用轴对称知识,将图形进行翻折变换,如图,她分别以AB 、AC 为对称轴,画出ABD ∆、ACD ∆的轴对称图形,D 点的对称轴为E 、F 延长EB 、FC 相交于G 点,得到四边形AEGF 是正方形。
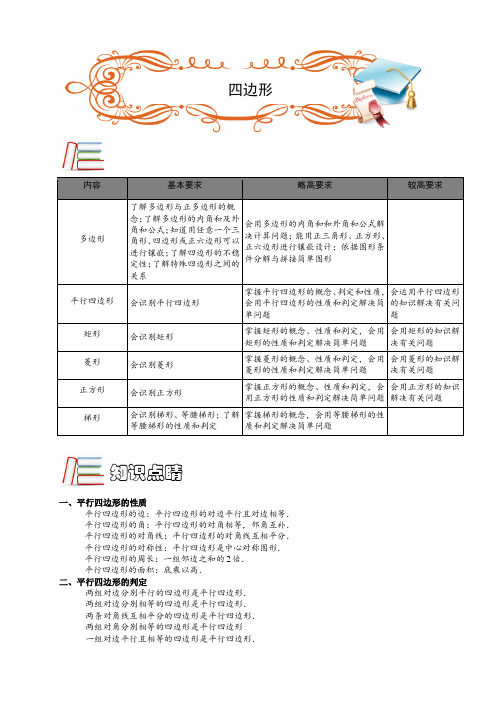
内容基本要求略高要求较高要求多边形了解多边形与正多边形的概念;了解多边形的内角和及外角和公式;知道用任意一个三角形、四边形或正六边形可以进行镶嵌;了解四边形的不稳定性;了解特殊四边形之间的关系会用多边形的内角和和外角和公式解决计算问题;能用正三角形、正方形、正六边形进行镶嵌设计;依据图形条件分解与拼接简单图形平行四边形会识别平行四边形掌握平行四边形的概念、判定和性质,会用平行四边形的性质和判定解决简单问题 会运用平行四边形的知识解决有关问题 矩形 会识别矩形 掌握矩形的概念、性质和判定,会用矩形的性质和判定解决简单问题 会用矩形的知识解决有关问题 菱形 会识别菱形 掌握菱形的概念、性质和判定,会用菱形的性质和判定解决简单问题 会用菱形的知识解决有关问题 正方形 会识别正方形掌握正方形的概念、性质和判定,会用正方形的性质和判定解决简单问题 会用正方形的知识解决有关问题梯形 会识别梯形、等腰梯形;了解等腰梯形的性质和判定 掌握梯形的概念,会用等腰梯形的性质和判定解决简单问题一、平行四边形的性质平行四边形的边:平行四边形的对边平行且对边相等. 平行四边形的角:平行四边形的对角相等,邻角互补. 平行四边形的对角线:平行四边形的对角线互相平分. 平行四边形的对称性:平行四边形是中心对称图形. 平行四边形的周长:一组邻边之和的2倍. 平行四边形的面积:底乘以高. 二、平行四边形的判定两组对边分别平行的四边形是平行四边形. 两组对边分别相等的四边形是平行四边形. 两条对角线互相平分的四边形是平行四边形. 两组对角分别相等的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形.知识点睛四边形三、矩形1.定义:有一个角是直角的平行四边形叫做矩形.2.矩形的性质矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:①边的性质:对边平行且相等.②角的性质:四个角都是直角.③对角线性质:对角线互相平分且相等.④对称性:矩形是中心对称图形,也是轴对称图形.直角三角形斜边上的中线等于斜边的一半.直角三角形中,30 角所对的边等于斜边的一半.点评:这两条直角三角形的性质在教材上是应用矩形的对角线推得,用三角形知识也可推得.3.矩形的判定判定①:有一个角是直角的平行四边形是矩形.判定②:对角线相等的平行四边形是矩形.判定③:有三个角是直角的四边形是矩形.四、菱形1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质菱形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:①边的性质:对边平行且四边相等.②角的性质:邻角互补,对角相等.③对角线性质:对角线互相垂直平分且每条对角线平分一组对角.④对称性:菱形是中心对称图形,也是轴对称图形.菱形的面积等于底乘以高,等于对角线乘积的一半.点评:其实只要四边形的对角线互相垂直,其面积就等于对角线乘积的一半.3.菱形的判定判定①:一组邻边相等的平行四边形是菱形.判定②:对角线互相垂直的平行四边形是菱形.判定③:四边相等的四边形是菱形.4.三角形的中位线中位线:连结三角形两边的中点所得的线段叫做三角形的中位线.也可以过三角形一边的中点作平行于三角形另外一边交于第三边所得的线段也是中位线.以上是中位线的两种作法,第一种可以直接用中位线的性质,第二种需要说明理由为什么是中位线,再用中位线的性质.中点中点平行中点定理:三角形的中位线平行第三边且长度等于第三边的一半.五、正方形1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.2.正方形的性质正方形是特殊的平行四边形、矩形、菱形.它具有前三者的所有性质:①边的性质:对边平行,四条边都相等.②角的性质:四个角都是直角.③对角线性质:两条对角线互相垂直平分且相等,•每条对角线平分一组对角.④对称性:正方形是中心对称图形,也是轴对称图形.平行四边形、矩形、菱形和正方形的关系:(如图)正方形菱形矩形平行四边形3.正方形的判定判定①:有一组邻边相等的矩形是正方形. 判定②:有一个角是直角的菱形是正方形.六、梯形 1.定义:四边形中还有一类特殊的四边形,它们的一组对边平行而另一组对边不平行,这样的特殊四边形就叫做梯形.研究梯形主要是研究两类:等腰梯形和直角梯形.AB CD ABCD AD BC ⎫⇒⎬⎭∥叫做梯形. C B A D底角腰底高2.等腰梯形AB CD AD BC AD BC ⎫⎪=⇒⎬⎪⎭∥.ABCD DAB CBA ADC BCD AC BD ∠=∠∠=∠=是等腰梯形,,,B CAD3. 直角梯形AB CD CB AB ABCD AD BC ⎫⎪⊥⇒⎬⎪⎭∥是直角梯形. CAB D4.平行线等分线段定理1234l l l l AB BC CD ⎫⇒⎬==⎭∥∥∥111111A B B C C D ==.l 4l 3l 2l1D 1C 1B 1A 1DC B A5.中位线定理⑴ 三角形中位线定理 ABC ∆中:1122AM BM MN BC MN BC AN CN =⎫⇒=⎬=⎭∥,. BN C MA⑵ 梯形中位线定理 梯形ABCD 中:AB CD AM DM BN CN ⎫⎪=⇒⎬⎪=⎭∥()12MN AB CD MN AB CD =+∥∥,B NC A MD八、等腰梯形1. 等腰梯形的性质①等腰梯形同一底边上的两个角相等; ②等腰梯形的两条对角线相等.③等腰梯形是轴对称图形,它只有一条对称轴,底边的垂直平分线是它的对称轴;2. 等腰梯形的判定①同一底上两个内角相等的梯形是等腰梯形. ②对角线相等的梯形是等腰梯形.九、梯形中常见的辅助线我们可以看到,梯形本身的性质并不多,所以实际解梯形的问题时,往往通过添加辅助线将梯形分成三角形或平行四边形,三角形是最简单的直线形,而平行四边形具有很好的对称性质.下面给出几个常见的添加辅助线的方法.1. 作梯形的高:一般是过梯形的一个顶点作高,其好处是将梯形分成一个直角三角形和一个直角梯形,从而可以用勾股定理,如果过梯形的两个顶点分别作高,则会出现矩形.2. 过梯形的一个顶点作另一腰的平行线:这样便将梯形分成了一个平行四边形和一个三角形,这样做的好处是可以将两条腰拉到同一个三角形中,并且三角形的另一条边恰好是梯形的两底之差,从而将问题集中到三角形中.3. 延长梯形的两腰交于一点:这样做可以同样地使问题转化为三角形的问题.4. 过梯形一腰的中点作另一腰的平行线:可以将梯形等积变换成一个平行四边形.5. 连接梯形一个顶点和另一腰上的中点并延长交另一底边:可以将梯形等积变换成一个三角形. 常见的辅助线添加方式如下:梯形中的辅助线较多,其实质是采用割补法将梯形问题划归为三角形、平行四边形问题处理.解题时要根据题目的条件和结论来确定作哪种辅助线.【例1】 如图,已知:在平行四边形ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC ∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.FGE DCBA【解析】⑴ ①(答案不惟一)⑵ ∵四边形ABCD 是平行四边形(已知)∴AD BC ∥,AB CD =(平行四边形的对边平行且相等)∴GBC BGA ∠=∠,BCE CED ∠=∠(两直线平行,内错角相等) 又∵BG 平分ABC ∠,CE 平分BCD ∠(已知)∴ABG GBC ∠=∠,BCE ECD ∠=∠(角平分线定义) ∴ABG AGB ∠=∠,ECD CED ∠=∠.∴AB AG =,CE DE =(在同一个三角形中,等角对等边) ∴AG DE =∴AG EG DE EG -=-,即AE DG =【答案】⑴ ①(答案不惟一)⑵ ∵四边形ABCD 是平行四边形(已知)∴AD BC ∥,AB CD =(平行四边形的对边平行且相等)∴GBC BGA ∠=∠,BCE CED ∠=∠(两直线平行,内错角相等) 又∵BG 平分ABC ∠,CE 平分BCD ∠(已知)∴ABG GBC ∠=∠,BCE ECD ∠=∠(角平分线定义) ∴ABG AGB ∠=∠,ECD CED ∠=∠.∴AB AG =,CE DE =(在同一个三角形中,等角对等边) ∴AG DE =∴AG EG DE EG -=-,即AE DG =【例2】 如图,四边形ABCD 是正方形,△ECF 是等腰直角三角形,其中CE =CF ,G 是CD 与EF 的交点.(1)求证:△BCF ≌△DCE .(2)若BC =5,CF =3,∠BFC =900,求DG :GC 的值.GFEDCBA【解析】 【答案】(1)∵四边形 ABCD 是正方形∴∠BCF +∠FCD =90°,BC =CD ∵△ECF 是等腰直角三角形, ∴∠ECD +∠FCD =90︒. CF =CE ∴∠BCF =∠ECD. ∴△BCF ≌△DCE(2)在△BFC 中,BC =5,CF =3,∠BFC =900.∴BF4 ∵△BCF ≌△DCE ,∴DE =BF =4,∠BFC =∠DEC =∠FCE =900.∴DE ∥FC∴△DGE ∽△CGF ∴DG :GC =DE :CF =4:3【例3】 如图,在四边形ABCD 中,AB =BC ,BF 平分∠ABC ,AF ∥DC , 连接AC ,CF . 求证:(1)AF =CF ;(2)CA 平分∠DCF .FDCBA【解析】略 【答案】(1)∵ BF 平分ABC ∠,∴ ABF CBF ∠=∠. 在△ABF 与△CBF 中,,,,AB CB ABF CBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴ △ABF ≌△CBF . ∴ AF CF =.(2)∵ AF CF =, ∴ FCA FAC ∠=∠. ∵ AF ∥DC ,∴ FAC DCA ∠=∠.∴ FCA DCA ∠=∠,即CA 平分DCF ∠.【例4】 如图,在梯形ABCD 中,AB ∥DC ,5AD BC ==,10AB =,4CD =,连结并延长BD 到E ,使DE BD =,作EF AB ⊥,交BA 的延长线于点F .(1)求tan ABD ∠的值;(2)求AF 的长.FEDCBA【解析】略【答案】(1)作DM ⊥AB 于点M ,CN ⊥AB 于点N .(如图3)∵AB ∥DC ,DM ⊥AB ,CN ⊥AB , ∴ ∠DMN =∠CNM =∠MDC =90︒. ∴ 四边形MNCD 是矩形. ∵4CD =, ∴ MN =CD = 4.∵ 在梯形ABCD 中,AB ∥DC ,5AD BC ==,NM FEDCBA∴ ∠DAB =∠CBA ,DM =CN . ∴ △ADM ≌△BCN . 又∵10AB =,∴ AM =BN =()11(104)322AB MN -=⨯-=. ∴ MB =BN +MN =7.∵ 在Rt AMD △中,∠AMD =90︒,AD =5,AM =3,∴4DM .∴4tan 7DM ABD BM ∠== (2)∵EF AB ⊥, ∴ ∠F =90︒. ∵∠DMN =90︒, ∴ ∠F =∠DMN . ∴ DM ∥EF .∴ △BDM ∽△BEF . ∵ DE BD =,∴12BM BD BF BE ==. ∴BF =2BM =14∴AF =BF -AB =14-10=4【例5】 梯形ABCD 中DC ∥AB , AB =2DC ,对角线AC 、BD 相交于点O , BD =4,过AC 的中点H 作EF ∥BD 分别交AB 、AD 于点E 、F ,求EF 的长.【解析】略【答案】过点C 作CP ∥BD 交AB 的延长线于P∵DC ∥AB ,∴四边形BPCD 是平行四边形. ∴ DB ∥CP , DC =BP . ∵AB =2DC ,设DC =x , ∴BP =x ,AB =2x . ∴AP =3x .∵EF ∥BD ,CP ∥BD , ∴EF ∥CP .又∵点H 为AC 的中点, ∴12AE AH AP AC ==. ∴AE =12AP =32x .∴33224xAE AB x == ∵EF ∥BD ,∴BDEFAB AE =. ∵BD =4, ∴344EF =.∴EF =3ABC D EFO HPHO FED C BA【例6】 如图,在梯形ABCD 中,AD //BC ,BD ⊥CD ,∠C =60°,AD =3,BC =43,求AB 的长.A BCD【解析】略【答案】如图,分别过点A 、D 作AE ⊥BC 于点E ,DF ⊥BC 于点F∴AE //DF . 又∵AD //BC ,∴四边形AEFD 是矩形. ∴EF =AD =3∵BD ⊥CD ,∠C =60°,BC =43,∴DC =BC·cos60°=143232⨯=.∴CF =DC·cos60°=12332⨯=.∴ AE =DF = DC·sin60°=32332⨯= ∴23BE BC EF CF =--= 在Rt △ABE 中,∠AEB =90°,∴ AB =22223(23)21AE BE +=+=【例7】 如图:正方形ABCD 的边长为6cm ,E 是AD 的中点,点P 在AB 上,且∠ECP =45°。


在二次函数与四边形的综合问题中,“平行四边形”“梯形”的存在性问题是主要考察内容。
考查学生对“平行四边形”“梯形”有关性质的理解和应用,“分类讨论思想”依然是本类问题考查的重点之一题型一:动点与平行四边形存在性题型说明:在解决此类问题时,需要注意“平行四边形”的四个顶点中是有一个动点或二个动点。
如果只有一个动点,则先求点坐标,然后代入检验;如果有两个动点,则常用的方法有两个,①引入坐标代入函数解析式后建立方程,注意最后要检验。
;②从已知条件直接进行分析【例1】如图,在平面直角坐标系中,抛物线经过(10)A -,,(30)B ,,(01)C -,三点.⑴求该抛物线的表达式;⑵点Q 在y 轴上,点P 在抛物线上,要使以点Q 、P 、A 、B 为顶点的四边形是平行四边形,求所有满足条件的点P 的坐标.【答案】⑴所求抛物线的表达式为212133y x x =--⑵①当AB 为边时,只要PQ AB ∥,且4PQ AB ==即可又知点Q 在y 轴上,∴点P 的横坐标为4或4-这时,符合条件的点P 有两个当4x =时,53y =;当4x =-时,7y =∴15(4)3P ,,2(47)P-, ②当AB 为对角线时,只要线段PQ 与线段AB 互相平分即可 又知点Q 在y 轴上,且线段AB 中点的横坐标为1 ∴点P 的横坐标为2,这时,符合条件的点P 只有一个 当2x =时,1y =- ∴3(21)P -,综上,满足条件的点P 有三个,其坐标分别为:15(4)3P ,,2(47)P -,,3(21)P -, 【注意】此给出的方法就是“直接分析”。
如果采用引入方程的方法,只需给出Q 点坐标,求出P 点坐标代入解析式即可【例2】在平面直角坐标系中,已知抛物线经过(40)A -,,(04)B -,,(20)C ,三点.例题精讲二次函数与四边形⑴求抛物线的解析式;⑵若点P 是抛物线上的动点,点Q 是直线y x =-上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,请求出相应的点Q【答案】⑴抛物线的解析式为2142y x x =+-⑵满足题意的Q 点的坐标有四个,分别是:(44)-,,(44)-,(22-+-,(22--+【注意】本题第⑵的解决过程中,就可以从两个角度入手,各有特点 切入点一:直接计算∵点Q 在直线y x =-上,设()Q m m -,(0m ≠)则P 点坐标可表示为(4)m m --,或(4)m m --,或(4)m m -+,分别代入2142y x x =+-计算即可切入点二:可以通过讨论①PQ OB ∥或②PQ 为对角线入手【例3】如图,已知抛物线2y ax bx c =++(0a ≠)的顶点坐标为(21)Q -,,且与y 轴交于点(03)C ,,与x 轴交于A 、B 两点(点A 在点B 的右侧),点P 是该抛物线上一动点,从点C 沿抛物线向点A 运动(点P 与A 不重合),过点P 作PD y ∥轴,交AC 于点D . ⑴求该抛物线的函数关系式;⑵当ADP ∆是直角三角形时,求点P 的坐标;⑶在题⑵的结论下,若点E 在x 轴上,点F 在抛物线上,问是否存在以A 、P 、E 、F 为顶点的平行四边形?若存在,求点F 的坐标;若不存在,请说明理由.【答案】⑴243y x x =-+⑵如图1,有两种情况:①当点P 为直角顶点时,点P 与点B 重合 令0y =,得2430x x -+=,解得11x =,23x = ∵点A 在点B 的右侧,∴B (10),,(30)A , ∴1(10)P ,②当点A 为直角顶点时∵OA OC =,90AOC ∠=︒,∴245OAD ∠=︒当2290D AP ∠=︒时,245OAP ∠=︒,∴AO 平分22D AP ∠ 又∵22P D y ∥轴,∴22P D AO ⊥,∴2P 、2D 关于x 轴对称 设直线AC 的函数关系式为y kx b =+ 将(30)A ,,(03)C ,代入解得:3y x =-+ ∵2D 在3y x =-+上,2P 在243y x x =-+上 ∴设2(3)D x x -+,,22(43)P x x x -+,∴2(3)(43)0x x x -++-+=,即2560x x -+= 解得12x =,23x =(舍去) ∴当2x =时,2431y x x =-+=-∴2P 的坐标为2(21)P -,(即为抛物线顶点) ∴P 点坐标为1(10)P ,,2(21)P -, 图1⑶由题⑵知,当点P 的坐标为1(10)P ,时,不能构成平行四边形 当点P 的坐标为2(21)P -,(即顶点Q )时如图2,平移直线AP 交x 轴于点E ,交抛物线于点F 当AP FE =时,四边形APEF 是平行四边形 ∵(21)P -,,∴可令(1)F x ,∴2431x x -+=,解得12x =22x =+故存在以A 、P 、E 、F 为顶点的平行四边形,点F的坐标为:1(21)F -,2(21)F +【例4】如图,抛物线交x 轴于点(20)A -,,点(40)B ,,交y 轴于点(04)C -,.⑴求抛物线的解析式,并写出顶点D 的坐标; ⑵设P 为直线MN 上的动点,过P 作PF ED ∥交直线MN 下方的抛物线于点F .问:在直线MN 上是否存在点P ,使得以P 、E 、D 、F 为顶点的四边形是平行四边形?若存在,请求出点P 及相应的点F 的坐标;若不存在,请说明理由.【答案】⑴设抛物线的解析式为2y ax bx c =++(0)a ≠∵点A 、B 、C 均在此抛物线上∴42016404a b c a b c c -+=⎧⎪++=⎨⎪=-⎩∴⎩⎪⎨⎪⎧a =21b =-1c =-4∴所求的抛物线的解析式为2142y x x =--,顶点D 的坐标为9(1)2-,⑵解:存在 ∵PF ED ∥∴要使以P 、E 、D 、F 为顶点的四边形是平行四边形,只要使PF ED = ∵点E 是抛物线的对称轴1x =和直线y x =-的交点∴E 点的坐标为(11)-,∴971()22ED =---=∵点P 是直线y x =-上的动点∴设P 点的坐标为()k k -,,且点F 是抛物线和直线PF∴F 的坐标为21(4)2k k k --,∴2211(4)422PF k k k k =----=-+,∴217422k -+= ∴k =当1k =时,点P 的坐标为(11)-,,F 的坐标为9(1)2-,此时PF 与ED 重合,不存在以P 、F 、D 、E 为顶点的平行四边形当1k =-时,点P 的坐标为(11)-,,F 的坐标为5(1)2--,此时,四边形PFDE 是平行四边形【例5】已知抛物线2y x bx c =++交y 轴于点A ,点A 关于抛物线对称轴的对称点为(34)B -,,直线14y x =与抛物线在第一象限的交点为C ,连结OB .⑴求抛物线的解析式; ⑵如图⑴,点P 在射线..OC 上运动,连结BP ,设点P 的横坐标为x ,OBP ∆的面积为y ,求y 与x 之间的函数关系式; ⑶如图⑵,点P 在直.线.OC 上运动,点Q 在抛物线上运动,试问点P 、Q 在运动过程中是否存在以O 、B 、P 、Q 为顶点的四边形是平行四边形的情况,若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】⑴∵(34)B -,点A 与点B 关于抛物线的对称轴对称,(04)A -,把(04)A -,、(34)B -,代入2y x bx c =++得: 4934c b c =-⎧⎨++=-⎩ ∴34b c =-⎧⎨=-⎩ ∴抛物线的解析式为234yx x =--⑵如图⑴,连结AB ,作PD y ⊥轴,则1(0)4D x ,S 梯形ABPD=21(x +3)(41x +4)=81x2+819x +6S △AOB=21×3×4=6,S △DOP=21×x ×41x =81x2∴y =S 梯形ABPD -S △AOB -S △DOP=819x⑶平移线段OB ,使点B 落在直线y =41x 上,落点为P ,点O 落在抛物线上,落点为Q ,则四边形OBPQ 为平行四边形 设P (x ,41x ),∵O (0,0),B (3,-4)∴Q (x -3,41x +4)∵点Q 在抛物线上,∴41x +4=(x -3)2-3(x -3)-4整理得:4x2-37x +40=0,解得:x =8或x =45∴P 1(8,2),P 2(45,165) 平移线段OB ,使点O 落在直线y =41x 上,落点为P ,点B 落在抛物线上,落点为Q ,则四边形图(1) 图(2) 备用图图(2)图(1)OBQP 为平行四边形设P (x ,41x ),∵O (0,0),B (3,-4),∴Q (x +3,41x -4)∵点Q 在抛物线上,∴41x -4=(x +3)2-3(x +3)-4整理得:4x2+11x =0,解得:x =0(舍去)或x =-411∴P 3(-411,-1611)平移线段OP 3,使点P 3与点O 重合,则点O 落在直线y =41x 上点P 4处,四边形OPBQ 为平行四边形∴P 4(411,1611)综上所述,符合条件的点P 有4个,分别是:P 1(8,2),P 2(45,165),P 3(-411,-1611),P 4(411,1611)题型二:动点与梯形问题题型说明:本类题型主要考查两点,①梯形,等腰梯形,直角梯形的性质的理解和应用;②两直线平行时,k 值相等,当然并不仅仅局限于这两种考查方式。

中考数学第9讲函数复习教案(新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(中考数学第9讲函数复习教案(新版)北师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为中考数学第9讲函数复习教案(新版)北师大版的全部内容。
课题:第九讲函数复习目标:1.理解平面直角坐标系的有关概念,了解坐标平面内点的坐标特征。
2.了解函数概念,会求自变量取值范围和函数值,会用描点法画函数图象。
3.会结合图象对实际问题进行分析,对变量的变化规律进行预测;用适当的函数表示问题中变量之间的关系.复习重点和难点:重点:掌握坐标平面内点的坐标特征,了解函数概念,会求自变量取值范围和函数值。
难点:结合图象对实际问题进行分析,对变量的变化规律进行预测。
课前准备:教师准备:PPT课件.学生准备:完成导学案“课前热身"和“知识梳理”两部分内容.教学过程:一、课前热身知识回顾(多媒体出示“课前热身”题组,并引导学生分组展示)请同学们先根据你课前的准备,派小组代表完成“课前热身”的展示.1.已知点M到x轴的距离为1,到y轴的距离为2,且点M在第二象限,则点M的坐标为()A.(2,-1) B.(-2,1) C.(1,-2)D.(-1,2)2.夏天到了,某小区准备开放游泳池,物业管理处安排一名清洁工对一个无水的游泳池进行清洗.该工人先只打开一个进水管,蓄了少量水后关闭进水管并立即进行清洗,一段时间后,再同时打开两个出水管将池内的水放完,随后将两个出水管关闭,并同时打开两个进水管将水蓄满.已知每个进水管的进水速度与每个出水管的出水速度相同.从工人最先打开一个进水管开始,所用的时间为x,游泳池内的蓄水量为y ,则下列各图中能够反映y与x 的函数关系的大致图象是( )3. 已知点M(1-2m ,m -1)关于x 轴的对称点在第一象限,则m 的取值范围是__ __.4。



在各种考试的几何压轴题压轴题中,平移,轴对称,旋转中,旋转考查的最多,但是很多题目之间,都有很多类似的地方,也就是“共性”问题,充分的掌握这些“共性”问题的分析思路和解决方法,能够使学生快速的发现解决问题的关键因素。
本讲会给出与旋转有关,且经常在考试中出现的几种基本模型模型一:共顶点旋转模型模型说明:本模型是由全等三角形中一道最基本,最经典的题型,由此题型可演变出很多变化,注意让学生体会,各种变化之间相同点和不同点。
下面给出基本模型,此部分内容系个人总结,如果还有不完善的地方,或者还有其他补充,亦或者还有更好的命名方式,易于学生记忆和理解,请到教师论坛→初数版块→疑难交流区进行反馈,大家一起讨论以下图形虽然很多,但都是一个基本模型,共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形例题精讲旋转与几何探究共顶点等腰三角形以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化而我们都知道,“全等三角形”是“相似三角形”的一种特殊情况,因此此模型进一步延伸,可引出相似三角形,也就是此模型的最一般的情况,也就是“通法”“共性”,下面也会给出几组连续变化的图形,注意仔细体会各种变化之间的区别与联系共性:ADAB=AEACCEEDCBA共顶点相似的直角三角形共顶点相似的一般三角形共顶点相似的直角三角形各部分阴影三角形相似的判定方法,均是:“两边成比例且夹角相等的两个三角形相似”,类比“SAS”真题体验【例1】以ABC∆的两边AB、AC为腰分别向外作等腰Rt ABD∆和等腰Rt ACE∆,90BAD CAE∠=∠=︒.连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.⑴如图①当ABC∆为直角三角形时,AM与DE的位置关系是;线段AM与DE的数量关系是 ;⑵将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转θ︒(090θ<<)后,如图②所示,⑴问中得到的两个结论是否发生改变?并说明理由.【答案】此题方法不唯一⑴AM DE ⊥,12AM DE =;⑵结论仍然成立。
如图,延长CA 至F ,使FA AC =,FA 交DE 于点P ,并连结BF .∵DA BA EA AF ⊥⊥,,∴90BAF DAF EAD ∠=︒+∠=∠. 在FAB ∆与EAD ∆中,FA AEBAF EAD BA DA =⎧⎪∠=∠⎨⎪=⎩∴FAB EAD ∆∆≌.∴BF DE F AEN =∠=∠,.∴90FPD F APE AEN ∠+∠=∠+∠=︒. ∴FB DE ⊥. 又CA AF =,CM MB =,∴AM FB ∥且12AM FB =∴12AM DE AM DE ⊥=,. 【例2】 ⑴ 如图所示,在四边形ABCD 中,AB AD =,60BAD ∠=,120BCD ∠=,证明:BC +DC AC =.⑵ 如图所示,在四边形ABCD 中,AB BC =,60ABC ∠=,P 为四边形ABCD 内部一点,120APD ∠=,证明:PA PD PC BD ++≥.DCBAPDCBA【答案】方法不唯一:⑴延长CB 到点E 使得BE CD =,连接AE 证明ABE ADC ∆∆≌即可,过程略⑵延长DP 到点Q ,使PQ AP =,连接AQ ,BQ ,AC ,BDFPN MEDCBA图①NM EDC BA图②NM EDCBABED易证ABC∆,APQ∆均为等边三角形,下略【例3】已知:PA=4PB=,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.⑴如图,当45APB∠=︒时,求AB及PD的长;⑵当APB∠变化,且其它条件不变时,求PD的最大值及相应APB∠的大小.PDCBAEABCDP【答案】⑴过点A作AE AP⊥,且AE AP=,连接PE,EB,证明AEB APD∆∆≌,即可求出BE,PD 过点A作AF PB⊥,应用解直角三角形的知识即可求出AB,过程略相信会有部分学生认为,前面的模型好理解,但是为什么这个题的辅助线,我就想不到呢?老师,你是怎么思考的呢?其实这就是对上述模型的理解,第一种理解方式,如图,已知的是两个等边或等腰三角形,证明全等第二种理解方式,如图,一个三角形绕着一个顶点旋转会形成两个等腰或等边或等腰直角三角形第二种理解方式第一种理解方式下面给出连续的变化图,辅助线就是这样想出来的,属于第二种理解方式,包括例1,例2的辅助线也是从这个角度去出发,CP BBP⑵当135APB∠=︒时,PD取得最大值为6思考方式:如图,∵AP6PB=固定不变,所以无论APB∠如何变化,ADP ABE∆∆≌,2PE=,BE PD=这些条件始终不变,因此就将此问转变成“已知PE,PB的长度,求BE的最大值”,因此只有E,P,B三点共线时,由此反求135APB∠=︒EABCDP【例4】 如图1,在平行四边形ABCD 中,AE BC ⊥于点E ,E 恰为BC 的中点,tan 2B =.⑴求证:AD AE =;⑵如图2,点P 在线段BE 上,作EF DP ⊥于点F ,连结AF .求证:DF EF -; ⑶请你在图3中画图探究:当P 为线段EC 上任意一点(P 不与点E 重合)时,作EF 垂直直线DP ,垂足为点F ,连结AF ,线段DF 、EF 与AF 之间有怎样的数量关系?直接写出你的结论.图3图2图1FPABCDE AB CDE E DCBA【答案】⑴略;⑵在DP 上取一点M ,使得DM EF =,连接AM ,证明AFE AMD ∆∆≌即可其他略辅助线思路MF PAB CEDB DB⑶结论:DF EF +=辅助线:延长FD 到点M 使得DM EF =,连接AM ,证明AEF ADM ∆∆≌即可辅助线思路B【例5】 如图①,已知ABC ∆是等腰直角三角形,BAC ∠,点D 是BC 的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接AE 、BG .⑴试猜想线段BG 和AE 的数量关系,请直接写出你得到的结论.⑵将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于︒0,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.⑶若2BC DE ==,在②的旋转过程中,当AE 为最大值时,求AF 的值.AB CD EFG②①G FEDC BA【答案】⑴BG AE =;第⑵,⑶问的提示如下:过程略,AE 的最大值为3AGEFGGC【例6】 已知:如图,OAB ∆与OCD ∆为等腰直角三角形,90AOB COD ∠=∠=︒.⑴如图①,点C 、D 分别在边OA 、OB 上,联结AD 、BC ,点M 为线段BC 的中点,联结OM ,请你猜想OM 与AD 的数量关系: (直接写出答案,不必证明); ⑵如图②,在图1的基础上,将OCD ∆绕点O 逆时针旋转一个角度α(︒<<︒900α). ①OM 与AD 的数量关系是否仍成立,若成立请证明,若不成立请说明理由; ②求证:OM AD ⊥.②①MACOD BMODCBA【答案】⑴2AD OM =;⑵方法不唯一:如图,延长CO 到点N ,使ON OC =,连接BN ,其他略ABD O CAM【例7】 已知ABC ∆,以AC 为边在ABC ∆外作等腰ACD ∆,其中AC AD =。
⑴如图①,若2DAC ABC ∠=∠,AC BC =,四边形ABCD 是平行四边形,则_____ABC ∠= ⑵如图②,若30ABC ∠=︒,ACD ∆是等边三角形,3AB =,4BC =,求BD 的长;⑶如图③,若ACD ∠为锐角,作AH BC ⊥于H ,当2224BD AH BC =+时,2DAC ABC ∠=∠是否成立?若不成立,请说明你的理由;若成立,证明你的结论。
③②①AH CBDDCBADCBA【答案】⑴略;⑵如图,以AE 为边作等边三角形ABE ,连接BE 、CE ,其他略CB C B B C⑶如图,辅助线虽然相对容易能够知道位置,但是本题比较特殊,或难点在于如何利用给出的已知条件2224BD AH BC =+,如何描述辅助线,将直接影响到能否解决本问HC BH CBBCH下面给出参考方法,注意体会为什么这样做辅助线,而不是像以前的题型一样,为什么按照其他的辅助线的作法不能解决第⑶问:(谁有更好的方法欢迎在论坛发帖探讨)如图,在BC 上取点G ,使得HG BH =,连接GA 并延长到点F ,使得AF AG =,连接BF FC = 易证BFG ∆为直角三角形,且2BF AH =,∴BFC ∆也为直角三角形,由勾股定理可得222BF BC FC +=,∴2224BC AH FC +=,∵2224BD AH BC =+,∴FC BD =此时,易证BAD FAC ∆∆≌(SSS),则易证2FAB DAC ABC ∠=∠=∠HCB全等三角形的例子就举例到这里了还有很多,下面举出一些相似例子【例8】 我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形⑴写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称:_______________ ⑵如图①,在梯形ABCD 中,AD BC ∥,AC BD ⊥,垂足为O 求证:2222AD BC AB DC +=+⑶如果将①中的AOD ∆绕点O 按逆时针方向旋转角α(090α︒<<︒)后得到图②,那么四边形ABCD 能否成为等平方和四边形?若能,请证明;若不能,请说明理由。
①ODCBAABCDO②【答案】⑴略;⑵提示:四个勾股定理;⑶如图:证明AOC DOB ∆∆∽即可,其他略ABCDOBBB【例9】 如图①,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:⑴请直接写出图①中线段BG ,线段DE 的数量关系及所在直线的位置关系;⑵将图①中的正方形CEFG 绕点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图②,图③的情况,请你通过观察,测量等方法判断①中得到的结论是否仍然成立,并选取图②证明你的判断③②①O ABCDEFGABCDEFG G FE DC BA⑶将原题中正方形改为矩形(如图④~⑥),且,,,AB a BC b CE ka CG kb ==== (,0)a b k ≠> ,试判断⑵中得到的结论哪个成立,哪个不成立?并写出你的判断,请用图⑤进行证明.⑷在图⑤中,连结DG 、BE ,且14,2,2a b k ===,则22BE DG += . ⑥⑤④OA BCDEFG ABC DEF GGFEDC BA【答案】略,请参考上面例题的思路【例10】 如图①,在ABC ∆中,D 、E 分别是AB 、AC 上的点,且DE BC ∥,将ADE ∆绕A 点顺时针旋转一定角度,连结BD 、CE ,得到图②,然后将BD 、CE 分别延长至M 、N ,使12DM BD =,12EN CE =,连结AM 、AN 、MN ,得到图③,请解答下列问题:⑴若AB AC =,请探究下列数量关系:①在图②中,BD 与CE 的数量关系是________________;②在图③中,猜想AM 与AN 的数量关系、MAN ∠与BAC ∠的数量关系,并证明你的猜想; ⑵若AB k AC =⋅(1k >),按上述操作方法,得到图④,请继续探究:AM 与AN 的数量关系、MAN ∠与BAC ∠的数量关系,直接写出你的猜想,不必证明.【答案】略【例11】 已知ABC ∆中,点D 在AC 上,点E 在BC 上,且DE AB ∥.将CDE ∆绕点C 按顺时针方向旋转得到''CD E ∆('180BCE ∠<︒),连接'AD 、'BE ,设直线'BE 与AC 、'AD 分别交于点O 、F .⑴如图1,若ABC ∆为等边三角形,则''AD BE 的值为________,AFB ∠的度数为________;⑵如图2,若ABC ∆满足60ACB ∠=︒,AC,BC =①求''AD BE 的值和AFB ∠的度数;②若E 是BC 的中点,求OBC ∆面积的最大值.D BC A E图① D B C A 图②ED B C A图③ E MND B CA 图④E M N图2图1ABCD E D'E'F OOF E'D'E D C BA【答案】略:提示思路,第⑴问全等三角形,第⑵问相似三角形图2图2BD'BD'CE D'图1第⑵问的②问,解决思路如下,当CDE ∆在旋转的过程中,点E 在以点C 为圆心,12BC 为半径的圆上,∴易证,当E 运动到圆C 与线段AC 的交点时,BE AC ⊥,此时CE 达到最大值,O 与E 重合,此时OBC ∆OE'ED CBA图2模型二:对角互补类—四边形模型模型说明:本模型是模型一的延伸和变形,所以从某种程度上,两个模型有相通之处,而之所以提出此类模型,是因为在不同的题目之间,所给出已知条件以及图形的展现形式不同。