大学物理思考题答案第四章

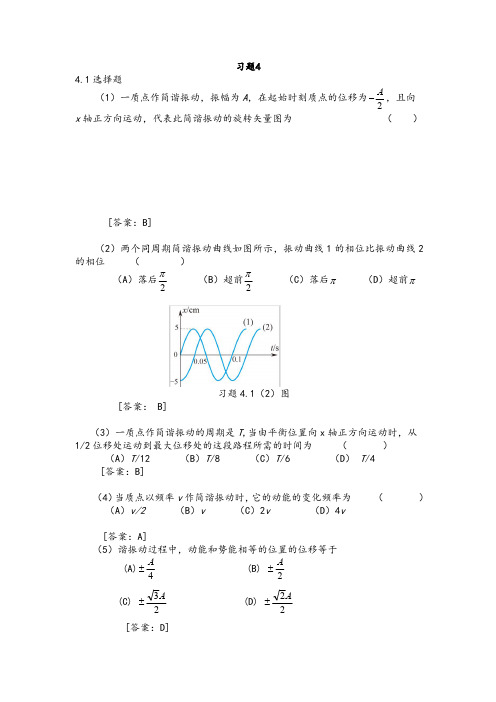
第四章机械振动4．1一物体沿x 轴做简谐振动，振幅A = 0.12m ，周期T = 2s ．当t = 0时，物体的位移x = 0.06m ，且向x 轴正向运动．求：（1）此简谐振动的表达式；（2）t = T /4时物体的位置、速度和加速度；（3）物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间． [解答]（1）设物体的简谐振动方程为x = A cos(ωt + φ)，其中A = 0.12m ，角频率ω = 2π/T = π．当t = 0时，x = 0.06m ，所以cos φ = 0.5，因此φ = ±π/3． 物体的速度为v = d x /d t = -ωA sin(ωt + φ)．当t = 0时，v = -ωA sin φ，由于v > 0，所以sin φ< 0，因此：φ = -π/3．简谐振动的表达式为：x = 0.12cos(πt – π/3)．（2）当t = T /4时物体的位置为;x = 0.12cos(π/2 – π/3) = 0.12cosπ/6 = 0.104(m)． 速度为；v = -πA sin(π/2 – π/3) = -0.12πsinπ/6 = -0.188(m·s -1)．加速度为：a = d v /d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s -2)． （3）方法一：求时间差．当x = -0.06m 时，可得cos(πt 1 - π/3) = -0.5， 因此πt 1 - π/3 = ±2π/3．由于物体向x 轴负方向运动，即v < 0，所以sin(πt 1 - π/3) > 0，因此πt 1 - π/3 = 2π/3，得t 1 = 1s ．当物体从x = -0.06m 处第一次回到平衡位置时，x = 0，v > 0，因此cos(πt 2 - π/3) = 0， 可得 πt 2 - π/3 = -π/2或3π/2等．由于t 2> 0，所以πt 2 - π/3 = 3π/2， 可得t 2 = 11/6 = 1.83(s)．所需要的时间为：Δt = t 2 - t 1 = 0.83(s)．方法二：反向运动．物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m ，即从起点向x 轴正方向运动第一次回到平衡位置所需的时间．在平衡位置时，x = 0，v < 0，因此cos(πt - π/3) = 0，可得 πt - π/3 = π/2，解得t = 5/6 = 0.83(s)．[注意]根据振动方程x = A cos(ωt + φ)，当t = 0时，可得φ = ±arccos(x 0/A )，（-π<φ<= π）， 初位相的取值由速度决定．由于v = d x /d t = -ωA sin(ωt + φ)，当t = 0时，v = -ωA sin φ，当v > 0时，sin φ< 0，因此 φ = -arccos(x 0/A )；当v < 0时，sin φ> 0，因此φ = arccos(x 0/A )π/3．可见：当速度大于零时，初位相取负值；当速度小于零时，初位相取正值．如果速度等于零，当初位置x 0 = A 时，φ = 0；当初位置x 0 = -A 时，φ = π．4．2已知一简谐振子的振动曲线如图所示，试由图求：（1）a ，b ，c ，d ，e 各点的位相，及到达这些状态的时刻t 各是多少？已知周期为T ； （2）振动表达式； （3）画出旋转矢量图． [解答]方法一：由位相求时间．（1）设曲线方程为x = A cos Φ，其中A 表示振幅，Φ = ωt + φ表示相位． 由于x a = A ，所以cos Φa = 1，因此Φa = 0．由于x b = A /2，所以cos Φb = 0.5，因此Φb = ±π/3；由于位相Φ随时间t 增加，b 点位相就应该大于a 点的位相，因此Φb = π/3．由于x c = 0，所以cos Φc = 0，又由于c 点位相大于b 位相，因此Φc = π/2．同理可得其他两点位相为：Φd = 2π/3，Φe = π．c 点和a 点的相位之差为π/2，时间之差为T /4，而b 点和a 点的相位之差为π/3，时间之差应该为T /6．因为b 点的位移值与O 时刻的位移值相同，所以到达a 点的时刻为t a = T /6． 到达b 点的时刻为t b = 2t a = T /3．图4.2到达c 点的时刻为t c = t a + T /4 = 5T /12． 到达d 点的时刻为t d = t c + T /12 = T /2． 到达e 点的时刻为t e = t a + T /2 = 2T /3．（2）设振动表达式为：x = A cos(ωt + φ)，当t = 0时，x = A /2时，所以cos φ = 0.5，因此φ =±π/3； 由于零时刻的位相小于a 点的位相，所以φ = -π/3， 因此振动表达式为． 另外，在O 时刻的曲线上作一切线，由于速度是位置对时间的变化率，所以切线代表速度的方向；由于其斜率大于零，所以速度大于零，因此初位相取负值，从而可得运动方程．（3）如图旋转矢量图所示．方法二：由时间求位相．将曲线反方向延长与t 轴 相交于f 点，由于x f = 0，根据运动方程，可得所以：．显然f 点的速度大于零，所以取负值，解得t f = -T /12．从f 点到达a 点经过的时间为T /4，所以到达a 点的时刻为：t a = T /4 + t f = T /6， 其位相为：． 由图可以确定其他点的时刻，同理可得各点的位相．4．3 有一弹簧，当其下端挂一质量为M 的物体时，伸长量为9.8×10-2m ．若使物体上下振动，且规定向下为正方向．（1）t = 0时，物体在平衡位置上方8.0×10-2m 处，由静止开始向下运动，求运动方程；（2）t = 0时，物体在平衡位置并以0.60m·s -1速度向上运动，求运动方程． [解答]当物体平衡时，有：Mg – kx 0 = 0， 所以弹簧的倔强系数为：k = Mg/x 0， 物体振动的圆频率为：s -1)． 设物体的运动方程为：x = A cos(ωt + φ)．（1）当t = 0时，x 0 = -8.0×10-2m ，v 0 = 0，因此振幅为：=8.0×10-2(m)；由于初位移为x 0 = -A ，所以cos φ = -1，初位相为：φ = π． 运动方程为：x = 8.0×10-2cos(10t + π)．（2）当t = 0时，x 0 = 0，v 0 = -0.60(m·s -1)，因此振幅为：v 0/ω|=6.0×10-2(m)；由于cos φ = 0，所以φ = π/2；运动方程为：x = 6.0×10-2cos(10t +π/2)．4．4 质量为10×10-3kg 的小球与轻弹簧组成的系统，按的规律作振动，式中t 以秒(s)计，x 以米(m)计．求： （1）振动的圆频率、周期、振幅、初位相； （2）振动的速度、加速度的最大值；（3）最大回复力、振动能量、平均动能和平均势能；cos(2)3t x A T ππ=-cos(2)03t T ππ-=232f t Tπππ-=±203a a t T πΦπ=-=ω==0||A x ==A =20.1cos(8)3x t ππ=+（4）画出这振动的旋转矢量图，并在图上指明t 为1，2，10s 等各时刻的矢量位置． [解答]（1）比较简谐振动的标准方程：x = A cos(ωt + φ)，可知圆频率为：ω =8π，周期T = 2π/ω = 1/4 = 0.25(s)，振幅A = 0.1(m)，初位相φ = 2π/3．（2）速度的最大值为：v m = ωA = 0.8π = 2.51(m·s -1)； 加速度的最大值为：a m = ω2A = 6.4π2 = 63.2(m·s -2)． （3）弹簧的倔强系数为：k = mω2，最大回复力为:f = kA = mω2A = 0.632(N)； 振动能量为:E = kA 2/2 = mω2A 2/2 = 3.16×10-2(J)， 平均动能和平均势能为:= kA 2/4 = mω2A 2/4 = 1.58×10-2(J)． （4）如图所示，当t 为1，2，10s 等时刻时，旋转矢量的位置是相同的．4．5 两个质点平行于同一直线并排作同频率、同振幅的简谐振动．在振动过程中，每当它们经过振幅一半的地方时相遇，而运动方向相反．求它们的位相差，并作旋转矢量图表示．[解答]设它们的振动方程为:x = A cos(ωt + φ)， 当x = A /2时，可得位相为:ωt + φ = ±π/3．由于它们在相遇时反相，可取Φ1 = (ωt + φ)1 = -π/3，Φ2 = (ωt + φ)2 = π/3，它们的相差为:ΔΦ = Φ2 – Φ1 = 2π/3，或者:ΔΦ` = 2π –ΔΦ = 4π/3．矢量图如图所示．4．6一氢原子在分子中的振动可视为简谐振动．已知氢原子质量m = 1.68×10-27kg ，振动频率v = 1.0×1014Hz ，振幅A = 1.0×10-11m ．试计算：（1）此氢原子的最大速度； （2）与此振动相联系的能量．[解答]（1）氢原子的圆频率为:ω = 2πv = 6.28×1014(rad·s -1)， 最大速度为:v m = ωA = 6.28×103(m·s -1)．（2）氢原子的能量为:= 3.32×10-20(J)．4．7 如图所示，在一平板下装有弹簧，平板上放一质量为1.0kg 的重物，若使平板在竖直方向上作上下简谐振动，周期为0.50s ，振幅为2.0×10-2m ，求：（1）平板到最低点时，重物对平板的作用力；（2）若频率不变，则平板以多大的振幅振动时，重物跳离平板？ （3）若振幅不变，则平板以多大的频率振动时，重物跳离平板？ [解答]（1）重物的圆频率为：ω = 2π/T = 4π，其最大加速度为：a m = ω2A ，合力为：F = ma m ，方向向上．重物受到板的向上支持力N 和向下的重力G ，所以F = N – G ． 重物对平板的作用力方向向下，大小等于板的支持力： N = G + F = m (g +a m ) = m (g +ω2A ) = 12.96(N)．（2）当物体的最大加速度向下时，板的支持为：N = m (g - ω2A )． 当重物跳离平板时，N = 0，频率不变时，振幅为：A = g/ω2 = 3.2×10-2(m)．（3）振幅不变时，频率为：3.52(Hz)．4．8 两轻弹簧与小球串连在一直线上，将两弹簧拉长后系在固定点A 和B 之间，整个系统放在光滑水平面上．设两弹簧的原长分别为l 1和l 2，倔强系统分别为k 1和k 2，A和B 间距为L ，小球的质量为m ．（1）试确定小球的平衡位置；k pE E =212m E mv=2ωνπ==（2）使小球沿弹簧长度方向作一微小位移后放手，小球将作振动，这一振动是否为简谐振动？振动周期为多少？[解答]（1）这里不计小球的大小，不妨设L > l 1 + l 2，当小球平衡时，两弹簧分别拉长x 1和x 2，因此得方程：L = l 1 + x 1 + l 2 + x 2；小球受左右两边的弹簧的弹力分别向左和向右，大小相等，即k 1x 1 = k 2x 2． 将x 2 = x 1k 1/k 2代入第一个公式解得：．小球离A 点的距离为：．（2）以平衡位置为原点，取向右的方向为x 轴正方向，当小球向右移动一个微小距离x 时，左边弹簧拉长为x 1 + x ，弹力大小为：f 1 = k 1(x 1 + x )， 方向向左；右边弹簧拉长为x 1 - x ，弹力大小为：f 2 = k 2(x 2 - x )， 方向向右．根据牛顿第二定律得：k 2(x 2 - x ) - k 1(x 1 + x ) = ma ，利用平衡条件得：，即小球做简谐振动．小球振动的圆频率为：．4．9如图所示，质量为10g 的子弹以速度v = 103m·s -1水平射入木块，并陷入木块中，使弹簧压缩而作简谐振动．设弹簧的倔强系数k = 8×103N·m -1，木块的质量为4.99kg ，不计桌面摩擦，试求：（1）振动的振幅；（2）振动方程．[解答]（1）子弹射入木块时，由于时间很短，木块还来不及运动，弹簧没有被压缩，它们的动量守恒，即：mv = (m + M)v 0．解得子弹射入后的速度为：v 0 = mv/(m + M) = 2(m·s -1)，这也是它们振动的初速度．子弹和木块压缩弹簧的过程机械能守恒，可得：(m + M ) v02/2 = kA 2/2， 所以振幅为：10-2(m)． （2）振动的圆频率为：= 40(rad·s -1)．取木块静止的位置为原点、向右的方向为位移x 的正方向，振动方程可设为：x = A cos(ωt + φ)．当t = 0时，x = 0，可得：φ = ±π/2；由于速度为正，所以取负的初位相，因此振动方程为：x = 5×10-2cos(40t - π/2)．4．10如图所示，在倔强系数为k 的弹簧下，挂一质量为M 的托盘．质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞，而使其作简谐振动，设两物体碰后瞬时为t = 0时刻，求振动方程．[解答]物体落下后、碰撞前的速度为：物体与托盘做完全非弹簧碰撞后，根据动量守恒定律可得它们的共同速度为，这也是它们振动的初速度．设振动方程为：x = A cos(ωt + φ)，211212()k x L l l k k =--+211111212()k L l x l L l l k k =+=+--+2122d ()0d xm kk x t++=ω=22T πω==A v =ω=v =0m v v m M ==+图4.9 图4.10其中圆频率为：物体没有落下之前，托盘平衡时弹簧伸长为x 1，则：x 1 = Mg/k ．物体与托盘磁盘之后，在新的平衡位置，弹簧伸长为x 2，则：x 2= (M + m )g/k ． 取新的平衡位置为原点，取向下的方向为正，则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k ．因此振幅为：初位相为：4．11 装置如图所示，轻弹簧一端固定，另一端与物体m 间用细绳相连，细绳跨于桌边定滑轮M 上，m 悬于细绳下端．已知弹簧的倔强系数为k = 50N·m -1，滑轮的转动惯量J = 0.02kg·m 2，半径R = 0.2m ，物体质量为m = 1.5kg ，取g = 10m·s -2．（1）试求这一系统静止时弹簧的伸长量和绳的张力；（2）将物体m 用手托起0.15m ，再突然放手，任物体m 下落而整个系统进入振动状态．设绳子长度一定，绳子与滑轮间不打滑，滑轮轴承无摩擦，试证物体m 是做简谐振动； （3）确定物体m 的振动周期；（4）取物体m 的平衡位置为原点，OX 轴竖直向下，设振物体m 相对于平衡位置的位移为x ，写出振动方程．[解答]（1）在平衡时，绳子的张力等于物体的重力T = G = mg = 15(N)．这也是对弹簧的拉力，所以弹簧的伸长为：x 0 = mg/k = 0.3(m)．（2）以物体平衡位置为原点，取向下的方向为正，当物体下落x 时，弹簧拉长为x 0 + x ，因此水平绳子的张力为：T 1 = k (x 0+ x )．设竖直绳子的张力为T 2，对定滑轮可列转动方程：T 2R – T 1R = Jβ， 其中β是角加速度，与线加速度的关系是：β = a/R ．对于物体也可列方程：mg - T 2 = ma ． 转动方程化为：T 2 – k (x 0 + x ) = aJ/R 2，与物体平动方程相加并利用平衡条件得：a (m + J/R 2) = –kx ，可得微分方程：，故物体做简谐振动． （3）简谐振动的圆频率为：s -1)． 周期为：T 2 = 2π/ω = 1.26(s)．（4）设物体振动方程为：x = A cos(ωt + φ)，其中振幅为：A = 0.15(m)． 当t = 0时，x = -0.15m ，v 0 = 0，可得：cos φ = -1，因此φ = π或-π， 所以振动方程为：x = 0.15cos(5t + π)，或x = 0.15cos(5t - π)．4．12一匀质细圆环质量为m ，半径为R ，绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动，求摆动的周期．[解答]通过质心垂直环面有一个轴，环绕此轴的转动惯量为：I c = mR 2．根据平行轴定理，环绕过O 点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2．当环偏离平衡位置时，重力的力矩为：M = mgR sin θ， 方向与角度θ增加的方向相反．ω=A ==00arctan v x ϕω-==222d 0d /x kx t m J R +=+ω=根据转动定理得：Iβ = -M ，即，由于环做小幅度摆动，所以sin θ≈θ，可得微分方程：． 摆动的圆频率为：周期为：4．13 重量为P 的物体用两根弹簧竖直悬挂，如图所示，各弹簧的倔强系数标明在图上．试求在图示两种情况下，系统沿竖直方向振动的固有频率．[解答]（1）前面已经证明：当两根弹簧串联时，总倔强系数为k = k1k 2/(k 1 + k 2)，因此固有频率为（2）前面还证明：当两根弹簧并联时，总倔强系数等于两个弹簧的倔强系数之和，因此固有频率为．4．14质量为0.25kg 的物体，在弹性力作用下作简谐振动，倔强系数k = 25N·m -1，如果开始振动时具有势能0.6J ，和动能0.2J ，求：（1）振幅；（2）位移多大时，动能恰等于势能？（3）经过平衡位置时的速度．[解答]物体的总能量为：E = E k + E p = 0.8(J)．（1）根据能量公式E = kA2/2，得振幅为：．（2）当动能等于势能时，即E k = E p ，由于E = E k + E p ，可得：E = 2E p ，即，解得：= ±0.179(m)． （3）再根据能量公式E = mv m2/2，得物体经过平衡位置的速度为： 2.53(m·s -1)．4．15 两个频率和振幅都相同的简谐振动的x-t 曲线如图所示，求： （1）两个简谐振动的位相差；（2）两个简谐振动的合成振动的振动方程． [解答]（1）两个简谐振动的振幅为：A = 5(cm)， 周期为：T = 4(s)，圆频率为：ω =2π/T = π/2，它们的振动方程分别为：x 1 = A cos ωt =5cosπt /2， x 2 = A sin ωt =5sinπt /2 =5cos(π/2 - πt /2)即x 2=5cos(πt /2 - π/2)．位相差为：Δφ = φ2 - φ1 = -π/2． （2）由于x = x 1 + x 2 = 5cosπt /2 +5sinπt /2 = 5(cosπt /2·cosπ/4 +5sinπt /2·sinπ/4)/sinπ/4 合振动方程为：(cm)．22d sin 0d I mgR tθθ+=22d 0d mgRt Iθθ+=ω=222T πω===2ωνπ===2ωνπ===A =2211222kA kx =⨯/2x =m v =cos()24x t ππ=- (b)图4.134．16 已知两个同方向简谐振动如下：，．（1）求它们的合成振动的振幅和初位相； （2）另有一同方向简谐振动x 3 = 0.07cos(10t +φ)，问φ为何值时，x 1 + x 3的振幅为最大？φ为何值时，x 2 + x 3的振幅为最小？（3）用旋转矢量图示法表示（1）和（2）两种情况下的结果．x 以米计，t 以秒计．[解答]（1）根据公式，合振动的振幅为：=8.92×10-2(m)． 初位相为：= 68.22°．（2）要使x 1 + x 3的振幅最大，则：cos(φ– φ1) = 1，因此φ– φ1 = 0，所以：φ = φ1 = 0.6π． 要使x 2 + x 3的振幅最小，则 cos(φ– φ2) = -1，因此φ– φ2 = π，所以φ = π + φ2 = 1.2π．（3）如图所示．4．17质量为0.4kg 的质点同时参与互相垂直的两个振动：， ．式中x 和y 以米(m)计，t 以秒(s)计．（1）求运动的轨道方程；（2）画出合成振动的轨迹；（3）求质点在任一位置所受的力．[解答]（1）根据公式：，其中位相差为：Δφ = φ2 – φ1 = -π/2，130.05cos(10)5x t π=+210.06cos(10)5x t π=+A =11221122sin sin arctancos cos A A A A ϕϕϕϕϕ+=+0.08cos()36x t ππ=+0.06cos()33y t ππ=-2222212122cos sin x y xyA A A A ϕϕ+-∆=∆所以质点运动的轨道方程为：． （2）合振动的轨迹是椭圆．（3）两个振动的圆频率是相同的ω = π/3，质点在x 方向所受的力为，即F x = 0.035cos(πt /3 + π/6)(N)．在y 方向所受的力为，即F y = 0.026cos(πt /3 - π/3)(N)．用矢量表示就是，其大小为，与x 轴的夹角为θ = arctan(F y /F x )．4．18 将频率为384Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ，在待测音叉的一端加上一小块物体，则拍频将减小，求待测音叉的固有频率．[解答]标准音叉的频率为v 0 = 384(Hz)， 拍频为Δv = 3.0(Hz)， 待测音叉的固有频率可能是v 1 = v 0 - Δv = 381(Hz)， 也可能是v 2 = v 0 + Δv = 387(Hz)．在待测音叉上加一小块物体时，相当于弹簧振子增加了质量，由于ω2 = k/m ，可知其频率将减小．如果待测音叉的固有频率v 1，加一小块物体后，其频率v`1将更低，与标准音叉的拍频将增加；实际上拍频是减小的，所以待测音叉的固有频率v 2，即387Hz ．4．19示波器的电子束受到两个互相垂直的电场作用．电子在两个方向上的位移分别为x = A cos ωt 和y = A cos(ωt +φ)．求在φ = 0，φ = 30º，及φ = 90º这三种情况下，电子在荧光屏上的轨迹方程．[解答]根据公式，其中Δφ = φ2 – φ1 = -π/2，而φ1 = 0，φ2 = φ．（1）当Δφ = φ = 0时，可得，质点运动的轨道方程为y = x ，轨迹是一条直线．（2）当Δφ = φ = 30º时，可得质点的轨道方程， 即，轨迹是倾斜的椭圆．（3）当Δφ = φ = 90º时，可得， 即x 2 + y 2 = A 2，质点运动的轨迹为圆．4．20三个同方向、同频率的简谐振动为，，．222210.080.06x y +=22d d x x x F ma m t==20.08cos()6m t πωω=-+22d d y y y F ma m t==20.06cos()3m t ωω=--πi+j x y F F F =F =2222212122cos sin x y xyA A A A ϕϕ+-∆=∆2222220x y xyA A A+-=222214x y A+=222/4x y A +=22221x y A A +=10.08cos(314)6x t π=+20.08cos(314)2x t π=+350.08cos(314)6x t π=+求：（1）合振动的圆频率、振幅、初相及振动表达式； （2）合振动由初始位置运动到所需最短时间（A 为合振动振幅）． [解答]合振动的圆频率为：ω = 314 = 100π(rad·s -1)． 设A 0 = 0.08，根据公式得：A x = A 1cos φ1 + A 2cos φ2 + A 3cos φ3 = 0，A y = A 1sin φ1 + A 2sin φ2 + A 3sin φ3 = 2A 0 = 0.16(m)， 振幅为：，初位相为：φ = arctan(A y /A x ) = π/2．合振动的方程为：x = 0.16cos(100πt + π/2)．（2）当时，可得：，解得：100πt + π/2 = π/4或7π/4．由于t > 0，所以只能取第二个解，可得所需最短时间为t = 0.0125s ．x A =A =/2x =cos(100/2)2t ππ+。

第四章 流体力学#4－1如本题图，试由多管压力计中水银面高度的读数确定压力水箱中A 点的相对压强（P －P 0）。

（所有读数均自地面算起，其单位为米） 解：根据gh P ρ=得）－（汞7.08.103g P P ρ=- ）－（水7.0232g P P ρ-=-）－（汞9.0221g P P ρ=- ）－（－水9.05.21g P P ρ=- m g m g P P 9.22.20⨯⨯=-∴水汞－ρρ4－2如本题图，将一充满水银的气压计下端浸在一个广阔的盛水银的容器中，其读数为 -25m N 10950.0⋅⨯=p 。

（1）求水银柱的高度h 。

(2)考虑到毛细现象后，真正的大气压强0p 多大? 已知毛细管的直径m 100.23-⨯=d ，接触角π=θ，水银的表面张力系数-1m N 49.0⋅=σ。

解：（1）gh p ρ=cm g p h 3.716.138.910950.05≈⨯⨯==∴ρ（2）Pa d p p 43500106.9100.1cos 49.021095.02cos 2'⨯=⨯⨯+⨯=+=-πθσ 4－3灭火筒每分钟喷出60m 3的水，假定喷口处水柱的截面积为1.5cm 2，问水柱喷到2m 高时其截面积有多大？ 解：流量2211S v S v Q ==且 gh v v 22122-=-s m m s m S Q v /107.6105.16060324311⨯≈⨯==∴- 2212235.42cm ghv Q v Q S =-==4－4油箱内盛有水和石油，石油的密度为0.9g ／cm 3，水的厚度为1m ，油的厚度为4m 。

求水自箱底小孔流出的速度。

解：如图，流线上1、2点分别是油面和小孔处的两点。

根据伯努利方程水习题4－1图习题4－2图恒量=++p gh v ρρ221 得： 水水水油油gh v gh ρρρ-=221s m h h g v /5.9)(2≈+=∴水油水油ρρ 4－5一截面为5.0cm 2的均匀虹吸管从容积很大的容器中把水吸出。

第四章 刚体的定轴转动4–1 半径为20cm 的主动轮，通过皮带拖动半径为50cm 的被动轮转动，皮带与轮之间无相对滑动，主动轮从静止开始作匀角加速度转动，在4s 内被动轮的角速度达到π/s 8，则主动轮在这段时间内转过了 圈。

解：被动轮边缘上一点的线速度为 πm/s 45.0π8222=⨯==r ωv在4s 内主动轮的角速度为πrad/s 202.0π412111====r r v v ω 主动轮的角速度为2011πrad/s 540π2==∆-=t ωωα 在4s 内主动轮转过圈数为20π520ππ2(π212π212121=⨯==αωN （圈） 4–2绕定轴转动的飞轮均匀地减速，t ＝0时角速度为0ω＝5rad/s ，t ＝20s 时角速度为08.0ωω=，则飞轮的角加速度α＝ ，t ＝0到t ＝100s 时间内飞轮所转过的角度θ＝ 。

解：由于飞轮作匀变速转动，故飞轮的角加速度为20s /rad 05.020558.0-=-⨯=-=t ωωα t ＝0到t ＝100s 时间内飞轮所转过的角度为 rad 250100)05.0(21100521220=⨯-⨯+⨯=+=t t αωθ 4–3 转动惯量是物体 量度，决定刚体的转动惯量的因素有 。

解：转动惯性大小，刚体的形状、质量分布及转轴的位置。

4–4 如图4-1，在轻杆的b 处与3b 处各系质量为2m 和m 的质点，可绕O 轴转动，则质点系的转动惯量为 。

解：由分离质点的转动惯量的定义得 221i i i r m J ∆=∑=22)3(2b m mb +=211mb = 4–5 一飞轮以600r/min 的转速旋转，转动惯量为2.5kg·m 2，现加一恒定的制动力矩使飞轮在1s 内停止转动，则该恒定制动力矩的大小M ＝_________。

解：飞轮的角加速度为20s /rad 20160/π26000-=⨯-=-=t ωωα 制动力矩的大小为 m N π50π)20(5.2⋅-=-⨯==αJ M负号表示力矩为阻力矩。

思 考 题4.1 阿伏伽德罗定律指出：在温度和压强相同的条件下，相同体积中含有的分子数是相等的，与气体的种类无关。

试用气体动理论予以说明。

答： 据压强公式 p nkT = ，当压强和温度相同时，n 也相同，与气体种类无关； 4.2 对一定量的气体来说，当温度不变时，气体的压强随体积的减小而增大。

当体积不变时，压强随温度的升高而增大。

从微观角度看，两种情况有何区别。

答：气体压强是器壁单位面积上受到大量气体分子频繁地碰撞而产生的平均作用力的结果。

当温度不变时，若体积减小，分子数密度增大，单位时间内碰撞器壁的分子数增加，从而压强增大；而当体积不变时，若温度升高，分子的平均平动动能增大，分子碰撞器壁的力度变大，从而压强增大；4.3 从气体动理论的观点说明：（1）当气体的温度升高时，只要适当地增大容器的容积，就可使气体的压强保持不变。

（2）一定量理想气体在平衡态（p 1，V 1，T 1）时的热动平衡状况与它在另一平衡态（p 2，V 2，T 2）时相比有那些不同?设气体总分子数为N ，p 2< p 1，V 2< V 1。

（3）气体在平衡状态下，则222213x y z v v v v ===， 0x y z v v v ===。

(式中x v 、y v 、z v ，是气体分子速度v 的三个分量)。

答：（1）由p nkT = 可知，温度升高时，n 适当地减小，可使压强不变；（2） 在平衡态（2p ，2V ,2T ）时分子的平均平动动能较在平衡态（1p ，1V ，1T ）时小，但分子数密度较大；（3） 因分子向各方向运动的概率相同，并且频繁的碰撞，速度的平均值为零，速度平方的平均值大小反映平均平动动能的大小，所以各分量平方平均值相等；4.4 有人说“在相同温度下，不同气体分子的平均平动动能相等，氧分子的质量比氢分子的大，所以氢分子的速率一定比氧分子大”。

这样讲对吗？答：不对，只能说氢分子的速率平方平均值比氧分子的大。

实验四、波器及其应用1．在示波器状况良好的情况下，荧光屏看不见亮点，怎样才能找到亮点显示的图形不清晰怎么办首先将亮点旋钮调至适中位置,不宜过大,否则损坏荧光屏，也不宜聚焦。

在示波器面板上关掉扫描信号后（如按下x－y键），调节上下位移键或左右位移键。

调整聚焦旋钮，可使图形更清晰。

2．如果正弦电压信号从Y轴输入示波器，荧光屏上要看到正弦波，却只显示一条铅直或水平直线，应该怎样调节才能显示出正弦波如果是铅直直线，则试检查x方向是否有信号输入。

如x－y键是否弹出，或者（t/div）扫描速率是否在用。

如果是水平直线，则试检查y方向是否信号输入正常。

如（v/div）衰减器是否打到足够档位。

3.观察正弦波图形时，波形不稳定时如何调节调节（t/div）扫描速率旋钮及（variable)扫描微调旋钮，以及（trig level)触发电平旋钮。

4.观察李萨如图形时，如果只看到铅直或水平直线的处理方法因为李萨如图形是由示波器x方向的正弦波信号和y方向的正弦波信号合成。

所以，试检查CH1通道中的（v/div)衰减器旋钮或CH2通道中的（v/div)衰减器旋钮。

5.用示波器测量待测信号电压的峰－峰值时，如何准确从示波器屏幕上读数在读格数前，应使“垂直微调”旋到CAL处。

建议用上下位移（position)旋钮将正弦波的波峰或波谷对齐某一横格再数格数，就不会两头数格时出现太大的误差。

6.用示波器怎样进行时间（周期）的测量在读格数前，应使“垂直微调”旋到CAL处。

根据屏幕上x轴坐标刻度，读得一个周期始末两点间得水平距离（多少div),如果t/div档示值为div，则周期＝水平距离（div）×div。

7.李萨如图形不稳定怎么办调节y方向信号的频率使图形稳定。

实验六、霍尔效应（Hall Effect）1、实验过程中导线均接好，开关合上，但Vh无示数，Im和Is示数正常,为什么（1）Vh组的导线可能接触不良或已断。

仔细检查导线与开关连接以及导线是否完好正常。

第四章 气体动理论一、基本要求1．理解平衡态的概念。

2．了解气体分子热运动图像和理想气体分子的微观模型，能从宏观和统计意义上理解压强、温度、内能等概念。

3．初步掌握气体动理论的研究方法，了解系统的宏观性质是微观运动的统计表现。

4．理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义，理解气体分子运动的最概然速率、平均速率、方均根速率的意义，了解玻尔兹曼能量分布律。

5．理解能量按自由度均分定理及内能的概念，会用能量均分定理计算理想气体的内能。

6．了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。

二、基本内容1. 平衡态在不受外界影响的条件下，一个系统的宏观性质不随时间改变的状态。

2. 理想气体状态方程在平衡态下，理想气体各参量之间满足关系式pV vRT =或 n k T p =式中v 为气体摩尔数，R 为摩尔气体常量 118.31R J mol K --=⋅⋅，k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质，在微观统计上32t kT ε=5. 能量均分定理在平衡态下，分子热运动的每个自由度的平均动能都相等，且等于2kT 。

以i 表示分子热运动的总自由度，则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p =≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间（粒子能量为ε）的粒子数正比于kT e /ε-。

重力场中粒子数密度按高度的分布（温度均匀）：kT m gh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型，对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=， 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触，经过足够长的时间后，系统也可以达到一个宏观性质不随时间变化的状态。

第4章 刚体的定轴转动习 题一 选择题4-1 有两个力作用在一个有固定转轴的刚体下，对此有以下几种说法：（1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零；（2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；(3）当这两个力的合力为零时，它们对轴的合力矩也一定是零；（4）当这两个力对轴的合力矩为零时，它们的合力也一定是零．对L 述说法下述判断正确的是[ ]（A ）只有（l ）是正确的 （B ）（1）、（2）正确，（3）、（4）错误 （C ）(1)、（2）、（3）都正确 （D ）（1）、（2）、（3）、（4）都正确 解析：力矩是描述力对刚体转动的作用，=⨯M r F 。

因此合力为零时，合力矩不一定为零；合力矩为零时，合力也不一定为零。

两者并没有一一对应的关系。

答案选B 。

4-2 有A 、B 两半径相同，质量相同的细圆环。

A 环的质量均匀分布，B 环的质量不均匀分布，设它们对过环心的中心轴的转动惯量分别为A I 和B I ，则有[ ]（A ）A B I I > （B ）A B I I < （C ）无法确定哪个大 （D ）A B I I = 解析：转动惯量2i i iI m r =∆∑，由于A 、B 两细圆环半径相同，质量相同，所以转动惯量相同2A B I I mR ==，而与质量分布均匀与否无关。

选D 。

4-3 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图4-3所示．今使棒从水平位置由静止开始自由下落，在棒摆到竖直位置的过程中，下述说法正确的是[ ]（A ）角速度从小到大，角加速度不变 （B ）角速度从小到大，角加速度从小到大（C ）角速度从小到大，角加速度从大到小 （D ）角速度不变，角加速度为零解析：在棒摆到竖直位置的过程中，重力势能和转动动能相互转化，因此转速越来越大，即角速度从小到大。

整个过程中棒只受到重力矩的作用，211cos 23M mg l J ml θαα===，所以3cos 2gl αθ=，随着转角θ逐渐增大，角加速度α由大变小。

第四章 动量守恒定律与能量守恒定律4-1 用锤压钉，很难把钉子压入木块，如果用锤击钉，钉子就很容易进入木块。

这是为什么？答：要将钉子压入木块中，受到木块的阻力是很大的，仅靠锤压钉子上面的重量远远不够，只有挥动锤子，使锤子在极短的时间内速度从很大突然变为零，在这过程中可获得较大的冲量，即:0F t mv =-又因为t 很短，所以可获得很大的冲力，这样才足以克服木块的阻力，将钉子打进木块中去。

4-2 一人躺在地上，身上压一块重石板，另一人用重锤猛击石板，但见石板碎裂，而下面的人毫无损伤。

何故？答：石板受击所受到的冲量很大，亦即)(v m d p d dt F ==很大。

但是，由于石板的质量m 很大，所以，石板的速度变化并不大。

又因为用重锤猛击石板时，冲击力F 很大，此力作用于石板，易击碎石板；但是，由于石板的面积很大，故作用于人体单位面积上的力并不大，所以下面的人毫无损伤。

4-3 两个质量相同的物体从同一高度自由下落，与水平地面相碰，一个反弹回去，另一个却贴在地上，问哪一个物体给地面的冲击较大？答：贴地：00)(0mv mv t F =--=∆反弹：)()(00v v m mv mv t F +=--=∆'F F >'∴，则反弹回去的物体对地面冲击大。

4-4 两个物体分别系在跨过一个定滑轮的轻绳两端。

若把两物体和绳视为一个系统，哪些力是外力？哪些力是内力？答：取系统21,m m 和绳，内力：2211,;,T T T T ''外力：g m g m 21,，绳与滑轮摩擦力f ，滑轮对绳支持力N 。

4-5 在系统的动量变化中内力起什么作用？有人说：因为内力不改变系统的动量，所以不论系统内各质点有无内力作用，只要外力相同，则各质点的运动情况就相同。

这话对吗？答：这话是错的。

由质点系动量定理21t ex t F dt p =⎰可知，在系统动量变化中，外力改变系统的动量，内力不改变系统的动量；但内力改变各质点的动量，所以各质点的运动情况就不相同。

⼤学物理学（第三版）第四章课后答案解析（主编）赵近芳习题44.1 选择题（1）在⼀惯性系中观测，两个事件同时不同地，则在其他惯性系中观测，他们[ ]。

（A）⼀定同时（B）可能同时（C）不可能同时，但可能同地（D）不可能同时，也不可能同地[答案：D ]（2）在⼀惯性系中观测，两个事件同地不同时，则在其他惯性系中观测，他们[ ]。

（A）⼀定同地（B）可能同地（C）不可能同地，但可能同时（D）不可能同地，也不可能同时[答案：D ]（3）宇宙飞船相对于地⾯以速度v作匀速直线飞⾏，某⼀时刻飞船头部的宇航员向飞船尾部发出⼀个光讯号，经过t?（飞船上的钟）时间后，被尾部的接收器收到，则由此可知飞船的固有长度为（c表⽰真空中光速）[ ]。

（A）c t??（B）v t??（C（D）c t[答案：A ]（4）⼀宇航员要到离地球5光年的星球去旅⾏。

如果宇航员希望把这路程缩短为3光年，则他所乘的⽕箭相对于地球的速度v应为[ ]。

（A）0.5c （B）0.6c（C）0.8c （D）0.9c[答案：C ]（5）某宇宙飞船以0.8c的速度离开地球，若地球上测到它发出的两个信号之间的时间间隔为10s。

则宇航员测出的相应的时间间隔为[ ]。

（A）6s （B）8s（C）10s （D）10/3s[答案：A ]4.2 填空题（1）有⼀速度为ｕ的宇宙飞船沿Ｘ轴正⽅向飞⾏，飞船头尾各有⼀个脉冲光源在⼯作，处于船尾的观察者测得船头光源发出的光脉冲的传播速度⼤⼩为_________；处于船头的观察者测得船尾光源发出的光脉冲的传播速度⼤⼩为__________。

[答案：c ，c ； ]S 系相对S 系沿x 轴匀速运动的速度为0.8c ，在'S 中观测，两个事件的时间间隔'7510t s -?=?，空间间隔是'120x m ?=-，则在S 系中测得的两事件的空间间隔x ?= ，时间间隔t ?= 。

[答案：0，7310s -? ]（3）⽤v 表⽰物体的速度，则当v c = 时，02m m =；vc= 时，0k E E =。

第四章 习题解答（仅供参考）4．3 如图所示，质量为10g 的子弹以速度v = 103m·s -1水平射入木块，并陷入木块中，使弹簧压缩而作简谐振动．设弹簧的倔强系数k = 8×103N·m -1，木块的质量为4.99kg ，不计桌面摩擦，试求：（1）振动的振幅； （2）振动方程．[解答]（1）子弹射入木块时，由于时间很短，木块还来不及运动，弹簧没有被压缩，它们的动量守恒，即mv = (m + M )v 0． 解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m·s -1)， 这也是它们振动的初速度．子弹和木块压缩弹簧的过程机械能守恒，可得 (m + M ) v 02/2 = kA 2/2， 所以振幅为A v =10-2(m)． （2）振动的圆频率为ω=s -1)．取木块静止的位置为原点、向右的方向为位移x 的正方向，振动方程可设为x = A cos(ωt + φ)．当t = 0时，x = 0，可得 φ = ±π/2；由于速度为正，所以取负的初位相，因此振动方程为 x = 5×10-2cos(40t - π/2)．4．4 如图所示，在倔强系数为k 的弹簧下，挂一质量为M 的托盘．质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞，而使其作简谐振动，设两物体碰后瞬时为t = 0时刻，求振动方程．[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后，根据动量守恒定律可得它们的共同速度为0m v v m M ==+，这也是它们振动的初速度．设振动方程为 x = A cos(ωt + φ)， 其中圆频率为ω=物体没有落下之前，托盘平衡时弹簧伸长为x 1，则x 1 = Mg/k ．物体与托盘磁盘之后，在新的平衡位置，弹簧伸长为x 2，则x 2 = (M + m )g/k ．图4.3图4.4取新的平衡位置为原点，取向下的方向为正，则它们振动的初位移为x0 = x1 - x2 = -mg/k．因此振幅为A===初位相为arctanvx ϕω-==4．14三个同方向、同频率的简谐振动为10.08cos(314)6x t π=+，20.08cos(314)2x t π=+，350.08c o s(314)6x t π=+．求：（1）合振动的圆频率、振幅、初相及振动表达式；（2）合振动由初始位置运动到x A=所需最短时间（A为合振动振幅）．[解答] 合振动的圆频率为ω = 314 = 100π(rad·s-1)．设A0 = 0.08，根据公式得A x = A1cosφ1 + A2cosφ2 + A3cosφ3 = 0，A y = A1sinφ1 + A2sinφ2 + A3sinφ3 = 2A0 = 0.16(m)，振幅为A=，初位相为φ = arctan(A y/A x) = π/2．合振动的方程为x = 0.16cos(100πt + π/2)．（2）当/2x=时，可得cos(100/2)2tππ+，解得100πt + π/2 = π/4或7π/4．由于t > 0，所以只能取第二个解，可得所需最短时间为t = 0.0125s．。