下载文档原格式
如何评估股票的价值
评估股票的价值是一个相对复杂的过程，需要分析多个因素。
以下是一个简要的股票价值评估的方法：
1.基本分析：基本分析是通过对公司的财务状况和业绩进行研
究来评估股票的价值。
主要的指标包括收入增长率、利润增长率、股息支付比率等。
分析这些指标可以帮助判断公司的盈利能力和成长潜力，从而评估其价值。
2.市盈率法：市盈率是衡量股票价格相对于每股收益的指标。
通过比较公司的市盈率与行业或市场的平均市盈率，可以判断股票是否被高估或低估。
通常来说，低市盈率意味着投资者可以较低的价格购买每单位的盈利，因此可能是较好的投资机会。
3.股息法：股息法是通过计算股票的股息和股息支付比率来评
估股票的价值。
股息是公司根据每股股数支付给股东的分红。
股息法假设股票的价值等于未来股息的现值，通常对于偏重于收益的投资者较为适用。
4.现金流量法：现金流量法是通过分析公司的自由现金流量来
确定股票的价值。
自由现金流量是指公司从经营活动中获得的可用于支付债务、投资和分红的现金。
通过折现自由现金流量，可以得出股票的内在价值。
5.技术分析：技术分析主要研究股票的图表和历史价格走势，
以确定价格的趋势和未来的走势。
技术分析的方法包括移动平均线、相对强弱指数、波动率等。
技术分析主要适用于短期交
易和投机行为，对于长期投资价值评估的有效性较低。
综上所述，评估股票的价值需要综合考虑基本分析、市盈率法、股息法、现金流量法和技术分析等多个因素。
通过对这些因素进行综合分析，可以帮助投资者更好地判断股票是否被高估或低估，并制定相应的投资策略。
第七章长期投资的评估一、填空题1.长期投资是企业短期投资以外的投资，通常指不准备随时变现，持有时间超过（1）一年的投资类型。
2.长期股权投资按投资的形式，又可分为和（3）直接投资和间接投资两类。
3.由于长期投资是以对其他企业享有的权益而存在的，因此，长期投资的评估主要是对（4）长期投资所代表的权益进行评估。
4.债券是政府、企业、银行等债务人为了筹集资金，按照法定程序发行、并向债权人承诺（5）于指定日期还本付息的有价证券。
5.股票评估与股票的（6）票面价格、发行价格及账面价格关系并不十分紧密，而与股票的（7）内在价格、（8）清算价格和市场价格有关。
6.在股市发育完全、股票交易比较正常的情况下，股票的（9）市场价格基本上可以作为评估股票的基本依据。
7.长期待摊费用是指企业已经支出，但（10）摊销期在1年以下（不含1年）的各项费用。
二、单项选择题1.非上市交易的债券和股票一般可采用（ C ）进行评估。
A.成本法B.市场法C.收益法D.清算价格法2.对于非控股长期投资评估基本上采用（C ）。
A.成本法B.市场法C.收益法D.清算价格法3.长期待摊费用能否作为评估对象在于它（ D ）。
A.是否已摊销B.摊销的具体方式C.能否变现D.能否带来经济效益4.到期一次性还本付息的债券其评估值一般为（C ）。
A.本金现值B.利息现值C.本金现值与利息现值之和D.本金现值与利息现值之差5.股票的清算价格是清算时（ C）。
A.公司的资产总额与企业股票总数的比值B.公司的资产总额与企业股票总数的比值再乘以-个折现系数C.公司的净资产与公司股票总数之比值D.公司的净资产总额与企业股票总数的比值再乘以一个折现系数6.上市交易的债券最适合运用（ B ）进行评估。
A.成本法B.市场法C.收益法D.价格指数法7.股票的内在价值属于股票的（B）。
A.账面价值B.理论价格C.无面值价值D.发行价格8.股票的未来收益的现值是（B）。
A.账面价值B.内在价值C.票面价值D.清算价值9.在股市发育不全、交易不规范的情况下，作为长期投资中的股票投资的评估值应以（C）为基本依据。
2015年注册会计师资格考试内部资料财务成本管理第七章 企业价值评估知识点：企业价值评估的对象● 详细描述：（一）含义企业价值评估的一般对象是企业整体的经济价值。
企业整体的经济价值是指企业作为一个整体的公平市场价值。
【提示】明确评估对象是“企业整体价值”还不够，还需要进一步明确是“哪一种”整体价值。
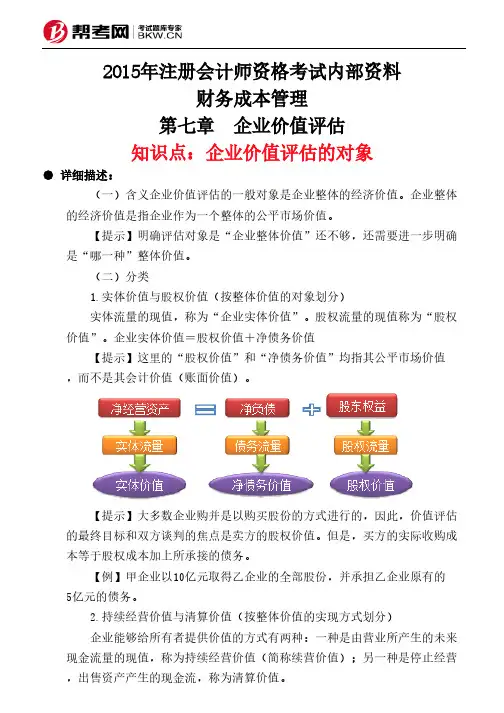
（二）分类 1.实体价值与股权价值（按整体价值的对象划分） 实体流量的现值，称为“企业实体价值”。
股权流量的现值称为“股权价值”。
企业实体价值＝股权价值＋净债务价值 【提示】这里的“股权价值”和“净债务价值”均指其公平市场价值，而不是其会计价值（账面价值）。
【提示】大多数企业购并是以购买股份的方式进行的，因此，价值评估的最终目标和双方谈判的焦点是卖方的股权价值。
但是，买方的实际收购成本等于股权成本加上所承接的债务。
【例】甲企业以10亿元取得乙企业的全部股份，并承担乙企业原有的5亿元的债务。
2.持续经营价值与清算价值（按整体价值的实现方式划分） 企业能够给所有者提供价值的方式有两种：一种是由营业所产生的未来现金流量的现值，称为持续经营价值（简称续营价值）；另一种是停止经营，出售资产产生的现金流，称为清算价值。
一个企业的公平市场价值，应当是续营价值与清算价值中较高的一个。
3.少数股权价值与控股权价值（按整体价值的实现前提划分）少数股权价值是在现有管理和战略条件下，企业能够给股票投资人带来的现金流量现值；控股权价值是企业进行重组，改进管理和经营战略后可以为投资人带来的未来现金流量的现值。
控股权价值与少数股权价值的差额称为控股权溢价，它是由于转变控股权而增加的价值。
控股权溢价＝V（新的）－V（当前） 【提示】在进行企业价值评估时，首先要明确拟评估的对象是什么，搞清楚是企业实体价值还是股权价值，是续营价值还是清算价值，是少数股权价值还是控股权价值。
例题：1.经济价值是经济学家所持的价值观念，下列有关表述不正确的是（）。
股票价值评估一、 股利折现模型威廉斯（Williams ，1938）提出了股利折现模型（Discounted dividend model ），认为股票价值等于未来股利的折现值，即股票价值为未来每年股利除以当年折现率之和，公式为：∑+=∞=+1)1(τττr d V t t . （1-1）V t = t 时间的股票价值d t+τ = t+τ时的股利r = 无风险报酬率该模型是确定性环境下的股票估值，而拓展到不确定的环境下后，模型演变为期望股利折现模型（present value of expected dividends ，PVED ）：∑∞=++=1)1()(τττr d E V t t t ， （1-2） （PVED ）E t = 根据T 期获得信息的期望算子r = 风险调整后的贴现率模型中预期的股利发放受股利政策影响，很难预测，为了增强模型的实用性，一般假定公司的股利政策不变并将公司的收益假设为稳定增长、两阶段增长或三阶段增长，使得对预期股利的度量转化为对预期收益的度量，后者更易预测且具有不同公司间的可比性。
模型代表的是一种“在手之鸟”的思想，即预期股利发放率越高，公司的价值就越大，若假定的“股利发放率”不同则模型有不同的结果。
而为了使模型具有实用价值，在实际应用中又不得不假定一个恒定的股利发放率，而这实际上是一种股利政策无关论的思想，这使得模型很难在理论与应用上找到一个平衡点。
单纯从实际应用的角度来说，股利折现模型也存在很多缺陷，公式的分子未来股利是一个不确定的值，取决于公司未来的经营业绩和股利政策：公司的经营业绩受多方面因素制约，在基期对多期间的收益进行合理估计并将其与风险相联系从而预计一个贴现率几乎是不可能的；股利政策由公司的管理层决定，它取决于公司的现金流量、投资计划、生命周期和管理层偏好，因而不可能是恒定不变的。
二、 自由现金流量折现模型为了克服预期股利的发放受股利政策的影响难以预测的弊端，科普兰和默瑞(Copleland and Murrin,1994）提出了自由现金流量折现模型，以股东所能获取的自由现金流量来替代股利，表达式为：1(1)t t t FCF V r ∞+τ+ττ==+∑ （1-3） t FCF +τ=属于股东的自由现金流量 将模型拓展到不确定性环境下，令t FCF +τ= cr t+τ-ci t+τ，则： V t = ∑∞=1τE t [cr t+τ-ci t+τ] / （1+r ）τ [PVCF] （1-4）E t = 根据T 期获得信息的期望算子r = 风险调整后的贴现率cr t =t 时期的现金流量ci t =t 时期的投资性支出式中cr t+τ-ci t+τ即为自由现金流量（free cash flow ），表示满足全部净现值为正的项目之后的剩余现金流量。
第一节期权的概述、类型和投资策略1、F股票的当前市价为100元，市场上有以该股票为标的物的期权交易，有关资料如下：（1）F股票的到期时间为1年的看跌期权，执行价格为100元，期权价格2.56元。
（2）F股票半年后市价的预测情况如下：投资者甲以当前市价购入1股F股票，同时购入F股票的1股看跌期权。
要求：（1）判断甲采取的是哪种投资策略；（2）计算该投资组合的预期收益。
【答案】【解析】（1）甲采取的是保护性看跌期权投资策略。
（2）投资组合预期收益计算如下：组合预期收益＝（－2.56）×0.2＋（－2.56）×0.3＋17.44×0.3＋47.44×0.2＝13.44（元）2、对于购买1份股票，同时购买该股票1份看跌期权组成的保护性看跌期权（执行价格为购买股票时股价），下列说法中正确的有（）。
A.组合最大净损失为期权价格B.组合最大净收益为期权价格C.股价大于执行价格组合净收益小于股票净收益D.股价大于执行价格组合净收益大于股票净收益【答案】AC【解析】股票净损益＝股价－股票购入价格，股价小于执行价格时，看跌期权净损益＝执行价格－股价－期权成本，即：组合净损益＝（股价－股票购入价格）＋（执行价格－股价－期权成本）＝执行价格－股票购入价格－期权成本，因此，执行价格等于股票购入价格时，组合净损益＝－期权成本，所以选项A正确，选项B错误；股价大于执行价格，看跌期权不执行，期权净收入=0，期权净损益=0-期权买价=0-期权价格，组合净损益=股票净损益+期权净损益=股票净损益-期权价格，所以选项C正确，选项D错误。
3、关于看跌期权多头净损益，下列表述正确的有（）。
A.净损失最大值为期权价格B.净损失最大值为期权价格与执行价格之和C.净收益最大值为执行价格与期权价格的差额D.净收益最大值为执行价格【答案】AC【解析】多头看跌期权净损益＝多头看跌期权到期日价值－期权成本，所以多头看跌期权净损益的最大值是当看跌期权到期日价值最大时，此时的最大净收益为执行价格－期权成本；多头看跌期权最大损失为不行权时，损失期权费，所以净损失最大值为期权价格。
如何评估股票的价值股票是金融市场中最受欢迎的投资品种之一，对于投资者而言，如何评估一只股票是否具有投资价值是非常关键的。
本文将从多个角度介绍如何评估股票的价值。
一、基本面分析基本面分析是评估股票价值的最基本方法之一。
基本面包括公司财务数据、经营指标、行业发展状况等。
投资者可以通过分析公司的盈利能力、偿债能力、资产负债状况等财务数据，来评估一家公司的健康程度。
此外，还可以通过分析公司的营收、净利润、毛利率、净资产收益率等经营指标，来了解公司的盈利水平和运营效率。
行业发展状况也是考虑一家公司价值的重要因素，如果所处行业景气度高，公司的成长性会更好。
二、股票估值方法股票估值方法包括P/E比、P/B比、PEG比等。
其中，P/E比是最常见的一种方法，它指的是市盈率，即股价与每股收益的比值，其计算公式为：市盈率=股价/每股收益。
一般而言，市盈率越低，投资价值越高。
但是，需要注意的是，不同行业、不同公司的市盈率也会有所差异，投资者需要对行业和公司进行比较再做决策。
三、技术分析技术分析是一种研究股票价格走势的方法，通过分析价格图形、交易量等数据，来预测未来股价走势。
技术分析包括趋势分析、形态分析、量价分析等。
其中，趋势分析是最基本的一种方法，它可以反映市场的主要方向和走势变化，有助于判断股价是处于上涨还是下跌状态。
四、风险评估风险评估是评估股票价值的重要组成部分，包括市场风险、行业风险、公司风险等。
市场风险指的是市场整体风险，通常反映在指数上，如上证指数、深证成指等。
行业风险指的是所处行业的风险，如果所处行业处于萎靡状态或者存在政策风险，公司投资价值会受到影响。
公司风险指的是公司本身的风险，如破产、财务丑闻等，会使公司的股价暴跌，投资者需要及时减仓或者抛售。
五、估值误差估值误差是指股票估值结果与实际价值存在偏差的情况，其中包括估值过高或者过低。
估值过高意味着投资者可能买入了一只高估的股票，而估值过低则意味着股票可能被低估了。
股票价值评估方法(完整版)股票价值评估方法评估股票价值的方法主要有三种：1.市盈率法：市盈率是指公司市值与其净利润之间的比值，这种方法适用于有稳定盈利的公司。
2.市净率法：市净率是指公司市值与其净资产之间的比值，这种方法适用于有固定资产的公司。
3.资产重估法：资产重估法是指对公司资产进行重新评估，从而得出新的价值。
这种方法一般适用于对公司进行重新评估或者公司资产发生重大变化时。
股票价值评估方法分析股票价值评估方法通常包括绝对投资方法和相对投资方法。
绝对投资方法是通过计算股票的内在价值来评估股票的价值。
这个价值通常是通过对公司未来的预期收益和折现率来估计。
绝对投资方法包括现金流折现法、资本金计算法、剩余收益法等方法。
这些方法的优点是可以充分考虑公司的未来收益和风险，并且不受市场波动的影响。
但是，绝对投资方法需要预测公司的未来收益，而这些预测通常是基于假设和估计，因此可能存在误差。
相对投资方法是通过比较类似的公司或者股票市场指数来评估股票的价值。
相对投资方法包括市盈率法、市净率法、市盈增长率法等方法。
这些方法的优点是简单易用，并且不需要预测公司的未来收益，但是它们可能受到市场波动的影响，并且可能低估或者高估股票的价值。
在选择股票价值评估方法时，应该根据评估的目的、公司的特点以及市场情况来选择。
例如，如果需要评估公司的长期价值，那么绝对投资方法可能更合适；如果需要评估股票的市场表现，那么相对投资方法可能更合适。
股票价值评估方法有哪些股票价值评估方法有以下几种：1.直接法：包括现金流量折现法和利润折现法。
前者以公司未来的净现金流量为依据折现其未来值；后者以公司未来所获得的净现金流量与公司的净收益为基础计算其未来值。
2.间接法：包括资本成本法和市场价值法。
前者以公司所承担的所有债务和优先股股本成本作为资本成本，如果公司发行普通股，则应以反映资本成本的资本成本收益率来计算公司投资资本成本，并据以确定股票的内在价值。
