结构化学 第三章习题(周公度)

【1.15】已知在一维势箱中粒子的归一化波函数为()n n x x l πϕ=1,2,3n =⋅⋅⋅ 式中l 是势箱的长度，x 是粒子的坐标)x l <，求粒子的能量，以及坐标、动量的平均值。

解：（1）将能量算符直接作用于波函数，所得常数即为粒子的能量：222n222h d n πx h d n πx ˆH ψ(x )-)-)8πm d x l 8πm d x l ==(sin )n n n x l l l πππ=⨯-22222222()88n h n n x n h x m l l ml ππψπ=-⨯= 即：2228n h E ml =（2）由于ˆˆx ()(),x n n x c x ψψ≠无本征值，只能求粒子坐标的平均值：()()x l x n sin l x l x n sin l x x ˆx x l *ln l*n d 22d x 000⎰⎰⎰⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==ππψψ()x l x n cos x l dx l x n sin x l l l d 22122002⎰⎰⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=ππ2000122sin sin d 222l l l x l n x l n x x x l n l n l ππππ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎣⎦⎰ 2l =（3）由于()()ˆˆp,p x n n x x c x ψψ≠无本征值。

按下式计算p x的平均值:()()1*ˆd x n x n p x px x ψψ=⎰0d 2n x ih d n x x l dx l πππ⎛=- ⎝⎰20sin cos d 0l nih n x n x x l l l ππ=-=⎰【1.20】若在下一离子中运动的π电子可用一维势箱近似表示其运动特征：估计这一势箱的长度 1.3l nm =，根据能级公式222/8n E n h ml =估算π电子跃迁时所吸收的光的波长，并与实验值510.0nm 比较。

【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kg υ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长： （a ）质量为10-10kg ，运动速度为0.01m·s -1的尘埃；（b ）动能为0.1eV 的中子； （c ）动能为300eV 的自由电子。

解：根据关系式： (1)34221016.62610J s6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅34-11 (2) 9.40310mh p λ-==⨯ 34(3) 7.0810mh p λ-==⨯【1.7】子弹（质量0.01kg ，速度1000m ·s -1），尘埃（质量10-9kg ，速度10m ·s -1）、作布郎运动的花粉（质量10-13kg ，速度1m ·s -1）、原子中电子（速度1000 m ·s -1）等，其速度的不确定度均为原速度的10%，判断在确定这些质点位置时，不确定度关系是否有实际意义？解：按测不准关系，诸粒子的坐标的不确定度分别为： 子弹：343416.2610 6.63100.01100010%h J sx mm v kg m s ---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃：3425916.62610 6.6310101010%h J sx m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉：34201316.62610 6.631010110%h J sx mm v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子：3463116.626107.27109.10910100010%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅ 【1.9】用不确定度关系说明光学光栅（周期约610m -）观察不到电子衍射（用100000V 电压加速电子）。

《结构化学》第三章习题答案3001 ( A, C )3002 H ab =∫ψa [-21∇2- a r 1 - br 1 +R 1 ] ψb d τ =E H S ab + R 1 S ab - ∫a r 1ψa ψb d τ= E H S ab + K因 E H = -13.6e V , S ab 为正值,故第一项为负值; 在分子的核间距条件下, K 为负值。

所以 H ab 为负值。

3003 ∫ψg ψu d τ=(4 - 4S 2)-1/2∫(ψa s 1+ψb s 1)((ψa s 1-ψb s 1)d τ = (4 - 4S 2)-1/2∫[ψa s 12 -ψb s 12 ] d τ= (4 - 4S 2)-1/2 [ 1 - 1 ] = 0故相互正交。

3004 ( C )3006 描述分子中单个电子空间运动状态的波函数叫分子轨道。

两个近似 (1) 波恩 - 奥本海默近似 ( 核质量 >> 电子质量 )(2) 单电子近似 (定态)3007 单个电子3008 (B)3009 (1) 能级高低相近(2) 对称性匹配(3) 轨道最大重叠3010 不正确3011 (B)3012 ψ= (0.8)1/2φA + (0.2)1/2φB3013 能量相近, 对称性匹配, 最大重叠> , < 或 < , >3014 正确3015 不正确3016 σ π π δ30173018 z3019 (C)3020 π3021 σ轨道: s -s , s -p z , s -d z , p z –p z , p z -2z d , 2z d -2z d ,π轨道p x –p x ,p x –d xz ,p y –p y ,p y –d yz ,d yz –d yz ,d xz –d xzδ轨道:d xy -d xy , d 22y x -- d 22y x -3022 σ δ π 不能 不能3023 (B)3024 原子轨道对 分子轨道p z -d xy ×p x -d xz πd 22y x -- d 22y x - δ2z d -2z d σp x –p x π3025 1σ22σ21π43σ2 , 3 , 反磁3026 d xy , δ3027 p y , d xy3028 C 2 ( 1σg )2( 1σu )2( 1πu )2+2 s -p 混杂显著.因1σu 为弱反键,而1σg 和1πu 均为强成键,故键级在2-3之间.3029 N 2: (1σg )2(1σu )2(1πu )4(2σg )2O 2: σ2s 2σ2s σ2pz 2π2px 2π2py 2π2px *π2py *1或 ( 1σg )2(1σu )22σg 2(1πu )4(1πg )23030 ( 1σg )2( 1σu )2( 1πu )4( 2σg )2的三重键为 1 个σ键 (1σg )2,2个π键 (1πu )4,键级为 3( 1σu )2和(2σg )2分别具有弱反键和弱成键性质, 实际上成为参加成键作用很小的两对孤对电子,可记为 :N ≡N: 。

习题1. CO 是一个极性较小的分子还是极性较大的分子？其偶极矩的方向如何？为什么？2. 下列AB型分子：N2，NO，O2，C2，F2，CN，CO，XeF中，哪几个是得电子变为AB–后比原来中性分子键能大？哪几个是失电子变为AB+ 后比原来中性分子键能大？3. 按分子轨道理论说明Cl2的键比Cl2+ 的键强还是弱？为什么？4. 下列分子中，键能比其正离子的键能小的是____________________ 。

键能比其负离子的键能小的是________________________ 。

O2，NO，CN，C2，F25. 比较下列各对分子和离子的键能大小：N2，N2+( )O2，O2+( )OF，OF–( )CF，CF+( )Cl2，Cl2+( )6. 写出O2+，O2，O2–和O22–的键级、键长长短次序及磁性。

7. 按分子轨道理论写出NF，NF+ 和NF–基态时的电子组态，说明它们的键级、不成对电子数和磁性。

8. 判断NO 和CO 哪一个的第一电离能小，原因是什么？9. HF分子以何种键结合？写出这个键的完全波函数。

10.试用分子轨道理论讨论SO分子的电子结构，说明基态时有几个不成对电子。

11.下列AB型分子：N2，NO，O2，C2，F2，CN，CO，XeF中，哪几个是得电子变为AB–后比原来中性分子键能大？哪几个是失电子变为AB+ 后比原来中性分子键能大？12.OH分子于1964年在星际空间被发现。

（a）试按分子轨道理论只用O原子的2 p轨道和H原子的1 s轨道叠加，写出其电子组态。

（b）在哪个分子轨道中有不成对电子？（c）此轨道是由O和H的原子轨道叠加形成，还是基本上定域于某个原子上？（d）已知OH的第一电离能为13.2eV，HF的第一电离能为16.05eV，它们的差值几乎与O原子和F原子的第一电离能（15.8eV和18.6eV）的差值相同，为什么？（e）写出它的基态光谱项。

13.试写出在价键理论中描述H2运动状态的、符合Pauli 原理的波函数，并区分其单态和三重态。

01.量子力学基础知识【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm，这是Li原子由电子组态(1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J·mol-1为单位的能量。

解：811412.99810m s4.46910s670.8mcνλ--⨯⋅===⨯【1.3】金属钾的临阈频率为5.464×10-14s-1，如用它作为光电极的阴极当用波长为300nm的紫外光照射该电池时，发射光电子的最大速度是多少？解：212hv hv mv =+【1.4】计算下列粒子的德布罗意波的波长：（a）质量为10-10kg，运动速度为0.01m·s-1的尘埃；（b）动能为0.1eV的中子；（c）动能为300eV的自由电子。

解：根据关系式：(1)34221016.62610J s6.62610m10kg0.01m shmvλ----⨯⋅===⨯⨯⋅【1.6】对一个运动速度cυ（光速）的自由粒子，有人进行了如下推导：结果得出12m mυυ=的结论。

上述推导错在何处？请说明理由。

解：微观粒子具有波性和粒性，两者的对立统一和相互制约可由下列关系式表达：式中，等号左边的物理量体现了粒性，等号右边的物理量体现了波性，而联系波性和粒性的纽带是Planck 常数。

根据上述两式及早为人们所熟知的力学公式：知①，②，④和⑤四步都是正确的。

微粒波的波长λ服从下式：式中，u是微粒的传播速度，它不等于微粒的运动速度υ，但③中用了/u vλ=，显然是错的。

在④中，E hv=无疑是正确的，这里的E是微粒的总能量。

若计及E中的势能，则⑤也不正确。

【1.7】子弹（质量0.01kg，速度1000m·s-1），尘埃（质量10-9kg，速度10m·s-1）、作布郎运动的花粉（质量10-13kg，速度1m·s-1）、原子中电子（速度1000 m·s-1）等，其速度的不确定度均为原速度的10%，判断在确定这些质点位置时，不确定度关系是否有实际意义？解：按测不准关系，诸粒子的坐标的不确定度分别为：子弹：343416.26106.63100.01100010%h J sx m m v kg m s---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃：3425916.626106.6310101010%h J sx m m v kg m s----⨯⋅∆===⨯⋅∆⨯⨯⋅花粉：34201316.62610 6.631010110%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⋅电子：3463116.626107.27109.10910100010%h J s x m m v kg m s ----⨯⋅∆===⨯⋅∆⨯⨯⨯⋅【1.8】电视机显象管中运动的电子，假定加速电压为1000V ，电子运动速度的不确定度υ∆为υ的10%，判断电子的波性对荧光屏上成像有无影响？解：在给定加速电压下，由不确定度关系所决定的电子坐标的不确定度为：34102/10%3.8810h x m m eV m mυ--==⨯==⨯这坐标不确定度对于电视机（即使目前世界上最小尺寸最小的袖珍电视机）荧光屏的大小来说，完全可以忽略。

姓名： 班级： 学号：3001 H 2+的H ˆ= 21∇2- a r 1 - b r 1 +R 1， 此种形式已采用了下列哪几种方法： ------------------------------ ( A C )(A) 波恩-奥本海默近似 (B) 单电子近似(C) 原子单位制 (D) 中心力场近似3002 分析 H 2+的交换积分(β积分) H ab 为负值的根据。

H ab =∫ψa [-21∇2- a r 1 - b r 1 +R 1 ] ψb d τ=E H S ab + R 1 S ab - ∫a r 1ψa ψb d τ = E H S ab + K 因 E H = -13.6e V , S ab 为正值,故第一项为负值; 在分子的核间距条件下, K 为负值。

所以 H ab 为负值3003 证明波函数()()()()b a b a ψψψψψψS S s 1s 121us 1s 121g 221221--=++=是相互正交的。

∫ψg ψu d τ=(4 - 4S 2)-1/2∫(ψa s 1+ψb s 1)((ψa s 1-ψb s 1)d τ = (4 - 4S 2)-1/2∫[ψa s 12 -ψb s 12 ] d τ = (4 - 4S 2)-1/2 [ 1 - 1 ] = 0 故相互正交3004 通过变分法计算得到的微观体系的能量总是：----------------- ( C )(A) 等于真实基态能量(B) 大于真实基态能量(C) 不小于真实基态能量(D) 小于真实基态能量3006 什么叫分子轨道？按量子力学基本原理做了哪些近似以后才有分子轨道的概念？ 这些近似的根据是什么？描述分子中单个电子空间运动状态的波函数叫分子轨道。

3个近似 (1) 波恩 - 奥本海默近似 (2) 非相对论近似(3) 单电子近似3007 描述分子中 ______单个电子_________ 空间运动状态的波函数称为分子轨道。

01.量子力学基础知识【】将锂在火焰上燃烧，放出红光，波长λ=，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。

解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯ 41711 1.49110cm 670.810cm νλ--===⨯⨯3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--==⨯⋅⨯⨯⨯⨯=⋅【】 实验测定金属钠的光电效应数据如下： 波长λ/nm光电子最大动能E k /10-19J 作“动能-频率”，从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。

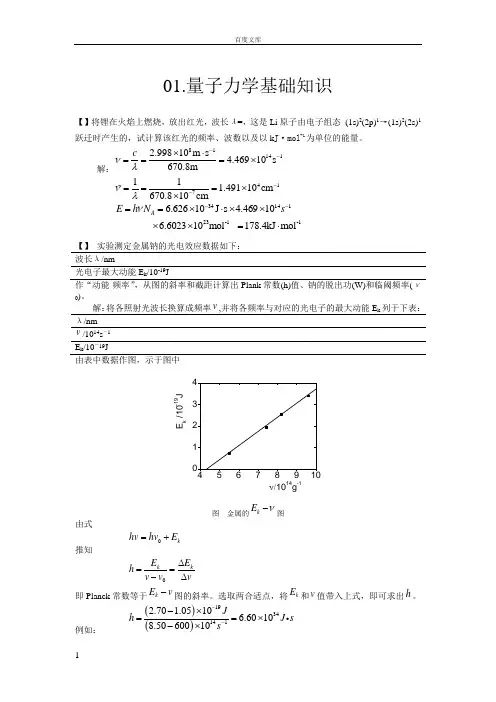
解：将各照射光波长换算成频率v ,并将各频率与对应的光电子的最大动能E k 列于下表： λ/nmv /1014s －1E k /10－19J由表中数据作图，示于图中4567891001234E k /10-19Jν/1014g-1图 金属的k E ν-图由式 0k hv hv E =+ 推知0k kE E h v v v ∆==-∆即Planck 常数等于kE v -图的斜率。

选取两合适点，将k E 和v 值带入上式，即可求出h 。

例如：()()19341412.70 1.0510 6.60108.5060010J h J ss ---⨯==⨯-⨯图中直线与横坐标的交点所代表的v 即金属的临界频率0v ，由图可知，1410 4.3610v s -=⨯。

因此，金属钠的脱出功为：341410196.6010 4.36102.8810W hv J s s J---==⨯⨯⨯=⨯【】金属钾的临阈频率为×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【】计算下列粒子的德布罗意波的波长： （a ） 质量为10-10kg ，运动速度为·s -1的尘埃； （b ） 动能为的中子；（c ） 动能为300eV 的自由电子。

【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。

解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯ 41711 1.49110cm670.810cm νλ--===⨯⨯3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--==⨯⋅⨯⨯⨯⨯=⋅【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长：（a ） 质量为10-10kg，运动速度为0.01m ·s -1的尘埃； （b ） 动能为0.1eV 的中子； （c ） 动能为300eV 的自由电子。

解：根据关系式：(1)34221016.62610J s 6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅ 34-11 (2) 9.40310mh p λ-====⨯3411(3) 7.0810mh p λ--====⨯【1.6】对一个运动速度c υ（光速）的自由粒子，有人进行了如下推导：1v vv v 2h h E m p m νλ=====①②③④⑤结果得出12m m υυ=的结论。

【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。

解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯ 41711 1.49110cm670.810cm νλ--===⨯⨯3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--==⨯⋅⨯⨯⨯⨯=⋅【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长：（a ） 质量为10-10kg，运动速度为0.01m ·s -1的尘埃； （b ） 动能为0.1eV 的中子； （c ） 动能为300eV 的自由电子。

解：根据关系式：(1)34221016.62610J s 6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅ 34-11 (2) 9.40310mh p λ-====⨯3411(3) 7.0810mh p λ--====⨯【1.6】对一个运动速度c υ（光速）的自由粒子，有人进行了如下推导：1v vv v 2h h E m p m νλ=====①②③④⑤结果得出12m m υυ=的结论。

结构化学基础第五版周公度答案目录01.量子力学基础知识 ...................................................................................................................... 1 02 原子的结构和性质 ................................................................................................................. 13 04分子的对称性 ............................................................................................................................ 48 05 多原子分子中的化学键 ........................................................................................................... 61 06配位化合物的结构和性质 ........................................................................................................ 91 07晶体的点阵结构和晶体的性质 .............................................................................................. 103 08金属的结构和性质 .................................................................................................................. 119 09离子化合物的结构化学 .......................................................................................................... 135 10次级键及超分子结构化学 (153)01.量子力学基础知识【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。

【】金属钾的临阈频率为×10-14s-1，如用它作为光电极的阴极当用波长为300nm的紫外光照射该电池时，发射光电子的最大速度是多少？解：【】计算下列粒子的德布罗意波的波长：（a）质量为10-10kg，运动速度为·s-1的尘埃；（b）动能为的中子；（c）动能为300eV的自由电子。

解：根据关系式：(1)【】子弹（质量，速度1000m·s-1），尘埃（质量10-9kg，速度10m·s-1）、作布郎运动的花粉（质量10-13kg，速度1m·s-1）、原子中电子（速度1000 m·s-1）等，其速度的不确定度均为原速度的10%，判断在确定这些质点位置时，不确定度关系是否有实际意义？解：按测不准关系，诸粒子的坐标的不确定度分别为：子弹：尘埃：花粉：电子：【】用不确定度关系说明光学光栅（周期约）观察不到电子衍射（用电压加速电子）。

解：解法一：根据不确定度关系，电子位置的不确定度为：这不确定度约为光学光栅周期的10－5倍，即在此加速电压条件下电子波的波长约为光学光栅周期的10－5倍，用光学光栅观察不到电子衍射。

解法二：若电子位置的不确定度为10－6m，则由不确定关系决定的动量不确定度为：在104V的加速电压下，电子的动量为：由Δp x和p x估算出现第一衍射极小值的偏离角为：这说明电子通过光栅狭缝后沿直线前进，落到同一个点上。

因此，用光学光栅观察不到电子衍射。

【】是算符的本征函数，求其本征值。

解：应用量子力学基本假设Ⅱ（算符）和Ⅲ（本征函数，本征值和本征方程）得：因此，本征值为。

【】和对算符是否为本征函数？若是，求出本征值。

解：，所以，是算符的本征函数，本征值为。

而所以不是算符的本征函数。

【】证明在一维势箱中运动的粒子的各个波函数互相正交。

证：在长度为的一维势箱中运动的粒子的波函数为：=1，2，3，……令n和n’表示不同的量子数，积分：和皆为正整数，因而和皆为正整数，所以积分：根据定义，和互相正交。

10次级键及超分子结构化学【10.1】在硫酸盐和硼酸盐中，24SO -和23BO -的构型分别为正四面体和平面正三角形，S O -键和B O -键的键长平均值分别为和，试计算S O -和B O -键的键价以及S 原子和B 原子的键价和。

解：将查得的0R 值和B 值数据代入计算价键的公式。

24SO -： 162.4148exp 1.4837pm pm S pm ⎡⎤-==⎢⎥⎣⎦S 原子的键价和为4 1.48 5.92⨯=。

此值和S 原子的氧化态6相近。

33BO -：137.1136.6exp 1.0137pm pm S pm ⎡⎤-==⎢⎥⎣⎦B 原子的键价和为3 1.01 3.03⨯=。

此值和B 原子的原子价3相近。

【10.2】2ClO -（弯曲形）、3ClO -（三角锥形）和4ClO -（四面体形）离子中，Cl O -键的平均键长值分别为157pm ，148pm 和142.5pm ，试分别计算其键价及键价和。

解：2ClO -： 171157exp 1.4637pm pm S pm ⎡⎤-==⎢⎥⎣⎦2ClO -中Cl 原子键价和为2 1.46 2.92⨯=和氧化态为3相近。

3ClO -： 167148exp 1.6737pm pm S pm ⎡⎤-==⎢⎥⎣⎦3ClO -中Cl 原子的键价和为3 1.67 5.01⨯=和氧化态为5相近。

4ClO -： 163.2142.5exp 1.7537pm pm S pm ⎡⎤-==⎢⎥⎣⎦4ClO -中Cl 原子的键价和为4 1.757.0⨯=和氧化态为7相近。

【10.3】试计算下列化合物已标明键长值的Xe F -键键价。

说明稀有气体Xe 原子在不同条件下和其他原子形成化学键的情况。

[按（7.1.3）式计算Xe F -键时0R 值为()2200Xe pm ，()4193Xe pm ，()6189Xe pm ，B 值为37pm ]。

（a ）XeF 2（直线形）： Xe-F200pm（b ）[][]236Xe F SbF +-：XeXe F FF210pm190pm151o+（c ）[][]2213NO Xe F +-：F 5XeFF XeF 6255pm-（d ）()[]26342,6F C H Xe BF +--⎡⎤⎣⎦：C CC CC C FHHHXe FBF 3279pm（e ）[][]45Me N XeF +-： 平面五角形的5XeF -离子中Xe F -202pm解： （a ）Xe F ：200200exp 1.0037pm pm S pm ⎡⎤-==⎢⎥⎣⎦ （b ）XeF ：200190exp 1.3137pm pm S pm ⎡⎤-==⎢⎥⎣⎦ XeF ：200214exp 0.6837pm pm S pm ⎡⎤-==⎢⎥⎣⎦ （c ）Xe F ：189255exp 0.1737pm pm S pm ⎡⎤-==⎢⎥⎣⎦ （d ）XeF ：200279exp 0.1237pm pm S pm ⎡⎤-==⎢⎥⎣⎦（e ）Xe F -：193202exp 0.7837pm pm S pm ⎡⎤-==⎢⎥⎣⎦Xe 和F 的范德华半径和为216pm ＋147pm=363pm 。

2. 写出HCN,CO2,H2O2,CH2=CH2和C6H6(苯)分子的对称元素以及所属点群。

解：
HCN：旋转轴反映面点群：C∞v
CO2: 对称中心i，反映面，旋转轴点群：D∞h
H2O2: 1条C2旋转轴，点群：C2
CH2=CH2:
3条C2旋转轴(其中与平面垂直的作为主轴) ，一个σh对称中心i 点群：D2h
C6H6: 6条C2旋转轴，1条C6旋转主轴，对称面σh对称中心i D6h
3. 写出ClHC=CHCl(反式)分子全部对称操作及其乘法表。

解：分子点群为C2h
对称操作：1条C2旋转轴，一个σh
乘法表：
4. 自己动手制作下列分子模型，找出它们的对称元素及所属分子点群，并指出它们是否有偶极矩和旋光性。

(1)CH2Cl2对称中心，C2对称轴，两个σv对称面点群：C2v 有偶极矩无旋光性
(2)CH2=CH-CH=CH2(反式) C2对称轴，σh点群：C2h 无偶极矩无旋光性
(3)OCS 无对称中心线形分子点群：C∞v有偶极矩和旋光性
(4)IF7(五角双锥) 对称中心，C5对称轴5个C2对称轴，1个σh对称面
点群：D5h 没有偶极矩和旋光性
(5)CH4对称元素：4个C3,3个C2，3个S4对称轴，对称中心，6个σd对称面
T d点群没有偶极矩和旋光性
(6)B2H6 对称中心，C2对称轴2个C2对称轴，1个σh对称面
点群：D2h 没有偶极矩和旋光性
(7)H3BO3(平面型) 对称中心，C3对称轴3个C2对称轴，1个σh对称面
点群：C3h 没有偶极矩和旋光性。

01.量子力学基础知识【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。

解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯41711 1.49110cm670.810cm νλ--===⨯⨯ 3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N s ν--==⨯⋅⨯⨯⨯⨯=⋅【1.2】 实验测定金属钠的光电效应数据如下：波长λ/nm 312.5365.0404.7546.1光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”，从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。

解：将各照射光波长换算成频率v ,并将各频率与对应的光电子的最大动能E k 列于下表：λ/nm 312.5 365.0 404.7 546.1v /1014s －19.59 8.21 7.41 5.49 E k /10－19J 3.412.561.95 0.75由表中数据作图，示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的k E ν-图由式 0k hv hv E =+ 推知0k kE E h v v v ∆==-∆即Planck 常数等于k E v -图的斜率。

选取两合适点，将k E 和v 值带入上式，即可求出h 。

例如：()()19341412.70 1.0510 6.60108.5060010J h J ss ---⨯==⨯-⨯图中直线与横坐标的交点所代表的v 即金属的临界频率0v ，由图可知，1410 4.3610v s -=⨯。

因此，金属钠的脱出功为：341410196.6010 4.36102.8810W hv J s s J---==⨯⨯⨯=⨯【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长：（a ） 质量为10-10kg ，运动速度为0.01m ·s -1的尘埃；（b ） 动能为0.1eV 的中子；（c ） 动能为300eV 的自由电子。