高中立体几何证明平行的专题训练
- 格式:docx
- 大小:295.26 KB
- 文档页数:2

立体几何线面平行垂直、面面平行垂直专题一、解答题(本大题共27小题,共324.0分)1.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.2.如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=AD,∠BAD=∠ABC=90°,E是PD的中点.BC=12(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.3.如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.(1)求证:AE⊥B1C;(2)求异面直线AE与A1C所成的角的大小;(3)若G为C1C中点,求二面角C-AG-E的正切值.4.如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=√6,AP=4AF.(Ⅰ)求证:PO⊥底面ABCD;(Ⅱ)求直线CP与平面BDF所成角的大小;(Ⅲ)在线段PB上是否存在一点M,使得CM∥平面BDF如果存在,求BM的值,如果不存在,请说明理BP由.5.如图,在直三棱柱ABC-A1B l C1中,AC=BC=√2,∠ACB=90°.AA1=2,D为AB的中点.(Ⅰ)求证:AC⊥BC1;(Ⅱ)求证:AC1∥平面B1CD:(Ⅲ)求异面直线AC1与B1C所成角的余弦值.6.如图,正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.7.如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=√6,AB=4.(1)求证:M为PB的中点;(2)求二面角B-PD-A的大小;(3)求直线MC与平面BDP所成角的正弦值.8.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=√3,三棱锥P-ABD的体积V=√3,求A到平面PBC的距4离.9.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(Ⅰ)证明:BE⊥DC;(Ⅱ)求直线BE与平面PBD所成角的正弦值;(Ⅲ)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.10.如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.11.如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.(I)求证:EM⊥AD;(II)求证:MN∥平面ADE;(III)求点A到平面BCE的距离.12.已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2.(Ⅰ)求证:平面EBD⊥平面BCF;(Ⅱ)求点B到平面ECD的距离.13.如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.(1)求证:EF∥平面PAD;(2)求证:平面AEF⊥平面PAB;(3)设AB=√2AD,求直线AC与平面AEF所成角θ的正弦值.14.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45∘,AD=AC=2,O为AC的中点,PO⊥平面ABCD且PO=6,M为BD的中点.(1)证明:AD⊥平面PAC;(2)求直线AM与平面ABCD所成角的正切值.15.如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=√2,点D为A1C1的中点.(I)求证:BC1∥平面AB1D;(II)求证:A1C⊥平面AB1D;(Ⅲ)求异面直线AD与BC1所成角的大小.16.如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.(Ⅰ)求证:BD⊥平面APQ;(Ⅱ)求直线PB与平面PDQ所成角的正弦值.17.如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.(1)求证:A1C⊥平面C1EB;(2)求直线CC1与平面ABC所成角的余弦值.18.如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AB=6,BC=2√3,AC=2√6,D为线段AB上的点,且AD=2DB,PD⊥AC.(1)求证:PD⊥平面ABC;,求点B到平面PAC的距离.(2)若∠PAB=π419.如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC为正三角形,D是BC边的中点,AA1=AB=1.(1)求证:平面ADB1⊥平面BB1C1C;(2)求点B到平面ADB1的距离.20.如图,在三棱锥P-ABC中,点D,E,F分别为棱PC,AC,AB的中点,已知PA⊥平面ABC,AB⊥BC,且AB=BC.(1)求证:平面BED⊥平面PAC;(2)求二面角F-DE-B的大小;(3)若PA=6,DF=5,求PC与平面PAB所成角的正切值.21.如图,在四棱锥P—ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2√2.(1)证明PA∥平面BDE;(2)证明AC⊥平面PBD;(3)求直线BC与平面PBD所成的角的正切值.22.如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.(Ⅰ)若M为CD中点,求证:AM⊥平面AA1B1B;(Ⅱ)求直线DD1与平面A1BD所成角的正弦值.=√2.23.如图,在直三棱柱ABC−A1B1C1中,∠ACB=90°,E为A1C1的中点,CC1C1E(Ⅰ)证明:CE⊥平面AB1C1;(Ⅱ)若AA1=√6,∠BAC=30°,求点E到平面AB1C的距离.24.如图,在四棱锥E-ABCD中,底面ABCD是边长为√2的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.(Ⅰ)求证:BE∥平面ACF;(Ⅱ)求证:CD⊥DE;(Ⅲ)求FC与平面ABCD所成角的正弦值.25.已知:平行四边形ABCD中,∠DAB=45°,AB=√2AD=2√2,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=√2,M为线段BC的中点.(1)求证:直线MF∥平面BED;(2)求证:平面BED⊥平面EAD;(3)求直线BF与平面BED所成角的正弦值.26.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=√2,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AC=√2,AB=BC=1,E为AD中点.(Ⅰ)求证:PE⊥平面ABCD;(Ⅱ)求异面直线PB与CD所成角的余弦值;(Ⅲ)求平面PAB与平面PCD所成的二面角.27.如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.答案和解析1.【答案】(1)证明:法一、如图,取PB 中点G ,连接AG ,NG ,∵N 为PC 的中点, ∴NG ∥BC ,且NG =12BC ,又AM =23AD =2,BC =4,且AD ∥BC , ∴AM ∥BC ,且AM =12BC ,则NG ∥AM ,且NG =AM ,∴四边形AMNG 为平行四边形,则NM ∥AG , ∵AG ⊂平面PAB ,NM ⊄平面PAB , ∴MN ∥平面PAB ; 法二、在△PAC 中,过N 作NE ⊥AC ,垂足为E ,连接ME , 在△ABC 中,由已知AB =AC =3,BC =4,得cos ∠ACB =42+32−322×4×3=23,∵AD ∥BC ,∴cos ∠EAM =23,则sin ∠EAM =√53,在△EAM 中,∵AM =23AD =2,AE =12AC =32,由余弦定理得:EM =√AE 2+AM 2−2AE ⋅AM ⋅cos∠EAM =√94+4−2×32×2×23=32,∴cos ∠AEM =(32)2+(32)2−42×32×32=19,而在△ABC 中,cos ∠BAC =32+32−422×3×3=19,∴cos ∠AEM =cos ∠BAC ,即∠AEM =∠BAC , ∴AB ∥EM ,则EM ∥平面PAB .由PA ⊥底面ABCD ,得PA ⊥AC ,又NE ⊥AC , ∴NE ∥PA ,则NE ∥平面PAB . ∵NE ∩EM =E ,∴平面NEM ∥平面PAB ,则MN ∥平面PAB ;(2)解:在△AMC 中,由AM =2,AC =3,cos ∠MAC =23,得CM 2=AC 2+AM 2-2AC •AM •cos ∠MAC =9+4−2×3×2×23=5.∴AM 2+MC 2=AC 2,则AM ⊥MC , ∵PA ⊥底面ABCD ,PA ⊂平面PAD ,∴平面ABCD ⊥平面PAD ,且平面ABCD ∩平面PAD =AD , ∴CM ⊥平面PAD ,则平面PNM ⊥平面PAD .在平面PAD 内,过A 作AF ⊥PM ,交PM 于F ,连接NF ,则∠ANF 为直线AN 与平面PMN 所成角.在Rt△PAC中,由N是PC的中点,得AN=12PC=12√PA2+PC2=52,在Rt△PAM中,由PA•AM=PM•AF,得AF=PA⋅AMPM =√42+22=4√55,∴sin∠ANF=AFAN =4√5552=8√525.∴直线AN与平面PMN所成角的正弦值为8√525.【解析】本题考查直线与平面平行的判定,考查直线与平面所成角的求法,考查数学转化思想方法,考查了空间想象能力和计算能力,是中档题.(1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG=12BC,再由已知得AM∥BC,且AM=12BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;法二、证明MN∥平面PAB,转化为证明平面NEM∥平面PAB,在△PAC中,过N作NE⊥AC,垂足为E,连接ME,由已知PA⊥底面ABCD,可得PA∥NE,通过求解直角三角形得到ME∥AB,由面面平行的判定可得平面NEM∥平面PAB,则结论得证;(2)由勾股定理得CM⊥AD,进一步得到平面PNM⊥平面PAD,在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.然后求解直角三角形可得直线AN与平面PMN所成角的正弦值.2.【答案】(1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,所以EF∥AD,EF=12AD,AB=BC=12AD,∠BAD=∠ABC=90°,∴BC∥AD,EF∥BC,EF=BC,∴四边形BCEF是平行四边形,可得CE∥BF,BF⊂平面PAB,CE⊄平面PAB,∴直线CE∥平面PAB;(2)解:如图所示,取AD中点O,连接PO,CO,由于△PAD为正三角形,则PO⊥AD,因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PO⊥平面ABCD,所以PO⊥CO. 因为AO=AB=BC=12AD,且∠BAD=∠ABC= 90∘,所以四边形ABCO是矩形,所以CO⊥AD,以O为原点,OC为x轴,OD为y轴,OP为z轴建立空间直角坐标系,不妨设AB=BC=12AD=1,则OA=OD=AB=CO=1.又因为△POC为直角三角形,|OC|=√33|OP|,所以∠PCO=60∘.作MN⊥CO,垂足为N,连接BN,因为PO ⊥CO ,所以MN //PO ,且PO ⊥平面ABCD ,所以MN ⊥平面ABCD ,所以∠MBN 即为直线BM 与平面ABCD 所成的角, 设CN =t ,因为∠PCO =60∘,所以MN =√3t ,BN =√BC 2+CN 2=√t 2+1. 因为∠MBN =45∘,所以MN =BN ,即√3t =√t 2+1,解得t =√22,所以ON =1−√22,MN =√62,所以A (0,−1,0),B (1,−1,0),M (1−√22,0,√62),D (0,1,0),则AB ⃗⃗⃗⃗⃗ =(1,0,0),AD⃗⃗⃗⃗⃗⃗ =(0,2,0),AM ⃗⃗⃗⃗⃗⃗ =(1−√22,1,√62). 设平面MAB 和平面DAB 的法向量分别为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1),n 2⃗⃗⃗⃗ =(x 2,y 2,z 2), 则{AB ⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0AM ⃗⃗⃗⃗⃗⃗ ·n 1⃗⃗⃗⃗ =0,即{x 1=0(1−√22)x 1+y 1+√62z 1=0, 可取z 1=−2,则n 1⃗⃗⃗⃗ =(0,√6,−2), 同理可得n 2⃗⃗⃗⃗ =(0,0,1),所以.因为二面角M -AB -D 是锐角,所以其余弦值为√105.【解析】本题考查直线与平面平行的判定定理的应用,空间向量求二面角夹角,考查空间想象能力以及计算能力,属于中档题.(1)取PA 的中点F ,连接EF ,BF ,通过证明CE ∥BF ,利用直线与平面平行的判定定理证明即可.(2)取AD 中点O ,连接PO ,CO ,作MN ⊥CO ,垂足为N ,以O 为原点,OC 为x 轴,OD 为y 轴,OP 为z 轴建立空间直角坐标系,即可求出二面角M -AB -D 的余弦值.3.【答案】证明:(1)因为BB 1⊥面ABC ,AE ⊂面ABC ,所以AE ⊥BB 1,由AB =AC ,E 为BC 的中点得到AE ⊥BC , ∵BC ∩BB 1=B ,BC 、BB 1⊂面BB 1C 1C , ∴AE ⊥面BB 1C 1C ,,∴AE ⊥B 1C ;解:(2)取B 1C 1的中点E 1,连A 1E 1,E 1C ,则AE ∥A 1E 1, ∴∠E 1A 1C 是异面直线AE 与A 1C 所成的角, 设AC =AB =AA 1=2,则由∠BAC =90°, 可得A 1E 1=AE =√2,A 1C =2√2,E 1C 1=EC =12BC =√2,∴E 1C =√E 1C 12+C 1C 2=√6,∵在△E 1A 1C 中,cos ∠E 1A 1C =2+8−62⋅√2⋅2√2=12, 所以异面直线AE 与A 1C 所成的角为π3;(3)连接AG ,设P 是AC 的中点,过点P 作PQ ⊥AG 于Q ,连EP ,EQ ,则EP ⊥AC ,又∵平面ABC ⊥平面ACC 1A 1,平面ABC ∩平面ACC 1A 1=AC ∴EP ⊥平面ACC 1A 1, 而PQ ⊥AG ∴EQ ⊥AG .∴∠PQE 是二面角C -AG -E 的平面角, 由(2)假设知:EP =1,AP =1, Rt △ACG ∽Rt △AQP ,PQ =CG·AP AG=1√5,故tan ∠PQE =PEPQ =√5,所以二面角C -AG -E 的平面角正切值是√5.【解析】本题考查异面直线的夹角,线线垂直的判定,属于中档题,熟练掌握线面垂直,线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义,是解答本题的关键,属于较难题.(1)由BB 1⊥面ABC 及线面垂直的性质可得AE ⊥BB 1,由AC =AB ,E 是BC 的中点,及等腰三角形三线合一,可得AE ⊥BC ,结合线面垂直的判定定理可证得AE ⊥面BB 1C 1C ,进而由线面垂直的性质得到AE ⊥B 1C ;(2)取B 1C 1的中点E 1,连A 1E 1,E 1C ,根据异面直线夹角定义可得,∠E 1A 1C 是异面直线A 与A 1C 所成的角,设AC =AB =AA 1=2,解三角形E 1A 1C 可得答案. (3)连接AG ,设P 是AC 的中点,过点P 作PQ ⊥AG 于Q ,连EP ,EQ ,则EP ⊥AC ,由直三棱锥的侧面与底面垂直,结合面面垂直的性质定理,可得EP ⊥平面ACC 1A 1,进而由二面角的定义可得∠PQE 是二面角C -AG -E 的平面角.4.【答案】(Ⅰ)证明:因为底面ABCD 是菱形,AC ∩BD =O ,所以O 为AC ,BD 中点.-------------------------------------(1分)又因为PA =PC ,PB =PD ,所以PO ⊥AC ,PO ⊥BD ,---------------------------------------(3分)所以PO ⊥底面ABCD .----------------------------------------(4分)(Ⅱ)解:由底面ABCD 是菱形可得AC ⊥BD , 又由(Ⅰ)可知PO ⊥AC ,PO ⊥BD .如图,以O 为原点建立空间直角坐标系O -xyz .由△PAC 是边长为2的等边三角形,PB =PD =√6,可得PO =√3,OB =OD =√3.所以A(1,0,0),C(−1,0,0),B(0,√3,0),P(0,0,√3).---------------------------------------(5分)所以CP ⃗⃗⃗⃗⃗ =(1,0,√3),AP ⃗⃗⃗⃗⃗ =(−1,0,√3). 由已知可得OF ⃗⃗⃗⃗⃗ =OA⃗⃗⃗⃗⃗ +14AP ⃗⃗⃗⃗⃗ =(34,0,√34)-----------------------------------------(6分) 设平面BDF 的法向量为n −=(x ,y ,z ),则{√3y =034x +√34z =0令x =1,则z =−√3,所以n ⃗ =(1,0,-√3).----------------------------------------(8分) 因为cos <CP ⃗⃗⃗⃗⃗ ,n ⃗ >=CP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗|CP ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=-12,----------------------------------------(9分) 所以直线CP 与平面BDF 所成角的正弦值为12,所以直线CP 与平面BDF 所成角的大小为30°.-----------------------------------------(10分)(Ⅲ)解:设BMBP =λ(0≤λ≤1),则CM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +λBP ⃗⃗⃗⃗⃗ =(1,√3(1−λ),√3λ).---------------------------------(11分)若使CM ∥平面BDF ,需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ,---------------------(12分) 解得λ=13∈[0,1],----------------------------------------(13分) 所以在线段PB 上存在一点M ,使得CM ∥平面BDF . 此时BM BP =13.-----------------------------------(14分)【解析】(Ⅰ)证明PO ⊥底面ABCD ,只需证明PO ⊥AC ,PO ⊥BD ;(Ⅱ)建立空间直角坐标系,求出直线CP 的方向向量,平面BDF 的法向量,利用向量的夹角公式可求直线CP 与平面BDF 所成角的大小;(Ⅲ)设BMBP =λ(0≤λ≤1),若使CM ∥平面BDF ,需且仅需CM −⋅n ⃗ =0且CM ⊄平面BDF ,即可得出结论.本题考查线面垂直,考查线面平行,考查线面角,考查向量知识的运用,正确求出向量的坐标是关键.5.【答案】解:(I )证明:∵CC 1⊥平面ABC ,AC ⊂平面ABC ,∠ACB =90°, ∴CC 1⊥AC ,AC ⊥BC ,又BC ∩CC 1=C ,∴AC ⊥平面BCC 1,BC 1⊂平面BCC 1, ∴AC ⊥BC 1.(II )证明:如图,设CB 1∩C 1B =E ,连接DE , ∵D 为AB 的中点,E 为C 1B 的中点,∴DE ∥AC 1, ∵DE ⊂平面B 1CD ,AC 1⊄平面B 1CD , ∴AC 1∥平面B 1CD .(III )解:由DE ∥AC 1,∠CED 为AC 1与B 1C 所成的角,在△CDE 中,DE =12AC 1=12√AC 2+CC 12=√62, CE =12B 1C =12√BC 2+BB 12=√62,CD =12AB =12√AC 2+BC 2=1,cos ∠CED =CE 2+DE 2−CD 22×CE×DE=32+32−12×√62×√62=23,∴异面直线AC 1与B 1C 所成角的余弦值为23.【解析】本题考查线线垂直的判定、线面平行的判定、异面直线及其所成的角. (I )先证线面垂直,再由线面垂直证明线线垂直即可; (II )作平行线,由线线平行证明线面平行即可;(III )先证明∠CED 为异面直线所成的角,再在三角形中利用余弦定理计算即可. 6.【答案】解:如图,在正三棱柱ABC -A 1B 1C 1中, 设AC ,A 1C 1的中点分别为O ,O 1, 则,OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,故以{OB ⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底, 建立空间直角坐标系O -xyz ,∵AB =AA 1=2,A (0,-1,0),B (√3,0,0), C (0,1,0),A 1(0,-1,2),B 1(√3,0,2),C 1(0,1,2).(1)点P 为A 1B 1的中点.∴P(√32,−12,2),∴BP ⃗⃗⃗⃗⃗ =(−√32,−12,2),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2). |cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=|−1+4|√5×2√2=3√1020.∴异面直线BP 与AC 1所成角的余弦值为:3√1020; (2)∵Q 为BC 的中点.∴Q (√32,12,0)∴AQ ⃗⃗⃗⃗⃗ =(√32,32,0),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2),设平面AQC 1的一个法向量为n⃗ =(x ,y ,z ), 由{AQ ⃗⃗⃗⃗⃗ ·n ⃗ =√32x +32y =0AC 1⃗⃗⃗⃗⃗⃗⃗ ·n⃗ =2y +2z =0,可取n⃗ =(√3,-1,1), 设直线CC 1与平面AQC 1所成角的正弦值为θ, sinθ=|cos|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n⃗ |=2√5×2=√55, ∴直线CC 1与平面AQC 1所成角的正弦值为√55.【解析】本题考查了向量法求空间角,属于中档题.设AC ,A 1C 1的中点分别为O ,O 1,以{OB ⃗⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底,建立空间直角坐标系O -xyz ,(1)由|cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗⃗ ⋅AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP ⃗⃗⃗⃗⃗⃗ |⋅|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |可得异面直线BP 与AC 1所成角的余弦值;(2)求得平面AQC 1的一个法向量为n⃗ ,设直线CC 1与平面AQC 1所成角的正弦值为θ,可得sinθ=|cos <CC 1⃗⃗⃗⃗⃗⃗⃗ ,n⃗ >|=|CC 1⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||CC 1⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |,即可得直线CC 1与平面AQC 1所成角的正弦值.7.【答案】(1)证明:如图,设AC ∩BD =O ,∵ABCD 为正方形,∴O 为BD 的中点,连接OM ,∵PD ∥平面MAC ,PD ⊂平面PBD ,平面PBD ∩平面AMC =OM , ∴PD ∥OM ,则BOBD =BM BP,即M 为PB 的中点;(2)解:取AD 中点G , ∵PA =PD ,∴PG ⊥AD ,∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD =AD , ∴PG ⊥平面ABCD ,则PG ⊥AD ,连接OG ,则PG ⊥OG ,由G 是AD 的中点,O 是AC 的中点,可得OG ∥DC ,则OG ⊥AD .以G 为坐标原点,分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系, 由PA =PD =√6,AB =4,得D (2,0,0),A (-2,0,0),P (0,0,√2),C (2,4,0),B (-2,4,0),M (-1,2,√22),DP ⃗⃗⃗⃗⃗ =(−2,0,√2),DB⃗⃗⃗⃗⃗⃗ =(−4,4,0). 设平面PBD 的一个法向量为m ⃗⃗⃗ =(x ,y ,z),则由{m ⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0,得{−2x +√2z =0−4x +4y =0,取z =√2,得m ⃗⃗⃗ =(1,1,√2). 取平面PAD 的一个法向量为n ⃗ =(0,1,0).∴cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗ |m ⃗⃗⃗ ||n ⃗⃗ |=12×1=12. ∴二面角B -PD -A 的大小为60°;(3)解:CM ⃗⃗⃗⃗⃗⃗ =(−3,−2,√22),平面BDP 的一个法向量为m ⃗⃗⃗ =(1,1,√2).∴直线MC 与平面BDP 所成角的正弦值为|cos <CM ⃗⃗⃗⃗⃗⃗ ,m ⃗⃗⃗ >|=|CM ⃗⃗⃗⃗⃗⃗⋅m ⃗⃗⃗|CM ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||=|−2√9+4+12×1|=2√69.【解析】本题考查线面角与面面角的求法,训练了利用空间向量求空间角,属中档题.(1)设AC ∩BD =O ,则O 为BD 的中点,连接OM ,利用线面平行的性质证明OM ∥PD ,再由平行线截线段成比例可得M 为PB 的中点;(2)取AD 中点G ,可得PG ⊥AD ,再由面面垂直的性质可得PG ⊥平面ABCD ,则PG ⊥AD ,连接OG ,则PG ⊥OG ,再证明OG ⊥AD .以G 为坐标原点,分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐标系,求出平面PBD 与平面PAD 的一个法向量,由两法向量所成角的大小可得二面角B -PD -A 的大小;(3)求出CM⃗⃗⃗⃗⃗⃗ 的坐标,由CM ⃗⃗⃗⃗⃗⃗ 与平面PBD 的法向量所成角的余弦值的绝对值可得直线MC 与平面BDP 所成角的正弦值.8.【答案】解:(Ⅰ)证明:设BD 与AC 的交点为O ,连结EO , ∵ABCD 是矩形, ∴O 为BD 的中点 ∵E 为PD 的中点, ∴EO ∥PB .EO ⊂平面AEC ,PB ⊄平面AEC ∴PB ∥平面AEC ;(Ⅱ)∵AP =1,AD =√3,三棱锥P -ABD 的体积V =√34,∴V =16PA ⋅AB ⋅AD =√36AB =√34,∴AB =32,PB =√1+(32)2=√132.作AH ⊥PB 交PB 于H , 由题意可知BC ⊥平面PAB , ∴BC ⊥AH ,故AH ⊥平面PBC .又在三角形PAB 中,由射影定理可得:AH =PA⋅AB PB=3√1313A 到平面PBC 的距离3√1313.【解析】本题考查直线与平面垂直,点到平面的距离的求法,考查空间想象能力以及计算能力.(Ⅰ)设BD 与AC 的交点为O ,连结EO ,通过直线与平面平行的判定定理证明PB ∥平面AEC ;(Ⅱ)通过AP =1,AD =√3,三棱锥P -ABD 的体积V =√34,求出AB ,作AH ⊥PB 角PB于H ,说明AH 就是A 到平面PBC 的距离.通过解三角形求解即可. 9.【答案】证明:(I )∵PA ⊥底面ABCD ,AD ⊥AB , 以A 为坐标原点,建立如图所示的空间直角坐标系,∵AD =DC =AP =2,AB =1,点E 为棱PC 的中点. ∴B (1,0,0),C (2,2,0),D (0,2,0), P (0,0,2),E (1,1,1)∴BE⃗⃗⃗⃗⃗ =(0,1,1),DC ⃗⃗⃗⃗⃗ =(2,0,0) ∵BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0, ∴BE ⊥DC ;(Ⅱ)∵BD ⃗⃗⃗⃗⃗⃗ =(-1,2,0),PB ⃗⃗⃗⃗⃗ =(1,0,-2),设平面PBD 的法向量m⃗⃗⃗ =(x ,y ,z ), 由{m ⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0m⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0,得{−x +2y =0x −2z =0, 令y =1,则m⃗⃗⃗ =(2,1,1), 则直线BE 与平面PBD 所成角θ满足: sinθ=m⃗⃗⃗ ⋅BE ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |⋅|BE ⃗⃗⃗⃗⃗⃗ |=2√6×√2=√33, 故直线BE 与平面PBD 所成角的正弦值为√33.(Ⅲ)∵BC⃗⃗⃗⃗⃗ =(1,2,0),CP ⃗⃗⃗⃗⃗ =(-2,-2,2),AC ⃗⃗⃗⃗⃗ =(2,2,0), 由F 点在棱PC 上,设CF⃗⃗⃗⃗⃗ =λCP ⃗⃗⃗⃗⃗ =(-2λ,-2λ,2λ)(0≤λ≤1), 故BF ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CF⃗⃗⃗⃗⃗ =(1-2λ,2-2λ,2λ)(0≤λ≤1), 由BF ⊥AC ,得BF ⃗⃗⃗⃗⃗ •AC ⃗⃗⃗⃗⃗ =2(1-2λ)+2(2-2λ)=0, 解得λ=34,即BF ⃗⃗⃗⃗⃗ =(-12,12,32), 设平面FBA 的法向量为n ⃗ =(a ,b ,c ), 由{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =0n ⃗ ⋅BF ⃗⃗⃗⃗⃗ =0,得{a =0−12a +12b +32c =0令c =1,则n⃗ =(0,-3,1), 取平面ABP 的法向量i =(0,1,0), 则二面角F -AB -P 的平面角α满足: cosα=|i ⋅n ⃗⃗ ||i|⋅|n ⃗⃗ |=3√10=3√1010,故二面角F -AB -P 的余弦值为:3√1010【解析】本题考查的知识点是空间二面角的平面角,建立空间直角坐标系,将二面角问题转化为向量夹角问题,是解答的关键.(I )以A 为坐标原点,建立空间直角坐标系,求出BE ,DC 的方向向量,根据BE ⃗⃗⃗⃗⃗ •DC ⃗⃗⃗⃗⃗ =0,可得BE ⊥DC ;(II )求出平面PBD 的一个法向量,代入向量夹角公式,可得直线BE 与平面PBD 所成角的正弦值;(Ⅲ)根据BF ⊥AC ,求出向量BF ⃗⃗⃗⃗⃗ 的坐标,进而求出平面FAB 和平面ABP 的法向量,代入向量夹角公式,可得二面角F -AB -P 的余弦值. 10.【答案】证明:(Ⅰ)取AD 的中点F ,连接EF ,CF ,∵E 为PD 的中点,∴EF ∥PA ,EF ∥平面PAB ,在四边形ABCD 中,BC ∥AD ,AD =2DC =2CB ,F 为中点,∴四边形CBAF 为平行四边形,故CF ∥AB ,CF ∥平面PAB ,∵CF ∩EF =F ,EF ∥平面PAB ,CF ∥平面PAB , ∴平面EFC ∥平面ABP , ∵EC ⊂平面EFC , ∴EC ∥平面PAB .解:(Ⅱ)连接BF ,过F 作FM ⊥PB 于M ,连接PF , ∵PA =PD ,∴PF ⊥AD ,∵DF ∥BC ,DF =BC ,CD ⊥AD ,∴四边形BCDF 为矩形,∴BF ⊥AD , 又AD ∥BC ,故PF ⊥BC ,BF ⊥BC ,又BF ∩PF =F ,BF 、PF ⊂平面PBF ,BC ⊄平面PBF , ∴BC ⊥平面PBF ,∴BC ⊥PB ,设DC =CB =1,由PC =AD =2DC =2CB ,得AD =PC =2, ∴PB =√PC 2−BC 2=√4−1=√3, BF =PF =1,∴MF =√12−(√32)2=12,又BC ⊥平面PBF ,∴BC ⊥MF ,又PB ∩BC =B ,PB 、BC ⊂平面PBC ,MF ⊄平面PBC , ∴MF ⊥平面PBC ,即点F 到平面PBC 的距离为12,∵MF =12,D 到平面PBC 的距离应该和MF 平行且相等,均为12, E 为PD 中点,E 到平面PBC 的垂足也为所在线段的中点,即中位线, ∴E 到平面PBC 的距离为14,在△PCD 中,PC =2,CD =1,PD =√2,,故由余弦定理得CE =√2, 设直线CE 与平面PBC 所成角为θ,则sinθ=14CE=√28.【解析】本题考查线面平行的证明,考查线面角的正弦值的求法,考查空间中线线、能力,考查数形结合思想、化归与转化思想,属于中档题.(Ⅰ)取AD的中点F,连结EF,CF,推导出EF∥PA,CF∥AB,从而平面EFC∥平面ABP,由此能证明EC∥平面PAB.(Ⅱ)连结BF,过F作FM⊥PB于M,连结PF,推导出四边形BCDF为矩形,从而BF⊥AD,进而AD⊥平面PBF,由AD∥BC,得BC⊥PB,再求出BC⊥MF,由此能求出sinθ.11.【答案】证明:(Ⅰ)∵EA=EB,M是AB的中点,∴EM⊥AB,∵平面ABE⊥平面ABCD,平面ABE∩平面ABCD=AB,EM⊂平面ABE,∴EM⊥平面ABCD,∵AD⊂平面ABCD,∴EM⊥AD;(Ⅱ)取DE的中点F,连接AF,NF,∵N是CE的中点,∴NF=//12CD,∵M是AB的中点,∴AM=//12CD,∴NF=//AM,∴四边形AMNF是平行四边形,∴MN∥AF,∵MN⊄平面ADE,AF⊂平面ADE,∴MN∥平面ADE;解:(III)设点A到平面BCE的距离为d,由(I)知ME⊥平面ABC,BC=BE=2,MC=ME=√3,则CE=√6,BN=√BE2−EN2=√102,∴S△BCE=12CE⋅BN=√152,S△ABC=12BA×BC×sin60°=√3,∵V A-BCE=V E-ABC,即13S△BCE×d=13S△ABC×ME,解得d=2√155,故点A到平面BCE的距离为2√155.【解析】本题考查线线垂直、线面平行的证明,考查点到平面的距离的求法,涉及到力、数据处理能力,考查数形结合思想,是中档题.(Ⅰ)推导出EM ⊥AB ,从而EM ⊥平面ABCD ,由此能证明EM ⊥AD ;(Ⅱ)取DE 的中点F ,连接AF ,NF ,推导出四边形AMNF 是平行四边形,从而MN ∥AF ,由此能证明MN ∥平面ADE ;(III )设点A 到平面BCE 的距离为d ,由V A -BCE =V E -ABC ,能求出点A 到平面BCE 的距离.12.【答案】(I )证明:∵AB ∥CD ,AD ⊥DC ,AB =AD =1,CD =2,∴BD =BC =√2, ∴BD 2+BC 2=CD 2, ∴BD ⊥BC ,∵EA ⊥平面ABCD ,BD ⊂平面ABCD , ∴EA ⊥BD ,∵EA ∥FC , ∴FC ⊥BD ,又BC ⊂平面BCF ,FC ⊂平面BCF ,BC ∩CF =C , ∴BD ⊥平面FBC , 又BD ⊂平面BDE ,∴平面BDE ⊥平面BCF .(II )解:过A 作AM ⊥DE ,垂足为M , ∵EA ⊥平面ABCD ,CD ⊂平面ABCD , ∴EA ⊥CD ,又CD ⊥AD ,EA ∩AD =A , ∴CD ⊥平面EAD ,又AM ⊂平面EAD , ∴AM ⊥CD ,又AM ⊥DE ,DE ∩CD =D , ∴AM ⊥平面CDE ,∵AD =AE =1,EA ⊥AD ,∴AM =√22,即A 到平面CDE 的距离为√22,∵AB ∥CD ,CD ⊂平面CDE ,AB ⊄平面CDE , ∴AB ∥平面CDE ,∴B 到平面CDE 的距离为√22.【解析】(I )先计算BD ,BC ,利用勾股定理的逆定理证明BD ⊥BC ,再利用EA ⊥平面ABCD 得出AE ⊥BD ,从而有CF ⊥BD ,故而推出BD ⊥平面FBC ,于是平面EBD ⊥平面BCF ;(II )证明AB ∥平面CDE ,于是B 到平面CDE 的距离等于A 到平面CDE 的距离,过A 作AM ⊥DE ,证明AM ⊥平面CDE ,于是AM 的长即为B 到平面CDE 的距离. 本题考查了线面垂直、面面垂直的判定与性质,空间距离的计算,属于中档题. 13.【答案】证明:方法一:(1)取PA 中点G ,连结DG 、FG . ∵F 是PB 的中点, ∴GF ∥AB 且GF =12AB ,又底面ABCD 为矩形,E 是DC 中点, ∴DE ∥AB 且DE =12AB∴GF ∥DE 且GF =DE ,∴EF ∥DG∵DG ⊂平面PAD ,EF ⊄平面PAD , ∴EF ∥平面PAD .(2)∵PD ⊥底面ABCD ,AB ⊂面ABCD ∴PD ⊥AB又底面ABCD 为矩形 ∴AD ⊥AB 又PD ∩AD =D ∴AB ⊥平面PAD ∵DG ⊂平面PAD ∴AB ⊥DG∵AD =PD ,G 为AP 中点 ∴DG ⊥AP又AB ∩AP =A , ∴DG ⊥平面PAB又由(1)知EF ∥DG ∴EF ⊥平面PAB ,又EF ⊂面AEF ∴平面AEF ⊥平面PAB .证法二:(1)以D 为坐标原点,DA 、DC 、DP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系.设AB =a . ∵AD =PD =2,∴A (2,0,0),B (2,a ,0),C (0,a ,0),P (0,0,2), ∵E 、F 分别为CD ,PB 的中点 ∴E (0,a2,0),F (1,a2,0).∴EF ⃗⃗⃗⃗⃗ =(1,0,1), ∵DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =(0,0,2)+(2,0,0)=(2,0,2), ∴EF ⃗⃗⃗⃗⃗ =12(DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ )=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ , 故EF ⃗⃗⃗⃗⃗ 、DP ⃗⃗⃗⃗⃗ 、DA ⃗⃗⃗⃗⃗ 共面, 又EF ⊄平面PAD ∴EF ∥平面PAD .(2)由(1)知EF ⃗⃗⃗⃗⃗ =(1,0,1),AB ⃗⃗⃗⃗⃗ =(0,a ,0),AP⃗⃗⃗⃗⃗ =(−2,0,2). ∴EF ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =0,EF ⃗⃗⃗⃗⃗ •AP ⃗⃗⃗⃗⃗ =-2+0+2=0, ∴EF ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ,EF ⃗⃗⃗⃗⃗ ⊥AP ⃗⃗⃗⃗⃗ , 又AB ∩AP =A ,∴EF ⊥平面PAB , 又EF ⊂平面AEF ,∴平面AEF ⊥平面PAB , (3)AB =2√2由(1)知,∴AE ⃗⃗⃗⃗⃗ =(-2,√2,0),EF⃗⃗⃗⃗⃗ =(1,0,1)设平面AEF 的法向量n ⃗ =(x ,y ,z),则{n⃗ ⋅AE ⃗⃗⃗⃗⃗ =0n ⃗ ⋅EF ⃗⃗⃗⃗⃗ =0即−2x +√2y =0令x =1,则y =√2,z =-1, ∴n⃗ =(1,√2,-1), 又AC⃗⃗⃗⃗⃗ =(-2,2√2,0), ∴cos <AC⃗⃗⃗⃗⃗ ,n ⃗ >=−2+4+02√12=√36, ∴sinθ=|cos <AC⃗⃗⃗⃗⃗ ,n ⃗ >|=√36.【解析】方法一;(1)取PA 中点G ,连结DG 、FG ,要证明EF ∥平面PAD ,我们可以证明EF 与平面PAD 中的直线AD 平行,根据E 、F 分别是PB 、PC 的中点,利用中位线定理结合线面平行的判定定理,即可得到答案. (2)根据线面垂直的和面面垂直的判断定理即可证明.方法二:(1)求出直线EF 所在的向量,得到EF ⃗⃗⃗⃗⃗ =12(DP ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ )=12DP ⃗⃗⃗⃗⃗ +12DA ⃗⃗⃗⃗⃗ ,即可证明EF ∥平面PAD .(2)再求出平面内两条相交直线所在的向量,然后利用向量的数量积为0,根据线面垂直的判定定理得到线面垂直,即可证明平面AEF ⊥平面PAB(3)求出平面的法向量以及直线所在的向量,再利用向量的有关运算求出两个向量的夹角,进而转化为线面角,即可解决问题.本题考查了本题考查的知识点是直线与平面平行的判定,面面垂直,直线与平面所成的角,解决此类问题的关键是熟练掌握几何体的结构特征,进而得到空间中点、线、面的位置关系,利于建立空间之间坐标系,利用向量的有关知识解决空间角与空间距离以及线面的位置关系等问题,属于中档题.14.【答案】解:(1)证明:∵PO ⊥平面ABCD ,且AD ⊂平面ABCD , ∴PO ⊥AD , ∵∠ADC =45°且AD =AC =2, ∴∠ACD =45°, ∴∠DAC =90°, ∴AD ⊥AC ,∵AC ⊂平面PAC ,PO ⊂平面PAC ,且AC ∩PO =O , ∴由直线和平面垂直的判定定理知AD ⊥平面PAC . (2)解:取DO 中点N ,连接MN ,AN , 由PO ⊥平面ABCD ,得MN ⊥平面ABCD , ∴∠MAN 是直线AM 与平面ABCD 所成的角, ∵M 为PD 的中点, ∴MN ∥PO ,且MN =12PO =3, AN =12DO =√52,在Rt △ANM 中,tan ∠MAN =MNAN =3√52=6√55, 即直线AM 与平面ABCD 所成角的正切值为6√55.【解析】(1)由PO ⊥平面ABCD ,得PO ⊥AD ,由∠ADC =45°,AD =AC ,得AD ⊥AC ,从而证明AD ⊥平面PAC .(2)取DO 中点N ,连接MN ,AN ,由M 为PD 的中点,知MN ∥PO ,由PO ⊥平面出直线AM 与平面ABCD 所成角的正切值.本题考查直线与平面垂直的证明,考查直线与平面所成角的正切值的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题. 15.【答案】证明:(I )在三棱柱ABC -A 1B 1C 1中,连接A 1B ,交AB 1于O 点,连接OD∵在△A 1BC 1中,A 1D =DC 1,A 1O =OB , ∴OD ∥BC 1,又∵OD ⊂平面AB 1D ,BC 1⊄平面AB 1D ; ∴BC 1∥平面AB 1D ;(II )在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面A 1B 1C 1; ∵B 1D ⊂平面A 1B 1C 1; ∴A 1A ⊥B 1D在△A 1B 1C 1中,D 为A 1C 1的中点 ∴B 1D ⊥A 1C 1又∵A 1A ∩A 1C 1=A 1,A 1A ,A 1C 1⊂平面AA 1C 1C , ∴B 1D ⊥平面AA 1C 1C , 又∵A 1C ⊂平面AA 1C 1C , ∴B 1D ⊥A 1C又∵A 1D AA 1=AA1AC =√22∴∠DA 1A =∠A 1AC =90°∴△DA 1A ∽△A 1AC ,∠ADA 1=∠CA 1A∵∠DA 1C +∠CA 1A =90° ∴∠DA 1C +∠ADA 1=90°∴A 1C ⊥AD又∵B 1D ∩AD =D ,B 1D ,AD ⊂平面AB 1D ; ∴A 1C ⊥平面AB 1D ;解:(III )由(I )得,OD ∥BC 1, 故AD 与BC 1所成的角即为∠ADO在△ADO 中,AD =√3,OD =12BC 1=√62,AO =12A 1B =√62,∵AD 2=OD 2+AO 2,OD =AO∴△ADO 为等腰直角三角形故∠ADO =45°即异面直线AD 与BC 1所成角等于45°【解析】(I )连接A 1B ,交AB 1于O 点,连接OD ,由平行四边形性质及三角形中位线定理可得OD ∥BC 1,进而由线面平行的判定定理得到BC 1∥平面AB 1D ;(II )由直棱柱的几何特征可得A 1A ⊥B 1D ,由等边三角形三线合一可得B 1D ⊥A 1C 1,进而由线面垂直的判定定理得到B 1D ⊥平面AA 1C 1C ,再由三角形相似得到A 1C ⊥AD 后,可证得A 1C ⊥平面AB 1D .(III )由(I )中OD ∥BC 1,可得异面直线AD 与BC 1所成角即∠ADO ,解△ADO 可得答案.本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,直线与平面平行的判定,(I )的关键是证得OD ∥BC 1,(II )的关键是熟练掌握线面垂直与线线垂直之间的转化,(III )的关键是得到异面直线AD 与BC 1所成角即∠ADO .16.【答案】(Ⅰ)证明:由P -ABD ,Q -BCD 是相同正三棱锥,且∠APB =90°,分别过P 、Q 作PE ⊥平面ABD ,QF ⊥平面BCD ,垂足分别为E 、F ,则E 、F 分别为底面正三角形ABD 与BCD 的中心. 连接EF 交BD 于G ,则G 为BD 的中点,连接PG 、QG ,则PG ⊥BD ,QG ⊥BD ,又PG ∩QG =G ,∴BD ⊥平面PQG ,则BD ⊥PQ , 再由正三棱锥的性质可得PA ⊥BD , 又PQ ∩PA =P ,∴BD ⊥平面APQ ;(Ⅱ)∵正三棱锥的底面边长为1,且∠APB =90°,∴PQ =EF =2EG =2×13AG =2×13×√32=√33, PE =√(√22)2−(√33)2=√66,则V B−PQD =13×12×√33×√66×1=√236.△PDQ 底边PQ 上的高为√(√22)2−(√36)2=√156,∴S △PDQ =12×√33×√156=√512.设B 到平面PQD 的距离为h ,则13×√512ℎ=√236,得h =√105.∴直线PB 与平面PDQ 所成角的正弦值为√105√22=2√55.【解析】(Ⅰ)由题意分别过P 、Q 作PE ⊥平面ABD ,QF ⊥平面BCD ,可得E 、F 分别为底面正三角形ABD 与BCD 的中心.连接EF 交BD 于G ,可得PG ⊥BD ,QG ⊥BD ,由线面垂直的判定及性质可得BD ⊥PQ ,再由正三棱锥的性质可得PA ⊥BD ,则BD ⊥平面APQ ;(Ⅱ)由已知求得PQ ,PE 的长,求得四面体B -PQD 的体积,利用等积法求出B 到平面PQD 的距离,则直线PB 与平面PDQ 所成角的正弦值可求.本题考查直线与平面所成的角,考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题. 17.【答案】(1)证明:如图:∵AB =BC ,E 为AC 的中点,∴BE ⊥AC ,∵平面A 1ACC 1⊥平面ABC ,平面A 1ACC 1∩平面ABC =AC , ∴BE ⊥平面A 1ACC 1,∵A 1C ⊂平面A 1ACC 1,∴BE ⊥A 1C .(2)解:∵面A1ACC1⊥面ABC,∴C1在面ABC上的射影H在AC上,∴∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,在Rt△C1CM中,CM=CC1cos∠C1CM=2cos60°=1.在Rt△CMH中,CH=CMcos∠ACB =2√33.∴在Rt△C1CH中,cos∠C1CH=CHCC1=23√32=√33.∴直线C1C与面ABC所成的角的余弦值为√33.【解析】(1)证明BE⊥平面A1ACC1,可得BE⊥A1C,即可证明:A1C⊥平面C1EB;(2)判断∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,即可求直线CC1与平面ABC所成角的余弦值.本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.18.【答案】证明:(1)连接CD,据题知AD=4,BD=2,∵AC2+BC2=AB2,∴∠ACB=90°,∴cos∠ABC=2√36=√33,∴CD2=4+12−2×2×2√3cos∠ABC=8,∴CD=2√2,∴CD2+AD2=AC2,∴CD⊥AB,又∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,CD⊂平面ABC,∴CD⊥平面PAB,∵PD⊂平面PAB,∴CD⊥PD,∵PD⊥AC,CD∩AC=C,CD、AC⊂平面ABC,∴PD⊥平面ABC.解:(2)∵∠PAB=π4,∴PD=AD=4,∴PA=4√2,在Rt△PCD中,PC=√PD2+CD2=2√6,∴△PAC是等腰三角形,∴S△PAC=8√2,设点B到平面PAC的距离为d,由V B-PAC=V P-ABC,得13S△PAC×d=13S△ABC×PD,∴d==3,故点B到平面PAC的距离为3.【解析】本题考查线面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.(1)连接CD,推导出CD⊥AB,CD⊥PD,由此能证明PD⊥平面ABC.(2)设点B到平面PAC的距离为d,由V B-PAC=V P-ABC,能求出点B到平面PAC的距离.19.【答案】解:(1)证明:∵ABC-A1B1C1中,A1A⊥平面ABC,又BB 1⊂平面BB 1C 1C , ∴平面BB 1C 1C ⊥平面ABC ,∵△ABC 为正三角形,D 为BC 的中点, ∴AD ⊥BC ,又平面BB 1C 1C ∩平面ABC =BC , ∴AD ⊥平面BB 1C 1C , 又AD ⊂平面ADB 1,∴平面ADB 1⊥平面BB 1C 1C ;(2)由(1)可得△ADB 1为直角三角形, 又AD =√32,B 1D =√52,∴S △ADB 1=12×AD ×B 1D =√158,又S △ADB =12S △ABC =√38,设点B 到平面ADB 1的距离为d , 则V B−ADB 1=V B 1−ADB , ∴13S △ADB 1⋅d =13S △ADB ⋅BB 1, ∴点B 到平面ADB 1的距离d =S △ADB ⋅BB 1S △ADB 1=√3√15=√55.【解析】本题考查面面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.(1)推导出BB 1⊥平面ABC ,从而平面BB 1C 1C ⊥平面ABC ,推导出AD ⊥BC ,从而AD ⊥平面BB 1C 1C ,由此能证明平面ADB 1⊥平面BB 1C 1C ;(2)设点B 到平面ADB 1的距离为d ,由V B−ADB 1=V B 1−ADB ,能求出点B 到平面ADB 1的距离.20.【答案】证明:(1)∵PA ⊥平面ABC ,BE ⊂平面ABC , ∴PA ⊥BE .∵AB =BC ,E 为AC 的中点, ∴BE ⊥AC ,又PA ⊂平面PAC ,AC ⊂平面PAC ,PA ∩AC =A , ∴BE ⊥平面PAC ,又BE ⊂平面BED , ∴平面BED ⊥平面PAC .(2)∵D ,E 是PC ,AC 的中点, ∴DE ∥PA ,又PA ⊥平面ABC ,∴DE ⊥平面ABC ,∵EF ⊂平面ABC ,BE ⊂平面ABC , ∴DE ⊥EF ,DE ⊥BE .∴∠FEB 为二面角F -DE -B 的平面角.∵E ,F 分别是AC ,AB 的中点,AB =AC , ∴EF =12BC =12AB =BF ,EF ∥BC .又AB ⊥BC ,∴BF ⊥EF ,∴△BEF 为等腰直角三角形,∴∠FEB =45°. ∴二面角F -DE -B 为45°.∴PA⊥BC,又BC⊥AB,PA⊂平面PAB,AB⊂平面PAB,PA∩AB=A,∴BC⊥平面PAB.∴∠CPB为直线PC与平面PAB所成的角.∵PA=6,∴DE=12PA=3,又DF=5,∴EF=√DF2−DE2=4.∴AB=BC=8.∴PB=√PA2+AB2=10.∴tan∠CPB=BCPB =4 5.【解析】(1)通过证明BE⊥平面PAC得出平面BED⊥平面PAC;(2)由DE∥PA得出DE⊥平面ABC,故DE⊥EF,DE⊥BE,于是∠FEB为所求二面角的平面角,根据△BEF为等腰直角三角形得出二面角的度数;(3)证明BC⊥平面PAB得出∠CPB为所求角,利用勾股定理得出BC,PB,即可得出tan∠CPB.本题考查了线面垂直,面面垂直的判定,空间角的计算,做出空间角是解题关键,属于中档题.21.【答案】解:(1)证明:设AC∩BD=H,连接EH,在△ADC中,因为AD=CD,且DB平分∠ADC,所以H为AC的中点,又有题设,E为PC的中点,故EH∥PA,又HE⊂平面BDE,PA⊄平面BDE,所以PA∥平面BDE(2)证明:因为PD⊥平面ABCD,AC⊂平面ABCD,所以PD⊥AC由(1)知,BD⊥AC,PD∩BD=D,故AC⊥平面PBD(3)由AC⊥平面PBD可知,BH为BC在平面PBD内的射影,所以∠CBH为直线与平面PBD所成的角.由AD⊥CD,AD=CD=1,DB=2√2,可得DH=CH=√22,BH=3√22在Rt△BHC中,tan∠CBH=CHBH =13,所以直线BC与平面PBD所成的角的正切值为13.【解析】(1)欲证PA∥平面BDE,根据直线与平面平行的判定定理可知只需证PA与平面BDE内一直线平行,设AC∩BD=H,连接EH,根据中位线定理可知EH∥PA,而又HE⊂平面BDE,PA⊄平面BDE,满足定理所需条件;(2)欲证AC⊥平面PBD,根据直线与平面垂直的判定定理可知只需证AC与平面PBD内两相交直线垂直,而PD⊥AC,BD⊥AC,PD∩BD=D,满足定理所需条件;(3)由AC⊥平面PBD可知,BH为BC在平面PBD内的射影,则∠CBH为直线与平面PBD所成的角,在Rt△BHC中,求出此角即可.本小题主要考查直线与平面平行.直线和平面垂直.直线和平面所成的角等基础知识,考查空间想象能力、运算能力和推理能力.。
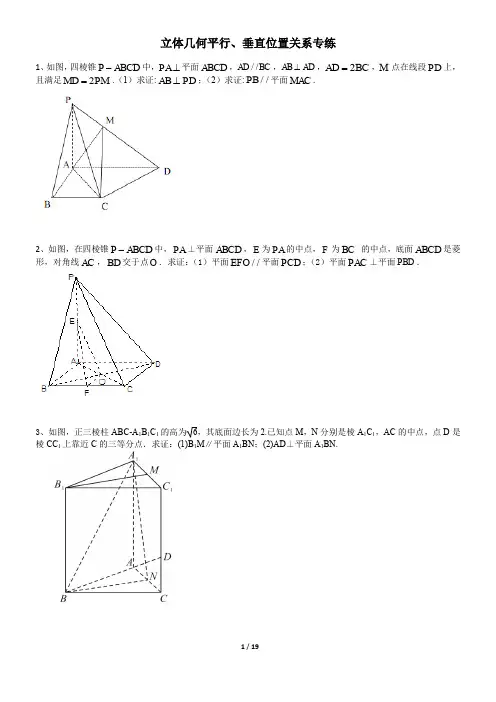
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点。
1)证明EFGH是平行四边形。
2)已知BD=23,AC=2,EG=2,求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图,已知空间四边形ABCD中,BC=AC,AD=BD,E 是AB的中点。
1)证明AB垂直于平面CDE。
2)证明平面CDE垂直于平面ABC。
3.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90,SA垂直于面ABC,AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点。
1)证明C1O平行于面AB1D1.2)证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1)证明AC垂直于平面B1D1D。
2)证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1)证明平面A1BD平行于平面B1DC。
2)已知E、F分别是AA1、CC1的中点,证明平面EB1D1平行于平面FBD。
8.四面体ABCD中,AC=BD,E、F分别为AD、BC的中点,且EF=AC/2,∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点,PA=PB,CB垂直于平面PAB,M是PC的中点,N是AB上的点,AN=3NB。
1)证明XXX垂直于AB。
2)当∠APB=90,AB=2BC=4时,求MN的长度。
10.如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
1)证明A1C平行于平面BDE。
2)证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD,PA垂直于平面ABCD,AB=2,PA=AD=4,E为BC的中点。
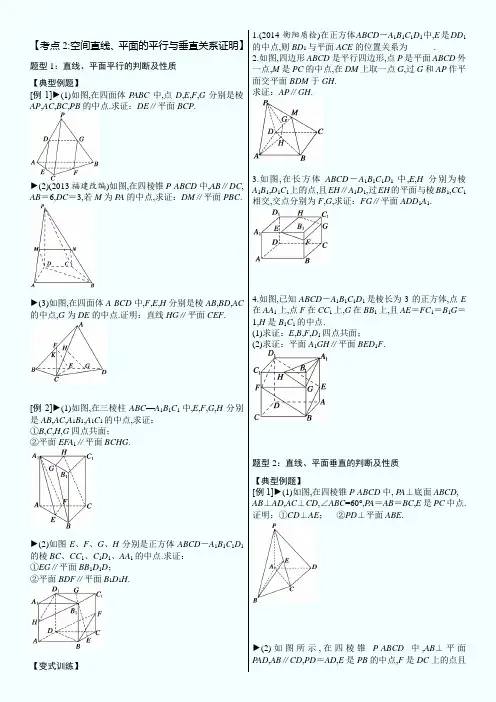
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。

立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨:证明直线与平面的平行与垂直问题,一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
直线与平面的平行有两种方法:一是在面内找线;二是通过面面平行转化。
直线与平面垂直关键是找两条相交直线例1、如图,在四棱锥PABCD中,M,N分别为棱PA,PD的中点.已知侧面PAD⊥底面ABCD,底面ABCD是矩形,DA=DP.求证:(1)MN∥平面PBC;MD⊥平面PAB.例2、如图所示,在三棱柱ABCA1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F 分别是侧面AA1B1B,BB1C1C对角线的交点.(1) 求证:EF∥平面ABC;(2) 求证:BB1⊥AC.例3、如图,在三棱柱ABCA1B1C1中,AB=AC,A1C⊥BC1,AB1⊥BC1,D,E分别是AB1和BC的中点.求证:(1)DE∥平面ACC1A1;(2)AE⊥平面BCC1B1.例4、如图,三棱锥DABC中,已知AC⊥BC,AC⊥DC,BC=DC,E,F分别为BD,CD的中点.求证:(1) EF∥平面ABC;(2) BD⊥平面ACE.例5、如图,在直三棱柱ABCA1B1C1中,侧面BCC1B1为正方形,A1B1⊥B1C1.设A1C与AC1交于点D,B1C 与BC1交于点E.求证:(1) DE∥平面ABB1A1;(2) BC1⊥平面A1B1C.例6、如图,在正三棱柱ABCA1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:(1) 直线A1E∥平面ADC1;(2) 直线EF⊥平面ADC1.题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题,一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
平面与平面的平行关键是在一个平面内找两条相交直线;平面与平面垂直可以从二面角入手页可以从线面垂直进行转化。

立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
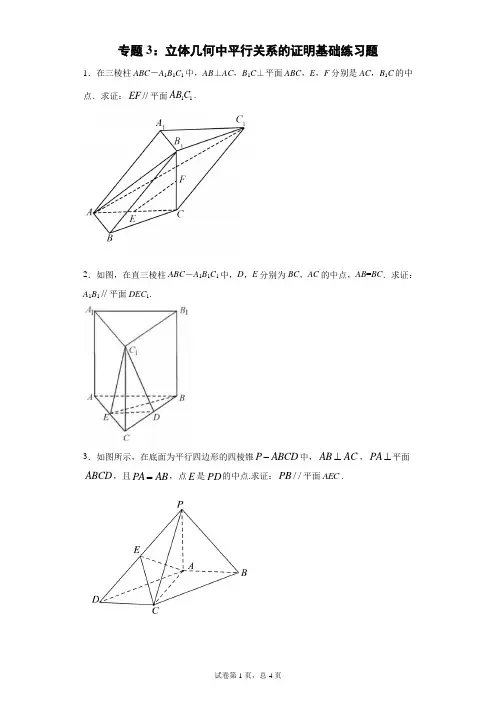

专题:平行问题主要考点:线面平行面面平行线面平行的判定定理:如果一个平面内的一条直线和另平面内的一条直线平行,那么这条直线和这个平面平行。
定理模式:, , ////a b a b a ααα⊄⊂⇒面面平行的判定定理:如果一个平面内有两条相交直线都平行于一个平面,那么这两个平面平行。
定理的模式://////a b a b P a b ββαβαα⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭1、如右图所示,已知P 、Q 是正方体的面11A B BA 和面ABCD 的中心.证明:PQ ∥平面11C B BC2、如图,在底面为平行四边形的四棱锥P ABCD -中,点E 是PD 的中点.求证://PB 平面AEC.3、如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD,AB=4, BC=CD=2, AA 1=2,E 、E 1、F 分别是棱AD 、AA 1、AB 的中点。
证明:直线EE 1//平面FCC 1;4、两个全等的正方形ABCD 和ABEF 所在平面相交于AB ,M ∈AC ,N ∈FB ,且AM =FN ,求证:MN ∥平面BCE 。
E E 1 A B 11D _ P5、已知在四棱锥P-ABCD 中,ABCD 为平行四边形,E 为PC 的中点,O 为BD 的中点. 求证:OE //平面ADP6、在四棱锥P-ABCD 中,底面四边形ABCD 是平行四边形,E,F 分别是AB ,PD 的中点. 求证://AF 平面PCE3、如图所示,ABC ∆为正三角形,EC ⊥平面ABC ,//BD CE ,且2CE CA BD ==,F 、M 是CE 、EA 的中点。
求证:(1)//DM 平面ABC ;(2)面//FDM 面ABC .10.P 是△ABC 所在平面外一点,A ′、B ′、C ′分别是△PBC 、△PCA 、△PAB 的重心。
(1)求证:平面A ′B ′C ′∥平面ABC ;(2)S △A′B′C′∶S △ABC 的值。

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1},E,F分别是AB,BC的中点,求证:EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中,因为E,F分别是AB,BC的中点,所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中:- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D,EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理,所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中,D是AB的中点,求证:AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1},交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中,E为BC_{1}的中点。
2. 因为D是AB的中点:- 所以在 ABC_{1}中,DE∥ AC_{1}。
- 又DE⊂平面CDB_{1},AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理,可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中,底面ABCD是正方形,PA = PB = PC = PD,求证:PA⊥平面ABCD。
解析1. 连接AC,BD交于点O,连接PO。
- 因为底面ABCD是正方形,所以O为AC,BD中点。
- 又PA = PC,PB = PD,根据等腰三角形三线合一的性质:- 可得PO⊥ AC,PO⊥ BD。
- 而AC∩ BD = O,AC⊂平面ABCD,BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理,所以PO⊥平面ABCD。
- 又PA = PB = PC = PD,AO = BO = CO = DO,所以 PAO≅ PBO≅ PCO ≅ PDO。

立体几何平行判定与性质定理专题突破训练一、单选题1.如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线交点为O ,M 为PB 的中点,下列结论正确的个数为( )①//OM 平面PBC ②//OM 平面PCD ③//OM 平面PDA ④//OM 平面PBA A .1个B .2个C .3个D .4个2.a 、b 、l 是直线,α是平面,则下列说法正确的是( ) A .l 平行于α内的无数条直线,则//l α B .a 不在面α,则//a α C .若//a b ,b α⊂,则//a αD .若//a b ,b α⊂,则a 平行于α内的无数条直线3.若l ,m 是平面α外的两条不同直线,且//m α,则“//l m ”是“//l α”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.在以下四个命题中:①直线与平面没有公共点,则直线与平面平行;②直线与平面内的任意一条直线都不相交,则直线与平面平行;③直线与平面内的无数条直线不相交,则直线与平面平行;④平面外的一条直线与平面内的一条直线平行,则直线与平面不相交.正确的命题是( ) A .①②B .①②③C .①③④D .①②④5.已知两条不同直线,m n 和平面α,下列判断正确的是( ) A .若//,//,m n αα则//m n B .若,,m n αα⊥⊥则m n ⊥ C .若//,//,m m n α则//n α D .若,//,m m n α⊥则n α⊥6.下列命题正确的是( )A .一个平面内两条直线都平行于另一个平面,那么这两个平面平行B .如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行C .平行于同一直线的两个平面一定相互平行D .如果一个平面内的无数条直线都平行于另一个平面,那么这两个平面平行 7.已知α,β是不同的平面,m ,n 是不同的直线,则下列命题不正确的是( ) A .若m ⊥α,m ∥n ,n ⊂β,则α⊥β B .若m ∥n ,α∩β=m ,则n ∥α,n ∥β C .若m ∥n ,m ⊥α,则n ⊥α D .若m ⊥α,m ⊥β,则α∥β8.下列命题中:(1)平行于同一直线的两个平面平行;(2)平行于同一平面的两个平面平行;(3)垂直于同一直线的两直线平行;(4)垂直于同一平面的两直线平行.其中正确的个数有( ) A .1B .2C .3D .49.如图,在四棱锥P-ABCD 中,M ,N 分别为AC ,PC 上的点,且MN ∥平面P AD ,则( )A .MN ∥PDB .MN ∥P AC .MN ∥AD D .以上均有可能10.如图,在三棱锥P —ABC 中,点D ,E 分别为棱PB ,BC 的中点.若点F 在线段AC 上,且满足AD //平面PEF ,则AFFC的值为( )A .1B .2C .12D .2311.在正方体1111ABCD A B C D -中,M 是1AA 的中点,过M 在平面11ACC A 内作直线MN 交11A C 于N ,若//MN 平面1BC D ,则111A NA C =( ) A .14B .13C .12D.2二、多选题12.如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线的交点为O ,M 为PB 的中点,给出以下结论,其中正确的是( )A .OM ∥PDB .OM ∥平面P AC C .OM ∥平面PDAD .OM ∥平面PBA13.设a ,b 为两条直线,α,β为两个平面,下列四个命题中,错误的命题是 A .若a ,b 与α所成的角相等,则//a b B .若//a α,b β//,//αβ,则//a b C .若a α⊂,b β⊂,//b α,则//αβ D .若a α⊥,b β⊥,αβ⊥,是a b ⊥14.如图,在棱长为2的正方体1111ABCD A B C D -中,O 为正方体的中心,M 为1DD 的中点,F 为侧面正方形11AA D D 内一动点,且满足1//B F 平面1BC M ,则( )A .若P 为正方体表面上一点,则满足OPA 的面积为2的点有12个 B .动点F 的轨迹是一条线段C .三棱锥1F BC M -的体积是随点F 的运动而变化的D .若过A ,M ,1C 三点作正方体的截面Ω,Q 为截面Ω上一点,则线段1A Q 长度的取值范围为⎣ 15.如图,在四棱锥P ABCD -中,M 、N 分别为AC 、PC 上的点,且//MN 平面PAD ,则( )A .//MN PDB .//MN 平面PABC .//MN AD D .//MN PA三、双空题16.如图,在棱长为1的正方体1111ABCD A B C D -,点E ,F 分别是棱BC ,1CC 的中点,P 是侧面11BCC B 内一点(含边界),若1//A P 平面AEF ,点P 的轨迹长度为________,三棱锥P AEF -的体积为________.17.已知正方体1111ABCD A B C D -的棱长为2,点,M N 分别是棱1,BC CC 的中点,则异面直线AN 与BC 所成角的余弦值为___________;若动点P 在正方形11BCC B (包括边界)内运动,且1PA //平面AMN ,则线段1PA 的长度范围是___________.18.如图,直三棱柱111ABC A B C -的所有棱长都为4,P Q R 、、分别在棱111AA AB B C 、、上,123AP AQ B R ===,,过P Q R 、、三点的平面截三棱柱所得的截面是________边形,该截面的面积是___________.19.如图,已知斜三棱柱111ABC A B C -中,点D ,1D 分别为11,AC A C 上的点.若1//BC 平面11AB D ,则1111A D D C =________;若平面1//BC D 平面11AB D ,则AD DC=_______.20.已知四棱锥P ABCD -的底面ABCD 是边长为3的正方形,PD ⊥平面ABCD ,6PD =,E 为PD 中点,过EB 作平面α分别与线段P A 、PC 交于点M ,N ,且//AC α,则PMPA=________;四边形EMBN 的面积为________.四、解答题21.已知四棱锥P ABCD -中,//CD AB ,取PA 的中点M ,BC 的中点N ,求证://MN 平面PDC .22.如图,四棱锥P ABCD -中,点M 、N 分别为直线,PB PD 上的点,且满足PM PNPB PD=,求证://MN 平面ABCD.23.如图,在三棱柱111ABC A B C -中,1AA AC ⊥且1AA AC =,点E ,F 分别为11B C 和BC 的中点,1B A 与1A B 相交于点G .(1)证明:平面//EFG 平面11A ACC ; (2)求异面直线GE 和AC 所成角的大小.24.如图,在正方体1111ABCD A B C D -中,S 是B 1D 1的中点,E ,F ,G 分别是BC ,CD ,SC 的中点,求证:(1)EG ∥平面BDD 1B 1; (2)平面EFG ∥平面BDD 1B 1.25.如图,长方体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,点P 为DD 1的中点.(1)求证:直线BD 1∥平面P AC ; (2)求异面直线BD 1与AP 所成角的大小.26.如图,AB 是圆O 的直径.C 是圆O 上的点,P 为平面ABC 外一点.设Q 为P A 的中点,G 为AOC △的重心,求证://QG 平面PBC .27.如图,已知//αβ,点P 是平面,αβ外的一点,直线PA 和PC 分别与β相交于B 和D .(1)求证://AC BD ;(2)已知4cm,5cm,3cm PA AB PC ===,求PD 的长.28.如图所示,已知α,β,γ都是平面,且////αβγ,两条直线l ,m 分别与平面α,β,γ相交于点A ,B ,C 和点D ,E ,F . 求证:AB DEBC EF=.29.如图所示,两条异面直线,AB CD 与三个平行平面,,αβγ分别相交于,,A E B 及 ,,C F D 又AD BC 、与平面β的交点为,H G .求证:四边形EHFG 为平行四边形.30.如图,在四棱锥O ABCD -中,底面ABCD 是矩形.(1)设M 为OA 上靠近A 的三等分点,N 为BC 上靠近B 的三等分点.求证://MN 平面OCD .(2)设E 是OD 上靠近点D 的一个三等分点,试问:在OD 上是否存在一点F ,使//BF 平面ACE 成立?若存在,请予以证明;若不存在,说明理由.31.如图,已知在直三棱柱111ABC A B C -中,,,,M N P Q 分别是1111,,,AA BB AB B C 的中点.(1)在图中画出过,,M N Q 三点的截面,并说出截面图形的形状(不必说明画法与理由); (2)求证:1PC //平面MNQ .32.如图,在三棱柱111ABC A B C -中,点D ,1D 分别为AC ,11A C 上的动点,若平面1//BC D 平面11AB D ,请问ADDC是否为定值.若为定值求出该值,若不是定值,说明理由.33.(如图1)在直角梯形ABCD 中,//AB DC ,90BAD ∠=︒,4AB =,2AD =,3DC =,点E 在CD 上,且2DE =.将ADE 沿AE 折起,使得平面ADE ⊥平面ABCE (如图2).(1)求证:BE AD ;(2)在线段BD 上是否存在点P ,使得//CP 平面ADE ?若存在,求:PD BP 的值;若不存在,请说明理由.参考答案1.B【分析】证明//OM PD ,即可证明②③正确;M ∈平面PBC ,故①错误,M ∈平面PAB ,故④错误.【详解】对于①,M ∈平面PBC ,故①错误;对于②,由于O 为BD 的中点,M 为PB 的中点,则//OM PD , OM ⊂平面PCD ,PD ⊂平面PCD ,则//OM 平面PCD ,故②正确;对于③,由于//OM PD ,OM ⊂平面PAD ,PD ⊂平面PAD ,则//OM 平面PAD ,故③正确;对于④,由于M ∈平面PAB ,故④错误.故选:B2.D【分析】利用线面平行的判定定理和性质定理逐个分析判断即可【详解】对于A ,当l 平行于α内的无数条直线,若l α⊂,则l 与α不平行,所以A 错误, 对于B ,当a 不在面α时,a 与α有可能相交,所以B 错误,对于C ,当//a b ,b α⊂时,若a α⊂,则a 与α不平行,所以C 错误,对于D ,当//a b ,b α⊂时,由线面平行的性质可知a 平行于α内的无数条直线,所以D 正确,故选:D3.A【分析】根据线线、线面的平行关系,结合条件间的推出关系,判断“//l m ”、“//l α”之间的充分、必要关系.【详解】∵l ,m 是平面α外的两条不同的直线,//m α,∴若//l m ,则推出“//l α”;若//l α,则//l m 或l 与m 相交;∴若l ,m 是平面α外的两条不同直线,且//m α,则“//l m ”是“//l α”的充分不必要条件. 故选:A.4.D【分析】根据线面平行的定义及判定定理可判断.【详解】定义:一条直线与一个平面无公共点(不相交),称为直线与平面平行.可知①②正确;线面平行的判定定理:平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行. 可知④正确;当线在面内时,直线与平面内的无数条直线不相交(平行时),所以③不正确.故选:D.5.D【分析】根据线线、线面、面面的平行与垂直的位置关系即可判断.【详解】解:对于选项A :若//,//m n αα,则m 与n 可能平行,可能相交,可能异面,故选项A 错误;对于选项B :若,m n αα⊥⊥,则//m n ,故选项B 错误;对于选项C :当n ⊂α时不满足//n α,故选项C 错误;综上,可知选项D 正确.故选:D.6.B【分析】根据面面平行的知识对选项逐一分析,由此确定正确选项.【详解】对于A 选项,这两个平面可能相交,故A 选项错误.对于B 选项,如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行,正确,故B 选项正确.对于C 选项,这两个平面可能相交,故C 选项错误.对于D 选项,这两个平面可能相交,故D 选项错误.故选:B7.B【分析】根据空间垂直、平行逐项讨论,即可得出结论.【详解】选项A:m ⊥α,m ∥n ,可得n ⊥α,n ⊂β,则α⊥β,该选项正确;选项B:m ∥n ,α∩β=m ,直线n 可能在α或β内,该选项不正确;选项C:是线面垂直的判定,故正确;选项D:是面面平行的判定,故正确.故选:B【点睛】本题考查有关空间线面平行、垂直性质和判定定理,属于基础题.8.B【分析】举特例说明可判断命题(1),(3);利用面面平行的传递性可判断(2);利用线面垂直的性质可判断(4)即可得解.【详解】对于命题(1),长方体1111ABCD A B C D -中,平面ABCD 与平面11ABB A 都与直线11C D 平行,而这两个平面却相交,(1)不正确;对于命题(2),由平面与平面平行的传递性知,平行于同一平面的两个平面平行是正确的,(2)正确;对于命题(3),长方体1111ABCD A B C D -中,棱AB ,AD 都垂直于棱AA 1,而AB 与AD 相交,(3)不正确;对于(4),由直线与平面垂直的性质知,垂直于同一平面的两直线平行是正确的,(4)正确, 所以命题(2),(4)都正确,有2个.故选:B9.B【分析】直接利用线面平行的性质分析解答.【详解】∵MN ∥平面P AD ,MN ⊂平面P AC ,平面P AD ∩平面P AC=P A ,∴MN ∥P A.故选:B10.C【分析】连接CD ,交PE 于G ,连接FG ,由//AD 平面PEF ,得到//AD FG ,由点D ,E 分别为棱PB ,BC 的中点,得到G 是PBC 的重心,由此能求出结果.【详解】解:连接CD ,交PE 于G ,连接FG ,如图,//AD 平面PEF ,平面ADC平面PEF FG =,//AD FG ∴, 点D ,E 分别为棱PB ,BC 的中点.G ∴是PBC 的重心, ∴12AF DG FC GC ==. 故选:C .11.A【分析】连接AC 、BD ,AC BD E =,连接1C E ,取11A C 的中点F ,连接AF ,根据正方体的性质可得1//AF EC ,再由线面平行的性质得到1//MN C E ,从而得到//MN AF ,即可得解;解:连接AC 、BD ,AC BD E =,连接1C E ,取11A C 的中点F ,连接AF ,在正方体1111ABCD A B C D -中1AE C F =,1//AE C F ,所以四边形1AEC F 为平行四边形,所以1//AF EC ,又//MN 平面1BC D ,MN ⊂平面11ACC A ,平面11ACC A 平面11BC D C E =,所以1//MN C E ,所以//MN AF ,因为M 是1AA 的中点,所以N 为1A F 的中点,所以11114A N AC =,即11114A N A C = 故选:A12.AC【分析】根据已知条件,利用三角形中位线定理判定A 正确;利用线面平行的判定定理判定C 正确;根据线面平行的定义——没有公共点,判定BD 错误.【详解】因为矩形对角线的交点为O ,所以O 是BD 的中点, 又M 为PB 的中点,OM ∴为△PBD 的中位线,//OM PD ∴,又OM ⊄平面PAD ,PD ⊂平面PAD ,所以OM ∥平面PDA ,故AC 正确;OM 与平面PAC 有公共点O ,与平面PBA 有公共点M ,故BD 错误.故选:AC .13.ABC根据题意,依次分析选项,A 、用直线的位置关系判断.B 、用长方体中的线线,线面,面面关系验证.C 、用长方体中的线线,线面,面面关系验证.D 、由a α⊥,αβ⊥,可得到a β⊂或//a β,再由b β⊥得到结论.【详解】解:A 、直线a ,b 的方向相同时才平行,不正确;B 、用长方体验证.如图,设11A B 为a ,平面AC 为α,BC 为b ,平面11A C 为β,显然有//a α,b β//,//αβ,但得不到//a b ,不正确;C 、可设11A B 为a ,平面1AB 为α,CD 为b ,平面AC 为β,满足选项C 的条件却得不到//αβ,不正确;D 、a α⊥,αβ⊥,a β∴⊂或//a β又b β⊥,a b ∴⊥,D 正确故选:ABC【点睛】本题考查线线平行与垂直、线面平行的判定.把线面关系放到长方体中有助于问题解决,是解题中是常用的方法;本题是基础题.14.BD【分析】选项A :设O '为底面正方形ABCD 的中心,根据OO A '的面积为12AO OO ''⋅=,由此可判断选项A ;选项B :分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD ;证明平面1B GH ∥平面1BC M ,从而得到点F 的轨迹为线段GH .选项C :根据选项B 可得出GH ∥平面1BC M ,从而得到点F 到平面1BC M 的距离为定值,再结合1BC M 的面积也为定值,从而可得到三棱锥1F BC M -的体积为定值.选项D :设N 为1BB 的中点,从而根据面面平行的性质定理可得到截面Ω即为面1AMC N ,从而线段1A Q 长度的最大值为线段11A C 的长,最小值为四棱锥11A AMC N -以1A 为顶点的高.【详解】对于A :设O '为底面正方形ABCD 的中心,连接AO ,AO ',OO ',则12AO AC '=1112OO AA '==,所以OO A '的面积为11122AO OO ''⋅== 所以在底面ABCD 上点P 与点O '必重合,同理正方形11ABB A 的中心,正方形11ADD A 的中心都满足题意.又当点P 为正方体各条棱的中点时也满足OPA A 不正确; 对于B :如图①,分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD . 因为11B H C M ∥,1GH BC ∥,1B H ⊂平面BHG ,1C M ⊂平面1BC M ,GH ⊂平面BHG ,1C B ⊂面1BC M ,111BC C M C ⋂=,所以平面1B GH ∥平面1BC M ,而1B F ∥平面1BC M ,所以1B F ⊂平面1B GH ,所以点F 的轨迹为线段GH ,故B 正确; 对于C :由选项B 可知,点F 的轨迹为线段GH ,因为GH ∥平面1BC M ,则点F 到平面1BC M 的距离为定值,同时1BC M 的面积也为定值,则三棱锥1F BC M -的体积为定值,故C 不正确; 对于D :如图②,设平面Ω与平面11AA B B 交于AN ,N 在1BB 上.因为截面Ω⋂平面11AA D D AM =,平面11AA D D ∥平面11BB C C ,所以1AM C N ∥.同理可证1AN C M ∥,所以截面1AMC N 为平行四边形,所以点N 为1BB 的中点.在四棱锥11A AMC N -中,侧棱11A C 最长,且11AC =设棱锥11A AMC N -的高为h ,因为1AM C M ==1AMC N 为菱形,所以1AMC 的边1AC 1AC =则112AMC S =⨯△1111111142223323C AA M AA M V SD C -=⋅=⨯⨯⨯⨯=△,所以111111433A AMC AMC C AA M V S h V --=⋅===△,解得h =.综上,可知1A Q 长度的取值范围是⎣,故D 正确.故选:BD .15.BD【分析】利用线面平行的性质结合线面平行的判定可得出结论.【详解】因为//MN 平面PAD ,MN ⊂平面PAC ,平面PAC 平面PAD PA =,//MN PA ∴, PA ⊂平面PAB ,MN ⊄平面PAB ,因此,//MN 平面PAB .故选:BD.16 112 【分析】分别取棱1BB ,11B C 的中点M ,N ,连接1A M ,1A N ,MN ,1BC ,NE ,推导出//MN 平面AEF ,1//A N 平面AEF ,得到平面1//A MN 平面AEF ,由此得以点P 的轨迹是线段MN , 借助等积变换可得三棱锥P AEF -的体积.【详解】解:如图,分别取棱1BB ,11B C 的中点M ,N ,连接1A M ,1A N ,MN ,1BC ,NE , M ,N ,E ,F 分别是其所在棱的中点,1//MN BC ∴,1//EF BC ,//MN EF ∴,MN ⊂/平面AEF ,EF ⊂平面AEF ,//MN ∴平面AEF ,1//AA NE ,1AA NE =,∴四边形1AENA 为平行四边形,1//A N AE ∴,1A N ⊂/平面AEF ,AE ⊂平面AEF ,1//A N ∴平面AEF ,1A N M N N =,∴平面1//A MN 平面AEF , P 是侧面11BCC B 内一点,且1//A P 平面AEF ,∴点P 必在线段MN 上,∴点P 的轨迹长度为112MN BC =∵//MN 平面AEF , ∴1111133412P AEF N AEF A NE NE F F V V V S AB ---===⋅=⨯⨯= .112.17.23 【分析】异面直线AN 与BC 所成的角就是∠DAN ,计算得3AN =,所以2cos 3DAN ∠=;由面面平行的性质得点P 在1BB 与11B C 中点的连线EF 上,设EF 中点为H ,则1A H 最短,1A E 或1A F同时最大,所以所求范围是. 【详解】 因为BC ∥AD, 异面直线AN 与BC 所成的角就是直线AN 与AD 所成的角,即∠DAN 为异面直线AN 与BC 所成的角,3AC AN == 所以2cos 3AD DAN AN ∠==; 取11B C 的中点E ,1BB 的中点F ,连接1A E ,1A F ,EF ,取EF 中点O ,连接1A O ,点M ,N 分别是棱长为2的正方体1111ABCD A B C D -中棱BC ,1CC 的中点,1//AM A E ∴,//MN EF , AM M N M =,1A E EF E =,∴平面//AMN 平面1A EF ,动点P 在正方形11BCC B (包括边界)内运动,且1//PA 面AMN ,∴点P 的轨迹是线段EF ,11A E A F ====EF1AO EF ∴⊥,∴当P 与O 重合时,1PA 的长度取最小值1A O =,当P 与E (或)F 重合时,1PA 的长度取最大值为11A E A F ==1PA ∴的长度范围为. 故答案为:23;. 【点睛】求异面直线的夹角一般要通过平行转换成平面角,第二个问题中动点的轨迹要点是求出直线的轨迹,是通过面面平行的思想转换的,做题时可以通过单独画截面图求解.18.五【分析】延长PQ 和1B B 交于M ,连RM 交BC 于E ,连QE ,延长QP 和11B A 交于N ,连RN 交11A C 于F ,连FP ,则过P Q R 、、三点的平面截三棱柱所得的截面是五边形PQERF ,通过计算可得ME EQ ⊥,RF MR ⊥,利用大直角三角形的面积减去两个小三角形的面积可得结果.【详解】如图:延长PQ 和1B B 交于M ,连RM 交BC 于E ,连QE ,延长QP 和11B A 交于N ,连RN 交11A C 于F ,连FP ,则过P Q R 、、三点的平面截三棱柱所得的截面是五边形PQERF , 依题意可知,P Q 为1,AA AB 的中点,所以PAQ △与MBQ 全等,所以2MB PA ==, 因为1//BE B R ,所以11BE MB B R MB =,所以2316BE ⨯==,所以ME因为QE ==MQ所以222ME EQ MQ +=,所以ME EQ ⊥,因为平面MRN 与两平行平面ABC 和111A B C 的交线为EQ 和RF ,所以//EQ RF ,所以RF MR ⊥,MR =MN =所以RN因为22211RN B R B N +=,所以1NR B R ⊥,又13FC R π∠=,所以1122FC RC ==,所以FR ==NF RN FR =-==cos RN FNP MN ∠===sin FNP ∠==所以12NPF S =⨯=△12MEQ S ==△又1122MRN S MR RN =⨯=⨯=△,所以截面面积为MNR NPF MEQ S S S --==△△△故答案为:五;.【点睛】关键点点睛:利用平面的基本性质作出截面是解题关键.19.1 1【分析】连接1A B 交1AB 于点O ,连接1OD ,由1//BC 平面11AB D 得性质定理得到11//BC OD ,又在11A BC 中,O 为1A B 的中点,可知1D 为11A C 的中点,即可求得结果;根据平面1//BC D 平面11AB D 的性质定理可知11//BC OD ,同理11//AD DC ,再根据比例关系即可求得结果.【详解】如图,连接1A B 交1AB 于点O ,由三棱柱性质知,O 为1A B 的中点,连接1OD1//BC 平面11AB D ,1BC ⊂平面11A BC ,平面11A BC ⋂平面111AB D OD =,11//BC OD ∴,又在11A BC 中,O 为1A B 的中点,故1D 为11A C 的中点,所以11111A D D C = 若平面1//BC D 平面11AB D , 又平面11A BC ⋂平面11BDC BC =,平面11A BC ⋂平面111AB D OD =,11//BC OD ∴,同理11//AD DC ,11111A D A O D C OB ∴=,1111A D D C DC AD= 又11AO OB =,1DC AD=,则1AD DC =【点睛】关键点睛:本题考查线面平行,及面面平行的性质定理,解题的关键是熟记线面平行证线线平行的性质定理,及面面平行证线线平行的性质定理,考查学生的逻辑推理能力与空间想象能力,属于中档题.20.23【分析】延伸平面α,交AC 所在的平面ABCD 于RS ,即平面α平面ABCD RS =,可得//AC RS ,在三角形PAD △和RED 中,利用平面几何三角形全等和平行线中的比例关系可得PM PA;至于四边形EMBN 的面积,连接MN ,BD ,可证明MN BE ⊥,求出,MN BE 的长度,通过面积公式12MN EB ⋅可得答案. 【详解】延伸平面α,交AC 所在的平面ABCD 于RS ,即平面α平面ABCD RS =,又B ∈平面α平面ABCD , B RS ∴∈,即,,R S B 三点共线,又//AC α,由线面平行的性质定理可得//AC RS ,则4ARB ABR π∠=∠=,即AR AB =,∴点A 为RD 的中点,又E 为PD 中点, 则6,3,2PD RD DA DE PDA ADP π====∠=∠=,PAD RED ∴≅,MPE MRA ∴∠=∠,又,PME RMA PE RA ∠=∠=,PME RMA ∴≅,则ME MA =,过M 作MK PD ⊥交PD 于点K ,222PM MK MK ME MA PA AD DR RE PA∴==⋅=⋅=⋅, 则2PM MA =,2233PM MA PA MA ∴==; 连接MN ,BD 由23PM PA =同理可得23PN PC =, //MN AC ∴,又PD ⊥平面ABCD ,AC ⊂平面ABCD ,PD AC ∴⊥,又,BD AC BD PD D ⊥=,AC ∴⊥面PBD ,又BE ⊂面PBD ,AC BE ∴⊥,MN BE ∴⊥,23MN PM AC PA ==, 2233MN AC ∴==⨯又EB ==所以四边形EMBN 的面积为1122MN EB ⋅=⨯=故答案为:23;【点睛】本题考查空间线面平行的判定和性质,考查空间线面垂直的判定和性质,关键是利用线面平行的性质合理作出图像,考查学生的作图能力和计算能力,是中档题.21.证明见解析【分析】如图,连接AN并延长,交DC的延长线于点E,连接PE,可得N为AE的中点,再由三角形中位线定理可得MN∥PE,然后由线面平行的判定定理可证得结论【详解】证明:如图,连接AN并延长,交DC的延长线于点E,连接PE.因为CD∥AB,N为BC的中点,所以N为AE的中点.因为M为PA的中点,所以MN∥PE.因为MN⊄平面PDC,PE⊂平面PDC,所以MN∥平面PDC.22.证明见解析【分析】MN平面ABCD.通过线线平行来证得//【详解】连接BD , ∵PM PN PB PD=,∴//MN BD , ∵MN ⊄平面ABCD ,BD ⊂平面ABCD ,∴//MN 平面ABCD .23.(1)证明见解析;(2)45︒【分析】(1)连接11,A C AC ,通过证明//FG 平面11A ACC 与//EG 平面11A ACC ,可得平面//EFG 平面11A ACC ;(2)找到1C AC ∠为异面直线GE 和AC 所成角,求1C AC ∠即可.【详解】证明:(1)由题意可得,点,F G 分别是BC 和1BA 的中点,连接11,A C AC ,1//FG A C ∴,又FG ⊄平面111,A ACC A C ⊂平面11A ACC ,//FG ∴平面11A ACC ,同理:1//EF C C ,则 //EF 平面11A ACC ,又,FG EF F FG =⊂平面,EFG EF ⊂平面EFG ,∴平面//EFG 平面11A ACC ;(2)点,G E 分别是1B A 和11B C 的中点,1//GE AC ∴,1C AC ∴∠为异面直线GE 和AC 所成角,由题意知,四边形11ACC A 为正方形,所以145C AC ︒∠=,即GE 和AC 所成角为45︒.【点睛】本题考查通过线面平行证明面面平行,考查异面直线所成的角,是基础题.24.(1)证明见解析;(2)证明见解析.【分析】(1)连接SB ,得到EG ∥SB ,结合线面平行的判定定理,即可证得EG ∥平面BDD 1B 1. (2)连接SD ,得到FG ∥SD ,证得FG ∥平面BDD 1B 1,再由EG ∥平面BDD 1B 1,面面平行的判定定理,即可证得平面EFG ∥平面BDD 1B 1.【详解】(1)如图所示,连接SB ,因为E ,G 分别是BC ,SC 的中点,所以EG ∥SB ,又因为SB ⊂平面BDD 1B 1,且EG ⊄平面BDD 1B 1,所以直线EG ∥平面BDD 1B 1.(2)如图所示,连接SD ,因为F ,G 分别是CD ,SC 的中点,所以FG ∥SD , 又因为SD ⊂平面BDD 1B 1,且FG ⊄平面BDD 1B 1,所以FG ∥平面BDD 1B 1,又由EG ∥平面BDD 1B 1,EG ⊂平面EFG ,FG ⊂平面EFG ,EG ∩FG =G ,所以平面EFG ∥平面BDD 1B 1.25.(1)证明见解析(2)30︒【分析】(1)连结PO ,先证线线平行,再证线面平行即可;(2)由(1)知,1PO BD ∥,所以APO ∠即为异面直线1BD 与AP 所成的角,然后再解三角形即可.(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点.连结PO ,又因为P 是1DD 的中点,所以1PO BD ∥.又因为PO ⊂平面1,PAC BD ⊄平面PAC所以直线1BD ∥平面PAC .(2)由(1)知,1PO BD ∥,所以APO ∠即为异面直线1BD 与AP 所成的角.在ADP △中可得PA =因为12PA PC AO AC ===且PO AO ⊥,所以1sin2AO APO AP ∠===. 又090APO ︒︒<∠≤,所以30APO ︒∠=故异面直线1BD 与AP 所成角的大小为30︒.26.证明见解析【分析】连接OG 并延长,交AC 于点M ,连接QM ,QO ,由已知可得M 为AC 的中点,//QM PC ,//OM BC ,可证//QM 平面PBC ,//OM 平面PBC ,从而平面//QMO 平面PBC , 即可证明结论.【详解】证明:如图,连接OG 并延长,交AC 于点M ,连接QM ,QO .由G 为AOC △的重心,得M 为AC 的中点.由Q 为M 的中点,得//QM PC ,PC ⊂平面PBC ,QM ⊄平面PBC ,所以//QM 平面PBC ,又O 为AB 的中点,所以//OM BC .同理可证//OM 平面PBC ,因为QM MO M ⋂=,QM ⊂平面QMO ,MO ⊂平面QMO ,所以平面//QMO 平面PBC .因为QG ⊂平面QMO ,所以//QG 平面PBC .【点睛】本题考查利用面面平行的性质定理证明线面平行,属于基础题.27.(1)证明见解析;(2)274 【分析】(1)由面面平行的性质定理得证线线平行;(2)由平行线的性质可求得线段长.【详解】(1)PB PD P =,所以,PB PD 确定一个平面PBD ,由题意平面PBD AC α=,平面PBD BD β=,//αβ所以//AC BD ;(2)由(1)//AC BD ,所以PA PC AB CD =,所以351544PC AB CD PA ⋅⨯===, 所以1527344PD PC CD =+=+=. 28.证明见解析【分析】连接DC ,设DC 与平面β相交于点G ,连,BG GE ,根据面面平行的性质定理,可得//BG AD ,利用三角形相似关系,即可证明结论.【详解】证明:连接DC ,设DC 与平面β相交于点G ,则平面ACD 与平面α,β分别相交于直线AD ,BG ,平面DCF 与平面β,γ分别相交于直线GE ,CF .因为//αβ,所以//BG AD ,因此CBG CAD ,因此AB DG BC GC=.同理可得DG DE GC EF =.因此AB DE BC EF =. 【点睛】本题考查根据面面平行的性质定理,以及线线平行的性质,属于基础题.29.证明见解析.【分析】由αβ∥得到AC EG HF ,同理得到BD EH GF ,所以四边形EHFG 为平行四边形.【详解】证明:∵平面ABC平面AC α=, 平面ABC平面BC β=,且αβ∥AC EG ∴. 同理可证AC HF .EG HF ∴.同理可证∥EH FG .∴四边形EHFG 为平行四边形.【点睛】本题考查面面平行的性质,属于简单题.30.(1)证明见解析;(2)在OD 上是存在OE 中点F ,使//BF 平面ACE 成立,证明见解析.【分析】(1)取AD 上靠近A 的三等分点G ,连接MG NG ,,可得//MG OD ,进而证明//MG 平面OCD ,同理证明//NG 平面OCD ,得出面//MNG 平面OCD 即可证明;(2)存在OE 中点F ,连BF BD ,,使=BD AC P ⋂,连PE ,得出//PE BF 即可证明. 【详解】(1)如图,取AD 上靠近A 的三等分点G ,连接MG NG ,,AOD △中,:1:2:=1:2AM MO AG GD =,, 则//MG OD ,又MG ⊄平面OCD ,OD ⊂平面OCD ,//MG ∴平面OCD ,同理,//NG 平面OCD ,又=MG NG G ⋂,∴平面//MNG 平面OCD ,又MN ⊂平面MNG ,∴//MN 平面OCD .(2)存在OE 中点F ,使//BF 平面ACE 成立.取OE 中点F ,连BF BD ,,使=BD AC P ⋂,连PE .ABCD 是矩形,P ∴是BD 的中点,又E 是OD 上靠近点D 的一个三等分点,且F 是OE 中点,E ∴是FD 的中点,BDF ∴中,//PE BF ,又PE ⊂平面ACE ,BF ⊄平面ACE ,//BF ∴平面ACE ,故在OD 上是存在OE 中点F ,使//BF 平面ACE 成立.【点睛】关键点睛:本题考查线面平行的证明,解题的关键是正确理解线面平行的判定定理以及面面平行的性质.31.(1)MHQN 是过,,M N Q 三点的截面,梯形;(2)证明见解析.【分析】(1)取11A C 中点H ,连接 HQ QN ,, NM ,MH ,即可得出结果; (2)连接11,BC AC ,根据面面平行的判定定理,得到平面//MNQ 平面1ABC ,进而可得线面平行.【详解】(1)取11A C 中点H ,连接 HQ QN ,, NM ,MH ,则梯形MHQN 是过,,M N Q 三点的截面,如图所示.(2)连接11,BC AC .∵三棱柱111ABC A B C -是直三棱柱,∴四边形11ABB A 是矩形.∵,M N 分别是11,AA BB 的中点,∴//MN AB .在11B C B 中,,Q N 分别是111,B C BB 的中点,∴1//NQ BC .又∵1,AB BC B MN NQ N ⋂=⋂=,∴平面//MNQ 平面1ABC .又∵P 是AB 的中点,∴1PC ⊂平面1ABC ,∴1//PC 平面MNQ .【点睛】本题主要考查几何体过点的截面图形,以及证明线面平行,熟记面面平行的判定定理与性质定理即可,属于常考题型.32.是定值1,理由见解析.【分析】连接1A B 交1AB 于点O ,连接1OD ,由平面1BC D ∥平面11AB D ,得到1BC ∥1OD ,1AD ∥1DC ,则四边形11ADC D 是平行四边形,根据111112C D AC =,得到11111122AD C D AC AC ===,从而可得1AD DC = 【详解】解:如图,连接1A B 交1AB 于点O ,连接1OD ,由棱柱的性质,可知四边形11A ABB 为平行四边形,所以O 为1A B 的中点,因为平面1BC D ∥平面11AB D ,且平面11A BC ⋂平面111AB D D O =,平面11A BC ⋂平面11BC D BC =,所以1BC ∥1OD ,所以1D 为线段11A C 的中点,所以111112C D AC =, 因为平面1BC D ∥平面11AB D ,平面11AAC C平面11BDC DC =,平面11AAC C 平面111AB D AD =, 所以1AD ∥1DC ,因为AD ∥11C D ,所以四边形11ADC D 是平行四边形, 所以11111122AD C D AC AC ===, 所以1AD DC =,33.(1)证明见解析;(2)存在,13=PD BP . 【分析】 (1)首先根据题意易证AE EB ⊥,再根据面面垂直的性质得到EB ⊥平面AED ,从而得到EB AD ⊥.(2)首先在AB 上取一点的F ,满足14AF AB =,在BD 上取一点的P ,满足14DP DB =,连接,,PF PC FC ,易证//PF 平面ADE ,//PF 平面ADE ,从而得到平面//PFC 平面ADE ,再利用面面平行的性质得到//PC 平面ADE ,从而得到13=PD BP . 【详解】(1)在梯形ABCE 中,取AB 的中点H ,连接EH ,BE ,如图所示所以AE ==BE == 又因为4AB =,所以222AE BE AB +=,即AE EB ⊥. 在图2中,因为平面ADE ⊥平面ABCE AE =,AE EB ⊥,所以EB ⊥平面AED .又因为AD ⊂平面AED ,所以EB AD ⊥.(2)在AB 上取一点的F ,满足14AF AB =, 在BD 上取一点的P ,满足14DP DB =,连接,,PF PC FC ,如图所示:因为//AF EC ,AF EC =,所以四边形AFCE 为平行四边形, 所以//FC AE .又因为AE ⊂平面ADE ,⊄FC 平面ADE ,所以//FC 平面ADE , 因为34BF BP BA BD ==,所以//PF AD . 又因为AD ⊂平面ADE ,PF ⊄平面ADE ,所以//PF 平面ADE , 又因为PF ⊂平面PFC ,PC ⊂平面PFC ,FCPF F =, 所以平面//PFC 平面ADE .又因为PC ⊂平面PFC ,所以//PC 平面ADE . 所以13=PD BP .。

立体证明题(2)1•如图,直二面角D- AB- E中,四边形ABCD是正方形,AE=EB F为CE上的点,且BF丄平面ACE(1) 求证:AE丄平面BCE(2) 求二面角B-AC- E的余弦值.2•等腰△ ABC中, AC=BC= AB=2, E、F分别为AC BC的中点,将△ EFC沿EF折起,使得C 至U P,得至U四棱锥P— ABFE 且AP=BP=(1) 求证:平面EFP!平面ABFE(2) 求二面角B-AP- E的大小.3•如图,在四棱锥P- ABCD中,底面是正方形,侧面PADL底面ABCD且PA=PD= AD,若E、F分别为PC BD的中点.(I)求证:EF//平面PAD(n)求证:EF丄平面PDC4•如图:正△ ABC与Rt△ BCD所在平面互相垂直,且/ BCD=90°,/ CBD=30°(1)求证:AB丄CD(2)求二面角D- AB- C的正切值.5•如图,在四棱锥P- ABCD中,平面PADL平面ABCD^ PAD是等边三角形,四边形ABCD 是平行四边形,/ ADC=120 , AB=2AD(1)求证:平面PADL平面PBD(2)求二面角A- PB- C的余弦值.6•如图,在直三棱柱ABC- A1B1C1 中,/ ACB=90°, AC=CB=CC2, E是AB中点.(I)求证:AB丄平面ACE(H)求直线AG与平面ACE所成角的正弦值.7•如图,在四棱锥P- ABCD中, PA丄平面ABCD / DAB为直角,AB// CD, AD=CD=2AB=2E, F分别为PC, CD的中点.(I)证明:AB丄平面BEF;(H)若PA=求二面角E- BD- C.8•如图,在四棱锥P-ABCD 中,PA丄平面ABCD , PA=AB=AD=2,四边形ABCD 满足AB 丄AD , BC // AD 且BC=4,点M 为PC 中点.(I)求证:DM丄平面PBC;BE(2)若点E为BC边上的动点,且一一,是否存在实数人使得二面角P- DE - B的EC2余弦值为-?若存在,求出实数入的值;若不存在,请说明理由.39•如图,ABED是长方形,平面ABEDL平面ABC AB=AC=5 BC=BE=6且M是BC的中点(I) 求证:AM L平面BEC(H) 求三棱锥B- ACE的体积;(川)若点Q是线段AD上的一点,且平面QECL平面BEC求线段AQ的长.10. 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB// CD AB丄BC, AB=2CD=2BC EA L EB(1)求证:EA丄平面EBC(2)求二面角C- BE- D的余弦值.11. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD// BC, / ADC=90°,平面PADL 底面ABCD O为AD中点,M是棱PC上的点,AD=2BC(1)求证:平面POBL平面PAD12. 如图,三棱柱ABC- A1B1C中,侧棱AA丄平面ABC △ ABC为等腰直角三角形,/BAC=90,且AB=AA, E、F 分别是CC, BC的中点.(1)求证:平面ABF丄平面AEF;(2)求二面角B1- AE- F 的余弦值.13. 如图,在菱形ABCD中,/ ABC=60°, AC与BD相交于点Q AE丄平面ABCD CF/ AE, AB=AE=2.(I )求证:BD丄平面ACFE(II )当直线FO与平面BDE所成的角为45。
立体几何之平行、垂直的性质与证明重难点突破重难点突破一 线线、线面与面面平行的性质例1.(1)、(2022·宁夏·银川一中模拟预测(文))如图,在下列四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,则在这四个正方体中,直线AB 不平行于平面MNQ 的是( )A .B .C .D .(2)、已知l ,m ,n 是三条不同的直线,α,β,γ是三个不同的平面,则下列命题一定正确的是( ) A .若//m α,//m n ,则//n αB .若m α⊂,n ⊂α,且满足//m β,βn//,则//αβC .若l αβ=,m αγ=,n βγ=,且满足//l m ,则//m nD .若m α⊂,n ⊂α,l β⊂,且//m β,//n l ,则//αβ 【变式训练1-1】、(2022·浙江·海宁中学模拟预测)已知a b c ,,是不全平行的直线,αβγ,,是不同的平面,则下列能够得到//αβ的是( )A .αβγγ⊥⊥,B .////a b a b ααββ⊂⊂,,,C .//////a b c a b c αααβββ⊂⊂⊂,,,,,D .////b b αβ,【变式训练1-2】、(2022·广东广州·三模)一几何体的平面展开图如图所示,其中四边形ABCD 为正方形,E F 、分别为PB PC 、的中点,在此几何体中,下面结论错误的是( )A.直线AE与直线BF异面B.直线AE与直线DF异面C.直线EF平面PAD D.直线EF平面ABCD 重难点突破二线线、线面与面面平行的证明例2.(1)如图,在四棱锥PABCD中,AD∥BC,AB=BC=12AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.(1)求证:AP∥平面BEF;(2)求证:GH∥平面PAD.(2)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,,,,EAB FBC GCD HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.(1)证明://EF平面ABCD;(2)求该包装盒的容积(不计包装盒材料的厚度).【变式训练2-1】、(2022·全国·模拟预测)在四棱锥P ABCD-中,PA⊥平面ABCD,四边形ABCD是矩形,1,,2AB AP AD E F ==分别是AP BC ,的中点.求证://EF 平面PCD ;例3、如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,124AA AB ==,M ,N ,P 分别是11,,AD DD CC 的中点.(1)证明:平面//MNC 平面1AD P .(2)求三棱锥1D ADP -的体积.【变式训练3-1】、(2022·河南·模拟预测(文))如图,在四棱柱1111ABCD A B C D -中,四边形ABCD 是正方形,E ,F ,G分别是棱1BB ,11B C ,1CC 的中点.(1)证明:平面1//A EF 平面1AD G ;(2)若点1A 在底面ABCD 的投影是四边形ABCD 的中心,124A A AB ==,求三棱锥11A AD G -的体积.【变式训练3-2】、已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BFDE ⊥.重难点突破三 线线、线面与面面垂直的性质例4.(1)、(北京市第十一中学一模)设m ,n 是两条不同的直线,α,β是两个不同的平面,则下列说法正确的是( )A .若m ⊥n ,n ∥α,则m ⊥αB .若m ∥β,β⊥α,则m ⊥αC .若m ⊥β,n ⊥β,n ⊥α,则m ⊥αD .若m ⊥n ,n ⊥β,β⊥α,则m ⊥α【变式训练4-1】.(多选题)(重庆一中高三月考)已知平面α和两条不同的直线m ,n ,下面的条件中一定可以推出m n⊥的是( )A .m α⊥,//n αB .m α⊥,n α⊥C .m α⊂,n α⊥D .//m α,//n α【变式训练4-2】、(2022·四川省泸县第二中学模拟预测(理))如图,在梯形ABCD 中,,90,2,1AB CD ABC AB BC CD ∠=︒===∥,点E 为AB 中点,将ADE 沿直线DE 向上折起到A DE '的位置(平面A DE '与平面ABCD 不重合).在折叠的过程中,给出下列结论:①任意时刻都有BC ∥平面A DE ';②任意时刻都有平面BCD ⊥平面A BE '﹔③存在某个位置,使得'AA DB ⊥﹔④当平面A DE '⊥平面BCDE 时,直线AD 与平面A DB '6其中所有正确结论的序号是___________.重难点突破四 线线、线面与面面垂直的证明例5.((2019·全国Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥E -BB 1C 1C 的体积.【变式训练5-1】、(如图,在三棱锥ABCD 中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E ,F (E 与A ,D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF∥平面ABC;(2)AD⊥AC.例6、如图,三棱锥P-ABC中,底面ABC是边长为2的正三角形,P A⊥PC,PB=2.(1)求证:平面P AC⊥平面ABC;(2)若P A=PC,求三棱锥P-ABC的体积.例6-2如图,正方体的棱长为1,B′C∩BC′=O,求:(1)AO与A′C′所成角的大小;(2)AO与平面ABCD所成角的正切值;(3)平面AOB与平面AOC所成角的大小.【变式训练6-1】、(在矩形ABCD中,AB=2AD=4,E是AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥P -BCDE.(1)若平面PDE⊥平面BCDE,求四棱锥P-BCDE的体积;(2)若PB=PC,求证:平面PDE⊥平面BCDE.【变式训练6-2】、如图,已知点E,F分别在正方体ABCD-A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则平面AEF 与平面ABC 所成的二面角的正切值为________.重难点突破五 平行、垂直关系中的探索性问题例7、(2021·湖南·长沙市第二十一中学高一期中)如图:在正方体1111ABCD A B C D -中,E 为1DD 的中点.(1)求证:1//BD 平面AEC ;(2)1CC 上是否存在一点F ,使得平面//AEC 平面1BFD ,若存在请说明理由.【变式训练7-1】、(2021·全国·高一单元测试)如图①,O 的直径2AB =,圆上两点,C D 在直线AB 的两侧,且45CAB ∠=︒,60DAB ∠=︒,沿直线AB 将半圆ACB 折起,使两个半圆所在的平面互相垂直(如图②),F 为BC 的中点,E 为AO 的中点.根据图②解答下列各题:(1)求三棱锥C BOD -的体积;(2)求证:CB DE ⊥;(3)在BD 上是否存在一点G ,使得//FG 平面ACD ?若存在,试确定点G 的位置;若不存在,请说明理由.例8、如图1,在Rt ABC ∆中,90C ∠=︒,D ,E 分别为AC ,AB 的中点,点F 是线段CD 上的一点,将ADE ∆沿DE折起到1A DE △的位置,使1A F CD ⊥,如图2.(1)证明:1A F BE ⊥;(2)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?若存在,求出11A Q A B 的值;若不存在,说明理由.【变式训练8-1】、(2021·陕西·西安)如图,在四棱锥P ABCD -中四边形ABCD 为平行四边形,90BAP CDP ∠=∠=︒,PAD △是正三角形,且PA AB =.(1)当点M 在线段PA 上什么位置时,有DM ⊥平面PAB ?(2)在(1)的条件下,点N 在线段PB 上什么位置时,有平面DMN ⊥平面PBC ?课时精练1.如图,在四棱锥PABCD中,M,N分别为棱PA,PD的中点.已知侧面PAD⊥底面ABCD,底面ABCD是矩形,DA =DP.求证:(1)MN∥平面PBC;MD⊥平面PAB.2.如图,三棱锥DABC中,已知AC⊥BC,AC⊥DC,BC=DC,E,F分别为BD,CD的中点.求证:(1) EF∥平面ABC;(2) BD⊥平面ACE.3.如图,在直三棱柱ABCA1B1C1中,D,E分别为AB,AC的中点.(1) 求证:B 1C 1∥平面A 1DE ;(2) 若平面A 1DE ⊥平面ABB 1A 1,求证:AB ⊥DE.4.如图,在直三棱柱ABCA 1B 1C 1中,∠ABC =90°,AB =AA 1,M ,N 分别是AC ,B 1C 1的中点.求证: (1) MN ∥平面ABB 1A 1; (2) AN ⊥A 1B.5.如图,在直三棱柱111ABC A B C -中,90,2BAC AB AC ∠=︒==,点M 为11A C 的中点,点N 为1AB 上一动点.(1)是否存在点N ,使得线段//MN 平面11BB C C ?若存在,指出点N 的位置,若不存在,请说明理由; (2)若点N 为1AB 的中点,且CM MN ⊥,求三棱锥M NAC -的体积.6.(2021·全国·高一课时练习)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 为直角梯形,//,AB CD AB AD ⊥,且2CD AB =.(1)若AB AD =,直线PB 与CD 所成的角为45︒,求二面角P CD B --的大小;(2)若E 为线段PC 上一点,试确定点E 的位置,使得平面EBD ⊥平面ABCD ,并说明理由.。
立体证明题(2)1.如图,直二面角D﹣AB﹣E中,四边形ABCD是正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(1)求证:AE⊥平面BCE;(2)求二面角B﹣AC﹣E的余弦值.2.等腰△ABC中,AC=BC=,AB=2,E、F分别为AC、BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP=.(1)求证:平面EFP⊥平面ABFE;(2)求二面角B﹣AP﹣E的大小.3.如图,在四棱锥P﹣ABCD中,底面是正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,若E、F分别为PC、BD的中点.(Ⅰ)求证:EF∥平面PAD;(Ⅱ)求证:EF⊥平面PDC.4.如图:正△ABC与Rt△BCD所在平面互相垂直,且∠BCD=90°,∠CBD=30°.(1)求证:AB⊥CD;(2)求二面角D﹣AB﹣C的正切值.5.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD 是平行四边形,∠ADC=120°,AB=2AD.(1)求证:平面PAD⊥平面PBD;(2)求二面角A﹣PB﹣C的余弦值.6.如图,在直三棱柱ABC ﹣A 1B 1C 1中,∠ACB=90°,AC=CB=CC 1=2,E 是AB 中点.(Ⅰ)求证:AB 1⊥平面A 1CE ;(Ⅱ)求直线A 1C 1与平面A 1CE 所成角的正弦值.7.如图,在四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,∠DAB 为直角,AB ∥CD ,AD=CD=2AB=2,E ,F 分别为PC ,CD 的中点.(Ⅰ)证明:AB ⊥平面BEF ;(Ⅱ)若PA=,求二面角E ﹣BD ﹣C .8.如图,在四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,PA=AB=AD=2,四边形ABCD 满足AB ⊥AD ,BC ∥AD 且BC=4,点M 为PC 中点.(1)求证:DM ⊥平面PBC ;(2)若点E 为BC 边上的动点,且λ=EC BE ,是否存在实数λ,使得二面角P ﹣DE ﹣B 的余弦值为32?若存在,求出实数λ的值;若不存在,请说明理由.9.如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点(Ⅰ)求证:AM⊥平面BEC;(Ⅱ)求三棱锥B﹣ACE的体积;(Ⅲ)若点Q是线段AD上的一点,且平面QEC⊥平面BEC,求线段AQ的长.10.如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB(1)求证:EA⊥平面EBC(2)求二面角C﹣BE﹣D的余弦值.11.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.(1)求证:平面POB⊥平面PAD;12.如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E、F分别是CC1,BC的中点.(1)求证:平面AB1F⊥平面AEF;(2)求二面角B1﹣AE﹣F的余弦值.13.如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.( I)求证:BD⊥平面ACFE;( II)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦角.14.如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.(1)证明:平面PAD⊥平面ABFE;(2)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是.15.如图,已知斜三棱柱ABC一A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.(Ⅰ)求证:AC1⊥平面A1BC;(Ⅱ)求二面角A﹣A1B﹣C的平面角的余弦值.试卷答案1.【考点】与二面角有关的立体几何综合题;直线与平面垂直的判定.【分析】(1)由已知中直二面角D﹣AB﹣E中,四边形ABCD是正方形,且BF⊥平面ACE,我们可以证得BF⊥AE,CB⊥AE,进而由线面垂直的判定定理可得AE⊥平面BCE.(2)连接BD与AC交于G,连接FG,设正方形ABCD的边长为2,由三垂线定理及二面角的平面角的定义,可得∠BGF是二面角B﹣AC﹣E的平面角,解Rt△BFG即可得到答案.【解答】证明:(1)∵BF⊥平面ACE∴BF⊥AE…∵二面角D﹣AB﹣E为直二面角,且CB⊥AB,∴CB⊥平面ABE∴CB⊥AE…∴AE⊥平面BCE.…解:(2)连接BD与AC交于G,连接FG,设正方形ABCD的边长为2,∴BG⊥AC,BG=,…∵BF垂直于平面ACE,由三垂线定理逆定理得FG⊥AC∴∠BGF是二面角B﹣AC﹣E的平面角…由(1)AE⊥平面BCE,得AE⊥EB,∵AE=EB,BE=.∴在Rt△BCE中,EC==,…由等面积法求得,则∴在Rt△BFG中,故二面角B﹣AC﹣E的余弦值为.…2.【考点】二面角的平面角及求法;平面与平面垂直的判定.【分析】(1)用分析法找思路,用综合法证明.取EF中点O,连接OP、OC.等腰三角形CEF中有CO⊥EF,即OP⊥EF.根据两平面垂直的性质定理,平面PEF和平面ABFE的交线是EF,且PO⊥EF,分析得PO⊥平面ABFE.故只需根据题中条件证出PO⊥平面ABFE,即可利用面面垂直的判定定理证得平面EFP⊥平面ABFE.(2)根据第一问分析空间位置关系,可建立空间直角坐标线求得平面ABP和平面AEP的法向量的所成角,利用向量角和二面角关系,确定二面角大小.【解答】解:(1)证明:在△ABC中,D为AB中点,O为EF中点.由AC=BC=,AB=2.∵E、F分别为AC、BC的中点,∴EF为中位线,得CO=OD=1,CO⊥EF∴四棱锥P﹣ABFE中,PO⊥EF,…2分∵OD⊥AB,AD=OD=1,∴AO=,又AP=,OP=1,∴四棱锥P﹣ABFE中,有AP2=AO2+OP2,即OP⊥AO,…4分又AO∩EF=O,EF、AO⊂平面ABFE,∴OP⊥平面ABFE,…5分又OP⊂平面EFP,∴平面EFP⊥平面ABFE.…6分(2)由(1)知OD,OF,OP两两垂直,以O为原点,建立空间直角坐标系(如图):则A(1,﹣1,0),B(1,1,0),E(0,,0),P(0,0,1)…7分∴,,设,分别为平面AEP、平面ABP的一个法向量,则⇒取x=1,得y=2,z=﹣1∴.…9分同理可得,…11分由于=0,所以二面角B﹣AP﹣E为90°.…12分3.【考点】空间中直线与平面之间的位置关系.【专题】证明题.【分析】对于(Ⅰ),要证EF∥平面PAD,只需证明EF平行于平面PAD内的一条直线即可,而E、F分别为PC、BD的中点,所以连接AC,EF为中位线,从而得证;对于(Ⅱ)要证明EF⊥平面PDC,由第一问的结论,EF∥PA,只需证PA⊥平面PDC即可,已知PA=PD=AD,可得PA⊥PD,只需再证明PA⊥CD,而这需要再证明CD⊥平面PAD,由于ABCD是正方形,面PAD⊥底面ABCD,由面面垂直的性质可以证明,从而得证.【解答】证明:(Ⅰ)连接AC,则F是AC的中点,在△CPA中,EF∥PA(3分)且PA⊂平面PAD,EF⊊平面PAD,∴EF∥平面PAD(6分)(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA(9分)又PA=PD=AD,所以△PAD是等腰直角三角形,且∠APD=,即PA⊥PD(12分)而CD∩PD=D,∴PA⊥平面PDC,又EF∥PA,所以EF⊥平面PDC(14分)【点评】本题考查线面平行的判定及线面垂直的判定,而其中的转化思想的应用值得注意,将线面平行转化为线线平行;证明线面垂直,转化为线线垂直,在证明线线垂直时,往往还要通过线面垂直来进行.4.【考点】与二面角有关的立体几何综合题;空间中直线与直线之间的位置关系.【分析】(1)利用平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,可得DC⊥平面ABC,利用线面垂直的性质,可得DC⊥AB;(2)过C作CE⊥AB于E,连接ED,可证∠CED是二面角D﹣AB﹣C的平面角.设CD=a,则BC==,从而EC=BCsin60°=,在Rt△DEC中,可求tan∠DEC.【解答】(1)证明:∵DC⊥BC,且平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,∴DC⊥平面ABC,又AB⊂平面ABC,∴DC⊥AB.…(2)解:过C作CE⊥AB于E,连接ED,∵AB⊥CD,AB⊥EC,CD∩EC=C,∴AB⊥平面ECD,又DE⊂平面ECD,∴AB⊥ED,∴∠CED是二面角D﹣AB﹣C的平面角,…设CD=a,则BC==,∵△ABC是正三角形,∴EC=BCsin60°=,在Rt△DEC中,tan∠DEC=.…5.【考点】MT:二面角的平面角及求法;LY:平面与平面垂直的判定.【分析】(1)令AD=1,求出BD=,从而AD⊥BD,进而BD⊥平面PAD,由此能证明平面PAD⊥平面PBD.(2)以D为坐标原点,DA为x轴,DC为y轴,过D作垂直于平面ABCD的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PB﹣C的余弦值.【解答】证明:(1)在平行四边形ABCD中,令AD=1,则BD==,在△ABD中,AD2+BD2=AB2,∴AD⊥BD,又平面PAD⊥平面ABCD,∴BD⊥平面PAD,BD⊂平面PBD,∴平面PAD⊥平面PBD.解:(2)由(1)得AD⊥BD,以D为坐标原点,DA为x轴,DC为y轴,过D作垂直于平面ABCD的直线为z轴,建立空间直角坐标系,令AD=1,则A(1,0,0),B(0,,0),C(﹣1,,0),P(,0,),=(﹣1,,0),=(﹣),=(﹣1,0,0),设平面PAB的法向量为=(x,y,z),则,取y=1,得=(),设平面PBC的法向量=(a,b,c),,取b=1,得=(0,1,2),∴cos<>===,由图形知二面角A﹣PB﹣C的平面角为钝角,∴二面角A﹣PB﹣C的余弦值为﹣.6.【考点】直线与平面垂直的判定;直线与平面所成的角.【分析】(Ⅰ)由ABC﹣A1B1C1是直三棱柱,可知CC1⊥AC,CC1⊥BC,∠ACB=90°,AC⊥BC.建立空间直角坐标系C﹣xyz.则A,B1,E,A1,可得,,,可知,根据,,推断出AB1⊥CE,AB1⊥CA1,根据线面垂直的判定定理可知AB1⊥平面A1CE.(Ⅱ)由(Ⅰ)知是平面A1CE的法向量,,进而利用向量数量积求得直线A1C1与平面A1CE所成角的正弦值【解答】(Ⅰ)证明:∵ABC﹣A1B1C1是直三棱柱,∴CC1⊥AC,CC1⊥BC,又∠ACB=90°,即AC⊥BC.如图所示,建立空间直角坐标系C﹣xyz.A(2,0,0),B1(0,2,2),E(1,1,0),A1(2,0,2),∴,,.又因为,,∴AB1⊥CE,AB1⊥CA1,AB1⊥平面A1CE.(Ⅱ)解:由(Ⅰ)知,是平面A1CE的法向量,,∴|cos<,>|==.设直线A1C1与平面A1CE所成的角为θ,则sinθ=|cos<,>|=.所以直线A1C1与平面A1CE所成角的正弦值为.7.【考点】二面角的平面角及求法;直线与平面垂直的判定.【分析】(Ⅰ)只需证明AB⊥BF.AB⊥EF即可.(Ⅱ)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,求出平面CDB的法向量为,平面EDB的法向量为,设二面角E﹣BD﹣C的大小为θ,则=,【解答】解:(Ⅰ)证:由已知DF∥AB且∠DAB为直角,故ABFD是矩形,从而AB⊥BF.又PA⊥底面ABCD,∴平面PAD⊥平面ABCD,∵AB⊥AD,故AB⊥平面PAD,∴AB⊥PD,在△PCD内,E、F分别是PC、CD的中点,EF∥PD,∴AB⊥EF.由此得AB⊥平面BEF…(Ⅱ)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,则设平面CDB的法向量为,平面EDB的法向量为,则可取设二面角E﹣BD﹣C的大小为θ,则=,所以,…8.【考点】二面角的平面角及求法;直线与平面垂直的判定.【分析】(1)取PB中点N,连结MN,AN.由三角形中位线定理可得四边形ADMN为平行四边形.由AP⊥AD,AB⊥AD,由线面垂直的判定可得AD⊥平面PAB.进一步得到AN⊥MN.再由AP=AB,得AN⊥PB,则AN⊥平面PBC.又AN∥DM,得DM⊥平面PBC;(2)以A为原点,方向为x轴的正方向,方向为y轴的正方向,方向为z轴的正方向,建立如图所示的空间直角坐标系.设E(2,t,0)(0≤t≤4),再求得P,D,B的坐标,得到的坐标,求出平面PDE的法向量,再由题意得到平面DEB的一个法向量,由两法向量夹角的余弦值得到实数λ的值.【解答】(1)证明:如图,取PB中点N,连结MN,AN.∵M是PC中点,∴MN∥BC,MN=BC=2.又∵BC∥AD,AD=2,∴MN∥AD,MN=AD,∴四边形ADMN为平行四边形.∵AP⊥AD,AB⊥AD,AP∩AB=A,∴AD⊥平面PAB.∵AN⊂平面PAB,∴AD⊥AN,则AN⊥MN.∵AP=AB,∴AN⊥PB,又MN∩PB=N,∴AN⊥平面PBC.∵AN∥DM,∴DM⊥平面PBC;(2)解:存在符合条件的λ.以A为原点,方向为x轴的正方向,方向为y轴的正方向,方向为z轴的正方向,建立如图所示的空间直角坐标系.设E(2,t,0)(0≤t≤4),P(0,0,2),D(0,2,0),B(2,0,0),则,.设平面PDE的法向量=(x,y,z),则,令y=2,则z=2,x=t﹣2,取平面PDE的一个法向量为=(2﹣t,2,2).又平面DEB即为xAy平面,故其一个法向量为=(0,0,1),∴cos<>==.解得t=3或t=1,∴λ=3或.9.【考点】棱柱、棱锥、棱台的体积;平面与平面垂直的判定.【分析】(Ⅰ)推导出BE⊥AM,BC⊥AM,由此能证明AM⊥平面BEC.(Ⅱ)由V B﹣ACE=V E﹣ABC,能求出三棱锥B﹣ACE的体积.(Ⅲ)在平面QEC内作QN⊥EC,QN交CE于点N.QN与AM共面,设该平面为a,推导出四边形AMNQ是平行四方形,由此能求出AQ.【解答】证明:(Ⅰ)∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,BE⊥AB,BE⊂平面ABED,∴BE⊥平面ABC,又AM⊂平面ABC,∴BE⊥AM.又AB=AC,M是BC的中点,∴BC⊥AM,又BC∩BE=B,BC⊂平面BEC,BE⊂平面BEC,∴AM⊥平面BEC.解:(Ⅱ)由(Ⅰ)知,BE⊥平面ABC,∴h=BE=6.在Rt△ABM中,,又,∴.(Ⅲ)在平面QEC内作QN⊥EC,QN交CE于点N.∵平面QEC⊥平面BEC,平面QEC∩平面BEC﹣EC,∴QN⊥平面BEC,又AM⊥平面BEC.∴QN∥AM.∴QN与AM共面,设该平面为a,∵ABED是长方形,∴AQ∥BE,又Q⊄平面BEC,BE⊂平面BEC,∴AQ∥平面BEC,又AQ⊂α,α∩平面BEC=MN,∴AQ∥MN,又QN∥AM,∴四边形AMNQ是平行四方形.∴AQ=MN.∵AQ∥BE,AQ∥MN,∴MN∥BE,又M是BC的中点.∴,∴AQ=MN=3.10.【考点】二面角的平面角及求法;直线与平面垂直的判定.【分析】(1)根据线面垂直的判定定理即可证明EA⊥平面EBC;(2)求出平面的法向量,利用向量法进行求解即可.【解答】(1)∵平面ABE⊥平面ABCD,且AB⊥BC,∴BC⊥平面ABE∵EA⊂平面ABE,∴EA⊥BC,∵EA⊥EB,EB∩BC=B,∴EA⊥平面EBC(2)取AB中O,连接EO,DO.∵EB=EA,∴EO⊥AB.∵平面ABE⊥平面ABCD,∴EO⊥平面ABCD∵AB=2CD,AB∥CD,AB⊥BC,∴DO⊥AB,建立如图的空间直角坐标系O﹣xyz如图:设CD=1,则A(0,1,0),B(0,﹣1,0),C(1,﹣1,0),D(1,0,0),E(0,0,1),由(1)得平面EBC的法向量为=(0,1,﹣1),设平面BED的法向量为=(x,y,z),则,即,设x=1,则y=﹣1,z=1,则=(1,﹣1,1),则|cos<,>|===,故二面角C﹣BE﹣D的余弦值是.11.【考点】平面与平面垂直的判定;直线与平面平行的判定.【分析】(1)证明四边形BCDO是平行四边形,得出OB⊥AD;再证明BO⊥平面PAD,从而证明平面POB⊥平面PAD;(2)解法一:由,M为PC中点,证明N是AC的中点,MN∥PA,PA∥平面BMO.解法二:由PA∥平面BMO,证明N是AC的中点,M是PC的中点,得.【解答】解:(1)证明:∵AD∥BC,,O为AD的中点,∴四边形BCDO为平行四边形,∴CD∥BO;又∵∠ADC=90°,∴∠AOB=90°,即OB⊥AD;又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴BO⊥平面PAD;又∵BO⊂平面POB,∴平面POB⊥平面PAD;(2)解法一:,即M为PC中点,以下证明:连结AC,交BO于N,连结MN,∵AD∥BC,O为AD中点,AD=2BC,∴N是AC的中点,又点M是棱PC的中点,∴MN∥PA,∵PA⊄平面BMO,MN⊂平面BMO,∴PA∥平面BMO.解法二:连接AC,交BO于N,连结MN,∵PA∥平面BMO,平面BMO∩平面PAC=MN,∴PA∥MN;又∵AD∥BC,O为AD中点,AD=2BC,∴N是AC的中点,∴M是PC的中点,则.12.【考点】与二面角有关的立体几何综合题;平面与平面垂直的判定.【分析】(1)连结AF,由已知条件推导出面ABC⊥面BB1C1C,从而AF⊥B1F,由勾股定理得B1F⊥EF.由此能证明平面AB1F⊥平面AEF.(2)以F为坐标原点,FA,FB分别为x,y轴建立直角坐标系,利用向量法能求出二面角B1﹣AE﹣F的余弦值.【解答】(1)证明:连结AF,∵F是等腰直角三角形△ABC斜边BC的中点,∴AF⊥BC.又∵三棱柱ABC﹣A1B1C1为直三棱柱,∴面ABC⊥面BB1C1C,∴AF⊥面BB1C1C,AF⊥B1F.…设AB=AA 1=1,则,EF=,.∴=,∴B 1F ⊥EF .又AF ∩EF=F ,∴B 1F ⊥平面AEF .…而B 1F ⊂面AB 1F ,故:平面AB 1F ⊥平面AEF .…(2)解:以F 为坐标原点,FA ,FB 分别为x ,y 轴建立直角坐标系如图, 设AB=AA 1=1,则F (0,0,0),A (),B 1(0,﹣,1),E (0,﹣,),,=(﹣,,1).…由(1)知,B 1F ⊥平面AEF ,取平面AEF 的法向量:=(0,,1).…设平面B 1AE 的法向量为,由,取x=3,得.…设二面角B 1﹣AE ﹣F 的大小为θ,则cos θ=|cos <>|=||=.由图可知θ为锐角,∴所求二面角B 1﹣AE ﹣F 的余弦值为.…13.【考点】MT:二面角的平面角及求法;LW:直线与平面垂直的判定.【分析】( I)只需证明DB⊥AC,BD⊥AE,即可得BD⊥平面ACFE;( II)取EF的中点为M,以O为坐标原点,以OA为x轴,以OB为y轴,以OM为z轴,建立空间直角坐标系,则,D(0,﹣,0),F(﹣1,0,h),E(1,0,2),则,,利用向量法求解【解答】( I)证明:在菱形ABCD中,可得DB⊥AC,又因为AE⊥平面ABCD,∴BD⊥AE,且AE∩AC=A,BD⊥平面ACFE;( II)解:取EF的中点为M,以O为坐标原点,以OA为x轴,以OB为y轴,以OM为z 轴,建立空间直角坐标系,则,D(0,﹣,0),F(﹣1,0,h),E(1,0,2),则,,设平面BDE的法向量,由,可取,|cos|=,⇒h=3,故F(﹣1,0,3),,,设平面BFE的法向量为,由,可取,,设平面DFE的法向量为,由,可取,cos=,二面角B﹣EF﹣D的余弦值为.14.【考点】MT:二面角的平面角及求法;LY:平面与平面垂直的判定.【分析】(Ⅰ)证明:AD⊥平面ABFE,即可证明平面PAD⊥平面ABFE;(Ⅱ)建立空间坐标系,求出平面的法向量,利用向量法建立方程关系即可求正四棱锥P ﹣ABCD的高.【解答】(Ⅰ)证明:直三棱柱ADE﹣BCF中,AB⊥平面ADE,所以:AB⊥AD,又AD⊥AF,所以:AD⊥平面ABFE,AD⊂平面PAD,所以:平面PAD⊥平面ABFE….(Ⅱ)∵AD⊥平面ABFE,∴建立以A为坐标原点,AB,AE,AD分别为x,y,z轴的空间直角坐标系如图:设正四棱锥P﹣ABCD的高为h,AE=AD=2,则A(0,0,0),F(2,2,0),C(2,0,2),=(2,2,0),=(2,0,2),=(1,﹣h,1),=(x,y,z)是平面AFC的法向量,则,令x=1,则y=z=﹣1,即=(1,﹣1,﹣1),设=(x,y,z)是平面ACP的法向量,则,令x=1,则y=﹣1,z=﹣1﹣h,即=(1,﹣1,﹣1﹣h),∵二面角C﹣AF﹣P的余弦值是.∴cos<,>===.得h=1或h=﹣(舍)则正四棱锥P﹣ABCD的高h=1.15.【考点】二面角的平面角及求法;直线与平面垂直的判定.【专题】证明题;数形结合;综合法;空间位置关系与距离.【分析】(1)推导出BC⊥AC,BC⊥AC1,BA1⊥AC1,由此能证明AC1⊥平面A1BC.(2)推导出平面A1AB⊥平面BCF,过C作CH⊥BF于H,则CH⊥面A1AB,求出CH=,过H作HG⊥A1B于G,连CG,则CG⊥A1B,从而∠CGH为二面角A﹣A1B﹣C的平面角,由此能求出二面角A﹣A1B﹣C的平面角的余弦值.【解答】证明:(1)因为A1D⊥平面ABC,所以,平面AA1C1C⊥平面ABC,又BC⊥AC,所以,BC⊥平面AA1C1C,得BC⊥AC1,又BA1⊥AC1,所以,AC1⊥平面A1BC.解:(2)因为AC1⊥A1C,所以四边形AA1C1C为菱形,故AA1=AC=2,又D为AC中点,知∠A1AC=60°,取AA1的中点F,则AA1⊥平面BCF,从而,平面A1AB⊥平面BCF,过C作CH⊥BF于H,则CH⊥面A1AB,在Rt△BCF,BC=2,CF=,故CH=,过H作HG⊥A1B于G,连CG,则CG⊥A1B,从而∠CGH为二面角A﹣A1B﹣C的平面角,在Rt△A1BC中,A1C=BC=2,所以,CG=,在Rt△CGH中,sin∠CGH=,cosCGH==.故二面角A﹣A1B﹣C的平面角的余弦值为.【点评】本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.。
线面平行的判定与性质练习一、基本内容 1.线面平行的判定2.线面平行的性质二、练习题题型一:概念性习题1.下列命题正确的是 ( ) A 一直线与平面平行,则它与平面内任一直线平行B 一直线与平面平行,则平面内有且只有一个直线与已知直线平行C 一直线与平面平行,则平面内有无数直线与已知直线平行,它们在平面内彼此平行D 一直线与平面平行,则平面内任意直线都与已知直线异面2.若直线l 与平面α的一条平行线平行,则l 和α的位置关系是 ( ) A. α⊂l B.α//l C.αα//l l 或⊂ D.相交和αl3.若直线a 在平面α内,直线a,b 是异面直线,则直线b 和α平面的位置关系是 ( ) A .相交 B.平行 C.相交或平行 D.相交且垂直4.下列各命题中假命题的个数为 ( )(1) 经过两条平行直线中一条直线的平面必平行于另一条直线; (2) 若一条直线平行于两相交平面,则这条直线和交线平行;(3) 空间四边形中三条边的中点所确定平面和这个空间四边形的两条对角线都平行。
A 0B 1C 2D 35.若直线上有两点P 、Q 到平面α的距离相等,则直线l 与平面α的位置关系是 ( ) A 平行 B 相交 C 平行或相交 D 或平行、或相交、或在内 6.a,b 为两异面直线,下列结论正确的是 ( ) A 过不在a,b 上的任何一点,可作一个平面与a,b 都平行 B 过不在a,b 上的任一点,可作一直线与a,b 都相交 C 过不在a,b 上任一点,可作一直线与a,b 都平行 D 过a 可以并且只可以作一个平面与b 平行 7.判断下列命题是否正确:(1)过平面外一点可作无数条直线与这个平面平行 ( )(2)若直线α⊄l ,则l 不可能与α内无数条直线相交 ( ) (3)若直线l 与平面α不平行,则l 与α内任一直线都不平行 ( ) (4)经过两条平行线中一条直线的平面平行于另一条直线 ( )(5)若平面α内有一条直线和直线l 异面,则α⊄l ( ) 题型二:证明题8.P 为平行四边形ABCD 外一点,E 是PA 的中点,O 是AC 和BD 的交点,求证:OE//平面PBC 。
立体几何线面平行-题型全归纳题型一利用三角形中位线例题1、如图所示,在三棱柱ABC-111C B A 中,侧棱⊥1AA 底面ABC ,AB ⊥BC ,D 为AC 的中点。
求证:1AB //平面DBC 1证明:连接C B 1,交1BC 于点O,再连接OD,平面11B BCC 是平行四边形,∴O是1BC 的中点,又D是AC的中点,∴OD是1ACB ∆的中位线,1//AB OD ∴,⊂OD 平面D BC 1,⊄1AB 平面D BC 1,//OD ∴平面D BC 1。
解题步骤(1)把直线通过平移到平面上,得到线线平行的初步形状;(2)连接平行四边形的对角线,再连接两个中点,恰好为平移所得到的线段;(3)通过延长两条线段的端点,构成一个三角形,即可得到三角形的中位线。
变式训练1、如图,在直四棱柱ABCD-1111D C B A 中,底面ABCD 为菱形,E 为1DD 中点。
求证:1BD //平面ACE ;证明:连接BD,交AC于点O,再连接OE,在直四棱柱ABCD-1111D C B A 中,O为BD的中点,且E为1DD 的中点,∴OE是1BDD ∆的中位线,1//BD OE ∴,又OE⊂平面ACE,⊄1BD 平面ACE,∴1BD //平面ACE 。
变式训练2、如图,在斜三棱柱ABC-111C B A 中,CA=CB ,D 、E 分别是AB ,C B 1的中点,求证:DE//平面11A ACC ;证明:连接1BC ,连接1AC ,在斜三棱柱ABC-111C B A 中,∴点E在线段1BC 上,∴点E是1BC 的中点,又点D是AB的中点,∴DE是1ABC ∆的中位线,∴DE//1AC ,⊄DE 平面11A ACC ,⊂1AC 平面11A ACC ∴DE//平面11A ACC 变式训练3、如图所示,正三棱柱ABC-111C B A 的高为2,点D 是B A 1的中点,点E 是11C B 的中点,求证:DE//平面11A ACC证明:连接1AB ,连接1AC ,在正三棱柱ABC-111C B A 中,∴点D在线段1AB 上,∴点D是1AB 的中点,又点E是11C B 的中点,∴DE是11C AB ∆的中位线,∴DE//1AC ,⊄DE 平面11A ACC ,⊂1AC 平面11A ACC ∴DE//平面11A ACC题型二利用平行四边形的对边平行例题2、如图,在多面体ABCDE 中,AEB 为等边三角形,AD//BC ,BC AD 21=,F 为EB 的中点。
立体几何-平行与垂直练习题1. 空间四边形SABC中,SO⊥平面ABC,O为∆ABC的垂心,求证:(1)AB⊥平面SOC(2)平面SOC⊥平面SABO D CA2. 如图所示,在正三棱柱ABC- A1B1C1中,E,M分别为BB1,A1C的中点,求证:(1)EM⊥平面A A1C1C; (2)平面A1EC⊥平面AA1C1C;EMA1B1C1ABC3. 如图,矩形ABCD中,AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.(1)求证:AE⊥平面BCE.(2)求证:AE∥平面BFD.4. 设P,Q是边长为a的正方体AC1的面AA1D1D,面A1B1C1D1的中心,如图,(1)证明PQ∥平面AA1B1B;(2)求线段PQ的长.5. 如图,在四棱锥P-ABCD 中,PD ABCD ⊥面,//AB DC ,AB AD ⊥,5BC =,3DC =,4AD =,60PAD ∠=.(Ⅰ)当主视图方向与向量AD 的方向相同时,画出四棱锥P ABCD -的三视图.(要求标出尺寸);(Ⅱ)若M 为PA 的中点,求证:DM //面PBC .6. 已知直四棱柱ABCD —A 1B 1C 1D 1的底面是菱形,且∠DAB=60°,AD=AA 1,F 为棱BB 1的中点,M 为线段AC 1的中点. 求证:(1)直线MF∥平面ABCD ;(2)平面AFC 1⊥平面ACC 1A 1.7. 如图,PA⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点. (1)求证:MN∥平面PAD ;(2)求证:MN⊥CD;(3)若二面角P-DC-A=45°,求证:MN⊥平面PDC.8. 如图,在三棱柱ABC -A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M ,N 分别是AB ,A1C 的中点.(1)求证:MN ∥平面BCC1B1;(2)求证:MN ⊥平面A1B1C ;(3)求三棱锥M-A1B1C的体积.9. 如图所示,在四棱锥S—ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=2.求证:平面SAD⊥平面SBC.10. 如图所示,在直.三棱柱...ABC-A1B1C1中,AC⊥BC.(1) 求证:平面AB1C1⊥平面AC1;(2) 若AB1⊥A1C,求线段AC与AA1长度之比;(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.11. 如图,把等腰Rt△ABC沿斜边AB旋转至△ABD的位置,使CD=AC,(1)求证:平面ABD⊥平面ABC;(2)求二面角C-BD-A的余弦值.12. 如图,在四棱锥P—ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、D、N三点的平面交PC 于M,E为AD的中点.(1)求证:EN∥平面PCD;(2)求证:平面PBC⊥平面ADMN;(3)求平面PAB与平面ABCD所成二面角的正切值.A1C D1B113.如图,AB为⊙O直径,C为⊙O上一点,PA⊥平面ABC,A在PB,PC上的射影分别为E,F,求证:PB⊥平面AFE.14.在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,AB=BC=1,DC=2,点E在PB上.(1)求证:平面AEC⊥平面PAD.(2)当PD∥平面AEC时,求PE∶EB的值.15. 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=12AB,N为AB上一点,AB=4AN,M,D,S分别为PB,AB,BC的中点.(1)求证:PA∥平面CDM;(2)求证:SN⊥平面CDM.16. 一个多面体的直观图和三视图如图所示,其中M,G分别是AB,DF的中点.(1)求证:CM⊥平面FDM;(2)在线段AD上(含A,D端点)确定一点P,使得GP∥平面FMC,并给出证明.。
一、单选题1.m 、n 是平面α外的两条直线,在m ∥α的前提下,m ∥n 是n ∥α的().A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的().A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.设α,β为两个平面,则α∥β的充要条件是().A.α内有无数条直线与β平行B.α,β平行与同一个平面C.α内有两条相交直线与β内两条相交直线平行D.α,β垂直与同一个平面4.已知l ,m 是两条不同的直线,m //平面α,则().A.若l //m ,则l //αB.若l //α,则l //mC.若l ⊥m ,则l ⊥αD.若l ⊥α,则l ⊥m5.设α,β为两个平面,则α∥β的充要条件是().A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面6.如果用m ,n 表示不同直线,α,β,γ表示不同平面,下列叙述正确的是().A.若m //α,m //n ,则n //αB.若m //n ,m ⊂α,n ⊂β,则α//βC.若α⊥γ,β⊥γ,则α//βD.若m ⊥α,n ⊥α,则m //n7.如图1,点P 在正方体ABCD -A 1B 1C 1D 1的面对角线BC 1上运动,则下列四个结论:图1①三棱锥A -D 1PC 的体积不变;②A 1P //平面ACD 1;③DP ⊥BC 1;④平面PDB 1⊥平面ACD 1.其中正确的结论的个数是().A.1个B.2个C.3个D.4个8.如图2,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则().图2A.BM =EN ,且直线BM ,EN 是相交直线B.BM ≠EN ,且直线BM ,EN 是相交直线C.BM =EN ,且直线BM ,EN 是异面直线D.BM ≠EN ,且直线BM ,EN 是异面直线9.如下图所示的四个正方体中,A ,B 正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,能得出AB //平面MNP 的图形的序号为().59A.①②B.②③C.③④D.①②③10.如图3,在直角梯形ABCD中,BC⊥CD,AB=BC=2,CD=4,E为CD中点,M,N分别为AD,BC的中点,将△ADE沿AE折起,使点D到D1,M到M1,在翻折过程中,有下列命题:图3①||M1M的最小值为1;②M1N//平面CD1E;③存在某个位置,使M1E⊥DE;④无论M1位于何位置,均有M1N⊥AE.其中正确命题的个数为().A.1B.2C.3D.4二、多选题11.已知α,β是两个不重合的平面,m,n是两条不重合的直线,则下列命题正确的是().A.若m//n,m⊥α,则n⊥αB.若m//α,α⋂β=n,则m//nC.若m⊥α,m⊥β,则α//βD.若m⊥α,m//n,n⊥β,则α//β12.已知菱形ABCD中,∠BAD=60°,AC与BD 相交于点O,将△ABD沿BD折起,使顶点A至点M,在折起的过程中,下列结论正确的是().A.BD⊥CMB.存在一个位置,使△CDM为等边三角形C.DM与BC不可能垂直D.直线DM与平面BCD所成的角的最大值为60°13.己知m、n为两条不重合的直线,α、β为两个不重合的平面,则下列说法正确的是().A.若m//α,n//β且α//β,则m//nB.若m//n,m⊥α,n⊥β,则α//βC.若m//n,n⊂α,α//β,m⊄β,则m//βD.若m//n,n⊥α,α⊥β,则m//β14.如图4,在正方体ABCD-A1B1C1D1中,N为底面ABCD的中心,P为线段A1D1上的动点(不包括两个端点),M为线段AP的中点,则().图4A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P,A,C三点的正方体的截面一定是等腰梯形15.已知四棱锥P-ABCD,底面ABCD为矩形,侧面PCD⊥平面ABCD,BC=23,CD=PC=PD=26.若点M为PC的中点,则下列说法正确的为().A.BM⊥平面PCDB.PA//面MBDC.四棱锥M-ABCD外接球的表面积为36πD.四棱锥M-ABCD的体积为6三、填空题16.如图5,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.其中正确的有_______.(把所有正确的序号都填上)图517.已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:_______.18.已知α,β是两个不同的平面,l,m是两条不同的直线,有如下四个命题:①若l⊥α,l⊥β,则α∥β;②若l⊥α,α⊥β,则l∥β;③若l∥α,l⊥β,则α⊥β;④若l∥α,α⊥β,则l⊥β.其中真命题为______(填所有真命题的序号).19.已知α,β是两个不同的平面,l,m是两条不同60,C⊥平面ABB.图622.如图7,在直三棱柱ABC为BC,AC的中点,AB=BC.(1)求证:A1B1∥平面DEC1;(2)求证:BE⊥C1E.23.如图8,在四棱锥P-ABCDPA,PD的中点.已知侧面PAD⊥是矩形,DA=DP.(1)求证:MN∥平面PBC;图8图9图11P-ABCD中,已知底BC=1,E,F分别是AB,;平面PDE.如图13,取PD中点G。
高中立体几何证明平行
的专题训练
WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】
P
E
D
C
B
A
1. 如图,四棱锥P -A B C D 的底面是平行四边形,点
E 、
F 分
别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ;
2、如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1,BC =2,CD =1+
3,
过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC. (1)求证:求证:FG ∥面BCD ;
3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点,M 为BE 的中点, AC ⊥BE. 求证: C 1D ∥平面B 1FM.
4、如图所示, 四棱锥P -ABCD 底面是直角梯形,
,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明:
//EB PAD 平面;
5、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。
求证:
PA ∥平面BDE
6.如图,三棱柱ABC —A 1B 1C 1中, D 为AC 的中点. 求证:AB 11C
2
1
中点为PD E 求证:AE ∥平面PBC ; 9、在如图所示的几何体中,四边形ABCD 为平行四边形,∠?ACB=90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF.
M是线段AD的中点,求证:GM∥平面ABFE;
10、S 是平行四边形ABCD 平面外一点,M 、N 分别是SA 、BD 上的
点,且
SM
AM =
ND
BN
, 求证:MN ∥平面SDC 11、如图,三棱锥ABC P -中,PB ⊥底面ABC ,90BCA ∠=,PB=BC=CA ,E 为PC 的中点,M 为AB 的中点,点F 在PA 上,且2AF FP =.求证://CM 平面BEF ;
E
F
B
A
C
D
P。