2014年天津市中考数学试题(含答案)

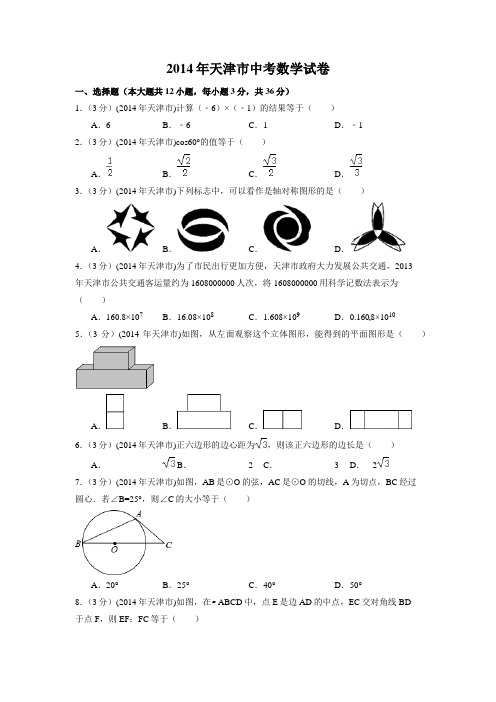
2014年天津市中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）(2014年天津市)计算（﹣6）×（﹣1）的结果等于（）A．6 B．﹣6 C．1D．﹣12．（3分）(2014年天津市)cos60°的值等于（）A．B．C．D．3．（3分）(2014年天津市)下列标志中，可以看作是轴对称图形的是（）A．B．C．D．4．（3分）(2014年天津市)为了市民出行更加方便，天津市政府大力发展公共交通，2013年天津市公共交通客运量约为1608000000人次，将1608000000用科学记数法表示为（）A．160.8×107B．16.08×108C．1.608×109D．0.1608×10105．（3分）(2014年天津市)如图，从左面观察这个立体图形，能得到的平面图形是（）A．B．C．D．6．（3分）(2014年天津市)正六边形的边心距为，则该正六边形的边长是（）A． B． 2 C． 3 D．27．（3分）(2014年天津市)如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°8．（3分）(2014年天津市)如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：29．（3分）(2014年天津市)已知反比例函数y=，当1＜x＜2时，y的取值范围是（）A．0＜y＜5 B．1＜y＜2 C．5＜y＜10 D．y＞1010．（3分）(2014年天津市)要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A．x（x+1）=28 B．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28 11．（3分）(2014年天津市)某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：4的权．根据四人各自的平均成绩，公司将录取（）A．甲B．乙C．丙D．丁12．（3分）(2014年天津市)已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1C．2D．3二、填空题（本大题共6小题，每小题3分，满分18分）13．（3分）(2014年天津市)计算x5÷x2的结果等于．14．（3分）(2014年天津市)已知反比例函数y=（k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为．15．（3分）(2014年天津市)如图，是一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点数小于9的概率为．16．（3分）(2014年天津市)抛物线y=x2﹣2x+3的顶点坐标是．17．（3分）(2014年天津市)如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．18．（3分）(2014年天津市)如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（Ⅰ）计算AC2+BC2的值等于；（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）．三、解答题（本大题共7小题，共66分）19．（8分）(2014年天津市)解不等式组请结合题意填空，完成本题的解答：（Ⅰ）解不等式①，得；（Ⅱ）解不等式②，得；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为．20．（8分）(2014年天津市)为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为，图①中m的值为；（Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？21．（10分）(2014年天津市)已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB 的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．22．（10分）(2014年天津市)解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁．（Ⅰ）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至A′C′的位置时，A′C′的长为m；（Ⅱ）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°，已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）．23．（10分）(2014年天津市)“黄金1号”玉米种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子的价格打8折．（Ⅰ）根据题意，填写下表：（Ⅲ）若小张一次购买该种子花费了30元，求他购买种子的数量．24．（10分）(2014年天津市)在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．（Ⅰ）如图①，当α=90°时，求AE′，BF′的长；（Ⅱ）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；（Ⅲ）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．25．（10分）(2014年天津市)在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1，﹣1），①当点F的坐标为（1，1）时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．（Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．2014年天津市中考数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）(2014年天津市)计算（﹣6）×（﹣1）的结果等于（）A．6 B．﹣6 C．1D．﹣1【考点】有理数的乘法．【分析】根据有理数的乘法运算法则进行计算即可得解．【解答】解：（﹣6）×（﹣1），=6×1，=6．故选A．【点评】本题考查了有理数的乘法运算，是基础题，熟记运算法则是解题的关键．2．（3分）(2014年天津市)cos60°的值等于（）A．B．C．D．【考点】特殊角的三角函数值．【分析】根据特殊角的三角函数值解题即可．【解答】解：cos60°=．故选A．【点评】本题考查特殊角的三角函数值，准确掌握特殊角的函数值是解题关键．3．（3分）(2014年天津市)下列标志中，可以看作是轴对称图形的是（）A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、不是轴对称图形，是中心对称图形，不符合题意；B、不是轴对称图形，是中心对称图形，不符合题意；C、不是轴对称图形，是中心对称图形，不符合题意；D、是轴对称图形，符合题意．故选：D．【点评】此题主要考查了中心对称图形和轴对称图形的定义，掌握中心对称图形与轴对称图形的概念，解答时要注意：判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合；判断中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．4．（3分）(2014年天津市)为了市民出行更加方便，天津市政府大力发展公共交通，2013年天津市公共交通客运量约为1608000000人次，将1608000000用科学记数法表示为（）A．160.8×107B．16.08×108C．1.608×109D．0.1608×1010【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将1608000000用科学记数法表示为：1.608×109．故选：C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5．（3分）(2014年天津市)如图，从左面观察这个立体图形，能得到的平面图形是（）A．B．C．D．【考点】简单组合体的三视图．【分析】根据从左面看得到的图形是左视图，可得答案．【解答】解；从左面看下面一个正方形，上面一个正方形，故选：A．【点评】本题考查了简单组合体的三视图，从左面看得到的图形是左视图．6．（3分）(2014年天津市)正六边形的边心距为，则该正六边形的边长是（）A． B． 2 C． 3 D．2【考点】正多边形和圆．【分析】运用正六边形的性质，正六边形边长等于外接圆的半径，再利用勾股定理解决．【解答】解：∵正六边形的边心距为，∴OB=，AB=OA，∵OA2=AB2+OB2，∴OA2=（OA）2+（）2，解得OA=2．故选B．【点评】本题主要考查了正六边形和圆，注意：外接圆的半径等于正六边形的边长．7．（3分）(2014年天津市)如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°【考点】切线的性质．【分析】连接OA，根据切线的性质，即可求得∠C的度数．【解答】解：如图，连接OA，∵AC是⊙O的切线，∴∠OAC=90°，∵OA=OB，∴∠B=∠OAB=25°，∴∠AOC=50°，∴∠C=40°．【点评】本题考查了圆的切线性质，以及等腰三角形的性质，已知切线时常用的辅助线是连接圆心与切点．8．（3分）(2014年天津市)如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：2【考点】平行四边形的性质；相似三角形的判定与性质．【分析】根据题意得出△DEF∽△BCF，进而得出=，利用点E是边AD的中点得出答案即可．【解答】解：∵▱ABCD，故AD∥BC，∴△DEF∽△BCF，∴=，∵点E是边AD的中点，∴AE=DE=AD，∴=．故选：D．【点评】此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识，得出△DEF∽△BCF是解题关键．9．（3分）(2014年天津市)已知反比例函数y=，当1＜x＜2时，y的取值范围是（）A．0＜y＜5 B．1＜y＜2 C．5＜y＜10 D．y＞10【考点】反比例函数的性质．【分析】将x=1和x=2分别代入反比例函数即可确定函数值的取值范围．【解答】解：∵反比例函数y=中当x=1时y=10，当x=2时，y=5，∴当1＜x＜2时，y的取值范围是5＜y＜10，故选C．【点评】本题考查了反比例函数的性质：（1）反比例函数y=（k≠0）的图象是双曲线；（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．10．（3分）(2014年天津市)要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A．x（x+1）=28 B．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28 【考点】由实际问题抽象出一元二次方程．【分析】关系式为：球队总数×每支球队需赛的场数÷2=4×7，把相关数值代入即可．【解答】解：每支球队都需要与其他球队赛（x﹣1）场，但2队之间只有1场比赛，所以可列方程为：x（x﹣1）=4×7．故选B．【点评】本题考查了由实际问题抽象出一元二次方程，解决本题的关键是得到比赛总场数的等量关系，注意2队之间的比赛只有1场，最后的总场数应除以2．11．（3分）(2014年天津市)某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：候选人甲乙丙丁测试成绩（百分制）面试86 92 90 83笔试90 83 83 92 如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）A．甲B．乙C．丙D．丁【考点】加权平均数．【分析】根据题意先算出甲、乙、丙、丁四位候选人的加权平均数，再进行比较，即可得出答案．【解答】解：甲的平均成绩为：（86×6+90×4）÷10=87.6（分），乙的平均成绩为：（92×6+83×4）÷10=88.4（分），丙的平均成绩为：（90×6+83×4）÷10=87.2（分），丁的平均成绩为：（83×6+92×4）÷10=86.6（分），因为乙的平均分数最高，所以乙将被录取．故选B．【点评】此题考查了加权平均数的计算公式，注意，计算平均数时按6和4的权进行计算．12．（3分）(2014年天津市)已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1C．2D．3【考点】二次函数图象与系数的关系．【分析】由图象可知二次函数y=ax2+bx+c与x轴有两个交点，进而判断①；先根据抛物线的开口向下可知a＜0，由抛物线与y轴的交点判断c与0的关系，根据对称轴在y轴右侧得出b与0的关系，然后根据有理数乘法法则判断②；一元二次方程ax2+bx+c﹣m=0没有实数根，则可转化为ax2+bx+c=m，即可以理解为y=ax2+bx+c和y=m没有交点，即可求出m的取值范围，判断③即可．【解答】解：①∵二次函数y=ax2+bx+c与x轴有两个交点，∴b2﹣4ac＞0，故①正确；②∵抛物线的开口向下，∴a＜0，∵抛物线与y轴交于正半轴，∴c＞0，∵对称轴x=﹣＞0，∴ab＜0，∵a＜0，∴b＞0，∴abc＜0，故②正确；③∵一元二次方程ax2+bx+c﹣m=0没有实数根，∴y=ax2+bx+c和y=m没有交点，由图可得，m＞2，故③正确．故选D．【点评】本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．二、填空题（本大题共6小题，每小题3分，满分18分）13．（3分）(2014年天津市)计算x5÷x2的结果等于x3．【考点】同底数幂的除法．【分析】同底数幂相除底数不变，指数相减，【解答】解：x5÷x2=x3故答案为：x3．【点评】此题考查了同底数幂的除法，解题要注意细心明确指数相减．14．（3分）(2014年天津市)已知反比例函数y=（k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为1．【考点】反比例函数的性质．【专题】开放型．【分析】反比例函数y=（k为常数，k≠0）的图象在第一，三象限，则k＞0，符合上述条件的k的一个值可以是1．（正数即可，答案不唯一）【解答】解：∵反比例函数的图象在一、三象限，∴k＞0，只要是大于0的所有实数都可以．例如：1．故答案为：1．【点评】此题主要考查反比例函数图象的性质：（1）k＞0时，图象是位于一、三象限；（2）k＜0时，图象是位于二、四象限．15．（3分）(2014年天津市)如图，是一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点数小于9的概率为．【考点】概率公式．【分析】抽出的牌的点数小于9有1，2，3，4，5，6，7，8共8个，总的样本数目为13，由此可以容易知道事件抽出的牌的点数小于9的概率．【解答】解：∵抽出的牌的点数小于9有1，2，3，4，5，6，7，8共8个，总的样本数目为13，∴从中任意抽取一张，抽出的牌点数小于9的概率是：．故答案为：．【点评】此题主要考查了概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．16．（3分）(2014年天津市)抛物线y=x2﹣2x+3的顶点坐标是（1，2）．【考点】二次函数的性质．【专题】计算题．【分析】已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．【解答】解：∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=（x﹣1）2+2，∴抛物线y=x2﹣2x+3的顶点坐标是（1，2）．【点评】此题考查了二次函数的性质，二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．17．（3分）(2014年天津市)如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为45（度）．【考点】等腰三角形的性质．【分析】设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°﹣∠ACE=90°﹣x﹣y，根据等边对等角得出∠ACE=∠AEC=x+y，∠BDC=∠BCD=∠BCE+∠DCE=90°﹣y．然后在△DCE中，利用三角形内角和定理列出方程x+（90°﹣y）+（x+y）=180°，解方程即可求出∠DCE的大小．【解答】解：设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°﹣∠ACE=90°﹣x﹣y．∵AE=AC，∴∠ACE=∠AEC=x+y，∵BD=BC，∴∠BDC=∠BCD=∠BCE+∠DCE=90°﹣x﹣y+x=90°﹣y．在△DCE中，∵∠DCE+∠CDE+∠DEC=180°，∴x+（90°﹣y）+（x+y）=180°，解得x=45°，∴∠DCE=45°．故答案为45．【点评】本题考查了等腰三角形的性质及三角形内角和定理，设出适当的未知数列出方程是解题的关键．18．（3分）(2014年天津市)如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（Ⅰ）计算AC2+BC2的值等于11；（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）如图所示：．【考点】作图—应用与设计作图．【分析】（1）直接利用勾股定理求出即可；（2）首先分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；进而得出答案．【解答】解：（Ⅰ）AC2+BC2=（）2+32=11；故答案为：11；（2）分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；延长DE交MN于点Q，连接QC，平移QC至AG，BP位置，直线GP分别交AF，BH于点T，S，则四边形ABST即为所求．【点评】此题主要考查了应用设计与作图，借助网格得出正方形是解题关键．三、解答题（本大题共7小题，共66分）19．（8分）(2014年天津市)解不等式组请结合题意填空，完成本题的解答：（Ⅰ）解不等式①，得x≥﹣1；（Ⅱ）解不等式②，得x≤1；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为﹣1≤x≤1．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．【解答】解：（I）解不等式①，得x≥﹣1；（II）解不等式②得，x≤1，（III）在数轴上表示为：；（IN）故此不等式的解集为：﹣1≤x≤1．故答案分别为：x≥﹣1，x≤1，﹣1≤x≤1．【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20．（8分）(2014年天津市)为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为40，图①中m的值为15；（Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？【考点】条形统计图；用样本估计总体；扇形统计图；中位数；众数．【专题】计算题．【分析】（Ⅰ）根据条形统计图求出总人数即可；由扇形统计图以及单位1，求出m的值即可；（Ⅱ）找出出现次数最多的即为众数，将数据按照从小到大顺序排列，求出中位数即可；（Ⅲ）根据题意列出算式，计算即可得到结果．【解答】解：（Ⅰ）本次接受随机抽样调查的学生人数为6+12+10+8+4=40，图①中m的值为100﹣30﹣25﹣20﹣10=15；故答案为：40；15；（Ⅱ）∵在这组样本数据中，35出现了12次，出现次数最多，∴这组样本数据的众数为5；∵将这组样本数据从小到大得顺序排列，其中处于中间的两个数都为36，∴中位数为=36；（Ⅲ）∵在40名学生中，鞋号为35的学生人数比例为30%，∴由样本数据，估计学校各年级中学生鞋号为35的人数比例约为30%，则计划购买200双运动鞋，有200×30%=60双为35号．【点评】此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．21．（10分）(2014年天津市)已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB 的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．【考点】圆周角定理；等边三角形的判定与性质；勾股定理．【分析】（Ⅰ）利用圆周角定理可以判定△CAB和△DCB是直角三角形，利用勾股定理可以求得AC的长度；利用圆心角、弧、弦的关系推知△DCB也是等腰三角形，所以利用勾股定理同样得到BD=CD=5；（Ⅱ）如图②，连接OB，OD．由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形，则BD=OB=OD=5．【解答】解：（Ⅰ）如图①，∵BC是⊙O的直径，∴∠CAB=∠BDC=90°．∵在直角△CAB中，BC=10，AB=6，∴由勾股定理得到：AC===8．∵AD平分∠CAB，∴=，∴CD=BD．在直角△BDC中，BC=10，CD2+BD2=BC2，∴易求BD=CD=5；（Ⅱ）如图②，连接OB，OD．∵AD平分∠CAB，且∠CAB=60°，∴∠DAB=∠CAB=30°，∴∠DOB=2∠DAB=60°．又∵OB=OD，∴△OBD是等边三角形，∴BD=OB=OD．∵⊙O的直径为10，则OB=5，∴BD=5．【点评】本题综合考查了圆周角定理，勾股定理以及等边三角形的判定与性质．此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形．22．（10分）(2014年天津市)解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁．（Ⅰ）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至A′C′的位置时，A′C′的长为23.5m；（Ⅱ）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°，已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）．【考点】解直角三角形的应用．【专题】应用题．【分析】（1）根据中点的性质即可得出A′C′的长；（2）设PQ=x，在Rt△PMQ中表示出MQ，在Rt△PNQ中表示出NQ，再由MN=40m，可得关于x的方程，解出即可．【解答】解：（I）∵点C是AB的中点，∴A'C'=AB=23.5m．（II）设PQ=x，在Rt△PMQ中，tan∠PMQ==1.4，∴MQ=，在Rt△PNQ中，tan∠PNQ==3.3，∴NQ=，∵MN=MQ﹣NQ=40，即﹣=40，解得：x≈97．答：解放桥的全长约为97m．【点评】本题考查了解直角三角形的应用，解答本题的关键是熟练锐角三角函数的定义，难度一般．23．（10分）(2014年天津市)“黄金1号”玉米种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子的价格打8折．（Ⅰ）根据题意，填写下表：购买种子的数量/kg 1.5 2 3.5 4 …付款金额/元7.5 1016 18…（Ⅱ）设购买种子数量为xkg，付款金额为y元，求y关于x的函数解析式；（Ⅲ）若小张一次购买该种子花费了30元，求他购买种子的数量．【考点】一次函数的应用；一元一次方程的应用．【分析】（1）根据单价乘以数量，可得答案；（2）根据单价乘以数量，可得价格，可得相应的函数解析式；（3）根据函数值，可得相应的自变量的值．【解答】解：（Ⅰ）10，8；（Ⅱ）根据题意得，当0≤x≤2时，种子的价格为5元/千克，∴y=5x，当x＞2时，其中有2千克的种子按5元/千克计价，超过部分按4元/千克计价，∴y=5×2+4（x﹣2）=4x+2，y关于x的函数解析式为y=；（Ⅲ）∵30＞2，∴一次性购买种子超过2千克，∴4x+2=30．解得x=7，答：他购买种子的数量是7千克．【点评】本题考查了一次函数的应用，分类讨论是解题关键．24．（10分）(2014年天津市)在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．（Ⅰ）如图①，当α=90°时，求AE′，BF′的长；（Ⅱ）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；（Ⅲ）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．【考点】几何变换综合题；三角形的外角性质；全等三角形的判定与性质；含30度角的直角三角形；勾股定理．【专题】综合题．【分析】（1）利用勾股定理即可求出AE′，BF′的长．（2）运用全等三角形的判定与性质、三角形的外角性质就可解决问题．（3）首先找到使点P的纵坐标最大时点P的位置（点P与点D′重合时），然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值．【解答】解：（Ⅰ）当α=90°时，点E′与点F重合，如图①．∵点A（﹣2，0）点B（0，2），∴OA=OB=2．∵点E，点F分别为OA，OB的中点，∴OE=OF=1∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的，∴OE′=OE=1，OF′=OF=1．在Rt△AE′O中，AE′=．在Rt△BOF′中，BF′=．∴AE′，BF′的长都等于．（Ⅱ）当α=135°时，如图②．∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得，∴∠AOE′=∠BOF′=135°．在△AOE′和△BOF′中，，∴△AOE′≌△BOF′（SAS）．∴AE′=BF′，且∠OAE′=∠OBF′．∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB，∠CAO=∠CBP，∴∠CPB=∠AOC=90°∴AE′⊥BF′．（Ⅲ）在第一象限内，当点D′与点P重合时，点P的纵坐标最大．过点P作PH⊥x轴，垂足为H，如图③所示．∵∠AE′O=90°，E′O=1，AO=2，∴∠E′AO=30°，AE′=．∴AP=+1．∵∠AHP=90°，∠PAH=30°，∴PH=AP=．∴点P的纵坐标的最大值为．【点评】本题是在图形旋转过程中，考查了全等三角形的判定与性质、勾股定理、三角形的外角性质、30°角所对的直角边等于斜边的一半等知识，而找到使点P的纵坐标最大时点P的位置是解决最后一个问题的关键．25．（10分）(2014年天津市)在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1，﹣1），①当点F的坐标为（1，1）时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．（Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．【考点】一次函数综合题．【分析】（Ⅰ）①利用待定系数法求得直线OF与EA的直线方程，然后联立方程组，求得该方程组的解即为点P的坐标；②由已知可设点F的坐标是（1，t）．求得直线OF、EA的解析式分别是y=tx、直线EA的解析式为：y=（2+t）x﹣2（2+t）．则tx=（2+t）x﹣2（2+t），整理后即可得到y关于x的函数关系式y=x2﹣2x；（Ⅱ）同（Ⅰ），易求P（2﹣，2t﹣）．则由PQ⊥l于点Q，得点Q（1，2t﹣），则OQ2=1+t2（2﹣）2，PQ2=（1﹣）2，所以1+t2（2﹣）2=（1﹣）2，化简得到：t（t ﹣2m）（t2﹣2mt﹣1）=0，通过解该方程可以求得m与t的关系式．【解答】解：（Ⅰ）①∵点O（0，0），F（1，1），∴直线OF的解析式为y=x．设直线EA的解析式为：y=kx+b（k≠0）、∵点E和点F关于点M（1，﹣1）对称，∴E（1，﹣3）．又A（2，0），点E在直线EA上，∴，解得，∴直线EA的解析式为：y=3x﹣6．∵点P是直线OF与直线EA的交点，则，解得，∴点P的坐标是（3，3）．②由已知可设点F的坐标是（1，t）．∴直线OF的解析式为y=tx．设直线EA的解析式为y=cx+dy（c、d是常数，且c≠0）．由点E和点F关于点M（1，﹣1）对称，得点E（1，﹣2﹣t）．又点A、E在直线EA上，∴，解得，∴直线EA的解析式为：y=（2+t）x﹣2（2+t）．∵点P为直线OF与直线EA的交点，∴tx=（2+t）x﹣2（2+t），即t=x﹣2．则有 y=tx=（x﹣2）x=x2﹣2x；（Ⅱ）由（Ⅰ）可得，直线OF的解析式为y=tx．直线EA的解析式为y=（t﹣2m）x﹣2（t﹣2m）．∵点P为直线OF与直线EA的交点，∴tx=（t﹣2m）x﹣2（t﹣2m），化简，得 x=2﹣．有 y=tx=2t﹣．∴点P的坐标为（2﹣，2t﹣）．∵PQ⊥l于点Q，得点Q（1，2t﹣），∴OQ2=1+t2（2﹣）2，PQ2=（1﹣）2，∵OQ=PQ，∴1+t2（2﹣）2=（1﹣）2，化简，得 t（t﹣2m）（t2﹣2mt﹣1）=0．又t≠0，∴t﹣2m=0或t2﹣2mt﹣1=0，解得 m=或m=．则m=或m=即为所求．【点评】本题考查了一次函数的综合题型．涉及到了待定系数法求一次函数解析式，一次函数与直线的交点问题．此题难度不大，掌握好两直线间的交点的求法和待定系数法求一次函数解析式就能解答本题．祝福语祝你考试成功!。

天津市2014 年初中毕业生学业考试数学答案解析第Ⅰ卷一、选择题1.【答案】A【解析】两数相乘，同号得正，异号得负，并把绝对值相乘，(-6) ⨯(-1) = 6 ，故选A. 【考点】有理数的计算2.【答案】A【解析】cos 60︒=1 . 2【考点】特殊角的三角函数值3.【答案】D【解析】轴对称图形沿对称轴折叠，直线两旁的部分能够重合，图形D 沿竖直的直线折叠两旁的部分能重合，D 是轴对称图形，故选D.【考点】轴对称图形的概念4.【答案】C【解析】科学计数法是将一个数写成a ⨯10n 的形式，其中1≤| a |<10 ，n 为整数.当原数的绝对值≥ 10 时，n 为正整数，n 等于原数的整数位数减1；当原数的绝对值< 1 时，n 为负整数，n 的绝对值等于原数中左起第一个非零数前零的个数（含整数位上的零），1608000000=1.608⨯109，故选C.【考点】科学计数法5.【答案】A【解析】此立体图形从左面能看到的图形是，故选A.【考点】三视图6.【答案】B【解析】正多边形的边长等于正六边形外接圆的半径，正六边形的边心距、外接圆的半径、边长的一半三条线段可以构成含有30︒角的直角三角形，由三角函数求得正六边形外接圆的半径为2，即边长为2，故选B. 【考点】正多边形的性质7.【答案】C【解析】连接OA ，则OA ⊥OC ，由∠B = 25︒知∠AOC = 50︒，所以∠C = 40︒，故选C.【考点】切线的性质8.【答案】D【解析】因为E 是平行四边形ABCD 中边AD 的中点，所以△EDF∽△CBF ，所以EF : FC =ED : BC =1: 2 ，故选D.【考点】相似三角形的性质9.【答案】C【解析】由反比例函数的性质结合图像写出取值范围.当x = 1 时，y = 10 ；当x = 2 时，y = 5 ，所以y 的取值范围是5 <y <10 ，故选C.【考点】反比例函数的性质10.【答案】B【解析】根据题意得共可进行28 场比赛，由于每两个队都要进行比赛，所以1x(x -1) = 28 ，故选B.2【考点】一元二次方程解决实际问题11.【答案】B【解析】首先根据权重计算四人的平均成绩，再根据平均成绩的大小确定录取人，甲的平均成绩：86⨯0.6 + 90⨯0.4 =87.6 ，乙的平均成绩：92⨯0.6 +83⨯0.4 = 88.4 ，丙的平均成绩：90⨯0.6 +83⨯0.4 = 87.2 ，丁的平均成绩：83⨯0.6 +92⨯0.4 =86.6，因为乙的平均成绩最高，所以公司将录取乙，故选B.【考点】加权平均数的计算12.【答案】D【解析】二次函数y =ax2 +bx +c 的图像与x 轴有两个交点，所以∆=b2 -4ac > 0 ，故①正确；由图像知a < 0 ，b > 0 ，c > 0 ，所以abc < 0 ，故② 正确；由二次函数y =ax2 +bx +c 的最大值为2，ax2 +bx +c -m = 0 没有实根，知ax2 +bx +c -m ≤ 2 -m < 0 ，m > 2 ，故③ 正确，所以正确的结论有三个，故选D.【考点】二次函数的图像和性质第Ⅱ卷二、填空题13.【答案】x3【解析】同底数幂相除，底数不变，指数相减，所以x5 ÷x2 =x3 .【考点】同底数幂的除法14. 【答案】1（满足 k > 0 即可）【解析】反比例函数 y = k (k ≠ 0) 位于第一、第三象限，只需k > 0 ，故 k 的值可以为 1.x【考点】反比例函数的性质15. 【答案】 813【解析】此 13 张牌中小于 9 的有 8 张，故从中任意抽取一张，抽到的牌的点数小于 9 的概率是 8 .13【考点】概率的计算16.【答案】(1, 2)b 4ac - b 22 2【解析】顶点坐标的计算有两种方法，一是公式法(- , 2a 4a 2) ；二是配方法，y = x - 2x + 3 = (x -1) + 2 ，故顶点坐标为（1, 2）.【考点】二次函数顶点坐标的计算17.【答案】45 【解析】设∠A = a ，由题意知∠ACE = (180o - a ) ÷ 2 = 90o - 1 a ，∠DCB = [180o - (90o - a )] ÷ 2 = 45o + 1 a ，2 2∠ACE + ∠DCB = (90o - 1 a ) + (45o + 1 a ) = 135o = ∠ACB + ∠DCE = 90o + ∠DCE ，2 2所以∠DCE = 45o .【考点】三角形内角和，等腰三角形的性质18.【答案】（1）11（2）分别以 AC ， BC ， AB 为一遍作正方形 ACED ，正方形 BCNM ，正方形 ABHF ；延长 DE 交 NM 于点Q ，连接QC ；平移QC 至 AG ， BP 位置；直线GP 分别交 AF ， BH 于点T ， S ，则四边形 ABST 即为 所求【解析】（1） AC 2 + BC 2 = ( 2)2 + 32 =112 （2） 连接 DG ，利用切割补形，可以得到四边形 DGPB 中，平行四边形 AGPB 的面积为 11，再作矩形 ATSB 使之与平行四边形 AGPB 等高即可.【考点】勾股定理，尺规作图三、解答题19.【答案】（1） x ≥ -1 .（2） x ≤ 1 .（3） 【解析】解：（1） 2x +1≥ -1则2x ≥ -2 ，解得 x ≥ -1 .（2） 2x +1≤ 3，则2x ≤ 2 ，解得 x ≤ 1 .（3） 如图所示【考点】不等式组的解法20.【答案】（1）40，15（2）36（3）60【解析】解：（1）40，15（2） 在这组样本数据中，35 出现了 12 次，出现的次数最多，∴这组样本数据的众数为 35.将这组样本数据从大到小的顺序排列，其中处于中间的两个数都是 361 有 36 + 36 = 36 ，2∴这组样本数据的中位数为 36.（3） 在 40 名学生中，鞋号为 35 的学生人数比例为30% ，∴由样本数据，估计学校各年级学生中鞋号为 35 的人数比例约为30%于是，计划购买 200 双运动鞋时，有200⨯30% = 60 .∴建议购买 35 号运动鞋 60 双【考点】扇形统计图，条形统计图解决实际问题21.【答案】（1） AC = 8 ， BD = 50 ， CD = 5 .（2） BD = 5【解析】解：（1）由已知， BC 为 O 的直径，得∠CAB = ∠BDC = 90.BC 2 - AB 2 102 - 62 2在 Rt △CAB 中， BC =10 ， AB = 6 ，∴ AC = = = 8 .AD 平分∠CAB .∴ CD =BD .∴ CD = BD .在 Rt △BDC 中， BC =10 ， CD 2 + BD 2 = BC 2 ，∴ BD 2 = CD 2 = 50 ，∴BD = CD = 5 .（2）如图，连接OB ,OD .AD 平分∠CAB ，且∠CAB = 60，∴ ∠DAB = 1 ∠CAB = 30 .2∴∠DOB = 2∠DAB = 60 .又 O 中OB = OD ，∴△OBD是等边三角形.O 的直径为 10，有OB = 5 ，∴BD = 5【考点】圆周角定理及其推论，勾股定理，等边三角形的判定及性质⎨ 4x + 2, x > 2.22.【答案】（1） 23.5（2）解放桥的全长约为 97 m.【解析】解：（1） A 'C ' = AC = 1 AB= 23.52（2）如图，根据题意， ∠PMQ = 54︒ ， 在 Rt △MPQ 中， tan ∠PMQ =PQ， MQ ∠PNQ = 73︒,∠PQM = 90︒, MN = 40. ∴PQ = MQ tan 54︒.在 Rt △NPM 中， tan ∠PNQ = PQ ，NQPQ = NQ tan 73︒.∴MQ tan54︒ = NQ tan 73︒.又 NQ = MN + NQ .∴(40 + NQ ) tan54︒ = NQ 40tan54︒tan73︒-tan54︒∴PQ = NQ40tan54︒ tan73︒ ≈ 40⨯1.4⨯3.3 ≈ 97 . tan73︒-tan54︒ 3.3+1.4答，解放桥的全长 PQ 约为 97m【考点】直角三角形的应用.23.【答案】（1）10，18（2） y 关于 x 的函数解析式为 y = ⎧5x , 0 ≤ x ≤ 2,⎩（3） 小张购买了 7 kg 种子.【解析】解：（1）10，18.（2）根据题意，当0 ≤ x ≤ 2 时，种子的价格为 5 元/kg 计价，tan 73︒tan 73︒ = NQ =即OA 2 + OE 2 22 +12 ⎩∴ y = 5x ;当 x > 2 时，其中有2kg 的种子按 5 元/kg 计价， 其余的(x - 2) kg 种子按 4 元/kg (即 8 折)计价， ∴ y = 5⨯ 2 + 4(x - 2) = 4x + 2 .⎧5x , 0 ≤ x ≤ 2, ∴ y 关于 x 的函数解析式为 y = ⎨ 4x + 2, x > 2. （3） 30 >10 ，∴一次性购买种子的数量超过 2 kg .∴30 = 4x + 2 ，解得 x = 7 .【考点】利用一次函数解决实际问题24.【答案】（1） AE ' =BF ' =（2）略（3） 1 + 3 .2【解析】解：（1）当α = 90︒ 时，如图，点 E ' 与点 F ' 重合. 点 A (-2,0) ，点 B (0, 2) ，∴OA = OB = 2 .点 E ，点 F 分别为OA ,OB 的中点，∴OE = OF =1.正方形OE 'D 'F '是正方形OEDF 旋转后得到的， ∴OE ' = OE =1,OF ' = OF =1.在 Rt △AE 'O 中，AE ' == = 5 .在 Rt △BOF ' 中，55OB2 +OF'222 +125BF'===.（2）当α=135︒时，如图，正方形OE'D'F'是正方形OEDF 旋转后得到的，∴∠AOE'=∠BOD'.又OE'=OF'，OA =OB ，∴△AOE'≌△BOF'.∴AE'=BF'，且∠1 =∠2 .AE'与OB 相交，可得∠3 =∠4 .∴∠1+∠3 =∠2 +∠4 .记AE'与BF'相交于点P .∴∠APB =180︒- (∠2 +∠4) .又∠AOB =180︒- (∠1+∠3) .∴∠APB =∠AOB = 90︒.即AE'⊥BF'.（3）1 + 3. 2【考点】图形的旋转25.【答案】（1）①P(3,3)② y 关于x 的函数解析式为y =x2 - 2x .（2）m =t或m =2t2 -12t【解析】解：（1）①点O(0,0)，点F(1,1)，∴直线OD 的解析式为y =x .设直线EA 的解析式为y =kx +b ，由点E 和点F 关于点M (1, -1) 对称，得点E(1, -3) . 又点A(2,0) ，点 E 在直线EA 上，t t ⎧0 = 2k + b , ⎧ k = 3, ∴⎨-3 = k + b , 解得⎨ = -6.⎩ ⎩b∴直线 EA 的解析式为 y = 3x - 6 .直线点 P 是直线OF 与直线 EA 的交点，⎧ y = x , ⎧ x = 3, 有⎨ y = 3x - 6. 解得⎨ y = 3.⎩ ⎩∴点 P 的坐标为(3,3) .②由已知，设点 F (1,t ) ，∴直线OF 的解析式为 y = tx ，设直线 EA 的解析式为 y = kx + b ，由点 E 和点 F 关于点 M (1, -1) 对称，得点 E (1, -2 - t ) . 又点 A 、点 E 在直线 EA 上，⎧ 0 = 2k + b , ⎧ k = 2 + t ∴ ⎨-2 - t = k + b . 解得⎨b = -2(2 + t ).⎩ ⎩∴直线 EA 的解析式为 y = (2 + t )x - 2(2 + t ) ， 点 P 为直线OF 与直线 EA 的交点，∴tx = (2 + t )x - 2(2 + t ) ，化简，得t = x - 2.有 y = tx = (x - 2)x = x 2 - 2x .∴ y 关于 x 的函数解析式为 y = x 2 - 2x .（2）根据题意，同（1）可得直线OF 的解析式为 y = tx ，直线 EA 的解析式为 y = (t - 2m )x - 2(t - 2m ) . 点 P 为直线OF 与直线 EA 的交点，∴tx = (t - 2m )x - 2(t - 2m ), m ≠ 0.化简，得 x = 2 - 2 . 有 y = tx = 2t - . m m t t 2∴点 P 的坐标为(2 - , 2 t - ) . m mt 2 PQ ⊥ l 于点Q ，得点Q (1, 2t - ) . m∴OQ 2 = 1+ t 2 (2 - t )2 ， PQ 2 = (1- t )2 .M m∴OQ =PQ ，∴1+t2 (2 -t)2 = (1-t)2 . m m化简，得t(t - 2m)(t 2 - 2mt -1) = 0 .又t ≠ 0 ，∴t - 2m = 0 或t2 - 2mt -1 = 0 .t t2 -1∴m =或m =即为所求.2 2t【考点】点的运动变化，待定系数法求函数解析式，一元二次方程的应用11 / 10。

2014年北京市初中毕业生学业考试数学试题（含答案全解全析）第Ⅰ卷(选择题,共36分)一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算(-6)×(-1)的结果等于( )A.6B.-6C.1D.-12.cos 60°的值等于( )A. B. C. D.3.下列标志中,可以看作是轴对称图形的是( )4.为让市民出行更加方便,天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1 608 000 000人次.将1 608 000 000用科学记数法表示应为( )A. 60.8× 07B. 6.08× 08C. .608× 09D.0. 60 8× 0105.如图,从左面观察这个立体图形,能得到的平面图形是( )6.正六边形的边心距为,则该正六边形的边长是( )A. B.2 C.3 D.27.如图,AB是☉O的弦,AC是☉O的切线,A为切点,BC经过圆心,若∠B= 5°,则∠C的大小等于( )A. 0°B. 5°C.40°D.50°8.如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF∶FC等于( )A. ∶B. ∶C. ∶D. ∶9.已知反比例函数y= 0,当1<x<2时,y的取值范围是( )A.0<y<5B.1<y<2C.5<y<10D.y>1010.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A.x(x+1)=28B.x(x-1)=28C.x(x+1)=28D.x(x-1)=2811.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示:如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,公司将录取( )A.甲B.乙C.丙D.丁12.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m> .其中,正确结论的个数是( )A.0B.1C.2D.3第Ⅱ卷(非选择题,共84分)二、填空题(本大题共6小题,每小题3分,共18分)13.计算x5÷x2的结果等于.14.已知反比例函数y=(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k 的值为.15.如图,是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为.16.抛物线y=x2-2x+3的顶点坐标是.17.如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为(度).18.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上. (Ⅰ)计算AC2+BC2的值等于;(Ⅱ)请在如图所示的网格中,用无刻度．．．的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2,并简要说明画图方法(不要求证明) .三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)19.(本小题8分)解不等式组- ,①.②请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得;(Ⅱ)解不等式②,得;(Ⅲ)把不等式①和②的解集在数轴上表示出来:(Ⅳ)原不等式组的解集为.20.(本小题8分)为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(Ⅰ)本次接受随机抽样调查的学生人数为,图①中m的值为;(Ⅱ)求本次调查获取的样本数据的众数和中位数;(Ⅲ)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?21.(本小题10分)已知☉O的直径为10,点A,点B,点C在☉O上,∠CAB的平分线交☉O于点D.(Ⅰ)如图①,若BC为☉O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.22.(本小题10分)解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47 m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 m;(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=7 °.已知PQ⊥MQ,MN=40 m,求解放桥的全长PQ(tan 54°≈ .4,tan 7 °≈ . ,结果保留整数).23.(本小题10分)“黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子的价格打8折.(Ⅰ)根据题意(Ⅱ)设购买种子数量为x kg,付款金额为y元,求y关于x的函数解析式;(Ⅲ)若小张一次购买该种子花费了30元,求他购买种子的数量.24.(本小题10分)在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE'D'F',记旋转角为α.(Ⅰ)如图①,当α=90°时,求AE',BF'的长;(Ⅱ)如图②,当α= 5°时,求证AE'=BF',且AE'⊥BF';(Ⅲ)若直线AE'与直线BF'相交于点P,求点P的纵坐标的最大值(直接写出结果即可).25.(本小题10分)在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E、点F、点M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.(Ⅰ)若点M的坐标为(1,-1).①当点F的坐标为(1,1)时,如图,求点P的坐标;②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.(Ⅱ)若点M(1,m),点F(1,t),其中t≠0.过点P作PQ⊥l于点Q,当OQ=PQ时,试用含t的式子表示m.答案全解全析：一、选择题1.A 根据有理数乘法法则,先确定符号为“+”,再把绝对值相乘,得(- )×(-6)=6,故选A.2.A 本题考查特殊角的三角函数值,60°角的余弦值是,故选A.3.D A 、B 、C 三个选项中的图形是中心对称图形,D 选项中的图形是轴对称图形,故选D. 评析 本题考查轴对称图形与中心对称图形的区别,属基础题.4.C 根据科学记数法的表示方法,知 608 000 000= .608× 09,故选C.5.A 本题考查立体图形的三视图,选项A 是左视图,选项B 是主视图,选项D 是俯视图,故选A.6.B 由题意可知,△OAB 是等边三角形,OG⊥AB 于G,在Rt△OAG 中,sin∠OAG=,所以OA=sin∠ =sin60°=2,所以AB=OA=2,故选B.7.C 连结OA,☉O 中,OA=OB,所以∠B=∠BAO= 5°,因为∠AOC 是△OAB 的外角,所以∠AOC=∠B+∠BAO=50°,又因为AC 是☉O 的切线,所以OA⊥AC,在Rt△OAC 中,∠C=90°-∠AOC=40°,故选C.8.D 平行四边形ABCD中,AD∥BC且AD=BC,因为E为AD的中点,所以DE=AD=BC,因为AD∥BC,所以△DEF∽△BCF,所以EF∶FC=DE∶BC= ∶ ,故选D.9.C 当1<x<2时,反比例函数y= 0的图象在第一象限,且y随x的增大而减小,当x=1时,y=10,当x=2时,y=5,所以5<y<10,故选C.10.B 对每一个队而言,都要和其余(x-1)个队比赛一场,考虑到重复性,故总共要比赛x(x-1)场,根据题意,总共比赛4×7= 8场,可列出方程x(x-1)=28,故选B.11.B 甲的平均成绩=86×0.6+90×0.4=87.6分,乙的平均成绩=9 ×0.6+8 ×0.4=88.4分,丙的平均成绩=90×0.6+8 ×0.4=87. 分,丁的平均成绩=8 ×0.6+9 ×0.4=86.6分,乙的平均成绩最高,故录取乙,选B.12.D 因为抛物线与x轴有两个交点,所以b2-4ac>0,结论①成立;因为抛物线开口向下,所以a<0,对称轴在y轴右侧,则a与b符号相反,所以b>0,因为抛物线与y轴的交点在y轴正半轴上,所以c>0,所以abc<0,结论②成立;ax2+bx+c-m=0可化为ax2+bx+c=m,设直线y=m,该方程无实数根,即直线y=m与抛物线y=ax2+bx+c无交点,由题图可知,m>2,结论③也成立.故选D.二、填空题13.答案x3解析根据同底数幂的除法法则,底数不变,指数相减,可得x5÷x2=x5-2=x3.14.答案1(答案不唯一,满足k>0即可)解析若反比例函数y=(k≠0)的图象位于第一、第三象限,则k>0,所以只要填一个大于0的数即可.15.答案8解析在这13张牌中,只有A、2、3、4、5、6、7、8这8张的牌点数小于9,每张牌被抽到的可能性相同,故抽出的牌点数小于9的概率为8.16.答案(1,2)解析解法一:可把抛物线解析式配方成顶点式为y=(x-1)2+2,由顶点式可知,顶点坐标为(1,2).解法二:可根据抛物线y=ax2+bx+c的顶点坐标公式-,4-4,直接求出顶点坐标为(1,2).17.答案45解析因为BD=BC,所以∠BCD=∠BDC,因为AE=AC,所以∠ACE=∠AEC.设∠BCD=∠BDC=α,∠ACE=∠AEC=β,∠DCE=γ,根据△CDE内角和为 80°及∠ACB=90°,可列出方程组80°,①-90°,②由①-②得 γ=90°,所以γ=45°,即∠DCE=45°.18.答案(Ⅰ)(Ⅱ)分别以AC,BC,AB为一边作正方形ACED,正方形BCNM,正方形ABHF;延长DE交NM于点Q,连结QC;平移QC至AG,BP位置;直线GP分别交AF,BH于点T,S.则四边形ABST即为所求解析(Ⅰ)由题图可知,AC=,BC=3,所以AC2+BC2=()2+32=2+9=11.(Ⅱ)BCNM的面积=BCQJ的面积=BCKP的面积,ACED的面积=ACKG的面积,所以BCNM的面积+ ACED的面积= BCKP的面积+ ACKG的面积=AGKPB的面积+△ABC的面积=AGKPB的面积+△KGP的面积=AGPB的面积=ABST的面积.评析本题考查面积的割补及面积的转化,图中的四边形面积可根据同底等高的原则进行转化.三、解答题19.解析(Ⅰ)x≥-1.(Ⅱ)x≤ .(Ⅲ)(Ⅳ)- ≤x≤ .20.解析(Ⅰ)40; 5.(Ⅱ)∵在这组样本数据中,35出现了12次,出现的次数最多,∴这组样本数据的众数为35. ∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是36,有 6 6=36,∴这组样本数据的中位数为36.(Ⅲ)∵在40名学生中,鞋号为35的学生人数比例为30%,∴由样本数据,估计学校各年级学生中鞋号为35的人数比例约为30%,于是,计划购买200双运动鞋时, 00× 0%=60(双).∴建议购买35号运动鞋60双.21.解析(Ⅰ)由已知,BC为☉O的直径,得∠CAB=∠BDC=90°.在Rt△CAB中,BC=10,AB=6,∴AC=-A= 0-6=8.∵AD平分∠CAB,∴=.∴CD=BD.在Rt△BDC中,BC=10,CD2+BD2=BC2,∴BD 2=CD 2=50.∴BD=CD=5 . (Ⅱ)如图,连结OB,OD.∵AD 平分∠CAB,且∠CAB=60°, ∴∠DAB=∠CAB= 0°.∴∠DOB= ∠DAB=60°. 又∵在☉O 中,OB=OD, ∴△OBD 是等边三角形.∵☉O 的直径为 0,∴OB=5,∴BD=5. 22.解析 (Ⅰ) .5.(Ⅱ)如图,根据题意知,∠PMQ=54°,∠PNQ=7 °,∠PQM=90°,MN=40.∵在Rt△MPQ 中,tan∠PMQ=,∴PQ=MQ·tan 54°.∵在Rt△NPQ 中,tan∠PNQ=,∴PQ=NQ·tan 7 °,∴MQ·tan 54°=NQ·tan 7 °. 又MQ=MN+NQ,∴(40+NQ)tan 54°=NQ·tan 7 °, 即NQ=40tan54°tan7 °-tan54°.∴PQ=NQ·tan 7 °=40tan54°·tan7 °tan7 °-tan54°≈40 .4 . . - .4≈97(m).答:解放桥的全长PQ 约为97 m.评析 本题是一个典型的用基础图形测量实际物体长度的问题,综合运用了三角函数、方程的思想,对学生有较高的能力要求. 23.解析 (Ⅰ) 0; 8.(Ⅱ)根据题意,当0≤x≤ 时,种子的价格为5元/kg, ∴y=5x;当x>2时,其中有2 kg 的种子按5元/kg 付款, 其余的(x-2)kg 种子按4元/kg(即8折)付款, ∴y=5× +4(x -2)=4x+2.∴y 关于x 的函数解析式为y= 5 , 0 x ,4 ,x .(Ⅲ)∵ 0> 0,∴一次购买种子的数量超过2 kg. ∴ 0=4x+ ,解得x=7.答:小张购买了7 kg 种子. 24.解析 (Ⅰ)当α=90°时,如图,点E'与点F 重合. ∵点A(-2,0),点B(0,2), ∴OA=OB= .∵点E,点F 分别为OA,OB 的中点, ∴OE=OF= .∵正方形OE'D'F'是由正方形OEDF 旋转后得到的, ∴OE'=OE= ,OF'=OF= . 在Rt△AE'O 中,AE'= OE'= = 5. 在Rt△BOF'中,BF'= OF' = = 5. (Ⅱ)证明:当α= 5°时,如图,∵正方形OE'D'F'是由正方形OEDF 旋转后得到的,∴∠AOE'=∠BOF'. 又OE'=OF',OA=OB, ∴△AOE'≌△BOF'. ∴AE'=BF',且∠ =∠ .由AE'与OB 相交,可得∠ =∠4, ∴∠ +∠ =∠ +∠4. 记AE'与BF'相交于点G, ∴∠AGB= 80°-(∠ +∠4). 又∠AOB= 80°-(∠ +∠ ),∴∠AGB=∠AOB=90°,即AE'⊥BF'. (Ⅲ). 25.解析 (Ⅰ)①∵点O(0,0),点F(1,1),∴直线OF 的解析式为y=x. 设直线EA 的解析式为y=kx+b,由点E 和点F 关于点M(1,-1)对称,得点E(1,-3). 又点A(2,0),点E 在直线EA 上, ∴ 0 ,- ,解得 ,-6.∴直线EA 的解析式为y=3x-6.∵点P 是直线OF 与直线EA 的交点,∴由 , -6解得 , . ∴点P 的坐标为(3,3). ②由已知,设点F(1,t),∴直线OF的解析式为y=tx.设直线EA的解析式为y=kx+b,由点E和点F关于点M(1,-1)对称,得点E(1,-2-t). 又点A,点E在直线EA上,∴由0,--解得,- ( ).∴直线EA的解析式为y=(2+t)x-2(2+t).∵点P为直线OF与直线EA的交点,∴tx=( +t)x-2(2+t),化简,得t=x-2.∴y=tx=(x-2)x=x2-2x.∴y关于x的函数解析式为y=x2-2x.(Ⅱ)根据题意,同(Ⅰ)可得直线OF的解析式为y=tx,直线EA的解析式为y=(t-2m)x-2(t-2m).∵点P为直线OF与直线EA的交点,∴tx=(t-2m)x-2(t- m),m≠0.化简,得x=2-.有y=tx=2t-.∴点P的坐标为-, t-.∵PQ⊥l于点Q,得点Q , -,∴OQ2=1+t2-,PQ2=-.∵OQ=PQ,∴ +t2-=-.化简,得t(t-2m)(t2-2mt-1)=0.又t≠0,∴t-2m=0或t2-2mt-1=0.∴m=或m=-.11。

2014年天津市初中毕业生学业考试试卷数 学本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2.本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算（-6）×（-1）的结果等于（A ）6（B ）-6 （C ）1 （D ）-1 （2）cos60o 的值等于（A ）21 （B ）33 （C ）23 （D ）3（3）下列标志中，可以看作是轴对称图形的是（A ） （B ） （C ） （D ）（4）为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608 000000人次.将1608 000 000用科学记数法表示应为（A ）160.8×107（B ）16.08×108 （C ）1.608×109 （D ）0.1608×1010（5）如图，从左面观察这个立体图形，能得到的平面图形是（A ） （B ）（C ） （D ）（6）正六边形的边心距为3，则该正六边形的边长是（A ）3 （B ）2 （C ）3 （D ）32 （7）如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.若∠B ＝25o ，则∠C 的大小等于（A ）20o（B ）25o （C ）40o （D ）50o （8）如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于（A ）3：2（B ）3：1 （C ）1：1（D ）1：2 （9）已知反比例函数x y 10=，当1<x <2时，y 的取值范围是 （A ）0<y <5（B ）1<y <2 （C ）5<y <10 （D ）y>10（10）要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为（A ）()28121=+x x （B ）()28121=-x x （C ）()281=+x x （D ）()281=-x x（11）某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：第（5）题第（7）题第（8）题如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取（A ）甲 （B ）乙 （C ）丙 （D ）丁（12）已知二次函数y =ax 2+b x+c （a ≠0）的图象如下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有下列结论：①b 2-4ac >0；②abc <0；③m >2.其中，正确结论的个数是 （A ）0（B ）1 （C ）2 （D ）32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷 注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。

数学试卷 第1页（共28页）数学试卷 第2页（共28页）绝密★启用前天津市2014年初中毕业生学业考试数 学本试卷满分120分,考试时间100分钟.第Ⅰ卷(选择题 共36分)一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.计算(6)(1)-⨯-的结果等于( )A .6B .6-C .1D .1- 2.cos60的值等于( )A .12B .33C .32D .3 3.下列标志中,可以看作是轴对称图形的是( )ABCD4.为让市民出行更加方便,天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608000000用科学记数法表示应为( )A .7160.810⨯B .816.0810⨯C .91.60810⨯D .100.160810⨯ 5.如图,从左面观察这个立体图形,能得到的平面图形是( )AB CD6.正六边形的边心距为3,则该正六边形的边长是( )A .3B .2C .3D .237.如图,AB 是O 的弦,AC 是O 的切线,A 为切点,BC 经过圆心.若25B ∠＝,则C ∠的大小等于( )A .20B .25C .40D .508.如图,在□ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则:EF FC 等于 ( ) A .3:2 B .3:1 C .1:1D .1:29.已知反比例函数10y x=,当12x ＜＜时,y 的取值范围是( )A .05y ＜＜B .12y ＜＜C .510y ＜＜D .10y ＞10.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x 个队参赛,则x 满足的关系式为( )A .1(1)282x x += B .1(1)282x x -=C .(1)28x x +=D .(1)28x x -=11.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如下表所示：候选人甲 乙 丙 丁 测试成绩 (百分制)面试 86 92 90 83 笔试90838392如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,公司将录取( ) A .甲B .乙C .丙D .丁12.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,且关于x的一元二次方程20ax bx c m ++-=没有实数根,有下列结论： ①240b ac -＞；②0abc ＜； ③2m ＞.其中,正确结论的个数是( )A .0B .1C .2D .3毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页（共28页） 数学试卷 第4页（共28页）第Ⅱ卷(非选择题 共84分)二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上) 13.计算52x x ÷的结果等于 . 14.已知反比例函数ky x=(k 为常数,0k ≠)的图象位于第一、第三象限,写出一个符合条件的k 的值为 .15.如图是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为 .16.抛物线223y x x =-+的顶点坐标是 .17.如图,在Rt ABC △中,,D E 为斜边AB 上的两个点,且,BD BC AE AC ==,则DCE ∠的大小为 (度).18.如图,将ABC △放在每个小正方形的边长为1的网格中,点A ,点B ,点C 均落在格点上.(1)计算22AC BC +的值等于 ；(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB 为一边的矩形,使该矩形的面积等于22AC BC +,并简要说明画图方法(不要求证明) .三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤) 19.(本小题满分8分) 解不等式组21,21.x x +⎧⎨+⎩≥-1①≤3②请结合题意填空,完成本小题的解答. (1)解不等式①,得 ； (2)解不等式②,得 ；(3)把不等式①和②的解集在数轴上表示出来：(4)原不等式组的解集为 . 20.(本小题满分8分)为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图1和图2,请根据有关信息,解答下列问题：(1)本次接受随机抽样调查的学生人数为 ,图1中m 的值是 ； (2)求本次调查获取的样本数据的众数和中位数；(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双？数学试卷 第5页（共28页） 数学试卷 第6页（共28页）21.(本小题满分10分)已知O 的直径为10,点A ,点B ,点C 是在O 上,CAB ∠的平分线交O 于点D .(1)如图1,若BC 为O 的直径,6AB ＝,求,,AC BD CD 的长； (2)如图2,若60CAB ∠＝,求BD 的长.22.(本小题满分10分)解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.(1)如图1,已知解放桥可开启部分的桥面的跨度AB 等于47m ,从AB 的中点C 处开启,则AC 开启至A C ''的位置时,A C ''的长为 m ；(2)如图2,某校兴趣小组要测量解放桥的全长PQ ,在观景平台M 处测得=54PMQ ∠,沿河岸MQ 前行,在观景平台N 处测得73PNQ ∠＝.已知PQ MQ ⊥,=40m MN ,求解放桥的全长PQ (tan54 1.4,tan73 3.3≈≈,结果保留整数).毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页（共28页） 数学试卷 第8页（共28页）23.(本小题满分10分)“黄金1号”玉米种子的价格为5元/kg .如果一次购买2kg 以上的种子,超过2kg 的部分的种子的价格打8折.(1)根据题意,填写下表：购买种子的数量/kg1.5 2 3.54 … 付款金额/元7.516…(2)设购买种子的数量为kg x ,付款金额为y 元,求y 关于x 的函数解析式； (3)若小张一次购买该种子花费了30元,求他购买种子的数量.24.(本小题满分10分)在平面直角坐标系中,O 为原点,点(2,0)A -,点(0,2)B ,点E ,点F 分别为,OA OB 的中点.若正方形OEDF 绕点O 顺时针旋转,得正方形OE D F ''',记旋转角为α.(1)如图1,当90α=时,求,AE BF ''的长；(2)如图2,当135α＝时,求证：AE BF ''＝,且AE BF ''⊥； (3)若直线AE '与直线BF '相交于点P ,求点P 的纵坐标的最大值(直接写出结果即可).25.(本小题满分10分)在平面直角坐标系中,O 为原点,直线:1l x ＝,点(2,0)A ,点E 、点F 、点M 都在直线l 上,且点E 和点F 关于点M 对称,直线EA 与直线OF 交于点P . (1)若点M 的坐标为(1,1)-.①当点F 的坐标为(1,1)时,如图,求点P 的坐标；②当点F 为直线l 上的动点时,记为(,)P x y ,求y 关于x 的函数解析式；(2)若点(1,)M m ,点(1,)F t ,其中0t ≠.过点P 作PQ l ⊥于点Q ,当=OQ PQ 时,试用含t 的式子表示m .5 / 14天津市2014年初中毕业生学业考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】两数相乘，同号得正，异号得负，并把绝对值相乘，(6)(1)6-⨯-=，故选A. 【考点】有理数的计算 2.【答案】A 【解析】1cos602︒=. 【考点】特殊角的三角函数值 3.【答案】D【解析】轴对称图形沿对称轴折叠，直线两旁的部分能够重合，图形D 沿竖直的直线折叠两旁的部分能重合，D 是轴对称图形，故选D. 【考点】轴对称图形的概念 4.【答案】C【解析】科学计数法是将一个数写成10n a ⨯的形式，其中11|0|a ≤<，n 为整数.当原数的绝对值10≥时，n 为正整数，n 等于原数的整数位数减1；当原数的绝对值1<时，n 为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位上的零），91 608 000 000 1.60810=⨯，故选C. 【考点】科学计数法 5.【答案】A【解析】此立体图形从左面能看到的图形是，故选A.【考点】三视图 6.【答案】B【解析】正多边形的边长等于正六边形外接圆的半径，正六边形的边心距、外接圆的半径、边长的一半三条线段可以构成含有30︒角的直角三角形，由三角函数求得正六边形外接圆的半径为2，即边长为2，故选B.数学试卷 第11页（共28页）数学试卷 第12页（共28页）【考点】正多边形的性质 7.【答案】C【解析】连接OA ，则OA OC ⊥，由25B ∠=︒知50AOC ∠=︒，所以40C ∠=︒，故选C. 【考点】切线的性质 8.【答案】D【解析】因为E 是平行四边形ABCD 中边AD 的中点，所以EDF CBF △∽△，所以::1:2EF FC ED BC ==，故选D.【考点】相似三角形的性质 9.【答案】C【解析】由反比例函数的性质结合图像写出取值范围.当1x =时，10y =；当2x =时，5y =，所以y 的取值范围是510y <<，故选C. 【考点】反比例函数的性质 10.【答案】B【解析】根据题意得共可进行28场比赛，由于每两个队都要进行比赛，所以1(1)282x x -=，故选B.【考点】一元二次方程解决实际问题 11.【答案】B【解析】首先根据权重计算四人的平均成绩，再根据平均成绩的大小确定录取人，甲的平均成绩：860.6900.487.6⨯+⨯=，乙的平均成绩：920.6830.488.4⨯+⨯=，丙的平均成绩：900.6830.487.2⨯+⨯=，丁的平均成绩：830.6920.486.6⨯+⨯= ，因为乙的平均成绩最高，所以公司将录取乙，故选B. 【考点】加权平均数的计算 12.【答案】D【解析】二次函数2y ax bx c =++的图像与x 轴有两个交点，所以240b ac ∆=->，故①正确；由图像知0a <，0b >，0c >，所以0abc <，故②正确；由二次函数2y ax bx c =++的最大值为2，20ax bx c m ++-=没有实根，知220ax bx c m m ++-≤-<，2m >，故③正确，所以正确的结论有三个，故选D.【考点】二次函数的图像和性质第Ⅱ卷7 / 14二、填空题 13.【答案】3x【解析】同底数幂相除，底数不变，指数相减，所以523x x x ÷=. 【考点】同底数幂的除法14.【答案】1（满足0k >即可）【解析】反比例函数(0)ky k x =≠位于第一、第三象限，只需0k >，故k 的值可以为1.【考点】反比例函数的性质15.【答案】813【解析】此13张牌中小于9的有8张，故从中任意抽取一张，抽到的牌的点数小于9的概率是813. 【考点】概率的计算 16.【答案】(1,2)【解析】顶点坐标的计算有两种方法，一是公式法24(,)224b ac b a a --；二是配方法，2223(1)2y x x x =-+=-+，故顶点坐标为1,2（）. 【考点】二次函数顶点坐标的计算 17.【答案】45【解析】设A a ∠=，由题意知o o 1(180)2902ACE a a ∠=-÷=-，o o o 1[180(90)]2452DCB a a ∠=--÷=+，o o o o 11(90)(45)1359022ACE DCB a a ACB DCE DCE ∠+∠=-++==∠+∠=+∠，所以o 45DCE ∠=.【考点】三角形内角和，等腰三角形的性质 18.【答案】（1）11（2）分别以AC ，BC ，AB 为一遍作正方形ACED ，正方形BCNM ，正方形ABHF ；延长DE 交NM 于点Q ，连接QC ；平移QC 至AG ，BP 位置；直线GP 分别交AF ，BH 于点T ，S ，则四边形ABST 即为所求数学试卷 第15页（共28页）数学试卷 第16页（共28页）【解析】（1）2222311AC BC +=+=（2）连接DG ，利用切割补形，可以得到四边形DGPB 中，平行四边形AGPB 的面积为11，再作矩形ATSB使之与平行四边形AGPB 等高即可. 【考点】勾股定理，尺规作图 三、解答题19.【答案】（1）1x ≥-. （2）1x ≤.（3）【解析】解：（1）211x +≥- 则22x ≥-，解得1x ≥-. （2）213x +≤，则22x ≤，解得1x ≤. （3）如图所示【考点】不等式组的解法 20.【答案】（1）40，15 （2）36 （3）60【解析】解：（1）40，15（2）在这组样本数据中，35出现了12次，出现的次数最多，∴这组样本数据的众数为35.将这组样本数据从大到小的顺序排列，其中处于中间的两个数都是361有3636362+=， ∴这组样本数据的中位数为36.（3）在40名学生中，鞋号为35的学生人数比例为30%，9 / 14∴由样本数据，估计学校各年级学生中鞋号为35的人数比例约为30%于是，计划购买200双运动鞋时，有20030%60⨯=.∴建议购买35号运动鞋60双【考点】扇形统计图，条形统计图解决实际问题 21.【答案】（1）8AC =，50BD =，CD = （2）5BD =【解析】解：（1）由已知，BC 为O 的直径，得90CAB BDC ∠=∠=.在Rt CAB △中，10BC =，6AB =，∴8AC ===.AD 平分CAB ∠. ∴CD BD =. ∴CD BD =.在Rt BDC △中，10BC =，222CD BD BC +=，∴2250BD CD ==，BD CD ∴==（2）如图，连接,OB OD .AD 平分CAB ∠，且60CAB ∠=，数学试卷 第19页（共28页）数学试卷 第20页（共28页）∴130.2DAB CAB ∠=∠=260.DOB DAB ∴∠=∠=又O 中OB OD =，OBD ∴△是等边三角形.O 的直径为10，有5OB =，5BD ∴=【考点】圆周角定理及其推论，勾股定理，等边三角形的判定及性质 22.【答案】（1）23.5 （2）解放桥的全长约为97 m. 【解析】解：（1）123.52A C AC AB ''===（2）如图，根据题意，54PMQ ∠=︒， 73,90,40.PNQ PQM MN ∠=︒∠=︒= 在Rt MPQ △中，tan PQPMQ MQ∠=， tan54PQ MQ ∴=︒.在Rt NPM △中，tan PQPNQ NQ∠=， tan73PQ NQ =︒.tan54tan73MQ NQ ∴︒=︒.又NQ MN NQ =+.(40)tan54tan73NQ NQ ∴+︒=︒即40tan54tan73tan54NQ ︒︒︒=-40tan54tan73401.43.3tan 7397tan73tan54 3.31.4PQ NQ ︒︒︒︒⨯⨯∴=︒=≈≈-+.答，解放桥的全长PQ 约为97m【考点】直角三角形的应用.23.【答案】（1）10，18（2）y 关于x 的函数解析式为5,02,42, 2.x x y x x ≤≤⎧=⎨+>⎩（3）小张购买了7 kg 种子.【解析】解：（1）10，18.（2）根据题意，当02x ≤≤时，种子的价格为5元/kg 计价，5;y x ∴=当2x >时，其中有2kg 的种子按5元/kg 计价，其余的(2)kg x -种子按4元/kg (即8折)计价，524(2)42y x x ∴=⨯+-=+.y ∴关于x 的函数解析式为5,02,42, 2.x x y x x ≤≤⎧=⎨+>⎩（3）3010>，∴一次性购买种子的数量超过2kg .3042x ∴=+，解得7x =.【考点】利用一次函数解决实际问题24.【答案】（1）AE '=BF '=（2）略（3 【解析】解：（1）当90α=︒时，如图，点E '与点F '重合.点(2,0)A -，点(0,2)B ， 2OA OB ∴==.点E ，点F 分别为,OA OB 的中点，1OE OF ∴==.正方形OE D F '''是正方形OEDF 旋转后得到的，1,1OE OE OF OF ''∴====.在Rt AE O '△中，AE '=在Rt BOF '△中，BF '===.（2）当135α=︒时，如图，正方形OE D F '''是正方形OEDF 旋转后得到的，AOE BOD ''∴∠=∠.又OE OF ''=，OA OB =，AOE BOF ''∴△≌△.AE BF ''∴=，且12∠=∠.AE '与OB 相交，可得34∠=∠.1324∴∠+∠=∠+∠.记AE '与BF '相交于点P .180(24)APB ∴∠=︒-∠+∠.又180(13)AOB ∠=︒-∠+∠.90APB AOB ∴∠=∠=︒.即AE BF ''⊥.（3）12+. 【考点】图形的旋转25.【答案】（1）①(3,3)P②y 关于x 的函数解析式为22y x x =-.（2）2t m =或212t m t -= 【解析】解：（1）①点(0,0)O ，点(1,1)F ，∴直线OD 的解析式为y x =.设直线EA 的解析式为y kx b =+，由点E 和点F 关于点(1,1)M -对称，得点(1,3)E -.又点(2,0)A ，点E 在直线EA 上，02,3,k b k b =+⎧∴⎨-=+⎩解得3,6.k b =⎧⎨=-⎩∴直线EA 的解析式为36y x =-.直线点P 是直线OF 与直线EA 的交点，有,3 6.y x y x =⎧⎨=-⎩解得3,3.x y =⎧⎨=⎩∴点P 的坐标为(3,3).②由已知，设点(1,)F t ，∴直线OF 的解析式为y tx =，设直线EA 的解析式为y kx b =+，由点E 和点F 关于点(1,1)M -对称，得点(1,2)E t --.又点A 、点E 在直线EA 上，∴02,2.k b t k b =+⎧⎨--=+⎩解得22(2).k t b t =+⎧⎨=-+⎩∴直线EA 的解析式为(2)2(2)y t x t =+-+，点P 为直线OF 与直线EA 的交点，(2)2(2)tx t x t ∴=+-+，化简，得 2.t x =-有2(2)2y tx x x x x ==-=-.y ∴关于x 的函数解析式为22y x x =-.（2）根据题意，同（1）可得直线OF 的解析式为y tx =，直线EA 的解析式为(2)2(2)y t m x t m =---.点P 为直线OF 与直线EA 的交点，(2)2(2),0.tx t m x t m m ∴=---≠ 化简，得2.t x m=-有22t y tx t m ==-. ∴点P 的坐标为2(2,2t )t t m m--. PQ l ⊥于点Q ，得点2(1,2)t Q t m-. 2221(2)t OQ t M ∴=+-，22(1)t PQ m=-. OQ PQ ∴=，2221(2)(1)t t t m m∴+-=-. 化简，得2(2)(21)0t t m t mt ---=.又0t ≠，20t m ∴-=或2210t mt --=.2t m ∴=或212t m t -=即为所求. 【考点】点的运动变化，待定系数法求函数解析式，一元二次方程的应用。

2014年天津市初中毕业生学业考试试卷数 学本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2.本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算（-6）×（-1）的结果等于（A ）6 （B ）-6（C ）1（D ）-1（2）cos60o 的值等于（A ）21 （B ）33 （C ）23 （D ）3（3）下列标志中，可以看作是轴对称图形的是（A ） （B ） （C ） （D ）（4）为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608 000 000用科学记数法表示应为 （A ）160.8×107（B ）16.08×108（C ）1.608×109（D ）0.1608×1010（5）如图，从左面观察这个立体图形，能得到的平面图形是（A ） （B ）（C ） （D ）（6）正六边形的边心距为3，则该正六边形的边长是（A ）3（B ）2（C ）3（D ）32（7）如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.若∠B ＝25o ，则∠C 的大小等于（A ）20o （B ）25o（C ）40o（D ）50o（8）如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于（A ）3：2 （B ）3：1 （C ）1：1（D ）1：2（9）已知反比例函数xy 10=，当1<x <2时，y 的取值范围是 （A ）0<y <5 （B ）1<y <2 （C ）5<y <10（D ）y>10（10）要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为 （A ）()28121=+x x （B ）()28121=-x x （C ）()281=+x x（D ）()281=-x x（11）某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：候选人 甲 乙 丙 丁 测试成绩（百分制） 面试86 92 90 83 笔试90838392如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取第（5）题第（7）题第（8）题（A ）甲 （B ）乙 （C ）丙 （D ）丁（12）已知二次函数y =ax 2+b x+c （a ≠0）的图象如下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有下列结论：①b 2-4ac >0；②abc <0；③m >2. 其中，正确结论的个数是 （A ）0 （B ）1（C ）2（D ）32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。

2014年天津市初中毕业生学业考试试卷数 学本试卷分为第Ⅰ卷〔选择题〕、第Ⅱ卷〔非选择题〕两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷总分值120分。

考试时间100分钟。

答卷前，考生务必将自己的、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2题，共36分。

一、选择题〔本大题共12小题，每题3分，共36分．在每题给出的四个选项中，只有一项是符合题目要求的〕〔1〕计算〔-6〕×〔-1〕的结果等于〔A 〕6 〔B 〕-6〔C 〕1〔D 〕-1〔2〕cos60o 的值等于〔A 〕21 〔B 〕33 〔C 〕23 〔D 〕3〔3〕以下标志中，可以看作是轴对称图形的是〔A 〕 〔B 〕 〔C 〕 〔D 〕〔4〕为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608 000 000用科学记数法表示应为 〔A 〕×107〔B 〕×108〔C 〕×109〔D 〕×1010〔5〕如图，从左面观察这个立体图形，能得到的平面图形是〔A 〕 〔B 〕〔C 〕 〔D 〕〔6〕正六边形的边心距为3，则该正六边形的边长是〔A 〕3〔B 〕2〔C 〕3〔D 〕32〔7〕如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.假设∠B ＝25o ，则∠C 的大小等于〔A 〕20o 〔B 〕25o〔C 〕40o〔D 〕50o〔8〕如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于〔A 〕3：2 〔B 〕3：1 〔C 〕1：1〔D 〕1：2〔9〕已知反比例函数xy 10=，当1<x <2时，y 的取值范围是 〔A 〕0<y <5 〔B 〕1<y <2 〔C 〕5<y <10〔D 〕y>10〔10〕要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为 〔A 〕()28121=+x x 〔B 〕()28121=-x x 〔C 〕()281=+x x〔D 〕()281=-x x〔11〕某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：候选人 甲 乙 丙 丁 测试成绩〔百分制〕 面试86 92 90 83 笔试90838392如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取第〔5〕题第〔7〕题第〔8〕题〔A 〕甲 〔B 〕乙 〔C 〕丙 〔D 〕丁〔12〕已知二次函数y =ax 2+b x+c 〔a ≠0〕的图象如以下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有以下结论：①b 2-4ac >0；②abc <0；③m >2. 其中，正确结论的个数是 〔A 〕0 〔B 〕1〔C 〕2〔D 〕32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。

2014年天津市中考数学试卷一、选择题（本大题共12小题.每小题3分.共36分）1．（3分）（2014•天津）计算（﹣6）×（﹣1）的结果等于（）A．6B．﹣6 C．1D．﹣1考点：有理数的乘法．分析：根据有理数的乘法运算法则进行计算即可得解．解答：解：（﹣6）×（﹣1）=6×1=6．故选A．点评：本题考查了有理数的乘法运算.是基础题.熟记运算法则是解题的关键．2．（3分）（2014•天津）cos60°的值等于（）A．B．C．D．考点：特殊角的三角函数值．分析：根据特殊角的三角函数值解题即可．解答：解：cos 60°=．故选A．点评：本题考查特殊角的三角函数值.准确掌握特殊角的函数值是解题关键．3．（3分）（2014•天津）下列标志中.可以看作是轴对称图形的是（）A．B．C．D．考点：轴对称图形．分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、不是轴对称图形.是中心对称图形.不符合题意；B、不是轴对称图形.是中心对称图形.不符合题意；C、不是轴对称图形.是中心对称图形.不符合题意；D、是轴对称图形.符合题意．故选：D．点评：此题主要考查了中心对称图形和轴对称图形的定义.掌握中心对称图形与轴对称图形的概念.解答时要注意：判断轴对称图形的关键是寻找对称轴.图形两部沿对称轴叠后可重合；判断中心对称图形是要寻找对称中心.图形旋转180度后与原图重合．4．（3分）（2014•天津）为了市民出行更加方便.天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608000000用科学记数法表示为（）A．160.8×107B．16.08×108C．1.608×109D．0.1608×1010考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式.其中1≤|a|＜10.n为整数．确定n的值时.要看把原数变成a时.小数点移动了多少位.n的绝对值与小数点移动的位数相同．当原数绝对值＞1时.n是正数；当原数的绝对值＜1时.n是负数．解答：解：将1608000000用科学记数法表示为：1.608×109．故选：C．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式.其中1≤|a|＜10.n为整数.表示时关键要正确确定a的值以及n的值．5．（3分）（2014•天津）如图.从左面观察这个立体图形.能得到的平面图形是（）A．B．C．D．考点：简单组合体的三视图．分析：根据从左面看得到的图形是左视图.可得答案．解答：解；从左面看下面一个正方形.上面一个正方形.故选：A．点评：本题考查了简单组合体的三视图.从左面看得到的图形是左视图．6．（3分）（2014•天津）正六边形的边心距为.则该正六边形的边长是（）A．B．2C．3D．2考点：正多边形和圆．分析：运用正六边形的性质.正六边形边长等于外接圆的半径.再利用勾股定理解决．解答：解：∵正六边形的边心距为.∴OB =.AB =OA.∵OA2=AB2+OB2.∴OA2=（OA）2+（）2.解得OA=2．故选B．点评：本题主要考查了正六边形和圆.注意：外接圆的半径等于正六边形的边长．7．（3分）（2014•天津）如图.AB是⊙O的弦.AC是⊙O的切线.A为切点.BC经过圆心．若∠B=25°.则∠C的大小等于（）A．20°B．25°C．40°D．50°考点：切线的性质．分析：连接OA.根据切线的性质.即可求得∠C的度数．解答：解：如图.连接OA.∵AC是⊙O的切线.∴∠OAC=90°.∵OA=OB.∴∠B=∠OAB=25°.∴∠AOC=50°.∴∠C=40°．点评：本题考查了圆的切线性质.以及等腰三角形的性质.已知切线时常用的辅助线是连接圆心与切点．8．（3分）（2014•天津）如图.在▱ABCD中.点E是边AD的中点.EC交对角线BD于点F.则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：2考点：平行四边形的性质；相似三角形的判定与性质．分析：根据题意得出△DEF∽△BCF.进而得出=.利用点E是边AD的中点得出答案即可．解答：解：∵▱ABCD.故AD∥BC.∴△DEF∽△BCF.∴=.∵点E是边AD的中点.∴AE=DE=AD.∴=．故选：D．点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识.得出△DEF∽△BCF是解题关键．9．（3分）（2014•天津）已知反比例函数y=.当1＜x＜2时.y的取值范围是（）A．0＜y＜5 B．1＜y＜2 C．5＜y＜10 D．y＞10考点：反比例函数的性质．分析：将x=1和x=2分别代入反比例函数即可确定函数值的取值范围．解答：解：∵反比例函数y=中当x=1时y=10.当x=2时.y=5.∴当1＜x＜2时.y的取值范围是5＜y＜10.故选C．点评：本题考查了反比例函数的性质：（1）反比例函数y=（k≠0）的图象是双曲线；（2）当k＞0.双曲线的两支分别位于第一、第三象限.在每一象限内y随x的增大而减小；（3）当k＜0.双曲线的两支分别位于第二、第四象限.在每一象限内y随x的增大而增大．10．（3分）（2014•天津）要组织一次排球邀请赛.参赛的每个队之间都要比赛一场.根据场地和时间等条件.赛程计划安排7天.每天安排4场比赛．设比赛组织者应邀请x个队参赛.则x满足的关系式为（）A．x（x+1）=28 B．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28考点：由实际问题抽象出一元二次方程．分析：关系式为：球队总数×每支球队需赛的场数÷2=4×7.把相关数值代入即可．解答：解：每支球队都需要与其他球队赛（x﹣1）场.但2队之间只有1场比赛.所以可列方程为：x（x﹣1）=4×7．故选B．点评：本题考查了由实际问题抽象出一元二次方程.解决本题的关键是得到比赛总场数的等量关系.注意2队之间的比赛只有1场.最后的总场数应除以2．11．（3分）（2014•天津）某公司欲招聘一名公关人员.对甲、乙、丙、丁四位候选人进行了面试和笔试.他们的成绩如表：候选人甲乙丙丁测试成绩（百分制）面试86 92 90 83笔试90 83 83 92如果公司认为.作为公关人员面试的成绩应该比笔试的成绩更重要.并分别赋予它们6和4的权．根据四人各自的平均成绩.公司将录取（）A．甲B．乙C．丙D．丁考点：加权平均数．分析：根据题意先算出甲、乙、丙、丁四位候选人的加权平均数.再进行比较.即可得出答案．解答：解：甲的平均成绩为：（86×6+90×4）÷10=87.6（分）.乙的平均成绩为：（92×6+83×4）÷10=88.4（分）.丙的平均成绩为：（90×6+83×4）÷10=87.2（分）.丁的平均成绩为：（83×6+92×4）÷10=86.6（分）.因为乙的平均分数最高.所以乙将被录取．故选B．点评：此题考查了加权平均数的计算公式.注意.计算平均数时按6和4的权进行计算．12．（3分）（2014•天津）已知二次函数y=ax2+bx+c（a≠0）的图象如图.且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根.有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中.正确结论的个数是（）A．0B．1C．2D．3考点：二次函数图象与系数的关系．分析：由图象可知二次函数y=ax2+bx+c与x轴有两个交点.进而判断①；先根据抛物线的开口向下可知a＜0.由抛物线与y轴的交点判断c与0的关系.根据对称轴在y轴右侧得出b与0的关系.然后根据有理数乘法法则判断②；一元二次方程ax2+bx+c﹣m=0没有实数根.则可转化为ax2+bx+c=m.即可以理解为y=ax2+bx+c和y=m没有交点.即可求出m的取值范围.判断③即可．解答：解：①∵二次函数y=ax2+bx+c与x轴有两个交点.∴b2﹣4ac＞0.故①正确；②∵抛物线的开口向下.∴a＜0.∵抛物线与y轴交于正半轴.∴c＞0.∵对称轴x=﹣＞0.∴ab＜0.∵a＜0.∴b＞0.∴abc＜0.故②正确；③∵一元二次方程ax2+bx+c﹣m=0没有实数根.∴y=ax2+bx+c和y=m没有交点.由图可得.m＞2.故③正确．故选D．点评：本题主要考查图象与二次函数系数之间的关系.会利用对称轴的范围求2a与b的关系.以及二次函数与方程之间的转换.根的判别式的熟练运用．二、填空题（本大题共6小题.每小题3分.满分18分）13．（3分）（2014•天津）计算x5÷x2的结果等于x3．考点：同底数幂的除法．分析：同底数幂相除底数不变.指数相减.解答：解：x5÷x2=x3故答案为：x3．点评：此题考查了同底数幂的除法.解题要注意细心明确指数相减．14．（3分）（2014•天津）已知反比例函数y=（k为常数.k≠0）的图象位于第一、第三象限.写出一个符合条件的k的值为 1 ．考点：反比例函数的性质．专题：开放型．分析：反比例函数y=（k为常数.k≠0）的图象在第一.三象限.则k＞0.符合上述条件的k的一个值可以是1．（正数即可.答案不唯一）解答：解：∵反比例函数的图象在一、三象限.∴k＞0.只要是大于0的所有实数都可以．例如：1．故答案为：1．点评：此题主要考查反比例函数图象的性质：（1）k＞0时.图象是位于一、三象限；（2）k＜0时.图象是位于二、四象限．15．（3分）（2014•天津）如图.是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上.从中任意抽取一张.则抽出的牌点数小于9的概率为．考点：概率公式．分析：抽出的牌的点数小于9有1.2.3.4.5.6.7.8共8个.总的样本数目为13.由此可以容易知道事件抽出的牌的点数小于9的概率．解答：解：∵抽出的牌的点数小于9有1.2.3.4.5.6.7.8共8个.总的样本数目为13.∴从中任意抽取一张.抽出的牌点数小于9的概率是：．故答案为：．点评：此题主要考查了概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．16．（3分）（2014•天津）抛物线y=x2﹣2x+3的顶点坐标是（1.2）．考点：二次函数的性质．专题：计算题．分析：已知抛物线的解析式是一般式.用配方法转化为顶点式.根据顶点式的坐标特点.直接写出顶点坐标．解答：解：∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=（x﹣1）2+2.∴抛物线y=x2﹣2x+3的顶点坐标是（1.2）．点评：此题考查了二次函数的性质.二次函数y=a（x﹣h）2+k的顶点坐标为（h.k）.对称轴为x=h.此题还考查了配方法求顶点式．17．（3分）（2014•天津）如图.在Rt△ABC中.D.E为斜边AB上的两个点.且BD=BC.AE=AC.则∠DCE的大小为45 （度）．考点：等腰三角形的性质．分析：设∠DCE=x.∠ACD=y.则∠ACE=x+y.∠BCE=90°﹣∠ACE=90°﹣x﹣y.根据等边对等角得出∠ACE=∠AEC=x+y.∠BDC=∠BCD=∠BCE+∠DCE=90°﹣y．然后在△DCE中.利用三角形内角和定理列出方程x+（90°﹣y）+（x+y）=180°.解方程即可求出∠DCE的大小．解答：解：设∠DCE=x.∠ACD=y.则∠ACE=x+y.∠BCE=90°﹣∠ACE=90°﹣x﹣y．∵AE=AC.∴∠ACE=∠AEC=x+y.∵BD=BC.∴∠BDC=∠BCD=∠BCE+∠DCE=90°﹣x﹣y+x=90°﹣y．在△DCE中.∵∠DCE+∠CDE+∠DEC=180°.∴x+（90°﹣y）+（x+y）=180°.解得x=45°.∴∠DCE=45°．故答案为45．点评：本题考查了等腰三角形的性质及三角形内角和定理.设出适当的未知数列出方程是解题的关键．18．（3分）（2014•天津）如图.将△ABC放在每个小正方形的边长为1的网格中.点A.点B.点C均落在格点上．（Ⅰ）计算AC2+BC2的值等于11 ；（Ⅱ）请在如图所示的网格中.用无刻度的直尺.画出一个以AB为一边的矩形.使该矩形的面积等于AC2+BC2.并简要说明画图方法（不要求证明）如图所示：．考点：作图—应用与设计作图．分析：（1）直接利用勾股定理求出即可；（2）首先分别以AC、BC、AB为一边作正方形ACED.正方形BCNM.正方形ABHF；进而得出答案．解答：解：（Ⅰ）AC2+BC2=（）2+32=11；故答案为：11；（2）分别以AC、BC、AB为一边作正方形ACED.正方形BCNM.正方形ABHF；延长DE交MN于点Q.连接QC.平移QC至AG.BP位置.直线GP分别交AF.BH于点T.S.则四边形ABST即为所求．点评：此题主要考查了应用设计与作图.借助网格得出正方形是解题关键．三、解答题（本大题共7小题.共66分）19．（8分）（2014•天津）解不等式组请结合题意填空.完成本题的解答：（Ⅰ）解不等式①.得x≥﹣1 ；（Ⅱ）解不等式②.得x≤1；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为﹣1≤x≤1．考点：解一元一次不等式组；在数轴上表示不等式的解集．分析：分别求出各不等式的解集.再求出其公共解集.并在数轴上表示出来即可．解答：解：（I）解不等式①.得x≥﹣1；（II）解不等式②得.x≤1.（III）在数轴上表示为：；（IN）故此不等式的解集为：﹣1≤x≤1．故答案分别为：x≥﹣1.x≤1.﹣1≤x≤1．点评：本题考查的是解一元一次不等式组.熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20．（8分）（2014•天津）为了推动阳光体育运动的广泛开展.引导学生走向操场.走进大自然.走到阳光下.积极参加体育锻炼.学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号.绘制了如下的统计图①和图②.请根据相关信息.解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为40 .图①中m的值为15 ；（Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据.若学校计划购买200双运动鞋.建议购买35号运动鞋多少双？考点：条形统计图；用样本估计总体；扇形统计图；中位数；众数．专题：计算题．分析：（Ⅰ）根据条形统计图求出总人数即可；由扇形统计图以及单位1.求出m的值即可；（Ⅱ）找出出现次数最多的即为众数.将数据按照从小到大顺序排列.求出中位数即可；（Ⅲ）根据题意列出算式.计算即可得到结果．（Ⅰ）本次接受随机抽样调查的学生人数为6+12+10+8+4=40.图①中m的值为100﹣30﹣25﹣20﹣10=15；解答：解：故答案为：40；15；（Ⅱ）∵在这组样本数据中.35出现了12次.出现次数最多.∴这组样本数据的众数为5；∵将这组样本数据从小到大得顺序排列.其中处于中间的两个数都为36.∴中位数为=36；（Ⅲ）∵在40名学生中.鞋号为35的学生人数比例为30%.∴由样本数据.估计学校各年级中学生鞋号为35的人数比例约为30%.则计划购买200双运动鞋.有200×30%=60双为35号．点评：此题考查了条形统计图.扇形统计图.以及用样本估计总体.弄清题意是解本题的关键．21．（10分）（2014•天津）已知⊙O的直径为10.点A.点B.点C在⊙O上.∠CAB的平分线交⊙O于点D．（Ⅰ）如图①.若BC为⊙O的直径.AB=6.求AC.BD.CD的长；（Ⅱ）如图②.若∠CAB=60°.求BD的长．考点：圆周角定理；等边三角形的判定与性质；勾股定理．分析：（Ⅰ）利用圆周角定理可以判定△CAB和△DCB是直角三角形.利用勾股定理可以求得AC的长度；利用圆心角、弧、弦的关系推知△DCB也是等腰三角形.所以利用勾股定理同样得到BD=CD=5；（Ⅱ）如图②.连接OB.OD．由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形.则BD=OB=OD=5．解答：解：（Ⅰ）如图①.∵BC是⊙O的直径.∴∠CAB=∠BDC=90°．∵在直角△CAB中.BC=10.AB=6.∴由勾股定理得到：AC===8．∵AD平分∠CAB.∴=.∴CD=BD．在直角△BDC中.BC=10.CD2+BD2=BC2.∴易求BD=CD=5；（Ⅱ）如图②.连接OB.OD∵AD平分∠CAB.且∠CAB=60°.∴∠DAB=∠CAB=30°.∴∠DOB=2∠DAB=60°．又∵OB=OD.∴△OBD是等边三角形.∴BD=OB=OD．∵⊙O的直径为10.则OB=5.∴BD=5．点评：本题综合考查了圆周角定理.勾股定理以及等边三角形的判定与性质．此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形．22．（10分）（2014•天津）解放桥是天津市的标志性建筑之一.是一座全钢结构的部分可开启的桥梁．（Ⅰ）如图①.已知解放桥可开启部分的桥面的跨度AB等于47m.从AB的中点C处开启.则AC开启至A′C′的位置时.A′C′的长为23.5 m；（Ⅱ）如图②.某校数学兴趣小组要测量解放桥的全长PQ.在观景平台M处测得∠PMQ=54°.沿河岸MQ前行.在观景平台N处测得∠PNQ=73°.已知PQ⊥MQ.MN=40m.求解放桥的全长PQ（tan54°≈1.4.tan73°≈3.3.结果保留整数）．考点：解直角三角形的应用．专题：应用题．分析：（1）根据中点的性质即可得出A′C′的长；（2）设PQ=x.在Rt△PMQ中表示出MQ.在Rt△PNQ中表示出NQ.再由MN=40m.可得关于x的方程.解出即可．解答：解：（I）∵点C是AB的中点.∴A'C'=AB=23.5m．（II）设PQ=x.在Rt△PMQ中.tan∠PMQ==1.4.∴MQ=.在Rt△PNQ中.tan∠PNQ==3.3.∴NQ=.∵MN=MQ﹣NQ=40.即﹣=40.解得：x≈97．答：解放桥的全长约为97m．点评：本题考查了解直角三角形的应用.解答本题的关键是熟练锐角三角函数的定义.难度一般．23．（10分）（2014•天津）“黄金1号”玉米种子的价格为5元/kg.如果一次购买2kg以上的种子.超过2kg部分的种子的价格打8折．（Ⅰ）根据题意.填写下表：购买种子的数量/kg 1.5 2 3.5 4 …付款金额/元7.5 10 16 18 …（Ⅱ）设购买种子数量为xkg.付款金额为y元.求y关于x的函数解析式；（Ⅲ）若小张一次购买该种子花费了30元.求他购买种子的数量．考点：一次函数的应用；一元一次方程的应用．分析：（1）根据单价乘以数量.可得答案；（2）根据单价乘以数量.可得价格.可得相应的函数解析式；（3）根据函数值.可得相应的自变量的值．解答：解：（Ⅰ）10.8；（Ⅱ）根据题意得.当0≤x≤2时.种子的价格为5元/千克.∴y=5x.当x＞2时.其中有2千克的种子按5元/千克计价.超过部分按4元/千克计价.∴y=5×2+4（x﹣2）=4x+2.y关于x的函数解析式为y=；（Ⅲ）∵30＞2.∴一次性购买种子超过2千克.∴4x+2=30．解得x=7.答：他购买种子的数量是7千克．点评：本题考查了一次函数的应用.分类讨论是解题关键．24．（10分）（2014•天津）在平面直角坐标系中.O为原点.点A（﹣2.0）.点B（0.2）.点E.点F分别为OA.OB 的中点．若正方形OEDF绕点O顺时针旋转.得正方形OE′D′F′.记旋转角为α．（Ⅰ）如图①.当α=90°时.求AE′.BF′的长；（Ⅱ）如图②.当α=135°时.求证AE′=BF′.且AE′⊥BF′；（Ⅲ）若直线AE′与直线BF′相交于点P.求点P的纵坐标的最大值（直接写出结果即可）．考点：几何变换综合题；三角形的外角性质；全等三角形的判定与性质；含30度角的直角三角形；勾股定理．专题：综合题．分析：（1）利用勾股定理即可求出AE′.BF′的长．（2）运用全等三角形的判定与性质、三角形的外角性质就可解决问题．（3）首先找到使点P的纵坐标最大时点P的位置（点P与点D′重合时）.然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值．解答：解：（Ⅰ）当α=90°时.点E′与点F重合.如图①．∵点A（﹣2.0）点B（0.2）.∴OA=OB=2．∵点E.点F分别为OA.OB的中点.∴OE=OF=1∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的.∴OE′=OE=1.OF′=OF=1．在Rt△AE′O中.AE′=．在Rt△BOF′中.BF′=．∴AE′.BF′的长都等于．（Ⅱ）当α=135°时.如图②．∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得.∴∠AOE′=∠BOF′=135°．在△AOE′和△BOF′中..∴△AOE′≌△BOF′（SAS）．∴AE′=BF′.且∠OAE′=∠OBF′．∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB.∠CAO=∠CBP.∴∠CPB=∠AOC=90°∴AE′⊥BF′．（Ⅲ）在第一象限内.当点D′与点P重合时.点P的纵坐标最大．过点P作PH⊥x轴.垂足为H.如图③所示．∵∠AE′O=90°.E′O=1.AO=2.∴∠E′AO=30°.AE′=．∴AP=+1．∵∠AHP=90°.∠PAH=30°.∴PH=AP=．∴点P的纵坐标的最大值为．点评：本题是在图形旋转过程中.考查了全等三角形的判定与性质、勾股定理、三角形的外角性质、30°角所对的直角边等于斜边的一半等知识.而找到使点P的纵坐标最大时点P的位置是解决最后一个问题的关键．25．（10分）（2014•天津）在平面直角坐标系中.O为原点.直线l：x=1.点A（2.0）.点E.点F.点M都在直线l上.且点E和点F关于点M对称.直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1.﹣1）.①当点F的坐标为（1.1）时.如图.求点P的坐标；②当点F为直线l上的动点时.记点P（x.y）.求y关于x的函数解析式．（Ⅱ）若点M（1.m）.点F（1.t）.其中t≠0.过点P作PQ⊥l于点Q.当OQ=PQ时.试用含t的式子表示m．考点：一次函数综合题．分析：（Ⅰ）①利用待定系数法求得直线OF与EA的直线方程.然后联立方程组.求得该方程组的解即为点P的坐标；②由已知可设点F的坐标是（1.t）．求得直线OF、EA的解析式分别是y=tx、直线EA的解析式为：y=（2+t）x﹣2（2+t）．则tx=（2+t）x﹣2（2+t）.整理后即可得到y关于x的函数关系式y=x2﹣2x；（Ⅱ）同（Ⅰ）.易求P（2﹣.2t﹣）．则由PQ⊥l于点Q.得点Q（1.2t﹣）.则OQ2=1+t2（2﹣）2.PQ2=（1﹣）2.所以1+t2（2﹣）2=（1﹣）2.化简得到：t（t﹣2m）（t2﹣2mt﹣1）=0.通过解该方程可以求得m与t的关系式．解答：解：（Ⅰ）①∵点O（0.0）.F（1.1）.∴直线OF的解析式为y=x．设直线EA的解析式为：y=kx+b（k≠0）、∵点E和点F关于点M（1.﹣1）对称.∴E（1.﹣3）．又A（2.0）.点E在直线EA上.∴.解得.∴直线EA的解析式为：y=3x﹣6．∵点P是直线OF与直线EA的交点.则.解得.∴点P的坐标是（3.3）．②由已知可设点F的坐标是（1.t）．∴直线OF的解析式为y=tx．设直线EA的解析式为y=cx+dy（c、d是常数.且c≠0）．由点E和点F关于点M（1.﹣1）对称.得点E（1.﹣2﹣t）．又点A、E在直线EA上.∴.解得.∴直线EA的解析式为：y=（2+t）x﹣2（2+t）．∵点P为直线OF与直线EA的交点.∴tx=（2+t）x﹣2（2+t）.即t=x﹣2．则有y=tx=（x﹣2）x=x2﹣2x；（Ⅱ）由（Ⅰ）可得.直线OF的解析式为y=tx．直线EA的解析式为y=（t﹣2m）x﹣2（t﹣2m）．∵点P为直线OF与直线EA的交点.∴tx=（t﹣2m）x﹣2（t﹣2m）.化简.得x=2﹣．有y=tx=2t﹣．∴点P的坐标为（2﹣.2t﹣）．∵PQ⊥l于点Q.得点Q（1.2t﹣）.∴OQ2=1+t2（2﹣）2.PQ2=（1﹣）2.∵OQ=PQ.∴1+t2（2﹣）2=（1﹣）2.化简.得t（t﹣2m）（t2﹣2mt﹣1）=0．又t≠0.∴t﹣2m=0或t2﹣2mt﹣1=0.解得m=或m=．则m=或m=即为所求．点评：本题考查了一次函数的综合题型．涉及到了待定系数法求一次函数解析式.一次函数与直线的交点问题．此题难度不大.掌握好两直线间的交点的求法和待定系数法求一次函数解析式就能解答本题．。

-12014年天津市中考数学试卷、选择题（本大题共 12小题，每小题3分，共36 分）1.（ 3分）（2014年天津市）计算（-6） X （ - 1）的结果等于（） A.6 B .- 6 C .1 D .考点： 有理数的乘法.分析： 根据有理数的乘法运算法则进行计算即可得解. 解答： 解：（-6） X （- 1）, =6X1, =6. 故选A .点评： 本题考查了有理数的乘法运算，是基础题，熟记运算法则是解题的关键.2. （ 3分）（2014年天津市）cos60°的值等于（ ）A .-B.2-C -P -£3考点： 特殊角的三角函数值.分析： 根据特殊角的三角函数值解题即可.解答：解：cos60°=—2故选A .点评：本题考查特殊角的三角函数值，准确掌握特殊角的函数值是解题关键.考点： 轴对称图形.分析： 根据轴对称图形与中心对称图形的概念求解.解答： 解：A 、不是轴对称图形，是中心对称图形，不符合题意； B 、 不是轴对称图形，是中心对称图形，不符合题意； C 、 不是轴对称图形，是中心对称图形，不符合题意； D 、 是轴对称图形，符合题意. 故选：D .点评： 此题主要考查了中心对称图形和轴对称图形的定义， 掌握中心对称图形与轴对称图形的概念，解答时要注意：3. （ 3分）（2014年天津市）下列标志中，可以看作是轴对称图形的是（B .)D .A .判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合；判断中心对称 是要寻找对称中心，图形旋转180度后与原图重合.4. （ 3分）（2014年天津市）为了市民出行更加方便，天津市政府大力发展公共交通， 2013年 天津市公共交通客运量约为 1608000000人次，将1608000000用科学记数法表示为（）789A . 160.8X10B . 16.08XI0C . 1.608>10D .100.160 8 X 0考点： 科学记数法一表示较大的数.分析： 科学记数法的表示形式为 a X 0n 的形式，其中1弓a|v 10, n 为整数.确定n 的值时， 要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同•当原数 绝对值〉1时，n 是正数；当原数的绝对值v 1时，n 是负数.解答： 解：将1608000000用科学记数法表示为：1.608X 09.故选：C .点评： 此题考查科学记数法的表示方法.科学记数法的表示形式为 a X 0n 的形式，其中1哼a| v 10, n 为整数，表示时关键要正确确定a 的值以及n 的值.5. （ 3分）（2014年天津市）如图，从左面观察这个立体图形，能得到的平面图形是（）.分析： 根据从左面看得到的图形是左视图，可得答案. 解答： 解；从左面看下面一个正方形，上面一个 正方形，故选：A .点评： 本题考查了简单组合体的三视图，从左面看得到的图形是左视图.6. （ 3分）（2014年天津市）正六边形的边心距为 ；，则该正六边形的边长是（_） A . 二 B . 2 C . 3 D . 2 二考点： 正多边形和圆.分析： 运用正六边形的性质，正六边形边长等于外接圆的半径，再利用勾股定理解决.解答： 解：•••正六边形的边心距为 匚， •••OB= ；, AB=—OA ,22 2 2•••OA =AB +OB ,图形C .D .A .•••0A 2= ( OA ) 2+ ( 7) 2,2解得OA=2 . 故选 B .x_k_b_i点评： 本题主要考查了正六边形和圆，注意：外接圆的半径等于正六边形的边长.7. （ 3分）（2014年天津市）如图，AB 是O O 的弦，AC 是O O 的切线，A 为切点，BC 经过••• AC 是O O 的切线, •••/ OAC=90 ° •/ OA=OB , •••/ B= / OAB=25 ° •••/ AOC=50 ° •••/ C=40°点评： 本题考查了圆的切线性质， 以及等腰三角形的性质， 已知切线时常用的辅助线是连 接圆心与切点.& （ 3分）（2014年天津市）如图，在？ABCD 中，点E 是边AD 的中点, 点F ,则EF : FC 等于(& ¥ ____ DC . 1: 1D . 1 : 225° C . 40° D . 50考点：切线的性质.分析： 连接OA ，根据切线的性质，即可求得/ 解答： 解：如图，连接 OA ,C 的度数.EC 交对角线BD 于3： 2 C考点：平行四边形的性质；相似三角形的判定与性质.分析：根据题意得出△ DEFBCF ,进而得出1= '「，利用点E是边AD的中点得出答BC FC案即可.解答：解：?ABCD，故AD // BC,•••△DEFBCF ,•丁一“… =——,BC FC•••点E是边AD的中点，• AE=DE= _AD ,2•匚一- -- = ・FC 2故选：D.点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识，得出△ DEF BCF是解题关键.9. （3分）（2014年天津市）已知反比例函数y=「，当1 v x V 2时，y的取值范围是（）xA . 0v y v 5B . 1 v y v 2C . 5v y v 10D . y>10考点：反比例函数的性质.分析：将x=1和x=2分别代入反比例函数即可确定函数值的取值范围.解答：解：T反比例函数y=二-中当x=1时y=10，当x=2时，y=5,•••当1 v x v 2时，y的取值范围是5v y v 10, 故选C .点评：本题考查了反比例函数的性质：（1）反比例函数y=^ （k旳）的图象是双曲线；（2）x当k> 0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；（3）当k v 0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大.10 . （3分）（2014年天津市）要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛.设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A . x （x+1 ）=28B . x （x - 1）=28C . x （x+1 ）=28D .2 2x （x - 1）=28考点：由实际问题抽象出一元二次方程.分析：关系式为：球队总数x每支球队需赛的场数吃=4 >7，把相关数值代入即可.解答：解：每支球队都需要与其他球队赛（x - 1）场，但2队之间只有1场比赛，所以可列方程为： x （x - 1） =4 >7.2故选B .点评： 本题考查了由实际问题抽象出一元二次方程，解决本题的关键是得到比赛总场数的等量关系，注意2队之间的比赛只有1场，最后的总场数应除以 2.11.（3分）（2014年天津市）某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进 行了面试和笔试，他们的成绩如表： 候选人甲 乙 丙 丁测试成绩（百分制）面试86929083笔试 90 83 8392 如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们 6和4的权.根据四人各自的平均成绩，公司将录取（）A .甲B .乙C .丙D .丁考点： 加权平均数.分析： 根据题意先算出甲、乙、丙、丁四位候选人的加权平均数，再进行比较，即可得出 答案.解答： 解：甲的平均成绩为： （86 0+90 >4）勻0=87.6 （分）， 乙的平均成绩为：（92>6+83 >4） ^10=88.4 （分）， 丙的平均成绩为：（900+83 >4） ^10=87.2 （分）， 丁的平均成绩为：（83 >6+92 >4） ^10=86.6 （分）， 因为乙的平均分数最高， 所以乙将被录取. 故选B .点评： 此题考查了加权平均数的计算公式，注意，计算平均数时按6和4的权进行计算.212 . （3分）（2014年天津市）已知二次函数y=ax +bx+c （a 用）的图象如图，且关于 x 的一元2二次方程ax +bx+c - m=0没有实数根，有下列结论：O① b - 4ac >0;② abc v 0;③ m >2 .其中，正确结论的个数是（）考点: 二次函数图象与系数的关系.分析: 由图象可知二次函数 y=ax +bx+c 与x 轴有两个交点，进而判断 ①; 先根据抛物线的开口向下可知 a v 0，由抛物线与y 轴的交点判断c 与0的关系，根据对称 轴在y 轴右侧得出b 与0的关系，然后根据有理数乘法法则判断 ②；一 2 21 C . 2D . 3B .一元二次方程ax+bx+c - m=0没有实数根，则可转化为ax+bx+c=m，即可以理解为2y=ax +bx+c和y=m没有交点，即可求出m的取值范围，判断③即可. 解答：解：①•••二次函数y=ax2+bx+c与x轴有两个交点，2••• b - 4ac> 0,故① 正确；②•••抛物线的开口向下，• a v 0,•••抛物线与y轴交于正半轴，• c> 0,•••对称轴x= - —> 0,2a• ab v 0,•/ a v 0,• b > 0,• abc v0，故②正确；2③•••一元二次方程ax +bx+c - m=0没有实数根，2• y=ax +bx+c和y=m没有交点，由图可得，m>2，故③正确.故选D .点评：本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用.二、填空题（本大题共6小题，每小题3分，满分18分）5 2 313. （3分）（2014年天津市）计算x次的结果等于x .考点：同底数幕的除法.分析：同底数幕相除底数不变，指数相减，解答：解：X5畝2=x3 故答案为：x3.点评：此题考查了同底数幕的除法，解题要注意细心明确指数相减.14. （3分）（2014年天津市）已知反比例函数沪（k为常数，k用）的图象位于第一、第三象限，写出一个符合条件的k的值为 1 .考点：反比例函数的性质.专题：开放型.分析：反比例函数y=‘ （k为常数，k老）的图象在第一，三象限，则k > 0，符合上述条x件的k的一个值可以是1.（正数即可，答案不唯一）解答：解：•••反比例函数的图象在一、三象限，• k > 0,只要是大于0的所有实数都可以.例如：1.故答案为：1.故答案为：一.点评： 此题主要考查了概率的求法.2 一16. （3分）（2014年天津市）抛物线y=x - 2x+3的顶点坐标是 （1, 2）考点： 二次函数的性质. 专题： 计算题.分析： 已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点， 直接写出顶点坐标.2 2 2解答： 解：••• y=x 2 - 2x+3=x 2 - 2x+1 - 1+3= （x - 1） 2+2,2•抛物线y=x - 2x+3的顶点坐标是（1, 2）. .§k §b,点评： 此题考查了二次函数的性质，二次函数y=a （x - h ） 2+k 的顶点坐标为（h , k ）,对称轴为x=h ，此题还考查了配方法求顶点式.17. （3分）（2014年天津市）如图，在Rt △ ABC 中，D , E 为斜边AB 上的两个点，且BD=BC , AE=AC ，则/ DCE 的大小为 45（度）.考点： 等腰三角形的性质.点评： 此题主要考查反比例函数图象的性质： （1） k >0时，图象是位于一、三象限；（2）k v 0时，图象是位于二、四象限.15. （ 3分）（2014年天津市）如图，是一副普通扑克牌中的 向下放在桌子上，从中任意抽取一张，则抽出的牌点数小于13张黑桃牌，将它们洗匀后正面 9的概率为 —一13—考点： 概率公式.分析： 抽出的牌的点数小于 9有1, 2, 3, 4, 5, 6, 由此可以容易知道事件抽出的牌的点数小于 9的概率.解答： 解：•••抽出的牌的点数小于 9有1 , 2, 3, 4,为13,8共8个，总的样本数目为 13, 6, 7, 8共8个，总的样本数目•••从中任意抽取一张，抽出的牌点数小于 9的概率是:用到的知识点为: 概率=所求情况数与总情况数之比.分析：设/ DCE=x，/ ACD=y，则/ ACE=x+y，/ BCE=90ACE=90 °- x - y,根据等边对等角得出/ ACE= / AEC=x+y，/ BDC= / BCD= / BCE+ / DCE=90 °- y.然后在△ DCE中，利用三角形内角和定理列出方程x+ (90°-y) + (x+y) =180°解方程即可求出/ DCE的大小.解答：解：设/ DCE=x，/ ACD =y，则/ ACE=x+y，/ BCE=90。

2014年天津市初中毕业生学业考试试卷数学本试卷分为第I 卷（选择题）、第n 卷（非选择题）两部分。

第I 卷为第 1页至第3页，第n 卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“ 答题卡”上，并在规定 位置粘贴考试用条形码。

答题时，务必将答案涂写在“ 答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利！注意事项：1. 每题选出答案后，用 2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡 皮擦干净后，再选涂其他答案标号的信息点。

2. 本卷共12题，共36分。

目要求的）000000人次.将1608 000 000用科学记数法表示应为 、选择题（本大题共 12小题，每小题3分， 共36分•在每小题给出的四个选项中，只有一项是符合题(1) 计算（-6 ）x （-1）的结果等于(A) 6(B) -6(C ) 1(D) -1(2) cos60°的值等于 V3(B )E(D) •、3(3) F 列标志中，可以看作是轴对称图形的是(4) （A ）（ B ） 为让市民出行更加方便，天津市政府大力发展公共交通（D ）.2013年天津市公共交通客运量约为1608(5) (A ) 160.8X 1078(B ) 16.08X 10(C ) 91.608 x 10,、 10(D ) 0.1608X 10如图，从左面观察这个立体图形，能得到的平面图形是(C )(11) 某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：候选人甲乙 丙 丁 测试成绩 面试 86 92 90 83 (百分制)笔试90838392如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们 6和4的权.公司将录取(6) (7) °25 , (8) 等于(9) (D)正六边形的边心距为 .,3，则该正六边形的边长是如图，AB 是O O 的弦, 则/ C 的大小等于(A) (C ) 如图, 20° 40° □ ABCD (A ) 3: 2 (C ) 1 : 1已知反比例函数(A) 0<y<5(C ) 5<y<10(B) 2(C ) 3(D) 2 3AC 是O O 的切线，A 为切点，BC 经过圆心.若/ B =(B ) 25° (D ) 50°中 占 I •)E 是边AD 的中点，EC 交对角线 BD 于点F ,则(B ) 3: 1 (D ) 1 : 2y 二10，当1<x<2时，y 的取值范围是 x(B) 1<y<2 (D) y>10(10)要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为1 (A) x x 1 =282 1(B) x x - 1 =282 (C ) x x 1 =28(D ) xx-1 ]=28(B)第(5 )题（A ）甲 （B ）乙 （C ）丙 （12）已知二次函数 y=ax 2+bx+c （0）的图象如下图所示，且关于 有实数根，有下列结论：① b 2-4ac>0 :②abc<0 :③m>2. 其中，正确结论的个数是 （A ） 0（ B ） 1（ C ） 22014年天津市初中毕业生学业考试试卷数学第口卷注意事项：1. 用黑色墨水的钢笔或签字笔将答案写在“ 答题卡”上。

2014年天津市初中毕业生学业考试试卷数 学本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2.本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算（-6）×（-1）的结果等于（A ）6 （B ）-6（C ）1（D ）-1（2）cos60o 的值等于（A ）21 （B ）33 （C ）23 （D ）3（3）下列标志中，可以看作是轴对称图形的是（A ） （B ） （C ） （D ）（4）为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608 000 000用科学记数法表示应为 （A ）160.8×107（B ）16.08×108（C ）1.608×109（D ）0.1608×1010（5）如图，从左面观察这个立体图形，能得到的平面图形是（A ） （B ）（C ） （D ）（6）正六边形的边心距为3，则该正六边形的边长是（A ）3（B ）2（C ）3（D ）32（7）如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.若∠B ＝25o ，则∠C 的大小等于（A ）20o （B ）25o（C ）40o（D ）50o（8）如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于（A ）3：2 （B ）3：1 （C ）1：1（D ）1：2（9）已知反比例函数xy 10=，当1<x <2时，y 的取值范围是 （A ）0<y <5 （B ）1<y <2 （C ）5<y <10（D ）y>10（10）要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为 （A ）()28121=+x x （B ）()28121=-x x （C ）()281=+x x（D ）()281=-x x（11）某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：候选人 甲 乙 丙 丁 测试成绩（百分制） 面试86 92 90 83 笔试90838392如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取第（5）题第（7）题第（8）题（A ）甲 （B ）乙 （C ）丙 （D ）丁（12）已知二次函数y =ax 2+b x+c （a ≠0）的图象如下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有下列结论：①b 2-4ac >0；②abc <0；③m >2. 其中，正确结论的个数是 （A ）0 （B ）1（C ）2（D ）32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。

2014年天津市中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）计算（﹣6）×（﹣1）的结果等于（）A．6 B．﹣6 C．1 D．﹣12．（3分）cos60°的值等于（）A．B．C．D．3．（3分）下列标志中，可以看作是轴对称图形的是（）A．B． C．D．4．（3分）为了市民出行更加方便，天津市政府大力发展公共交通，2013年天津市公共交通客运量约为1608000000人次，将1608000000用科学记数法表示为（）A．160.8×107B．16.08×108C．1.608×109D．0.1608×10105．（3分）如图，从左面观察这个立体图形，能得到的平面图形是（）A． B．C．D．6．（3分）正六边形的边心距为，则该正六边形的边长是（）A．B．2 C．3 D．27．（3分）如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°8．（3分）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：29．（3分）已知反比例函数y=，当1＜x＜2时，y的取值范围是（）A．0＜y＜5 B．1＜y＜2 C．5＜y＜10 D．y＞1010．（3分）要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A ．x（x+1）=28B ．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28 11．（3分）某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：候选人甲乙丙丁86929083测试成绩（百分制）面试90838392笔试如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）A．甲B．乙C．丙D．丁12．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1 C．2 D．3二、填空题（本大题共6小题，每小题3分，满分18分）13．（3分）计算x5÷x2的结果等于．14．（3分）已知反比例函数y=（k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为．15．（3分）如图，是一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点数小于9的概率为．16．（3分）抛物线y=x2﹣2x+3的顶点坐标是．17．（3分）如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为（度）．18．（3分）如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（Ⅰ）计算AC2+BC2的值等于；（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）．三、解答题（本大题共7小题，共66分）19．（8分）解不等式组请结合题意填空，完成本题的解答：（Ⅰ）解不等式①，得；（Ⅱ）解不等式②，得；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为．20．（8分）为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为，图①中m的值为；（Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？21．（10分）已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．22．（10分）解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁．（Ⅰ）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至AC′的位置时，AC′的长为m；（Ⅱ）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°，已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）．23．（10分）“黄金1号”玉米种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子的价格打8折．（Ⅰ）根据题意，填写下表：1.52 3.54…购买种子的数量/kg付款金额/元7.516…（Ⅱ）设购买种子数量为xkg，付款金额为y元，求y关于x的函数解析式；（Ⅲ）若小张一次购买该种子花费了30元，求他购买种子的数量．24．（10分）在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．（Ⅰ）如图①，当α=90°时，求AE′，BF′的长；（Ⅱ）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；（Ⅲ）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．25．（10分）在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1，﹣1），①当点F的坐标为（1，1）时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．（Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．2014年天津市中考数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．（3分）计算（﹣6）×（﹣1）的结果等于（）A．6 B．﹣6 C．1 D．﹣1【分析】根据有理数的乘法运算法则进行计算即可得解．【解答】解：（﹣6）×（﹣1），=6×1，=6．故选：A．【点评】本题考查了有理数的乘法运算，是基础题，熟记运算法则是解题的关键．2．（3分）cos60°的值等于（）A．B．C．D．【分析】根据特殊角的三角函数值解题即可．【解答】解：cos60°=．故选：A．【点评】本题考查特殊角的三角函数值，准确掌握特殊角的函数值是解题关键．3．（3分）下列标志中，可以看作是轴对称图形的是（）A．B． C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、不是轴对称图形，是中心对称图形，不符合题意；B、不是轴对称图形，是中心对称图形，不符合题意；C、不是轴对称图形，是中心对称图形，不符合题意；D、是轴对称图形，符合题意．故选：D．【点评】此题主要考查了中心对称图形和轴对称图形的定义，掌握中心对称图形与轴对称图形的概念，解答时要注意：判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合；判断中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．4．（3分）为了市民出行更加方便，天津市政府大力发展公共交通，2013年天津市公共交通客运量约为1608000000人次，将1608000000用科学记数法表示为（）A．160.8×107B．16.08×108C．1.608×109D．0.1608×1010【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n 是负数．【解答】解：将1608000000用科学记数法表示为：1.608×109．故选：C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5．（3分）如图，从左面观察这个立体图形，能得到的平面图形是（）A． B．C．D．【分析】根据从左面看得到的图形是左视图，可得答案．【解答】解；从左面看下面一个正方形，上面一个正方形，故选：A．【点评】本题考查了简单组合体的三视图，从左面看得到的图形是左视图．6．（3分）正六边形的边心距为，则该正六边形的边长是（）A．B．2 C．3 D．2【分析】运用正六边形的性质，正六边形边长等于外接圆的半径，再利用勾股定理解决．【解答】解：∵正六边形的边心距为，∴OB=，AB=OA，∵OA2=AB2+OB2，∴OA2=（OA）2+（）2，解得OA=2．故选：B．【点评】本题主要考查了正六边形和圆，注意：外接圆的半径等于正六边形的边长．7．（3分）如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°【分析】连接OA，根据切线的性质，即可求得∠C的度数．【解答】解：如图，连接OA，∵AC是⊙O的切线，∴∠OAC=90°，∵OA=OB，∴∠B=∠OAB=25°，∴∠AOC=50°，∴∠C=40°．故选：C．【点评】本题考查了圆的切线性质，以及等腰三角形的性质，已知切线时常用的辅助线是连接圆心与切点．8．（3分）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：2【分析】根据题意得出△DEF∽△BCF，进而得出=，利用点E是边AD的中点得出答案即可．【解答】解：∵▱ABCD，故AD∥BC，∴△DEF∽△BCF，∴=，∵点E是边AD的中点，∴AE=DE=AD，∴=．故选：D．【点评】此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识，得出△DEF∽△BCF是解题关键．9．（3分）已知反比例函数y=，当1＜x＜2时，y的取值范围是（）A．0＜y＜5 B．1＜y＜2 C．5＜y＜10 D．y＞10【分析】将x=1和x=2分别代入反比例函数即可确定函数值的取值范围．【解答】解：∵反比例函数y=中当x=1时y=10，当x=2时，y=5，∴当1＜x＜2时，y的取值范围是5＜y＜10，故选：C．【点评】本题考查了反比例函数的性质：（1）反比例函数y=（k≠0）的图象是双曲线；（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y 随x的增大而减小；（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．10．（3分）要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A．x（x+1）=28 B．x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28【分析】关系式为：球队总数×每支球队需赛的场数÷2=4×7，把相关数值代入即可．【解答】解：每支球队都需要与其他球队赛（x﹣1）场，但2队之间只有1场比赛，所以可列方程为：x（x﹣1）=4×7．故选：B．【点评】本题考查了由实际问题抽象出一元二次方程，解决本题的关键是得到比赛总场数的等量关系，注意2队之间的比赛只有1场，最后的总场数应除以2．11．（3分）某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如表：候选人甲乙丙丁86929083测试成绩（百分制）面试90838392笔试如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）A．甲B．乙C．丙D．丁【分析】根据题意先算出甲、乙、丙、丁四位候选人的加权平均数，再进行比较，即可得出答案．【解答】解：甲的平均成绩为：（86×6+90×4）÷10=87.6（分），乙的平均成绩为：（92×6+83×4）÷10=88.4（分），丙的平均成绩为：（90×6+83×4）÷10=87.2（分），丁的平均成绩为：（83×6+92×4）÷10=86.6（分），因为乙的平均分数最高，所以乙将被录取．故选：B．【点评】此题考查了加权平均数的计算公式，注意，计算平均数时按6和4的权进行计算．12．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1 C．2 D．3【分析】由图象可知二次函数y=ax2+bx+c与x轴有两个交点，进而判断①；先根据抛物线的开口向下可知a＜0，由抛物线与y轴的交点判断c与0的关系，根据对称轴在y轴右侧得出b与0的关系，然后根据有理数乘法法则判断②；一元二次方程ax2+bx+c﹣m=0没有实数根，则可转化为ax2+bx+c=m，即可以理解为y=ax2+bx+c和y=m没有交点，即可求出m的取值范围，判断③即可．【解答】解：①∵二次函数y=ax2+bx+c与x轴有两个交点，∴b2﹣4ac＞0，故①正确；②∵抛物线的开口向下，∴a＜0，∵抛物线与y轴交于正半轴，∴c＞0，∵对称轴x=﹣＞0，∴ab＜0，∵a＜0，∴b＞0，∴abc＜0，故②正确；③∵一元二次方程ax2+bx+c﹣m=0没有实数根，∴y=ax2+bx+c和y=m没有交点，由图可得，m＞2，故③正确．故选：D．【点评】本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．二、填空题（本大题共6小题，每小题3分，满分18分）13．（3分）计算x5÷x2的结果等于x3．【分析】同底数幂相除底数不变，指数相减，【解答】解：x5÷x2=x3故答案为：x3．【点评】此题考查了同底数幂的除法，解题要注意细心明确指数相减．14．（3分）已知反比例函数y=（k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为1．【分析】反比例函数y=（k为常数，k≠0）的图象在第一，三象限，则k＞0，符合上述条件的k的一个值可以是1．（正数即可，答案不唯一）【解答】解：∵反比例函数的图象在一、三象限，∴k＞0，只要是大于0的所有实数都可以．例如：1．故答案为：1．【点评】此题主要考查反比例函数图象的性质：（1）k＞0时，图象是位于一、三象限；（2）k＜0时，图象是位于二、四象限．15．（3分）如图，是一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点数小于9的概率为．【分析】抽出的牌的点数小于9有1，2，3，4，5，6，7，8共8个，总的样本数目为13，由此可以容易知道事件抽出的牌的点数小于9的概率．【解答】解：∵抽出的牌的点数小于9有1，2，3，4，5，6，7，8共8个，总的样本数目为13，∴从中任意抽取一张，抽出的牌点数小于9的概率是：．故答案为：．【点评】此题主要考查了概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．16．（3分）抛物线y=x2﹣2x+3的顶点坐标是（1，2）．【分析】已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．【解答】解：∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=（x﹣1）2+2，∴抛物线y=x2﹣2x+3的顶点坐标是（1，2）．故答案为：（1，2）．【点评】此题考查了二次函数的性质，二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．17．（3分）如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为45（度）．【分析】设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°﹣∠ACE=90°﹣x﹣y，根据等边对等角得出∠ACE=∠AEC=x+y，∠BDC=∠BCD=∠BCE+∠DCE=90°﹣y．然后在△DCE中，利用三角形内角和定理列出方程x+（90°﹣y）+（x+y）=180°，解方程即可求出∠DCE的大小．【解答】解：设∠DCE=x，∠ACD=y，则∠ACE=x+y，∠BCE=90°﹣∠ACE=90°﹣x ﹣y．∵AE=AC，∴∠ACE=∠AEC=x+y，∵BD=BC，∴∠BDC=∠BCD=∠BCE+∠DCE=90°﹣x﹣y+x=90°﹣y．在△DCE中，∵∠DCE+∠CDE+∠DEC=180°，∴x+（90°﹣y）+（x+y）=180°，解得x=45°，∴∠DCE=45°．故答案为：45．【点评】本题考查了等腰三角形的性质及三角形内角和定理，设出适当的未知数列出方程是解题的关键．18．（3分）如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（Ⅰ）计算AC2+BC2的值等于11；（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）如图所示：．【分析】（1）直接利用勾股定理求出即可；（2）首先分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；进而得出答案．【解答】解：（Ⅰ）AC2+BC2=（）2+32=11；故答案为：11；（2）方法一：分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；延长DE交MN于点Q，连接QC，平移QC至AG，BP位置，直线GP分别交AF，BH于点T，S，则四边形ABST即为所求．方法二：如图1，所求矩形的面积等于两个粉色正方形的面积和小正方形面积为2，大正方形面积为9，如图2，第一次变化，图中绿色三角形的面积等于粉色小正方形的面积，如图3，第二次变化，图中蓝色平行四边形的面积等于粉色小正方形的面积，如图4，第三次，将粉色大正方形变形为平行四边形，经过几次变形以后，如图5，两块阴影所示的面积和，还是等于11，，如图6，然后进行一次割补，上面黑色阴影与△ABC全等，把黑色割补到△ABC，则平行四边形ABEF的面积也是11，下面再进行最后一次等积变形，过A，B两点分别做AB的垂，然后延长EF，与这两条垂线分别相交于M，N如图7，矩形ABMN与平行四边形ABEF面积相等，都是11．【点评】此题主要考查了应用设计与作图，借助网格得出正方形是解题关键．三、解答题（本大题共7小题，共66分）19．（8分）解不等式组请结合题意填空，完成本题的解答：（Ⅰ）解不等式①，得x≥﹣1；（Ⅱ）解不等式②，得x≤1；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为﹣1≤x≤1．【分析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．【解答】解：（I）解不等式①，得x≥﹣1；（II）解不等式②得，x≤1，（III）在数轴上表示为：；（IN）故此不等式的解集为：﹣1≤x≤1．故答案分别为：x≥﹣1，x≤1，﹣1≤x≤1．【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20．（8分）为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）本次接受随机抽样调查的学生人数为40，图①中m的值为15；（Ⅱ）求本次调查获取的样本数据的众数和中位数；（Ⅲ）根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？【分析】（Ⅰ）根据条形统计图求出总人数即可；由扇形统计图以及单位1，求出m的值即可；（Ⅱ）找出出现次数最多的即为众数，将数据按照从小到大顺序排列，求出中位数即可；（Ⅲ）根据题意列出算式，计算即可得到结果．【解答】解：（Ⅰ）本次接受随机抽样调查的学生人数为6+12+10+8+4=40，图①中m的值为100﹣30﹣25﹣20﹣10=15；故答案为：40；15；（Ⅱ）∵在这组样本数据中，35出现了12次，出现次数最多，∴这组样本数据的众数为35；∵将这组样本数据从小到大得顺序排列，其中处于中间的两个数都为36，∴中位数为=36；（Ⅲ）∵在40名学生中，鞋号为35的学生人数比例为30%，∴由样本数据，估计学校各年级中学生鞋号为35的人数比例约为30%，则计划购买200双运动鞋，有200×30%=60双为35号．【点评】此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．21．（10分）已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．【分析】（Ⅰ）利用圆周角定理可以判定△CAB和△DCB是直角三角形，利用勾股定理可以求得AC的长度；利用圆心角、弧、弦的关系推知△DCB也是等腰三角形，所以利用勾股定理同样得到BD=CD=5；（Ⅱ）如图②，连接OB，OD．由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形，则BD=OB=OD=5．【解答】解：（Ⅰ）如图①，∵BC是⊙O的直径，∴∠CAB=∠BDC=90°．∵在直角△CAB中，BC=10，AB=6，∴由勾股定理得到：AC===8．∵AD平分∠CAB，∴=，∴CD=BD．在直角△BDC中，BC=10，CD2+BD2=BC2，∴易求BD=CD=5；（Ⅱ）如图②，连接OB，OD．∵AD平分∠CAB，且∠CAB=60°，∴∠DAB=∠CAB=30°，∴∠DOB=2∠DAB=60°．又∵OB=OD，∴△OBD是等边三角形，∴BD=OB=OD．∵⊙O的直径为10，则OB=5，∴BD=5．【点评】本题综合考查了圆周角定理，勾股定理以及等边三角形的判定与性质．此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形．22．（10分）解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁．（Ⅰ）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至AC′的位置时，AC′的长为23.5m；（Ⅱ）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°，已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）．【分析】（1）根据中点的性质即可得出A′C′的长；（2）设PQ=x，在Rt△PMQ中表示出MQ，在Rt△PNQ中表示出NQ，再由MN=40m，可得关于x的方程，解出即可．【解答】解：（I）∵点C是AB的中点，∴A'C'=AB=23.5m．（II）设PQ=x，在Rt△PMQ中，tan∠PMQ==1.4，∴MQ=，在Rt△PNQ中，tan∠PNQ==3.3，∴NQ=，∵MN=MQ﹣NQ=40，即﹣=40，解得：x≈97．答：解放桥的全长约为97m．【点评】本题考查了解直角三角形的应用，解答本题的关键是熟练锐角三角函数的定义，难度一般．23．（10分）“黄金1号”玉米种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子的价格打8折．（Ⅰ）根据题意，填写下表：1.52 3.54…购买种子的数量/kg付款金额/元7.5101618…（Ⅱ）设购买种子数量为xkg，付款金额为y元，求y关于x的函数解析式；（Ⅲ）若小张一次购买该种子花费了30元，求他购买种子的数量．【分析】（1）根据单价乘以数量，可得答案；（2）根据单价乘以数量，可得价格，可得相应的函数解析式；（3）根据函数值，可得相应的自变量的值．【解答】解：（Ⅰ）10，18；（Ⅱ）根据题意得，当0≤x≤2时，种子的价格为5元/千克，∴y=5x，当x＞2时，其中有2千克的种子按5元/千克计价，超过部分按4元/千克计价，∴y=5×2+4（x﹣2）=4x+2，y关于x的函数解析式为y=；（Ⅲ）∵30＞10，∴一次性购买种子超过2千克，∴4x+2=30．解得x=7，答：他购买种子的数量是7千克．【点评】本题考查了一次函数的应用，分类讨论是解题关键．24．（10分）在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．（Ⅰ）如图①，当α=90°时，求AE′，BF′的长；（Ⅱ）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；（Ⅲ）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．【分析】（1）利用勾股定理即可求出AE′，BF′的长．（2）运用全等三角形的判定与性质、三角形的外角性质就可解决问题．（3）首先找到使点P的纵坐标最大时点P的位置（点P与点D′重合时），然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值．【解答】解：（Ⅰ）当α=90°时，点E′与点F重合，如图①．∵点A（﹣2，0）点B（0，2），∴OA=OB=2．∵点E，点F分别为OA，OB的中点，∴OE=OF=1∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的，∴OE′=OE=1，OF′=OF=1．在Rt△AE′O中，AE′=．在Rt△BOF′中，BF′=．∴AE′，BF′的长都等于．（Ⅱ）当α=135°时，如图②．∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得，∴∠AOE′=∠BOF′=135°．在△AOE′和△BOF′中，，∴△AOE′≌△BOF′（SAS）．∴AE′=BF′，且∠OAE′=∠OBF′．∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB，∠CAO=∠CBP，∴∠CPB=∠AOC=90°∴AE′⊥BF′．（Ⅲ）∵∠BPA=∠BOA=90°，∴点P、B、A、O四点共圆，∴当点P在劣弧OB上运动时，点P的纵坐标随着∠PAO的增大而增大．∵OE′=1，∴点E′在以点O为圆心，1为半径的圆O上运动，∴当AP与⊙O相切时，∠E′AO（即∠PAO）最大，此时∠AE′O=90°，点D′与点P重合，点P的纵坐标达到最大．过点P作PH⊥x轴，垂足为H，如图③所示．∵∠AE′O=90°，E′O=1，AO=2，∴∠E′AO=30°，AE′=．∴AP=+1．∵∠AHP=90°，∠PAH=30°，∴PH=AP=．∴点P的纵坐标的最大值为．【点评】本题是在图形旋转过程中，考查了全等三角形的判定与性质、勾股定理、三角形的外角性质、30°角所对的直角边等于斜边的一半等知识，而找到使点P 的纵坐标最大时点P的位置是解决最后一个问题的关键．25．（10分）在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．（Ⅰ）若点M的坐标为（1，﹣1），①当点F的坐标为（1，1）时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．（Ⅱ）若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．【分析】（Ⅰ）①利用待定系数法求得直线OF与EA的直线方程，然后联立方程组，求得该方程组的解即为点P的坐标；②由已知可设点F的坐标是（1，t）．求得直线OF、EA的解析式分别是y=tx、直线EA的解析式为：y=（2+t）x﹣2（2+t）．则tx=（2+t）x﹣2（2+t），整理后即可得到y关于x的函数关系式y=x2﹣2x；（Ⅱ）同（Ⅰ），易求P（2﹣，2t﹣）．则由PQ⊥l于点Q，得点Q（1，2t ﹣），则OQ2=1+t2（2﹣）2，PQ2=（1﹣）2，所以1+t2（2﹣）2=（1﹣）2，化简得到：t（t﹣2m）（t2﹣2mt﹣1）=0，通过解该方程可以求得m与t的关系式．【解答】解：（Ⅰ）①∵点O（0，0），F（1，1），∴直线OF的解析式为y=x．设直线EA的解析式为：y=kx+b（k≠0）、∵点E和点F关于点M（1，﹣1）对称，∴E（1，﹣3）．又∵A（2，0），点E在直线EA上，∴，解得，∴直线EA的解析式为：y=3x﹣6．∵点P是直线OF与直线EA的交点，则，解得，∴点P的坐标是（3，3）．②由已知可设点F的坐标是（1，t）．∴直线OF的解析式为y=tx．设直线EA的解析式为y=cx+d（c、d是常数，且c≠0）．由点E和点F关于点M（1，﹣1）对称，得点E（1，﹣2﹣t）．又点A、E在直线EA上，∴，解得，∴直线EA的解析式为：y=（2+t）x﹣2（2+t）．∵点P为直线OF与直线EA的交点，∴tx=（2+t）x﹣2（2+t），即t=x﹣2．则有y=tx=（x﹣2）x=x2﹣2x；（Ⅱ）由（Ⅰ）可得，直线OF的解析式为y=tx．直线EA的解析式为y=（t﹣2m）x﹣2（t﹣2m）．∵点P为直线OF与直线EA的交点，∴tx=（t﹣2m）x﹣2（t﹣2m），化简，得x=2﹣．有y=tx=2t﹣．∴点P的坐标为（2﹣，2t﹣）．∵PQ⊥l于点Q，得点Q（1，2t﹣），∴OQ2=1+t2（2﹣）2，PQ2=（1﹣）2，∵OQ=PQ，∴1+t2（2﹣）2=（1﹣）2，化简，得t（t﹣2m）（t2﹣2mt﹣1）=0．又∵t≠0，∴t﹣2m=0或t2﹣2mt﹣1=0，解得m=或m=．则m=或m=即为所求．【点评】本题考查了一次函数的综合题型．涉及到了待定系数法求一次函数解析式，一次函数与直线的交点问题．此题难度不大，掌握好两直线间的交点的求法和待定系数法求一次函数解析式就能解答本题．第31页（共31页）。

2014年天津市初中毕业生学业考试试卷数 学本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝各你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2.本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算（-6）×（-1）的结果等于（A ）6 （B ）-6（C ）1（D ）-1（2）cos60o 的值等于（A ）21 （B ）33 （C ）23 （D ）3（3）下列标志中，可以看作是轴对称图形的是（A ） （B ） （C ） （D ）（4）为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608000000人次.将1608 000 000用科学记数法表示应为 （A ）160.8×107（B ）16.08×108（C ）1.608×109（D ）0.1608×1010（5）如图，从左面观察这个立体图形，能得到的平面图形是（A ） （B ）（C ） （D ）（6）正六边形的边心距为3，则该正六边形的边长是（A ）3（B ）2（C ）3（D ）32（7）如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.若∠B ＝25o ，则∠C 的大小等于（A ）20o （B ）25o（C ）40o（D ）50o（8）如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于（A ）3：2 （B ）3：1 （C ）1：1（D ）1：2（9）已知反比例函数xy 10=，当1<x <2时，y 的取值范围是 （A ）0<y <5 （B ）1<y <2 （C ）5<y <10（D ）y>10（10）要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为 （A ）()28121=+x x （B ）()28121=-x x （C ）()281=+x x（D ）()281=-x x（11）某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：候选人 甲 乙 丙 丁测试成绩（百分制） 面试86 92 90 83 笔试90838392如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取第（5）题第（7）题第（8）题（A ）甲 （B ）乙 （C ）丙 （D ）丁（12）已知二次函数y =ax 2+b x+c （a ≠0）的图象如下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有下列结论：①b 2-4ac >0；②abc <0；③m >2. 其中，正确结论的个数是 （A ）0 （B ）1（C ）2（D ）32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。

天津市2014年中考数学试卷本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分。

第Ⅰ卷为第1页至第3页，第Ⅱ卷为第4页至第8页。

试卷满分120分。

考试时间100分钟。

答卷前，考生务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝你考试顺利!第Ⅰ卷注意事项：1.每题选出答案后，用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2.本卷共12题，共36分。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）（1）计算（-6）×（-1）的结果等于（A）6 （B）-6 （C）1 （D）-1（2）cos60o的值等于（A（B C（D（3）下列标志中，可以看作是轴对称图形的是（A）（B）（C）（D）（4）为让市民出行更加方便，天津市政府大力发展公共交通.2013年天津市公共交通客运量约为1608 000000人次.将1608 000 000用科学记数法表示应为（A ）160.8×107 （B ）16.08×108 （C ）1.608×109（D ）0.1608×1010（5）如图，从左面观察这个立体图形，能得到的平面图形是（A ） （B ）（C ） （D ）（6）正六边形的边心距为3，则该正六边形的边长是（A ）3（B ）2（C ）3（D ）32（7）如图，AB 是⊙O 的弦，AC 是⊙O 的切线，A 为切点，BC 经过圆心.若∠B ＝25o ，则∠C 的大小等于（A ）20o （B ）25o（C ）40o（D ）50o（8）如图，□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF:FC 等于（A ）3：2 （B ）3：1 （C ）1：1（D ）1：2（9）已知反比例函数xy 10=，当1<x <2时，y 的取值范围是 （A ）0<y <5 （B ）1<y <2 （C ）5<y <10（D ）y>10（10）要组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x 个队参赛，则x 满足的关系式为 （A ）()28121=+x x （B ）()28121=-x x （C ）()281=+x x（D ）()281=-x x（11）某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：第（5）题第（7）题第（8）题如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权.公司将录取 （A ）甲（B ）乙（C ）丙（D ）丁（12）已知二次函数y =ax 2+b x+c （a ≠0）的图象如下图所示，且关于x 的一元二次方程ax 2+bx +c -m =9没有实数根，有下列结论：①b 2-4ac >0；②abc <0；③m >2. 其中，正确结论的个数是 （A ）0 （B ）1（C ）2（D ）32014年天津市初中毕业生学业考试试卷数 学第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上。