中考数学压轴题合集【精品永久免费】

中考数学压轴题100题精选【含答案】2中考数学压轴题100题精选【含答案】【001】如图，已知抛物线2(1)y a x =-+a ≠0）经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．3【002】如图16，在Rt △ABC 中，∠C=90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，来的速度沿AC 返回；点Q 从点A 秒1个单位长的速度向点B Q 的运动，DE 保持垂直平分PQ ，交折线QB-BC-CP 于点E ．点P 、同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当t = 2时，AP = ，点Q 到AC 的距离是 ；（2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围） （3）在点E 从B 向C 运动的过程中，四边形QBED 能否成为直角梯形？若能，求t 的值．若不能，请说明理由；（4）当DE 经过点C 时，请直接写出t 的值． P D 图【003】如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标，并求出抛物线的解析式；(2)动点P从点A出发．沿线段AB向终点B 运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E，①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。

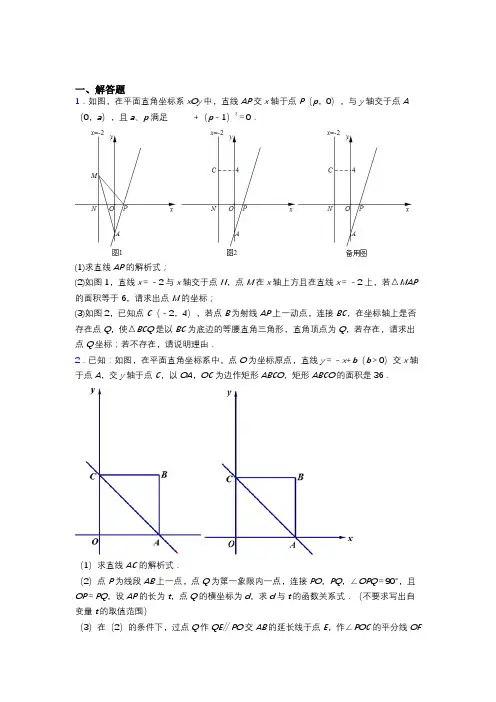
一、解答题1．如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），与y轴交于点A （0，a），且a、p满足+（p﹣1）2＝0．(1)求直线AP的解析式；(2)如图1，直线x＝﹣2与x轴交于点N，点M在x轴上方且在直线x＝﹣2上，若△MAP 的面积等于6，请求出点M的坐标；(3)如图2，已知点C（﹣2，4），若点B为射线AP上一动点，连接BC，在坐标轴上是否存在点Q，使△BCQ是以BC为底边的等腰直角三角形，直角顶点为Q，若存在，请求出点Q坐标；若不存在，请说明理由．2．已知：如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，以OA，OC为边作矩形ABCO，矩形ABCO的面积是36．（1）求直线AC的解析式．（2）点P为线段AB上一点，点Q为第一象限内一点，连接PO，PQ，∠OPQ＝90°，且OP＝PQ，设AP的长为t，点Q的横坐标为d，求d与t的函数关系式．（不要求写出自变量t的取值范围）（3）在（2）的条件下，过点Q作QE∥PO交AB的延长线于点E，作∠POC的平分线OF交PE于点F，交PQ于点K，若KQ＝2EF，求点Q的坐标．3．如图1，ΔABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点．（1）求证：∠BDE=∠ACD；（2）若DE=2DF，过点E作EG//AC交AB于点G，求证：AB=2AG；（3）将“点D在BA的延长线上，点E在BC上”改为“点D在AB上，点E在CB的延长线上”，“点F是DE与AC的交点”改为“点F是ED的延长线与AC的交点”，其它条件不变，如图2．①求证：AB·BE=AD·BC；②若DE=4DF，请直接写出SΔABC:SΔDEC的值．4．在平面直角坐标系xOy中，⊙O的半径为1．对于点A和线段BC，给出如下定义：若将线段BC绕点A旋转可以得到⊙O的弦B′C′（B′，C′分别是B，C的对应点），则称线段BC是⊙O的以点A为中心的“关联线段”．（1）如图，点A，B1，C1，B2，C2，B3，C3的横、纵坐标都是整数．在线段B1C1，B2C2，B3C3中，⊙O的以点A为中心的“关联线段”是；（2）△ABC是边长为1的等边三角形，点A（0，t），其中t≠0．若BC是⊙O的以点A 为中心的“关联线段”，求t的值；（3）在△ABC中，AB＝1，AC＝2．若BC是⊙O的以点A为中心的“关联线段”，直接写出OA的最小值和最大值，以及相应的BC长．5．综合与探究如图，在平面直角坐标系中，点()0,10A ，点B 是x 轴的正半轴上的一个动点，连接AB ，取AB 的中点M ，将线段MB 绕着点B 按顺时针方向旋转90°，得到线段BC ．过点B 作x 轴的垂线交直线AC 于点D ．设点B 坐标是(),0t（1）当6t =时，点M 的坐标是 ；（2）用含t 的代数式表示点C 的坐标；（3）是否存在点B ，使四边形AOBD 为矩形？若存在，请求出点B 的坐标；若不存在，请说明理由；（4）在点B 的运动过程中，平面内是否存在一点N ，使得以A 、B 、N 、D 为顶点的四边形是菱形？若存在，请直接写出点N 的纵坐标（不必要写横坐标）；若不存在，请说明理由．6．抛物线1C ：211211y x t x t ---≠＝（）（）（）与x 轴交于A 、B 两点（点A 在点B 的左侧）（1）若2t -＝，求线段AB 的长；（2）猜想：随着t 的变化，A 、B 两点是否会有一定点？若会，请求出该定点的坐标；若不会，请说明理由；（3）求线段AB 的长（用t 表示）（4）若1t ＞，将抛物线1C 经过适当平移后，得到抛物线2C ：221y x t t --＝（）＋，A 、B 的对应点分别为D m （、n ），2E m （＋、n ）； ①求抛物线2C 的解析式；②将抛物线2C 位于直线DE 下方的部分沿直线DE 向上翻折，连同G 在DE 上方的部分组成一个新图形，记为图形G ，若直线132y x b b -＝＋（＜）与圆形G 有且只有两个公共点，求b 的取值范围．7．如图1，直线l 1：y ＝kx 与直线l 2：y ＝﹣12x ＋b 相交于点A （4，3），直线l 2：y ＝﹣12x ＋b 与x 轴交于点B ，点E 为线段AB 上一动点，过点E 作EF ∥y 轴交直线l 1于点F ，连接BF ．（1）求k、b的值；（2）如图2，若点F坐标为（8，6），∠OFE的角平分线交x轴于点M．①求线段OM的长；②点N在直线l1的上方，当△OFN和△OFM全等时，直接写出点N的坐标．8．如图，△ABC为等腰三角形，AB＝AC，将CA绕点C顺时针旋转至CD，连接AD，E为直线CD上一点，连接AE；（1）如图1，若∠BAC＝60°，∠ACD＝90°，E为CD中点，23AB=，求△BCE的面积；（2）如图2，若∠ACD＝90°，点E在线段CD上且∠DAE＋∠ABC＝90°，AE的延长线与BC的延长线交于点F，连接DF，求证：2=；BC DF（3）如图3，AB＝1，∠BAC＝90°，∠ACD＝105°，若BE恰好平分∠AEC，点P为线段AE上的动点，点E′与点E关于直线DP对称，AE′与CD交于点Q，连接CE′，当'+-''的值最小时，直接写出CQ的值．2CE AE CE9．如图1，已知数轴上的点A、B对应的数分别是﹣5和1．（1）若P到点A、B的距离相等，求点P对应的数；（2）动点P从点A出发，以2个单位/秒的速度向右运动，设运动时间为t秒，问：是否存在某个时刻t，恰好使得P到点A的距离是点P到点B的距离的2倍？若存在，请求出t 的值；若不存在，请说明理由；（3）如图2在数轴上的点M和点N处各竖立一个挡板（点M在原点左侧，点N在原点右侧且OM＞ON），数轴上甲、乙两个弹珠同时从原点出发，甲弹珠以2个单位/秒的速度沿数轴向右运动，乙弹珠以5个单位/秒的速度沿数轴向左运动．当弹珠遇到挡板后立即以原速度向反方向运动，若甲、乙两个弹珠相遇的位置恰好到点M和点N的距离相等，试探究点M对应的数m与点N对应的数n是否满足某种数量关系，请写出它们的关系式，并说明理由．10．在平面直角坐标系xOy中，已知点A（1，0）和点B（5，0）．对于线段AB和直线AB外的一点C，给出如下定义：点C到线段AB两个端点的连线所构成的夹角∠ACB叫做线段AB关于点C的可视角，其中点C叫做线段AB的可视点．(1)在点D（-2，2）、E（1，4）、F（3，-2）中，使得线段AB的可视角为45°的可视点是；(2)⊙P为经过A，B两点的圆，点M是⊙P上线段AB的一个可视点.① 当AB为⊙P的直径时，线段AB的可视角∠AMB为度；② 当⊙P的半径为4时，线段AB的可视角∠AMB为度；(3)已知点N为y轴上的一个动点，当线段AB的可视角∠ANB最大时，求点N的坐标．11．图形的旋转变换是研究数学相关问题的重要手段之一，在研究三角形的旋转过程中，发现下列问题：如图1，在ABC中，AB AC∠=，MN分别为AB、BC边上一=，BACα点，连接MN，且MN AC∥，将ABC绕点B在平面内旋转．(1)观察猜想 ABC 绕点B 旋转到如图2所示的位置，若60α=︒，则AM CN 的值为______． (2)类比探究 若90α=︒，将ABC 绕点B 旋转到如图3所示的位置，求AM CN 的值． (3)拓展应用若90α=︒，M 为AB 的中点，4AB =，当AM BN ⊥时，请直接写出CN 的值．12．如图1，抛物线y 14=-x 2+bx +c 经过点C （6，0），顶点为B ，对称轴x ＝2与x 轴相交于点A ，D 为线段BC 的中点．(1)求抛物线的解析式；(2)P 为线段BC 上任意一点，M 为x 轴上一动点，连接MP ，以点M 为中心，将△MPC 逆时针旋转90°，记点P 的对应点为E ，点C 的对应点为F ．当直线EF 与抛物线y 14=-x 2+bx +c 只有一个交点时，求点M 的坐标．(3)△MPC 在（2）的旋转变换下，若PC 2=2）．①求证：EA ＝ED ．②当点E 在（1）所求的抛物线上时，求线段CM 的长．13．如图1，在平面直角坐标系中，已知△ABC 中，∠ABC ＝90°，B (4，0)，C (8，0)，tan∠ACB ＝2，抛物线y ＝ax 2+bx 经过A ，C 两点．(1)求点A的坐标及抛物线的解析式；(2)如图2，过点A作AD⊥AB交BC的垂线于点D，动点P从点A出发，沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动，速度均为每秒1个单位长度，运动时间为t秒，过点P作PE⊥AB交AC于点E．①过点E作EF⊥AD于点F，交抛物线于点G．当t为何值时，线段EG取得最大值？最大值是多少？②连接EQ，在点P，Q运动过程中，t为何值时，使得△CEQ与△ABC相似？14．在平面直角坐标系中，抛物线：与x轴交于点A，B（点B 在点A的右侧）．抛物线顶点为C点，△ABC为等腰直角三角形．(1)求此抛物线解析式．(2)若直线与抛物线有两个交点，且这两个交点与抛物线的顶点所围成的三角形面积等于6，求k的值．(3)若点，且点E，D关于点C对称，过点D作直线2l交抛物线于点M，N，过点E作直线轴，过点N作于点F，求证：点M，C，F三点共线．15．如图1：抛物线y＝ax2+bx﹣4交x轴于点A、B，连接AC、BC，tan∠ABC＝1，tan∠BAC＝4．(1)抛物线的解析式为；(2)点P在第三象限的抛物线上，连接PC、PA，若点P横坐标为t，△PAC的面积为S，求S与t的函数关系式；(3)如图2，在（2）的条件下，当S＝6时，点G为第四象限抛物线上一点，连接PG，CH ⊥PG 于点H ，连接OH ，若tan∠OHG 34=，求GH 的长． 16．已知抛物线24y ax bx =++（a ≠0）与x 轴交于点A （3-，0）、B （2，0），与y 轴交于点C ，直线y mx n =+经过两点A 、C ．(1)求a ，b 的值；(2)如图1，点Р在已知抛物线上，且位于第二象限，当四边形PABC 的面积最大时，求点P 的坐标．(3)如图2，将已知抛物线向左平移12个单位，再向下平移2个单位．记平移后的抛物线为'y ，若抛物线'y 与原抛物线的对称轴交于点Q ．点E 是新抛物线'y 的对称轴上一动点，在（2）的条件下，当△PQE 是等腰三角形时，请直接写出点E 的坐标．17．如图，已知四边形ABCD 内接于⊙O ，直径DF 交BC 于点G ．(1)如图1，求证：∠BAD －∠BCF ＝90°；(2)如图2，连接AC ，当∠BAC ＝∠CFD ＋∠ACD 时，求证：CA ＝CB ；(3)如图3，在（2）的条件下，AC 交DF 于点H ，∠BAC ＝∠DGB ，45CG BG =，AC ＝9，求△CDH 的面积．18．同学们学过正方形与等腰三角形发现它们都是轴对称图形，它们之间有很多相似，在正边形ABCD 中，E 是对角线AC 上一点（不与点A 、C 重合），以AD 、AE 为邻边作平行四边形AEGD ，GE 交CD 于点M ，连接CG ．(1)如图1，当12AE AC <时，过点E 作EF BE ⊥交CD 于点F ，连接GF 并延长交AC 于点H ．求证：EB EF =；(2)在ABC 中，AB AC =，90BAC ∠=︒．过点A 作直线AP ，点C 关于直线AP 的对称点为点D ，连接BD ，CD 直线BD 交直线AP 于点E ．如图2，①依题意补全图形；②请用等式表示线段EB ，ED ，BC 之间的数量关系，并予以证明．19．已知抛物线y 14=-kx 212-（k ﹣2）x +2与y 轴交于点A ，与x 轴交于B 、C （点B 在点C 的左边）．(1)直接写出点B 的坐标；(2)当k ＝1时（如图），求：①在直线AC 上方的抛物线上一点M ，求点M 到直线AC 的最大距离及此时点M 的坐标；②将线段OA 绕x 轴上的动点P （m ，0）顺时针旋转90°得到线段O ′A ′，若线段O ′A ′与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．20．如图，在平面直角坐标系中，抛物线的对称轴是直线1x =，且与x 轴交于A ，B 两点，与y 轴交于点()0,3C -，OB OC =．（1）求抛物线的解析式．（2）在抛物线上是否存在点Q，使得BCQ△是以BC为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．（3）设抛物线上的一点P的横坐标为m，且在直线BC的下方，求使BCP的面积为最大整数时点P的坐标．【参考答案】**科目模拟测试一、解答题1．(1)y=3x-3；(2)（-2，3）；(3)Q的坐标为（-72，0）或（0，74）或（0，132）【解析】【分析】（1）根据算术平方根的非负性及偶次方的非负性得到a+3=0，p-1=0，求出a，p，得到点P，A的坐标，设直线AP的解析式为y=kx+b，利用待定系数法求出函数解析式；（2）过M作MD交x轴于D，连接AD，由MD，△MAP的面积等于6，顶点△DAP的面积等于6，求出DP，得到点D坐标，求出直线DM的解析式，即可求出M的坐标；（3）设B（t，3t-3），分三种情况，①当点Q在轴负半轴时，过B作BE⊥x轴于E，证明△BEQ≌△QNC（AAS），得到O Q=QE-OE=ON+QN，即4-t=2+3-3t，求出t值即可；②当Q在y轴正半轴上时，过C作CF⊥y轴于F，过B作BG⊥y轴于G，证明△CQF≌△QBG（AAS），得到O Q=OG-QG=OF-QF，即3t-3-2=4-t，求出t即可；③当Q在y轴正半轴上时，过点C作CF⊥y轴于F，过B作BT⊥y轴于T，同②可证△CFQ≌△QTB（AAS），得到OQ=OT+QT=OF+QF，即3t-3+2=4+t，求出t值即可．(1)解：∵+（p﹣1）2＝0．∴a+3=0，p-1=0，解得a=-3，p=1，∴P(1,0)，A(0,-3)，设直线AP的解析式为y=kx+b，∴，解得，∴直线AP的解析式为y=3x-3；(2)解：过M作MD交x轴于D，连接AD，∵MD，△MAP的面积等于6，∴△DAP的面积等于6，∴，即，∴DP=4，∴D（-3，0）设直线DM的解析式为y=3x+c，则，∴c=9，∴直线DM的解析式为y=3x+9，令x=-2，得y=3，∴M（-2，3）；(3)解：存在设B（t，3t-3），①当点Q在x轴负半轴时，过B作BE⊥x轴于E，如图，∴OE=t，BE=3-3t，∵△BCQ是以BC为底边的等腰直角三角形，∴BQ=CQ，∠BQC=90°，∴∠BQE=90°-∠NQC=∠QCN，又∵∠BEQ=∠QN C，∴△BEQ≌△QNC（AAS），∴QN=BE=3-3t，QE=CN=4，∴OQ=QE-OE=ON+QN，即4-t=2+3-3t，∴t=12，∴OQ=72，∴Q（-72，0）；②当Q在y轴正半轴上时，过C作CF⊥y轴于F，过B作BG⊥y轴于G，如图，∴BG=t，OG=3t-3，∵△BCQ是以BC为底边的等腰直角三角形，∴BQ=CQ，∠BCQ=90°，∴∠CQF=90°-∠BQG=∠GBQ，又∵∠CFQ=∠BGQ=90°，∴△CQF≌△QBG（AAS），∴CF=QG=2，QF=BG=t，∴O Q=OG-QG=OF-QF，即3t-3-2=4-t，∴t=94，∴OQ=4-t=74，∴Q（0，74）；③当Q在y轴正半轴上时，过点C作CF⊥y轴于F，过B作BT⊥y轴于T，如图，∴BT=t，OT=3t-3，同②可证△CFQ≌△QTB（AAS），∴CF=BT=t，QF=CF=2，∴O Q=OT+QT=OF+QF，即3t-3+2=4+t，∴t=52，∴OQ=4+t=132，∴Q（0，132）；综上，Q的坐标为（-72，0）或（0，74）或（0，132）．【点睛】此题是一次函数与图形的综合题，考查了待定系数法求函数解析式，全等三角形的判定即性质，等腰直角三角形的性质，算术平方根的非负性及偶次方的非负性，熟记全等三角形的判定即性质是解题的关键．2．（1）直线AC的解析式为y＝﹣x+6；（2）d=4-t；（3）Q（212，1）．【解析】【分析】（1）先由解析式求出得A、C点的坐标，得OA=OC，得四边形ABCO为正方形，再根据正方形的面积求得边长，便可得b的值；（2）过点Q作QG⊥AB交AB延长沿于点G，证明Rt△AOP≌Rt△GPQ（AAS），得到AP=GQ，进而求得结论便可；（3）过点P作PH⊥OF于点H，延长PH交EQ的延长线于点R，EQ的延长线与x轴交于点N，过Q作QM⊥x轴于点M．证明Rt△AOP≌Rt△GPQ（CCS），得PK=QR，∠R=∠OKP，再证明∠R=∠FPR，得EP=ER，再证FE=NR，设FE=NR=k，NQ=m，在Rt△PQE中，由勾股定理列出方程，得到k与m的关系，解Rt△PQE得tan∠PEQ，进而把这个函数值运用到△OAP中，求得t的值，再运用（2）中结论得Q的纵坐标d的值，再运用到△QNM中求得NM，NQ的值，进而求得ON，便可得Q的横坐标的值．【详解】解：（1）∵直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，A b C b，∴(,0),(0,)∴OA=OC=b，∴矩形ABCO为正方形，∵矩形ABCO的面积是36．∴b=6，即直线AC的解析式为y＝﹣x+6；（2）如图，过点Q作QG⊥AB交AB延长沿于点G，∵∠OPQ=90°，∴∠APO+∠GPQ=90°，∵∠APO+∠AOP=90°，∴∠AOP=∠GPQ，∵在矩形ABCO，∠OAP=90°，QG⊥AB,∴∠QGP=∠OAP=90°，∵PQ=OP，∴Rt△AOP≌Rt△GPQ（AAS），∴AP=GQ，∵AP=t，∴GQ=t，∴d=4-t；（2）过点P 作PH ⊥OF 于点H ，延长PH 交EQ 的延长线于点R ，EQ 的延长线与y 轴交于点N ，过Q 作QM ⊥y 轴于点M ．则AP =t ，QM =d ，且d =6-t ．∵OF 平分∠POC ，∴∠POF =∠COF =∠PFO ，∴PF =PO ，∵PH ⊥OF ，∠OPQ ＝90°，∴∠OPH =∠FPH ，∠KPH =∠POH ，在△OPK 和△PQR 中，90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝， ∴△OPK ≌△PQR （ASA ），∴PK =QR ，∠R =∠OKP ，∵∠OKP +∠POK =∠POK +∠OPH =90°，∴∠OKP =∠OPH ，∴∠R =∠OPH ，∵PO =PF ，PH ⊥OF ，∴∠OPH =∠FPH ，∴∠R =∠FPR ，∴EP =ER ，∵PE ∥ON ，OP ∥EN ，∴四边形OPEN 是平行四边形，∴EN =PO =PF ，∴PE -PF =ER -EN ，∴FE =NR ，设FE=NR=k，则KQ=2FE=2k，又设NQ=m，∴PK=QR=m+k，∴PQ=m+3k，∴PO=EN=PF=m+3k，∴QE=EN-QR=m+3k-m=3k，PE=PF+FE=4k+m，在Rt△PQE中，∵PE2=PQ2+QE2，∴（4k+m）2=（3k+m）2+（3k）2，∴k1=0（舍去），k2=m，∴PQ=4m，QE=3m，∴tan∠PEN=43 PQQE=，∵OP∥EN，∴∠OPA=∠PEN，∴tan∠APO=43，∵AO=6，∴AP=4.5，∴t=4.5，∴QM=d=6-t=1.5，∵PE∥OC，∴∠QNM=∠PEN，∴tan∠QNM=tan∠PEN=43，∴NM=9 tan8QMQNM=∠，∴m=NQ158 =，∴PE=ON=4k+m=5m=758，∴OM=ON+NM=212，∴Q（212，1）．【点睛】本题是一次函数与四边形的综合题，主要考查了一次函数的图象与性质，全等三角形的性质与判定，正方形的性质，旋转的性质，解直角三角形的应用，等腰三角形的性质与判定，平行四边形的性质与判定，是一道综合性极强的题目，解决这类问题常用到数形结合、方程和转化等数学思想方法．构造全等三角形是解题的关键，也是问题的突破口．3．（1）见解析；（2）见解析；（3）①见解析；②16:15．【解析】【分析】（1）运用等腰三角形的性质及三角形的外角性质就可解决问题．（2）如图1，证明△DCA ≌△EDG （AAS ），得AD =EG ，根据等腰三角形的判定得：DG =AB ，由平行线分线段成比例定理得：2DE DG DF AD ==，由此可得结论； （3）①如图2，作辅助线，构建三角形全等，证明△DCA ≌△EDG （AAS ），得DA =EG ，再证明△ACB ∽△GEB ，列比例式可得结论；②如图3，作辅助线，构建△ABC 和△DCE 的高线，先得14AF AD EG DG ==，设AF =a ，则EG =AD =4a ，DG =16a ，根据AH ∥PD ，得123164PD BD a AH AB a ===，设PD =3h ，AH =4h ，根据EG ∥AC ，同理得41164BG BE a AB BC a ===，设BE =y ，BC =4y ，利用三角形面积公式代入可得结论．【详解】（1）证明：∵AC =AB ，∴∠ACB =∠B ，∵DC =DE ，∴∠DCE =∠DEC ，∴∠ACD +∠ACB =∠B +∠BDE ，∴∠BDE =∠ACD ；（2）证明：如图1，∵EG ∥AC ，∴∠DAC =∠DGE ，∠BEG =∠ACB ，由（1）知：∠DCA =∠BDE ，∵DC =DE ，∴△DCA ≌△EDG （AAS ），∴AD =EG ，∵∠B =∠ACB =∠BEG ，∴EG =BG =AD ，∵DE =2DF ，AF ∥EG ， ∴2DE DG DF AD==， ∴DG =2AD =2AG ，∴AB =DG =2AG ；（3）解：①如图2，过点E 作EG ∥AC ，交AB 的延长线于点G ，则有∠A =∠G ，∵AB =AC ，CD =DE ，∴∠ACB =∠ABC ，∠DCE =∠DEC ，∴∠ACD +∠DCE =∠EDG +∠DEC ，∴∠ACD =∠EDG ，在△DCA 和△EDG 中，∵ACD EDG A G CD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△DCA ≌△EDG （AAS ）．∴DA =EG ，∵AC ∥EG ，∴△ACB ∽△GEB ，∴AC BC EG BE=， ∵EG =AD ，AC =AB ，∴AB •BE =AD •BC ；②如图3，过A 作AH ⊥BC 于H ，过D 作DP ⊥BC 于P ，则AH ∥PD ，∴AF AD DF EG DG DE==，∵DE=4DF，∴14 AF ADEG DG==，设AF=a，则EG=AD=4a，DG=16a，∵∠ACB=∠ABC，∴∠GBE=∠BEG，∴BG=EG=4a，∴BD=12a，∵AH∥PD，∴123164 PD BD aAH AB a===，设PD=3h，AH=4h，∵EG∥AC，∴41164 BG BE aAB BC a===，设BE=y，BC=4y，∴S△ABC=12BC•AH=4?42y h=162yh=8yh，S△DCE=12CE•PD=5?32y h=152yh，∴S△ABC：S△DEC=8yh：152yh=16：15．【点睛】本题是三角形的综合题，考查了相似三角形的判定与性质、全等三角形的判定与性质、平行线分线段成比例、等腰三角形的性质和判定等知识，第三问有难度，利用参数表示各线段的长是本题的关键，综合性较强．4．（1）B2C2；（23）OA最小值为1，相应的BC=OA最大值为2，相应的BC=【解析】【分析】（1）结合题意，根据旋转和圆的性质分析，即可得到答案；（2）根据题意，分B C''在x轴上方和x轴上方两种情况；根据等边三角形、勾股定理、全等三角形的性质，得AD OD==（3）结合题意，得当AC'为⊙O的直径时，OA取最小值；当A、B'、O三点共线时，OA 取最大值；根据勾股定理、等腰三角形的性质计算，即可得到答案．【详解】（1）线段B 1C 1绕点A 旋转得到的11B C ''，均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”；线段B 2C 2绕点A 旋转得到的22B C ''，如下图：∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”；线段B 3C 3绕点A 旋转得到的33B C ''，均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”；故答案为：B 2C 2；（2）∵△ABC 是边长为1的等边三角形，点A （0，t ），⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况：当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：∵1OB OC ''== ∴1122B D B C '''==∴2232OD OB B D ''=-= ∵△ABC 是边长为1的等边三角形，即△AB C ''是边长为1的等边三角形，∴AC D OC D ''∠=∠，AD B C ''⊥∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =；当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：同理，3AO AD OD =+=∴()0,3A -；∴t 3=-；∴3t =或3-；（3）当AC '为⊙O 的直径时，OA 取最小值，如下图：∴OA 最小值为1，90AB C ''∠=︒∴223BC B C AC AB ''''==-=当A 、B '、O 三点共线时，OA 取最大值，2OA AC '== ，如下图：作AE OC '⊥交OC '于点E ，作C F AO '⊥交AO 于点F ，如下图∵2OA AC '== ∴1122OE OC '== ∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '== ∴2214OF OC C F ''=-= ∴34B F OB OF ''=-= ∴26BC B C C F B F ''''==+=∴OA 最小值为1，相应的3BC =；OA 最大值为2，相应的62BC =． 【点睛】 本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识；解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质，从而完成求解．5．（1）(3,5)M ，（2）1(5,)2C t t +；（3）(20,0)B ；（4）154或10． 【解析】【分析】（1）利用中点坐标公式计算即可．（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．证明()MEB BFC AAS ∆≅∆，利用全等三角形的性质即可解决问题．（3）如图2中，存在．由题意当CF OA =时，可证四边形AOBD 是矩形，构建方程即可解决问题．（4）分三种情形：①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为6．③因为BD AB ≠，所以不存在以AD 为对角线的菱形．【详解】解：（1）如图1中，(0,10)A ，(6,0)B ，AM BM =，(3,5)M ∴，（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．//ME OA ，AM BM =，12OE EB t ∴==，152ME OA ==， 90MEB CFB CBM ∠=∠=∠=︒，90MBE CBF ∴∠+∠=︒，90MBE BME ∠+∠=︒，BME CBF ∴∠=∠，BM BC =，()MEB BFC AAS ∴∆≅∆，5BF ME ∴==，12CF BE t ==， 5OF OB BF t ∴=+=+，1(5,)2C t t ∴+． （3）存在．如图2中，作ME OB ⊥于E ，CF x ⊥轴于F ．理由：由题意当=10CF OA =时，//OA CF ，∴四边形AOFC 是平行四边形，90AOF ∠=︒，∴四边形AOFC 是矩形，90DAO AOB DBO ∴∠=∠=∠=︒，∴四边形AOBD 是矩形，又∵由（2）得12CF BE t ==，即：1102t =，解得：20t =．(20,0)B ∴． （4）①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．AD BD =，BAD ABD ∴∠=∠，//BD y 轴，OAB ABD ∴∠=∠，OAB BAD ∴∠=∠．tan tan OAB BAD ∴∠=∠， ∴12OB BC OA BA ==，即1102t =， 5t ∴=，5OB ∴=，设AN NB m ==，在Rt OBN △中，则有2225(10)m m =+-，解得254m =， 25151044ON OA AN ∴=-=-=， ∴点N 的纵坐标为154． ②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为10．③BD AB ≠，∴不存在以AD 为对角线的菱形．综上所述，满足条件的点N 的纵坐标为154或10． 【点睛】本题属于四边形综合题，考查了矩形的判定和性质，菱形的判定和性质，翻折变换，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．6．（1）6；（2）会，（1，0）；（3）22t -；（4）①y 2=（x -2）2+1；②52＜b ＜3． 【解析】【分析】（1）根据题意令y 1=0，解得x ，即AB 点的横坐标，进而即可求得AB 的长；（2）由题意可知当x =1时，y 1=0，进而可以得出该定点的坐标；（3）由（1）可知AB 点的横坐标，进而即可用t 表示线段AB 的长；（4）①由题意可知t ＞1时，点A 、B 的坐标分别为：（1，0），（2t -1，0），进而依据AB =DE ，即可求解；②根据题意将点D 、E 的坐标代入抛物线表达式得：m =1，故点D 、E 的坐标为：（1，2）、（3，2），当直线过点D 时，2=-12×1+b ，解得：b =52，同理直线过点E 时，b =72，而b ＜3，即可求解． 【详解】解：（1）令y 1=0，解得：x =1或2t -1，当t =-2，则x =1或-5，所以线段AB =1-（2t -1）=2-2t =6； （2）会有一定点，理由如下：当x =1时，y 1=0，所以会有一定点（1，0）；（3）由（1）可知当y 1=0，解得：x =1或2t -1，所以线段AB 的长为：1(21)22t t --=-；（4）①t ＞1时，点A 、B 的坐标分别为：（1，0），（2t -1，0），因为平移距离相等可得AB =DE ，即2t -1-1=m +2-m =2，解得：t =2，所以点B （3，1），把t =2，代入221y x t t --＝（）＋， 可得抛物线C 2的解析式为：y 2=（x -2）2+1；②将点D 、E 的坐标代入抛物线表达式得：n =（m -2）2+1=（m +2-2）2+1，解得：m =1，故点D 、E 的坐标为：（1，2）、（3，2）；图象G 如下图所示，当直线过点D 时，2=-12×1+b ，解得：b =52， 同理直线过点E 时，b =72，而b ＜3， 所以b 的取值范围为：52＜b ＜3． 【点睛】 本题考查的是二次函数综合运用，涉及到一次函数、图形过定点等，其中（3），要注意分类讨论避免遗漏．7．（1）34k =，5b =；（2）①OM =5；②()3,6N 或724,55N ⎛⎫ ⎪⎝⎭【解析】【分析】（1）分别将将(4,3)A 代入y kx =和12y x b =-+中，求解即可； （2）①设直线AB 与y 轴交与点C ，与FM 交于点D ,证明△AFD ≌△EFD ，得到AD =ED ，利用中点坐标公式求得点D 坐标，用待定系数法求得直线FD 的函数表达式，令0y =,即可求得点M 的坐标，从而求得OM ；②点N 在直线l 1的上方，当△OFN 和△OFM 全等时，满足题意的点N 有两个，分别画出相关的图形，分类讨论求解即可．【详解】解：（1）∵直线l 1：y kx =和直线l 2：12y x b =-+相交于点A ∴将(4,3)A 代入y kx =中，得：43k =解得：34k = ∴将(4,3)A 代入12y x b =-+中，得：1432b -⨯+= 解得：5b =∴3,54k b == （2）① 设直线AB 与y 轴交与点C ，与FM 交于点D ,如下图：∵34k =，5b = ∴直线l 1的函数表达式为34y x =，直线l 2的函数表达式为152y x =-+ ∵(4,3)A∴22345OA +设直线AB 与y 轴交与点C ，与FM 交于点D则()0,5C∴5OC =∴5OA OC ==∴∠OCA =∠OAC∵//FE y 轴∴∠OCA =∠FEA又∵∠OAC =∠FAE∴∠FAE =∠FEA∴FA =FE又∵FM 是∠OFE 的角平分线∴∠AFM =∠EFM又∵FD =FD∴△AFD ≌△EFD∴AD =ED∴点D 为AE 的中点∵//FE y 轴∴点F 和点E 的横坐标相同将8x =代入152y x =-+中，得1y = ∴()8,1E∵(4,3)A ，()8,1E∴()6,2D设线段FM 所在的直线函数表达式为()0y ax b a =+≠将()()8,6,6,2F D 代入y ax b =+中，得：8662k b k b +=⎧⎨+=⎩解得：210k b =⎧⎨=-⎩∴线段FM 所在的直线函数表达式为210y x =-令0y =，得2100x -=解得：5x =∴()5,0M∴OM =5② 当,OFN FOM 全等时，有两种情况，情况一，如下图所示：∵OFN FOM ≅△△∴∠OFN =∠FOM ，FN =OM ,ON =FM∴//FN OM∵OM =5∴FN =5,8F x =∴853N x =-=,6N F y y ==∴()3,6N情况二，当△OMF 和△ONF 关于直线l 1对称时，如下图所示：∵OFN FOM ≅△△∴ON =OM =5，∠NOF =∠MOF∵OP =OP∴△NOP ≌△MOP∴PN =PM∵()8,6F ∴226810OF + 又∵1122OMF F S OM y OF PM =⋅=⋅ ∴F OM y OF PM ⋅=⋅ ∴56==310PM ⨯ ∴MN =2PM =6，OP 2222534OM PM -- ∵1122OMN N S MN OP OM y =⋅=⋅△ ∴642455N y ⨯== ∴2222247555N N x ON y ⎛⎫=-=- ⎪⎝⎭∴724,55N ⎛⎫ ⎪⎝⎭ 综上所述，满足题意点有两个，分别是：()3,6N 或724,55N ⎛⎫ ⎪⎝⎭ 【点睛】本题考查用待定系数法求一次函数表达式，三角形全等的性质和证明，两条直角交点的求法以及三角形的等面积法等知识点，牢记相关内容并能灵活应用数形结合思想解题是本题的关键．8．（1）32；（2）见解析；（3）222- 【解析】【分析】（1）过点,,A E D 分别作BC 的垂线，垂足分别为,,H I G ，连接BE ，证明Rt AHC Rt CGD △≌△，根据含30度角的直角三角形的性质求得CE ,进而求得EI ,根据三角形的面积公式求解即可；（2）过点,A D 分别作BC 的垂线，交BC 及BC 的延长线于点,H G ，证明Rt AHC Rt CGD △≌△，进而可得HAF △是等腰直角三角形，DGF 是等腰直角三角形，即可证明2222DF DG HC BC ===，即2BC DF =； （3）延长,EA EC ，过点B 分别作,BN EN BM CM ⊥⊥，垂足分别为,N N ，解直角三角形Rt ABN △可得45ABN ∠=︒，进而可得30AEC NEM ∠=∠=︒，进求得DE 的长度，由点P 为线段AE 上的动点，点E ′与点E 关于直线DP 对称，AE ′与CD 交于点Q ，连接CE ′，构造相似三角形，在线段DC 上截取322DF =-,连接E F '，则CDE E DF ''△∽△，求得目标等量关系()21E F CE ''=-，根据()221CE AE CE CE AE E F AE AF '''''+-=-+=+≥''则当,,A E F '三点共线时，取得最小值，此时Q 点与F 点重合，根据CQ CF CD FD ==-即可求得答案．【详解】（1）如图，过点,,A E D 分别作BC 的垂线，垂足分别为,,H I G ，连接BE ，AB ＝AC ，将CA 绕点C 顺时针旋转至CD ，AC CD ∴=∠BAC ＝60°，ABC ∴是等边三角形，AC CD ∴=，60BAC ∠=︒AH BC ⊥ 1302CAH CAB ∴∠=∠=︒ ,AH HC DG GC ⊥⊥，∠ACD ＝90°，90AHC CGD ∴∠=∠=︒90ACH DCG ACH HAC ∴∠+∠=∠+∠=︒DCG HAC ∴∠=∠Rt AHC Rt CGD ∴△≌△HC GD ∴=,30CAH DCG ∠=∠=︒ E 为CD 中点，23AB =， 11322CE CD AB ∴=== 在Rt CEI △中，30ECI ∠=︒1322EI CE ∴== 1133232222BCE S BC EI ∴=⋅⋅=⨯⨯=△ （2）如图，过点,A D 分别作BC 的垂线，交BC 及BC 的延长线于点,H G ，,AH HC DG GC ⊥⊥，∠ACD ＝90°，90AHC CGD ∴∠=∠=︒90ACH DCG ACH HAC ∴∠+∠=∠+∠=︒DCG HAC ∴∠=∠Rt AHC Rt CGD ∴△≌△AH CG ∴=,DG HC =AC CD =， AH BC ⊥∴BAH HAC ∠=∠，90ABC BAH ∠+∠=︒∠DAE ＋∠ABC ＝90°，DAE HAC DCG ∴∠=∠=∠AC CD =，∠ACD ＝90°，45DAC ∴∠=︒DAE EAC CAH EAC ∴∠+∠=∠+∠45HAF =∠=︒即45HAF ∠=︒HAF ∴△是等腰直角三角形AH HF ∴=CG HF ∴=CG CF HF CF ∴-=-即HC FG =又DG HC =FG DG ∴= ∴DGF 是等腰直角三角形 2222DF DG HC BC ∴=== 即2BC DF =（3）如图，延长,EA EC ，过点B 分别作,BN EN BM CM ⊥⊥，垂足分别为,N N ，BE 恰好平分∠AEC ，BM BN ∴=∠BAC ＝90°，∠ACD ＝105°，AB ＝AC ，AB ＝1，在Rt ABC 中，2BC 45ABC ACB ∴∠=∠=︒150BCE ACB ACE ∴∠=∠+∠=︒30BCM ∴∠=︒60CBM ∴∠=︒22BM ∴= 2BN BM ∴==在Rt ABN △中21,AB BN ==2cos BN ABN AB ∴∠==45ABN ∴∠=︒90NBC ∴∠=︒9060150NBM NBC CBM ∴∠=∠+∠=︒+︒=︒在四边形ENBM 中，90,150M N NBM ∠=∠=︒∠=︒30AEC NEM ∴∠=∠=︒ 1152BEC AEC ∴∠==︒ 又30BCM BEC CBE ∠=∠+∠=︒15CBE CEB ∴∠=∠=︒CB CE ∴=2= 1CD CA AB ===21DE CE CD ∴=-=-如图，点P 为线段AE 上的动点，点E ′与点E 关于直线DP 对称，AE ′与CD 交于点Q ，连接CE ′， ∴21DE DE '==-211DE CD '-= 若211DF E D -='，则322DF =- 在线段DC 上截取322DF =-,连接E F '，则DF ED E D CD'='，又E DF CDE ''∠=∠ CDE E DF ''∴△∽△ 21CE CD E F E D '∴==''-()21E F CE ''= ∴()221CE AE CE CE AE E F AE AF '''''+-=+=+≥'' 则当,,A E F '三点共线时，取得最小值，此时Q 点与F 点重合，此时1(322)22CQ CF CD FD ==-=--=【点睛】本题考查了三角形全等的性质与判定，相似三角形的性质与判定，角平分线的性质，解直角三角形，第三问是阿氏圆模型，找到点F 的位置是解题的关键．9．（1）点P 对应的数为-2；（2）当t =2或6时，恰好使得P 到点A 的距离是点P 到点B 的距离的2倍；（3）m +13n =0．【解析】【分析】（1）设点P 对应的数为x ，表示出BP 与PA ，根据BP =PA 求出x 的值，即可确定出点P 对应的数；（2）表示出点P 对应的数，进而表示出PA 与PB ，根据PA =2PB 求出t 的值即可；（3）因为OM ＞ON ，只有甲乙均反弹之后在中点相遇一种情况，设点M 对应的数为m ，点N 对应的数为n ，时间为t ，则M 、N 的中点对应的数为2m n +，根据甲、乙两个弹珠相遇的位置恰好到点M 和点N 的距离相等列出关系式即可．【详解】解：（1）点A 、B 对应的数分别是﹣5和1，设点P 对应的数为x ，则BP =1-x ，PA =x +5，∵BP =PA ，∴1-x =x +5，解得：x =-2，∴点P 对应的数为-2；（2）P 对应的数为-5+2t ，∴PA =2t ，PB =|-5+2t -1|=|2t -6|，∵PA =2PB ，∴2t =2|2t -6|，当t =2t -6时，t =6；当t +2t -6=0时，t =2；答：当t =2或6时，恰好使得P 到点A 的距离是点P 到点B 的距离的2倍；（3）设点M 对应的数为m ，点N 对应的数为n ，时间为t ，则M 、N 的中点对应的数为2m n +， ∴MN =n -m ，OM =-m ，ON =n ，∴()()252502t t n m m n t m m ⎧+=-⎪+⎨⎛⎫=-+- ⎪⎪⎝⎭⎩，即()()351073352t n m n m t ⎧=-⎪⎨-=⎪⎩， 化简得m +13n =0．【点睛】本题考查了二元一次方程的应用，数轴，两点间的距离，运用分类讨论思想、方程思想及数形结合思想是解题的关键．10．(1)点E(2)① 90；② 30或150(3)N（00，【解析】【分析】（1）AE、BE、AB满足勾股定理，且AE=AB，可知ABE△为等腰直角三角形，则∠AEB=45°，故E点可使线段AB的可视角为45°．（2）①由半径所对的圆周角为90°即可得出∠AMB为90°．②连接AP、BP，即可得出ABP△为等边三角形，由圆周角定理即可求得∠AMB为30°或150°．（3）以AB为弦作圆M且过点N，由圆周角定理可得出当圆心角AMB最大时，圆周角ANB最大，由直线与圆的位置关系得出当y轴与圆M相切时圆心角AMB最大，进而可求得N点坐标．(1)连接AE，BE∵AE=4，AB=4，AE⊥AB∴ABE△为等腰直角三角形∴∠AEB=45°．故使得线段AB的可视角为45°的可视点是点E．(2)①有题意可知，此时AB为⊙P直径由半径所对的圆周角为90°可知∠AMB为90°②当⊙P的半径为4时，AB为⊙P一条弦，连接AP，BP∵BP=AP=4，AB=4∴ABP△为等边三角形∴∠APB=60°当点M在圆心一侧由圆周角定理知∠AMB=当点M不在圆心一侧由内切四边形性质可知∠AMB=180°-30°=150°。

中考数学综合压轴题100题（附答案）一、中考压轴题1．在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得△A1B1C1，使点C1落在直线BC上（点C1与点C不重合），（1）如图，当∠C＞60°时，写出边AB1与边CB的位置关系，并加以证明；（2）当∠C＝60°时，写出边AB1与边CB的位置关系（不要求证明）；（3）当∠C＜60°时，请你在如图中用尺规作图法作出△AB1C1（保留作图痕迹，不写作法），再猜想你在（1）、（2）中得出的结论是否还成立并说明理由．【分析】（1）AB1∥BC．因为等腰三角形，两底角相等，再根据平行线的判定，内错角相等两直线平行，可证明两直线平行．（2）当∠C＝60°时，写出边AB1与边CB的位置关系也是平行，证明方法同（1）题．（3）成立，根据旋转变换的性质画出图形．利用三角形全等即可证明．【解答】解：（1）AB1∥BC．证明：由已知得△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（5分）（2）如图1，∠C＝60°时，AB1∥BC．（7分）（3）如图，当∠C＜60°时，（1）、（2）中的结论还成立．证明：显然△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∴∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（13分）【点评】考查图形的旋转，等腰三角形的性质，平行线的判定．本题实质是考查对图形旋转特征的理解，旋转前后的图形是全等的．2．已知：y关于x的函数y＝（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．（1）求k的取值范围；（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2＝4x1x2．①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最小值．【分析】（1）分两种情况讨论，当k＝1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0．（2）①根据（k﹣1）x12+2kx2+k+2＝4x1x2及根与系数的关系，建立关于k的方程，求出k 的值；②充分利用图象，直接得出y的最大值和最小值．【解答】解：（1）当k＝1时，函数为一次函数y＝﹣2x+3，其图象与x轴有一个交点．当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，令y＝0得（k﹣1）x2﹣2kx+k+2＝0．△＝（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1．综上所述，k的取值范围是k≤2．（2）①∵x1≠x2，由（1）知k＜2且k≠1，函数图象与x轴两个交点，∴k＜2，且k≠1．由题意得（k﹣1）x12+（k+2）＝2kx1①，将①代入（k﹣1）x12+2kx2+k+2＝4x1x2中得：2k（x1+x2）＝4x1x2．又∵x1+x2＝，x1x2＝，∴2k•＝4•．解得：k1＝﹣1，k2＝2（不合题意，舍去）．∴所求k值为﹣1．②如图，∵k1＝﹣1，y＝﹣2x2+2x+1＝﹣2（x﹣）2+．且﹣1≤x≤1．由图象知：当x＝﹣1时，y最小＝﹣3；当x＝时，y最大＝．∴y的最大值为，最小值为﹣3．【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值，充分利用图象是解题的关键．3．广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．（1）求平均每次下调的百分率．（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【分析】（1）根据题意设平均每次下调的百分率为x，列出一元二次方程，解方程即可得出答案；（2）分别计算两种方案的优惠价格，比较后发现方案①更优惠．【解答】解：（1）设平均每次下调的百分率为x，则6000（1﹣x）2＝4860，解得：x1＝0.1＝10%，x2＝1.9（舍去），故平均每次下调的百分率为10%；（2）方案①购房优惠：4860×100×（1﹣0.98）＝9720（元）；方案②可优惠：80×100＝8000（元）．故选择方案①更优惠．【点评】本题主要考查一元二次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解，属于中档题．4．我们学习了利用函数图象求方程的近似解，例如：把方程2x﹣1＝3﹣x的解看成函数y ＝2x﹣1的图象与函数y＝3﹣x的图象交点的横坐标．如图，已画出反比例函数y＝在第一象限内的图象，请你按照上述方法，利用此图象求方程x2﹣x﹣1＝0的正数解．（要求画出相应函数的图象；求出的解精确到0.1）【分析】根据题意可知，方程x2﹣x﹣1＝0的解可看做是函数y＝和y＝x﹣1的交点坐标，所以根据图象可知方程x2﹣x﹣1＝0的正数解约为1.1．【解答】解：∵x≠0，∴将x2﹣x﹣1＝0两边同时除以x，得x﹣1﹣＝0，即＝x﹣1，把x2﹣x﹣1＝0的正根视为由函数y＝与函数y＝x﹣1的图象在第一象限交点的横坐标．如图：∴正数解约为1.1．【点评】主要考查了反比例函数和一元二次方程之间的关系．一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解．5．如图，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．（1）当PQ∥AD时，求x的值；（2）当线段PQ的垂直平分线与BC边相交时，求x的取值范围；（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S关于x的函数关系式，并写出S的取值范围．【分析】（1）根据已知条件，证明四边形APQD是矩形，再根据矩形的性质和AP＝CQ 求x即可；（2）连接EP、EQ，则EP＝EQ，设BE＝y，列出等式（8﹣x）2+y2＝（6﹣y）2+x2然后根据函数的性质来求x的取值范围；（3）由图形的等量关系列出方程，再根据函数的性质来求最值．【解答】解：（1）当PQ∥AD时，则∠A＝∠APQ＝90°，∠D＝∠DQP＝90°，又∵AB∥CD，∴四边形APQD是矩形，∴AP＝QD，∵AP＝CQ，AP＝CD＝，∴x＝4．（2）如图，连接EP、EQ，则EP＝EQ，设BE＝y．∴（8﹣x）2+y2＝（6﹣y）2+x2，∴y＝．∵0≤y≤6，∴0≤≤6，∴≤x≤．（3）S△BPE＝•BE•BP＝••（8﹣x）＝，S△ECQ＝＝•（6﹣）•x＝，∵AP＝CQ，∴S BPQC＝，∴S＝S BPQC﹣S△BPE﹣S△ECQ＝24﹣﹣，整理得：S＝＝（x﹣4）2+12（），∴当x＝4时，S有最小值12，当x＝或x＝时，S有最大值．∴12≤S≤．【点评】解答本题时，涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点，这是一道综合性比较强的题目，所以在解答题目时，一定要把各个知识点融会贯通，这样解题时才会少走弯路．6．九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，求旗杆AB的高度．【分析】利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB＝EF＝1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出，把相关条件代入即可求得AH＝11.9，所以AB＝AH+HB＝AH+EF＝13.5m．【解答】解：∵CD⊥FB，AB⊥FB，∴CD∥AB∴△CGE∽△AHE∴即：∴∴AH＝11.9∴AB＝AH+HB＝AH+EF＝11.9+1.6＝13.5（m）．【点评】主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．7．如图，已知△BEC是等边三角形，∠AEB＝∠DEC＝90°，AE＝DE，AC，BD的交点为O．（1）求证：△AEC≌△DEB；（2）若∠ABC＝∠DCB＝90°，AB＝2 cm，求图中阴影部分的面积．【分析】（1）在△AEC和△DEB中，已知AE＝DE，BE＝CE，且夹角相等，根据边角边可证全等．（2）由图可知，在连接EO并延长EO交BC于点F，连接AD之后，整个图形是一个以EF所在直线对称的图形．即△AEO和△DEO面积相等，只要求出其中一个即可，而三角形AEO面积＝•OE•FB，所以解题中心即为求出OE和FB，有（1）中结论和已知条件即可求解．【解答】（1）证明：∵∠AEB＝∠DEC＝90°，∴∠AEB+∠BEC＝∠DEC+∠BEC，即∠AEC＝∠DEB，∵△BEC是等边三角形，∴CE＝BE，又AE＝DE，∴△AEC≌△DEB．（2）解：连接EO并延长EO交BC于点F，连接AD．由（1）知AC＝BD．∵∠ABC＝∠DCB＝90°，∴∠ABC+∠DCB＝180°，∴AB∥DC，AB＝＝CD，∴四边形ABCD为平行四边形且是矩形，∴OA＝OB＝OC＝OD，又∵BE＝CE，∴OE所在直线垂直平分线段BC，∴BF＝FC，∠EFB＝90°．∴OF＝AB＝×2＝1，∵△BEC是等边三角形，∴∠EBC＝60°．在Rt△AEB中，∠AEB＝90°，∠ABE＝∠ABC﹣∠EBC＝90°﹣60°＝30°，∴BE＝AB•cos30°＝，在Rt△BFE中，∠BFE＝90°，∠EBF＝60°，∴BF＝BE•cos60°＝，EF＝BE•sin60°＝，∴OE＝EF﹣OF＝＝，∵AE＝ED，OE＝OE，AO＝DO，∴△AOE≌△DOE．∴S△AOE＝S△DOE∴S阴影＝2S△AOE＝2וEO•BF＝2×××＝（cm2）．【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质，进行逻辑推理能力和运算能力．8．如图，⊙O是等边△ABC的外接圆，AB＝2，M、N分别是边AB、AC的中点，直线MN交⊙O于E、F两点，BD∥AC交直线MN于点D．求出图中线段DM上已有的一条线段的长．【分析】连接OA交MN于点G，则OA⊥BC，由三角形的中位线的性质可得MN的长，易证得△BMD≌△AMN，有DM＝MN，由相交弦定理得ME•MF＝MA•MB，就可求得EM，DE的值．【解答】解：∵M，N分别是边AB，AC的中点∴MN∥BC，MN＝BC＝1又∵BD∥AC∴∠DBA＝∠A＝60°∵BM＝AM，∠BMD＝∠AMN∴△BMD≌△AMN∴DM＝MN＝1连接OA交MN于点G，则OA⊥BC∴OA⊥EF∴EG＝FG，MG＝FN由相交弦定理得：ME•MF＝MA•MB∴EM（EM+1）＝1解得EM＝（EM＝不合题意，舍去）∴DE＝DM﹣EM＝∴DE（3﹣DE）＝1解得DE＝（DE＝不合题意，舍去）．【点评】本题利用了三角形的中位线的性质，等边三角形的性质，全等三角形的判定和性质，一元二次方程的解法求解．9．如图，有一直径MN＝4的半圆形纸片，其圆心为点P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴向右翻滚至位置Ⅴ，其中，位置Ⅰ中的MN平行于数轴，且半⊙P与数轴相切于原点O；位置Ⅱ和位置Ⅳ中的MN垂直于数轴；位置Ⅲ中的MN在数轴上；位置Ⅴ中的点N到数轴的距离为3，且半⊙P与数轴相切于点A．解答下列问题：（1）位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；（2）求位置Ⅲ中的圆心P在数轴上表示的数；（3）纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时，求点N所经过路径长及该纸片所扫过图形的面积；（4）求OA的长．[（2），（3），（4）中的结果保留π]．【分析】（1）先求出圆的半径，再根据切线的性质进行解答；（2）根据位置Ⅰ中的长与数轴上线段ON相等求出的长，再根据弧长公式求出的长，进而可得出结论；（3）作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形，在Rt△NPH中，根据sin∠NPH＝＝即可∠NPH、∠MP A的度数，进而可得出的长，【解答】解：（1）∵⊙P的直径＝4，∴⊙P的半径＝2，∵⊙P与直线有一个交点，∴位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；故答案为：2，相切；（2）位置Ⅰ中的长与数轴上线段ON相等，∵的长为＝π，NP＝2，∴位置Ⅲ中的圆心P在数轴上表示的数为π+2．（3）点N所经过路径长为＝2π，S半圆＝＝2π，S扇形＝＝4π，半⊙P所扫过图形的面积为2π+4π＝6π．（4）如图，作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形．在Rt△NPH中，PN＝2，NH＝NC﹣HC＝NC﹣P A＝1，于是sin∠NPH＝＝，∴∠NPH＝30°．∴∠MP A＝60°．从而的长为＝，于是OA的长为π+4+π＝π+4．【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式，在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系．10．已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图（1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC＝CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图（3），若C是⊙O1内的一点，判断（2）中的结论是否成立？【分析】（1）连接C01，利用直径所对圆周角等于90度，以及垂直平分线的性质得出即可；（2）根据已知得出四边形AEDB内接于⊙O1，得出∠ABC＝∠E，再利用＝，得出∠E＝∠AO1C，进而得出CO1∥ED即可求出；（3）根据已知得出∠B＝∠EO1C，又∠E＝∠B，即可得出∠EO1C＝∠E，得出CO1∥ED，即可求出．【解答】（1）证明：连接C01∵AC为⊙O2直径∴∠AO1C＝90°即CO1⊥AD，∵AO1＝DO1∴DC＝AC（垂直平分线的性质）；（2）证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵四边形AEDB内接于⊙O1，∴∠E+∠ABD＝180°，∵∠ABC+∠ABD＝180°，∴∠ABC＝∠E，又∵＝，∴∠ABC＝∠AO1C，∴∠E＝∠AO1C，∴CO1∥ED，又AE为⊙O1的直径，∴ED⊥AD，∴O1C⊥AD，（3）（2）中的结论仍然成立．证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵∠B+∠AO1C＝180°，∠EO1C+∠AO1C═180°，∴∠B＝∠EO1C，又∵∠E＝∠B，∴∠EO1C＝∠E，∴CO1∥ED，又ED⊥AD，∴CO1⊥AD．【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质，根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键．11．如图①，有四张编号为1、2、3、4的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．（1）从中随机抽取一张，抽到的卡片是眼睛的概率是多少？（2）从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：（1）所求概率为；（2）方法①（树状图法）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为，方法②（列表法）1 2 3 4第一次抽取第二次抽取1（2，1）（3，1）（4，1）2（1，2）（3，2）（4，2）3（1，3）（2，3）（4，3）4（1，4）（2，4）（3，4）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3），∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．12．如图，菱形、矩形与正方形的形状有差异，我们将菱形、矩形与正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度”相等．（1）设菱形相邻两个内角的度数分别为m°和n°，将菱形的“接近度”定义为|m﹣n|，于是|m﹣n|越小，菱形越接近于正方形．①若菱形的一个内角为70°，则该菱形的“接近度”等于40；②当菱形的“接近度”等于0时，菱形是正方形．（2）设矩形相邻两条边长分别是a和b（a≤b），将矩形的“接近度”定义为|a﹣b|，于是|a﹣b|越小，矩形越接近于正方形．你认为这种说法是否合理？若不合理，给出矩形的“接近度”一个合理定义．【分析】（1）根据相似图形的定义知，相似图形的形状相同，但大小不一定相同，相似图形的“接近度”相等．所以若菱形的一个内角为70°，则该菱形的“接近度”等于|m﹣n|；当菱形的“接近度”等于0时，菱形是正方形；（2）不合理，举例进行说明．【解答】解：（1）①∵内角为70°，∴与它相邻内角的度数为110°．∴菱形的“接近度”＝|m﹣n|＝|110﹣70|＝40．②当菱形的“接近度”等于0时，菱形是正方形．（2）不合理．例如，对两个相似而不全等的矩形来说，它们接近正方形的程度是相同的，但|a﹣b|却不相等．合理定义方法不唯一．如定义为，越接近1，矩形越接近于正方形；越大，矩形与正方形的形状差异越大；当时，矩形就变成了正方形，即只有矩形的越接近1，矩形才越接近正方形．【点评】正确理解“接近度”的意思，矩形的“接近度”|a﹣b|越小，矩形越接近于正方形．这是解决问题的关键．13．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）①画出△ABC关于x轴对称的△A1B1C1；②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2；③△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标．【分析】（1）将三角形的各顶点，向x轴作垂线并延长相同长度得到三点的对应点，顺次连接；（2）将三角形的各顶点，绕原点O按逆时针旋转90°得到三点的对应点．顺次连接各对应点得△A2B2C2；（3）从图中可发现成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，做它的垂直平分线；（4）成中心对称图形，画出两条对应点的连线，交点就是对称中心．【解答】解：如下图所示：（3）成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，作它的垂直平分线，或连接A1C1，A2C2的中点的连线为对称轴．（4）成中心对称，对称中心为线段BB2的中点P，坐标是（，）．【点评】本题综合考查了图形的变换，在图形的变换中，关键是找到图形的对应点．14．图（1）是一个10×10格点正方形组成的网格．△ABC是格点三角形（顶点在网格交点处），请你完成下面的两个问题：（1）在图（1）中画出与△ABC相似的格点△A1B1C1和△A2B2C2，且△A1B1C1与△ABC的相似比是2，△A2B2C2与△ABC的相似比是；（2）在图（2）中用与△ABC，△A1B1C1，△A2B2C2全等的格点三角形（每个三角形至少使用一次），拼出一个你熟悉的图案，并为你设计的图案配一句贴切的解说词．【分析】（1）△A1B1C1与△ABC的相似比是2，则让△ABC的各边都扩大2倍就可．△A2B2C2与△ABC的相似比是；△ABC的直角边是2，所以△A2B2C2与的直角边是即一个对角线的长度．斜边为2．依此画图即可；（2）拼图有审美意义即可，答案不唯一．【解答】解：【点评】本题主要考查了相似图形的画法，做这类题时根据的是相似图形的性质，即相似比相等．对应角相等．15．如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．（1）试判断DE与BD是否相等，并说明理由；（2）如果BC＝6，AB＝5，求BE的长．【分析】（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD＝∠BAD，根据圆周角定理即可得出∠DEB＝∠DBE，便可证得DE＝DB．（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出AC•BE＝CB•AD．进而求出BE的长．【解答】解：（1）DE＝BD证明：连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD＝∠BAD（等腰三角形三线合一），∴＝，∴DE＝BD；（2）∵AB＝5，BD＝BC＝3，∴AD＝4，∵AB＝AC＝5，∴S△ABC＝•AC•BE＝•CB•AD，∴BE＝4.8．【点评】本题主要考查了等腰三角形的性质，圆周角定理等知识点的运用，用等腰三角形三线合一的特点得出圆周角相等是解题的关键．16．如图，在Rt△ABC中，∠C＝90°，Rt△BAP中，∠BAP＝90°，已知∠CBO＝∠ABP，BP交AC于点O，E为AC上一点，且AE＝OC．（1）求证：AP＝AO；（2）求证：PE⊥AO；（3）当AE＝AC，AB＝10时，求线段BO的长度．【分析】（1）根据等角的余角相等证明即可；（2）过点O作OD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CO＝DO，利用“SAS”证明△APE和△OAD全等，根据全等三角形对应角相等可得∠AEP＝∠ADO＝90°，从而得证；（3）设C0＝3k，AC＝8k，表示出AE＝CO＝3k，AO＝AP＝5k，然后利用勾股定理列式求出PE＝4k，BC＝BD＝10﹣4k，再根据相似三角形对应边成比例列式求出k＝1然后在Rt △BDO中，利用勾股定理列式求解即可．【解答】（1）证明：∵∠C＝90°，∠BAP＝90°∴∠CBO+∠BOC＝90°，∠ABP+∠APB＝90°，又∵∠CBO＝∠ABP，∴∠BOC＝∠APB，∵∠BOC＝∠AOP，∴∠AOP＝∠APB，∴AP＝AO；（2）证明：如图，过点O作OD⊥AB于D，∵∠CBO＝∠ABP，∴CO＝DO，∵AE＝OC，∴AE＝OD，∵∠AOD+∠OAD＝90°，∠P AE+∠OAD＝90°，∴∠AOD＝∠P AE，在△AOD和△P AE中，，∴△AOD≌△P AE（SAS），∴∠AEP＝∠ADO＝90°∴PE⊥AO；（3）解：设AE＝OC＝3k，∵AE＝AC，∴AC＝8k，∴OE＝AC﹣AE﹣OC＝2k，∴OA＝OE+AE＝5k．由（1）可知，AP＝AO＝5k．如图，过点O作OD⊥AB于点D，∵∠CBO＝∠ABP，∴OD＝OC＝3k．在Rt△AOD中，AD＝＝＝4k．∴BD＝AB﹣AD＝10﹣4k．∵OD∥AP，∴，即解得k＝1，∵AB＝10，PE＝AD，∴PE＝AD＝4K，BD＝AB﹣AD＝10﹣4k＝6，OD＝3在Rt△BDO中，由勾股定理得：BO＝＝＝3．【点评】本题考查了全等三角形的判定与性质，角平分线上的点到角的两边的距离相等的性质，勾股定理，相似三角形的判定与性质，（2）作辅助线构造出过渡线段DO并得到全等三角形是解题的关键，（3）利用相似三角形对应边成比例求出k＝1是解题的关键．17．如图，AD是⊙O的直径．（1）如图①，垂直于AD的两条弦B1C1，B2C2把圆周4等分，则∠B1的度数是22.5°，∠B2的度数是67.5°；（2）如图②，垂直于AD的三条弦B1C1，B2C2，B3C3把圆周6等分，分别求∠B1，∠B2，∠B3的度数；（3）如图③，垂直于AD的n条弦B1C1，B2C2，B3C3，…，B n∁n把圆周2n等分，请你用含n的代数式表示∠B n的度数（只需直接写出答案）．【分析】根据条件可以先求出圆的各段弧的度数，根据圆周角等于所对弧的度数的一半，就可以求出圆周角的度数．【解答】解：（1）垂直于AD的两条弦B1C1，B2C2把圆周4等分，则是圆的，因而度数是45°，因而∠B1的度数是22.5°，同理的度数是135度，因而，∠B2的度数是67.5°；（2）∵圆周被6等分∴＝＝＝360°÷6＝60°∵直径AD⊥B1C1∴＝＝30°，∴∠B1＝＝15°∠B2＝＝×（30°+60°）＝45°∠B3＝＝×（30°+60°+60°）＝75°；（3）B n∁n把圆周2n等分，则弧BnD的度数是：，则∠B n AD＝，在直角△AB n D中，．【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题，依据是圆周角等于所对弧的度数的一半．18．下框中是小明对一道题目的解答以及老师的批改．题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？解：设矩形蔬菜种植区域的宽为xm，则长为2xm，根据题意，得x•2x＝288．解这个方程，得x1＝﹣12（不合题意，舍去），x2＝12所以温室的长为2×12+3+1＝28（m），宽为12+1+1＝14（m）答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．结果为何正确呢？（1）请指出小明解答中存在的问题，并补充缺少的过程：变化一下会怎样…（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB＝2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．【分析】（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以应设矩形蔬菜种植区域的宽为xm，则长为2xm，然后由题意得，矩形蔬菜种植区域的长与宽之比为2：1，再利用小明的解法求解即可；（2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得，即，然后利用比例的性质，即可求得答案．【解答】解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由．在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：设温室的宽为xm，则长为2xm．则矩形蔬菜种植区域的宽为（x﹣1﹣1）m，长为（2x﹣3﹣1）m．∵，∴矩形蔬菜种植区域的长与宽之比为2：1；（2）要使矩形A′B′C′D′∽矩形ABCD，就要，即，即，即2AB﹣2（b+d）＝2AB﹣（a+c），∴a+c＝2（b+d），即．【点评】此题考查了相似多边形的性质．此题属于阅读性题目，注意理解题意，读懂题目是解此题的关键．19．二次函数y＝ax2+bx+c图象的一部分如图所示，则a的取值范围是﹣1＜a＜0．【分析】由抛物线的开口方向判断a的符号，由抛物线与y轴的交点得出c的值，然后根据图象经过的点的情况进行推理，进而推出所得结论．【解答】解：抛物线开口向下，a＜0，图象过点（0，1），c＝1，图象过点（1，0），a+b+c＝0，∴b＝﹣（a+c）＝﹣（a+1）．由题意知，当x＝﹣1时，应有y＞0，∴a﹣b+c＞0，∴a+（a+1）+1＞0，∴a＞﹣1，∴实数a的取值范围是﹣1＜a＜0．【点评】根据开口判断a的符号，根据与x轴，y轴的交点判断c的值以及b用a表示出的代数式．难点是推断出当x＝﹣1时，应有y＞0．20．今年，我国政府为减轻农民负担，决定在5年内免去农业税．某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同．（1）求降低的百分率；（2）若小红家有4人，明年小红家减少多少农业税？（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税？【分析】（1）设降低的百分率为x，则降低一次后的数额是25（1﹣x），再在这个数的基础上降低x，则变成25（1﹣x）（1﹣x）即25（1﹣x）2，据此即可列方程求解；（2）每人减少的税额是25x，则4个人的就是4×25x，代入（1）中求得的x的值，即可求解；（3）每个人减少的税额是25x，乘以总人数16000即可求解．【解答】解：（1）设降低的百分率为x，依题意有，25（1﹣x）2＝16，解得，x1＝0.2＝20%，x2＝1.8（舍去）；（2）小红全家少上缴税25×20%×4＝20（元）；（3）全乡少上缴税16000×25×20%＝80 000（元）．答：降低的增长率是20%，明年小红家减少的农业税是20元，该乡农民明年减少的农业税是80 000元．【点评】本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2＝b．21．如图，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连接DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．（1）求y关于x的函数关系式；（2）若m＝8，求x为何值时，y的值最大，最大值是多少？（3）若y＝，要使△DEF为等腰三角形，m的值应为多少？【分析】（1）利用互余关系找角相等，证明△BEF∽△CDE，根据对应边的比相等求函数关系式；（2）把m的值代入函数关系式，再求二次函数的最大值；（3）∵∠DEF＝90°，只有当DE＝EF时，△DEF为等腰三角形，把条件代入即可．【解答】解：（1）∵EF⊥DE，∴∠BEF＝90°﹣∠CED＝∠CDE，又∠B＝∠C＝90°，∴△BEF∽△CDE，∴＝，即＝，解得y＝；（2）由（1）得y＝，将m＝8代入，得y＝﹣x2+x＝﹣（x2﹣8x）＝﹣（x﹣4）2+2，所以当x＝4时，y取得最大值为2；（3）∵∠DEF＝90°，∴只有当DE＝EF时，△DEF为等腰三角形，∴△BEF≌△CDE，∴BE＝CD＝m，此时m＝8﹣x，解方程＝，得x＝6，或x＝2，当x＝2时，m＝6，当x＝6时，m＝2．【点评】本题把相似三角形与求二次函数解析式联系起来，在解题过程中，充分运用相似三角形对应边的比相等，建立函数关系式．22．在△ABC中，AB＝AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F．设DE＝a，DF＝b，且实数a，b满足9a2﹣24ab+16b2＝0，并有＝2566，∠A使得方程x2﹣x•sin A+sin A﹣＝0有两个相等的实数根．（1）试求实数a，b的值；（2）试求线段BC的长．【分析】（1）由题意可知：2a2b＝2566，则2a2b＝248，则a2b＝48．化简9a2﹣24ab+16b2＝0得：（3a﹣4b）2＝0，则3a﹣4b＝0，即3a＝4b，则根据，可求得a与b的值；（2）要求BC的长需求出BD和CD的长，知BD、CD分别是直角三角形BDE和直角三角形CDF中的斜边．又知在△ABC中，AB＝AC，则∠B＝∠C，则根据三角函数只要知道∠B或∠C的读数即可，要求∠B或∠C的读数需求的∠A的读数，根据判别式可以求得∠A的读数．【解答】解：（1）由条件有，解得；（2）又由关于x的方程的判别式△＝sin2A﹣sin A+＝（sin A﹣）2＝0，则sin A＝，而∠A为三角形的一个内角，所以∠A1＝60°或∠A2＝120° 2分当∠A＝60°时，△ABC为正三角形，∠B＝∠C＝60°于是分别在Rt△BDE和Rt△CDF中有BD＝，CD＝所以BC＝BD+DC＝．当∠A＝120°时，△ABC为等腰三角形，∠B＝∠C＝30°同上方法可得BC＝14． 3分所以线段BC的长应为或14．【点评】考查了解直角三角形以及判别式的应用．23．某市城建部门经过长期市场调查发现，该市年新建商品房面积P（万平方米）与市场新房均价x（千元/平方米）存在函数关系P＝25x；年新房销售面积Q（万平方米）与市场新房均价x（千元/平方米）的函数关系为Q＝﹣10；（1）如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；（2）在（1）的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少？变化了多少？结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议．（字数不超过50）【分析】（1）根据“新建商品房的面积与年新房销售面积相等”作为相等关系求x的值即可；（2）分别求算出市场新房均价上涨1千元后的新建商品房面积P，年新房销售面积Q再来求算其变化的量和积压的情况．【解答】解：（1）根据题意得：25x＝﹣10，解得x1＝2，x2＝﹣（舍去），则Q＝﹣10＝50万平方米，所以市场新房均价为2千元．则年新房销售总额为2000×500000＝10亿元．。

中考数学选填压轴题练习一．根的判别式（共1小题）1．（2023•广州）已知关于x的方程x2﹣（2k﹣2）x+k2﹣1＝0有两个实数根，则的化简结果是（）A．﹣1B．1C．﹣1﹣2k D．2k﹣3【分析】首先根据关于x的方程x2﹣（2k﹣2）x+k2﹣1＝0有两个实数根，得判别式Δ＝[﹣（2k﹣2）]2﹣4×1×（k2﹣1）≥0，由此可得k≤1，据此可对进行化简．【解答】解：∵关于x的方程x2﹣（2k﹣2）x+k2﹣1＝0有两个实数根，∴判别式Δ＝[﹣（2k﹣2）]2﹣4×1×（k2﹣1）≥0，整理得：﹣8k+8≥0，∴k≤1，∴k﹣1≤0，2﹣k＞0，∴＝﹣（k﹣1）﹣（2﹣k）＝﹣1．故选：A．二．函数的图象（共1小题）2．（2023•温州）【素材1】某景区游览路线及方向如图1所示，①④⑥各路段路程相等，⑤⑦⑧各路段路程相等，②③两路段路程相等．【素材2】设游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④⑤⑥⑦⑧用时3小时25分钟；小州游路线①②⑧，他离入口的路程s与时间t的关系（部分数据）如图2所示，在2100米处，他到出口还要走10分钟．【问题】路线①③⑥⑦⑧各路段路程之和为（）A．4200米B．4800米C．5200米D．5400米【分析】设①④⑥各路段路程为x米，⑤⑦⑧各路段路程为y米，②③各路段路程为z米，由题意及图象可知，然后根据“游玩行走速度恒定，经过每个景点都停留20分钟，小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解．【解答】解：由图象可知：小州游玩行走的时间为75+10﹣40＝45（分钟），小温游玩行走的时间为205﹣100＝105（分钟），设①④⑥各路段路程为x米，⑤⑦⑧各路段路程为y米，②③各路段路程为z米由图象可得：，解得：x+y+z＝2700，∴游玩行走的速度为：（2700﹣2100）÷10＝60 （米/分），由于游玩行走速度恒定，则小温游路线①④⑤⑥⑦⑧的路程为：3x+3y＝105×60＝6300，∴x+y＝2100，∴路线①③⑥⑦⑧各路段路程之和为：2x+2y+z＝x+y+z+x+y＝2700+2100＝4800（米）．故选：B．三．动点问题的函数图象（共1小题）3．（2023•河南）如图1，点P从等边三角形ABC的顶点A出发，沿直线运动到三角形内部一点，再从该点沿直线运动到顶点B．设点P运动的路程为，图2是点P运动时y随x变化的关系图象，则等边三角形ABC的边长为（）A．6B．3C．D．【分析】如图，令点P从顶点A出发，沿直线运动到三角形内部一点O，再从点O沿直线运动到顶点B，结合图象可知，当点P在AO上运动时，PB＝PC，AO＝，易知∠BAO＝∠CAO＝30°，当点P在OB上运动时，可知点P到达点B时的路程为，可知AO＝OB＝，过点O作OD⊥AB，解直角三角形可得AD＝AO•cos30°，进而得出等边三角形ABC的边长．【解答】解：如图，令点P从顶点A出发，沿直线运动到三角形内部一点O，再从点O沿直线运动到顶点B，\结合图象可知，当点P在AO上运动时，，∴PB＝PC，，又∵△ABC为等边三角形，∴∠BAC＝60°，AB＝AC，∴△APB≌△APC（SSS），∴∠BAO＝∠CAO＝30°，当点P在OB上运动时，可知点P到达点B时的路程为，∴OB＝，即AO＝OB＝，∴∠BAO＝∠ABO＝30°，过点O作OD⊥AB，垂足为D，∴AD＝BD，则AD＝AO•cos30°＝3，∴AB＝AD+BD＝6，即等边三角形ABC的边长为6．故选：A．四．反比例函数系数k的几何意义（共1小题）4．（2023•宁波）如图，点A，B分别在函数y＝（a＞0）图象的两支上（A在第一象限），连结AB交x 轴于点C．点D，E在函数y＝（b＜0，x＜0）图象上，AE∥x轴，BD∥y轴，连结DE，BE．若AC ＝2BC，△ABE的面积为9，四边形ABDE的面积为14，则a﹣b的值为12，a的值为9．【分析】依据题意，设A（m，），再由AE∥x轴，BD∥y轴，AC＝2BC，可得B（﹣2m，﹣），D （﹣2m，﹣），E（，），再结合△ABE的面积为9，四边形ABDE的面积为14，即可得解．【解答】解：设A（m，），∵AE∥x轴，且点E在函数y＝上，∴E（，）．∵AC＝2BC，且点B在函数y＝上，∴B（﹣2m，﹣）．∵BD∥y轴，点D在函数y＝上，∴D（﹣2m，﹣）．∵△ABE的面积为9，∴S△ABE＝AE×（+）＝（m﹣）（+）＝m••＝＝9．∴a﹣b＝12．∵△ABE的面积为9，四边形ABDE的面积为14，∴S△BDE＝DB•（+2m）＝（﹣+）（）m＝（a﹣b）••（）•m＝3（）＝5．∴a＝﹣3b．又a﹣b＝12．∴a＝9．故答案为：12，9．五．反比例函数图象上点的坐标特征（共2小题）5．（2023•德州）如图，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（6，3），D是OA的中点，AC，BD交于点E，函数的图象过点B．E．且经过平移后可得到一个反比例函数的图象，则该反比例函数的解析式（）A．y＝﹣B．C．D．【分析】先根据函数图象经过点B和点E，求出a和b，再由所得函数解析式即可解决问题．【解答】解：由题知，A（6，0），B（6，3），C（0，3），令直线AC的函数表达式为y1＝k1x+b1，则，解得，所以．又因为点D为OA的中点，所以D（3，0），同理可得，直线BD的函数解析式为y2＝x﹣3，由得，x＝4，则y＝4﹣3＝1，所以点E坐标为（4，1）．将B，E两点坐标代入函数解析式得，，解得．所以，则，将此函数图象向左平移3个单位长度，再向下平移4个单位长度，所得图象的函数解析式为：．故选：D．6．如图，O是坐标原点，Rt△OAB的直角顶点A在x轴的正半轴上，AB＝2，∠AOB＝30°，反比例函数y＝（k＞0）的图象经过斜边OB的中点C．（1）k＝；（2）D为该反比例函数图象上的一点，若DB∥AC，则OB2﹣BD2的值为4．【分析】（1）根据直角三角形的性质，求出A、B两点坐标，作出辅助线，证得△OPC≌△APC（HL），利用勾股定理及待定系数法求函数解析式即可解答．（2）求出AC、BD的解析式，再联立方程组，求得点D的坐标，分两种情况讨论即可求解．【解答】解：（1）在Rt△OAB中，AB＝2，∠AOB＝30°，∴，∴，∵C是OB的中点，∴OC＝BC＝AC＝2，如图，过点C作CP⊥OA于P，∴△OPC≌△APC（HL），∴，在Rt△OPC中，PC＝，∴C（，1）．∵反比例函数y＝（k＞0）的图象经过斜边OB的中点C，∴，解得k＝．故答案为：．（2）设直线AC的解析式为y＝k1x+b（k≠0），则，解得，∴AC的解析式为y＝﹣x+2，∵AC∥BD，∴直线BD的解析式为y＝﹣x+4，∵点D既在反比例函数图象上，又在直线BD上，∴联立得，解得，，当D的坐标为（2+3，）时，BD2＝＝9+3＝12，∴OB2﹣BD2＝16﹣12＝4；当D的坐标为（2﹣3，）时，BD2＝+＝9+3＝12，∴OB2﹣BD2＝16﹣12＝4；综上，OB2﹣BD2＝4．故答案为：4．六．反比例函数与一次函数的交点问题（共1小题）7．（2023•湖州）已知在平面直角坐标系中，正比例函数y＝k1x（k1＞0）的图象与反比例函数（k2＞0）的图象的两个交点中，有一个交点的横坐标为1，点A（t，p）和点B（t+2，q）在函数y＝k1x的图象上（t≠0且t≠﹣2），点C（t，m）和点D（t+2，n）在函数的图象上．当p﹣m与q﹣n的积为负数时，t的取值范围是（）A．或B．或C．﹣3＜t＜﹣2或﹣1＜t＜0D．﹣3＜t＜﹣2或0＜t＜1【分析】将交点的横坐标1代入两个函数，令二者函数值相等，得k1＝k2．令k1＝k2＝k，代入两个函数表达式，并分别将点A、B的坐标和点C、D的坐标代入对应函数，进而分别求出p﹣m与q﹣n的表达式，代入解不等式（p﹣m）（q﹣n）＜0并求出t的取值范围即可．【解答】解：∵y＝k1x（k1＞0）的图象与反比例函数（k2＞0）的图象的两个交点中，有一个交点的横坐标为1，∴k1＝k2．令k1＝k2＝k（k＞0），则y＝k1x＝kx，＝．将点A（t，p）和点B（t+2，q）代入y＝kx，得；将点C（t，m）和点D（t+2，n）代入y＝，得．∴p﹣m＝kt﹣＝k（t﹣），q﹣n＝k（t+2）﹣＝k（t+2﹣），∴（p﹣m）（q﹣n）＝k2（t﹣）（t+2﹣）＜0，∴（t﹣）（t+2﹣）＜0．∵（t﹣）（t+2﹣）＝•＝＜0，∴＜0，∴t（t﹣1）（t+2）（t+3）＜0．①当t＜﹣3时，t（t﹣1）（t+2）（t+3）＞0，∴t＜﹣3不符合要求，应舍去．②当﹣3＜t＜﹣2时，t（t﹣1）（t+2）（t+3）＜0，∴﹣3＜t＜﹣2符合要求．③当﹣2＜t＜0时，t（t﹣1）（t+2）（t+3）＞0，∴﹣2＜t＜0不符合要求，应舍去．④当0＜t＜1时，t（t﹣1）（t+2）（t+3）＜0，∴0＜t＜1符合要求．⑤当t＞1时，t（t﹣1）（t+2）（t+3）＞0，∴t＞1不符合要求，应舍去．综上，t的取值范围是﹣3＜t＜﹣2或0＜t＜1．故选：D．七．二次函数图象与系数的关系（共3小题）8．（2023•乐至县）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，且过点（1，0）．现有以下结论：①abc＜0；②5a+c＝0；③对于任意实数m，都有2b+bm≤4a﹣am2；④若点A（x1，y1）、B（x2，y2）是图象上任意两点，且|x1+2|＜|x2+2|，则y1＜y2，其中正确的结论是（）A．①②B．②③④C．①②④D．①②③④【分析】根据题意和函数图象，利用二次函数的性质，可以判断各个小题中的结论是否正确，从而可以解答本题．【解答】解：由图象可得，a＞0，b＞0，c＜0，∴abc＜0，故①正确，∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，且过点（1，0）．∴﹣＝﹣2，a+b+c＝0，∴b＝4a，∴a+b+c＝a+4a+c＝0，故5a+c＝0，故②正确，∵当x＝﹣2时，y＝4a﹣2b+c取得最小值，∴am2+bm+c≥4a﹣2b+c，即2b+bm≥4a﹣am2（m为任意实数），故③错误，∵抛物线开口向上，对称轴为直线x＝﹣2，若点A（x1，y1）、B（x2，y2）是图象上任意两点，且|x1+2|＜|x2+2|，∴y1＜y2，故④正确；故选：C．9．（2023•丹东）抛物线y＝ax2+bx+c（a≠0）与x轴的一个交点为A（﹣3，0），与y轴交于点C，点D是抛物线的顶点，对称轴为直线x＝﹣1，其部分图象如图所示，则以下4个结论：①abc＞0；②E（x1，y1），F（x2，y2）是抛物线y＝ax2+bx（a≠0）上的两个点，若x1＜x2，且x1+x2＜﹣2，则y1＜y2；③在x轴上有一动点P，当PC+PD的值最小时，则点P的坐标为；④若关于x的方程ax2+b（x﹣2）+c ＝﹣4（a≠0）无实数根，则b的取值范围是b＜1．其中正确的结论有（）A．1个B．2个C．3个D．4个【分析】根据所给函数图象可得出a，b，c的正负，再结合抛物线的对称性和增减性即可解决问题．【解答】解：根据所给函数图象可知，a＞0，b＞0，c＜0，所以abc＜0，故①错误．因为抛物线y＝ax2+bx的图象可由抛物线y＝ax2+bx+c的图象沿y轴向上平移|c|个单位长度得到，所以抛物线y＝ax2+bx的增减性与抛物线y＝ax2+bx+c的增减性一致．则当x＜﹣1时，y随x的增大而减小，又x1＜x2，且x1+x2＜﹣2，若x2＜﹣1，则E，F两点都在对称轴的左侧，此时y1＞y2．故②错误．作点C关于x轴的对称点C′，连接C′D与x轴交于点P，连接PC，此时PC+PD的值最小．将A（﹣3，0）代入二次函数解析式得，9a﹣3b+c＝0，又，即b＝2a，所以9a﹣6a+c＝0，则c＝﹣3a．又抛物线与y轴的交点坐标为C（0，c），则点C坐标为（0，﹣3a），所以点C′坐标为（0，3a）．又当x＝﹣1时，y＝﹣4a，即D（﹣1，﹣4a）．设直线C′D的函数表达式为y＝kx+3a，将点D坐标代入得，﹣k+3a＝﹣4a，则k＝7a，所以直线C′D的函数表达式为y＝7ax+3a．将y＝0代入得，x＝．所以点P的坐标为（，0）．故③正确．将方程ax2+b（x﹣2）+c＝﹣4整理得，ax2+bx+c＝2b﹣4，因为方程没有实数根，所以抛物线y＝ax2+bx+c与直线y＝2b﹣4没有公共点，所以2b﹣4＜﹣4a，则2b﹣4＜﹣2b，解得b＜1，又b＞0，所以0＜b＜1．故④错误．所以正确的有③．故选：A．10．（2023•河北）已知二次函数y＝﹣x2+m2x和y＝x2﹣m2（m是常数）的图象与x轴都有两个交点，且这四个交点中每相邻两点间的距离都相等，则这两个函数图象对称轴之间的距离为（）A．2B．m2C．4D．2m2【分析】求出三个交点的坐标，再构建方程求解．【解答】解：令y＝0，则﹣x2+m2x＝0和x2﹣m2＝0，∴x＝0或x＝m2或x＝﹣m或x＝m，∵这四个交点中每相邻两点间的距离都相等，若m＞0，则m2＝2m，∴m＝2，若m＜0时，则m2＝﹣2m，∴m＝﹣2．∵抛物线y＝x2﹣m2的对称轴为直线x＝0，抛物线y＝﹣x2+m2x的对称轴为直线x＝，∴这两个函数图象对称轴之间的距离＝＝2．故选：A．八．二次函数图象上点的坐标特征（共1小题）11．（2023•广东）如图，抛物线y＝ax2+c经过正方形OABC的三个顶点A，B，C，点B在y轴上，则ac 的值为（）A．﹣1B．﹣2C．﹣3D．﹣4【分析】过A作AH⊥x轴于H，根据正方形的性质得到∠AOB＝45°，得到AH＝OH，利用待定系数法求得a、c的值，即可求得结论．【解答】解：过A作AH⊥x轴于H，∵四边形ABCO是正方形，∴∠AOB＝45°，∴∠AOH＝45°，∴AH＝OH，设A（m，m），则B（0，2m），∴，解得am＝﹣1，m＝，∴ac的值为﹣2，故选：B．九．二次函数与不等式（组）（共1小题）12．（2023•西宁）直线y1＝ax+b和抛物线（a，b是常数，且a≠0）在同一平面直角坐标系中，直线y1＝ax+b经过点（﹣4，0）．下列结论：①抛物线的对称轴是直线x＝﹣2；②抛物线与x轴一定有两个交点；③关于x的方程ax2+bx＝ax+b有两个根x1＝﹣4，x2＝1；④若a ＞0，当x＜﹣4或x＞1时，y1＞y2.其中正确的结论是（）A．①②③④B．①②③C．②③D．①④【分析】根据直线y1＝ax+b经过点（﹣4，0）．得到b＝4a，于是得到＝ax2+4ax，求得抛物线的对称轴是直线x＝﹣﹣＝2；故①正确；根据Δ＝16a2＞0，得到抛物线与x轴一定有两个交点，故②正确；把b＝4a，代入ax2+bx＝ax+b得到x2+3x﹣4＝0，求得x1＝﹣4，x2＝1；故③正确；根据a＞0，得到抛物线的开口向上，直线y1＝ax+b和抛物线交点横坐标为﹣4，1，于是得到结论．【解答】解：∵直线y1＝ax+b经过点（﹣4，0）．∴﹣4a+b＝0，∴b＝4a，∴＝ax2+4ax，∴抛物线的对称轴是直线x＝﹣﹣＝2；故①正确；∵＝ax2+4ax，∴Δ＝16a2＞0，∴抛物线与x轴一定有两个交点，故②正确；∵b＝4a，∴方程ax2+bx＝ax+b为ax2+4ax＝ax+4a得，整理得x2+3x﹣4＝0，解得x1＝﹣4，x2＝1；故③正确；∵a＞0，抛物线的开口向上，直线y1＝ax+b和抛物线交点横坐标为﹣4，1，∴当x＜﹣4或x＞1时，y1＜y2.故④错误，故选：B．一十．三角形中位线定理（共1小题）13．（2023•广州）如图，在Rt△ABC中，∠ACB＝90°，AB＝10，AC＝6，点M是边AC上一动点，点D，E分别是AB，MB的中点，当AM＝2.4时，DE的长是 1.2.若点N在边BC上，且CN＝AM，点F，G分别是MN，AN的中点，当AM＞2.4时，四边形DEFG面积S的取值范围是3≤S≤4．【分析】依据题意，根据三角形中位线定理可得DE＝AM＝1.2；设AM＝x，从而DE＝x，由DE∥AM，且DE＝AM，又FG∥AM，FG＝AM，进而DE∥FG，DE＝FG，从而四边形DEFG是平行四边形，结合题意可得DE边上的高为（4﹣x），故四边形DEFG面积S＝4x﹣x2，进而利用二次函数的性质可得S的取值范围．【解答】解：由题意，点D，E分别是AB，MB的中点，∴DE是三角形ABM的中位线．∴DE＝AM＝1.2．如图，设AM＝x，∴DE＝AM＝x．由题意得，DE∥AM，且DE＝AM，又FG∥AM，FG＝AM，∴DE∥FG，DE＝FG．∴四边形DEFG是平行四边形．由题意，GF到AC的距离是x，BC＝＝8，∴DE边上的高为（4﹣x）．∴四边形DEFG面积S＝2x﹣x2，＝﹣（x﹣4）2+4．∵2.4＜x≤6，∴3≤S≤4．故答案为：1.2；3≤S≤4．一十一．矩形的性质（共2小题）14．（2023•宁波）如图，以钝角三角形ABC的最长边BC为边向外作矩形BCDE，连结AE，AD，设△AED，△ABE，△ACD的面积分别为S，S1，S2，若要求出S﹣S1﹣S2的值，只需知道（）A．△ABE的面积B．△ACD的面积C．△ABC的面积D．矩形BCDE的面积【分析】作AG⊥ED于点G，交BC于点F，可证明四边形BFGE是矩形，AF⊥BC，可推导出S﹣S1﹣S2＝ED•AG﹣BE•EG﹣CD•DG＝ED•AG﹣FG•ED＝BC•AF＝S△ABC，所以只需知道S△ABC，就可求出S﹣S1﹣S2的值，于是得到问题的答案．【解答】解：作AG⊥ED于点G，交BC于点F，∵四边形BCDE是矩形，∴∠FBE＝∠BEG＝∠FGE＝90°，BC∥ED，BC＝ED，BE＝CD，∴四边形BFGE是矩形，∠AFB＝∠FGE＝90°，∴FG＝BE＝CD，AF⊥BC，∴S﹣S1﹣S2＝ED•AG﹣BE•EG﹣CD•DG＝ED•AG﹣FG•ED＝BC•AF＝S△ABC，∴只需知道S△ABC，就可求出S﹣S1﹣S2的值，故选：C．15．（2023•河南）矩形ABCD中，M为对角线BD的中点，点N在边AD上，且AN＝AB＝1．当以点D，M，N为顶点的三角形是直角三角形时，AD的长为2或1+．【分析】以点D，M，N为顶点的三角形是直角三角形时，分两种情况：如图1，当∠MND＝90°时，如图2，当∠NMD＝90°时，根据矩形的性质和等腰直角三角形的性质即可得到结论．【解答】解：以点D，M，N为顶点的三角形是直角三角形时，分两种情况：①如图1，当∠MND＝90°时，则MN⊥AD，∵四边形ABCD是矩形，∴∠A＝90°，∴MN∥AB，∵M为对角线BD的中点，∴AN＝DN，∵AN＝AB＝1，∴AD＝2AN＝2；如图2，当∠NMD＝90°时，则MN⊥BD，∵M为对角线BD的中点，∴BM＝DM，∴MN垂直平分BD，∴BN＝DN，∵∠A＝90°，AB＝AN＝1，∴BN＝AB＝，∴AD＝AN+DN＝1+，综上所述，AD的长为2或1+．故答案为：2或1+．一十二．正方形的性质（共2小题）16．如图，在边长为4的正方形ABCD中，点G是BC上的一点，且BG＝3GC，DE⊥AG于点E，BF∥DE，且交AG于点F，则tan∠EDF的值为（）A．B．C．D．【分析】由正方形ABCD的边长为4及BG＝3CG，可求出BG的长，进而求出AG的长，证△ADE∽△GAB，利用相似三角形对应边成比例可求得AE、DE的长，证△ABF≌△DAE，得AF＝DE，根据线段的和差求得EF的长即可．【解答】解：∵四边形ABCD是正方形，AB＝4，∴BC＝CD＝DA＝AB＝4，∠BAD＝∠ABC＝90°，AD∥BC，∴∠DAE＝∠AGB，∵BG＝3CG，∴BG＝3，∴在Rt△ABG中，AB2+BG2＝AG2，∴AG＝，∵DE⊥AG，∴∠DEA＝∠DEF＝∠ABC＝90°，∴△ADE∽△GAB，∴AD：GA＝AE：GB＝DE：AB，∴4：5＝AE：3＝DE：4，∴AE＝，DE＝，又∵BF∥DE，∴∠AFB＝∠DEF＝90°，又∵AB＝AD，∠DAE＝∠ABF（同角的余角相等），∴△ABF≌△DAE，∴AF＝DE＝，∴EF＝AF﹣AE＝，∴tan∠EDF＝，故选：A．17．（2023•湖州）如图，标号为①，②，③，④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD，相邻图形之间互不重叠也无缝隙，①和②分别是等腰Rt△ABE和等腰Rt△BCF，③和④分别是Rt△CDG和Rt△DAH，⑤是正方形EFGH，直角顶点E，F，G，H分别在边BF，CG，DH，AE上．（1）若EF＝3cm，AE+FC＝11cm，则BE的长是4cm．（2）若，则tan∠DAH的值是3．【分析】（1）将AE和FC用BE表示出来，再代入AE+FC＝11cm，即可求出BE的长；（2）由已知条件可以证明∠DAH＝∠CDG，从而得到tan∠DAH＝tan∠CDG，设AH＝x，DG＝5k，GH ＝4k，用x和k的式子表示出CG，再利用tan∠DAH＝tan∠CDG列方程，解出x，从而求出tan∠DAH 的值．【解答】解：（1）∵Rt△ABE和Rt△BCF都是等腰直角三角形，∴AE＝BE，BF＝CF，∵AE+FC＝11cm，∴BE+BF＝11cm，即BE+BE+EF＝11cm，即2BE+EF＝11cm，∵EF＝3cm，∴2BE+3cm＝11cm，∴BE＝4cm，故答案为：4；（2）设AH＝x，∵，∴可设DG＝5k，GH＝4k，∵四边形EFGH是正方形，∴HE＝EF＝FG＝GH＝4k，∵Rt△ABE和Rt△BCF都是等腰直角三角形，∴AE＝BE，BF＝CF，∠ABE＝∠CBF＝45°，∴CG＝CF+GF＝BF+4k＝BE+8k＝AH+12k＝x+12k，∠ABC＝∠ABE+∠CBF＝45°+45°＝90°，∵四边形ABCD对角互补，∴∠ADC＝90°，∴∠ADH+∠CDG＝90°，∵四边形EFGH是正方形，∴∠AHD＝∠CGD＝90°，∴∠ADH+∠DAH＝90°，∴∠DAH＝∠CDG，∴tan∠DAH＝tan∠CDG，∴，即，整理得：x2+12kx﹣45k2＝0，解得x1＝3k，x2＝﹣15k（舍去），∴tan∠DAH＝＝＝3．故答案为：3．一十三．正多边形和圆（共1小题）18．（2023•河北）将三个相同的六角形螺母并排摆放在桌面上，其俯视图如图1，正六边形边长为2且各有一个顶点在直线l上．两侧螺母不动，把中间螺母抽出并重新摆放后，其俯视图如图2，其中，中间正六边形的一边与直线l平行，有两边分别经过两侧正六边形的一个顶点．则图2中：（1）∠α＝30度；（2）中间正六边形的中心到直线l的距离为2（结果保留根号）．【分析】（1）作图后，结合正多边形的外角的求法即可得到结论；（2）把问题转化为图形问题，首先作出图形，标出相应的字母，把正六边形的中心到直线l的距离转化为求ON＝OM+BE，再根据正六边形的性质以及三角函数的定义，分别求出OM，BE即可．【解答】解：（1）作图如图所示，∵多边形是正六边形，∴∠ACB＝60°，∵BC∥直线l，∴∠ABC＝90°，∴α＝30°；故答案为：30°；（2）取中间正六边形的中心为O，作图如图所示，由题意得，AG∥BF，AB∥GF，BF⊥AB，∴四边形ABFG为矩形，∴AB＝GF，∵∠BAC＝∠FGH，∠ABC＝∠GFH＝90°，∴△ABC≌△GFH（SAS），∴BC＝FH，在Rt△PDE中，DE＝1，PE＝，由图1知AG＝BF＝2PE＝2，OM＝PE＝，∵，∴，∴，∵，∴，∴．∴中间正六边形的中心到直线l的距离为2，故答案为：2．一十四．扇形面积的计算（共1小题）19．（2023•温州）图1是4×4方格绘成的七巧板图案，每个小方格的边长为，现将它剪拼成一个“房子”造型（如图2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形CDEF作为题字区域（点A，E，D，B在圆上，点C，F在AB上），形成一幅装饰画，则圆的半径为5．若点A，N，M在同一直线上，AB∥PN，DE＝EF，则题字区域的面积为．【分析】根据不共线三点确定一个圆，根据对称性得出圆心的位置，进而垂径定理、勾股定理求得r，连接OE，取ED的中点T，连接OT，在Rt△OET中，根据勾股定理即可求解．【解答】解：如图所示，依题意，GH＝2＝GQ，∵过左侧的三个端点Q，K，L作圆，QH＝HL＝4，又NK⊥QL，∴O在KN上，连接OQ，则OQ为半径，∵OH＝r﹣KH＝r﹣2，在Rt△OHQ中，OH2+QH2＝QO2，∴（r﹣2）2+42＝r2，解得：r＝5；连接OE，取ED的中点T，连接OT，交AB于点S，连接PB，AM，过点O作OU⊥AM于点U.连接OA．由△OUN∽△NPM，可得＝＝，∴OU＝．MN＝2，∴NU＝，∴AU＝＝，∴AN＝AU﹣NU＝2，∴AN＝MN，∵AB∥PN，∴AB⊥OT，∴AS＝SB，∴NS∥BM，∴NS∥MP，∴M，P，B共线，又NB＝NA，∴∠ABM＝90°，∵MN＝NB，NP⊥MP，∴MP＝PB＝2，∴NS＝MB＝2，∵KH+HN＝2+4＝6，∴ON＝6﹣5＝1，∴OS＝3，∵，设EF＝ST＝a，则，在Rt△OET中，OE2＝OT2+TE2，即，整理得5a2+12a﹣32＝0，即（a+4）（5a﹣8）＝0，解得：或a＝﹣4，∴题字区域的面积为．故答案为：．一十五．轴对称-最短路线问题（共1小题）20．（2023•安徽）如图，E是线段AB上一点，△ADE和△BCE是位于直线AB同侧的两个等边三角形，点P，F分别是CD，AB的中点．若AB＝4，则下列结论错误的是（）A．P A+PB的最小值为3B．PE+PF的最小值为2C．△CDE周长的最小值为6D．四边形ABCD面积的最小值为3【分析】延长AD，BC交于M，过P作直线l∥AB，由△ADE和△BCE是等边三角形，可得四边形DECM 是平行四边形，而P为CD中点，知P为EM中点，故P在直线l上运动，作A关于直线l的对称点A'，连接A'B，当P运动到A'B与直线l的交点，即A'，P，B共线时，P A+PB＝P A'+PB最小，即可得P A+PB 最小值A'B＝＝2，判断选项A错误；由PM＝PE，即可得当M，P，F共线时，PE+PF 最小，最小值为MF的长度，此时PE+PF的最小值为2，判断选项B正确；过D作DK⊥AB于K，过C作CT⊥AB于T，由△ADE和△BCE是等边三角形，得KT＝KE+TE＝AB＝2，有CD≥2，故△CDE周长的最小值为6，判断选项C正确；设AE＝2m，可得S四边形ABCD＝（m﹣1）2+3，即知四边形ABCD面积的最小值为3，判断选项D正确．【解答】解：延长AD，BC交于M，过P作直线l∥AB，如图：∵△ADE和△BCE是等边三角形，∴∠DEA＝∠MBA＝60°，∠CEB＝∠MAB＝60°，∴DE∥BM，CE∥AM，∴四边形DECM是平行四边形，∵P为CD中点，∴P为EM中点，∵E在线段AB上运动，∴P在直线l上运动，由AB＝4知等边三角形ABM的高为2，∴M到直线l的距离，P到直线AB的距离都为，作A关于直线l的对称点A'，连接A'B，当P运动到A'B与直线l的交点，即A'，P，B共线时，P A+PB ＝P A'+PB最小，此时P A+PB最小值A'B＝＝＝2，故选项A错误，符合题意；∵PM＝PE，∴PE+PF＝PM+PF，∴当M，P，F共线时，PE+PF最小，最小值为MF的长度，∵F为AB的中点，∴MF⊥AB，∴MF为等边三角形ABM的高，∴PE+PF的最小值为2，故选项B正确，不符合题意；过D作DK⊥AB于K，过C作CT⊥AB于T，如图，∵△ADE和△BCE是等边三角形，∴KE＝AE，TE＝BE，∴KT＝KE+TE＝AB＝2，∴CD≥2，∴DE+CE+CD≥AE+BE+2，即DE+CE+CD≥AB+2，∴DE+CE+CD≥6，∴△CDE周长的最小值为6，故选项C正确，不符合题意；设AE＝2m，则BE＝4﹣2m，∴AK＝KE＝m，BT＝ET＝2﹣m，DK＝AK＝m，CT＝BT＝2﹣m，∴S△ADK＝m•m＝m2，S△BCT＝（2﹣m）（2﹣m）＝m2﹣2m+2，S梯形DKTC ＝（m+2﹣m）•2＝2，∴S四边形ABCD＝m2+m2﹣2m+2+2＝m2﹣2m+4＝（m﹣1）2+3，∴当m＝1时，四边形ABCD面积的最小值为3，故选项D正确，不符合题意；故选：A．一十六．翻折变换（折叠问题）（共2小题）21．（2023•乐至县）如图，在平面直角坐标系xOy中，边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动，将△ABC沿BC所在直线翻折得到△DBC，则OD的最大值为+1．【分析】过点D作DF⊥AB，交AB延长线于点F，取AB的中点E，连接DE，OE，OD，在Rt△ABO 中利用斜边中线性质求出OE，根据OE+DE≥OD确定当D、O、E三点共线时OD最大，最大值为OD ＝OE+DE．【解答】解：如图，过点D作DF⊥AB，交AB延长线于点F，取AB的中点E，连接DE，OE，OD，∵等边三角形ABC的边长为2，∴AB＝2，∠ABC＝60°，由翻折可知：∠DBC＝∠ABC＝60°，DB＝AB＝2，∴∠DBF＝60°，∵DF⊥AB，∴∠DFB＝90°，∴∠BDF＝30°，∴BF＝BD＝1，∴DF＝BF＝，∵E是AB的中点，∴AE＝BE＝OE＝AB＝1，∴EF＝BE+BF＝2，∴DE＝＝＝，∴OD≤DE+OE＝+1，∴当D、E、O三点共线时OD最大，最大值为+1．故答案为：+1．22．（2023•南京）如图，在菱形纸片ABCD中，点E在边AB上，将纸片沿CE折叠，点B落在B′处，CB′⊥AD，垂足为F．若CF＝4cm，FB′＝1cm，则BE＝cm．【分析】作EH⊥BC于点H，由CF＝4cm，FB′＝1cm，求得B′C＝5cm，由折叠得BC＝B′C＝5cm，由菱形的性质得BC∥AD，DC＝BC＝5cm，∠B＝∠D，因为CB′⊥AD于点F，所以∠BCB′＝∠CFD ＝90°，则∠BCE＝∠B′CE＝45°，DF＝＝3cm，所以∠HEC＝∠BCE＝45°，则CH＝EH，由＝sin B＝sin D＝，＝cos B＝cos D＝，得CH＝EH＝BE，BH＝BE，于是得BE+BE ＝5，则BE＝cm．【解答】解：作EH⊥BC于点H，则∠BHE＝∠CHE＝90°，∵CF＝4cm，FB′＝1cm，∴B′C＝CF+FB′＝4+1＝5（cm），由折叠得BC＝B′C＝5cm，∠BCE＝∠B′CE，∵四边形ABCD是菱形，∴BC∥AD，DC＝BC＝5cm，∠B＝∠D，∵CB′⊥AD于点F，∴∠BCB′＝∠CFD＝90°，∴∠BCE＝∠B′CE＝∠BCB′＝×90°＝45°，DF＝＝＝3（cm），∴∠HEC＝∠BCE＝45°，∴CH＝EH，∵＝sin B＝sin D＝＝，＝cos B＝cos D＝＝，∴CH＝EH＝BE，BH＝BE，∴BE+BE＝5，∴BE＝cm，故答案为：．一十七．旋转的性质（共1小题）23．（2023•西宁）如图，在矩形ABCD中，点P在BC边上，连接P A，将P A绕点P顺时针旋转90°得到P A′，连接CA′，若AD＝9，AB＝5，CA′＝2，则BP＝2．【分析】过A′点作A′H⊥BC于H点，如图，根据旋转的性质得到P A＝P A′，再证明△ABP≌△PHA′得到PB＝A′H，PH＝AB＝5，设PB＝x，则A′H＝x，CH＝4﹣x，然后在Rt△A′CH中利用勾股定理得到x2+（4﹣x）2＝（2）2，于是解方程求出x即可．【解答】解：过A′点作A′H⊥BC于H点，如图，∵四边形ABCD为矩形，∴BC＝AD＝9，∠B＝90°，∵将P A绕点P顺时针旋转90°得到P A′，∴P A＝P A′，∵∠P AB+∠APB＝90°，∠APB+∠A′PH＝90°，∴∠P AB＝∠A′PH，在△ABP和△PHA′中，，∴△ABP≌△PHA′（AAS），∴PB＝A′H，PH＝AB＝5，设PB＝x，则A′H＝x，CH＝9﹣x﹣5＝4﹣x，在Rt△A′CH中，x2+（4﹣x）2＝（2）2，解得x1＝x2＝2，即BP的长为2．故答案为：2．一十八．相似三角形的判定与性质（共2小题）24．（2023•杭州）如图，在△ABC中，AB＝AC，∠A＜90°，点D，E，F分别在边AB，BC，CA上，连接DE，EF，FD，已知点B和点F关于直线DE对称．设＝k，若AD＝DF，则＝（结果用含k的代数式表示）．【分析】方法一：先根据轴对称的性质和已知条件证明DE∥AC，再证△BDE∽△BAC，推出EC＝k•AB，通过证明△ABC∽△ECF，推出CF＝k2•AB，即可求出的值．方法二：证明AD＝DF＝BD，可得BF⊥AC，设AB＝AC＝1，BC＝k，CF＝x，则AF＝1﹣x，利用勾股定理列方程求出x的值，进而可以解决问题．【解答】解：方法一：∵点B和点F关于直线DE对称，∴DB＝DF，∵AD＝DF，∴AD＝DB，∵AD＝DF，∴∠A＝∠DF A，∵点B和点F关于直线DE对称，∴∠BDE＝∠FDE，∵∠BDE+∠FDE＝∠BDF＝∠A+∠DF A，∴∠FDE＝∠DF A，∴DE∥AC，∴∠C＝∠DEB，∠DEF＝∠EFC，∵点B和点F关于直线DE对称，∴∠DEB＝∠DEF，∴∠C＝∠EFC，∵AB＝AC，∴∠C＝∠B，∵∠ACB＝∠EFC，∴△ABC∽△ECF，∴＝，∵DE∥AC，∴∠BDE＝∠A，∠BED＝∠C，∴△BDE∽△BAC，∴＝＝，∴EC＝BC，∵＝k，∴BC＝k•AB，∴EC＝k•AB，∴＝，∴CF＝k2•AB，∴＝＝＝＝．方法二：如图，连接BF，∵点B和点F关于直线DE对称，∴DB＝DF，∵AD＝DF，∴AD＝DB＝DF，∴BF⊥AC，设AB＝AC＝1，则BC＝k，设CF＝x，则AF＝1﹣x，由勾股定理得，AB2﹣AF2＝BC2﹣CF2，∴12﹣（1﹣x）2＝k2﹣x2，∴x＝，∴AF＝1﹣x＝，∴＝．故答案为：．25．（2023•广东）边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上（如图），则图中阴影部分的面积为15．【分析】根据相似三角形的性质，利用相似比求出梯形的上底和下底，用面积公式计算即可．【解答】解：如图，∵BF∥DE，∴△ABF∽△ADE，∴＝，∵AB＝4，AD＝4+6+10＝20，DE＝10，∴＝，∴BF＝2，∴GF＝6﹣2＝4，∵CK∥DE，∴△ACK∽△ADE，∴＝，∵AC＝4+6＝10，AD＝20，DE＝10，∴＝，∴CK＝5，∴HK＝6﹣5＝1，∴阴影梯形的面积＝（HK+GF）•GH＝（1+4）×6＝15．故答案为：15．一十九．相似三角形的应用（共1小题）26．（2023•南京）如图，不等臂跷跷板AB的一端A碰到地面时，另一端B到地面的高度为60cm；当AB 的一端B碰到地面时，另一端A到地面的高度为90cm，则跷跷板AB的支撑点O到地面的高度OH是（）A．36cm B．40cm C．42cm D．45cm【分析】过点B作BC⊥AH，垂足为C，再证明A字模型相似△AOH∽△ABC，从而可得＝，过点A作AD⊥BH，垂足为D，然后证明A字模型相似△ABD∽△OBH，从而可得＝，最后进行计算即可解答．【解答】解：如图：过点B作BC⊥AH，垂足为C，∵OH⊥AC，BC⊥AC，∴∠AHO＝∠ACB＝90°，∵∠BAC＝∠OAH，∴△AOH∽△ABC，∴＝，∴＝，如图：过点A作AD⊥BH，垂足为D，∵OH⊥BD，AD⊥BD，∴∠OHB＝∠ADB＝90°，∵∠ABD＝∠OBH，∴△ABD∽△OBH，∴＝，∴＝，∴+＝+，∴+＝，∴+＝1，解得：OH＝36，∴跷跷板AB的支撑点O到地面的高度OH是36cm，故选：A．二十．解直角三角形（共1小题）27．（2023•丹东）如图，在平面直角坐标系中，点O是坐标原点，已知点A（3，0），B（0，4），点C在x 轴负半轴上，连接AB，BC，若tan∠ABC＝2，以BC为边作等边三角形BCD，则点C的坐标为（﹣2，0）；点D的坐标为（﹣1﹣2，2+）或（﹣1+2，2﹣）．【分析】过点C作CE⊥AB于E，先求处AB＝5，再设BE＝t，由tan∠ABC＝2得CE＝2t，进而得BC ＝，由三角形的面积公式得S△ABC＝AC•OB＝AB•CE，即5×2t＝4×（3+OC），则OC＝﹣3，然后在Rt△BOC中由勾股定理得，由此解出t1＝2，t2＝10（不合题意，舍去），此时OC＝﹣3＝2，故此可得点C的坐标；设点D的坐标为（m，n），由两点间的距离公式得：BC2＝20，BD2＝（m﹣0）2+（n﹣4）2，CD2＝（m+2）2+（n﹣0）2，由△BCD为等边三角形得，整理：，②﹣①整理得m＝3﹣2n，将m＝3﹣2n代入①整理得n2﹣4n+1＝0，解得n＝，进而再求出m即可得点D的坐标．【解答】解：过点C作CE⊥AB于E，如图：∵点A（3，0），B（0，4），由两点间的距离公式得：AB＝＝5，设BE＝t，∵tan∠ABC＝2，在Rt△BCE中，tan∠ABC＝，∴＝2，∴CE＝2t，由勾股定理得：BC＝＝t，∵CE⊥AB，OB⊥AC，AC＝OC+OA＝3+OC，∴S△ABC＝AC•OB＝AB•CE，即：5×2t＝4×（3+OC），∴OC＝﹣3，在Rt△BOC中，由勾股定理得：BC2﹣OB2＝OC2，即，整理得：t2﹣12t+20＝0，解得：t1＝2，t2＝10（不合题意，舍去），∴t＝2，此时OC＝﹣3＝2，∴点C的坐标为（﹣2，0），设点D的坐标为（m，n），由两点间的距离公式得：BC2＝（﹣2﹣0）2+（0﹣4）2＝20，BD2＝（m﹣0）2+（n﹣4）2，CD2＝（m+2）2+（n﹣0）2，∵△BCD为等边三角形，∵BD＝CD＝BC，∴，整理得：，②﹣①得：4m+8n＝12，∴m＝3﹣2n，将m＝3﹣2n代入①得：（3﹣2n）2+n2﹣8n＝4，整理得：n2﹣4n+1＝0，解得：n＝，当n＝时，m＝3﹣2n＝，当n＝时，m＝3﹣2n＝，∴点D的坐标为或．故答案为：（﹣2，0）；或．二十一．解直角三角形的应用（共1小题）28．（2023•杭州）第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（△DAE，△ABF，△BCG，△CDH）和中间一个小正方形EFGH 拼成的大正方形ABCD中，∠ABF＞∠BAF，连接BE．设∠BAF＝α，∠BEF＝β，若正方形EFGH与正方形ABCD的面积之比为1：n，tanα＝tan2β，则n＝（）A．5B．4C．3D．2【分析】设AE＝a，DE＝b，则BF＝a，AF＝b，解直角三角形可得，化简可得（b﹣a）2＝ab，a2+b2＝3ab，结合勾股定理及正方形的面积公式可求得S正方形EFGH；S正方形ABCD＝1：3，进而可求解n的值．【解答】解：设AE＝a，DE＝b，则BF＝a，AF＝b，∵tanα＝，tanβ＝，tanα＝tan2β，∴，∴（b﹣a）2＝ab，∴a2+b2＝3ab，∵a2+b2＝AD2＝S正方形ABCD，（b﹣a）2＝S正方形EFGH，∴S正方形EFGH：S正方形ABCD＝ab：3ab＝1：3，∵S正方形EFGH：S正方形ABCD＝1：n，∴n＝3．故选：C．。

一、解答题1．（1）回归教材：北师大七年级下册P 44，如图1所示，点P 是直线m 外一点，，点O 是垂足，点A 、B 、C 在直线m 上，比较线段PO ，PA ，PB ，PC 的长短，你发现了什么？最短线段是______，于是，小明这样总结：直线外一点与直线上各点连接的所有线段中，______．（2）小试牛刀：如图2所示，Rt ABC △中，AB c =，，．则点P 为AB 边上一动点，则CP 的最小值为______． （3）尝试应用：如图3所示ABC 是边长为4的等边三角形，其中点P 为高AD 上的一个动点，连接BP ，将BP 绕点B 顺时针旋转60°得到BE ，连接PE 、DE 、CE ．①请直接写出DE 的最小值．②在①的条件下求的面积．（4）拓展提高：如图4，顶点F 在矩形ABCD 的对角线AC 上运动，连接AE ．．3AB =，4BC =，请求出AE 的最小值．2．如图1，在平面直角坐标系中，直线55y x =-+与x 轴，y 轴分别交于A 、C 两点，抛物线2y x bx c =++经过A 、C 两点，与x 轴的另一交点为B ．（1）求抛物线解析式；（2）若点M 为x 轴下方抛物线上一动点，MN ⊥x 轴交BC 于点N ，当点M 运动到某一位置时，线段MN 的长度最大，求此时点M 的坐标及线段MN 的长度；（3）如图2，以B 为圆心，2为半径的⊙B 与x 轴交于E 、F 两点（F 在E 右侧），若P 点是⊙B 上一动点，连接PA ，以PA 为腰作等腰Rt PAD △，使90PAD ∠=︒（P 、A 、D 三点为逆时针顺序），连接FD ．①将线段AB 绕A 点顺时针旋转90°，请直接写出B 点的对应点的坐标；②求FD 长度的取值范围．3．在ABC 中，AB BC =，45B ∠=︒，AD 为BC 边上的高．（1）如图1，若1AD =，求线段CD 的长度；（2）如图2，点E ，点F 在AB 边上，且满足AE BF =，连接CE ，CF 分别交线段AD 于点M ，点N ，若点M 为线段CE 的中点，求证：2AN CD AB +=；（3）在（2）问条件下，若2AC =，点K 为AC 边上一动点，点Р为ACF 内一点且满足ACP CAD ∠=∠，当PK PA +取最小值时，请直接写出CPK S △的值．4．在平面直角坐标系xOy 中，⊙O 的半径为1．对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′（B ′，C ′分别是B ，C 的对应点），则称线段BC 是⊙O 的以点A 为中心的“关联线段”．（1）如图，点A ，B 1，C 1，B 2，C 2，B 3，C 3的横、纵坐标都是整数．在线段B 1C 1，B 2C 2，B 3C 3中，⊙O 的以点A 为中心的“关联线段”是 ；（2）△ABC 是边长为1的等边三角形，点A （0，t ），其中t ≠0．若BC 是⊙O 的以点A 为中心的“关联线段”，求t 的值；（3）在△ABC 中，AB ＝1，AC ＝2．若BC 是⊙O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．5．如图，抛物线26y ax bx =+-交x 轴于(2,0),(6,0)A B -两点，交y 轴于点C (0,6)-，点Q 为线段BC 上的动点．（1）求抛物线的解析式；（2）求QA QO +的最小值；（3）过点Q 作QP AC 交抛物线的第四象限部分于点P ，连接,PA PB ，记PAQ △与PBQ △的面积分别为12,S S ，设12S S S =+，当S 最大时，求点P 的坐标，并求S 的最大值．6．如图1，在平面直角坐标系中，直线y ＝2x ＋8与x 轴交于点A ，与y 轴交于点B ，过点B 的另一条直线483y x =-+交x 轴正半轴于点C ．（1）写出C 点坐标 ；（2）若M 为线段BC 上一点，且满足S △AMB ＝ S △AOB ，请求出点M 的坐标；（3）如图2，设点F 为线段AB 中点，点G 为y 轴正半轴上一动点，连接FG ，以FG 为边向FG 右侧作正方形FGQP ，在G 点的运动过程中，当顶点Q 落在直线BC 上时，求出点G 的坐标．7．已知抛物线y ＝ax 2+32x +4的对称轴是直线x ＝3，与x 轴相交于A ，B 两点（点B 在点A 右侧），与y 轴交于点C ．（1）求抛物线的解析式和A ，B 两点的坐标；（2）如图1，若点P 是抛物线上B 、C 两点之间的一个动点（不与B 、C 重合），是否存在点P ，使四边形PBOC 的面积最大？若存在，求点P 的坐标及四边形PBOC 面积的最大值；若不存在，请说明理由；（3）如图2，若点M 是抛物线上任意一点，过点M 作y 轴的平行线，交直线BC 于点N ，当MN ＝3时，求点M 的坐标．8．如图，已知抛物线2(0)y ax bx c a =++≠与x 轴交于点(1,0)A 和点，与y 轴交于点C ，且OC OB =．（1）求此抛物线的解析式；（2）若点E 为第二象限抛物线上一动点，连接BE ，CE ，BC ，求BCE 面积的最大值；（3）点P 在抛物线的对称轴上，若线段PA 绕点P 逆时针旋转90︒后，点A 的对应点'A 恰好也落在此抛物线上，求点P 的坐标．9．问题发现如图1，在Rt ABC △和Rt CDE △中，90ACB DCE ∠=∠=︒，45CAB CDE ∠=∠=︒，点D 是线段AB 上一动点，连接BE ．（1）填空： ①BE AD的值为______； ②DBE ∠的度数为______．（2）类比探究如图2，在Rt ABC △和Rt CDE △中，90ACB DCE ∠=∠=︒，60CAB CDE ∠=∠=︒，点D 是线段AB 上一动点，连接BE ．请求出BE AD的值及DBE ∠的度数，并说明理由； （3）拓展延伸如图3，在Rt ABC △和Rt CDE △中，90ACB DCE ∠=∠=︒，CAB CDE ∠=∠，点D 是线段AB 上一动点，连接BE ，M 为DE 中点．若4BC =，3AC =，在点D 从A 点运动到B 点的过程中，请直接写出M 点经过的路径长．10．如图，抛物线y ＝ax 2＋bx ﹣3经过A 、B 、C 三点，点A （﹣3，0）、C （1，0），点B在y轴上．点P是直线AB下方的抛物线上一动点（不与A、B重合）．(1)求此抛物线的解析式；(2)过点P作x轴的垂线，垂足为D，交直线AB于点E，动点P在什么位置时，PE最大，求出此时P点的坐标；(3)点Q是抛物线对称轴上一动点，是否存在点Q，使以点A、B、Q为顶点的三角形为直角三角形？若存在，请求出点Q坐标；若不存在，请说明理由．11．如图1，直线y12=-x+b与地物线y＝ax2交于A．B两点，与y轴于点Ｃ，其中点A的坐标为（﹣4，8）．(1)求a，b的值；(2)将点A绕点C逆时针旋转90°得到点D．①试说明点D在抛物线上；②如图2，将直线AB向下平移，交抛物线于E，F两点（点E在点F的左侧），点G在线段OC上．若GEF DBA∽（点G，E，F分别与点D，B，A对应），直接写出点G的坐标．12．如图1，在平面直角坐标系中，一次函数y12=x﹣2的图象与x轴交于点B，与y轴交于点C，二次函数y bx+c的图象经过B，C两点，且与x轴的负半轴交于点A．(1)求二次函数的表达式．(2)如图2，连接AC，点M为线段BC上的一点，设点M的横坐标为t，过点M作y轴的平行线，过点C作x轴的平行线，两者交于点N，将△MCN沿MC翻折得到△MCN'．①当点N'落在线段AB上，求此时t的值；②求△MCN′与△ACB重叠的面积S与t的函数关系式．(3)如图3，点D在直线BC下方的二次函数图象上，过点D作DM⊥BC于点M，是否存在点D，使得△CDM中的某个角恰好等于∠ABC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．13．如图，直线y＝﹣2x+10分别与x轴，y轴交于点A，B两点，点C为OB的中点，抛物线y＝x2+bx+c经过A，C两点．(1)求抛物线的函数表达式；(2)点D是直线AB下方的抛物线上的一点，且ABD的面积为，求点D的坐标；(3)点P为抛物线上一点，若APB是以AB为直角边的直角三角形，求点P到抛物线的对称轴的距离．14．等腰△ABC中，BA＝BC，过点A作AD⊥BC于点D，平面上有一点E，连接ED，EB，ED＝2EB，作∠BED的角平分线交BC于点F．(1)如图1，当∠EBC ＝90°时，若∠BAD ＝45°，BE ＝23，求线段DC 的长；(2)如图2，当∠EBC ＞90°时，过点F 作FG ⊥AC ，分别交AC ，AD 于点G ，H ，若AD ＝2BF ，P 为EF 中点，连接BP ，求证：AB ﹣3BP ＝DH ；(3)如图3，在（1）问的条件下，BE 上取点O ，BO ，点M ，N 为线段BD 上的两个动点（点M 在点N 的左侧），连接AN ，将△AND 绕点D 逆时针旋转得到△A ′N ′D ，若满足A ′D ⊥AN 于点P ，连接OM ，MP ，当OM +MP 的值最小时，直接写出△OMP 的面积．15．已知抛物线24y ax bx =++（a ≠0）与x 轴交于点A （3-，0）、B （2，0），与y 轴交于点C ，直线y mx n =+经过两点A 、C ．(1)求a ，b 的值；(2)如图1，点Р在已知抛物线上，且位于第二象限，当四边形PABC 的面积最大时，求点P的坐标．(3)如图2，将已知抛物线向左平移1个单位，再向下平移2个单位．记平移后的抛物线为2'y，若抛物线'y与原抛物线的对称轴交于点Q．点E是新抛物线'y的对称轴上一动点，在（2）的条件下，当△PQE是等腰三角形时，请直接写出点E的坐标．16．如图，矩形ABCD中，对角线AC、BD相交于点O，∠AOB＝60°，AB＝2，将一张和△ABC一样大的纸片和△ABC重叠放置，点E是边BC上一点（不含点B、C），将△OCE 沿着OE翻折，点C落在点P处．(1)直接写出∠OBC、∠OCB的数量关系是．(2)连接DE，设△OPE的面积为S1，△ODE的面积为S2，在点E取边BC上每一点（除点B、C）的过程中，S1+S2的值是否变化？如果变化，请求出它的取值范围；如果不变，请求出S1+S2的值；(3)分别连接PD、PC，当点P与点B重合时，易知PO•PC＝PE•PD，当点P不与点B重合时，PO•PC＝PE•PD是否成立？请在图3、图4中选一种情况进行证明．17．抛物线2=-++交x轴于点A，B（A在B的左边），交y轴于点C，顶点为y x2x3M，对称轴MD交x轴于点D，E是线段MD上一动点，以OB，BE为邻边作平行四边形OBEF，EF交抛物线于点P，G（P在G的左边），交y轴于点H．(1)求点A，B，C的坐标；(2)如图1，当EG FP=时，求DE的长；(3)如图2，当1DE=时，①求直线FC 的解析式，并判断点M 是否落在该直线上．②连接CG ，MG ，CP ，MP ，记CGM △的面积为1S ，CPM △的面积为2S ，则12S S =__________． 18．在平面直角坐标系中，抛物线y 12=-x 22x +3与x 轴交于A 、B 两点（A 在B 左侧），与y 轴交于点C ，抛物线的顶点为D ，过点B 作BC 的垂线，交对称轴于E ．(1)如图1，点P 为第一象限内的抛物线上一动点，当△PAE 面积最大时，在对称轴上找一点M ，在y 轴上找一点N ，使得OM +MN +NP 最小，求此时点M 的坐标及OM +MN +NP 的最小值；(2)如图2，平移抛物线，使抛物线的顶点D 在射线AD 上移动，点D 平移后的对应点为D '，点A 的对应点A '，设原抛物线的对称轴与x 轴交于点F ，将△FBC 沿BC 翻折，使点F 落在点F ′处，在平面上找一点G ，使得以A '、D '、F '、G 为顶点的四边形为菱形．直接写出D ′的坐标．19．如图1，在平面直角坐标系xOy 中，直线:4l y x =+交x 轴于点C ，交y 轴于点D ，AB CD ，()2,3A ，点P 是直线l 上一动点，连接AP ，BP ．(1)求直线AB 的表达式；(2)求22AP CP+的最小值；(3)如图2，将三角形ABP沿BP翻折得到A BP'，当点A'落在坐标轴上时，请直接写出直线BP的表达式．20．如图，在平面直角坐标系xOy中，抛物线与x轴交于两点与y轴交于点C，点M是抛物线的顶点，抛物线的对称轴l与BC交于点D，与x轴交于点E．(1)求抛物线的对称轴及B点的坐标(2)如果，求抛物线的表达式；(3)在（2）的条件下，已知点F是该抛物线对称轴上一点，且在线段BC的下方，，求点F的坐标【参考答案】参考答案**科目模拟测试一、解答题1．（1）PO，垂线段最短；（2）；（3）①DE的最小值是1；②△BPE的面积为；（4）AE的最小值为．【解析】【分析】（1）根据垂线段的性质即可解答；（2）由（1）知当PC⊥AB时，PC取得最小值，利用面积法即可求解；（3）①根据旋转的性质，旋转前后的图形对应线段、对应角相等，可证得△ABP≌△CBE，得到∠BCE=30°．得到点E在射线CE上，根据“垂线段最短”这一定理，当∠DEC=90°时，DE最短，据此求解即可；②利用勾股定理求得ECAP AD、PD、BP的长，即可求解；（4）作出如图的辅助线，先判断出点E在直线GH上运动，根据“垂线段最短”这一定理，当当AE⊥GH时，AE最短，利用相似三角形的判定和性质、勾股定理以及三角形面积公式即可求解．【详解】解：（1）∵PO⊥直线m，∴从直线外一点到这条直线所作的垂线段最短．故答案为：PO，垂线段最短；（2）由（1）知当PC⊥AB时，PC取得最小值，S△ABC=12AC BC=12AB PC，∴PC=，即CP的最小值为，故答案为：；（3）①由旋转知∠PBE=60°，BP=BE，∴△PBE是等边三角形，∵△ABC是等边三角形，AD⊥BC，边长为4，∴AB=BC，∠ABC=60°，∠ABD=∠CBD=30°，BD=CD=2，∴∠ABP=∠CBE，∴△ABP≌△CBE（SAS），∴∠BCE=∠BAD=30°；∵点P为高AD上的一个动点，∴点E在射线CE上，根据“垂线段最短”可知，当DE⊥CE时，DE最短．∵∠BCE=30°，CD=2，∴DE=12CD=1，即DE的最小值是1；②由①得CD=2，DE=1，∴CE=，∵△ABP≌△CBE，∴AP=CE3，在Rt△BDA中，AB=4，BD=2，∴AD=，∴PD=AD-AP=3，∴PB=，∴等边三角形△PBE的高为，∴△BPE的面积为=；（4）过点B作BH⊥AC于点H，则∠BHC=90°，∴∠HBC+∠HCB=90°，∠ACD+∠HCB=90°，∴∠HBC=∠ACD，∵∠EBF=∠ACD，∴∠HBC=∠EBF，此时点F与点C重合，点E与点H重合，∵AB=3，BC=4，∴AC=，∵S△ABC=12AB BC=12AC BH，∴BH=125，∴AH=，取AB中点G，过点G作GI⊥AB交AC于点I，则∠BGI=90°，∴∠GBI=∠BAC，∵∠EBF=∠ACD=∠BAC，∴∠GBI=∠EBF，此时点F与点I重合，点E与点G重合，顶点F在矩形ABCD的对角线AC上运动，且，四点共圆，∴点E在直线GH上运动，根据“垂线段最短”这一定理，当AE⊥GH时，AE最短，过点H作HP⊥AB于点P，∴△APH~△ABC，∴，即，∴PH=，AP=，∴PG=AG-AP=，∴GH=，∵S△AGH=12AG PH=12GH AE，∴AE =，∴AE 的最小值为． 【点睛】本题考查了相似三角形的判定和性质，全等三角形的性质与判定，垂线段最短，勾股定理，等边三角形的判定和性质，四点共圆的判定等知识，解决本题的关键是正确寻找相似三角形解决问题．2．（1）265y x x =-+；（2）当M 运动到515(,)24- 时，线段MN 的长度最大为254；（3）①(1,4)-；②22FD ≤≤．【解析】【分析】（1）先求得直线与坐标轴的交点坐标，然后代入到抛物线解析式即可求解；（2）设设2(,65)M m m m -+，则(,5)N m m -+，则2(5)(65)MN m m m =-+--+，整理可得225255()24MN m m m =-+=--+，可求得当52m =时，MN 的最大值为254，进而求得M 坐标；（3）①由（1），（2）可求得514AB AB OB OA '==-=-=，从而求得点B '坐标；②根据点P 的运动情况，来确定点D 的运动轨迹，是与点P 半径相等的圆，圆心为B '，作射线FB '，与⊙B '交于1D ，2D ，从而确定FD 的范围．【详解】解：（1）∵直线55y x =-+与x 轴、y 轴分别交于A ，C 两点，∴当0x =时，5y =，所以(0,5)C ，当0y =时，1x =，所以(1,0)A ，∵抛物线2y x bx c =++经过A ，C 两点，∴5c =，150b ++=，解得6b =-，∴抛物线解析式为265y x x =-+．（2）令0y =，∴265=0-+x x ，解得：11x =，25x =，∴(5,0)B ，∴直线BC 的解析式为：5y x =-+，设2(,65)M m m m -+，则(,5)N m m -+，∴2(5)(65)MN m m m =-+--+， ∴225255()24MN m m m =-+=--+，∴当52m =时，MN 的最大值为254， ∴当M 运动到515(,)24- 时，线段MN 的长度最大为254．（3）①将线段AB 绕A 点顺时针旋转90°，∴B A BA '⊥，∵(1,0)A ，(5,0)B ，∴514AB AB OB OA '==-=-=，∴(1,4)B '-；②连接PB ，B D '，由①可得4AB AB '==，又已知PAD △是等腰直角三角形，90BAB PAD '∠=∠=︒，AD AP =，∴(SAS)DAB PAB '≌△△，∴2B D BP '==，∴当P 点在⊙B 上运动时，点D 在以B '为圆心，半径为2的圆上，∴作射线FB '，与⊙B '交于1D ，2D 两点，情况一：当交点为1D 时，1FD 为最小值，即11FD FB B D ''=-，已知(1,0)A ，(5,0)B ，2BF =，∴426AF AB BF =+=+=,4AB AB '==,∴在Rt AFB '△中，222246FB AB AF ''=+=+ ,即213FB '=，∴12132FD =-；情况二：当交点为2D 时，2FD 为最大值，即22FD FB B D ''=+，已知(1,0)A ，(5,0)B ，2BF =，∴426AF AB BF =+=+=,4AB AB '==,∴在Rt AFB '△中，222246FB AB AF ''++即213FB '=∴22132FD =；综上21322132FD ≤≤．【点睛】本题考查二次函数的综合问题，待定系数法确定函数解析式，抛物线与线段最值问题，以及瓜豆原理在二次函数中的应用问题，其中利用点P ，确定点D 的运动轨迹是本题的解题关键．3．（121；（2）证明见解析；（321- 【解析】【分析】（1）证明,AD BD = 再利用勾股定理求解,,AB BC 从而可得答案；（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥ 证明,EHM CDM ≌ 可得22,AE EH CD == 同理：22,BF FQ BQ == 而,AE BF = 再证明,FQC DCA ≌ 可得,FCQ CAD ∠=∠ 再证明,AF AN = 从而可得结论；（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒ 证明,22.5,CF CA CAD =∠=︒ 可得CP 平分,ACF ∠ 则,A F 关于直线CP 对称，,PF PA = 过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+= 所以PA PK +最短，设,PK n = 则1,21,PF PA n AK ==-= 再利用勾股定理求解,n 即可得到答案.【详解】解：（1）45B ∠=︒，AD 为BC 边上的高，90,45,ADB B BAD ∴∠=︒∠=∠=︒221,112,AD BD AB ∴==+=AB BC =，2,2 1.BC CD BC BD ∴==-=-（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥则90,EHM CDM ∠=∠=︒M 为CE 的中点，,HME DMC ∠=∠ ,EM CM ∴=,EHM CDM ∴≌,EH CD ∴=45,90,BAD AHE EHM ∠=︒∠=∠=︒22,AE EH CD ∴==同理：22,BF FQ BQ == 而,AE BF =,FQ BQ CD EH ∴===,BD CQ AD ∴==90,ADC CQF ∠=∠=︒,FQC DCA ∴≌,FCQ CAD ∴∠=∠,AB BC =,BAC BCA ∴∠=∠,BAD ACF ∴∠=∠ 而,B BAD ∠=∠,,B FCQ AFN ANF ACF CAD ∠+∠=∠∠=∠+∠,AFN ANF ∴∠=∠,AF AN ∴=2.AN CD AF AE AF BF AB ∴=+=+=（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒,45,BA BC B =∠=︒67.5,BAC BCA ∴∠=∠=︒67.5,CFA BAC ∴∠=︒=∠,22.5,CF CA CAD ∴=∠=︒22.5,ACP CAD ∠=∠=︒CP ∴平分,ACF ∠,,CP AF AL FL ∴⊥=则,A F 关于直线CP 对称，,PF PA =过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+=所以PA PK +最短，2,AC ∴= 则2,CF = 而45,ACF ∠=︒1,CK FK ∴==设,PK n = 则1,21,PF PA n AK ==-=())222121,n n ∴-=+ 解得：21,n = )121121.22CPK S ∴=⨯⨯= 【点睛】本题考查的是全等三角形的判定与性质，等腰直角三角形的判定与性质，等腰三角形的判定与性质，勾股定理的应用，本题综合性较强，是压轴题，知识的系统化是解题的关键.4．（1）B 2C 2；（233-3）OA 最小值为1，相应的3BC =OA 最大值为2，相应的6BC =【解析】【分析】（1）结合题意，根据旋转和圆的性质分析，即可得到答案；（2）根据题意，分B C ''在x 轴上方和x 轴上方两种情况；根据等边三角形、勾股定理、全等三角形的性质，得3AD OD == （3）结合题意，得当AC '为⊙O 的直径时，OA 取最小值；当A 、B '、O 三点共线时，OA 取最大值；根据勾股定理、等腰三角形的性质计算，即可得到答案．【详解】（1）线段B 1C 1绕点A 旋转得到的11B C ''，均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”；线段B 2C 2绕点A 旋转得到的22B C ''，如下图：∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”；线段B 3C 3绕点A 旋转得到的33B C ''，均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”；故答案为：B 2C 2；（2）∵△ABC 是边长为1的等边三角形，点A （0，t ），⊙O 的半径为1∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况：当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：∵1OB OC ''== ∴1122B D BC '''==∴2232OD OB B D ''=-= ∵△ABC 是边长为1的等边三角形，即△AB C ''是边长为1的等边三角形，∴AC D OC D ''∠=∠，AD B C ''⊥∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =；当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：同理，3AO AD OD =+=∴()0,3A -；∴t 3=-；∴3t =或3-；（3）当AC '为⊙O 的直径时，OA 取最小值，如下图：∴OA 最小值为1，90AB C ''∠=︒∴223BC B C AC AB ''''==-=当A 、B '、O 三点共线时，OA 取最大值，2OA AC '== ，如下图：作AE OC '⊥交OC '于点E ，作C F AO '⊥交AO 于点F ，如下图∵2OA AC '== ∴1122OE OC '== ∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '== ∴2214OF OC C F ''=-= ∴34B F OB OF ''=-= ∴26BC B C C F B F ''''==+=∴OA 最小值为1，相应的BC =OA 最大值为2，相应的BC =． 【点睛】 本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识；解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质，从而完成求解．5．（1）y =12x 2−2x −6；（2）QO ＋QA 有最小值10；（3）P （3，−152）时，S 有最大值152【解析】【分析】（1）运用待定系数法设y ＝a （x ＋2）（x −6），将C （0，−6）代入，即可求得答案；（2）如图1，作点O 关于直线BC 的对称点O ′，连接AO ′，QO ′，CO ′，BO ′，由O 、O ′关于直线BC 对称，得出四边形BOCO ′是正方形，根据QA ＋QO ′≥AO ′，QO ′＝QO ，得出答案；（3）运用待定系数法求出直线BC 、AC 、PQ 的解析式，设P （m ，12m 2−2m −6），联立方程组，得：261362y x y x m m ⎪--⎧⎪-⎨⎩＝＝＋＋，求得Q （22128m m +-，22608m m +-），再运用三角形面积公式求得答案．【详解】解：（1）∵抛物线交x 轴于A （−2，0），B （6，0）两点，∴设y ＝a （x ＋2）（x −6），将C （0，−6）代入，得：−12a ＝−6，解得：a ＝12， ∴y ＝12（x ＋2）（x −6）＝12x 2−2x −6， ∴抛物线的解析式为y =12x 2−2x −6；（2）如图1，作点O 关于直线BC 的对称点O ′，连接AO ′，QO ′，CO ′，BO ′，∵OB＝OC＝6，∠BOC＝90°，∴∠BCO＝45°，∵O、O′关于直线BC对称，∴BC垂直平分OO′，∴OO′垂直平分BC，∴四边形BOCO′是正方形，∴O′（6，−6），在Rt△ABO′中，AO′＝2222+=+=，AB O B'8610∵QA＋QO′≥AO′，QO′＝QO，∴QO＋QA＝QA＋QO′≥AO′＝5，即点Q位于直线AO′与直线BC交点时，QO＋QA有最小值10；（3）设直线BC的解析式为y＝kx＋d，∵B（6，0），C（0，−6），∴606k d d ⎨⎩-⎧＋＝＝，解得：16k d =⎧⎨=-⎩， ∴直线BC 的解析式为y ＝x −6，设直线AC 的解析式为y ＝mx ＋n ，∵A （−2，0），C （0，−6），∴206m n n ⎧⎨⎩--＋＝＝，解得：36m n =-⎧⎨=-⎩， ∴直线AC 的解析式为y ＝−3x −6，∵PQ ∥AC ，∴直线PQ 的解析式可设为y ＝−3x ＋b ，由（1）可设P （m ，12m 2−2m −6），代入直线PQ 的解析式， 得：12m 2−2m −6＝−3m ＋b ，解得：b ＝12m 2＋m −6，∴直线PQ 的解析式为y ＝−3x ＋12m 2＋m −6， 联立方程组，得：261362y x y x m m ⎪--⎧⎪-⎨⎩＝＝＋＋， 解得：2221282608m m x m m y ⎧+-=⎪⎪⎨+-⎪=⎪⎩， ∴Q （22128m m +-，22608m m +-）， 由题意：S ＝S △PAQ ＋S △PBQ ＝S △PAB −S △QAB ，∵P ，Q 都在第四象限，∴P ，Q 的纵坐标均为负数，∴S ＝12|AB |•（−12m 2＋2m ＋6）−12|AB |•（22608m m +--） ＝23962m m -+-2315(3)22m =--+， 由题意，得0＜m ＜6，∴m ＝3时，S 最大，即P （3，−152）时，S 有最大值152． 【点睛】 本题是二次函数综合题，主要考查了二次函数图象和性质，待定系数法求函数解析式，将军饮马的最值问题，利用二次函数求最值等，熟练掌握二次函数图象和性质等相关知识，运用数形结合思想是解题关键．6．（1）点C （6，0）；（2）点1224(,)55M ；（3）满足条件的点G 坐标为34(0,)7或(0,-2)．【解析】【分析】（1）直接利用直线483y x =-+，令y=0，解方程即可； （2）结合图形，由S △AMB ＝S △AOB 分析出直线OM 平行于直线AB ，再利用两直线相交建立方程组2483y x y x =⎧⎪⎨=-+⎪⎩，解方程组求得交点M 的坐标； （3）分两种情形：①当n ＞4时，如图2-1中，点Q 落在BC 上时，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ．求出Q （n-4，n-2）．②当n ＜4时，如图2-2中，同法可得Q （4-n ，n +2），代入直线BC 的解析式解方程即可解决问题．【详解】解：（1）∵直线483y x =-+交x 轴正半轴于点C ． ∴当y =0时，48=03x -+， 解得x =6∴点C （6，0）故答案为（6，0）；（2）连接OM 并双向延长，∵S △AMB ＝S △AOB ，∴点O 到AB 与点M 到AB 的距离相等，∴直线OM 平行于直线AB ，∵AB 解析式为y ＝2x ＋8，故设直线OM 解析式为：2y x =，将直线OM 的解析式与直线BC 的解析式联立得方程组得：2483y x y x =⎧⎪⎨=-+⎪⎩， 解得：125245x y ⎧=⎪⎪⎨⎪=⎪⎩故点1224(,)55M ； （3）∵直线y ＝2x ＋8与x 轴交于点A ，与y 轴交于点B ，∴令y=0，2x ＋8=0，解得x =-4，∴A （-4，0），令x =0，则y ＝8∴B （0，8），∵点F 为AB 中点，点F 横坐标为()1-4+0=-22，纵坐标为()10+8=42∴F （-2，4），设G （0，n ），①当n ＞4时，如图2-1中，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ．∵四边形FGQP 是正方形，∴FG =QG ，∠FGQ =90°，∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°，∵FM ⊥MN ，QN ⊥MN ，∴∠M =∠N =90°，∴∠MFG +∠MGF =90°，∴∠MFG =∠NGQ ，在△FMG 和△GNQ 中，M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FMG ≌△GNQ ，∴MG =NQ =2，FM =GN =n -4，∴Q （n -4，n -2），∵点Q 在直线483y x =-+上， ∴42(4)43n n -=--+， ∴34=7n , ∴34(0,)7G ． ②当n ＜4时，如图2-2中，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ．∵四边形FGQP 是正方形，∴FG =QG ，∠FGQ =90°，∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°，∵FM ⊥MN ，QN ⊥MN ，∴∠M =∠N =90°，∴∠MFG +∠MGF =90°，∴∠MFG =∠NGQ ，在△FMG 和△GNQ 中，M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FMG ≌△GNQ ，∴MG =NQ =2，FM =GN = 4-n ，∴Q （4- n ， n +2），∵点Q 在直线483y x =-+上， ∴42(4)83n n +=--+，∴n =-2，∴(0,-2)G ．综上所述，满足条件的点G 坐标为34(0,)7或(0,-2)． 【点睛】本题属于一次函数综合题，考查了一次函数与坐标轴的交点，平行线性质，两直线联立解方程组，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．7．（1）213442y x x =-++，点A 的坐标为（﹣2，0），点B 的坐标为（8，0）；（2）存在，点P （4，6）；（3）点M 的坐标为（4﹣771）或（77﹣1）．【解析】【分析】（1）由抛物线的对称轴是直线x ＝3，解出a 的值，即可求得抛物线解析式，在令其y 值为零，解一元二次方程即可求出A 和B 的坐标；（2）易求点C 的坐标为（0，4），设直线BC 的解析式为y ＝kx +b （k ≠0），将B （8，0），C （0，4）代入y ＝kx +b ，解出k 和b 的值，即得直线BC 的解析式；设点P 的坐标为（x ，213442x -++），过点P 作PD ∥y 轴，交直线BC 于点D ，则点D 的坐标为（x ，142x -+），利用关系式S 四边形PBOC ＝S △BOC +S △PBC 得出关于x 的二次函数，从而求得其最值；（3）设点M 的坐标为（m ，213442m m -++）则点N 的坐标为（m ，142m -+），MN ＝2213114(4)24224m m m m m -++--+=-+，分当0＜m ＜8时，或当m ＜0或m ＞8时来化简绝对值，从而求解．【详解】解：（1）∵抛物线的对称轴是直线x ＝3，3232a∴-= 14a ∴=- ∴抛物线的解析式为：213442y x x =-++． 当y ＝0时，2130442x x =-++，解得x 1＝﹣2，x 2＝8， ∴点A 的坐标为（﹣2，0），点B 的坐标为（8，0）．答：抛物线的解析式为：213442y x x =-++；点A 的坐标为（﹣2，0），点B 的坐标为（8，0）．（2）当x ＝0时，2134442y x x =-++=， ∴点C 的坐标为（0，4）．设直线BC 的解析式为y ＝kx +b （k ≠0），将B （8，0），C （0，4）代入y ＝kx +b 得804k b b +=⎧⎨=⎩，解得124k b ⎧=-⎪⎨⎪=⎩ ∴直线BC 的解析式为142y x =-+． 假设存在点P ，使四边形PBOC 的面积最大，设点P 的坐标为（x ，213442x x -++），如图1所示，过点P 作PD ∥y 轴，交直线BC 于点D ，则点D 的坐标为（x ，142x -+），则PD ＝2211314222()444-++-++-=-x x x x x ， ∴S 四边形PBOC ＝S △BOC +S △PBC118422PD OB =⨯⨯+⋅ 211168(2)24x x =+⨯-+ 2816x x =-++2(4)32x =--+∴当x ＝4时，四边形PBOC 的面积最大，最大值是32∵0＜x ＜8，∴存在点P （4，6），使得四边形PBOC 的面积最大．答：存在点P ，使四边形PBOC 的面积最大；点P 的坐标为（4，6），四边形PBOC 面积的最大值为32．（3）设点M 的坐标为（m ，213442m m -++）则点N 的坐标为（m ，142m -+）， ∴MN ＝2213114(4)24224m m m m m -++--+=-+ 又∵MN ＝3，21234m m ∴-+= 当0＜m ＜8时，212304m m -+-=，解得m 1＝2，m 2＝6， ∴点M 的坐标为（2，6）或（6，4）；当m ＜0或m ＞8时，212304m m -+-=，解得m 3＝4-m 4＝4+，∴点M 的坐标为（4-1）或（4+，1）．答：点M 的坐标为（2，6）、（6，4）、（4-1）或（4+，1）．【点睛】本题属于二次函数压轴题，综合考查了待定系数法求解析式，解析法求面积及点的坐标的存在性，最大值等问题，难度较大．8．（1）223y x x =--+；（2）278；（3）P （-1，1）或（-1，-2）． 【解析】【分析】（1）由题意已知抛物线过A 、B 两点，可将两点的坐标代入抛物线的解析式中，用待定系数法即可求出二次函数的解析式；（2）根据题意连接BC ，过点E 作EF ⊥x 轴于点F ，设E （a ，-a 2-2a +3）（-3＜a ＜0），可得EF =-a 2-2a +3，BF =a +3，OF =-a ，根据S △BEC =S 四边形BOCE -S △BOC ，构建二次函数，利用二次函数的性质求解即可．（3）根据题意由P 在抛物线的对称轴上，设出P 坐标为（-1，m ），如图所示，过A ′作A ′N ⊥对称轴于N ，由旋转的性质得到一对边相等，再由同角的余角相等得到一对角相等，根据一对直角相等，利用AAS 得到△A ′NP ≌△PMA ，由全等三角形的对应边相等得到A ′N =PM =|m |，PN =AM =2，表示出A ′坐标，将A ′坐标代入抛物线解析式中求出相应m 的值，即可确定出P 的坐标．【详解】解：（1）∵抛物线y =ax 2+bx +c （a ≠0）与x 轴交于点A （1，0）和点B （-3，0）， ∴OB =3，∵OC =OB ，∴OC =3，∴c =3，∴， 解得：， ∴所求抛物线解析式为：223y x x =--+；（2）如图2，连接BC ，过点E 作EF ⊥x 轴于点F ，设E （a ，-a 2-2a +3）（-3＜a ＜0），∴EF =-a 2-2a +3，BF =a +3，OF =-a ，∴S △BEC =S 四边形BOCE -S △BOC =12BF •EF +12（OC +EF ）•OF -12•OB •OC =12（a +3）•（-a 2-2a +3）+12（-a 2-2a +6）•（-a ）-92 =-32a 2-92a=-32（a+32）2+278，∴当a=-32时，S△BEC最大，且最大值为278．（3）∵抛物线y=-x2-2x+3的对称轴为x=-1，点P在抛物线的对称轴上，∴设P（-1，m），∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，①当m≥0时，∴PA=PA′，∠APA′=90°，如图3，过A′作A′N⊥对称轴于N，设对称轴于x轴交于点M，∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°，∴∠NA′P=∠NPA，在△A′NP与△PMA中，，∴△A′NP≌△PMA（AAS），∴A′N=PM=m，PN=AM=2，∴A′（m-1，m+2），代入y=-x2-2x+3得：m+2=-（m-1）2-2（m-1）+3，解得：m=1，m=-2（舍去），②当m＜0时，要使P2A=P2A2，由图可知A2点与B点重合，∵∠AP2A2=90°，∴MP2=MA=2，∴P2（-1，-2）．∴满足条件的点P 的坐标为P （-1，1）或（-1，-2）．【点睛】本题考查全等三角形的判定与性质，待定系数法求二次函数，二次函数的性质，四边形的面积．利用数形结合、分类讨论及方程思想是解题的关键．9．（1）①1；②90°；（2）BE AD =90DBE ∠=︒，理由见解析；（3）256 【解析】【分析】（1）①证明ACD △≌BCE 即可求得BE AD的值；②由①的结论，可得DBE ABC CBE ∠=∠+∠，进而可得DBE ∠的度数； （2）由已知条件证明Rt ACB △∽Rt DCE ，可得AC CD BC CE =，又ACD BCE ∠=∠，可得ACD △∽BCE，进而根据AC BC =BE BC AD AC ==1）可得DBE ABC CBE ∠=∠+∠，进而可得DBE ∠的度数；（3）设AB 的中点为P ，BE 的中点为Q ，由题意M 的路径长为PQ 的长，根据（2）的结论可得ACD △∽BCE ，进而求得CE 的长，根据中位线定理即可求得PQ ，即M 点经过的路径长．【详解】（1）∵90ACB DCE ∠=∠=︒，45CAB CDE ∠=∠=︒，∴45ABC CAB CDE CED ∠=∠=︒=∠=∠，∴AC BC =，CD CE =，∵90ACB DCE ∠=∠=︒，∴ACD BCE ∠=∠，在ACD △和BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ∴ACD △≌BCE （S A S ），∴BE AD =，45CAB CBE ∠=∠=︒，∴90DBE ABC CBE ∠=∠+∠=︒，1BE AD=． 故答案为：1，90°．（2）BE AD =90DBE ∠=︒． 理由如下：∵90ACB DCE ∠=∠=︒，60CAB CDE ∠=∠=︒，∴30CED ABC ∠=∠=︒，ACB DCB DCE DCB ∴∠-∠=∠-∠，即ACD BCE ∠=∠， ∴3tan tan 303AC ABC BC ∠=︒==． ∵90ACB DCE ∠=∠=︒，60CAB CDE ∠=∠=︒，∴Rt ACB △∽Rt DCE ，∴AC CD BC CE =， ∴AC BC CD CE=，且ACD BCE ∠=∠， ∴ACD △∽BCE ， ∴3BE BC AD AC ==，60CBE CAD ∠=∠=︒， ∴90DBE ABC CBE ∠=∠+∠=︒．（3）如图，设AB 的中点为P ，BE 的中点为Q ，点D 是线段AB 上一动点， M 为DE 中点,在点D 从A 点运动到B 点的过程中，M 点从AB 的中点P 运动到BE 的中点Q ，当D 点与B 点重合时，M 点与Q 点重合，此时如图，则M 点的运动路径长为PQ 的长，由（2）可得ACD △∽BCE ，4BC =，3AC =，90ACB ∠=︒,∴43BE BC EC AD AC CD ===，5AB =， 4CD BC ==，163EC ∴=， 1625333AE AC EC ∴=+=+=， ,P Q 分别为,AD BE 的中点，则256PQ =， ∴M 点的运动路径长为256． 【点睛】本题考查了三角形全等的性质与判定，相似三角形的性质与判定，解直角三角形，综合运用以上知识是解题的关键．10．(1)y ＝x 2+2x ﹣3；(2)（﹣32，154-） (3)（-1，2）或（-1，﹣4）或（-1，）或（-1，）【解析】【分析】（1）把点A ，B 代入y ＝ax 2+bx ﹣3即可； （2）设P （x ，x 2+2x ﹣3），求出直线AB 的解析，用含x 的代数式表示出点E 坐标，即可用含x 的代数式表示出PE 的长度，由函数的思想可求出点P 的横坐标，进一步求出其纵坐标；（3）设点Q （-1，a ），然后分类讨论利用勾股定理列出关于a 的方程求解．(1)解：把A （﹣3，0）和C （1，0）代入y ＝ax 2+bx ﹣3，得，， 解得，，∴抛物线解析式为y ＝x 2+2x ﹣3；(2)解：设P （x ，x 2+2x ﹣3），直线AB 的解析式为y ＝kx +b ，由抛物线解析式y ＝x 2+2x ﹣3，令x ＝0，则y ＝﹣3，∴B （0，﹣3），把A（﹣3，0）和B（0，﹣3）代入y＝kx+b，得，，解得，，∴直线AB的解析式为y＝﹣x﹣3，∵PE⊥x轴，∴E（x，﹣x﹣3），∵P在直线AB下方，∴PE＝﹣x﹣3﹣（x2+2x﹣3）＝﹣x2﹣3x＝﹣（x+32）2+94，当x＝﹣32时，y＝x2+2x﹣3＝154-，∴当PE最大时，P点坐标为（﹣32，154-）；(3)存在，理由如下，∵x＝﹣＝-1，∴抛物线的对称轴为直线x＝-1，设Q（-1，a），∵B（0，-3），A（-3，0），①当∠QAB＝90°时，AQ2+AB2＝BQ2，∴22+a2+32+32＝12+（3+a）2，解得：a＝2，∴Q1（-1，2），②当∠QBA＝90°时，BQ2+AB2＝AQ2，∴12+（3+a）2+32+32＝22+a2，解得：a＝﹣4，∴Q2（-1，﹣4），③当∠AQB＝90°时，BQ2+AQ2＝AB2，∴12+（3+a）2+22+a2＝32+32，解得：a1＝或a1＝，∴Q3（-1，），Q4（-1，），综上所述：点Q的坐标是（-1，2）或（-1，﹣4）或（-1，）或（-1，）．【点睛】本题是二次函数的综合题，主要考查了二次函数图象上点的坐标特征、待定系数法求函数的解析式、二次函数的性质、勾股定理，解题的关键是用含有未知数的代数式表达点的坐标和线段的长度．11．(1)126a b ⎧=⎪⎨⎪=⎩ (2)①见解析；②20(0,)9G 【解析】【分析】（1）利用待定系数法，把问题转化为解方程组即可．（2）①如图1中，分别过点A ，D 作AM ⊥y 轴于点M ，DN ⊥y 轴于点N ．利用全等三角形的性质求出点D 的坐标，可得结论． ②设21(,)2E t t ，求出直线EG ，FG 的解析式，构建方程组求出点G 的坐标，再根据点G 的横坐标为0，构建方程组求出t ，即可解决问题．(1) 解：由题意，得21(4)82(4)8b a ⎧-⨯-+=⎪⎨⎪-⨯=⎩， 解得126a b ⎧=⎪⎨⎪=⎩． (2)解：①如图1中，分别过点A ，D 作AM ⊥y 轴于点M ，DN ⊥y 轴于点N ．由（1）可知，直线AB 的解析式为162y x =-+， ∴C （0，6），∵A （-4，8），∴AM =4，OM =8，OC =6，∴CM =2，90AMC DNC ACD ∠=∠=∠=︒，∴90ACM DCN ∠+∠=︒，90DCN CDN ∠+∠=︒，∴=ACM CDN ∠∠，∵CA ＝CD ，∴AMC CND AAS ≌（），。

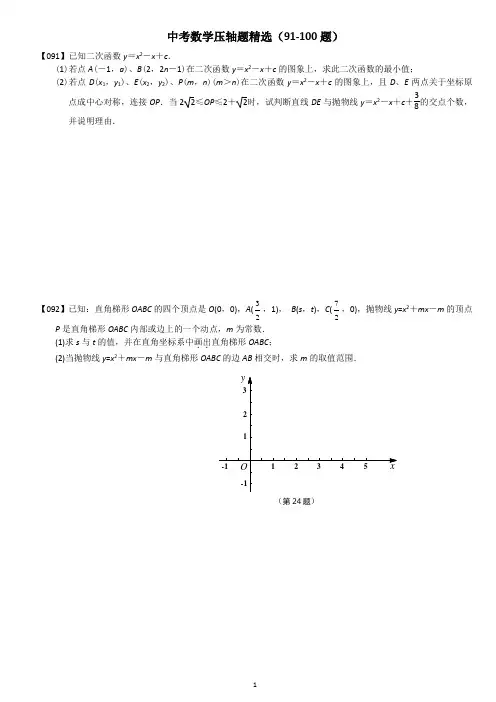
中考数学压轴题精选（91-100题）【091】已知二次函数y＝x2－x＋c．(1)若点A(－1，a)、B(2，2n－1)在二次函数y＝x2－x＋c的图象上，求此二次函数的最小值；(2)若点D(x1，y1)、E(x2，y2)、P(m，n)(m＞n)在二次函数y＝x2－x＋c的图象上，且D、E两点关于坐标原点成中心对称，连接OP．当22≤OP≤2＋2时，试判断直线DE与抛物线y＝x2－x＋c＋38的交点个数，并说明理由．【092】已知：直角梯形OABC的四个顶点是O(0，0)，A(32，1)，B(s，t)，C(72，0)，抛物线y=x2＋mx－m的顶点P是直角梯形OABC内部或边上的一个动点，m为常数．(1)求s与t的值，并在直角坐标系中画出．．直角梯形OABC；(2)当抛物线y=x2＋mx－m与直角梯形OABC的边AB相交时，求m的取值范围．（第24题）【093】已知在平面直角坐标系中，四边形OABC 是矩形，点A 、C 的坐标分别为()3A 0，、()04C ，，点D 的坐标为()D 5-0，，点P 是直线AC 上的一动点，直线DP 与y 轴交于点M ．问：（1）当点P 运动到何位置时，直线DP 平分矩形OABC 的面积，请简要说明理由，并求出此时直线DP 的函数解析式；（2）当点P 沿直线AC 移动时，是否存在使DOM △与ABC △相似的点M ，若存在，请求出点M 的坐标；若不存在，请说明理由；（3）当点P 沿直线AC 移动时，以点P 为圆心、半径长为R （R ＞0）画圆，所得到的圆称为动圆P ．若设动圆P的直径长为AC ，过点D 作动圆P 的两条切线，切点分别为点E 、F ．请探求是否存在四边形DEPF 的最小面积S ，若存在，请求出S 的值；若不存在，请说明理由． 注：第（3）问请用备用图解答．【094】在平面直角坐标系中，已知(40)A -，，(10)B ，，且以AB 为直径的圆交y 轴的正半轴于点(02)C ，，过点C 作圆的切线交x 轴于点D ．（1）求过A B C ，，三点的抛物线的解析式 （2）求点D 的坐标（3）设平行于x 轴的直线交抛物线于E F ，两点，问：是否存在以线段EF 为直径的圆，恰好与x 轴相切？若存在，求出该圆的半径，若不存在，请说明理由？备用图【095】）如图1，已知：抛物线212y x bx c =++与x轴交于A B 、两点，与y 轴交于点C ，经过B C 、两点的直线是122y x =-，连结AC ． （1）B C 、两点坐标分别为B （_____，_____）、C （_____，_____），抛物线的函数关系式为______________； （2）判断ABC △的形状，并说明理由； （3）若ABC △内部能否截出面积最大的矩形DEFC （顶点D E F 、、、G 在ABC △各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．[抛物线2y ax bx c =++的顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭]【096】如图12，已知抛物线经过坐标原点O 和x 轴上另一点E ，顶点M 的坐标为 (2,4)；矩形ABCD 的顶点A 与点O 重合，AD 、AB 分别在x 轴、y 轴上，且AD=2，AB=3. （1）求该抛物线所对应的函数关系式；（2）将矩形ABCD 以每秒1个单位长度的速度从图12所示的位置沿x 轴的正方向匀速平行移动，同时一动点P也以相同的速度．．．．．从点A 出发向B 匀速移动，设它们运动的时间为t 秒（0≤t ≤3），直线AB 与该抛物线的交点为N （如图13所示）.① 当t=25时，判断点P 是否在直线ME 上，并说明理由；② 设以P 、N 、C 、D 为顶点的多边形面积为S ，试问S 是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．图1图2(备用)（第26题）【097】矩形OABC 在平面直角坐标系中位置如图13所示，A C 、两点的坐标分别为(60)A ，，(03)C -，，直线34y x =-与BC 边相交于D 点． （1）求点D 的坐标；（2）若抛物线294y ax x =-经过点A ，试确定此抛物线的表达式；（3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P 为对称轴上一动点，以P O M 、、为顶点的三角形与OCD △相似，求符合条件的点P 的坐标．【098】如图，在平面直角坐标系中，点A （0，6），点B 是x 轴上的一个动点，连结AB ，取AB 的中点M ，将线段MB 绕着点B 按顺时针方向旋转90o ，得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是（t ，0）. （1）当t =4时，求直线AB 的解析式； （2）当t >0时，用含t 的代数式表示点C 的坐标及△ABC 的面积；（3）是否存在点B ,使△ABD 为等腰三角形?若存在，请求出所有符合条件的点B 的坐标；若不存在，请说明理由.【099】我们所学的几何知识可以理解为对“构图”的研究：根据给定的（或构造的）几何图形提出相关的概念和．．．．．．．．．．．．．．．．．．．．．．．问题（或者根据问题构造图形），并加以研究．．．．．．．．．．．．．．．．．．．．. 例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三·y OA x备用图条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）.请你用上面的思想和方法对下面关于圆的问题进行研究：(1) 如图1，在圆O 所在平面上，放置一条．．直线m （m 和圆O 分别交于点A 、B ），根据这个图形可以提出的概念或问题有哪些（直接写出两个即可）？(2) 如图2，在圆O 所在平面上，请你放置与圆O 都相交且不同时经过圆心．．．．．．．的两条．．直线m 和n （m 与圆O 分别交于点A 、B ，n 与圆O 分别交于点C 、D ）. 请你根据所构造的图形提出一个结论，并证明之. (3) 如图3，其中AB 是圆O 的直径，AC 是弦，D 是的中点，弦DE ⊥AB 于点F . 请找出点C 和点E 重合的条件，并说明理由.【100】抛物线)0(2≠++=a c bx ax y 的顶点为M ，与x 轴的交点为A 、B （点B 在点A 的右侧），△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。

中考数学压轴题集锦精选100题（含答案）一、中考压轴题1．如图，在△ABC中，∠BAC＝30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且＝，弦AD的延长线交切线PC于点E，连接BC．（1）判断OB和BP的数量关系，并说明理由；（2）若⊙O的半径为2，求AE的长．【分析】（1）首先连接OC，由PC切⊙O于点C，可得∠OCP＝90°，又由∠BAC＝30°，即可求得∠COP＝60°，∠P＝30°，然后根据直角三角形中30°角所对的直角边等于斜边的一半，证得OB＝BP；（2）由（1）可得OB＝OP，即可求得AP的长，又由＝，即可得∠CAD＝∠BAC＝30°，继而求得∠E＝90°，继而在Rt△AEP中求得答案．【解答】解：（1）OB＝BP．理由：连接OC，∵PC切⊙O于点C，∴∠OCP＝90°，∵OA＝OC，∠OAC＝30°，∴∠OAC＝∠OCA＝30°，∴∠COP＝60°，∴∠P＝30°，在Rt△OCP中，OC＝OP＝OB＝BP；（2）由（1）得OB＝OP，∵⊙O的半径是2，∴AP＝3OB＝3×2＝6，∵＝，∴∠CAD＝∠BAC＝30°，∴∠BAD＝60°，∵∠P＝30°，∴∠E＝90°，在Rt△AEP中，AE＝AP＝×6＝3．【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理．此题难度适中，注意掌握数形结合思想的应用，注意掌握辅助线的作法．2．如图，在矩形ABCD中，AB＝8，AD＝6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP＝CQ．设AP＝x．（1）当PQ∥AD时，求x的值；（2）当线段PQ的垂直平分线与BC边相交时，求x的取值范围；（3）当线段PQ的垂直平分线与BC相交时，设交点为E，连接EP、EQ，设△EPQ的面积为S，求S关于x的函数关系式，并写出S的取值范围．【分析】（1）根据已知条件，证明四边形APQD是矩形，再根据矩形的性质和AP＝CQ 求x即可；（2）连接EP、EQ，则EP＝EQ，设BE＝y，列出等式（8﹣x）2+y2＝（6﹣y）2+x2然后根据函数的性质来求x的取值范围；（3）由图形的等量关系列出方程，再根据函数的性质来求最值．【解答】解：（1）当PQ∥AD时，则∠A＝∠APQ＝90°，∠D＝∠DQP＝90°，又∵AB∥CD，∴四边形APQD是矩形，∴AP＝QD，∵AP＝CQ，AP＝CD＝，∴x＝4．（2）如图，连接EP、EQ，则EP＝EQ，设BE＝y．∴（8﹣x）2+y2＝（6﹣y）2+x2，∴y＝．∵0≤y≤6，∴0≤≤6，∴≤x≤．（3）S△BPE＝•BE•BP＝••（8﹣x）＝，S△ECQ＝＝•（6﹣）•x＝，∵AP＝CQ，∴S BPQC＝，∴S＝S BPQC﹣S△BPE﹣S△ECQ＝24﹣﹣，整理得：S＝＝（x﹣4）2+12（），∴当x＝4时，S有最小值12，当x＝或x＝时，S有最大值．∴12≤S≤．【点评】解答本题时，涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点，这是一道综合性比较强的题目，所以在解答题目时，一定要把各个知识点融会贯通，这样解题时才会少走弯路．3．汽车产业的发展，有效促进我国现代化建设．某汽车销售公司2005年盈利1500万元，到2007年盈利2160万元，且从2005年到2007年，每年盈利的年增长率相同．（1）该公司2006年盈利多少万元？（2）若该公司盈利的年增长率继续保持不变，预计2008年盈利多少万元？【分析】（1）需先算出从2005年到2007年，每年盈利的年增长率，然后根据2005年的盈利，算出2006年的利润；（2）相等关系是：2008年盈利＝2007年盈利×每年盈利的年增长率．【解答】解：（1）设每年盈利的年增长率为x，根据题意得1500（1+x）2＝2160解得x1＝0.2，x2＝﹣2.2（不合题意，舍去）∴1500（1+x）＝1500（1+0.2）＝1800答：2006年该公司盈利1800万元．（2）2160（1+0.2）＝2592答：预计2008年该公司盈利2592万元．【点评】本题的关键是需求出从2005年到2007年，每年盈利的年增长率．等量关系为：2005年盈利×（1+年增长率）2＝2160．4．如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，连接PC并延长PC交y轴于点D（0，3）．（1）求证：△POD≌△ABO；（2）若直线l：y＝kx+b经过圆心P和D，求直线l的解析式．【分析】（1）首先连接PB，由直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，可求得∠APB＝∠DPO＝60°，∠ABO＝∠POD＝90°，即可得△P AB是等边三角形，可得AB＝OP，然后由ASA，即可判定：△POD≌△ABO；（2）易求得∠PDO＝30°，由OP＝OD•tan30°，即可求得点P的坐标，然后利用待定系数法，即可求得直线l的解析式．【解答】（1）证明：连接PB，∵直径为OA的⊙P与x轴交于O、A两点，点B、C把三等分，∴∠APB＝∠DPO＝×180°＝60°，∠ABO＝∠POD＝90°，∵P A＝PB，∴△P AB是等边三角形，∴AB＝P A，∠BAO＝60°，∴AB＝OP，∠BAO＝∠OPD，在△POD和△ABO中，∴△POD≌△ABO（ASA）；（2）解：由（1）得△POD≌△ABO，∴∠PDO＝∠AOB，∵∠AOB＝∠APB＝×60°＝30°，∴∠PDO＝30°，∴OP＝OD•tan30°＝3×＝，∴点P的坐标为：（﹣，0）∴，解得：，∴直线l的解析式为：y＝x+3．【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式．此题综合性较强，难度适中，注意准确作出辅助线，注意数形结合思想的应用．5．广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．（1）求平均每次下调的百分率．（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【分析】（1）根据题意设平均每次下调的百分率为x，列出一元二次方程，解方程即可得出答案；（2）分别计算两种方案的优惠价格，比较后发现方案①更优惠．【解答】解：（1）设平均每次下调的百分率为x，则6000（1﹣x）2＝4860，解得：x1＝0.1＝10%，x2＝1.9（舍去），故平均每次下调的百分率为10%；（2）方案①购房优惠：4860×100×（1﹣0.98）＝9720（元）；方案②可优惠：80×100＝8000（元）．故选择方案①更优惠．【点评】本题主要考查一元二次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解，属于中档题．6．用两种方法解答：已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，求代数式（m2+mp+1）（n2+np+1）的值．【分析】本题主要是利用韦达定理来计算．已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，有四个等式可供使用：m+n＝2﹣p①，mn＝1②，m2+（p﹣2）m+1＝0③，n2+（p﹣2）n+1＝0④．通过变形方法，合理地选择解题方法．【解答】解：∵m、n是x2+（p﹣2）x+1＝0的根，∴m+n＝2﹣p，mn＝1．方法一：m2+（p﹣2）m+1＝0，n2+（p﹣2）n+1＝0．即m2+pm+1＝2m，n2+pn+1＝2n．原式＝2m×2n＝4mn＝4．方法二：（m2+mp+1）（n2+np+1）＝（m2+mp）（n2+np）+m2+mp+n2+np+1＝m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1＝1+mp+np+p2+m2+n2+mp+np+1＝2+p2+m2+n2+2（m+n）p＝2+p2+m2+n2+2（2﹣p）p＝2+p2+m2+n2+4p﹣2p2＝2+（m+n）2﹣2mn+4p﹣2p2+p2＝2+（2﹣p）2﹣2+4p﹣2p2+p2＝4﹣4p+p2+4p﹣p2＝4．【点评】本题主要是通过根与系数的关系来求值．注意把所求的代数式转化成m+n＝2﹣p，mn＝1的形式，正确对所求式子进行变形是解题的关键．7．如图，⊙O是等边△ABC的外接圆，AB＝2，M、N分别是边AB、AC的中点，直线MN交⊙O于E、F两点，BD∥AC交直线MN于点D．求出图中线段DM上已有的一条线段的长．【分析】连接OA交MN于点G，则OA⊥BC，由三角形的中位线的性质可得MN的长，易证得△BMD≌△AMN，有DM＝MN，由相交弦定理得ME•MF＝MA•MB，就可求得EM，DE的值．【解答】解：∵M，N分别是边AB，AC的中点∴MN∥BC，MN＝BC＝1又∵BD∥AC∴∠DBA＝∠A＝60°∵BM＝AM，∠BMD＝∠AMN∴△BMD≌△AMN∴DM＝MN＝1连接OA交MN于点G，则OA⊥BC∴OA⊥EF∴EG＝FG，MG＝FN由相交弦定理得：ME•MF＝MA•MB∴EM（EM+1）＝1解得EM＝（EM＝不合题意，舍去）∴DE＝DM﹣EM＝∴DE（3﹣DE）＝1解得DE＝（DE＝不合题意，舍去）．【点评】本题利用了三角形的中位线的性质，等边三角形的性质，全等三角形的判定和性质，一元二次方程的解法求解．8．如图，已知△BEC是等边三角形，∠AEB＝∠DEC＝90°，AE＝DE，AC，BD的交点为O．（1）求证：△AEC≌△DEB；（2）若∠ABC＝∠DCB＝90°，AB＝2 cm，求图中阴影部分的面积．【分析】（1）在△AEC和△DEB中，已知AE＝DE，BE＝CE，且夹角相等，根据边角边可证全等．（2）由图可知，在连接EO并延长EO交BC于点F，连接AD之后，整个图形是一个以EF所在直线对称的图形．即△AEO和△DEO面积相等，只要求出其中一个即可，而三角形AEO面积＝•OE•FB，所以解题中心即为求出OE和FB，有（1）中结论和已知条件即可求解．【解答】（1）证明：∵∠AEB＝∠DEC＝90°，∴∠AEB+∠BEC＝∠DEC+∠BEC，即∠AEC＝∠DEB，∵△BEC是等边三角形，∴CE＝BE，又AE＝DE，∴△AEC≌△DEB．（2）解：连接EO并延长EO交BC于点F，连接AD．由（1）知AC＝BD．∵∠ABC＝∠DCB＝90°，∴∠ABC+∠DCB＝180°，∴AB∥DC，AB＝＝CD，∴四边形ABCD为平行四边形且是矩形，∴OA＝OB＝OC＝OD，又∵BE＝CE，∴OE所在直线垂直平分线段BC，∴BF＝FC，∠EFB＝90°．∴OF＝AB＝×2＝1，∵△BEC是等边三角形，∴∠EBC＝60°．在Rt△AEB中，∠AEB＝90°，∠ABE＝∠ABC﹣∠EBC＝90°﹣60°＝30°，∴BE＝AB•cos30°＝，在Rt△BFE中，∠BFE＝90°，∠EBF＝60°，∴BF＝BE•cos60°＝，EF＝BE•sin60°＝，∴OE＝EF﹣OF＝＝，∵AE＝ED，OE＝OE，AO＝DO，∴△AOE≌△DOE．∴S△AOE＝S△DOE∴S阴影＝2S△AOE＝2וEO•BF＝2×××＝（cm2）．【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质，进行逻辑推理能力和运算能力．9．如图，有一直径MN＝4的半圆形纸片，其圆心为点P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴向右翻滚至位置Ⅴ，其中，位置Ⅰ中的MN平行于数轴，且半⊙P与数轴相切于原点O；位置Ⅱ和位置Ⅳ中的MN垂直于数轴；位置Ⅲ中的MN在数轴上；位置Ⅴ中的点N到数轴的距离为3，且半⊙P与数轴相切于点A．解答下列问题：（1）位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；（2）求位置Ⅲ中的圆心P在数轴上表示的数；（3）纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时，求点N所经过路径长及该纸片所扫过图形的面积；（4）求OA的长．[（2），（3），（4）中的结果保留π]．【分析】（1）先求出圆的半径，再根据切线的性质进行解答；（2）根据位置Ⅰ中的长与数轴上线段ON相等求出的长，再根据弧长公式求出的长，进而可得出结论；（3）作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形，在Rt△NPH中，根据sin∠NPH＝＝即可∠NPH、∠MP A的度数，进而可得出的长，【解答】解：（1）∵⊙P的直径＝4，∴⊙P的半径＝2，∵⊙P与直线有一个交点，∴位置Ⅰ中的MN与数轴之间的距离为2；位置Ⅱ中的半⊙P与数轴的位置关系是相切；故答案为：2，相切；（2）位置Ⅰ中的长与数轴上线段ON相等，∵的长为＝π，NP＝2，∴位置Ⅲ中的圆心P在数轴上表示的数为π+2．（3）点N所经过路径长为＝2π，S半圆＝＝2π，S扇形＝＝4π，半⊙P所扫过图形的面积为2π+4π＝6π．（4）如图，作NC垂直数轴于点C，作PH⊥NC于点H，连接P A，则四边形PHCA为矩形．在Rt△NPH中，PN＝2，NH＝NC﹣HC＝NC﹣P A＝1，于是sin∠NPH＝＝，∴∠NPH＝30°．∴∠MP A＝60°．从而的长为＝，于是OA的长为π+4+π＝π+4．【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式，在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系．10．如图，△ABC内接于⊙O，AB＝6，AC＝4，D是AB边上一点，P是优弧BAC的中点，连接P A、PB、PC、PD．（1）当BD的长度为多少时，△P AD是以AD为底边的等腰三角形？并证明；（2）在（1）的条件下，若cos∠PCB＝，求P A的长．【分析】（1）根据等弧对等弦以及全等三角形的判定和性质进行求解；（2）过点P作PE⊥AD于E．根据锐角三角函数的知识和垂径定理进行求解．【解答】解：（1）当BD＝AC＝4时，△P AD是以AD为底边的等腰三角形．∵P是优弧BAC的中点，∴＝．∴PB＝PC．又∵∠PBD＝∠PCA（圆周角定理），∴当BD＝AC＝4，△PBD≌△PCA．∴P A＝PD，即△P AD是以AD为底边的等腰三角形．（2）过点P作PE⊥AD于E，由（1）可知，当BD＝4时，PD＝P A，AD＝AB﹣BD＝6﹣4＝2，则AE＝AD＝1．∵∠PCB＝∠P AD（在同圆或等圆中，同弧所对的圆周角相等），∴cos∠P AD＝cos∠PCB＝，∴P A＝．【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理．11．在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得△A1B1C1，使点C1落在直线BC上（点C1与点C不重合），（1）如图，当∠C＞60°时，写出边AB1与边CB的位置关系，并加以证明；（2）当∠C＝60°时，写出边AB1与边CB的位置关系（不要求证明）；（3）当∠C＜60°时，请你在如图中用尺规作图法作出△AB1C1（保留作图痕迹，不写作法），再猜想你在（1）、（2）中得出的结论是否还成立并说明理由．【分析】（1）AB1∥BC．因为等腰三角形，两底角相等，再根据平行线的判定，内错角相等两直线平行，可证明两直线平行．（2）当∠C＝60°时，写出边AB1与边CB的位置关系也是平行，证明方法同（1）题．（3）成立，根据旋转变换的性质画出图形．利用三角形全等即可证明．【解答】解：（1）AB1∥BC．证明：由已知得△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（5分）（2）如图1，∠C＝60°时，AB1∥BC．（7分）（3）如图，当∠C＜60°时，（1）、（2）中的结论还成立．证明：显然△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∴∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（13分）【点评】考查图形的旋转，等腰三角形的性质，平行线的判定．本题实质是考查对图形旋转特征的理解，旋转前后的图形是全等的．12．九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，求旗杆AB的高度．【分析】利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB＝EF＝1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出，把相关条件代入即可求得AH＝11.9，所以AB＝AH+HB＝AH+EF＝13.5m．【解答】解：∵CD⊥FB，AB⊥FB，∴CD∥AB∴△CGE∽△AHE∴即：∴∴AH＝11.9∴AB＝AH+HB＝AH+EF＝11.9+1.6＝13.5（m）．【点评】主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．13．一个不透明的口袋里有红、黄、绿三种颜色的球（除颜色外其余都相同），其中红球有2个，黄球有1个，任意摸出一个黄球的概率为．（1）试求口袋里绿球的个数；（2）若第一次从口袋中任意摸出一球（不放回），第二次任意摸出一球，请你用树状图或列表法，求出两次都摸到红球的概率．【分析】（1）根据概率的求解方法，利用方程求得绿球个数；（2）此题需要两步完成，所以采用树状图法或者列表法都比较简单，解题时要注意是放回实验还是不放回实验，此题为不放回实验．【解答】解：（1）设口袋里绿球有x个，则，解得x＝1．故口袋里绿球有1个．（2）红一红二黄绿红一红二，红一黄，红一绿，红一红二红一，红二黄，红一绿，红二黄红一，黄红二，黄绿，黄绿红一，绿红二，绿黄，绿故，P（两次都摸到红球）＝．【点评】（1）解题时要注意应用方程思想；（2）列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．14．已知：y关于x的函数y＝（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．（1）求k的取值范围；（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2＝4x1x2．①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最小值．【分析】（1）分两种情况讨论，当k＝1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0．（2）①根据（k﹣1）x12+2kx2+k+2＝4x1x2及根与系数的关系，建立关于k的方程，求出k 的值；②充分利用图象，直接得出y的最大值和最小值．【解答】解：（1）当k＝1时，函数为一次函数y＝﹣2x+3，其图象与x轴有一个交点．当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，令y＝0得（k﹣1）x2﹣2kx+k+2＝0．△＝（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1．综上所述，k的取值范围是k≤2．（2）①∵x1≠x2，由（1）知k＜2且k≠1，函数图象与x轴两个交点，∴k＜2，且k≠1．由题意得（k﹣1）x12+（k+2）＝2kx1①，将①代入（k﹣1）x12+2kx2+k+2＝4x1x2中得：2k（x1+x2）＝4x1x2．又∵x1+x2＝，x1x2＝，∴2k•＝4•．解得：k1＝﹣1，k2＝2（不合题意，舍去）．∴所求k值为﹣1．②如图，∵k1＝﹣1，y＝﹣2x2+2x+1＝﹣2（x﹣）2+．且﹣1≤x≤1．由图象知：当x＝﹣1时，y最小＝﹣3；当x＝时，y最大＝．∴y的最大值为，最小值为﹣3．【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值，充分利用图象是解题的关键．15．如图①，有四张编号为1、2、3、4的卡片，卡片的背面完全相同．现将它们搅匀并正面朝下放置在桌面上．（1）从中随机抽取一张，抽到的卡片是眼睛的概率是多少？（2）从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处，然后再随机抽取一张贴在大头娃娃的右眼处，用树状图或列表法求贴法正确的概率．【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【解答】解：（1）所求概率为；（2）方法①（树状图法）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为，方法②（列表法）1 2 3 4第一次抽取第二次抽取1（2，1）（3，1）（4，1）2（1，2）（3，2）（4，2）3（1，3）（2，3）（4，3）4（1，4）（2，4）（3，4）共有12种可能的结果：（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3），∵其中有两种结果（1，2），（2，1）是符合条件的，∴贴法正确的概率为．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．16．经统计分析，某市跨河大桥上的车流速度v（千米/小时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为80千米/小时，研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．（1）求大桥上车流密度为100辆/千米时的车流速度；（2）在交通高峰时段，为使大桥上的车流速度大于40千米/小时且小于60千米/小时，应控制大桥上的车流密度在什么范围内？（3）车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量＝车流速度×车流密度．求大桥上车流量y的最大值．【分析】（1）当20≤x≤220时，设车流速度v与车流密度x的函数关系式为v＝kx+b，根据题意的数量关系建立方程组求出其解即可；（2）由（1）的解析式建立不等式组求出其解即可；（3）设车流量y与x之间的关系式为y＝vx，当x＜20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论．【解答】解：（1）设车流速度v与车流密度x的函数关系式为v＝kx+b，由题意，得，解得：，∴当20≤x≤220时，v＝﹣x+88，当x＝100时，v＝﹣×100+88＝48（千米/小时）；（2）由题意，得，解得：70＜x＜120．∴应控制大桥上的车流密度在70＜x＜120范围内；（3）设车流量y与x之间的关系式为y＝vx，当0≤x≤20时y＝80x，∴k＝80＞0，∴y随x的增大而增大，∴x＝20时，y最大＝1600；当20≤x≤220时y＝（﹣x+88）x＝﹣（x﹣110）2+4840，∴当x＝110时，y最大＝4840．∵4840＞1600，∴当车流密度是110辆/千米，车流量y取得最大值是每小时4840辆．【点评】本题考查了车流量＝车流速度×车流密度的运用，一次函数的解析式的运用，一元一次不等式组的运用，二次函数的性质的运用，解答时求出函数的解析式是关键．17．如图，反比例函数的图象经过点A（4，b），过点A作AB⊥x轴于点B，△AOB 的面积为2．（1）求k和b的值；（2）若一次函数y＝ax﹣3的图象经过点A，求这个一次函数的解析式．【分析】（1）由△AOB的面积为2，根据反比例函数的比例系数k的几何意义，可知k的值，得出反比例函数的解析式，然后把x＝4代入，即可求出b的值；（2）把点A的坐标代入y＝ax﹣3，即可求出这个一次函数的解析式．【解答】解：（1）∵反比例函数的图象经过点A，AB⊥x轴于点B，△AOB的面积为2，A（4，b），∴OB×AB＝2，×4×b＝2，∴AB＝b＝1，∴A（4，1），∴k＝xy＝4，∴反比例函数的解析式为y＝，即k＝4，b＝1．（2）∵A（4，1）在一次函数y＝ax﹣3的图象上，∴1＝4a﹣3，∴a＝1．∴这个一次函数的解析式为y＝x﹣3．【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．18．图（1）是一个10×10格点正方形组成的网格．△ABC是格点三角形（顶点在网格交点处），请你完成下面的两个问题：（1）在图（1）中画出与△ABC相似的格点△A1B1C1和△A2B2C2，且△A1B1C1与△ABC的相似比是2，△A2B2C2与△ABC的相似比是；（2）在图（2）中用与△ABC，△A1B1C1，△A2B2C2全等的格点三角形（每个三角形至少使用一次），拼出一个你熟悉的图案，并为你设计的图案配一句贴切的解说词．【分析】（1）△A1B1C1与△ABC的相似比是2，则让△ABC的各边都扩大2倍就可．△A2B2C2与△ABC的相似比是；△ABC的直角边是2，所以△A2B2C2与的直角边是即一个对角线的长度．斜边为2．依此画图即可；（2）拼图有审美意义即可，答案不唯一．【解答】解：【点评】本题主要考查了相似图形的画法，做这类题时根据的是相似图形的性质，即相似比相等．对应角相等．19．如图，矩形ABCD的边AD、AB分别与⊙O相切于点E、F，（1）求的长；（2）若，直线MN分别交射线DA、DC于点M、N，∠DMN＝60°，将直线MN沿射线DA方向平移，设点D到直线的距离为d，当时1≤d≤4，请判断直线MN与⊙O的位置关系，并说明理由．【分析】（1）连接OE、OF，利用相切证明四边形AFOE是正方形，再根据弧长公式求弧长；（2）先求出直线M1N1与圆相切时d的值，结合1≤d≤4，划分d的范围，分类讨论．【解答】解：（1）连接OE、OF，∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F，∴∠A＝90°，∠OEA＝∠OF A＝90°∴四边形AFOE是正方形∴∠EOF＝90°，OE＝AE＝∴的长＝＝π．（2）如图，将直线MN沿射线DA方向平移，当其与⊙O相切时，记为M1N1，切点为R，交AD于M1，交BC于N1，连接OM1、OR，∵M1N1∥MN∴∠DM1N1＝∠DMN＝60°∴∠EM1N1＝120°∵MA、M1N1切⊙O于点E、R∴∠EM1O＝∠EM1N1＝60°在Rt△EM1O中，EM1＝＝＝1∴DM1＝AD﹣AE﹣EM1＝+5﹣﹣1＝4．过点D作DK⊥M1N1于K在Rt△DM1K中DK＝DM1×sin∠DM1K＝4×sin∠60°＝2即d＝2，∴当d＝2时，直线MN与⊙O相切，当1≤d＜2时，直线MN与⊙O相离，当直线MN平移到过圆心O时，记为M2N2，点D到M2N2的距离d＝DK+OR＝2+＝3＞4，∴当2＜d≤4时，MN直线与⊙O相交．【点评】本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定．20．如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．（1）试判断DE与BD是否相等，并说明理由；（2）如果BC＝6，AB＝5，求BE的长．【分析】（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD＝∠BAD，根据圆周角定理即可得出∠DEB＝∠DBE，便可证得DE＝DB．（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出AC•BE＝CB•AD．进而求出BE的长．【解答】解：（1）DE＝BD证明：连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD＝∠BAD（等腰三角形三线合一），∴＝，∴DE＝BD；（2）∵AB＝5，BD＝BC＝3，∴AD＝4，∴S△ABC＝•AC•BE＝•CB•AD，∴BE＝4.8．【点评】本题主要考查了等腰三角形的性质，圆周角定理等知识点的运用，用等腰三角形三线合一的特点得出圆周角相等是解题的关键．21．如图，在Rt△ABC中，∠C＝90°，Rt△BAP中，∠BAP＝90°，已知∠CBO＝∠ABP，BP交AC于点O，E为AC上一点，且AE＝OC．（1）求证：AP＝AO；（2）求证：PE⊥AO；（3）当AE＝AC，AB＝10时，求线段BO的长度．【分析】（1）根据等角的余角相等证明即可；（2）过点O作OD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CO＝DO，利用“SAS”证明△APE和△OAD全等，根据全等三角形对应角相等可得∠AEP＝∠ADO＝90°，从而得证；（3）设C0＝3k，AC＝8k，表示出AE＝CO＝3k，AO＝AP＝5k，然后利用勾股定理列式求出PE＝4k，BC＝BD＝10﹣4k，再根据相似三角形对应边成比例列式求出k＝1然后在Rt △BDO中，利用勾股定理列式求解即可．【解答】（1）证明：∵∠C＝90°，∠BAP＝90°∴∠CBO+∠BOC＝90°，∠ABP+∠APB＝90°，又∵∠CBO＝∠ABP，∴∠BOC＝∠APB，∵∠BOC＝∠AOP，∴∠AOP＝∠APB，∴AP＝AO；（2）证明：如图，过点O作OD⊥AB于D，∵∠CBO＝∠ABP，∵AE＝OC，∴AE＝OD，∵∠AOD+∠OAD＝90°，∠P AE+∠OAD＝90°，∴∠AOD＝∠P AE，在△AOD和△P AE中，，∴△AOD≌△P AE（SAS），∴∠AEP＝∠ADO＝90°∴PE⊥AO；（3）解：设AE＝OC＝3k，∵AE＝AC，∴AC＝8k，∴OE＝AC﹣AE﹣OC＝2k，∴OA＝OE+AE＝5k．由（1）可知，AP＝AO＝5k．如图，过点O作OD⊥AB于点D，∵∠CBO＝∠ABP，∴OD＝OC＝3k．在Rt△AOD中，AD＝＝＝4k．∴BD＝AB﹣AD＝10﹣4k．∵OD∥AP，∴，即解得k＝1，∵AB＝10，PE＝AD，∴PE＝AD＝4K，BD＝AB﹣AD＝10﹣4k＝6，OD＝3在Rt△BDO中，由勾股定理得：BO＝＝＝3．【点评】本题考查了全等三角形的判定与性质，角平分线上的点到角的两边的距离相等的性质，勾股定理，相似三角形的判定与性质，（2）作辅助线构造出过渡线段DO并得到全等三角形是解题的关键，（3）利用相似三角形对应边成比例求出k＝1是解题的关键．22．如图，AD是⊙O的直径．（1）如图①，垂直于AD的两条弦B1C1，B2C2把圆周4等分，则∠B1的度数是22.5°，∠B2的度数是67.5°；（2）如图②，垂直于AD的三条弦B1C1，B2C2，B3C3把圆周6等分，分别求∠B1，∠B2，∠B3的度数；（3）如图③，垂直于AD的n条弦B1C1，B2C2，B3C3，…，B n∁n把圆周2n等分，请你用含n的代数式表示∠B n的度数（只需直接写出答案）．【分析】根据条件可以先求出圆的各段弧的度数，根据圆周角等于所对弧的度数的一半，就可以求出圆周角的度数．【解答】解：（1）垂直于AD的两条弦B1C1，B2C2把圆周4等分，则是圆的，因而度数是45°，因而∠B1的度数是22.5°，同理的度数是135度，因而，∠B2的度数是67.5°；（2）∵圆周被6等分∴＝＝＝360°÷6＝60°∵直径AD⊥B1C1∴＝＝30°，∴∠B1＝＝15°∠B2＝＝×（30°+60°）＝45°∠B3＝＝×（30°+60°+60°）＝75°；（3）B n∁n把圆周2n等分，则弧BnD的度数是：，则∠B n AD＝，在直角△AB n D中，．【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题，依据是圆周角等于所对弧的度数的一半．23．今年，我国政府为减轻农民负担，决定在5年内免去农业税．某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同．（1）求降低的百分率；（2）若小红家有4人，明年小红家减少多少农业税？（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税？【分析】（1）设降低的百分率为x，则降低一次后的数额是25（1﹣x），再在这个数的基础上降低x，则变成25（1﹣x）（1﹣x）即25（1﹣x）2，据此即可列方程求解；（2）每人减少的税额是25x，则4个人的就是4×25x，代入（1）中求得的x的值，即可求解；（3）每个人减少的税额是25x，乘以总人数16000即可求解．【解答】解：（1）设降低的百分率为x，依题意有，25（1﹣x）2＝16，解得，x1＝0.2＝20%，x2＝1.8（舍去）；（2）小红全家少上缴税25×20%×4＝20（元）；（3）全乡少上缴税16000×25×20%＝80 000（元）．答：降低的增长率是20%，明年小红家减少的农业税是20元，该乡农民明年减少的农业税是80 000元．【点评】本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2＝b．24．在△ABC中，AB＝AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F．设DE＝a，DF＝b，且实数a，b满足9a2﹣24ab+16b2＝0，并有＝2566，∠A使得方程x2﹣x•sin A+sin A﹣＝0有两个相等的实数根．（1）试求实数a，b的值；（2）试求线段BC的长．【分析】（1）由题意可知：2a2b＝2566，则2a2b＝248，则a2b＝48．化简9a2﹣24ab+16b2＝0得：（3a﹣4b）2＝0，则3a﹣4b＝0，即3a＝4b，则根据，可求得a与b的值；（2）要求BC的长需求出BD和CD的长，知BD、CD分别是直角三角形BDE和直角三角形CDF中的斜边．又知在△ABC中，AB＝AC，则∠B＝∠C，则根据三角函数只要知道∠B或∠C的读数即可，要求∠B或∠C的读数需求的∠A的读数，根据判别式可以求得∠A的读数．【解答】解：（1）由条件有，解得；（2）又由关于x的方程的判别式△＝sin2A﹣sin A+＝（sin A﹣）2＝0，则sin A＝，而∠A为三角形的一个内角，所以∠A1＝60°或∠A2＝120° 2分当∠A＝60°时，△ABC为正三角形，∠B＝∠C＝60°于是分别在Rt△BDE和Rt△CDF中有BD＝，CD＝所以BC＝BD+DC＝．当∠A＝120°时，△ABC为等腰三角形，∠B＝∠C＝30°同上方法可得BC＝14． 3分所以线段BC的长应为或14．【点评】考查了解直角三角形以及判别式的应用．25．某市城建部门经过长期市场调查发现，该市年新建商品房面积P（万平方米）与市场新房均价x（千元/平方米）存在函数关系P＝25x；年新房销售面积Q（万平方米）与市场新房均价x（千元/平方米）的函数关系为Q＝﹣10；（1）如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；（2）在（1）的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少？变化了多少？结合年新房销售总额和积压面积的变化情况，请你提出一条合理。

一、解答题1．平面直角坐标系中，点在y轴正半轴，点在x轴正半轴，以线段AB为边在第一象限内作等边ABC，点C关于y轴的对称点为点D，连接AD，BD，且BD交y 轴于点E．(1)补全图形，并填空；①若点，则点D的坐标是__________；②若，则________．(2)若，求证：AD垂直平分BC；(3)若时，探究的数量关系，并证明．2．如图，在平面直角坐标系中，已知一次函数y＝kx+b(k>0，b>0)的图象与x轴交于A，与y轴交于C．双曲线y＝ax（x＞0）的图象交一次函数的图像于第一象限内的点B，BD⊥x轴于D．E是AB中点，直线DE交y轴于F，连接AF．（1）若k=1，点B(2，6)时．①求一次函数和反比例函数的解析式；②求AFD的面积．（2）当k=2，a=12时，求AFD的面积．（3）求证：当k，b，a为任意常数时，AFD的面积恒等于1 2 a3．已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．（1）如图1，当∠MBN 绕B 点旋转到AE =CF 时，求证：AE +CF =EF ．（2）如图2，当∠MBN 绕B 点旋转到AE ≠CF 时，上述结论是否成立？若成立，请给予证明；若不成立，线段AE ，CF ，EF 又有怎样的数量关系？请写出你的猜想，并证明． （3）当∠MBN 绕B 点继续旋转到图3位置时，AE =10，CF =2．求EF 的长度．4．抛物线212y x mx n =-++与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，已知(1,0)A -，(0,2)C ．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在点P ，使PCD 是以CD 为腰的等腰三角形？如果存在，求出P 点的坐标；如果不存在，请说明理由；（3）点E 是线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，当四边形CDBF 的面积最大时，求点E 的坐标．5．如果抛物线1C 的顶点在抛物线2C 上，同时，抛物线2C 的顶点在抛物线1C 上，那么我们称抛物线1C 与2C 关联．（1）已知抛物线①221y x x =+-，判断下列抛物线②221y x x =-++；③221y x x =++与已知抛物线①是否关联，并说明理由．（2）抛物线211:(1)28C y x =+-，动点P 的坐标为(,2)t ，将抛物线绕点(,2)P t 旋转180︒得到抛物线2C ，若抛物线1C 与2C 关联，求抛物线2C 的解析式．（3）点A 为抛物线211:(1)28C y x =+-的顶点，点B 为与抛物线1C 关联的抛物线顶点，是否存在以AB 为斜边的等腰直角ABC ，使其直角顶点C 在y 轴上，若存在，求出C 点的坐标；若不存在，请说明理由．6．已知二次函数2y x bx c =+-图象通过两点(1,),(2,10)P a Q a ． （1）如果a ，b ，c 是整数，且8c b a <<，求a ，b ，c 值．（2）设二次函数2y x bx c =+-图象和x 轴交点为A 、B ，和y 轴交点为C ．如果有关x 方程20x bx c +-=两个根都是整数，求ABC 面积．7．如图1，直线AB 与x 轴，y 轴分别交于A ，B 两点，点C 在x 轴负半轴上，这三个点的坐标分别为A (4，0)，B (0，4)，C (−1，0) ． （1）请求出直线AB 的解析式；（2）连接BC，若点E是线段AC上的一个动点（不与A，C重合），过点E作EF//BC交AB于点F，当△BEF的面积是52时，求点E的坐标；（3）如图2，将点B向右平移1个单位长度得到点D，在x轴上存在动点P，若∠DCO+∠DPO=∠α，当tan∠α=4时，请直接写出点P的坐标．8．如图①，在平面直角坐标系中，点A、B的坐标分别为A（4，0）、B（0，3），连结AB．抛物线经过点B，且对称轴是直线．（1）求抛物线的函数关系式．（2）将图①中的△ABO沿x轴向左平移得到△DCE（如图②），当四边形ABCD是菱形时，说明点C和点D都在该抛物线上．（3）在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），过点M作MN∥y轴交直线CD于点N．设点M的横坐标为m，线段MN的长为l．求l与m之间的函数关系式．（4）在（3）的条件下，直接写出m为何值时，以M、N、C、E为顶点的四边形是平行四边形．9．如图1，ABC内接于O，弦AE交BC于点D，连接BO，且ABO DAC∠∠．（1）求证：AE BC⊥；（2）如图2，点F在弧AC上，连接CF、BF，BF交AE于点M，若ACF OBC∠=∠，求证：MD ED=；（3）如图3，在（2）的条件下，3AM=时，求弦CF∠=∠，若10BFC EACBM=，3的长．10．如图，在△ABC中，AB＝6，AC＝BC＝5，CD⊥AB于点D，点P从点A出发，以每秒5个单位长度的速度沿折线AC—CB向终点B运动，当点P不与A，B，C重合时，过点P作PQ⊥AB交AB于点Q，过点P作PM⊥PQ，使得PM＝2PQ，点M、点D在PQ的同侧，连结MQ，设点P的运动时间为t（s）（1）线段CD＝．（2）当点P在线段BC上时，PC＝．（用含t的代数式表示）（3）当点M落在△BCD的内部时，求t的取值范围；（4）连结CM，当△CPM为锐角三角形时，直接写出t的取值范围．11．在四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，过点A作AE⊥BC于点E．（1）如图1，求证：AE＝CE；（2）如图2，点F是线段CE．上一点，CF＝BE，FG⊥BC交BD于点G，连接AG，求证：AG＝BE+FG；（3）如图3，在（2）的条件下，若EF＝10，FG＝7，求AG的长．12．在ABC中，AB AC=，D是边AC上一点，F是边AB上一点，连接BD、CF交于点E，连接AE，且．(1)如图1，若90BAC∠=︒，，，求点B到AE的距离；(2)如图2，若E为BD中点，连接FD，FD平分，G为CF上一点，且，求证：；(3)如图3，若，12△沿着AB翻折得，点H为的BC=，将ABD中点，连接HA、HC，当周长最小时，请直接写出的值．13．如图1，抛物线y＝ax2＋bx＋3过点A（﹣1，0），点B（3，0），与y轴交于点C．M是抛物线任意一点，过点M作直线l⊥x轴，交x轴于点E，设M的横坐标为m（0＜m＜3）．(1)求抛物线的解析式及tan∠OBC的值；(2)当m＝1时，P是直线l上的点且在第一象限内，若△ACP是直角三角形时，求点P的坐标；(3)如图2，连接BC，连接AM交y轴于点N，交BC于点D，连接BM，设△BDM的面积为S1，△CDN的面积为S2，求S1﹣S2的最大值．14．如图，抛物线y＝ax2+bx+2与直线AB相交于A（﹣1，0），B（3，2），与x轴交于另一点C．(1)求抛物线的解析式；(2)在y上是否存在一点E，使四边形ABCE为矩形，若存在，请求出点E的坐标；若不存在，请说明理由；DB的最小值．(3)以C为圆心，1为半径作⊙C，D为⊙O上一动点，求DA+5515．如图，已知抛物线y＝ax2＋bx＋5（a≠0）与x轴交于点A（﹣5，0），点B（1，0）（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点，连接BD．直线y＝经过点A，且与y轴交于点E．(1)求抛物线的解析式；(2)点N是抛物线上的一点，当△BDN是以DN为腰的等腰三角形时，求点N的坐标；(3)点F为线段AE上的一点，点G为线段OA上的一点，连接FG，并延长FG与线段BD 交于点H（点H在第一象限），当∠EFG＝3∠BAE且HG＝2FG时，求出点F的坐标．16．如图1，点A，点B的坐标分别（a，0），（0，b），且b＝+4，将线段BA绕点B逆时针旋转90°得到线段BC．(1)直接写出a ＝ ，b ＝ ，点C 的坐标为 ；(2)如图2，作CD ⊥x 轴于点D ，点M 是BD 的中点，点N 在△OBD 内部，ON ⊥DN ，求证：2MN +ON ＝DN ．(3)如图3，点P 是第二象限内的一个动点，若∠OPB ＝90°，求线段CP 的最大值． 17．如图，在长方形ABCD 中，10AB =，9BC =，点E 在AB 上，点G 在AD 上，AEFG 为正方形．点M ，N 分别为BC ，CD 上的动点，MO BC ⊥，NO CD ⊥，且点O 始终在正方形AEFG 的内部，MO 交EF 于点P ，NO 交FG 于点Q ．(1)设CM AE a ==，①用含a 的代数式表示四边形EBMP 的周长；②若四边形OPFQ ，GQND 的周长之和恰好为四边形EBMP 周长的两倍，求a 的值． (2)设3CM x =，2CN x =，AE n CN =，是否存在正整数x ，n ，使得EBMP GQND S S =四边形四边形若存在，求出x ，n 的值；若不存在，请说明理由．18．如图，抛物线24y ax bx =++的对称轴是直线x ＝3，与x 轴交于()2,0A -，B 两点，与y 轴交于点C ．(1)求抛物线的函数表达式；(2)若M 是抛物线上任意一点，过点M 作y 轴的平行线，交直线BC 于点N ，若3MN =，求点M 的坐标；(3)设点D ，E 是直线3x =上两动点，且1DE =，点D 在点E 上方，求四边形ACDE 周长的最小值．19．已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B （1，0）两点，与y 轴交于点()03C -，．(1)求二次函数的表达式及A 点坐标；(2)D 是二次函数图象上位于第三象限内的点，若点D 的横坐标为m ，ACD △的面积为S ，求S 与m 之间的函数关系式，并写出ACD △的面积取得最大值时点D 的坐标； (3)M 是二次函数图象对称轴上的点，在二次函数图象上是否存在点N ．使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．20．如图1，已知二次函数y ＝ax 232+x +c 的图象与y 轴交于点C （0，4），与x 轴交于点A 、点B ，点B 坐标为（8，0）．（1）请直接写出二次函数的解析式；（2）在直线BC 上方的抛物线上是否存在点P ，使△PBC 的面积为16？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）在（2）的结论下，过点P作PF⊥x轴于点F，交直线BC于点E，连接AE，点N是抛物线对称轴上的动点，在抛物线上是否存在点M，使得以M、N、A、E为顶点的四边形是平行四边形？如果存在，请直接写出点M的坐标；如果不存在，请说明理由．【参考答案】**科目模拟测试一、解答题1．(1)①D(-2，3) ②∠BEO=60°；(2)答案见解析；(3)DE= AE+2EO，证明见解析．【解析】【分析】（1）①根据关于y轴的对称的性质可得答案，关于y轴的对称的两点，横坐标互为相反数，纵坐标不变；②根据C、D两点关于y轴的对称，可知y轴是线段CD的垂直平分线，得AD=AC、∠CAF=∠DAF，然后由等边△ABC得AC=AB，最后得AD=AB，∠ADB=∠ABD，即可得答案；（2）由|a−3|+b2−6b+9=0，得a=b，得∠BAO=45°，然后根据平角得∠CAF的度数、∠CAG的度数，即可得答案；（3）先证∠EBO=30°，得BE=2EO，然后作HE=AE，证△ADE≌△ABH，得DE=BH，最后证BH= AE+2EO，即可得答案．(1)解：补全图形如下图①∵C、D两点关于y轴的对称的两点，∴横坐标互为相反数，纵坐标不变，∵C(2，3)，∴D(-2，3)；②∵C、D两点关于y轴的对称，∠CAD=140°，=70°∴∠CAF=∠DAF=140°×12∵△ABC是等边三角形，∴∠CAB=60°，AC=AB，∴∠BAE=180°-70°-60°=50°，∵C、D两点关于y轴的对称，∴AD=AC，∴AD=AB，∴∠ADB=∠ABD=[180°-（360°-140°-60°）] ×1=10°2∴∠BEO=∠BAE+∠ABD=50°+10°=60°；(2)如下图：延长DA交BC于点G，∵|a−3|+b2−6b+9=0，∴|a−3|+（b−3）2=0，∴a=b=3，∴AO=BO，∴∠BAO=45°，∴∠CAF=180°-45°-60°=75°，∴∠CAG=180°-75°-75°=30°，∴∠BAG=60°-30°=30°，∴∠CAG=∠BAG，∴AD垂直平分BC；(3)如下图：作HE=AE，连接AH，∵C、D两点关于y轴的对称，∴∠CAF=∠DAF，∴∠CAE=∠DAE，∵∠CAE=60°+∠BAO，∴∠DAE=60°+∠BAO，∴∠DAB=60°+2∠BAO，=60°－∠BAO，∴∠DBA=[ 180°－（60°+2∠BAO）] ×12∴∠BEO=∠BAO+∠DBA=∠BAO+60°－∠BAO=60°，∴∠EBO=30°，∵∠AOB=90°，∴BE=2EO，∵HE=AE，∠BEA=∠AEH=60°，∴△AEH是等边三角形，∴AH=AE，∠HAE=60°，∴∠DAH=∠BAO，∵∠DAE=∠DAH+60°，∠BAH=∠BAO+60°，∴∠DAE=∠BAH，在△ADE和△ABH中，，∴△ADE≌△ABH，∴DE =BH ， ∵HE =AE ，BE =2EO ， ∴BH =BE +HE = AE +2EO ， ∴DE = AE +2EO ． 【点睛】本题考查了关于y 轴的对称的性质、等边三角形的性质、三角形的内角与外角的性质，垂直平分线的判定、在直角三角形中，30°的所对的边是斜边的一半、全等三角形的判定和性质，做题的关键是作辅助线，构造△ADE ≌△ABH ．2．（1）①y =x +4，12y x=； ②6；（2）6；（3）见解析 【解析】 【分析】（1）①把点B （2，6）分别代入y ＝x ＋b 和y ＝kx （x ＞0），根据待定系数法即可求得； ②求出D ，E 的坐标，求出直线DE 的解析式，得到F 点坐标，故可求出△ADF 的面积； （2）联立两函数求出B 点坐标，再得到E 点坐标，求出直线DE 的解析式，从而得到F 点坐标，根据三角形的面积公式即可求出AFD 的面积 （3）与（2）同理即可求解． 【详解】解：（1）①∵一次函数y ＝x ＋b 的图象与反比例函数y ＝ax（x ＞0）的图象交于B ，B （2，6）， ∴6＝2＋b ，6＝2a ， ∴b ＝4，a ＝12，∴一次函数解析式为y ＝x ＋4，反比例函数解析式为12y x=； ②令一次函数y ＝x ＋4=0 解得x =-4 ∴A （-4，0）∵E 是AB 中点，B （2，6） ∴E （-1，3） ∵BD ⊥x 轴于D ∴D （2，0）设直线DE 的解析式为y =mx +n ，代入E （-1，3）、D （2，0）得302m nm n =-+⎧⎨=+⎩解得12m n =-⎧⎨=⎩∴直线DE 的解析式为y =-x +2，令x =0，得y =2 ∴F （0，2） ∴OF =2 ∴AFD 的面积为1162622AD OF ⨯=⨯⨯=； （2）∵一次函数y ＝2x ＋b ，反比例函数12y x= 联立得2x ＋b =12x∴2x 2+bx -12=0解得xx舍去）∴B由A （12b -，0）得到E∵D0）设直线DE 的解析式为y =mx +n ，代入ED）得0m n m n ⎧=⎪=+⎪⎩解得2m n =-⎧⎪⎨=⎪⎩∴直线DE 的解析式为y =-2x令x =0，y∴F （0∴OF∵A （12b -，0），D0） ∴AD =12b∴AFD的面积为11622AD OF ⨯==；（3）∵一次函数y ＝kx ＋b ，反比例函数ay x= 联立得kx 2+bx -a =0解得xx舍去）∴B由A （bk -，0）得到E∵D0）设直线DE 的解析式为y =mx +n ，代入ED）得0m n m n ⎧=+⎪=+⎪⎩解得m kn =-⎧⎪⎨=⎪⎩∴直线DE 的解析式为y =-kx令x =0，y∴F （0∴OF∵A （bk -，0），D0）∴AD =b k∴AFD的面积为11212282ak AD OF a k ⨯===．【点睛】本题是反比例函数与一次函数的交点问题，解题的关键是熟知待定系数法求函数的解析式，三角形的面积及一元二次方程的解法．3．（1）见解析；（2）成立，理由见解析；（3）EF =8． 【解析】 【分析】（1）根据SAS 证明Rt △ABE ≌Rt △CBF ，求得BF =BE ，易求得△BEF 是等边三角形，可得BF =2CF ，即可解题；（2）将Rt △ABE 顺时针旋转120°，可得FG =CG +CF =AE +CF ，易证∠GBF =∠EBF =60°，即可求证△GBF ≌△EBF ，可得FG =EF ，即可解题；（3）将Rt △ABE 顺时针旋转120°，可得FG =CG -CF =AE -CF ，易证∠GBF =∠EBF =60°，即可求证△GBF ≌△EBF ，可得FG =EF ，即可解题． 【详解】证明：（1）∵Rt △ABE 和Rt △CBF 中，AB =BC ，CF =AE ，∠C =∠A =90°， ∴Rt △ABE ≌Rt △CBF （SAS ）， ∴∠CBF =∠ABE ，BF =BE ， ∵∠ABC =120°，∠MBN =60°，∴∠CBF =∠ABE =30°，△BEF 是等边三角形， ∴BF =2CF ，BE =2AE ，BF =EF ， ∴EF =BF =2CF =AE +CF ； （2）成立，理由如下：如图2，将Rt △ABE 顺时针旋转120°，∵AB =BC ，∠ABC =120°，∴A 点与C 点重合，AE =CG ，BG =BE ， ∵∠BCG =∠BCF =90°， ∴点G 、C 、F 共线， ∴FG =CG +CF =AE +CF ，∵∠ABC =120°，∠MBN =60°，∠ABE =∠CBG ， ∴∠GBF =60°， 在△GBF 和△EBF 中， 60BG BE GBF EBF BF BF =⎧⎪∠=∠=︒⎨⎪=⎩，∴△GBF ≌△EBF （SAS ）， ∴FG =EF ， ∴EF =AE +CF ；（3）如图3，将Rt △ABE 顺时针旋转120°，∵AB =BC ，∠ABC =120°，∴A 点与C 点重合，AE =CG ，BG =BE ， ∵∠BCG =∠BCD =90°， ∴点G 、C 、D 共线， ∴FG =CG +CF =AE +CF ， ∵∠ABC =∠ABE +∠CBE =120°， ∴∠CBG +∠CBE =∠GBE =120°， ∵∠MBN =60°， ∴∠GBF =60°， 在△BFG 和△BFE 中， 60BG BE GBF EBF BF BF =⎧⎪∠=∠=︒⎨⎪=⎩， ∴△BFG ≌△BFE ，（SAS ） ∴GF =EF ，∴EF =AE -CF =10-2=8． 【点睛】本题考查了全等三角形的判定和性质，30°角所对直角边是斜边一半的性质，旋转的性质等知识点，本题中求证△BFG ≌△BFE 是解题的关键．4．（1）213222y x x =-++；（2）存在，13(,4)2P ，235(,)22P ，335(,)22P -；（3）点()2,1E【解析】 【分析】（1）把()1,0A -，()0,2C 代入抛物线的解析式，利用待定系数法求解即可；（2）先求解抛物线的对称轴3,2x = 再求解CD 的长，由CDP 是以CD 为腰的等腰三角形，可得123CP DP DP CD ===．再作CH ⊥对称轴于点H ，从而可得答案； （3）先求解()4,0B ．再求解直线BC 的解析式为122y x =-+．过点C 作CM EF ⊥于M ，设1,22E a a ⎛⎫-+ ⎪⎝⎭，213,222F a a a ⎛⎫-++ ⎪⎝⎭，根据BCDCEFBEFCDBF S SSS=++四边形111222BD OC EF CM EF BN =⋅+⋅+⋅列函数关系式，从而可得答案. 【详解】解：（1）∵抛物线212y x mx n =-++经过()1,0A -，()0,2C ，∴10,22,m n n ⎧--+=⎪⎨⎪=⎩解得3,22.m n ⎧=⎪⎨⎪=⎩ ∴抛物线的解析式为213222y x x =-++．（2）∵22131325222228y x x x ⎛⎫=-++=--+⎪⎝⎭， ∴抛物线的对称轴是直线32x =． ∴32OD =． ∵()0,2C ，∴2OC =．在Rt OCD △中，由勾股定理，得2235222CD ⎛⎫=+ ⎪⎝⎭． ∵CDP 是以CD 为腰的等腰三角形， ∴123CP DP DP CD ===． 作CH ⊥对称轴于点H ， ∴12HP HD ==．∴14DP =．∴13(,4)2P ，235(,)22P ，335(,)22P -． （3）当0y =时，由2132022x x -++=，解得11x =-，24x =，∴()4,0B ．设直线BC 的解析式为y kx b =+，得2,40,b k b =⎧⎨+=⎩解得1,22.k b ⎧=-⎪⎨⎪=⎩∴直线BC 的解析式为122y x =-+． 过点C 作CM EF ⊥于M ，设1,22E a a ⎛⎫-+ ⎪⎝⎭，213,222F a a a ⎛⎫-++ ⎪⎝⎭，∴2213112222222EF a a a a a ⎛⎫=-++--+=-+ ⎪⎝⎭．∵BCDCEFBEFCDBF S SSS=++四边形111222BD OC EF CM EF BN =⋅+⋅+⋅ 2215111122(4)2222222a a a a a a ⎛⎫⎛⎫=⨯⨯+-++--+ ⎪ ⎪⎝⎭⎝⎭225134(2)22a a a =-++=--+． ∴根据题意04a ≤≤，∴当2a =时，CDBF S 四边形的最大值为132，此时点()2,1E ． 【点睛】本题考查的是利用待定系数法求解抛物线的解析式，二次函数与等腰三角形，图形面积的最值问题，灵活运用二次函数的图象与性质解决问题是解题的关键.5．（1）①、②关联，理由见解析；（2）21(7)68y x =--+或21(9)68y x =-++；（3）存在，（0，1）或（0，3+420，3-42 【解析】 【分析】（1）首先求得抛物线①的顶点坐标，然后检验是否此点在抛物线②与③上，再求得抛物线②的顶点坐标，检验是否在抛物线①上即可求得答案；（2）首先求得抛物线C 1的顶点坐标，则可得：点P 在直线y =2上，则可作辅助线：作M 关于P 的对称点N ，分别过点M 、N 作直线y =2的垂线，垂足为E ，F ，则可求得：点N 的坐标，利用顶点式即可求得结果；（3）分别从当A ，B ，C 逆时针分布时与当A ，B ，C 顺时针分布时分析，根据全等三角形的知识，即可求得点C 的坐标，注意别漏解． 【详解】解：（1）∵①抛物线y =x 2+2x -1=（x +1）2-2的顶点坐标为M （-1，-2）， ∴②当x =-1时，y =-x 2+2x +1=-1-2+1=-2， ∴点M 在抛物线②上；∵③当x =-1时，y =x 2+2x +1=1-2+1=0， ∴点M 不在抛物线③上； ∴抛物线①与抛物线②有关联；∵抛物线②y =-x 2+2x +1=-（x -1）2+2，其顶点坐标为（1，2）， 经验算：（1，2）在抛物线①上， ∴抛物线①、②是关联的；（2）抛物线C 1：211:(1)28C y x =+-的顶点M 的坐标为（-1，-2），∵动点P 的坐标为（t ，2）， ∴点P 在直线y =2上，作M 关于P 的对称点N ，分别过点M 、N 作直线y =2的垂线，垂足为E ，F ，则ME =NF =4，∴点N 的纵坐标为6，当y =6时，21(1)268x +-=，解得：x 1=7，x 2=-9，①设抛物C 2的解析式为：y =a （x -7）2+6， ∵点M （-1，-2）在抛物线C 2上， ∴-2=a （-1-7）2+6，∴a =18-，∴抛物线C 2的解析式为：21(7)68y x =--+，②设抛物C 2的解析式为：y =a （x +9）2+6， ∵点M （-1，-2）在抛物线C 2上， ∴-2=a （-1+9）2+6，∴a =18-，∴抛物线C 2的解析式为：21(9)68y x =-++；（3）点C 在y 轴上的一动点，以AC 为腰作等腰直角△ABC ，令C 的坐标为（0，c ），则点B 的坐标分两类：①当A ，B ，C 逆时针分布时，如图中B 点，过点A ，B 作y 轴的垂线，垂足分别为H ，F ， 在等腰直角△ABC 中，AC =BC ，∠ACB =90°，即∠ACH +∠BCH =90°， ∵∠ACH +∠CAH =90°，∴∠CAH =∠BCH ，又∠AHC =∠BFC =90°， 则△BCF ≌△CAH （AAS ），∴CF =AH =1，BF =CH =c +2，点B 的坐标为（c +2，c -1），当点B 在抛物线C 1：y =221(1)8x +-上时，c -1=18（c +2+1）2-2，解得：c =1．②当A ，B ，C 顺时针分布时，如图中B ′点，过点B ′作y 轴的垂线，垂足为D ， 同理可得：点B ′的坐标为（-c -2，c +1），当点B ′在抛物线C 1：y =18（x +1）2-2上时，c +1=18（-c -2+1）2-2，解得：c =3+42c =3-42综上所述，存在三个符合条件的等腰直角三角形，其中C 点的坐标分别为：C 1（0，1），C 2（0，3+42C 3（0，3-42【点睛】此题考查了待定系数法求二次函数的解析式以及二次函数的顶点坐标的求解方法，全等三角形的性质等知识．此题综合性很强，难度较大，注意数形结合思想与分类讨论思想的应用．6．（1）a=2，b=15，c=14；（2）1【解析】【分析】（1）代入两点坐标，求得b、c（用a表示），再由已知c＜b＜8a，联立不等式组求得a、b、c的值；（2）设出程x2+bx-c=0的两个根，根据根与系数的关系与因式分解求得两根，得出函数解析式，进一步求得图象与x、y轴的交点A、B、C三点解答问题．【详解】解：点P（1，a）、Q（2，10a）在二次函数y=x2+bx-c的图象上，故1+b-c=a，4+2b-c=10a，解得b=9a-3，c=8a-2；（1）由c＜b＜8a知8293 938a aa a-<-⎧⎨-<⎩，解得1＜a＜3，又a为整数，所以a=2，b=9a-3=15，c=8a-2=14；（2）设m，n是方程的两个整数根，且m≤n．由根与系数的关系可得m+n=-b=3-9a，mn=-c=2-8a，消去a，得9mn-8（m+n）=-6，两边同时乘以9，得81mn-72（m+n）=-54，分解因式，得（9m-8）（9n-8）=10．∴9819810mn-=⎧⎨-=⎩或9810981mn-=-⎧⎨-=-⎩或985982mn-=-⎧⎨-=-⎩或982985mn-=⎧⎨-=⎩，解得：12mn=⎧⎨=⎩或2979mn⎧=-⎪⎪⎨⎪=⎪⎩或1323mn⎧=⎪⎪⎨⎪=⎪⎩或109139mn⎧=⎪⎪⎨⎪=⎪⎩；又∵m，n是整数，所以后面三组解舍去，故m=1，n=2．因此，b=-（m+n）=-3，c=-mn=-2，二次函数的解析式为y=x2-3x+2．令y=0，则x=1或x=2，令x=0，则y=2，∴点A、B的坐标为（1，0）和（2，0），点C的坐标为（0，2），∴△ABC的面积为12×(2−1)×2＝1．【点睛】此题主要考查二次函数图象上点的坐标特点、根与系数的关系、不等式组、以及三角形的面积计算公式．7．（1）4y x =-+；（2）点E 坐标为3,02⎛⎫⎪⎝⎭；（3）点P 的坐标为(19，0)或(-17，0)．【解析】 【分析】（1）利用待定系数法即可求解；（2）同理利用待定系数法求得直线BC 的解析式为y =4x +4，再求得直线EF 的解析式，联立求得点F 的坐标，利用BEF OAB OBE AEF S S S S ∆∆∆∆=--列式求解即可； （3）计算得到tan 4DGDOG OG∠==，推出∠α=∠DOG ，∠DPO =∠CDO ，设点P 的坐标为(p ，0)，分p <0和p >0两种情况讨论，利用相似三角形的判定和性质求解即可． 【详解】解：（1）∵直线AB 经过点A (4，0)，B (0，4)， ∴设直线AB 的解析式为y =kx +4， 把A (4，0)代入得：4k +4=0， 解得：k =-1，∴直线AB 的解析式为y =-x +4； （2）设点E (m ，0)，同理求得直线BC 的解析式为y =4x +4， ∵EF //BC ，∴设直线EF 的解析式为：4y x n =+，将点E 坐标代入上式并解得：04m n =+， ∴4n m =-，∴直线EF 的解析式为：44y x m =-， ∴444x x m -+=-， 解得：()415x m =+， 把x 的值代入4y x =-+，得1645my -=．∴点F 坐标为4416455m m +-⎛⎫⎪⎝⎭，， ()1111645444422252BEF OAB OBE AEF m S S S S m m -=--=⨯⨯-⨯--⨯=△△△△，解得：32m =， ∴点E 坐标为302⎛⎫⎪⎝⎭，； （3）将点B (0，4)向右平移1个单位长度得到点D ，则D (1，4)， 过点D 作DG ⊥x 轴于点G ，则∠OGD =90°，OG =1，GD =4，CG =2， ∴tan 4DGDOG OG∠==，OD =22224117DG OG +=+=， 在Rt △CDG 中，CD =22222425CG DG +=+=， ∵tan ∠α=4， ∴∠α=∠DOG ，∵∠DCO +∠DPO =∠α，∠DCO +∠CDO =∠DOG ， ∴∠DPO =∠CDO ， ∵点P 在x 轴上∴设点P 的坐标为(p ，0)，当p <0时，PO =-p ，∵∠POD =∠DOC ，∠DPO =∠CDO ， ∴△POD ~△DOC ， ∴PO DODO CO=， ∴PO =2171DO CO ==17，此时，点P 的坐标为(-17，0)；当p>0时，PO=p，PC=p+1，∵∠PCD=∠DCO，∠DPC=∠ODC，∴△PCD~△DCO，∴PC DC DC CO=，∴PC=(22201DCCO==，∴p=PC-1=19，此时，点P的坐标为(19，0)；综上，点P的坐标为(19，0)或(-17，0)．【点睛】本题是一次函数综合题，主要考查了待定系数法，角平分线的性质，相似三角形的性质和判定，三角形函数等，分类讨论是解第（3）问的关键．8．(1) y=；（2）见解析；（3）l=或l=；（4）m=或或−3时，以点M、N、C、E为顶点的四边形是平行四边形．【解析】【分析】（1）把点B的坐标代入抛物线解析式、联合对称轴x=列出关于系数b、c的方程组，通过解方程组来求它们的值；（2）由平移的性质易求点C、D的坐标，将它们的坐标分别代入抛物线解析式进行验证即可；（3）根据点C、D的坐标易求直线CD的解析式为y=．根据已知条件知点M、N 的横坐标都是m，则l的值就是点M、N的纵坐标之差．(4)由平行四边形的对边相等的性质推知MN=CE=3，利用所求的l与m间的函数式可以求得相应的m的值．【详解】解：（1）由已知，得，解得，∴二次函数的解析式为y=；（2）在Rt△ABO中，∵OA=4，OB=3，∴AB=5．又∵四边形ABCD是菱形，∴BC=AD=AB=5．∵△ABO沿x轴向左平移得到△DCE，∴CE=OB=3．∴C(−5，3)、D(−1，0)．当x=−5时，y==3，当x=−1时，y==0，∴C、D在该抛物线上；（3）设直线CD的解析式为y=kx+b，则，解得，∴y=，∵MN//y轴，∴M、N的横坐标均为m，当M在直线CD的上方时，有l=MN=()−()=；当M在直线CD的下方时，有l=MN=()− ()=．∴l与m之间的函数解析式为l=或l=．(4)由于MN//CE，要使以点M、N、C、E为顶点的四边形是平行四边形，只需MN=CE=3，当=3时，解得；当=3时，解得．即当m=或或−3时，以点M、N、C、E为顶点的四边形是平行四边形．【点睛】本题综合考查了待定系数法求一次函数、二次函数解析式，平行四边形的性质．在求有关动点问题时要注意分析题意分情况讨论结果．9．（1）见解析；（2）见解析；（3）53．【解析】【分析】（1）作⊙O的直径AF，连接BF，证明∠ACD+∠CAE=90°即可；（2）连接BE，利用角的转换证明∠BMD=∠BEM，从而可得BM=BE，进而根据等腰三角形三线合一即可得出结论；（3）如图3，证明BEM AEB得2=即可求出DE长，进而由勾股定理求出BE EM AEBD，再由相交线弦定理求出CD，即可得出CE长，EC FC=．=可得EC FC【详解】解：（1）如图1，作⊙O的直径AF，连接BF，∴∠AFB+∠OAB=90°，∵OA=OB，∴∠ABO=∠OAB，又∵∠DAC=∠ABO，∴∠DAC=∠ABO=∠OAB．∵AB AB=∵∠AFB=∠ACD，∵AF是直径∴∠AFB+∠OAB=90°，∴∠ACD+∠CAE=90°，∴∠ADC=90°，即AE⊥BC；（2）连接BE，∵AF AF=∴∠ACF=∠ABF，又∵∠ACF=∠OBC，∴∠ABF=∠OBC，∴∠ABO+∠OBF=∠FBC+∠OBF，∴∠ABO=∠FBC，∵∠DAC=∠ABO，∴∠DAC=∠MBC，∵∠BMD+∠MBC=∠ACD+∠DAC=90°，∴∠BMD=∠ACD，∵AB AB=∴∠BEM=∠ACD，∴∠BMD=∠BEM，∴BM=BE，∵AE⊥BC，∴MD=ED；（3）如图2，连接EC，∵BC BC=∴BFC BAC∠=∠，∵3BFC EAC∠=∠，∴3BAC EAC∠=∠，∴2BAE BAC EAC EAC∠=∠-∠=∠，∵EBC FBC DAC∠=∠=∠，∴=2MBE EBC FBC EAC∠=∠+∠∠，∴MBE BAE∠=∠，又∵E E∠=∠，∴BEM AEB，∴BE AE EM BE=，∵10BM BE=3AM= 1010=1010=∴=2EM，由（2）可知MD =ED ，BM =BE ，∴1DM DE ==，314AD AM DM =+=+=在Rt BDM 中，BD =，在Rt BDA 中，AB =， ∵=BE BE ， ∴BAD DCE ∠=∠， 又∵BDA CDE ∠=∠， ∴BDA EDC ，∴=EC DE AB BD，即1=53EC ∴5=3EC ，∵CAE FBC ∠=∠， ∴EC FC =，∴5=3EC FC =【点睛】本题是圆的综合题，主要考查了圆周角定理，涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点，解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系，从而利用相似或勾股定理解题．10．（1）4；（2）；（3）或；（4）或．【解析】 【分析】（1）首先根据等腰三角形三线合一的性质得到，然后根据勾股定理即可求出线段CD 的长度；（2）根据点P 运动的速度求出点P 运动的路程，然后减去AC 的长度即可求出PC 的长度；（3）分两种情况，当点P 在线段AC 上时和点P 在线段BC 上时，分别利用相似三角形的性质计算出点M 在线段CD 上时和点M 在线段BC 上时的时间，即可求出t 的取值范围； （4）分两种情况，当点P 在线段AC 上时和点P 在线段BC 上时，分别得出点M 在线段CD 上时和点M 在线段BC 上时是直角三角形，然后利用相似三角形的性质求出t 的值，即可得出△CPM 为锐角三角形时t 的取值范围． 【详解】解：（1）∵在△ABC 中，AC ＝BC ＝5 ∴ABC ∆是等腰三角形 ∵CD ⊥AB 于点D∴（三线合一）∴在中，由勾股定理得，故答案为：4；（2）∵点P从点A出发，以每秒5个单位长度的速度沿折线AC—CB向终点B运动∴点P运动的路程为5t∴当点P在线段BC上时，故答案为：；（3）当点P在线段AC上时，由题意得，，AC＝5，如图所示，当点M在线段CD上时，∵PQ⊥AB，CD⊥AB，∴∴∴∴，即，解得：，，∴，∵PM＝2PQ，∴，∵CD⊥AB，PQ⊥AB，PM⊥PQ，∴四边形PQDM是矩形，∴，∴，解得：，如图所示，当点M在线段BC上时，同理可得，，，，，，∵PQ⊥AB，PM⊥PQ，∴∴∴∴，即，解得：，∴当时，点M落在△BCD的内部；如图所示，当点P在线段BC上时，当点M在线段CD上时，设，则，同理可得，四边形MDQP是矩形，，∴，，∴，即，解得：，∴，∴，∴，当点P运动到B点时，，∴当时，点M落在△BCD的内部，综上所述，当点M落在△BCD的内部时，t的取值范围是或；（4）当点M在线段CD上时，，即是直角三角形，由（3）可得，此时，当时，如图所示，∵，，，则，，∵，，又∵，∴∴，即，解得：，∴当时，是锐角三角形；当点M在线段BC上时，当时，即是直角三角形，如图所示，设，则，，，，同理可得，，∴，即，解得：，∴，∴，∵当点M在CD上时，此时，即是直角三角形，由（3）可得，此时，∴当时，是锐角三角形，∴综上所述，当△CPM为锐角三角形时，t的取值范围是或．【点睛】此题考查了相似三角形的性质和判定，等腰三角形的性质，勾股定理，三角形动点问题等知识，解题的关键是根据题意画出相应的图形，分情况讨论利用相似三角形的性质求解．11．（1）见详解；（2）见详解；（3）29 2【解析】【分析】（1）过点D作DM⊥AE于点M，证明ABE△≌DAM△，即可得到结论；（2）延长GF到点M，使FM=BE，则BE+FG=MG，先证明ABE△≌BMF，再证明ABG≌MBG△，进而即可得到结论；（3）过点G作GN⊥AE，设BE=x，则AG=BE+FG=x+7，AN= 3+x，结合勾股定理，列出方程，进而即可求解．【详解】解：（1）过点D作DM⊥AE于点M，∵∠DME=∠MEC=∠C=90°，∴四边形CDME是矩形，∴DM=CE，又∵∠BAD=∠AMD=90°，∴∠1+∠EAD=∠2+∠EAD=90°，∴∠1=∠2，在ABE△和DAM△中，∵1290AMD AEB AB AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴ABE △≌DAM △， ∴AE=DM ， ∴AE =CE ；（2）延长GF 到点M ，使FM =BE ，则BE +FG =MG ，∵BE =CF ， ∴BF =CE =AE ， 在ABE △和BMF 中，∵90AE BF AEB BFM BE MF =⎧⎪∠=∠=︒⎨⎪=⎩， ∴ABE △≌BMF ， ∴∠BAE =∠MBF ，AB =BM ， ∵∠BAE +∠ABE =90°， ∴∠MBF +∠ABE =90°， ∴∠ABM =90°， ∵∠BAD =90°，AB =AD ， ∴∠A BD=45°， ∴∠DBM =45°， ∴∠ABD =∠DBM ， ∴ABG ≌MBG △， ∴AG=MG=BE +FG ；（3）过点G 作GN ⊥AE ，设BE =x ，则AG =BE +FG =x +7，∵∠GNE =∠NEF=EFG =90°， ∴四边形EFGN 是矩形， ∴NG =EF =10，EN=FG =7， 又∵AE =BF =10+x ， ∴AN =AE -EN =10+x -7=3+x ，在直角ANG 中，()()2223107x x ++=+，解得：x =152， ∴AG =x +7=152+7=292．【点睛】本题主要考查矩形的性质，全等三角形的判定和性质，勾股定理，等腰自交三角形的性质，添加辅助线构造全等三角形，掌握“截长补短法”是解题的关键．12．3(2)证明见解析 (3)【解析】 【分析】（1）如图所示，过点B作BG⊥AE交AE延长线于G，先证明∠ACF=∠GAB，即可证明△ABG≌△CAE得到BG=AE，由勾股定理得，再由，得到，则点B到AE的距离为（2）如图所示，延长AE到H使得，AE=HE，连接DH，CH，先证明△AEB≌△HED得到AB=HD=AC，∠ABE=∠HDE，则∠HCD=∠HDC，AB∥DH，从而推出∠BAC=∠HDC=∠HCD，再证明CE是AH的垂直平分线，得到AC=HC，则∠ACE=∠HCE，即∠HCA=2∠ACE，然后推出∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD，GD=GC，即可证明△AFD≌△GFD（AAS），得到AF=GF，则CF=GF+CG=AF+DG；（3）如图所示，连接，延长交BC于F，作直线BE⊥BC，由翻折的性质可知，，，，然后证明，得到，则点D在线段BC的垂直平分线上，即AF⊥BC，求出，由H 是的中点，得到直线A关于点H的对称点A'在直线BE上，则要使△AHC的周长最小，则要最小，即最小，即当A'、C、H、三点共线时有最小值，如图所示，连接交于，交AF于P，连接BP，先证明，得到，由平行线之间的间距相等，得到，然后求出，再证明，求出，由此求解即可．(1)解：如图所示，过点B作BG⊥AE交AE延长线于G，∵AE⊥CF，AG⊥BG，∴∠BAC=∠AGB=∠AEF=∠AEC=90°，∠AFC+∠ACF=90°，∴∠FAE+∠AFE=90°，∴∠ACF=∠GAB，又∵AB=CA，∴△ABG≌△CAE（AAS），∴BG=AE，在直角△AFC中，由勾股定理得，∵，∴，∴点B到AE(2)解：如图所示，延长AE到H使得，AE=HE，连接DH，CH，∵FD平分∠AFC，∴∠AFD=∠CFD，∵E是BD的中点，∴BE=DE，又∵AE=HE，∠AEB=∠HED，∴△AEB≌△HED（SAS），∴AB=HD=AC，∠ABE=∠HDE，∴∠HCD=∠HDC，∴∠BAC=∠HDC=∠HCD，∴∠ACE=∠HCE，即∠HCA=2∠ACE，∵∠GDC=∠GCD，∠FGD=∠GDC+∠GCD，∴∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD，GD=GC，又∵FD=FD，∠AFD=∠GFD，∴△AFD≌△GFD（AAS），∴AF=GF，∴CF=GF+CG=AF+DG；(3)解：如图所示，连接，延长交BC于F，作直线BE⊥BC，由翻折的性质可知，，，，∴，又∵AB=AC，，∴，∴，∴点D在线段BC的垂直平分线上，即AF⊥BC，∴，∵H是的中点，∴直线A关于点H的对称点A'在直线BE上，∴，∴要使△AHC的周长最小，则要最小，即最小，∴当A'、C、H、三点共线时有最小值，如图所示，连接交于，交AF于P，连接BP，∵BE⊥BC，AF⊥BC，∴，∴，，又∵，∴，∴，∵，BC⊥BE，∴,∵平行线之间的间距相等，∴∵AB=AC，∠BAC=120°，∴∠ABC=∠ACB=30°，∴AB=2AF，∴，∴，∴，∵P在线段BC的垂直平分线上，∴PB=PC，∴∠PBC=∠PCB，∵，∴，∴，∴，∴，∴，∴，∴【点睛】本题主要考查了全等三角形的性质与判定，线段垂直平分线的性质，等腰三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，平行线的性质与判定等等，熟练掌握相关知识是解题的关键．13．(1)y＝﹣x2+2x+3，1(2)（1，1）或（1，2）或（1，83）(3)【解析】【分析】（1）用待定系数法即可求解；（2）①当为直角时，证明，则，即，即可求解；②当为直角时，同理可解；③当为直角时，同理可解；（3）；，即可求解．(1)解：设抛物线的表达式为，则，则，解得1a=-，故抛物线的表达式为2y x2x3=-++，则；(2)解：当1m=时，则直线l为抛物线的对称轴，如图1，连接AC，设点(1,)P m，①当为直角时，则，，，，过点C作于点N，，，，，即，∴，解得1m=或2，故点P的坐标为(1,1)或(1,2)；②当为直角时，同理可得：点P'的坐标为8 (1,)3；③当为直角时，。

一、解答题1．如图，在直角梯形ABCD 中，AB ∥CD ，∠B ＝90°，AB ＝4，BC ＝8，CD ＝2m （m ＞2），P 为CD 中点，以P 为圆心，CP 为半径作半圆P ，交线段AC 于点E ，交线段AD 于点F ．（1）当E 为CA 中点时，①求证：E 是弧CF 的中点．②求此时m 的值．（2）连结PF ，若PF 平行△ABC 的某一边时求出满足条件的m 值．（3）连结PE ，将PE 绕着点E 顺时针旋转90°得到EP '，连结AP '，当AP '⊥AC 时，求此时CE 的长．2．如图1，在菱形ABCD 中，∠D ＝120°，AB ＝8，点M 从A 开始，以每秒1个单位的速度向点B 运动；点N 从C 出发，沿C →D →A 方向，以每秒2个单位的速度向点A 运动，若M 、N 同时出发，其中一点到达终点时，另一个点也随之停止运动．设运动的时间为t 秒，过点N 作NQ ⊥DC ，交AC 于点Q ．（1）当t ＝2时，求线段NQ 的长；（2）设△AMQ 的面积为S ，直接写出S 与t 的函数关系式及t 的取值范围；（3）在点M 、N 运动过程中，是否存在t 值，使得△AMQ 为等腰三角形？若存在，请求出t 的值；若不存在，请说明理由．3．如图，在平面直角坐标系中，抛物线2y x bx c =-++，与y 轴交于点A 与x 轴交于点E 、B ．且点()0,5A ，()5,0B ，点P 为抛物线上的一动点．（1）求二次函数的解析式；（2）如图1，过点A 作AC 平行于x 轴，交抛物线于点C ，若点P 在AC 的上方，作PD 平行于y 轴交AB 于点D ，连接PA ，PC ，当245AOE APCD S S ∆=四边形时，求点P 坐标； （3）设抛物线的对称轴与AB 交于点M ，点Q 在直线AB 上，当以点M 、E 、P 、Q 为顶点的四边形为平行四边形时，请直接写出点Q 的坐标．4．如图，抛物线2y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于C 点，OA =1，OB =OC =3．（1）求抛物线的表达式；（2）如图1，点D 为第一象限抛物线上一动点，连接DC ，DB ，BC ，设点D 的横坐标为m ，△BCD 的面积为S ，求S 的最大值；（3）如图2，点P (0，n )是线段OC 上一点(不与点O 、C 重合)，连接PB ，将线段PB 以点P 为中心，旋转90°得到线段PQ ，是否存在n 的值，使点Q 落在抛物线上？若存在，请求出满足条件的n 的值，若不存在，请说明理由．5．如图，抛物线223y x x =--+与x 轴交于A 、B 两点，与y 轴交于C 点．（1）在第二象限内的抛物线上确定一点P ，使四边形PBOC 的面积最大．求出点P 的坐标．（2）点M 为抛物线上一动点，x 轴上是否存在一点Q ，使点B 、C 、M 、Q 的顶点的四边形是平行四边形，若存在，请直接写出Q 点的坐标；若不存在，请说明理由．6．已知抛物线经过()30A -,，()1,0B ，52,2C ⎛⎫ ⎪⎝⎭三点，其对称轴交x 轴于点H ，一次函数()0y kx b k =+≠的图象经过点C ，与抛物线交于另一点D （点D 在点C 的左边），与抛物线的对称轴交于点E ． （1）求抛物线的解析式；（2）在抛物线上是否存在点F ，使得点A 、B 、E 、F 构成的四边形是平行四边形，如果存在，求出点F 的坐标，若不存在请说明理由（3）设∠CEH=α，∠EAH =β，当αβ>时，直接写出k 的取值范围7．如图1，直线l 1：y ＝kx 与直线l 2：y ＝﹣12x ＋b 相交于点A （4，3），直线l 2：y ＝﹣12x ＋b 与x 轴交于点B ，点E 为线段AB 上一动点，过点E 作EF ∥y 轴交直线l 1于点F ，连接BF ．（1）求k、b的值；（2）如图2，若点F坐标为（8，6），∠OFE的角平分线交x轴于点M．①求线段OM的长；②点N在直线l1的上方，当△OFN和△OFM全等时，直接写出点N的坐标．8．如图，抛物线y＝ax2+bx+c与x轴交于A（﹣2，0）、B（6，0）两点，与y轴交于点C．直线l与抛物线交于A、D两点，与y轴交于点E，点D的坐标为（4，3）．（1）求抛物线的解析式与直线l的解析式；（2）若点P是抛物线上的点且在直线l上方，连接PA、PD，求当△PAD面积最大时点P 的坐标及该面积的最大值；（3）若点Q是y轴上的点，且∠ADQ＝45°，求点Q的坐标．9．如图，在△ABC中，AB＝AC，⊙是△ABC的外接圆，连接BO并延长交边AC于点D．（1）如图1，求证：∠BAC＝2∠ABD；（2）如图2，过点B作BH⊥AC于点H，延长BH交⊙O于点G，连接OC，CG，OC交BG于点F，求证：BF＝2HG；（3）如图3，在（2）的条件下，若AD＝2，CD＝3，求线段BF的长．10．如图1，在平面直角坐标系中，抛物线y＝ax2+154x+c与x轴负半轴相交于点A（﹣20，0），与y轴相交于点B（0，﹣15）．（1）求抛物线的函数表达式及直线AB的函数表达式；（2）如图2，点C是第三象限内抛物线上的一个动点，连接AC、BC，直线OC与直线AB 相交于点D，当△ABC的面积最大时，求此时△ABC面积的最大值及点C的坐标；（3）在（2）的条件下，点E为线段OD上的一个动点，点E从点O开始沿OD以每秒10个单位长度的速度向点D运动（运动到点D时停止），以OE为边，在OD的左侧做正方形OEFG，设正方形OEFG与△OAD重叠的面积为S，运动时间为t秒．当t＞3时，请直接写出S与t之间的函数关系式为（不必写出t的取值范围）．11．在平面直角坐标系xOy中，点A(a，b)和点B(c，d)．给出如下定义：以AB为边，作等边三角形ABC，按照逆时针方向排列A，B，C三个顶点，则称等边三角形ABC为点A，B的逆序等边三角形．例如，当1,0,3,0a b c d=-===时，点A，B的逆序等边三角形ABC如图①所示．(1)已知点A(-1，0)，B(3，0)，则点C的坐标为___；请在图①中画出点C，B的逆序等边三角形CBD，点D的坐标为___．(2)图②中，点B(3，0)，点A在以点M(-2，0)为圆心1为半径的圆上，求点A，B的逆序等边三角形ABC的顶点C的横坐标取值范围．(3)图③中，点A在以点M(-2，0)为圆心1为半径的圆上，点B在以N(3，0)为圆心2为半径的圆上，且点B的纵坐标0d>，点A，B的逆序等边三角形ABC如图③所示．若点C 恰好落在直线y x t=+上，直接写出t的取值范围．12．已知：如图1，一次函数y＝mx＋5m的图像与x轴、y轴分别交于点A、B，与函数y＝－23x的图像交于点C，点C的横坐标为－3．（1）求点B的坐标；（2）若点Q为直线OC上一点，且S△QAC＝2S△AOC，求点Q的坐标；（3）如图2，点D为线段OA上一点，∠ACD＝∠AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．①在图2中，只利用圆规．．．．．作图找到点P的位置； (保留作图痕迹，不得在图2中作无关元素．)②求点P的坐标．13．在平面直角坐标系xOy中，⊙O的半径为1．对于线段AB，给出如下定义：若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′，则称线段AB是⊙O的以直线l为对称轴的“反射线段”，直线l称为“反射轴”．（1）如图，线段CD，EF，GH中是⊙O的以直线l为对称轴的“反射线段”有；（2）已知A点坐标为（0，2），B点坐标为（1，1），①若线段AB是⊙O的以直线l为对称轴的“反射线段”，求反射轴l与y轴的交点M的坐标．②若将“反射线段”AB沿直线y＝x的方向向上平移一段距离S，其反射轴l与y轴的交点的纵坐标yM的取值范围为12≤yM136≤，求S．（3）已知点M，N是在以原点为圆心，半径为2的圆上的两个动点，且满足MN＝1，若MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，求反射轴l未经过的区域的面积．（4）已知点M，N是在以（2，013MN2=MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，请直接写出反射轴l与y轴交点的纵坐标的取值范围．14．△ABC为等边三角形，AB=4，AD⊥BC于点D，点E为AD的中点．(1)如图1，将AE绕点A顺时针旋转60°至AF，连接EF交AB于点G，求证：G为EF中点．(2)如图2，在（1）的条件下，将△AEF绕点A顺时针旋转，旋转角为α，连接BE，H为BE的中点，连接DH，GH．当30°＜α＜120°时，猜想∠DHG的大小是否为定值，并证明你的结论．(3)在△AEF绕点A顺时针旋转过程中，H为BE的中点，连接CH，问线段CH何时取得最大值，请说明理由，并直接写出此时△ADH的面积．15．在ABC中，AB AC=，D是边AC上一点，F是边AB上一点，连接BD、CF交于点E，连接AE，且．(1)如图1，若90BAC∠=︒，，，求点B到AE的距离；(2)如图2，若E为BD中点，连接FD，FD平分，G为CF上一点，且，求证：；(3)如图3，若，12BC=，将ABD△沿着AB翻折得，点H为的中点，连接HA、HC，当周长最小时，请直接写出的值．16．在平面直角坐标系xOy中，已知抛物线y＝x2﹣2x﹣3与x轴交于A、B两点，与y轴交于C点，D为抛物线顶点．(1)连接AD，交y轴于点E，P是抛物线上的一个动点．①如图一，点P是第一象限的抛物线上的一点，连接PD交x轴于F，连接，若，求点P的坐标．②如图二，点P在第四象限的抛物线上，连接AP、BE交于点G，若，则w有最大值还是最小值？w的最值是多少？(2)如图三，点P是第四象限抛物线上的一点，过A、B、P三点作圆N，过点P作PM x⊥轴，垂足为I，交圆N于点M，点P在运动过程中，线段是否变化？若有变化，求出MI的取值范围；若不变，求出其定值．(3)点Q是抛物线对称轴上一动点，连接OQ、AQ，设AOQ外接圆圆心为H，当的值最大时，请直接写出点H的坐标．17．如图，在平面直角坐标系中，矩形OABC，点A在y轴上，点C在x轴上，其中B（﹣2，3），已知抛物线y＝﹣34x2＋bx＋c经过点A和点B．(1)求抛物线解析式；(2)如图1，点D （﹣2，﹣1）在直线BC 上，点E 为y 轴右侧抛物线上一点，连接BE 、AE ，DE ，若S △BDE ＝4S △ABE ，求E 点坐标；(3)如图2，在（2）的条件下，P 为射线DB 上一点，作PQ ⊥直线DE 于点Q ，连接AP ，AQ ，PQ ，若△APQ 为直角三角形，请直接写出P 点坐标．18．如图1，点A ，点B 的坐标分别（a ，0），（0，b ），且b ＝+4，将线段BA 绕点B 逆时针旋转90°得到线段BC ．(1)直接写出a ＝ ，b ＝ ，点C 的坐标为 ；(2)如图2，作CD ⊥x 轴于点D ，点M 是BD 的中点，点N 在△OBD 内部，ON ⊥DN ，求2+ON ＝DN ．(3)如图3，点P 是第二象限内的一个动点，若∠OPB ＝90°，求线段CP 的最大值．19．如图1，已知抛物线)(3343y x x =+-与x 轴交于A 、B 两点，与y 轴交于点C ，(1)写出A 、B 、C 三点的坐标．(2)若点P 为OBC 内一点，求OP BP CP ++的最小值．(3)如图2，点Q 为对称轴左侧抛物线上一动点，点()4,0D ，直线DQ 分别与y 轴、直线AC 交于E 、F 两点，当CEF △为等腰三角形时，请直接写出CE 的长．20．已知等边△ABC ，M 在边BC 上，MN ⊥AC 于N ，交AB 于点P ．（1）求证：BP ＝BM ；（2）若MC ＝2BM ，求证：MP ＝MN ．（3）若E ，F 分别在AB 、AC 上，且△MEF 为等边三角形，当MEF ABC S S ∆∆的值最小时，BM BC＝ ．【参考答案】**科目模拟测试 一、解答题 1．（1）①见解析；②5m =；（2）m 的值为25或6；（3）25CE =【解析】【分析】（1）①连接DE ，证明ADC ∆是等腰三角形，根据“三线合一”的性质可得ADE CDE ∠=∠，证得EC EF =，从而可得结论；②根据勾股定理得到AC 45=，由E 为AC 中点得EC 25=，再证明DEC CBA ，由相似三角形的性质列出比例式，求出m 的值即可；（2）分PF //AC 和PF //BC 两种情况求解即可； （3）设CE =x ，作PG ⊥AC ，则2x GE =，45AE x =- 证明PGE EAP '≅得AP GE '=，再证明AP EBAC '，列比例式求出x 的值即可．【详解】解：（1）如图，连接DE∵CD 是圆P 的直径，∴∠DEC =90°，即DE ⊥AC∵E 为CA 中点∴AE =CE∴AD =CD∴ADE CDE ∠=∠∴EC EF =∴E 是CF 的中点；②在Rt △ABC 中，∠B ＝90°，AB ＝4，BC ＝8，∴22224845AC AB BC +=+∵E 是AC 的中点∴11452522EC AC ==⨯= ∵AB //CD ，90B ∠=︒∴90B DCB ∠+∠=︒∴90DCB∠=︒，即90DCE BCA∠+∠=︒∵90CDE DCE∠+∠=︒∴CDE BCA∠=∠又90B DEC∠=∠=︒∴DEC CBA∆∆∽∴CE DCAB AC=，即252=445m解得，5m=；（2）分两种情况：①当PF//AC时，如图，则有PDF CDA∆∆∴PF PDAC CD=，即245PF mm=∴25=PF∴25m=②当PF//BC时，如图，过点A作AH⊥DC，垂足为H，则四边形AHCB是矩形，∴AH//BC，HC=AB=4，AH=BC=8∴PF//AH∵90DCB∠=︒∴90FPD∠=︒∴45PDF PFD∠=∠=︒∴45HAD HDA∠=∠=︒∴DH=AH，即248m-=解得，6m=综上，m的值为256；（3）过点P 作PG AC ⊥于点G ，如图，∵PE =PC ∴1,2GE CE EPG CPG =∠=∠ ∵90PEP '∠=︒∴90P EA PEG '∠+∠=︒又90PEG GPE ∠+∠=︒∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒，PE P E '=∴P AE EPG '∆≅∆∴AP GE '=设CE x =，则45,2x AE x GE AP '=== ∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒∴GPC BCA ∠=∠∴EPG BCP ∠=∠∴P EA BCA '∠=∠又90P AE B '∠=∠=︒∴AP E BAC '∆∆ ∴AP AB AE BC '=42825x = ∴5x =25CE =【点睛】本题主要考查了全等三角形的判定与性质，圆的基本概念，相似三角形的判定与性质，正确作出辅助线以及进行分类讨论是解答本题的关键．2．（143；（2）S =()()22330434348t t t ⎧+≤≤⎪⎪⎨⎪≤⎪⎩＜；（3）存在，当t =247s 或（32-163）s或163s时，△AMQ为等腰三角形．【解析】【分析】（1）首先求得CN的长，在直角△CNQ中利用三角函数即可求得NQ的长；（2）当0≤t≤4时，N在CD上，首先求得CQ，则AQ长即可求得，再根据△CAB=30°，AM=t，据此即可求得△AMQ的长；当4＜t≤8时，利用相似求得AQ的长，进而求得△AMQ的面积，得到函数解析式；（3）分三种情形讨论求解即可．【详解】解：（1）当t=2时，CN=2×2=4，∵在△ACD中，AD=DC，∴∠DCA=1801202︒-︒=30°，在直角△CNQ中，NQ=CN•tan30°=4×33=433；（2）由题意得，AM=t，当0≤t≤4时，CN=2t，∵∠D=120°，AB=CD=8，∴∠DCA=30°，连接BD，与AC相交于点定O，过点Q作QG⊥AB于点G，∴OC=CD•cos30︒3AC3∴在Rt△CNQ中，NQ23t，CQ43t，∴AQ=AC-CQ343，QG=12AQ，∴S=12AM• QG =233t+，当4＜t≤8时，延长QN，交AB于G，交CD延长线于H，如图：ND =2t -8，∠HDN =60°，∴HD =12ND =t -4， ∴CH =t -4+8=t +4，∴CQ =23cos303CH =︒(t +4)， ∴AQ =AC -CQ =83-233(t +4)，QG =12AQ ， S =12•AM • QG 234363t t =-+． 综上，S =()()223230433434863t t t t t t ⎧-+≤≤⎪⎪⎨⎪-+≤⎪⎩＜； （3）①当0＜t ≤4时，只有MA =MQ 符合条件，过点M 作ME ⊥AC 于点E ，则AE =EQ =AM •cos30︒=32t ， ∴AQ =3t ，由（2）知AQ 343， 3433， 解得t =247； ②当4＜t ≤8时，由（2）知AQ 323t +4)，AQ =AM 时，)4t +=t ，解得tAQ =MQ 时，AM ，t )4t ⎤+⎥⎦， 解得t =163．综上所述，当t =247s 或（s 或163s 时，△AMQ 为等腰三角形． 【点睛】本题考查了菱形的性质以及三角函数，正确进行分请情况进行讨论是关键．3．（1）245y x x =-++；（2）1(2,9)P ，2(3,8)P ；（3）1(9,4)Q -，2(0,5)Q ，3(1,6)Q -，4(5,10)Q -【解析】【分析】（1）直接将(0,5)A ，(5,0)B 代入2y x bx c =-++，求解即可；（2）先求出AB 的解析式，设点P 的横坐标为t ，则()2,45P t t t -++，(,5)D t t -+，用t 表示出PD ，最后利用245AOE APCD S S ∆=四边形求出结果； （3）分三种情况讨论解答：①当EM 为平行四边形的对角线时；②当EP 为对角线时；③当EQ 为对角线时．【详解】（1）将点(0,5)A ，(5,0)B 分别代入2y x bx c =-++得25505b c c -++=⎧⎨=⎩， 45b c =⎧∴⎨=⎩， ∴二次函数的解析式为245y x x =-++；（2）//AC x 轴，点()0,5A ，∴当5y =时，2455x x -++=，10x ∴=，24x =，()4,5C ∴，4AC ∴=，设直线AB 的解析式为y mx n =+，将(0,5)A ，(5,0)B 分别代入得505n m n =⎧⎨=+⎩， 解得：1m =-，5n =∴直线AB 的解析式为5y x =-+；设点P 的横坐标为t ，则()2,45P t t t -++，(,5)D t t -+()2245(5)5PD t t t t t ∴=-++--+=-+，4AC =，()22114521022APCD S AC PD t t t t ∴=⨯=⨯⨯-+=-+四边形 函数245y x x =-++，当0y =时，有2450x x -++=，11x ∴=-，25x =，(1,0)E ∴-，1OE ∴=，又5OA =，11515222AOE S OE OA ∆∴=⨯⨯=⨯⨯=， 245AOE APCD S S ∆=四边形， 22452101252t t ∴-+=⨯=， 解得：12t =，23t =，∴点1(2,9)P ，2(3,8)P ；（3）∵2(2)9y x =--+，∴当x =2时，y =-2+5=3，∴M (2,3),设P (m ，2(2)9m --+，(,5)Q n n -+，而E (-1，0)，①当EM 为平行四边形的对角线时，(平行四边形的对角线互相平分)得：21222(2)950322m n m n +-+⎧=⎪⎪⎨--+-++⎪=⎪⎩， 解得121261,52m m n n ==-⎧⎧⎨⎨=-=⎩⎩ (舍)， ∴点Q 的坐标为（-5,10）；②当EP 为对角线时，212220(2)93522m m m n -++⎧=⎪⎪⎨--+-+⎪=⎪⎩，解得121223,10m m n n ==⎧⎧⎨⎨=-=⎩⎩， ∴点Q 的坐标为（-1,6）或（0,5）；③当EQ 为对角线时，21222053(2)922n m n m -++⎧=⎪⎪⎨-+--+⎪=⎪⎩， 解得121261,92m m n n ==-⎧⎧⎨⎨==⎩⎩（舍）， 点Q 的坐标为（9,-4），综上所得：1(9,4)Q -，2(0,5)Q ，3(1,6)Q -，4(5,10)Q -．【点睛】本题考查了待定系数法求函数关系式，平行四边形的性质和判定，解本题的关键是分类思想的运用．4．（1）2y x 2x 3=-++；（2）278；（3）存在，n =1或n 3+33- 【解析】【分析】（1）通过待定系数法求解函数解析式即可；（2）作DF ⊥x 轴于点F ，交BC 于点E ，根据12S DE OB =⋅求得S 关于m 的解析式，根据二次函数的性质求解即可；（3）过点P 作PB 的垂线，交抛物线于点1Q 和2Q ，作1Q M y ⊥轴于点M ，2Q N y ⊥轴于点N ，利用全等三角形的性质求解即可．【详解】解：(1)设函数关系式为2y ax bx c =++由题意，得A (－1，0)，B (3，0)，C (0，3)∴(1)(3)y a x x =+-把C (0，3)代入得，1a =-∴2y x 2x 3=-++(2)作DF ⊥x 轴于点F ，交BC 于点E设直线BC 关系式为y =kx ＋b ，代入(3，0)，(0，3)得k =－1，b =3，∴y =－x ＋3∵点D 的横坐标为m ，则DF =223m m -++，EF =－m ＋3∴DE =23m m -+22133327(3)()22228S DE OB m m m =⋅=-+=--+ ∵302-<，∴S 的最大值是278(3)过点P 作PB 的垂线，交抛物线于点1Q 和2Q ，作1Q M y ⊥轴于点M ，2Q N y ⊥轴于点N∴1290Q MP Q NP BOP ∠=∠=∠=︒∵1190Q PM PQ M ∠+∠=︒，190Q PM BPO ∠+∠=︒，∴1PQ M BPO ∠=∠又∵1BP PQ =，∴1Q PM PBO △≌△∴1MQ OP n ==，3MP OB ==，∴1()3Q n n +，代入抛物线，得2323n n n +=-++解得11n =，20n =(舍去)同理，2PN Q PBO ≌，∴2Q (－n ，n －3)代入抛物线，得2323n n n =-+－－ 解得13+33n -=2333n --=舍去) 综上，存在n 的值，n =1或n 3+33-【点睛】 此题考查了二次函数与几何的综合应用，涉及了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，解题的关键是熟练掌握二次函数以及全等三角形的判定与性质．5．（1）315,24⎛⎫- ⎪⎝⎭；（2）Q 1（-5,0），Q 2（-1,0），Q 3 ()720，，Q 4)720，． 【解析】【分析】（1）分别求出点B 、C 的坐标，连接PB ，PC ，PO ，设点P 坐标为()2,23m m m --+，四边形PBOC 的面积为S ，根据=BOP COP S S S +△△得到S 关于m 的二次函数解析式，根据二次函数的性质即可求解；（2）分点M 在x 轴上方或点M 在x 轴下方两种情况讨论，分别求出点M 的坐标，根据平行四边形的性质即可求出点Q 的坐标． 【详解】解：（1）把0x =代入223y x x =--+得y =3， ∴点C 坐标为（0,3）；把y =0代入223y x x =--+得2x 2x 30--+=， 解得123,1x x =-=， ∵点B 在x 轴负半轴上， ∴点B 坐标为（-3,0）； 如图1，连接PB ，PC ，PO ，∵点P 在第二象限抛物线223y x x =--+上，∴设点P 坐标为()2,23m m m --+（-3＜m ＜0），设四边形PBOC 的面积为S ， ∴=BOP COP S S S +△△2211232m m OB O m C =--++ ()()2332223m m m +=+--- 2399222m m =--+， ∵302-＜，∴当322b m a =-=-时，S 有最大值， 此时，215234m m --+=， ∴当点P 坐标为315,24⎛⎫- ⎪⎝⎭时，四边形PBOC 的面积最大；（2）存在，如图2，分点M 在x 轴上方或点M 在x 轴下方两种情况讨论． ①当点M 在x 轴上方时，点M 与点C 纵坐标相等，∴2233x x --+=， 解得122,0x x =-=， ∴CM 1=2，∵四边形BQCM 1是平行四边形， ∴CM =BQ =2，∴满足条件的点Q 有两个，分别是Q 1（-5,0），Q 2（-1,0）； ②当点M 在x 轴下方时，点M 与点C 纵坐标互为相反数， ∴2233x x --+=-， 解得1271,71x x =--=-，∴点M 2坐标为()713---，，点M 3坐标为()713--，，由平行四边形的性质得点B 向右平移3个单位，向上平移3个单位得到点C ，∴点M 2向右平移3个单位，向上平移3个单位得到点Q 3，点M 3向右平移3个单位，向上平移3个单位得到点Q 4，∴Q 3的坐标为()720-+，，Q 4的坐标为()720+，；综上所述，满足条件的点Q 的坐标有四个，分别是Q 1（-5,0），Q 2（-1,0），Q 3()720-+，，Q 4()720+，．【点睛】本题为二次函数综合题，难度较大，解决第（1）步，关键是理解函数图象上点的坐标特点，将四边形分割为两个三角形，分别表示出三角形面积，得到函数解析式，并利用二次函数性质求解；解决第（2）步关键是理解平行四边形的性质，利用分类讨论思想求解，注意要充分考虑各种情况，不要漏解．6．（1）y ＝12x 2＋x −32；（2）（3，6）或（-5，6）或（−1，-2）；（3）−12＜k ＜56且k≠0或56＜k＜43【解析】【分析】（1）把A（−3，0），B（1，0），52,2C⎛⎫⎪⎝⎭代入y＝ax2＋bx＋c，解方程组即可；（2）把C点坐标代入直线CD，得2k＋b＝52，分两种情况：①若AB为平行四边形的边时，②若AB为平行四边形的对角线时，得关于k、b的方程组，解方程组即可求解；（3）分两种情况：①当E点在x轴上方时，②E点在x轴下方时，根据当α＝β时，列方程，可求出k的值，进而求出k的取值范围．【详解】解：（1）设抛物线的解析式为y＝ax2＋bx＋c，∵抛物线经过A（−3，0），B（1，0），C（2，52）三点，∴9305 422a b ca b ca b c⎧⎪-+=⎪++=⎨⎪⎪++=⎩，∴12132abc⎧⎪⎪⎨⎪⎪-⎩＝＝＝，∴抛物线的解析式为y＝12x2＋x−32；（2）如图1所示，将C点坐标代入直线CD，得2k＋b＝52，当x＝−1时，y＝−k＋b，即E（−1，−k＋b）．①若AB为平行四边形的边时，则F（-1+4，−k＋b）或F（-1-4，−k＋b），即：F（3，−k ＋b ）或F （-5，−k ＋b ）， 把F （3，−k ＋b ）代入y ＝12x 2＋x −32，得−k ＋b =6， 把F （-5，−k ＋b ），代入y ＝12x 2＋x −32，得−k ＋b =6， 又∵2k ＋b ＝52， ∴k =76-，b =296∴F （3，6）或（-5，6）；②若AB 为平行四边形的对角线时，则F 和E 关于x 轴对称， ∴F （−1，k -b ）， ∴k -b =-2， 又∵2k ＋b ＝52， ∴k =16，b =136，∴F （−1，-2），综上所述：F 的坐标为（3，6）或（-5，6）或（−1，-2）； （3）如图2所示，①当E 点在x 轴上方时，如图2所示，当α＝β时，∵∠EHA ＝90°， ∴∠AEC ＝90°， ∴∠AEH =∠EGH ， ∵∠AHF =∠FHG =90°， ∴AHF FHG ∽， ∴AE AHEG EH=， ∵A （−3，0），E （−1，−k ＋b ），G （bk-，0），∴()()2222221k bk bbk bk+-+=-+⎛⎫-++-+⎪⎝⎭，∴k2−bk−2＝0，联立方程220522k bkk b⎧--=⎪⎨+=⎪⎩，解得k＝−12（k＝43舍去），随着E点向下移动，∠CEH的度数越来越大，∠EAH的度数越来越小，当E点和H点重合时（如图3所示），α和β均等于0，此时联立方程522k bk b⎧+⎪⎨⎪-+⎩＝＝，解得5656kb⎧=⎪⎪⎨⎪=⎪⎩，因此当−12＜k＜56且k≠0时，α＞β；②E点在x轴下方时，如图4所示，当α＝β时，∵∠EHA＝90°，∴∠AEC＝90°，根据①可得此时k＝43（k＝−12舍去），随着E点向下移动，∠CEH的度数越来越小，∠EAH的度数越来越大，因此当56＜k ＜43时，α＞β．综上所述可得，当α＞β时，k 取值范围为−12＜k ＜56且k ≠0或56＜k ＜43．【点睛】本题考查的是一次函数、二次函数和相似三角形的判定和性质的综合应用，掌握待定系数法求函数解析式和数形结合思想方法是解题的关键．7．（1）34k =，5b =；（2）①OM =5；②()3,6N 或724,55N ⎛⎫ ⎪⎝⎭【解析】 【分析】（1）分别将将(4,3)A 代入y kx =和12y x b =-+中，求解即可；（2）①设直线AB 与y 轴交与点C ，与FM 交于点D ,证明△AFD ≌△EFD ，得到AD =ED ，利用中点坐标公式求得点D 坐标，用待定系数法求得直线FD 的函数表达式，令0y =,即可求得点M 的坐标，从而求得OM ；②点N 在直线l 1的上方，当△OFN 和△OFM 全等时，满足题意的点N 有两个，分别画出相关的图形，分类讨论求解即可． 【详解】解：（1）∵直线l 1：y kx =和直线l 2：12y x b =-+相交于点A∴将(4,3)A 代入y kx =中，得：43k = 解得：34k =∴将(4,3)A 代入12y x b =-+中，得：1432b -⨯+=解得：5b =∴3,54k b == （2）① 设直线AB 与y 轴交与点C ，与FM 交于点D ,如下图：∵34k =，5b = ∴直线l 1的函数表达式为34y x =，直线l 2的函数表达式为152y x =-+∵(4,3)A ∴22345OA +设直线AB 与y 轴交与点C ，与FM 交于点D 则()0,5C ∴5OC = ∴5OA OC == ∴∠OCA =∠OAC ∵//FE y 轴 ∴∠OCA =∠FEA 又∵∠OAC =∠FAE ∴∠FAE =∠FEA ∴FA =FE又∵FM 是∠OFE 的角平分线 ∴∠AFM =∠EFM 又∵FD =FD ∴△AFD ≌△EFD ∴AD =ED ∴点D 为AE 的中点 ∵//FE y 轴∴点F 和点E 的横坐标相同 将8x =代入152y x =-+中，得1y =∴()8,1E ∵(4,3)A ，()8,1E ∴()6,2D设线段FM 所在的直线函数表达式为()0y ax b a =+≠将()()8,6,6,2F D 代入y ax b =+中，得：8662k b k b +=⎧⎨+=⎩解得：210k b =⎧⎨=-⎩∴线段FM 所在的直线函数表达式为210y x =- 令0y =，得2100x -= 解得：5x = ∴()5,0M ∴OM =5② 当,OFN FOM 全等时，有两种情况，情况一，如下图所示：∵OFN FOM ≅△△∴∠OFN =∠FOM ，FN =OM ,ON =FM ∴//FN OM ∵OM =5 ∴FN =5,8F x =∴853N x =-=,6N F y y == ∴()3,6N情况二，当△OMF 和△ONF 关于直线l 1对称时，如下图所示：∵OFN FOM ≅△△∴ON =OM =5，∠NOF =∠MOF ∵OP =OP ∴△NOP ≌△MOP ∴PN =PM ∵()8,6F∴10OF 又∵1122OMFF SOM y OF PM =⋅=⋅ ∴F OM y OF PM ⋅=⋅ ∴56==310PM ⨯∴MN =2PM =6，OP 4 ∵1122OMN N S MN OP OM y =⋅=⋅△ ∴642455N y ⨯==∴75N x ==∴724,55N ⎛⎫⎪⎝⎭综上所述，满足题意点有两个，分别是：()3,6N 或724,55N ⎛⎫⎪⎝⎭【点睛】本题考查用待定系数法求一次函数表达式，三角形全等的性质和证明，两条直角交点的求法以及三角形的等面积法等知识点，牢记相关内容并能灵活应用数形结合思想解题是本题的关键．8．（1）y 14=-x 2+x +3；y 12=x +1；（2）△PAD 的面积的最大值为274，P （1，154）；（3）点Q 的坐标为（0，133）或（0，﹣9） 【解析】 【分析】（1）由A （﹣2，0）、B （6，0）设抛物线的解析式为y ＝a （x +2）（x ﹣6），把D （4，3）的代入解析式解方程即可，再利用待定系数法求解一次函数的解析式； （2）如图1中，过点P 作PT y ∥轴交AD 于点T ．设P （m ，14- m 2+m +3），则T（m，12m+1），再利用面积列函数关系式，再利用二次函数的性质求解最值即可；（3）如图2中，将线段AD绕点A逆时针旋转90°得到AT，则T（﹣5，6），设DT交y轴于点Q，则∠ADQ＝45°，再求解直线DT的解析式为y13=-x133+，作点T关于AD的对称点T′（1，﹣6），求解直线DT′的解析式为y＝3x﹣9，设DQ′交y轴于点Q′，则∠ADQ′＝45°，从而可得答案．【详解】解：（1）∵抛物线y＝ax2+bx+c与x轴交于A（﹣2，0）、B（6，0）两点，∴设抛物线的解析式为y＝a（x+2）（x﹣6），∵D（4，3）在抛物线上，∴3＝a（4+2）×（4﹣6），解得a14 =-，∴抛物线的解析式为y14=-（x+2）（x﹣6）14=-x2+x+3，∵直线l经过A（﹣2，0）、D（4，3），设直线l的解析式为y＝kx+m（k≠0），则2043k mk m-+=⎧⎨+=⎩，解得，121km⎧=⎪⎨⎪=⎩，∴直线l的解析式为y12=x+1；（2）如图1中，过点P作PT y∥轴交AD于点T．设P（m，14-m2+m+3），则T（m，12m+1）．∵S△PAD12=•（xD﹣xA）•PT＝3PT，∴PT的值最大值时，△PAD的面积最大，∵PT14=-m2+m+312-m﹣114=-m212+m+214=-（m﹣1）294+，∵14-<0，抛物线开口向下，∴m＝1时，PT的值最大，最大值为94，此时△PAD的面积的最大值为274，P（1，154）．（3）如图2中，将线段AD绕点A逆时针旋转90°得到AT，过D作DM x⊥轴于,M过T作TN x轴于,N90,,TNA AMD TAD AD AT90,TAN ATN TAN DAM,ATN DAM,ATN DAM≌6,3,235,TN AM AN DM ON∴T（﹣5，6），设DT交y轴于点Q，则∠ADQ＝45°，∵D（4，3），∴直线DT的解析式为y13=-x133+，∴Q（0，133），作点T关于AD的对称点T'，同理可得T'（1，﹣6），则直线DT′的解析式为y＝3x﹣9，设DQ′交y轴于点Q′，则∠ADQ′＝45°，∴Q′（0，﹣9），综上所述，满足条件的点Q的坐标为（0，133）或（0，﹣9）．【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，待定系数法，等腰直角三角形的性质等知识，解题的关键是学会利用参数构建二次函数解决最值问题，学会构造特殊三角形解决问题，属于中考压轴题．二次函数综合题中面积问题的解题通法:（1）直角坐标系中图形面积的求法，以“S三角形=12×水平底×铅直高”为基础求解.（2）图形面积的数量关系：①找出所求图形的顶点，其中动点的坐标根据函数关系式用含未知数的代数式表示出来；②结合图形作辅助线，并将关键线段的长度用含未知数的代数式表示出来；③利用面积公式用含未知数的代数式表示出图形的面积；④列方程求解.（3）图形面积的最值,解题思路跟（1）中的前三步相同，然后利用函数的增减性求解.9．（1）证明见解析；（2）证明见解析，（3）15714BF=．【解析】【分析】（1）连接OA并延长AO交BC于E，证明∠BAC=2∠BAE和∠ABD=∠BAE即可得结论，（2）利用直角三角形两锐角互余、圆周角定理进行导角，得出MCG△和△FCG是等腰三角形，得出BM=MC=FG=CG，MH=HG，进而由BF=BM+MH-FH=FG-FH+HG，得出结论；（3）过O点作OP⊥AC，由垂径定理得出12PD=，再由52ABOADOS AB BOS AD OD===和平行线分线段成比例定理求出7724DH DP==，由勾股定理进而可求BH，再利用相似三角形对应边成比例求出HG，即可得BF长．【详解】解：（1）连接OA并延长AO交BC于E，∵AB=AC，∴AB AC=，∵AE过圆心O，∴AE BC⊥，BE EC=，∴∠BAC=2∠BAE，∵OA=OB，∴∠ABD=∠BAE，∴∠BAC=2∠ABD；（2）如解图（2），连接OA并延长AO交BC于E，AE交BF于M，连接MC，设2BACα∠=，则ABD BAE EACα∠=∠=∠=∵AE =EC ，AE ⊥BC ，∴BM =MC ，∴∠MBC =∠MCB ，∵BG ⊥AC ，AE ⊥BC ，∴∠EAC +∠ACE =90°，∠HBC +∠ACE =90°，∴EAC HBC MCB α∠=∠=∠=，∴2CMG MBC MCB α∠=∠+∠=，∵BC BC =，∴2G BAC α∠=∠=，∴∠G =∠CMG ，∴CG =CM =BM ，∵AC ⊥BG ，∴MH =HG ，∵OA =OC ，∴ACO EAC α∠=∠=∴9090CFG ACO α∠=︒-∠=︒-，∵180FCG CFG G ∠=︒-∠-∠，即180(90)290FCG ααα∠=︒-︒--=︒-，∴FCG CFG ∠=∠，∴FG =CG ，∴BM =MC =FG =CG ，又∵MH =HG ，∴BF =BM +MH -FH =FG -FH +HG ，∴BF =2HG ．（3）过O 点作OP ⊥AC ，如解图（3）∵AO 是∠BAC 的角平分线，∴点O 到AB 、AC 的距离相等， ∴ABO ADO SAB BO S AD OD==， ∵AD =2，CD =3，∴AB =AC =5， ∴5=2BO OD ，即：2=7OD BD ， ∵OP ⊥AC ，∴52AP PC ==，12PD =， ∵BH AC ⊥， ∴OP //BH ，∴27DP OP OD DH BH BD ===， ∴7724DH DP ==， ∴154AH AD DH =+=，5-4HC DC DH ==，∵在Rt ABH中，BH == ∵BAH G ∠=∠，AHB GHC ∠=∠， ∴AHB GHC △△，∴AH BH HG CH = 即：AH HC BHHG =， 51544=⨯， ∴HG =， 由（2）得BF =2HG ，∴BF = 【点睛】 本题是圆的综合题，主要考查了圆周角定理，涉及了相似三角形的判定和性质、勾股定理、等腰三角形的判定和性质等知识点，解题关键是利用同弧或等弧所对圆周角相等、直角三角形的两锐角相等找出图中角之间的关系，从而利用相似或勾股定理解题．10．（1）291515404y x x =+-，y ＝﹣34x ﹣15；（2）面积最大值225，C （﹣10，﹣30）；（3）S ＝﹣2553t +160t ﹣240． 【解析】【分析】（1）利用待定系数法将点A （﹣20，0），B （0，﹣15）代入抛物线y ＝ax 2+154x +c 即可求出抛物线的函数表达式；设AB 的函数表达式是y ＝kx +b ，然后利用待定系数法将点A （﹣20，0），B （0，﹣15）代入y ＝kx +b 即可求出直线AB 的函数表达式；（2）作CE ⊥OA 于E ，交AB 于F ，设C （a ，940a 2+154a ﹣15），F （a ，﹣34a ﹣15），根据题意表示出CF 的长度，进而表示出ABC S ∆，然后利用二次函数的性质求解即可；（3）作AN ⊥OD 于N ，AD 与FG 交于点I ，首先根据题意求出OC 的解析式，然后联立33154y x y x =⎧⎪⎨=--⎪⎩求出点D 的坐标，然后求出AD OD =，利用等腰三角形三线合一性质求出ON 的长度，进而利用勾股定理求出AN 的长度，表示出S △AON ，然后证明出△GFI ∽△OGH ∽△ANO ，利用相似三角形的性质表示出S △IJF ＝803（t ﹣3）2，S △GOH ＝253t ，最后利用面积之间的关系即可求出S 与t 之间的函数关系式．【详解】解：（1）由题意得，将点A （﹣20，0），B （0，﹣15）代入抛物线y ＝ax 2+154x +c 得， 21515(20)(20)04c a c =-⎧⎪⎨-+⨯-+=⎪⎩， ∴15940c a =-⎧⎪⎨=⎪⎩， ∴291515404y x x =+-， 设AB 的函数表达式是y ＝kx +b ，将点A （﹣20，0），B （0，﹣15）代入y ＝kx +b 得，∴15200b k b =-⎧⎨-+=⎩， ∴1534b k =-⎧⎪⎨=-⎪⎩， ∴y ＝﹣34x ﹣15； （2）如图1，作CE ⊥OA 于E ，交AB 于F ，设C （a ，940a 2+154a ﹣15），F （a ，﹣34a ﹣15）， ∴FC ＝（﹣315)4a -﹣（2940a +154a ﹣15）＝﹣2940a ﹣92a ， ∴ABC S ∆＝12CF •AO ＝12（﹣2940a ﹣92a ）×20＝﹣94（a +10）2+225， ∴当a ＝﹣10时，ABC S ∆＝225， 当a ＝﹣10时，y ＝29(10)40⨯-+()15104⨯-﹣15＝﹣30， ∴C （﹣10，﹣30）；（3）如图2，作AN ⊥OD 于N ，∵C （﹣10，﹣30），∴OC 的解析式是：y ＝3x ，由33154y x y x =⎧⎪⎨=--⎪⎩得， 412x y =-⎧⎨=-⎩， ∴D （﹣4，﹣12），∵A （﹣20，0），OD 22412+10∴AD ()2220412-++=20，∴AD OD=，又∵AN⊥OD，∴ON＝12OD=AN=S△AON＝1160 22AN ON=⨯=，∵OE，OD＝，∴DE＝，∴JE＝3（），∴FJ＝EF﹣JEt﹣3（t）＝（t﹣3），∵OG AN FJ∥∥，∴GOH OAN DAN AJF∠=∠=∠=∠，又∵90G ANO F∠=∠=∠=︒，∴△GFI∽△OGH∽△ANO，∴IJFAONSS∆∆＝（FJAN）2＝2，GOHAONSS∆∆＝（OGAN）2）2，∴S△IJF＝803（t﹣3）2，S△GOH＝253t，∴S＝S正方形OEFG﹣S△IJF﹣S△GOH＝10t2﹣53t2﹣803（t﹣3）2＝﹣2553t+160t﹣240，故答案是：S＝﹣2553t+160t﹣240．【点睛】此题考查了待定系数法求二次函数和一次函数表达式，二次函数与一次函数综合问题，相似三角形的性质和判定，二次函数中最大面积问题等知识，解题的关键是正确分析题目中的条件，设出点的坐标，根据相似三角形的性质以及勾股定理表示出相应的线段和面积．11．(1)(1,，图见解析(2)1322Cx-≤≤1122t<≤【解析】【分析】（1）根据等边三角形的性质，勾股定理求解即可；（2）根据题意以MB为边作等边三角形MM B'，以M'为圆心1为半径作M'，根据线段中点坐标公式求解即可；（3）在（2）的基础上，先求得最小值，再确定2个圆心，第1个是A 点运动点C 对应的圆心P '，第2个是点B 的运动时点C 轨迹的对应的圆心P ，进而根据线段和最大，当,,P P Q '共线时候，t 最大，根据（2）的方法求解即可．(1)过点C 作CE x ⊥轴于点E ，作出点C ，B 的逆序等边三角形CBD ，如图1，()()1,03,0A B -,，ABC 是等边三角形()1131222AE BE AB ∴===--=，33CE AE ==()1,0E ∴，(1,3C ,ABC BCD 是等边三角形∴60DCB ABC ∠=∠=︒，AB AC BC CD BD ====,CD AB CD AB ∴=∥(5,23D ∴ 故答案为：(1,23，(5,23(2)如图2，以MB 为边作等边三角形MM B '，以M '为圆心1为半径作M '， 点B (3，0)，点A 在以点M (-2，0)为圆心1为半径的圆上， ∴点A ，B 的逆序等边三角形ABC 的顶点C 在M '23122M x '-+∴== M '的半径为1∴111122C x -≤≤+ 即1322C x -≤≤(3)如图3，设N 与x 轴交于点G ，以GM 为边向上作等边三角形MGH ，以点H 为圆心1为半径，作H ，设直线y x =为1l ，y x t =+为2l ，过点H 作1HJ l ⊥，交x 轴于点J ，交1l 于点S ，交2l 于点L ，过点H ，作HI x ⊥轴于点I ，设2l 与x 轴的交点为T ，则OT t =根据题意，当C 点在第二象限时，能找到t 的最小值，根据定义可知，B 点与G 点重合时，A 点在M 上运动，则C 点在H 上运动，当2l 与H 相切时，t 最小， ()2,0M -,()3,0N ，M 的半径为1，N 的半径为2， 2,321OM OG ∴==-=3MG ∴=33HI ∴=1322MI MG == 1,02I ⎛⎫∴- ⎪⎝⎭ 1332H ⎛∴- ⎝⎭1l 与x 轴的夹角为45°，1HJ l ⊥，HI x ⊥轴， HIJ ∴是等腰直角三角形 HI IJ ∴=HJ ∴===12OI =12OJ ∴1,02J ⎫∴⎪⎪⎝⎭1LJ HJ HL ∴=-=12l l ∥ LTJ ∴是等腰直角三角形1TJ ∴===⎝3122OJ =1122TO TJ JO ⎫=-==⎪⎪⎝⎭即t 12， B 的纵坐标0d >，则12t > 如图4，作,M N 的逆序等边三角形MNP '，以P '为圆心，1为半径作P '，则1PP AM '==，连接,AM PP ',ANP MNP '是等边三角形，,,60AN NP MN NP ANP MNP ''∴==∠=∠=︒PNP ANM '∴∠=∠PP N AMN '≌∴当,,P P Q '共线时候，t 最大以P 为圆心，2为半径作半圆P ，当直线y x t =+与半圆P 相切时，设切点为Q ，当C 点与Q 点重合时，即可取得t 的最大值，最大值即为T O '的长，()()2,0,3,0M N - ∴1532P ⎛' ⎝⎭过点P '作P P x '''⊥轴于点P ''，如图，。

一、解答题1．如图，已知正方形ABCD ，将AD 绕点A 逆时针方向旋转到AP 的位置，分别过点作，垂足分别为点E 、F ．(1)求证：；(2)联结，如果，求的正切值； (3)联结，如果，求n 的值．2．在ABC 中，AB BC =，45B ∠=︒，AD 为BC 边上的高． （1）如图1，若1AD =，求线段CD 的长度；（2）如图2，点E ，点F 在AB 边上，且满足AE BF =，连接CE ，CF 分别交线段AD 于点M ，点N ，若点M 为线段CE 的中点，求证：2AN CD AB +=；（3）在（2）问条件下，若2AC =，点K 为AC 边上一动点，点Р为ACF 内一点且满足ACP CAD ∠=∠，当PK PA +取最小值时，请直接写出CPK S △的值．3．如图，点D 、E 分别在等边△ABC 的边AB 、BC 上，且BD ＝CE ，CD ，AE 交于点F ． （1）求∠AFD 的度数；（2）如图2，若D ，E ，M ，N 分别是△ABC 各边上的三等分点，BM ，CD 交于Q ．若△ABC 的面积为S ，则四边形ANQF 的面积为______；（只写出答案即可，不要求写解题过程）（3）如图3，延长CD 到点P ，使∠BPD ＝30°，设AF ＝a ，CF ＝b ，请用含a ，b 的式子表示PC 的长，并说明理由．4．如图1，在平面直角坐标系xOy中，矩形OABC的顶点A、C的坐标分别为（0，6）、（5，0），点P为线段OA上的一个动点，将矩形OABC在直线PC上方的部分沿直线PC翻折，点B落在点D处，点A落在点E处，直线CD交y轴于点F．（1）如图2，当点P与点A重合时，求点F的坐标；（2）点P从A向O运动的过程中，点D、P、C、B能否构成菱形，若能，求出符合条件的点D的坐标，若不能，请说明理由；（3）点P从A向O运动的过程中，当△DPC的重心刚好落在y轴上时，求出此时点P的坐标．5．问题提出（1）如图①，在△ABC中，BC＝2，将△ABC绕点B顺时针旋转60°得到△A′B′C′，则CC′＝；问题探究（2）如图②，在△ABC中，AB＝BC＝3，∠ABC＝30°，点P为△ABC内一点，连接PA、PB、PC，求PA＋PB＋PC的最小值，并说明理由；问题解决（3）如图③，在四边形ABCD中，AD∥BC，AB＝6，AD＝4，∠ABC＝∠BCD＝60°．在四边形ABCD内部有一点，满足∠APD＝120°，连接BP、CP，点Q为△BPC内的任意一点，是否存在一点P和一点Q，使得PQ＋BQ＋CQ有最小值？若存在，请求出这个最小值；若不存在，请说明理由．6．折叠变换是特殊的轴对称变换，我们生活中常对矩形纸片进行折叠，这其中蕴含着丰富的数学知识和思想．（1）如图1，矩形ABCD中，AB＝6，BC＝4，点E是DC的中点，将矩形ABCD沿BE折叠，点C落在点F的位置．①求证：DF∥BE；②求DF的长度．（2）如图2，在直角坐标系中，把矩形OABC沿对角线AC所在的直线折叠，点B落在点D处，AD与y轴交于点E，OA＝2，OC＝23，点G是直线AC上的一个动点，在坐标平面内存在点H，使得以点E，A，G，H为顶点的四边形是菱形，请直接写出点H坐标．7．“数学建模”是中学数学的核心素养，平时学习过程中能归纳一些几何模型，解决几何问题就能起到事半功倍的作用．（1）如图1，正方形ABCD中，45=；∠=︒，且DE BFEAF=，求证：EG AG（2）如图2，正方形ABCD中，45∠=︒，延长EF交AB的延长线于点G，（1）中的EAF结论还成立吗？请说明理由；⊥，垂足为点Q，交AF于点N，连结DN，求（3）如图3在（2）的条件下，作GQ AE证：45∠=︒．NDC8．如图，在平面直角坐标系中，点B的坐标是（0，2），动点A从原点O出发，沿着x 轴正方向移动，△ABP是以AB为斜边的等腰直角三角形（点A、B、P顺时针方向排列），当点A与原点O重合时，得到等腰直角△OBC（此时点P与点C重合）．（1）BC＝；当OA＝2时，点P的坐标是；（2）设动点A的坐标为（t，0）（t≥0）．①点A在移动过程中，△ABP的顶点P在射线OC上吗？请说明理由；②用含t的代数式表示点P的坐标为：（，）；（3）分别过点P、A做x轴、y轴的平行线，两条平行线交于点Q，是否存在这样的Q，使得△AQB是等腰三角形？若存在，请直接写出Q的坐标，若不存在，请说明理由．9．抛物线y＝ax2+b经过点A（4，0），B（0，﹣4），直线EC过点E（4，﹣1），C （0，﹣3），点P是抛物线上点A、B间的动点（不含端点A、B），过P作PD⊥x轴于点D，连接PC、PE．（1）求抛物线与直线CE的解析式；（2）求证：PC+PD为定值；（3）若△PEC的面积为1，求满足条件的点P的坐标．10．如图，在直角梯形ABCD中，AB∥CD，∠B＝90°，AB＝4，BC＝8，CD＝2m（m＞2），P为CD中点，以P为圆心，CP为半径作半圆P，交线段AC于点E，交线段AD于点F．（1）当E为CA中点时，①求证：E是弧CF的中点．②求此时m的值．（2）连结PF，若PF平行△ABC的某一边时求出满足条件的m值．（3）连结PE，将PE绕着点E顺时针旋转90°得到EP'，连结AP'，当AP'⊥AC时，求此时CE的长．11．已知抛物线214y x bx c =-++与直线AC 相交于A 、C 两点，且()2,0A -、()4,3C ．(1)填空：b =______，c =______；(2)长度为5的线段DE 在线段AC 上移动，点G 与点F 在上述抛物线上，且线段DG 与EF 始终平行于y 轴．①连接FG ，求四边形DEFG 的面积的最大值，并求出对应点D 的坐标；②CH AB ⊥，垂足为点H ，线段DE 在移动的过程中，是否存在点D ，使△DEG 与△ACH 相似？若存在，请求出此时点D 的坐标；若不存在，试说明理由． 12．如图，抛物线交x 轴于A ，B 两点，交y 轴于点C ，直线经过点B ，C ．(1)求抛物线的解析式；(2)抛物线的对称轴l 与直线BC 相交于点P ，连接AC ，AP ，判定△APC 的形状，并说明理由；(3)在直线BC 上是否存在点M ，使AM 与直线BC 的夹角等于∠ACB 的2倍?若存在，请求出点M 的坐标；若不存在，请说明理由．13．如图，在平面直角坐标系中，矩形OABC ，点A 在y 轴上，点C 在x 轴上，其中B（﹣2，3），已知抛物线y＝﹣34x2＋bx＋c经过点A和点B．(1)求抛物线解析式；(2)如图1，点D（﹣2，﹣1）在直线BC上，点E为y轴右侧抛物线上一点，连接BE、AE，DE，若S△BDE＝4S△ABE，求E点坐标；(3)如图2，在（2）的条件下，P为射线DB上一点，作PQ⊥直线DE于点Q，连接AP，AQ，PQ，若△APQ为直角三角形，请直接写出P点坐标．14．如图，已知二次函数的解析式为y=﹣12x2+bx+c，A(-1,0)，C(4,0)，P为二次函数上的动点．(1)求二次函数的解析式．(2)若P在第一象限上，求S△BCP的最大值．(3)在x轴上是否存在点Q，使得BQ=BP且BP⊥BQ若存在，请直接写出所有点Q的坐标，若不存在，请说明理由．15．（1）[感知]如图1，在正△ABC的外角∠CAH内引射线AM，作点C关于AM的对称点E（点E在∠CAH内），连接BE，BE、CE分别交AM于点F、G．求∠FEG的度数．（2）[探究]把（1）中的“正△ABC”改为“正方形ABDC，其余条件不变，如图2，类比探究，可得：①∠FEG＝°；②猜想线段BF、AF、FG之间的数量关系，并说明理由．（3）[拓展]如图3，点A在射线BH上，AB＝AC，∠BAC＝α（0°＜α＜180°），在∠CAH 内引射线AM，作点C关于AM的对称点E（点E在∠CAH内），连接BE，BE、CE分别交AM于点F．G．则线段BF、AF、GF之间的数量关系为．16．在平面直角坐标系中，抛物线：与x轴交于点A，B（点B 在点A的右侧）．抛物线顶点为C点，△ABC为等腰直角三角形．(1)求此抛物线解析式．(2)若直线与抛物线有两个交点，且这两个交点与抛物线的顶点所围成的三角形面积等于6，求k的值．(3)若点，且点E，D关于点C对称，过点D作直线2l交抛物线于点M，N，过点E作直线轴，过点N作于点F，求证：点M，C，F三点共线．17．在平面直角坐标系中，抛物线交x轴于A、B两点（点A在点B的左），交y轴于点C(1)当3a =时，①如图1，求△ABC 的面积； ②如图2，若抛物线上有一点P ，且，求点P 的坐标(2)过点B 且与抛物线仅有一个交点的直线y kx b =+交y 轴于点D ，求的值．18．已知：在⊙O 中，弦AC ⊥BD 于点E ，连接OC 、BC 、CD ．(1)如图1，求证：∠B ＋∠OCD ＝90°．(2)如图2，连接OE 、OD ，若EO 平分∠AED ，求证：2=CD OC ．(3)如图3，在（2）的条件下，延长OE 交⊙O 于点F ，连接FC 、FD ，点K 为OD 上一点，KC 交FD 于点H ，FD 交OC 于点G ，若CK ＝5，552DG =，∠ODF ＝2∠KCD 时，求FC 的长． 19．问题提出：如图①所示，在矩形AOCB 和矩形ODEF 中，CO FOk AO DO==，点A ，O ，D 不在同一直线上，连接,AD CF ．HO 是AOD △的中线，那么,HO CF 之间存在怎样的关系？HO CF的数量关(1)问题探究：先将问题特殊化，如图②所示，当1k=且90AOD∠=︒时，,系是________，位置关系是________．(2)问题拓展：再探究一般情形如图③所示，当1k=，90∠≠︒时，证明（1）中的结论AOD仍然成立．HO CF之间存在怎样的关系（数量关系用k表示）？(3)问题解决：回归图①所示，探究,20．如图，△ABC为等腰三角形，AB＝AC，将CA绕点C顺时针旋转至CD，连接AD，E 为直线CD上一点，连接AE；（1）如图1，若∠BAC＝60°，∠ACD＝90°，E为CD中点，23AB=，求△BCE的面积；（2）如图2，若∠ACD＝90°，点E在线段CD上且∠DAE＋∠ABC＝90°，AE的延长线与BC的延长线交于点F，连接DF，求证：2=；BC DF（3）如图3，AB＝1，∠BAC＝90°，∠ACD＝105°，若BE恰好平分∠AEC，点P为线段AE上的动点，点E′与点E关于直线DP对称，AE′与CD交于点Q，连接CE′，当'+-''的值最小时，直接写出CQ的值．2CE AE CE【参考答案】**科目模拟测试一、解答题1．(1)证明见解析；(2)2；3(3)30【解析】【分析】（1）作CG⊥CE，交FD延长线于G点，可根据题意得出四边形FECG为矩形，再结合矩形和正方形的性质推出△BCE≌△DCG，从而得到CE=CG，即四边形FECG为正方形，即可证得结论；（2）在（1）的基础之上，连接CF，首先通过旋转的性质和三角形的内角定理推出△CEF 和△DFP均为等腰直角三角形，进而利用相似三角形的判定与性质推出PF和EF之间的关系，从而表示出BE的长度，即可求出∠BCE的正切值，再根据余角的关系证明∠ABP=∠BCE，即可得出结论；（3）根据正方形的性质以及前面两个问题的求解过程推断出A、C、D、F四点共圆，即可得到在变化过程中，∠AFC始终为90°，从而在Rt△ACF中运用特殊角的三角函数值求解角度即可得出结论．(1)：如图所示，作CG⊥CE，交FD延长线于G点，∵CE⊥BP，DF⊥BP，CG⊥CE，∴∠EFG=∠FEC=∠ECG=∠BEC=90°，∴四边形FECG为矩形，∠G=90°，∵四边形ABCD为正方形，∴∠BCD=90°，BC=DC，∵∠BCD=∠BCE+∠ECD，∠ECG=∠ECD+∠DCG，∴∠BCE+∠ECD=∠ECD+∠DCG，即：∠BCE=∠DCG，在△BCE和△DCG中，∴△BCE≌△DCG(AAS)，∴CE=CG，∴四边形FECG为正方形，∴CE=EF；(2)解：如图所示，连接CF，由（1）知，CE=EF，CE⊥EF，则△CEF为等腰直角三角形，由旋转的性质得：∠PAD=n°，AP=AD，∴∠PAB=90°+n°，∠APD=12（180°-∠PAD）=90°-12n°，∵AP=AB，∴∠APB=12（180°-∠PAB）=45°-12n°，∴∠FPD=∠APD-∠APB=45°，∵DF⊥AB，∴∠DFP=90°，∴△DFP也为等腰直角三角形，PF=DF，∴△DFP∽△CEF，∵，∴，设PF= DF=x，则FE=CE=3x，由（1）知四边形CEFG为正方形，∴FG=FE=3x，∴DG=FG-DF=2x，∵△BCE≌△DCG，∴BE=DG=2x，∴在Rt△BEC中，，∵∠ABP+∠EBC=90°，∠EBC+∠BCE=90°，∴∠ABP=∠BCE，∴；(3)解：∵，∴如图所示，连接AF和对角线AC，由（2）可知，∠EFC=45°，∠EFD=90°，∴∠CFD=45°，∵AC为正方形ABCD的对角线，∴∠CAD=45°，AC2，∴∠CAD=∠CFD，∴点A、C、D、F四点共圆，∴∠AFC=∠ADC=90°，∵AF=22AB，∴AF=12AC，则在Rt△AFC中，，∵∠ACF为锐角，∴∠ACF=30°，∠FAC=90°-30°=60°，∵∠CAD=45°，∴∠FAD=60°-45°=15°，∵AP=AD，AF=AF，PF=DF，∴△AFP≌△AFD，∴∠FAD=∠FAP=15°，∴∠PAD=30°，∴n=30．【点睛】本题考查正方形的判定与性质，相似三角形的判定与性质，以及旋转的性质和解直角三角形等，掌握图形的基本性质和判定方法，具有较强的综合分析能力是解题关键．2．（121；（2）证明见解析；（321- 【解析】【分析】（1）证明,AD BD = 再利用勾股定理求解,,AB BC 从而可得答案；（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥ 证明,EHM CDM ≌ 可得22,AE EH CD == 同理：22,BF FQ BQ == 而,AE BF = 再证明,FQC DCA ≌ 可得,FCQ CAD ∠=∠ 再证明,AF AN = 从而可得结论；（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒ 证明,22.5,CF CA CAD =∠=︒ 可得CP 平分,ACF ∠ 则,A F 关于直线CP 对称，,PF PA = 过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+= 所以PA PK +最短，设,PK n = 则1,21,PF PA n AK ==-= 再利用勾股定理求解,n 即可得到答案.【详解】解：（1）45B ∠=︒，AD 为BC 边上的高，90,45,ADB B BAD ∴∠=︒∠=∠=︒221,112,AD BD AB ∴==+=AB BC =，2,2 1.BC CD BC BD ∴=-=（2）如图，过E 作EH AD ⊥于,H 过F 作FQ BC ⊥于,Q 而,AD CD ⊥则90,EHM CDM ∠=∠=︒ M 为CE 的中点，,HME DMC ∠=∠,EM CM ∴=,EHM CDM ∴≌,EH CD ∴=45,90,BAD AHE EHM ∠=︒∠=∠=︒22,AE EH CD ∴==同理：22,BF FQ BQ == 而,AE BF =,FQ BQ CD EH ∴===,BD CQ AD ∴==90,ADC CQF ∠=∠=︒,FQC DCA ∴≌,FCQ CAD ∴∠=∠,AB BC =,BAC BCA ∴∠=∠,BAD ACF ∴∠=∠ 而,B BAD ∠=∠,,B FCQ AFN ANF ACF CAD ∠+∠=∠∠=∠+∠,AFN ANF ∴∠=∠,AF AN ∴=2.AN CD AF AE AF BF AB ∴=+=+=（3）如图，记CP 与AB 的交点为,L 由（2）得：45,ACF BAD ∠=∠=︒,45,BA BC B =∠=︒67.5,BAC BCA ∴∠=∠=︒67.5,CFA BAC ∴∠=︒=∠,22.5,CF CA CAD ∴=∠=︒22.5,ACP CAD ∠=∠=︒CP ∴平分,ACF ∠,,CP AF AL FL ∴⊥=则,A F 关于直线CP 对称，,PF PA =过F 作FK AC ⊥于,K 则此时,PA PK PF PK FK +=+=所以PA PK +最短，2,AC ∴= 则2,CF = 而45,ACF ∠=︒1,CK FK ∴==设,PK n = 则1,21,PF PA n AK ==-=())222121,n n ∴-=+ 解得：21,n = )121121.22CPK S ∴=⨯⨯= 【点睛】本题考查的是全等三角形的判定与性质，等腰直角三角形的判定与性质，等腰三角形的判定与性质，勾股定理的应用，本题综合性较强，是压轴题，知识的系统化是解题的关键.3．（1）60°；（2）13S ；（3）a +2b ，理由见解析 【解析】【分析】（1）由等边三角形的性质AB =AC =BC ，∠ABC =∠ACE =∠BAC =60°，且BD =CE ，可证△BDC ≌△CEA ，由三角形的外角性质可求∠AFD 的度数；（2）由等边三角形的性质可得BD =CE =AM =DN ，且AB =AC =BC ，∠ABC =∠ACE =∠BAC =60°，可证△ABM ≌△CAE ≌△BCD 和△BDQ ≌△CEF ，由全等三角形的性质和三等分点性质，可求四边形ANQF 的面积；（3）在AC 上截取AM =CE ，由题意可证△BHC ≌△CFA ，可得BH =CF =b ，AF =CH =a ，∠PHB =60°，即可求PC 的长．【详解】解：（1）∵△ABC 是等边三角形∴AB =AC =BC ，∠ABC =∠ACE =∠BAC =60°，且BD =CE ，∴△BDC≌△CEA（SAS），∴∠CAE=∠BCD，∵∠AFD=∠CAE+∠ACF=∠BCD+∠ACD=∠ACB，∴∠AFD=60°；（2）∵D，E，M，N分别是△ABC各边上的三等分点，∴BD=CE=AM=DN，且AB=AC=BC，∠ABC=∠ACE=∠BAC=60°，∴△ABM≌△CAE≌△BCD（SAS），∴∠CAE=∠ABM=∠BCD，∠AMB=∠AEC=∠BDC，且BD=CE，∴△BDQ≌△CEF（ASA），∴S△BDQ=S△CEF，∵BD=DN，∴S△BDQ=S△DNQ=S△CEF，∵D，E是AB，BC上三等分点，∴S△BDC=S△CEA=13S△ABC=13S，∵四边形ANQF的面积=S△ABC-S△AEC-S△DNQ-S四边形DFEB=S-13S-13S=13S；（3）PC=a+2b．理由如下：如图，在AC上截取AM=CE，即AM=CE=BD，∵AM=CE=BD，∠ABC=∠BAC=∠ACB=60°，AB=AC=CB．∴△CBD≌△ACE≌△BAM（SAS），∴∠CAE=∠BCD=∠ABM，且∠ABC=∠ACE，∴∠MBC=∠ACD，且BC=AC，∠EAC=∠BCD，∴△BHC≌△CFA（ASA），∴BH=CF=b，AF=CH=a，∵∠PHB=∠MBH+∠HCB=∠ABM+∠MBC=∠ABC，∴∠PHB=60°，且∠BPD=30°，∴∠PBH=90°，且∠BPH=30°，∴PH=2BH=2b，∴PC=PH+HC=a+2b．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等边三角形的性质，三角形的外角的性质，添加恰当的辅助线构造全等三角形是本题的关键．4．（1）F（0，3112）；（2）能，D（0，－31）；（3）P的坐标为（0，5）或（0，1）．【解析】【分析】（1）由矩形的性质和折叠的性质，求出AF=CF，设OF＝x，然后利用勾股定理求出x，即可得到答案；（2）当四边形DPBC为菱形时，PB∥DC，PD∥BC，利用菱形的性质和勾股定理求出31AP ，然后求出OD的长度，即可得到答案；（3）当重心在y轴上时，F一定是DC的中点，过D作DH⊥x轴于H，利用勾股定理求出DH=4，然后得到点D的坐标，即可求出点P的坐标．【详解】解：（1）如图：在矩形OABC中，OA∥BC，∴∠1＝∠2，又∵∠2＝∠3，∴∠1＝∠3，∴AF＝FC，设OF＝x，∴AF＝FC＝6－x，∴(6－x)2＝x2＋52，解得：x＝31 12，∴F（0，31 12）（2）能，当四边形DPBC为菱形时，PB∥DC，PD∥BC，∴点D在y轴上，且PB＝BC＝6，在Rt△APB中，AP2＋AB2＝PB2，∴AP2＝62－(5)2，∴AP＝31，∵AO＝PD＝6，∴OD＝31，∴D（0，－31）；（3）当重心在y轴上时，F一定是DC的中点，过D作DH⊥x轴于H，∴OH＝OC5∴CH＝5∴DH2246(25)∴D5454）当D54）时，F（0，2），∴AP＝1（6－4）＝12∴OP＝5，∴P（0，5）当D（－5，－4）时，F(0，－2)，AP＝12（6＋4）＝5，∴OP＝1，∴P（0，1）综上，P的坐标为（0，5）或（0，1）．【点睛】本题考查了矩形的性质，折叠的性质，勾股定理，坐标与图形等知识，解题的关键是熟练掌握所学的知识，正确的作出辅助线进行解题．5．（1）2；（2）32；（3）存在，223 3【解析】【分析】（1）如图①，根据等边三角形的判定和性质解决问题即可．（2）如图②，将△ABP绕点B逆时针旋转60°得到△BFE，连接PF，EC．易证PA＋PB＋PC＝PC＋PF＋EF，因为PC＋PF＋EF≥EC，推出当P，F在直线EC上时，PA＋PB＋PC的值最小，求出EC的长即可解决问题．（3）如图③−1中，将△PBQ绕点B逆时针旋转60°得到△EBG，则PQ＝EG，△BQG是等边三角形，易知PQ＋BQ＋CQ＝EG＋GQ＋QC≥EC，推出EC的值最小时，QP＋QB＋QC的值最小，如图③−2中，延长BA交CD的延长线于J，作△ADJ的外接圆⊙O，将线段BO，BP绕点B逆时针旋转60°得到线段BO′，BE，连接EO′，OB，OP．易证△BEO′≌△BPO（SAS），推出EO′＝OP＝433，推出点E的运动轨迹是以O′为圆心，433为半径的圆，推出当点E在线段CO′上时，EC的值最小，最小值＝CO′−EO′．【详解】（1）如图①，由旋转的性质可知：△BCC′是等边三角形，∴CC′＝BC＝2，故答案为2．（2）如图②，将△ABP 绕点B 逆时针旋转60°得到△BFE ，连接PF ，EC ．由旋转的性质可知：△PBF 是等边三角形，∴PB ＝PF ，∵PA ＝EF ，∴PA +PB +PC ＝PC +PF +EF ，∵PC +PF +EF ≥EC ，∴当P ，F 在直线EC 上时，PA +PB +PC 的值最小，根据旋转以及翻折的性质可得BC ＝BE ＝BA ＝3，∵,30EBF ABP ABP PBC ∠=∠∠+∠=︒，∴90FBP EBF PBC ∠+∠+=︒,∵EB ⊥BC ，∴EC ＝2BC ＝32，∴PA +PB +PC 的最小值为32．（3）如图③﹣1中，将△PBQ 绕点B 逆时针旋转60°得到△EBG ，则PQ ＝EG ，△BQG 是等边三角形，∴BQ ＝QG ，PQ ＝EG ，∴PQ +BQ +CQ ＝EG +GQ +QC ≥EC ，∴EC 的值最小时，QP +QB +QC 的值最小，如图③﹣2中，延长BA 交CD 的延长线于J ，作△ADJ 的外接圆⊙O ，将线段BO ，BP 绕点B 逆时针旋转60°得到线段BO ′，BE ，连接EO ′，OB ，OP ．∵,,BO BO BE BP O BE OBP ==∠=∠''，∴△BEO ′≌△BPO （SAS ），∴EO ′＝OP ，∵∠APD +∠AJD ＝180°，∴A ，P ，D ，J 四点共圆，∴OP 43 ∴EO 43， ∴点E 的运动轨迹是以O 43为半径的圆， ∴当点E 在线段CO ′上时，EC 的值最小，最小值＝CO ′﹣EO ′，连接OO ′，延长OO ′到R ，使得O ′R ＝OO ′，连接BR ，则∠OBR ＝90°，作RH ⊥CB 交CB 的延长线于H ，O ′T ⊥CH 于T ，OM ⊥BC 于M ．在Rt △OBM 中，BM ＝5，OM 113 ∴OB 22OM BM +113 ∴BR 3＝14，由△BHR ∽△OMB ， ∴RH BM ＝BR OB， ∴RH ＝3∵HR ∥O ′T ∥OM ，OO ′＝RO ′，∴TM ＝TH ，∴O ′T ＝2RH OM +133 ∴BT 22O B O T -''3，∴CO ，∴CO ′﹣EO∴QP +QB +QC 【点睛】 本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，等边三角形的判定和性质，解直角三角形等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．6．（1）①见解析；②185；（2）在坐标平面内存在点2,03H ⎛⎫ ⎪⎝⎭或4,H ⎛ ⎝⎭或2H ⎫⎪⎝⎭或2H ⎛⎫+ ⎪⎝⎭使得以点E ，A ，G ，H 为顶点的四边形是菱形． 【解析】【分析】（1）①由折叠的性质可知EF =EC ，∠BEF =∠BEC ，E 是CD 的中点，得到DE =EC =EF ，则∠EDF =∠EFD ，即可证明∠EDF =∠BEC ，得到DF ∥BE ；②过点E 作EG ⊥DF 于G ，先证明△EGD ∽△BCE ，得到DE DG BE CE=，利用勾股定理求出5BE ，由此求解即可；（2）先证明△CDE ≌△AEO 得到AE =CE ，设OE x =，则AE CE OC OE x ==-=，由222AE OE OA =+，得到()2222x x =+，可求得E ⎛ ⎝⎭，AE =求出直线AC的解析式为y =+，设(,G a +，(),H m n ，然后分当AE 是菱形的对角线时，则AG =EG ，当AG 是菱形的对角线时，AE =EG ，当AH 为菱形对角线时，AE =AG ，三种情况进行讨论求解即可．【详解】解：（1）①由折叠的性质可知EF =EC ，∠BEF =∠BEC ，∵E 是CD 的中点，∴DE =EC =EF ，∴∠EDF =∠EFD ，∵∠FEC =∠EDF +∠EFD =∠BEF +∠BEC ，∴∠EDF =∠BEC ，∴DF ∥BE ；②如图所示，过点E 作EG ⊥DF 于G ，∴FD=2DG，∵四边形ABCD是矩形，∴CD=AB=6，∠C=90°，∵∠EGD=∠BCE，∠EDG=∠BEC，∴△EGD∽△BCE，∴DE DG BE CE=，∵E为CD中点，∴132DE CE CD===，∴225 BE BC CE=+=，∴353DG =，∴95 DG=，∴185 DF=；（2）∵2OA=，3OC=∴A（2，0），C（0，23∵四边形OABC是矩形，∴BC=OA，∠ABC=90°，由折叠的性质可知CD=CB=OA，∠CDE=∠AOE=90°，又∵∠CED=∠AEO，∴△CDE≌△AOE（AAS），∴AE=CE，设OE x=，则3AE CE OC OE x==-=，∵222AE OE OA=+，∴()222232x x=+，解得23 x=∴23E⎛⎝⎭，43AE=设直线AC的解析式为y kx b=+，∴20k b b +=⎧⎪⎨=⎪⎩，∴k b ⎧=⎪⎨=⎪⎩， ∴直线AC的解析式为y =+设(,G a +，(),H m n ，∴AGEG =当AE 是菱形的对角线时，则AG =EG ，∴()(222a -++=22a ⎛++ ⎝⎭，解得43a =， 由AE 与HG的中点坐标相同得：0222032a m ++⎧=⎪⎪⎨⎪=⎪⎩ 解得230m n ⎧=⎪⎨⎪=⎩； ∴2,03H ⎛⎫ ⎪⎝⎭当AG 是菱形的对角线时，AE =EG ，22163a ⎛++= ⎝⎭， 解得2a =或0a =（舍去），由AG 与EH的中点坐标相同得2202232m n ++⎧=⎪⎪= 解得4m n =⎧⎪⎨=⎪⎩∴4,H ⎛ ⎝⎭； 当AH 为菱形对角线时，AE =AG ，∴()()221623233a a -+-+=， 解得2323a =±， 由AH 与EG 的中点坐标相同得2022233230322m a a n ++⎧=⎪⎪⎨-++⎪+=⎪⎩， 解得2332323m n ⎧=⎪⎪⎨⎪=-⎪⎩或2332323m n ⎧=-⎪⎪⎨⎪=+⎪⎩； ∴2323,233H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫-+ ⎪⎝⎭； ∴综上所述，在坐标平面内存在点2,03H ⎛⎫ ⎪⎝⎭或234,3H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫- ⎪⎝⎭或2323,233H ⎛⎫-+ ⎪⎝⎭使得以点E ，A ，G ，H 为顶点的四边形是菱形．【点睛】本题主要考查了坐标与图形，一次函数与几何综合，全等三角形的性质与判定，等腰三角形的性质与判定，平行线的判定，矩形的性质，菱形的性质等等，解题的关键在于能够熟练掌握相关知识进行求解．7．（1）见解析；（2）结论依然成立，理由见解析；（3）见解析【解析】【分析】（1）根据半角旋转模型，把△ABF 逆时针旋转90°，则AB 与AD 重合，设F 对应的点为M ，即可证明AME AFE ≅，得到AEM AEF ∠=∠，再结合AEM EAG ∠=∠，可得AEM AEF ∠=∠，可得EG AG =；（2）结论依然成立，证明方法与（1）一样；（3）又等腰三角形三线合一的性质可得GQ 垂直平分EA ，可得△ANE 是等腰直角三角形，可得A 、D 、E 、N 四点共圆，根据圆周角45NDC EAN ∠=∠=︒【详解】（1）把△ABF 逆时针旋转90°，则AB 与AD 重合，设F 对应的点为M ，∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB ∥CD∴AEM EAG ∠=∠∴AEG EAG ∠=∠∴EG AG =（2）结论依然成立，EG AG =把△ABF 逆时针旋转90°，则AB 与AD 重合，设F 对应的点为M ，∴AMD AFB ≅∴90,,MDA FBA AM AF MAD FAB ∠=∠=︒=∠=∠∴M 、D 、C 三点共线∵45EAF ∠=︒∴45EAD FAB EAD MAD MAE ∠+∠=∠+∠=∠=︒∴()AME AFE SAS ≅∴AEM AEG ∠=∠∵AB ∥CD∴AEM EAG ∠=∠∴AEG EAG ∠=∠∴EG AG =（3）连接EN由（2）得EG AG =∵GQ AE ⊥∴GQ 垂直平分AE∴EN =AN∵45EAF ∠=︒∴90ANE ADE ∠=︒=∠∴A 、D 、E 、N 四点在以AE 为直径的同一个圆上，∴45NDC EAN ∠=∠=︒．【点睛】本题考查半角旋转模型，熟练根据模型做出辅助线是解题的关键．第（3）问根据四点共圆证明是本题的难点．8．（12 ；（2，2）；（2）① 在，理由见解析； ②22t +，22t +；（3）存在，（2，2）（6，4）【解析】【分析】（1）作PM ⊥y 轴于M ，PN ⊥OA 于N ，根据全等三角形的判定及性质可得：PMB PNA ≌，PM PN =，BM AN =，再依据正方形的判定及性质即可得出结果；（2）①利用角平分线的判定定理证明OP 平分AOB ∠即可；②由（1）可知：22OM OB OA t =+=+，即可得出点P 的坐标；（3）过点A 作平行于y 轴的直线交过点M 作平行于x 轴的直线于点Q ，连接QB ，由（1）（2）结论可知：2,2t Q t +⎛⎫ ⎪⎝⎭，可得22t QA +=，根据点坐标及勾股定理确定QB 、AB 长度，然后分三种情况讨论三角形为等腰三角形，得出一元二次方程求解即可得．【详解】 解：（1）作PM ⊥y 轴于M ，PN ⊥OA 于N ．∵OBC 是等腰直角三角形，2OB =，∴222BC OC OB +=，∴2BC =∵90PMB PNA PNO MON ∠=∠=∠=∠=︒，∴90MPN BPA ∠=∠=︒，四边形PMON 是矩形，∴MPB NPA ∠=∠，∵PBA △是等腰直角三角形，∴PB PA =，在PMB △与PNA 中，PMB PNA MPB NPA PB PA ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴PMB PNA ≌，∴PM PN =，BM AN =，∴24OB OA OM BM ON AN OM +=-++==，∴2OM ON ==，∴四边形PMON 是正方形，∴()2,2P ，2，（2，2）；（2）①由（1）可知：四边形PMON 是正方形，PM PN =，如图所示，∵PM OB ⊥，PN OA ⊥，∴OP 平分AOB ∠，∵45BOC ∠=︒，∴OC 平分AOB ∠，∴点P 在射线OC 上；②由（1）可知：22OM OB OA t =+=+， ∴22t OM ON +==， ∴22,22t t P ++⎛⎫ ⎪⎝⎭， 故答案为22,22t t ++； （3）如图，过点A 作平行于y 轴的直线交过点M 作平行于x 轴的直线于点Q ，连接QB ，由（1）可知：四边形PMON 是正方形，PM PN =，点()0,2B ，(),0A t ，由（2）可知：22,22t t P ++⎛⎫ ⎪⎝⎭， ∴点2,2t Q t +⎛⎫ ⎪⎝⎭， ∴22t QA +=， 根据勾股定理可得：222252124t QB t t t +⎛⎫=+-=-+ ⎪⎝⎭ 22224AB t t ++①当QA QB =时，即22t += 化简可得：220t t -=，解得：2t =或0=t （题中已给，舍去）， ∴222t +=， 故点()2,2Q ；②当QA AB =时，即22t +， 化简可得：234120t t -+=， ()2443120∆=--⨯⨯<，方程无解，故这种情况不存在；③当QB AB =时，= 化简可得：24120t t --=，解得：6t =或2t =-（舍去）， ∴242t +=， 故点()6,4Q ；综上可得：点()6,4Q 或()2,2Q ．【点睛】题目主要考查等腰直角三角形的性质，全等三角形的判定和性质，正方形的判定和性质角平分线的性质、勾股定理等知识点，理解题意，作出相应辅助线，综合运用这些知识点是解题关键．9．（1）2144y x =-，132y x =-；（2）见解析；（3）1(12)P +，2(13)P 【解析】【分析】（1）将A （4，0），B （0，﹣4）的坐标代入y ＝ax 2+b ，利用待定系数法得抛物线解析式，再将点E （4，﹣1），C （0，﹣3）的坐标代入y ＝mx +n 可得问题的答案；（2）设点21,44P t t ⎛⎫- ⎪⎝⎭ ，0＜t ＜4，如图，过点P 作PF ⊥y 轴于点F ，从而得PF 、PD 、PC 、FC 的长度，从而得到答案；（3）设DP 与EC 的交点为G ，设21,44P x x ⎛⎫- ⎪⎝⎭，①当点G 在点P 上方时，根据三角形面积公式可得答案；②当点G 在点P 下方时，根据三角形面积公式可得答案． 【详解】解：（1）将A （4，0），B （0，﹣4）的坐标代入y ＝ax 2+b ，得1604a b b +=⎧⎨=-⎩，解得，144a b ⎧=⎪⎨⎪=-⎩ ，∴抛物线的解析式为2144y x =-， 设直线CE 为y ＝mx +n ，将点E （4，﹣1），C （0，﹣3）的坐标代入y ＝mx +n 得，413m n n +=-⎧⎨=-⎩， 解得，123m n ⎧=⎪⎨⎪=-⎩ ，∴直线CE 的解析式是132y x =-；（2）证明：设点21,44P t t ⎛⎫- ⎪⎝⎭，0＜t ＜4，如图，过点P 作PF ⊥y 轴于点F ，则PF ＝t ，221143144FC t t =-+=- ，2144PD t =- ，222222111111444PC t t t t ⎛⎫⎛⎫=+-=+=+ ⎪ ⎪⎝⎭⎝⎭ ，所以221114544PC PD t t ⎛⎫⎛⎫+=++-= ⎪ ⎪⎝⎭⎝⎭ 为定值；（3）解：方法一：设DP 与EC 的交点为G ，设21,44P x x ⎛⎫- ⎪⎝⎭，①如图，当点G 在点P 上方时，()2211115434122422PEC S x x x ⎡⎤⎛⎫⎛⎫=⨯⨯---=--+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦△ ，∵S △PEC ＝1 ， ∴()2151122x --+=， 解得：113x =+ ，213x =- （负根舍去）， ∴()213134342y =+-=- ，即1313,32P ⎛⎫=+- ⎪ ⎪⎝⎭， ②如图，当点G 在点P 下方时，()2211115443124222PEC S x x x ⎡⎤⎛⎫⎛⎫=⨯⨯---=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦△，∵S △PEC ＝1， ∴()2151122x --= ， 解得：317x =，417x =（负根舍去），∴()217174242y =⨯+-=-，即2717,22P ⎛⎫+- ⎪ ⎪⎝⎭， 综上所述，满足条件的点有1313,32P ⎛⎫=+- ⎪ ⎪⎝⎭，2717,22P ⎛⎫+- ⎪ ⎪⎝⎭． 方法二：如图，分别过点P ，E 作PF ⊥CE ，EH ⊥y 轴，垂足为F ，H ，PD 交CE 于点G ，在Rt △EHC 中，EH ＝4，HC ＝2， ∴2225CE EH HC +=， ∵S △PEC ＝1， ∴12CE PF ＝1， 即5PF =， ∵PF ⊥CE ，PG ⊥EH ， ∴△PFG ∽△CHE ， ∴PG ECPF EH= ， 255= ， 解得12PG =， ∴过点P 与直线CE 平行，且与直线CE 5的直线有两条：1522y x =- 或1722y x =- ，依题意得：21441522y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩，解得：1x =（负根舍去），∴1x =+2y =- ，∴112P ⎛⎫ ⎪ ⎪⎝⎭， 21441722y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩，解得：1x =∴1x =+3y = ，∴2(13)P +，综上所述，满足条件的点有1(12)P +，2(13)P +-． 【点睛】此题考查的是二次函数综合题目，掌握待定系数法求解析式、由坐标得线段长度、相似三角形的判定与性质是解决此题关键．10．（1）①见解析；②5m =；（2）m的值为6；（3）CE =【解析】 【分析】（1）①连接DE ，证明ADC ∆是等腰三角形，根据“三线合一”的性质可得ADE CDE ∠=∠，证得EC EF =，从而可得结论；②根据勾股定理得到AC =，由E 为AC 中点得EC =DEC CBA ，由相似三角形的性质列出比例式，求出m 的值即可；（2）分PF //AC 和PF //BC 两种情况求解即可； （3）设CE =x ，作PG ⊥AC ，则2xGE =，AE x = 证明PGE EAP '≅得AP GE '=，再证明AP E BAC '，列比例式求出x 的值即可．【详解】解：（1）如图，连接DE∵CD是圆P的直径，∴∠DEC=90°，即DE⊥AC∵E为CA中点∴AE=CE∴AD=CD∴ADE CDE∠=∠∴EC EF=∴E是CF的中点；②在Rt△ABC中，∠B＝90°，AB＝4，BC＝8，∴22224845AC AB BC=+=+=∵E是AC的中点∴114525 22EC AC==⨯=∵AB//CD，90B∠=︒∴90B DCB∠+∠=︒∴90DCB∠=︒，即90DCE BCA∠+∠=︒∵90CDE DCE∠+∠=︒∴CDE BCA∠=∠又90B DEC∠=∠=︒∴DEC CBA∆∆∽∴CE DCAB AC=，即252=445m解得，5m=；（2）分两种情况：①当PF//AC时，如图，则有PDF CDA∆∆∴PF PDAC CD =，即245PF m m=∴25=PF ∴25m =②当PF //BC 时，如图，过点A 作AH ⊥DC ，垂足为H ，则四边形AHCB 是矩形， ∴AH //BC ，HC =AB =4，AH =BC =8 ∴PF //AH ∵90DCB ∠=︒ ∴90FPD ∠=︒ ∴45PDF PFD ∠=∠=︒ ∴45HAD HDA ∠=∠=︒ ∴DH =AH ，即248m -= 解得，6m =综上，m 的值为25或6；（3）过点P 作PG AC ⊥于点G ，如图，∵PE =PC∴1,2GE CE EPG CPG =∠=∠∵90PEP '∠=︒ ∴90P EA PEG '∠+∠=︒ 又90PEG GPE ∠+∠=︒ ∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒，PE P E '= ∴P AE EPG '∆≅∆ ∴AP GE '=设CE x =，则,2x AE x GE AP '===∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒ ∴GPC BCA ∠=∠ ∴EPG BCP ∠=∠ ∴P EA BCA '∠=∠ 又90P AE B '∠=∠=︒ ∴AP EBAC '∆∆∴AP ABAE BC'=48x=∴x =CE =【点睛】本题主要考查了全等三角形的判定与性质，圆的基本概念，相似三角形的判定与性质，正确作出辅助线以及进行分类讨论是解答本题的关键．11．(1)1，3；(2)①4；D (0，1)；②存在这样的D 使△DEG 与△ACH相似，坐标为1⎛ ⎝ 【解析】 【分析】（1）将A (-2，0)，C (4，3)代入抛物线方程214y x bx c =-++得b 与c 的值即可；（2）①过D 作EF 垂线交FE 延长线于P ，过C 作CH LAB 于H ，从而求出EP =1，DP =2，再求出直线AC 的函数关系式，D （x ，12x +1），则E （x +2，12x +2），G （x ，2134x x -++），F （x +2，()()212234x x -++++），最后列出关于四边形DEFG 的面积的关系式，再求其最大值；②分∠DGE =∠CAH 及∠GDE =∠CAH 两种情况进行讨论，设1,12D m m ⎛+⎫ ⎪⎝⎭，则21,34G m m m ⎛⎫-++ ⎪⎝⎭，根据三角函数值求出GD 的长，令其等于用坐标表示的GD 长，解方程求出满足要求的解即可，进而可得坐标． (1)将A (-2， 0)，C (4， 3)代入抛物线方程214y x bx c =-++得：()221443412204b c b c ⎧-⨯++=⎪⎪⎨⎪-⨯--+=⎪⎩， 解得：13b c =⎧⎨=⎩，故答案为 1，3； (2)①解：如图，过D 作EF 垂线交FE 延长线于P ，过C 作CH ⊥AB 于H则DP AB ∥，∠EDP = ∠CAH ，且CH =3，AH =4+2=6， 故tan ∠EDP =tan ∠CAH =CH ：AH =12，又DE 5 ∴EP =1，DP =2设直线AC 方程y =kx +a ，将A ，C 坐标代入得：2043k a k a -+=⎧⎨+=⎩，解得112a k =⎧⎪⎨=⎪⎩，设D （x ，12x +1），则E （x +2，12x +2），G （x ，2134x x -++），F （x +2，()()212234x x -++++）， ∴1S S S ()2DEFG DPFG DEP DP GD FP EP =-=+- 22111131(2)(2)324242x x x x x x ⎛⎫⎛⎫=-++-+-++++-+ ⎪ ⎪⎝⎭⎝⎭ 2142x =-+ 故当x =0时，四边形面积最大为4，此时D （0，1）； ②解：由题意知，DG CH ∥ ∴GDE ACH ∠=∠ ∵6AH =，3CH = ∴2235AC AH CH +∴sinCH CAH AC ∠==1tan 2CH CAH AH ∠== 由题意知△DEG 与△ACH 相似分两种情况求解： 情况一：90DGE ∠=︒时，DEG CAH ∽ ∴1tan tan 2DG DEG CAH GE ∠==∠= ∴2GE DG =∵DE 解得1DG =设1,12D m m ⎛+⎫ ⎪⎝⎭，则21,34G m m m ⎛⎫-++ ⎪⎝⎭∴21131142m m m -++--=整理得2240m m --=∴m =解得11m =21m =当1m =(1112y =⨯+=∴1D ⎛ ⎝⎭； 情况二：90DEG ∠=︒时，DGE CAH ∽ ∴sin sinDE DGE CAH DG ∠==∠=∴5DG =∴21131542m m m -++--=整理得22120m m -+= ∵()224120=--⨯< ∴方程无解，此时不存在；综上所述，存在这样的D 使△DEG 与△ACH 相似，坐标为1⎛ ⎝⎭． 【点睛】本题考查了二次函数综合，二次函数与几何图形面积问题及二次函数与相似相结合问题，勾股定理，三角函数值等知识．解题的关键在于熟练掌握二次函数的性质及几何图形有关性质．12．(1)(2)ACP △为直角三角形，理由见解析 (3)存在，点M 的坐标为或【解析】 【分析】(1)根据一次函数的解析式可求得()5,0B ，，再把这两点的坐标分别代入二次函数解析式，即可求得； (2) 抛物线的对称轴为直线3x =，可分别求得点A 、C 、P 的坐标，分别求得、、，根据勾股定理的逆定理即可证得；(3)分点M 在PA 左边和右边两种情况分别计算，根据两点间距离公式及等腰三角形判定与性质即可分别求得． (1) 解：由，得点B 的坐标为，点C 的坐标为.把()5,0B ，代入抛物线，得，解得1a =-，，∴抛物线的解析式为；(2)解：ACP △为直角三角形. 理由如下： 抛物线的对称轴为直线3x =， 当3x =时，， ∴点P 的坐标为，当0y =时，，得1x =或5，∴点A 的坐标为.∵， ∴. 同理，，，∴， ∴ACP △为直角三角形；(3)解：存在点M ，使AM 与直线BC 的夹角等于ACB ∠的2倍. 分两种情况：①点M 在PA 左边时，如图， ∵，，∴，∴，M在直线上，∵点1M的坐标为.设点1根据题意，得，，∴，解得，M的坐标为.∴点1②点M在PA右边时，如图，此时，∴，∵，∴点P是的中点∵，，∴.综上所述，点M的坐标为或．【点睛】本题考查了利用待定系数法求二次函数的解析式，两点间距离公式，勾股定理的逆定理，解决(3)的关键是分两种情况分别计算13．(1)(2)E（23，53）(3)（﹣2，1）或（﹣2，3）或（﹣2，9）【解析】【分析】（1）由矩形的性质及已知，易得点A的坐标，把A、B两点的坐标代入解析式中可得关于b、c的方程组，解方程组即可；（2）设E（m，﹣34m2﹣32m+3），由题意易得BD、AB的长，则可把△BDE、△ABE的面积表示出来，由S△BDE＝4S△ABE得关于m的方程，解方程即可；（3）用待定系数法可求得直线DE的解析式；分三种情况：当P、B重合时，易得△APQ 是等腰直角三角形，从而问题解决；当点P在线段DB的延长线，且AP⊥AQ时，过点Q 作QM⊥AB交BA的延长线于点M，易证△PAB∽△AQM，设P（﹣2，t），由相似三角形的性质可得关于t的方程，解方程即可求得t；当PQ⊥AQ时，易得AP∥DE，则可求得直线AP的解析式，易得点P的坐标．(1)∵B（﹣2，3），矩形OABC，∴A（0，3），∵抛物线y＝﹣34x2+bx+c经过点A和点B，∴，∴，∴y＝﹣34x2﹣32x+3；(2)∵D（﹣2，﹣1），∴BD＝4，设E（m，﹣34m2﹣32m+3），∴S△BDE＝12×4×（m+2）＝2（m+2），∵AB＝2，∴，∵S△BDE＝4S△ABE，∴2（m+2）＝4（），。

1.一个等腰三角形的底边长为10厘米，腰长为13厘米，求这个三角形的面积。

答案：底边上的高为12厘米，面积为60平方厘米。

2.解方程：2x^2 - 5x + 2 = 0。

答案：x1 = 1/2, x2 = 2。

3.一个圆的半径是7厘米，求这个圆的周长和面积。

答案：周长约为43.98厘米，面积约为153.94平方厘米。

4.一个长方体的长、宽、高分别是8厘米、6厘米和4厘米，求它的体积和表面积。

答案：体积为192立方厘米，表面积为192平方厘米。

5.一个数的2/3加上15等于这个数的1/2，求这个数。

答案：这个数是60。

6.一个班级有40名学生，其中女生占全班的5/8，求男生的人数。

答案：男生有15人。

7.一个三角形的两边长分别是8厘米和6厘米，夹角为90度，求这个三角形的面积。

答案：面积为24平方厘米。

8.一个圆柱的底面半径是5厘米，高是10厘米，求这个圆柱的体积。

答案：体积约为785.4立方厘米。

9.一个梯形的上底是6厘米，下底是10厘米，高是4厘米，求这个梯形的面积。

答案：面积为32平方厘米。

10.一个数的1/4减去5等于这个数的1/8，求这个数。

答案：这个数是40。

11.一个班级有50名学生，其中2/5是女生，求男生的人数。

答案：男生有30人。

12.一个三角形的两边长分别是9厘米和12厘米，夹角为60度，求这个三角形的面积。

答案：面积约为27.71平方厘米。

13.一个圆锥的底面半径是3厘米，高是4厘米，求这个圆锥的体积。

答案：体积约为37.68立方厘米。

14.一个梯形的上底是5厘米，下底是7厘米，高是3厘米，求这个梯形的面积。

答案：面积为18平方厘米。

15.一个数的3/5加上10等于这个数的2/3，求这个数。

答案：这个数是75。

16.一个班级有60名学生，其中1/3是男生，求女生的人数。

答案：女生有40人。

17.一个三角形的两边长分别是7厘米和5厘米，夹角为30度，求这个三角形的面积。

答案：面积约为5.92平方厘米。

中考数学压轴题100题精选【含答案】【001】如图，已知抛物线y a(x 3 3( a z 0)经过点A2 °)，抛物线的顶点为D , 过O作射线OM // AD •过顶点D平行于x轴的直线交射线OM于点C , B在x轴正半轴上，连结BC •(1)求该抛物线的解析式；(2)若动点P从点0出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为t(s) •问当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？(3)若0C °B，动点P和动点Q分别从点0和点B同时出发，分别以每秒1个长度单位和2 个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动•设它们的运动的时间为t (s)，连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长.【002】如图16,在Rt A ABC中，/ C=90 , AC = 3 , AB = 5 .点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动，DE保持垂直平分PQ,且交PQ于点D，交折线QB-BC-CP于点E.点P、Q同时出发，当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t >0).(1) 当t = 2时，AP = ，点Q到AC的距离是:(2) 在点P从C向A运动的过程中，求△ APQ的面积S与t的函数关系式；(不必写出t的取值范围)(3) 在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t的值.若不能，请说明理由；(4) 当DE经过点C时，请直接写出t的值.【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B (4, 0)、C ( 8, 0)、D ( 8,8) •抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标，并求出抛物线的解析式；(2) 动点P从点A出发.沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动.速度均为每秒1个单位长度，运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ.在点P、Q运动的过程中，判断有几个时刻使得△ CEQ是等腰三角形？请直接写出相应的t值。

中考数学压轴题100题精选【含答案】【001】如图，已知抛物线2(1)y a x=-+a≠0）经过点(2)A-，0，抛物线的顶点为D，过O作射线OM AD∥．过顶点D平行于x轴的直线交射线OM于点C，B在x轴正半轴上，连结BC．（1）求该抛物线的解析式；（2）若动点P从点O出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为()t s．问当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB=，动点P和动点Q分别从点O和点B同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t()s，连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长．【002】如图16，在Rt△ABC中，∠C=90°，AC = 3，AB = 5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当t = 2时，AP = ，点Q到AC的距离是；（2）在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；（不必写出t的取值范围）（3）在点E从B向C运动的过程中，四边形QBED能否成为直角梯形？若能，求t的值．若不能，请说明理由；（4）当DE经过点C 时，请直接写出t的值．AP 图16【003】如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B （4，0）、C （8，0）、D （8，8）.抛物线y=ax2+bx 过A 、C 两点.(1)直接写出点A 的坐标，并求出抛物线的解析式；(2)动点P 从点A 出发．沿线段AB 向终点B 运动，同时点Q 从点C 出发，沿线段CD向终点D 运动．速度均为每秒1个单位长度，运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ，①过点E 作EF ⊥AD 于点F ，交抛物线于点G.当t 为何值时，线段EG 最长?②连接EQ ．在点P 、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。

做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，在直角梯形OABC中，AB∥OC，BC⊥x轴于点C，A(1，1)，B(3，1)．动点P从点O出发，沿x轴正方向以每秒1个单位长度的速度移动．过点P作PQ⊥OA，垂足为Q．设点P移动的时间为t秒（0<t<4），△OPQ与直角梯形OABC重叠部分的面积为S．做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日三、解答题23. （11分）如图，抛物线22++=bx ax y 与x 轴交于A (-1，0)，B (4，0)两点，与y 轴交于点C ，与过点C 且平行于x 轴的直线交于另一点D ，点P 是抛物线上一动点．（1）求抛物线的解析式及点D 的坐标．（2）点E 在x 轴上，若以A ，E ，D ，P 为顶点的四边形是平行四边形，求此时点P 的坐标．（3）过点P 作直线CD 的垂线，垂足为Q ．若将△CPQ 沿CP 翻折，点Q 的对应点为Q ′，是否存在点P ，使点Q ′恰好在x 轴上？若存在，求出此时点P 的坐标；若不存在，请说明理由．备用图做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，已知直线112y x=-+与坐标轴交于A，B两点，以线段AB为边向上作正方形ABCD，过点A，D，C的抛物线与直线的另一个交点为E．（1）请直接写出C，D两点的坐标，并求出抛物线的解析式；（2个单位长度的速度沿射线AB下滑，直至顶点D落在x轴上时停止，设正方形落在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围；（3）在（2）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上C，E两点间的抛物线弧所扫过的面积．备用图做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，抛物线y=ax2+bx+c交x轴于点A(-3，0)，点B(1，0)，交y轴于点E(0，-3)．点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行．直线y=-x+m过点C，交y轴于点D．（1）求抛物线的解析式；（2）点K为线段AB上一动点，过点K作x轴的垂线，交直线CD于点H，交抛物线于点G，求线段HG长度的最大值；（3）在直线l上取点M，在抛物线上取点N，使以A，C，M，N为顶点的四边形是平行四边形，求点N的坐标．备用图做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日三、解答题23. （11分）如图，在平面直角坐标系中，直线3342y x =-与抛物线214y x bx c =-++交于A ，B 两点，点A 在x 轴上，点B 的横坐标为-8．（1）求抛物线的解析式．（2）点P 是直线AB 上方的抛物线上一动点（不与点A ，B 重合），过点P 作x 轴的垂线，垂足为C ，交直线AB 于点D ，作PE ⊥AB 于点E ． ①设△PDE 的周长为l ，点P 的横坐标为x ，求l 关于x 的函数关系式，并求出l 的最大值．②连接PA ，以PA 为边作图示一侧的正方形APFG ．随着点P 的运动，正方形的大小、位置也随之改变．当顶点F 或G 恰好落在y 轴上时，直接写出对应的点P 的坐标．备用图做题时间：_______至_______ 家长签字：_____________ 共__________分钟 日 期：_____月_____日三、解答题23. （11分）如图1，点A 为抛物线C 1：2122y x =-的顶点，点B 的坐标为(1，0)，直线AB 交抛物线C 1于另一点C ．（1）求点C 的坐标；（2）如图1，平行于y 轴的直线x =3交直线AB 于点D ，交抛物线C 1于点E ，平行于y 轴的直线x =a 交直线AB 于点F ，交抛物线C 1于点G ，若FG :DE =4:3，求a 的值；（3）如图2，将抛物线C 1向下平移m （m >0）个单位得到抛物线C 2，且抛物线C 2的顶点为P ，交x 轴负半轴于点M ，交射线AB 于点N ，NQ ⊥x 轴于点Q ，当NP 平分∠MNQ 时，求m 的值．图1 图2做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图1，在平面直角坐标系中，已知点A(0，，点B在x轴正半轴上，且∠ABO=30°．动点P在线段AB上，从点A向点B个单位长度的速度运动，设运动时间为t秒．在x轴上取两点M，N作等边三角形PMN．（1）求直线AB的解析式；（2）求等边三角形PMN的边长（用含有t的代数式表示），并求出当等边三角形PMN的顶点M运动到与原点O重合时t的值；（3）如果取OB的中点D，以OD为边在Rt△AOB内部作如图2所示的矩形ODCE，点C在线段AB上．设等边三角形PMN和矩形ODCE重叠部分的面积为S，请求出当0≤t≤2时S与t的函数关系式，并求出S的最大值．图2图1做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，平面直角坐标系xOy中，点A的坐标为( 2，2)，点B的坐标为(6，6)，抛物线经过A，O，B三点．连接OA，OB，AB，线段AB交y 轴于点E．（1）求点E的坐标；（2）求抛物线的函数解析式；（3）点F为线段OB上的一个动点（不与点O，B重合），直线EF与抛物线交于M，N两点（点N在y轴右侧），连接ON，BN，当点F在线段OB 上运动时，求△BON面积的最大值，并求出此时点N的坐标；（4）连接AN，当△BON面积最大时，在坐标平面内求使得△BOP与△OAN 相似（点B，O，P分别与点O，A，N对应）的点P的坐标．做题时间：_______至_______ 家长签字：_____________共__________分钟日期：_____月_____日三、解答题23.（11分）如图，在平面直角坐标系中，已知点A，B，C的坐标分别为( 1，0)，(5，0)，(0，2)．（1）求过A，B，C三点的抛物线解析式．（2）点P从点A出发，沿x轴正方向以每秒1个单位长度的速度向点B移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．设点P运动的时间为t（0≤t≤6）秒，△PBF的面积为S．①求S与t的函数关系式；②当t为何值时，△PBF的面积最大？最大面积是多少？（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．备用图做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(-4，0)，点B的坐标是(0，b)（b>0）．P是直线AB上的一个动点，作PC ⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连接PP′，P′A，P′C．设点P的横坐标为a．（1）当b=3时，①求直线AB的解析式；②若点P′的坐标是(-1，m)，求m的值．（2）若点P在第一象限，记直线AB与P′C的交点为D．当P′D:DC=1:3时，求a的值．（3）是否同时存在a，b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．23．（1）21433y x x =-+； （2）22102412311143422tt S t t t t t ⎧<⎪⎪=-<⎨⎪⎪-+-<<⎩≤≤（）（）（）； （3）存在，t =1或2．中考数学压轴题专项训练（二）参考答案23．（1）213222y x x =-++，(3 2)，D ； （2）123(0 2) 2) 2)，，，P P P --； （3）存在，点P的坐标为 (或．中考数学压轴题专项训练（三）参考答案中考数学压轴题专项训练（四）参考答案中考数学压轴题专项训练（六）参考答案中考数学压轴题专项训练（七）参考答案中考数学压轴题专项训练（八）参考答案中考数学压轴题专项训练（十）参考答案。

中考数学压轴题100题精选及答案全第一篇：数与代数1.下列各组数中，哪一组数最大？A. \frac{1}{2} ,\frac{2}{3},\frac{3}{4},\frac{4}{5}B. 0.99,0.999,0.9999,0.99999C. \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7}D. 1,10^2,10^3,10^42. 一个整数，十位数与各位数的和为9，再去掉该整数中的各位数，十位数与剩下的数字的和为40，该整数为__________。

A. 45B. 54C. 63D. 723. 已知 a+b=2, ab=-1，求a^2+b^2的值。

A. 3B. 5C. 7D. 94. 解方程 2x-5=3x+1。

A. x=-3.5B. x=-2C. x=2D. x=3.55. 有两个数，各位数字相同，但顺序颠倒，若它们的和为110，这两个数分别是多少？A. 47,74B. 49,94C. 56,65D. 59,956. 若x-3y=-7，x+4y=1，则y的值为__________。

A. -2B. -1C. 0D. 17. 16÷(a-2)=4，则 a 的值为__________。

A. 6B. 8C. 10D. 128. 若a:b=5:3，b:c=7:4，则a∶b∶c=__________。

A. 35:21:12B. 25:15:12C. 25:21:16D. 35:15:169. 若a+3b=5，3a-5b=7，则 a 的值为__________。

A. -2B. -1C. 0D. 110. 已知x+y=3，xy=2，则y的值为__________。

A. 1B. 2C. 3D. 4第二篇：几何图形11. 已知正方形 ABCD 的边长为6，以 BC 为边，画一个正三角形 BCE，连接 AE，AD，请问△ADE 和正方形 ABCD 的面积之比是多少？A. \frac{2}{9}B. \frac{1}{2}C. \frac{4}{9}D.\frac{5}{6}12. 把一张纸平整地放在桌上，在纸的中央画一个圆形，请问可以用多少个直径为5 厘米的圆去覆盖这个圆形（圆覆盖圆）？A. 1B. 2C. 3D. 413. 已知△ABC 是等腰三角形，AB=AC，E是BC中点，DE∥AC，AE=CD=2，求△ABC 的面积。

中考数学压轴题100题精选【含答案】【001】如图，已知抛物线2(1)y a x =-+a ≠0）经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ． （1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？ （3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．【002】如图16，在Rt △ABC 中，∠C=90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，到达点A 后立刻以原来的速度沿AC 返回；点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动．伴随着P 、Q 的运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交折线QB-BC-CP 于点E ．点P 、Q 同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）． （1）当t = 2时，AP = ，点Q 到AC 的距离是 ； （2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围）（3）在点E 从B 向C 运动的过程中，四边形QBED 能否成 为直角梯形？若能，求t 的值．若不能，请说明理由； （4）当DE 经过点C 时，请直接写出t 的值．【003】如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B （4，0）、C （8，0）、D （8，8）.抛物线y=ax2+bx 过A 、C 两点. (1)直接写出点A 的坐标，并求出抛物线的解析式；(2)动点P 从点A 出发．沿线段AB 向终点B 运动，同时点Q 从点C 出发，沿线段CD 向终点D 运动．速度均为每秒1个单位长度，运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ，①过点E 作EF ⊥AD 于点F ，交抛物线于点G .当t 为何值时，线段EG 最长? ②连接EQ ．在点P 、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。