滚动轴承的振动机理与信号特征
- 格式:docx
- 大小:230.87 KB
- 文档页数:11

西南交通大学本科毕业设计(论文)滚动轴承振动信号特性分析年级:2010级学号:**********:***专业:机械制造工艺及其设备****:***2014年 6月院系机械工程系专业机械设计制造及其自动化(机械制造)年级 2010级姓名刘元是题目滚动轴承振动信号特性分析指导教师评语指导教师 (签章) 评阅人评语评阅人 (签章) 成绩答辩委员会主任 (签章)年月日毕业设计(论文)任务书班级 2010机制1班学生姓名刘元是学号 20107151 发题日期:2014年 2月 24日完成日期: 6月 20日题目滚动轴承振动信号特性分析1、本论文的目的、意义:滚动轴承的优点众多,因此滚动轴承在工程实践中得到充分的应用。
但是滚动轴承有时的工作条件十分恶劣并且在机械设备中承载载荷、传递载荷。
滚动轴承损坏尤其是突然损坏不仅会导致机械设备的故障失效,甚至可能造成更为严重或许是灾难性的事故。
本论文主要针对滚动轴承振动信号进行研究,在对滚动轴承结构有一定了解的基础上,重点研究滚动轴承振动信号特点,并基于滚动轴承振动实测信号进行分析验证,掌握常见的信号谱分析方法,并尝试对滚动轴承零件故障进行分析。
2、学生应完成的任务(1)基于滚动轴承振动信号进行常见分析的分析方法,如时域分析、FFT分析、功率谱分析研究所实测振动信号,并得出相应结论。
(2)利用小波或其它信号分析方法研究所实测振动信号,并得出相应结论。
(3)利用MATLAB编制信号分析GUI,实现计算信号特征参数及实现简单的信号分析功能。
(4)完成毕业论文。
3、论文各部分内容及时间分配:(共 16 周)第一部分了解滚动轴承的功能、构成 (2周) 第二部分了解滚动轴承常见的失效形式(2周) 第三部分基于实测滚动轴承振动信号利用功率谱等方法分析其特性 (4周) 第四部分利用典型时频分析方法分析滚动轴承振动信号特性并编GUI(6周) 第五部分论文撰写(2周) 评阅及答辩(2周)备注(1)CNKI关于滚动轴承故障分析的论文.(2)功率谱分析、小波分析、希尔伯特-黄变换有关书籍(3)matlab编程方面的书籍指导教师:年月日审批人:年月日摘要滚动轴承在工程实践中得到了充分的应用,但是滚动轴承却十分容易损坏。


讲义:一.轴承振动的原理二.影响静音轴承的原因三.车间生产如何控制(注意哪些细节)前言随着高科技的发展,机械产品越来越向精密延伸。
轴承行业也在逐步地革新换代,同时用户对轴承的使用也越来越向“静音”高要求。
于是静音轴承成为了行业商场上的“紧俏品”,也成为了同行竞争的分档线。
一、轴承振动的原理我们知道轴承的结构主要由4大件组成:内外圈、保持架、钢球,加上润滑剂就是5大件了。
在轴承运转的过程中,这几大件相互之间形成的摩擦副有:外圈与保持架、内圈与保持架、滚动体与保持架、内、外圈与滚动体,结构是封闭式的摩擦副还存在密封圈(或防尘盖)与内外圈、油脂与机械物质等的摩擦。
以上这些摩擦副最终形成了轴承运转时发出的声音,这种本能固有的声音行业上称做轴承的“基础噪音”。
测振时这种声音一般表现的比较平稳、轻微、柔和,这与我们攻关的低噪音有所不同。
轴承运转的过程中,由于轴承滚道工作面、滚动体、润滑不良等缺陷的影响,在加速度测振仪上,这些缺陷经过传感器而产生的振动脉冲更大地激起轴承本身固有频率振动,从而产生出人耳听起来不舒服的异常音。
下面我讲一下影响低噪音轴承的因素。
二、影响静音轴承的因素1.产品结构的影响从最近几年轴承结构的不断更新来看,以消除噪音为目的来改进产品结构的还不少,比如:内外滚道的优化设计、宽边保持架的采用、钢球的球形偏差改进等等。
实际拆套中发现钢球往往有“猫眼”的,其实是保持架结构不合理导致。
我计算过6308、6309、6311目前所用的保持架结构,6309、6311的在实际受力的情况下比理论受力结构变形量增大了()mm,这样运转时钢球必然撞击保持架,则易产生磨痕,影响低噪音控制。
2.零件缺陷的影响(1). 钢球缺陷的影响在轴承几大件中,钢球对成品轴承的振动影响最大。
钢球的球形偏差及表面磕碰伤直接影响成品轴承的振动,因此严格控制钢球的球形偏差及表面磕碰伤,能够降低轴承的低频振动。
目前钢球厂家在钢球的加工过程中提高研磨盘的加工质量,控制研磨盘的沟形偏差,并选用优质精研液,以降低钢球表面粗糙度。

滚动轴承振动信号特性分析滚动轴承是一种常见的机械元件,在机械系统中起到支撑转动轴承、减少摩擦和传递载荷的作用。
然而,由于长期使用或其他原因,滚动轴承可能会出现一些故障,如疲劳破坏、过度磨损和松动等。
因此,滚动轴承的振动信号特性分析对于故障检测和预测具有重要的意义。
滚动轴承的振动信号是由于内外圈的滚珠与滚道之间的相对运动而产生的,这些振动信号可以通过加速度传感器等设备进行采集。
基于振动信号的特性分析,可以帮助我们了解滚动轴承在运行过程中的状况,从而判断是否存在故障。
下面将从不同的角度分析滚动轴承振动信号的特性。
首先,可以从时间域来分析滚动轴承的振动信号特性。
利用时间域信号,可以直观地观察到滚动轴承振动信号的波形变化。
通过观察振动信号的幅值和周期,可以初步判断是否存在异常。
通常情况下,正常的滚动轴承振动信号应该是稳定和准周期的。
如果出现振动信号的幅值波动较大或周期不规则,可能表示滚动轴承存在故障。
其次,可以从频域来分析滚动轴承的振动信号特性。
频域分析可以将信号从时域转换为频域,通过频谱图来观察不同频率分量的强度。
通过对滚动轴承振动信号进行傅里叶变换,可以得到其频谱图。
正常的滚动轴承振动信号的频谱图应该是窄带的,且主要集中在轴承的基频和谐波频率上。
如果出现频谱图突然增加了一些频率分量,可能表示滚动轴承存在故障,如滚珠松动、内圈或外圈的损伤等。
此外,滚动轴承的振动信号还可以通过时频分析方法进行特性分析。
时频分析可以将信号的时域信息和频域信息进行联合分析,可以观察到信号在时间和频率上的变化。
通过应用时频分析方法,如短时傅里叶变换(STFT)和小波变换,可以查看滚动轴承振动信号在时间和频率上的瞬态和局部特性。
这种分析方法可以帮助我们检测滚动轴承振动信号的瞬态特征和突变情况,提高故障检测和预测的准确性。
最后,滚动轴承的振动信号特性还可以通过统计学方法进行分析。
通过统计学参数,如均值、标准差和峭度等,可以观察滚动轴承振动信号的集中程度、离散程度和峰态等特性。


滚动轴承常见故障及其振动信号特征作者:武栋梁来源:《科技资讯》2012年第18期摘要:轴承为机械设备的关键部件之一,轴承损坏能直接影响设备正常运作,影响生产效率。
本文对轴承的常见故障原因及形式进行分析,并总结其故障检测方法和轴承在发生故障时的振动信号特征。
关键词:轴承故障振动信号中图分类号:TH133 文献标识码:A 文章编号:1672-3791(2012)06(c)-0085-02及时对系统关键部件进行维修和更换可以在一定程度上避免系统工作过程中关键部件损坏带来的系统故障造成的经济损失和人员伤害。
滚动轴承为旋转机械的关键部件,其运行状态直接决定转动部件的效率和安全,本文总结了常见的滚动轴承故障种类和轴承故障检测方法,并对轴承振动信号特点进行分析。
本文对轴承故障的诊断和设备的维修提供参考作用,有助于实现对轴承故障的原因和种类的预先判断。
1 轴承故障形式及原因分析滚动轴承在工作过程中,由于装配不当、润滑欠缺、异物侵入或者超负荷运转等都可能引发轴承损坏,或者过载等都可能引发轴承损坏,或者长时间工作后产生疲劳剥落或者自然磨损导致系统故障。
常见的轴承故障可总结为损伤和磨损两大类。
常见的损伤类故障有疲劳剥落、塑性变形、轴承烧伤、锈蚀、断裂、胶合六种;磨损类故障为轴承长期正常工作引起的渐变性故障。
1.1 疲劳剥落滚动轴承发生故障的典型方式是其滚动接触发生单纯的疲劳剥落。
在工作中,轴承滚子和滚道接触面相对滚动的同时又互相挤压,加上周期交变载荷的作用,长时间工作后,轴承部件接触面将产生小的剥落坑,最终发展为大面积剥落,该现象称作疲劳剥落。
1.2 塑性变形当工作载荷过重时,由于滚动轴承承受的过大的冲击力和静载荷的原因,轴承滚道的表面上形成的不均匀凹坑,这种现象主要发生在低速旋转的轴承上。
另外由于热变形而引起的额外的载荷也可能使轴承产生塑性变形[1]。
1.3 断裂过大的负荷是轴承内部部件断裂的主要原因,另外工作过程中摩擦产生的热应力过大时也能引起轴承零件的断裂。

滚动轴承振动信号处理及特征提取方法研究共3篇滚动轴承振动信号处理及特征提取方法研究1滚动轴承振动信号处理及特征提取方法研究随着工业自动化的推进和智能化的发展,机械设备的使用率越来越高,滚动轴承作为最常用的机械元件之一,其使用寿命的长短直接关系到整个机械设备的寿命。
如果能够在使用前预测轴承故障的发生,及时进行维护,就可以极大地提高设备的可靠性和使用寿命。
因此,如何对滚动轴承进行振动信号处理及特征提取成为了机械故障预测领域的热门研究方向。
滚动轴承的振动信号可以通过加速度、速度、位移等参数来表征。
振动信号处理的基本内容包括数据采集、滤波、去噪、分析和特征提取等步骤。
数据采集是为了获取原始振动信号,通常使用加速度传感器将振动信号转换成电信号采集下来。
然后对采集到的振动信号进行滤波和去噪处理来消除环境噪声和其他信号干扰,以便于分析和提取轴承特征信息。
在分析振动信号时,需要从几个方面入手。
首先是时域分析,通过对振动信号的时间序列进行统计分析,可以得到均值、方差、峰值、波形等信息。
其次是频域分析,可以将时域信号转化为频域信号来分析频率分布特征。
最后是时频域分析,可以将振动信号拆分成多个小时间段,然后在每个时间段内进行频域分析,进一步揭示振动信号的时变特性。
特征提取是对振动信号分析的最核心步骤。
特征提取旨在从振动信号中提取出对轴承状态诊断有意义的特征量,以实现机械设备健康状态的检测和故障诊断。
目前常用的特征量包括时域特征、频域特征、时频域特征等。
时域特征包括均值、方差、峰值、脉冲因子、裕度因子等;频域特征包括能量、均值频率、频率幅值、谱峰等;时频域特征包括小波包能量特征、小波包熵特征与小波包谱能量特征等。
总之,滚动轴承的振动信号处理及特征提取是机械预测维护的重要内容,其研究对于提高机械设备的可靠性和使用寿命具有重要的意义。
未来,随着新技术的不断引入和发展,机械故障诊断和维护模式也将不断升级,从而为滚动轴承振动信号处理及特征提取的研究提供更加广泛和多样化的应用场景滚动轴承是工业生产中不可或缺的机械零件,但其长期运行可能会受到各种因素的干扰而导致故障,因此开展振动信号处理及特征提取研究对于机械设备的预测维护具有重要的意义。

滚动轴承的振动形式及振动机理的研究滚动轴承是一种常见的机械元件,广泛应用于各种设备和机械系统中。
然而,滚动轴承在使用过程中常常会产生振动,这不仅会影响设备的正常运行,还会导致设备寿命的缩短。
因此,研究滚动轴承的振动形式及振动机理对于提高设备的可靠性和性能具有重要意义。
我们来探讨滚动轴承的振动形式。
滚动轴承的振动主要表现为径向振动和轴向振动两种形式。
径向振动是指滚动轴承在工作过程中产生的轴向位移,它可能由于滚动体与滚道之间的不匹配或轴承内部结构的不均匀等原因而引起。
轴向振动则是指滚动轴承在工作过程中产生的周向位移,它可能由于滚动体与保持架之间的不匹配或轴承内部结构的不均匀等原因而引起。
接下来,我们来研究滚动轴承振动的机理。
滚动轴承的振动源于多个因素的综合作用。
首先,滚动轴承在工作时承受着来自外部负载的力,这些力会引起滚动轴承的变形和位移,从而产生振动。
其次,滚动轴承内部的滚动体和保持架之间存在着摩擦力和碰撞力,这些力的作用也会导致滚动轴承的振动。
此外,滚动轴承的材料和制造工艺也会对其振动特性产生影响。
例如,滚动轴承的材料硬度不均匀或制造工艺不精细都会导致振动的增加。
为了研究滚动轴承的振动形式及振动机理,研究人员通常会采用实验方法和数值模拟方法进行研究。
实验方法通过在滚动轴承上安装加速度传感器等装置,测量滚动轴承的振动信号,并进行信号分析和处理,从而得到滚动轴承的振动特性。
数值模拟方法则是利用计算机模拟滚动轴承的工作过程,通过对滚动轴承内部力学和动力学特性的建模和计算,预测和分析滚动轴承的振动行为。
通过研究滚动轴承的振动形式及振动机理,可以帮助人们更好地理解滚动轴承的工作原理和振动特性,为改善滚动轴承的设计和制造提供理论依据和技术支持。
例如,可以通过优化滚动轴承的结构和材料,减小滚动轴承的振动幅值和频率,提高滚动轴承的工作效率和寿命。
此外,还可以通过改进滚动轴承的润滑和冷却方式,减少滚动轴承的热量和摩擦,从而降低滚动轴承的振动水平。

滚动轴承常见故障及其振动信号特征轴承长时间未使用或者存储环境不良会导致轴承表面生锈,进而引发轴承锈蚀故障。
另外,轴承在工作过程中也可能因为润滑不良或者介质腐蚀等原因产生锈蚀现象。
1.6胶合轴承在长期运行过程中,可能会因为润滑不足或者介质污染等原因导致轴承内部的胶合现象。
胶合现象会导致轴承的滚动体和滚道之间失去滚动性能,从而引发轴承故障。
2轴承故障检测方法轴承故障检测的方法主要包括视觉检测、声音检测、振动检测、温度检测和油液检测等。
其中,振动检测是最常用的一种方法。
轴承在故障发生时会产生特定的振动信号,通过对振动信号进行分析可以判断轴承是否发生故障,并确定故障的类型和程度。
3轴承故障的振动信号特征轴承故障时产生的振动信号具有一定的特征,不同类型的故障会产生不同的振动信号特征。
常见的轴承故障振动信号特征包括频率、振幅、相位和波形等。
通过对这些特征的分析,可以准确地判断轴承的故障类型和程度,并采取相应的维修措施。
总之,对轴承故障的诊断和维修具有重要意义。
通过本文对轴承常见故障形式、故障检测方法和振动信号特征的分析,可以帮助工程师更好地诊断和处理轴承故障,提高设备的运行效率和安全性。
轴承锈蚀的原因之一是水分侵入。
当轴承停止工作时,温度下降,空气中的水分容易在轴承表面凝结成水珠,如果不及时清理,就会引起轴承锈蚀。
另外,保护不当也会使水分直接进入轴承,导致轴承锈蚀。
在高速高负荷和润滑不足的情况下,轴承部件会迅速升温,摩擦产生的热量能引起轴承部件接触的金属表面相互粘接,这种现象称为胶合。
轴承滚子和滚道相对运动产生的挤压力和侵入轴承滚道的杂物也会引起轴承表面的磨损。
磨损会增大轴承的游隙,降低运转精度,增加工作噪音。
常见的滚动轴承故障检测方法包括油样分析法、温度监测法、声发射法和振动法。
油样分析法通过分析轴承润滑油中的金属颗粒来判断轴承的运转状况。
温度监测法通过监测轴承附近部件的温度来观测轴承是否正常运转。
声发射法可以通过分析发声周期来判断故障类型和部位。

滑动轴承、滚动轴承振动故障症状特征分析与解决处理方法(图文并茂详解)一、滚动轴承症状特征:(一)、滚动轴承故障发展的第一阶段症状特征:1、超声波频率范围(>250K赫兹) 内的最早的指示;2、利用振动加速度包络技术(振动尖峰能量gSE)可最好地评定频谱。
(二)、滚动轴承故障发展的第二阶段症状特征:1、轻微的故障激起滚动轴承部件的自振频率振动。
2、故障频率出现在500-2000赫兹范围内。
3、在滚动轴承故障发展第二阶段的末端,在自振频率的左右两侧出现边带频率。
(三)、滚动轴承故障发展的第三阶段症状特征:1、出现滚动轴承故障频率及其谐波频率。
2、随着磨损严重出现故障频率的许多谐波频率,边带数也增多。
3、在此阶段,磨损可以用肉眼看见,并环绕轴承的圆周方向扩展。
(四)、滚动轴承故障发展的第四阶段症状特征:1、离散的滚动轴承故障频率消失,被噪声地平形式的宽带随机振动取代之。
2、朝此阶段末端发展,甚至影响1X转速频率的幅值。
3、事实上,高频噪声地平的幅值和总量幅值可能反而减小。
二、滑动轴承症状特征:(一)、油膜振荡不稳定性症状特征:1、如果机器在2X转子临界转速下运转,可能出现油膜振荡。
2、当转子升速到转子第二阶临界转速时,油膜涡动接近转子临界转速,过大的振动将使油膜不能支承轴。
3、油膜振荡频率将锁定在转子的临界转速。
4、转速升高,油膜涡动频率也不升高。
(二)、油膜涡动不稳定性症状特征:1、通常出现在旋转转速的42-48%频率范围内。
2、有时,振动幅值非常大油膜涡动是固有不稳定的,因为它增大离心力,所以增大涡动力。
(三)、滑动轴承磨损/间隙故障症状特征:1、滑动轴承磨损故障后阶段将产生幅值很大的旋转转速频率的谐波频率振动。
2、当存在过大的滑动轴承间隙时,很小的不平衡或不对中将导致很大幅值的振动。

滚动轴承振动产⽣的可能原因及其特征频率通过前⾯的⽂章《滚动轴承的运动学》,我们了解了滚动轴承运转产⽣的特征频率,但实际上,除了这些频率之外,还存在⼀些其他的频率成分。
产⽣这些复杂的振动频率的原因可以分两类:第⼀类为外界激励所引起的,如轴不平衡、不对中、临界转速、结构共振等,这些故障(或缺陷)可以按照它们各⾃的特征频率来处理;第⼆类是由于滚动轴承⾃⾝结构特点以及故障缺陷所引起的。
通常,滚动轴承不会仅受到⼀种激励作⽤,更多是两种激励同时作⽤引起轴承振动,这就使得振动频谱更为错综复杂,对轴承的故障诊断增加难度。
另⼀⽅⾯,除了存在各⾃的特征频率成分及其谐波之外,还会存在相互调制效应,产⽣边频带。
当轴承各元件出现各种故障时,《滚动轴承的运动学》中的轴承频率公式提供了频率成分的理论计算,这些计算是基于这样的假设:当轴承各元件遭遇故障时,会产⽣⼀个理想的脉冲。
对于轴承局部故障,如滑动和点蚀,会产⽣短时尖的冲击,这些冲击将激起结构共振,相应的振动通过外部安装在轴承座上的传感器能测量到。
每次遭遇⼀个局部故障产⽣的冲击,测量到的振动信号将是按指数衰减的正弦振荡。
1载荷引起的振动滚动轴承在运转过程中,如受到通过轴⼼的轴向载荷,可以认为各个滚动体平均分担,即各滚动体受⼒相等。
但在受到径向载荷F r作⽤时,内圈沿径向载荷⽅向会移动⼀段路径δ0,如图1中虚线所⽰,此时上半圈滚动体不受⼒,下半圈的各个滚动体由于接触点上的弹性变形量δi不同⽽承受不同的载荷Q i。
处于F r作⽤线最下端位置的滚动体受⼒Q0最⼤,对应的变形量δ0也最⼤。
下半圈受载荷作⽤的其他各接触点滚动体的法向变形量为δi与径向载荷⽅向处变形量δ0的关系为图1 轴承元件上的受⼒分析各个接触点法向⼒Q i与沿径向载荷⽅向处的法向⼒Q0的关系为因此,在受载荷作⽤的半圈内,各接触点处的受⼒⼤致呈余弦分布状态,并引起相应规律的应⼒变化。
滚动轴承各元件在⼯作时承受变动的接触应⼒,如单颗滚动体受到的接触应⼒从⼩变⼤,然后再变⼩的周期性变化,⽽在不受载荷的半圈内不受接触应⼒作⽤,内圈上的某⼀点的接触应⼒也有类似的规律。

滚动轴承的振动机理与信号特征滚动轴承的振动可由外部振源引起,也可由轴承本身的结构特点及缺陷引起。
此外,润滑剂在轴承运转时产生的流体动力也可以是振动(噪声)源。
上述振源施加于轴承零件及附近的结构件上时都会激励起振动。
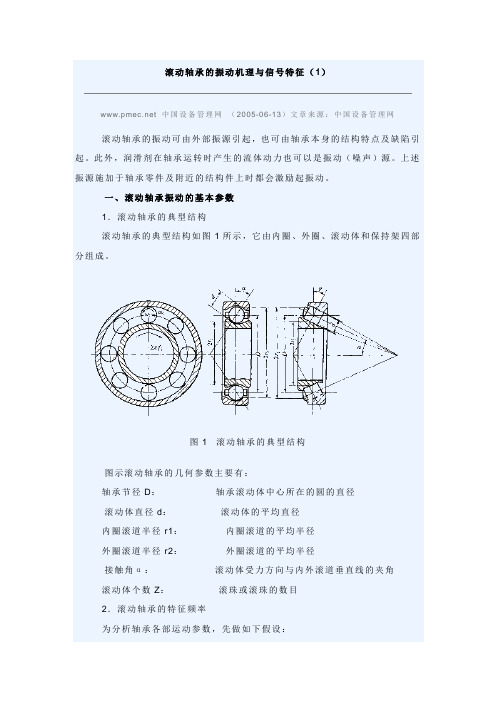
一、滚动轴承振动的基本参数1.滚动轴承的典型结构滚动轴承的典型结构如图1所示,它由内圈、外圈、滚动体和保持架四部分组成。
图1 滚动轴承的典型结构图示滚动轴承的几何参数主要有:轴承节径D:轴承滚动体中心所在的圆的直径滚动体直径d:滚动体的平均直径内圈滚道半径r1:内圈滚道的平均半径外圈滚道半径r2:外圈滚道的平均半径接触角α:滚动体受力方向与内外滚道垂直线的夹角滚动体个数Z:滚珠或滚珠的数目2.滚动轴承的特征频率为分析轴承各部运动参数,先做如下假设:(1)滚道与滚动体之间无相对滑动;(2)承受径向、轴向载荷时各部分无变形;(3)内圈滚道回转频率为fi;(4)外圈滚道回转频率为fO;(5)保持架回转频率(即滚动体公转频率为fc)。
参见图1,则滚动轴承工作时各点的转动速度如下:内滑道上一点的速度为:Vi=2πr1fi=πfi(D-dcosa)外滑道上一点的速度为:VO=2πr2fO=πfO(D+dcosa)保持架上一点的速度为:Vc=1/2(Vi+VO)=πfcD由此可得保持架的旋转频率(即滚动体的公转频率)为:从固定在保持架上的动坐标系来看,滚动体与内圈作无滑动滚动,它的回转频率之比与d/2r1成反比。
由此可得滚动体相对于保持架的回转频率(即滚动体的自转频率,滚动体通过内滚道或外滚道的频率)fbc根据滚动轴承的实际工作情况,定义滚动轴承内、外圈的相对转动频率为一般情况下,滚动轴承外圈固定,内圈旋转,即:同时考虑到滚动轴承有Z个滚动体,则滚动轴承的特征频率如下:滚动体在外圈滚道上的通过频率zfoc为:滚动体在内圈滚道上的通过频率Zfic为:滚动体在保持架上的通过频率(即滚动体自转频率fbc)为:3.止推轴承的特征频率止推轴承可以看作上述滚动轴承的一个特例,即α=90°,同时内、外环相对转动频率为轴的转动频率fr,此时滚动体在止推环滚道上的频率为:滚动体相对于保持架的回转频率为:以上各特征频率是利用振动信号诊断滚动轴承故障的基础,对故障诊断非常重要。

滚动轴承的振动形式及振动机理的研究滚动轴承是一种常见的机械元件,广泛应用于各种机械设备中。
在使用过程中,滚动轴承的振动问题一直是工程师们关注的焦点。
本文将介绍滚动轴承的振动形式及振动机理的研究。
滚动轴承的振动形式主要包括径向振动和轴向振动。
径向振动是指轴承内圈和外圈在径向方向上的振动,轴向振动则是指轴承内圈和外圈在轴向方向上的振动。
这些振动形式会导致轴承的噪声和寿命降低,因此需要对其进行研究和控制。
滚动轴承的振动机理主要包括内部因素和外部因素。
内部因素包括轴承结构、材料、制造工艺等,而外部因素则包括载荷、转速、温度、润滑等。
这些因素会影响轴承的刚度、阻尼、质量等特性,从而导致轴承的振动。
在研究滚动轴承的振动机理时,需要考虑轴承的动力学特性。
轴承的动力学特性包括刚度、阻尼、质量等,这些特性会影响轴承的振动响应。
因此,需要建立轴承的动力学模型,通过数值模拟等方法研究轴承的振动响应。
除了数值模拟,还可以通过实验研究轴承的振动特性。
实验方法包括模态分析、频率响应分析、阻尼比测试等。
这些实验方法可以直接观测到轴承的振动响应,从而更加深入地了解轴承的振动机理。
在控制滚动轴承的振动问题时,需要综合考虑内部因素和外部因素。
内部因素可以通过改变轴承结构、材料、制造工艺等来控制,而外部因素可以通过调整载荷、转速、温度、润滑等来控制。
此外,还可以采用主动控制、被动控制等方法来控制轴承的振动。
总之,滚动轴承的振动问题是一个复杂的问题,需要综合考虑多种因素。
通过建立动力学模型、数值模拟和实验研究等方法,可以更加深入地了解轴承的振动机理,从而控制轴承的振动问题,提高轴承的寿命和性能。

一、数控机床滚动轴承的特点与故障在数控机床上主轴轴承常用滚动轴承和滑动轴承。
滚动轴承摩擦阻力小,可以预紧,润滑维护简单,能在一定转速范围和载荷变动范围下稳定的运动。
数控机床最常用的滑动轴承是静压滑动轴承。
静压滑动轴承的油膜压强是由液压缸从外界供给的,与主轴的转速无关。
它的刚度大,回转精度高。
但静压轴承需要一套液压装置,成本较高,一般用于重型或高精度数控机床。
滚动轴承由专业化工厂生产,选购维修方便。
数控主轴组件在可能的条件下,尽量使用滚动轴承。
特别是大多数立式主轴和主轴装在套简内能够作轴向移动的主轴,用滚动轴承可以用润滑脂润滑避免漏油。
在数控机床上使用的滚动轴承主要有:球轴承,滚珠轴承,圆锥滚子轴承三大类。
箱式直线轴承滚动轴承的损伤和破坏形式主要有:磨损、疲劳、断裂、腐蚀、压痕和胶合。
可将这六种失效形式归类成三种类型的故障:表面皱裂、表面剥落和轴承烧损。
1 表面皱裂是由于轴承使用时间较长,磨损后滚动面全周慢慢劣化的异常形态。
此时轴承的振动与正常轴承振动具有相同的特点。
唯一区别是此时振动幅度变大了。
2 表面剥落是由疲劳、裂纹、压痕、胶合等失效形式造成滚动面的异常形态。
它们所引起的振动为冲击振动,振动信号中含有轴承的传输振动和轴承构件的固有振动。
可以通过查找这些固有振动中是否出现某一构件运行特征频率来判断轴承的故障。
3 烧损是由于轴承润滑状态恶化等原因造成的。
在到达烧伤程度的过程中,轴承的振动值急速增大。
润滑不良,载荷过大,冲击载荷,和转速过高是造成滚动轴承故障的主要原因。
其中润滑不良是主要原因。
数控机床由于本身的结构特点和切削工艺特点,其轴承受到的损坏也与普通机床不太一样。
在数控机床中,数控机床主轴的转动速度和进给轴的进给速度都是受数控系统的监控,很少出现转速过高的现象,所以转速过高不会成为数控机床轴承的故障原因。
数控机床的轴承一般采用强制润滑和油脂封入润滑,使用强制润滑的轴承不存在润滑不良的问题:采用油脂封入式润滑的轴承,才会因没有得到定期的保养而产生润滑不良的问题。

滚动轴承振动信号特性分析滚动轴承在工程实践中得到了充分的应用,但是滚动轴承却十分容易损坏。
滚动轴承的运行状态通常也会直接影响到整个机械设备的性能。
滚动轴承损坏尤其是突然损坏不仅会导致机械设备的故障失效,甚至造成更为严重或许是灾难性的事故。
对滚动轴承进行特征信号分析对其故障进行诊断可以有效地避免事故发生。
关键词:滚动轴承;信号;分析为了有效地提取滚动轴承故障信号特性,提出了一种基于共振解调技术和谱峭度法相结合的方法,并且将其应用到实际的滚动轴承的数据中进行分析处理。
发现能准确的找出其故障部位并得到其故障频率。
一、轴承结构和故障机理滚动轴承是一类广泛应用的精细的机械构件。
滚动轴承的作用是将运转的轴承座和轴相互的滑动类型的摩擦转换为滚动类型的摩擦。
其一般包括四个部分:滚动体,外圈,内圈和保持架。
内圈能和轴进行配合共同旋转。
外圈则是与轴承座进行配合并且起着支撑的作用。
滚动体均匀分布在内外圈之间,对轴承的运转性能和使用寿命有着重要的影响。
保持架起着让滚子分布均匀的功能,引领滚子旋转而且具有润滑功能以及避免滚子掉落。
总体说来轴承工作时的振动通常分为以下两种:与轴承工作面的裂痕、波纹相关和与轴承弹性相关的振动。
其中与轴承表面裂痕、波纹相关振动能够反映其损伤的情况。
工作面若有损坏,当滚子在损坏面运转的时侯,某种交变的激振力将会出现。
因为轴承滚动表面损伤形状并不规则。
由此,产生的振动也会是一种随机振动并包含了多种频率成分。
通常来说,轴运转的速率以及轴承面损坏样式是激振力的频率的首要性因素。
而激振系统传递相关的因素由轴承和外壳来决定。
总而言之,轴运转的速率、外壳和轴承的振动传递因数以及轴承面损坏样式等一起确定了因轴承异常而产生的振动频率。
一般而言,轴承具有越高的振动频率则表明轴有越严重的损伤或者有越高的旋转速度,另外滚动轴承的固有振动频率会随着滚动轴承尺寸的增大而有所降低。
因而,所有异常的轴承产生振动时都不会是一个特定的频率。

滚动轴承信号分析方法(测试特征频率)!一、故障信号三频段(三座大山)1.低频段:在8kHz以下,滚动轴承中与结构和运动关系相联系的故障信号在这个频率段,少数高速滚动轴承的信号频段能延展到B点以外。
因为轴的故障信号、齿轮的故障信号也在这个频段,因而这也是绝大部分在线故障监测与诊断系统所监测的频段。
2.高频段:位于Ⅱ区,这个频段的信号是轴承故障所激发的轴承自振频率的振动。
3.超高频段:位于Ⅲ区,它们是轴承内微裂纹扩张所产生的声发射超声波信号。
二、分析谱带的选择1.低频段:(1)低频率段指1kHz以下的频率范围;(2)一般可以采用低通滤波器(例如截止频率fb≤1kHz)滤去高频成分后再作频谱分析;(3)此法可直接观察频谱图上相应的特征谱线,做出判断;(4)这个频率范围容易受到机械及电源干扰,并且在故障初期反映故障的频率(5)成分在低频段的能量很小。
因此,信噪比低,故障检测灵敏度差。
2.中频段:(1)中频段指1k~20kHz频率范围;(2)使用截止频率为1kHz的高通滤波器滤去1kHz以下的低频成分,以消除机械干扰;(3)用信号的峰值、RMS值或峭度指标作为监测参数;(4)使用带通滤波器提取轴承零件或结构零件的共振频率成分,用通带内的信号总功率作为监测参数;3.高频段:(1)高频率段指20~80kHz频率范围;(2)轴承故障引起的冲击有很大部分冲击能量分布在高频段;(3)如果采用合适的加速度传感器和固定方式保证传感器较高的谐振频率,利用传感器的谐振或电路的谐振增强所得到衰减振动信号,对故障诊断非常有效;(4)瑞典的冲击脉冲计(SPM)和美国首创的IFD法就是利用这个频段。
三、测点的选择(1)测量点应尽量靠近被测轴承的承载区,应尽量减少中间传递环节,探测点离轴承外圈的距离越近越直接越好;(2)应尽量考虑在水平(x)、垂直(y)和轴向(z)三个方向上进行振动检测。
四、滚动轴承故障信号分析方法1.有效值与峰值判别法(1)有效值:可以用有效值作为轴承异常的判断指标。
滚动轴承的振动机理与信号特征(1) 中国设备管理网(2005-06-13)文章来源:中国设备管理网滚动轴承的振动可由外部振源引起,也可由轴承本身的结构特点及缺陷引起。
此外,润滑剂在轴承运转时产生的流体动力也可以是振动(噪声)源。
上述振源施加于轴承零件及附近的结构件上时都会激励起振动。
一、滚动轴承振动的基本参数1.滚动轴承的典型结构滚动轴承的典型结构如图1所示,它由内圈、外圈、滚动体和保持架四部分组成。
图1 滚动轴承的典型结构图示滚动轴承的几何参数主要有:轴承节径D:轴承滚动体中心所在的圆的直径滚动体直径d:滚动体的平均直径内圈滚道半径r1:内圈滚道的平均半径外圈滚道半径r2:外圈滚道的平均半径接触角α:滚动体受力方向与内外滚道垂直线的夹角滚动体个数Z:滚珠或滚珠的数目2.滚动轴承的特征频率为分析轴承各部运动参数,先做如下假设:(1)滚道与滚动体之间无相对滑动;(2)承受径向、轴向载荷时各部分无变形;(3)内圈滚道回转频率为fi;(4)外圈滚道回转频率为fO;(5)保持架回转频率(即滚动体公转频率为fc)。
参见图1,则滚动轴承工作时各点的转动速度如下:内滑道上一点的速度为:V i=2πr1f i=πf i(D-dcosa)外滑道上一点的速度为:V O=2πr2f O=πf O(D+dcosa)保持架上一点的速度为:V c=1/2(V i+V O)=πf c D由此可得保持架的旋转频率(即滚动体的公转频率)为:从固定在保持架上的动坐标系来看,滚动体与内圈作无滑动滚动,它的回转频率之比与d/2r1成反比。
由此可得滚动体相对于保持架的回转频率(即滚动体的自转频率,滚动体通过内滚道或外滚道的频率)fbc根据滚动轴承的实际工作情况,定义滚动轴承内、外圈的相对转动频率为一般情况下,滚动轴承外圈固定,内圈旋转,即:同时考虑到滚动轴承有Z个滚动体,则滚动轴承的特征频率如下:滚动体在外圈滚道上的通过频率zfoc为:滚动体在内圈滚道上的通过频率Zfic为:滚动体在保持架上的通过频率(即滚动体自转频率fbc)为:3.止推轴承的特征频率止推轴承可以看作上述滚动轴承的一个特例,即α=90°,同时内、外环相对转动频率为轴的转动频率fr,此时滚动体在止推环滚道上的频率为:滚动体相对于保持架的回转频率为:以上各特征频率是利用振动信号诊断滚动轴承故障的基础,对故障诊断非常重要。

滚动轴承时域特征
滚动轴承的时域特征主要包括以下几个方面:
1. 直接信号:滚动轴承在旋转运动中,产生的直接信号是指由于轴承内部故障引起的振动信号。
其频率通常与转速、内圈和外圈的配合不良、滚珠或滚道的损伤等有关。
直接信号的幅值通常较小,但在早期故障诊断中具有重要意义。
2. 谐波信号:滚动轴承在旋转运动中,产生的谐波信号是指由于轴承内部故障引起的与元件旋转频率成整数倍数关系的信号。
其频率通常是转速的倍数,幅值与故障类型有关,如滚珠或滚道的损伤会导致幅值变化较大的谐波信号。
3. 侧边波:滚动轴承在旋转运动中,产生的侧边波是指由于轴承内部故障引起的轴承运动轴线偏离旋转中心而产生的振动信号。
其频率通常等于转速,幅值与偏移量有关,故障类型主要包括外环和内环的偏心、滚珠间隙过大等。
4. 内部杂音:滚动轴承的内部杂音是指由于轴承内部故障引起的机械摩擦声、颤振声和碰撞声等杂音。
其幅值与故障类型有关,如滚珠和滚道的碰撞声会导致幅值较大的内部杂音。
通过对滚动轴承的时域特征进行分析,可以快速准确地检测出轴承内部的故障情况,及时进行维修和更换,保障设备的安全运行。
滚动轴承的振动机理与信号特征滚动轴承的振动可由外部振源引起,也可由轴承本身的结构特点及缺陷引起。
此外,润滑剂在轴承运转时产生的流体动力也可以是振动(噪声)源。
上述振源施加于轴承零件及附近的结构件上时都会激励起振动。
一、滚动轴承振动的基本参数1.滚动轴承的典型结构滚动轴承的典型结构如图1所示,它由内圈、外圈、滚动体和保持架四部分组成。
图1 滚动轴承的典型结构图示滚动轴承的几何参数主要有:轴承节径D:轴承滚动体中心所在的圆的直径滚动体直径d:滚动体的平均直径内圈滚道半径r1:内圈滚道的平均半径外圈滚道半径r2:外圈滚道的平均半径接触角α:滚动体受力方向与内外滚道垂直线的夹角滚动体个数Z:滚珠或滚珠的数目2.滚动轴承的特征频率为分析轴承各部运动参数,先做如下假设:(1)滚道与滚动体之间无相对滑动;(2)承受径向、轴向载荷时各部分无变形;(3)内圈滚道回转频率为fi;(4)外圈滚道回转频率为fO;(5)保持架回转频率(即滚动体公转频率为fc)。
参见图1,则滚动轴承工作时各点的转动速度如下:内滑道上一点的速度为:V i=2πr1f i=πf i(D-dcosa)外滑道上一点的速度为:V O=2πr2f O=πf O(D+dcosa)保持架上一点的速度为:V c=1/2(V i+V O)=πf c D由此可得保持架的旋转频率(即滚动体的公转频率)为:从固定在保持架上的动坐标系来看,滚动体与内圈作无滑动滚动,它的回转频率之比与d/2r1成反比。
由此可得滚动体相对于保持架的回转频率(即滚动体的自转频率,滚动体通过内滚道或外滚道的频率)fbc根据滚动轴承的实际工作情况,定义滚动轴承内、外圈的相对转动频率为一般情况下,滚动轴承外圈固定,内圈旋转,即:同时考虑到滚动轴承有Z个滚动体,则滚动轴承的特征频率如下:滚动体在外圈滚道上的通过频率zfoc为:滚动体在内圈滚道上的通过频率Zfic为:滚动体在保持架上的通过频率(即滚动体自转频率fbc)为:3.止推轴承的特征频率止推轴承可以看作上述滚动轴承的一个特例,即α=90°,同时内、外环相对转动频率为轴的转动频率fr,此时滚动体在止推环滚道上的频率为:滚动体相对于保持架的回转频率为:以上各特征频率是利用振动信号诊断滚动轴承故障的基础,对故障诊断非常重要。
4.滚动轴承的固有振动频率滚动轴承在运行过程中,由于滚动体与内圈或外圈冲击而产生振动,这时的振动频率为轴承各部分的固有频率。
固有振动中,内、外圈的振动表现最明显,如图2所示图2 滚动轴承套圈横截面简化图与径向弯曲振动振型示意图轴承圈在自由状态下的径向弯曲振动的固有频率为:式中n—振动阶数(变形波数),n=2,3,…;E—弹性模量,钢材为210GPa ;I—套圈横截面的惯性矩,mm 4;γ—密度,钢材为7.86X10-6kg /mm3;A—套圈横截面积,A≈bh,mm 2;D—套圈横截面中性轴直径,mm;g—重力加速度,g=9800mm /S2。
对钢材,将各常数代入式得有时钢球也会产生振动,钢球振动的固有频率为:式中R—钢球半径;E—弹性模量,钢材为210GPa ;γ—密度,钢材为7.86X10-6kg /mm3;g—重力加速度,g=9800mm /S2。
5.滚动轴承特征频率表为方便使用,将以上介绍的滚动轴承各特征频率列于表1中。
表1 滚动轴承特征频率表(假定外圈固定、内圈旋转)二、正常轴承的振动信号特征正常的轴承也有相当复杂的振动和噪声,有些是由轴承本身结构特点引起的;有些和制造装配有关,如滚动体和滚道的表面波纹、表面粗糙度以及几何精度不够高,在运转中都会引起振动和噪声。
1.轴承结构特点引起的振动滚动轴承在承载时,由于在不同位置承载的滚子数目不同,因而承载刚度会有所变化,引起轴心的起伏波动,振动频率为Zfoc(图3)。
要减少这种振动的振幅可以采用游隙小的轴承或加预紧力去除游隙。
2.轴承钢度非线性引起的振动滚动轴承的轴向刚度常呈非线性(图4),特别是当润滑不良时,易产生异常的轴向振动。
在刚度曲线呈对称非线性时,振动频率为fn, 2fn., 3f.n,…;在刚度曲线呈非对称非线性时,振动频率为…分数谐频(fn为轴回转频率)。
这是一种自激振动,常发生在深沟球轴承,自调心球轴承和滚柱轴承不常发生。
图3 滚动轴承的承载刚度和滚子位置的关系图4 轴承的轴向刚度3.轴承制造装配的原因(1)加工面波纹度引起的振动由轴承零件的加工面(内圈、外圈滚道面及滚动体面)的波纹度引起的振动和噪声在轴承中比较常见,这些缺陷引起的振动为高频振动(比滚动体在滚道上的通过频率高很多倍)。
高频振动及轴心的振摆不仅会引起轴承的径向振动,在一定条件下还会引起轴向振动。
表2列出的振动频率与波纹度峰数的关系。
表中,n为正整数,Z为球(滚动体)数,fic为单个滚动体在内圈滚道上的通过频率,fc为保持架转速,fbc 为滚动体相对于保持架的转动频率。
表2 振动频率与波纹度峰数的关系下面简单介绍一下这种振动的机理。
在图5中,轴承内圈加工过程中残留有波纹,球个数Z=8,内圈旋转,当内圈波纹峰数分别为nZ-1,nZ,nZ+1时,对外圈径向振动影响情况如下:图5 内圈波纹率引起外圈径向振动的机理(n=1,Z=8)在图中讨论编号为“1”的球与波峰接触时的情况。
当波峰为nZ时,外圈在径向无移动,但球与nZ士1个波峰数的波纹面接触时,在外圈箭头方向上有最大位移。
在另一种情况下,当编号为“1”的球与波谷接触时,波峰数为nZ个时,外圈则无径向位移;在nZ士1个波峰数时,外圈在与箭头相反方向有最大位移。
由此可以说明在波峰数等于nZ士1时产生振动的原因。
表2中所列的条件是理想的,即波纹是均匀分布,波纹形状是正弦变化的。
而对实际的波纹形状,可能有其他频率成分出现。
用类似方法可说明波峰数对轴向振动的影响。
对于精密轴承,波纹度引起的轴心摆动是不能忽视的。
图6所示为在机床中使用的加有预紧力的两个超精密向心球轴承,由于滚道波纹度引起轴心摆动轨迹。
此时轴心轨迹呈现内卷形和外卷形两种形式。
还应注意,不仅轴承滚道和滚动体的波纹度会引起轴承振动,轴承的内外配合面及轴颈和轴承座孔的波纹度对精密轴承也会引起类似的振动,因为在预紧力作用下,轴承装配后会引起套圈的相应变形。
图6 由轴承零件波纹度引起的轴心摆动(2)轴承偏心引起的振动如图7所示,当轴承游隙过大或滚道偏心时都会引起轴承振动,振动频率为nfn,fn为轴回转频率,n =1,2,…。
(3)滚动体大小不均匀引起轴心摆动如图8所示,滚动体大小不均匀会导致轴心摆动,还有支承刚性的变化。
振动频率为fc和nfc士fn,n=1,2,…,此处fc为保持架回转频率,fn为轴回转频率。
图7 轴承偏心引起的轴承振动图8 滚动体大小不均匀引起的轴心摆动(4)轴弯曲引起轴承偏斜轴弯曲会引起轴上所装轴承的偏移,造成轴承振动。
轴承的振动频率为nfc士fn,n=1, 2,…。
此处fc为保持架回转频率,fn为轴回转频率。
4.滚动轴承的声响滚动轴承在运转时由于各种原因会产生振动,并通过空气传播成为声音,声音中包含着轴承状态的信息。
轴承声响有如下几种:所谓轴承本质的声音是一切轴承都有的声音。
滚道声是滚动体在滚动面上滚动而发生的,是一种滑溜连续的声音。
它与套圈的固有振动有关,频率一般都在1kHz以上,并与轴承转速有关。
辗压声主要发生在脂润滑的低速重载圆柱滚动轴承中,类似于“咯吱咯吱”的声音。
保持架声音是由保持架的自激振动引起的,保持架振动时会与滚动体发生冲撞而发出声音。
高频振动声是由加工面的波纹度引起的振动而发出的声音。
在与使用有关的声音中,伤痕声是由滚动面上的压痕或锈蚀引起的,为周期性的振动和声音。
尘埃声是非周期性的。
综合以上所述,正常的轴承在运转时也会有十分复杂的振动和声响,而故障轴承的声音则更复杂。
三、故障轴承振动信号特点轴承发生故障后,其振动特征会有明显的变化,主要有以下几方面。
1.疲劳剥落损伤当轴承零件上产生了疲劳剥落坑后(图9以夸大的方式画出了疲劳剥落坑),在轴承运转中会因为碰撞而产生冲击脉冲。
图10给出了钢球落下产生的冲击过程的示意图。
在冲击的第一阶段,在碰撞点产生很大的冲击加速度〔图10(a)和(b)〕,它的大小和冲击速度v成正比(在轴承中与疲劳损伤的大小成正比)。
第二阶段,构件变形产生衰减自由振动(图c),振动频率取决于系统的结构,为其固有频率(图d)。
振幅的增加量A也与冲击速度v成正比(图e)。
在滚动轴承剥落坑处碰撞产生的冲击力的脉冲宽度一般都很小,大致为微秒级。
因力的频谱宽度与脉冲持续时间成反比,所以其频谱可从直流延展到100~500kHz。
疲劳剥落损伤可以在很宽的频率范围内激发起轴承一传感器系统的固有振动。
由于从冲击发生处到测量点的传递特性对此有很大影响,因此测点位置选择非常关键,测点应尽量接近承载区,振动传递界面越少越好。
图9 轴承零件上的疲劳剥落坑有疲劳剥落故障轴承的振动信号如图11(a)所示,图11(b)为其简化的波形。
T取决于碰撞的频率,T=1/f碰。
在简单情况下,碰撞频率就等于滚动体在滚道上的通过率ZF ic或Zf oc或滚动体自转频率f bc。
图10 冲击过程示意图图11 有疲劳剥落故障轴承的振动信号2.磨损随着磨损的进行,振动加速度峰值和RMS值缓慢上升,振动信号呈现较强的随机性,峰值与RMS 值的比值从5左右逐渐增加到5.5~6。
如果不发生疲劳剥落,最后振动幅值可比最初增大很多倍,变化情况见图12。
3.胶合图13为一运转过程中发生胶合的滚动轴承的振动加速度及外圈温度的变化情形。
在A点以前,振动加速度略微下降,温度缓慢上升。
A点之后振动值急剧上升,而温度却还有些下降,这一段轴承表面状态已恶化。
在B点以后振动值第二次急剧上升,以致超过了仪器的测量范围,同时温度也急剧上升。
在B点之前,轴承中已有明显的金属与金属的直接接触和短暂的滑动,B点之后有更频繁的金属之间直接接触及滑动,润滑剂恶化甚至发生炭化,直至发生胶合。
从图中可以看出,振动值比温度能更早地预报胶合的发生,由此可见轴承振动是一个比较敏感的故障参数。
图12 轴承磨损时振动加速度图13 发生胶合的轴承试验曲线</SPAN< p>。