同济【弹性力学试卷】2008年期终考试A-本科
- 格式:doc
- 大小:251.50 KB
- 文档页数:9

同济大学课程考核试卷(A卷)2008 — 2009 学年第 1 学期命题教师签名:审核教师签名:课号:190047课名:流体力学考试:此卷选为:期中考试( )、期终考试(√ )、重考( )试卷年级专业学号姓名得分一)选择题(30分)1.从力学的角度分析,一般流体和固体的区别在于流体_ __。
A. 能承受拉力,平衡时不能承受切应力。
B. 不能承受拉力,平衡时能承受切应力。
D. 能承受拉力,平衡时也能承受切应力。
2. 按连续介质概念,流体质点是指。
A. 流体的分子。
B. 流体内的固体颗粒。
C. 几何的点。
3.液体的粘性主要来自于液体_______。
A. 分子的热运动C. 易变形性D. 抗拒变形的能力4.定常流动中,流体质点的加速度。
A .等于零 B. 等于常数C. 随时间变化而变化5.流体作无旋运动的特征是。
A.所有流线都是直线B.所有迹线都是直线C.任意流体元的角变形为零6.沿流线成立的伯努利方程的限制条件不包含__ ___。
A.不可压缩流体B.无粘流体C.定常流动7.运用沿总流的伯努利方程时所选取的两个断面之间。
A. 可以是任何断面B. 必须是缓变流断面D. 之间必须是缓变流8.一维流动的连续性方程VA = C 成立的必要条件是。
A. 理想流体B. 粘性流体C.可压缩流体9.圆管内的流动为层流时,沿程阻力与平均速度的次方成正比。
B.1.5C.1.75 D.210.两根直径不同的圆管,在流动雷诺数Re相等时,它们的沿程损失系数 。
A.一定不相等B. 可能相等C. 粗管的一定比细管的大D. 粗管的一定比细管的小11.湍流附加切应力是由于而产生的。
A.分子的内聚力B.分子间的动量交换C.重力12.边界层内的流动特点之一是。
A.粘性力比惯性力重要C.压强变化可以忽略D.流动速度比外部势流小13.边界层的流动分离发生于。
A.物体后部B.零压梯度区D.后駐点14.欧拉数Eu代表的是之比。
B. 惯性力与重力C. 惯性力与表面张力D. 惯性力与粘性力15.汽车高速行驶时所受到的阻力主要来至于。

弹塑性力学试卷及习题解答弹塑性力学试卷配套教材《弹性与塑性力学》陈惠发1.是非题(认为该题正确,在括号中打√;该题错误,在括号中打×。
)(每小题 2 分)(1)物体内某点应变为0 值,则该点的位移也必为0 值。
(2)可用矩阵描述的物理量,均可采用张量形式表述。
3)因张量的分量是随坐标系的变化而变化,故张量本身也应随坐标系变化。
()4)弹性的应力和应变张量两者的主方向是一致性,与材料无关的。
()5)对于常体力平面问题,若应力函数x,y 满足双调和方程 2 20,那么,由x,y 确定的应力分量必然满足平衡微分方程。
()(6)若某材料在弹性阶段呈各向同性,故其弹塑性状态势必也呈各向同性。
()(7)Drucker 假设适合于任何性质的材料。
()(8)应变协调方程的几何意义是:物体在变形前是连续的,变形后也是连续的。
()(9)对于任何材料,塑性应变增量均沿着当前加载面的法线方向。
()(10)塑性应变增量的主方向与应力增量的主方向不重合。
P107;226 ()2.填空题(在每题的横线上填写必要的词语,以使该题句意完整。
)(每小题 2 分)(1)设x,y a1x a2x y a3y ,当a1,a2,a3满足_________________________________ 关系时x,y 能作为应力函数。
(2)弹塑性力学是研究固体受外界因素作用而产生的______________________ 的一门学科。
(3)导致后继屈曲面出现平移及扩大的主要原因是材料_______________________ 。
(4)π 平面上的一点对应于应力的失量的 _____________________ 。
P65(5)随动强化后继屈服面的主要特征为:__________________________________________ 。
(6)主应力轴和主应变轴总是重合的材料为_______________________ 。

弹性力学试题及答案一、选择题(每题10分,共40分)1. 在弹性力学中,下列哪个物理量表示应变能密度?A. 应力B. 应变C. 位移D. 应力能密度答案:D2. 在平面应力状态下,下列哪个方程是正确的?A. σ_x + σ_y = 0B. σ_x + σ_y = σ_zC. σ_x + σ_y = τ_xyD. σ_x + σ_y = 0答案:D3. 在弹性体中,应力与应变之间的关系可以用下列哪个关系式表示?A. σ = EεB. σ = GγC. τ = μγD. σ = λε答案:A4. 在弹性力学中,下列哪个方程表示平衡方程?A. σ_x + σ_y + σ_z = 0B. ε_x + ε_y +ε_z = 0 C. τ_xy = τ_yx D. σ_x + σ_y + σ_z = F答案:D二、填空题(每题10分,共30分)1. 弹性力学中的基本假设有:连续性假设、线性假设和________假设。
答案:各向同性2. 在三维应力状态下,应力分量可以表示为:σ_x, σ_y, σ_z, τ_xy, τ_xz, τ_yz。
其中,τ_xy表示________面上的切应力。
答案:xOy3. 在弹性力学中,位移与应变之间的关系可以用________方程表示。
答案:几何方程三、计算题(每题30分,共90分)1. 已知一弹性体在平面应力状态下的应力分量为:σ_x = 100 MPa,σ_y = 50 MPa,τ_xy = 25 MPa。
弹性模量E = 200 GPa,泊松比μ = 0.3。
求应变分量ε_x, ε_y, γ_xy。
解:首先,利用胡克定律计算应变分量:ε_x = σ_x / E = 100 MPa / 200 GPa = 0.0005ε_y = σ_y / E = 50 MPa / 200 GPa = 0.00025γ_xy = τ_xy / G = 25 MPa / (E / 2(1 + μ)) = 25 MPa / (200 GPa / 2(1 + 0.3)) = 0.000375答案:ε_x = 0.0005,ε_y = 0.00025,γ_xy = 0.0003752. 一弹性体在三维应力状态下的应力分量为:σ_x = 120 MPa,σ_y = 80 MPa,σ_z = 40 MPa,τ_xy = 30 MPa,τ_xz = 20 MPa,τ_yz = 10 MPa。

信阳师范学院成人教育学生专业课期终考试试卷《弹性力学》试卷(A )一、判断与改错题(每题4分,共32分)1、当物体可当作平面应力问题来处理时,总有0,0,0===yz xz z γγε。
( ⨯ ) 改:当物体可当作平面应变问题来处理时,总有0,0,0===yz xz z γγε。
2、在体力不是常量的情况下,引入了应力函数Yy xXx y y x -∂Φ∂=-∂Φ∂=Φ2222,,σσ且,yx xy∂∂Φ∂-=2τ平衡微分方程可以自动满足。
( ⨯ ) 改:在常体力情况下,————3、应力函数()y dx y cx by ax y x 3324,+++=Φ,不论d c b a ,,,取何值总能满足相容方程。
( ⨯ )改:系数应满足一定的关系才能满足相容方程。
4、轴对称圆板(单连域),若将坐标原点取在圆心,则应力公式中的系数A ,B 不一定为零。
( × )改:如存在A ,B ,当ρ=0时,则必产生无限大有应力,这当然是不合理的。
5、在弹性力学和材料力学里关于应力的正负号规定是一样的。
( ⨯ )(试卷第1页,共6页)改:两者正应力的正负号规定相同,剪应力的正负号规定不同。
6、对于轴对称问题,其单元体的环向平衡条件恒能满足。
( √ )改:7、厚壁圆环(多连体),位移计算公式ϕϕρρϕϕcos sin 4K I H EB U +-+=中的系数B 一定为零。
( √ )改:8、某一应力函数所能解决的问题与坐标系的选择无关。
( ⨯ ) 改:三次及三次以上的应力函数所能解答的问题与坐标系的选取有关。
二、填空题(每空2分,共32分)1、平面应力问题的几何形状特征是 等厚度薄板 。
2、弹性力学可分为数学弹性力学和实用弹性力学两个部分。
前者只用精确的数学推演而不引用任何关于应变状态或应力分布的 假定 ;在实用弹性力学里,和材料力学类同,也引用一些关于应变或应力分布的假设,以便简化繁复的数学推演,得出具有相当实用价值 近似解 。
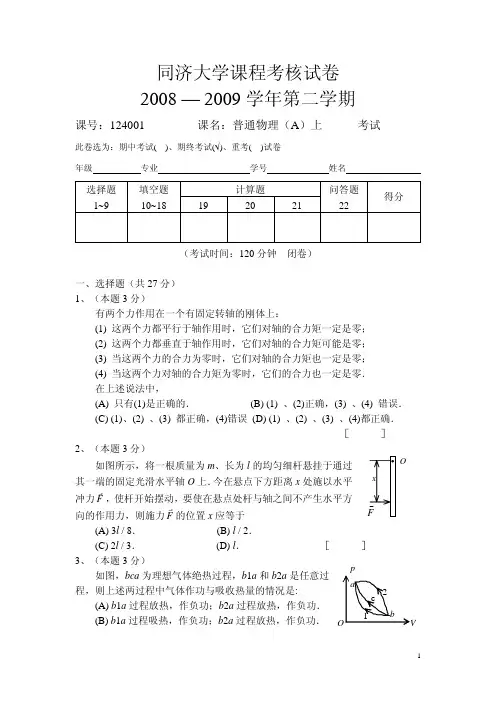
同济大学课程考核试卷 2008 — 2009学年第二学期课号:124001 课名:普通物理(A )上 考试此卷选为:期中考试( )、期终考试(√)、重考( )试卷年级 专业 学号 姓名计算题 选择题 1∼9 填空题 10∼18 19 20 21 问答题 22 得分(考试时间:120分钟 闭卷)一、选择题(共27分) 1、(本题3分)有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零; (2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零; (3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零; (4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零. 在上述说法中, (A) 只有(1)是正确的. (B) (1) 、(2)正确,(3) 、(4) 错误.(C) (1)、(2) 、(3) 都正确,(4)错误 (D) (1) 、(2) 、(3) 、(4)都正确.[ ]2、(本题3分)O如图所示,将一根质量为m 、长为l 的均匀细杆悬挂于通过其一端的固定光滑水平轴O 上.今在悬点下方距离x 处施以水平冲力,使杆开始摆动,要使在悬点处杆与轴之间不产生水平方向的作用力,则施力的位置x 应等于F rF r(A) 3l / 8. (B) l / 2.(C) 2l / 3. (D) l . [] 3、(本题3分)如图,bca 为理想气体绝热过程,b 1a 和b 2a 是任意过程,则上述两过程中气体作功与吸收热量的情况是:(A) b 1a 过程放热,作负功;b 2a 过程放热,作负功.(B) b 1a 过程吸热,作负功;b 2a 过程放热,作负功.(C) b 1a 过程吸热,作正功;b 2a 过程吸热,作负功.(D) b 1a 过程放热,作正功;b 2a 过程吸热,作正功.[ ] 4、(本题3分)甲说:“由热力学第一定律可证明任何热机的效率不可能等于1”乙说:“热力学第二定律可表述为效率等于 100%的热机不可能制造成功”丙说:“由热力学第一定律可证明任何卡诺循环的效率都等于.”丁说:“由热力学第一定律可证明理想气体卡诺热机(可逆的)循环的效率等于”对以上说法,有如下几种评论,哪种是正确的? )/(112T T −)/(112T T − (A) 甲、乙、丙、丁全对. (B) 甲、乙、丙、丁全错.(C) 甲、乙、丁对,丙错. (D) 乙、丁对,甲、丙错. [ ]5、(本题3分)静电场中某点电势的数值等于 (A) 单位正电荷置于该点时具有的电势能. (B) 单位试验电荷置于该点时具有的电势能. (C) 试验电荷置于该点时具有的电势能. 0q (D) 把单位正电荷从该点移到电势零点外力所作的功. [ ]6、(本题3分)如图所示,一封闭的导体壳A 内有两个导体B 和C 。

同济大学本科课程期终考试(考查)统一命题纸 A 卷2006—2007学年第 一 学期课程名称:弹性力学 课号: 任课教师:专业年级: 学号: 姓名: 考试(√)考查( ) 考试(查)日期: 2007 年1月 22 日 出考卷教师签名:朱合华、许强、王君杰、李遇春、陈尧舜、邹祖军、赖永瑾、蔡永昌教学管理室主任签名:1.是非题(认为该题正确,在括号中打√;该题错误,在括号中打×。
)(每小题2分)(1)薄板小挠度弯曲时,体力可以由薄板单位面积内的横向荷载q 来等代。
( )(2)对于常体力平面问题,若应力函数满足双调和方程,那么由),(y x ϕ022=∇∇ϕ确定的应力分量必然满足平衡微分方程。
),(y x ϕ( )(3)在求解弹性力学问题时,要谨慎选择逆解法和半逆解法,因为解的方式不同,解的结果会有所差别。
( )(4)如果弹性体几何形状是轴对称时,就可以按轴对称问题进行求解。
()(5)无论是对于单连通杆还是多连通杆,其截面扭矩均满足如下等式:,其中为扭转应力函数。
( ⎰⎰=dxdyy x F M ),(2),(y x F )(6)应变协调方程的几何意义是:物体在变形前是连续的,变形后也是连续的。
( )(7)平面应力问题和平面应变问题的应变协调方程相同,但应力协调方程不同。
()(8)对于两种介质组成的弹性体,连续性假定不能满足。
( )(9)位移变分方程等价于以位移表示的平衡微分方程及以位移表示的静力边界条件。
()(10)三个主应力方向一定是两两垂直的。
( )2.填空题(在每题的横线上填写必要的词语,以使该题句意完整。
)(共20分,每小题2分)(1)弹性力学是研究弹性体受外界因素作用而产生的 的一门学科。
(2)平面应力问题的几何特征是: 。
(3)平衡微分方程则表示物体 的平衡,应力边界条件表示物体 的平衡。
(4) 在通过同一点的所有微分面中,最大正应力所在的平面一定是 。
(5)弹性力学求解过程中的逆解法和半逆解法的理论基础是: 。


华 北 水 利 水 电 学 院 试 题 答 案 A 2010 ~2011 学年 第 一 学期 2008 级 工程力学 专业_弹性力学__课程一、填空(每空1分,共10×1=10分)1.平衡微分 几何 物理 应力 位移2.连续 均匀 各向同性 完全弹性 小变形二、判断(每题2分,共10分)1、×2、×3、×4、×5、×三、简答题(每题10分,共20分)1边界条件:主要边界条件:()20h y σ=±=()2h xy y q τ=±=- (4分) 次要边界条件: ()220cos hh x x dy F σα-==⎰()220h h x x ydy M σ-==-⎰ (4分) 固定端:()()11000x x y y u v ======100x y v x ==∂⎛⎫= ⎪∂⎝⎭ (2分) 2(1)求解未知量x σ、y σ、xy τ,使满足:平衡方程:第 1页 共 5 页0xy x X x y τσ∂∂++=∂∂0yxyY y x στ∂∂++=∂∂应力协调方程:()()21x y X Y v x y σσ⎛⎫∂∂+=-++⎪∂∂⎝⎭∇ 边界条件:x xy m X τσ+=x xy m l Y τσ+= (6分)(2)将求出的应力分量x σ、y σ、xy τ带入本构方程求出应变分量ε()1x x v y E σσε=- ()1y y x v E εσσ=- ()21xy xy v E γτ+= 并且()1z x y v v εεε=-+- 由几何方程x ux ε∂=∂y vy ε∂=∂2xy xy u v y x γε∂∂==+∂∂ 积分得到位移分量u ,v 其中积分常数由位移边界条件u u =,v v =确定并且z w z ε=或者w o ≈ (4分)第 2页 共 5 页四、计算题(共60分,每题20分)1、解:用半逆解法。

弹性力学与有限元分析复习题及其答案一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。
应力及其分量的量纲是L -1MT -2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。
6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa ,=2σ0MPa ,=1α6135' 。
8、已知一点处的应力分量,200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512 MPa ,=2σ-312 MPa ,=1α-37°57′。
9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
分为位移边界条件、应力边界条件和混合边界条件。
13、按应力求解平面问题时常采用逆解法和半逆解法。
14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。
其具体步骤分为单元分析和整体分析两部分。
15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。

弹性力学与有限元分析复习题及其答案一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。
应力及其分量的量纲是L -1MT -2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。
6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa ,=2σ0MPa ,=1α6135'ο。
8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512 MPa ,=2σ-312 MPa ,=1α-37°57′。
9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
分为位移边界条件、应力边界条件和混合边界条件。
13、按应力求解平面问题时常采用逆解法和半逆解法。
14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。
其具体步骤分为单元分析和整体分析两部分。
15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。

弹性力学与有限元分析复习题及其答案一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。
应力及其分量的量纲是L -1MT -2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。
6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa ,=2σ0MPa ,=1α6135' 。
8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512 MPa ,=2σ-312 MPa ,=1α-37°57′。
9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
分为位移边界条件、应力边界条件和混合边界条件。
13、按应力求解平面问题时常采用逆解法和半逆解法。
14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。
其具体步骤分为单元分析和整体分析两部分。
15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。
同济大学课程考核试卷(A 卷)2007 — 2008 学年第 一 学期 命题教师签名: 审核教师签名:课号:125112 课名:工程力学ⅱ 考试考查:考试此卷选为:期中考试( )、期终考试(√)、重考( )试卷年级 专业 学号 姓名 得分一、填空题(每小题5分,共20分)1.已知图示平行四边形O 1ABO 2机构的O 1A 杆以匀角速度ω绕O 1轴转动,则D 的速度为_______________;加速度为______________(二者方向要在图1.1上画出)。
2. 均质细圆环,半径为r ,质量为m ,与二等长无重刚性杆OA ,OB 连接,并在水平面内绕O 轴转动,已知:OE =2r ,图1.2示瞬时角速度为ω,则该瞬时圆环动量的大小为__________________________;动能为________________;对O 轴的动量矩_________________。
3.两个质量都是m 1,半径都是R 的均质圆盘Ⅰ,Ⅱ,以相同的角速度ω 和角加速度α 分别绕O 1,O 2轴转动。
质量为m 2的匀质直杆AB 铰接在二轮的轮缘上,而且有O 1O 2=AB =L 。
二轮及杆AB 的惯性力(包括惯性力偶)大小分别为_______________________________________________________________________。
(方向应图1.3中画出)。
4.均质细杆OA 长L ,重P ,其一端用光滑铰链与半径为r ,重为P 1的均质圆轮中心O 连接,今在圆轮上作用一常值转矩M ,使其沿水平直线作纯滚动。
则该系统有__________个自由度,若取x 及ϕ为广义坐标,则相应于x的广义力为________________________。
图1.1 图1.2 图1.4图1.3如图所示,凸轮以匀角速度ω绕O轴转动,杆AB的A端搁在凸轮上。
图示瞬时杆AB处于水平位置,OA连线为铅垂。
1、试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积21200mm A =,22300mm A =,23400mm A =,并求各横截面上的应力。
(10分)解:(1)求指定截面上的轴力kN N 2011-=-)(10201022kN N -=-=- )(1020102033kN N =-+=- (2)作轴力图轴力图如图所示。
(3)计算各截面上的应力M P a mm NA N 10020010202311111-=⨯-==--σ MPa mmN A N 3.3330010102322222-=⨯-==--σ MPa mmN A N 254001010233333=⨯==--σ图⋅NmkN ⋅30kN 20kN5.12⊕Θ图Q mkN ⋅30mkN ⋅20图M AC BBCA2、用区段叠加法作图示梁的内力图(10分)解:(1)求支座反力)(5.120412030kN R A -=+⨯+-= )(5.3220412030kN R C =+⨯+=(2)求控制截面的弯矩 m kN M A ⋅=30)(20120m kN M C ⋅-=⨯-=0=B M(3)画控制截面弯矩的竖标,连竖标叠加后得如图所示的弯矩图。
(4)根据支座反力和横力,作出如图所示的剪力图。
3、试用积分法求图示悬臂梁的挠曲线方程、最大挠度、梁端转角的表达式。
(10分)解:(1)写弯矩方程 e M x M -=)((2)写挠曲线近似微分方程,并积分)("x M E I w -= e M E I w="1'C x M E I we += 21221C x C x M E I w e ++=把边界条件:当0=x 时,0'=w ,0=w 代入以上方程得:01=C ,02=C 。
故:转角方程为: x M EI EIw e ==θ',EIxM e =θ 挠曲线方程:221x M EIw e =, EI x M w e 22=(3)求梁端的转角和挠度 EIlM l e B ==)(θθ EIl M l w w e B 2)(2==(最大挠度)4、刚性杆AB 的左端铰支,两根长度相等、横截面面积相同的钢杆CD 和EF 使该刚性杆处于水平位置,如所示。
同济大学课程考核试卷(A 卷) 2008 — 2009 学年第 一 学期命题教师签名: 审核教师签名: 课号:030192 课名: 弹性力学 考试考查:考试此卷选为:期中考试( )、期终考试(√ )、重考( )试卷年级 专业 学号 姓名 得分一.是非题(正确,在括号中打√;该题错误,在括号中打×。
)(共30分,每小题2分) 1. 三个主应力方向必定是相互垂直的。
( ) 2. 最小势能原理等价于平衡方程和面力边界条件。
( ) 3. 轴对称的位移对应的几何形状和受力一定是轴对称的。
( ) 4. 最大正应变是主应变。
( )5. 平面应力问题的几何特征是物体在某一方向的尺寸远小于另两个方向的尺寸。
( )6. 最大剪应力对应平面上的正应力为零。
( )7. 弹性体所有边界上的集中荷载均可以按照圣维南原理放松处理边界条件。
( ) 8. 用应力函数表示的应力分量满足平衡方程,但不一定满足协调方程。
( ) 9. 经过简化后的平面问题的基本方程及不为零的基本未知量(应力、应变和位移)均为8个。
( )10. 运动可能的位移必须满足已知面力的边界条件。
( ) 11. 实对称二阶张量的特征值都是实数。
( ) 12. 对单、多连通弹性体,任意给出的应变分量只要满足协调方程就可求出单值连续的位移分量。
( )13. 若整个物体没有刚体位移,则物体内任意点处的微元体都没有刚体位移。
( ) 14. 出现最大剪应力的微平面和某两个应力主方向成45度角。
( ) 15. 对任意弹性体,应力主方向和应变主方向一致。
( )二.分析题(共20分,每小题10分)1.已知应力张量为()()2211e e e e σ⊗-+⊗+=b a b a ,0>>a b(1) 设与xy 平面垂直的任意斜截面的法向矢量为21sin cos e e n θθ+=,试求该斜截面上的正应力与剪应力。
(2) 求最大和最小剪应力值。
2.已知应变张量:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=0000203a a a a ij ε试求:(1)主应变;(2)主应变方向;(3)应变不变量三.计算题(共50分)1、(13分) 如图1所示为一等截面简支梁,抗弯刚度为EI ,长为L ,受均布荷载q 和集中力P 作用,试采用瑞利——李兹(Rayleigh-Ritz) 法或者伽辽金(Galerkin)法(二法只选一种)求挠度函数w 。
提示:挠度函数可假设为:221)]1([)1()(ξξξξξ-+-=a a w ,其中L x /=ξ。
图12、(10分)证明应力函数2Mϕθπ=可以满足双调和方程,并求出相对应的应力分量。
设有内半径为a ,外半径为b 的圆环发生了上述应力(如图2),试求出边界上的面力,并图示之。
图23、(13分)如图3所示悬臂梁承受均布荷载q的作用(h<<l),设该问题的应力函数为523322Ay Bx y Cy Dx Ex yϕ=++++,试求出其应力分量。
图34、(14分)已知楔形的悬臂梁在0θ=的边界上受载荷作用(如图4),试计算各应力分量。
注:设应力函数为2(cos2sin2)2rA B C D ϕθθθ=+++图4qyOq1h同济大学本科课程期终考试统一命题纸 A 卷 标准答案2008—2009学年第 一 学期一.是非题(认为该题正确,在括号中打√;该题错误,在括号中打×。
)(每小题2分) 1. 三个主应力方向必定是相互垂直的。
(×)2. 最小势能原理等价于平衡方程和面力边界条件。
(√)3. 轴对称的位移对应的几何形状和受力一定是轴对称的。
(√)4. 最大正应变是主应变。
(√)5. 平面应力问题的几何特征是物体在某一方向的尺寸远小于另两个方向的尺寸。
(√)6. 最大剪应力对应平面上的正应力为零。
(×)7. 弹性体所有边界上的集中荷载可以按照圣维南原理放松处理边界条件。
(×) 8. 用应力函数表示的应力分量满足平衡方程,但不一定满足协调方程。
(√) 9. 经过简化后的平面问题的基本方程及不为零的基本未知量(应力、应变和位移)均为8个。
(×)10. 运动可能的位移必须满足已知面力的边界条件。
(×) 11. 实对称二阶张量的特征值都是实数。
(√) 12. 对单、多连通弹性体,任意给出的应变分量只要满足协调方程就可求出单值连续的位移分量。
(×)13. 若整个物体没有刚体位移,则物体内任意点处的微元体都没有刚体位移。
(×) 14. 出现最大剪应力的微平面和某两个应力主方向成45度角。
(√) 15. 对任意弹性体,应力主方向和应变主方向一致。
(×)二.分析题(共20分,每小题10分) 1.(1) 利用方程j i ij n n n σσ=⋅⋅=n σn ,即得()()θθθσ2cos sin cos 22b a b a b a n +=-++=再利用()()()()θθτσ222222sin cos b a b a n n -++=⋅⋅⋅=+n σn σ,可得()()()θθθθτ2sin 2cos sin cos 22222222b b a b a b a n =+--++= (6分)(2) 由于应力张量σ的剪应力分量全为零,因此3个正应力均为主应力。
又由于最大主应力为0>+=b a x σ,最小主应力为0<-=b a y σ,因此最大最小剪应力分别为b =max τ和b -=min τ,它们所对应的微分面法矢量与z 轴垂直,且与x 轴和y 轴的夹角(不计方向)均为45度。
(4分)2. (1)由0)(=-I εε解得主应变为,255,255321=+-=--=εεεa a (4分)(2)主应变方向 由1,1=i i n n ε得1n由1,2=i i n n ε得2n由1,3=ii n n ε得3n(4分)(3)应变不变量为0,5,53221==-=J a J a J(2分)三.计算题(共50分)1、采用瑞利——李兹 (Rayleigh-Ritz) 法(1) 设挠度函数为221)]1([)1()(ξξξξξ-+-=a a w ,其中L x /=ξ。
(2) 检查位移边界条件:当0=x 时,即0=ξ时,0=w ,满足; 当L x =时,即1=ξ时,0=w ,也满足。
(2分)(3) 求梁的总势能∏Ldx d 1=ξ )]21)(1(2)21([121ξξξξξξ--+-==a a Ldx d d dw dx dw )121222(1))((22221222ξξξξa a a a Ldx d dx dw d d dx w d +-+-== 200222)(21L x L L w P qwdx dx dx w d EI =--∏⎰⎰=)16141()30161()544(2121213a a P a a qL a a LEI +-+-=+ (6分)(4) 按采用瑞利——李兹 (Rayleigh-Ritz) 法,令01=∂∏∂a ,即P qL a LEI 4161413+= 解得:)32(4831P qL EIL a +=02=∂∏∂a ,即 P qL a LEI 1613015423+= 解得:)161301(4532P qL EI L a +=于是挠度近似函数为:)]554)(1([64)]1)(1([242324ξξξξξξξξ-+-+-+-=PL EI qL w(5分)2、(1)证明应力函数2Mϕθπ=自动满足双调和方程 (4分) (2)(6分)210,2r r M rθθσστπ===内边r=a 处 212r Ma θτπ=外边r=b 处 212r Mbθτπ=(1)将523322Ay Bx y Cy Dx Ex y ϕ=++++代入双调和方程:220ϕ∇∇=241200By Ay +=5B A ϕ∴=-时,可作为应力函数, 523322y 5A Ax y Cy Dx Ex y ϕ∴=-+++(3分)(2)232220306x Ay Ax y Cy yϕσ∂==-+∂ 2321022y Ay D Ey xϕσ∂==-++∂22302xyAxy Ex x yϕτ∂=-=-∂∂(3分)(3)边界条件/2:,0/2:0,0y xy y xy y h q y h στστ=-=-====2222220:000h h xy h h x h h x x dy dy ydy τσσ---====⎰⎰⎰将x σ、y σ代入上述边界条件可解出各系数 (5分)(4)将参数代入可得323332346353412632x y xy q q q y x y y h h h q y y h h q q xy x h hσστ=--⎛⎫=--+ ⎪⎝⎭=-(2分)检查该应力函数满足双调和方程 (3分)在已知应力函数的情况下应力表达式为cos 2sin 2cos 2sin 21(2sin 22cos 2)2r r A B C D A B C D B C D θθσθθθσθθθτθθ=--+=+++=--++ (4分)边界条件为(1)当0,q θθσ==-; (2)当0,0r θθτ==; (3)当,0θθασ==; (4)当,0r θθατ==。
这些条件给出如下方程组1(2)02cos 2sin 201(2sin 22cos 2)02A B qC D A B C D B C D ααααα+=--+=+++=--=(5分)解出这一方程组后,得111tan ,tan ,,222q q q q A K B C D K K K K αα-⎛⎫=-===- ⎪⎝⎭(2分)式中tan K αα=-。
Welcome To Download !!!欢迎您的下载,资料仅供参考!。