程序框图循环结构
- 格式:ppt
- 大小:1.07 MB
- 文档页数:40










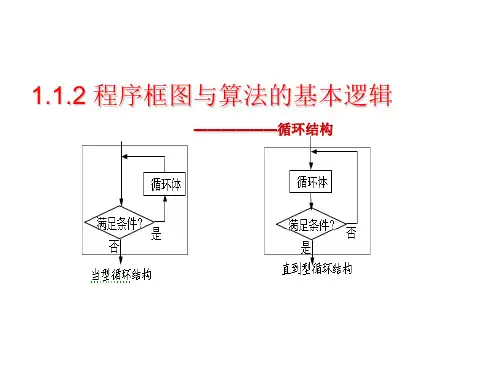
程序框图的循环结构算法初步是高中新课程中的一项新增内容,而且作为高中数学必修内容的一部分。
《新课程标准》里指出:算法是数学的重要组成部分,是计算理论、计算机理论和技术的基础。
可见算法的重要地位和作用。
在数学中,算法通常是按照一定规则解决某一类问题的明确和有限的步骤。
通俗地说,算法就是用计算机求解某一问题的方法,解决问题的过程就是实现算法的过程。
问题的不同求解过程就是不同的算法。
算法是程序设计的“灵魂”,但算法又独立于任何具体的程序设计语言,一个算法可以用各种程序设计语言来实现,比如:可以用BASIC语言,也可以用C语言等来实现。
由于BASIC语言具有简单、易学等特点,数学课本《必修3》介绍算法语句时就使用QBASIC(BASIC的一种)的语句形式和语法规则。
下面就结合我的教学实践并参考计算机教程《算法与程序设计》来谈谈一些认识。
一.程序框图的由来和含义自然语言、程序框图及程序是算法的不同表示形式。
用自然语言描述算法的优点是通俗易懂,但容易造成理解歧义,描述算法太长,不够精练。
当算法中存在循环或分支较多时,不易清晰表示出来。
与自然语言描述相比,用程序框图描述的算法形象、直观,更容易理解。
而且对于一个复杂的算法,如果直接编写程序语言很难保证程序的正确性,此时人们往往先用程序框图来描述算法,然后根据程序框图就可以方便地写出程序语言了。
所以程序框图的学习与掌握还是有必要的。
程序框图是一种用程序框、流程线及文字说明来表示算法的图形。
它是文科选修教材1-2第四章《框图》中介绍的流程图的一种,它不同于日常生活和工作中常见的诊病流程图、工序流程图等等。
程序框图是算法步骤的直观图示,它有一定的规范和标准,要求能编成计算机程序,并能在计算机上进行运行,而日常生活中用到的流程图则相对自由一些,它只要能较直观,明确地表示动态过程从开始到结束的全部步骤即可。
二.程序框图的基本逻辑结构算法的结构包括顺序结构,条件结构,循环结构等三种基本逻辑结构。