沪科版九上数学相似三角形知识点总结 (2)

初三数学《相似三角形》知识提纲一：比例的性质及平行线分线段成比例定理（一）相关概念：1.两条线段的比：两条线段的比就是两条线段长度的比 在同一长度单位下两条线段a ，b 的长度分别为m ，n ，那么就说这两条线段 的比是，或写成a ：b=m ：n ； 其中 a 叫做比的前项，b 叫做比的后项 2：比例尺= 图上距离／实际距离3：成比例线段：在四条线段a ，b ，c ，d 中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成比例线段，简称比例线段，记作：cda b =（或a ：b=c ：d ） ① 线段a ，d 叫做比例外项，线段b ，c 叫做比例内项， ② 线段a 叫首项，d 叫a ，b ，c 的第四比例项。

③ 比例中项:若c a b c a b cbb a ,,2是则即⋅==的比例中项. （二）比例式的性质 1.比例的基本性质:bc ad dcb a =⇔= 2. 合比：若，则或a b c d a b b c d d a b a c d c =±=±±=±3.等比：若……（若……）a b c d e f mn k b d f n =====++++≠0则…………a c e m b d f n a b mn k++++++++===4、黄金分割：把线段AB 分成两条线段AC ，BC （AC>BC ），并且使AC 是AB 和BC 的比例中项，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AC=215-AB ≈0.618AB ， (三)平行线分线段成比例定理1.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.如图：当AD∥BE∥CF 时，都可得到=.=，= ，语言描述如下：=，= ，=.（4）上述结论也适合下列情况的图形：nm b a =图（2） 图（3） 图（4） 图（5）2.推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.l 3l 2l 1ABCD E E D CBA D ECA l 1l 2l 3AB CD EA 型 X 型由DE ∥BC 可得：ACAEAB AD EA EC AD BD EC AE DB AD ===或或. 3.推论的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.如上图：若 = . = ，=，则AD ∥BE ∥CF此定理给出了一种证明两直线平行方法,即：利用比例式证平行线.4.定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边．．．．．．与原三角形．．．．三边．．对应成比例. 二：相似三角形： （一）：定义：1：对应角相等，对应边成比例的三角形，叫做相似三角形。

相似三角形知识点总结知识点1、三角对应相等，三边对应成比例的三角形叫相似三角形。

如△ABC 与△A /B /C /相似，记作: △ABC ∽△A /B /C /。

相似三角形的比叫相似比相似三角形的定义既是相似三角形的性质，也是三角形相似的判定方法。

注意：（1）相似比是有顺序的。

（2）对应性，两个三角形相似时，通常把对应顶点写在对应位置，这样写比较容易找到相似三角形的对应角和对应边。

（3）顺序性：相似三角形的相似比是有顺序的，若△ABC ∽△A /B /C /，相似比为k ，则△A /B /C /与△ABC 的相似比是1k知识点2、相似三角形与全等三角形的关系（1）两个全等的三角形是相似比为1的相似三角形。

（2）两个等边三角形一定相似，两个等腰三角形不一定相似。

（3）二者的区别在于全等要对应边相等，而相似要求对应边成比例。

知识点3、平行线分线段成比例定理1. 比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a bc da b c d a d b c a c ()b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC ，使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质：①基本性质：a bc dadbc ②合比性质：±±a b c d a b b c d d③等比性质：……≠……a bc dm nb dn a c m bdna b()03. 平行线分线段成比例定理（1）平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知l1∥l2∥l3,A D l1B E l2CF l3可得EF BC DEAB DFEF ACBC DFEF ABBC DFDE ACAB EFDE BCAB或或或或等.（2）推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. AD EBC由DE ∥BC 可得：AC AEABAD EAEC ADBD ECAE DBAD 或或.此推论较原定理应用更加广泛,条件是平行.（3）推论的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即：利用比例式证平行线.（4）定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. 知识点4：相似三角形的性质①相似三角形的对应角相等②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方知识点5：相似三角形的判定：①两角对应相等，两个三角形相似②两边对应成比例且夹角相等，两三角形相似③三边对应成比例，两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角形相似⑤平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似如果两个三角形的两角分别于另一个三角形的两角对应相等，那么这两个三角形相似。

九年级数学上22.2.1相似三角形的判定（最新沪科版）相似三角形的判定一、授目的与考点分析：相似三角形的判定二、授内容：(一)相似三角形1、定义：对应角相等，对应边成比例的两个三角形，叫做相似三角形．强调：①当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等，且三条对应边的比相等时，这两个(或几个)三角形叫做相似三角形，即定义中的两个条，缺一不可；②相似三角形的特征：形状一样，但大小不一定相等；③相似三角形的定义，可得相似三角形的基本性质：对应角相等，对应边成比例．2、相似三角形对应边的比叫做相似比．强调：①全等三角形一定是相似三角形，其相似比=1．所以全等三角形是相似三角形的特例．其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△AB∽△A′B′′的对应边的比，即相似比为，则△A′B′′∽△AB的相似比，当它们全等时，才有=′=1．③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数，这一点借助相似三角形可观察得出．3、如果两个边数相同的多边形的对应角相等，对应边成比例，那么这两个多边形叫做相似多边形．4、相似三角形的预备定理：平行于三角形的一条边直线，截其它两边所在的直线，截得的三角形与原三角形相似．强调：①定理的基本图形有三种情况，如图其符号语言：∵DE∥B，∴△AB∽△ADE；（双A型）②这个定理是用相似三角形定义推导出的三角形相似的判定定理．它不但本身有着广泛的应用，同时也是证明相似三角形三个判定定理的基础，故把它称为“预备定理”；③有了预备定理后，在解题时不但要想到“见平行，想比例”，还要想到“见平行，想相似”．(二)相似三角形的判定1、相似三角形的判定：判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

可简单说成：两角对应相等，两三角形相似。

例1、已知：如图，∠1=∠2=∠3，求证：△AB∽△ADE．例2、如图，E、F分别是△AB的边B上的点，DE∥AB,DF∥A ,求证：△AB∽△DEF判定定理2：如果三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

九年级数学相似三角形知识点咱来唠唠九年级数学里的相似三角形知识点哈。

一、相似三角形是啥玩意儿呢？简单来说，相似三角形就像是三角形家族里的“克隆兄弟”，它们形状相同，但大小可能不一样。

就好比你用放大镜看一个小三角形，放大后的三角形和原来的小三角形就是相似的。

二、相似三角形的判定方法1. 两角对应相等- 如果两个三角形有两个角分别相等，那这两个三角形就相似。

这就像是两个人，只要他们在两个关键的地方（角度）长得一样，那他们就有相似之处。

比如说三角形ABC和三角形DEF，要是∠A = ∠D，∠B = ∠E，那这两个三角形就相似啦。

2. 两边对应成比例且夹角相等- 想象一下，两个三角形的两条边的长度比例是一样的，而且这两条边所夹的角也相等。

就像两根一样比例的小棍，它们夹着相同角度的话，那这两个三角形也是相似的。

比如在三角形ABC和三角形DEF中，AB/DE = AC/DF，并且∠A = ∠D，那这两个三角形就相似喽。

3. 三边对应成比例- 这个就更好理解啦，三个边的长度比例都一样的两个三角形肯定相似。

就好比三个小伙伴，他们的身高、臂长、腿长的比例都相同，那他们就是相似的三角形啦。

如果AB/DE = BC/EF = AC/DF，那么三角形ABC和三角形DEF就是相似三角形。

三、相似三角形的性质1. 对应边成比例- 相似三角形的对应边的比例是相等的。

就像前面说的那些判定方法里的边的比例一样。

如果三角形ABC相似于三角形DEF，那么AB/DE = BC/EF = AC/DF，这个比例是固定的哦。

2. 对应角相等- 因为相似三角形形状相同嘛，所以它们的对应角肯定是相等的。

∠A = ∠D，∠B = ∠E，∠C = ∠F。

3. 相似三角形的周长比等于相似比- 相似比就是对应边的比例。

比如说相似三角形ABC和DEF的相似比是k （AB/DE = k），那么它们的周长比也是k。

就好比两个相似的图形，一个大一个小，大的图形的周长是小的图形周长的k倍。

24.2 相似三角形的判定[知识点1]相似三角形：1、两个三角形，如果各边对应成比例，各角对应相等，则这两个三角形相似。

2、各边对应成比例，各角对应相等是指三组对应角分别相等，三组对应边分别成比例。

3、△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”，书写时同三角形全等一样，要注意对应字母放在对应位置4、相似三角形的定义揭示了相似三角形的本质特性，即如果两个三角形相似，则各边对应成比例，各角对应相等，∴相似三角形的定义即是性质，又是判定。

5、全等三角形是相似比为1的相似三角形。

[知识点2]相似三角形判定方法：相似三角形的判定方法按照全等三角形的判定方法可记为“AA”、“SAS”、“SSS”和“HL”，只是这里对边要求是对应成比例，对角的要求是对应角相等。

1、“AA”：如果一个三角形的两个角分别与另一个三角形的两个角对应相等；那么这两个三角形相似。

可简单的说成：两角对应相等的两个三角形相似。

2、“SAS”：如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等，那么这两个三角形相似，可简单的说成：两边对应成比例且夹角相等的两个三角形相似。

3、“SSS”：如果一个三角形的三条边为另一个三角形的三条边对应成比例，那么这两个三角形相似，可以简单的说成：三边对应成比例的两个三角形相似。

4、“HL”：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三外形相似。

典型例题点拨例1、已知:如图，ΔABC中,AD＝DB，∠1＝∠2，求证:ΔABC∽ΔEAD。

例2、已知：如图，在正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，ΔADQ与ΔQCP是否相似？为什么？例3、如图，点C、D在线段AB上，△PCD是等边三角形。

（1）当AC、CD、DB满足怎样的关系时，△ACP∽△PDB？（2）当△ACP∽△PDB时，求∠APB的度数。

初中相似三角形知识点总结
相似三角形是指两个或多个三角形的对应角相等，对应边成比例的关系。

以下是初中相似三角形的知识点总结：
1. 相似三角形的定义：两个或多个三角形的对应角相等，对应边成比例。

2. 相似三角形的性质：
- 对应角相等：两个相似三角形的对应角相等，即角A = 角D，角B = 角E，角C = 角F。

- 对应边成比例：两个相似三角形的对应边成比例，即 AB/DE = BC/EF = AC/DF。

3. 相似三角形的判定：
- AA相似定理：如果两个三角形的两个角分别相等，则这两个三角形相似。

- SAS相似定理：如果两个三角形的两个边成比例，并且夹角相等，则这两个三角形相似。

4. 相似三角形的应用：
- 求比例关系：根据相似三角形的性质，可以利用已知的比例关系来求解未知的边长或角度。

- 利用相似三角形求高度：在一个相似三角形中，可以利用已知的比例关系来求解未知的高度。

5. 相似三角形的注意事项：
- 只有对应角相等和对应边成比例的三角形才是相似三角形。

- 相似三角形的比例关系可以用来计算边长，但不能用来计算面积。

相似三角形是初中数学中的重要概念，它在几何形状的比较和计算中有着广泛的应用。

理解相似三角形的性质和应用方法，对于解决与三角形相关的问题具有重要意义。

九年级数学相似三角形知识点九年级数学：相似三角形知识点1. 相似三角形的定义相似三角形是指两个三角形的对应角相等，且对应边成比例的三角形。

也就是说，如果两个三角形的三个角分别相等，且每组对应边的比值都相等，那么这两个三角形就是相似的。

2. 相似三角形的标记在标记相似三角形时，通常使用希腊字母来表示对应的顶点。

例如，如果三角形ABC与三角形DEF相似，我们可以标记为：△ABC ∼△DEF。

3. 相似三角形的性质- 对应角相等：∠A = ∠D, ∠B = ∠E, ∠C = ∠F。

- 对应边成比例：AB/DE = BC/EF = AC/DF。

- 对应高的比值也相等：AH/DH = BH/EH = CH/FH（其中H是三角形的高所在的顶点）。

- 对应中线的比值也相等：AM/DM = BM/EM = CM/FM（其中M是三角形的中线所在的顶点）。

4. 相似三角形的判定- 三角形相似的判定定理一：如果两个三角形的两组对应角分别相等，那么这两个三角形相似。

- 三角形相似的判定定理二：如果两个三角形的三组对应边的比值都相等，那么这两个三角形相似。

- 三角形相似的判定定理三：如果两个三角形的两组对应边的比值相等，且它们之间的夹角也相等，那么这两个三角形相似。

5. 相似三角形的应用- 解决实际问题：在建筑设计、地图制作等领域，相似三角形的概念可以用来解决比例缩放问题。

- 计算面积比：相似三角形的面积比等于对应边长的平方比。

即，如果AB/DE = x，则△ABC的面积与△DEF的面积之比为x²。

- 证明几何定理：在证明某些几何定理时，可以通过证明三角形相似来简化证明过程。

6. 相似三角形的计算- 使用比例关系解决实际问题时，通常需要先确定比例系数，然后利用这个系数来计算其他边长或角度。

- 在计算面积比时，应先计算出三角形的边长比，然后根据边长比计算面积比。

7. 相似三角形的证明- 在证明三角形相似时，需要明确指出所使用的判定定理，并确保所有的条件都满足。

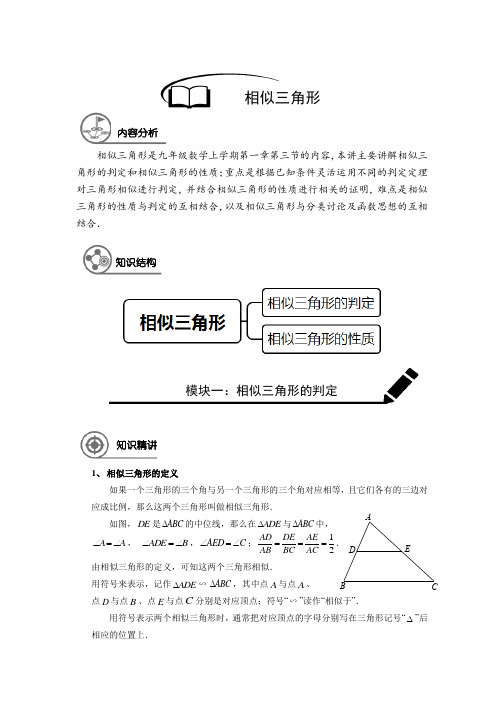
D ABCE相似三角形是九年级数学上学期第一章第三节的内容，本讲主要讲解相似三角形的判定和相似三角形的性质；重点是根据已知条件灵活运用不同的判定定理对三角形相似进行判定，并结合相似三角形的性质进行相关的证明，难点是相似三角形的性质与判定的互相结合，以及相似三角形与分类讨论及函数思想的互相结合．1、 相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三边对应成比例，那么这两个三角形叫做相似三角形．如图，DE 是ABC ∆的中位线，那么在ADE ∆与ABC ∆中，A A ∠=∠， ADEB ∠=∠，AEDC ∠=∠；12AD DE AE AB BC AC ===． 由相似三角形的定义，可知这两个三角形相似．用符号来表示，记作ADE ∆∽ABC ∆，其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点；符号“∽”读作“相似于”．用符号表示两个相似三角形时，通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上．相似三角形内容分析知识结构模块一：相似三角形的判定知识精讲2 / 16ABC A 1B 1C 1根据相似三角形的定义，可以得出：（1）相似三角形的对应角相等，对应边成比例；两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数）．（2）如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似． 2、 相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似． 如图，已知直线l 与ABC ∆的两边AB 、AC 所在直线分别交于点D 和点E ，则ADE ∆∽ABC ∆．3、 相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．可简述为：两角对应相等，两个三角形相似．如图，在ABC ∆与111A B C ∆中，如果1A A ∠=∠、1B B ∠=∠，那么ABC ∆∽111A B C ∆．常见模型如下：A BCDEABCDEABCDEABCA 1B 1C 1ABCA 1B 1C 14、 相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．可简述为：两边对应成比例且夹角相等，两个三角形相似．如图，在ABC ∆与111A B C ∆中，1A A ∠=∠，1111AB ACA B AC =，那么ABC ∆∽111A B C ∆．5、 相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．可简述为：三边对应成比例，两个三角形相似． 如图，在ABC ∆与111A B C ∆中，如果111111AB BC CAA B B C C A ==，那么ABC ∆∽111A B C ∆．6、 直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例，那么这两个直角三角形相似．可简述为：斜边和直角边对应成比例，两个直角三角形相似．如图，在Rt ABC ∆和111Rt A B C ∆中，如果190C C ∠=∠=︒，1111AB BCA B B C =，那么ABC ∆∽111A B C ∆．ABCA 1B 1C 14 / 16AB CABCDEABCP【例1】 如图，已知点P 是ABC ∆中边AC 上一点，联结BP ，要使ABP ∆∽ACB ∆，那么应添加的一个条件为____________，或____________，或____________．【例2】 下列命题正确的是（ ） A ．有一个角是40°的两个等腰三角形相似 B ．有一个角是106°的两个等腰三角形相似 C ．面积相等的两个直角三角形相似 D ．两边之比为3 : 5的两个直角三角形相似【例3】 下列4⨯4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与ABC ∆相似的三角形所在的网格图形是（ ）A ．B ．C ．D ．【例4】 如图，ABC ∆中，AE 交BC 于点D ，C E ∠=∠，:3:5AD DE =，AE = 8， BD = 4，则DC 的长等于（ ）A ．415B ．125C ．174D ．154例题解析ABCDPA BCDE FP【例5】 在研究相似问题时，甲、乙同学的观点如下：甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似；乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．对于两人的观点，下列说法正确的是（ ） A ．两人多对B ．两人都不对C ．甲对乙不对D ．甲不对，乙对【例6】 如图，ABC ∆中，AB = AC = 5，BC = 6，点M 为BC 中点，MN ⊥AC 于点N ，则MN =______．【例7】 如图，在平行四边形ABCD 中，F 是BC 上的一点，直线DF 与AB的延长线相交于点E ，BP // DF ，且与AD 相交于点P ，则图中有______对相似的三角形．【例8】 如图，在直角梯形ABCD 中，AD // BC ，90ABC ∠=︒，AB = 8，AD = 3，BC = 4，点P 为AB 边上一动点，若PAD ∆与PBC ∆是相似三角形，则满足条件的点P 的个数是（ ）A ．1个B ．2个C ．3个D ．4个图1图211 1 1111 AB CNM6 / 16A BCDEFAB CDE FGABCDEF 【例9】 如图，在Rt ABC ∆中，90ACB ∠=︒，BC = 3，AC = 4，AB 的垂直平分线DE 交BC的延长线于点E ，则CE 的长为（ ）A ．32B ．76C ．256D ．2【例10】如图，在平行四边形ABCD 中，过点A 作AE ⊥BC ，垂足为E ，连接DE ，F为线段DE 上一点，且AEF B ∠=∠．（1）求证：ADF ∆∽DEC ∆；（2）若AB = 8，AD =63，AF =43，求AE 的长．【例11】如图，梯形ABCD 中，AD // BC ，AB = DC ，对角线AC 、BD 相交于点F ，点E 是边BC 延长线上一点，且CDE ABD ∠=∠．（1）求证：四边形ACED 是平行四边形；（2）联结AE ，交BD 于点G ，求证：DG DFGB DB=．【例12】如图，在ABC ∆中，AB = AC ，点D 、E 分别是边AC 、AB 的中点，DF ⊥AC ，DF 与CE 相交于点F ，AF 的延长线与BD 相交于点G ．（1）求证：2AD DG BD =；（2）联结CG ，求证：ECB DCG ∠=∠．【例13】 在ABC ∆中，AB = 40，AC = 24，BC = 32，点D 是射线BC 上的一点（不与端点重合），联结AD ，如果ACD ∆与ABC ∆相似，求BD 的值．ABCDEAB C DE FG H QAB CDNM【例14】正方形ABCD 的边长为1，M 、N 分别是BC 、CD 上的两个动点，且始终保持AM ⊥MN ，求当BM 为多少时，四边形ABCN 的面积最大，最大面积为多少？【例15】 如图，将边长为6 cm 的正方形ABCD 折叠，使点D 落在AB 边的中点E 处，折痕为FH ，点C 落在Q 处，EQ 与BC 交于点G ，则EBG ∆的周长为______cm ．【例16】如图，Rt ABC ∆中，90ACB ∠=︒，AC = 4 cm ，BC = 2 cm ，D 为BC的中点，若动点E 以1 cm /s 的速度从A 点出发，沿着A B A →→的方向运动，设点E 的运动时间为t 秒，联结DE ，当t 为何值时，BDE ∆是直角三角形？【例17】如图，ABC ∆中，4AB = 5AC ，AD 为ABC ∆的角平分线，点E 在BC 的延长线上，EF ⊥AD 于点F ，点G 在AF 上，FG = FD ，联结EG 交AC 于点H ，若点H 是AC 的中点，求AGFD的值．A BCDE A BCDEF G H8 / 161、 相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比． 2、 相似三角形性质定理2 相似三角形周长的比等于相似比． 3、 相似三角形性质定理3相似三角形的面积的比等于相似比的平方．【例18】如果两个相似三角形的面积之比是9 : 25，其中小三角形一边上的中线长是12cm ，那么大三角形对应边上的中线长是______cm ．【例19】在ABC ∆中，DE // BC ，且D 在AB 边上，E 在AC 边上，若:1:4ADE BCED S S ∆=，则:ADE ABC C C ∆∆=______，:AD DB =______．【例20】如图，梯形ABCD 中，AD // BC ，90B ACD ∠=∠=︒，AB = 2，DC = 3，则ABC∆与DCA ∆的面积比为（ ）A ．2 : 3B ．2 : 5C ．4 : 9D ．2:3【例21】【例22】如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3、4及x ，那么x 的值为（ ）A ．只有1个B ．可以有2个C ．可以有3个D ．有无数个模块二：相似三角形的性质知识精讲例题解析ABCDABCD E ABCDE【例23】如图，D 、E 分别在ABC ∆的边AB 、AC 上，23AD AE DE AB AC BC ===，且ABC ∆与ADE ∆的周长之差为15 cm ，求ABC ∆与ADE ∆的周长．【例24】如图，在ABC ∆中，D 、E 分别是AB 、BC 上的点，且DE // AC ，若:1:4BDE CDE S S ∆∆=，则:BDE ACD S S ∆∆=______．【例25】如图，在ABC ∆中，90C ∠=︒，将ABC ∆沿直线MN 翻折后，顶点C 恰好落在AB 边上的点D 处，已知MN // AB ，MC = 6，23NC =，那么四边形MABN 的面积是______．【例26】如图，在平行四边形ABCD 中，AB = 6，AD = 9，BAD ∠的平分线交BC 于E ，交DC 的延长线与F ，BG AE ⊥于G ，则EFC ∆的周长为______．【例27】如图，在ABC ∆中，BE 平分ABC ∠交AC 于点E ，过点E 作ED // BC 交AB于点D ．（1）求证：AE BC BD AC =；（2）如果3ADE S ∆=，2BDE S ∆=，DE = 6，求BC 的长．AB CDEABCDNMABC DEFG10 / 16ABCD PQ【例28】如图，直角三角形ABC 中，90ACB ∠=︒，AB = 10，BC = 6，在线段AB 上取一点D ，作DF AB ⊥交AC 于点F ，现将ADF ∆沿DF 折叠，使点A 落在线段DB 上，对应点记为1A ，AD 的中点E 的对应点记为1E ，若11E FA ∆∽1E BF ∆， 则AD =______．【例29】如图，在Rt ABC ∆中，90C ∠=︒，AB = 5，BC = 3，点D 、E 分别在BC 、AC上，且BD = CE ，设点C 关于DE 的对称点为F ，若DF // AB ，则BD 的长为______．【例30】如图，在Rt ABC ∆中，90ACB ∠=︒，AC = 8，BC = 6，CD AB ⊥于点D ．点P从点D 出发，沿线段CD 向点C 运动，点O 从点C 出发，沿线段CA 向点A 运动，两点同时出发，速度都为每秒1个单位长度，当点P 运动到点C 时，两点都停止．设运动时间为t 秒．（1）求线段CD 的长；（2）设CPQ ∆的面积为S ，求S 与t 之间的关系式，并确定运动过程中是否存在某一时刻t ，使得:9:100CPQ ABC S S ∆∆=？若存在，求出t 的值；若不存在，请说明理由；（3）当t 为何值时，CPQ ∆为等腰三角形？ABCD E F A 1E 1 AB CDEA BCABCDE FGABCDE【习题1】 如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中ABC ∆相似的是（ ）A ．B ．C ．D ．【难度】★ 【答案】 【解析】【习题2】 如图，D 是ABC ∆的边AC 上一点，CBD ∠的平分线交AC 于点E ，AE = AB ，则长度为线段AD 、AC 长度比例中项的线段是______．【习题3】 如图，在ABC ∆中，D 、F 是AB 的三等分点，DE // FG // BC ，分别交AC 于E 、G ．记ADE ∆、四边形DFGE 、四边形FBCG 的面积分别为1S 、2S 、3S ，则123::S S S =______．【习题4】 如图，D 是ABC ∆的边BC 上一点，已知AB = 4，AD = 2，DAC B ∠=∠，若ABD ∆的面积为a ，则ACD ∆的面积为______．随堂检测ABCD12 / 16AB CPN MQA BCDEG Hx y xy xy xy O O O O 3 45 3 45 3 45 3 45 AB C D E FMG H【习题5】 如图，矩形ABCD 中，AB = 3，BC = 4，动点P 从A 点出发，按A B C →→的方向在AB 和BC 上移动，记P A = x ，点D 到直线P A 的距离为y ，则y 关于x 的函数图像大致是（ ）A ．B ．C ．D ．【习题6】 如图，已知点D 是等腰直角三角形ABC 斜边BC 上的一点，BC = 3BD ，CE ⊥AD ，则AE CE =______．【习题7】 在同一时刻，两根木竿在太阳光下的影子如图所示，其中木竿AB = 2 m ，它的影子BC = 1.6 m ，木竿PQ 的影子有一部分落在了墙上，PM = 1.2 m ，MN = 0.8 m ，则木竿PQ 的长度为______m ．【习题8】 如图，点E 是矩形ABCD 的边BC 上一点，EF ⊥AE ，EF 分别交AC 、CD 于点M 、F ，BG ⊥AC ，垂足为点G ，BG 交AE 于点H ．（1）求证：ABE ∆∽ECF ∆；（2）找出与ABH ∆相似的三角形，并证明；（3）若E 是BC 的中点，BC = 2AB ，AB = 2，求EM 的长．【习题9】 如图，在矩形ABCD 中，AB = 2，BC = 3，点E 、F 、G 、H分别在矩形ABCD 的各边上，EF // AC // HG ，EH // BD // FG ，求四边形EFGH 的周长．A B CDPx yA BC DEABCDEFmH【习题10】 如图，在ABC ∆中，AB = AC ，AD ⊥AB 于点D ，BC = 10 cm ，AD = 8 cm ．点P 从点B 出发，在线段BC 上以每秒3 cm 的速度向点C 匀速运动，与此同时，垂直于AD 的直线m 从底边BC 出发，以每秒2 cm 的速度沿DA 方向匀速平移，分别交AB 、AC 、AD 于E 、F 、H ，当点P 到达点C 时，点P 与直线m 同时停止运动，设运动时间为t 秒（t > 0）．（1）当t = 2时，连接DE 、DF ，求证：四边形AEDF 为菱形；（2）在整个运动过程中，所形成的PEF ∆的面积存在最大值，当PEF ∆的面积最大时，求线段BP 的长；（3）是否存在某一时刻t ，使PEF ∆为直角三角形？若存在，请求出此时刻t 的值；若不存在，请说明理由．14 / 16AB C DE A BCDEABCDE AB C D O【作业1】 如图，在ABC ∆中，DE // BC ，12AD DB =，则下列结论正确的是（ ） A ．12AE AC =B ．12DE BC = C ．13ADE ABC ∆=∆的周长的周长D ．13ADE ABC ∆=∆的面积的面积【作业2】 如图，在ABC ∆中，点D 和点E 分别在边AB 、AC 上，下列条件不能判定ABC∆∽AED ∆的是（ ）A ．AEDB ∠=∠B ．ADEC ∠=∠ C ．AD AC AE AB=D ．AD AE AB AC=【作业3】 一副三角尺按如图所示的方式叠放，则AOB ∆与DOC ∆的面积之比为____________．【作业4】 如图，点D 、E 分别在ABC ∆两边AB 、AC 上，且AD = 31，DB = 29，AE = 30，EC = 32．若50A ∠=︒，则关系式“○1ADE B ∠>∠；○2AED C ∠=∠；○3ADE C ∠>∠；○4AED B ∠=∠”中正确的有（ ） A ．1个 B ．2个 C ．3个 D ．4个【作业5】 在ABC ∆中，P 是AB 上的动点（P 异于A 、B ），过点P 的一条直线截ABC ∆，使截得的三角形与ABC ∆相似，我们不妨称这种直线为过点P 的相似线．如图，36A ∠=︒，AB = AC ，当点P 在AC 的垂直平分线上时，过点P 的ABC ∆的相 似线最多有______条．课后作业AB CPAB O xyAB CDE FGOAB CDEFA B CDE F NM【作业6】 如图，四边形ABCD 、CEFG 都是正方形，点G 在线段CD 上，连接BG 、DE ，DE 和FG 相交于点O ，设AB = a ，CG = b （a > b ），下列结论：○1BCG ∆≌DCE ∆；○2BG DE ⊥；○3DG GO GC CE=；○4()22EFO DGO a b S b S ∆∆-=，其中正确的个数是（ ） A ．4个 B ．3个 C ．2个 D ．1个【作业7】 已知，在菱形ABCD 中，CF ⊥AB ，垂直为E ；CE 与BD 相交于点F ．（1）求证：AB CFBE EF=；（2）求证：22DF DB BC =．【作业8】 如图，四边形ABCD 中，AC ⊥BD 交BD 与点E ，点F 、M 分别是AB ，BC 的中点，BN 平分ABE ∠交AM 于点N ，AB = AC = BD ，连接MF ，NF ． （1）判断BMN ∆的形状，并证明你的结论；（2）判断MFN ∆与BDC ∆之间的关系，并说明理由．【作业9】 如图，AOB ∆为等腰三角形，顶点A 的坐标为（2，5）底边OB 在x 轴上，将AOB ∆绕点B 按顺时针方向旋转一定角度后得''A O B ∆，点A 的对应点'A 在x 轴上，求点'O 的坐标．16 / 16ABCD EF GP Q【作业10】 已知：正方形ABCD 的边长为4，点E 为BC 边的中点，点P 为AB 边上一动点，沿PE 翻折得到BPE ∆，直线PF 交CD 边于点Q ，交直线AD 于点G ． （1）如图，当BP = 1.5时，求CQ 的长；（2）如图，当点G 在射线AD 上时，设BP = x ，DG = y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）延长EF 交直线AD 于点H ，若CQE ∆与FHG ∆相似，求BP 的长．。

沪科版九年级数学上册 相似三角形 知识点大总结知识点1 有关相似形的概念(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比(相似系数)．知识点2 比例线段的相关概念（1）如果选用同一单位量得两条线段的长度分别为，那么就说这两条线段的比是，或写b a ,n m ,nmb a =成．注：在求线段比时，线段单位要统一。

n m b a ::=（2）在四条线段中，如果的比等于的比，那么这四条线段叫做成比例线段，d c b a ,,,b a 和d c 和d c b a ,,,简称比例线段．注：①比例线段是有顺序的，如果说是的第四比例项，那么应得比例式为：a d cb ,,．②a 、d 叫比例外项，b 、c 叫比例内项, a 、c 叫比例前项，a d cb =()ac a b cd b d==在比例式：：中，b 、d 叫比例后项，d 叫第四比例项，如果b=c ，即 那么b 叫做a 、d 的比例中项， 此时有a b b d =：：。

2b ad =（3）黄金分割：把线段分成两条线段，且使是的比例中项，即AB )(,BC AC BC AC >AC BC AB 和，叫做把线段黄金分割，点叫做线段的黄金分割点，其中2AC AB BC =⋅AB C AB ≈0.618．即简记为：AB AC 215-=AB AC BC AB AC ==长短＝＝全长注：黄金三角形：顶角是360的等腰三角形。

黄金矩形：宽与长的比等于黄金数的矩形知识点3 比例的性质（注意性质立的条件：分母不能为0）（1） 基本性质：①；②．bc ad d c b a =⇔=::2::a b b c b a c =⇔=⋅注：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如，除bc ad =了可化为，还可化为，d c b a ::=d b c a ::=，，，，，．b a dc ::=c ad b ::=c d a b ::=b d a c ::=a b c d ::=a c b d ::=（2） 更比性质(交换比例的内项或外项)：()()()a bc d a c d cb db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩，交换内项，交换外项．同时交换内外项（3）反比性质(把比的前项、后项交换)：．a cb d b da c=⇔=（4）合、分比性质：．a c a b c d b d b d±±=⇔=注：实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间发生同样和差变化比例仍成立．如：等等．⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a（5）等比性质：如果，那么．)0(≠++++====n f d b n m f e d c b a ba n f db m ec a =++++++++ 注：①此性质的证明运用了“设法”（即引入新的参数k ）这样可以减少未知数的个数，这种方法是有关比例k 计算变形中一种常用方法．②应用等比性质时，要考虑到分母是否为零．③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立．如：；其中．baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322032≠+-f d b 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE∥BC 可得：ACAEAB AD EA EC AD BD EC AE DB AD ===或或注：①重要结论：平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.②三角形中平行线分线段成比例定理的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即：利用比例式证平行线.③平行线的应用：在证明有关比例线段时，辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD∥BE∥CF,可得等. AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或注：平行线分线段成比例定理的推论：平行线等分线段定理：两条直线被三条平行线所截，如果在其中一条上截得的线段相等，那么在另一条上截得的线段也相等。

相似三角形基本知识知识点一：放缩与相似形1.图形的放大或缩小，称为图形的放缩运动。

2.把形状相同的两个图形说成是相似的图形，或者就说是相似性。

3.相似多边形的性质：如果两个多边形是相似形，那么这两个多边形的对应角相等，对应边的长度成比例。

知识点二：比例线段有关概念及性质（1）有关概念1比：选用同一长度单位量得两条线段。

a、b 的长度分别是m、n，那么就说这两条线段的比是a：b＝m：n（或n mb a =）（2）比例性质1.基本性质:bc ad dcb a =⇔=（两外项的积等于两内项积）2.反比性质：cd a b d c b a =⇒=(把比的前项、后项交换)3.更比性质(交换比例的内项或外项)：()()()a bc d a c d c b d b ad bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩，交换内项，交换外项同时交换内外项4.合比性质：dd c b b a d c b a ±=±⇒=（分子加（减）分母,分母不变FE D CB A 知识点三：黄金分割1）定义：在线段AB 上，点C 把线段AB 分成两条线段AC 和BC （AC ＞BC ），如果ACBCAB AC =，即AC 2=AB×BC ，那么称线段AB 被点C 黄金分割，点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比。

其中AB AC 215-=≈0.618AB 。

知识点四：平行线分线段成比例定理1．平行线分线段成比例定理：两条直线被三条平行的直线所截，截得的对应线段成比例.用符号语言表示：AD∥BE∥CF,,,AB DE BC EF AB DEBC EF AC DF AC DF∴===.2．平行线等分线段定理：两条直线被三条平行的直线所截，如果在一直线上所截得的线段相等，那么在另一直线上所截得的线段也相等.用符号语言表示：AD BE CF AB BC DE DF ⎫⇒=⎬=⎭.重心定义：三角形三条中线相交于一点，这个交点叫做三角形的重心.重心的性质：三角形的重心到一个顶点的距离，等于它到对边中点的距离的两倍.知识点五：相似三角形1、相似三角形1）定义：如果两个三角形中，三角对应相等，三边对应成比例，那么这两个三角形叫做相似三角形。

初三数学：《相似三角形》知识点归纳
所谓的相似三角形,就是它们的形状相同,但大小不一样,然而只要其形状相同,不论大小怎样改变他们都相似,所以就叫做相似三角形。

三角对应相等，三边对应成比例的两个三角形叫做相似三角形。

相似三角形的判定方法有：
平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似，
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似，
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似，
如果两个三角形的三组对应边的比相等,那么这两个三角形相似，
直角三角形相似判定定理1：斜边与一条直角边对应成比例的两直角三角形相似。

直角三角形相似判定定理2：直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

射影定理
相似三角形的性质
1.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比。

2.相似三角形周长的比等于相似比。

3.相似三角形面积的比等于相似比的平方。

九年级数学相似三角形知识点相似三角形是九年级数学中的重要知识点之一，本文将详细介绍相似三角形的概念、判定方法及性质。

一、概念相似三角形是指具有相同形状但大小不同的三角形。

两个三角形相似的条件为对应角相等，并且对应边成比例。

记作△ABC∽△DEF。

二、判定方法1.角-角-角（AA）判定法若两个三角形的三个角分别相等，则它们一定相似。

2.角-边-角（ARJ）判定法若两个三角形的一个角相等，另一个角相等，且夹在已知边之间的两边成比例，则它们一定相似。

3.边-角-边（SAS）判定法若两个三角形的两边分别成比例，夹角相等，则它们一定相似。

注意：边-边-边（SSS）判定法不能判断两个三角形是否相似，因为只有边成比例不能保证角相等。

三、性质1.对应角相等性质相似三角形的对应角相等，即∠A=∠D，∠B=∠E，∠C=∠F。

2.对应边成比例性质相似三角形的对应边成比例，即AB/DE=BC/EF=AC/DF。

其中，k为比例因子，代表两个相似三角形的对应边之比。

3.周长比例性质相似三角形的周长之比等于任意一条对应边之比。

4.面积比例性质相似三角形的面积之比等于任意一条对应边平方的比。

5.高比例性质相似三角形的高之比等于任意一条对应边之比。

四、相似三角形的应用1.测量难以直接获取的长度利用相似三角形的边比例性质，可以通过测量一些直接长度，求解难以直接获取的长度，如高度、距离等。

2.解决图像与实物的相似问题在制图中，根据相似三角形的比例性质，可以将实物缩小或放大绘制，保持图像与实物相似，从而达到简化和便于研究的目的。

3.解决间接测量问题利用相似三角形的性质，可以通过测量一些已知长度和角度，间接计算出难以直接测量的距离或高度。

4.解决图形的包含和相似问题通过相似三角形的判定方法，可以判断一个三角形是否包含在另外一个三角形中，以及两个图形是否相似。

总结：相似三角形是九年级数学中的重要知识点，通过角-角-角、角-边-角和边-角-边三种判定方法，我们可以判断两个三角形是否相似。

相似三角形知识点1 相似图形形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形. 知识点2 比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,，那么就说这两条线段的比是nmb a =，或写成n m b a ::=． 注意：在求线段比时，线段单位要统一，单位不统一应先化成同一单位．在四条线段d c b a ,,,中，如果b a 和的比等于d c 和的比，那么这四条线段d c b a ,,,叫做成比例线段，简称比例线段．注意：(1)当两个比例式的每一项都对应相同，两个比例式才是同一比例式．(2)比例线段是有顺序的，如果说a 是d c b ,,的第四比例项，那么应得比例式为：adc b =．知识点3 比例的性质基本性质：(1)bc ad d c b a =⇔=::；(2)b a c b c c a ⋅=⇔=2::． 注意：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如bc ad =，除 了可化为d c b a ::=，还可化为d b c a ::=，b a d c ::=，c a d b ::=，c d a b ::=，b d a c ::=，a b c d ::=，a c b d ::=．更比性质(交换比例的内项或外项)：()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩，交换内项，交换外项．同时交换内外项 反比性质(把比的前项、后项交换)：cd a b d c b a =⇒=． 合比性质：dd c b b a d c b a ±=±⇒=． 注意：实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间发生同样和差变化比例仍成立．如：⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a 等等．等比性质：如果)0(≠++++====n f d b nmf e d c b a ，那么b a n f d b m ec a =++++++++ ． 注意：(1)此性质的证明运用了“设k 法” ，这种方法是有关比例计算，变形中一种常用方法． (2)应用等比性质时，要考虑到分母是否为零．(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立．如：baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322；其中032≠+-f d b ． 知识点4 比例线段的有关定理平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例． 推论：(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例． (2)平行于三角形一边并且和其它两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例．定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形第三边． 知识点5 黄金分割把线段AB 分成两条线段)(,BC AC BC AC >，且使AC 是BC AB 和的比例中项，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB AC 215-=≈0.618AB ． 知识点6 相似三角形的概念对应角相等，对应边成比例的三角形，叫做相似三角形． 相似用符号“∽”表示，读作“相似于” ．相似三角形对应边的比叫做相似比(或相似系数)． 相似三角形对应角相等，对应边成比例． 注意：①对应性：即两个三角形相似时，通常把表示对应顶点的字母写在对应位置上，这样写比较容易找到相似三角形的对应角和对应边． ②顺序性：相似三角形的相似比是有顺序的． ③两个三角形形状一样，但大小不一定一样．④全等三角形是相似比为1的相似三角形．二者的区别在于全等要求对应边相等，而相似要求对应边成比例．知识点7 相似三角形的基本定理定理：平行于三角形一边的直线和其它两边(或两边延长线)相交，所构成的三角形与原 三角形相似． 定理的基本图形：用数学语言表述是： BC DE // ，ADE ∆∴∽ABC ∆．知识点8 相似三角形的等价关系(1)反身性：对于任一ABC ∆有ABC ∆∽ABC ∆．(2)对称性：若ABC ∆∽'''C B A ∆，则'''C B A ∆∽ABC ∆．(3)传递性：若ABC ∆∽C B A '∆''，且C B A '∆''∽C B A ''''''∆，则ABC ∆∽C B A ''''''∆． 知识点9 三角形相似的判定方法1、定义法：对应角相等，对应边成比例的两个三角形相似．2、平行法：平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角 形与原三角形相似．3、判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两 个三角形相似．简述为：两角对应相等，两三角形相似．4、判定定理2：如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹 角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似．5、判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这 两个三角形相似．简述为：三边对应成比例，两三角形相似．6、判定直角三角形相似的方法： (1)以上各种判定均适用．(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似．直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。