当前位置：文档之家 › 网络计划--单代号网络图详解例题

网络计划--单代号网络图详解例题

  • 格式：ppt
  • 大小：2.35 MB
  • 文档页数：111

下载文档原格式

  / 111

合集下载

网络计划--单代号网络图详解例题

网络计划--单代号网络图详解例题

【解】（1）计算最早开始时间和最早完成时间
（2）计算相邻两项工作之间的时间间隔LAGij
（3）计算工作的总时差TFi 已知计划工期等于计算工期：Tp＝Tc＝15，故终点节点⑥节 点的总时差为零，即：
其他工作总时差为：
TF6＝0
（4）计算工作的自由时差FFi 已点知的计自划由工时期差等为于：计算工期：Tp＝Tc＝15，故终点节点⑥节
最早开始时间。
ESj＝Max［ EFi ］ 或 ESj ＝Max［ ESi ＋Di ］ 式中ESi －工作 j 的各项紧前工作的
（4）网络计划的计算工期TC
即：
TC等于网络计划的终点节点n的最早完成时间EFn，
TC ＝ EFn
2.计算相邻两项工作之间的时间间隔LAGij 相邻两项工作i和j之间的时间间隔，等于紧后工作j的最早 开始时间ESj和本工作的最早完成时间EFi之差，即：
（1）网络计划的起点节点的最早开始时间为零。如起点节 点的编号为1，则：
ESi＝0（＝1） （2）工作的最早完成时间等于该工作的最早开始时间加上 其持续时间：
ESi ＝ ESj ＋ Di （3）工作的最早开始时间等于该工作的各个紧前工作的最 早完成时间的最大值。如工作的紧前工作的代号为，则：
A
H
B
F
C
G
D
作业
（3）M的紧前工序为A、B、C;N的紧前工序为 B、C、D。AMB NhomakorabeaC
D
N
作业
（4）H的紧前工序为A、B、C;N的紧前工序为B、
C、D;P的紧前工序为C、D、E。
A
H
B
C
N
D
E
P
作业
作业6：根据表中逻辑关系，绘制双代号网络图。

(完整版) 单代号网络图和双代号网络图

(完整版) 单代号网络图和双代号网络图

9
F
1
5
实用文档
H 36I 7 Nhomakorabea4．节点与工作的关系：
i
前导工作 （紧前工作）
后续工作 （紧后工作）
5．节点编号：
⑴目的： ①便于网络图时间参数的计算； ②便于检查或识别各项工作。
⑵原则： ①编号从小到大，可不连续但不允许重复编号；
②箭尾编号必须小于箭头编号，即：i＜j。 实用文档
（三） 线路
1．概念：
A、B、C三项工作，A、B结束后， C才能开始
6
A、B、C、D四项工作，A、B结束 后，C、D才能开始
A、B、C、D四项工作，A完成后， 7 C才能开始，A、B完成后，D才能
开始
A、B、C、D、E五项工作，A、B、 8 C完成后， D才能开始，B、C完成
后， E才能开始
A、B、C、D、E五项工作，A、B 9 完成后， C才能开始，B、D完成
B
E
8
3
6
7
G 5
1
A 5
00
2 5 5 13 13 5
D 10
C ６
4
F
4
11 13
6 23 23 30 30 9
8
H 7
23 23
I 4
10
34 34
实用文档
（二）节点时间参数计算 5．利用标号法确定关键线路 （1）起始节点标号为0。 （2）其他节点为双标号：（源节点，标号值）
1）标号值的确定方法: bj=max(bi+Dij)
A
2
D
4
H
1
9
3
G 6
C 3
1
6
B
3

网络计划单代号

网络计划单代号

3、绘制规则方法 (节点位置法)
单代号网络图
单代号网络图的绘制规则 1、单代号网络图的绘制规则与双代号网络图基本相同。 2、当网络图中出现多项没有紧前工作的工作节点和多
项没有紧后工作的工作节点时，应在网络图的两端分别设置 虚拟的起点节点和虚拟的终点节点。
3、当只有一项没有紧前工作的工作节点和只有一项没 有紧后工作的工作节点时，不宜再设置虚拟的起点节点和虚 拟的终点节点。
2
3 FTS=0
A
B
10 LAG=0 15
0
0
10 10
25
1
15 0
STF=25
6
E
LAG=0 20
0
25 15
28 35 25 0
7 STS=5 F
LAG=5 10 0
35 25
35 35 0
8 FTS=0 Fin
0 LAG=0
0 35 35
35 35
0
22
13
FTS=0 LAG=0
FTF=5
LAG=7 FTS=0
St
A
B
0
10
15
STF=25
6
E
15
7 STS=5 F 10
8 FTS=0 Fin 0
FTF=5
5
D
22
STS=3
单代号搭接网络图绘图规则
1、根据施工顺序建立搭接关系。 2、通常情况下要设立开始节点和结束节点。 3、一个节点代表一项工作，箭线表示工作的先后顺序 和相互的塔接关系。 4、不能出现闭和回路。
单代号塔接网络计划时间参数的计算
标注图例
ESi TFi EFi
ESj TFj EFj

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)

后续工作 C、D E、G J F F H、I —— J —— ——
精选课件
持续时间 2 3 5 3 2 4 2 1 3 4
19
A 2
2
C 5
6
D3
H1
1
4
F
5
4
E2
B 3
3
G 2
J 4
I
7
3
精选课件
20
12.3.3 单位（土建）工程网络计划的编制步骤 1．熟悉施工图纸，研究原始资料，分析施工条件； 2．分解施工过程，明确施工顺序，确定工作名称和内容； 3．拟定施工方案，划分施工段； 4．确定工作持续时间； 5．绘制网络图； 6．网络图各项时间参数计算； 7．网络计划的优化； 8．网络计划的修改与调整
A
C
j
B
D
A、B、C、D四项工作，A 7 完成后，C才能开始，A、
B完成后，D才能开始
A、B、C、D、E五项工作，
8
A、B、C完成后， D才能 开始，B、C完成后， E才
能开始
A
C
i
B jD
A
D
i
B jE
C
A、B、C、D、E五项工作， 9 A、B完成后， C才能开始，
B、D完成后， E才能开始
A B 精选课D件
4．在单目标网络图中，只允许有一个终点节点，不允许出现没 有后续工作的“尽头”节点；
5．在网络图中，不允许出现重复编号的工作；
A
1
3
B
1
A
3
B5
6．在网络图中，不允许出现没有开始节点的工作；
精选课件
11
12.3.2网络图绘制的基本方法
1．网络图的布图技巧： ⑴网络图的布局要条理清晰，重点突出；

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)
⑶计划工期：根据计算工期和要求工期确定的工期。用 Tp 表示。
2.三种工期的关系：
Tc ≤ Tp ≤ Tr
◆无要求工期时，计算工期等于计划工期。
【示例】某网络计划的有关资料如图所示，试绘制双代号网络图， 并计算各项工作的时间参数，判定关键线路。
工 作A B C D E F G H
I
J
持续时间 2 3 5 2 3Hale Waihona Puke 3 2 31314
1 支Ⅰ 2
支Ⅱ
3
支Ⅲ
绑Ⅰ 4
5 绑Ⅱ 6
浇Ⅰ
8
绑Ⅲ 7
浇Ⅱ
浇Ⅲ
9
10
4．尽量减少不必要的节点和虚箭杆 5．网络图的分解 6．网络图的排列方法： 按工种排列法、按施工段排列法、按施工层排列法。
【示例】已知各项工作之间的逻辑关系如下表所示， 试绘制双代号网络图。
工作
A
紧前工作
—
B
C
D
—
A、B
5．在网络图中，不允许出现重复编号的工作；
A
1
3
B
1
A
3
B5
6．在网络图中，不允许出现没有开始节点的工作；
12.3.2网络图绘制的基本方法
1．网络图的布图技巧： ⑴网络图的布局要条理清晰，重点突出；
⑵关键工作、关键线路尽可能布置在中心位置；
⑶密切相关的工作，尽可能相邻布置，尽量减少箭杆交叉；
⑷尽量采用水平箭杆，减少倾斜箭杆。
B
A
C
B
D
A3
C
1 B2
4 D
【示例】已知各项工作之间的逻辑关系如下表所示， 试绘制双代号网络图。
工作 A
B

单代号网络计划图的绘制与计算

单代号网络计划图的绘制与计算

在单代号网络计划图中，总时差的概念与双代号网络图完全相同。
TFi=LFi-ESi-Di=LFi-EFi=LSi-ESi 2. 局部时差FFi
由于单代号网络计划图中，无节点时间参数，工作ｉ的所有紧后工作 最早可能开始时间不一定相同，故计算工作局部时差公式稍有变化：
FFi=min{ESj}-ESi-Di=min{ESj}-EFi 3.相干时差IFi : 4.独立时差DFi: IFi=LTi-FFi
2.工作最迟必须开始时间LS
1）定义：工作的最迟必须开始时间表示工作开工不能迟于这个时间， 若迟于这个时间，将会影响计划的总工期。 2）计算：
ES
LSi=LFi-Di
i EF 工代 LS Di LF
（三）工作的各种时差的计算
1.总时差TFi
ES
i EF 工代 LS Di LF
TF FF IF DF
D 4 A 5 0 1 B 3 2 2 C 10 3 7 G 1 F 3 4 5 E 5
6
9 3 I 2 K 25 11 11 L 5
15
8
J 5
10
3．计算局部时差 工作的局部时差，是工作在不影响其所有紧后工作的最早开始时间的前提下所具有的机动时间，所以其计算公式为： （12-13）
式中，工作j为工作 i的紧后工作。 4．计算总时差 任取一项工作i与它的一项紧后工作了进行研究，分析EFi至LSj这一时间段(如图12-39所示)。EFi至ESj这一时间段为工作i与工作j之间的时间间隔LAGi-j，而ESj至LSj这 （12-14） 插入原图29
——工作ｉ的持续时间； ——工作ｉ的最早开始时间； ——工作ｉ的最早结束时间； ——工作ｉ的最迟开始时间； ——工作ｉ的最迟结束时间； ——工作ｉ的总时差； ——工作ｉ的局部时差。 如果设有虚拟的开始节点，该节点的开始时间 和工作时间均为零。1．计算工作最早开始和最 早结束时间工作 j 的最早可能开始时间 ESj ， 取决于该工作所有紧前工作 i 的完成；而 ESj 加上工作j 的持续时间就可以求得最早可能结束 时间 ESj 。公式如 下： （12-11）2．计算前 后工作时间间隔为便于计算工作时差，我们引进 时间间隔参数LAGi-j，它表示某项工作 i ，的最 早可能结束时间EFi，至其某一项紧后工作j的最 早可能开始时间ESi的时间间隔， 即 （ 12-12）3．计算局部时差工作的局部时差，是 工作在不影响其所有紧后工作的最早开始时间的 前提下所具有的机动时间，所以其计算公式 为： （12-13）式中，工作j为工作 i的紧后工作。 4．计算总时差任取一项工作i与它的一项紧后工 作了进行研究，分析EFi至LSj这一时间段(如图 12-39所示)。EFi至ESj这一时间段为工作i与工 作j之间的时间间隔LAGi-j，而ESj至LSj这一时 间段为工作j的总时差TFj。由于工作z．的总时 差是工作i在不影响其所有紧后工作j的最迟必须 开始时间的前提下所具有的机动时间，所以当工 作的完成时间处于EFi至LSj这一时间段时，不会 影响总工期， 即 （12-14） 插入原图29 图12-39 时差分析图 计算各工作 的总时差时，结束节点工作的最迟必须结束时间 等于规定工期或最早可能结束时间，从而可以确 定最后一个节点工作的总时差，然后从后向前逆 向求出各节点的总时差。 5．计算工作最迟必 须开始时间和最迟必须结束时间 由总时差与 工作最早时间和最迟时间的关系式： 可 得 （12-15） 当然 也有

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)

序号 工作之间的逻辑关系 1 A、B两项工作依次施工
2
A、B、C三项工作同时 开始施工
3
A、B、C三项工作同时 结束
网络图中的表示方法
A
B
A B C A B C
说明 A制约B的开始，B 依赖A的结束
A、B、C三项工作 为平行施工方式
A、B、C三项工作 为平行施工方式
A、B、C三项工作，A 4 结束后，B、C才能开始
B A
C
A制约B、C的开始， B、C依赖A的结束， B、C为平行施工
9
序号 工作之间的逻辑关系
5
A、B、C三项工作，A、B 结束后，C才能开始
6
A、B、C、D四项工作，A、 B结束后，C、D才能开始
A、B、C、D四项工作，A 7 完成后，C才能开始，A、
B完成后，D才能开始
A、B、C、D、E五项工作，
②非关键线路上的工作,除了关键工作之外，都称为非关键 工作;
③非关键线路有时间储备,非关键工作也有时间储备;
④在网络图中,除了关键线路之外，其余的都是非关键线路;
⑤当管理人员由于工作疏忽,拖长了某些非关键工作的持续
时间，就可能使非关键线路转变为关键线路。
8
12.3 双代号网络图的绘制
12.3.1 绘制网络图的基本规则 1．必须正确表达已定的逻辑关系;
它表示该节点所有前导工作最迟必须结束的时间,它也限制 其后续工作的开始。
LTi min LTj Di j
23
【示例】计算下图节点时间参数。
13 13
23 25
B
E
8
3
6
7
G 5
1
A 5
00
2 5 5 13 13 5

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)

单代号网络图表示法:
编号 名称 时间
双代号网络图表示法:
i 工作名称 持续时间
j
2
13.1.3 网络计划技术的基本原理
1．利用网络图的形式表达一项工程中各项工作的先后顺序及逻辑 关系;
2．通过对网络图时间参数的计算,找出关键工作、关键线路;
3．利用优化原理,改善网络计划的初始方案，以选择最优方案;
6
13.2.3 线路
1．概念:
指网络图中从起点节点开始,沿箭线方向连续通过一系列箭线 与节点，最后到达终点节点的通路。
2．线路时间: 它是指线路所包含的各项工作持续时间的总和。
A
2
D
4
H
1
9
3
G 6
C 3
1
6
3．线路种类:
B
3
2
F 1
5
I 7
⑴关键线路: 在网络图中线路持续时间最长Байду номын сангаас线路。
⑵非关键线路:
4．在网络计划的执行过程中进行有效的控制和监督,保证合理地 利用资源，力求以最少的消耗获取最佳的经济效益和社会效益.
13.1.4 网络计划技术的优缺点
1．能全面而明确地反映出各项工作之间开展的先后顺序和它们之 间的相互制约、相互依赖的关系;
2．可以进行各种时间参数的计算;
3．能在工作繁多、错综复杂的计划中找出影响工程进度的关键工 作和关键线路,便于管理者抓住主要矛盾，集中精力确保工 期，避免盲目施工;
它表示该节点所有前导工作最迟必须结束的时间,它也限制 其后续工作的开始。
LTi min LTj Di j
23
【示例】计算下图节点时间参数。
13 13
23 25

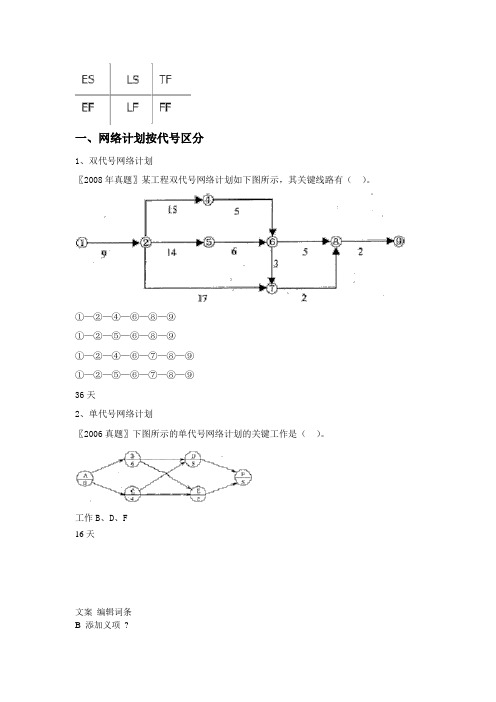
单代号与双代号网络计划图

单代号与双代号网络计划图

一、网络计划按代号区分1、双代号网络计划〖2008年真题〗某工程双代号网络计划如下图所示，其关键线路有（）。

①—②—④—⑥—⑧—⑨①—②—⑤—⑥—⑧—⑨①—②—④—⑥—⑦—⑧—⑨①—②—⑤—⑥—⑦—⑧—⑨36天2、单代号网络计划〖2006真题〗下图所示的单代号网络计划的关键工作是（）。

工作B、D、F16天文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

现在指的是公司或企业中从事文字工作的职位，就是以文字来表现已经制定的创意策略。

文案它不同于设计师用画面或其他手段的表现手法，它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程，多存在于广告公司，企业宣传，新闻策划等。

基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代，文案的称呼主要用在商业领域，其意义与中国古代所说的文案是有区别的。

在中国古代，文案亦作" 文按"。

公文案卷。

《北堂书钞》卷六八引《汉杂事》:"先是公府掾多不视事，但以文案为务。

"《晋书·桓温传》:"机务不可停废，常行文按宜为限日。

" 唐戴叔伦《答崔载华》诗:"文案日成堆，愁眉拽不开。

"《资治通鉴·晋孝武帝太元十四年》:"诸曹皆得良吏以掌文按。

"《花月痕》第五一回:" 荷生觉得自己是替他掌文案。

"旧时衙门里草拟文牍、掌管档案的幕僚，其地位比一般属吏高。

《老残游记》第四回:"像你老这样抚台央出文案老爷来请进去谈谈，这面子有多大!"夏衍《秋瑾传》序幕:"将这阮财富带回衙门去，要文案给他补一份状子。

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)

持续时间 2 3 5 3 2 4 2 1 3 4
19
A 2
2
C 5
6
D3
H1
1
4
F
5
4
E2
B 3
3
G 2
J 4
I
7
3
20
12.3.3 单位（土建）工程网络计划的编制步骤 1．熟悉施工图纸,研究原始资料，分析施工条件; 2．分解施工过程,明确施工顺序，确定工作名称和内容; 3．拟定施工方案,划分施工段; 4．确定工作持续时间; 5．绘制网络图; 6．网络图各项时间参数计算; 7．网络计划的优化; 8．网络计划的修改与调整
②形成条件:
ESi j ETi
h
i
FF i j
D i j
ES jk ETj
j
k
③计算公式:
FFij ETj ETi Dij ETj (ETi Dij ) ETj EFij
FF i j
27
13.4.4 关键工作和关键线路的确定 在网络计划中,总时差最小的工作称为关键工作。
【示例】计算下图各项时间参数。
⑶计划工期: 根据计算工期和要求工期确定的工期。用 Tp 表示。
2.三种工期的关系:
Tc ≤ Tp≤ Tr
◆无要求工期时,计算工期等于计划工期。
29
【示例】某网络计划的有关资料如图所示，试绘制双代号网络图， 并计算各项工作的时间参数，判定关键线路。
工 作A B C D E F G H
I
J
持续时间 2 3 5 2 3 3 2 3
5．在网络图中,不允许出现重复编号的工作;
A
1
A
3
1
3
B
B5

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)

A 2
2
C 5
6
D3
H1
1
4
F
5
4
E2
B 3
3
G 2
J 4
I
7
3
12.3.3 单位（土建）工程网络计划的编制步骤 1．熟悉施工图纸，研究原始资料，分析施工条件； 2．分解施工过程，明确施工顺序，确定工作名称和内容； 3．拟定施工方案，划分施工段； 4．确定工作持续时间； 5．绘制网络图； 6．网络图各项时间参数计算； 7．网络计划的优化； 8．网络计划的修改与调整
单代号网络图表示法：
编号 名称 时间
双代号网络图表示法：
i 工作名称 持续时间
j
13.1.3 网络计划技术的基本原理
1．利用网络图的形式表达一项工程中各项工作的先后顺序及逻辑 关系；
2．通过对网络图时间参数的计算，找出关键工作、关键线路；
3．利用优化原理，改善网络计划的初始方案，以选择最优方案；
4．在网络计划的执行过程中进行有效的控制和监督，保证合理地 利用资源，力求以最少的消耗获取最佳的经济效益和社会效益.
13.1.4 网络计划技术的优缺点 1．能全面而明确地反映出各项工作之间开展的先后顺序和它们之
间的相互制约、相互依赖的关系； 2．可以进行各种时间参数的计算； 3．能在工作繁多、错综复杂的计划中找出影响工程进度的关键工
作和关键线路，便于管理者抓住主要矛盾，集中精力确保工 期，避免盲目施工；
4．能够从许多可行方案中，选出最优方案；
正确的表达它们之 间的逻辑关系
引出虚工作 i j
正确的表达它们之 间的逻辑关系
2．网络图中，严禁出现循环回路；
2
2
2
4

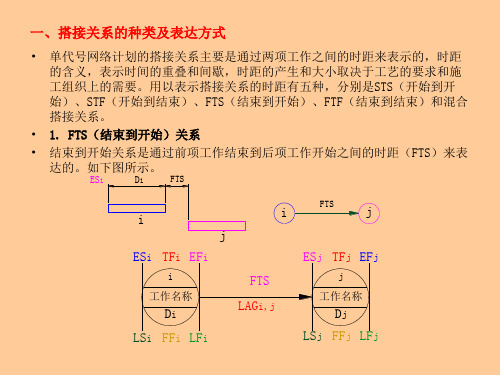
单代号搭接网络图实例讲解

单代号搭接网络图实例讲解

E 按STS关系：
S
j

ESi
STSijຫໍສະໝຸດ LS j LSi STSij
按FTF关系：EFj EFi FTFij
LFj LFi FTFij
如，某修筑道路工程，工作i是修筑路肩，工作j是修筑路面层，在组织这
两项工作时，要求路肩工作至少开始一定时距STS=4以后，才能开始修筑路
面层；而且面层工作不允许在路肩工作完成之前结束，必须延后于路肩完
FTF
ESi TFi EFi
ESj TFj EFj
i j
i 工作名称
Di LSi FFi LFi
FTF LAGi,j
j 工作名称
Dj LSj FFj LFj
• FTF搭接关系的时间参数计算式为：ESj＝ESi+Di+FTFi,j–Dj； • 如基坑排水工作结束一定时间后，浇注砼工作才能结束。
5d 基坑排水15d
例如：混凝土沉箱码头工程，沉箱在岸上预制后，要求静置一段养护存放的 时间，然后才可下水沉放。
• 2. STS（开始到开始）关系
• 开始到开始关系是通过前项工作开始到后项工作开始之间的时距（STS）
来表达的,表示在i工作开始经过一个规定的时距（STS）后，j工作才能开
始进行。
i j
STS
ESi TFi EFi
一、搭接关系的种类及表达方式
• 单代号网络计划的搭接关系主要是通过两项工作之间的时距来表示的，时距 的含义，表示时间的重叠和间歇，时距的产生和大小取决于工艺的要求和施 工组织上的需要。用以表示搭接关系的时距有五种，分别是STS（开始到开 始）、STF（开始到结束）、FTS（结束到开始）、FTF（结束到结束）和混合 搭接关系。

网络计划 单代号网络图详解例题共113页文档

网络计划 单代号网络图详解例题共113页文档

网络计划 单代号网络图详解例题
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯

46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特

单代号网络图和双代号网络图(习题)

单代号网络图和双代号网络图(习题)
5
3．节点种类:
i
i-j工作的 结束节点
j
i-j工作的 开始节点
4．节点与工作的关系:
j-k工作的 开始节点
j-k工作的 结束节点
k
i
前导工作 （紧前工作）
5．节点编号: ⑴目的: ①便于网络图时间参数的计算; ②便于检查或识别各项工作。
后续工作 （紧后工作）
⑵原则: ①不允许重复编号;
②箭尾编号必须小于箭头编号,即:i＜j。
它表示该节点所有前导工作最迟必须结束的时间,它也限制 其后续工作的开始。
LTi min LTj Di j
23
【示例】计算下图节点时间参数。
13 13
23 25
B
E
8
3
6
7
G 5
1
A 5
00
2 5 5 13 13 5
D 10
C ６
4
F
4
11 13
6 23 23 30 30 9
8
H 7
23 23
—
B
C
D
—
A、B
B
A
C
B
D
A3
C
1 B2
4 D
16
【示例】已知各项工作之间的逻辑关系如下表所示, 试绘制双代号网络图。
工作 A
B
C
D
E
F
紧前工作 —
—
—
A、B A、B、C D、E
A2 1B 3 D 5 F 6
C4E
17
【示例】已知各项工作之间的逻辑关系如下表所示, 试绘制双代号网络图。
工作 A
B
B A
C
A制约B、C的开始， B、C依赖A的结束， B、C为平行施工

网络图专题(非常全面,带案例)

网络图专题(非常全面,带案例)

1.关键线路与非关键线路 ：在一项计划的所有线路中，持续时间最长的线路，其对整 个工程的完工起着决定性作用，称为关键线路，其余线路称为非关键线路。关键线路 的持续时间即为该项计划的工期。关键线路宜用粗箭线、双箭线或彩色箭线标注，以 突出其在网络计划中的重要位置
A
D
F
2
4
2
2
2
1
2C
6
B 3
3
E
G
5
8
最迟完成时 在不影响工程工期的条件下，本工
间
作必须完成的最迟时刻
9
总时差
在不影响总工期的前提下，本工作 可以利用的机动时间
在不影响其紧后工作最早开始时间 10 自由时差 的前提下，本工作可以利用的机动
时间
表示方法
双单
ti-j
ti
Tc
Tr
Tp
ESi-j ESi
EFi-j EFi
LSi-j LSi
LFij
8、双代号网络图中应只有一个起点节点和一个终点节点（多目标网络计划除外）； 而其他所有节点均应是中间节点。如图所示。
（三）绘制步骤
（1）明确各项工作紧后工作 ； （2）根据逻辑关系，在满足绘图规则的前提下开始绘制； （3）检查
【例题1】：根据表中逻辑关系，绘制双代号网络 图。
工作 A
B
C
D
E
F
工作
A
B
C
D
E
F
紧前
-
-
-
A、B
B
C、D、 E
时间
3
3
3
8
5
4
【例题2】：根据表中逻辑关系，绘制双代号网络 图。

网络计划图例题

网络计划图例题

网络计划图例题(总4页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除节点的相关计算1.结点最早开始时间①当进入结点J的箭线只有一条时：ET(j)=ET(i)+t(i,j)②当进入结点J的箭线有多条时：ET(j)=max{ET(i k)+t(i k,j)}2.节点最迟结束时间①若节点i的后面只有一条箭线时：LT(i)=LT(j)-t(i,j)②若节点i的后面有多条箭线时：LT(i)=min{LT(j k)-t(i,j k)}3.节点时差：S（i）=LT（i）-ET（ i ）=最迟发生-最早发生作业的相关计算1.作业最早开始时间ES（i,j）=ET（i）或ES（i,j）=max{ES(h,i)+t(h,i)}2.作业最早结束时间EF（i,j）=ES (i,j)+t(i,j)3.作业最迟结束时间LF（i,j）=LT（j）1.作业最迟开始时间LS（i,j）=LF（I,j）- t(i,j)=LT（j）- t(i,j)5.作业时差1)作业总时差：不影响总工期的前提下，可以利用的机动时间ST(i, j)=LS(i, j)-ES(i, j)=最迟开始-最早开始=LF(i, j)-EF(i, j)=最迟结束-最早完成=LT( j)-ET(i)- t(i, j)1)作业单时差：不影响下一个作业的机动时间。

S(i, j)=ES(j, k)-EF(i, j)=ES(j, k)-ES(i, j)-t (i, j)=ET(j)-ET(i)-t (i, j)关键作业：总时差为零的作业称为关键作业。

关键路线：把所有关键作业连接起来，所得到的从始点到终点的路线。

路线时差=关键路线长度-该路线长度。

网络计划--单代号网络图详解例题共113页文档

网络计划--单代号网络图详解例题共113页文档

37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
40、人类法律，事物有规律，这是不 容忽视 的。— —爱献 生
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
网络计划--单代号网络图详解例题
36、如果我们国家的法律中只有某种 神灵， 而不是 殚精竭 虑将神 灵揉进 宪法， 总体上 来说， 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日，便是暴政兴起之 时。— —威· 量的。 ——菲 力普斯 39、一个判例造出另一个判例，它们 迅速累 聚，进 而变成 法律。 ——朱 尼厄斯

单代号搭接网络计算示例

单代号搭接网络计算示例
因为搭接网络计划存在着比较复杂的搭接关系特别是存在着stsstf搭接关系的节点之后使得其最后的终点节点的最早完成时间有可能小于前面有些节点的最早完成时间
某工程单代号搭接施工网络计划如图所示。 某工程单代号搭接施工网络计划如图所示。工程负责人 审查后发现，该工程施工网络计划的绘制有缺陷， 审查后发现，该工程施工网络计划的绘制有缺陷，并缺少工 的六个时间参数，建议工程计划人员修改。 作H的六个时间参数，建议工程计划人员修改。
ES TF EF
工作代号 工作名称 持续时间
时距 时间间隔
0
LS FF LF
图例
STF=6 3 0 0 1 A 5 0 5
3 3 B 7 0
7 FTF=10 FTS=3 10 10 3 22 7 D 12 4 17 29
2
0
0
0 0 0 St 0 0 0
3 17 9 E 15 0 5 20 FTF=2 STS=3
工作H (2) 工作H的最早开始时间和最早完成时间 EFE=17 ESH=max ESD+ STSD,H=10+3=13 EFD+ FTFD,H- DH=22+2-12=12 ESG+ STFG,H- DH=7+10-12=5 EFH= ESH+ DH=17+12=29 (3) A、C和G工作应作为重点控制对象，因为他们 工作应作为重点控制对象， 为关键工作。 为关键工作。 =17
参考答案： 参考答案： （1）该网络计划中工作B与起点节点没有建立直接或间接 该网络计划中工作B 的联系。因为工作B的最早开始时间为0 但工作B只与工作A 的联系。因为工作B的最早开始时间为0，但工作B只与工作A有 开始结束关系， 开始结束关系，不符合单代号搭接网络图中只有一个节点的规 则。 该施工网络计划中应设一个虚拟的终点节点。因为搭接网 该施工网络计划中应设一个虚拟的终点节点。 络计划存在着比较复杂的搭接关系，特别是存在着STS、STF搭 络计划存在着比较复杂的搭接关系，特别是存在着STS、STF搭 STS 接关系的节点之后，使得其最后的终点节点的最早完成时间有 接关系的节点之后， 可能小于前面有些节点的最早完成时间。 可能小于前面有些节点的最早完成时间。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

工作 A
B
C
D
紧前 工作
-
-
A
A
E
F
B
C、D
工作 A
B
C
D
紧前 工作
-
-
A
A
C 4
E
F
B
C、D
A
1 B
D
F
2
5
6
E 3
作业
作业9：根据表中逻辑关系，绘制双代号网络图。
工作 A
B
C
D
E
F
紧前 工作
-
A
A
B
B、C D、E
时间 2
5
3
4
8
5
工作 A
B
C
D
E
F
紧前 工作
-
A
A
B
B、C D、E
时间 2
5
770 15 15 0
E(8)
TP＝TC＝20天
作业
作业10：根据表中逻辑关系，绘制双代号网络图。
工作 A B C D E F G H
紧前 工作
-
A
B
B
B C、D C、E F、G
时间 1 3 1 6 2 4 2 1
工作 A B C D E F G H
紧前 工作
-
A
B
B
B C、D C、E F、G
时间 1 3 1 6 2 4 2 1
4.3单代号网络计划
4.3.1 单代号网络图的组成
编号 工作名称
时间
编号 工作名称 持续时间
节点表示工作；箭线表示工序之间的逻辑关系。
4.3.2单代号网络图的绘制
绘制原则、绘制方法与双代号网络图基本相同。
4.3.3 单代号网络计划时间参数计算
1．单代号网络计划时间参数的标注形式
ES i TFi EFi
ES TF EF
ESi , EFi
i
工作名称
LAGi, j
Di FF
关 键
TFi
FFi
LS
LF
线
路
LSi , LFi
单代号网络计划时间参数的计算过程:
(一)计算工作的最早开始时间和最早完成时间
工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始， 顺着箭线方向按节点编号从小到大的顺序依次进行。其计算步骤如下：
最早开始时间。
ESj＝Max［ EFi ］ 或 ESj ＝Max［ ESi ＋Di ］ 式中ESi －工作 j 的各项紧前工作的
❖（4）网络计划的计算工期TC
即：
TC等于网络计划的终点节点n的最早完成时间EFn，
TC ＝ EFn
2.计算相邻两项工作之间的时间间隔LAGij 相邻两项工作i和j之间的时间间隔，等于紧后工作j的最早 开始时间ESj和本工作的最早完成时间EFi之差，即：
i
工作名称
LAGi, j
Di FF
关 键
TFi
FFi
LS
LF
线
路
LSi , LFi
❖6.关键工作和关键线路的确定
（1）关键工作：总时差最小的工作是关键工作。
（2）关键线路的确定按以下规定：从起点节点开始到终点 节点均为关键工作，且所有工作的时间间隔为零的线路为关 键线路。
【例1】已知单代号网络计划如图所示，若计划工期等于计 算工期，试计算单代号网络计划的时间参数，将其标注在网 络计划上；并用双箭线标示出关键线路。
三、单代号网络图的绘图规则
❖（1）单代号网络图必须正确表达已定的逻辑关系。 ❖（2）单代号网络图中，严禁出现循环回路。 ❖（3）单代号网络图中，严禁出现双向箭头或无箭头的连 线。 ❖（4）单代号网络图中，严禁出现没有箭尾节点的箭线和 没有箭头节点的箭线。 ❖（5）绘制网络图时，箭线不宜交叉，当交叉不可避免时， 可采用过桥法或指向法绘制。
（1）工作i的最迟开始时间LSi等于该工作的最早开始时间 ESi加上其总时差TFi之和，即：
LSi ＝ ESi ＋ TFi （2）工作的最迟完成时间LFi等于该工作的最早完成时间EFi 加上其总时差TFi之和，即：
LFi ＝ EFi ＋ TFi
单代号网络计划时间参数的计算
ES TF EF
ESi , EFi
二、单代号网络图的基本符号 ❖1.节点 ❖单代号网络图中的每一个节点表示一项工作，节点宜用圆 圈或矩形表示。节点所表示的工作名称、持续时间和工作 代号等应标注在节点内，如图所示。
❖单代号网络图中的节点必须编号。编号标注在节点内，其 号码可间断，但严禁重复。箭线的箭尾节点编号应小于箭 头节点的编号。一项工作必须有惟一的一个节点及相应的 一个编号。
11110
440
2
3
B(3) 4 4
495 5 10 0
C(1)
4 10 6 6 12 0
E(2)
5 10 5 5 10 5
4 5 10
5 12 7 5 12 1
14 14 0 15 15
15 15 0
7
8
14 14 H(1)
6 12 6
8 14 6
6
G(2)
6 12
TP＝TC＝15天
作业：绘制双代号网络图； 复习时间参数有关内容。
D(6)
5 F(4)
1
2
3
4
A(1)
B(3)
C(1)
7
8
H(1)
E(2) 6 G(2)
工作 A B C D E F G H
紧前 工作
-
A
B
B
B C、D C、E F、G
时间 1 3 1 6 2 4 2 1
10 10
D(6) 5 F(4)
00
11
1
2
3
A(1)
B(3) 4 4 C(1)
4 5 10
15 15
A
H
B
F
C
G
D
作业
（3）M的紧前工序为A、B、C;N的紧前工序
为B、C、D。
A
M
B
C
D
N
作业
（4）H的紧前工序为A、B、C;N的紧前工序 为B、C、D;P的紧前工序为C、D、E。
A
H
B
C
N
D
E
P
作业
作业6：根据表中逻辑关系，绘制双代号网络图。
工作 A
B
C
D
E
F
紧前 工作
-
-
-
A、B
B C、D、E
❖ （6）单代号网络图只应有一个起点节点和一个终点节点；当网络图中有多项 起点节点或多项终点节点时，应在网络图的两端分别设置一项虚工作，作为 该网络图的起点节点（）和终点节点（），如图所示。
❖ 单代号网络图的绘图规则大部分与双代号网络图的绘图规则相同，故不再进 行解释。
四、单代号网络计划时间参数的计算
工作 A
B
C
D
E
F
紧前 工作
-
-
-
A、B
B C、D、E
A
D 3
B
E
F
1
2
4
5
C
作业
作业7：根据表中逻辑关系，绘制双代号网络图。
工作 A
B
C
D
E
F
紧前 工作
-
A
A
A B、C、D D
工作 A
紧前 工作
-
B
C
D
E
F
A
A
A B、C、D D
B
E
5
A
C
1
2
4
6
D
F
3
作业
作业8：根据表中逻辑关系，绘制双代号网络图。
(1)网络计划起点节点所代表的工作，其最早开始时间未规定时取值为零。 (2)工作的最早完成时间应等于本工作的最早开始时间与其持续时间之和。 (3)其他工作的最早开始时间应等于其紧前工作最早完成时间的最大值。 (4)网络计划的计算工期等于其终点节点所代表的工作的最早完成时间。 (二)计算相邻两项工作之间的时间间隔
（5）计算工作的最迟开始时间LSi和最迟完成时间LFi
❖ （6）关键工作和关键线路的确定 ❖ 根据计算结果，总时差为零的工作：A、C、E为关键工作； ❖ 从起点节点①节点开始到终点节点⑥节点均为关键工作，且所有工作
之间时间间隔为零的线路：①－③－⑤－⑥为关键线路，用双箭线标 示在下图中。
2．单代号网络计划时间参数的计算： ⑴工作最早时间的计算：
ES1 0
ES j max ESi Di EFj ES j D j ES j max EFi
⑵工作最迟时间的计算：
LFn T
或
LFi min LS j
LSi LFi Di
⑶时差计算：
LFn ESn
TFi LSi ESi
FFi min ES j EFi
单代号网络计划时间参数的计算
7
8
14 14 H(1)
6
E(2)
G(2)
6 12
TP＝TC＝15天
工作 A B C D E F G H
紧前 工作

-
A
B
B
B C、D C、E F、G
时间 1 3 1 6 2 4 2 1
00000 110
1 A(1)
440 10 10 0
D(6)
10 10 10 10 0 14 14 0
5 F(4)
❖【解】（1）计算最早开始时间和最早完成时间
❖（2）计算相邻两项工作之间的时间间隔LAGij
❖（3）计算工作的总时差TFi 已知计划工期等于计算工期：Tp＝Tc＝15，故终点节点⑥节 点的总时差为零，即：

相关主题