刍甍、羡除、刍童及楔形四棱台的体积公式

四棱台体积公式：①、[S上+S下+√(S上×S下)]*h /3 （可以用于四棱锥）[上面面积+下面面积+根号(上面面积×下面面积)]×高÷2②、(S上+S下)*h/2 （不能用于四棱锥）(上面面积+下面面积)x高÷2第②个最简便的公式，可以把正方体当作四棱台验证。

注意：如果把四棱锥可以看成上面面积为0的四棱台，第①个公式仍然可以用，但是四棱锥不能用第②个公式，切记！！！！！！！！。

拟棱台：对于一个多面体，如果有两个面互相平行，而其余的面均为顶点全在这两个平行面上的三角形、平行四边形或梯形，这样的多面体叫拟棱台。

若上下底面和中截面的面积分别是S1、S2、S0，高为H，则体积V=1/6(s1+s2+4s0)H正四棱台体积V=底面积S×高H圆锥体体积=底×高÷3长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15评论(14) | 80 12012-08-12 16:31 我只是碗馄饨| 四级体积的话叫棱台S1=上面的面积S2=下面的面积H是高V是体积V=（S1+S2+根号（S1×S2））×H ÷3评论(6) | 52 22012-05-08 23:50 绿锦小学| 十三级答：梯形是平面图形，没有体积，只有面积。

四棱台体积公式及推导过程
四棱台一种特殊台梯形体（好比正方形与长方形），即底面与顶面均为相似的四边形，侧面都是梯形，四条棱的延长线能够交汇于一点的一种台体。

它的体积计算公式是V=(S1+4S0+S2)*H/6。

四棱台体积公式正四棱台
V=H/3[S1+S2+√(S1S2)]
注：非通用公式,（s1是上底的面积，s2是下底的面积）
通用公式
V=[S1+4S0+S2]*H/6
注：上底面积S1，下底面积S2，中截面面积S0，高H，此体积公式多一个参量S0——中截面积,它有“万能公式”的美誉。

四棱台体积公式推导由相似三角形可得b/h1=a/(h1+h2)，所以h1=bh2/(a-b).
V台=a^2(h1+h2)/3-b^2*h1/3
=h1(a^2-b^2)/3+h2*a^2/3
=(a+b)*b*h2/3+a^2*h2/3
=（a^2+b^2+ab）*h2/3
四棱台体积计算公式①[S上+S下+√(S上×S下)]*h /3 （可以用于四棱锥）专[上面面积+下面面积+根号下(上面面积×属下面面积)]×高÷3 。

②(S上+S下)*h/2 （不能用于四棱锥）(上面面积+下面面积)x高÷2 。

注意：第②个最简便的公式可以把正方体当作四棱台验证2把四棱锥看成上面面积为0的四棱台适用于第①个公式但是四棱锥不能用第②个公式。

刍甍、羡除、刍童及楔形四棱台的体积公式
甘志国
【期刊名称】《新高考（高二数学）》
【年(卷),期】2017(000)009
【摘要】《九章算术》是中国古代数学的经典著作，里面提及了很多有趣但十分拗口的立体图形的名词，其中最有名气的，莫过于“鳖膈”了（请大家移步常老师的文章《从鳖膈谈起》）．除此之外，如阳马、刍甍、羡除、刍童等．
【总页数】4页(P33-36)
【作者】甘志国
【作者单位】北京丰台二中
【正文语种】中文
【相关文献】
1.古巴比伦正四棱台体积公式古证复原
2.《缀术》中的“刍甍,方亭之问”初探
3.刍甍的应用
4.正四棱台体积公式的再探索和教学尝试
5.学生的想法出乎我的意料--《正四棱台体积公式》教学尝试及所得
因版权原因，仅展示原文概要，查看原文内容请购买。

4棱台体积公式4棱台是个常见的几何体，它有数学家陈立群先生在1758-1838年研究出来的一个重要的几何定理。

根据这一定理，4棱台的体积是可以用公式来表示的，公式如下：V = ah/3，其中V表示4棱台的体积，a表示4棱台的底面积，h表示4棱台的高。

4棱台的底面积与其形状有关，通常4棱台的底面是正方形或者长方形，正方形底面积为a=a×a，而长方形底面积为a=a1×a2。

4棱台的高h与其形状也有关，通常在普通情况下，4棱台的高指的是其底部和顶部之间的距离。

一般来说，使用这个公式计算4棱台体积是非常方便的，不需要太多的数学知识就可以求出4棱台的体积。

例如，一个4棱台的底面积是4m×4m，高是2m，根据该公式，4棱台的体积可以得到：V=4×4×2/3=16/3，即16/3。

因此，4棱台体积公式：V=ah/3，上述公式可以用来计算4棱台体积，应用非常广泛。

4棱台是数学中一种重要的几何体，其体积公式更是几何学中非常常见的一种计算方法，常用于各种工程实践中。

在建筑工程中，4棱台的体积常常被用来计算建筑物的体积，因为4棱台是一种容易计算出体积的几何体，可以省去很多计算量。

比如说，一栋建筑的底面是正方形，则可以使用4棱台体积公式，根据该公式计算出这栋建筑的体积，从而可以更加准确地掌握建筑物的体积。

在石油勘探与储存工程中，也常常涉及到4棱台体积公式的使用，比如储气和水的储量计算。

因为4棱台体积公式可以准确计算出储气和水仓的容量，这既能够帮助人们更准确地估算储气和水的量，也能更好地控制人们的储量。

另外，4棱台体积公式在机械行业中也有着重要的应用，比如它可以用来求取各种金属零件的体积，这样就可以更准确地确定零件的重量，为机械行业的发展和提高工作效率提供了有力的支撑。

总的来说，4棱台体积公式在各种工程实践中都有着广泛的应用，是一个十分重要的数学公式。

其精准的计算方式在各种领域，特别是在建筑工程、石油勘探、机械行业等领域具有重要的意义，为现代人解决各种工程计算问题提供了极大的帮助。

不规则四棱台体积公式计算公式在我们的数学世界里，不规则四棱台的体积计算可是个有趣但又有点小挑战的问题。

先来说说啥是四棱台。

想象一下，有一个正四棱锥，就像金字塔那种，不过底面是正方形的。

然后呢，从它的顶部沿着平行于底面的方向切一刀，切下来的上面那部分就是四棱台啦。

那不规则四棱台又是什么呢？简单说，就是这个四棱台的上下底面不是那种规规矩矩的正方形或者长方形，形状有点“放飞自我”。

要计算它的体积，咱们有个公式：V = 1/3 × h × (S₁ + S₂ + √(S₁ ×S₂)) 。

这里的 V 就是体积，h 是四棱台的高，S₁和 S₂分别是上下底面的面积。

我记得有一次，我在给学生们讲这个知识点的时候，有个调皮的小家伙举手问我：“老师，这公式咋来的呀？感觉好复杂！”我笑着跟他们说：“别着急，咱们一步步来。

”我拿了个模型出来，就是一个简单的四棱台模型。

我先让他们观察这个模型的形状，然后我把它想象成是由一个大的四棱锥切掉上面一个小的四棱锥形成的。

接着，咱们分别算出大四棱锥和小四棱锥的体积。

大的四棱锥体积V₁ = 1/3 × h₁ × S₁，小四棱锥体积 V₂ = 1/3 × h₂ × S₂。

这里要注意啦，因为是从大的上面切下来的小的，所以 h₁ - h₂就是咱们要求的四棱台的高 h 。

然后通过一系列的推导，就能得出咱们前面说的那个公式啦。

学生们听我这么一讲，好像有点明白了，但还是有点迷糊。

我就让他们自己动手，用卡纸做几个简单的四棱台模型，标上尺寸，然后按照公式去计算体积，再和实际测量的体积对比一下。

嘿，这一招还真管用！他们通过自己动手，对这个公式的理解更深刻了。

回到这个公式，咱们在实际运用的时候，得先准确地求出上下底面的面积。

比如说，如果上底面是个不规则的四边形，咱们可以把它分成几个三角形或者梯形，分别求出面积再相加。

下底面也是同样的道理。

四棱台体积计算公式四棱台体积公式：①、[S上+S下+√(S上×S下)]*h /3 （可以用于四棱锥）[上面面积+下面面积+根号(上面面积×下面面积)]×高÷2②、(S上+S下)*h/2 （不能用于四棱锥）(上面面积+下面面积)x高÷2第②个最简便的公式，可以把正方体当作四棱台验证。

注意：如果把四棱锥可以看成上面面积为0的四棱台，第①个公式仍然可以用，但是四棱锥不能用第②个公式，切记。

拟棱台：对于一个多面体，如果有两个面互相平行，而其余的面均为顶点全在这两个平行面上的三角形、平行四边形或梯形，这样的多面体叫拟棱台。

若上下底面和中截面的面积分别是S1、S2、S0，高为H，则体积V=1/6(s1+s2+4s0)H正四棱台体积V=底面积S×高H圆锥体体积=底×高÷3长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6 圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12 (母线是圆弧形,圆心是桶的中心) V＝πh(2D2＋Dd＋3d2/4)/15 评论(14) | 80 12012-08-12 16:31 我只是碗馄饨| 四级体积的话叫棱台S1=上面的面积S2=下面的面积H是高V是体积V=（S1+S2+根号（S1×S2））×H ÷3评论(6) | 52 22012-05-08 23:50 绿锦小学| 十三级答：梯形是平面图形，没有体积，只有面积。

一节基于数学史的教学课例：正四棱台的体积公式
朱哲;张维忠
【期刊名称】《中学数学教学参考：教师版》
【年(卷),期】2004(000)003
【摘要】对中西古代数学文化的深入研究，特别是这种历史的挖掘，目的还是为了指向现实、着眼于未来。

本文给出的一节基于数学史的教学课例，正是笔者设想的在数学教育中通过数学史的渗透，在传统与现代之间架起一座桥梁，从而实现数学教育的现代化。

【总页数】4页(P8-11)
【作者】朱哲;张维忠
【作者单位】浙江师范大学数理学院
【正文语种】中文
【中图分类】G633.63
【相关文献】
1.古巴比伦正四棱台体积公式古证复原
2.刍甍、羡除、刍童及楔形四棱台的体积公式
3.正棱台体积和侧面积公式及应用
4.正四棱台体积公式的再探索和教学尝试
5.学生的想法出乎我的意料--《正四棱台体积公式》教学尝试及所得
因版权原因，仅展示原文概要，查看原文内容请购买。

四棱台体积公式及推导过程四棱台是一种特殊的多面体，由一个正方形底面和四个三角形侧面组成。

为了计算四棱台的体积，我们首先需要了解四棱台的基本特征，并推导出体积公式。

四棱台的特征：1.四棱台由一个正方形底面和四个三角形侧面组成。

2.四个侧面的顶点会汇集到一个顶点，这个顶点被称为四棱台的顶点。

3.正方形底面的边长被称为底边长，正方形底面的对角线被称为底对角线。

4.顶点到底边的距离被称为高。

推导四棱台体积的公式：假设四棱台的底边长为a，底对角线长为d，高为h。

首先，我们可以计算出正方形底面的面积S1，正方形的面积公式为：S1=a^2接下来，我们需要计算每个三角形侧面的面积。

我们可以将四棱台看作是由四个等腰三角形组成的。

每个等腰三角形的底边长为a，高为h。

那么等腰三角形的面积S2为：S2=(1/2)*a*h由于四棱台共有四个等腰三角形，所以四个等腰三角形的总面积S3为：S3=4*S2=2*a*h接下来，我们需要计算出四棱台的总面积S4四棱台的总面积S4可以通过底面积S1加上四个三角形侧面的面积S3来得到：S4=S1+S3=a^2+2*a*h最后，我们可以得到四棱台的体积V。

我们知道，四棱台的体积V可以通过底面积S1乘以高h来得到：V=S1*h将S1的表达式带入，可以得到：V=(a^2)*h综上所述，四棱台的体积V的公式为：V=(a^2)*h这就是四棱台体积的推导过程和公式。

【注意】在具体计算中，需要确保所有的长度单位一致。

此外，如果给定的是底边长和底对角线长，可以通过勾股定理计算出高的长度。

如果给定的是底边长和高的长度，可以通过勾股定理计算出底对角线的长度。

刍甍羡除刍童及楔形四棱台的体积公式一、刍甍的体积公式：刍甍是一种用土石建筑而成的燃烧炉，由燃烧室和煤气出口组成。

它的体积公式与燃烧室的形状和尺寸有关。

假设燃烧室的形状为一个长方体，长度为L，宽度为W，高度为H。

刍甍的体积公式可以表示为：V=L×W×H二、羡除的体积公式：羡除是一种类似刍甍的燃烧炉，常用于炼铁过程中。

它的燃烧室呈长方体形状，顶部有一段斜坡。

根据燃烧室的形状和尺寸，羡除的体积公式可以表示为：V=L×W×H+A×h×(L+W)/2其中，A表示斜坡的宽度，h表示斜坡的高度。

三、刍童的体积公式：刍童是一种类似刍甍的燃烧炉，常用于炼钢过程中。

它的燃烧室呈圆柱体形状，顶部有一段斜坡。

根据燃烧室的形状和尺寸，刍童的体积公式可以表示为：V=π×r^2×H+A×h×(2×π×r)/2其中，r表示燃烧室的半径，A表示斜坡的宽度，h表示斜坡的高度。

四、楔形四棱台的体积公式：楔形四棱台是一种几何体，其体积公式的推导需要通过几何性质和计算方法来解释。

假设楔形四棱台的顶面为一个正方形，边长为a；底面为一个矩形，长为b，宽为c；楔形四棱台的高为h。

首先计算楔形四棱台的上底面积和下底面积：上底面积A1=a^2下底面积A2=b×c然后计算楔形四棱台的体积：V=(A1+A2+√(A1×A2))×h/3以上即是楔形四棱台的体积公式的推导过程。

综上所述，刍甍、羡除、刍童以及楔形四棱台的体积公式都与燃烧室的形状和尺寸有关。

通过理解这些公式，我们可以计算出不同形状和尺寸的刍甍、羡除、刍童以及楔形四棱台的体积。

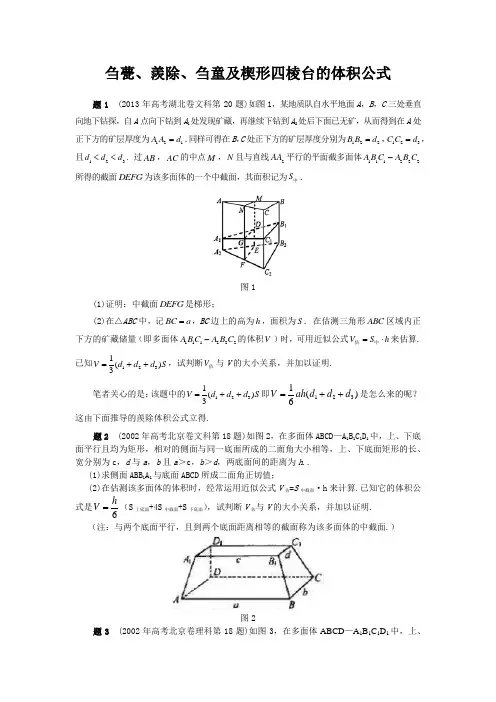
刍甍、羨除、刍童及楔形四棱台的体积公式题1 (2013年高考湖北卷文科第20题)如图1，某地质队自水平地面A ，B ，C 三处垂直向地下钻探，自A 点向下钻到A 1处发现矿藏，再继续下钻到A 2处后下面已无矿，从而得到在A 处正下方的矿层厚度为121A A d =．同样可得在B ，C 处正下方的矿层厚度分别为122B B d =，123C C d =，且123d d d <<. 过AB ，AC 的中点M ，N 且与直线2AA 平行的平面截多面体111222A B C A B C -所得的截面D E F G 为该多面体的一个中截面，其面积记为S 中．图1(1)证明：中截面D EFG 是梯形；(2)在△ABC 中，记BC a =，BC 边上的高为h ，面积为S . 在估测三角形ABC 区域内正下方的矿藏储量（即多面体111222A B C A B C -的体积V ）时，可用近似公式V S h =⋅估中来估算. 已知1231()3V d d d S =++，试判断V 估与V 的大小关系，并加以证明.笔者关心的是：该题中的1231()3V d d d S =++即)(61321d d d ah V ++=是怎么来的呢？这由下面推导的羨除体积公式立得.题2 (2002年高考北京卷文科第18题)如图2，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h .. (1)求侧面ABB 1A 1与底面ABCD 所成二面角正切值；(2)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图2题3 (2002年高考北京卷理科第18题)如图3，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E ，F 两点，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h ..(1)求侧面ABB 1A 1与底面ABCD 所成二面角的大小； (2)证明：EF//面ABCD(3)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图3笔者关心的是：高考题2,3中的6hV =（S 上底面+4S中截面+S下底面）即[(2)(2)]6hV a c b c a d =+++是怎么来的呢？这由下面推导的刍童体积公式立得.《九章算术·商功》篇有部分题目涉及到刍甍、羨除、刍童及楔形四棱台的体积公式，这些公式秦汉时人都已掌握，下面来推导它们.1.刍甍刍甍是图4所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是平行四边形.设a AB =，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)2(6c a HhV +=.图4证明 如图5所示.设点F E ,在面ABCD 上的射影分别是点F E '',.图5我们把平面ABCD 分成三块区域：区域I 指该平面位于直线AD 左侧的部分(不包括直线AD )，区域II 指该平面夹在直线BC AD 、之间的部分(包括直线这两条直线)，区域III 指该平面位于直线BC 右侧的部分(不包括直线BC ).应分六种情形来证明： (1)点F E '',均位于区域I ；(2)点E '位于区域I ，点F '位于区域II ； (3)点E '位于区域I ，点F '位于区域III ；(4)点F E '',均位于区域II ；(5)点E '位于区域II ，点F '位于区域III ；(6)点F E '',均位于区域III .下面只对情形(5)予以证明：过点E '作CD GH ⊥于H '，交AB 于G ；过点F '作CD IJ ⊥于I ，交AB 于J ，得H E E h GH ='=,，所以=-+=-)(BJIC AGHD FJI EGH V V V V 四棱锥四棱锥直三棱柱=-+=-+)(32)(32GJIH ABCD BJIC AGHD S S Hc Hh S S H c Hh )2(6)(32c a Hh ch ah H c Hh +=-+=证毕！ 2.羨除羨除是图6所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是梯形.设)(,b a b DC a AB >==，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)(6c b a HhV ++=.图6证明 用补形法可证.图7如图7所示，延长CD 至R ，使RC AB =，得刍甍ABCREF ，由刍甍的体积公式，得)(62)(3)2(6c b a Hh h b a H c a Hh V V V ADRE ABCREF ++=-⋅-+=-=-三棱锥刍甍注 羨除的体积公式是由刍甍的体积公式推得的；当羨除的下底面梯形变成平行四边形时(即图4所示中的b a =时的情形)，羨除就变成了刍甍，也得刍甍的体积公式是羨除的体积公式的极限情形.3.刍童刍童是图8所示中的六面体D C B A ABCD ''''-，其中面//ABCD面D C B A ''''，底面A B C D 、底面D C B A ''''均是平行四边形.设b B A a AB =''=,，直线CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A B C D ''''、之间的距离是H，则其体积])2()2[(6h a a h a a HV '+'+'+=.图8证明 如图9所示，可得面A B AB ''与平行平面D C B A ABCD ''''、的交线B A AB ''、平行,所以CD B A //''.连结C BD A '',.图9由刍甍的体积公式，得])2()2[(6h a a h a a HV V V D C B A CD ABCD A B '+'+'+=+=''''''刍甍刍甍 注 刍童的体积公式是由刍甍的体积公式推得的；当刍童的上底面平行四边形变成线段时(即图4所示中的0='h 时的情形)，刍童就变成了刍甍，也得刍甍的体积公式是刍童的体积公式的极限情形. 4.楔形四棱台楔形四棱台是图10所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面A B C D 、底面D C B A ''''均是梯形.设b D C b B A b CD a AB '=''=''==,,,，面CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A B C D ''''、之间的距离是H ，则其体积])()[(6h b b a h a b a HV '+'+'+'++=.图10 图11证明 如图11所示，可得CD B A //''.连结C B D A '',.由羨除的体积公式，得])()[(6h b b a h a b a HV V V D C B A CD ABCD A B '+'+'+'++=+=''''''羡除羡除 注 楔形四棱台的体积公式是由羨除的体积公式推得的；当楔形四棱台的上底面的梯形变成线段时(即图4中的0='h 时的情形)，楔形四棱台就变成了羨除，也得刍甍的体积公式是楔形四棱台的体积公式的极限情形.由刍甍的体积公式可推得羨除、刍童、楔形四棱台的体积公式，由楔形四棱台的体积公式也可推得刍甍的体积公式.题4 (1999年高考全国卷文科、理科第10题)如图12所示，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，23,//=EF AB EF ，EF 与面ABCD 的距离为2，则该多面体的体积为( )A.29 B.5 C.6 D.215图12解 D.由刍甍的体积公式可得.题5 (2007年全国高中数学联赛江苏赛区复赛第一试第9题)如图13，在多面体ABCDEF 中，已知四边形ABCD 是边长为3的正方形，3//,2EF AB EF =.若该多面体的体积为152，则EF 与AC 的距离为 .图13解 2.设直线EF 与平面AC 的距离为H ，由刍甍的体积公式可得153323262H ⋅⎛⎫=⋅+ ⎪⎝⎭2H =进而可得：异面直线,EF AC 的距离为2H =.题6 (2005年高考全国卷I 理科第4题即文科第5题)如图14，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE 、△BCF 均为正三角形，EF //AB ，EF =2，则该多面体的体积为( )A.32 B.33C.34D.23图14解 A.设棱,A D B C的中点分别是,S T ，在等腰梯形EFTS 中可得1,2,S T E F E S ===EF 与平面ABCD 的距离22=H . 所以由刍甍的体积公式可得多面体ABCDEF的体积为12(212)6⋅+=题7 (1983年美国邀请赛题)图15中的多面体的底面是边长为s 的正方形，上面的棱平行于底面，其长为s 2，其余棱长也都为s ，若26=s ，求这个多面体的体积.图15解 288.由刍甍的体积公式可得(先算得s H 22=).在该题中，当1=s 时就是高考题2.。

《九章算术》中的刍童、刍甍、羡除作者：甘大旺来源：《中学数学杂志(高中版)》2016年第04期2015年湖北省高考数学试卷文科第20题、理科第19题引入了《九章算术》中的“阳马”和“鳖臑”，这两个被多数同行认为的“新”名称的最近发展区是呼之欲出的刍童、刍甍、羡除.大约在25年前，我当时所在的湖北省咸宁高中数学组的几位老师就探讨着一类想象的六面体：两个平行底面是相似矩形、两组相对侧面分别是全等梯形的六面体一定是四棱台吗？经过争论和尝试后，我们画出下列两图：先画出两底面为长方形且两底面中心连线（对称轴）垂直于两底面的四棱台ABCD—A1B1C1D1（如图1），再将其上底面矩形A1B1C1D1绕对称轴按逆时针方向旋转90°，便可伴随得到“两个平行底面是相似矩形、两组相对侧面分别是全等梯形的六面体”（如图2），但这个六面体却不是四棱台.于是，我们当时统一了观点，所探讨的六面体不一定是四棱台.但是，这样旋转得到的六面体是否有一个名称呢？我们当时并不知道！若干年之后，我阅读相关数学史书籍，才知晓我国于公元前一世纪编成、公元一世纪修订的世界性名著《九章算术》上有着相关上述六面体的内容.用《九章算术》的名称，上述旋转得到的六面体是一种刍童.图1图2形似“草垛”的所谓刍童（包括曲池、盘池、冥谷），就是恰有两个矩形底面（不能全为正方形）、四条侧棱的延长线不交于一点的六面体[1][2].刍童的两个底面所在的平面互相平行，其实对于几何图形中所说的“两底”都默认其所在平面互相平行；刍童的四个侧面是梯形或平行四边形，但不能全为平行四边形（否则就退化成平行六面体）；刍童的四条侧棱所在直线交于两点（一个底面矩形的长、宽与另一个底面矩形的平行棱的大小关系不相反）或四点（一个底面矩形的长、宽与另一个底面矩形的平行棱的大小关系相反）.例1（2002年北京市高考题）如图3，在多面体ABCD—A1B1C1D1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E、F两点，上、下底面矩形的长、宽分别为c、d与a、b，且a>c，b>d，两底面间距离为h.（1）证明：EF∥平面ABCD；（2）在估测该多面体的体积时，经常运用近似公式V估=S中截面·h来计算，已知它的体积公式是V=16（S上底面+4S中截面+S下底面）·h，（Ⅰ）试判断V估与V的大小关系.审题①六面体ABCD—A1B1C1D1是一个刍童，四条侧棱所在直线交于两点，而不是交于四点；②公式（Ⅰ）是任意拟柱体的一般体积公式.解（1）由于下底面ABCD是矩形，则AB∥CD，则AB∥平面CDEF（线面平行的判定定理）.又因为平面ABFE∩平面CDEF=EF，则AB∥EF（线面平行的性质定理），即EF∥AB，则EF∥平面ABCD（线面平行的判定定理）.（2）根据梯形的中位线定理得到S中截面=a+c2·b+d2=ab+ad+bc+cd4，则V估-V=S中截面h-16（S上底面+4S中截面+S下底面）h=h6（2S中截面-S上底面-S下底面）=h6（ab+ad+bc+cd2-ab-cd）=h12（-ab+ad+bc-cd）.=-h12（a-c）（b-d）c，b>d）.所以，V估补注①此题可以启发我们领悟到刍童的一个性质——刍童的四条侧棱所在直线交于两点或四点，底面同侧的两点连线必定平行于底面；②根据拟柱体的一般体积公式（Ⅰ）可以推导出刍童特有求体积之“术”，请见下面的定理.定理1如图4和图5，如果刍童的高为h，下底面矩形的长为a1、宽为b1，上底面矩形的长为a2、宽为b2，那么此刍童的体积是[1][2]V=16[（2a1+a2）b1+（a1+2a2）b2]h.（Ⅱ）《九章算术》对于问题只给出“术”与终答，而对“术”却不证自明.下面补遗证明定理1.证明由于刍童是一类拟柱体，则运用公式（Ⅰ）得到V=16（S上底面+4S中截面+S下底面）·h=16（a1b1+4·a1+a22·b1+b22+a2b2）·h=16[a1b1+（a1b1+a1b2+a2b1+a2b2）+a2b2）]·h=16[（2a1+a2）b1+（a1+2a2）b2]h，所以，公式（Ⅱ）正确，故定理1证毕.如下列两图，将图6刍童ABCD-A1B1C1D1的两个顶点A1与D1合拢成一点E，同时将两个顶点B1与C1合拢成一点F，便形成图7而得到一个五面体EF—ABCD.按照《九章算术》的说法，这个由刍童退化演变出来的五面体是一个广义的刍甍.形似“草脊”的所谓刍甍，就是唯一顶棱平行于唯一矩形底面、三条平行棱不全等长的五面体.这是广义的刍甍，《九章算术》中狭义的刍甍还要限制顶棱的长度小于与它平行的两条等棱的长度[2]，此限制条件对于后面的体积公式（Ⅳ）没有影响.例2（2007年江苏省竞赛题改编题，1999年全国高考题）如图8，在多面体ABCDEF 中，已知面ABCD是边长为3的正方形，EF∥AB，EF=32，EF与面ABCD的距离为2，则该多面体的体积为.解作两个平行四边形AB1FE与DC1FE（图略），连B1C1，则题设的多面体（刍甍）EF—ABCD可以由四棱锥F—BB1C1C和三棱柱ADE—B1C1F所拼成，其中该三棱柱的直截面的底边长为3、高为2，于是所求多面体的体积为VEF—ABCD=VF-BB1C1C+VADE-B1C1F=13S矩形BB1C1C·2+S直截面·32=13·3·（3-32）·2+3·22·32=152（平方单位）.补注①在此例中，把矩形ABCD和线段EF放在距离等于2的两个平行平面中任意平行移动，刍甍EF-ABCD的体积都不会改变；②狭义的刍甍体积可以这样分割求得，那么另一类不狭义的刍甍体积是否也可以通过拼补求得呢？定理2在刍甍CC1-AA1B1B中，底面矩形的两边AA1=a、AB=l，顶棱CC1=c，顶棱CC1到底面AA1B1B的距离为h，则该刍甍的体积为[2]V=16（2a+c）lh.（Ⅲ）证明当c>a时，如图9，延长AA1至A0、延长BB1至B0，使AA0=BB0=CC1=c，连A0B0，则ABC—A0B0C1是三棱柱且其直截面三角形的底边长为l、高也为h，则此时刍甍CC1—AA1B1B的体积为V=VABC-A0B0C1-VC1-A1A0B0B1=S直截面·c-13·SA1A0B0B1·h=lh2·c-13·（c-a）l·h=16（2a+c）lh.当c对刍甍进行泛化想象（图略），假如将刍甍的底面矩形替换为底面梯形且刍甍有三条棱两两平行，那么《九章算术》把这种五面体称为羡除.形似“楔体”的所谓羡除，就是三个侧面都是梯形或平行四边形（其中最多只有一个平行四边形）、两个不平行对面是三角形的五面体[1][2].还能够想象，羡除可以由三棱柱的三个侧面与其两个三角形截面所围成的凸五面体，羡除是三棱柱的泛化图形，三棱柱是羡除的退化图形.《九章算术》给出求羡除体积的“术”是：“并三广，以深乘之，又以袤乘之，六而一”.其中的“广”是指羡除的三条平行侧棱之长、“深”是指一条侧棱到另两条侧棱所在平面的距离、“袤”是指这两条侧棱所在平行线之距.用现代语言描述，就是——定理3在羡除ABC—A1B1C1中，AA1∥BB1∥CC1，AA1=a，BB1=b，CC1=c，两条平行线AA1与BB1间的距离为l，直线CC1到平面AA1B1B的距离为h，则该羡除的体积为[1][2]V=16（a+b+c）lh.（Ⅳ）受定理2的证明过程的启发，下面因势利导地来推导羡除的体积公式.证明如图11，在羡除ABC-A1B1C1中，当c是a、b、c的最小者时，在棱AA1、BB1上分别取点A0、B0使得AA0=BB0=CC1=c，连A0B0，则此时羡除ABC-A1B1C1的体积为VABC—A1B1C1=VABC—A0B0C1+VC1—A1A0B0B1=S直截面·c+13·SA1A0B0B1·h=lh2·c+13·（a-c）+（b-c）2l·h=（c2+a+b-2c6）lh=16（a+b+c）lh.当c不是a、b、c的最小者时，不妨设b是a、b、c的最小者，令两条平行线AA1与CC1间的距离为l1，直线BB1到平面AA1C1C的距离为h1，则同理可证VABC—A1B1C1=16（a+b+c）l1h1.又因为l1h1=2S正截面=lh（为定值），则此时也有VABC—A1B1C1=16（a+b+c）lh.总之，定理3证毕.例3（2009年南京大学自主招生题）在四面体ABCD中，平行于AB与CD的平面π截该四面体得到截面EFGH，AB到π的距离为d1，CD到π的距离为d2，且d1=kd2.求立方体图形AB—EFGH与四面体ABCD的体积之比（用k表示）.图12解如图12，设两条异面直线AB、CD的距离与夹角分别为d与θ，则借用四面体的外接平行六面体可求得四面体ABCD的体积[3]为VABCD=d·AB·CD6·sinθ.这里，d=d1+d2.由于平行四边形EFGH的较小内角是θ，则两条平行线EF与GH间的距离l=EH·sinθ，根据已知条件、定理3、相似比求得VAB-EFGH=VAEH-BFG=16（AB+EF+GH）·l·d1=16（AB+2·EF）·（EH·sinθ）·d1=AB6·（1+2·d2d1+d2）（d1·CDd1+d2·sinθ）d1=VABCD·d1+3d2d1+d2·（d1d1+d2）2=VABCD·k2（k+3）（k+1）2.所以，立方体图形AB—EFGH与四面体ABCD的体积之比为k2（k+3）（k+1）2.补注命题组采用添加辅助线AF、AG、EG的方法解答此题，读者可对比阅读.回味上述定理，顿悟到可以由定理3证明定理2和定理1；经检验，公式（Ⅳ）也适合刍甍和三棱柱，于是我们可以概括出一个统一的结论——定理4在五面体ABC—A1B1C1中，AA1∥BB1∥CC1，AA1=a，BB1=b，CC1=c，且三条平行线AA1、BB1、CC1的直截面三角形的面积为S直截面，则该五面体（三棱柱、刍甍、羡除）的体积为V=13（a+b+c）S直截面.（Ⅴ）考虑篇幅，最后把例题改作习题留给读者探究.1.（2005年全国高考题改编题，1983年美国邀请赛题）图13的多面体的底面是边长为s 的正方形，上面的棱平行于底面，其长为2s，其余棱长也都为s，若s=62，求这个多面体的体积.图13图142.（2015年安徽省竞赛题）在如图14所示的多面体ABCDEF中，已知AD，BE，CF都与平面ABC垂直.设AD=a，BE=b，CF=c，AB=AC=BC=1.求四面体ABCE与BDEF公共部分的体积（用a，b，c表示）.3.（2013年湖北省文科高考题）如图15，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A1处发现矿藏，再继续下钻到A2处后下面已无矿，从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B，C处正下方的矿层厚度分别为B1B2=d2，C1C2=d3，d1点M，N且与直线AA2平行的平面截多面体A1B1C1—A2B2C2所得的截面DEFG为该多面体的一个中截面，其面积记为S中.（Ⅰ）证明：中截面DEFG是梯形；（Ⅱ）在△ABC中，记BC=a，BC边上的高为h，面积为S.在估测三角形ABC区域内正下方的矿藏储量（即多面体A1B1C1—A2B2C2的体积V）时，可用近似公式V估=S中·h来估算.已知V=13（d1+d2+d3）S，试判断V估与V的大小关系，并加以证明.参考文献[1]李文林.数学史概论[M].北京：高等教育出版社，2002：76～78[2]郭书春.中国传统数学史话[M].北京：中国国际广播出版社，2012：40～42[3]甘大旺.高考数学150专题[M].武汉：湖北教育出版社，2015：145。

四棱台体积公式及推导过程
四棱台一种特殊台梯形体（好比正方形与长方形），即底面与顶面均为相似的四边形，侧面都是梯形，四条棱的延长线能够交汇于一点的一种台体。

它的体积计算公式是V=(S1+4S0+S2)*H/6。

扩展资料
四棱台体积计算公式
①[S上+S下+√(S上×S下)]*h /3 （可以用于四棱锥）专 [上面面积+下面面积+根号下(上面面积×属下面面积)]×高÷3 。

②(S上+S下)*h/2 （不能用于四棱锥）(上面面积+下面面积)x高÷2 。

注意：第②个最简便的公式可以把正方体当作四棱台验证2把四棱锥看成上面面积为0的四棱台适用于第①个公式但是四棱锥不能用第②个公式。

刍童体积公式证明过程体积是空间物体占据的三维空间的大小，它描述了一个物体有多大。

而刍童体积公式是一种计算封闭几何体体积的方法。

在这个公式中，我们使用了切片的方法将一个几何体划分成许多薄片，然后通过对每个薄片的计算得到整个体积。

下面我们将详细阐述这个公式的证明过程。

我们可以看到，每个薄片的面积都是a^2，因为立方体的底面是正方形，边长为a。

而每个薄片的体积为a^2×h。

现在，我们来计算叠放的长方体的体积。

根据长方体的体积公式，我们知道，体积等于底面积乘以高度。

所以，这个叠放的长方体的体积为a^2 × nh。

另一方面，由于这个长方体是由n个薄片叠放而成的，所以它的体积也应该等于每个薄片的体积之和。

即：体积= a^2 × nh现在，我们来考虑一个更一般的情况，一个任意形状的物体。

为了计算这个物体的体积，我们可以将其切割成许多小薄片，并将它们叠放在一起。

类似于前面的例子，每个薄片的面积为S，厚度为h。

将这个物体切割成n个薄片，并叠放在一起，我们得到了一个形状为长方体的结构。

它的长、宽、高分别为a，b，nh。

根据长方体的体积公式，这个叠放的长方体的体积为S × nh。

另一方面，由于这个长方体是由n个薄片叠放而成的，所以它的体积也应该等于每个薄片的体积之和。

即：体积= S × nh由于这个物体是任意形状的，所以我们可以在整个物体上无限细化地切割并叠放小薄片，使得它们的厚度h趋近于零。

那么，当h趋近于零时，上述公式将近似于：体积≈S×h这就是刍童体积公式的核心思想，即将物体切割为无限细小的薄片，并在计算体积时使用这个公式。

总结一下，刍童体积公式的证明过程是从一个简单的立方体开始的，然后将立方体切割为薄片并叠放，得到了一个形状为长方体的结构。

通过比较长方体的体积公式和每个薄片的体积之和，我们证明了刍童体积公式的正确性。

当然，在实际应用中，我们通常使用积分的方法来计算连续的无限小薄片的体积。

四棱台体积公式①、［S上+S下+ V（S 上x S下）］*h /3 （可以用于四棱锥）［上面面积+下面面积+根号（上面面积x下面面积）］x高十2②、（S上+S下）*h/2 （不能用于四棱锥）（上面面积+下面面积）x高* 2 第②个最简便的公式，可以把正方体当作四棱台验证。

注意：如果把四棱锥可以看成上面面积为0的四棱台，第①个公式仍然可以用，但是四棱锥不能用第②个公式，切记！ !!!!!!! o拟棱台：对于一个多面体，如果有两个面互相平行，而其余的面均为顶点全在这两个平行面上的三角形、平行四边形或梯形，这样的多面体叫拟棱台。

若上下底面和中截面的面积分别是S1、S2、S0 ,高为H，则体积V=1/6（s1+s2+4s0）H正四棱台体积V=底面积s x高H 圆锥体体积=底X高十3 长方形的周长=（长+宽）X 2正方形的周长=边长X 4长方形的面积=长X宽正方形的面积=边长X边长三角形的面积=底X高十2 平行四边形的面积=底乂高梯形的面积=（上底+下底）X咼* 2 直径=半径X 2半径=直径十2 圆的周长=圆周率X直径= 圆周率X半径X 2圆的面积=圆周率X半径X半径长方体的表面积=（长X宽+长X高+宽X高）X 2 长方体的体积=长乂宽X高正方体的表面积=棱长X棱长X 6 正方体的体积=棱长X棱长X棱长圆柱的侧面积=底面圆的周长X高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积X高圆锥的体积=底面积X高十3 长方体（正方体、圆柱体）的体积=底面积X高平面图形名称符号周长C和面积S 正方形a—边长C= 4aS= a2长方形a和b—边长 C = 2(a+b)S= ab三角形a,b,c —三边长h—a边上的高s—周长的一半A,B,C —内角其中s= (a+b+c)/2 S = ah/2=ab/2 • sinC=[s(s-a)(s-b)(s-c)]1/2=a2si nBsi nC/(2si nA)四边形d,D —对角线长a 一对角线夹角S= dD/2 • sin a平行四边形a,b—边长h—a边的高a 一两边夹角S= ah=absin a菱形a—边长a —夹角D—长对角线长d —短对角线长S= Dd/2=a2sin a梯形a和b—上、下底长h —高m —中位线长S= (a+b)h/2=mh圆r —半径d一直径C= n d = 2 n rS= n r2=n d2/4扇形r—扇形半径a—圆心角度数C= 2r + 2n r X (a/360)S= n r2 X (a/360)弓形I—弧长b—弦长h —矢高r—半径a —圆心角的度数S= r2/2 • (n a /180-sin a ) =r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2=n a r2/360 - b/2 • [r2-(b/2)2]1/2=r(l-b)/2 + bh/2~ 2bh/3圆环R—外圆半径r —内圆半径D—外圆直径d—内圆直径S= n (R2-r2)=n (D2-d2)/4椭圆D —长轴d —短轴S= n Dd/4立方图形名称符号面积S和体积V正方体a—边长S = 6a2V = a3长方体a-长b—宽c—高S= 2(ab+ac+bc)V = abc棱柱S—底面积h —高V = Sh棱锥S—底面积h —高V = Sh/3棱台S1和S2 —上、下底面积h —高V = h[S1+S2+(S1S1)1/2]/3 拟柱体S1—上底面积S2—下底面积SO—中截面积h —高V = h(S1+S2+4S0)/6圆柱r—底半径h —高C—底面周长S底一底面积S侧一侧面积S表一表面积C = 2 n rS 底=n r2S 侧=ChS 表=Ch+2S 底V = S 底h=n r2h空心圆柱R—外圆半径r —内圆半径h —高V =n h(R2-r2)直圆锥r—底半径h —高V =n r2h/3圆台r—上底半径R—下底半径h —高V =n h(R2 + Rr + r2)/3球r —半径d —直径V = 4/3 n r3= n d2/6球缺h—球缺高r -球半径a—球缺底半径V =n h(3a2+h2)/6 =n h2(3r-h)/3a2= h(2r-h)球台r1和r2 —球台上、下底半径h —高V =n h[3(r12 + r22)+h2]/6 圆环体R—环体半径D-环体直径r —环体截面半径d —环体截面直径V = 2 n 2Rr2 =n 2Dd2/4桶状体D-桶腹直径d-桶底直径h —桶高V =n h(2D2 + d2)/12(母线是圆弧形，圆心是桶的中心)V = n h(2D2 + Dd + 3d2/4)/15评论(14) | 80 12012-08-12 16:31我只是碗馄饨|四级体积的话叫棱台S1=上面的面积S2=下面的面积H是高V是体积V= (S1+S2+根号(S1X S2)) X H - 3评论⑹| 52 22012-05-08 23:50绿锦小学|十三级答：梯形是平面图形，没有体积，只有面积。

四棱台体积公式：①、[S上+S下+√(S上×S下)]*h /3 （可以用于四棱锥）[上面面积+下面面积+根号(上面面积×下面面积)]×高÷2②、(S上+S下)*h/2 （不能用于四棱锥）(上面面积+下面面积)x高÷2第②个最简便的公式，可以把正方体当作四棱台验证。

注意：如果把四棱锥可以看成上面面积为0的四棱台，第①个公式仍然可以用，但是四棱锥不能用第②个公式，切记！！！！！！！！。

拟棱台：对于一个多面体，如果有两个面互相平行，而其余的面均为顶点全在这两个平行面上的三角形、平行四边形或梯形，这样的多面体叫拟棱台。

若上下底面和中截面的面积分别是S1、S2、S0，高为H，则体积V=1/6(s1+s2+4s0)H正四棱台体积V=底面积S×高H圆锥体体积=底×高÷3长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15评论(14) | 80 12012-08-12 16:31 我只是碗馄饨| 四级体积的话叫棱台S1=上面的面积S2=下面的面积H是高V是体积V=（S1+S2+根号（S1×S2））×H ÷3评论(6) | 52 22012-05-08 23:50 绿锦小学| 十三级答：梯形是平面图形，没有体积，只有面积。

刍甍、羨除、刍童及楔形四棱台的体积公式题1 (2013年高考湖北卷文科第20题)如图1，某地质队自水平地面A ，B ，C 三处垂直向地下钻探，自A 点向下钻到A 1处发现矿藏，再继续下钻到A 2处后下面已无矿，从而得到在A 处正下方的矿层厚度为121A A d =．同样可得在B ，C 处正下方的矿层厚度分别为122B B d =，123C C d =，且123d d d <<. 过AB ，AC 的中点M ，N 且与直线2AA 平行的平面截多面体111222A BC A B C -所得的截面DEFG 为该多面体的一个中截面，其面积记为S 中．图1(1)证明：中截面DEFG 是梯形；(2)在△ABC 中，记BC a =，BC 边上的高为h ，面积为S . 在估测三角形ABC 区域内正下方的矿藏储量（即多面体111222A B C A B C -的体积V ）时，可用近似公式V S h =⋅估中来估算. 已知1231()3V d d d S =++，试判断V 估与V 的大小关系，并加以证明.笔者关心的是：该题中的1231()3V d d d S =++即)(61321d d d ah V ++=是怎么来的呢？这由下面推导的羨除体积公式立得.题2 (2002年高考北京卷文科第18题)如图2，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h .. (1)求侧面ABB 1A 1与底面ABCD 所成二面角正切值；(2)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图2题3 (2002年高考北京卷理科第18题)如图3，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E ，F 两点，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h ..(1)求侧面ABB 1A 1与底面ABCD 所成二面角的大小； (2)证明：EF//面ABCD(3)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图3笔者关心的是：高考题2,3中的6hV =（S 上底面+4S中截面+S下底面）即[(2)(2)]6hV a c b c a d =+++是怎么来的呢？这由下面推导的刍童体积公式立得.《九章算术·商功》篇有部分题目涉及到刍甍、羨除、刍童及楔形四棱台的体积公式，这些公式秦汉时人都已掌握，下面来推导它们.1.刍甍刍甍是图4所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是平行四边形.设a AB =，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)2(6c a HhV +=.图4证明 如图5所示.设点F E ,在面ABCD 上的射影分别是点F E '',.图5我们把平面ABCD 分成三块区域：区域I 指该平面位于直线AD 左侧的部分(不包括直线AD )，区域II 指该平面夹在直线BC AD 、之间的部分(包括直线这两条直线)，区域III 指该平面位于直线BC 右侧的部分(不包括直线BC ).应分六种情形来证明： (1)点F E '',均位于区域I ；(2)点E '位于区域I ，点F '位于区域II ； (3)点E '位于区域I ，点F '位于区域III ；(4)点F E '',均位于区域II ；(5)点E '位于区域II ，点F '位于区域III ；(6)点F E '',均位于区域III .下面只对情形(5)予以证明：过点E '作CD GH ⊥于H '，交AB 于G ；过点F '作CD IJ ⊥于I ，交AB 于J ，得H E E h GH ='=,，所以=-+=-)(BJIC AGHD FJI EGH V V V V 四棱锥四棱锥直三棱柱=-+=-+)(32)(32GJIH ABCD BJIC AGHD S S Hc Hh S S H c Hh )2(6)(32c a Hh ch ah H c Hh +=-+=证毕！ 2.羨除羨除是图6所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是梯形.设)(,b a b DC a AB >==，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)(6c b a HhV ++=.图6证明 用补形法可证.图7如图7所示，延长CD 至R ，使RC AB =，得刍甍ABCREF ，由刍甍的体积公式，得)(62)(3)2(6c b a Hh h b a H c a Hh V V V ADRE ABCREF ++=-⋅-+=-=-三棱锥刍甍注 羨除的体积公式是由刍甍的体积公式推得的；当羨除的下底面梯形变成平行四边形时(即图4所示中的b a =时的情形)，羨除就变成了刍甍，也得刍甍的体积公式是羨除的体积公式的极限情形.3.刍童刍童是图8所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面A B C D 、底面D C B A ''''均是平行四边形.设b B A a AB =''=,，直线CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A B C D ''''、之间的距离是H，则其体积])2()2[(6h a a h a a HV '+'+'+=.图8证明 如图9所示，可得面A B AB ''与平行平面D C B A ABCD ''''、的交线B A AB ''、平行,所以CD B A //''.连结C BD A '',.图9由刍甍的体积公式，得])2()2[(6h a a h a a HV V V D C B A CD ABCD A B '+'+'+=+=''''''刍甍刍甍 注 刍童的体积公式是由刍甍的体积公式推得的；当刍童的上底面平行四边形变成线段时(即图4所示中的0='h 时的情形)，刍童就变成了刍甍，也得刍甍的体积公式是刍童的体积公式的极限情形. 4.楔形四棱台楔形四棱台是图10所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面A B C D 、底面D C B A ''''均是梯形.设b D C b B A b CD a AB '=''=''==,,,，面CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A BCD ''''、之间的距离是H ，则其体积])()[(6h b b a h a b a HV '+'+'+'++=.图10 图11证明 如图11所示，可得CD B A //''.连结C B D A '',.由羨除的体积公式，得])()[(6h b b a h a b a HV V V D C B A CD ABCD A B '+'+'+'++=+=''''''羡除羡除 注 楔形四棱台的体积公式是由羨除的体积公式推得的；当楔形四棱台的上底面的梯形变成线段时(即图4中的0='h 时的情形)，楔形四棱台就变成了羨除，也得刍甍的体积公式是楔形四棱台的体积公式的极限情形.由刍甍的体积公式可推得羨除、刍童、楔形四棱台的体积公式，由楔形四棱台的体积公式也可推得刍甍的体积公式.题4 (1999年高考全国卷文科、理科第10题)如图12所示，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，23,//=EF AB EF ，EF 与面ABCD 的距离为2，则该多面体的体积为( )A.29 B.5 C.6 D.215图12解 D.由刍甍的体积公式可得.题5 (2007年全国高中数学联赛江苏赛区复赛第一试第9题)如图13，在多面体ABCDEF 中，已知四边形ABCD 是边长为3的正方形，3//,2EF AB EF =.若该多面体的体积为152，则EF 与AC 的距离为 .图13解 2.设直线EF 与平面AC 的距离为H ，由刍甍的体积公式可得153323262H ⋅⎛⎫=⋅+ ⎪⎝⎭2H =进而可得：异面直线,EF AC 的距离为2H =.题6 (2005年高考全国卷I 理科第4题即文科第5题)如图14，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE 、△BCF 均为正三角形，EF //AB ，EF =2，则该多面体的体积为( )A.32 B.33C.34D.23图14解 A.设棱,A D B C的中点分别是,S T ，在等腰梯形EFTS 中可得1,2,2ST EF ES FT ====，可求得该等腰梯形的高即直线EF 与平面ABCD 的距离22=H . 所以由刍甍的体积公式可得多面体ABCDEF的体积为12(212)63⋅+=. 题7 (1983年美国邀请赛题)图15中的多面体的底面是边长为s 的正方形，上面的棱平行于底面，其长为s 2，其余棱长也都为s ，若26=s ，求这个多面体的体积.图15解 288.由刍甍的体积公式可得(先算得s H 22=).在该题中，当1=s 时就是高考题2.用排除法简解2015年高考全国卷I 理科第12题高考题 (2015年高考全国卷I 理科第12题)设函数f (x )＝e x (2x －1)－ax ＋a ，其中a <1，若存在唯一的整数x 0使得f (x 0)<0，则a 的取值范围是( )A.3,12e ⎡⎫-⎪⎢⎣⎭ B.33,2e 4⎡⎫-⎪⎢⎣⎭C.33,2e 4⎡⎫⎪⎢⎣⎭D.3,12e ⎡⎫⎪⎢⎣⎭解法1 (数形结合法)D.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又函数g (x )在x <12时g (x )<0，在x >12时g (x )>0，所以其大致图象如图1所示．图1直线y ＝ax －a 过点(1，0)．若a ≤0，则f (x )<0的整数解有无穷多个，因此只能a >0. 结合函数图象可知，存在唯一的整数x 0，使得f (x 0)<0，即存在唯一的整数x 0，使得点(x 0，ax 0－a )在点(x 0，g (x 0))的上方，得x 0只能是0，所以实数a 应满足⎩⎪⎨⎪⎧f （－1）≥0，f （0）<0，f （1）≥0，即⎩⎪⎨⎪⎧－3e －1＋2a ≥0，－1＋a <0，e ≥0，解得32e≤a <1.即实数a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭.解法2 (分离常数法)D.令1+=t x 后，得题设即关于t 的不等式)0(1)e (21≠<++t at t t 有唯一的整数解.若0t >，由a <1，可得1(21)e (21)e t t t t at ++>+>>所以题设即关于t 的不等式1(21)e(0)t t at t ++<<即1(21)e (0)t t a t t++><有唯一的整数解，也即关于t 的不等式1(21)e (1)t t a t t++>≤-有唯一的整数解. 设1(21)e ()(1)t t g t t t ++=≤-，得12e ()(1)(21)(1)t g t t t t t+'=+-≤-，所以函数)(t g 在(,1]-∞-上是增函数，得最大值为(1)1g -=.又lim ()0,(1)1t g t g →-∞=-=，由此可作出函数)(t g 的图象如图2所示：图2注意到图象()y g t =过点32,2e B ⎛⎫- ⎪⎝⎭且1<a ，所以由图2可得： 当32ea <时，满足()g t a >的整数t 有2,1--，所以此时不满足题意. 当1e23<≤a 时，满足()g t a >的整数t 只有1-，所以此时满足题意. 得所求a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭. 解法3 (排除法)D.当0a =时，不等式f (x )<0即e x (2x －1)<0也即12x <，它有无数个整数解，不满足题设.由此可排除选项A,B.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又g ′(0)＝1，所以可得曲线()y g x =在点(0,1)-处的切线为1y x =-，如图3所示．图3所以当a <1且1a →时满足题设(此时满足题设的唯一整数x 0=0).由此可排除选项C. 所以选D.注 小题不大做，还是解法3(排除法)简洁.本题对函数与方程思想、数形结合思想、分类讨论思想都有所考查.例谈用验证法解题——2010年高考数学安徽卷理科第20题的另解题1 解方程：(1)2121+=+x x ；(2)c c x x 11-=-；(3)c c x x 11+=+. 解 (1)容易观察出212，=x 均是该方程的解.按常规方法解此方程时，先去分母得到一元二次方程，该一元二次方程最多两个解，再检验(舍去使原方程中分母为零的解)，所以原方程最多有两个解.而已经找到了原方程的两个解212，=x ，所以这两个解就是原方程的所有解.(2)同理，可得原方程的所有解是cc x 1-=，. (3)容易观察出cc x 1，=均是该方程的解.同上得原方程最多有两个解，而已经找到了原方程的两个解cc x 1，=(因为对于任意的非零实数c ，c 和c 1都是原方程的解，所以应当把c 和c1理解成原方程的两个解)，所以这两个解就是原方程的所有解.题2 解方程22=+++x x x .解 设函数2)(+++=x x x x f ，易知它是增函数，所以方程2)(=x f 至多有一个根(当2在函数)(x f 的值域中时有一个根，否则没有根)，……所以原方程的根是2=x .题3 已知1tan ,51cos sin ->=+ααα，求αtan . 解 由⎪⎩⎪⎨⎧=+=+1cos sin 51cos sin 22αααα及“勾三股四弦五”可以猜出该方程组有两组解：⎪⎪⎩⎪⎪⎨⎧-==53cos 54sin αα 或 ⎪⎪⎩⎪⎪⎨⎧=-=54c o s 53s i n αα 该方程组即⎪⎪⎩⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛-+-=1sin 51sin sin 51cos 22αααα 因为关于αsin 的一元二次方程1sin 51sin 22=⎪⎭⎫ ⎝⎛-+αα最多有两个解，所以该方程组也最多有两组解，......所以上面猜出的两组解就是该方程组的全部解， (4)3tan -=α. 题4]1[ (2007年高考陕西卷理科第22(1)题)已知各项全不为零的数列}{k a 的前k 项和为k S ，且∈=+k a a S k k k (211N*)，其中11=a ，求数列}{k a 的通项公式. 解 由题设得kk k k k a a a a a S a )(22211+++==+ ，所以当k a a a ,,,21 确定时，1+k a 也唯一确定.所以由11=a 知，数列}{k a 是唯一确定的.可以观察出k a k =满足题设的所有条件，所以数列{}k 是满足题设的唯一数列，得k a k =.另解 (2),2)()((211111k k k kk k k k k k k k S S S S S k S S S S a a S +-=≥--==-++-+因为)2)(01≥≠=--k a S S k k k ①由题设得3,121==S S ，再由①知{}k S 是唯一确定的数列⎪⎪⎭⎫ ⎝⎛⎩⎨⎧≥-==-2,1,11k S S k S a k k k .再同上得k a k =.题5]1[ (2005年高考江苏卷第23(1)(2)题)设数列}{n a 的前n 项和为n S ，已知11,6,1321===a a a ，且∈+=+--+n B An S n S n n n ()25()85(1N*)，其中B A ,为常数.(1)求A 与B 的值；(2)证明数列}{n a 为等差数列；解 (1)8,20-=-=B A . (2) ∈-+--+=+n n n S n n S n n (8582085251N*)，11=S ②所以{}n S 是唯一确定的数列，}{n a 也是唯一确定的数列.又由11,6,1321===a a a 知，若}{n a 为等差数列，则45-=n a n ，于是)35(21-=n n S n . 容易验证)35(21-=n n S n 满足②，所以题中的45),35(21-=-=n a n n S n n ，}{n a 为等差数.题6]2[ 已知数列}{n a 满足nn a a a n n ++==+2111,21，求n a ； 解 首先，由首项211=a 及递推关系nn a a n n ++=+211知，满足题意的数列}{n a 是唯一确定的.所以，若能找到一个数列满足该题目的所有条件，则该数列的通项公式就是所求的答案.易得⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+-=+-=+=-+n k n k n n n n a a n n 111111121，即nk a n1-=（k 是常数）满足递推关系n n a a n n ++=+211，再由211=a ，得n a n123-=满足题目的所有条件，所以本题的答案就是na n 123-=.题7]2[ 已知数列}{n a 满足n n a n n a a 1,3211+==+，求n a . 解 易知本题的答案是是唯一确定的，所以只需寻求一个数列满足该题目的所有条件.易得k nk n kn na a n n (111+=+=+是非零常数），即n k a n =满足递推关系n n a n n a 11+=+，再由321=a ，得n a n 32=满足题目的所有条件，所以本题的答案就是na n 32=.注 因为绝大部分求数列通项公式的题目答案都是唯一的，所以只要能观察或求出满足所有题设的一个通项公式，则该通项公式就是所求的唯一答案.对于要求解的问题Ω，若能证明它最多有n n (是确定的正整数)个解，又找出了它的n 个解n ωωω,,,21 ，则这n 个解就是该问题的所有解.这就是本文要阐述的用验证法解题.下面再用这种方法解答一道高考题：题8 (2010·安徽·理·20)设数列 ,,,,21n a a a 中的每一项都不为0.证明{}n a 为等差数列的充分必要条件是：对任何∈n N*，都有1113221111++=+++n n n a a na a a a a a .证明 先证必要性.若数列{}n a 是公差为d 的等差数列： 当0=d 时，易得欲证成立.当0≠d 时，有⎪⎪⎭⎫⎝⎛-++-+-=++++++1132232112132211111n n n n n n a a a a a a a a a a a a d a a a a a a 111111111322111111111111+++++=-⋅=⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=n n n n n n a a na a a a d a a d a a a a a a d再证充分性.只需对)3(≥n n 用数学归纳法证明加强的结论：若),,3,2(1111113221n i a a ia a a a a a i i i ==+++++恒成立，则n a a a ,,,21 成等差数列，且na a n 1≠. 当3=n 时成立：当2=i 时，得2313132212,211a a a a a a a a a =+=+，所以321,,a a a 成等差数列，还可证313a a ≠(因为由313a a =可得023131313334=-=--+=+=a a a a a d a a ，而由3=i 时成立立知)04≠a .假设kn ,,4,3 =时成立：即ka a a ,,,21 成等差数列，且ka a a a a a k 11413,,4,3≠≠≠. 由k i ,,3,2 =时均成立及kaa a a a a k 11413,,4,3≠≠≠知，当21,a a 确定时，数列121,,,+n a a a 也是确定的，而由必要性的证明知，由21,a a 确定的等差数列121,,,+n a a a 满足题设，所以由题设及21,a a 确定的数列就是这个等差数列，即121,,,+n a a a 成等差数列，同上还可证111+≠+k a a k ，即1+=k n 时成立.所以要证结论成立，得充分性成立.参考文献1 甘志国.例谈用验证法求数列通项[J].中学数学月刊，2008(3)：462 甘志国著.初等数学研究(II)上[M].哈尔滨：哈尔滨工业大学出版社，2009.416-417用排除法简解2015年高考全国卷I 理科第12题高考题 (2015年高考全国卷I 理科第12题)设函数f (x )＝e x (2x －1)－ax ＋a ，其中a <1，若存在唯一的整数x 0使得f (x 0)<0，则a 的取值范围是( )A.3,12e ⎡⎫-⎪⎢⎣⎭ B.33,2e 4⎡⎫-⎪⎢⎣⎭C.33,2e 4⎡⎫⎪⎢⎣⎭D.3,12e ⎡⎫⎪⎢⎣⎭解法1 (数形结合法)D.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数． 又函数g (x )在x <12时g (x )<0，在x >12时g (x )>0，所以其大致图象如图1所示．图1直线y ＝ax －a 过点(1，0)．若a ≤0，则f (x )<0的整数解有无穷多个，因此只能a >0. 结合函数图象可知，存在唯一的整数x 0，使得f (x 0)<0，即存在唯一的整数x 0，使得点(x 0，ax 0－a )在点(x 0，g (x 0))的上方，得x 0只能是0，所以实数a 应满足⎩⎪⎨⎪⎧f （－1）≥0，f （0）<0，f （1）≥0，即⎩⎪⎨⎪⎧－3e －1＋2a ≥0，－1＋a <0，e ≥0，解得32e≤a <1.即实数a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭.解法2 (分离常数法)D.令1+=t x 后，得题设即关于t 的不等式)0(1)e (21≠<++t at t t 有唯一的整数解.若0t >，由a <1，可得1(21)e (21)e t t t t at ++>+>>所以题设即关于t 的不等式1(21)e(0)t t at t ++<<即1(21)e (0)t t a t t++><有唯一的整数解，也即关于t 的不等式1(21)e (1)t t a t t++>≤-有唯一的整数解. 设1(21)e ()(1)t t g t t t ++=≤-，得12e ()(1)(21)(1)t g t t t t t+'=+-≤-，所以函数)(t g 在(,1]-∞-上是增函数，得最大值为(1)1g -=.又lim ()0,(1)1t g t g →-∞=-=，由此可作出函数)(t g 的图象如图2所示：图2注意到图象()y g t =过点32,2e B ⎛⎫- ⎪⎝⎭且1<a ，所以由图2可得： 当32ea <时，满足()g t a >的整数t 有2,1--，所以此时不满足题意. 当1e23<≤a 时，满足()g t a >的整数t 只有1-，所以此时满足题意. 得所求a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭. 解法3 (排除法)D.当0a =时，不等式f (x )<0即e x (2x －1)<0也即12x <，它有无数个整数解，不满足题设.由此可排除选项A,B.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又g ′(0)＝1，所以可得曲线()y g x =在点(0,1)-处的切线为1y x =-，如图3所示．。