数学建模实验报告

数学建模实验报告1.流⽔问题问题描述：⼀如下图所⽰的容器装满⽔，上底⾯半径为r=1m，⾼度为H=5m，在下地⾯有⼀⾯积为B0.001m2的⼩圆孔，现在让⽔从⼩孔流出，问⽔什么时候能流完？解题分析：这个问题我们可以采⽤计算机模拟，⼩孔处的⽔流速度为V=sqrt[2*g*h]，单位时间从⼩孔流出的⽔的体积为V*B，再根据⼏何关系，求出⽔⾯的⾼度H，时间按每秒步进，记录点（H，t）并画出过⽔⾯⾼度随时间的变化图，当⽔⾯⾼度⼩于0.001m 时，可以近似认为⽔流完了。

程序代码：Methamatic程序代码：运⾏结果：（5）结果分析：计算机仿真可以很直观的表现出所求量之间的关系，从图中我们可以很⽅便的求出要求的值。

但在实际编写程序中，由于是初次接触methamatic 语⾔，对其并不是很熟悉，加上个⼈能⼒有限，所以结果可能不太精确，还请见谅。

2.库存问题问题描述某企业对于某种材料的⽉需求量为随机变量，具有如下表概率分布：每次订货费为500元，每⽉每吨保管费为50元，每⽉每吨货物缺货费为1500元，每吨材料的购价为1000元。

该企业欲采⽤周期性盘点的),(S s 策略来控制库存量，求最佳的s ，S 值。

（注：),(S s 策略指的是若发现存货量少于s 时⽴即订货，将存货补充到S ，使得经济效益最佳。

）问题分析：⽤10000个⽉进⾏模拟，随机产⽣每个⽉需求量的概率，利⽤计算机编程，将各种S 和s 的取值都遍历⼀遍，把每种S，s的组合对应的每⽉花费保存在数组cost数组⾥，并计算出平均⽉花费average，并⽤类answer来记录，最终求出对应的S和s。

程序代码：C++程序代码：#include#include#include#include#define Monthnumber 10000int Need(float x){int ned = 0;//求每个⽉的需求量if(x < 0.05)ned = 50;else if(x < 0.15)ned = 60;else if(x < 0.30)ned = 70;else if(x < 0.55)ned = 80;else if(x < 0.75)ned = 90;else if(x < 0.85)ned = 100;else if(x < 0.95)ned = 110;else ned = 120;return ned;}class A{public:int pS;int ps;float aver;};int main(){A answer;answer.aver=10000000;//int cost[Monthnumber+1]={0}; float average=0;int i;float x;int store[Monthnumber];//srand((int)time(0));for(int n=6;n<=12;n++){// int n=11;int S=10*n;for(int k=5;k{// int k=5;int s=k*10;average=0;int cost[Monthnumber+1]={0};for(i=1;i<=Monthnumber;i++){store[i-1]=S;srand(time(0));x=(float)rand()/RAND_MAX; //产⽣随机数//cout<<" "<//cout<int need=Need(x);if(need>=store[i-1]){cost[i]= 1000*S + (need - store[i-1])*1500 + 500;store[i]=S;}else if(need>=store[i-1]-s){cost[i]=1000*(need+S-store[i-1]) + 50*(store[i-1]-need) + 500; store[i]=S;}else{cost[i]=(store[i-1]-need)*50;store[i]=store[i-1]-need;}average=cost[i]+average;}average=average/Monthnumber;cout<<"n="<cout<<"花费最少时s应该为："<cout<<"平均每⽉最少花费为："<}运⾏结果：结果分析：⽤计算机模拟的结果和⽤数学分析的结果有⼀定的差异，由于计算机模拟时采⽤的是随机模型⽽我⽤time函数和rand函数产⽣真随机数，所以在每次的结果上会有所差异，但对于⼀般的⽣产要求亦可以满。

第1篇一、实验目的本次实验旨在让学生掌握数学建模的基本步骤，学会运用数学知识分析和解决实际问题。

通过本次实验，培养学生主动探索、努力进取的学风，增强学生的应用意识和创新能力，为今后从事科研工作打下初步的基础。

二、实验内容本次实验选取了一道实际问题进行建模与分析，具体如下：题目：某公司想用全行业的销售额作为自变量来预测公司的销售量。

表中给出了1977—1981年公司的销售额和行业销售额的分季度数据（单位：百万元）。

1. 数据准备：将数据整理成表格形式，并输入到计算机中。

2. 数据分析：观察数据分布情况，初步判断是否适合使用线性回归模型进行拟合。

3. 模型建立：利用统计软件（如MATLAB、SPSS等）进行线性回归分析，建立公司销售额对全行业的回归模型。

4. 模型检验：对模型进行检验，包括残差分析、DW检验等，以判断模型的拟合效果。

5. 结果分析：分析模型的拟合效果，并对公司销售量的预测进行评估。

三、实验步骤1. 数据准备将数据整理成表格形式，包括年份、季度、公司销售额和行业销售额。

将数据输入到计算机中，为后续分析做准备。

2. 数据分析观察数据分布情况，绘制散点图，初步判断是否适合使用线性回归模型进行拟合。

3. 模型建立利用统计软件进行线性回归分析，建立公司销售额对全行业的回归模型。

具体步骤如下：（1）选择合适的统计软件，如MATLAB。

（2）输入数据，进行数据预处理。

（3）编写线性回归分析程序，计算回归系数。

（4）输出回归系数、截距等参数。

4. 模型检验对模型进行检验，包括残差分析、DW检验等。

（1）残差分析：计算残差，绘制残差图，观察残差的分布情况。

（2）DW检验：计算DW值，判断随机误差项是否存在自相关性。

5. 结果分析分析模型的拟合效果，并对公司销售量的预测进行评估。

四、实验结果与分析1. 数据分析通过绘制散点图，观察数据分布情况，初步判断数据适合使用线性回归模型进行拟合。

2. 模型建立利用MATLAB进行线性回归分析，得到回归模型如下：公司销售额 = 0.9656 行业销售额 + 0.01143. 模型检验（1）残差分析：绘制残差图，观察残差的分布情况，发现残差基本呈随机分布，说明模型拟合效果较好。

数学建模实验报告姓名：学院：专业班级：学号：数学建模实验报告（一）——用最小二乘法进行数据拟合一．实验目的：1.学会用最小二乘法进行数据拟合。

2.熟悉掌握matlab软件的文件操作和命令环境。

3.掌握数据可视化的基本操作步骤。

4.通过matlab绘制二维图形以及三维图形。

二．实验任务：来自课本64页习题：用最小二乘法求一形如y=a+b x2的多项式，使之与下列数据拟合：三．实验过程：1.实验方法：用最小二乘法解决实际问题包含两个基本环节：先根据所给出数据点的变化趋势与问题的实际背景确定函数类；然后按照最小二乘法原则求最小二乘解来确定系数。

即要求出二次多项式: y=a+b x2的系数。

2．程序：x=[19 25 31 38 44]y=[19.0 32.3 49.0 73.3 97.8]ab=y/[ones(size(x));x.^2];a=ab(1),b=ab(2)xx=19:44;plot(xx,a+b*xx.^2,x,y,'.')3.上机调试得到结果如下：x = 19 25 31 38 44y=19.0000 32.3000 49.0000 73.3000 97.8000a = 0.9726b = 0.0500图形：四．心得体会通过本次的数学模型的建立与处理，我们学习并掌握了用最小二乘法进行数据拟合，及多项式数据拟合的方法，进一步学会了使用matlab软件，加深了我们的数学知识，提高了我们解决实际问题的能力，为以后深入学习数学建模打下了坚实的基础。

数学建模实验报告（二）——用Newton法求方程的解一．实验目的1.掌握Newton法求方程的解的原理和方法。

2.利用Matlab进行编程求近似解。

二．实验任务来自课本109页习题4-2：用Newton法求f(x)=x-cosx=0的近似解三．实验过程1.实验原理：把f(x)在x0点附近展开成泰勒级数f(x) = f(x0)+(x－x0)f'(x0)+(x－x0)^2*f''(x0)/2! +… 取其线性部分，作为非线性方程f(x) = 0的近似方程，即泰勒展开的前两项，则有f(x0)+f'(x0)(x－x0)=0 设f'(x0)≠0则其解为x1=x0－f(x0)/f'(x0) 这样，得到牛顿法的一个迭代序列：x(n+1)=x(n)－f(x(n))/f'(x(n))。

一、实验背景与目的随着科学技术的不断发展，数学建模作为一种解决复杂问题的有力工具，在各个领域都得到了广泛应用。

本实验旨在通过数学建模的方法，解决实际问题，提高学生的数学思维能力和解决实际问题的能力。

二、实验内容与步骤1. 实验内容本实验选取了一道具有代表性的实际问题——某城市交通拥堵问题。

通过对该问题的分析，建立数学模型，并利用MATLAB软件进行求解，为政府部门提供决策依据。

2. 实验步骤（1）问题分析首先，对某城市交通拥堵问题进行分析，了解问题的背景、目标及影响因素。

通过查阅相关资料，得知该城市交通拥堵的主要原因是道路容量不足、交通信号灯配时不当、公共交通发展滞后等因素。

（2）模型假设为简化问题，对实际交通系统进行以下假设：1）道路容量恒定，不考虑道路拓宽、扩建等因素；2）交通信号灯配时固定，不考虑实时调整；3）公共交通系统运行正常，不考虑公交车运行时间波动；4）车辆行驶速度恒定，不考虑车辆速度波动。

（3）模型构建根据以上假设，构建以下数学模型：1）道路容量模型：C = f(t)，其中C为道路容量，t为时间；2）交通流量模型：Q = f(t)，其中Q为交通流量；3）拥堵指数模型：I = f(Q, C)，其中I为拥堵指数。

（4）模型求解利用MATLAB软件，对所构建的数学模型进行求解。

通过编程实现以下功能：1）计算道路容量C与时间t的关系；2）计算交通流量Q与时间t的关系；3）计算拥堵指数I与交通流量Q、道路容量C的关系。

（5）结果分析与解释根据求解结果，分析拥堵指数与时间、交通流量、道路容量之间的关系。

针对不同时间段、不同交通流量和不同道路容量，提出相应的解决方案，为政府部门提供决策依据。

三、实验结果与分析1. 结果展示通过MATLAB软件求解，得到以下结果：（1）道路容量C与时间t的关系曲线；（2）交通流量Q与时间t的关系曲线；（3）拥堵指数I与交通流量Q、道路容量C的关系曲线。

2. 结果分析根据求解结果，可以得出以下结论：（1）在高峰时段，道路容量C与时间t的关系曲线呈现下降趋势，说明道路容量在高峰时段不足；（2）在高峰时段，交通流量Q与时间t的关系曲线呈现上升趋势，说明交通流量在高峰时段较大；（3）在高峰时段，拥堵指数I与交通流量Q、道路容量C的关系曲线呈现上升趋势，说明拥堵指数在高峰时段较大。

数学建模实习报告4篇数学建模实习报告篇1大一第二学期的第九周，我们建筑工程学院的学生在陈金陵院长，彭莉英和梁桥等老师的带领下进行了为期一周的认知实习。

众说周知。

建筑工程行业是相当注重实际经验的。

身为一名应用型本科土木专业的学生，经验对我们来说就更加重要了。

这次我们终于有机会去众多的建筑工地实地考察了。

一周以来，前两天天气炎热，后两天大于瓢泼，天气一直不好，我们先后去了长沙和湘潭等地考察，时间紧，路途远，是比较累的。

但一周以来，我却始终怀着兴奋的心情，认真听着老师和施工员，监理人员的实地讲解，这使我收获很大。

这不但使我对本专业的认识进一步加强，也是我对今后工作的选择有了初步的认识。

下面就是我本次实习的具体行程和我的体会。

一、实习地点及日程安排:2023年4月13日实习动员参观主校区2023年4月15日上午参观莲城大桥金屏村铁路桥晚上“招标与投标”专业知识讲座2023年4月16日上无参观并解工业厂房与民用住宅的异同观看湘潭市体育公园施工过程二、实习目的：认识实习是整个实习教学计划中的一个有机组成部分，是土木工程专业的一个重要的实践性环节。

通过组织参观和听取一些专题技术报告，收集一些与实习课题有关的资料和素材，为顺利完成实习打下坚实基础。

通过实习应达到以下目的：1.了解普通住宅结构2.初步了解体育馆结构设计及施工过程3.了解桥梁道路铁路桥梁等设计及结构4.了解工用与民用建筑的区别联系5.了解建筑结构领域的最新动态和发展方向6.提高艺术修养，加深对建筑与艺术的了解7.培养专业兴趣，明确学习目的三、实习过程及内容：2023年4月13号星期一晴上午，在图书馆第二报告厅内，我们认真聆听了陈院长和湘潭市建筑设计院的专家讲说。

陈院长概括了我们这次实习的行程安排，接着设计院的专家细致的为我们介绍了现在设计院内的工作要求，也就是告诉我们要达到怎们样的水平才有机会计入设计院工作。

这对我们既是鞭策是鼓励。

下午天气温和，我们怀着兴奋的心情，在陈院长的带领下参观我们学校的新校区。

第1篇一、实验背景随着信息技术的飞速发展，数字建模在各个领域中的应用越来越广泛。

数字应用建模是将现实世界的复杂问题转化为数学模型，通过计算机模拟和分析，为决策提供科学依据。

本实验旨在通过数字应用建模的方法，解决实际问题，提高学生对数学建模的理解和应用能力。

二、实验目的1. 理解数字应用建模的基本原理和方法；2. 掌握数学建模软件的使用；3. 提高解决实际问题的能力；4. 培养团队合作精神和沟通能力。

三、实验内容1. 实验题目：某城市交通流量优化研究2. 实验背景：随着城市人口的增加，交通拥堵问题日益严重。

为了缓解交通压力，提高城市交通效率，本研究旨在通过数字应用建模方法，优化该城市的交通流量。

3. 实验步骤：（1）数据收集：收集该城市主要道路的实时交通流量数据、道路长度、交叉口数量、道路等级等数据。

（2）建立数学模型：根据交通流量数据，建立交通流量的数学模型，如线性回归模型、多元回归模型等。

（3）模型求解：利用数学建模软件（如MATLAB、Python等）对建立的数学模型进行求解，得到最优交通流量分布。

（4）结果分析：对求解结果进行分析，评估优化后的交通流量分布对缓解交通拥堵的影响。

（5）模型改进：根据分析结果，对模型进行改进，以提高模型的准确性和实用性。

4. 实验结果：（1）通过建立数学模型，得到优化后的交通流量分布。

（2）优化后的交通流量分布较原始分布，道路拥堵程度明显降低，交通效率得到提高。

（3）通过模型改进，进一步优化交通流量分布，提高模型的准确性和实用性。

四、实验总结1. 本实验通过数字应用建模方法，成功解决了某城市交通流量优化问题，提高了交通效率，为城市交通管理提供了科学依据。

2. 在实验过程中，学生掌握了数学建模的基本原理和方法，熟悉了数学建模软件的使用，提高了解决实际问题的能力。

3. 实验过程中，学生学会了团队合作和沟通，提高了自己的综合素质。

五、实验心得1. 数字应用建模是一种解决实际问题的有效方法，通过建立数学模型，可以将复杂问题转化为可操作的解决方案。

一、实验目的1. 掌握数学建模的基本步骤，学会运用数学知识分析和解决实际问题。

2. 提高数学建模能力，培养创新思维和团队合作精神。

3. 熟练运用数学软件进行数据分析、建模和求解。

二、实验内容本次实验选取了以下三个题目进行建模：1. 题目一：某公司想用全行业的销售额作为自变量来预测公司的销售量，表中给出了1977—1981年公司的销售额和行业销售额的分季度数据（单位：百万元）。

2. 题目二：三个系学生共200名（甲系100，乙系60，丙系40），某公司计划招聘一批新员工，要求男女比例分别为1:1，甲系女生比例60%，乙系女生比例40%，丙系女生比例30%。

请为公司制定招聘计划。

3. 题目三：研究某市居民出行方式选择问题，收集了以下数据：居民年龄、收入、职业、出行距离、出行时间、出行频率等。

请建立模型分析居民出行方式选择的影响因素。

三、实验步骤1. 问题分析：对每个题目进行分析，明确问题背景、目标和所需求解的数学模型。

2. 模型假设：根据问题分析，对实际情况进行简化，提出合适的模型假设。

3. 模型构建：根据模型假设，选择合适的数学工具和方法，建立数学模型。

4. 模型求解：运用数学软件（如MATLAB、Python等）进行模型求解，得到结果。

5. 结果分析与解释：对求解结果进行分析，解释模型的有效性和局限性。

四、实验报告1. 题目一：线性回归模型（1）问题分析：利用线性回归模型预测公司销售量，分析行业销售额对销售量的影响。

（2）模型假设：假设公司销售量与行业销售额之间存在线性关系。

（3）模型构建：根据数据，建立线性回归模型y = β0 + β1x + ε，其中y为公司销售量，x为行业销售额，β0、β1为回归系数，ε为误差项。

（4）模型求解：运用MATLAB软件进行线性回归分析，得到回归系数β0、β1。

（5）结果分析与解释：根据模型结果，分析行业销售额对销售量的影响程度，并提出相应的建议。

2. 题目二：招聘计划模型（1）问题分析：根据男女比例要求，制定招聘计划，确保男女比例均衡。

数学建模实验报告班级:姓名:学号:元件可靠性问题一、实验问题:给出3种不同情况的元件连接方式, 分别求解他们的正常运行概率。

其中每个元件的正常运行概率均为p。

元件数为N, 方式2与方式3用到了与A元件相同的N个B元件。

连接方式如图：方式1:方式2:方式3:二、问题分析:Ｎ个元件的连接方式, 相当于电阻的串并联, 所以可以用电阻串并联的关系去分析各无件之间的关系:对于方式一来说, 相当于电阻的串联。

所以, 他的正常运行的概率为p^n.对于方式二来说, 相当于电阻先串联再并联。

所以, 他的正常运行的概率为：1-(1-P^n)(1-P^n)=2P^n-P^2n.对于方式三来说, 相当于电阻先并联再串联。

所以, 他的正常运行的概率为:(1-(1-P^n)^2)^n=(2p-p^2)^n现在再比较三个系统正常工作概率大小P1- P2= p^n–(2p^n-p^2n )= p^2n–p^n 由于0<p<1,所以易知P^2n-P^n<０。

所以有P1< P2P2- P3=(2p^n- p^2n)- (2p-p^2)^n= p^n［(2- p^n)-(2-p)^n］因为p^n>0,所以只要比较［(2- p^n)-(2-p)^n］大小即可。

对此式求导有-n［p^(n-1)-(2-p)^n-1］可见此式恒大于零,所以函数单调递增。

当p=１时, ［(2- p^n)-(2-p)^n］=0.所以P2- P3 <0, 再由上求导可知所以P2<P3所以P3最大。

即其的可靠性最高。

理发店问题实验题目:（１）某单人理发店有４反椅子接待顾客排队理发, 当４把椅子都坐满人时, 后来的顾客就不进店而离去。

顾客平均到达速率为４人／Ｈ, 理发时间平均10min/人。

设到达过程为泊松流, 服务时间服从负指数颁布。

求：（２）顾客一到达就能理发的概率；（３）系统中顾客数的期望值和排队等待顾客数的期望值；（４）顾客在理发店内逗留的全部时间的期望值；（５）在可能到达的顾客中因客满离开的概率。

数学建模社会实践报告范文大全第一篇：数学建模社会实践报告数学建模社会实践报告----暑期的心得摘要本文通过描写大学生参加数学建模培训的亲身经历，讲诉大学生社会实践酸甜苦辣，表达了大学生参加社会实践的重要性、必要性和重大意义。

通过这学期的数学建模训练，使我感触良多，它所教给我的不单是一些数学方面的知识，更多的其实是综合能力的培养、锻炼与提高。

它培养了我全面、多角度考虑问题的能力，使我的逻辑推理能力和量化分析能力得到很好的锻炼和提高。

它还让我了解了多种数学软件，以及运用数学软件对模型进行求解。

数学建模属于一门应用数学，学习这门课要求我们学会如何将实际问题经过分析、简化转化为一个数学问题，然后用适当的数学方法去解决。

数学建模是一种数学的思考方法，是运用数学的语言和方法，通过抽象、简化建立能近似刻画并“解决”实际问题的一种强有力的数学手段。

为了使描述更具科学性，逻辑性，客观性和可重复性，人们采用一种普遍认为比较严格的语言来描述各种现象，这种语言就是数学。

使用数学语言描述的事物就称为数学模型。

数学建模竞赛是本科生接触实际科学问题的第一步，是利用所学书本知识、广泛涉猎课外知识、利用数学和计算机工具、为某一具体问题建立抽象模型、给出求解方法并解决问题、最后撰写论文并给出客观评价的一个系统工程。

数学建模就是利用数学知识对一些实际问题建立模型，但又不是纯数学的。

它不仅要数学思维，还要计算机编程能力，论文写作能力，其实更重要的是团队协作能力，这是对以后工作有非常大的帮助的，更甚是人生。

总之，通过这次数学建模培训，我学了很多的知识，我也用了很多我们平时没有学到和听说过的知识，真是让我的眼界大开。

关键词：数学建模心得体会社会实践对数学建模的认识接近两个月的数学建模培训，我最大的收获可能就是我更深层次的了解了数模，得到很多资料，学到很多的知识。

在开始，在我大一的时候，对这个数学建模都有些迷茫，不知道这是干什么的，听名字就好陌生啊，觉得那是一件很高深的事情。

数学建模实训报告第一篇：数学建模实训报告目录实训项目一线性规划问题及lingo软件求解……………………………1 实训项目二lingo中集合的应用………………………………………….7 实训项目三lingo中派生集合的应用……………………………………9 实训项目四微分方程的数值解法一………………………………………13 实训项目五微分方程的数值解法二……………………………………..15 实训项目六数据点的插值与拟合………………………………………….17 综合实训作品…………………………………………………………….18 每次实训课必须带上此本子，以便教师检查预习情况和记录实验原始数据。

实验时必须遵守实验规则。

用正确的理论指导实践袁必须人人亲自动手实验，但反对盲目乱动，更不能无故损坏仪器设备。

这是一份重要的不可多得的自我学习资料袁它将记录着你在大学生涯中的学习和学习成果。

请你保留下来，若干年后再翻阅仍将感到十分新鲜，记忆犹新。

它将推动你在人生奋斗的道路上永往直前！项目一：线性规划问题及lingo软件求解一、实训课程名称数学建模实训二、实训项目名称线性规划问题及lingo软件求解三、实验目的和要求了解线性规划的基本知识，熟悉应用LINGO 解决线性规划问题的一般方法四：实验内容和原理内容一：某医院负责人每日至少需要下列数量的护士班次时间最少护士数1 6:00-10:00 60 2 10:00-14:00 70 3 14:00-18:00 60 4 18:00-22:00 50 5 22:00-02:00 20 6 02:00-06:00 30 每班的护士在值班的开始时向病房报道，连续工作8个小时，医院领导为满足每班所需要的护士数，最少需要多少护士。

内容二：内容三五：主要仪器及耗材计算机与Windows2000/XP系统；LINGO软件六：操作办法与实训步骤内容一：考虑班次的时间安排，是从6时开始第一班，而第一班最少需要护士数为60，故x1>=60，又每班护士连续工作八个小时，以此类推，可以看出每个班次的护士可以为下一个班次工作四小时，据此可以建立如下线性规划模型：程序编程过程：min=x1+x2+x3+x4+x5+x6;x1>=60;x1+x2>=70;x2+x3>=60; x3+x4>=50;x4+x5>=20;x5+x6>=30;编程结果：Global optimal solution found.Objective value:150.0000Infeasibilities:0.000000Total solver iterations:VariableValueReduced CostX160.000000.000000X210.000000.000000X350.000000.000000X40.0000001.000000X530.000000.000000X60.0000000.000000RowSlack or SurplusDual Price150.0000-1.0000000.000000-1.0000000.0000000.0000000.000000-1.0000000.0000000.00000010.000000.0000000.000000-1.000000 内容二：（1）max=6*x1+4*x2;2*x1+3*x2<100;4*x1+2*x2<120;x1,x2分别表示两种型号生产数量。

第1篇一、实验背景随着科学技术的飞速发展，数学建模作为一种重要的科学研究方法，越来越受到人们的重视。

初中数学建模实验旨在培养学生运用数学知识解决实际问题的能力，提高学生的创新思维和团队协作能力。

本实验以某市居民出行方式选择为研究对象，通过建立数学模型，分析不同因素对居民出行方式的影响。

二、实验目的1. 理解数学建模的基本概念和步骤。

2. 学会运用数学知识分析实际问题。

3. 培养学生的创新思维和团队协作能力。

4. 提高学生运用数学知识解决实际问题的能力。

三、实验方法1. 收集数据：通过网络、调查问卷等方式收集某市居民出行方式选择的相关数据。

2. 数据处理：对收集到的数据进行整理、清洗和分析，为建立数学模型提供依据。

3. 建立模型：根据数据分析结果，选择合适的数学模型，如线性回归模型、多元回归模型等。

4. 模型求解：运用数学软件或编程工具求解模型，得到预测结果。

5. 模型验证：将预测结果与实际数据进行对比，验证模型的准确性。

四、实验过程1. 数据收集：通过问卷调查的方式，收集了500份某市居民的出行方式选择数据，包括出行距离、出行时间、出行目的、出行方式等。

2. 数据处理：对收集到的数据进行整理和清洗，剔除无效数据，得到有效数据490份。

3. 建立模型：根据数据分析结果，选择多元回归模型作为本次实验的数学模型。

4. 模型求解：利用SPSS软件对多元回归模型进行求解，得到以下结果：- 模型方程：Y = 0.05X1 + 0.03X2 + 0.02X3 + 0.01X4 + 0.005X5 + 0.002X6 + 0.001X7 + 0.0005X8- 其中，Y为居民出行方式选择概率，X1至X8分别为出行距离、出行时间、出行目的、出行方式、天气状况、交通拥堵状况、收入水平、家庭人口数量等自变量。

5. 模型验证：将模型预测结果与实际数据进行对比，结果显示模型具有较高的预测准确性。

五、实验结果与分析1. 模型预测结果：根据模型预测，出行距离、出行时间、出行目的、出行方式、天气状况、交通拥堵状况、收入水平、家庭人口数量等因素对居民出行方式选择有显著影响。

数学建模试验报告（六）姓名学号 班级 问题：.（插值）在某海域测得一些点(x,y)处的水深z 由下表给出，船的吃水深度为5英尺，在矩形区域（75，200）*（-50，150）里的哪些地方船要避免进入。

问题的分析和假设：设该海域海底是平滑的，由于测量点散乱分布，先在平面上作出测量点的分布图，再利用三维插值法补充出一些点的水深，然后作出海底曲面图和等高线图，并求出水深小于2m 的海域分布范围图。

建模：该题只需用数学软件，运用已知各点画出相应的分布图、曲面图等就可分析出船要避免进入的范围，详解见Matlab 的程序代码和结果。

求解的Matlab 程序代码：clearX=[54.0 65.0 18.5 13.0 100.5 120.5 30.5 82.5 32.5 2.0 6.0 87.0 87.0 32.5];Y=[57.5 191.5 3.0 197.0 72.5 187.5 135.5 43.5 -31.0 53.0 106.5 -16.5 134.0 16.5];plot(X,Y ,'+');%绘制测量点分布图Z=[1.6 3.2 2.4 3.2 2.4 3.2 3.2 3.6 3.6 3.2 3.2 3.6 1.6 3.6];%a=linspace(0,150,100);………%线性等分向量%b=linspace(0,200,200);………%线性等分向量[x,y]=meshgrid(0:0.5:150,0:0.5:200);z=griddata(X,Y,Z,x,y,'cubic');%以三角形为基础的三次方程内插figure(2);meshz(x,y,z+2);%作海底地貌图figure(3);meshz(x,y,z);%作水深低于5英尺的部分海底曲面图figure(4);contour(x,y,z,[-2,2]);%作深度为5的海底等值线图xyz129 140 103.5 88 185.5 195 105 7.5 141.5 23 147 22.5 137.5 85.5 4 8 6 8 6 8 8 xyz 157.5 107.5 77 81 162 162 117.5 -6.5 -81 3 56.5 -66.5 84 -33.5 9 9 8 8 9 4 9计算结果与问题分析讨论：图1、测量分布图图2、海底地貌图图3、危险区域海底地貌图图4、海底危险区域平面图经过插值计算拟合后最终得到的图4中封闭曲线内部分则为“危险海域”，即落潮时海水深度小于2米的区域，船只应该避免进入。

第1篇一、实验背景数学建模是数学与其他学科交叉的一种研究方法，它通过建立数学模型来描述现实世界中的现象，从而为解决实际问题提供理论依据。

乘法作为基础的数学运算之一，广泛应用于各个领域。

本实验旨在通过数学建模的方法，探讨乘法运算在解决实际问题中的应用，提高学生对数学知识的理解和运用能力。

二、实验目的1. 了解数学建模的基本方法，掌握建立乘法模型的基本步骤。

2. 培养学生运用数学知识解决实际问题的能力。

3. 提高学生对乘法运算的理解和应用水平。

三、实验内容1. 问题提出假设某公司生产一种产品，每件产品成本为20元，售价为30元。

公司计划在一段时间内销售1000件产品，请建立数学模型预测公司在该时间段内的利润。

2. 模型建立（1）定义变量设公司销售产品的数量为x件，则公司获得的利润为y元。

（2）建立关系式根据题意，每件产品的利润为售价减去成本，即10元。

因此，公司销售x件产品的总利润为10x元。

（3）确定模型利润y与销售数量x之间的关系可以表示为：y = 10x。

3. 模型求解（1）确定模型参数根据题意，公司计划销售1000件产品，即x = 1000。

（2）代入参数求解将x = 1000代入模型y = 10x，得到y = 10 × 1000 = 10000。

（3）结果分析通过计算可知，公司在该时间段内的利润为10000元。

4. 模型验证为了验证模型的准确性，我们可以根据实际情况调整销售数量，重新计算利润，并与实际结果进行比较。

四、实验结果与分析通过本实验，我们成功建立了乘法模型，并预测了公司销售产品的利润。

实验结果表明，乘法模型能够有效地解决实际问题，为决策提供理论依据。

五、实验总结1. 数学建模是解决实际问题的重要方法，通过建立数学模型，我们可以将实际问题转化为数学问题，并运用数学知识进行求解。

2. 乘法模型在解决实际问题中具有广泛的应用，我们可以通过乘法模型预测、分析各种现象。

3. 在进行数学建模时，需要注意以下几点：（1）准确理解问题，明确模型的目标和变量。

在下面的题目中选做100分的题目，给出详略得当的答案。

一.通过举例简要说明数学建模的一般过程或步骤。

(15分)答：建立数学模型的方法大致有两种，一种是实验归纳的方法，即根据测试或计算数据，按照一定的数据，按照一定的数学方法，归纳出系统的数学模型；另一种是理论分析的方法，具体步骤有五步（以人口模型为例）：1、明确问题，提出合理简化的假设：首先要了解问题的实际背景，明确题目的要求，收集各种必要的信息2、建立模型：据所做的假设以及事物之间的联系，构造各种量之间的关系。

（查资料得出数学式子或算法）。

3、模型求解：利用数学方法来求解上一步所得到的数学问题，此时往往还要做出进一步的简化或假设。

注意要尽量采用简单的数学公具。

例如：马尔萨斯模型，洛杰斯蒂克模型4、模型检验：根据预测与这些年来人口的调查得到的数目进行对比检验5、模型的修正和最后应用：所建立的模型必须在实际应用中才能产生效益，根据预测模型，制定方针政策，以实现资源的合理利用和环境的保护。

二.把一张四条腿等长的正方形桌子放在稍微有些起伏的地面上，通常只有三只脚着地，然而只需稍为转动一定角度，就可以使四只脚同时着地，即放稳了。

(1) 请用数学模型来描述和证明这个实际问题; (2)讨论当桌子是长方形时，又该如何描述和证明？(15分)答：模型假设：1．椅子四条腿一样长，椅脚与地面的接触部分相对椅子所占的地面面积可视为一个点。

2．地面凹突破面世连续变化的，沿任何方向都不会出现间断（没有向台阶那样的情况），即地面可看作数学上的连续曲面。

3．相对椅脚的间距和椅子腿的长度而言，地面是相对平坦的，即使椅子在任何位置至少有三条腿同时着地。

4．椅子四脚连线所构成的四边形是圆内接四边形，即椅子四脚共圆。

5．挪动仅只是旋转。

我们将椅子这两对腿的交点作为坐标原点，建立坐标系，开始时AC、BD这两对腿都在坐标轴上。

将AC和BD这两条腿逆时针旋转角度θ。

记AC到地面的距离之和为f(θ)。

《数学建模》实验报告计算过程如下, 结果如下:画图程序命令如下:函数图象如下:实验题目二: 编写利用顺序Guass消去法求方程组解的M-函数文件,并计算方程组的解解: M-函数文件如下:方程组的计算结果如下:实验题目三: 编写“商人们安全过河”的Matlab程序解: 程序如下:function foot=chouxiang%%%%%%%%%%%%%%%%%%%%%% 程序开始需要知道商人数, 仆人数, 船的最大容量n=input('输入商人数目:');nn=input('输入仆人数目:');nnn=input('输入船的最大容量:');if nn>nn=input('输入商人数目:');nn=input('输入仆人数目:');nnn=input('输入船的最大容量:');end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 决策生成jc=1; % 决策向量存放在矩阵“d”中, jc为插入新元素的行标初始为1for i=0:nnnfor j=0:nnnif (i+j<=nnn)&(i+j>0) % 满足条件D={(u,v)|1<=u+v<=nnn,u,v=0,1,2}d(jc,1:3)=[i,j 1]; %生成一个决策向量后立刻将他扩充为三维（再末尾加“1”）d(jc+1,1:3)=[-i,-j,-1]; % 同时生成他的负向量jc=jc+2; % 由于一气生成两个决策向量,jc指标需要往下移动两个单位endendj=0;end再验证：程序结果说明在改变商人和仆人数目, 其他条件不变的条件下。

可能无法得到结果。

程序结果说明在改变商人和仆人数目，其他条件不变的条件下。

可能无法得到结果。

数学建模实习报告[定稿]第一篇：数学建模实习报告[定稿]数学建模实习报告一、实习目的数学建模主要是将显示对象的信息加以翻译、归纳的产物。

通过对数学模型的假设、求解、验证，得到数学上的解答，在经过翻译回到现实对象，给出分析、决策的结果。

数学建模对我们并不陌生，在我们的日常生活和工作中，经常会用到有关建模的概念。

例如，我们平时出远门，会考虑一下出行的路线，以达到既快速又经济的目的；一些厂长为了获得更大的利润，往往会策划出一个合理安排生产和销售的最优方案......这些问题和建模都有着很大的联系。

通过数学建模培训，就会知道解决问题的原理。

学习更多的数学方面的知识及其应用，数学建模的过程可以培养我们全面、多角度考虑问题的能力，使我们的逻辑推理能力和量化分析能力得到很好的锻炼和提高，它还可以让我了解多种数学软件以及如何运用数学软件对模型求解。

二、实习内容（一）实习单位简介西安财经学院统计学院数学建模组是以信息与计算科学系主任王培勋教授为组长的指导教师组，每年都组队参加高教社杯全国大学生数学建模竞赛，并取得了优异的成绩。

今年我院数学建模参赛队员的选拔是经过学生自愿报名、考试选拔、集中培训等环节来进行的。

30 名最后入选的学生，组建了10个队，经过一个暑假的培训，基本全部掌握了数学软件的计算机程序设计方法，掌握了常用的数学建模方法。

在三天三夜的竞赛过程中，各参赛小组学员勇于拼搏，力争创新，在规定的七十二小时内顺利完成了答卷。

（二）实习内容数学建模是运用数学思想、方法和知识解决实际问题的过程，它为我们学生提供了自主学习的空间，有助于我们体验数学在解决实际问题中的价值和作用，体验数学与日常生活和其他学科的联系，体验综合运用知识和方法解决实际问题的过程，增强应用意识；有助于激发我们学习数学的兴趣，发展我们的创新意识和实践能力。

数学建模与数学实验开创了大学生把数学理论和专业知识有机结合的新途径，是培养学生分析问题、解决问题和使用计算机进行科学计算的有效方法，是培养学生创新能力和实践能力的有效手段。

第1篇一、前言数学建模是现代科学技术领域的一种重要方法，它将数学理论与实际问题相结合，为解决实际问题提供了一种新的思路。

近年来，随着我国高等教育的快速发展，数学建模教学逐渐成为各高校教学的重要组成部分。

本文以某高校数学建模课程为例，对数学建模教学实践进行总结和分析。

二、教学目标与内容1. 教学目标（1）使学生掌握数学建模的基本理论和方法；（2）提高学生运用数学知识解决实际问题的能力；（3）培养学生的创新意识和团队协作精神。

2. 教学内容（1）数学建模的基本理论：数学建模的概念、数学建模的方法、数学建模的步骤等；（2）数学建模的常用工具：MATLAB、Mathematica、Excel等；（3）实际问题案例分析：从实际问题中提取数学模型，运用数学方法求解；（4）团队协作与论文撰写：培养学生团队合作精神和论文撰写能力。

三、教学方法与手段1. 教学方法（1）启发式教学：引导学生主动思考，激发学生的学习兴趣；（2）案例教学：通过实际案例，让学生了解数学建模的应用；（3）小组讨论：培养学生的团队协作精神，提高学生解决问题的能力；（4）实践操作：通过实际操作，让学生掌握数学建模的方法和工具。

2. 教学手段（1）多媒体课件：利用多媒体课件展示数学建模的理论和方法；（2）网络资源：利用网络资源，拓展学生的知识面；（3）实践平台：搭建实践平台，让学生在实际操作中提高数学建模能力。

四、教学过程1. 理论教学在理论教学中，教师重点讲解数学建模的基本理论和方法，引导学生掌握数学建模的步骤和常用工具。

同时，结合实际案例，让学生了解数学建模的应用。

2. 实践教学在实践教学环节，教师布置实际问题，要求学生运用所学知识进行建模和求解。

学生通过小组讨论、实践操作，提高数学建模能力。

教师对学生的作品进行点评和指导，帮助学生改进和完善。

3. 论文撰写在论文撰写环节，教师指导学生整理和总结建模过程，撰写论文。

通过论文撰写，培养学生的团队协作精神和论文撰写能力。

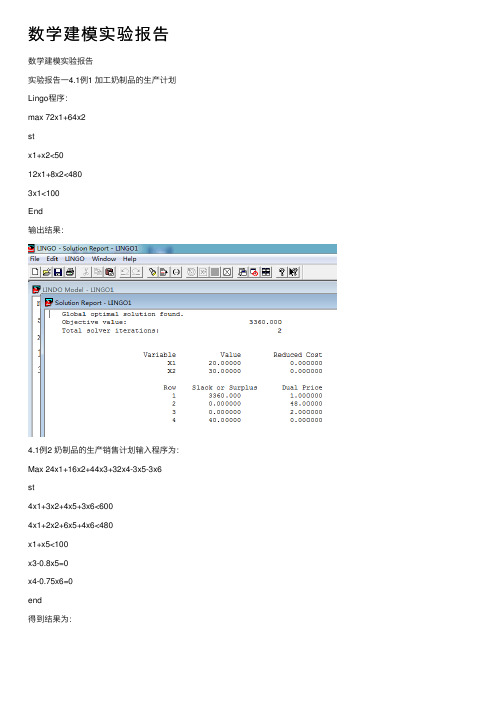
数学建模实验报告数学建模实验报告实验报告⼀4.1例1 加⼯奶制品的⽣产计划Lingo程序：max 72x1+64x2stx1+x2<5012x1+8x2<4803x1<100End输出结果：4.1例2 奶制品的⽣产销售计划输⼊程序为：Max 24x1+16x2+44x3+32x4-3x5-3x6st4x1+3x2+4x5+3x6<6004x1+2x2+6x5+4x6<480x1+x5<100x3-0.8x5=0x4-0.75x6=0end得到结果为：4.2例1 ⾃来⽔输送问题输⼊程序为：Min160x11+130x12+220x13+170x14+140x21+130x22+190x23+150x24+190x31+200x32 +230x33 stx11+x12+x13+x14=50x21+x22+x23+x24=60x31+x32+x33=50x11+x21+x31>30x11+x21+x31<80x12+x22+x32>70x12+x22+x32<140x13+x23+x33>10x13+x23+x33<30x14+x24>10x14+x24<50end输出结果：4.2例2 货运装机输⼊程序：Max3100x11+3100x22+3100x13+3800x21+3800x22+3800x23+3500x31+3500x32+3500x 33+2850x41+2850x42+2850x43stx11+x12+x13<18x21+x22+x23<15x31+x32+x33<23x41+x42+x43<12x11+x21+x31+x41<10x12+x22+x32+x42<16x13+x23+x366+x43<8480x11+650x21+580x31+390x41<6800 480x12+650x22+580x32+390x42<8700 480x13+650x23+580x33+390x43<5300 输出结果：4.3例1汽车⼚⽣产计划max 2x1+3x2+4x31.5x1+3x2+5x3<600280x1+250x2+400x3<60000 endgin 3输出结果：4.3例2 原油采购与加⼯max 4.8x11+4.8x21+5.6x12+5.6x22-10x1-8x2-6x3 st x-x1-x2-x3=0x11+x12-x<500x21+x22<10000.5x11-0.5x21>00.4x12-0.6x22>0x1-500y1<0x2-500y2<0x3-500y3<0x1-500y2>0x2-500y3>0int y1int y2int y3输出结果：4.4例1 混合泳接⼒队的选拔min 66.8x11+75.6x12+87x13+58.6x14 +57.2x21+66x22+66.4x23+53x24+78x31+67.8x32+84.6x33+59.4x34+70x41+74.2x42+69.4x43+57.1x44+67.4x51+71x52+83.8x53+62.4x54stx11+x12+x13+x14<=1x21+x22+x23+x24<=1x31+x32+x33+x34<=1x41+x42+x43+x44<=1x11+x21+x31+x41+x51=1x12+x22+x32+x42+x52=1x13+x23+x33+x43+x53=1x14+x24+x34+x44+x54=1endint 20输出结果：4.4例2 选课策略min x1+x2+x3+x4+x5+x6+x7+x8+x9 st x1+x2+x3+x4+x5>2x3+x5+x6+x8+x9>3 x4+x6+x7+x9>22x3-x1-x2<0x4-x7<02x5-x1-x2<0x6-x7<0x8-x5<02x9-x1-x2<0endint x1int x2int x3int x4int x5int x6int x7int x8int x9输出结果：实验报告⼆P236 例4.⼯作选择（1）对⼯作选择中的：贡献、收⼊、发展、声誉、关系、位置六个变量进⾏打分，分别为5，9，8，5，8，3。