算法笔试题总结
- 格式:doc
- 大小:80.00 KB
- 文档页数:5

java 经典笔试算法题一、排序算法1. 实现一个基于Java的快速排序算法。
答:快速排序是一种常用的排序算法,其核心思想是分治法。
首先选择一个基准元素,将数组分成两部分,一部分小于基准元素,一部分大于基准元素。
然后递归地对这两部分继续进行快速排序,直到整个数组有序。
2. 实现一个稳定的冒泡排序算法。
答:冒泡排序是一种简单的排序算法,通过重复地遍历待排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
稳定的冒泡排序算法是指在排序过程中,相同元素的相对位置不会改变。
3. 实现一个选择排序算法。
答:选择排序是一种简单直观的排序算法。
其工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
二、字符串操作算法1. 实现一个函数,将一个字符串反转。
答:可以使用StringBuilder类的reverse()方法来实现字符串的反转。
2. 实现一个函数,将一个字符串中的所有大写字母转换为小写字母,其余字符保持不变。
答:可以使用String类的replaceAll()方法和toLowerCase()方法来实现。
3. 实现一个函数,将一个字符串按空格分割成单词数组,并删除空字符串和null字符串。
答:可以使用split()方法和Java 8的流来处理。
三、数据结构算法1. 实现一个单向链表,并实现插入、删除、查找和打印链表的功能。
答:单向链表是一种常见的数据结构,可以通过定义节点类和链表类来实现。
插入、删除、查找和打印链表的功能可以通过相应的方法来实现。
2. 实现一个二叉搜索树(BST),并实现插入、查找、删除节点的功能。
答:二叉搜索树是一种常见的数据结构,它具有唯一的高度特性。
插入、查找和删除节点的功能可以通过相应的方法来实现,如左旋、右旋、递归等。
3. 实现一个哈希表(HashMap),并实现插入、查找和删除键值对的功能。
答:HashMap是一种基于哈希表的映射数据结构,它通过哈希码的方式将键映射到对应的值上。

ai算法岗位的笔试题一、问题描述在AI算法岗位的笔试题中,通常会涉及以下几个方面的内容:1. 基本概念:回答与AI算法相关的基本概念,如机器学习、深度学习、神经网络等的定义和特点,以及它们在实际应用中的作用和意义。
2. 数据预处理:描述常见的数据预处理方法,如标准化、归一化、缺失值处理、异常值处理等。
并解释为什么需要进行数据预处理,以及预处理的方法对算法效果的影响。
3. 机器学习算法:回答关于机器学习算法的问题,如逻辑回归、支持向量机、决策树、随机森林、梯度提升树等的原理和特点,以及它们的优缺点和适用场景。
4. 深度学习算法:阐述深度学习算法的基本原理,如卷积神经网络、循环神经网络、长短时记忆网络等的结构和作用,以及它们在计算机视觉、自然语言处理等领域的应用。
5. 模型评估与调优:介绍常见的模型评估指标,如准确率、召回率、F1值、AUC等,并说明如何选择适当的评估指标来评估模型的性能。
此外,描述常用的模型调优方法,如交叉验证、网格搜索、学习曲线等,以提高模型的泛化能力。
6. 算法实现:回答有关算法实现的问题,如特征选择、特征提取、模型训练、模型预测等的具体步骤和技巧,以及常见的编程语言和工具,如Python、Scikit-learn、TensorFlow等。
二、回答示例1. 基本概念:AI算法是指通过计算机模拟人类智能的算法。
机器学习是AI算法的一个重要分支,它是通过从数据中学习规律,从而实现对未知数据的预测和分类。
深度学习则是机器学习的一种方法,它模拟人脑的神经网络结构,通过多层次的神经元和权重来提取和学习数据的特征。
2. 数据预处理:数据预处理是在进行机器学习和深度学习之前对数据进行的一系列操作,以提高算法的性能和准确度。
常见的数据预处理方法包括标准化、归一化、缺失值处理和异常值处理。
标准化是将数据转化为均值为0,方差为1的分布;归一化是将数据缩放到0-1之间的范围;缺失值处理是对缺失值进行填充或删除;异常值处理是对超出正常范围的值进行处理。

一面:(35 分钟)1、重点讲两个项目就项目提问了一些问题在此不赘述2、说一下LSTM,3 个门的方程,输出由哪几个状态决定3、改良版是什么?GRU 改良了哪些结构4、BN 的参数,原理说一下5、推荐算法了解吗(我说不了解)6、有什么要问我的--------------------------------------------------------------------------------------------------------------------------------- ----------------二面:(1 个小时)1、你说你做DL 做得比较多是吧好把CNN 的发展历史从2010 年开始按时间轴顺序说一下,各个网络结构的特点优点,解决了之前什么问题(当时就斯密达了,忘了挺多,就重点说了下alexnet vgg resnet)2、你用的网络和文章里的结构差不多吗?有没有自己的创新?那你做和别人做有啥差别呢?2、resnet 说一下shortcut,两个mapping 、为啥可以无损传播梯度,为啥可以缓解网络退化3、除了深度做文章,还从哪些方面作文章(Inception)说一下4、做项目遇到过过拟合都是怎么解决的5、介绍一下正则,L1 L2 的比较,为啥L1 更稀疏6、tensorflow 或者caffe 的底层代码看过吗卷积是怎么实现的GPU 进行并行计算时如何计算矩阵卷积的7、感受野受哪几个参数的影响,给了一个距离例子,计算感受野的大小8、数据结构题目:如何判断一个链表上是否有环快慢指针如果快指针走3 步的话呢还能奏效吗? 如果快慢指针的起点不一样呢,还能奏效吗?9、数学题:凸函数有什么优点?如何证明一个n 元函数是凸函数?10、有什么想问我的--------------------------------------------------------------------------------------------------------------------------------- ----------------hr 面:11 分钟1、自我介绍2 分钟2、项目中最有成就感的一次最有挫折感的一次3、为什么想要加入jd?4、你性格上的优势和劣势是什么5、如果和leader 意见不统一如何解决6、你的职业生涯规划是什么7、有什么想问我的吗。

用ts笔试算法题什么是算法?算法是一种解决问题的方法或步骤。
它是一个有序的、确定性的计算过程,以解决某个特定问题或完成某个特定任务。
算法可以用来处理各种类型的数据,如数字、字符串、图形等。
算法的设计和分析是计算机科学的基础。
它涉及到选择合适的数据结构和算法来解决问题,以及评估算法的效率和复杂度。
TypeScript(TS)简介TypeScript是一种由微软开发的开源编程语言,它是JavaScript的超集。
TypeScript通过添加静态类型和其他编程概念来增强JavaScript,并提供了更好的开发工具和更强大的类型检查功能。
与JavaScript相比,TypeScript具有更严格的语法和类型检查,可以提前发现潜在的错误,并提供更好的代码补全和重构功能。
它还支持面向对象编程和模块化开发,使得开发大型应用程序更加容易。
算法题示例下面是一个示例算法题,用TypeScript编写一个函数,实现对一个数组进行排序。
function bubbleSort(arr: number[]): number[] {const n = arr.length;for (let i = 0; i < n - 1; i++) {for (let j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {const temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}return arr;}const arr = [64, 34, 25, 12, 22, 11, 90];console.log(bubbleSort(arr)); // [11, 12, 22, 25, 34, 64, 90]这个示例实现了冒泡排序算法,它是一种简单但效率较低的排序算法。
它的基本思想是通过重复比较相邻的两个元素,如果顺序不对则交换它们,直到整个数组排序完成。

多益算法工程师笔试题目
多益算法工程师的笔试题目一般会涉及数据结构、算法、编程语言等方面的知识,以下是一些可能出现的题目类型:
1. 数据结构类题目:例如,给定一个无序数组,要求找出其中出现次数超过一半的元素;或者给定一个二叉树,要求求出其中任意两个节点的最大距离等。
2. 算法类题目:例如,给定一个字符串,要求编写一个函数判断该字符串是否为回文字符串;或者给定一个无向图,要求求出其中的最小生成树等。
3. 编程语言类题目:例如,给定一个整数数组,要求编写一个函数将其排序并返回排序后的结果;或者给定一个字符串,要求编写一个函数将其转换为大写字母等。
除了以上这些题目类型,多益算法工程师的笔试题目还可能涉及数学、概率统计、逻辑思维等方面的知识,要求考生具备较为全面的知识和技能。

1. 什么是文本清洗?请简述其步骤。
2. 什么是词向量?如何训练词向量?
3. 简述朴素贝叶斯分类器的原理。
4. 什么是TF-IDF?它在信息检索中有何作用?
5. 请解释RNN、LSTM和GRU的区别和联系。
6. 什么是注意力机制?它在NLP中有何应用?
7. 请简述BERT模型的原理和作用。
8. 什么是词性标注和命名实体识别?请简述其算法。
9. 请解释什么是语义角色标注。
10. 请简述文本生成中的BLEU、ROUGE等评价指标的原理和应用。
以上题目涵盖了NLP领域的一些基本概念和算法,包括文本清洗、词向量、分类器、TF-IDF、RNN、注意力机制、BERT、词性标注、命名实体识别、语义角色标注和文本生成的评价指标等。
对于这些题目,需要了解相关的概念、原理和应用,并能够根据具体的问题进行解答和应用。

用ts笔试算法题用TS(时间序列)算法题时间序列数据是一种常见的统计数据类型,在很多领域都有广泛的应用。
本篇文档将介绍一个基于时间序列的算法题,并给出相应的解题思路和代码实现。
题目描述:给定一组时间序列数据,要求设计一个算法,根据给定的时间戳,快速查找指定时间点的时间序列数据。
时间序列数据可能包含缺失值或异常值,需要设计合理的算法进行处理。
解题思路:1. 数据预处理:对时间序列数据进行清洗和预处理,包括去除缺失值、异常值和噪声数据等。
可以使用一些统计方法和算法进行数据清洗,如均值填充、中位数填充等。
2. 时间戳排序:对时间序列数据进行排序,按照时间戳的顺序排列数据,以便后续查找。
3. 建立索引:为了提高查找效率,可以使用一些索引技术建立时间序列数据的索引。
常用的索引技术包括前缀索引、倒排索引等。
在本题中,可以使用前缀索引建立时间戳和对应的时间序列数据的映射关系。
4. 查找算法:根据时间戳进行查找时,可以利用索引快速定位到对应的时间序列数据。
常用的查找算法有二分查找、哈希查找等。
在本题中,可以使用哈希查找算法进行查找,根据时间戳计算哈希值,然后根据哈希值在索引中找到对应的记录。
代码实现:以下是一个基于Python的时间序列数据查找算法的实现示例:```pythonimport numpy as npfrom sklearn.preprocessing import MinMaxScalerfrom collections import defaultdictdef build_index(data):# 数据预处理:去除异常值和噪声数据data = np.array(data)data[data < np.min(data)] = np.min(data)data[data > np.max(data)] = np.max(data)# 数据排序data = data[np.argsort(data[:, 0])]# 建立前缀索引index = defaultdict(list)for i, (timestamp, value) in enumerate(data):index[timestamp].append((i, value))return indexdef hash_search(index, timestamp):# 根据时间戳计算哈希值hash_value = hash(str(timestamp)) % len(index)# 在索引中查找对应的记录result = []for timestamp, value in index[hash_value]:if timestamp == timestamp:result.append((timestamp, value))return result, len(index) > len(result)```上述代码中,`build_index`函数用于建立时间序列数据的索引,使用前缀索引技术。
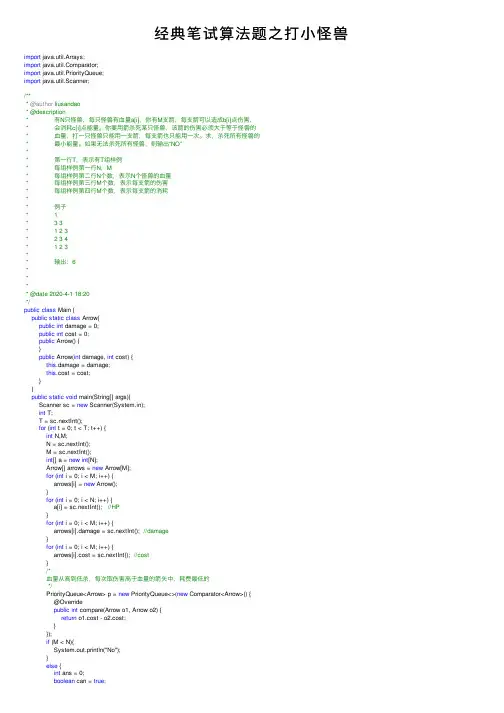
经典笔试算法题之打⼩怪兽import java.util.Arrays;import parator;import java.util.PriorityQueue;import java.util.Scanner;/*** @author liusandao* @description* 有N只怪兽,每只怪兽有⾎量a[i],你有M⽀箭,每⽀箭可以造成b[i]点伤害,* 会消耗c[i]点能量。
你要⽤箭杀死某只怪兽,该箭的伤害必须⼤于等于怪兽的* ⾎量,打⼀只怪兽只能⽤⼀⽀箭,每⽀箭也只能⽤⼀次。
求,杀死所有怪兽的* 最⼩能量。
如果⽆法杀死所有怪兽,则输出“NO”** 第⼀⾏T,表⽰有T组样例* 每组样例第⼀⾏N,M* 每组样例第⼆⾏N个数,表⽰N个怪兽的⾎量* 每组样例第三⾏M个数,表⽰每⽀箭的伤害* 每组样例第四⾏M个数,表⽰每⽀箭的消耗** 例⼦* 1* 3 3* 1 2 3* 2 3 4* 1 2 3** 输出:6**** @date 2020-4-1 18:20*/public class Main {public static class Arrow{public int damage = 0;public int cost = 0;public Arrow() {}public Arrow(int damage, int cost) {this.damage = damage;this.cost = cost;}}public static void main(String[] args){Scanner sc = new Scanner(System.in);int T;T = sc.nextInt();for (int t = 0; t < T; t++) {int N,M;N = sc.nextInt();M = sc.nextInt();int[] a = new int[N];Arrow[] arrows = new Arrow[M];for (int i = 0; i < M; i++) {arrows[i] = new Arrow();}for (int i = 0; i < N; i++) {a[i] = sc.nextInt(); //HP}for (int i = 0; i < M; i++) {arrows[i].damage = sc.nextInt(); //damage}for (int i = 0; i < M; i++) {arrows[i].cost = sc.nextInt(); //cost}/*⾎量从⾼到低杀,每次取伤害⾼于⾎量的箭⽮中,耗费最低的*/PriorityQueue<Arrow> p = new PriorityQueue<>(new Comparator<Arrow>() {@Overridepublic int compare(Arrow o1, Arrow o2) {return o1.cost - o2.cost;}});if (M < N){System.out.println("No");}else {int ans = 0;boolean can = true;Arrays.sort(a);Arrays.sort(arrows, new Comparator<Arrow>() {@Overridepublic int compare(Arrow o1, Arrow o2) {return o1.damage - o2.damage;}});int j = M - 1;for (int i = N - 1; i >= 0; i--) {while(j >= 0 && arrows[j].damage >= a[i]){p.offer(arrows[j]);j--;}//把伤害超过的⼸箭加进去if (p.size() == 0){System.out.println("No");can = false;break;}else {Arrow ar = p.poll();ans += ar.cost;}}if (can){System.out.println(ans);}}}}}很多⼈看到的第⼀反应是动态规划,感觉和背包问题很像,但是这题其实有更简便的⽅法,就是贪⼼。

美团笔试算法题范文这里我将给出一道美团的算法题,并给出一个解答思路和代码实现。
题目:排序数组的中位数给定一个包括n个整数的排序数组,找出数组中的中位数。
如果数组长度是偶数,返回中间两个数的平均值。
要求:时间复杂度为O(log n)思路:1.首先我们可以想到使用二分查找的思路来解决。
由于数组是有序的,我们可以使用二分查找法找到中位数。
2.我们可以将中位数划分为两个部分,即左边部分和右边部分。
如果数组长度n为奇数,左边部分将比右边部分多一个数;如果长度为偶数,左边部分和右边部分的数目相同。
3.假设左边部分的数目为k,则右边部分的数目为n-k。
由于左边部分的最大值小于等于右边部分的最小值,所以我们只需要找到一个数使得左边部分的最大值小于等于右边部分的最小值即可。
4.我们可以使用二分查找法来找到这样一个数,使其满足上面的条件。
5.具体的二分查找过程如下:- 定义两个指针l和r分别指向数组的第一个数和最后一个数,然后计算中位数下标mid = (l + r) // 2-判断当前的中位数是否满足左边部分的最大值小于等于右边部分的最小值,如果满足,则返回中位数。
- 如果左边部分的最大值大于右边部分的最小值,则说明中位数在左边部分,更新r为mid-1- 如果右边部分的最小值大于左边部分的最大值,则说明中位数在右边部分,更新l为mid+1-重复上面的步骤,直到找到中位数。
6.在二分查找过程中,我们可以使用逆向思维来判断左边部分的最大值和右边部分的最小值。
即将左边部分最大值和右边部分最小值初始化为负无穷和正无穷,然后通过比较当前中位数与这两个值来判断中位数的位置。
代码实现:```pythondef findMedian(nums):n = len(nums)l,r=0,n-1while l <= r:mid = (l + r) // 2left_max = float('-inf') # 左边部分的最大值if mid > 0:left_max = max(left_max, nums[mid - 1])right_min = float('inf') # 右边部分的最小值if mid < n:right_min = min(right_min, nums[mid])if left_max <= right_min:#当数组长度为奇数时,直接返回中位数if n % 2 != 0:return float(nums[mid])#当数组长度为偶数时,返回中间两个数的平均值else:if mid > 0:left_max = max(left_max, nums[mid - 1])if mid + 1 < n:right_min = min(right_min, nums[mid + 1]) return (left_max + right_min) / 2.0if left_max > right_min:r = mid - 1else:l = mid + 1return -1 # 如果出现异常情况,返回-1#测试样例nums = [1, 2, 3, 4, 5]print(findMedian(nums)) # 输出3nums = [1, 2, 3, 4]print(findMedian(nums)) # 输出2.5```该算法的时间复杂度为O(log n),符合题目要求。

以下是一些前端算法的笔试题及答案,供您参考:一、数组排序问题描述:给定一个整数数组,请你编写一个算法将该数组按照升序排序。
解题思路:可以使用快速排序、归并排序等常见排序算法,也可以手动实现冒泡排序、插入排序等简单排序算法。
二、链表操作问题描述:给定一个链表,请你编写一个算法将该链表反转。
解题思路:可以使用迭代或递归的方式,遍历链表一次,依次修改每个节点的指向,从而实现链表的反转。
三、二分查找问题描述:给定一个有序数组,请你编写一个算法在该数组中查找一个元素,并返回该元素的索引。
解题思路:可以使用二分查找算法,在有序数组中反复将查找范围缩小一半,直到找到目标元素或查找范围为空。
四、字符串匹配问题描述:给定两个字符串S和P,请你编写一个算法判断P是否是S的子串。
解题思路:可以使用KMP算法、Boyer-Moore算法等字符串匹配算法,也可以手动实现滑动窗口等简单算法。
五、动态规划问题描述:给定一个二维数组dp,其中dp[i][j]表示到达位置(i, j)所需的最小代价,请你编写一个算法求解dp数组的值。
解题思路:可以使用动态规划算法,将dp数组视为一个状态转移方程的表格,根据状态转移方程求解dp数组的值。
六、深度优先搜索(DFS)和广度优先搜索(BFS)问题描述:给定一个有向图或无向图,请你分别使用DFS和BFS遍历该图的所有节点。
解题思路:可以使用DFS或BFS算法遍历图的所有节点,根据图的拓扑结构选择合适的算法。
七、查找最大值和最小值问题描述:给定一组数字序列,请你编写一个算法找到该序列中的最大值和最小值。
解题思路:可以使用简单的循环遍历算法,依次比较每个元素的大小,找到最大值和最小值。
以上是部分前端算法的笔试题及答案,这些题目可以考察候选人的算法基础和思维能力,帮助他们更好地了解自己的编程能力和潜力。

美团算法岗笔试题
1.给定一个字符串,判断其是否是回文串。
2.给定一个有序数组和一个目标数,找出数组中两个数的和等于目标
数的索引。
3.给定一个整数数组,找出数组中出现频次最高的数字。
4.给定一个非负整数数组,计算数组中最大连续子数组的和。
5.给定一个字符串,找出其中的最长回文子串。
6.给定一个有序数组和一个目标数,找出数组中小于目标数的最大数。
7.给定一个整数数组和一个目标数,找出数组中两个数的乘积等于目
标数的索引。
8. 给定一个整数数组和一个目标数,找出数组中三个数的和等于目
标数的unique组合。
9.给定一个字符串和一个模式串,判断字符串是否符合模式串的规则。
10.给定一组边长,判断这些边能否组成一个三角形。
ai算法工程师笔试题目
AI算法工程师的笔试题目可能涉及多个领域,包括机器学习、深度学习、
计算机视觉、自然语言处理等。
以下是一些可能的AI算法工程师笔试题目:
1. 解释什么是过拟合,如何避免过拟合?
2. 请解释什么是损失函数,并给出几种常见的损失函数。
3. 请解释什么是梯度下降法,并给出其优缺点。
4. 请解释什么是反向传播算法,并简述其工作原理。
5. 请解释什么是卷积神经网络(CNN),并简述其在图像识别领域的应用。
6. 请解释什么是循环神经网络(RNN),并简述其在自然语言处理领域的
应用。
7. 请解释什么是长短期记忆网络(LSTM),并简述其工作原理。
8. 请解释什么是注意力机制,并简述其在神经网络中的应用。
9. 请解释什么是迁移学习,并简述其应用场景。
10. 请解释什么是数据预处理,并给出几种常见的数据预处理方法。
11. 请解释什么是特征工程,并给出几种常见的特征工程技术。
12. 请解释什么是欠拟合和过拟合,并给出避免过拟合的方法。
13. 请解释什么是交叉验证,并简述其在模型选择和参数调整中的应用。
14. 请解释什么是支持向量机(SVM),并简述其工作原理和应用场景。
15. 请解释什么是决策树和随机森林,并简述其工作原理和应用场景。
以上题目只是可能的AI算法工程师笔试题目的一部分,具体考试内容可能会根据具体的岗位和公司而有所不同。
一、二面问题汇总:
自我介绍;
非CS专业为什么做机器学习(我记得有本书上说机器学习产生于控制学科...);
看成绩单,因为我们学校信息学院分院之前自动化和计算机课程几乎相同,所以面试官比较满意;
与岗位相关的课程介绍;
分类器了解哪些,自己写过哪些;
熟悉的语言,用过哪些框架;
最熟悉哪个分类模型;
项目介绍;
项目中用到的算法详细;
树模型和熵介绍,为什么xgboost效果好;
除了课程外读了哪些书和视频公开课;
线性回归解析解的推导(三种方法),SVD与PCA的关系;
深度学习的适用场景;
深度学习与传统方法的区别,深度学习为什么效果这么好;
熟悉数据结构与算法吗;
贪婪在机器学习中有哪些应用;
想在哪个城市,为什么,为什么不去**城市;
面试了哪些公司,有哪些offer;
为什么去面试这些公司,找工作看重哪些方面;
有什么问题。
1. 反转链表
给定一个单链表,实现一个函数,将链表反转。
例如:输入1->2->3->4->5 ,输出5->4->3->2->1。
2. 两数相加
给出两个非空链表表示的两个非负整数。
位数按照逆序方式存储,每个节点只能存储一位数字。
将两个数相加返回一个新的链表。
例如:输入(2 -> 4 -> 3) + (5 -> 6 -> 4),输出7 -> 0 -> 8。
原因:342 + 465 = 807。
3. 合并两个有序链表
给出两个有序的链表,合并为一个新的有序链表并返回。
例如:输入1->2->4, 1->3->4,输出1->1->2->3->4->4。
4. K个一组翻转链表
给定一个链表和一个整数k,将链表的每k 个节点翻转一次。
例如:输入1->2->3->4->5,k=2,输出2->1->4->3->5。
5. 二叉树的最大深度
给定一个二叉树,找到它的最大深度。
二叉树的深度被定义为最长路径上的节点数,其中路径至少向下延伸一层。
例如:输入[3,9,20,null,null,15,7],输出3。
数据结构算法笔试题及答案一、选择题1. 在数据结构中,以下哪个选项不是线性结构?A. 栈B. 队列C. 树D. 链表答案:C2. 以下哪个排序算法的时间复杂度是O(nlogn)?A. 冒泡排序B. 快速排序C. 插入排序D. 选择排序答案:B3. 在哈希表中,以下哪个操作的时间复杂度通常是O(1)?A. 插入B. 删除C. 查找D. 遍历答案:C4. 下列关于二叉树的叙述中,错误的是?A. 二叉树的度最多为2B. 二叉树的节点数最多为n^2C. 二叉树的节点数最少为nD. 二叉树的节点数最多为2^n - 1答案:B5. 在图的遍历算法中,深度优先搜索(DFS)使用的是哪种数据结构?A. 队列B. 栈C. 链表D. 堆答案:B二、填空题1. 在二叉搜索树中,对于任意节点,其左子树中的所有节点的值都____。
答案:小于该节点的值2. 一个完全二叉树的第i层最多有____个节点。
答案:2^(i-1)3. 一个长度为n的链表,删除链表的倒数第k个节点的时间复杂度是____。
答案:O(n)4. 哈夫曼编码是一种基于字符出现频率进行编码的方法,它是一种____编码。
答案:前缀5. 在图的遍历算法中,广度优先搜索(BFS)使用的是____数据结构。
答案:队列三、简答题1. 请简述快速排序算法的基本思想。
答案:快速排序算法的基本思想是选择一个元素作为基准(pivot),然后将数组分为两部分,一部分是小于基准的元素,另一部分是大于基准的元素。
递归地在这两部分上重复这个过程,直到整个数组变为有序。
2. 什么是图的深度优先搜索(DFS)?答案:图的深度优先搜索(DFS)是一种遍历算法,它从一个节点开始,尽可能深地搜索图的分支。
搜索过程中,它会访问一个节点的所有未访问的邻接节点,直到所有可达的节点都被访问过。
3. 请解释什么是哈希表的冲突以及如何解决冲突。
答案:哈希表的冲突是指两个或多个不同的键值对通过哈希函数映射到同一个哈希值。
以下是一些可能出现在 AI 算法岗位笔试中的题目:
1. 请说明 PCA 算法的原理和应用场景。
2. 在机器学习中,什么是过拟合和欠拟合?如何解决这两种问题?
3. 假设有 1000 个样本,其中 900 个属于负类,100 个属于正类。
如果你使用一个预测模型对这些样本进行分类,假设输出结果为全部为负类,请计算准确率、召回率和 F1 分数。
4. 如何处理数据集中的缺失值?
5. 请解释 SVM 算法的原理,并说明其优点和缺点。
6. 请解释交叉验证的原理和作用。
7. 请说明决策树算法的原理和应用场景。
8. 请简述神经网络的结构和训练过程。
9. 请说明聚类算法的原理和应用场景。
10. 请说明深度学习算法的原理和应用场景。
以上是一些可能出现在 AI 算法岗位笔试中的题目,当然实际上可能会更具体和专业化一些。
希望这些题目能够帮助你更好地准备 AI 算法岗位的笔试。
一、递归和分制策略汉诺塔递归实现:Void hannoi(int n,char x,char y,char z){if (n ==1)move(x,1,z);//printf(“%i Move disk %i from %c to %c \n”,++c,n,x,z)//将编号1从x移到zelse{hanoi(n-1, x,z,y);//将x上编号1至n-1的移到y,z做辅助move(x,n,z);// 将编号n从x移到zhanoi(n-1, y,x,z);// 将y上编号1至n-1的移到z,x做辅助}}递归小结优点:结构清晰,可读性强,而且容易用数学归纳法来证明算法的正确性,因此它为设计算法、调试程序带来很大方便。
缺点:递归算法的运行效率较低,无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。
解决方法:在递归算法中消除递归调用,使其转化为非递归算法。
1.采用一个用户定义的栈来模拟系统的递归调用工作栈。
该方法通用性强,但本质上还是递归,只不过人工做了本来由编译器做的事情,优化效果不明显。
2.用递推来实现递归函数。
3.通过Cooper变换、反演变换能将一些递归转化为尾递归,从而迭代求出结果。
后两种方法在时空复杂度上均有较大改善,但其适用范围有限。
排序总结直接插入排序:void insertSort(listtp & r){ for(i=2; i<=n; i++){ r[0]=r[i]; /* 设置监视哨*/j=i-1; k=r[i].key;while(j>0&&r[j].key>k)/* 大值的记录后移*/ { r[j+1]=r[j]; j--; }r[j+1]=r[0]; /*插入位置*/}} /* straisort */希尔排序:将整个序列划分成若干子序列,分别进行直接插入排序。
void ShellSort(SeqList R,int dlta[],int t){For(k=0;k<t;k++)ShellInsert(R,dlta[k]); //一趟增量为dlta[k]的Shell插入排序} //ShellSort{ for(i=dk+1; i<=n; i++){ r[0]=r[i]; /* 设置监视哨*/j=i-dk; k=r[i].key;while( r[j].key>k)/* 大值的记录后移*/{ r[j+dk]=r[j]; j-=dk; }r[j+dk]=r[0]; /*插入位置*/}} /* straisort */冒泡排序:void buble_sort(listtp r){ for (i=1; i<=n-1; i++) /* 共计n-1趟 */for (j=1; j<=n-i ; j++)if (r[j].key>r[j+1].key){ x=r[j]; r[j]=r[j+1] r[j+1]=x;} } /* bubble_sort */快速排序:在快速排序中,记录的比较和交换是从两端向中间进行的,关键字较大的记录一次就能交换到后面单元,关键字较小的记录一次就能交换到前面单元,记录每次移动的距离较大,因而总的比较和移动次数较少。
private static void qSort(sqlist & L,int low, int high){if (low<high) { //int pivotloc=partition(L,low,high); //以a[pivotloc]为基准元素将a[low:high]划分成3段a[low: pivotloc -1],a[pivotloc]和a[pivotloc +1:high],使得a[low: pivotloc-1]中任何元素小于等于a[pivotloc],a[pivotloc +1:high]中任何元素大于等于a[pivotloc]。
下标pivotloc在划分过程中确定。
qSort (L,low, pivotloc-1); //对左半段排序qSort(L, pivotloc+1,high); //对右半段排序 }}Int Partition(sqlist &L,int low,int high){L.r[0]=L.r[low];//用子表第一个元素作为轴Pivotkey = L.r[low].key;While(low<high){While(low<high&&L.r[high].key>=privotkey )High--;If(L.r[high].key<privotkey)R[low]=r[high];While(low<high&&L.r[low].key<=privotkey)Low++;If(L.r[low].key>privotkey)R[high]=r[low];}L.r[low]=L.r[0];Return low;}归并排序:public static void mergeSort(Comparable a[], int left, int right){int m = (left+right)/2; //取中点if(left>=right)return;if(left+1==right){if(a[left]>a[right])std::swap(a[left], a[right]);return;}mergeSort(a, left, m);mergeSort(a, m+1, right);merge(a, left,m, right); //合并到数组a}}void Merge(A[], int l, int m, int h){int i = l;int j = m+1;int k = 0; while(i<=m&&j<=h){if(A[i]<A[j]){B[k++] = A[i];i++;}else{B[k++] = A[j];j++;}}while(i<=m)B[k++] = A[i++];while(j<=h)B[k++] = A[j++];for(i=l; i<=h; i++)A[i] = B[i-l];}二分法:#include<iostream>#define N 10using namespace std;int main(){int a[N],front,end,mid,x,i;cout<<"请输入已排好序的a数组元素:"<<endl;for(i=0;i<N;i++)cin>>a[i];cout<<"请输入待查找的数x:"<<endl;cin>>x;front=0;end=N-1;mid=(front+end)/2;while(front<=end&&a[mid]!=x){if(a[mid]<x)front=mid+1;if(a[mid]>x)end=mid-1;mid=(front+end)/2;}if(a[mid]!=x)cout<<"没找到!"<<endl;elsecout<<"找到了!在第"<<mid+1<<"项里。
"<<endl;return 0;}二叉树递归、非递归遍历package edu.cumt.jnotnull;import java.util.Stack;public class BinaryTree {protected Node root;public BinaryTree(Node root) {this.root = root;}public Node getRoot() {return root;}/** 构造树 */p ublic static Node init() {Node a = new Node('A');Node b = new Node('B', null, a);Node c = new Node('C');Node d = new Node('D', b, c);Node e = new Node('E');Node f = new Node('F', e, null);Node g = new Node('G', null, f);Node h = new Node('H', d, g);return h;// root}/** 访问节点 */p ublic static void visit(Node p) {System.out.print(p.getKey() + " ");}/** 递归实现前序遍历 */p rotected static void preorder(Node p) {if (p != null) {visit(p);preorder(p.getLeft());preorder(p.getRight());}}/** 递归实现中序遍历 */p rotected static void inorder(Node p) {if (p != null) {inorder(p.getLeft());visit(p);inorder(p.getRight());}}/** 递归实现后序遍历 */p rotected static void postorder(Node p) {if (p != null) {postorder(p.getLeft());postorder(p.getRight());visit(p);}}/** 非递归实现前序遍历 */protected static void iterativePreorder2(Node p) {Stack<Node> stack = new Stack<Node>();Node node = p;while (node != null || stack.size() > 0) {while (node != null) {//压入所有的左节点,压入前访问它visit(node);stack.push(node);node = node.getLeft();}if (stack.size() > 0) {//node = stack.pop();node = node.getRight();}}}/** 非递归实现后序遍历 */protected static void iterativePostorder(Node p) {Node q = p;Stack<Node> stack = new Stack<Node>();while (p != null) {// 左子树入栈for (; p.getLeft() != null; p = p.getLeft())stack.push(p);// 当前节点无右子或右子已经输出while (p != null && (p.getRight() == null || p.getRight() == q)) {visit(p);q = p;// 记录上一个已输出节点if (stack.empty())return;p = stack.pop();}// 处理右子stack.push(p);p = p.getRight();}}/** 非递归实现后序遍历双栈法 */p rotected static void iterativePostorder2(Node p) {Stack<Node> lstack = new Stack<Node>();Stack<Node> rstack = new Stack<Node>();Node node = p, right;do {while (node != null) {right = node.getRight();lstack.push(node);rstack.push(right);node = node.getLeft();}node = lstack.pop();right = rstack.pop();if (right == null) {visit(node);} else {lstack.push(node);rstack.push(null);}node = right;} while (lstack.size() > 0 ||rstack.size() > 0);}/** 非递归实现后序遍历单栈法*/p rotected static void iterativePostorder3(Node p) {Stack<Node> stack = new Stack<Node>();Node node = p, prev = p;while (node != null || stack.size() > 0) { while (node != null) {stack.push(node);node = node.getLeft();}if (stack.size() > 0) {Node temp = stack.peek().getRight();if (temp == null || temp == prev) {node = stack.pop();visit(node);prev = node;node = null;} else {node = temp;}}}}/** 非递归实现后序遍历4 双栈法*/p rotected static void iterativePostorder4(Node p) {Stack<Node> stack = new Stack<Node>();Stack<Node> temp = new Stack<Node>();Node node = p;while (node != null || stack.size() > 0) { while (node != null) {temp.push(node);stack.push(node);node = node.getRight();}if (stack.size() > 0) {node = stack.pop();node = node.getLeft();}}while (temp.size() > 0) {node = temp.pop();visit(node);}}/** 非递归实现中序遍历 */p rotected static void iterativeInorder2(Node p) {Stack<Node> stack = new Stack<Node>();Node node = p;while (node != null || stack.size() > 0) { while (node != null) {stack.push(node);node = node.getLeft();}if (stack.size() > 0) {node = stack.pop();visit(node);node = node.getRight();}}}/*** @param args*/p ublic static void main(String[] args) {BinaryTree tree = new BinaryTree(init());System.out.print(" Pre-Order:");preorder(tree.getRoot());System.out.println();System.out.print(" In-Order:");inorder(tree.getRoot());System.out.println();System.out.print("Post-Order:");postorder(tree.getRoot());System.out.println();System.out.print(" Pre-Order:");iterativePreorder(tree.getRoot());System.out.println();System.out.print("Pre-Order2:");iterativePreorder2(tree.getRoot());System.out.println();System.out.print(" In-Order:");iterativeInorder(tree.getRoot());System.out.println();System.out.print(" In-Order2:");iterativeInorder2(tree.getRoot());System.out.println();System.out.print(" Post-Order:");iterativePostorder(tree.getRoot());System.out.println();System.out.print("Post-Order2:");iterativePostorder2(tree.getRoot());System.out.println();System.out.print("Post-Order3:");iterativePostorder3(tree.getRoot());System.out.println();System.out.print("Post-Order4:");iterativePostorder4(tree.getRoot());System.out.println();}}字符串反转//字符串反转char *reverse(char *str){int len = strlen(str);char temp ;int i;char *str1;str1 = (char*)malloc(len);memset(str1,0,len);memcpy(str1,str,len);for( i=0; i <len/2; i++){temp = str1[i];str1[i] = str1[len-1-i];//*(str+len-1-i); //执行到该行出现系统错误str1[len-1-i]= temp;}return str1;}function reverse(arg) {if(arg.length == 0) {return arg;}else {return reverse(arg.substr(1,arg.length)) + arg.substr(0,1);}}alert(reverse("123456"));2009-01-23 00:26快速排序的原理倒是挺简单,选一个基准,将其余的元素与之对比分别放在左右两侧,左大右小,每次对比都是对其所有的元素,也就是说每一次都是n次对比。