(完整版)中考数学必考经典题型(最新整理)
- 格式:docx
- 大小:153.73 KB
- 文档页数:8

数学中考常见题型选择题汇总1. 选择题:已知等差数列{an}的通项公式为an=2n-1,求该数列的前n项和Sn。
2. 选择题:一个圆的半径为5cm,求该圆的面积和周长。
3. 选择题:解方程:2x^2-5x+3=0。
4. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
5. 选择题:计算下列代数式的值:2^3×4^2÷3^2。
6. 选择题:已知函数f(x)=x^2-2x+1,求函数的值域。
7. 选择题:一个正方体的边长为4cm,求该正方体的对角线长度。
8. 选择题:已知函数g(x)=x^3-3x^2+3x,求函数的导数。
9. 选择题:解不等式:3x^2-6x+2>0。
10. 选择题:已知等比数列{bn}的通项公式为bn=2^n,求该数列的前n项和Sn。
11. 选择题:计算下列代数式的值:(-3)^4÷(-2)^2。
12. 选择题:解方程:x^2-4x+3=0。
13. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
14. 选择题:一个圆的半径为5cm,求该圆的面积和周长。
15. 选择题:已知函数f(x)=x^2-2x+1,求函数的值域。
16. 选择题:一个正方体的边长为4cm,求该正方体的对角线长度。
17. 选择题:已知函数g(x)=x^3-3x^2+3x,求函数的导数。
18. 选择题:解不等式:3x^2-6x+2>0。
19. 选择题:已知等比数列{bn}的通项公式为bn=2^n,求该数列的前n项和Sn。
20. 选择题:计算下列代数式的值:(-3)^4÷(-2)^2。
21. 选择题:解方程:x^2-4x+3=0。
22. 选择题:已知a、b、c是三角形ABC的三边,且满足a^2+b^2-c^2=2ab,求三角形ABC的类型。
23. 选择题:一个圆的半径为5cm,求该圆的面积和周长。

初三数学经典总结题型包括但不限于以下几种:
1. 线段、角的计算与证明:包括线段长度的计算、角的度数计算、线段与角的综合问题等。
2. 函数问题:包括一次函数、二次函数等,涉及到函数的性质、图像、最值等问题。
3. 方程与不等式问题:包括一元一次方程、一元二次方程、不等式的解法及实际应用等。
4. 三角形问题:包括三角形的性质、全等三角形、相似三角形等,涉及到三角形的边长、角度、面积等问题。
5. 四边形问题:包括平行四边形、矩形、菱形、正方形等,涉及到四边形的性质、判定条件及面积计算等。
6. 圆的问题:包括圆的性质、圆与直线的位置关系、圆与圆的位置关系等,涉及到圆的半径、直径、周长、面积等问题。
7. 统计与概率问题:包括数据的收集与整理、概率初步知识与事件的概率等,涉及到数据的分析、预测及概率的计算等。
8. 综合题:包括多个知识点的综合应用,如函数与三角形、四边形、圆的综合应用等,需要学生综合运用所学知识进行分析和解答。

中考数学题型考点归纳中考数学重要考点及题型整理一、计算题:科学计数法、倒数相反数绝对值、简单概率运算、三视图求原图面积、三角形(相似、全等、内角外交关系)、统计(众数、中位数、平均数)、二次函数(顶点、对称轴、表达式)、函数图像关系二、填空题:因式分解、二次函数解析式求解、三角形(相似、周长面积计算)、坐标(坐标点运动规律)、直线和反比例函数图像问题三、解答题:次方、开方、三角函数、次幂(0次、-1次)计算;求解不等式组;分式、多项式化简(整体代入方法求值);方程组求解;几何图形中证明三角形边相等;一次函数与二次函数;四、解答题四边形边长、周长、面积求解;圆相关问题(切割线、圆周角、圆心角);统计图;在数轴中求三角形面积;五、解答题二次函数(解析式、直线方程);圆与直线关系;中考数学中常见的六种题型1线段、角的计算与证明中考的解答题一般是分两到三部分的。
第一部分基本上都是一些简单题或者中档题,目的在于考察基础。
第二部分往往就是开始拉分的中难题了。
对这些题轻松掌握的意义不仅仅在于获得分数,更重要的是对于整个做题过程中士气,军心的影响。
2一元二次方程与函数在这一类问题当中,尤以涉及的动态几何问题最为艰难。
几何问题的难点在于想象,构造,往往有时候一条辅助线没有想到,整个一道题就卡壳了。
相比几何综合题来说,代数综合题倒不需要太多巧妙的方法,但是对考生的计算能力以及代数功底有了比较高的要求。
中考数学当中,代数问题往往是以一元二次方程与二次函数为主体,多种其他知识点辅助的形式出现的。
一元二次方程与二次函数问题当中,纯粹的一元二次方程解法通常会以简单解答题的方式考察。
但是在后面的中难档大题当中,通常会和根的判别式,整数根和抛物线等知识点结合。
3多种函数交叉综合问题初中数学所涉及的函数就一次函数,反比例函数以及二次函数。
这类题目本身并不会太难,很少作为压轴题出现,一般都是作为一道中档次题目来考察考生对于一次函数以及反比例函数的掌握。
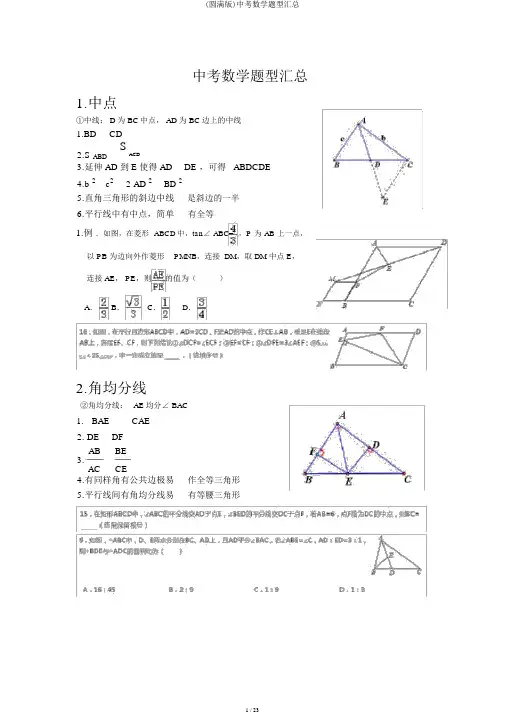
中考数学题型汇总1.中点①中线: D为 BC中点, AD为 BC边上的中线1.BD CD2.S ABD SACD3.延伸 AD 到 E使得 AD DE ,可得 ABDCDE4.b 2c2 2 AD 2BD 25.直角三角形的斜边中线是斜边的一半6.平行线中有中点,简单有全等1.例.如图,在菱形ABCD中,tan∠ABC=,P为AB上一点,以 PB 为边向外作菱形PMNB,连接 DM,取 DM 中点 E,连接 AE, PE,则的值为()A.B.C.D.2.角均分线②角均分线:AE均分∠ BAC1. BAE CAE2. DE DFAB BE3.AC CE4.有同样角有公共边极易作全等三角形5.平行线间有角均分线易有等腰三角形3. 高线③垂线: AF ⊥ BCBC 即 AFC 902.求高线可用等面积法3.充足利用 Rt4.多个直角,易有相像三 角形②直角三角形: AD 为中线 AE 为垂线1.两角互余: B C 902.斜边中线为斜边的一半: ADBD CD 1 BC2 3.等面积法: S ABC1 AC ? AB1 BC ? AE2 2 4.勾股定理: AC 2AB 2 BC 2 AB 2 BE ? BC ; AC 2 CE ? BC5.充足利用特别角 30 ,45 ,60 ,结构 Rt4.函数坐标公式公式 1:两点求斜率 ky1y2kABx2x1①与 x轴正方向夹角为45 时, k1②与 x轴正方向夹角为60 时, k3③与 x轴正方向夹角为30 时, k3 3④与 x轴正方向夹角为120 时, k3⑤与 x轴正方向夹角为135 时, k1公式 2:两点之间距离AB( x1 x2 ) 2( y1 y2 )2应用:弦长公式公式 3:中点公式AB 中点 (x 1 x 2 , y 1 y 2 ) 2 2 ABC 重心( x 1x 2 x 3 , y 1y 2 y 3 )32 应用:求中点坐标公式 4:两直线平行与垂直① l 1 // l 2k 1 k 2 ② l 1l 2 k 1 ? k 2 1应用:①平行与垂直②直角三角形5. 相像中的特别角tan () tan tan 1 tan tan6.将军引马7.旋转8.对称9.反比率函数1.面积与 k的关系2.坐标点的表示3.直线与反比率交点的关系4.反比率函数对于 y x对称5.看坐标求面积10.二次函数1.三大表达式及转变2.对称轴与极点及关系3.二次函数与二次方程或不等式4.二次函数的挪动5.二次函数中间的水平长与铅垂高6.二次函数中的三种线段最值园中的三个直角三角形1.园中的两个等腰三角形2.园中的内接四边形3.园中的圆周角,圆心角与弧度4.5.外接圆 - 外心,内切圆 -心里园中的对称与翻折6.7.弦长,弦心距,弧长,弧度,圆心角,圆周角11. 圆8.扇形的面积与弧长12规律题圆14应用题。

初三数学常考试题及答案一、选择题1. 已知一个二次函数的图像经过点A(-1,0)和点B(3,0),且函数的开口向上,则该二次函数的对称轴是()。
A. x = 0B. x = 1C. x = 2D. x = -1答案:B解析:二次函数的对称轴是其顶点的x坐标,由于函数图像经过点A(-1,0)和点B(3,0),且开口向上,根据二次函数的性质,对称轴是这两点x坐标的平均值,即x = (-1 + 3) / 2 = 1。
2. 下列哪个选项是不等式2x - 3 > 0的解集?A. x > 3/2B. x < 3/2C. x > 3D. x < 3答案:A解析:将不等式2x - 3 > 0移项得到2x > 3,再除以2得到x > 3/2,因此选项A是正确的。
二、填空题3. 计算绝对值:|-7| = _______。
答案:7解析:绝对值表示一个数距离0的距离,因此|-7|表示-7距离0的距离,即7。
4. 计算平方根:√9 = _______。
答案:±3解析:平方根是一个数的平方等于给定数的那个数,9的平方根是3,因为3的平方是9。
同时,-3的平方也是9,所以9的平方根是±3。
三、解答题5. 已知一个直角三角形的两条直角边长分别为3和4,求斜边的长度。
答案:5解析:根据勾股定理,直角三角形的斜边长度等于两直角边长度的平方和的平方根。
即斜边长度= √(3² + 4²) = √(9 + 16) = √25 = 5。
6. 某工厂生产一种零件,每件成本为10元,售价为15元,若该工厂希望获得的利润不低于1000元,问至少需要生产多少件零件?答案:100件解析:设需要生产的零件数量为x件,则总利润为(15 - 10)x = 5x元。
根据题意,5x ≥ 1000,解得x ≥ 200。
因此,至少需要生产200件零件。
四、证明题7. 证明:如果一个三角形的两边之和大于第三边,那么这个三角形是存在的。

初三数学考试题型及答案一、选择题(每题3分,共30分)1. 下列哪个选项是不等式的基本性质?A. 不等式两边同时乘以一个负数,不等号方向不变B. 不等式两边同时乘以一个正数,不等号方向不变C. 不等式两边同时加上同一个数,不等号方向不变D. 不等式两边同时除以一个正数,不等号方向不变答案:B2. 一个数的平方是9,那么这个数是:A. 3B. -3C. 3或-3D. 以上都不对答案:C3. 函数y=2x+1的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 一个圆的直径是10cm,那么这个圆的半径是:A. 5cmB. 10cmC. 15cmD. 20cm答案:A5. 一个等腰三角形的两个底角相等,那么这个三角形的顶角是:A. 90度B. 60度C. 30度D. 无法确定答案:D6. 一个数的相反数是-5,那么这个数是:A. 5B. -5C. 10D. -10答案:A7. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么这个长方体的体积是:A. 24cm³B. 12cm³C. 8cm³D. 6cm³答案:A8. 一个数的绝对值是5,那么这个数是:A. 5B. -5C. 5或-5D. 以上都不对答案:C9. 一个二次函数y=ax²+bx+c的图象开口向上,那么a的值是:A. 正数B. 负数C. 0D. 无法确定答案:A10. 一个等差数列的前三项是2,5,8,那么这个数列的公差是:A. 3B. 2C. 1D. 4答案:A二、填空题(每题3分,共30分)1. 一个数的立方是27,那么这个数是________。
答案:32. 一个直角三角形的两条直角边长分别是3cm和4cm,那么这个三角形的斜边长是________。
答案:5cm3. 一个数的倒数是1/2,那么这个数是________。
答案:24. 一个三角形的内角和是________度。

初中数学题经典题型一、代数式求值代数式求值是初中数学的基本题型之一,也是中考数学必考题型。
这类题主要考察学生的运算能力和对基本公式的掌握程度。
以下是一些典型的代数式求值题目:1. 求代数式(2x+3)/(x+1)的值,其中x=4。
2. 求代数式(2x+1)/(x+3)的值,其中x=2。
3. 求代数式(x^2-1)/(x+1)的值,其中x=3。
二、方程求解方程求解是初中数学中非常重要的一个知识点,也是中考数学必考题型。
这类题主要考察学生的运算能力和对方程的掌握程度。
以下是一些典型的方程求解题目:1. 求方程2x+3=7的解。
2. 求方程3x-2=5的解。
3. 求方程4x+2=7的解。
三、不等式求解不等式求解是初中数学中的一个重要知识点,也是中考数学必考题型。
这类题主要考察学生的运算能力和对不等式的掌握程度。
以下是一些典型的不等式求解题目:1. 求不等式5x+3>7的解集。
2. 求不等式2x-1<9的解集。
3. 求不等式4x-5>=0的解集。
四、函数与图像函数与图像是初中数学中的一个难点和重点,也是中考数学必考题型。
这类题主要考察学生的数形结合能力和对函数的掌握程度。
以下是一些典型的函数与图像题目:1. 已知函数y=2x-1,求当x=3时y的值。
2. 已知函数y=-x+4,求当y=3时x的值。
3. 已知函数y=x^2,求当y=4时x的值。
五、三角形与四边形三角形与四边形是初中数学中非常重要的一个知识点,也是中考数学必考题型。
这类题主要考察学生的空间思维能力和对几何图形的掌握程度。
以下是一些典型的三角形与四边形题目:1. 求等边三角形的边长为10厘米时,其面积和周长分别是多少?2. 一个矩形长为6厘米,宽为4厘米,求其对角线的长度是多少?。

初三中考数学必考题型
中考数学必考题型有很多,不同的考试和难度都会有所侧重。
以下是常见的一些题型和知识点,仅供您参考:
1. 选择题:考察基础概念和计算能力,包括代数式化简、方程求解、几何性质等。
2. 填空题:考察计算和推理能力,包括几何作图、代数变形、函数性质等。
3. 解答题:考察综合运用知识的能力,包括函数与方程、几何证明与计算、概率与统计等。
4. 综合题:考察知识整合和问题解决能力,包括函数与几何、方程与不等式、几何变换等。
无论考试形式如何变化,关键是要掌握数学基础知识和基本技能,同时提高自己的思维能力和问题解决能力。
如果您需要更详细的备考指导,建议查阅中考数学备考资料或咨询数学老师。

初中数学中考必考题型
题型一
运用同三角函数关系、诱导公式、和、差、倍、半等公式进行化简求
值类。
题型二
运用三角函数性质解题,通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心。
题型三
解三角函数问题、判断三角形形状、正余弦定理的应用。
题型四
数列的通向公式得求法。
题型五
数列的前n项求和的求法。
题型六
利用导数研究函数的极值、最值。
题型七
利用导数几何意义求切线方程。
题型八
利用导数研究函数的单调性,极值、最值
题型九
利用导数研究函数的图像。
题型十
求参数取值范围、恒成立及存在性问题。
题型十一
数形结合确定直线和圆锥曲线的位置关系。
题型十二
焦点三角函数、焦半径、焦点弦问题。
题型十三
动点轨迹方程问题。

中考数学必背题型归纳总结在中考数学中,各种题型繁多,但是在备考过程中,有一些题型是必须要掌握的,因为它们经常出现。
本文将对中考数学中的必背题型进行归纳总结,并提供相应的解题思路和方法。
一、选择题选择题在中考数学中占据重要的比重,因此必须要熟练掌握解题技巧。
以下是几种常见的选择题题型及解题思路:1. 增减百分数题增减百分数题是一种常见的选择题题型,要求计算某个数值的增加或减少百分之多少。
解题时,根据题目给出的百分数,将要计算的数值乘以相应的百分数即可。
例如,计算120的60%是多少,可以直接将120乘以0.6得到72,因此答案为72。
2. 几何图形题几何图形题在中考数学中也经常出现,解题时需要根据题目给出的条件进行分析。
常见的几何图形题有平行四边形的性质、三角形的性质等。
解题时可以根据题目条件绘制几何图形,并运用相应的几何定理进行推理。
3. 坐标题坐标题是中考数学中的基础题型,要求对平面上的点进行坐标定位。
解题时需要根据题目给出的条件,确定点的坐标,并进行相应的计算。
在解答坐标题时,可以通过绘制坐标图、运用距离公式等方法进行求解。
二、填空题填空题在中考数学中也是常见的题型之一,考查学生对基础知识的掌握程度。
以下是几种常见的填空题题型及解题思路:1. 算式填空题算式填空题要求填写适当的数值,使得等式成立。
解题时需要分析等式中各个数值的关系,并利用已知的条件来求解。
例如,对于等式5 + □ = 10,可以通过计算得到□的数值为5。
2. 几何图形填空题几何图形填空题主要考查学生对几何图形性质的理解。
解题时可以根据已知条件对图形进行推理,并根据已有的线段长度、角度等信息填空。
在解答几何图形填空题时,需要灵活运用几何定理和计算方法。
三、解答题解答题是中考数学中较为复杂的题型,要求学生进行详细的计算和推理。
以下是几种常见的解答题题型及解题思路:1. 单方程解答题单方程解答题要求求解方程中的未知数。
解答此类题目时,需要运用一些解方程的方法,如等式相加减、等式相乘除等,将方程转换为较简单的形式,并求解出方程中的未知数。

数学中考常见题型选择题汇总1. 选择题:已知一个等差数列的前三项分别是a、b、c,且a+b+c=9,a+b=11,a+c=8,求a、b、c的值。
2. 选择题:如果一个三角形的两个内角分别是120度和30度,那么第三个内角的度数是多少?3. 选择题:一个长方形的长是8厘米,宽是3厘米,求这个长方形的周长和面积。
4. 选择题:一个正方体的棱长是4厘米,求这个正方体的表面积和体积。
5. 选择题:一个圆的半径是5厘米,求这个圆的周长和面积。
6. 选择题:已知两个正方体的体积分别是16立方厘米和8立方厘米,求这两个正方体的棱长。
7. 选择题:一个长方体的长是8厘米,宽是3厘米,高是2厘米,求这个长方体的对角线长度。
8. 选择题:一个等差数列的前两项分别是3和7,公差是2,求这个等差数列的第10项。
9. 选择题:一个圆锥的底面半径是3厘米,高是4厘米,求这个圆锥的体积和表面积。
10. 选择题:已知一个三角形的两个内角分别是60度和90度,求第三个内角的度数。
11. 选择题:一个长方体的长是6厘米,宽是4厘米,高是2厘米,求这个长方体的对角线长度。
12. 选择题:一个正方体的棱长是6厘米,求这个正方体的表面积和体积。
13. 选择题:一个圆的半径是8厘米,求这个圆的周长和面积。
14. 选择题:已知一个等差数列的前两项分别是1和4,公差是3,求这个等差数列的第10项。
15. 选择题:一个圆锥的底面半径是4厘米,高是6厘米,求这个圆锥的体积和表面积。
16. 选择题:已知一个三角形的两个内角分别是45度和45度,求第三个内角的度数。
17. 选择题:一个长方体的长是5厘米,宽是3厘米,高是2厘米,求这个长方体的对角线长度。
18. 选择题:一个正方体的棱长是5厘米,求这个正方体的表面积和体积。
19. 选择题:一个圆的半径是10厘米,求这个圆的周长和面积。
20. 选择题:已知一个等差数列的前两项分别是2和7,公差是3,求这个等差数列的第10项。
初三数学必考题48题
初三数学的必考题通常涵盖了各个知识点,包括代数、几何、
数学应用题等。
在这里,我将列举一些可能出现的题目类型,以便
全面回答你的问题。
1. 代数题,可能包括一元一次方程、一元二次方程、分式方程等。
例如,“已知方程2x + 3 = 7,求x的值。
”。
2. 几何题,可能涉及到直角三角形、相似三角形、平行四边形
等内容。
例如,“已知直角三角形的两条直角边分别为3cm和4cm,求斜边长。
”。
3. 数学应用题,可能包括利润、利息、速度、工时等实际问题
的数学建模。
例如,“甲、乙两人同时从A、B两地相向而行,相遇
后甲行至B地还需2小时,乙行至A地还需3小时,求甲、乙两地
的距离。
”。
4. 综合题,可能结合多个知识点,考察学生的综合运用能力。
例如,“某商店举行促销活动,原价500元的商品打8折,再打9折,求促销后的价格。
”。
以上只是一些可能的题目类型,初三数学必考题还可能包括其他知识点。
学生在备考时,除了熟练掌握基础知识外,还需要注重综合运用能力和解题技巧的培养。
希望这些信息能够帮助你更好地准备初三数学考试。
【必考题】数学中考试卷(含答案)【必考题】数学中考试卷(含答案)第一题:计算下列各式的值:(1) $\frac{3}{4}-\frac{1}{2}+\frac{5}{6}$(2) $2\frac{1}{5}+\left(1\frac{1}{3}-\frac{5}{6}\right)$(3) $3\frac{2}{5}-\left(1\frac{1}{4}+\frac{3}{8}\right)$答案:(1) $\frac{3}{4}-\frac{1}{2}+\frac{5}{6}=\frac{9}{12}-\frac{6}{12}+\frac{10}{12}=\frac{13}{12}$(2) $2\frac{1}{5}+\left(1\frac{1}{3}-\frac{5}{6}\right)=\frac{11}{5}+\left(\frac{4}{3}-\frac{5}{6}\right)=\frac{11}{5}+\frac{8}{6}-\frac{5}{6}=\frac{71}{30}$(3) $3\frac{2}{5}-\left(1\frac{1}{4}+\frac{3}{8}\right)=\frac{17}{5}-\left(\frac{5}{4}+\frac{3}{8}\right)=\frac{44}{10}-\frac{13}{8}=\frac{47}{20}$第二题:已知$a=3,b=5$,求:(1) $2(a^2-b^2)+5(a+b)$(2) $\sqrt{4a^2+3b^2}$(1) $2(a^2-b^2)+5(a+b)=2(9-25)+5(3+5)=-32+40=8$(2) $\sqrt{4a^2+3b^2}=\sqrt{4\cdot 3^2+3\cdot 5^2}=\sqrt{4\cdot 9+3\cdot 25}=\sqrt{36+75}=\sqrt{111}$第三题:解方程:(1) $2x+5=17$(2) $3(2x-4)-5x=1$答案:(1) $2x+5=17$将方程中的常数项移到右边,得到$2x=17-5=12$再将方程两边同除以2,得到$x=\frac{12}{2}=6$所以方程的解为$x=6$(2) $3(2x-4)-5x=1$展开方程,并将同类项合并,得到$6x-12-5x=1$合并同类项,得到$x-12=1$将方程中的常数项移到右边,得到$x=1+12=13$所以方程的解为$x=13$求解下列不等式:(1) $2x+3>5x-1$(2) $4(x-3)>2x+7$答案:(1) $2x+3>5x-1$将方程中的常数项移到右边,得到$2x-5x>-1-3$合并同类项,得到$-3x>-4$将方程两边同除以$-3$,注意不等号方向的改变,得到$x<\frac{4}{3}$所以不等式的解为$x<\frac{4}{3}$(2) $4(x-3)>2x+7$展开方程,并将同类项合并,得到$4x-12>2x+7$合并同类项,得到$4x-2x>7+12$将方程两边合并同类项,并将常数项移到右边,得到$2x>19$将方程两边同时除以2,得到$x>\frac{19}{2}$所以不等式的解为$x>\frac{19}{2}$综上所述,本次数学中考试卷共含有四道题目,涉及到了基本的四则运算、方程的解和不等式的求解。
初三数学典型题精选一、选择题1. 下列哪个数是质数?A. 21B. 29C. 33D. 392. 若一个三角形的两边长分别为5厘米和12厘米,则第三边的长度可能是多少?A. 7厘米B. 13厘米C. 18厘米D. 20厘米3. 下列哪个图形的面积最大?A. 一个半径为2厘米的圆B. 一个边长为2厘米的正方形C. 一个长为4厘米,宽为2厘米的长方形D. 一个直径为4厘米的圆4. 下列哪个数是平方数?A. 15B. 16C. 17D. 185. 若一个等腰三角形的底边长为8厘米,腰长为5厘米,则该三角形的周长是多少?A. 18厘米B. 20厘米C. 22厘米D. 24厘米二、填空题1. 下列哪个数是质数?A. 21B. 29C. 33D. 392. 若一个三角形的两边长分别为5厘米和12厘米,则第三边的长度可能是多少?A. 7厘米B. 13厘米C. 18厘米D. 20厘米3. 下列哪个图形的面积最大?A. 一个半径为2厘米的圆B. 一个边长为2厘米的正方形C. 一个长为4厘米,宽为2厘米的长方形D. 一个直径为4厘米的圆4. 下列哪个数是平方数?A. 15B. 16C. 17D. 185. 若一个等腰三角形的底边长为8厘米,腰长为5厘米,则该三角形的周长是多少?A. 18厘米B. 20厘米C. 22厘米D. 24厘米三、解答题1. 设函数 $ f(x) = x^3 3x^2 + 2 $,求 $ f(x) $ 在 $ x =1 $ 处的切线方程。
2. 设函数 $ f(x) = e^x $,求 $ f(x) $ 在 $ x = 0 $ 处的切线方程。
3. 设函数 $ f(x) = \sin x $,求 $ f(x) $ 在 $ x =\frac{\pi}{2} $ 处的切线方程。
4. 设函数 $ f(x) = \ln x $,求 $ f(x) $ 在 $ x = 1 $ 处的切线方程。
5. 设函数 $ f(x) = x^2 $,求 $ f(x) $ 在 $ x = 2 $ 处的切线方程。
数学初三必考试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数的图像?A. 直线B. 抛物线C. 圆D. 双曲线答案:B2. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 2答案:A3. 一个等腰三角形的两边长分别为3和5,那么第三边的长度是:A. 3B. 5C. 8D. 不能确定答案:B4. 下列哪个选项是圆的面积公式?A. A = πrB. A = πr²C. A = 2πrD. A = r²答案:B5. 一个数的相反数是它自己,这个数是:A. 0B. 1C. -1D. 2答案:A6. 一个数的绝对值是它自己,这个数是:A. 正数B. 负数C. 0D. 非负数答案:D7. 一个数的倒数是它自己,这个数是:A. 1B. -1C. 0D. 2答案:A8. 一个数的立方等于它本身,这个数是:A. 0B. 1C. -1D. 2答案:A, B, C9. 一个数的平方等于它本身,这个数是:A. 0B. 1C. -1D. 2答案:A, B10. 一个数的平方根等于它的立方根,这个数是:A. 0B. 1C. -1D. 2答案:A二、填空题(每题4分,共20分)1. 一个数的平方是25,那么这个数是____。
答案:±52. 一个数的立方是-8,那么这个数是____。
答案:-23. 一个数的绝对值是5,那么这个数是____。
答案:±54. 一个数的倒数是2,那么这个数是____。
答案:1/25. 一个数的平方根是3,那么这个数是____。
答案:9三、解答题(每题10分,共50分)1. 已知一个等腰三角形的两边长分别为4和6,求第三边的长度。
答案:第三边的长度为6。
2. 已知一个数的平方是36,求这个数。
答案:这个数是±6。
3. 已知一个数的绝对值是7,求这个数。
答案:这个数是±7。
4. 已知一个数的倒数是3,求这个数。
中考数学必考经典题型题型一 先化简再求值命题趋势由河南近几年的中考题型可知,分式的化简求值是每年的考查重点,几乎都 以解答题的形式出现,其中以除法和减法形式为主,要求对分式化简的运算法则及分式有意义的条件熟练掌握。
例:先化简,再求值: ( 1 + x +1 1 ) ÷ x -1 x 2 - x x 2 - 2x +1, 其中 x =-1. 分析:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将 x 的值带入计算即可求值。
题型二阴影部分面积的相关计算命题趋势近年来的中考有关阴影面积的题目几乎每年都会考查到,而且不断翻新,精 彩纷呈.这类问题往往与变换、函数、相似等知识结合,涉及到转化、整体等数学思想方法,具有很强的综合性。
例如图 17,记抛物线 y =-x 2+1 的图象与 x 正半轴的交点为A ,将线段 OA 分成n 等份.设分点分别为 P 1,P 2,…,P n -1,过每个分点作 x 轴的垂线,分别与抛物线交于点 Q 1,Q 2,…,Q n -1,再记直角三角形 OP 1Q 1,P 1P 2Q 2,…的面积分别为 S 1,S 2,…,这样就有 S 1= n 2 -1 2n 3 ,S 2= n 2 - 42n 3…;记W=S 1+S 2+…+S n -1,当 n 越来越大时,你猜想 W 最接近的常数是()(A) 23 (B) 12(C) 13(D) 14分析 如图 17,抛物线 y =-x 2+1 的图象与 x 正半轴的交点为A(1,0),与 y 轴的交点为 8(0,1).设抛物线与 y 轴及 x 正半轴所围成的面积为 S ,M(x ,y )在图示抛物线上,则OM 2 = x 2 + y 223 3 2 从 而 = (1 - y ) + y 2⎛ 1 ⎫23 = y - ⎪ + . ⎝ ⎭ 4由 0≤y32≤1, 得 ≤OM ≤1.4这段图象在图示半径为 11个圆 面积之间,即4 、1 的两个 圆所夹的圆环内,所以 S 在图示两 243 1<S < π.164显然,当 n 的值越大时,W 的值就越来越接近抛物线与 y 轴和 x 正半轴所围成的面积的一半,所以3 1<W < π.328与其最接近的值是,故本题应选 C .题型三 解直角三角形的实际应用命题趋势解直角三角形的应用是中考的必考内容之一,它通常以实际生活为背景,考 查学生运用直角三角形知识建立数学模型的能力,解答这类问题的方法是运用 “遇斜化直”的数学思想,即通过作辅助线(斜三角形的高线)把它转化为直角三角形问题,然后根据已知条件与未知元素之间的关系,利用解直角三角形的知识, 列出方程来求解。
初三数学必考题
1.比例:题目类型包括等比例分割、比例的性质和应用、比例方程的解法等。
2.代数式和方程:题目类型包括代数式的化简、配方法、分式的化简、方程的解法、二元一次方程组的解法等。
3.几何:题目类型包括基本图形的性质和计算、平移、旋转、对称、相似、勾股定理、角平分线定理等。
4.统计与概率:题目类型包括频率分布表、直方图、折线图、散点图、概率的计算等。
5.函数:题目类型包括函数的定义、性质、图像、单调性、奇偶性、反函数等。
6.三角函数:题目类型包括正弦、余弦、正切的定义、性质、图像、解三角形等。
7.立体几何:题目类型包括立体图形的分类、性质、面积和体积的计算、欧拉定理等。
8.数系:题目类型包括有理数、无理数、实数的性质、大小比较、数轴等。
9.数论:题目类型包括最大公因数、最小公倍数、质数、因数、分解质因数等。
- 1 -。
中考数学必考经典题型题型一 先化简再求值命题趋势由河南近几年的中考题型可知,分式的化简求值是每年的考查重点,几乎都 以解答题的形式出现,其中以除法和减法形式为主,要求对分式化简的运算法则及分式有意义的条件熟练掌握。
例:先化简,再求值: ( 1 + x +1 1 ) ÷ x -1 x 2 - x x 2 - 2x +1, 其中 x =-1. 分析:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将 x 的值带入计算即可求值。
题型二阴影部分面积的相关计算命题趋势近年来的中考有关阴影面积的题目几乎每年都会考查到,而且不断翻新,精 彩纷呈.这类问题往往与变换、函数、相似等知识结合,涉及到转化、整体等数学思想方法,具有很强的综合性。
例如图 17,记抛物线 y =-x 2+1 的图象与 x 正半轴的交点为A ,将线段 OA 分成n 等份.设分点分别为 P 1,P 2,…,P n -1,过每个分点作 x 轴的垂线,分别与抛物线交于点 Q 1,Q 2,…,Q n -1,再记直角三角形 OP 1Q 1,P 1P 2Q 2,…的面积分别为 S 1,S 2,…,这样就有 S 1= n 2 -1 2n 3 ,S 2= n 2 - 42n 3…;记W=S 1+S 2+…+S n -1,当 n 越来越大时,你猜想 W 最接近的常数是()(A) 23 (B) 12(C) 13(D) 14分析 如图 17,抛物线 y =-x 2+1 的图象与 x 正半轴的交点为A(1,0),与 y 轴的交点为 8(0,1).设抛物线与 y 轴及 x 正半轴所围成的面积为 S ,M(x ,y )在图示抛物线上,则OM 2 = x 2 + y 223 3 2 从 而 = (1 - y ) + y 2⎛ 1 ⎫23 = y - ⎪ + . ⎝ ⎭ 4由 0≤y32≤1, 得 ≤OM ≤1.4这段图象在图示半径为 11个圆 面积之间,即4 、1 的两个 圆所夹的圆环内,所以 S 在图示两 243 1<S < π.164显然,当 n 的值越大时,W 的值就越来越接近抛物线与 y 轴和 x 正半轴所围成的面积的一半,所以3 1<W < π.328与其最接近的值是,故本题应选 C .题型三 解直角三角形的实际应用命题趋势解直角三角形的应用是中考的必考内容之一,它通常以实际生活为背景,考 查学生运用直角三角形知识建立数学模型的能力,解答这类问题的方法是运用 “遇斜化直”的数学思想,即通过作辅助线(斜三角形的高线)把它转化为直角三角形问题,然后根据已知条件与未知元素之间的关系,利用解直角三角形的知识, 列出方程来求解。
例 如图 2,学校旗杆附近有一斜坡。
小明准备测量旗杆 AB 的高度,他发现当斜坡正对着太阳时,旗杆 AB 的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长 BC=20 米,斜坡坡面上的影长 CD=8 米,太阳光线 AD 与水平地面 BC 成 30°角,斜坡 CD 与水平地面 BC 成 45°的角,求旗杆 AB 的高度。
( = 1.732,2 = 1.414,6 = 2.449 精确到 1 米)。
图 2简解:延长 AD 交 BC 延长线于 E ,作 DH ⊥BC 于 H 。
在 Rt △DCH 中,∠DCH=45°,DC=8,所以 DH=HC=8sin45° = 4在 Rt △DHE 中,∠E=30°HE =DH tan 30︒ = 4 2 = 433所以 BE=BC+CH+HE= 20 + 4 2 + 4 6= 20 + 5.656 + 9.796 = 35.452在 Rt △ABE 中,AB = BC ⋅ tan 30︒ = 35.452 ⨯3 ≈ 20(米) 。
3答:旗杆的高度约为 20 米。
点拨:解本题的关键在于作出适当的辅助线,构造直角三角形,并灵活地应用解直角三角形的知识去解决实际问题。
题型四 一次函数和反比例函数的综合题命题趋势一次函数和反比例函数的综合题近几年来几乎每年都会考到,基本上是在 19 题或者 20 题的位置出现,难度中等,问题主要为;求函数的解析式,利用数形结合思想求不等式的解集以及结合三角形,四边形知识的综合考查。
例 已知 A (m ,2) 是直线l 与双曲线 y = 3的交点。
x(1) 求 m 的值; (2) 若直线 l 分别与 x 轴、y 轴相交于 E ,F 两点,并且 Rt△OEF(O 是坐标原点)的外心为点 A ,试确定直线 l 的解析式;(3) 在双曲线 y = 3上另取一点 B 作 BK ⊥ x 轴于 K ;将(2)中的直线lx绕点 A 旋转后所得的直线记为 l ′,若 l ′与 y 轴的正半轴相交于点 C ,且OC = 1OF ,试问在 y 轴上是否存在点 p,使得S 4∆PCA = S ∆BOK若存在,请求出点 P 的坐标?若不存在,请说明理由.2 623解:(1)∵直线l 与双曲线y = x的一个交点为A(m ,2),3 3 ∴ m =2,即m = 2. 3∴A 点坐标为( 2,2).(2)作 AM⊥x 轴于 M .∵A 点是 Rt△OEF 的外心, ∴EA=FA .由 AM∥y 轴有 OM =ME . ∴OF=2OM .∵MA=2,∴OF=4. ∴F 点的坐标为(0,4). 设 l :y =kx +b ,则有⎧ 3 k +b =2, ⎧k 4 ⎪ ⎪ ⎨ ∴⎨ =- ,3⎪⎩b =4. ⎪⎩b =4. 4∴直线l 的解析式为y =- 3x +4.(3)∵OC = 1OF ,∴OC =1.4∴C 点坐标为(0,1).设 B 点坐标为(x 1,y 1,),则x 1y 1=3.1 3∴S △BOK = 2 |x 1 |·|y 1 |= 2.设 P 点坐标为(0,y),满足 S △PCA =S △BOK . ①当点 P 在 C 点上方时,y >1,有1 3 S = (y -1)3 (y -1) 3△PCA2 × = = . 2 4 2∴y=3.②当点 P 在 C 点下方时,y<1,有S△PCA1 3=2(1-y)=2.∴y=-2.综上知,在 y 轴存在点 P(0,3)与(0,-2),使得 S△PAC=S△BOK总结:直线与双曲线的综合题的重要组成部分是两种图象的交点,这是惟一能沟通它们的要素,应用交点时应注意:(1)交点既在直线上也在双曲线上,交点坐标既满足直线的解析式也满足双曲线的解析式.(2)要求交点坐标时,应将两种图象对应的解析式组成方程组,通过解方程组求出交点坐标.(3)判断两种图象有无交点时,可用判别式确定,也可以画出草图直观地确定.题型五实际应用题命题趋势中考考查的实际应用题知识点主要集中在一次方程(组),一次不等式,一次函数的实际应用及其相关方案的设计问题,此类问题近几年每年必考,且分值相对稳定。
例某学校为开展“阳光体育”活动,计划拿出不超过 3000 元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为 8︰3︰2,且其单价和为 130 元.⑴请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?⑵若要求购买篮球、羽毛球拍和乒乓球拍的总数量是 80 个(副),羽毛球拍的数量是篮球数量的 4 倍,且购买乒乓球拍的数量不超过 15 副,请问有几种购买方案?解题方法指导:列方程解应用题的一般步骤:(1)审题,弄清题意。
即全面分析已知量与未知量,已知量与未知量的关系;(2)根据题目需要设合适的未知量;(3)找出题目中的等量关系,并列出方程;(4)解方程,求出未知数的值;(5)检验并作答,对方称的解进行检验,看是否符合题意,针对问题做出答案。
题型六函数动态变化问题命题趋势函数动态变化问题最近几年每年必考,该类问题综合性强,题目难度较大,题型,题序及分值都很稳定,每年均在 23 题以解答题的形式命题。
一般为 3 问,第一问常常考查待定系数法确定二次函数解析式;第二问结合三角形周长,面积及线段长等问题考查二次函数解析式及最值问题;第三问多是几何图形的探究问题。
例已知:在矩形AOBC 中,OB = 4 ,OA = 3 .分别以OB,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B,C 重合),过Fy =k(k > 0)点的反比例函数x 的图象与AC 边交于点E .(1)求证:△AOE 与△BOF 的面积相等;(2)记S =S△OEF -S△ECF ,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.思路分析本题看似几何问题,但是实际上△AOE 和△FOB 这两个直角三角形的底边和高恰好就是E,F 点的横坐标和纵坐标,而这个乘积恰好就是反比例函数的系数K。
所以直接设点即可轻松证出结果。
第二问有些同学可能依然纠结这个△EOF 的面积该怎么算,事实上从第一问的结果就可以发现这个矩形中的三个RT△面积都是异常好求的。
于是利用矩形面积减去三个小RT△面积即可,经过一系列化简即可求得表达式,利用对称轴求出最大值。
第三问的思路就是假设这个点存在,看看能不能证明出来。
因为是翻折问题,翻折之后大量相等的角和边,所以自然去利用三角形相似去求解,于是变成一道比较典型的几何题目,做垂线就可以了.方法指导针对函数与几何图形结合的题目,首先要考虑代数与几何知识之间的相互关联,找出其内在的联系,然后设出要求的解析式,用待定系数法求解即可。
对于涉及存在探究性问题,首先假设条件的存在,然后再通过证明推理及计算,探究所假设的结果是否与已知,推理过程相矛盾,若矛盾则假设不成立,否则假设成立。
“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。