八年级上册数学《轴对称》作轴对称图形 知识点整理

第十三章轴对称一、概念1.把一个图形沿着一条直线折叠，如果直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

这时我们也说这个图形关于这条直线（成轴）对称。

2. 把一个图形沿着某一条直线折叠，如果它能与另一个图形完全重合，那么就说这两个图关于这条直线对称。

这条直线叫做对称轴。

折叠后重合的点是对应点,叫做对称点3、让学生知道轴对称图形（一个图形，有一条或多条对称轴）和轴对称（两个图形，只有一条对称轴）的区别与联系4.轴对称的性质①关于某直线对称的两个图形是全等形。

②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

③轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

④如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

二、线段的垂直平分线1.经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫中垂线。

2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点，在线段的垂直平分线上三、用坐标表示轴对称小结：在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点（x, y）关于x轴对称的点的坐标为（x,- y）.点（x, y）关于y轴对称的点的坐标为（-x, y）.注意：像类似点（x，y）关于X=1对称的题目要学会做法2.三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等注意：知道角平分线交点（到边相等）和垂直平分线交点（到点相等）的区别四、等腰三角形1.等腰三角形的性质①.等腰三角形的两个底角相等。

（等边对等角）②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

（三线合一）2、等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等。

（等角对等边）注意：三线合一不能直接来判定等腰三角形，需要证明全等。

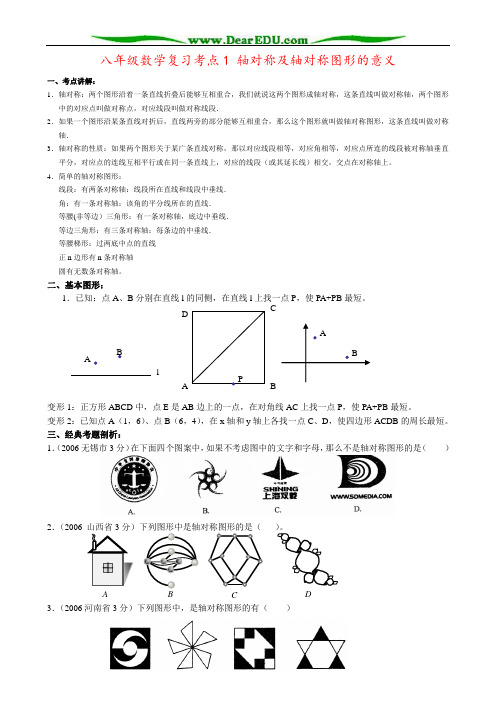
ABCDP八年级数学复习考点1 轴对称及轴对称图形的意义一、考点讲解：1．轴对称：两个图形沿着一条直线折叠后能够互相重合，我们就说这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点，对应线段叫做对称线段．2．如果一个图形沿某条直线对折后，直线两旁的部分能够互相重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴．3．轴对称的性质：如果两个图形关于某广条直线对称，那以对应线段相等，对应角相等，对应点所连的线段被对称轴垂直平分，对应点的连线互相平行或在同一条直线上，对应的线段（或其延长线）相交，交点在对称轴上。

4．简单的轴对称图形：线段：有两条对称轴：线段所在直线和线段中垂线． 角：有一条对称轴：该角的平分线所在的直线． 等腰(非等边）三角形：有一条对称轴，底边中垂线． 等边三角形：有三条对称轴：每条边的中垂线． 等腰梯形：过两底中点的直线 正n 边形有n 条对称轴 圆有无数条对称轴。

二、基本图形：1．已知：点A 、B 分别在直线l 的同侧，在直线l 上找一点P ，使PA+PB 最短。

变形1：正方形ABCD 中，点E 是AB 边上的一点，在对角线AC 上找一点P ，使PA+PB 最短。

变形2：已知点A （1，6）、点B （6，4），在x 轴和y 轴上各找一点C 、D ，使四边形ACDB 的周长最短。

三、经典考题剖析：1．（2006无锡市3分）在下面四个图案中，如果不考虑图中的文字和字母，那么不是轴对称图形的是（ ）2．（2006 山西省3分）下列图形中是轴对称图形的是（ ）。

3．（2006河南省3分）下列图形中，是轴对称图形的有（ ）ABABlB A CDＡ．4个Ｂ．3个Ｃ．2个Ｄ．1个4．（2006鸡西市3分）在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )(A) (B) (C) (D)5．（2006苏州市3分）如图，如果直线m 是多边形ABCDE 的对称轴，其中∠A=1300， ∠B=1100．那么∠BCD 的度数等于 （ ） A. 400B.500C ．60D.7006．（2006梅州市3分）小明在镜中看到身后墙上的时钟，实际时间最接近8时的是下图中的（ ）7．（2006 湛江市6分）如图5，请你画出方格纸中的图形关于点O 的中心对称图形，并写出整个图形的对称轴的条数．四、针对性训练：1．（2006宜昌市3分）从汽车的后视镜中看见某车车牌的后5位号码是 ，该车的后5位号码实际是 。

第十三章（精编）轴对称《轴对称、线段垂直平分线、、等腰三角形、等边三角形》轴对称图形如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，•这个图形就叫做轴对称图形，这条直线就是它的对称轴．有的轴对称图形的对称轴不止一条，如圆就有无数条对称轴．轴对称有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，•那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．图形轴对称的性质如果两个图形成轴对称，•那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线．画一图形关于某条直线的轴对称图形的步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

轴对称与轴对称图形的区别轴对称是指两个图形之间的形状与位置关系，•成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．考点一、关于“轴对称图形”与“轴对称”的认识1.下列几何图形中，○1线段○2角○3直角三角形○4半圆，其中一定是轴对称图形的有【】A．1个B．2个C．3个D．4个2．图中，轴对称图形的个数是【】A．4个 B．3个 C．2个 D．1个3．正n 边形有___________条对称轴，圆有_____________条对称轴线段的垂直平分线 （1）经过线段的中点并且垂直于这条线段的直线，•叫做这条线段的垂直平分线（或线段的中垂线）．（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，•与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．考点二、线段垂直平分线的性质4．如图，△ABC 中，∠A ＝90°，BD 为∠ABC 平分线，DE ⊥BC ，E 是BC 的中点，求∠C 的度数。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）；2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

八年级上册数学轴对称知识点在初中数学中，轴对称是一个非常重要的知识点。

轴对称是指在一个平面上，如果有一条直线，把这个平面分成两个对称的部分，那么我们就说这个平面是轴对称的。

八年级上册的数学课程中，轴对称被涉及到了，下面我们来详细地探讨一下轴对称的相关知识点。

一、轴对称的定义和性质轴对称的定义如上所述，即沿着一条直线进行对称，这条直线就称为轴线或者对称轴。

在轴对称的情况下，通过轴对称得到的镜像图形和原图形完全重合，这也就是轴对称的性质。

轴对称有如下的性质：（1）轴对称图形共有或自成一类轴对称得到的镜像图形和原图形完全重合，因此当把某个图形做轴对称后，得到的图形和原图形形状相同，只是位置不同。

所以，轴对称得到的镜像图形和原图形共有或自成一类。

（2）轴对称的两个对称图形的距离等于轴到这两个图形的距离我们知道，轴对称的求法是以轴线为轴进行对称，而轴线到对称位置不同的点的距离不同，因此，轴对称的两个对称图形的距离等于轴到这两个图形的距离。

（3）轴对称保持长度、角度不变轴对称能够保持长度和角度不变的原因是，轴对称的两个对称图形都是完全重合的，所以它们的长度和角度是相同的。

二、轴对称的基本步骤下面我们来看轴对称的基本步骤：（1）确定轴对称的轴线首先，要确定轴对称的轴线，它必须是平面内的一条直线。

（2）确定轴对称的中心点确定轴对称的中心点，这个点一般都在轴线上，它是轴线的中点。

（3）确定轴对称的象限确定轴对称的象限，即确定轴对称得到的镜像图形和原图形的位置关系。

（4）确定轴对称的顺序确定轴对称的顺序，从哪一端开始进行对称。

一般情况下，我们可以从离中心点近的位置开始对称。

三、轴对称的应用轴对称的应用十分广泛，下面我们来看一下轴对称在实际生活中的应用：（1）轮子的轴对称自行车、汽车等车辆的轮子都采用了轴对称的原理。

（2）建筑物的轴对称建筑物在建造过程中也采用了轴对称的方法，比如古希腊罗马建筑中的神殿、半圆形壳体建筑等。

轴对称知识点一、轴对称图形轴对称图形的定义：一个图形沿着某直线折叠，直线两旁的部分能完全重合，这个图形就叫做轴对称图形，该直线就是它的对称轴.要点诠释：轴对称图形是指一个图形，图形被对称轴分成的两部分能够互相重合．一个轴对称图形的对称轴不一定只有一条，也可能有两条或多条，因图形而定.知识点二、轴对称1.轴对称定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称（或说这两个图形成轴对称），这条直线叫做对称轴．折叠后重合的点是对应点，也叫做对称点要点诠释：轴对称指的是两个图形的位置关系，两个图形沿着某条直线对折后能够完全重合．成轴对称的两个图形一定全等.2.轴对称图形与轴对称的区别：轴对称是指两个图形，而轴对称图形是一个图形.知识点三、轴对称与轴对称图形的性质轴对称的性质：若两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的性质：轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线．知识点四、线段的垂直平分线定义：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫线段的中垂线．性质：性质1：线段垂直平分线上的点到线段两端点的距离相等；性质2：与一条线段两个端点距离相等的点在这条线段的垂直平分线上．要点诠释：三角形三边垂直平分线交于一点，该点到三角形三顶点的距离相等，这点是三角形外接圆的圆心——外心.类型一、轴对称变换1.如图，在平面直角坐标系中，ABC ∆三个顶点坐标分别为(1,6)A -，(5,3)B -，(3,1)C -．（1）ABC ∆关于y 轴对称的图形△111A B C （其中1A ，1B ，1C 分别是A ，B ，C 的对称点），请写出点1A ，1B ，1C 的坐标；（2）若直线l 过点(1,0)，且直线//l y 轴，请在图中画出ABC ∆关于直线l 对称的图形△222A B C （其中2A ，2B ，2C 分别是A ，B ，C 的对称点，不写画法），并写出点2A ，2B ，2C 的坐标．类型二、线段垂直平分线知识点① 线段垂直平分线的性质2. 如图，已知ABC ∆，AB 、AC 的垂直平分线的交点D 恰好落在BC 边上．（1）判断ABC ∆的形状；（2）若点A 在线段DC 的垂直平分线上，求AC BC的值．知识点② 线段垂直平分线的判定3. 如图所示，在ABC ∆中，AB AC =，BE CD =，且BD 与CE 相交于点O ，求证：点O 在线段BC 的垂直平分线上．类型三、利用轴对称的性质求图形的面积4. 在ABC ∆中，90BAC ∠=︒，点A 关于BC 边的对称点为A '，点B 关于AC 边的对称点为B '，点C 关于AB 边的对称点为C '，若1ABC S ∆=，求A B C S '''．类型四、“将军饮马”问题5. 如图，点P、Q为MON内两点，分别在OM与ON上找点A、B，使四边形PABQ的周长最小．类型五、角平分线与线段垂直平分线的综合6. 如图，在△ABC中，AD是∠BAC平分线，线段AD的垂直平分线分别交AB于点F，交BC的延长线于E（1）在图①中，连接DF，证明DF//AC（2）在图①中，连接AE，证明∠EAC=∠B（3）如图②，若线段CD上存在一点M，使∠MPD=∠ACD，AM与EF交于点P，连接DP 并延长与AC交于点N，求证：AN=DM.①②【复习巩固】一．选择题（共7小题）1．如图，ABC ∆中，D 点在BC 上，将D 点分别以AB 、AC 为对称轴，画出对称点E 、F ，并连接AE 、AF ．根据图中标示的角度，求EAF ∠的度数为何？( )A ．113︒B ．124︒C ．129︒D ．134︒2．如图所示，在四边纸片ABCD 中，//AD BC ，//AB CD ，将纸片沿EF 折叠，点A ，D 分别落在A '，D '处，且A D ''经过点B ，FD '交BC 于点G ，连接EG ，若EG 平分FEB ∠，//EG A D ''，80D FC '∠=︒，则A ∠的度数是( )A ．65︒B ．70︒C ．75︒D ．80︒3．如图，直线MN 是四边形AMBN 的对称轴，点P 是直线MN 上的点，下列判断错误的是( )A ．AM BM =B ．AP BN =C ．M AP M BP ∠=∠D ．ANM BNM ∠=∠4．如图，在ABC ∆中，AB 边的中垂线DE ，分别与AB 边和AC 边交于点D 和点E ，BC 边的中垂线FG ，分别与BC 边和AC 边交于点F 和点G ，又BEG ∆周长为16，且1GE =，则AC 的长为( )A ．13B ．14C ．15D ．165．如图，50∠的平分线BE交AD于点E，连接∠=︒，AD垂直平分线段BC于点D，ABCABC∠的度数是()EC，则AECA．115︒B．75︒C．105︒D．50︒6．如图，四边形ABCD中，AB AD=，点B关于AC的对称点B'恰好落在CD上，若110∠=︒，BAD则ACB∠的度数为()A．40︒B．35︒C．60︒D．70︒7．如图，P是AOB∠两边上的点，点P关于OA的对称点Q恰∠外的一点，M，N分别是AOB好落在线段MN上，点P关于OB的对称点R恰好落在MN的延长线上．若 2.5PN=，PM=，3 MR=，则线段QN的长为()7A．1 B．1.5 C．2 D．2.5二．解答题（共3小题）8如图，点A、B在直线l同侧，请你在直线l上画出一点P，使得PA PB+的值最小，画出图形并证明．9．如图，OBC ∆中，BC 的垂直平分线DP 交BOC ∠的平分线于D ，垂足为P ．（1）若60BOC ∠=︒，求BDC ∠的度数；（2）若BOC α∠=，则BDC ∠= （直接写出结果）．10．如图，ABC ∆中，BD 平分ABC ∠，BC 的中垂线交BC 于点E ，交BD 于点F ，连接CF ．（1）若60A ∠=︒，24ABD ∠=︒，求ACF ∠的度数；（2）若5BC =，:5:3BF FD =，10BCF S ∆=，求点D 到AB 的距离．。

5、垂直平分线(中垂线)定义垂直并且平分⼀条线段的直线，叫做这条线段的垂直平分线．书写格式：判定：∵AO＝A′O，∠1＝90°，∴l 是AA′的垂直平分线．性质：∵l是AA′的垂直平分线，∴AO＝A′O，∠1＝∠2＝90° ．6、轴对称性质成轴对称的两个图形全等，且(1)对应点的连线被对称轴垂直平分．(2)对应点的连线互相平⾏(或在同⼀条直线上)．(3)对应线段相等，对应⾓相等．(4)对应线段所在直线的交点在对称轴上(或对应线段所在直线互相平⾏)．如图：(1)AA′，BB′，CC′，DD′，被l垂直平分．(2)AA′∥BB′∥CC′，CC′、DD′在同⼀直线上．(3)AB＝A′B′，BC＝B′C′，CD＝C′D′，AD＝A′D′，∠BAD＝∠B′A′D′，∠ABC＝∠A′B′C′，∠BCD＝∠B′C′D′，∠CDA＝∠C′D′A′．(4)BA、B′A′，BC、B′C′，CD、C′D′的延长线交点在l上．DA、D′A′的延长线平⾏．7、对称轴的作法法1：作⼀条对应点的连线，并作其中垂线．法2：作两条对应点的连线，并分别作其中点，两点确定⼀条直线．法3：分别延长两对对应线段，确定两个交点，两点确定⼀条直线．8、给出⼀个图形及对称轴，作其对称图形的作法过原图形各点画对称轴的垂线，以各点到垂⾜的距离为半径，截取相等，将所作对应点分别相连．⼆、实战演练例1：请在下列三个2×2的⽅格中，各画出⼀个三⾓形，要求所画三⾓形与图中三⾓形成轴对称，且所画的三⾓形顶点与⽅格中的⼩正⽅形顶点重合，并将所画三⾓形涂上阴影．分析：我们应该利⽤轴对称图形的性质，先选择不同的直线当对称轴，再作对称图形．显然⼤⽅格作为正⽅形，有4条对称轴，⽽还有⼀条⽐较难想，对称轴可以经过斜边和直⾓边的中点．解答：例2：如图，桌⾯上有A、B两球，若要将B球射向桌⾯任意⼀边，使⼀次反弹后击中A球，则可以瞄准的点有哪些？分析：本题中，对于桌⾯反弹的问题，其实属于物理中的光路问题，⼊射⾓等于反射⾓，⽽将⼊射⾓作对称后，恰好与反射⾓是对顶⾓，光线在同⼀直线上，因此我们考虑作对称．解答：变式：如图是⼀个台球桌⾯的⽰意图，图中四个⾓上的阴影部分分别表⽰四个⼊球孔.若⼀个球按图中所⽰的⽅向被击出(球可以经过多次反弹)，则该球最后落⼊的球袋是______袋.分析：本题与例2类似，但如果每次都作对称，未免太过⿇烦，我们不难发现⼊射线与桌边的夹⾓为45°，则反射后的夹⾓也为45°，问题得解．解答：例3：如图，已知∠AOB＝60°，点P为∠AOB内⼀点，分别作点P关于OA，OB的对称点P1，P2，连接P1P2，交OA于点M，交OB于点M．(1)连接OP1，OP2，求∠P1OP2的度数．(2)若P1P2＝8，求△PMN周长．分析：(1)要求∠P1OP2的度数，直接求显然很困难，我们不妨从对应线段考虑，则想到连接OP．(2)同样的，将组成三⾓形的三条线段中，能找到对应相等的线段找出，进⾏转化．解答：变式：如图，△ABC和△A′B′C′关于直线MN对称，△A′B′C′和△A′′B′′C′′关于直线EF对称．(1)画出直线EF；(2)直线MN与EF相交于点O，试探究∠BOB′′与直线MN、EF所夹锐⾓α的数量关系．分析：(1)问不难，只需⽤3种⽅法中的任意⼀种即可．(2)问与例3类似，准确依据题意，画出图形后，根据对称性，连接对应线段就能有所突破．解答：(1)如图，连接B′B′′，C′C′′，各取中点，连接后，直线EF即为所求．(2)连接OB′，∵△ABC和△A′B′C′关于直线MN对称，∴∠BOM＝∠B′OM，同理可得∠B′OE＝∠B′′OE，∴∠BOB′′＝∠BOB′＋∠B′OB′′＝2∠B′OM＋2∠B′OE＝2∠MOE＝2α．。

八年级上册数学轴对称知识点总结一、引言数学作为一门基础学科，其所包含的内容广泛而深刻。

在八年级上册中，轴对称作为其中的一个重要知识点，对学生来说具有一定的挑战性。

在本文中，我们将以八年级上册数学轴对称知识点为主题，进行全面的评估和总结，帮助学生更好地理解和掌握这一知识点。

二、基本概念1. 关于轴对称轴对称是指平面上存在一条直线，使得图形关于这条直线对称。

一个图形如果可以分成两部分，且其中一部分经过旋转、翻转或平移后可以和另一部分完全重合，那么这个图形就是关于这条直线对称的。

2. 轴对称的性质- 轴对称的图形关于对称轴是对称的。

- 轴对称的图形的对称中心在对称轴上。

- 轴对称的图形的每一点经过对称轴的对称变换后都能恰好在图形上。

三、基本题型在八年级上册数学中，关于轴对称的题型主要包括：1. 判断图形是否轴对称2. 找出图形的对称中心和对称轴3. 根据轴对称的性质，解决相关的计算题目四、实例分析以具体的实例来分析轴对称的知识点：题目：如图，判断图形是否关于虚线对称。

[图片]解析：根据图形可以看出，通过对折可以发现，图形A和图形B可以重合，因此该图形是关于虚线对称的。

又如，若已知一个三角形的对称轴为边AC，对称中心为边BC的中点O，求证△ABC是个等腰三角形。

解析：根据轴对称的性质，可以证明线段BO和OA相等，从而得到△ABC为等腰三角形。

五、拓展应用除了基本的题型和实例分析，八年级上册数学中的轴对称知识点还涉及到一些拓展应用，在真实生活中也是有一定的应用场景的。

在建筑设计中，轴对称的思想可以帮助设计师更好地进行建筑设计和规划，保证建筑物的整体美观和稳定性。

在工程制图和艺术设计中，轴对称也扮演着重要的角色。

六、总结与展望通过对八年级上册数学轴对称知识点的全面评估和总结，我们更深入地理解了轴对称的基本概念、基本题型和实例分析，以及在拓展应用中的意义。

在今后的学习中，我们应该更加注重轴对称知识点的理解和应用，结合实际情况进行综合训练，提高解决问题的能力和思维方式，为未来的学习和生活打下坚实的基础。

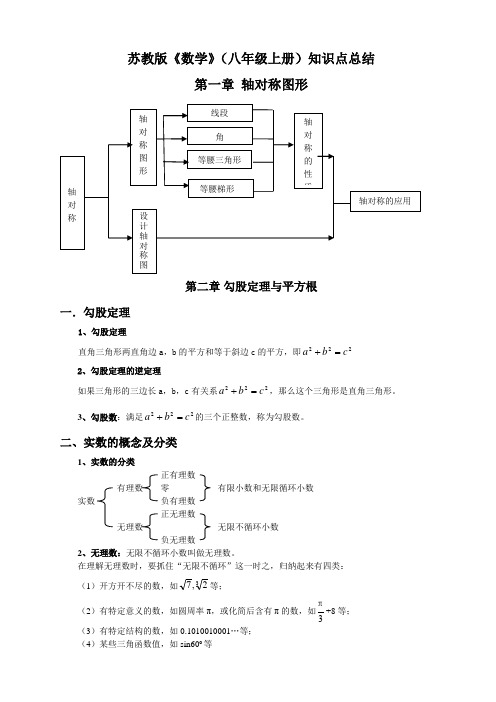
苏教版《数学》（八年级上册）知识点总结第一章 轴对称图形第二章 勾股定理与平方根一．勾股定理1、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+ 2、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

3、勾股数：满足222c b a =+的三个正整数，称为勾股数。

二、实数的概念及分类1、实数的分类 正有理数有理数 零 有限小数和无限循环小数 实数 负有理数 正无理数无理数 无限不循环小数 负无理数2、无理数：无限不循环小数叫做无理数。

在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类： （1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等； （3）有特定结构的数，如0.1010010001…等； （4）某些三角函数值，如sin60o 等轴对称轴对称的性质轴对称图形线段 角 等腰三角形 轴对称的应用等腰梯形设计轴对称图案三、平方根、算数平方根和立方根1、算术平方根：一般地，如果一个正数x 的平方等于a ，即x 2=a ，那么这个正数x 就叫做a 的算术平方根。

特别地，0的算术平方根是0。

表示方法：记作“a ”，读作根号a 。

性质：正数和零的算术平方根都只有一个，零的算术平方根是零。

2、平方根：一般地，如果一个数x 的平方等于a ，即x 2=a ，那么这个数x 就叫做a 的平方根（或二次方根）。

表示方法：正数a 的平方根记做“a ±”，读作“正、负根号a ”。

性质：一个正数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。

开平方：求一个数a 的平方根的运算，叫做开平方。

0≥a注意a 的双重非负性：a ≥03、立方根一般地，如果一个数x 的立方等于a ，即x 3=a 那么这个数x 就叫做a 的立方根（或三次方根）。

表示方法：记作3a性质：一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

八年级上册数学轴对称知识点总结八年级上册数学轴对称知识点总结1.对称轴：如果一个图形沿某条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形;这条直线叫做对称轴。

2.性质：(1)轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

(2)角平分线上的点到角两边距离相等。

(3)线段垂直平分线上的任意一点到线段两个端点的距离相等。

(4)与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

(5)轴对称图形上对应线段相等、对应角相等。

3.等腰三角形的性质：等腰三角形的两个底角相等，(等边对等角)4.等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三线合一〞。

5.等腰三角形的判定：等角对等边。

6.等边三角形角的特点：三个内角相等，等于60°，7.等边三角形的判定：三个角都相等的三角形是等腰三角形。

有一个角是60°的.等腰三角形是等边三角形有两个角是60°的三角形是等边三角形。

8.直角三角形中，30°角所对的直角边等于斜边的一半。

9.直角三角形斜边上的中线等于斜边的一半。

数学学习方法诀窍1细心地发掘概念和公式很多同学对概念和公式不够重视，这类问题反映在三个方面：一是，对概念的理解只是停留在文字表面，对概念的特殊情况重视不够。

例如，在代数式的概念(用字母或数字表示的式子是代数式)中，很多同学忽略了“单个字母或数字也是代数式〞。

二是，对概念和公式一味的死记硬背，缺乏与实际题目的联系。

这样就不能很好的将学到的知识点与解题联系起来。

三是，一部分同学不重视对数学公式的记忆。

记忆是理解的基础。

如果你不能将公式烂熟于心，又怎能够在题目中熟练应用呢?我们的建议是：更细心一点(观察特例)，更深入一点(了解它在题目中的常见考点)，更熟练一点(无论它以什么面目出现，我们都能够应用自如)。

2养成良好的解题习惯要想学好数学，多做题目是难免的，熟悉掌握各种题型的解题思路。

暑期预习 | 八年级上册〔新初二〕【轴对称】知识点梳理+讲解+习题《轴对称》一、知识框架：二、知识概念：1.根本概念：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的局部能够相互重合，这个图形就叫做轴对称图形.⑵两个图形成轴对称：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称.⑶线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线.⑷等腰三角形：有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角.⑸等边三角形：三条边都相等的三角形叫做等边三角形.2.根本性质：⑴对称的性质：①不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一对对应点所连线段的垂直平分线.②对称的图形都全等.⑵线段垂直平分线的性质：①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.⑶关于坐标轴对称的点的坐标性质⑷等腰三角形的性质：①等腰三角形两腰相等.②等腰三角形两底角相等〔等边对等角〕.③等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合.④等腰三角形是轴对称图形，对称轴是三线合一〔1条〕.⑸等边三角形的性质：①等边三角形三边都相等.②等边三角形三个内角都相等，都等于60°③等边三角形每条边上都存在三线合一.④等边三角形是轴对称图形，对称轴是三线合一〔3条〕.3.根本判定：⑴等腰三角形的判定：①有两条边相等的三角形是等腰三角形.②如果一个三角形有两个角相等，那么这两个角所对的边也相等〔等角对等边〕.⑵等边三角形的判定：①三条边都相等的三角形是等边三角形.②三个角都相等的三角形是等边三角形.③有一个角是60°的等腰三角形是等边三角形.4.根本方法：⑴做已知直线的垂线：⑵做已知线段的垂直平分线：⑶作对称轴：连接两个对应点，作所连线段的垂直平分线.⑷作已知图形关于某直线的对称图形：⑸在直线上做一点，使它到该直线同侧的两个已知点的距离之和最短.。

三一文库（）/初中二年级〔苏教版八年级数学轴对称图形知识点〕为大家整理的苏教版八年级数学轴对称图形知识点的文章，供大家学习参考！更多最新信息请点击一、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形沿某直线对折能够完全重合，是两个图形之间的一种关系，而轴对称图形是两部分能完全重合的一个图形。

联系：两者都有完全重合的特征，都有对称轴，都有对称点。

二、轴对称的性质1、定义——垂直并且平分一条线段的直线，叫做这条线段的垂直平分线。

2、把一个图形沿着一条直线折叠，如果它能够与另一个图形重合，那么称这两个图形关于这条直线对称，也称这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点。

第1页共3页3、把一个图形沿着一条某直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴。

4、成轴对称的两个图形全等。

如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线。

三、线段、角的轴对称性1、线段是轴对称图形，线段的垂直平分线是它的对称轴。

线段的垂直平分线上的点到线段两端的距离相等;2、到线段两端距离相等的点，在这条线段的垂直平分线上;线段的垂直平分线是到线段两端距离相等的点的集合。

3、角是轴对称图形，角平分线所在直线是它的对称轴。

角平分线上的点到角的两边距离相等;角的内部到角的两边距离相等的点，在这个角的平分线上。

四、等腰三角形的轴对称性1、等腰三角形是轴对称图形，顶角平分线所在直线是它的对称轴。

2、等腰三角形的两个底角相等(简称“等边对等角”)。

等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

3、如果一个三角形有两个角相等，那么这两个角所对的边也相等(简称“等角对等边”)。

23。

八年级数学上册“第十三章轴对称”必背知识点一、轴对称与轴对称图形的定义1. 轴对称：如果两个图形关于某一条直线对称，那么这两个图形就叫做关于这条直线的轴对称图形，这条直线叫做对称轴。

折叠后重合的点是对应点，叫做对称点。

2. 轴对称图形：如果一个图形沿着一条直线折叠，直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

二、轴对称的性质1. 对应点性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

2. 对应线段与对应角：轴对称图形上对应线段相等、对应角相等。

三、线段的垂直平分线1. 定义：经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）。

2. 性质：线段垂直平分线上的点与这条线段两个端点的距离相等。

与一条线段两个端点距离相等的点，在线段的垂直平分线上。

四、坐标表示轴对称1. 关于x轴对称：点(x, y)关于x轴对称的点的坐标为(x, -y)。

2. 关于y轴对称：点(x, y)关于y轴对称的点的坐标为(-x, y)。

五、等腰三角形与等边三角形的性质1. 等腰三角形：性质：等腰三角形的两个底角相等 （等边对等角）；顶角平分线、底边上的中线、底边上的高互相重合 （三线合一）。

判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）。

2. 等边三角形：性质：等边三角形的三个角都相等，并且每一个角都等于60°；等边三角形具有等腰三角形所有的性质。

判定：三条边都相等的三角形是等边三角形；三个角都相等的三角形是等边三角形；有一个角是60°的等腰三角形是等边三角形。

六、特殊线段的性质1. 三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线。

三角形的中位线平行于第三边，并且等于它的一半。

2. 三角形三条边的垂直平分线：三角形的三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等。

专题13.12轴对称（全章知识梳理与考点分类讲解）第一部分【知识点归纳】【知识点一】轴对称1.轴对称图形和轴对称（1）轴对称图形如果一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形的性质：轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.（2）轴对称定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴.成轴对称的两个图形的性质：①关于某条直线对称的两个图形形状相同，大小相等，是全等形；②如果两个图形关于某条直线对称，则对称轴是任何一对对应点所连线段的垂直平分线；③两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么它们的交点在对称轴上.（3）轴对称图形与轴对称的区别和联系区别:轴对称是指两个图形的位置关系，轴对称图形是指具有特殊形状的一个图形；轴对称涉及两个图形，而轴对称图形是对一个图形来说的.联系：如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形关于这条轴对称；如果把成轴对称的两个图形看成一个整体，那么它就是一个轴对称图形．2.线段的垂直平分线线段的垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等.反过来，与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.【知识点二】作轴对称图形（1）几何图形都可以看作由点组成，我们只要分别作出这些点关于对称轴的对应点，再连接这些点，就可以得到原图形的轴对称图形；（2）对于一些由直线、线段或射线组成的图形，只要作出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形.【知识点三】等腰三角形1.等腰三角形（1）定义：有两边相等的三角形，叫做等腰三角形.（2）等腰三角形性质①等腰三角形的两个底角相等，即“等边对等角”；②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合（简称“三线合一”）.特别地，等腰直角三角形的每个底角都等于45°.（3）等腰三角形的判定如果一个三角形有两个角相等，那么这两个角所对的边也相等（即“等角对等边”）.2.等边三角形（1）定义：三条边都相等的三角形，叫做等边三角形.（2）等边三角形性质：等边三角形的三个角相等，并且每个角都等于60°.（3）等边三角形的判定：①三条边都相等的三角形是等边三角形；②三个角都相等的三角形是等边三角形；③有一个角为60°的等腰三角形是等边三角形.3.直角三角形的性质定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.第二部分【题型展示与方法点拨】【题型1】利用轴对称的性质求值【例1】（2024八年级上·江苏·专题练习）如图，点P 在四边形ABCD 的内部，且点P 与点M 关于AD 对称，PM 交AD 于点G ，点P 与点N 关于BC 对称，PN 交BC 于点H ，MN 分别交AD BC ，于点E F ，．（1）连接PE PF ，，若12cm MN =，求PEF !的周长；（2）若134C D ∠+∠=︒，求HPG ∠的度数．【变式1】（23-24七年级下·广东深圳·期末）如图，四边形ABCD 中，AB AD =，将ABC V 沿着AC 折叠，使点B 恰好落在CD 上的点B '处，若110BAD ∠=︒，则ACB =∠（）A ．55︒B ．45︒C ．40︒D ．35︒【变式2】（22-23八年级上·江苏镇江·阶段练习）如图，APT △与CPT △关于直线PT 对称，A APT ∠=∠，延长AT 交PC 于点F ，当A ∠=︒时，FTC C ∠=∠．【题型2】利用折叠的特征求值【例2】（23-24七年级下·河南新乡·期末）如图，在长方形纸片ABCD 中，点E 在边AD 上，点F 在边BC 上，四边形CDEF 沿EF 翻折得到四边形C D EF ''且点D ¢恰好落在边AB 上；将AED '△沿ED '折叠得到A ED ''△且点A '恰好落在边BC 上．（1）若77BFE ∠=︒，则BFC '∠=．（2）若50A D B '∠='︒，求A EF '∠的度数．【变式1】（23-24九年级上·山东枣庄·开学考试）如图，四边形ABCD 为一矩形纸带，点E F 、分别在边AB CD 、上，将纸带沿EF 折叠，点A D 、的对应点分别为A ''、D ，若235∠=︒，则1∠的度数为（）A ．62.5︒B ．72.5︒C ．55︒D ．45︒【变式2】（2024八年级上·江苏·专题练习）如图，在ABC V 和DCB △中，90,,A D AC BD ∠=∠=︒相交于点E ，AE DE =．将CDE 沿CE 折叠，点D 落在点D ¢处，若30BED ∠='︒，则BCD '∠的大小为．【题型3】线段垂直平分线的性质与判定求值【例3】（23-24八年级上·江苏宿迁·期中）如图，AD 是ABC 的角平分线，DE DF 、分别是ABD △和ACD 的高．（1）试说明AD 垂直平分EF ；（2）若8628ABC AB AC S === ，，，求DE 的长．【变式1】（23-24八年级上·四川巴中·期末）如图，在ABC V 中，分别以点A 和点B 为圆心，大于12AB长为半径画弧，两弧相交于点M 、N ，作直线MN ，交BC 于点D ，连接AD ．若7AC =，12BC =，则ADC △的周长为（）A ．12B ．14C ．19D ．26【变式2】（23-24九年级上·重庆·期末）如图在ABC V 中，D 为AB 中点，DE AB ⊥，180ACE BCE ∠+∠=︒，EF BC ⊥交BC 于F ，8AC =，12BC =，则BF 的长为．【题型4】利用等腰三角形的性质与判定求值或证明【例4】（2024八年级上·江苏·专题练习）如图，在ABC V 中，AC BC =，120ACB ∠=°，CD 是AB 边上的中线，BD 的垂直平分线EF 交BC 于点E ，交AB 于点F ，15CDG ∠=︒．（1）求证：AD AG =；（2）试判断CDE 的形状，并说明理由．【变式1】（23-24八年级上·湖南株洲·期末）在ABC V 中，36A ∠=︒，72B ∠=︒，则ABC V 是（）A ．钝角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形【变式2】（23-24八年级上·重庆沙坪坝·期末）如图，在ABC ∆中，AB AC =，AD BD =，DE AB ⊥于点E ，若4BC =，BDC 的周长为10，则AE 的长为．【题型5】利用等边三角形的性质与判定求值或证明【例5】（2024八年级上·江苏·专题练习）如图，已知Rt ABC △中，90ACB ∠=︒，CD AB ⊥于D ，BAC ∠的平分线分别交BC ，CD 于E 、F ．（1）试说明CEF △是等腰三角形．（2）若点E 恰好在线段AB 的垂直平分线上，试说明线段AC 与线段AB 之间的数量关系．【变式1】（23-24八年级上·福建福州·期末）如果,,a b c 为三角形的三边长，且满足()()()0a b b c c a ---=，那么该三角形的形状为（）A ．等腰三角形B ．等边三角形C ．不等边三角形D ．无法确定【变式2】（23-24九年级上·河北邯郸·期末）如图1，ABC V 和ADE V 是等边三角形，连接BD ，CE 交于点F ．（1）BD CE 的值为；（2）BFC ∠的度数为︒.【题型6】利用30度所对的直角边等于斜边一半求值或证明【例6】（2024八年级上·江苏·专题练习）在Rt ABC △中，90ACB ∠=︒，M 是边AB 的中点，CH AB ⊥于点H ，CD 平分ACB ∠．（1）求证：CD 平分MCH ∠；（2）过点M 作AB 的垂线交CD 的延长线于点E ，求证：CM EM =；（3）AEM △是什么三角形？证明你的猜想．【变式1】（23-24九年级上·安徽合肥·期末）如图，ABC V 中，9030ACB A ∠=︒∠=︒，，CD AB ⊥于点D ，若1BD =，则AD 的长度为（）A ．5B ．4C ．3D ．2【变式2】（23-24七年级下·陕西西安·阶段练习）如图，在Rt ABC △中，90C ∠=︒，AD 是CAB △的平分线，DE 垂直平分AB ，若3CD =，则BD =．第三部分【中考链接与拓展延伸】1、直通中考【例1】（2024·四川巴中·中考真题）如图，在ABC V 中，D 是AC 的中点，CE AB ⊥，BD 与CE 交于点O ，且BE CD =．下列说法错误的是（）A ．BD 的垂直平分线一定与AB 相交于点EB ．3BDC ABD ∠=∠C ．当E 为AB 中点时，ABC V 是等边三角形D ．当E 为AB 中点时，34BOC AEC S S =△△【例2】（2024·江苏宿迁·中考真题）如图，在ABC V 中，5030B C ︒∠∠=︒=，，A 是高，以点A 为圆心，A 长为半径画弧，交AC 于点E ，再分别以B 、E 为圆心，大于12BE 的长为半径画弧，两弧在BAC ∠的内部交于点F ，作射线AF ，则DAF ∠=．2、拓展延伸【例】（22-23八年级上·吉林长春·阶段练习）在等腰ABC V 中，CA CB =，30B ∠=︒，将一块足够大的直角三角尺PMN （90M ∠=︒、30MPN ∠=︒）按如图所示放置，顶点P 在线段AB 上滑动，三角尺的直角边PM 始终经过点C ，并且与CB 的夹角PCB α∠=，斜边PN 交AC 于点D ．（1）当P 运动到AB 中点时，α=__________度；（2）当45α=︒时，请写出图中所有的等腰三角形（ABC V 除外）__________．（3）在点P 的滑动过程中，当PCD △的形状是以PC 为底的等腰三角形时，请在指定位置画出此时形成的图形，并指出此时图中的所有直角三角形（PMN 除外）．不用说明理由．。

第十三章轴对称13.1 轴对称（对称点）轴对称图形：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合。

这条直线就是它的对称轴。

垂直平分线：经过线段中点并且垂直于这条线段的直线。

图形轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

线段垂直平分线的性质：垂直平分线上的点到两端的距离相等。

若PA=PB，点C为AB中点，则PC⊥AB或点P在线段AB的垂直平分线上。

13.2 画轴对称图形先画对称点（过该点画对称轴的垂线，取等长），然后连接对称点，形成轴对称图形。

13.3 等腰三角形概念：有两边相等的三角形。

性质：等边对等角，三线合一（顶角平分线、底边上的中线、底边上的高）。

判定：等角对等边等边三角形：三边都相等的特殊的等腰三角形。

三个内角都相等，每个内角60º。

（判定：三个角都相等的三角形；有一个角是60º的等腰三角形。

）在RtΔ中，如果一个锐角等于30º，那么它所对的直角边等于斜边的一半。

（在RtΔ中，斜边上的中线等于斜边的一半。

）13.4 课题学习最短路径问题利用轴对称、平移作出最短路径选择。

（两点之间线段最短）作者留言：非常感谢！您浏览到此文档。

为了提高文档质量，欢迎您点赞或留言告诉我文档的不足之处，以便于对该文档进行完善优化，在此本人深表感谢！祝您天天快乐！制定学习计划有什么好处？一、计划是实现目标的蓝图。

目标不是什么花瓶，你需要制定计划，脚踏实地、有步骤地去实现它。

通过计划合理安排时间和任务，使自己达到目标，也使自己明确每一个任务的目的。

二、促使自己实行计划。

学习生活是千变万化的，它总是在引诱你去偷懒。

制定学习计划，可以促使你按照计划实行任务，排除困难和干扰。

三、实行计划是意志力的体现。

持实行计划可以磨练你的.意志力，而意志力经过磨练，你的学习收获又会更一步提升。

这些进步只会能使你更有自信心，取得更好的成功。

四、有利于学习习惯的形成。

八年级数学上册知识点：轴对称1轴对称：把一个图形沿着某一条直线折叠，若是它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，两个图形中的对应点叫做对称点，对应线段叫做对称线段。

2轴对称图形：若是一个图形沿着一条直线折叠，直线两旁的部份能够相互重合，那么那个图形叫做轴对称图形，这条直线确实是它的对称轴。

注意：对称轴是直线而不是线段3轴对称的性质：关于某条直线对称的两个图形是全等形;若是两个图形关于某条直线对称，那么对称轴是对应点连线的垂直平分线;两个图形关于某条直线对称，若是它们的对应线段或延长线相交，那么交点在对称轴上;若是两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

4线段垂直平分线：概念：垂直平分一条线段的直线是这条线的垂直平分线。

性质：①线段垂直平分线上的点到这条线段两个端点的距离相等;②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

注意：依照线段垂直平分线的这一特性能够推出：三角形三边的垂直平分线交于一点，而且这一点到三个极点的距离相等。

角的平分线：概念：把一个角分成两个相等的角的射线叫做角的平分线性质：①在角的平分线上的点到那个角的两边的距离相等②到一个角的两边距离相等的点，在那个角的平分线上注意：依照角平分线的性质，三角形的三个内角的平分线交于一点，而且这一点到三条边的距离相等6等腰三角形的性质与判定：性质：对称性：等腰三角形是轴对称图形，等腰三角形底边上的中线所在的直线是它的对称轴，或底边上的高所在的直线是它的对称轴，或顶角的平分线所在的直线是它的对称轴;三线合一：等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合;等边对等角：等腰三角形的两个底角相等。

说明：等腰三角形的性质除“三线合一”外，三角形中的要紧线段之间也存在着特殊的性质，如：①等腰三角形两底角的平分线相等;②等腰三角形两腰上的中线相等;③等腰三角形两腰上的高相等;④等腰三角形底边上的中点到两腰的距离相等。