线面平行与面面平行的判定
- 格式:ppt
- 大小:214.00 KB
- 文档页数:23


创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、两条直线垂直的判定(1)在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
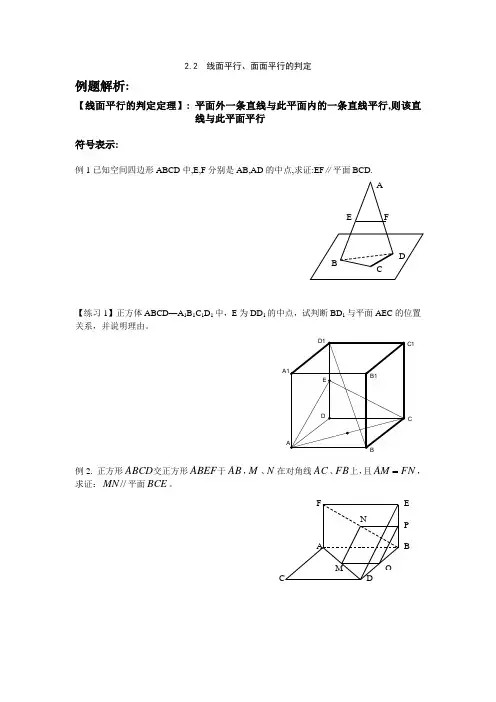
2.2 线面平行、面面平行的判定例题解析:【线面平行的判定定理】: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行符号表示:例1已知空间四边形ABCD 中,E,F 分别是AB,AD 的中点,求证:EF ∥平面BCD.【练习1】正方体ABCD —A 1B 1C 1D 1中,E 为DD 1的中点,试判断BD 1与平面AEC 的位置关系,并说明理由。
例2. 正方形ABCD 交正方形ABEF 于AB ,M 、N 在对角线AC 、FB 上,且FN AM ,求证://MN 平面BCE 。
C1A C【练习求证:例3.已知P 是平行四边形ABCD 所在平面外一点,E 、F 分别为AB 、PD 的中点,求证:AF ∥平面PEC【练习3】:在正方体ABCD -A 1B 1C 1D 1中,E 、F BC 、C 1D 1的中点 求证:EF ∥平面BB 1D 1DPDBA C1A CA例4.(如图)已知正方体ABCD-A 1B 1C 1D 1,求证平面AB 1D 1∥平面C 1BD练习4 正方体ABCD-A 1B 1C 1D 1,中,M,N,E,F 分别为棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点,求证: 平面AMN ∥平面EFDB例5:在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 、P 、Q 、R 分别是所在棱AB 、BC 、BB '、A 'D '、D 'C '、DD '的中点,求证:平面PQR ∥平面EFG 。
CB 1A 1C 1D 1ABDC'CB 1A 1C 1D 1ABD练习5:已知四棱锥P-ABCD 中,地面ABCD 为平行四边形,点M,N,Q 分别为PA,BD,PD 上的中点,求证:平面MNQ ∥平面PBC【巩固练习】一、选择题1、a ∥β,则a 平行于β内的( ) A 、一条确定的直线 B 、任意一条直线 C 、所有直线 D 、无数多条平行线2、如果直线a ∥平面a ,那么直线a 与平面a 内的( ) A 、一条直线不相交 B 、两条直线不相交 C 、无数条直线不相交 D 、任意一条直线都不相交3 两条平行线中的一条平行于一个平面,那么另一条与此平面的位置关系是( ) A.平行 B.相交或平行C.平行或在平面内.D.相交或平行或在平面内 4. 已知直线l ∥平面α,直线a α⊂,则l 与 a 必定 ( ) A.平行. B.异面. C.相交. D.无公共点.5、直线a ∥面α,面α内有n 条互相平行的直线,那么这n 条直线和直线a ( ) A 、全平行B 、全异面C 、全平行或全异面D 、不全平行也不全异面6、直线a ∥平面a ,平面a 内有n 条直线相交于一点,那么这n 条 直线中与直线a 平行的( ) A 、至少有一条B 、至多有一条C 、有且只有一条D 、不可能有二、填空题7、若直线a ∥平面 α,直线b ∥平面β,且 a ⊂β,b ⊂α,且 α∩β=c ,则 a 、b 的位置关系是8、若直线a ∥平面 α,直线b ∥ 平面β,a ⊂β,b ⊂α,则a 、b 的位置关系是B9. 空间四边形ABCD 中,AC=2cm ,BD=4cm ,AC 与BD 成45°角,M ,N ,P ,Q 分别是四边中点,则四边形MNPQ 的面积是 . 三.解答题10.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE :EB=CF :FB=1:3,则对角线AC 和平面DEF 的位置关系如何?11.正方体ABCD —A 1B 1C 1D 1的棱长为a ,E ,F 是线段AD 1,DB 上的点,且AE =BF . 求证:EF ∥平面CD 1.12.已知,如图P 是平行四边形ABCD 外一点同M ,N 分别是PC ,AB 的中点。

2.2.3 直线与平面平行的性质 2.2.4 平面与平面平行的性质1.文字语言:一条直线与一个平面平行,则__过这条直线的任一平面与此平面的交线__与该直线平行.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫a ∥α__a ⊂β____α∩β=b __⇒a ∥b 4.作用:线面平行⇒线线平行.要点二 面面平行的性质定理1.文字语言:如果两个平行平面同时和第三个平面__相交__,那么它们的交线__平行__.2.图形语言:3.符号语言:⎭⎪⎬⎪⎫α∥β__α∩γ=a ____β∩γ=b __⇒a ∥b 4.作用:面面平行⇒线线平行.要点三 平行关系性质的应用1.若平面α与平面β平行,则α上的任何直线与平面β的位置关系是__平行__. 2.若两个面互相平行,则分别在这两个平行平面内的直线的关系是__平行或异面__. 3.A 是异面直线a ,b 外一点,过A 最多可作__0或1__个平面同时与a ,b 平行. 4.过平面外一点能作__无数__条直线和这个平面平行.思考: 如果两个平面平行,那么分别位于两个平面内的直线也互相平行,这句话正确吗?为什么?提示 不正确,因为这两个平面平行,那么位于两个平面内的直线没有公共点,它们平行或异面.考点一线面平行、面面平行的性质定理定理可简记为“线面平行,则线线平行”“面面平行,则线线平行”.定理揭示了直线与平面平行中蕴涵着直线与直线平行,即通过直线与平面平行、平面与平面平行可得到直线与直线平行,这给出了一种作平行线的方法.【例题1】在下列命题中,正确的有__④__(填序号).①若α∩β=a,b⊂α,则a∥b;②若a∥平面α,b⊂α,则a∥b;③若平面α∥平面β,a⊂α,b⊂β,则a∥b;④平面α∥平面β,点P∈α,a∥β且P∈a,则a⊂α.思维导引:此类题一般是以符号语言为载体的判断题,熟悉相关定理是前提,全面分析是关键,一般通过合理利用模型及排除法解题.解析①若α∩β=a,b⊂α,则a,b可能平行也可能相交,①不正确;②若a∥α,b⊂α,则a与b异面或a∥b,②不正确;③若α∥β,a⊂α,b⊂β,则a∥b或a与b异面,③不正确;④若α∥β,点P∈α,知P∉β,所以过点P且平行于β的直线a必在α内,故④正确.【变式1】(1)若直线a,b均平行于平面α,那么a与b的位置关系是__平行、相交或异面__.(2)若直线a∥b,且a∥平面β,则b与β的位置关系是__b∥β或b⊂β__.(3)若直线a,b是异面直线,且a∥β,则b与β的关系是__b∥β或b⊂β或b与β相交__.解析(1)a∥α,b∥α,则知a,b与α无公共点,而a,b平行、相交、异面都有可能.(2)a∥b,a∥β知b∥β或b在β内.(3)b与β的三种位置关系都有可能.考点二线面平行的性质及应用利用线面平行的性质定理判断两直线平行的步骤:(1)先找过已知直线且与已知平面相交的平面;(2)再找两个平面的交线;(3)由定理得出结论.【例题2】如图,已知两条异面直线AB与CD,平面MNPQ与AB,CD都平行,且点M,N,P,Q依次在线段AC,BC,BD,AD上,求证:四边形MNPQ是平行四边形.思维导引:AB∥平面MNPQ,CD∥平面MNPQ→MN∥PQ,NP∥MQ→四边形MNPQ是平行四边形证明因为AB∥平面MNPQ,且过AB的平面ABC交平面MNPQ于MN,所以AB∥MN.又过AB的平面ABD交平面MNPQ于PQ,所以AB∥PQ,所以MN∥PQ.同理可证NP ∥MQ.所以四边形MNPQ为平行四边形.【变式2】如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于点F.求证:EF∥B1C.证明由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD 为平行四边形,从而B1C∥A1D,又A1D⊂平面A1DFE,B1C⊄平面A1DFE,于是B1C∥平面A1DFE.又B1C⊂平面B1CD1,平面A1DFE∩平面B1CD1=EF,所以EF∥B1C.考点三面面平行的性质及应用应用平面与平面平行的性质定理的基本思路:【例题3】在长方体ABCD-A1B1C1D1中,E为棱DD1上的点.当平面AB1C∥平面A1EC1时,点E的位置是__与D重合__.思维导引:平面AB1C∥平面A1EC1,且都与对角面BB1D1D相交,则交线平行.在平行四边形BB1D1D中再来论证平行线的位置.解析如图,连接B1D1,BD,设B1D1∩A1C1=M,BD∩AC=O.连接ME,B1O,因为平面AB1C∥平面A1EC1,平面AB1C∩平面BDD1B1=B1O,平面A1EC1∩平面BDD1B1=ME,所以B1O∥ME.又由长方体的性质可知四边形B1MDO为平行四边形,则B1O∥MD.故E与D重合.【变式3】已知三棱柱ABC-A′B′C′中,D是BC的中点,D′是B′C′的中点,设平面A′D′B∩平面ABC=a,平面ADC′∩平面A′B′C′=b,判断直线a,b的位置关系,并证明.解析直线a,b的位置关系是平行.如图所示,连接DD′.因为平面ABC∥平面A′B′C′,平面A′D′B∩平面ABC=a,平面A ′D ′B ∩平面A ′B ′C ′=A ′D ′, 所以A ′D ′∥a . 同理可证AD ∥b .又D 是BC 的中点,D ′是B ′C ′的中点,所以DD ′BB ′,又BB ′AA ′,所以DD ′AA ′,所以四边形AA ′D ′D 为平行四边形,所以A ′D ′∥AD ,所以a ∥b .考点四 空间平行关系的相互转换线线平行、线面平行、面面平行这三种关系是紧密相连的,可以进行转换.相互间的转换关系如下.【例题4】 如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别是AD 1,BD 的中点.(1)求证:PQ ∥平面DCC 1D 1; (2)求PQ 的长;思维导引:通过作辅助线构造平面,从而证得线面平行;或通过线线平行证得线面平行. 解析 (1)证明:方法一 如图,连接AC ,CD 1.AC 与BD 交于点Q .因为P ,Q 分别是AD 1,AC 的中点,所以PQ ∥CD 1. 又PQ ⊄平面DCC 1D 1, CD 1⊂平面DCC 1D 1, 所以PQ ∥平面DCC 1D 1.方法二 取AD 的中点G ,连接PG ,GQ , 则有PG ∥DD 1,GQ ∥DC ,且PG ∩GQ =G , 则平面PGQ ∥平面DCC 1D 1.又因为PQ ⊂平面PGQ ,则PQ ∥平面DCC 1D 1. (2)由(1)易知PQ =12D 1C =22a .【变式4】 如图,在正方体ABCD -A 1B 1C 1D 1中,侧面对角线AB 1,BC 1上分别有两点E ,F ,且B 1E =C 1F .求证:EF ∥平面ABCD .证明 过E 作EG ∥AB 交BB 1于点G ,连接GF ,则B 1E B 1A =B 1GB 1B.因为B 1E =C 1F ,B 1A =C 1B ,所以C 1F C 1B =B 1GB 1B .所以FG ∥B 1C 1∥BC ,又因为EG ∩FG =G ,AB ∩BC =B , 所以平面EFG ∥平面ABCD ,又因为EF ⊂平面EFG ,EF ⊄平面ABCD , 所以EF ∥平面ABCD .。

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平ab a //面平行。
符合表示:a// b2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:aa//a // bab二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
n // b m // aa b M //mnN符号表示:2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
//符号表示:l l// d (更加实用的性质:一个平d面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直a c线垂直这个平面。
符号表示: a b ab c M$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直aoApoa oA A2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平 面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、 判定定理:经过一个平面的垂线的平面与该平面垂直。
a , a2、 性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一 个平面。
, b, a ,a b a 符号表示:a PA。

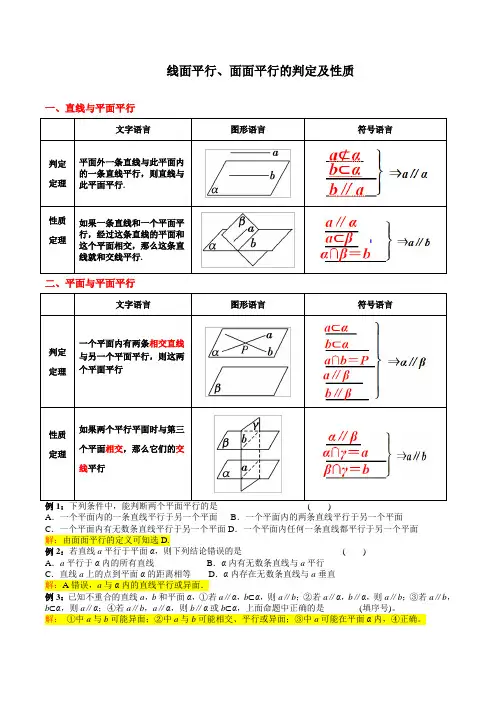
线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行,则直线与此平面平行.性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行,则这两个平面平行性质定理如果两个平行平面时与第三个平面相交,那么它们的交线平行A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面解:由面面平行的定义可知选D.例2:若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直解:A错误,a与α内的直线平行或异面.例3:已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a∥α,则b∥α或b⊂α,上面命题中正确的是________(填序号)。
解:①中a与b可能异面;②中a与b可能相交、平行或异面;③中a可能在平面α内,④正确。
例4:已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且n ⊄α,n ⊄β,则n ∥α且n ∥β其中正确命题的个数是 ( ) A .1 B .2 C .3 D .4解:对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,选B.例5:已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题:(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ;(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A .0 B .1 C .2 D .3 解:若⎩⎪⎨⎪⎧ m ⊥α,n ⊥α,则m ∥n ,即命题(1)正确;若⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ,则n ∥α或n ⊂α,即命题(2)不正确;若⎩⎪⎨⎪⎧m ⊥αn ∥α,则m ⊥n ,即命题(3)正确;综上可得,真命题共有2个.选C例6:已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是 ( )A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2解:由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.例7:在下列条件中,可判断平面α与β平行的是( ).A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线,且l ∥β,m ∥βD. l 、m 是两条异面直线,且l ∥α,m ∥α,l ∥β,m ∥β 解:排除法,A中α、β可以是相交平面;B中三点可面平面两侧;C中两直线可以不相交.故选D,也可直接证明.例8:经过平面外的两点作该平面的平行平面可以作( ).A. 0个B. 1个C. 0个或1个D. 1个或2个解:这两点可以是在平面同侧或两侧.选C 。

正在空间“线线仄止、线里仄止、里里仄止”的判决要领之阳早格格创做一、二条曲线仄止的判决要领(1)正在共一仄里内不大众面的二条曲线仄止(定义)(2)先证正在共一仄里内,再用仄里几许中的仄止线的判决理大概者相闭图形的本量举止说明.如①正在共一仄里内,二条曲线被第三条曲线所截,如果共位角大概内错角相等,大概共旁内角互补,则二曲线仄止.②三角形、梯形中位线定理.③仄止四边形、矩形、菱形、正圆形本量(对于边仄止).④正在共一个仄里内,共笔曲于一条曲线的二条曲线仄止(注意:此论断正在空间不符合).(3)(线里仄止的本量)如果一条曲线战一个仄里仄止,则通过那条曲线的一个仄里取那个仄里相接,那么那条曲线战接线仄止.(4)如果二曲线皆仄止于第三条曲线,那么那二条曲线互相仄止(仄止的传播性).(5)(里里仄止的本量)如果二个仄止仄里分别战第三个仄里相接,则它们的接线仄止.(6)(线里笔曲的本量之一)如果二条曲线笔曲于共一个仄里,那么那二条曲线仄止.(7)用背量说明.二、一条曲线战一个仄里仄止的判决(1)如果背来线战一仄里不大众面,那么那条曲线便战那个仄里仄止(定义)(2)仄里中的一条曲线,如果战那个仄里内的一条曲线仄止,那么那条曲线便战那个仄里仄止(线里仄止的判决定理).(3)如果二个仄里相互仄止,那么正在一个仄里内的所有一条曲线皆仄止于另一个仄里.(线里仄止的本量).(4)背量法.三、二个仄里仄止的判决(1)如果二个仄里不大众面,那么那二个仄里互相仄止(定义)(2)如果一个仄里内的二条相接曲线分别战另一个仄里仄止,那么那二个仄里仄止.(3)如果一个仄里内的二条相接曲线分别仄止于另一个仄里内的二条相接曲线,那么那二个仄里仄止.(4)如果二个仄里分别仄止于第三个仄里,那么那二个仄里仄止.(5)如果二个仄里笔曲于共一条曲线,那么那二个仄里仄止.正在空间“线线笔曲、线里笔曲、里里笔曲”的判决要领一、二条曲线笔曲的判决(1)正在共一个明里内说明二条曲线笔曲可依照仄里几许的有闭定理战要领判决.①说明二条曲线产生的角等于90°②正圆形、矩形本量(四个角皆是曲角);③正圆形、菱形对于角线互相笔曲;④勾股定理顺定理;⑤“曲角三角形斜边上的中线等于斜边的一半”的顺定理.⑥说明一个三角形二个内角战为90°,则另一个内角为90°.⑦说明一个三角形战一个曲角三角形齐等,利用齐等三角形对于应角相等说明曲角.⑧说明二个邻补角相等且战为180°,则每一个角为90°(此二个角有大众定面,有一条大众边,非大众边互为反背延少线).⑨等腰三角形本量(三线合一).⑩曲径所对于的圆周角是曲角.(2)如果一条曲线笔曲于一个仄里,那么它笔曲于那个仄里内的所有一条曲线.(3)如果仄里内的一条曲线战此仄里的一条斜线正在仄里内的射影笔曲,那么它也战那条斜线笔曲(三垂线定理)(4)如果仄里内的一条曲线战那个仄里的一条斜线笔曲,那么它也战那条斜线正在仄里内的射影笔曲(三垂线定理的顺定理).(5)如果一条曲线笔曲于二条仄止线中的一条曲线,那么它也笔曲于另一条曲线(此定理正在仄里战空间皆符合).(6)说明空间二条同里曲线相互笔曲,可说明那二条曲线所成的角为90°.(7)背量法.二、背来线战一个仄里笔曲的判决(1)如果一条曲线战一个仄里内的所有一条曲线皆笔曲,那么那条曲线便笔曲于那个仄里.(2)如果一条曲线战一个仄里内的二条相接曲线笔曲,那么那条曲线便战那个仄里笔曲.(3)如果二条仄止线中的一条笔曲于一个仄里,那么另一条也笔曲于那个仄里.(4)如果一条曲线笔曲于二个仄止仄里中的一个仄里,那么它也笔曲于另一个仄里.(5)如果二个仄里互相笔曲,那么正在一个仄里内笔曲于接线的曲线必笔曲于另一个仄里(里里笔曲的本量定理).(6)如果二个相接仄里α战β皆笔曲于仄里γ,那么它们的接线也笔曲于仄里γ(不克不迭当定理引用).(7)背量法.三、二仄里笔曲的判决(1)如果二相接仄里所成的二里角为曲二里角,那么那二个仄里互相笔曲(定义).(2)如果一个仄里通过另一个仄里的垂线,那么那二个仄里互相笔曲(线里笔曲本量定理).四、有闭曲线取仄里位子闭系中的几个本量定理(1)夹正在二个仄止仄里之间仄止线段的少相等.(2)二仄止仄里间的距离到处相等.(3)二曲线如果被三个仄止仄里所截,那么所截得下对于应线段成比率.(4)如果二个角的二边分别仄止且目标相共,那么那二个角相等.五、重心分解(1)线线、线里、里里仄止闭系的转移(2)线线、线里、里里笔曲闭系的转移。


线面、面面平行的判定与性质(教师版)知识回顾1.线面平行的判定(1)直线与平面平行的定义:直线与平面无公共点. (2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 用符号表示为:a ⊄α,b ⊂α,且a ∥b ⇒a ∥α. 2.线面平行的性质直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行符号语言描述:⎭⎪⎬⎪⎫a ∥αa ⊂ββ∩α=b ⇒a ∥b . 3. 面面平行的判定(1)平面α与平面β平行的定义:两平面无公共点. (2)直线与平面平行的判定定理:下面的命题在“________”处缺少一个条件,补上这个条件,使其构成真命题(m ,n 为直线,α,β为平面),则此条件应为m ,n 相交.⎭⎪⎬⎪⎫m ⊂αn ⊂αm ∥βn ∥β⇒α∥β 4.面面平行的性质平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.符号表示为:⎭⎪⎬⎪⎫α∥βα∩γ=a β∩γ=b ⇒a ∥b . 题型讲解题型一 利用三角形中位线证明线面平行例1、如图,ABCD 是平行四边形,S 是平面ABCD 外一点,M 为SC 的中点.求证:SA∥平面MDB.答案:证明:连结AC交BD于N,因为ABCD是平行四边形,所以N是AC的中点.又因为M是SC的中点,所以MN∥SA.因为MN平面MDB,所以SA∥平面MDB.例2、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,求证:MN∥平面PB1C.答案证明:如图,连结AC,则P为AC的中点,连结AB1,∵M、N分别是A1A与A1B1的中点,∴MN∥AB1.又∵平面PB1C,平面PB1C,故MN∥面PB1C.例3、如图所示,P是▱ABCD所在平面外一点,E、F分别在PA、BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.证明连接AF延长交BC于G,连接PG.在▱ABCD中,易证△BFG∽△DFA.∴GFFA=BFFD=PEEA,∴EF∥PG.而EF⊄平面PBC,PG⊂平面PBC,∴EF∥平面PBC.练习在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过点A,E,C的平面的位置关系是______.答案:平行题型二利用平行四边形证明线面平行例1、如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点.求证:EF∥平面BDD1B1.证明:取D1B1的中点O,连接OF,OB.∵OF 12B1C1,BE12B1C1,∴OF BE.∴四边形OFEB是平行四边形,∴EF∥BO.∵EF⊄平面BDD1B1,BO⊂平面BDD1B1,∴EF∥平面BDD1B1.例2、如图所示,已知正方体ABCD-A1B1C1D1中,面对角线AB1、BC1上分别有两点E、F,且B1E=C1F.求证:EF∥平面ABCD.证明方法一过E、F分别作AB、BC的垂线,EM、FN分别交AB、BC于M、N,连接MN.∵BB1⊥平面ABCD,∴BB1⊥AB,BB1⊥BC,∴EM∥BB1,FN∥BB1,∴EM∥FN,∵AB1=BC1,B1E=C1F,∴AE=BF,又∠B1AB=∠C1BC=45°,∴Rt△AME≌Rt△BNF,∴EM=FN.∴四边形MNFE是平行四边形,∴EF∥MN.又MN⊂平面ABCD,EF⊄平面ABCD,∴EF∥平面ABCD.方法二过E作EG∥AB交BB1于G,连接GF,∴B1EB1A=B1GB1B,B1E=C1F,B1A=C1B,∴C1FC1B=B1GB1B,∴FG∥B1C1∥BC.又∵EG∩FG=G,AB∩BC=B,∴平面EFG∥平面ABCD.又EF⊂平面EFG,∴EF∥平面ABCD.题型三利用面面平行证明线面平行例. 如图,在四棱锥中,是平行四边形,,分别是,的中点.求证:平面.答案:证明:如图,取的中点,连接,,分别是,的中点,,,P ABCDABCD M N AB PCMN//PADCD E NE ME∵M N AB PCNE PD∴//ME AD//可证明平面,平面.又,平面平面,又平面,平面.题型四面面平行的证明例1、如图所示,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?解:当Q为CC1的中点时,平面D1BQ∥平面PAO.∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.∵P、O为DD1、DB的中点,∴D1B∥PO.又PO∩PA=P,D1B∩QB=B,D1B∥平面PAO,QB∥平面PAO,∴平面D1BQ∥平面PAO.题型五平行性质NE//PAD ME//PADNE ME E=∴MNE//PADMN⊂MNE∴MN//PAD例1、如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是()A.平行 B.相交C.异面 D.平行和异面答案:A例2、ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.证明如图所示,连接AC交BD于O,连接MO,∵ABCD是平行四边形,∴O是AC中点,又M是PC的中点,∴AP∥OM.根据直线和平面平行的判定定理,则有PA∥平面BMD.∵平面PAHG∩平面BMD=GH,根据直线和平面平行的性质定理,∴AP∥GH.练习、如图,在三棱柱ABC-A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.求证:N为AC的中点.证明 ∵平面AB 1M ∥平面BC 1N , 平面ACC 1A 1∩平面AB 1M =AM , 平面BC 1N∩平面ACC 1A 1=C 1N , ∴C 1N ∥AM ,又AC ∥A 1C 1, ∴四边形ANC 1M 为平行四边形, ∴AN 綊C 1M =12A 1C 1=12AC ,∴N 为AC 的中点.跟踪训练1.如右图所示的三棱柱ABC -A 1B 1C 1中,过A 1B 1的平面与平面ABC 交于直线DE ,则DE 与AB 的位置关系是( )A .异面B .平行C .相交D .以上均有可能 答案:B[解析] ∵A 1B 1∥AB ,AB ⊂平面ABC ,A 1B 1⊄平面ABC , ∴A 1B 1∥平面ABC.又A 1B 1⊂平面A 1B 1ED ,平面A 1B 1ED∩平面ABC =DE ,∴DE ∥A 1B 1. 又AB ∥A 1B 1,∴DE ∥AB.2.已知直线l ,m ,平面α,β,下列命题正确的是( ) A .l ∥β,l ⊂α⇒α∥βB .l ∥β,m ∥β,l ⊂α,m ⊂α⇒α∥βC .l ∥m ,l ⊂α,m ⊂β⇒α∥βD .l ∥β,m ∥β,l ⊂α,m ⊂α,l ∩m =M ⇒α∥β 答案:D3、直线a ∥平面α,α内有n 条直线交于一点,则这n 条直线中与直线a 平行的直线( )A.至少有一条 B.至多有一条C.有且只有一条 D.没有答案:B4、给出下列结论,正确的有()①平行于同一条直线的两个平面平行;②平行于同一平面的两个平面平行;③过平面外两点,不能作一个平面与已知平面平行;④若a,b为异面直线,则过a与b平行的平面只有一个.A.1个 B.2个 C.3个 D.4个答案:B5.正方体EFGH—E1F1G1H1中,下列四对截面中,彼此平行的一对截面是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G答案:A6.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.答案:平行四边形[解析]∵平面ABFE∥平面CDHG,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面CDHG=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH的形状是平行四边形.7. 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点,求证:BC1∥平面CA1D.证明:如图所示,连接AC1交A1C于点O,连接OD,则O是AC1的中点.∵点D是AB的中点,∴OD∥BC1.又∵OD⊂平面CA1D,BC1⊄平面CA1D,∴BC1∥平面CA1D.8.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC和SC的中点.求证:平面EFG∥平面BDD 1B1.证明如图所示,连接SB,SD,∵F、G分别是DC、SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴直线FG∥平面BDD1B1.同理可证EG∥平面BDD1B1,又∵EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.9.(本小题满分12分)在四棱锥S-ABCD中,底面ABCD是正方形, M、N分别为AB、SC的中点,SA⊥底面ABCD.求证://MN平面SAD;答案.证明(Ⅰ): E 为SD 中点,连接AE ,NE ,因为M 、N 分别为AB 、SC 的中点,所以AM//EN ,AM=EN ,即四边形AMNE 是平行四边形,所以MN//AE ,可得//MN 平面SAD ;10. 一个多面体的直观图及三视图如图所示:(其中M 、N 分别是AF 、BC 的中点).(1)求证:MN ∥平面CDEF ;(2)求多面体A -CDEF 的体积.答案 由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE-BCF ,且AB =BC =BF=2,DE =CF=2,∴∠CBF =. (1)证明:取BF 的中点G ,连结MG 、NG ,由M 、N 分别为AF 、BC 的中点可得,NG ∥CF ,MG ∥EF ,∴平面MNG ∥平面CDEF ,又MN ⊂平面MNG ,∴MN ∥平面CDEF .(2)取DE 的中点H .∵AD =AE ,∴AH ⊥DE , 在直三棱柱ADE-BCF 中,平面ADE ⊥平面CDEF ,平面A DE ∩平面CDEF=DE .∴AH ⊥平面CDEF.∴多面体A-CDEF 是以AH 为高,以矩形CDE F 为底面的棱锥,在△ADE 中,AH =. S 矩形CDEF =DE ·EF =4,∴棱锥A-CDEF 的体积为2222V=·S 矩形CDEF ·AH =×4×= 解法2:13218222323A CDEF AED BFC A BFCAED V V V S AB S AB ---=-=⨯-⨯⨯=⨯⨯⨯⨯=△△BFC 11如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,且AB =2CD ,在棱AB 上是否存在一点F ,使平面C 1CF ∥平面ADD 1A 1?若存在,求点F 的位置;若不存在,请说明理由.答案 存在这样的点F ,使平面C 1CF ∥平面ADD 1A 1,此时点F 为AB的中点,证明如下:∵AB ∥CD ,AB =2CD ,∴AF ∥CD ,∴四边形AFCD 是平行四边形,∴AD ∥CF ,又AD ⊂平面ADD 1A 1,CF ⊄平面ADD 1A 1,∴CF ∥平面ADD 1A 1.又CC 1∥DD 1,CC 1⊄平面ADD 1A 1,DD 1⊂平面ADD 1A 1,∴CC 1∥平面ADD 1A 1,又CC 1、CF ⊂平面C 1CF ,CC 1∩CF =C ,∴平面C 1CF ∥平面ADD 1A 1.12. 如图,在底面是平行四边形的四棱锥P -ABCD 中,点E 在PD 上,且PE ∶ED =2∶1,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?证明你的结论.答案 存在.证明如下:取棱PC 的中点F ,线段PE 的中点M ,连接BD .设BD ∩AC =O .连接BF ,MF ,BM ,OE .13132283∵PE ∶ED =2∶1,F 为PC 的中点,M 是PE 的中点,E 是MD的中点,∴MF ∥EC ,BM ∥OE .∵MF ⊄平面AEC ,CE ⊂平面AEC ,BM ⊄平面AEC ,OE ⊂平面AEC ,∴MF ∥平面AEC ,BM ∥平面AEC .∵MF ∩BM =M ,∴平面BMF ∥平面AEC .又BF ⊂平面BMF ,∴BF ∥平面AEC .13. (北京)如图,在四面体PABC 中,PC ⊥AB ,PA ⊥BC ,点D ,E ,F ,G 分别是棱AP ,AC ,BC ,PB 的中点.(1)求证:DE ∥平面BCP ;(2)求证:四边形DEFG 为矩形;(3)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由.答案 (1)证明:因为D ,E 分别为AP ,AC 的中点,所以DE ∥PC .又因为DE ⊄平面BCP ,PC ⊂平面BCP ,所以DE ∥平面BCP .(2)证明:因为D ,E ,F ,G 分别为AP ,AC ,BC ,PB 的中点所以DE ∥PC ∥FG ,DG ∥AB ∥EF ,所以四边形DEFG 为平行四边形.又因为PC ⊥AB ,所以DE ⊥DG ,所以四边形DEFG 为矩形.(3)存在点Q 满足条件,理由如下:连接DF ,EG ,设Q 为EG 的中点.由(2)知,DF ∩EG =Q ,且QD =QE =QF =QG =12EG .分别取PC ,AB 的中点M ,N ,连接ME ,EN ,NG ,MG ,MN .与(2)同理可证四边形MENG 为矩形,其对象线交点为EG 的中点Q ,且QM =QN =12EG ,所以EG 的中点Q 是满足条件的点.。

在空间“线线平行、线面平行、面面平行”的判定方法一、两条直线平行的判定方法(1)在同一平面内没有公共点的两条直线平行(定义)(2)先证在同一平面内,再用平面几何中的平行线的判定理或者相关图形的性质进行证明。
如①在同一平面内,两条直线被第三条直线所截,如果同位角或内错角相等,或同旁内角互补,则两直线平行。
②三角形、梯形中位线定理。
③平行四边形、矩形、菱形、正方形性质(对边平行)。
④在同一个平面内,同垂直于一条直线的两条直线平行(注意:此结论在空间不适合)。
(3)(线面平行的性质)如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
(4)如果两直线都平行于第三条直线,那么这两条直线互相平行(平行的传递性)。
(5)(面面平行的性质)如果两个平行平面分别和第三个平面相交,则它们的交线平行。
(6)(线面垂直的性质之一)如果两条直线垂直于同一个平面,那么这两条直线平行。
(7)用向量证明。
二、一条直线和一个平面平行的判定(1)如果一直线和一平面没有公共点,那么这条直线就和这个平面平行(定义)(2)平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
(3)如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.(线面平行的性质)。
(4)向量法。
三、两个平面平行的判定(1)如果两个平面没有公共点,那么这两个平面互相平行(定义)(2)如果一个平面内的两条相交直线分别和另一个平面平行,那么这两个平面平行。
(3)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
(4)如果两个平面分别平行于第三个平面,那么这两个平面平行。
(5)如果两个平面垂直于同一条直线,那么这两个平面平行。
在空间“线线垂直、线面垂直、面面垂直”的判定方法一、 两条直线垂直的判定(1) 在同一个明面内证明两条直线垂直可按照平面几何的有关定理和方法判定。
面面平行的判定定理和性质定理
面面平行的性质定理:
一、线线平行
1、同位角成正比两直线平行:在同一平面内,两条直线被第三条直线所封盖,如果
内错角成正比,那么这两条直线平行。
2、内错角相等两直线平行:在同一平面内,两条直线被第三条直线所截,如果同旁
内角互补,那么这两条直线平行。
3、同旁内角优势互补两直线平行。
二、线面平行
1、利用定义:证明直线与平面并无公共点;
2、利用判定定理:从直线与直线平行得到直线与平面平行;
3、利用面面平行的性质:两个平面平行,则一个平面内的'直线必平行于另一个平面。
平行平面间的距离处处相等。
已知:α∥β,ab⊥α,dc⊥α,且a、d∈α,b、
c∈β求证:ab=cd证明:连接ad、bc由线面垂直的性质定理可知ab∥cd,那么ab和cd
构成了平面abcd∵平面abcd∩α=ad,平面abcd∩β=bc,且α∥β∴ad∥bc(定理2)
∴四边形abcd是平行四边形∴ab=cd。