地面观测值归算至椭球面算法
- 格式:doc
- 大小:204.50 KB
- 文档页数:3



椭球面坐标与大地测量的转换方法与公式椭球面坐标是地球表面上的一种坐标系统, 它将地球视为一个近似椭球体, 提供了一种测量和计算地球上点的方法。
在实际的测量和定位任务中, 经常需要将椭球面坐标转换为其他坐标系统, 或者反过来。
这就需要使用一些转换方法和公式。
一、椭球面坐标系统椭球面坐标系统是大地测量学中常用的一种坐标系统。
它使用经度、纬度和高程来描述地球上的点。
其中,经度表示点在东西方向上的位置,纬度表示点在南北方向上的位置,而高程表示点相对于基准面的高度。
在椭球面坐标系统中,常用的参考椭球体包括WGS84、CGCS2000等。
二、椭球面坐标与地心坐标的转换将椭球面坐标转换为地心坐标是大地测量中常见的任务。
地心坐标是以地球质心为原点的坐标系统,它与椭球体的长短轴、扁率等参数有关。
在转换过程中,需要考虑到椭球体的参数,包括椭球体的半长轴a、扁率f等。
常用的转换方法包括勒让德多项式展开法、球面三角法等。
三、椭球面坐标与笛卡尔坐标的转换将椭球面坐标转换为笛卡尔坐标是另一个常见的任务。
笛卡尔坐标是三维坐标系,它使用直角坐标系来表示地球上的点。
在转换过程中,需要考虑到椭球体的参数,包括椭球体的半长轴a、扁率f等。
常用的转换方法包括克里金插值法、最小二乘法等。
四、大地测量中的应用椭球面坐标与大地测量的转换方法和公式在实际测量和定位任务中发挥着重要的作用。
它们被广泛应用于地理信息系统、导航定位、地质勘探等领域。
例如,在导航定位中,利用椭球面坐标与笛卡尔坐标的转换,可以实现卫星导航系统的精确定位。
在地质勘探中,利用椭球面坐标与地心坐标的转换,可以确定地下矿藏的位置和分布。
总结:椭球面坐标与大地测量的转换方法与公式是地球科学中的重要内容。
通过了解和掌握这些方法和公式,我们可以更好地进行地球测量和定位任务。
椭球面坐标系统提供了一种描述地球表面上点的方式,而转换方法和公式则是实现不同坐标系统之间转换的关键。
在实际应用中,我们需要根据具体任务的要求选择适当的转换方法和公式,以保证测量和定位的精度和准确性。


地面观测值归算至椭球面的计算
一、计算目的:经过大地测量学基础课程的学习,在掌握了大地测量有关基本理
论、基本知识、基本方法的基础上,通过计算掌握野外地面观测的水平角归算至椭球面大地线上相应的水平角以及野外地面观测的距离归算至椭球面上大地线的长度的计算方法。
二、计算内容:
(一)地面水平角观测值归算至椭球面的计算
1、计算垂线偏差改正;
2、计算标高差改正;
3、计算截面差改正;
4、水平角归算;
(二)地面观测距离归算至椭球面的计算
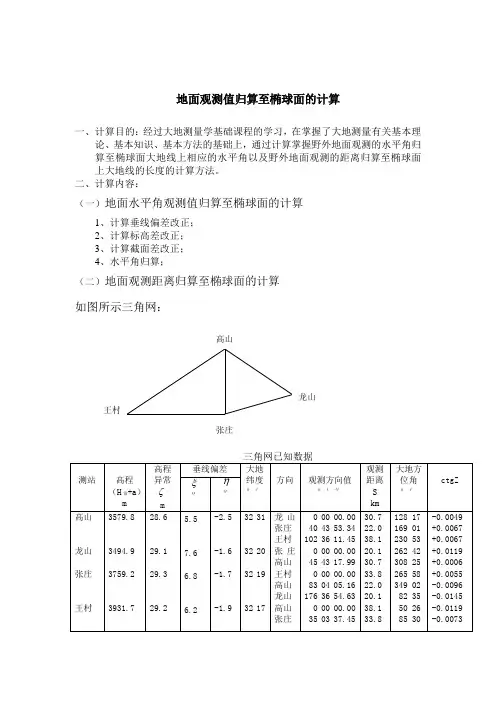
如图所示三角网:
(一)地面水平角观测值归算至椭球面的计算
三差改正计算(小数取到0.0001位)
(二) 地面观测距离归算至椭球面大地线的计算。


§6.4 将地面观测值归算至椭球面6.4.1 概述参考椭球面是测量计算的基准面。
在野外的各种测量都是在地面上进行,观测的基准线不是各点相应的椭球面的法线,而是各点的垂线,各点的垂线与法线存在着垂线偏差。
因此不能直接在地面上处理观测成果,而应将地面观测元素(包括方向和距离等)归算至椭球面。
在归算中有两条基本要求:(1)以椭球面的法线为基准;(2)将地面观测元素化为椭球面上大地线的相应元素。
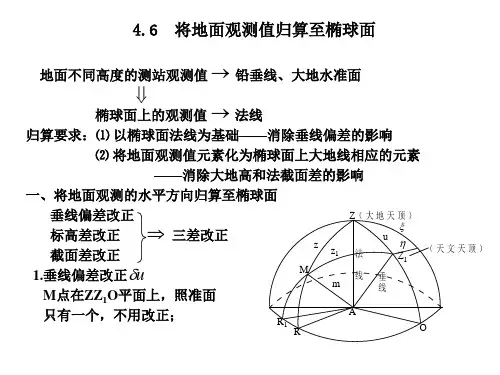
6.4.2 将地面观测的水平方向归算至椭球面 1.垂线偏差改正u δ地面上所有水平方向的观测都是以垂线为根据的,而在椭球面上则要求以该点的法线为依据。
把以垂线为依据的地面观测的水平方向值归算到以法线为依据的方向值而应加的改正定义为垂线偏差改正,以u δ表示。
如图所示,以测站A 为中心作出单位半径的辅助球,u 是垂线偏差,它在子午圈和卯酉圈上的分量分别以ηξ,表示,M 是地面观测目标m 在球面上的投影。
垂线偏差改正的计算公式是:1cot )cos sin (Z A A m m uηξδ''-''-='' 1tan )cos sin (αηξm m A A ''-''-=式中:ηξ,为测站点上的垂线偏差在子午圈及卯酉圈上的分量,它们可在测区的垂线偏差分量图中内插取得;m A 为测站点至照准点的大地方位角;1Z 为照准点的天顶距;1α为照准点的垂直角。
垂线偏差改正的数值主要与测站点的垂线偏差和观测方向的天顶距(或垂直角)有关。
2.标高差改正h δ 标高差改正又称由照准点高度而引起的改正。
不在同一子午面或同一平行圈上的两点的法线是不共面的。
当进行水平方向观测时,如果照准点高出椭球面某一高度,则照准面就不能通过照准点的法线同椭球面的交点,由此引起的方向偏差的改正叫做标高差改正,以h δ表示。
如图所示,A 为测站点,如果测站点观测值已加垂线偏差改正,则可认为垂线同法线一致。
§7.7将地面观测的长度归算到椭球面根据测边使用仪器的不同,地面长度的归算可分为两种:一是基线尺量距的归算;二是电磁波测距的归算,现分别进行研究。
7.7.1基线尺量距的归算将基线尺测量求得的长度加入尺段倾斜改正后,可认为它是基线平均水准面上的长度值,用s 0表示。
而我们所求的是椭球面上的大地线的长度s ,因此产生了长度归算问题。
1. 垂线偏差对长度归算的影响由于垂线偏差的存在,使得垂线和法线不一致,水准面不平行于椭球面。
为此在长度归算中应首先消除这种影响。
假设垂线偏差沿基线是线性变化的,则垂线偏差u 对长度归算的影响式是:)(22122121H H u u h u u s u -''''+''=∆''''+''=∆∑ρρ (7-97) 式中1u ''和2u ''为在基线端点1和2处垂线偏差在基线方向上的分量;∑∆h 为各个测段测量的高差总和;H 1和H 2为基线端点1和2处的大地高。
从式中可以看出,垂线偏差对基线长度归算的影响,主要与垂线偏差分量u 及基线端点的大地高差∑∆h 有关,其数值一般比较小,此项改正是否需要应结合测区及计算精度要求的实际情况进行具体分析。
2. 高程对长度归算的影响假设基线两端点已经过垂线偏差改正,则基线平均水准面平行于椭球体面。
此时由于水准面离开椭球体面一定距离,也引起长度归算的改正。
AB 为平均高程水准面上的基线长度,以0S 表示,现要计算其在椭球面上的长度S ,由图可知由此得椭球面上的长度为 10)1(-+=RH S S m (7-98) 式中)(2121H H H m +=,即基线端点平均大地高程;R 为基线方向法截线曲率半径,按(7-55)式计算。
如果将上式展开级数,取至二次项,则有)1(220RH R H S S m m +-= (7-99) 由此式可得由高程引起的基线归化改正数公式2200R H S R H S S m m H +-=∆ (7-100)可见此项改正数主要与基线的平均高程m H 及长度有关。
§6.4 将地面观测值归算至椭球面
6.4.1 概述
参考椭球面是测量计算的基准面。
在野外的各种测量都是在地面上进行,观测的基准线不是各点相应的椭球面的法线,而是各点的垂线,各点的垂线与法线存在着垂线偏差。
因此不能直接在地面上处理观测成果,而应将地面观测元素(包括方向和距离等)归算至椭球面。
在归算中有两条基本要求:(1)以椭球面的法线为基准;(2)将地面观测元素化为椭球面上大地线的相应元素。
6.4.2 将地面观测的水平方向归算至椭球面 1.垂线偏差改正u δ
地面上所有水平方向的观测都是以垂线为根据的,而在椭球面上则要求以该点的法线为依据。
把以垂线为依据的地面观测的水平方向值归算到以法线为依据的方向值而应加的改正定义为垂线偏差改正,以u δ表示。
如图所示,以测站A 为中心作出单位半径的辅助球,u 是垂线偏差,它在子午圈和卯酉圈上的分量分别以ηξ,表示,M 是地面观测目标m 在球面上的投影。
垂线偏差改正的计算公式是:
1cot )cos sin (Z A A m m u
ηξδ''-''-='' 1tan )cos sin (αηξm m A A ''-''-=
式中:ηξ,为测站点上的垂线偏差在子午圈及卯酉圈上的分量,它们可在测区的垂线偏差分量图中内插取得;m A 为测站点至照准点的大地方位角;1Z 为照准点的天顶距;1α为照准点的垂直角。
垂线偏差改正的数值主要与测站点的垂线偏差和观测方向的天顶距(或垂直角)有关。
2.标高差改正h δ 标高差改正又称由照准点高度而引起的改正。
不在同一子午面或同一平行圈上的两点的法线是不共面的。
当进行水平方向观测时,如果照准点高出椭球面某一高度,则照准面就不能通过照准点的法线同椭球面的交点,
由此引起的方向偏差的改正叫做标高差改正,以h δ表示。
如图所示,A 为测站点,如果测站点观测值已加垂线偏差改正,则可认为垂线同法线一致。
这时测站点在椭球面上或者高出椭球面某一高度,对水平方向是没有影响的。
这是因为测站点法线不变,则通过某一照准点只能有一个法截面。
设照准点高出椭球面的高程为a An H ,2和b Bn 分别为A 点及B 点的法线,B 点法线与椭球面的交点为b 。
因为通常a An 和b Bn 不在同一平面内,所以在A 点照准B 点得出的法截线是b A '而不是Ab ,因而产生了Ab 同b A '方向的差异。
按归算的要求,地面各点都应沿自己法线方向投影到椭球面上,即需要的是Ab 方向值而不是b A '方向值,因此需加入标高差改正数h δ,以便将b A '方向改到Ab 方向。
标高差改正的计算公式是
1222222sin cos )1(2
A B H e h =''δ
式中:2B 为照准点大地纬度;1A 为测站点至照准点的大地方位角;2H 为照准点高出椭球
面的高程,它由三部分组成:
a H H ++=ζ常2
其中常H 为照准点标石中心的正常高,ζ为高程异常,a 为照准点的觇标高。
22/)1(M ρ''=,
2M 是与照准点纬度2B 相应的子午圈曲率半径。
标高差改正主要与照准点的高程有关。
经过此项改正后,便将地面观测的水平方向值归化为椭球面上相应的法截弧方向。
3.截面差改正g δ
在椭球面上,纬度不同的两点由于其法线不共面,所以在对向观测时相对法截弧不重合,应当用两点间的大地线代替相对法截弧。
这样将法截弧方向化为大地线方向应加的改正叫截面差改正,用g δ表示。
如图所示,AaB 是A 至B 的法截弧,它在A 点处的大地方位角为1A ',ASB 是AB 间的大地线,它在A 点的大地方位角是1A ,1A 与1A '之差g δ就是截面差改正。
截面差改正的计算公式为
1122
1222sin cos )2(12A B S e g ρδ'
'-=''
式中S 为AB 间大地线长度,1
1)2(N ρ'
'=
,1N 为测站点纬度1B 相对
应的卯酉圈曲率半径。
现令
在一般情况下,一等三角测量应加三差改正,二等三角测量应加垂线偏差改正和标高差改正,而不加截面差改正;三等和四等三角测量可不加三差改正。
但当01''>=ηξ时或者H >2 000m 时,则应分别考虑加垂线偏差改正和标高差改正。
在特殊情况下,应该根据测区的实际情况作具体分析,然后再做出加还是不加改正的规定。
如下表所示:
6.4.3 电磁波测距边长归算椭球面
电磁波测距仪测得的长度是连接地面两点间的直线斜距,也应将它归算到参考椭球面上。
如图,大地点
1Q 和2Q 的大地高分别为1H 和2H 。
其间用电磁波测距仪测得的斜距为D ,现要求大地点在椭球面上沿法线
的投影点1Q '和2
Q '间的大地线的长度S 。
在工程测量中边长一般都是几公里,最长也不过十几公里,
因此,所求的大地线的长度可以认为是半径
1
212
2
cos cos 1A B e N
R A '+=
相应的圆弧长。
电磁波测距边长归算椭球面上的计算公式为:
2
3
22421A
A m R D R H D D h D S +-∆-= 式中)(2
1
21H H H m +=。
电磁波测距边长归算的几何意义为:
(1)计算公式中右端第二项是由于控制点之高差引起的倾斜改正的主项,经过此项改正,测线已变成平距;
(2)第三项是由平均测线高出参考椭球面而引起的投影改正,经此项改正后,测线已变成弦线;
(3)第四项则是由弦长改化为弧长的改正项。
电磁波测距边长归算至椭球面上的计算公式还可用下式表达:
232
2
241A
A m R D R H h D S +⎪⎪⎭⎫ ⎝⎛-∆-= 显然第一项即为经高差改正后的平距。