常微分方程解的存在唯一性定理

谈谈常微分方程解的存在唯一性定理的教学作者：罗勇来源：《新一代》2017年第10期摘要：本文以高等学校常微分方程解的存在唯一性定理的教学为例，阐述高等学校数学教育，提高教学效率和效果的可能的途径和应该注意的问题。

本文的观点主要基于作者亲身的教学经验和总结，同时力图使本文的教学观点和建议具有一般性和广泛的意义。

关键词：高校数学教育；常微分方程基本定理；教学方法在各高校的许多本科专业，如数学，物理，计算机，经济与管理，工科等在大二或大三的时候都会开设常微分方程这门课程。

笔者从事经济与管理学院金融专业的常微分方程的教学工作已有两年，今年已经是第三次主讲这门课程了。

因为对这门课程积累了较多的教学经验，难免心中有一些感悟，不发不快。

今天就来简单讲讲这门课程其中的一个章节：常微分方程解的存在唯一性的教学的一些经验体会，算是对自己教学经验的小结，希望能够启发自己和读者。

笔者比较了现在国内几本主要的常微分方程教材，比如复旦大学出版社出版，张晓梅教授等人主编的《常微分方程》；高等教育出版社出版，东北师范大学微分方程教研室主编的《常微分方程》以及高等教育出版社出版，北京大学丁同仁教授等人编写的经典教材《常微分方程教程》之后发现，不同的教材在编写常微分方程解的存在唯一性定理的时候，选材是大同小异的，几乎都以Picard存在唯一性定理为主，兼顾着介绍一下Euler的解的存在性定理。

但是由于不同的教材假想的受众不太一样，各个教材还是会有一些差异。

常微分方程在高校的所有数学课程中，总的来说是一门比较简单的基础专业课，但是它又为应用高等数学和线性代数来解决很多实际问题，提供了一个很重要的例子。

因此笔者认为它具有很独特的地位。

尤其是在解的存在唯一性定理的讲解中，提供了一个全方位锻炼大学生数学思维能力的机会。

笔者接下来就来展开说明为什么是这样。

Picard存在唯一性定理是说，如果方程的右端函数f（x，y）在以（x_0，y_0）点为中心，长a宽b的矩形区域上连续，并且关于y变量在该区域上满足Lipschitz连续性条件，那么常微分方程的初值问题存在唯一的解，其中解的存在区间在a和b除f在矩形区域上的最大值的商中取小。

Banach空间中常微分方程解的存在唯一性定理總婷婷(XX帅X学院数学与鋭计学院,XX,XX,741000)描要:在Banach空同中，常械分方程解的存在唯一性定理中力=｝，初值冋題的解y(f)的变量『在t o-h<t<t o+ht变化，把f的变化X围扩大为心％「5+%, 为此给出f变化X围后的Banach 空间中常做分方程解的存在唯一性定理，并对定理给予明确的证明.关维词:存在唯一;常撤分方程;数学IJ3细袪;皮卡逐步II近法\ Banach空间引言常撤分方程解的存在唯一性定理明确地肯定了在一定条件下方程的解的存在性和唯一性，它是常ta分方程理论中最基本且实用的定理，有其重大的理论怠义，另一方面，它也是近做求解法的前提和理论基硝.对于人们裁知的Banach空同中常撤分方程解的存在唯一性定理,解的存在区同较小,只限制在一个小的球形邻裁内,(球形邻域的半径若为5, U需满足Ld<\,且辭只在以儿为中心以5为半径的冈球B t5(y0) = (yeX|||y-y0||<J)存在唯一，其中X是Banach空间)因此在应用过程中受到了一定的眼制.如今我们尝试扩大了解的存在XIJ.U而使此重要的定理今后有更加广泛的应用.1预备定理我们给岀Banach空同中常做分方程解的存在唯一性定理如下设X是Banach空同，UuX是一f开集.f :U i X上关干 >，满足利普希茨(Lipschitz)条件，即存在常数厶>0,使得不等式］/(/, ”)- /(/, y2)|| <厶卜】一儿||，对于所有y^y2eu部成立.® y.eU ,在u内，以儿为中心作一个半径为“的冈球3心())=© eX|||y-儿||詡’对所有的y e B b(y0)都成立，且有,取h = min{%,%^},则存在唯一的C、曲线y(t)，使得在r0-h<t< t0+h上满足y w B h(y0), 并有y' = /(/,y),y(G)=)b・2结果与证明笔者通il改进对力的限歟即仅取〃 = %/，硕备定理仍然成立,从而使定理的应用进一步广泛.2.1改进条件后的定理定理假设条件同上预备定理，设初值为仇,儿)，则存在唯一的C、曲线y(『),对任恿的G 一%/ ° "u + %r满足y €场(儿),且使得V = /(/, y) , Wo)=儿.显然可有% —〃，心 + 幻 U〔5 - ，心 + % ］，目"min{%,%} •2.2定理舸证明证明证明过程中我们利用皮卡(Picard)逐步逼近法•为了简单起见，只就区同对干区间t.<t<t.+y M的讨论完全一样.2.2.1定理证明的思想现在先简单叙述一下运用皮卡逐步逼近法证明的壬要思想.首先证明条件 H), xu=y0等价于求枳分方程y(Q = %+j\/a，y)〃•⑴再证明积分方程的解的存在唯一性.任取一个儿⑴为连续函数，将它代人方程⑴的右常，可得到函数卩⑴=y(> +J；./■(/,%)〃/,显然，儿⑴也为连续函数•若x⑴=y o(0,1可知y()⑴就是方程⑴的解•若不然，我ill a把川)代人枳分方程⑴的右竭m,y)，可得到函数儿⑴=儿+J；“/(/')〉)/•若y2(0 = >'i(0 JO可知莎⑴就是方程(1)的解•若不然，我们如此下去,可作连续函红儿(/) = + j* ：＞/(/，y”-i M ・(2)这算就得到连续函数列儿(0，”(/)，儿⑴,…，儿⑴，…若畑⑴=儿⑴,那么儿⑴就是枳分方程的解，如果始终不发生眩种悄猊，我们可以证明上面的函数序列有一个极眼函数y(t), fill liin y…(t) = y(f)存在，因而对(2)式两jfi取枚限时,就得到巴y n(0 = y0 + lim J :/(f,y…_,)dt = y0+J ；o lim/(r,儿“)/ =儿 + J ；o/(r,y)dt, 即y(0 = y0 + J；/(心)力謔就是说M)是枳分方程的解•在定理的假设条件下，以上的步骤是可以实现的.2.2.2定理iil明的步骤下面我门分五个命题来证明定理.金題1设y = y(r)是y'5，y)的定义于区同心％““上,满足初值条件〉仇)=儿(3)的解厲y = y(r)是枳分方程W)=儿+ 定义于心一夕缶上的连续解，反之亦衆证明因为y = y(0是方程y' = /(/, y)的解，故有竽5,刃.at对上式两fflU/o到「取定枳分得到W) - W())= J ；＞ /(/，y W ‘ 5 - ％ o()‘把(3)式代入上式,即有y(f) = ＞o+J 财(人曲5-%；"")•⑷因此,y = XO是(4)的定义于上的连续解.反之，如果y = y（f）是⑷的连续解,）心）=儿+J: <t<t0.fit分之，得到弊局）•ata把心心代人⑷式，得到y（G =儿，S此,y = y（r）是方程 H）的定义于区间且満足初值条件（3）的解.金题1込毕.现在取y。

Banach 空间中常微分方程解的存在唯一性定理魏婷婷(天水师范学院 数学与统计学院,甘肃,天水,741000)摘要: 在Banach 空间中, 常微分方程解的存在唯一性定理中},1min{M b L h =,初值问题的解)(t y 的变量t 在h t t h t +≤≤-00上变化,把t 的变化范围扩大为Mbt t Mbt +≤≤-00,为此给出t 变化范围后的Banach 空间中常微分方程解的存在唯一性定理,并对定理给予明确的证明.关键词: 存在唯一;常微分方程;数学归纳法;皮卡逐步逼近法;Banach 空间引言常微分方程解的存在唯一性定理明确地肯定了在一定条件下方程的解的存在性和唯一性,它是常微分方程理论中最基本且实用的定理,有其重大的理论意义,另一方面,它也是近似求解法的前提和理论基础.对于人们熟知的Banach 空间中常微分方程解的存在唯一性定理,解的存在区间较小, 只限制在一个小的球形邻域内,(球形邻域的半径若为δ,还需满足1<δL ,且解只在以0y 为中心以δ为半径的闭球δδ≤-∈=00)(y y X y y B 存在唯一,其中X 是Banach 空间)因此在应用过程中受到了一定的限制.如今我们尝试扩大了解的存在范围,从而使此重要的定理今后有更加广泛的应用.1 预备定理我们给出Banach 空间中常微分方程解的存在唯一性定理如下设X 是Banach 空间, X U ⊂是一个开集. X U f →:上关于y 满足利普希茨)(Lipschitz 条件,即存在常数0>L ,使得不等式2121),(),(y y L y t f y t f -≤-,对于所有U y y ∈21,都成立.取U y ∈0,在U 内,以0y 为中心作一个半径为b 的闭球b y y X y y B b ≤-∈=00)(,对所有的)(0y B y b ∈都成立,且有M y f ≤)(,取},1min{Mb L h =,则存在唯一的1C 曲线)(t y ,使得在h t t h t +≤≤-00上满足)(0y B y b ∈,并有),(y t f y =',00)(y t y =.2 结果与证明笔者通过改进对h 的限制,即仅取Mb h =,预备定理仍然成立,从而使定理的应用进一步广泛.2.1改进条件后的定理定理 假设条件同上预备定理,设初值为),(00y t ,则存在唯一的1C 曲线)(t y ,对任意的Mbt t Mbt +≤≤-00,满足)(0y B y b ∈,且使得),(y t f y =',00)(y t y =.显然可有],[],[0000Mbt M bt h t h t +-⊂+-,且},1min{MbL h =.2.2定理的证明证明 证明过程中我们利用皮卡)(Picard 逐步逼近法.为了简单起见,只就区间00t t Mbt ≤≤-进行讨论,对于区间Mbt t t +≤≤00的讨论完全一样.2.2.1定理证明的思想现在先简单叙述一下运用皮卡逐步逼近法证明的主要思想. 首先证明条件),(y t f y =',00)(y t y =等价于求积分方程dt y t f y t y t t ),()(00⎰+=.(1)再证明积分方程的解的存在唯一性.任取一个)(0t y 为连续函数,将它代入方程(1)的右端),(y t f ,可得到函数dt y t f y t y t t ),()(0010⎰+=,显然,)(1t y 也为连续函数.若)()(01t y t y =,则可知)(0t y 就是方程(1)的解.若不然,我们又把)(1t y 代入积分方程(1)的右端),(y t f ,可得到函数dt y t f y t y t t ),()(1020⎰+=.若)()(12t y t y =,则可知)(1t y 就是方程(1)的解.若不然,我们如此下去,可作连续函数,dt y t f y t y n t t n ),()(100-⎰+=. (2)这样就得到连续函数列),(,),(),(),(210t y t y t y t y n若)()(1t y t y n n =+,那么)(t y n 就是积分方程的解,如果始终不发生这种情况,我们可以证明上面的函数序列有一个极限函数)(t y ,即)()(lim t y t y n n =∞→存在,因而对(2)式两边取极限时,就得到dt y t f y dt y t f y dt y t f y t y t t n n t t n t t n n n ⎰⎰⎰+=+=+=-∞→-∞→∞→),(),(lim ),(lim )(lim 00001010,即dt y t f y t y t t ),()(00⎰+=,这就是说,)(t y 是积分方程的解.在定理的假设条件下,以上的步骤是可以实现的. 2.2.2定理证明的步骤下面我们分五个命题来证明定理.命题1 设)(t y y =是),(y t f y ='的定义于区间00t t Mbt ≤≤-上,满足初值条件00)(y t y = (3) 的解,则)(t y y =是积分方程dt y t f y t y t t ),()(00⎰+=定义于00t t M b t ≤≤-上的连续解,反之亦然.证明 因为)(t y y =是方程),(y t f y ='的解,故有),()(y t f dtt dy =. 对上式两边从0t 到t 取定积分得到dt y t f t y t y t t ⎰=-),()()(00,00t t M b t ≤≤-,把(3)式代入上式,即有dt y t f y t y t t ⎰+=),()(00,00t t M b t ≤≤-. (4)因此, )(t y y =是(4)的定义于00t t Mbt ≤≤-上的连续解.反之,如果)(t y y =是(4)的连续解, dt y t f y t y t t ⎰+=),()(00,00t t M b t ≤≤-.微分之,得到),()(y t f dtt dy =. 又把0t t =代入(4)式,得到00)(y t y =,因此, )(t y y =是方程),(y t f y ='的定义于区间00t t Mbt ≤≤-,且满足初值条件(3)的解.命题1证毕.现在取00)(y t y =,构造皮卡逐步逼近函数序列如下⎪⎩⎪⎨⎧=≤≤-+==⎰-),2,1(,),()()(0010000 n t t M b t dt y t f y t y y t y n t t n(5) 命题2 对于所有的n ,(5)中函数)(t y n 在00t t Mb t ≤≤-上有定义,连续且满足不等式b y t y n ≤-0)(.证明 用数学归纳法可以证明,如下)()(0y B t y b n ∈,对于任意N n ∈,00t t Mbt ≤≤-,当1=n 时, ξξd y f y t y t t ),()(0010⎰+=,显然)(1t y 在00t t Mb t ≤≤-上有定义,连续且有b t t M d y f d y f y t y t t t t ≤-≤≤=-⎰⎰)(),(),()(0000100ξξξξ.设当k n =时有)()(0y B t y b k ∈,也即)(t y k 在00t t Mbt ≤≤-上有定义,连续且满足不等式b y t y k ≤-0)(,这时ξξd y f y t y k t t k ),()(001⎰+=+.由假设,命题2当k n =时成立,则可知)(1t y k +在00t t Mb t ≤≤-上有定义,连续且有当1+=k n 时b t t M d y f d y f y t y k t t k t t k ≤-≤≤=-⎰⎰+)(),(),()(00100ξξξξ,即命题2当1+=k n 时也成立,从而得知命题2对于所有的n 均成立.命题2证毕.命题3 函数序列)}({t y n 在00t t Mb t ≤≤-上是一致收敛的.证明 我们考虑级数∑∞=--+110)]()([)(k k k t y t y t y ,00t t Mbt ≤≤-,(6)(6)式级数的部分和为)()]()([)(110t y t y t y t y n nk k k =-+∑=-,因此,要证明函数序列)}({t y n 在00t t Mbt ≤≤-上一致收敛,我们仅证明级数(6)在00t t Mbt ≤≤-上一致收敛.因此,我们可进行如下计算,由)(),(),()(0000100t t M d y f d y f y t y t t t t -≤≤=-⎰⎰ξξξξ, (7)及ξξξd y f y f t y t y t t ⎰-≤-),(),()()(01120,利用利普希茨)(Lipschitz 条件及(7)式可知对于任意的n 为正整数,不等式n n n n t t n ML t y t y )(!)()(011-≤---成立. 则由利普希茨条件,当00t t Mbt ≤≤-时,有为此,由数学归纳法可知,对于所有的正整数k ,可有如下的式子成立,k k k k t t k ML t y t y )(!)()(011-≤---,00t t M b t ≤≤-.因此可有,当k k kk k k M b k ML t t k ML t y t y )(!)(!)()(1011---≤-≤-, (8) (8)式右端为收敛的正项级数∑∞=-11)(!k k k M bk ML 的一般项. 由魏尔斯特拉斯)(s Weierstras 判别法,级数(6)在00t t Mb t ≤≤-上是一致收敛的,因此序列)}({t y n 也在00t t Mbt ≤≤-上一致收敛,命题3证毕.现设)()(lim t y t y n n =∞→,为此)(t y 也在00t t Mbt ≤≤-上连续,且由命题2又可知b y t y ≤-0)(,命题4 )(t y 是积分方程dt y t f y t y t t ),()(00⎰+=的定义在区间00t t M b t ≤≤-上的连续解.证明 由利普希茨条件)()(),(),(t y t y L y t f y t f n n -≤-以及)}({t y n 在2000112)(!2)()()()()(0t t ML d t M L d y y L t y t y t t t t -=-≤-≤-⎰⎰ξξξξξ100111)()!1()(!)()(),(),()()(000+--+-+=-≤-≤-≤-⎰⎰⎰n nnt t n n n t t n n t t n n t t n ML d t n ML d y y L d y f y f t y t y ξξξξξξξξ00t t Mbt ≤≤-上一致收敛于)(t y ,且函数列)}({t y n 逐项连续,即知序列))}(({t y f n 在00t t Mbt ≤≤-上一致收敛于))((t y f .因而对(5)式两边取极限,得到ξξξξd y f y d y f y t y n n t t n t t n n n ),(lim ),(lim )(lim 101000-∞→-∞→∞→⎰⎰+=+=即ξξd y f y t y t t ),()(00⎰+=,这就是说, )(t y 是积分方程dt y t f y t y t t ),()(00⎰+=的定义于00t t Mbt ≤≤-上的连续解.命题4证毕.命题5 (证明解的唯一性)设)(t x 是积分方程dt y t f y t y t t ),()(00⎰+=定义于00t t Mbt ≤≤-上的另一个连续解,则)()(t x t y =,00t t Mbt ≤≤-.证明 现在我们证明)(t x 也是序列)}({t y n 的一致收敛极限函数.为此,从00)(y t y =,.),()(100ξξd y f y t y n t t n ⎰-+= )1(≥n ,ξξd x f y t x t t ),()(00⎰+=,可以进行如下的估计,)(),(),()()(0000t t M d x f d x f t x t y t t t t -≤≤=-⎰⎰ξξξξ200001)(!2)()()(),(),()()(000t t MLd t ML d x y L d x f y f t x t y t t t t t t -=-≤-≤-≤-⎰⎰⎰ξξξξξξξξ现在我们可以假设n n n t t n ML t x t y )(!)()(011-≤---,则有 .)()!1()(!)()(),(),()()(10011000+---+=-≤-≤-≤-⎰⎰⎰n nnt t n n t t n t t n t t n ML d t n ML d x y L d x f y f t x t y ξξξξξξξξ故由数学归纳法得知,对于所有的正整数n ,有下面的估计式10)()!1()()(+-+≤-n nn t t n ML t x t y ,于是我们可知在00t t Mbt ≤≤-上有110)()!1()()!1()()(+++≤-+≤-n n n n n Mb n ML t t n ML t x t y , (9)1)()!1(++n n M b n ML 是收敛级数的公项,且当∞→n 时, 0)()!1(1→++n n Mb n ML . 因而)}({t y n 在00t t Mbt ≤≤-上一致收敛于)(t x .根据极限的唯一性,即可知)()(t x t y =,00t t Mbt ≤≤-.命题5证毕.综合命题1～5,即得到Banach 空间中常微分方程解的存在唯一性定理的证明. 例题 求初值问题⎪⎩⎪⎨⎧=--=0)1(22y yt dtdy 其中R :[]0,2-∈t ,[]1,1-∈y 的解的存在区间,并求第二次近似解,给出在解的存在区间的误差估计.解 ()4),(max ,==∈y t f M Ry t则利用本文的结果41==Mbh , 在R 上函数22),(y t y t f -=的利普希茨常数可取2=L ,因为L y yf=≤-=∂∂22. 0)(0=t y ,313))(()(220211+=-=⎰-t d y t y t ξξξ,4211631893))(()(74321212+---=-=⎰-t t t t d y t y t ξξξ.在本文的估计式(9)中令)()(t y t x =,则有误差估计式110)()!1()()!1()()(+++≤-+≤-n n n n n Mb n ML t t n ML t y t y ,从而可得241)41(!324)()(322=⨯⨯≤-t y t y .利用本文结果,初值问题解的存在区间为Mbt t Mbt +≤≤-00为此将10-=t ,41=Mb代入上式,可得解的存在区间为4345-≤≤-t ; 第二次近似解为42116318937432+---=t t t t y ;在解的存在区间的误差估计为2412≤-y y . 结束语在Banach 空间中,通过运用皮卡的逐步逼近法,从证明解的存在性,到解的唯一性,采用严密的逻辑推理和理论证明,得到扩大解的存在区间后Banach 空间中常微分方程解的存在唯一性定理,从而使定理更加实用.当然,展望未来,我们还可以利用所得到的结果进一步作为探究其他问题的可靠性依据.参考文献[1] 王高雄,周之铭,朱思铭,王寿松,编.常微分方程[M].北京：高等教育出版社,2006.[2] 郭大均,孙经先.抽象空间常微分方程[M].济南:山东科学技术出版社,2003.[3] 王兴涛,编.常微分方程[M].哈尔滨:哈尔滨工业大学出版社,2004.[4] 邓海荣,马兆丰.Banach空间中常微分方程解的存在唯一性定理的注[J].扬州大学学报:自然科学版,2007,10（1）: 1～3.[5] 房琦贵.关于常微分方程解的存在唯一问题的讨论[J].高校讲坛,2010.[6] 王声望,郑伟行,编.实变函数与泛函分析概要[M].北京：高等教育出版社,2005.如不慎侵犯了你的权益，请联系告知！致谢在完成终稿的今天,在敲完最后一个句号的时刻,我的思想同周围凝固的热气一样停驻了,不知道是慰藉还是悲伤,大学四年的生活就这样结束了,而眼前的路还很长,虽然似乎有些迷茫,但我必须整理心情,背上行囊,坚定的踏上新的征程……我要感谢,非常感谢我的指导老师何老师.在忙碌的教学工作中挤出时间来审查修改我的论文,循循善诱的教导和不拘一格的思路给予我无尽的启迪.他为人随和热情﹑治学严谨细心﹑广博的学识﹑深厚的学术素养,在论文的写作和措辞等方面他也总会以专业标准严格要求,从选题﹑定题﹑开始,一直到论文的反复修改,何老师始终认真负责地给予我深刻而细致地指导,帮助我开拓研究思路,精心点拨﹑热忱鼓励.正是何老师的无私帮助与热忱鼓励,我的毕业论文才能够得以顺利完成,谢谢何老师.再次,我还要认真地谢谢我身边所有的朋友和同学,你们对我的关心﹑帮助和支持是我不断前进的动力之一,我的大学生活因为有你们而更加精彩.最后,向在百忙中抽出时间对本文进行评审并提出宝贵意见的各位专家表示衷心地感谢!（本资料素材和资料部分来自网络，仅供参考。

常微分方程解的存在唯一性定理一阶微分方程⑴其中. 是在矩形域丄」’叭」上的连续函数。

定义1如果存在常数二11，使得不等式”（础）-/（砒）冏肝川对于所有--■■-1--- 都成立，贝U函数/、•称为在二上关于：'满足Lipschitz 条件。

定理1如果「二，在二上连续且关于「满足Lipschitz 条件，则方程（1）存在唯一的解y=叭心，定义于区间M ■阳卜月上，连续且满足初始条件W八-卄 A = r—）M = max' ■-.，这里」f，•心「。

Picard逐步逼近法来证明这个定理的主要思想首先证明求微分方程的初值冋题的解等价于求积分方程的连续解。

然后去证明积分方程的解的存在唯一性。

任取一个连续函数代入上面积分方程右端的,就得到函数俅沪）Vp（Z（）⑴）必，显然J 也是连续函数，如果,那末l:-'就是积分方程的解。

否则，我们又把J二代入积分方程右端的「，得到汀0恥）皿，如果氛沪仍⑴，那末仇⑴就是积分方程的解。

否则我们继续这个步骤。

一般地作函数惦（3.1.1.4）这样就得到连续函数序列，...，〔「」，…如果二, 那末就是积分方程的解。

如果始终不发生这种情况，我们可以证明上面的函数序列有一个极限函数厂：;；1，即'厂…I存在，因而对©Ji/）取极限时，就得到f「打「X FJr=y0+l=y0+祕幼必Jf祕x）=y n+/（X 矶兀））必/ 、即•血，这就是说机x）是积分方程的解。

这种一步一步地求出方程的解的方法就称为逐步逼近法。

函数''■■■■■'称为初值问题的第：次近似解。

命题1设—是方程（1）的定义于区间V —'■'‘上，满足初始条件Jf瞅）=刃的解，则厂曲）是积分方程y=y°+y （2曲碳心砒的定义于V ——'■上的连续解。

反之亦然。

现在取，构造皮卡逐步逼近函数序列如下: 京（X）=丹；保（方=丹+ f于（乙矶_1©）時从“英肿hJ*D（聊=12…）1命题2对于所有的卜，函数在J■:上有定义、连续且满足不等式命题3 函数序列"I「在J ------------ '."上是一致收敛的。

常微分方程解的唯一性定理及其应用1.1引言1.1.1 课题意义:常微分方解的唯一性定理是微分方程理论中的基本定理,也是微分方程近似计算的前提和根据，更是动力系统中重要的定理之一。

对解的存在唯一性的探讨是研究微分方程的重要内容，这更好的促进于微分方程解集的研究，使得微分方程内容的丰富。

对微分方程解的唯一性定理的研究将很好地解答了初值问题解的存在性与唯一性，这也是人们对微分方程目前研究的一个重要内容。

本文在前人研究的基础上对解的唯一性定理的证明进行归纳总结，并在此基础上延伸对定理的应用,增加其得实用性,将数学来源于生活并回归于生活得之真切表现。

1.1.2 目前发展状况：在前人们的研究都致力于对定理的证明及其证明方法的改进以及对定理的条件的改进与对方程的初值条件的优化,而对定理得实际应用确微乎其微。

从17世界微分方程的发展，数学家们致力于研究关于微分方程的初等解法。

到1740年数学家们已经知道几乎所有求解一阶方程的初等方法。

随着微分方程的发展，人们要求满足某种附加条件的特解，即定值问题的解，从而致使人们开始从事对定解问题的研究，其通常包括边值问题与初值问题。

对微分方程解的存在唯一性定理得研究,A Cauchy 在1820年首先严格证明了在相当一般条件下微分方程解的存在唯一性定理，为微分方程理论的研究奠定了坚实的基础。

1876年，R Lipschitz使用“Lischitz条件”简化了A Cauchy 关于微分方程的存在唯一性定理的证明。

1838年，J Liouville在研究热传导方程时提出了逐次逼近法。

1896年 C Picard 在1896年给出了逐次逼近法的普遍形式，这个定理的证明为日后人们研究解的存在唯一性奠定了坚实的基础。

但是从定理本身来看，其条件是比较严格的，因而更多的研究处在于对定理的条件的消弱的证明，以及将其朝其它数学分支的发展。

[1]Picard利用逐次逼近法证明了这个定理，将求微分方程的初值问题的解等价于求积分方程的连续解，再证明积分方程的解的存在唯一性。

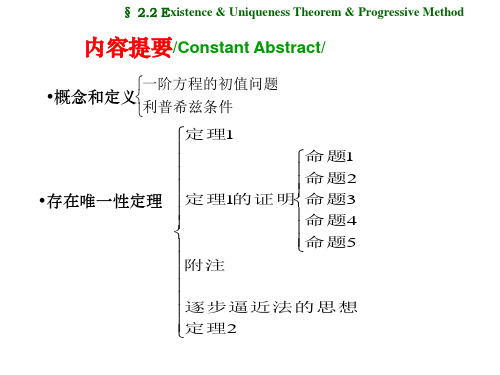
1解的存在唯一性
解的存在唯一性定理是指方程的解在一定条件下的存在性和唯一性，它是常微分方程理论中最基本的定理，有其重大的理论意义，另一方面由于能求得精确解的微分方程并不多，常微分方程的近似解法具有十分重要的意义，而解的存在唯一性又是近似解的前提，试想，如果解都不存在，花费精力去求其近似解有什么意义呢？如果解存在但不唯一，但不知道要确定的是哪一个解，又要去近似的求其解，又是没有意义的。

2解的存在唯一性定理一
定理1
如果函数f(x,y)在矩形域R上连续且关于y满足利普希茨条件，则方程
dx/dy=f(x,y);存在唯一的解y=φ(x)，定义于区间|x-x0|<=h上，连续且满足初值条件φ(x0)=y0,这里h=min(a,b/M) , M=max|f(x,y)|。

命题1
设y=φ(x)是方程的定义于区间x0<=x<=x0+h上，满足初值条件φ(x0)=y0的解，则y=φ(x)是积分方程y=y0+∫f(x,y)dx,x0<=x<=x0+h的定义于x0<=x<=x0+h上的连续解，反之亦然。

命题2
对于所有的n，皮卡逐步逼近函数φn(x)在 x0<=x<=x0+h上有定义，连续且满足不等式|φn(x)-y0|<=b。

命题3
函数序列{φn(x)} 在x0<=x<=x0+h上已收敛的。

命题4
φn(x)是积分方程的定义于x0<=x<=x0+h上的连续解
命题5
设ψ(x)是积分方程的定义于 x0<=x<=x0+h的另一个解，则
ψ(x)=φ(x)(x0<=x<=x0+。

常微分方程的解的存在唯一性定理常微分方程是研究变量之间关系的数学工具。

在许多科学和工程领域，我们经常需要求解常微分方程来描述和预测系统的行为。

而常微分方程的解的存在唯一性定理则为我们提供了一种保证求解过程的准确性和可靠性的方法。

1. 引言常微分方程是研究变量之间关系的数学工具，广泛应用于物理、生物、经济等领域。

解常微分方程是求解系统行为和预测未来发展的重要方法，但如何确保解的唯一性和存在性一直是研究的焦点。

2. 定理的表述常微分方程的解的存在唯一性定理指出，如果一个常微分方程满足一定条件，则该方程存在且只存在一个解。

具体表述如下：定理：设F(t, y)在区域D上连续且关于y满足Lipschitz条件，即存在常数L>0，使得对于任意的(t, y1)和(t, y2)∈D，有|F(t, y1) - F(t, y2)| ≤ L|y1 - y2|。

那么对于初值问题y' = F(t, y)，y(t0) = y0，存在唯一的解y(t)。

3. 论证和证明为了证明上述定理，我们可以使用柯西-利普希茨定理。

柯西-利普希茨定理指出，如果一个函数满足Lipschitz条件，那么它的微分方程必然存在唯一解。

4. 柯西-利普希茨定理的推导柯西-利普希茨定理的推导主要包括以下几个步骤：（1）定义导数：我们首先定义导数，即一个函数在某一点的斜率。

（2）利用导数定义微分方程：我们将导数的定义应用到微分方程中，得到一个关于导数的等式。

（3）引入Lipschitz条件：我们引入Lipschitz条件来限制导数的变化范围，确保解的唯一性。

（4）证明柯西-利普希茨定理：通过数学分析和推导，我们最终证明了柯西-利普希茨定理。

5. 应用实例常微分方程的解的存在唯一性定理在实际应用中具有重要意义。

以下是几个应用实例：（1）物理学中的运动方程：物体在运动中往往涉及到速度的变化，可以使用常微分方程来描述物体的运动轨迹。

解的存在唯一性定理保证了我们能够准确地求解出物体的运动轨迹。

常微分方程的解的存在唯一性定理常微分方程是数学中的一门重要分支，它涉及到许多实际问题的理论分析和计算求解，尤其是在物理、化学等领域有着广泛的应用。

而常微分方程的解的存在唯一性定理则是研究常微分方程解的基础，下面我将对这一定理进行详细阐述。

1. 常微分方程的定义及初值问题常微分方程（ODE）是指未知函数 $y(t)$ 的某个数量关系式：$$F(t,y,y',y'',\cdots ,y^{(n)})=0$$其中 $y'$，$y''$，$\cdots$，$y^{(n)}$ 分别表示 $y$ 的一阶、二阶、$\cdots$，$n$ 阶导数，$F$ 是已知的函数。

这个方程称为$n$ 阶常微分方程。

方程的初值问题是指，在确定 $n$ 阶常微分方程中的 $n$ 个初始条件：$$y(t_0)=y_0,\ y'(t_0)=y_1,\ \cdots,\ y^{(n-1)}(t_0)=y_{n-1}$$后，求解函数 $y(t)$ 在整个定义域上的解。

2. 解的存在唯一性定理的三个条件常微分方程的解的存在唯一性定理是指在一定的条件下，常微分方程仅有唯一的解。

下面给出常微分方程存在唯一性定理的三个条件。

2.1 连续性设函数 $F(t,y,y',y'',\cdots ,y^{(n)})$ 是定义于某个区域上的$C^{m+1}$ 级函数，即 $F$ 及其 $m$ 个偏导数（一直到$y^{(m)}$）都是连续的。

2.2 局部存在性对于同一初值问题，存在一个足够小的区间 $I$，使得在此区间内存在解 $y(t)$，并且 $y(t)$ 函数及其前 $n-1$ 阶导数都是$C^{m}$ 级函数。

2.3 局部唯一性在区间 $I$ 上，对于同一初值问题，解 $y(t)$ 是唯一的。

3. 解的存在唯一性定理的证明解的存在唯一性定理可转化为证明常微分方程方程的解满足某种 Lipschitz 条件，即：$$\forall \ y_1,y_2\in C([a,b])\ \text{and}\ y_1(t_0)=y_2(t_0)$$$$\Rightarrow \ \exists L>0,\ \text{s.t.}\ |y_1(t)-y_2(t)|\le L\cdot \max_{t\in [t_0,T]}\{|y_1(t)-y_2(t)|\}$$其中，$C([a,b])$ 表示在区间 $[a,b]$ 内连续的函数集合，$L$ 是 Lipschitz 常数。

常微分方程的解的存在唯一性定理常微分方程是数学中一个重要的研究对象，它描述了自变量是连续变化的函数与自变量的导数之间的关系。

研究常微分方程的解的存在唯一性定理是常微分方程理论的基石之一，对于解的存在性和唯一性的判断具有重要的意义。

定理一：皮卡尔(Picard)存在定理假设函数f(x, y)在矩形区域D={(x, y)：a≤x≤b,α≤y≤β}上连续，且满足利普希茨条件：存在正数L，使得在D上任意点(x, y1)和(x, y2)，有|f(x, y1) - f(x, y2)|≤L|y1-y2|。

则初值问题y' = f(x, y)，y(x0) = y0在区间[a, b]上存在唯一的解。

证明：（略）定理二：格朗沃尔(Gronwall)不等式假设函数y(x)满足不等式y(x)≤K+∫[a,x]f(t,y(t))dt，其中K为常数且f(x, y)为非负函数。

则有0≤y(x)≤Kexp(∫[a,x]f(t,y(t))dt)。

证明：（略）根据皮卡尔存在定理和格朗沃尔不等式，我们可以推导出常微分方程解的存在唯一性定理。

定理三：常微分方程解的存在唯一性定理假设函数f(x, y)在区域D上连续，且满足利普希茨条件：存在正数L，使得在D上任意点(x, y1)和(x, y2)，有|f(x, y1) - f(x, y2)|≤L|y1-y2|。

则对于初值问题y' = f(x, y)，y(x0) = y0，在定义区间上存在唯一的解。

证明：（略）常微分方程解的存在唯一性定理的推导过程相对较为复杂，涉及到一些数学理论和定理的运用。

但是这个定理为我们研究和求解常微分方程提供了重要的理论支持，确保了我们在解决实际问题中得到的解是存在且唯一的。

除了皮卡尔存在定理和格朗沃尔不等式外，我们还可以利用其他方法来证明常微分方程解的存在唯一性，比如利用分离变量法、变换方法、级数法等。

在实际应用中，根据具体问题的特点选择适合的方法进行求解。