数据结构第6章二叉树自测题参考答案
- 格式:doc
- 大小:398.00 KB
- 文档页数:11

数据结构第6章树和二叉树一、下面是有关二叉树的叙述,请判断正误(√)1.若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n-1个非空指针域。
n个结点的二叉树有n-1条分支(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2k-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i -1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,即有后继链接的指针仅n-1个,还有n+1个空指针。
)采用二叉链表存储有2n个链域,空链域为:2n-(n-1)=n+1(√)10.具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[ n/2] =6,再求n2=n0-1=5 [n/2] 除的结果四舍五入二、填空1.由3个结点所构成的二叉树有5种形态。
2. 一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
(或:总结点数为n=2k-1=26-1=63,叶子数为n0= [ n/2] =32,满二叉数没有度为1的结点,由n0=n2+1得n2=n0-1=32-1=31)3.一棵具有257个结点的完全二叉树,它的深度为9。

一、概念题(每空1分,共55分)1.树(及一切树形结构)是一种“________”结构。
在树上,________结点没有直接前趋。
对树上任一结点X来说,X是它的任一子树的根结点惟一的________。
2.由3个结点所构成的二叉树有种形态。
3.一棵深度为6的满二叉树有个分支结点和个叶子。
4.一棵具有257个结点的完全二叉树,它的深度为。
5.二叉树第i(i>=1)层上至多有______个结点;深度为k(k>=1)的二叉树至多有______个结点。
6.对任何二叉树,若度为2的节点数为n2,则叶子数n0=______。
7.满二叉树上各层的节点数已达到了二叉树可以容纳的______。
满二叉树也是______二叉树,但反之不然。
8.设一棵完全二叉树有700个结点,则共有个叶子结点。
9.设一棵完全二叉树具有1000个结点,则此完全二叉树有个叶子结点,有个度为2的结点,有个结点只有非空左子树,有个结点只有非空右子树。
10.一棵含有n个结点的k叉树,可能达到的最大深度为,最小深度为。
11.二叉树的基本组成部分是:根(N)、左子树(L)和右子树(R)。
因而二叉树的遍历次序有六种。
最常用的是三种:前序法(即按N L R次序),后序法(即按次序)和中序法(也称对称序法,即按L N R次序)。
这三种方法相互之间有关联。
若已知一棵二叉树的前序序列是BEFCGDH,中序序列是FEBGCHD,则它的后序序列必是。
12.中序遍历的递归算法平均空间复杂度为。
13.二叉树通常有______存储结构和______存储结构两类存储结构。
14.如果将一棵有n个结点的完全二叉树按层编号,则对任一编号为i(1<=i<=n)的结点X有:(1)若i=1,则结点X是______;若i〉1,则X的双亲PARENT(X)的编号为______。
(2)若2i>n,则结点X无______且无______;否则,X的左孩子LCHILD(X)的编号为______。

第六章树和二叉树试题一、单项选择题1.树中所有结点的度等于所有结点数加()。
A. 0B. 1C. -1D. 22.在一棵树中,()没有前驱结点。
A. 分支结点B. 叶结点C. 根结点D. 空结点3.在一棵二叉树的二叉链表中,空指针域数等于非空指针域数加()。
A. 2B. 1C. 0D. -14.在一棵具有n个结点的二叉树中,所有结点的空子树个数等于()。
A. nB. n-1C. n+1D. 2*n5.在一棵具有n个结点的二叉树的第i层上(假定根结点为第0层,i大于等于0而小于等于树的高度),最多具有()个结点。
A. 2iB. 2i+1C. 2i-1D. 2n6.在一棵高度为h(假定根结点的层号为0)的完全二叉树中,所含结点个数不小于()。
A. 2h-1B. 2h+1C. 2h-1D. 2h7.在一棵具有35个结点的完全二叉树中,该树的高度为()。
假定空树的高度为-1。
A. 5B. 6C. 7D. 88.在一棵具有n个结点的完全二叉树中,分支结点的最大编号为()。
假定树根结点的编号为0。
A. ⎣(n-1)/2⎦B. ⎣n/2⎦C. ⎡n/2⎤D. ⎣n/2⎦ -19.在一棵完全二叉树中,若编号为i的结点存在左孩子,则左子女结点的编号为()。
假定根结点的编号为0A. 2iB. 2i-1C. 2i+1D. 2i+210.在一棵完全二叉树中,假定根结点的编号为0,则对于编号为i(i>0)的结点,其双亲结点的编号为()。
A. ⎣(i+1)/2⎦B. ⎣(i-1)/2⎦C. ⎣i/2⎦D. ⎣i/2⎦-111.在一棵树的左子女-右兄弟表示法中,一个结点的右孩子是该结点的()结点。
A. 兄弟B. 子女C. 祖先D. 子12.在一棵树的静态双亲表示中,每个存储结点包含()个域。
A. 1B. 2C. 3D. 413.已知一棵二叉树的广义表表示为a (b (c), d (e ( , g (h) ), f ) ),则该二叉树的高度为()。

第六章树和二叉树作业一、选择题(每题2分,共24分)。
1. 一棵二叉树的顺序存储情况如下:树中,度为2的结点数为( C )。
A.1 B.2 C.3 D.42. 一棵“完全二叉树”结点数为25,高度为(B )。
A.4 B.5 C.6 D.不确定3.下列说法中,(B )是正确的。
A. 二叉树就是度为2的树B. 二叉树中不存在度大于2的结点C. 二叉树是有序树D. 二叉树中每个结点的度均为24.一棵二叉树的前序遍历序列为ABCDEFG,它的中序遍历序列可能是(B )。
A. CABDEFGB. BCDAEFGC. DACEFBGD. ADBCFEG5.线索二叉树中的线索指的是(C )。
A.左孩子 B.遍历 C.指针 D.标志6. 建立线索二叉树的目的是(A )。
A. 方便查找某结点的前驱或后继B. 方便二叉树的插入与删除C. 方便查找某结点的双亲D. 使二叉树的遍历结果唯一7. 有 D )示意。
A.B.C.D.8. 一颗有2046个结点的完全二叉树的第10层上共有(B )个结点。
A. 511B. 512C. 1023D. 10249. 一棵完全二叉树一定是一棵(A )。
A. 平衡二叉树B. 二叉排序树C. 堆D. 哈夫曼树10.某二叉树的中序遍历序列和后序遍历序列正好相反,则该二叉树一定是( C )的二叉树。
A .空或只有一个结点B .高度等于其结点数C .任一结点无左孩子D .任一结点无右孩子11.一棵二叉树的顺序存储情况如下:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15A B C D E 0 F 0 0 G H 0 0 0 X结点D 的左孩子结点为( D )。
A .EB .C C .FD .没有12.一棵“完全二叉树”结点数为25,高度为( B )。
A .4B .5C .6D .不确定二、填空题(每空3分,共18分)。
1. 树的路径长度:是从树根到每个结点的路径长度之和。
对结点数相同的树来说,路径长度最短的是 完全 二叉树。

第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DE D.-+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D 3. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( ) 【南京理工大学1999 一、20(2分)】 A. A*B+C/(D*E)+(F-G) B. (A*B+C)/(D*E)+(F-G) C. (A*B+C)/(D*E+(F-G )) D. A*B+C/D*E+F-G 4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D .8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是( )【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2; ③二叉树的左右子树可任意交换;④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③B .②③④C .②④D .①④6. 设森林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,森林F 中第一棵树的结点个数是( )A .m-nB .m-n-1C .n+1D .条件不足,无法确定 【南京理工大学2000一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T 。
其余结点分成为m (m>0)个((2))的集合T1,T2, …,Tm ,每个集合又都是树,此时结点T 称为Ti 的父结点,Ti 称为T的子结点(1≤i ≤m )。

第6章树和二叉树答案一、判断正误(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2i-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。
用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。
)即有后继链接的指针仅n-1个。
(√)10. 〖01年计算机系研题〗具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5二、填空题1.由3个结点所构成的二叉树有5种形态。
2. 一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为9。
(注:用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.设一棵完全二叉树有700个结点,则共有350个叶子结点。

第 6 章树和二叉树1.选择题( 1)把一棵树变换为二叉树后,这棵二叉树的形态是()。
A.独一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子( 2)由 3 个结点能够结构出多少种不一样的二叉树?()A. 2 B . 3 C . 4 D. 5( 3)一棵完整二叉树上有1001 个结点,此中叶子结点的个数是()。
A. 250 B . 500 C . 254 D. 501( 4)一个拥有 1025 个结点的二叉树的高h 为()。
A. 11 B . 10 C.11 至 1025 之间 D .10 至 1024 之间( 5)深度为 h 的满 m叉树的第 k 层有()个结点。
(1=<k=<h)k-1B kCh-1 hA. m . m-1 . m D.m-1( 6)利用二叉链表储存树,则根结点的右指针是()。
A.指向最左孩子 B .指向最右孩子 C .空 D .非空( 7)对二叉树的结点从 1 开始进行连续编号,要求每个结点的编号大于其左、右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,可采纳()遍历实现编号。
A.先序 B. 中序 C. 后序 D.从根开始按层次遍历(8)若二叉树采纳二叉链表储存结构,要互换其全部分支结点左、右子树的地点,利用()遍历方法最适合。
A.前序B.中序C.后序D.按层次(9)在以下储存形式中,()不是树的储存形式?A.双亲表示法 B .孩子链表表示法 C .孩子兄弟表示法D.次序储存表示法( 10)一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树必定满足()。
A.全部的结点均无左孩子B.全部的结点均无右孩子C.只有一个叶子结点D.是随意一棵二叉树( 11)某二叉树的前序序列和后序序列正好相反,则该二叉树必定是()的二叉树。
A.空或只有一个结点B.任一结点无左子树C.高度等于其结点数 D .任一结点无右子树( 12)若 X 是二叉中序线索树中一个有左孩子的结点,且 X 不为根,则 X 的前驱为()。

一、基础知识题6.1设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,求树T中的叶子数。
【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm,结点总数为n,分枝数为B,则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即: n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点,求叶子结点的个数。
【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系:n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1,则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中,度为1的结点数n1至多为1,叶子数n0是整数。
本题中度为1的结点数n1只能是0,故叶子结点的个数n0为501.注:解本题时要使用以上公式,不要先判断完全二叉树高10,前9层是满二叉树,第10层都是叶子,……。
虽然解法也对,但步骤多且复杂,极易出错。
6.3 一棵124个叶结点的完全二叉树,最多有多少个结点。
【解答】由公式n=2n0+n1-1,当n1为1时,结点数达到最多248个。
6.4.一棵完全二叉树有500个结点,请问该完全二叉树有多少个叶子结点?有多少个度为1的结点?有多少个度为2的结点?如果完全二叉树有501个结点,结果如何?请写出推导过程。
【解答】由公式n=2n0+n1-1,带入具体数得,500=2n0+n1-1,叶子数是整数,度为1的结点数只能为1,故叶子数为250,度为2的结点数是249。
若完全二叉树有501个结点,则叶子数251,度为2的结点数是250,度为1的结点数为0。
6.5 某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树的总结点数是多少。
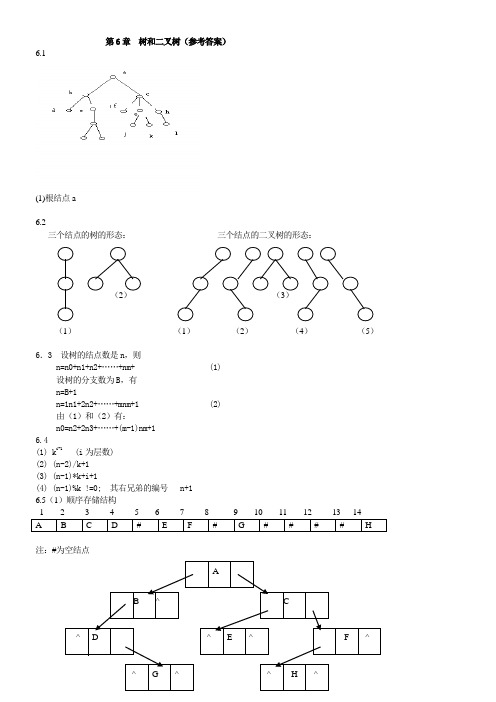
第6章 树和二叉树(参考答案)6.1(1)根结点a6.2三个结点的树的形态: 三个结点的二叉树的形态:(1) (1) (2) (4) (5)6.3 设树的结点数是n ,则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ,有n=B+1n=1n1+2n2+……+mnm+1 (2)由(1)和(2)有:n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5(1)顺序存储结构注:#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树,本算法求二叉树bt的高度{ int bl,br; // 局部变量,分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1(根) }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树,i是数// 组下标,初始调用时为1。
本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈,栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针,栈空时top=0if (n<=0) { printf(“输入错误”);exit(0);}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空,其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈,先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法,“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组,n是数组元素个数。
第6章树和二叉树部分答案解释如下。
12. 由二叉树结点的公式:n=n0+n1+n2=n0+n1+(n0-1)=2n0+n1-1,因为n=1001,所以1002=2n0+n1,在完全二叉树树中,n1只能取0或1,在本题中只能取0,故n=501,因此选E。
42.前序序列是“根左右”,后序序列是“左右根”,若要这两个序列相反,只有单支树,所以本题的A和B均对,单支树的特点是只有一个叶子结点,故C是最合适的,选C。
A或B 都不全。
由本题可解答44题。
47. 左子树为空的二叉树的根结点的左线索为空(无前驱),先序序列的最后结点的右线索为空(无后继),共2个空链域。
52.线索二叉树是利用二叉树的空链域加上线索,n个结点的二叉树有n+1个空链域。
部分答案解释如下。
6.只有在确定何序(前序、中序、后序或层次)遍历后,遍历结果才唯一。
19.任何结点至多只有左子树的二叉树的遍历就不需要栈。
24. 只对完全二叉树适用,编号为i的结点的左儿子的编号为2i(2i<=n),右儿子是2i+1(2i+1<=n)37. 其中序前驱是其左子树上按中序遍历的最右边的结点(叶子或无右子女),该结点无右孩子。
38 . 新插入的结点都是叶子结点。
42. 在二叉树上,对有左右子女的结点,其中序前驱是其左子树上按中序遍历的最右边的结点(该结点的后继指针指向祖先),中序后继是其右子树上按中序遍历的最左边的结点(该结点的前驱指针指向祖先)。
44.非空二叉树中序遍历第一个结点无前驱,最后一个结点无后继,这两个结点的前驱线索和后继线索为空指针。
三.填空题1.(1)根结点(2)左子树(3)右子树2.(1)双亲链表表示法(2)孩子链表表示法(3)孩子兄弟表示法3.p->lchild==null && p->rchlid==null 4.(1) ++a*b3*4-cd (2)18 5.平衡因子6. 97. 128.(1)2k-1 (2)2k-19.(1)2H-1 (2)2H-1(3)H=⎣log2N⎦+110. 用顺序存储二叉树时,要按完全二叉树的形式存储,非完全二叉树存储时,要加“虚结点”。

第6章树和二叉树自测卷解答一、下面是有关二叉树的叙述,请判断正误(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2i-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。
用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。
)即有后继链接的指针仅n-1个。
(√)10. 具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5二、填空(每空1分,共15分)1.由3个结点所构成的二叉树有5种形态。
2. 一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为9。
(注:用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.设一棵完全二叉树有700个结点,则共有350个叶子结点。

数据结构(本)单元6树和二叉树单元测试数据结构(本)单元6树和二叉树单元测试(题+答案)题目1、假定一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为()。
A. 15B. 16C. 47D. 17题目2、已知某二叉树的后续遍历序列是dabec,中序遍历是debac,则它的先序遍历序列是()。
A. cedbaB. decabC. acbedD. deabc题目3、二叉树第k层上最多有()个结点。
A.B.C.D. 2k题目4、二叉树的深度为k,则二叉树最多有()个结点。
A.B.C. 2kD. 2k-1题目5、设某一二叉树先序遍历为abdec,中序遍历为dbeac,则该二叉树后序遍历的顺序是()。
A. debacB. debcaC. abedcD. abdec题目6、设某一二叉树中序遍历为badce,后序遍历为bdeca,则该二叉树先序遍历的顺序是()。
A. debacB. decabC. adbecD. abcde题目7、树最适合于用来表示()。
A. 元素之间有包含和层次关系的数据B. 元素之间无前驱和后继关系的数据C. 顺序结构的数据D. 线性结构的数据题目8、一棵非空的二叉树,先序遍历与后续遍历正好相反,则该二叉树满足()。
A. 任意二叉树B. 无左孩子C. 只有一个叶子结点D. 无右孩子题目9、设a,b为一棵二叉树的两个结点,在后续遍历中,a在b前的条件是()。
A. a在b左方B. a在b右方C. a在b上方D. a在b下方题目10、权值为{1,2,6,8}的四个结点构成的哈夫曼树的带权路径长度是()。
A. 29B. 18C. 19D. 28题目11、如果将给定的一组数据作为叶子数值,所构造出的二叉树的带权路径长度最小,则该树称为()。
A. 哈夫曼树B. 平衡二叉树C. 二叉树D. 完全二叉树题目12、下列有关二叉树的说法正确的是()。
A. 完全二叉树中,任何一个结点的度,或者为0或者为2B. 二叉树中度为0的结点的个数等于度为2的结点的个数加1C. 二叉树的度是2D. 二叉树中结点个数必大于0题目13、二叉树是非线性数据结构,所以()。

数据结构(本)单元6树和二叉树单元测试(题+答案)题目1、假定一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为()。
A. 15B. 16C. 47D. 17题目2、已知某二叉树的后续遍历序列是dabec,中序遍历是debac,则它的先序遍历序列是()。
A. cedbaB. decabC. acbedD. deabc题目3、二叉树第k层上最多有()个结点。
A.B.C.D. 2k题目4、二叉树的深度为k,则二叉树最多有()个结点。
A.B.C. 2kD. 2k-1题目5、设某一二叉树先序遍历为abdec,中序遍历为dbeac,则该二叉树后序遍历的顺序是()。
A. debacB. debcaC. abedcD. abdec题目6、设某一二叉树中序遍历为badce,后序遍历为bdeca,则该二叉树先序遍历的顺序是()。
A. debacB. decabC. adbecD. abcde题目7、树最适合于用来表示()。
A. 元素之间有包含和层次关系的数据B. 元素之间无前驱和后继关系的数据C. 顺序结构的数据D. 线性结构的数据题目8、一棵非空的二叉树,先序遍历与后续遍历正好相反,则该二叉树满足()。
A. 任意二叉树B. 无左孩子C. 只有一个叶子结点D. 无右孩子题目9、设a,b为一棵二叉树的两个结点,在后续遍历中,a在b前的条件是()。
A. a在b左方B. a在b右方C. a在b上方D. a在b下方题目10、权值为{1,2,6,8}的四个结点构成的哈夫曼树的带权路径长度是()。
A. 29B. 18C. 19D. 28题目11、如果将给定的一组数据作为叶子数值,所构造出的二叉树的带权路径长度最小,则该树称为()。
A. 哈夫曼树B. 平衡二叉树C. 二叉树D. 完全二叉树题目12、下列有关二叉树的说法正确的是()。
A. 完全二叉树中,任何一个结点的度,或者为0或者为2B. 二叉树中度为0的结点的个数等于度为2的结点的个数加1C. 二叉树的度是2D. 二叉树中结点个数必大于0题目13、二叉树是非线性数据结构,所以()。

一、基础知识题6.1设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,求树T中的叶子数。
【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm,结点总数为n,分枝数为B,则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即: n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点,求叶子结点的个数。
【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系:n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1,则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中,度为1的结点数n1至多为1,叶子数n0是整数。
本题中度为1的结点数n1只能是0,故叶子结点的个数n0为501.注:解本题时要使用以上公式,不要先判断完全二叉树高10,前9层是满二叉树,第10层都是叶子,……。
虽然解法也对,但步骤多且复杂,极易出错。
6.3 一棵124个叶结点的完全二叉树,最多有多少个结点。
【解答】由公式n=2n0+n1-1,当n1为1时,结点数达到最多248个。
6.4.一棵完全二叉树有500个结点,请问该完全二叉树有多少个叶子结点?有多少个度为1的结点?有多少个度为2的结点?如果完全二叉树有501个结点,结果如何?请写出推导过程。
【解答】由公式n=2n0+n1-1,带入具体数得,500=2n0+n1-1,叶子数是整数,度为1的结点数只能为1,故叶子数为250,度为2的结点数是249。
若完全二叉树有501个结点,则叶子数251,度为2的结点数是250,度为1的结点数为0。
6.5 某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树的总结点数是多少。

第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DE D. -+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D 3. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( ) 【南京理工大学1999 一、20(2分)】 A. A*B+C/(D*E)+(F-G) B. (A*B+C)/(D*E)+(F-G) C. (A*B+C)/(D*E+(F-G )) D. A*B+C/D*E+F-G4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D .8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是( )【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2; ③二叉树的左右子树可任意交换; ④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③B .②③④C .②④D .①④6. 设森林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,森林F 中第一棵树的结点个数是( )A .m-nB .m-n-1C .n+1D .条件不足,无法确定 【南京理工大学2000 一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T 。
其余结点分成为m (m>0)个((2))的集合T1,T2, …,Tm ,每个集合又都是树,此时结点T 称为Ti 的父结点,Ti 称为T 的子结点(1≤i ≤m )。


第六章课后习题6、1、各层的结点数目是:K2、编号为n的结点的双亲结点是:<=(n-2)/k的最大整数3、编号为n的结点的第i个孩子结点编号是:k*(n-1)+1+i4、编号为n的结点有右兄弟的条件是:(n-1)能被k整除右兄弟的编号是:n+1.7、1、先序序列和中序序列相同:空二叉树或没有左子树的二叉树。
2、中序序列和后序序列相同:空二叉树或没有右子树的二叉树。
3、先序序列和后序序列相同:空二叉树或只有根的二叉树。
9、中序序列:BDCEAFHG和后序序列:DECBHGFA的二叉树为:AB FC GD E H先序序列:ABCDEFGH算法设计:3、typedef struct{int data[100];int top;}seqstack;seqstack *s;Perorder(char a[],int n){int i=1,count=1;s->top=-1;if(n==0)return(0);else{if(I<=n){s->top++;s->data[s->top]=a[I];}while(count<n){printf(“%c”,s->data[s->top]);count++;s->top--;if(s->data[s->top]);==a[i]){ printf(“%c”,s->data[s->top]);count++;s->top--;}if((2*i+1)<n){i=2*i;s->top++;s->data[s->top]=a[i+1];s->top++;s->data[s->top]=a[i];}else if(a*i<n){i=2*i;s->top++;s->data[s->top]=a[i];}else if(i/2%2==1)i=i/2/2+1;else i=i/2+1;}}}main(){char A[]=“kognwyuvb”;int n=strlen(A);s=(seqstack *)malloc(sizeof(seqstack)); printf(“\n”);Perorder(A,n);}。

数据结构第6章树和⼆叉树第六章树和⼆叉树⼀、选择题1.已知⼀算术表达式的中缀形式为 A+B*C-D/E,后缀形式为ABC*+DE/-,其前缀形式为( )A.-A+B*C/DE B. -A+B*CD/E C.-+*ABC/DE D. -+A*BC/DE2.设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T中的叶⼦数为()A.5 B.6 C.7 D.83.在下述结论中,正确的是()①只有⼀个结点的⼆叉树的度为0; ②⼆叉树的度为2;③⼆叉树的左右⼦树可任意交换;④深度为K的完全⼆叉树的结点个数⼩于或等于深度相同的满⼆叉树。
A.①②③ B.②③④ C.②④ D.①④4.设森林F对应的⼆叉树为B,它有m个结点,B的根为p,p的右⼦树结点个数为n,森林F中第⼀棵树的结点个数是()A.m-n B.m-n-1 C.n+1 D.条件不⾜,⽆法确定5.⼀棵完全⼆叉树上有1001个结点,其中叶⼦结点的个数是()A.250 B. 254 C.500 D.5016.设给定权值总数有n 个,其哈夫曼树的结点总数为( )A.不确定 B.2n C.2n+1 D.2n-17.有关⼆叉树下列说法正确的是()A.⼆叉树的度为2 B.⼀棵⼆叉树的度可以⼩于2 C.⼆叉树中⾄少有⼀个结点的度为2 D.⼆叉树中任何⼀个结点的度都为2 8.⼆叉树的第I层上最多含有结点数为()A.2I B. 2I-1-1 C. 2I-1 D.2I -19.⼀个具有1025个结点的⼆叉树的⾼h为()A.11 B.10 C.11⾄1025之间 D.10⾄1024之间10.⼀棵⼆叉树⾼度为h,所有结点的度或为0,或为2,则这棵⼆叉树最少有( )结点A.2h B.2h-1 C.2h+1 D.h+111.⼀棵具有 n个结点的完全⼆叉树的树⾼度(深度)是()A.?log2n?+1 B.log2n+1 C.?log2n? D.log2n-112.深度为h的满m叉树的第k层有()个结点。
第6章树和二叉树自测卷解答一、下面是有关二叉树的叙述,请判断正误(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2i-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。
用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。
)即有后继链接的指针仅n-1个。
(√)10. 具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5二、填空(每空1分,共15分)1.由3个结点所构成的二叉树有5种形态。
2. 一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为9。
(注:用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.设一棵完全二叉树有700个结点,则共有350个叶子结点。
答:最快方法:用叶子数=[n/2]=3505. 设一棵完全二叉树具有1000个结点,则此完全二叉树有500个叶子结点,有499个度为2的结点,有1个结点只有非空左子树,有0个结点只有非空右子树。
答:最快方法:用叶子数=[n/2]=500 ,n2=n0-1=499。
另外,最后一结点为2i属于左叶子,右叶子是空的,所以有1个非空左子树。
完全二叉树的特点决定不可能有左空右不空的情况,所以非空右子树数=0.6. 一棵含有n个结点的k叉树,可能达到的最大深度为n,最小深度为2。
答:当k=1(单叉树)时应该最深,深度=n(层);当k=n-1(n-1叉树)时应该最浅,深度=2(层),但不包括n=0或1时的特例情况。
教材答案是“完全k叉树”,未定量。
)7.二叉树的基本组成部分是:根(N)、左子树(L)和右子树(R)。
因而二叉树的遍历次序有六种。
最常用的是三种:前序法(即按N L R次序),后序法(即按L R N次序)和中序法(也称对称序法,即按L N R次序)。
这三种方法相互之间有关联。
若已知一棵二叉树的前序序列是BEFCGDH,中序序列是FEBGCHD,则它的后序序列必是 F E G H D C B。
解:法1:先由已知条件画图,再后序遍历得到结果;法2:不画图也能快速得出后序序列,只要找到根的位置特征。
由前序先确定root,由中序先确定左子树。
例如,前序遍历BEFCGDH中,根结点在最前面,是B;则后序遍历中B一定在最后面。
法3:递归计算。
如B在前序序列中第一,中序中在中间(可知左右子树上有哪些元素),则在后序中必为最后。
如法对B的左右子树同样处理,则问题得解。
8.中序遍历的递归算法平均空间复杂度为O(n)。
答:即递归最大嵌套层数,即栈的占用单元数。
精确值应为树的深度k+1,包括叶子的空域也递归了一次。
9.用5个权值{3, 2, 4, 5, 1}构造的哈夫曼(Huffman)树的带权路径长度是33 。
解:先构造哈夫曼树,得到各叶子的路径长度之后便可求出WPL=(4+5+3)×2+(1+2)×3=33(15)(9) (6) (注:两个合并值先后不同会导致编码不同,即哈夫曼编码不唯一)4 5 3 (3) (注:合并值应排在叶子值之后)1 2(注:原题为选择题:A.32 B.33 C.34 D.15)三、单项选择题(每小题1分,共11分)(C)1.不含任何结点的空树。
(A)是一棵树; (B)是一棵二叉树;(C)是一棵树也是一棵二叉树; (D)既不是树也不是二叉树答:以前的标答是B,因为那时树的定义是n≥1(C)2.二叉树是非线性数据结构,所以。
(A)它不能用顺序存储结构存储; (B)它不能用链式存储结构存储;(C)顺序存储结构和链式存储结构都能存储; (D)顺序存储结构和链式存储结构都不能使用(C)3. 具有n(n>0)个结点的完全二叉树的深度为。
(A) ⎡log2(n)⎤(B) ⎣ log2(n)⎦(C) ⎣ log2(n) ⎦+1 (D) ⎡log2(n)+1⎤注1:⎡x ⎤表示不小于x的最小整数;⎣ x⎦表示不大于x的最大整数,它们与[ ]含义不同!注2:选(A)是错误的。
例如当n为2的整数幂时就会少算一层。
似乎⎣ log2(n) +1⎦是对的?(A)4.把一棵树转换为二叉树后,这棵二叉树的形态是。
(A)唯一的(B)有多种(C)有多种,但根结点都没有左孩子(D)有多种,但根结点都没有右孩子5. 从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在答卷的对应栏内。
树是结点的有限集合,它A 根结点,记为T。
其余的结点分成为m(m≥0)个 B的集合T1,T2,…,Tm,每个集合又都是树,此时结点T称为T i的父结点,T i称为T的子结点(1≤i≤m)。
一个结点的子结点个数为该结点的 C 。
供选择的答案A:①有0个或1个②有0个或多个③有且只有1个④有1个或1个以上B: ①互不相交②允许相交③允许叶结点相交④允许树枝结点相交C:①权②维数③次数(或度)④序答案:ABC=1,1,36.从供选择的答案中,选出应填入下面叙述?内的最确切的解答,把相应编号写在答卷的对应栏内。
二叉树A 。
在完全的二叉树中,若一个结点没有 B ,则它必定是叶结点。
每棵树都能惟一地转换成与它对应的二叉树。
由树转换成的二叉树里,一个结点N的左子女是N在原树里对应结点的 C ,而N的右子女是它在原树里对应结点的 D 。
供选择的答案A:①是特殊的树②不是树的特殊形式③是两棵树的总称④有是只有二个根结点的树形结构B: ①左子结点②右子结点③左子结点或者没有右子结点④兄弟C~D:①最左子结点②最右子结点③最邻近的右兄弟④最邻近的左兄弟⑤最左的兄弟⑥最右的兄弟答案:A= B= C= D = 答案:ABCDE =2,1,1,3四、简答题(每小题4分,共20分)1.设如下图所示的二叉树B 的存储结构为二叉链表,root 为根指针,结点结构为:(lchild,data,rchild )。
其中lchild ,rchild 分别为指向左右孩子的指针,data 为字符型,root为根指针,试回答下列问题:1. 对下列二叉树B ,执行下列算法traversal(root),试指出其输出结果;2. 假定二叉树B 共有n 个结点,试分析算法traversal(root)的时间复杂度。
(共8分)二叉树B解:这是“先根再左再根再右”,比前序遍历多打印各结点一次,输出结果为:A B C C E E B A D F F D G G特点:①每个结点肯定都会被打印两次;②但出现的顺序不同,其规律是:凡是有左子树的结点,必间隔左子树的全部结点后再重复出现;如A ,B ,D 等结点。
反之马上就会重复出现。
如C ,E ,F ,G 等结点。
时间复杂度以访问结点的次数为主,精确值为2*n ,时间渐近度为O(n). 2.给定二叉树的两种遍历序列,分别是:前序遍历序列:D ,A ,C ,E ,B ,H ,F ,G ,I ; 中序遍历序列:D ,C ,B ,E ,H ,A ,G ,I ,F , 试画出二叉树B ,并简述由任意二叉树B 的前序遍历序列和中序遍历序列求二叉树B 的思想方法。
解:方法是:由前序先确定root ,由中序可确定root 的左、右子树。
然后由其左子树的元素集合和右子树的集合对应前序遍历序列中的元素集合,可继续确定root 的左右孩子。
将他们分别作为新的root ,不断递归,则所有元素都将被唯一确定,问题得解。
DAC FE G B H I3.略五、阅读分析题(每题5分,共20分)1.试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列。
答:DLR :A B D F J G K C E H I L M LDR: B F J D G K A C H E L I M LRD :J F K G D B H L M I E C AA B D C F G E C 的结点类型定义如下:struct node{char data;struct node *lchild, rchild;};C 算法如下:void traversal(struct node *root){if (root){printf(“%c”, root ->data);traversal(root->lchild);printf(“%c”, root ->data);traversal(root->rchild);}}2825 3340 60 08 54 552.把如图所示的树转化成二叉树。
答:注意全部兄弟之间都要连线(包括度为2的兄弟),并注意原有连线结点一律归入左子树,新添连线结点一律归入右子树。
A BE CK F H D L G I M J3.阅读下列算法,若有错,改正之。
4.画出和下列二叉树相应的森林。
答:注意根右边的子树肯定是森林, 而孩子结点的右子树均为兄弟。
六、算法设计题1.编写递归算法,计算二叉树中叶子结点的数目。
解:思路:输出叶子结点比较简单,用任何一种遍历递归算法,凡是左右指针均空者,则为叶子,将其打印出来。
法一:核心部分为:DLR(liuyu *root) /*中序遍历 递归函数*/ {if(root!=NULL){if((root->lchild==NULL)&&(root->rchild==NULL)){sum++; printf("%d\n",root->data);} DLR(root->lchild); DLR(root->rchild); } return(0);BiTree InSucc(BiTree q){//已知q 是指向中序线索二叉树上某个结点的指针, //本函数返回指向*q 的后继的指针。