圆曲线、缓和曲线计算方法

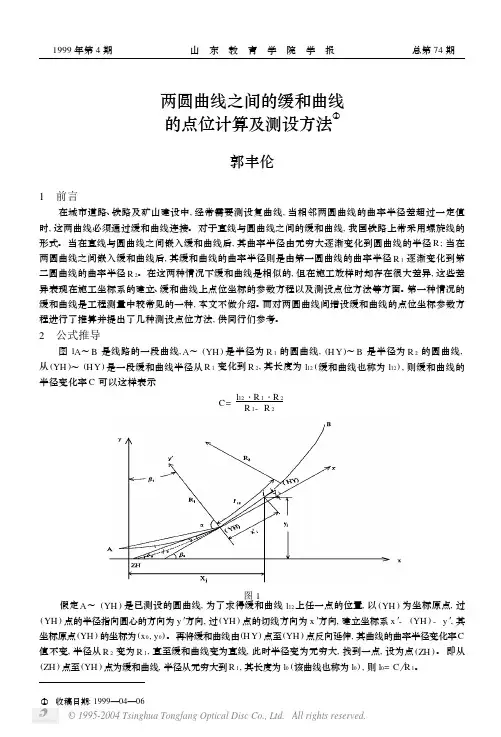
缓和曲线、竖曲线、圆曲线、匝道（计算公式）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”) 求：①线路匝道上点的坐标：xy②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x0时sgn(x)=1，当x=0时sgn(x)=0。

● 圆曲线方法一：sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二：11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三：180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角，A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段：先由JD1以及JD2的坐标算出JD1到JD2的方位角，即直线段方位角A ，故可算出HZ 、ZH 坐标及其直线段各点坐标。

2、缓和曲线：以HZ 、ZH 为起点，缓和曲线上任意一点离HZ 、ZH 距离为l ，利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标，利用arctan y x算出该点相对起点的方位角B ，再根据线路走向及直线段方位角可算出该点的方位角C （顺时针加，逆时针减），用可求出该点相对起点的距离D ，最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。

（00(,)x y 为缓和曲线起点的坐标）3、圆曲线：用上述方法求出圆曲线两端点HY 、YH 坐标，算出HY 到YH 的方位角F ，以及两点间的距离E ，用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ，根据线路走向求出起点到圆心的方位角H （H=F+/-G ），00(,)x y 圆曲线为起点坐标，根据00cos sin x x R H y y R H=+⎧⎨=+⎩，求出圆心坐标。

缓和曲线连同圆曲线的曲线主点测设一、缓和曲线常数计算曲线要素计算前，应进行必要的常数计算。

缓和曲线的常数包括：缓和曲线、切垂距m（切线增长值）、内移距p。

切线角β缓和曲线切线角——过HY（或YH）点的切线与ZH（或HZ）点的切线组成的角。

即，圆曲线被缓和曲线所代替的那一段弧长对应的圆心角。

向切线作垂线的垂足到缓和曲线起点的距离。

切垂距——由圆心O2内移距——加缓和曲线后，圆曲线相对于切线的内移量。

缓和曲线常数按下式计算：二、缓和曲线要素计算、切曲差q。

各曲线要缓和曲线要素包括：切线长T、曲线总长L、外矢距E素按下式计算：式中 L′——HY点到YH点的曲线长。

三、主点里程计算主点里程计算是根据交点里程和缓和曲线要素推算而得，如图4.5.2所示。

铁路习惯推算方法：公路习惯推算方法：四、主点测设方法举例【例4.6.1】已知某线路，交点里程为DK281＋578.59，圆曲线半径R＝500m，转向角α右＝18°22′00″，缓和曲线长l＝40 m。

试计算曲线要素与主点里程。

【解】（1）缓和曲线常数计算：（2）缓和曲线要素计算：（3）主点里程计算：校核：（4）主点测设方法：缓和曲线的圆曲线主点测设与单圆曲线主点测设方法基本相同，ZH、HZ、QZ 的测设方法和精度要求与ZY、YZ、QZ相同。

用直角坐标法（即切线支距法）测设HY、YH点。

如图4.7.1所示，HY、YH点的坐标，按式（4.6.12）、（4.6.13）计算，当l＝l0时，则x、y为：置镜于ZH（HZ）点，后视交点方向，沿视线方向测设x，得HY（HY）点的，得HY（HY）垂足，仪器搬到垂足点，后视切线方向，拨90°角，沿视线测设y点。

一、公路平曲线坐标计算公式1、缓和曲线：Lb1 0{K,D}①T=A2/R ②L=J（K-O）+T ③B=T2 /2/A2 *180/π④M=（L-T）-（L5-T5）/40/A4+（L9-T9）/3456/A8-（L13-T13）/599040/A12+（L17-T17）/17542600/A165.N=(L3-T3)/6/A2-(L7-T7)/336/A6+(L11-T11)/42240/A10-(L15-T15) /9676800/A14+(L19-T19)/3530097000/A18⑥I=(L2-T2)*180/2/A2/π⑦X=C+Mcos(Q-ZB)-ZNsin(Q-ZB)+Dcon(Q+ZI+S)◢⑧Y=F+Msin(Q-ZB)+ZNcos(Q-ZB)+Dsin(Q+ZI+S)◢Goto 0注：A：缘和曲线参数 R：起点半径 J：曲率半径判定值（当曲率半径由小到大取1,否则取-1）（当起点半径到终点半径是由大或无穷大到小取+1，反之则取-1） K：欲求点里程 O：缘和曲线起点里程 C：缘和曲线起点X坐标Q：起始方位角（当J=-1时，方位角应+180。

） Z：偏角判定值(当J=1时，左偏为-1，右偏为1；当J=-1时，左偏为1，右偏为-1) D：距中桩的距离 S：斜交角度 F：缘和曲线起点Y坐标2、圆曲线Lb1 0{K,D}①L=K-0②X=C+R[sin(Q+L/R*180/π)-sinQ]+Dcos(Q+L/R*180/π+S)◢③Y=F-R[cos(Q+L/R*180/π)-cosQ]+Dsin(Q+L/R*180/π+S)◢ Goto 0注：K：欲求点里程 O：圆曲线起点里程 C：圆曲线起点X坐标 R：圆曲线半径 (左偏为负) Q：起始方位角 D：距中桩的距离 S：斜交角度 F：圆曲线起点Y坐标3、直线Lb1 0{K,D}①L=K-0②X=C+LcosQ+Dcos(Q+S)◢③Y=F+LsinQ+Dsin(Q+S)◢Goto 0注：K：欲求点里程 O：直线起点里程 C：直线起点X坐标 Q：起始方位角 D：距中桩的距离 S：斜交角度 F：直线起点Y坐标二、竖曲线计算公式Lb1 0①{K} ②L=K-（0-T）③H=M-IT+LI-ZL2 /2/R◢ Goto 0 注：K：欲求点里程;O：顶点里程;T：切线长;M：顶点高程;I：坡度;Z：竖曲线判定值三、预拱度计算公式Lb1 0①{K} ②H=D-(4D÷B2)×(B/2-(K-O)) 2◢ Goto 0注：D：跨中最大设计预拱度 H：要计算的预拱度 K：欲求点里程桩号（距支座的距离） O：起点桩号 B：本跨净长。

缓和曲线坐标计算公式：
S=L-(L5)/(90×R2×K2)◢ B= L2×180/(6×R×K×π)◢ Q=W＋B◢X=U＋S×CosQ◢ Y=V＋S×SinQ◢
其中：L为缓和曲线起点至计算桩号的弧长，R为缓和曲线后接圆曲线的半径，K为缓曲线总长，W为缓和曲线起点的切线方位角，U为缓和曲线起点的X坐标，V为缓和曲线起点的Y坐标。

左转角半径为负，右转角为正。

圆曲线坐标计算公式：
B=K×90/(R×π)+L×180/(R×π)◢ Q=K/2-(K×K2)/(240×R2)◢P=K2/(24×R)◢ M=R×SinB+Q◢N= R×(1- CosB)+P◢
E=tan-1 (N/M)◢ F=∫(M2+N2 )◢ T=W+E◢X=U+F×CosT◢Y=V+F×SinT◢∫：开根号
K为缓和曲线总长，R为圆曲线半径，L为圆曲线起点至计算点的弧长，W为缓和曲线起点的切线方位角，U为缓和曲线起点的坐标，V 为缓和曲线起点的坐标.
左转角半径为负，右转角为正。

公路缓和曲线计算公式讲解公路缓和曲线是指在设计公路线形时为了使车辆在曲线上能够顺利转弯而采用的一种曲线形式。

在公路设计中，缓和曲线的设计是非常重要的，因为它直接关系到车辆在曲线上的安全行驶和舒适性。

在本文中，我们将对公路缓和曲线的计算公式进行详细的讲解，希望能够帮助大家更好地理解和应用这一知识。

一、缓和曲线的类型。

在公路设计中，常见的缓和曲线类型有三种，分别是圆曲线、过渡曲线和螺旋曲线。

圆曲线是一种由圆弧组成的曲线形式，它的曲率是恒定的。

过渡曲线是一种由直线段和圆弧段组成的曲线形式，它的曲率是逐渐变化的。

螺旋曲线是一种由圆弧和直线段交替组成的曲线形式，它的曲率也是逐渐变化的。

在实际的公路设计中，我们需要根据具体的情况选择合适的缓和曲线类型，以确保车辆在曲线上的安全行驶和舒适性。

二、缓和曲线的计算公式。

1. 圆曲线的计算公式。

在公路设计中，圆曲线的计算是非常常见的。

圆曲线的计算公式如下：L = (V^2) / (127R)。

其中，L表示圆曲线的长度（单位，米），V表示车辆的设计速度（单位，公里/小时），R表示圆曲线的半径（单位，米）。

根据这个公式，我们可以计算出圆曲线的长度，从而确定圆曲线的位置和形状。

2. 过渡曲线的计算公式。

过渡曲线是一种由直线段和圆弧段组成的曲线形式，它的计算公式如下：L = (V^2) / (a)。

其中，L表示过渡曲线的长度（单位，米），V表示车辆的设计速度（单位，公里/小时），a表示过渡曲线的加速度（单位，米/秒^2）。

根据这个公式，我们可以计算出过渡曲线的长度，从而确定过渡曲线的位置和形状。

3. 螺旋曲线的计算公式。

螺旋曲线是一种由圆弧和直线段交替组成的曲线形式，它的计算公式比较复杂。

螺旋曲线的计算需要考虑曲线的曲率变化和车辆的行驶轨迹，因此通常需要借助计算机软件来进行精确计算。

三、缓和曲线的设计原则。

在公路设计中，缓和曲线的设计需要遵循一些基本原则，以确保车辆在曲线上的安全行驶和舒适性。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

平曲线计算公式摘要：一、引言二、平曲线计算公式介绍1.圆曲线2.缓和曲线三、计算方法1.圆曲线计算方法2.缓和曲线计算方法四、实际应用1.在道路设计中的应用2.在铁路设计中的应用五、结论正文：一、引言平曲线计算公式是道路和铁路设计中非常重要的一个概念，它涉及到道路和铁路的曲率半径、超高缓和段长度等关键参数的计算。

本文将详细介绍平曲线计算公式及其在实际工程中的应用。

二、平曲线计算公式介绍平曲线分为圆曲线和缓和曲线两种，下面分别介绍这两种曲线的计算公式。

1.圆曲线圆曲线是最简单的平曲线形式，其计算公式如下：R = (V^2 / g) / (1 + (h / R)^2)其中，R 为曲率半径，V 为设计速度，g 为重力加速度，h 为超高缓和段长度。

2.缓和曲线缓和曲线是为了克服圆曲线在高速行驶时产生的离心力而设计的曲线形式。

缓和曲线的计算公式较为复杂，通常需要通过数值方法求解。

三、计算方法1.圆曲线计算方法根据圆曲线计算公式，可以求解出曲率半径R。

在实际应用中，需要根据设计速度V 和超高缓和段长度h 这两个已知条件，计算出合适的曲率半径R。

2.缓和曲线计算方法缓和曲线的计算方法通常采用数值方法，例如牛顿法、梯度下降法等。

在实际应用中，需要根据设计要求设定初始值，然后通过迭代计算，逐步逼近最优解。

四、实际应用1.在道路设计中的应用平曲线计算公式在道路设计中具有重要意义，它直接影响到道路的行驶安全性、舒适性和经济性。

正确使用平曲线计算公式，可以为道路设计提供科学依据，提高道路设计的质量。

2.在铁路设计中的应用与道路设计类似，平曲线计算公式在铁路设计中也具有重要意义。

在高速列车行驶过程中，平曲线的设置将直接影响到列车的运行安全、舒适性和能耗。

因此，在铁路设计中，需要根据列车设计速度和线路条件，合理设置平曲线，以满足列车运行要求。

五、结论平曲线计算公式是道路和铁路设计中的关键概念，掌握平曲线计算公式对于提高设计质量和保障工程安全具有重要意义。

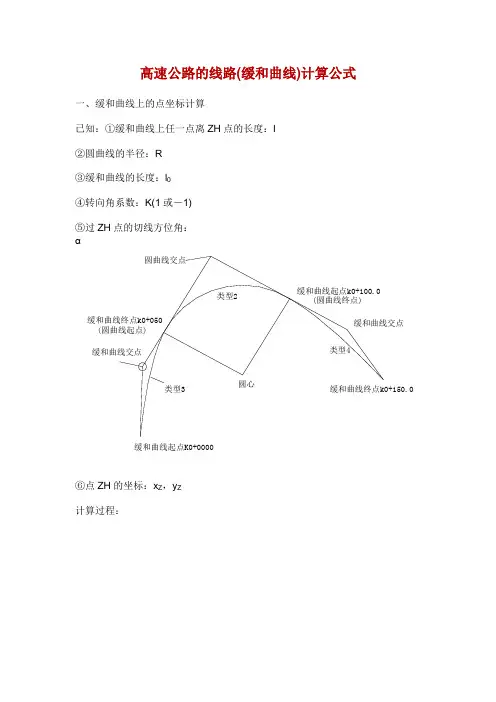
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y ②待求点的切线方位角：αT计算过程：。