当前位置：文档之家 › 半导体物理习题第六章第七章答案

半导体物理习题第六章第七章答案

  • 格式：doc
  • 大小：327.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

半导体物理课后习题答案(精)

半导体物理课后习题答案(精)

第一章习题1．设晶格常数为a的一维晶格，导带极小值附近能量Ec(k)和价带极大值附近能量EV(k)分别为：h2k2h2(k-k1)2h2k213h2k2Ec= +,EV(k)=-3m0m06m0m0m0为电子惯性质量，k1=（1）禁带宽度;（2）导带底电子有效质量;（3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化解：（1）导带：2 2k2 2(k-k1)由+=03m0m03k14d2Ec2 22 28 22=+=>03m0m03m0dk得：k=所以：在k=价带：dEV6 2k=-=0得k=0dkm0d2EV6 2又因为=-<0,所以k=0处，EV取极大值2m0dk2k123=0.64eV 因此：Eg=EC(k1)-EV(0)=412m02=2dECdk23m0 8πa,a=0.314nm。

试求： 3k处，Ec取极小值4 (2)m*nC=3k=k14(3)m*nV 2=2dEVdk2=-k=01m06(4)准动量的定义：p= k所以：∆p=( k)3k=k14 3-( k)k=0= k1-0=7.95⨯10-25N/s42. 晶格常数为0.25nm的一维晶格，当外加102V/m，107 V/m的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：f=qE=h(0-∆t1=-1.6⨯10∆k ∆k 得∆t= ∆t-qEπa)⨯10)=8.27⨯10-13s2-19=8.27⨯10-8s (0-∆t2=π-1.6⨯10-19⨯107第三章习题和答案100π 21. 计算能量在E=Ec到E=EC+ 之间单位体积中的量子态数。

*22mLn31*2V（2mng(E)=(E-EC)2解232πdZ=g(E)dEdZ 单位体积内的量子态数Z0=V22100π 100h Ec+Ec+32mnl8mnl1*2（2mn1V Z0=g(E)dE=⎰(E-EC)2dE23⎰VEC2π EC 23100h*2 =V（2mn2(E-E)Ec+8m*L2Cn32π2 3Ecπ =10003L32. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

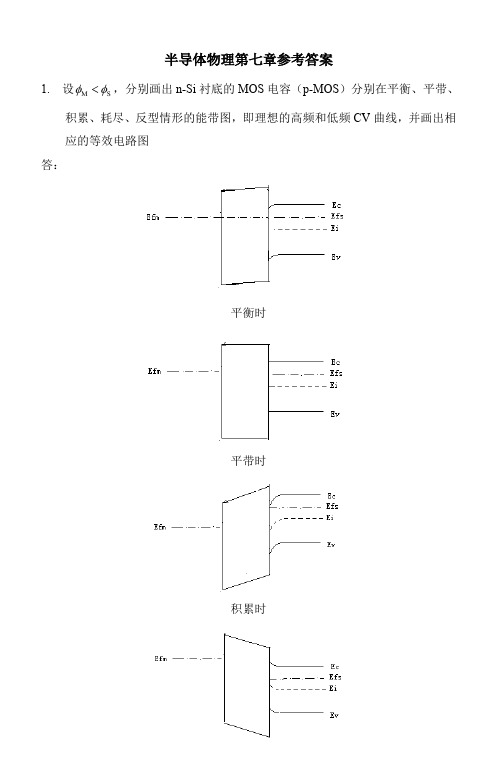
半导体物理第七章参考答案

半导体物理第七章参考答案

半导体物理第七章参考答案1. 设M S φφ<，分别画出n-Si 衬底的MOS 电容（p-MOS ）分别在平衡、平带、积累、耗尽、反型情形的能带图，即理想的高频和低频CV 曲线，并画出相应的等效电路图 答：平衡时平带时积累时耗尽时弱反时强反时理想的高频和低频CV曲线等效电路图2. 设氧化层厚度为1μm 的Si MOS 结构的p 型衬底的掺杂浓度分别为N ＝1015/cm 3和1016/cm 3，比较这两种结构的耗尽层电容和MOS 电容的极小值。

答：1) 耗尽层电容由耗尽层厚度决定，而耗尽层厚度与Si 表面势有关，根据耗尽层厚度、表面势，可求得耗尽层电容为：()d Sid sdd Q C d W εψ-==又由MOS 电容为氧化层电容与耗尽层电容串联而成：dox C C C 111+= 以及栅压方程：g fb s oxV V ψ-=消去表面势s ψ，可得：C =显然，相同氧化层厚度，即相同氧化层电容，相同栅压下，衬底掺杂浓度高的MOS 结构耗尽层电容大。

2) 由C =MOS 电容的极小值出现在强反型时，此时耗尽层厚度最大，表面势为2B φ：max d W ==min maxSid d C W ε==则：1minmin 11ox d C C C -⎛⎫=+ ⎪⎝⎭当N ＝1015/cm 3时，12min min 1126.7ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭当N ＝1016/cm 3时，12min min 1131.3ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭3. 从物理上说明F B i C C 随氧化层厚度及掺杂浓度的变化趋势，并计算315/10cm N =，nm t ox 10=的Si MOS 结构的FB i C C 值和德拜长度。

答：由公式：11ox D FB i Si ox t L C C εε=+=+有：11FB D i iSi C L C C ε==+ 其中oxi oxC t ε=。

半导体物理习题答案

半导体物理习题答案

第一章半导体中的电子状态例1.证明:对于能带中的电子，K状态和-K状态的电子速度大小相等,方向相反。

即：v(k)= －v(－k)，并解释为什么无外场时，晶体总电流等于零。

解：K状态电子的速度为：（1）同理，－K状态电子的速度则为：（2）从一维情况容易看出：（3）同理有：（4）（5）将式（3）（4）（5）代入式（2）后得：（6）利用（1）式即得：v(－k)= －v(k)因为电子占据某个状态的几率只同该状态的能量有关，即：E(k)=E(－k)故电子占有k状态和-k状态的几率相同，且v(k)=－v(－k)故这两个状态上的电子电流相互抵消，晶体中总电流为零。

例2.已知一维晶体的电子能带可写成：式中，a为晶格常数。

试求：（1）能带的宽度；（2）能带底部和顶部电子的有效质量。

解：（1）由E(k)关系（1）（2）令得：当时，代入（2）得：对应E(k)的极小值。

当时，代入（2）得：对应E(k)的极大值。

根据上述结果，求得和即可求得能带宽度。

故：能带宽度（3）能带底部和顶部电子的有效质量：习题与思考题：1 什么叫本征激发？温度越高，本征激发的载流子越多，为什么？试定性说明之。

2 试定性说明Ge、Si的禁带宽度具有负温度系数的原因。

3 试指出空穴的主要特征。

4 简述Ge、Si和GaAs的能带结构的主要特征。

5 某一维晶体的电子能带为其中E0=3eV，晶格常数a=5×10-11m。

求：（1）能带宽度；（2）能带底和能带顶的有效质量。

6原子中的电子和晶体中电子受势场作用情况以及运动情况有何不同？原子中内层电子和外层电子参与共有化运动有何不同？7晶体体积的大小对能级和能带有什么影响？8描述半导体中电子运动为什么要引入“有效质量”的概念？用电子的惯性质量描述能带中电子运动有何局限性？9 一般来说，对应于高能级的能带较宽，而禁带较窄，是否如此？为什么？10有效质量对能带的宽度有什么影响？有人说：“有效质量愈大，能量密度也愈大，因而能带愈窄。

半导体物理作业(六)答案

半导体物理作业(六)答案

两边杂质浓度为 N A = 1016 cm −3 ， N D = 1020 cm −3 ，求温度 300K 时的势垒高度和势 垒宽度。
VD = kT N A N D 1016 × 10 20 0 . 026 ln = ln = 0.026 × ln 9.61168781× 1015 =0.9568 (V) 2 2 10 q ni 1.02 × 10
τp
半导体物理作业（六）
学号：
姓名：
4/6 页
(1.02 ×10 ) =
9 × 10
14
10 2
× 1.602 × 10 −19 ×
0.026 × 460 =6.40×10-11（A/cm2） −6 10
.3 ⎛ qV ⎞ ⎛ 0.0026 ⎞ -6 2 kT ⎜ ⎟ ⎜ 3) J = J s ⎜ e − 1⎟ = 0.16 × ⎜ e − 1⎟ ⎟ =6.5×10 （A/cm ） ⎝ ⎠ ⎝ ⎠
qD p pn 0 Lp =
=
μ p N A μ nτ n N A μ pτ n 5 × 1017 × 460 × 1 = =508 = μ n N D μ pτ p N D μ nτ p 9 × 1014 × 550 × 1
q kTμ p
2） J s ≈
Dp kTμ p ni2 n2 n2 = i q = i q τp qτ p ND ND ND
qD p qDn n p0 + pn 0 Ln Lp
半导体物理作业（六）
学号：
姓名：
2/6 页
2. 若 N D = 5 ×1015 cm −3 , N A = 1017 cm−3 ，求室温下 Ge 突变 pn 结的 VD。(300K 时锗 的本征载流子浓度为 2.33×1013 cm-3) 解： VD =

半导体物理学第七版完整答案修订版

半导体物理学第七版完整答案修订版

半导体物理学第七版完整答案修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E C （K ）=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ （1）禁带宽度;（2）导带底电子有效质量;（3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化解：（1）2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a ）(100)晶面 （b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=（， 式中a 为 晶格常数，试求（1）布里渊区边界；（2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π= （n=0，?1，?2…）进一步分析an k π)12(+= ，E （k ）有极大值，ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()mak E k E MINMAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==（4）电子的有效质量能带底部 an k π2=所以m m n2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

《半导体物理学》刘恩科、朱秉生版上海科技1-12章课后答案

《半导体物理学》刘恩科、朱秉生版上海科技1-12章课后答案

第 1 页第一章 半导体中的电子状态1. 设晶格常数为 a 的一维晶格，导带极小值附近能量 E c （k ）和价带极大值附近 能量 E v （k ）分别为：E c (k)=2 2h k + 3m 02h (k − m 0k1) 2和 E v (k)= 2 2h k － 6m 0322h k ； m 0m 0为电子惯性质量，k 1＝1/2a ；a ＝0.314nm 。

试求： ①禁带宽度；②导带底电子有效质量； ③价带顶电子有效质量；④价带顶电子跃迁到导带底时准动量的变化。

[解] ①禁带宽度 Eg22h k − k ＝0；可求出对应导带能量极小值 E min的 k 值：根据 dEc (k ) ＝2h k ＋2( dk 3m 0m 03 ，1 )k min＝ k 14由题中 E C式可得：E min＝E C(K)|k=k min=h k 2；m 401 由题中 E V式可看出，对应价带能量极大值 Emax 的 k 值为：k max＝0；2 2 2h 2并且 E min＝E V(k)|k=k max＝k ；∴Eg ＝E min－E max＝hk 1＝ h 21 6m 12m48m a 20 −27 20 0＝×−28× (6.62 ×10) −8 2 ×× −11＝0.64eV48 × 9.1 10(3.14 ×10 1.6 10②导带底电子有效质量 m n22 2 22d E C= 2h + 2h = 8h ；∴ m n＝ h2 / d E C =3 m 0dk 23m 0 m 0 3m 0dk 28 ③价带顶电子有效质量 m ’222d E V= −6h'=，∴ mh2/ d E V= − 1 mdk 2m 0ndk 2 6 0④准动量的改变量h△k ＝ h (k min-k max)=3 4h k1=3h 8a2. 晶格常数为 0.25nm 的一维晶格，当外加 102V/m ，107V/m 的电场时，试分别 计算电子自能带底运动到能带顶所需的时间。

半导体物理与器件习题

半导体物理与器件习题

半导体物理与器件习题目录半导体物理与器件习题 (1)一、第一章固体晶格结构 (2)二、第二章量子力学初步 (2)三、第三章固体量子理论初步 (2)四、第四章平衡半导体 (3)五、第五章载流子输运现象 (5)六、第六章半导体中的非平衡过剩载流子 (5)七、第七章pn结 (6)八、第八章pn结二极管 (6)九、第九章金属半导体和半导体异质结 (7)十、第十章双极晶体管 (7)十一、第十一章金属-氧化物-半导体场效应晶体管基础 (8)十二、第十二章MOSFET概念的深入 (9)十三、第十三章结型场效应晶体管 (9)一、第一章固体晶格结构1．如图是金刚石结构晶胞，若a 是其晶格常数，则其原子密度是。

2．所有晶体都有的一类缺陷是：原子的热振动，另外晶体中常的缺陷有点缺陷、线缺陷。

3．半导体的电阻率为10-3～109Ωcm。

4．什么是晶体？晶体主要分几类？5．什么是掺杂？常用的掺杂方法有哪些？答：为了改变导电性而向半导体材料中加入杂质的技术称为掺杂。

常用的掺杂方法有扩散和离子注入。

6．什么是替位杂质？什么是填隙杂质？7．什么是晶格？什么是原胞、晶胞？二、第二章量子力学初步1．量子力学的三个基本原理是三个基本原理能量量子化原理、波粒二相性原理、不确定原理。

2．什么是概率密度函数？3．描述原子中的电子的四个量子数是：、、、。

三、第三章固体量子理论初步1．能带的基本概念◼能带（energy band）包括允带和禁带。

◼允带（allowed band）：允许电子能量存在的能量范围。

◼禁带（forbidden band）：不允许电子存在的能量范围。

◼允带又分为空带、满带、导带、价带。

◼空带（empty band）：不被电子占据的允带。

◼满带（filled band）：允带中的能量状态（能级）均被电子占据。

导带：有电子能够参与导电的能带，但半导体材料价电子形成的高能级能带通常称为导带。

价带:由价电子形成的能带，但半导体材料价电子形成的低能级能带通常称为价带。

半导体物理习题答案完整版

半导体物理习题答案完整版

半导体物理习题答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第一章半导体中的电子状态例1.证明:对于能带中的电子，K状态和-K状态的电子速度大小相等,方向相反。

即：v(k)= －v(－k)，并解释为什么无外场时，晶体总电流等于零。

解：K状态电子的速度为：（1）同理，－K状态电子的速度则为：（2）从一维情况容易看出：（3）同理有：（4）（5）将式（3）（4）（5）代入式（2）后得：（6）利用（1）式即得：v(－k)= －v(k)因为电子占据某个状态的几率只同该状态的能量有关，即：E(k)=E(－k)故电子占有k状态和-k状态的几率相同，且v(k)=－v(－k)故这两个状态上的电子电流相互抵消，晶体中总电流为零。

例2.已知一维晶体的电子能带可写成：式中，a为晶格常数。

试求：（2）能带底部和顶部电子的有效质量。

解：（1）由E(k)关系（1）（2）令得：当时，代入（2）得：对应E(k)的极小值。

当时，代入（2）得：对应E(k)的极大值。

根据上述结果，求得和即可求得能带宽度。

故：能带宽度（3）能带底部和顶部电子的有效质量：习题与思考题：1 什么叫本征激发温度越高，本征激发的载流子越多，为什么试定性说明之。

2 试定性说明Ge、Si的禁带宽度具有负温度系数的原因。

3 试指出空穴的主要特征。

4 简述Ge、Si和GaAs的能带结构的主要特征。

5 某一维晶体的电子能带为其中E0=3eV，晶格常数a=5×10-11m。

求：（2）能带底和能带顶的有效质量。

6原子中的电子和晶体中电子受势场作用情况以及运动情况有何不同原子中内层电子和外层电子参与共有化运动有何不同7晶体体积的大小对能级和能带有什么影响？8描述半导体中电子运动为什么要引入“有效质量”的概念？用电子的惯性质量描述能带中电子运动有何局限性？9 一般来说，对应于高能级的能带较宽，而禁带较窄，是否如此为什么10有效质量对能带的宽度有什么影响？有人说：“有效质量愈大，能量密度也愈大，因而能带愈窄。

半导体物理学(刘恩科第七版)课后习题答案

半导体物理学(刘恩科第七版)课后习题答案
第一章习题
1．设晶格常数为 a 的一维晶格，导带极小值附近能量 Ec(k)和价带极大值附近 能量 EV(k)分别为： h 2 k 2 h 2 ( k k1 ) 2 h 2 k 21 3h 2 k 2 Ec= , EV (k ) 3m0 m0 6m0 m0 m0 为电子惯性质量，k1
1
在E ~ E dE空间的状态数等于k空间所包含的 状态数。 即d z g (k ' ) Vk ' g (k ' ) 4k ' dk 2( m m m ) 1 3 2 1 dz ' t t l ( E Ec ) 2 V g (E) 4 2 dE h 对于si导带底在100个方向，有六个对称的旋转椭球， 锗在（ 111）方向有四个，
解： （1）由
dE (k ) n 0 得 k dk a
（n=0，1，2…） 进一步分析 k ( 2n 1)

a
，E（k）有极大值，
E（k ) MAX k 2n
2 2 ma 2

a
时，E（k）有极小值
所以布里渊区边界为 k ( 2n 1)

a
2 2 ma 2
7. 锑化铟的禁带宽度 Eg=0.18eV，相对介电常数r=17，电子的有效质量
m* n =0.015m0, m0 为电子的惯性质量，求①施主杂质的电离能，②施主的弱束
缚电子基态轨道半径。
解：根据类氢原子模型：
* 4 * mn q mn E0 13.6 E D 0.0015 2 7.1 10 4 eV 2 2 2 m0 r 2(4 0 r ) 17
(2)能带宽度为 E（k ) MAX E ( k ) MIN (3）电子在波矢 k 状态的速度 v （4）电子的有效质量

半导体物理 课后习题答案

半导体物理 课后习题答案

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2） 导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。

解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C 22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**）（）（单位体积内的量子态数）（2. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

半导体物理参考答案第六章

半导体物理参考答案第六章

= − qNd 2ε n
(x
+
xn )2
+ ϕin (−xn )
ϕip (x)=
qNa εp
(x
−
xp )2
+ ϕin (xp )
则：
ϕin =
ϕin (−xn ) − ϕin (0) =
qNd 2ε n
xn 2
ϕip
=ϕin (0) − ϕin (xp )
=qNa 2ε p
xp2
(−xn ≤ x ≤ 0) (0 < x ≤ xp )
xp2
Байду номын сангаас
则耗尽层厚度为：
xp
=
( 2φsε Si qNa
1
)2
7.试求出肖特基二极管的接触电阻表达式，并讨论和降低接触电阻、形成欧姆接 触的有效途径。
解：通过肖特基二极管的电流为 I ≈ I0 eqVA kT −1
其中 I0
=
Aq2Dn NC kT
[ 2qNd (φi ε Si
−
VA
)
1
]2

d
ϕ2 ip
dx2
=
qNa εp
(−xn ≤ x ≤ 0) (0 < x ≤ xp )
在 x= −xn 和 x= xp 处电场为零，即：
− dϕin
= − dϕip = 0
dx x= − xn
dx x=xp
电中性条件：
qNd xn
=
qNa xp ，得
xn xp
=
Na Nd
解泊松方程得：
ϕin (x)
(−xn ≤ x ≤ 0) (0 < x ≤ xp )

半导体物理学习题答案（有目录）

半导体物理学习题答案（有目录）

半导体物理学习题答案（有目录）半导体物理习题解答目录1－1．（P32）设晶格常数为a的一维晶格，导带极小值附近能量E c（k）和价带极大值附近能量E v（k）分别为： (2)1－2．（P33）晶格常数为0.25nm的一维晶格，当外加102V/m，107V/m的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

(3)3－7．（P81）①在室温下，锗的有效状态密度Nc＝1.05×1019cm－3，Nv＝5.7×1018cm－3，试求锗的载流子有效质量mn*和mp*。

(3)3－8．（P82）利用题7所给的Nc和Nv数值及Eg＝0.67eV，求温度为300k和500k时，含施主浓度ND＝5×1015cm-3，受主浓度NA＝2×109cm-3的锗中电子及空穴浓度为多少？ (4)3－11．（P82）若锗中杂质电离能△ED＝0.01eV，施主杂质浓度分别为ND＝1014cm-3及1017cm-3，计算(1)99%电离，(2)90%电离，(3)50%电离时温度各为多少？ (5)3－14．（P82）计算含有施主杂质浓度ND＝9×1015cm-3及受主杂质浓度为1.1×1016cm-3的硅在300k 时的电子和空穴浓度以及费米能级的位置。

(6)3－18．（P82）掺磷的n型硅，已知磷的电离能为0.04eV，求室温下杂质一般电离时费米能级的位置和磷的浓度。

(7)3－19．（P82）求室温下掺锑的n型硅，使EF＝(EC＋ED)/2时的锑的浓度。

已知锑的电离能为0.039eV。

(7)3－20．（P82）制造晶体管一般是在高杂质浓度的n型衬底上外延一层n型的外延层，再在外延层中扩散硼、磷而成。

①设n型硅单晶衬底是掺锑的，锑的电离能为0.039eV，300k时的EF位于导带底下面0.026eV处，计算锑的浓度和导带中电子浓度。

(8)4－1．（P113）300K时，Ge的本征电阻率为47Ω.cm，如电子和空穴迁移率分别为3900cm2/V.S和1900cm2/V.S，试求本征Ge的载流子浓度。

半导体物理 课后习题答案

半导体物理 课后习题答案

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2） 导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。

解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C 22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**）（）（单位体积内的量子态数）（2. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

半导体物理课后习题(保密)

半导体物理课后习题(保密)

解: 须先求出本征载流子浓度ni，即
代入数据得，ni=1.86 ×1013cm-3 根据电中性条件有 p0+ND+=n0+NA-
ni
q( n p )
i

1 i ( n p )
联立 载流子浓度公式
n0p0=ni2
可求解得 n0=3.89 ×1013cm-3, p0=8.89 ×1012cm-3 所以样品的电导率为：
解: 由图3-7查得T=500k时，Si的本征载流子浓度ni=3.5×1014cm-3 联立方程
p0=ni2/n0
解得， ND=3.5×1014cm-3时，n0≈4.3×1014cm-3, p0=2.8×1014cm-3 —— n0,p0差别不显著，杂质导电特性不很明显 ND=1012cm-3时，n0≈ni=3.5×1014cm-3, p0=3.5×1014cm-3,即n0=p0. —— 进入本征 半导体材料在某一温度下所处的区域与杂质浓度相关 或 杂质浓度不同，材料进入同一区域所需要的温度不一样。
m0为电子惯性质量，k1=1/2a; a=0.314nm。试求： （1）禁带宽度； （2）导带底电子有效质量； （3）价带顶电子有效质量； （4）价带顶电子跃迁到导带底时准动量的变化。
练习2-课后习题2
第一章 半导体中的电子状态
2.晶格常数为0.25nm的一维晶格，当外加102V/m和107V/m 的电 场时，试分别计算电子自能带底运动到能带顶所需的时间。
作业-课后习题14
第三章 半导体中载流子的统计分布
计算含有施主杂质浓度ND=9×1015cm-3与受主杂质浓度为1.1×1016cm-3 的硅在室温时的电子和空穴浓度以及费米能级的位置。

半导体物理 课后习题答案解析

半导体物理 课后习题答案解析

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2） 导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。

解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C 22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**）（）（单位体积内的量子态数）（2. 试证明实际硅、锗中导带底附近状态密度公式为式（3-6）。

电子科技大学-半导体物理答案

电子科技大学-半导体物理答案

第一篇 半导体中的电子状态习题1-1、 什么叫本征激发？温度越高，本征激发的载流子越多，为什么？试定性说明之。

1-2、 试定性说明Ge 、Si 的禁带宽度具有负温度系数的原因。

1-3、试指出空穴的主要特征。

1-4、简述Ge 、Si 和GaAS 的能带结构的主要特征。

1-5、某一维晶体的电子能带为[])sin(3.0)cos(1.01)(0ka ka E k E --=其中E 0=3eV ，晶格常数a=5х10-11m 。

求：（1） 能带宽度；（2） 能带底和能带顶的有效质量。

题解：1-1、 解：在一定温度下，价带电子获得足够的能量（≥E g ）被激发到导带成为导电电子的过程就是本征激发。

其结果是在半导体中出现成对的电子-空穴对。

如果温度升高，则禁带宽度变窄，跃迁所需的能量变小，将会有更多的电子被激发到导带中。

1-2、 解：电子的共有化运动导致孤立原子的能级形成能带，即允带和禁带。

温度升高，则电子的共有化运动加剧，导致允带进一步分裂、变宽；允带变宽，则导致允带与允带之间的禁带相对变窄。

反之，温度降低，将导致禁带变宽。

因此，Ge 、Si 的禁带宽度具有负温度系数。

1-3、 解：空穴是未被电子占据的空量子态，被用来描述半满带中的大量电子的集体运动状态，是准粒子。

主要特征如下：A 、荷正电：+q ；B 、空穴浓度表示为p （电子浓度表示为n ）；C 、E P =-E nD 、m P *=-m n *。

1-4、 解：（1） Ge 、Si:a ）Eg (Si ：0K) = 1.21eV ；Eg (Ge ：0K) = 1.170eV ；b ）间接能隙结构c ）禁带宽度E g 随温度增加而减小；（2） GaAs ：a ）E g （300K ）= 1.428eV ，Eg (0K) = 1.522eV ；b ）直接能隙结构；c ）Eg 负温度系数特性： dE g /dT = -3.95×10-4eV/K ；1-5、 解：（1） 由题意得：[][])sin(3)cos(1.0)cos(3)sin(1.002220ka ka E a kd dEka ka aE dk dE +=-=eVE E E E a kd dEa k E a k d dEa k a k a k ka tg dkdE o ooo1384.1min max ,01028.2)4349.198sin 34349.198(cos 1.0,4349.198,01028.2)4349.18sin 34349.18(cos 1.0,4349.184349.198,4349.1831,04002222400222121=-=∆<⨯-=+==>⨯=+====∴==--则能带宽度对应能带极大值。

刘恩科半导体物理第六章课后习题最全答案

刘恩科半导体物理第六章课后习题最全答案
①
d 2V x 0 2 dx dV x x c dx
令 V 0 0 ，则 A 0 ，V x cx
E(x) c<0 0 V(x) x c>0 c>0
dV x V x dx x dx cx A dx
2 11.6 8.85 10 14 0.94 19 16 1.6 10 10
1 2
12.2 10

1 10 2

3.5 105 cm
（2） 画出 x 和 V x 的图线
+ + + + + + + + V + + + + + + + +
kT n ， p kT p ，Ln Dn n ， 又 Dn D q q L p D p p
Jp Jn D p N A Ln Dn N D L p


p N A Dn n n N D D p p
p N A n n n N D p p

1.56 10 x 3.47 10
9
5
V
cm
2
2 x
dV x dx
2

qN D x n
1.56 109 x 3.47 109 V cm2
V1 x qN A x 2 r 0
8 2 p
r 0
J s 400 6 10 1.6 10 5 J s 300 1.5 10 10
12 2
解法二：

半导体物理课后习题答案(1-12章)

半导体物理课后习题答案(1-12章)
h2 k12 h 2 k12 h2 并且 Emin＝EV(k)|k=kmax＝ ；∴Eg＝Emin－Emax＝ ＝ 48m0 a 2 12m0 6 m0
＝
(6.62 × 10 − 27 ) 2 ＝0.64eV 48 × 9.1 × 10 − 28 × (3.14 × 10 − 8 ) 2 × 1.6 × 10 − 11
② 77k 时，由（3－46）式得到： Ec － ED ＝ 0.01eV ； T ＝ 77k ； k0 ＝ 1.38×10-23J/K; n0 ＝ 1017 cm − 3 ； Nc ＝ 1.365×1019cm-3； Po 可忽略不计，由于 n 0 = n D ，即
° m0 q 4 ε 0 h2 = 13.6 e V a = = 0.53A ， 0 8ε r2 h2 m0 e2π
∗ 当 ε r = 11.1 ， m p = 0.86m0 时
m∗p E0 13.6 ∆ EA = � 2 � 0.86 m0 ε r 11.12 r1, p = ε r (
9.49 10− 2 eV
( 2mdn ) 4π V
h3
32
(E−
Ec ) 2
1
蝌
E1
E2
dZ = 4π
32
( 2mdn )
h3
32
骣 h2 Ec + 100 琪 ∗ 2 琪8 m L 桫 n Ec 3 2
(E−
Ec ) 2 dE
1
( 2mdn )
h3
2 骣 h2 创 琪100 ∗ 2 3 桫 8mn L
故： Z=1000π 3L3 7. ① 在室温下，锗的有效状态密度 Nc＝1.05×1019cm－3，Nv＝5.7×1018cm－3， 试求锗的载流子有效质量 mn*和 mp*。计算 77k 时的 Nc 和 Nv。已知 300k 时，Eg＝
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第6章 p-n 结1、一个Ge 突变结的p 区和n 区掺杂浓度分别为N A =1017cm -3和N D =5⨯1015cm -3，求该pn 结室温下的自建电势。

解：pn 结的自建电势 2(ln )D A D iN N kTV q n =已知室温下，0.026kT =eV ，Ge 的本征载流子密度1332.410 cm i n -=⨯代入后算得：1517132510100.026ln 0.36(2.410)D V V ⨯⨯=⨯=⨯ 4.证明反向饱和电流公式（6-35）可改写为20211()(1)i s n n p pb k T J b q L L σσσ=++ 式中npb μμ=，n σ和p σ分别为n 型和p 型半导体电导率，i σ为本征半导体电导率。

证明：将爱因斯坦关系式p p kT D q μ=和n n kT D qμ=代入式（6-35）得 0000()p n pnS p n n p npn pp nn p J kTn kTp kT L L L L μμμμμμ=+=+因为002i p p n n p =，02i n n n p n =，上式可进一步改写为221111()()S n p i n p i n p p p n n n pp nJ kT n qkT n L p L n L L μμμμμμσσ=+=+又因为()i i n p n q σμμ=+22222222()(1)i i n p i p n q n q b σμμμ=+=+即22222222()(1)i i i n p p n q q b σσμμμ==++ 将此结果代入原式即得证2222221111()()(1)(1)n p i i S p n p p n n p p nqkT b kT J q b L L q b L L μμσσμσσσσ=+=⋅⋅+++ 注：严格说，迁移率与杂质浓度有关，因而同种载流子的迁移率在掺杂浓度不同的p 区和n区中并不完全相同，因而所证关系只能说是一种近似。

5.一硅突变pn 结的n 区ρn =5Ω⋅cm ，τp =1μs ；p 区ρp =0.1Ω⋅cm ，τn =5μs ，计算室温下空穴电流与电子电流之比、饱和电流密度，以及在正向电压0.3V 时流过p-n 结的电流密度。

解：由5n cm ρ=Ω⋅，查得143910D N cm -=⨯，3420/p cm V s μ=⋅由0.1p cm ρ=Ω⋅，查得173510A N cm -=⨯，3500/n cm V s μ=⋅ ∴由爱因斯坦关系可算得相应的扩散系数分别为2142010.5 cm /40p p kT D s q μ==⨯=，2150012.5 cm /40n n kT D s q μ==⨯= 相应的扩散长度即为33.2410p L cm -===⨯37.910n L cm -===⨯对掺杂浓度较低的n 区，因为杂质在室温下已全部电离，0143910n n cm -=⨯，所以0021025314(1.510) 2.510910i n n n p cm n -⨯===⨯⨯ 对p 区，虽然N A =5⨯1017cm -3时杂质在室温下已不能全部电离，但仍近似认为p p0=N A ，0021022317(1.510) 4.510510i p p n n cm p -⨯===⨯⨯ 于是，可分别算得空穴电流和电子电流为∴0195UU 31.61010.52.510(1)(1)3.2410q q n kTkTp PPp J qD ee L --⨯⨯⨯⨯=-=-⨯101.3010(1)qVkTe-=⨯-019231.61012.5 4.510(1)(1)7.910qVqV p kTkTn nnn J qD ee L --⨯⨯⨯⨯=-=-⨯131.1410(1)qVkTe-=⨯-空穴电流与电子电流之比 103131.3010 1.14101.1410pn J J --⨯==⨯⨯饱和电流密度：0010131021.3010 1.1410 1.3010/n p S PnPnp n J qD qD A cm L L ---=+=⨯+⨯=⨯当U =0.3V 时：0.30.310100.0260.026(1) 1.3010(1) 1.3010qVkTS J J eee--=-=⨯⨯-=⨯⨯=521.2910A /cm -⨯6．条件与上题相同，计算下列电压下的势垒区宽度和单位面积上的势垒电容： ①－10V ；②0V ；③0.3V 。

解：对上题所设的p +n 结，其势垒宽度D X ===式中，1417021021910510()ln 0.026ln 0.74(1.510)n p A D D F F i k T N N V E E V q q n ⋅⨯⨯⨯=-===⨯ 外加偏压U 后，势垒高度D V 变为()D V U -，因而 ① U =－10V 时，势垒区宽度和单位面积势垒电容分别为43.9410D X cm -===⨯ 14920411.68.8510 2.610 F/cm 3.9410r T DC x εε---⨯⨯===⨯⨯ ② U =0V 时，势垒区宽度和单位面积势垒电容分别为41.0310D x cm -==⨯ 1492411.68.85109.9710 F/cm 1.0310T C ---⨯⨯==⨯⨯ ③ U =0.3V57.9710D x cm -==⨯ 正向偏压下的pn 结势垒电容不能按平行板电容器模型计算，但近似为另偏压势垒电容的4倍，即982T 4(0)49.9710410 F/cm T C C --==⨯⨯=⨯7.计算当温度从300K 增加到400K 时，硅pn 结反向电流增加的倍数。

解：根据反向饱和电流J S 对温度的依赖关系（讲义式(6－26)或参考书p.193）：(3/2)(0)exp()g S E J TkTγ+∝-式中，E g (0)表示绝对零度时的禁带宽度。

由于3/2T γ+比其后之指数因子随温度的变化缓慢得多，S J 主要是由其指数因子决定，因而1.24 1.2440012.4512001.24300(400) 2.4310(300)kS k S kJ K ee e J K e --====⨯12、分别计算硅p +n 结在平衡和反向电压45V 时的最大电场强度。

已知V D =0.7V ，153510D N cm -=⨯。

解：势垒宽度：D X ==⑴平衡时，即U=0V 时54.2710D X cm -==⨯ 最大场强：191554141.610510 4.2710 3.3310/8.851011.6B mm r qN X V cm εεε---⨯⨯⨯⨯⨯===⨯⨯⨯ ⑵45D V V =-时：43.4510D X cm -==⨯ 最大场强191545141.610510 3.45102.710/8.851011.6B mm r qN X V cm εεε---⨯⨯⨯⨯⨯===⨯⨯⨯ 13. 求题5所给硅p +n 的反向击穿电压、击穿前的空间电荷区宽度及其中的平均电场强度。

解：按突变结击穿电压与低掺杂区电阻率的关系，可知其雪崩击穿电压U B = 95.1443ρ＝95.14⨯751/4=318 V或按其n 区掺杂浓度9⨯1014/cm 3按下式算得U B =603164(10/)B N =60⨯ (100/9)3/4=365（V ）二者之间有计算误差。

以下计算取300V 为击穿前的临界电压。

击穿前的空间电荷区宽度32.110cm D X -===⨯ 空间电荷区中的平均电场强度53300/ 1.4310 V /cm 2.110B D E U X -===⨯⨯ 注：硅的临界雪崩击穿电场强度为3⨯105 V/cm ，计算结果与之基本相符。

14.设隧道长度40x nm = ，求硅、锗、砷化镓在室温下电子的隧穿几率。

解：隧穿几率])2(38exp[2/12*x h E m P g n ∆-=π⑴对硅：*01.08n m m =， 1.12g E ev =，121 1.610ev -=⨯尔格128212830.714227282 1.089.110P exp[()(1.12 1.610)410] 4.65103(6.6210)e π------⨯⨯⨯=-⋅⋅⨯⨯⋅⨯==⨯⨯ ⑵对锗：*00.56n m m =，0.67g E ev =128212816.782272820.569.110exp[()(0.67 1.610)410] 5.4103(6.6210)p e π-----⨯⨯⨯=-⋅⋅⨯⨯⋅⨯==⨯⨯ ⑶对砷化镓：*00.068n m m =， 1.35g E ev =12821288.2742272820.0689.110exp[()(1.35 1.610)410] 2.5103(6.6210)p e π------⨯⨯⨯=-⋅⋅⨯⨯⋅⨯==⨯⨯ 第7章 金属和半导体的接触1、求Al-Cu 、Au-Cu 、W-Al 、Cu-Ag 、Al-Au 、Mo-W 、Au-Pt 的接触电势差，并标出电势的正负。

对功函数不同的两种材料的理想化接触，其接触电势差为：()()A B B AAB A B W W W W V V V q q q-=-=---=故： 4.59 4.180.41Cu Al Al Cu W W V ev q q ---=== 4.59 5.200.61Cu Au Au Cu W W V ev q q ---===- 4.18 4.550.37Al W W Al W W V ev q q---===- 4.42 4.590.17Ag CuCu Ag W W V ev qq---===- 5.20 4.181.02Au Al Al Au W W V ev q q ---=== 4.59 4.180.34W Mo Mo W W W V ev q q ---=== 5.43 5.200.23Pt Au Au Pt W W V ev q q---=== 2、两种金属A 和B 通过金属C 相接触，若温度相等，证明其两端a 、b 的电势差同A 、B 直接接触的电势差一样。

如果A 是Au ，B 是Ag ，C 是Cu 或Al ，则V ab 为多少伏？解：∵温度均相等，∴不考虑温差电动势∵C A AC W W V q -=，B CCB W W V q-= 两式相加得：B AAC CB AB W W V V V q-==＋ 显然，V AB 与金属C 无关。

若A 为Au ，B 为Ag ，C 为Al 或Cu ，则V AB 与Cu 、Al 无关，其值只决定于W Au =5.2eV ，W Ag =4.42eV ，即4.425.200.78V Ag AuAu Ag W W V qq---===- 3、求N D =1017cm -3的n 型硅在室温下的功函数。

相关主题