四川大学2009数学分析

四川大学2009年攻读硕士学位研究生入学考试题一、解答下列各题.1.（5分）设)(x f 是数域F 上次数为2008的多项式，证明：20092不可能是)(x f 的根.F 为有理数域该命题成立如题：设)(x f 是有理数域Q 上一个m 次多项式（0≥m ），n 是大于m 的正整数，证明：n2不可能是)(x f 的根.证明：反证法：假设n2是)(x f 的根，有)2()2(--n nx x 对于2-nx ，存在素数2=p110,,,-n a a a p Λ、p 不能整除n a 、2p 不能整除0a由艾森斯坦判别法，有2-nx 在有理数域不可约，则有)()2(x f x n -则n x f ≥∂))((与题设矛盾，故假设不成立，即n 2不可能是)(x f 的根.2.(10分)用代数基本定理证明，实数域R 上的任意不可约多项式只能是一次多项式或满足042<-ac b 的二次多项式：c bx ax ++2.证明：由代数基本定理，任意多项式在复数域都可以分解为一次多项式的乘积 则令多项式为)())(()(21n a x a x a x k x f ---=Λ （C a i ∈，R k ∈且0≠k ） 当R a i ∈时，则i a x -是实数域R 上的一次不可约多项式当R a i ∉时，有i a 也是)(x f 的根，有i i i i i i a a x a a x a x a x ++-=--)())((2i i i i a a x a a x ++-)(2满足042<-ac b由)(i i a a +-，R a a i i ∈，则i i i i a a x a a x ++-)(2是实数域R 上的二次不可约多项式故实数域R 上的任意不可约多项式只能是一次多项式或满足042<-ac b 的二次多项式：c bx ax ++2.3.（5分）设A 是数域F 上的n 阶方阵.要求不用Hamilton-Caylay 定理，证明：存在F 上的多项式)(x f 使得O A f =)(. 证明：取A 的特征多项式A E g -=λλ)(设)(λB 为A E -λ的伴随矩阵，有E g E A E A E B )())((λλλλ=-=- 由)(λB 的元素是A E -λ各个代数余子式，则1))((-≤∂n B λ 有11201)(---+++=n n n B B B B Λλλλ令n n n a a g +++=-Λ11)(λλλ，得E a E a E E g n n n +++=-Λ11)(λλλ ①A B A B B A B B A B B B A E B n n n n n n 1211220110)()()())((-------++-+-+=-λλλλλλΛ ②比较①、②，有⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-=-=-=-=----E a A B Ea A B B E a A B B E a A B B EB n n n n n 11212121010ΛΛΛ，得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-=-=-=-=---------Ea A B A a A B A B A a A B A B A a A B A B A A B n n n n n n n n n nn n n 11221221122110110ΛΛΛ左边和右边全部相加，有O E g =)(λ，即0)(=λg 任取)()()(x g x q x f =，则有O A f =)(4.（10分）设1α、2α、3α是多项式123)(3++=x x x f 的全部根.求下式的值 ))()((212331223221ααααααααα+++解:由根与系数的关系得0321=++ααα、32323121=++αααααα、31321-=ααα)31)(31)(31())()((323222121212331223221ααααααααααααααα---=+++]1)()([91)1)(1)(1(271333231333233313231333231333231321-+++++--=---=αααααααααααααααααα)(91)(9124328333231333233313231ααααααααα++-++-=① )(91)111(243124328333231333231αααααα++-++-=)(91243124328333231333231333233313231αααααααααααα++-++-= ② 由①、②得，0333233313231=++αααααα，则原式)(9124328333231ααα++-=由13))((3)(3213231213213321333231-=+++++-++=++αααααααααααααααααα得原式24355=二、解答下列各题.1（10分）叙述并证明线性方程组的克莱默（Cramer ）法则.2（5分）设F ，K 都是数域且K F ⊆，设β=AX 是数域F 上的线性方程组. 证明：β=AX 在F 上有解当且仅当β=AX 在K 上有解. 证明：令A 为n m ⨯矩阵 必要性：令X 为β=AX 在F 上的解，有n F X ∈，由K F ⊆，得nK X ∈X 也为β=AX 在K 上的解充分性：β=AX 在K 上有解， 有)()(A r A r =由A ，)(F M A n m ⨯∈，则在F 上，也有)()(A r A r =，故β=AX 在F 上有解3.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=142412222A （1）（5分）在任意数域F 上，A 能否相似于一个对角阵？说明理由. （2）（5分）求A 的极小多项式.（3）（5分）设AX X X f ')(=，其中)',,(321x x x X =是列向量.求)(X f 的一个标准型.解：（1）)6()3(1424122222+-=+---+--=-λλλλλλA EA 的特征值为3，3，6-当3=λ时，000002214424422213-=----=-A E基础解系由2)3(=--A E r n 个线性无关的向量构成)'1,1,4(-、)'1,1,0(当6-=λ时，0009904525424522286--→-------=--A E 基础解系由1)6(=---A E r n 个向量构成)'2,2,1(- 故A 对应3个线性无关的特征向量，A 可对角化取⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=211211104P ，则有)6,3,3(1-=-diag AP P 由)(,3Q M C A ∈、又Q ∈-6,3，则A 在有理数域可以对角化由任何数域都包含有理数域，故在任意数域F 上，A 都能相似于一个对角阵（2）A 的特征多项式为O E A E A A f =+-=)6()3()(2由O E A E A =+-)6)(3(，有A 的极小多项式为)6)(3()(+-=λλλm（3）把P 的列向量单位化，得⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=32212313221231310234C ，C 为正交矩阵 令CY X =，有232221633''')(y y y ACY C Y AX X X f -+===4.（10分）证明：在任意数域F 上矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=111001012A 与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110011001B 都不相似. 证明：3)1(11101012-=----=-λλλλλA E 有A 的特征值为1，1，1 1=λ时，00000001101101111-=---=-A E基础解系有2)(=--A E r n 个线性无关的向量构成 ①3)1(11011001-=-----=-λλλλλB E 有B 的特征值为1，1，1 1=λ时，01000100--=-B E 基础解系有1)(=--B E r n 个向量构成 ②由①、②，得在任意数域F 上矩阵A 与B 都不相似5.（5分）设A 是n 阶实对称矩阵.证明：A 是正定矩阵的充分必要条件是，对任意整数k ，k A 也是正定的.证明：必要性：令A 的特征值为i λ（n i ,,2,1Λ=），则k A 的特征值为k i λ A 是正定矩阵，0>i λ，则0>ki λ，有k A 为正定矩阵充分性：k A 的特征值为k i λ，有0>ki λ，由k 的任意性，有0>i λ，故A 是正定矩阵三、（15分）设)(F M n 是数域F 上的全体n 阶方阵组成的集合.对任意可逆矩阵)(F M A n ∈，定义集合})({1X XA A F M X n A =∈=T -. 设A A F M A n V T =≠∈0):(I，即V 是所有可能的A T 的交集（A 可逆）.求V dim 和V 的一个基.解： 取)(F M n 的一个基nn E E E Λ,,1211，令n n ij a A ⨯=)(、n n ij x X ⨯=)( 有nn nn E a E a E a A +++=Λ12121111由X XA A =-1，有AX XA =，则X E XE ij ij =有行第列第i 111j 21⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=j j j ijnii i ij x x x X E x x x XE ΛM 得0=ij x （j i ≠）且nn x x x ===Λ2211，故kE X =为数量矩阵 有)(E L A =T ，则V 由数量矩阵和全体对角元素为零的矩阵构成令V B ∈，有∑=+=nj i ij ij E k kE B 1,（j i ≠），有1dim 2+-=n n VE 与全体ij E （j i ≠）构成V 的一个基.四、设)(12F M r +是数域F 上的全体12+r 阶方阵组成的集合.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=O E O E O O O OM r r 2是分块矩阵，其中r E 是r 阶单位阵.设}')({12O MX M X F M X B r =+∈=+，其中'X 表示X 的转置矩阵.进一步B X ∈，设∑∞==0!1k kXX k e .已知：)(12F M e r X+∈.1.（15分）求B dim 和B 的一个基.2.（15分）证明：对任意B X ∈都有行列式1)det(=Xe3.（10分）设列向量空间12+r F上的一个双线性函数),(--在它的基)'0,,0,1(1Λ=ε，)'0,,1,0(2Λ=ε，……，)'1,,0,0(12Λ=+r ε下的度量矩阵为上述M .证明：对任意B X ∈和列向量12,+∈r Fβα都有),(),(βαβα=XX e e .1.解：令⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211X X X X X X X X x X （12X 、13X 为r 维行向量，21X 、31X 为r 维列向量，22X 、23X 、32X 、33X 为r 阶方阵）有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=232221333231131211222X X X X X X X X x MX ，有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='''2'''2''2)'(233313223212213111X X X X X X X X x MX 由O MX M X =+'，又M 为对称矩阵，有O MX MX =+)'(则O X X X X X X X X X X XX X X X X x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++++2323223321133322323231121321123111'''2'''22'2'4，有011=x 自由变量有12X 、13X 、22X 、23X 、32X 且23X 、32X 为反对称矩阵有r r r r r r r r r B +=-+-+++=2222222dim2.证明：根据矩阵指数的性质，有)()det(X tr X e e =)'()()'()()()()(3322332233223322X X tr X tr X tr X tr X tr X X tr X tr e e e e e ++++====由O X X =+3322'，有10)'(3322==+e e X X tr ，则1)det(=X e注：关于)()det(X tr X e e =的证明由存在可逆矩阵P ，使得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-n XP P λλλ******211O有121******-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=P P X k n kk k λλλO11020100******!1***!1***!1!121--∞=∞=∞=∞=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=∑∑∑∑P e e e P P k k k P X k n k nk kk k k k kλλλλλλOO有)(2121)det(X tr Xe e e e e e n n ===+++λλλλλλΛΛ3.证明：五、（20分）证明：在数域F 上的任意n 元多项式都是线性多项式（即：一次齐次多项式）的幂的线性组合.证明：由任何一个m 次n 元多项式f 都可以唯一的表示成∑==mi i f f 0，其中i f 是n 元i 次齐次多项式由i f 是i 次齐次多项式,那么n x x x ,,,21Λ有ii n C k 1-+=种组合方式令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=+++=--k i n i i i n k i i i b b b x x x x x b x x b x b f M ΛΛ212111211211),,,(取k 个一次齐次多项式k g g g ,,,21Λ，它们的i 次方为ik i i g g g ,,,21Λ令ij g 的k 个系数为kj j j a a a ,,,21Λ（k j ,,2,1Λ=）⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=+++=--kj j j i n i i i n kj i j i j i j a a a x x x x x a x x a x a g M ΛΛ212111211211),,,( 得到系数方程⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡k k kk k k k k b b b y y y a a a a a aa a a M MΛM MM ΛΛ2121212222111211 只要k g g g ,,,21Λ选取得当，则此方程有解则有∑==+++=kl i ll i kki ii g y g y g y g y f 12211Λ，故∑∑===m i kl il l g y f 01，即证.。

四川大学2009数学分析考研真题与解析1·求下列极限。

（a ）∑=∞→nk k nn Cn2.ln 1lim解： 原极限=()221111121ln ln limln 1limnn C C Cn n k nk kn k n n k nnk n ++-=∑∑∑+==+∞→=∞→=∑=∞→-++nk n k n nn 11ln 121lim =∑=∞→∞→--⋅+n k n n nk n n n 1111ln 1lim 12lim =⎰=--1021)1ln(21dx x(b)().sin lim 22n n n +∞→π解： 原极限=nn n nn n n n n ++=-+∞→∞→22sinlim )sin(lim πππ=12sin 111limsin ==⎪⎪⎭⎫ ⎝⎛++∞→ππn n （c ）().sin sin lim2302dtt t t tdtx x x ⎰⎰-→解： 原极限=()().1262limsin sin 2lim 53302230=⎥⎦⎤⎢⎣⎡+--=-⋅→→x x x x x x x x x x x x ο （d ）xx xe x x cos 11lim 0----+→ 解： 原极限=()()()⎥⎦⎤⎢⎣⎡++--⎥⎦⎤⎢⎣⎡+--++→222222024218212lim x x x x x x x x x οοο =.32418121-=--2·计算下列积分。

（a ）,222dxdy y x yx D⎰⎰--+其中{()}1;R ,222≤+∈=y x y x D 解： 原积分=rdr r r r d ⎰⎰-+12202sin cos θθθπ=dr r r d 220104sin ⎰⎰-⎪⎭⎫⎝⎛+ππθθ=()()θθθπθθd dr r r dr r r ⎰⎰⎰⎥⎦⎤⎢⎣⎡-+-201sin 23sin 032sin sin=θθθπd ⎰⎪⎪⎭⎫ ⎝⎛+-204413sin 6sin =85π(b) ⎰l yzds ,其中l 是球面⎪⎪⎭⎫ ⎝⎛>=++332222a a z y x 与平面1=++z y x 的交线.解： 原积分=()ds z z ds zx yz l l ⎰⎰-=+121)(21 =()()ds z y x ds z y x l l ⎰⎰++-++2226161 =⎰-l ds a 612 =().3131312612222--=-⋅-a a a a ππ（c ）设()x f 在()+∞∞-,内有连续导函数，求积分()()[]dy xy f y y x dx y xy f y L11222-++⎰，其中L 是从点⎪⎭⎫⎝⎛32,3A 到()2,1B 的直线段。

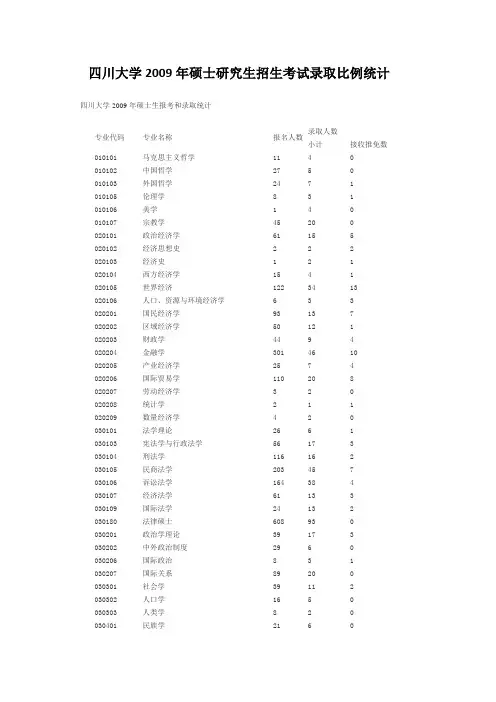
四川大学2009年硕士研究生招生考试录取比例统计四川大学2009年硕士生报考和录取统计专业代码专业名称报名人数录取人数小计接收推免数010101 马克思主义哲学11 4 0 010102 中国哲学27 5 0 010103 外国哲学24 7 1 010105 伦理学8 3 1 010106 美学 1 4 0 010107 宗教学45 20 0 020101 政治经济学61 15 5 020102 经济思想史 2 2 2 020103 经济史 1 2 1 020104 西方经济学15 4 1 020105 世界经济122 34 13 020106 人口、资源与环境经济学 6 3 3 020201 国民经济学93 13 7 020202 区域经济学50 12 1 020203 财政学44 9 4 020204 金融学301 46 10 020205 产业经济学25 7 4 020206 国际贸易学110 20 8 020207 劳动经济学 3 2 0 020208 统计学 2 1 1 020209 数量经济学 4 2 0 030101 法学理论26 6 1 030103 宪法学与行政法学56 17 3 030104 刑法学116 16 2 030105 民商法学203 45 7 030106 诉讼法学164 38 4 030107 经济法学61 13 3 030109 国际法学24 13 2 030180 法律硕士608 93 0 030201 政治学理论39 17 3 030202 中外政治制度29 6 0 030206 国际政治8 3 1 030207 国际关系89 20 0 030301 社会学39 11 2 030302 人口学16 5 0 030303 人类学8 2 0 030401 民族学21 6 0030405 中国少数民族艺术12 3 3 030501 马克思主义基本原理35 11 1 030503 马克思主义中国化研究26 11 0 030505 思想政治教育64 14 0 040106 高等教育学72 10 0 040203 应用心理学223 18 4 040301 体育人文社会学11 3 0 040302 运动人体科学8 1 0 040303 体育教育训练学105 22 2 040304 民族传统体育学 2 2 0 050101 文艺学81 20 3 050102 语言学及应用语言学306 34 3 050103 汉语言文字学78 27 3 050104 中国古典文献学32 12 7 050105 中国古代文学188 25 3 050106 中国现当代文学165 27 4 050107 中国少数民族语言文学 5 0 0 050108 比较文学与世界文学160 31 9 050120 文艺与传媒31 4 0 050121 文化批评20 7 0 050122 文学人类学23 11 4 050123 佛教语言文学 5 6 0 050124 广播影视文艺学26 4 1 050201 英语语言文学242 45 11 050202 俄语语言文学7 5 2 050205 日语语言文学41 18 3 050211 外国语言学及应用语言学477 63 22 050301 新闻学286 45 8 050302 传播学313 51 9 050401 艺术学93 23 8 050403 美术学191 36 6 050404 设计艺术学261 36 13 060101 史学理论及史学史 4 1 0 060102 考古学及博物馆学51 13 5 060103 历史地理学25 4 0 060104 历史文献学14 4 0 060105 专门史52 11 2 060106 中国古代史49 16 3 060107 中国近现代史165 31 3 060108 世界史64 18 5 060123 中国儒学9 1 0 070101 基础数学121 31 12 070102 计算数学31 11 6 070103 概率论与数理统计34 9 6070104 应用数学26 4 1 070105 运筹学与控制论26 5 3 070120 不确定性处理的数学24 5 3 070121 信息安全22 5 3 070201 理论物理35 8 2 070202 粒子物理与原子核物理53 15 1 070203 原子与分子物理130 45 1 070205 凝聚态物理101 39 8 070207 光学165 39 5 070208 无线电物理12 6 2 070220 生物医学物理 3 2 0 070221 应用电子物理12 6 2 070222 高压科学与技术24 12 0 070301 无机化学29 10 1 070302 分析化学88 25 5 070303 有机化学115 38 11 070304 物理化学20 17 4 070305 高分子化学与物理30 16 5 070320 绿色化学32 11 0 070321 化学生物学30 26 2 071001 植物学93 30 5 071002 动物学23 12 1 071005 微生物学197 33 7 071007 遗传学104 37 7 071009 细胞生物学138 51 6 071010 生物化学与分子生物学189 54 7 071012 生态学20 9 4 071020 生物信息学27 4 0 071021 生物安全29 6 0 071022 结构生物学 1 0 0 077301 物理电子学23 10 2 077401 计算机系统结构23 4 1 077402 计算机软件与理论206 57 13 077403 计算机应用技术549 179 27 077501 环境科学197 38 4 080102 固体力学7 3 2 080103 流体力学 2 1 1 080104 工程力学 5 2 1 080201 机械制造及其自动化136 36 11 080202 机械电子工程21 9 8 080203 机械设计及理论52 24 13 080204 车辆工程12 2 0 080300 光学工程12 17 4 080401 精密仪器及机械13 5 3080402 测试计量技术及仪器33 10 3 080501 材料物理与化学40 24 4 080502 材料学238 100 26 080503 材料加工工程129 52 12 080520 高分子科学与工程148 50 5 080521 纳米材料与纳米技术18 8 1 080522 复合材料28 6 0 080601 冶金物理化学 1 1 1 080602 钢铁冶金7 5 1 080603 有色金属冶金7 4 3 080706 化工过程机械31 12 9 080801 电机与电器11 1 0 080802 电力系统及其自动化127 37 17 080803 高电压与绝缘技术 4 1 1 080804 电力电子与电力传动45 5 2 080805 电工理论与新技术33 5 1 080902 电路与系统51 22 4 080903 微电子学与固体电子学25 9 4 080904 电磁场与微波技术15 9 4 081001 通信与信息系统288 49 11 081002 信号与信息处理148 48 9 081101 控制理论与控制工程43 11 5 081102 检测技术与自动化装置34 10 4 081104 模式识别与智能系统19 15 4 081280 软件工程47 4 4 081302 建筑设计及其理论22 10 5 081303 城市规划与设计28 16 6 081304 建筑技术科学12 4 1 081401 岩土工程25 21 6 081402 结构工程51 16 12 081403 市政工程15 7 4 081501 水文学及水资源53 13 5 081502 水力学及河流动力学55 29 12 081503 水工结构工程73 20 8 081504 水利水电工程17 7 2 081505 港口、海岸及近海工程 3 1 0 081520 水电建设工程管理16 6 0 081521 城市水利与水安全 3 2 0 081701 化学工程43 14 3 081702 化学工艺115 37 6 081703 生物化工33 16 8 081704 应用化学62 25 6 081705 工业催化 4 3 0 081720 制药工程48 16 6081721 化工安全工程与技术9 4 2 082102 纺织材料与纺织品设计11 3 2 082103 纺织化学与染整工程8 5 1 082104 服装11 5 4 082203 发酵工程7 4 1 082204 皮革化学与工程21 21 8 082504 人机与环境工程 2 1 0 082703 核技术及应用9 5 1 082802 农业水土工程26 7 1 083001 环境科学 1 1 0 083002 环境工程76 18 7 083100 生物医学工程49 30 13 083120 医学信息工程 5 1 1 083201 食品科学43 13 8 090403 农药学16 5 1 090706 园林植物与观赏园艺50 15 3 090707 水土保持与荒漠化防治 6 2 1 097202 粮食、油脂及植物蛋白工程 1 0 0 097203 农产品加工及贮藏工程20 10 1 100101 人体解剖与组织胚胎学 4 4 0 100102 免疫学17 7 1 100103 病原生物学11 3 0 100104 病理学与病理生理学90 20 4 100105 法医学61 13 7 100120 医学生物化学及细胞生物学24 6 0 100121 医学神经生物学 1 0 0 100122 医学生理学与时间生物学15 3 0 100201 内科学414 72 8 100202 儿科学68 10 2 100203 老年医学20 6 0 100204 神经病学87 11 0 100205 精神病与精神卫生学57 6 1 100206 皮肤病与性病学76 7 0 100207 影像医学与核医学81 14 0 100208 临床检验诊断学27 8 2 100209 护理学110 12 4 100210 外科学480 64 3 100211 妇产科学208 26 3 100212 眼科学84 9 0 100213 耳鼻咽喉科学51 8 0 100214 肿瘤学103 27 3 100215 康复医学与理疗学13 2 0 100216 运动医学10 1 0 100217 麻醉学96 23 2100218 急诊医学12 2 0 100220 循证医学8 6 0 100221 移植科学与工程学7 5 5 100222 临床药物与器械评价科学 4 0 0 100223 眼视光学 6 2 2 100225 人类重大疾病生物治疗 4 2 1 100301 口腔基础医学8 14 1 100302 口腔临床医学331 77 0 100401 流行病与卫生统计学67 31 7 100402 劳动卫生与环境卫生学12 9 2 100403 营养与食品卫生学71 17 3 100404 儿少卫生与妇幼保健学11 3 1 100405 卫生毒理学 4 2 0 100420 健康与社会行为学11 4 1 100421 公共卫生检验学27 13 4 100602 中西医结合临床29 8 0 100701 药物化学101 36 6 100702 药剂学77 30 10 100703 生药学15 6 2 100704 药物分析学85 20 2 100705 微生物与生化药学9 4 0 100706 药理学59 25 5 100720 临床药学26 9 2 100721 药事管理学 4 1 0 100722 天然药物化学26 11 5 107200 生物医学工程25 28 1 120100 管理科学与工程131 37 15 120124 医院管理与卫生政策 4 3 3 120201 会计学182 27 9 120202 企业管理451 48 15 120203 旅游管理283 55 9 120204 技术经济及管理48 10 3 120280 工商管理硕士571 398 0 120401 行政管理447 93 2 120402 社会医学与卫生事业管理42 14 5 120403 教育经济与管理142 32 0 120404 社会保障164 54 4 120405 土地资源管理131 20 1 120501 图书馆学25 13 3 120502 情报学61 26 6 120503 档案学20 10 4。

四川大学2009年攻读硕士学位研究生入学考试题一、（每题7分，共28分）求下列极限1. ∑=∞→nk k nn Cn2ln 1lim解：定理（∞∞型Stolz 公式，数列极限）设}{n x 严格递增（即N n ∈∀，有1+<n n x x ），且+∞=∞→n n x lim . 若1）a x x y y n n n n n =----∞→11lim（有限数），则a x y nnn =∞→lim . 2）a 为∞+或∞-，结论任然成立. 因2n ↗∞+，用Stolz 公式1211ln lim 12ln lim )1(ln ln lim ln 1lim 00122010102+-++=+=-+-=∑∑∑∑∑=∞→=+∞→=+=+∞→=∞→n k n n n C C n n C C C n nk n nk kn k n n nk kn n k k n n n k k n n 12ln )1ln()1(lim12)1ln()1ln(lim 11+-++=+-+-+=∑∑∑+=∞→==∞→n kn n n k n n n k n nk n k n （再次用Stolz 公式）212)11ln(lim )12()12()ln ln (]ln )1ln()1[(lim111=+=--+---++=∞→=+=∞→∑∑nn n k n k n n n n k n n k n n2. )(sin lim 22n n n +∞→π 解：)111(sin )(sin )(sin 22222++=-+=+nn n n n n ππππ 初等函数在有定义的地方皆连续12s i n l i m )111(s i n l i m )(s i n l i m 2222==++=+∞→∞→∞→πππn n n nn n3. dtt t t dtt x x x ⎰⎰-+→0230)sin (sin lim 2解：x x x x x x x x x x x x x dt t t t dtt x x x x x x sin 2lim )sin ()(2)(sin lim )sin ()(sin 2lim )sin (sin lim 30232223202320002302-=-⋅=-=-++++→→→→⎰⎰1226lim cos 16lim 22020==-=++→→x x x x x x4. xx xe x x cos 11lim 0----→ 解：泰勒公式∑∞==++++++=032!!!3!21n nn xn x n x x x x e ，（+∞<<∞-x ） +----++--+-++=+!)]1([)2)(1(!3)2)(1(!2)1(1)1(2n n x x x ααααααααααα，（11<<-x ）∑∞=-=+-+-+-+-=022642)!2()1()!2()1(!6!4!21cos n n n n n n x n x x x x x ，（+∞<<∞-x ） )](!4)(!2)(1[)(!2)121(21)(2111)(21lim cos 11lim 24222220x o x x x o x x xx o x x x x xe x x x ++--+-+-+--+++=----→→3)(24181)(2lim 222220-=+--+=→x o x x x o x x二、（每题10分，共40分）计算下列积分 （1）dxdy y x yx D⎰⎰--+222，其中}1:),{(222≤+∈=y x R y x D 解：2222)221()221(412----=--+y x y x y x 当),(y x 在41)221()221(22=-+-y x 内和上时0222≥--+y x yx ，记作1D ； 当),(y x 在41)221()221(22=-+-y x 外，且在122≤+y x 内时0222<--+y x y x ，记作2D 则dxdy y x yx dxdy y x y x I D D ⎰⎰⎰⎰--+---+=21)2()2(2222 2122222)2()2(2211I I d x d y y x y x d x d y y x y x I DD D D -=--+---+=⎰⎰⎰⎰=+ d x d y y x y x I D ⎰⎰--+=1)2(221 令θcos 221r x =-、θsin 221r y =- πθπ321)81(213201=-=⎰⎰dr r r d I d x d y y x yx I D⎰⎰--+=)2(222 令θcos r x =、θsin r y = πθθθπ21)2c o s s i n (1032202-=-+=⎰⎰dr r r d Iπ169221=-=I I I（2）ds yz l⎰，其中l 是球面2222a z y x =++与平面1=++z y x 的交线。

国内数学分析主要参考书⽬_数学分析书籍花了半天时间，对国内部分⼤学所编数学分析(/⾼等数学/微积分)教材做了个汇总，发于此，肯定有很多遗漏，(期待有兴趣的⾍友帮我⼀起补充,补充格式:⼤学名，精确书名，编写作者....)。

国内部份⼤学常⽤数学分析(⾼数,微积分)教材总汇清华⼤学《数学分析教程》常庚哲.史济怀.《数学分析》(三册).何琛史济怀徐森林《数学分析》(三册).徐森林,.⾦亚东,.薛春华《数学分析讲义》(三册).陈天权《数学分析习题课讲义》谢惠民等北京⼤学《数学分析》沈燮昌著第⼀册，⽅企勤著第⼆册，廖可⼈、李正元著第三册《数学分析习题课教材》（第⼀版）《数学分析解题指南》（第⼆版）林源渠，⽅企勤《数学分析习题集》林源渠，⽅企勤等《数学分析新讲》张筑⽣(三册)《数学分析简明教程》邓东翱,尹⼩铃著《数学分析上、下册》彭⽴中、谭⼩江著复旦⼤学《数学分析》《数学分析》陈传璋，⾦福临，朱学炎，欧阳光中著第⼆版《数学分析》欧阳光中，朱学炎，⾦福临，陈传璋著第三版《数学分析》陈纪修等著《数学分析》欧阳光中，姚允龙著同济⼤学《⾼等数学》（同济⼤学数学系第六版,上、下册）《⾼等数学讲义》樊映川等编..华东师范⼤学《数学分析》华东师范⼤学数学系著《数学分析精读讲义》华东师范⼤学数学系著《数学分析习题精解》吴良森，⽑⽻辉等?中国科学技术⼤学《数学分析教程》常庚哲，史济怀著《简明微积分》龚昇《⾼等数学引论》华罗庚《数学分析》徐森林著《数学分析的⽅法及例题选讲》徐利治南开⼤学《数学分析上、下册》李成章，黄⽟民《在南开⼤学的演讲》陈省⾝南京⼤学《数学分析讲义》梅加强《数学分析教程》许绍浦等北京师范⼤学《简明数学分析（第⼀版）》王昆扬《简明数学分析（第⼆版）》郇中丹，刘永平，王昆扬《微积分学讲义（第⼆版）》邝荣⾬武汉⼤学《⾼等数学上、下册》（⾼等教育出版社，齐民友主编）《重温微积分》齐民友著吉林⼤学《数学分析》东北师范⼤学《数学分析讲义》刘⽟琏，傅沛仁著天津⼤学《⾼等数学上、下册》蔡⾼厅叶宗泽《⾼等数学试题精选与解答》（蔡⾼厅等编）内蒙古⼤学《微积分学简明教程》曹之江等著[ Last edited by hylpy on 2014-9-15 at 12:38 ]国内数学分析主要参考书⽬[1].刘⽟琏,傅沛仁,林玎,苑德馨,刘宁编.数学分析讲义(上),第四版.北京:⾼等教育出版社,2003.[2].刘⽟琏,傅沛仁,林玎,苑德馨,刘宁编.数学分析讲义(下),第四版.北京:⾼等教育出版社,2003.[3].刘⽟琏,扬奎元,吕风编.数学分析讲义学习辅导书(上),第⼆版,北京:⾼等教育出版社.2003.[4].刘⽟琏,扬奎元,吕风编.数学分析讲义学习辅导书(下),第⼆版,北京:⾼等教育出版社.2003.[5].华东师范⼤学数学系编.数学分析(上),第三版.北京:⾼等教育出版社,2002.[6].华东师范⼤学数学系编.数学分析(下),第三版.北京:⾼等教育出版社,2002.[7].吴良森,⽑⽻辉,韩⼠安,吴畏编著.数学分析学习指导书(上).北京:⾼等教育出版社.2004.[8].吴良森,⽑⽻辉,韩⼠安,吴畏编著.数学分析学习指导书(下).北京:⾼等教育出版社.2004.[9].吴良森,⽑⽻辉编著.数学分析习题精解(单变量部分).北京:科学出版社.2002.[10].吴良森,⽑⽻辉编著.数学分析习题精解(多变量部分).北京:科学出版社.2003.[11].薛宗慈,曾昭著,邝荣⾬,陈平尚编.数学分析习作课讲义(上).北京:北京师范⼤学出版社,1985.[12].薛宗慈,曾昭著,邝荣⾬,陈平尚编.数学分析习作课讲义(下).北京:北京师范⼤学出版社,1987.[13].谢惠民,恽⾃求,易法槐,钱定边编.数学分析习题课讲义(上).北京:⾼等教育出版社,2004.[14].谢惠民,恽⾃求,易法槐,钱定边编.数学分析习题课讲义(下).北京:⾼等教育出版社,2004.[15].徐利治,王兴华.数学分析的⽅法与例题选讲.北京:⾼等教育出版社,2002.[16].钱吉林等主编.数学分析解题精粹.武汉:崇⽂书局,2003.[17].裴礼⽂.数学分析中的典型问题与⽅法,第⼆版.北京: ⾼等教育出版社,2006.[18].周民强编著.数学分析习题演练(第⼀册).北京:科学出版社,2006.[19].周民强编著.数学分析习题演练(第⼆册).北京:科学出版社,2006.[20].裘兆泰.王承国,章仰⽂编.数学分析学习指导.北京:科学出版社,2004.[21].孙涛编.数学分析经典习题解析.北京:⾼等教育出版社,2004.[22].胡晓敏,李承家编著.数学分析考研教案,第⼆版.西安:西北⼯业⼤学出版社, 2006.[23].孙本旺,汪浩主编.数学分析中的典型例题和⽅法.长沙:湖南科学技术出版社,1983.[24].⽑⽻辉编著.数学分析选论.北京:科学出版社,2003.[25].王昆扬编.数学分析专题研究.北京:⾼等教育出版社,2001.[26].胡适耕,姚云飞编著.数学分析:定理问题⽅法.北京:科学出版社,2007.[27].徐利治编著.数学分析的⽅法及例题选讲:分析学的思想、⽅法与技巧.⼤连:⼤连理⼯⼤学出版社,2007.[28].沈燮昌.数学分析纵横谈.北京:北京⼤学出版社,1991.[29].G.波利亚.数学分析中的问题和定理(第⼀卷).上海:上海科技出版社,1981.[30].舒斯会编著.数学分析选讲.北京:北京⼤学出版社,2007.[31].刘三阳,于⼒,李⼴民编.数学分析选讲.北京:科学出版社,2007.[32].李克典,马云苓编著.数学分析选讲.厦门:厦门⼤学出版社,2007.[33].⾟钦著.数学分析⼋讲.武汉:武汉⼤学出版社,1999.[34].[美]克莱鲍尔著.数学分析.上海:上海科技出版社,1981.[35].朱时编著.数学分析札记.贵阳:贵州教育出版社,1994.[36].[苏]B.Π.吉⽶多维奇.数学分析习题集.北京:⾼等教育出版社,1985.[37].林源渠.数学分析习题集.北京:⾼等教育出版社,1986.[38].吕通庆编.数学分析中⼀些重要概念及其⽭盾概念.北京:⼈民教育出版社,1979.[39].赵显曾著.数学分析拾遗.南京:东南⼤学出版社,2006.[40].强⽂久,李元章,黄雯荣.数学分析的基本概念与⽅法.北京:⾼等教育出版社,1989.[41].⽅企勤,林源渠编著.数学分析习题课教材.北京:北京⼤学出版社,1990.[42].王向东主编.数学分析的概念与⽅法(上).上海:上海科学技术⽂献出版社,1989.[43].王向东主编.数学分析的概念与⽅法(下).上海:上海科学技术⽂献出版社,1989.[44].朱匀华,周健伟.数学分析选讲.⼴州:⼴东科技出版社,1995.[45].明清河.数学分析的思想与⽅法.济南:⼭东⼤学出版社,2004.[46].李惜雯.数学分析例题解析及难点注释(上).西安:西安交通⼤学出版社,2004.[47].李惜雯.数学分析例题解析及难点注释(下).西安:西安交通⼤学出版社,2004.[48].宋国柱编.分析中的基本定理和典型⽅法.北京:科学出版社,2004.[49].周忠群主编.数学分析⽅法选讲.重庆:西南师范⼤学出版社,1990.[50].王⼽平编.数学分析选讲.徐州:中国矿业⼤学出版社,2002.[51].林安浩,张国杰,王智青编演.数学分析(1983-1984全国⾼等院校硕⼠研究⽣⼊学试题解答).天津:天津科学技术出版社,1985.[52].皱节铣,陈强编.数学试题选解(1980-1985全国招考研究⽣).长沙:湖南科学技术出版社,1986.[53].庄亚栋,⽅洪锦,姚林编.基础数学试题选解(研究⽣⼊选考试).苏州:江苏科技术学出版社,1986.[54].蔡林,张继昌编著.研究⽣数学⼊学考试精编,第三版.杭州:浙江⼤学出版社,1999.[55].牟俊霖,李青吉主编.洞穿考研数学.北京:航空⼯业出版社,2003.[56].刘光祖,卢恩双主编.⼤学数学辅导与考研指导.北京:科学出版社,2002.[57].西安交通⼤学⼗教授考研班主编.考研数学成功指南,第三版.西安:世界图书出版公司西安公司,2004.[58].余长安主编.⼤学数学考研题型精讲与解题技巧集粹.北京:科学出版社,2005.[59].邵剑,陈维新,张继昌,何勇编著.⼤学数学考研专题复习.北京:科学出版社,2001.[60].李沛恒主编.考研数学新编考试参考书.北京:中国⼈民⼤学出版社,2004.[61].龚冬宝（保）主编.数学考研教程,第三版.西安:西北交通⼤学出版社,2004.[62].龚怀云,胡清徽,杨泽⾼,张可村.研究⽣⾼等数学⼊学考试指南.西安:西北交通⼤学出版社,1985.[63].陈⽂灯,莫先开主编.数学复习指南.北京:世界图书出版公司北京公司,2002.[64].齐民友主编.微积分学习指导.武汉:武汉⼤学出版社,2004.[65].汪林.数学分析中的问题和反例.昆明:云南科技出版社,1990.[66].汪林,戴正徳,杨富春,郑喜印.数学分析问题与研究评注.北京:科学出版社,1995.[67].陈纪修,於崇华,⾦路.数学分析(上).北京:⾼等教育出版社,2000.[68].陈纪修,於崇华,⾦路.数学分析(下).北京:⾼等教育出版社,2000[69].王晓敏,李晓奇,惠兴杰主编.数学分析学习⽅法与解题指导.沈阳:东北⼤学出版社,2005.[70].赵焕光,林长盛编著.数学分析(上).成都:四川⼤学出版社,2006.[71].赵焕光,林长盛编著.数学分析(下).成都:四川⼤学出版社,2006.[72].陈传章,⾦福临,朱学炎,欧阳光中.数学分析(上),第⼆版.北京:⾼等教育出版社,1983.[73].陈传章,⾦福临,朱学炎,欧阳光中.数学分析(下),第⼆版.北京:⾼等教育出版社,1983.[74].⽅企勤编.数学分析(1).北京:⾼等教育出版社,1986.[75].沈燮昌编.数学分析(2).北京:⾼等教育出版社,1986.[76].廖可⼈,李正元编.数学分析(3).北京:⾼等教育出版社,1986.[77].许绍溥,姜东平,宋国柱,任福贤.数学分析教程(上).南京:南京⼤学出版社,1990.[78].宋国柱,任福贤,许绍溥,姜东平.数学分析教程(下).南京:南京⼤学出版社,1990.[79].武汉⼤学数学系编.数学分析(上).北京:⼈民教育出版社,1978.[80].武汉⼤学数学系编.数学分析(下).北京:⼈民教育出版社,1978.[81].吉林⼤学数学系编.数学分析(上).北京:⾼等教育出版社,1979.[82].吉林⼤学数学系编.数学分析(中).北京:⾼等教育出版社,1979.[83].吉林⼤学数学系编.数学分析(下).北京:⾼等教育出版社,1979.[84].常庚哲,史济怀编.数学分析教程(上).北京:⾼等教育出版社,2003.[85].常庚哲,史济怀编.数学分析教程(下).北京:⾼等教育出版社,2003.[86].复旦⼤学数学系编.数学分析(上).上海:上海科学技术出版社,1978.[87].复旦⼤学数学系编.数学分析(下).上海:上海科学技术出版社,1978.[88].邓东皋,尹⼩玲编著.数学分析简明教程(上).北京:⾼等教育出版社,1999.[89].邓东皋,尹⼩玲编著.数学分析简明教程(下).北京:⾼等教育出版社,1999.[90].欧阳光中编.数学分析(上).上海:上海科学技术出版社,1982.[91].欧阳光中编.数学分析(下).上海:上海科学技术出版社,1982.[92].周性伟.数学分析(上).天津:南开⼤学出版社,1982.[93].周性伟.数学分析(下).天津:南开⼤学出版社,1982.[94].彭⽴中,谭⼩江编著.数学分析(第1册).北京:⾼等教育出版社,2005.[95].严⼦谦,尹景学,张然编著.数学分析(第⼀册).北京:⾼等教育出版社,2004.[96].马富明,⾼⽂杰编著.数学分析(第⼆册).北京:⾼等教育出版社,2005.[97].徐森林,薛春华编著.数学分析(第⼆册).北京:清华⼤学出版社,2006.[98].王慕三,庄亚栋.数学分析(上).北京:⾼等教育出版社,1990.[99].王慕三,庄亚栋.数学分析(中).北京:⾼等教育出版社,1990.[100].王慕三,庄亚栋.数学分析(下).北京:⾼等教育出版社,1990.[101].邓东皋,尹⼩玲编撰.数学分析简明教程.北京:⾼等教育出版社,1997.[102].李成章,黄⽟明编.数学分析(上).北京:科学出版社,2004.[103].李成章,黄⽟明编.数学分析(下).北京:科学出版社,2004.[104].张筑⽣.数学分析新讲(第⼀册).北京:北京⼤学出版社,1999.[105].张筑⽣.数学分析新讲(第⼆册).北京:北京⼤学出版社,1999.[106].张筑⽣.数学分析新讲(第三册).北京:北京⼤学出版社,1999.[107].朱永庚.数学分析(上).西安:陕西师范⼤学出版社,1989.[108].朱永庚.数学分析(下).西安:陕西师范⼤学出版社,1989.[109].东北师⼤等校数学系编.数学分析(上).北京:⾼等教育出版社,1983.[110].东北师⼤等校数学系编.数学分析(下).北京:⾼等教育出版社,1983.[111].吴传⽣,张⼩柔主编.数学分析(下册)习题精解.合肥:中国科学技术⼤学出版社,2007. [112].吴传⽣,张⼩柔主编.数学分析(下册)习题精解).合肥:中国科学技术⼤学出版社,2007. [113].郑英元.数学分析习题课教程(上).北京:⾼等教育出版社,1991.[114].郑英元.数学分析习题课教程(下).北京:⾼等教育出版社,1991.[115].郑美元.数学分析中的习题课教程(上).北京:⾼等教育出版社,1991.[116].郑美元.数学分析中的习题课教程(下).北京:⾼等教育出版社,1991.[117].邵漪漪.⾼等数学选择题集.上海:上海科学技术出版社,1989.[118].孟繁铎.微积分标准化试题库.⼤连:⼤连理⼯⼤学出版社,1989.[119].李承家,胡晓敏编.数学分析导教•导学•导考.西安:西北⼯业⼤学出版社,2003. [120].贺⾃树等编.数学分析习题课选讲.重庆:重庆⼤学出版社,2007.[ Last edited by hylpy on 2018-9-2 at 18:39 ][121].李忠⽅丽萍编.数学分析教程上,2008.[122].李忠⽅丽萍编.数学分析教程下,2008.[123].梅加强编.《数学分析》⾼等教育出版社,2011.07.[124].邹应编.数学分析.上册.⾼等教育出版社.1995.[125].邹应编.数学分析.下册.⾼等教育出版社.1995.[126].郭⼤钧等编著.数学分析（上册）（第2版）,2002.[127].郭⼤钧等编著.数学分析（下册）（第2版）,2002.[128].沐定夷.数学分析（上）,1993.[129].沐定夷.数学分析（下）,1993.[130].欧阳光中，姚允龙，周渊编著.数学分析（上册）,2003.[131].欧阳光中，姚允龙，周渊编著.数学分析（下册）,2003.[132].数学分析-卷I-秦曾复、朱学炎-⾼等教育出版社1991.[133].数学分析-卷Ⅱ-秦曾复、朱学炎-⾼等教育出版社1991.[134].数学分析-卷Ⅲ-秦曾复、朱学炎-⾼等教育出版社1991.[ Last edited by hylpy on 2018-9-5 at 19:19 ][135].数学分析1-徐森林,.薛春华.清华⼤学出版社,2005.[136].数学分析2-徐森林,薛春华.清华⼤学出版社,2007.[137].数学分析3-徐森林,⾦亚东,薛春华.清华⼤学出版社,2007.[138].数学分析精选习题全解(上)-薛春华,徐森林,2009.[139].数学分析精选习题全解(下)-薛春华,徐森林,2010.[ Last edited by hylpy on 2018-9-7 at 18:06 ][140].伍胜健.数学分析第⼆版，(第⼀册),北京⼤学数学教学系列丛书,2009.[141].伍胜健.数学分析第⼆版，(第⼆册),北京⼤学数学教学系列丛书,2009.[142].伍胜健.数学分析第⼆版，(第三册),北京⼤学数学教学系列丛书,2009.国内数学分析主要参考书⽬本帖隐藏的内容[1].刘⽟琏,傅沛仁,林玎,苑德馨,刘宁编.数学分析讲义(上),第四版.北京:⾼等教育出版社,2003.[2].刘⽟琏,傅沛仁,林玎,苑德馨,刘宁编.数学分析讲义(下),第四版.北京:⾼等教育出版社,2003.[3].刘⽟琏,扬奎元,吕风编.数学分析讲义学习辅导书(上),第⼆版,北京:⾼等教育出版社.2003.[4].刘⽟琏,扬奎元,吕风编.数学分析讲义学习辅导书(下),第⼆版,北京:⾼等教育出版社.2003.[5].华东师范⼤学数学系编.数学分析(上),第三版.北京:⾼等教育出版社,2002.[6].华东师范⼤学数学系编.数学分析(下),第三版.北京:⾼等教育出版社,2002.[7].吴良森,⽑⽻辉,韩⼠安,吴畏编著.数学分析学习指导书(上).北京:⾼等教育出版社.2004.[8].吴良森,⽑⽻辉,韩⼠安,吴畏编著.数学分析学习指导书(下).北京:⾼等教育出版社.2004.[9].吴良森,⽑⽻辉编著.数学分析习题精解(单变量部分).北京:科学出版社.2002.[10].吴良森,⽑⽻辉编著.数学分析习题精解(多变量部分).北京:科学出版社.2003.[11].薛宗慈,曾昭著,邝荣⾬,陈平尚编.数学分析习作课讲义(上).北京:北京师范⼤学出版社,1985.[12].薛宗慈,曾昭著,邝荣⾬,陈平尚编.数学分析习作课讲义(下).北京:北京师范⼤学出版社,1987.[13].谢惠民,恽⾃求,易法槐,钱定边编.数学分析习题课讲义(上).北京:⾼等教育出版社,2004.[14].谢惠民,恽⾃求,易法槐,钱定边编.数学分析习题课讲义(下).北京:⾼等教育出版社,2004.[15].徐利治,王兴华.数学分析的⽅法与例题选讲.北京:⾼等教育出版社,2002.[16].钱吉林等主编.数学分析解题精粹.武汉:崇⽂书局,2003.[17].裴礼⽂.数学分析中的典型问题与⽅法,第⼆版.北京: ⾼等教育出版社,2006.[18].周民强编著.数学分析习题演练(第⼀册).北京:科学出版社,2006.[19].周民强编著.数学分析习题演练(第⼆册).北京:科学出版社,2006.[20].裘兆泰.王承国,章仰⽂编.数学分析学习指导.北京:科学出版社,2004.[21].孙涛编.数学分析经典习题解析.北京:⾼等教育出版社,2004.[22].胡晓敏,李承家编著.数学分析考研教案,第⼆版.西安:西北⼯业⼤学出版社, 2006.[23].孙本旺,汪浩主编.数学分析中的典型例题和⽅法.长沙:湖南科学技术出版社,1983.[24].⽑⽻辉编著.数学分析选论.北京:科学出版社,2003.[25].王昆扬编.数学分析专题研究.北京:⾼等教育出版社,2001.[26].胡适耕,姚云飞编著.数学分析:定理问题⽅法.北京:科学出版社,2007.[27].徐利治编著.数学分析的⽅法及例题选讲:分析学的思想、⽅法与技巧.⼤连:⼤连理⼯⼤学出版社,2007.[28].沈燮昌.数学分析纵横谈.北京:北京⼤学出版社,1991.[29].G.波利亚.数学分析中的问题和定理(第⼀卷).上海:上海科技出版社,1981.[30].舒斯会编著.数学分析选讲.北京:北京⼤学出版社,2007.[31].刘三阳,于⼒,李⼴民编.数学分析选讲.北京:科学出版社,2007.[32].李克典,马云苓编著.数学分析选讲.厦门:厦门⼤学出版社,2007.[33].⾟钦著.数学分析⼋讲.武汉:武汉⼤学出版社,1999.[34].[美]克莱鲍尔著.数学分析.上海:上海科技出版社,1981.[35].朱时编著.数学分析札记.贵阳:贵州教育出版社,1994.[36].[苏]B.Π.吉⽶多维奇.数学分析习题集.北京:⾼等教育出版社,1985.[37].林源渠.数学分析习题集.北京:⾼等教育出版社,1986.[38].吕通庆编.数学分析中⼀些重要概念及其⽭盾概念.北京:⼈民教育出版社,1979.[39].赵显曾著.数学分析拾遗.南京:东南⼤学出版社,2006.[40].强⽂久,李元章,黄雯荣.数学分析的基本概念与⽅法.北京:⾼等教育出版社,1989.[41].⽅企勤,林源渠编著.数学分析习题课教材.北京:北京⼤学出版社,1990.[42].王向东主编.数学分析的概念与⽅法(上).上海:上海科学技术⽂献出版社,1989.[43].王向东主编.数学分析的概念与⽅法(下).上海:上海科学技术⽂献出版社,1989.[44].朱匀华,周健伟.数学分析选讲.⼴州:⼴东科技出版社,1995.[45].明清河.数学分析的思想与⽅法.济南:⼭东⼤学出版社,2004.[46].李惜雯.数学分析例题解析及难点注释(上).西安:西安交通⼤学出版社,2004.[47].李惜雯.数学分析例题解析及难点注释(下).西安:西安交通⼤学出版社,2004.[48].宋国柱编.分析中的基本定理和典型⽅法.北京:科学出版社,2004.[49].周忠群主编.数学分析⽅法选讲.重庆:西南师范⼤学出版社,1990.[50].王⼽平编.数学分析选讲.徐州:中国矿业⼤学出版社,2002.[51].林安浩,张国杰,王智青编演.数学分析(1983-1984全国⾼等院校硕⼠研究⽣⼊学试题解答).天津:天津科学技术出版社,1985.[52].皱节铣,陈强编.数学试题选解(1980-1985全国招考研究⽣).长沙:湖南科学技术出版社,1986.[53].庄亚栋,⽅洪锦,姚林编.基础数学试题选解(研究⽣⼊选考试).苏州:江苏科技术学出版社,1986.[54].蔡林,张继昌编著.研究⽣数学⼊学考试精编,第三版.杭州:浙江⼤学出版社,1999.[55].牟俊霖,李青吉主编.洞穿考研数学.北京:航空⼯业出版社,2003.[56].刘光祖,卢恩双主编.⼤学数学辅导与考研指导.北京:科学出版社,2002.[57].西安交通⼤学⼗教授考研班主编.考研数学成功指南,第三版.西安:世界图书出版公司西安公司,2004.[58].余长安主编.⼤学数学考研题型精讲与解题技巧集粹.北京:科学出版社,2005.[59].邵剑,陈维新,张继昌,何勇编著.⼤学数学考研专题复习.北京:科学出版社,2001.[60].李沛恒主编.考研数学新编考试参考书.北京:中国⼈民⼤学出版社,2004.[61].龚冬宝（保）主编.数学考研教程,第三版.西安:西北交通⼤学出版社,2004.[62].龚怀云,胡清徽,杨泽⾼,张可村.研究⽣⾼等数学⼊学考试指南.西安:西北交通⼤学出版社,1985.[63].陈⽂灯,莫先开主编.数学复习指南.北京:世界图书出版公司北京公司,2002.[64].齐民友主编.微积分学习指导.武汉:武汉⼤学出版社,2004.[65].汪林.数学分析中的问题和反例.昆明:云南科技出版社,1990.[66].汪林,戴正徳,杨富春,郑喜印.数学分析问题与研究评注.北京:科学出版社,1995.[67].陈纪修,於崇华,⾦路.数学分析(上).北京:⾼等教育出版社,2000.[68].陈纪修,於崇华,⾦路.数学分析(下).北京:⾼等教育出版社,2000[69].王晓敏,李晓奇,惠兴杰主编.数学分析学习⽅法与解题指导.沈阳:东北⼤学出版社,2005.[70].赵焕光,林长盛编著.数学分析(上).成都:四川⼤学出版社,2006.[71].赵焕光,林长盛编著.数学分析(下).成都:四川⼤学出版社,2006.[72].陈传章,⾦福临,朱学炎,欧阳光中.数学分析(上),第⼆版.北京:⾼等教育出版社,1983.[73].陈传章,⾦福临,朱学炎,欧阳光中.数学分析(下),第⼆版.北京:⾼等教育出版社,1983.[74].⽅企勤编.数学分析(1).北京:⾼等教育出版社,1986.[75].沈燮昌编.数学分析(2).北京:⾼等教育出版社,1986.[76].廖可⼈,李正元编.数学分析(3).北京:⾼等教育出版社,1986.[77].许绍溥,姜东平,宋国柱,任福贤.数学分析教程(上).南京:南京⼤学出版社,1990.[78].宋国柱,任福贤,许绍溥,姜东平.数学分析教程(下).南京:南京⼤学出版社,1990.[79].武汉⼤学数学系编.数学分析(上).北京:⼈民教育出版社,1978.[80].武汉⼤学数学系编.数学分析(下).北京:⼈民教育出版社,1978.[81].吉林⼤学数学系编.数学分析(上).北京:⾼等教育出版社,1979.[82].吉林⼤学数学系编.数学分析(中).北京:⾼等教育出版社,1979.[83].吉林⼤学数学系编.数学分析(下).北京:⾼等教育出版社,1979.[84].常庚哲,史济怀编.数学分析教程(上).北京:⾼等教育出版社,2003.[85].常庚哲,史济怀编.数学分析教程(下).北京:⾼等教育出版社,2003.[86].复旦⼤学数学系编.数学分析(上).上海:上海科学技术出版社,1978.[87].复旦⼤学数学系编.数学分析(下).上海:上海科学技术出版社,1978.[88].邓东皋,尹⼩玲编著.数学分析简明教程(上).北京:⾼等教育出版社,1999.[89].邓东皋,尹⼩玲编著.数学分析简明教程(下).北京:⾼等教育出版社,1999.[90].欧阳光中编.数学分析(上).上海:上海科学技术出版社,1982.[91].欧阳光中编.数学分析(下).上海:上海科学技术出版社,1982.[92].周性伟.数学分析(上).天津:南开⼤学出版社,1982.[93].周性伟.数学分析(下).天津:南开⼤学出版社,1982.[94].彭⽴中,谭⼩江编著.数学分析(第1册).北京:⾼等教育出版社,2005.[95].严⼦谦,尹景学,张然编著.数学分析(第⼀册).北京:⾼等教育出版社,2004.[96].马富明,⾼⽂杰编著.数学分析(第⼆册).北京:⾼等教育出版社,2005.[97].徐森林,薛春华编著.数学分析(第⼆册).北京:清华⼤学出版社,2006.[98].王慕三,庄亚栋.数学分析(上).北京:⾼等教育出版社,1990.[99].王慕三,庄亚栋.数学分析(中).北京:⾼等教育出版社,1990.[100].王慕三,庄亚栋.数学分析(下).北京:⾼等教育出版社,1990.[101].邓东皋,尹⼩玲编撰.数学分析简明教程.北京:⾼等教育出版社,1997.[102].李成章,黄⽟明编.数学分析(上).北京:科学出版社,2004.[103].李成章,黄⽟明编.数学分析(下).北京:科学出版社,2004.[104].张筑⽣.数学分析新讲(第⼀册).北京:北京⼤学出版社,1999.[105].张筑⽣.数学分析新讲(第⼆册).北京:北京⼤学出版社,1999.[106].张筑⽣.数学分析新讲(第三册).北京:北京⼤学出版社,1999.[107].朱永庚.数学分析(上).西安:陕西师范⼤学出版社,1989.[108].朱永庚.数学分析(下).西安:陕西师范⼤学出版社,1989.[109].东北师⼤等校数学系编.数学分析(上).北京:⾼等教育出版社,1983.[110].东北师⼤等校数学系编.数学分析(下).北京:⾼等教育出版社,1983.[111].吴传⽣,张⼩柔主编.数学分析(上册)习题精解.合肥:中国科学技术⼤学出版社,2007.[112].吴传⽣,张⼩柔主编.数学分析(下册)习题精解).合肥:中国科学技术⼤学出版社,2007.[113].郑英元.数学分析习题课教程(上).北京:⾼等教育出版社,1991.[114].郑英元.数学分析习题课教程(下).北京:⾼等教育出版社,1991.[115].郑美元.数学分析中的习题课教程(上).北京:⾼等教育出版社,1991.[116].郑美元.数学分析中的习题课教程(下).北京:⾼等教育出版社,1991.[117].邵漪漪.⾼等数学选择题集.上海:上海科学技术出版社,1989.[118].孟繁铎.微积分标准化试题库.⼤连:⼤连理⼯⼤学出版社,1989.[119].李承家,胡晓敏编.数学分析导教•导学•导考.西安:西北⼯业⼤学出版社,2003. [120].贺⾃树等编.数学分析习题课选讲.重庆:重庆⼤学出版社,2007.[121].李忠⽅丽萍编.数学分析教程上,2008.[122].李忠⽅丽萍编.数学分析教程下,2008.[123].梅加强编.《数学分析》⾼等教育出版社,2011.07.[124].邹应编.数学分析.上册.⾼等教育出版社.1995.[125].邹应编.数学分析.下册.⾼等教育出版社.1995.[126].郭⼤钧等编著.数学分析（上册）（第2版）,2002.[127].郭⼤钧等编著.数学分析（下册）（第2版）,2002.[128].沐定夷.数学分析（上）,1993.[129].沐定夷.数学分析（下）,1993.[130].欧阳光中，姚允龙，周渊编著.数学分析（上册）,2003.[131].欧阳光中，姚允龙，周渊编著.数学分析（下册）,2003.[132].数学分析-卷I-秦曾复、朱学炎-⾼等教育出版社1991.[133].数学分析-卷Ⅱ-秦曾复、朱学炎-⾼等教育出版社1991.[134].数学分析-卷Ⅲ-秦曾复、朱学炎-⾼等教育出版社1991.[135].数学分析1-徐森林,.薛春华.清华⼤学出版社,2005.[136].数学分析2-徐森林,薛春华.清华⼤学出版社,2007.[137].数学分析3-徐森林,⾦亚东,薛春华.清华⼤学出版社,2007.[138].数学分析精选习题全解(上)-薛春华,徐森林,2009.[139].数学分析精选习题全解(下)-薛春华,徐森林,2010.[140].伍胜健.数学分析第⼆版，(第⼀册),北京⼤学数学教学系列丛书,2009.[141].伍胜健.数学分析第⼆版，(第⼆册),北京⼤学数学教学系列丛书,2009.[142].伍胜健.数学分析第⼆版，(第三册),北京⼤学数学教学系列丛书,2009.这⾥列的参考书，本论坛⼤部分都有电⼦版分享。

2009四川大学理科录取分数线（陕西）小编为方便您今年的报考工作，特意为您收集整理了2010年的高考录取分数线，更多更详细的高考资讯，尽在高考频道。

如果您有问题，可以随时联系我们。

我们新增了高考满分作文频道，欢迎您进入。

本页内容主要有2009年陕西地区四川大学理科高考分数线信息。

为您作为今年的高考报考提供尽所能及的帮助。

谢谢您的访问！最后，预祝各位考生在今年的高考中能够取得优异成绩。

四川大学在陕西地区录取分数线--文科专业类型平均分最高分最低分录取批次金属材料工程594 619 -- 第一批纺织工程556 560 -- 第一批制药工程583 589 -- 第一批数学类596 614 -- 第一批热能与动力工程595 619 -- 第一批临床医学626 640 -- 第一批材料物理597 609 -- 第一批安全工程557 560 -- 第一批轻工生物技术560 573 -- 第一批生物科学类605 615 -- 第一批轻化工程561 572 -- 第一批预防医学608 616 -- 第一批医学检验608 614 -- 第一批化学基地班609 626 -- 第一批金融学605 615 -- 第一批高分子材料与工程611 621 -- 第一批口腔医学639 658 -- 第一批经济学603 611 -- 第一批机械设计制造及其自动化600 633 -- 第一批电子信息科学类600 642 -- 第一批电气信息类599 620 -- 第一批核工程与核技术613 619 -- 第一批广播电视新闻学598 608 -- 第一批管理科学593 605 -- 第一批建筑学593 615 -- 第一批环境工程592 611 -- 第一批水利类591 610 -- 第一批微电子学589 600 -- 第一批化学工程与工艺577 583 -- 第一批高分子材料加工工程581 590 -- 第一批日语582 597 -- 第一批信息安全584 620 -- 第一批软件工程584 607 -- 第一批测控技术与仪器585 596 -- 第一批无机非金属材料工程586 609 -- 第一批光信息科学与技术587 598 -- 第一批土建类585 600 -- 第一批计算机科学与技术587 598 -- 第一批英语575 582 -- 第一批工程力学573 602 -- 第一批生命科学与技术基地班593 596 -- 第一批医学技术592 597 -- 第一批农业水利工程563 571 -- 第一批工程管理563 593 -- 第一批材料成型及控制工程565 574 -- 第一批护理学565 601 -- 第一批工业工程565 578 -- 第一批过程装备与控制工程566 570 -- 第一批工业设计567 575 -- 第一批化学类581 585 -- 第一批医学信息工程567 571 -- 第一批数学基地班568 576 -- 第一批药学571 591 -- 第一批食品科学与工程573 607 -- 第一批查看：2013陕西高考分数线 2009陕西高考分数线专题:全国历年高考理科分数线汇总全国历年高考文科分数线汇总四川大学介绍：四川大学是由原四川大学、原成都科技大学、原华西医科大学三所全国重点大学于1994年4月和2000年9月两次“强强合并”组建而成的教育部直属全国重点大学，也是国家“211工程”和“985工程”重点建设的大学。

课程号：20100440 课程名：泛函分析课程英文名：Functional Analysis学时：68 学分：4先修课程：实变函数、高等代数基本面向：数学学院教材：《泛函分析》江泽坚、孙善利编高等教育出版社1998 一版参考书：1.《实变函数与泛函分析》（下册）夏道行等等教育出版社1984 一版2.《实变函数与泛函分析》（下册）曹广福、严从荃编人民教育出版社第2版3. W.Rudin，Functional Analysis，McGraw_HillBook Company，1973课程简介：线性赋范空间，Banach空间，Hilbert空间（包括有界，紧集，列紧集，完全有界集等）。

Banach 空间上有界线性算子（包括算子范数，有界性，连续性，Hahn-Banach定理，闭图象定理，逆算子定理，谱理论，紧算子Riesz-Schauder理论等）Hilbert 空间上的有界线性算子（射影定理、Riesz表示定理）。

课程号：20100640 课程名：概率统计课程英文名Probability and Statistics学时：68 学分：4先修课程：数学分析、线性代数基本面向：数学学院各专业教材：《概率论基础》（第二版）李贤平高等教育出版社1997参考书：1．《概率论》（第一册概率论基础）复旦大学高等教育出版社，1979。

2．《概率论引论》汪仁官北京大学出版社19943．《概率论及数理统计》（第二版）（上）梁之舜等高等教育出版社1988课程简介：事件与概率，条件概率与统计独立性，随机变量与分布函数，数字特征与特征函数，极限定理。

课程号：20100850 课程名：高等代数-1课程英文名：Advanced Algebra-1学时：102 学分：5先修课程：高中数学基本面向：数学数院各专业教材：《Advanced Algebra》彭国华、李德琅高等教育出版社-Springer（计划2004年出版参考书：1。

《高等代数》北京大学数学系几何代数教研空编高等教育出版社2．《高等代数》张禾瑞、郝锅新高等教育出版社3．《Linear Slgebra》B。