南京工业大学 工程力学弯曲应力习题答案

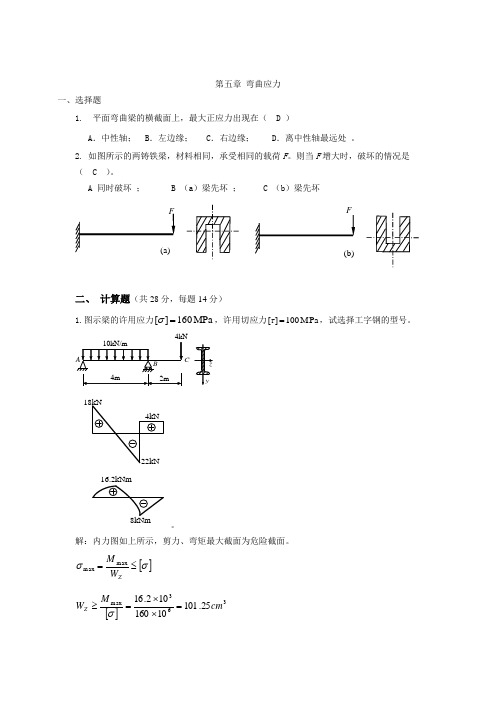
第五章弯曲应力一、选择题1.平面弯曲梁的横截面上，最大正应力出现在（ D ）A．中性轴； B．左边缘； C．右边缘； D．离中性轴最远处。

2. 如图所示的两铸铁梁，材料相同，承受相同的载荷F。

则当F增大时，破坏的情况是（ C ）。

A 同时破坏；B （a）梁先坏；C （b）梁先坏二、计算题（共28分，每题14分）MPa100][=τ，试选择工字钢的型号。

16.2kNm8kNm。

解：内力图如上所示，剪力、弯矩最大截面为危险截面。

[]σσ≤=ZWMmaxmax[]363max25.10110160102.16cmMWZ=⨯⨯=≥σ选用14号工字钢，并用其计算剪应力。

此时，cm bcm S I Z Z 5.5,12*== Z Z bI S Q *max max=τ []MPa MPa 100331012105.51022233max =≤=⨯⨯⨯⨯=--ττ 说明14号工字钢剪应力强调满足强度要求，故选用14号工字钢。

2.梁AB 为10号工字钢，W z =49cm 3，已知梁下表面C 处横截面上的正应力σc =60MPa 。

试求载荷F 的值。

（14分）解 C 处的弯矩为 F M C 1.0= （3分） 由zC C W M =σ得 z C C W M ⋅=σ （5分） 即 66104910601.0-⨯⨯⨯=F （3分）得 4.29=F kN （1分）3.一矩形截面外伸木梁，截面尺寸及荷载如图示。

q=1.3 kN/m 。

已知需用弯曲正应力[]10MPa σ=，许用切应力2MPa τ=（1）求二支座支反力（2）画出对应的剪力图与弯矩图。

（3）试校核梁的正应力和切应力强度。

（15分）解：（1）max max 1.61 3.912.29 1.02A B F KN F KN Q KN M KN m ====⋅；；（2） 对应的剪力图和弯矩图如下：（3）[]6max 2z M 1.02106σ7.08MPa W 60120σ⨯⨯===<⨯ []3max 3Q 3 2.2910τ0.477MPa 2A 212060τ⨯⨯===<⨯⨯ 故梁的正应力和切应力均满足强度要求。

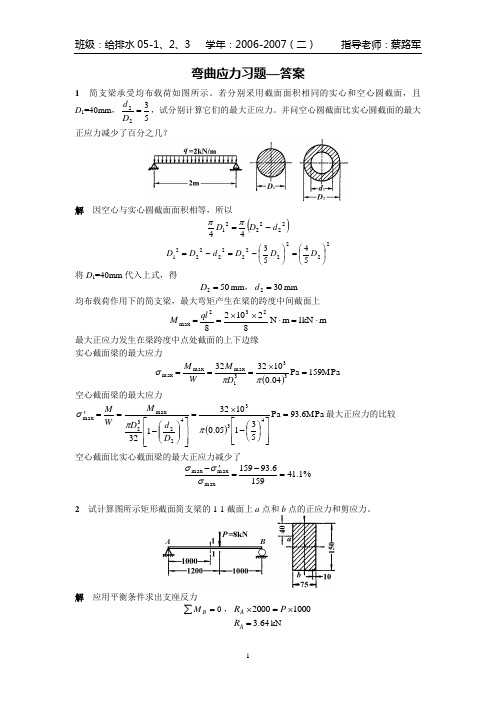
弯曲应力习题—答案1 简支梁承受均布载荷如图所示。

若分别采用截面面积相同的实心和空心圆截面，且D 1=40mm ，5322=D d ，试分别计算它们的最大正应力。

并问空心圆截面比实心圆截面的最大正应力减少了百分之几？解 因空心与实心圆截面面积相等，所以()22222144d D D -=ππ2222222222215453⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-=-=D D D d D D 将D 1=40mm 代入上式，得502=D mm ，302=d mm均布载荷作用下的简支梁，最大弯矩产生在梁的跨度中间截面上m 1kN m N 821028232max ⋅=⋅⨯⨯==ql M最大正应力发生在梁跨度中点处截面的上下边缘 实心截面梁的最大应力()159MPa Pa 04.01032323331max max max=⨯===ππσD M W M空心截面梁的最大应力()93.6MPa Pa 53105.010********42232max max =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=='ππσD d D M W M 最大正应力的比较 空心截面比实心截面梁的最大正应力减少了%1.411596.93159max max max =-='-σσσ2 试计算图所示矩形截面简支梁的1-1截面上a 点和b 点的正应力和剪应力。

解 应用平衡条件求出支座反力0=∑B M ，10002000⨯=⨯P R A64.3=A R kN1－1截面内力Q =R A =3.64kN ，m kN 64.31⋅=⨯=A R Ma 点的正应力和剪应力6.03MPa Pa 15.010*******)4075(1064.333331=⨯⨯⨯⨯-⨯⨯==--z a I My σ0.379MPa Pa 107515.01075121105575401064.333393=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯==---*b I QS Z Z a τb 点的正应力和剪应力12.9MPa Pa 15.0075.0611064.323=⨯⨯⨯==W M b σ0=b τ3 ⊥形截面铸铁悬臂梁，尺寸及载荷如图所示。

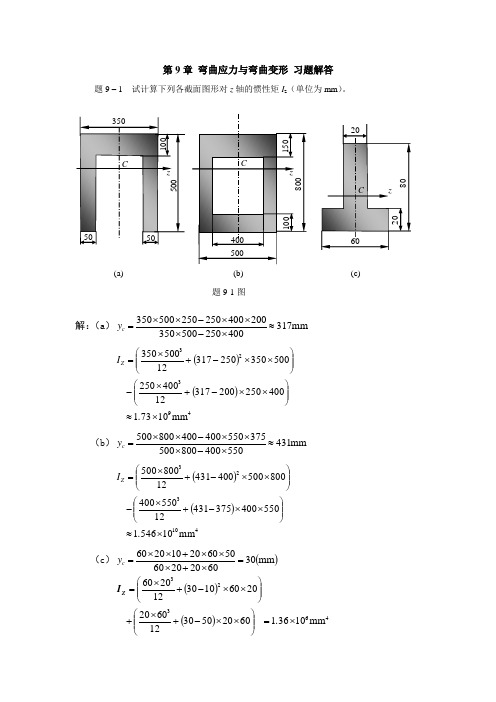
第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z （单位为mm ）。

解：（a ）mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （b ）mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （c ）()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a) (b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。

设q = 60kN/m ，F = 100kN 。

试求（1）梁1– 1截面上A 、B 两点的正应力。

（2）整个梁横截面上的最大正应力和最大切应力。

解：（1）求支反力kN 220100260=+⨯=A F （↑）m kN 32021001260⋅=⨯+⨯⨯=A M （ ） （2）画F S 、M 图（3）求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点：MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点：MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c （4）求最大正应力和最大切应力MPa 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzMPa 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。

第 五 章 弯 曲 应 力一、是非判断题1、设某段梁承受正弯矩的作用，则靠近顶面和靠近底面的纵向纤维分别是伸长的和缩短的。

（×）2、中性轴是梁的横截面与中性层的交线。

梁发生平面弯曲时，其横截面绕中性轴旋转。

（√）3、 在非均质材料的等截面梁中，最大正应力maxσ不一定出现在maxM的截面上。

（ × ）4、等截面梁产生纯弯曲时，变形前后横截面保持为平面，且其形状、大小均保持不变。

5、梁产生纯弯曲时，过梁内任一点的任一截面上的剪应力都等于零。

（ × ）6、控制梁弯曲强度的主要因素是最大弯矩值。

（ × ）7、横力弯曲时，横截面上的最大切应力不一定发生在截面的中性轴上。

（ √ ）二、填空题1、应用公式y I Mz=σ时，必须满足的两个条件是 满足平面假设 和 线弹性 。

2、跨度较短的工字形截面梁，在横力弯曲条件下，危险点可能发生在 翼缘外边缘 、 翼缘腹板交接处 和 腹板中心 处。

3、 如图所示的矩形截面悬臂梁，其高为h 、宽为b 、长为l ，则在其中性层的水平剪力4、梁的三种截面形状和尺寸如图所示，则其抗弯截面系数分别为226161bH BH -、 H Bh BH 66132- 和 Hbh BH 66132- 。

）2、 如图所示的两铸铁梁，材料相同，承受相同的载荷F 。

则当F 增大时，破坏的情况是 （ C ）。

A 同时破坏 ；B （a ）梁先坏 ；C （b ）梁先坏3、为了提高混凝土梁的抗拉强度，可在梁中配置钢筋。

若矩形截面梁的弯矩图如图所示，则梁内钢筋（图中虚线所示）配置最合理的是（ D ）x四、计算题1、长为l 的矩形截面梁，在自由端作用一集中力F ，已知m h 18.0=，m b 12.0=，m y 06.0=，m a 2=，kN F 1=，求C 截面上K 点的正应力。

解：MPa I y M Z C K1.21218.012.006.0210133=⨯⨯⨯⨯==σ2、⊥形截面铸铁悬臂梁，尺寸及载荷如图所示。

第四章 弯曲应力4-1 试求图示各梁中指定横截面上的剪力和弯矩。

解：（a ）m kN M kN F m kN M F s s ⋅−=−=⋅−==12 ,5 ,2 ,02211 （b ）m kN M kN F m kN M kN F s s ⋅=−=⋅==6 ,3 ,6 ,22211 （c ）m kN M kN F m kN M kN F s s ⋅−==⋅==6 ,4 ,4 ,42211 （d ） ,5 ,67.111m kN M kN F s ⋅==（e ）e e s e e s M M aMF M M a M F −=−=−=−=2211 ,4 ,4 ,4, e s M M F −==33 ,0 （f ）m kN M kN F m kN M kN F s s ⋅−=−=⋅−==25.15 ,81.11 ,25.15 ,5.122211 （g ）m kN M F m kN M kN F s s ⋅−==⋅−==40 ,0 ,45 ,302211（h ）34 ,0 ,1211 ,4302220101aq M F a q M a q F s s ====4-3 试利用载荷集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。

解：（a）（b）（c）（g）（d）（e）（f）4-4 试作下列具有中间铰的梁的剪力图和弯矩图。

解：有中间铰的梁的内力图画法与普通梁无异，关键是求出约束反力。

4-6 已知简支梁的剪力图如图所示。

试作梁的弯矩图和载荷图。

已知梁上没有集中力偶作用。

解：（a ）A 、B 、D 截面剪力突变，说明截面上有集中力作用，集中力的值等于该截面剪力的突变值。

CD 段剪力图为下斜直线，说明该段上有向下的均布载荷作用，载荷集度等于该段剪力图的斜率。

（b ）A 、C 、D 截面剪力突变，说明截面上有集中力作用，集中力的值等于相应截面上剪力的突变值。

AC 段剪力图为下斜直线，说明该段上有向下的均布载荷作用，载荷集度等于该段剪力图的斜率。

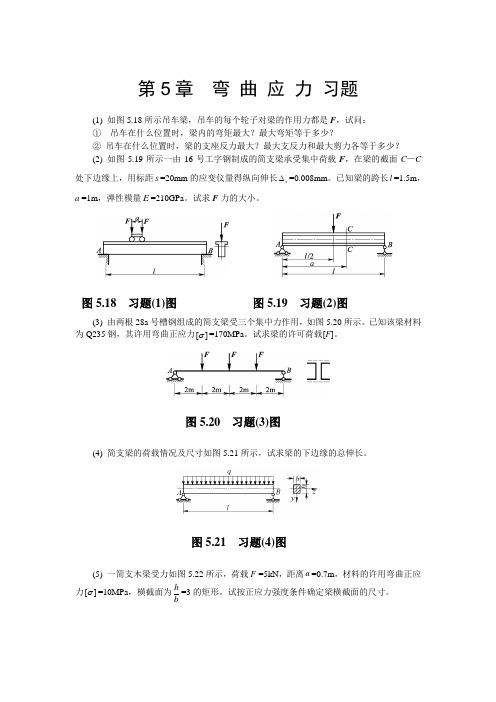
第5章 弯 曲 应 力 习题(1) 如图5.18所示吊车梁，吊车的每个轮子对梁的作用力都是F ，试问： ① 吊车在什么位置时，梁内的弯矩最大？最大弯矩等于多少？② 吊车在什么位置时，梁的支座反力最大？最大支反力和最大剪力各等于多少？(2) 如图5.19所示一由16号工字钢制成的简支梁承受集中荷载F ，在梁的截面C —C 处下边缘上，用标距s =20mm 的应变仪量得纵向伸长s ∆=0.008mm 。

已知梁的跨长l =1.5m ，a =1m ，弹性模量E =210GPa 。

试求F 力的大小。

图5.18 习题(1)图图5.19 习题(2)图(3) 由两根28a 号槽钢组成的简支梁受三个集中力作用，如图5.20所示。

已知该梁材料为Q235钢，其许用弯曲正应力[]σ=170MPa 。

试求梁的许可荷载[F ]。

图5.20 习题(3)图(4) 简支梁的荷载情况及尺寸如图5.21所示，试求梁的下边缘的总伸长。

图5.21 习题(4)图(5) 一简支木梁受力如图5.22所示，荷载F =5kN ，距离a =0.7m ，材料的许用弯曲正应力[]σ=10MPa ，横截面为bh =3的矩形。

试按正应力强度条件确定梁横截面的尺寸。

图5.22 习题(5)图(6) 如图5.23所示，一矩形截面简支梁由圆柱形木料锯成。

已知F =5kN ， 1.5a =m ，[]σ=10MPa 。

试确定弯曲截面系数为最大时矩形截面的高宽比bh ，以及梁所需木料的最小直径d 。

图5.23 习题(6)图(7) 一正方形截面悬臂木梁的尺寸及所受荷载如图5.24所示。

木料的许用弯曲正应力[]σ=10MPa 。

现需在梁的截面C 上中性轴处钻一直径为d 的圆孔，试问在保证梁强度的条件下，圆孔的最大直径d (不考虑圆孔处应力集中的影响)可达多大？图5.24 习题(7)图(8) 当荷载F 直接作用在跨长为l =6m 的简支梁AB 之中点时，梁内最大正应力超过许可值30%。

第6章弯曲应力6-1 选择题答案：Aa σb σ材料和横截面均相同的两根梁，变形后其轴线为两同心圆弧，如图所示。

梁a 、b 内的最大弯曲正应力分别为和 ，则比较二者可知_____。

R aabR ba bσσ<a b σσ=a bσσ>A. B. C. D. 其大小关系不定 1=,,a a b b a b a b a bM EIR R M M M EI ρρρρσσρρ==>=<<，，显然，由知，所以6-2 选择题答案：C图示截面的抗弯截面模量 A.B.C. z W =_____。

32π1326d bh -43π16412d bh -431π1326d bh d ⎛⎫-⎪⎝⎭431π1326d bh h ⎛⎫-⎪⎝⎭D. 43max max π1,,64122z z z I d dW I bh y y ==-=其中bhzd6-3 选择题答案：B三根正方形截面梁如图所示，其长度、横截面面积和受力状态相同，其中(b)、(c)梁的截面为两个形状相同 的矩形拼合而成，拼合后无胶接。

在三根梁中，____梁内的最大正应力相等。

FAB(a)Fz(b)Fz 1 z 1b /2 (c)Fzb /2b /2 b /2A ．(a)和(b) B. (a)和(c) C. (b)和(c) D. (a)、 (b)和(c)max,(a)(c)z M Fl W =与相同。

3max 336=,6/6z b Fl FlW b bσ==max σ(b)12331max 3112,,/6224224z b b Fl b Flz W b bσ⎛⎫⎛⎫=⋅=== ⎪ ⎪⎝⎭⎝⎭所以 相等。

而 的两层截面各自的中性轴为(a)a Aa aBM 06-4 选择题答案：CA. B. C. D. 200GPa E =0M 43.010ε-=⨯max σ=图(a)所示工字钢简支梁，弹性模量 。

若在力偶矩 作用下测得横截面A 处梁顶面的纵向应变，则梁内最大弯曲正应力 _____。

班级： 学号： 姓名：《工程力学》弯曲应力测试题一、判断题（每小题2分，共20分）1、弯曲变形梁，其外力、外力偶作用在梁的纵向对称面内，梁产生对称弯曲。

（ √ ）2、铁路的钢轨制成工字形，只是为了节省材料。

（ × ）3、为了提高梁的强度和刚度，只能通过增加梁的支撑的办法来实现。

（ × ）4、中性轴是中性层与横截面的交线。

（ √ ）5、最大弯矩M max 只可能发生在集中力F 作用处，因此只需校核此截面强度是否满足梁的 强度条件。

（ × ）6、大多数梁只进行弯曲正应力强度校核，而不计算弯曲切应力，这是因为他们横截面上只有正应力存在。

（ × ）7、抗弯截面系数仅与截面形状和尺寸有关，与材料种类无关。

（ √ ）8、矩形截面梁，若其截面高度和宽度都增加一倍，则强度提高到原来的16倍。

（ × ）9、在梁的弯曲正应力公式中，I z 为梁截面对于形心轴的惯性矩。

（ √ ） 10、梁弯曲最合理的截面形状，是在横截面积相同条件下W z 值最大的截面形状。

（ √ ） 二、单项选择题（每小题2分，共20分）1、材料弯曲变形后（ B ）长度不变。

A ．外层 B ．中性层 C ．内层2、梁弯曲时横截面上的最大正应力在（ C ）。

A. 中性轴上B. 对称轴上C. 离中性轴最远处的边缘上3、一圆截面悬臂梁，受力弯曲变形时，若其它条件不变，而直径增加一倍，则其最大正 应力是原来的（ A ）倍。

A.81B. 8C. 2D.214、图示受横力弯曲的简支梁产生纯弯曲变形的梁段是（ D ）A. AC 段B. CD 段C. DB 段D. 不存在 5、由梁弯曲时的平面假设，经变形几何关系分析得到（ C ）A. 中性轴通过截面形心B. 梁只产生平面弯曲；C. y ερ=；D. 1zM EI ρ=6、图示的两铸铁梁，材料相同，承受相同的载荷F 。

当F 增大时，破坏的情况是（ C ）。

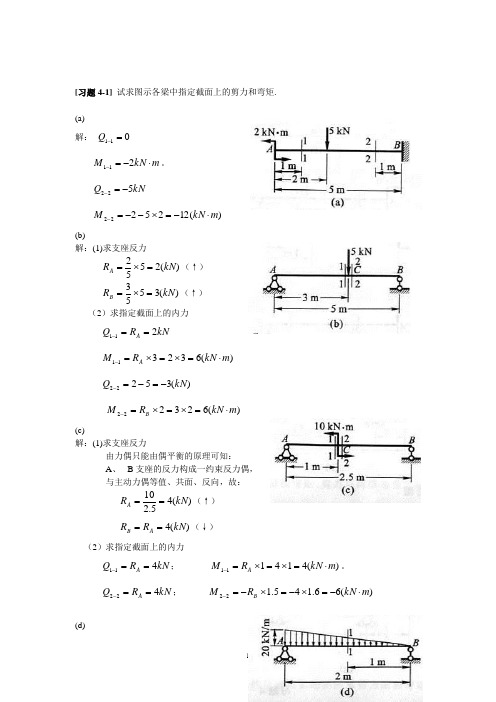
[习题4-1] 试求图示各梁中指定截面上的剪力和弯矩.(a)解： 011=-Qm kN M ⋅-=-211。

kN Q 522-=-)(1225222m kN M ⋅-=⨯--=-(b)解：(1)求支座反力)(2552kN R A =⨯=（↑） )(3553kN R B =⨯=（↑） （2）求指定截面上的内力kN R Q A 211==-)(632311m kN R M A ⋅=⨯=⨯=-)(35222kN Q -=-=-)(623222m kN R M B ⋅=⨯=⨯=-(c)解：(1)求支座反力由力偶只能由偶平衡的原理可知：A 、B 支座的反力构成一约束反力偶，与主动力偶等值、共面、反向，故：)(45.210kN R A ==（↑） )(4kN R R A B ==（↓）（2）求指定截面上的内力kN R Q A 411==-； )(414111m kN R M A ⋅=⨯=⨯=-。

kN R Q A 422==-； )(66.145.122m kN R M B ⋅-=⨯-=⨯-=-(d)解：(1)求支座反力因为AB 平衡，所以：① 0=∑A M032)20221(2=⨯⨯⨯-⋅B R )(667.6320kN R B ==（↑） ② 0=∑Y020221=⨯⨯-+B A R R 020667.6=-+A R)(333.13kN R A =（↑）（2）求指定截面上的内力kN R Q A 667.121)2010(333.1311-=⨯+-==-)(531)10121(1667.611m kN M ⋅=⨯⨯⨯-⨯=-。

（e ）解：(1)求支座反力由力偶只能由偶平衡的原理可知：A （左）、C （右）支座的反力构成一约束反力偶，与主动力偶等值、共面、反向，故：a M R e A 4=（↓）；aM R R e A C 4==（↑） （2）求指定截面上的内力a M R Q e A 411-=-=-； 4411e e A M a a M a R M -=⋅-=⨯-=-。

216-3、图示矩形截面梁受集中力作用，试计算1-1横截面上a 、b 、c 、d 四点的正应力。

解：（1）外力分析，判变形。

荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。

中性轴z 轴过形心C 与载荷垂直，沿水平方向。

（2）内力分析，弯矩图如图（b ）所示，1-1横截面的弯矩为：1115230(M-=-⨯=-⋅kN m )（3）应力分析，梁上边有弯矩图，上侧纤维受拉。

1-1横截面上的a 点处于拉伸区，正应力为正；c 点处于中性层上，正应力为零；b 、d 两点处于压缩区，正应力为负。

3111111m ax 2301011.1110.1800.36a a zzzM M M y y I I W σ---⨯=⋅=⋅===⨯⨯P a M P a 。

11.11b a σσ=-=-M Pa0c σ=31133010(0.1500.050)7.4110.1800.312d d zM y I σ-⨯=-⋅=-⨯-=-⨯⨯P a M P a37.5M kN ·m)V 图(kN )(a)(c)(b)30-(c)(e)(d)10102+q l /8M kN ·m)(f)20201z+25001150015bd (b)18015kNac (a)BqAlaz z az 22题6-3图 题6-5图6-5、两根矩形截面简支木梁受均布荷载q 作用，如图所示。

梁的横截面有两种情况，一是如图(b)所示是整体，另一种情况如图(c)所示是由两根方木叠合而成（二方木间不加任何联系且不考虑摩擦）。

若已知第一种情况整体时梁的最大正应力为10MPa ，试计算第二种情况时梁中的最大正应力，并分别画出危险截面上正应力沿高度的分布规律图示。

解：（1）外力分析，判变形。

荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。

第一种情况中性层为过轴线的水平纵向面，中性轴z 轴过整体形心C 与载荷垂直，沿水平方向。

而第二种情况，两根木梁以各自的水平纵向面为中性层发生弯曲，两根中性轴为与荷载垂直的水平形心主轴。

第七章 组合变形本章主要讨论建筑工程中常见的组合变形的强度计算问题。

其中斜弯曲、拉（压）与弯曲、偏心拉（压）组合变形的强度计算问题是本章的重点。

第一节 组合变形的概念前面的章节分别研究了杆件在轴向拉（压）、剪切、扭转、平面弯曲基本变形下的强度和刚度计算。

但在工程实际中，结构中一些杆件的受力情况是复杂的，往往同时发生两种或者两种以上的基本变形，这种由两种或两种以上的基本变形组合而成的变形称为组合变形。

例如，图7-1a 所示的烟囱，除自重引起的轴向压缩外，还有水平方向的风力引起的弯曲变形，即同时产生两种基本变形。

又如，图7-1b 所示的备有吊车的厂房柱，作用在立柱上的荷载1F 和2F ,其合力的作用线一般不在立柱轴线上，此时，立柱即发生压缩变形又发生弯曲变形。

再如，图7-1c 所示的曲拐轴，在荷载F 作用下，曲拐AB 段同时发生扭转和弯曲变形。

上述这些杆件的变形，都是结构杆件发生组合变形的工程实例。

图7-1由上一章梁的弯曲可知：外力沿横向作用在梁的纵向对称平面内，梁将发生平面弯曲变形。

那么，外力虽然沿梁的横向（垂直于轴线），但不作用在纵向对称平面内时，梁会发生怎样的变形呢?实验及理论研究得知，此时梁轴线变形后弯成的曲线已不在荷载的作用平面内，即不属于平面弯曲，这种弯曲称为斜弯曲。

若外力不沿梁的横向（斜交于轴线），但力作用仍在纵向对称平面内，梁将发生拉（压）与弯曲组合变形。

若作用外力虽然沿杆件轴向方向，但不与轴线重合，杆件也将发生拉（压）与弯曲组合变形，称为偏心拉（压）。

对发生组合变形的杆件计算应力和变形时，可将荷载进行简化或分解，使简化或分解后得到的静力等效的荷载，每类荷载各自只引起一种基本变形，分别计算，再进行叠加，就得到由原来的荷载所引起的组合变形的应力和变形，这就是组合变形的分析方法和组合变形计算的叠加原理。

这里需要强调的是：叠加原理是在满足小变形和力与位移成线性关系的条件下才适用。

本章将主要讨论斜弯曲、拉压与弯曲、偏心拉伸（压缩）组合变形的强度计算问题。