初二数学《分式》能力测试题

初二数学分式有意义练习题分式在数学中占据着重要的地位，它们是我们在解决实际问题中常常会遇到的形式。

为了提高初二学生解决分式相关问题的能力，以下是一些有意义的练习题。

1. 甲班有 120 名学生，乙班有 150 名学生。

如果甲班的学生又增加了 1/3，而乙班的学生又减少了 1/4，两班现在的学生人数相等了。

求甲班增加的学生人数。

解答:设甲班增加的学生人数为 x。

则甲班现在的学生人数为 120 + x，乙班现在的学生人数为 150 - 1/4 * 150 = 150 - 37.5 = 112.5。

根据题意，有 120 + x = 112.5。

解方程可得 x = 112.5 - 120 = -7.5。

由于人数不能是负数，所以甲班增加的学生人数为 0，即甲班没有增加学生。

2. 甲乙丙三个水龙头同时放水，甲水龙头每分钟放水 1/4 升，乙水龙头每分钟放水 1/3 升，丙水龙头每分钟放水 1/5 升。

如果三个水龙头同时放水 5 分钟后，一共放了多少升水？解答:甲水龙头每分钟放水 1/4 升，所以 5 分钟后甲水龙头放了 5 * 1/4 =5/4 升水。

乙水龙头每分钟放水 1/3 升，所以 5 分钟后乙水龙头放了 5 * 1/3 =5/3 升水。

丙水龙头每分钟放水 1/5 升，所以 5 分钟后丙水龙头放了 5 * 1/5 =1 升水。

三个水龙头共放水量为 5/4 + 5/3 + 1 = 8/4 + 5/3 + 1 = 21/4 升水。

所以，五分钟后三个水龙头一共放了 21/4 升水。

通过以上的两个例题，我们可以看到分式在解决实际问题中的应用。

希望同学们通过这些练习题的实践，能够更好地理解和掌握数学中的分式知识。

初二人教版数学分式练习题分式是数学中的重要概念，初中数学中也有大量的分式运算和解题。

下面是一些初二人教版数学中的分式练习题，希望能帮助同学们更好地理解和掌握分式的知识。

1. 求下列各分式的值：a) $\frac{3}{4} + \frac{1}{2}$b) $\frac{2}{3} - \frac{5}{6}$c) $\frac{3}{5} \times \frac{4}{9}$d) $\frac{2}{3} \div \frac{3}{4}$2. 化简下列各分式：a) $\frac{24}{36}$b) $\frac{10x}{12y}$c) $\frac{16a^2}{12b^3}$d) $\frac{3m^2n^3}{4m^5n^4}$3. 将下列混合数改写成带分数的形式：a) $2\frac{5}{6}$b) $4\frac{1}{3}$c) $5\frac{3}{4}$d) $7\frac{2}{5}$4. 计算下列各式的值：a) $5 - \frac{3}{4}$b) $3 \times \left(\frac{1}{5} - \frac{2}{3}\right)$c) $8 + \frac{1}{2} \div \frac{1}{4}$d) $(\frac{2}{3} - \frac{1}{4}) \times (\frac{3}{5} + \frac{2}{3})$5. 求下列各分式的最简形式：a) $\frac{12}{36}$b) $\frac{8x^2y^3}{12x^4y^2}$c) $\frac{9a^3b^2c^4}{6a^2bc^3}$d) $\frac{15x^2y^4z^3}{20x^3y^2z^2}$6. 求下列各分式的整数部分和小数部分：a) $\frac{7}{2}$b) $\frac{11}{4}$c) $\frac{23}{8}$d) $\frac{17}{5}$这些练习题旨在帮助同学们熟悉和巩固初二数学中的分式知识，并能够熟练运用分式进行计算和解题。

初二数学分式练习题及答案分式是数学中的重要概念，也是初中数学的基础知识之一。

在初中数学学习中，分式的运算是一个关键的内容。

为了帮助同学们更好地掌握分式的运算，以下将提供一些初二数学分式练习题及答案。

一、基础练习题1. 计算下列分式的值：(1) $\frac{2}{3}+\frac{1}{6}$(2) $\frac{5}{7}-\frac{2}{7}$(3) $\frac{3}{4}\times\frac{2}{5}$(4) $\frac{6}{13}\div\frac{2}{3}$2. 按照要求变换下列分式：(1) 化简：$\frac{4x^2-2x}{2x}$(2) 分解：$\frac{5}{xy}-\frac{7}{yx}$(3) 合并：$\frac{a}{b}\times\frac{b}{c}$(4) 变形：$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}$3. 求解方程：(1) $\frac{7}{10}x=\frac{35}{4}$(2) $\frac{5}{6}+\frac{x}{4}=\frac{7}{8}$(3) $\frac{3}{x}-\frac{2}{x-1}=\frac{5}{x(x-1)}$二、提高练习题1. 小明在旅行中用一辆摩托车以每小时40千米的速度行驶，计划经过$\frac{2}{5}$小时后休息10分钟，然后以每小时50千米的速度行驶到终点。

求小明旅行一段的总时间。

2. 甲，乙两个工程队共同进行一项工程，甲队完成全工程的$\frac{2}{5}$，乙队完成剩下的部分。

如果两队同时施工，还需6天可以完成全工程；如果只由甲队自行施工，需要10天完成全工程。

请问乙队自行施工需要多少天才能完成全工程？3. 甲、乙两人一起做一件工作，甲独立完成全工作需要8小时，乙独立完成全工作需要12小时。

他们两人合作完成全工作，需要多少小时？三、答案基础练习题答案：1.(1) $\frac{2}{3}+\frac{1}{6}=\frac{4}{6}+\frac{1}{6}=\frac{5}{6}$(2) $\frac{5}{7}-\frac{2}{7}=\frac{3}{7}$(3)$\frac{3}{4}\times\frac{2}{5}=\frac{3\times2}{4\times5}=\frac{3}{10}$(4)$\frac{6}{13}\div\frac{2}{3}=\frac{6}{13}\times\frac{3}{2}=\frac{6}{13 }\times\frac{3}{2}=\frac{9}{13}$2.(1) 化简：$\frac{4x^2-2x}{2x} = \frac{2x(2x-1)}{2x}=2x-1$(2) 分解：$\frac{5}{xy}-\frac{7}{yx}=\frac{5}{xy}-\frac{7}{xy}=\frac{5-7}{xy}=-\frac{2}{xy}$(3) 合并：$\frac{a}{b}\times\frac{b}{c}=\frac{a\times b}{b\timesc}=\frac{a}{c}$(4) 变形：$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}$ 通过分数的通分，两边同乘以$xy$得到等式$\frac{xy}{x}+\frac{xy}{y}=x+y$，化简得到$x+y=x+y$3.(1) $\frac{7}{10}x=\frac{35}{4}$，两边同乘以$\frac{10}{7}$得到等式$x=\frac{35}{4}\times\frac{10}{7}=\frac{25}{2}$(2) $\frac{5}{6}+\frac{x}{4}=\frac{7}{8}$，先通分得到等式$\frac{10}{12}+\frac{3x}{12}=\frac{7}{8}$，化简得到$\frac{10+3x}{12}=\frac{7}{8}$，两边同乘以12得到$10+3x=12\times\frac{7}{8}$，解方程得到$x=\frac{63}{8}$(3) $\frac{3}{x}-\frac{2}{x-1}=\frac{5}{x(x-1)}$，先通分得到等式$\frac{3(x-1)-2x}{x(x-1)}=\frac{5}{x(x-1)}$，化简得到$\frac{3x-3-2x}{x(x-1)}=\frac{5}{x(x-1)}$，整理得到$\frac{x-3}{x(x-1)}=\frac{5}{x(x-1)}$，可以得到方程$x-3=5$，解方程得到$x=8$。

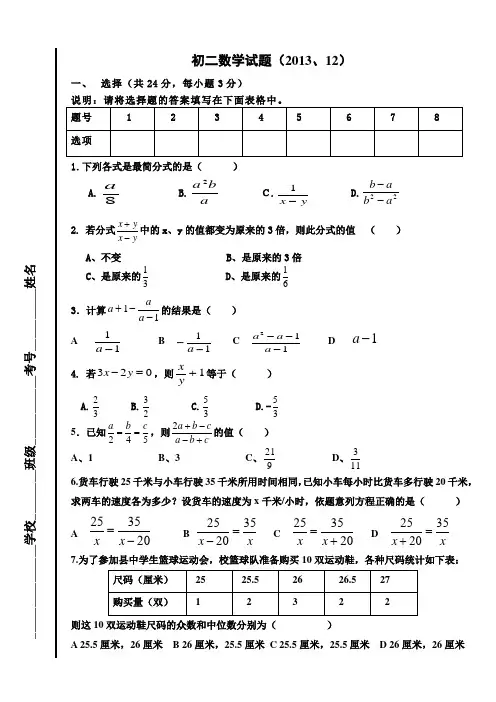
初二数学试题（2013、12）一、 选择（共24分，每小题3分）1.下列各式是最简分式的是（ ）A.8aB.a b a 2 Ｃ.yx -1D.22a b a b -- 2. 若分式x yx y+-中的x 、y 的值都变为原来的3倍，则此分式的值 （ ） A 、不变 B 、是原来的3倍C 、是原来的13D 、是原来的163．计算11--+a aa 的结果是（ ） A 11-a B 11--a C 112---a a a D1-a4. 若023=-y x ，则1+yx等于（ ） A.32 B.23 C.35 D.-35 5．已知542c b a ==，则cb a cb a +--+2的值（ ）A 、1B 、3C 、921 D 、1136.货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x 千米/小时，依题意列方程正确的是（ ） A203525-=x x B x x 352025=-C 203525+=x xD xx 352025=+ 7.为了参加县中学生篮球运动会，校篮球队准备购买10双运动鞋，各种尺码统计如下表：则这10双运动鞋尺码的众数和中位数分别为（ ）A 25.5厘米，26厘米B 26厘米，25.5厘米C 25.5厘米，25.5厘米D 26厘米，26厘米_______________学校________班级___________考号__________姓名8.有8个数的平均数是12，还有12个数的平均数是17，则这20个数的平均数是（ ） A 15.6 B 15.9 C 15 D 14 二、填空题（共24分，每小题3分） 1、当______x 时，分式55+x x有意义； 2、当x= 时，分式392+-x x 的值为0；3、某工厂原计划a 天完成b 件产品，若现在需要提前x 天完成，则现在每天要比原来多生产产品__________ 件；4、m 取 时，方程323-=--x m x x 会产生增根； 5、分式,21x xy y51,212-的最简公分母为 。

第十六章 分式单元复习一、选择题1．下列各式中，不是分式方程的是（ ） 2．如果分式2||55x x x-+的值为0，那么x 的值是（ ）A ．0B ．5C ．－5D ．±5 3．把分式22x yx y+-中的x ，y 都扩大2倍，则分式的值（ ）A ．不变B ．扩大2倍C ．扩大4倍D ．缩小2倍 4．下列分式中，最简分式有（ ）A ．2个B ．3个C ．4个D ．5个 5．分式方程2114339x x x +=-+-的解是（ ） A ．x=±2 B ．x=2 C ．x=－2 D ．无解6．若2x+y=0，则2222x xy y xy x++-的值为（ ） A ．－13.55B - C ．1 D ．无法确定7．关于x 的方程233x k x x =+--化为整式方程后，会产生一个解使得原分式方程的最简公分母为0，则k 的值为（ ）A ．3B ．0C ．±3D ．无法确定 8．使分式224x x +-等于0的x 值为（ ） A ．2 B ．－2 C ．±2 D ．不存在 9．下列各式中正确的是（ ） 10．下列计算结果正确的是（ ） 二、填空题1．若分式||55y y--的值等于0，则y= __________ ． 2．在比例式9:5=4:3x 中，x=_________________ ．3．计算:1111b a b a a b a b++---=_________________ ．4．当x> __________时，分式213x--的值为正数．5．计算:1111x x++-=_______________ ． 6．当分式2223211x x x x x +++--与分式的值相等时，x 须满足_______________ ． 7．已知x+1x =3，则x 2+21x = ________ ． 8．已知分式212x x +-:当x= _ 时，分式没有意义；当x= _______时，分式的值为0；当x=－2时，分式的值为_______．9．当a=____________时，关于x 的方程23ax a x +-=54的解是x=1．10．一辆汽车往返于相距akm 的甲、乙两地，去时每小时行mkm ，•返回时每小时行nkm ，则往返一次所用的时间是_____________． 三、解答题 1．计算题: 2．化简求值．（1）（1+11x -）÷（1－11x -），其中x=－12； （2）213(2)22x x x x x -÷-+-++，其中x=12． 3．解方程: （1）1052112x x +--=2； （2）2233111x x x x +-=-+-．4．课堂上，李老师给大家出了这样一道题：当x=3，5－求代数式22212211x x x x x -+-÷-+的值．小明一看，说：“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？•请你写出具体的解题过程． 5．对于试题：“先化简，再求值：23111x x x----，其中x=2．”小亮写出了如下解答过程：∵2313111(1)(1)1x x x x x x x ---=----+- ① 31(1)(1)(1)(1)x x x x x x -+--+-+ ②=x －3－（x+1）=2x －2， ③ ∴当x=2时，原式=2×2－2=2． ④（1）小亮的解答在哪一步开始出现错误： ① （直接填序号）；（2）从②到③是否正确： 不正确 ；若不正确，错误的原因是 把分母去掉了 ； （3）请你写出正确的解答过程．6．小亮在购物中心用12.5元买了若干盒饼干，但他在一分利超市发现，同样的饼干，这里要比购物中心每盒便宜0.5元．因此当他第二次买饼干时，便到一分利超市去买，如果用去14元，买的饼干盒数比第一次买的盒数多25，•问他第一次在购物中心买了几盒饼干？ 答案一、选择题1．下列各式中，不是分式方程的是（D ） 2．如果分式2||55x x x-+的值为0，那么x 的值是（B ）A ．0B ．5C ．－5D ．±5 3．把分式22x yx y+-中的x ，y 都扩大2倍，则分式的值（A ）A ．不变B ．扩大2倍C ．扩大4倍D ．缩小2倍 4．下列分式中，最简分式有（C ）A ．2个B ．3个C ．4个D ．5个 5．分式方程2114339x x x +=-+-的解是（B ） A ．x=±2 B ．x=2 C ．x=－2 D ．无解6．若2x+y=0，则2222x xy y xy x++-的值为（B ）A ．－13.55B - C ．1 D ．无法确定7．关于x 的方程233x k x x =+--化为整式方程后，会产生一个解使得原分式方程的最简公分母为0，则k 的值为（A ）A ．3B ．0C ．±3D ．无法确定 8．使分式224x x +-等于0的x 值为（D ） A ．2 B ．－2 C ．±2 D ．不存在 9．下列各式中正确的是（C ） 10．下列计算结果正确的是（B ） 二、填空题 1．若分式||55y y--的值等于0，则y= －5 ． 2．在比例式9：5=4：3x 中，x=2027． 3．1111b a b a a b a b ++---的值是 2()a b ab+ ．4．当x> 13 时，分式213x --的值为正数．5．1111x x ++-= 221x - ． 6．当分式2223211x x x x x +++--与分式的值相等时，x 须满足 x ≠±1 ． 7．已知x+1x =3，则x 2+21x = 7 ． 8．已知分式212x x +-，当x= 2 时，分式没有意义；当x= －12 时，分式的值为0；当x=－2时，分式的值为 34．9．当a= －173 时，关于x 的方程23ax a x +-=54的解是x=1．10．一辆汽车往返于相距akm 的甲、乙两地，去时每小时行mkm ，•返回时每小时行nkm ，则往返一次所用的时间是 （a am n+）h ． 三、解答题 1．计算题．2．化简求值．（1）（1+11x -）÷（1－11x -），其中x=－12； 解：原式=1111111122x x x x xx x x x x -+---÷==-----．当x=－12时，原式=15．（2）213(2)22x x x x x -÷-+-++，其中x=12． 解：原式=22(1)(2)(2)3121(2)(1)2211x x x x x x x x x x ---+++÷=-=-+-++--． 当x=12时，原式=43．3．解方程．（1）1052112x x +--=2； 解：x=74．（2）2233111x x x x +-=-+-． 解：用（x+1）（x －1）同时乘以方程的两边得， 2（x+1）－3（x －1）=x+3． 解得 x=1． 经检验，x=1是增根． 所以原方程无解．4．课堂上，李老师给大家出了这样一道题：当x=3，5－求代数式22212211x x x x x -+-÷-+的值．小明一看，说：“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？•请你写出具体的解题过程．解：原式=2(1)1(1)(1)2(1)x x x x x -++--=12．由于化简后的代数中不含字母x ，故不论x 取任何值，所求的代数式的值始终不变．所以当x=3，5－12． 5．对于试题：“先化简，再求值：23111x x x----，其中x=2．”小亮写出了如下解答过程：∵2313111(1)(1)1x x x x x x x ---=----+- ① 31(1)(1)(1)(1)x x x x x x -+--+-+ ②=x －3－（x+1）=2x －2， ③ ∴当x=2时，原式=2×2－2=2． ④（1）小亮的解答在哪一步开始出现错误： ① （直接填序号）；（2）从②到③是否正确： 不正确 ；若不正确，错误的原因是 把分母去掉了 ； （3）请你写出正确的解答过程． 解：正确的应是：23111x x x ----=312(1)(1)(1)(1)1x x x x x x x -++=-+-++ 当x=2时，原式=23．6．小亮在购物中心用12.5元买了若干盒饼干，但他在一分利超市发现，同样的饼干，这里要比购物中心每盒便宜0.5元．因此当他第二次买饼干时，便到一分利超市去买，如果用去14元，买的饼干盒数比第一次买的盒数多25，•问他第一次在购物中心买了几盒饼干？ 解：设他第一次在购物中心买了x 盒，则他在一分利超市买了75x 盒． 由题意得：12.51475x x -=0.5 解得 x=5．经检验，x=5是原方程的根．答：他第一次在购物中心买了5盒饼干．初中数学分式方程同步练习题一、选择题（每小题3分，共30分） 1．下列式子是分式的是（ ）A ．2x B ．x2C ．πxD ．2yx +2．下列各式计算正确的是（ ）A ．11--=b a b aB ．abb a b 2= C ．()0,≠=a ma na m n D ．a m a n m n ++=3．下列各分式中，最简分式是（ ）A ．()()y x y x +-73B ．n m n m +-22C ．2222ab b a b a +-D ．22222yxy x y x +-- 4．化简2293m m m --的结果是（ ）A.3+m m B.3+-m mC.3-m mD.m m -3 5．若把分式xyyx +中的x 和y 都扩大2倍，那么分式的值（ ）A ．扩大2倍B ．不变C ．缩小2倍D ．缩小4倍6．若分式方程xa xa x +-=+-321有增根，则a 的值是（ ） A ．1 B ．0 C ．—1 D ．—27．已知432c b a ==，则c b a +的值是（ ） A ．54 B. 47 C.1 D.458．一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？设江水的流速为x 千米/时，则可列方程（ ）A ．x x -=+306030100 B ．306030100-=+x xC ．x x +=-306030100D ．306030100+=-x x9．某学校学生进行急行军训练，预计行60千米的路程在下午5时到达，后来由于把速度加快20% ，结果于下午4时到达，求原计划行军的速度。

第十六章分式单元复习一、选择题1．以下各式中，不是分式方程的是〔〕111..(1)1111.1.[(1)1]110232x A B x x x xx x x C D x x x-=-+=-+=--=+- 2．如果分式2||55x x x-+的值为0，那么x 的值是〔〕 A ．0 B ．5 C ．－5 D ．±53．把分式22x y x y+-中的x ，y 都扩大2倍，那么分式的值〔〕 A ．不变 B ．扩大2倍 C ．扩大4倍 D ．缩小2倍4．以下分式中，最简分式有〔〕322222222222212,,,,312a x y m n m a ab b x x y m n m a ab b -++-++---- A ．2个 B ．3个 C ．4个 D ．5个5．分式方程2114339x x x +=-+-的解是〔〕 A ．x=±2 B ．x=2 C ．x=－2 D ．无解6．假设2x+y=0，那么2222x xy y xy x++-的值为〔〕 A ．－13.55B -C ．1D ．无法确定 7．关于x 的方程233x k x x =+--化为整式方程后，会产生一个解使得原分式方程的最简公分母为0，那么k 的值为〔〕 A ．3 B ．0 C ．±3 D ．无法确定8．使分式224x x +-等于0的x 值为〔〕 A ．2 B ．－2 C ．±2 D ．不存在9．以下各式中正确的选项是〔〕....a b a b a b a bA B a b a b a b a b a ba ba b a b C D a b a b a b b a -++--==-----++--+-+-==-+-+-10．以下计算结果正确的选项是〔〕22222211..()223..()955b a a b A B a ab a b aba a m n n xy xy C D xy x x m a a --=-÷-=-÷=÷= 二、填空题1．假设分式||55y y--的值等于0，那么y=__________． 2．在比例式9:5=4:3x 中，x=_________________ ．3．计算:1111b a b a a b a b++---=_________________ ． 4．当x> __________时，分式213x--的值为正数． 5．计算:1111x x ++-=_______________ ． 6．当分式2223211x x x x x +++--与分式的值相等时，x 须满足_______________． 7．x+1x =3，那么x 2+21x= ________． 8．分式212x x +-:当x= _时，分式没有意义；当x= _______时，分式的值为0；当x=－2时，分式的值为_______． 9．当a=____________时，关于x 的方程23ax a x +-=54的解是x=1． 10．一辆汽车往返于相距akm 的甲、乙两地，去时每小时行mkm ，•返回时每小时行nkm ，那么往返一次所用的时间是_____________．三、解答题1．计算题:2222444(1)(4);282a a a a a a a --+÷-+--222132(2)(1).441x x x x x x x --+÷+-+-2．化简求值．〔1〕〔1+11x -〕÷〔1－11x -〕，其中x=－12；〔2〕213(2)22xx x x x -÷-+-++，其中x=12．3．解方程: 〔1〕1052112x x +--=2；〔2〕2233111x x x x +-=-+-．4．课堂上，李教师给大家出了这样一道题：当x=3，5－22212211x x x x x -+-÷-+的值．小明一看，说：“太复杂了，怎么算呢？〞你能帮小明解决这个问题吗？•请你写出具体的解题过程．5．对于试题：“先化简，再求值：23111x x x ----，其中x=2．〞小亮写出了如下解答过程： ∵2313111(1)(1)1x x x x x x x ---=----+-① 31(1)(1)(1)(1)x x x x x x -+--+-+② =x －3－〔x+1〕=2x －2， ③∴当x=2时，原式=2×2－2=2． ④〔1〕小亮的解答在哪一步开场出现错误：①〔直接填序号〕；〔2〕从②到③是否正确： 不正确 ；假设不正确，错误的原因是 把分母去掉了 ；〔3〕请你写出正确的解答过程．6．小亮在购物中心用12.5元买了假设干盒饼干，但他在一分利超市发现，同样的饼干，这里要比购物中心每盒廉价0.5元．因此当他第二次买饼干时，便到一分利超市去买，如果用去14元，买的饼干盒数比第一次买的盒数多25，•问他第一次在购物中心买了几盒饼干？答案一、选择题1．以下各式中，不是分式方程的是〔D 〕111..(1)1111.1.[(1)1]110232x A B x x x x x x x C D x x x -=-+=-+=--=+-2．如果分式2||55x x x -+的值为0，那么x 的值是〔B 〕A ．0B ．5C ．－5D ．±53．把分式22x yx y +-中的x ，y 都扩大2倍，那么分式的值〔A 〕A ．不变B ．扩大2倍C ．扩大4倍D ．缩小2倍4．以下分式中，最简分式有〔C 〕322222222222212,,,,312a x y m n m a ab b x x y m n m a ab b -++-++----A ．2个B ．3个C ．4个D ．5个5．分式方程2114339x x x +=-+-的解是〔B 〕A ．x=±2B ．x=2C ．x=－2D ．无解6．假设2x+y=0，那么2222x xy y xy x ++-的值为〔B 〕A ．－13.55B - C ．1 D ．无法确定7．关于x 的方程233x k x x =+--化为整式方程后，会产生一个解使得原分式方程的最简公分母为0，那么k 的值为〔A 〕 A ．3 B ．0 C ．±3 D ．无法确定8．使分式224x x +-等于0的x 值为〔D 〕 A ．2 B ．－2 C ．±2 D ．不存在9．以下各式中正确的选项是〔C 〕....a b a b a b a bA B a b a b a b a b a ba ba b a b C D a b a b a b b a -++--==-----++--+-+-==-+-+- 10．以下计算结果正确的选项是〔B 〕22222211..()223..()955b a a b A B a ab a b aba a m n n xy xy C D xy x x m a a --=-÷-=-÷=÷= 二、填空题1．假设分式||55y y --的值等于0，那么y=－5 ． 2．在比例式9：5=4：3x 中，x=2027． 3．1111b a b a a b a b ++---的值是 2()a b ab+ ． 4．当x> 13 时，分式213x--的值为正数． 5．1111x x ++-= 221x - ． 6．当分式2223211x x x x x +++--与分式的值相等时，x 须满足 x ≠±1 ． 7．x+1x =3，那么x 2+21x= 7 ． 8．分式212x x +-，当x= 2 时，分式没有意义；当x= －12 时，分式的值为0；当x=－2时，分式的值为 34． 9．当a= －173 时，关于x 的方程23ax a x +-=54的解是x=1． 10．一辆汽车往返于相距akm 的甲、乙两地，去时每小时行mkm ，•返回时每小时行nkm ，那么往返一次所用的时间是 〔a a m n+〕h ． 三、解答题1．计算题．2222222444(1)(4);28241(2)1.(2)(4)424a a a a a a a a a a a a a a --+÷-+----==-+--+解:原式 2222132(2)(1).441(1)(1)1(1)(2)1.(2)112x x x x x x x x x x x x x x x x --+÷+-+-+----==-+--解:原式 2．化简求值．〔1〕〔1+11x -〕÷〔1－11x -〕，其中x=－12； 解：原式=1111111122x x x x x x x x x x -+---÷==-----． 当x=－12时，原式=15． 〔2〕213(2)22x x x x x -÷-+-++，其中x=12． 解：原式=22(1)(2)(2)3121(2)(1)2211x x x x x x x x x x ---+++÷=-=-+-++--． 当x=12时，原式=43． 3．解方程．〔1〕1052112x x +--=2； 解：x=74． 〔2〕2233111x x x x +-=-+-． 解：用〔x+1〕〔x －1〕同时乘以方程的两边得，2〔x+1〕－3〔x －1〕=x+3．解得 x=1．经检验，x=1是增根．所以原方程无解．4．课堂上，李教师给大家出了这样一道题：当x=3，5－22212211x x x x x -+-÷-+的值．小明一看，说：“太复杂了，怎么算呢？〞你能帮小明解决这个问题吗？•请你写出具体的解题过程．解：原式=2(1)1(1)(1)2(1)x x x x x -++--=12． 由于化简后的代数中不含字母x ，故不管x 取任何值，所求的代数式的值始终不变．所以当x=3，5－12． 5．对于试题：“先化简，再求值：23111x x x ----，其中x=2．〞小亮写出了如下解答过程： ∵2313111(1)(1)1x x x x x x x ---=----+-① 31(1)(1)(1)(1)x x x x x x -+--+-+② =x －3－〔x+1〕=2x －2， ③∴当x=2时，原式=2×2－2=2． ④〔1〕小亮的解答在哪一步开场出现错误：①〔直接填序号〕；〔2〕从②到③是否正确： 不正确 ；假设不正确，错误的原因是 把分母去掉了 ；〔3〕请你写出正确的解答过程．解：正确的应是：23111x x x ----=312(1)(1)(1)(1)1x x x x x x x -++=-+-++ 当x=2时，原式=23． 6．小亮在购物中心用12.5元买了假设干盒饼干，但他在一分利超市发现，同样的饼干，这里要比购物中心每盒廉价0.5元．因此当他第二次买饼干时，便到一分利超市去买，如果用去14元，买的饼干盒数比第一次买的盒数多25，•问他第一次在购物中心买了几盒饼干？解：设他第一次在购物中心买了x 盒，那么他在一分利超市买了75x 盒． 由题意得：12.51475x x -=0.5 解得 x=5．经检验，x=5是原方程的根．答：他第一次在购物中心买了5盒饼干．初中数学分式方程同步练习题一、选择题〔每题3分，共30分〕1．以下式子是分式的是〔 〕A ．2xB ．x 2C ．πxD ．2y x + 2．以下各式计算正确的选项是〔 〕A ．11--=b a b aB ．abb a b 2= C ．()0,≠=a ma na m n D ．a m a n m n ++= 3．以下各分式中，最简分式是〔 〕A ．()()y x y x +-73B ．n m n m +-22C ．2222ab b a b a +-D ．22222y xy x y x +-- 4．化简2293m m m --的结果是〔 〕 A.3+m m B.3+-m m C.3-m m D.m m -3 5．假设把分式xy y x +中的x 和y 都扩大2倍，那么分式的值〔 〕 A ．扩大2倍 B ．不变 C ．缩小2倍 D ．缩小4倍6．假设分式方程xa x a x +-=+-321有增根，那么a 的值是〔 〕 A ．1 B ．0 C ．—1 D ．—27．432c b a ==，那么c b a +的值是〔 〕A ．54 B. 47 C.1 D.458．一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？设江水的流速为x 千米/时，那么可列方程〔 〕A ．x x -=+306030100B ．306030100-=+x x C ．x x +=-306030100D ．306030100+=-x x 9．某学校学生进展急行军训练，预计行60千米的路程在下午5时到达，后来由于把速度加快20%，结果于下午4时到达，求原方案行军的速度。

初二数学分式练习题带答案1、在11x2?13xy3x22?x?y、a?1m中分式的个数有有意义，则x应满足A．x≠-1B．x≠C．x≠±1D．x≠-1且x≠2、下列约分正确的是Axx2?x3； Bx?yx?y?0； Cx?y12xy21x2?xy?x； D4x2y?24、如果把分式xyx?y中的x和y都扩大2倍，则分式的值 A、扩大4倍；B、扩大2倍；C、不变；D缩小2倍5、化简m2?3m9?m2的结果是A、mm? B、?mmmm?3C、m?D、3?m6、下列分式中,最简分式是A.a?bx2?2?ab?aB.x2?y2x?yC.4x?D.a2?4a??a7、根据分式的基本性质，分式a?b可变形为aa?a?bb?a?aa?a?ba?b8、对分式y2x，x3y，124xy通分时，最简公分母是 A．24x2y B．12ｘ2ｙＣ．24ｘｙＤ．12ｘｙ、下列式子x?y1b?aa?bx2?y2?x?y；c?a?a?c；b?aa?b??1；?x?yx?y?x?y?x?y中正确个数有 A 、1个 B 、个 C、个 D、个 10、x-y的倒数的相反数 A．-1x?y B．1?x?y C．1x?y D．?1x?y二、填空题11、当x 时，分式1x?5有意义.12、当x 时，分式x2?1x?1的值为零。

13、当x=1x-y2,y=1时，分式xy-1的值为_________________14、计算：yx?y?x?y????x??15、用科学计数法表示：—aa16、如果b?23，那么a?b?____ 。

17、若x?5x?4?14?x?5有增根，则增根为___________。

?118、20080-22+??1?3??=?19、方程7x?2?5x的解是。

0、某工厂库存原材料x吨，原计划每天用a 吨，若现在每天少用b吨，则可以多用天。

三、解答题21、计算题1?a2a?a?1x2?2x?1x2?1?x?1x2?x22、先化简，再求值：???1?1?x?1???xx2?1，其中：x=-223、解方程2x?3?3x3x?1x?2?xx?1?124、勐捧中学162班和163班的学生去河边抬砂到校园内铺路，经统计发现：162班比163班每小时多抬30kg，162班抬900kg所用的时间和163班抬600kg所用的时间相等，两个班长每小时分别抬多少砂？25、已知y=x?1，x取哪些值时：?3xy的值是零；分式无意义； y的值是正数； y的值是负数．第16章分式参考答案11. x≠12. x=1 13. 1y314. ?3x15. -3.02?10 16.?4217. x=418. 0 19． x=-5x20.a?b三、解答题分式练习题一、选择题：1.下列运算正确的是A.x10÷x5=xB.x-4·x=x-C.x3·x2=xD.-3=-8x62. 一件工作,甲独做a小时完成,乙独做b小时完成,则甲、乙两人合作完成需要小时. 1111ab? B. C. D. ababa?ba?bab?3.化简等于 a?ba?bA.a2?b22a2?b22A. B. C.D.2222a?ba?ba?ba?bx2?44.若分式2的值为零,则x的值是 x?x?2A.2或-2B.2C.-2D.45y5.不改变分式的值,把分子、分母中各项系数化为整数,结果是x?y32x?A.2x?15y4x?5y6x?15y12x?15yB.C.D.x?3y4x?6y4x?y4x?2ya?2a?b14a,②,③,④中,最简分式有a2?3a2?b2x?2126.分式:①A.1个B.2个C.3个D.4个7.计算?A. -x?4x?x的结果是 ????x?2x?2?2?x11B.C.-1D.1 x?2x?2x?ac? 有解,则必须满足条件.若关于x的方程b?xdA. a≠b ，c≠dB. a≠b ，c≠-dC.a≠-b , c≠dC.a ≠-b , c≠-d9.若关于x的方程ax=3x-5有负数解,则a的取值范围是A.a C.a≥D.a≤310.解分式方程236??2,分以下四步,其中,错误的一步是 x?1x?1x?1A.方程两边分式的最简公分母是B.方程两边都乘以,得整式方程2+3=6C.解这个整式方程,得x=1D.原方程的解为x=1二、填空题:11.把下列有理式中是分式的代号填在横线上．x2?1m2?1x52213m?2－3x；；xy?7xy；－x；；；－； . x?1?yy?3380.512.当a时，分式-1a?1有意义．a?313.若则x+x=__________.14.某农场原计划用m天完成A公顷的播种任务,如果要提前a天结束,那么平均每天比原计划要多播种_________公顷.?1?15.计算????5?0的结果是_________. ?2?2?1s1?s,则t=___________. t?1xm?2?17.当m=______时,方程会产生增根. x?3x?316.已知u=18.用科学记数法表示:12.5毫克=________吨.19.当x 时，分式3?x的值为负数．?xx2y220.计算·=____________. ?2x?yy?x三、计算题:6x?5xy2x4yx2?21.?; 2.. ???x1?xx2?xx?yx?yx4?y4x2?y2四、解方程:3.1212??2。

分式方程姓名——1. 在以下方程中，对于x 的分式方程的个数（ a 为常数）有（）① 1x22 x 4 0② . x 4③ . 2 3a⑥ x 1 x 12 . 个个个个aaa 4; ④ .x 29 1; ⑤ 1 6; xx3 x 22. 方程15 3 的根是（）x 2x 111 xA. x =1B.x =-1C.x =3D.x =24 40, 那么283. 1的值是（）xx 2x4 以下分式方程去分母后所得结果正确的选项是（ ）A.1x 2去分母得， x1(x 1)( x 2) 1 ；1x1x 1B.x51 ，去分母得， x 52 x 5 ；52x2x 5C.x2 x 2 x x ，去分母得， ( x 2)2 x 2 x(x2) ；x2 x 2 42D.21 , 去分母得，2 ( x 1)x 3 ；x3x 15 . 赵强同学借了一本书，共280 页，要在两周借期内读完 . 当他读了一半书时，发现均匀每日要多读21 页才能在借期内读完 . 他读前一半时，均匀每日读多少页假如设读前一半时，均匀每日读 x 页，则下边所列方程中，正确的是 ()A. 140140 =14B. 280280 =14 xx 21xx 21 C. 140140 =14 D.1010 =1xx 21xx 216. 对于 x 的方程m1 x x 10 ，有增根，则 m 的值是（） A3x 17 若方程AB2 x 1, 那么 A 、 B 的值为（）x 3x 4( x 3)( x4)， 1 ， 2， 1， -18 假如 xa 1,b 0, 那么ab （ ）1B.x1 C. x 1 D.x 1b3a b 2xx1xx19 使分式4与的值相等的 x 等于（）x 2x 6 x 24 x 2 5x 6二、填空题（每题 3 分，共 30 分）10 知足方程：12的 x 的值是 ________.x 1 x 211当 x=________时，分式1x的值等于1. 5x212分式方程x22x0 的增根是. x213一汽车从甲地开往乙地，每小时行驶v1千米， t 小时可抵达，假如每小时多行驶v2千米，可提早抵达__小时 . 14农机厂员工到距工厂15 千米的某地检修农机，一部分人骑自行车先走40 分钟后，其他人乘汽车出发，结果他们同时抵达，已知汽车速度为自行车速度的 3 倍，若设自行车的速度为x 千米/时，则所列方程为.15 已知x4 ,则x2y 2. y5x 2y 216 a时，对于 x 的方程x12a3的解为零 . x2a517飞机从 A 到 B 的速度是v1,，返回的速度是v2，来回一次的均匀速度是.18当 m时，对于 x 的方程m21有增根 . x29x 3x 319某市在旧城改造过程中，需要整修一段全长2400m 的道路．为了尽量减少施工对城市交通所造成的影响，实质工作效率比原计划提升了20%，结果提早8 小时达成任务．求原计划每小时修路的长度．若设原计划每小时修路x m，则依据题意可得方程.三、解答题（共 5 大题，共 60 分）20.解以下方程(1)14x4x 3x 1（3）x1．23(2)x2 4 x 2x 21x2x 3x x 2421 有一项工程，若甲队独自做，恰幸亏规定日期达成，若乙队独自做要超出规定日期 3 天达成；此刻先由甲、乙两队合做 2 天后，剩下的工程再由乙队独自做，也恰幸亏规定日期达成，问规定日期多少天22 小兰的妈妈在供销大厦用元买了若干瓶酸奶，但她在百货商场食品自选室内发现，相同的酸奶，这里要比供销大厦每瓶廉价元钱，所以，当第二次买酸奶时，便到百货商场去买，结果用去元钱，买的瓶数比第一次买的瓶数多35倍，问她第一次在供销大厦买了几瓶酸奶第一讲分式的运算（一）、分式定义及相关题型题型一：考察分式的定义b , x2y21【例 1】以下代数式中：x ,1x y,a, x y ，是分式的有：.2a b x y x y 题型二：考察分式存心义的条件【例 2】当x有何值时，以下分式存心义（ 1）x4（2）3x（ 3）2（4）6x（ 5）1 x 4x22x21| x | 31xx题型三：考察分式的值为0 的条件【例 3】当x取何值时，以下分式的值为0.（ 1）x1（2） | x | 2（3） x 22x 3 x3x24x 2 5 x6题型四：考察分式的值为正、负的条件【例 4】（ 1）当x为什么值时，分式4为正；8x（ 2）当x 为什么值时，分式5x3(x1)2 为负；（ 3）当x为什么值时，分式x 2为非负数 .x3练习：1．当x取何值时，以下分式存心义：（ 1）1（2）3x（ 3）16 | x | 3( x 1) 2111x2．当x为什么值时，以下分式的值为零：（ 1）5| x 1 |（2）25x2 x 4x26x 53．解以下不等式（ 1）| x | 20（2）x2x50x12x3（二）分式的基天性质及相关题型1．分式的基天性质：A A M A MB B M B M2．分式的变号法例：a a a a bbbb题型一：化分数系数、小数系数为整数系数【例 1】不改变分式的值，把分子、分母的系数化为整数.12xy（ 1） 23（2）1 x 1 yb34题型二：分数的系数变号【例 2】不改变分式的值，把以下分式的分子、分母的首项的符号变成正号 .（ 1）x y （ 2）a （ 3）ax ya bb题型三：化简求值题【例 3】已知：11 5，求 2x3xy 2y的值 .xyx2xyy提示：整体代入，①x y5xy ，②转变出11 .xy【例 4】已知： x1 2 ，求 x 2 1的值 .xx 2【例 5】若 | x y1 | (2x3)2 0 ，求1 2y 的值 .4x练习：1．不改变分式的值，把以下分式的分子、分母的系数化为整数.0.2 y3 b（ 1）（2） 50.5 y11ab4 102．已知： x 13 ，求 x 21的值 .x3．已知：11 3 ，求2a3ab2b的值 .a bb ab a4．若a 22 a b 26 10 0，求 2a b 的值 .b 3a 5b5．假如 1x 2 ，试化简| x 2 |x 1 | x | 2x| x 1 |.x（三）分式的运算题型一：通分【例 1】将以下各式分别通分 .（ 1）cb a；（ 2）ab；2ab,3a 2 c ,5b 2c,a b 2b 2a（ 3）1 x2；（ 4） a2, 1 2x,1 2x x2 ,x 2x 2 2 ax题型二：约分【例 2】约分：（ 1） 16 x 2y ；（ 3） n2m 2；（3） x2x 2 .20xy 3m nx 2x 6题型三：分式的混淆运算【例 3】计算：（ 1） ( a 2b )3 (c 2)2( bc ) 4 ；（ 2） ( 3a3)3 ( x2y 2)(yx ) 2 ；c abaxyy x（ 3）m2 nn2 m ；（ 4）a 2a 1 ;m nn1n m m a （ 5） ( 2 x 24x 1) ( x 22x )x 4x 42x 1题型四：化简求值题【例 4】先化简后求值（ 1）已知： x1 ，求分子 1x 284[( x24 1) ( 1 1)] 的值；4x 2 x（ 2）已知：xy z ，求 xy2 yz 3xz 的值；234x 2y 2 z 2（ 3）已知：23 1 02 11a，试求 (aa 2 )(aa ) 的值 .a题型五：求待定字母的值【例 5】若13x MN ，试求 M , N 的值 .x 2 1x 1 x 1练习：1．计算（ 1）2a 5a 12a 3 ； （ 2） a 2b b 2 2ab ；2( a 1)2(a 1)2(a 1)a b a（ 4） a b2b 2 ；(5)(ab4abb4ab ) ；aa)( aa b bb2．先化简后求值（ 1） a 1 a 241，此中 a1a 2 a22a 1 a231（ 2）已知 x : y2 :3 ，求 ( x2y 2) [( xy) (xy )3 ] x 的值 .xyxy 23．已知：5x 4AB ，试求 A 、 B 的值 .1)( 2x 1)x 12x1( x（四）、整数指数幂与科学记数法题型一：运用整数指数幂计算【例 1】计算：（1） (a2 ) 3(bc 1) 3 （ 2） (3x 3 y 2 z 1) 2 (5xy 2 z 3 ) 2 （ 3） [ ( a b) 3( ab)5 ] 2（ 4） [( x y)3 ( x y) 2 ] 2 (x y) 624(a b) ( a b)题型二：化简求值题【例 2】已知 xx 1 5 ，求（ 1） x 2 x 2 的值；（ 2）求 x 4 x 4 的值 .题型三：科学记数法的计算【例 3】计算：（1） (310 3 )102 )2；（ 2） (4 10 3 ) 2 (2 10 2 ) 3 .练习 ：1．计算：（ 1） (11) ( 1) 2|1 | (1 3 )0 ( 0.25)2007 420083 553（ 2） (3 1 m 3n 2 ) 2 (m 2 n) 3（ 3）(2ab 2 ) 2 (a 2b) 2(3a 3 b 2 ) (ab 3 ) 22．已知 x 25x 1 0 ，求（ 1） x x 1 ，（ 2） x 2x 2 的值 .二讲 分式方程题型一：用惯例方法解分式方程【例 1】解以下分式方程（ 1） 13；（ 2） 21 0 ；（3）x 1x 241 ；（ 4）5 x x 5x 1 xx 3xx 1 1x 3 4 x提示易犯错的几个问题：①分子不添括号；②漏乘整数项；③约去相同因式至使漏根；④忘掉验根 .题型二：求待定字母的值【例 4】若对于 x 的分式方程2 1 m有增根，求 m 的值 .x 3x3【例 5】若分式方程2 x a 1的解是正数，求a 的取值范围 .x2提示： 2 a 0 且 x2 ，a 2 且 a4 .x3题型三：解含有字母系数的方程【例 6】解对于 x 的方程x a c (c d0)b xd提示：（ 1） a, b, c, d 是已知数；（ 2） c d0 .题型四：列分式方程解应用题（略）练习：1．解以下方程： （ 1）x 12 x 0 ； （2）x 24 ；x 11 2xx 3x 3（ 3）2x32 ； （4）7 37 x 2x 2 x 2x2x x x212 1x 2．解对于 x 的方程：（ 1）11 2(b 2a) ；（ 2）1a 1 b(ab) .a xb a x b x3．假如解对于 x 的方程k 2x会产生增根，求 k 的值 .x 2x24．当 k 为什么值时，对于x 的方程x3k1的解为非负数 . x2(x 1)( x2)5．已知对于x的分式方程2a1 a 无解，试求 a 的值. x1。

初二分式所有练习题在初二数学学习中，分式是一个重要的知识点，也是学生们比较容易犯错的地方。

为了帮助同学们巩固分式的知识，下面我将提供一些初二分式的练习题，供大家练习。

题目1：简化分式将分式$\frac{12x^3y^2}{4x^2y^3}$进行简化。

解答：首先，我们可以进行分子和分母的因式分解。

分子可以写成$2^2 \times 3 \times x^3 \times y^2$，分母可以写成$2^2 \times x^2 \times y^3$。

然后，我们可以将相同的因式约掉，得到简化后的结果：$\frac{3x}{y}$。

题目2：分式加法计算$\frac{3}{4} + \frac{2}{5}$。

解答：首先，我们需要找到两个分式的公共分母。

对于$\frac{3}{4}$和$\frac{2}{5}$，其最小公倍数为20。

然后，我们将两个分式的分子乘以相应的公倍数得到同分母的分式，即$\frac{15}{20} + \frac{8}{20}$。

最后，我们将分子相加，保持分母不变，得到$\frac{23}{20}$。

如果需要，我们可以将其化简为$\frac{23}{20}$。

题目3：分式乘法计算$\frac{2}{3} \times \frac{4}{5}$。

解答：将$\frac{2}{3}$和$\frac{4}{5}$的分子相乘，分母相乘，得到$\frac{8}{15}$。

题目4：分式除法计算$\frac{5}{8} \div \frac{2}{3}$。

解答：将$\frac{5}{8}$乘以$\frac{3}{2}$的倒数，即$\frac{5}{8} \times \frac{3}{2}$。

然后，进行分子相乘，分母相乘，得到$\frac{15}{16}$。

题目5：分式的整体倍数计算$2 \times \left(\frac{1}{3} + \frac{2}{5}\right)$。

解答：首先，我们需要将两个分式相加，得到$\frac{5}{15} +\frac{6}{15}$。

八年级数学分式测试题(含答案)
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学分式测试题(含答案)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学分式测试题(含答案)的全部内容。

403 Forbidden
JSP3/2.0。

14
ª_。

初二下册数学分式方程练习题及答案一、单选题（共8题；共16分）1、已知函数y＝8x－11，要使y＞0，那么x应取 ( )A、x＞B、x＜C、x＞0D、x＜02、观察函数y1和y2的图象，当x=0，两个函数值的大小为（）A、y1＞y2B、y1＜y2C、y1=y2D、y1≥y23、若函数y=kx+b的图象如图所示，那么当y＞0时，x的取值范围是（）A、x＞1B、x＞2C、x＜1D、x＜24、（2016百色）直线y=kx+3经过点A（2，1），则不等式kx+3≥0的解集是（）A、x≤3C、x≥﹣3D、x≤05、若一次函数y=（1﹣2m）x+m的图象经过点A（x1 ， y1）和点B （x2 ， y2），当x1＜x2时，y1＜y2 ，且与y轴相交于正半轴，则m的取值范围是（）A、m＞0B、m＜C、0＜m＜D、m＞6、一次函数y=a1x+b1与y=a2x+b2的图象在同一平面直角坐标系中的位置如图所示，小华根据图象写出下面三条信息：①a1＞0，b1＜0；②不等式a1x+b1≤a2x+b2的解集是x≥2；③方程组的解是，你认为小华写准确（）A、0个B、1个C、2个D、3个7、若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是（）A、ab＞0B、a﹣b＞0C、a2+b＞08、直线l1：y=k1x+b与直线l2：y=k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k2x＞k1x+b的解集为（）A、x＞3B、x＜3C、x＞﹣1D、x＜﹣1二、填空题（共6题；共6分）9、已知关于x的不等式kx﹣2＞0（k≠0）的解集是x＜﹣3，则直线y=﹣kx+2与x轴的交点是________10、直线y=2x+b经过点（3，5），则关于x的不等式2x+b≥0的解集为________．11、已知直线y1=x，y2= x+1，y3=﹣ x+5的图象如图所示，若无论x 取何值，y总取y1 ， y2 ， y3中的最小值，则y的值为________12、如图，已知函数y=2x+b与函数y=kx﹣3的图像交于点P，则不等式kx﹣3＞2x+b的解集是________．13、已知关于x的一元一次不等式组有解，则直线y=﹣x+b不经过第________ 象限．14、小明家准备春节前举行80人的聚餐，需要去某餐馆订餐．据了解餐馆有10人坐和8人坐两种餐桌，要使所订的每个餐桌刚好坐满，则订餐方案共有________ 种．三、解答题（共6题；共30分）15、利用一次函数图象求方程2x+1=0的解．16、已知函数y=ax+b，y随x增大而减少，且交x轴于A（3，0），求不等式（a﹣b）x﹣2b＜0的解集．17、如图，函数y=2x和y= x+4的图象相交于点A，（1）求点A的坐标；（2）根据图象，直接写出不等式2x≥ x+4的解集．18、如图是一次函数y=2x﹣5的图象，请根据给出的图象写出一个一元一次方程和一个一元一次不等式，并用图象求解所写出的方程和不等式．19、函数y=2x与y=ax+4的图象相交于点A（m，2），求不等式2x＜ax+4的解集．20、已知一次函数y1=﹣2x﹣3与y2= x+2．（1）在同一平面直角坐标系中，画出这两个函数的图象；（2）根据图象，不等式﹣2x﹣3＞ x+2的解集为多少？（3）求两图象和y轴围成的三角形的面积．一、单选题题号 1 2 3 4 5 6 7 8答案 A A A A C C C D解析：1、A解：函数y=8x-11，要使y＞0，则8x-11＞0，解得x＞，2、A解：由图可知：当x=0时，y1=3，y2=2，y1＞y2 ．故选A．3、A解：因为直线y=kx+b过点（3，2）和（2，1），所以其解析式为：y=x-1，故 y=x-1＞0， x＞1.故选A．5、C解：∵如下图所示，一次函数y=（1﹣2m）x+m的图象经过点A（x1 ， y1）和点B（x2 ，y2），且当x1＜x2时，y1＜y2 ，∴一次函数y=（1﹣2m）x+m中y随x增大而增大，即：自变量的系数1﹣2m＞0，又∵函数图象与y轴的交点在x轴的上方，∴函数图象与y轴的交点的纵坐标m＞0，即：∴m的取值范围是：0＜m＜故：选C解：如图，∵直线y=a1x+b1经过一、二、三象限，∴a1＞0，b1＞0，故①错误；∵当x≥2时，直线y=a1x+b1在y=a2x+b2下方，∴不等式a1x+b1≤a2x+b2的解集是x≥2，故②准确；∵直线y=a1x+b1与y=a2x+b2的交点坐标为（2，3），∴方程组的解是，故③准确．故选C．7、C解：∵一次函数y=ax+b的图象经过第一、二、四象限，∴a＜0，b＞0，∴ab＜O，故A错误，a﹣b＜0，故B错误，a2+b＞0，故C准确，a+b不一定大于0，故D错误．故选C．8、D解：当x＜﹣1时，k2x＞k1x+b，所以不等式k2x＞k1x+b的解集为x＜﹣1．故选D．二、填空题9、（﹣3，0）解：解关于x的不等式kx﹣2＞0，移项得到；kx＞2，而不等式kx﹣2＞0（k≠0）的解集是：x＜﹣3，∴ =﹣3，解得：k=﹣，∴直线y=﹣kx+2的解析式是：y= x+2，在这个式子中令y=0，解得：x=﹣3，因而直线y=﹣kx+2与x轴的交点是（﹣3，0）．故本题答案为：（﹣3，0）．10、x≥解：∵直线y=2x+b经过点（3，5），∴5=2×3+b，解得：b=﹣1，∴不等式2x+b≥0变为不等式2x﹣1≥0，解得：x≥ ，故答案为：x≥ ．11、解：如图，分别求出y1 ， y2 ， y3交点的坐标A（，）；B （，）；C（，）当x＜，y=y1；当≤x＜，y=y2；当≤x＜，y=y2；当x≥ ，y=y3 ．∵y总取y1 ， y2 ， y3中的最小值，∴y的取值为图中红线所描述的部分，则y1 ， y2 ， y3中最小值的值为C点的纵坐标，∴y= ．12、x＜4解：把P（4，﹣6）代入y=2x+b得，﹣6=2×4+b解得，b=﹣14把P（4，﹣6）代入y=kx﹣3解得，k=﹣把b=﹣14，k=﹣代入kx﹣3＞2x+b得，﹣ x﹣3＞2x﹣14解得，x＜4．故答案为：x＜4．13、三解：根据题意得：b+2＜3b﹣2，解得：b＞2．当b＞2时，直线经过第一、二、四象限，不过第三象限．故填：三．14、3解：设10人桌x张，8人桌y张，根据题意得：10x+8y=80∵x、y均为整数，∴x=0，y=10或x=4，y=5或x=8，y=0共3种方案．故答案是3．三、解答题15、解：函数y=2x+1的图象如下所示：由图象可知，直线y=2x+1与x轴交点坐标为（﹣，0），所以方程2x+1=0的解为x=﹣．16、解：函数y=ax+b，y随x增大而减少，且交x轴于A（3，0），得a＜0，b＞0，3a+b=0，b=﹣3a．把b=﹣3a代入（a﹣b）x﹣2b＜0，得4ax+6a＜0．解得x＞﹣．17、解：（1）由，解得：，∴A的坐标为（，3）；（2）由图象，得不等式2x≥﹣ x+4的解集为：x≥ ．19、解：∵函数y=2x与y=ax+4的图象相交于点A（m，2），∴2m=2，2=ma+4，解得：m=1，a=﹣2，2x＜﹣2x+4，4x＜4，x＜1．20、解：（1）函数y1=﹣2x﹣3与x轴和y轴的交点分别是（﹣1.5，0）和（0，﹣3），y2= x+2与x轴和y轴的交点分别是（﹣4，0）和（0，2），其图象如图：（2）观察图象可知，函数y1=﹣2x﹣3与y2= x+2交于点（﹣2，1），当x＜﹣2时，直线y1=﹣2x﹣3的图象落在直线y2= x+2的上方，即﹣2x﹣3＞ x+2，所以不等式﹣2x﹣3＞ x+2的解集为x＜﹣2；故答案为x＜﹣2；（3）∵y1=﹣2x﹣3与y2= x+2与y轴分别交于点A（0，﹣3），B（0，2），∴AB=5，∵y1=﹣2x﹣3与y2= x+2交于点C（﹣2，1），∴△ABC的边AB上的高为2，∴S△ABC= ×5×2=5．。

初二数学分式试题练习及答案（精练）计算：（分析）本题中有四个分式相加减，如果采用直接通分化成同分母的分式相加减，公分母比较复杂，其运算难度较大.不过我们注意到若把前两个分式相加，其结果却是非常简单的.因此我们可以采用逐项相加的办法.（解）===（知识大串联）1．分式的有关概念设A、B表示两个整式．如果B中含有字母，式子就叫做分式．注意分母B的值不能为零，否则分式没有意义分子与分母没有公因式的分式叫做最简分式．如果分子分母有公因式，要进行约分化简2、分式的基本性质（M为不等于零的整式）3．分式的运算分式的`运算法则与分数的运算法则类似．异分母相加，先通分；4．零指数5．负整数指数注意正整数幂的运算性质可以推广到整数指数幂，也就是上述等式中的m、 n可以是O或负整数．分式是初中代数的重点内容之一，其运算综合性强，技巧性大，如果方法选取不当，不仅使解题过程复杂化，而且出错率高．下面通过例子来说明分式运算中的种种策略，供同学们学习参考．1．顺次相加法例1：计算：（分析）本题的解法与例1完全一样.（解）===2．整体通分法（例2）计算：（分析）本题是一个分式与整式的加减运算.如能把（-a-1）看作一个整体，并提取“-”后在通分会使运算更加简便.通常我们把整式看作分母是1的分式.（解）==.3．化简后通分分析：直接通分，极其繁琐，不过，各个分式并非最简分式，有化简的余地，显然，化简后再通分计算会方便许多．4．巧用拆项法例4计算：.分析：本题的10个分式相加，无法通分，而式子的特点是：每个分式的分母都是两个连续整数的积（若a是整数），联想到，这样可抵消一些项.解：原式====5．分组运算法例5：计算：分析：本题项数较多，分母不相同.因此，在进行加减时，可考虑分组.分组的原则是使各组运算后的结果能出现分子为常数、相同或倍数关系，这样才能使运算简便.解：=====（错题警示）一、错用分式的基本性质例1 化简错解：原式分析：分式的基本性质是“分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式的值不变”，而此题分子乘以3，分母乘以2，违反了分式的基本性质.正解：原式二、错在颠倒运算顺序例2 计算错解：原式分析：乘除是同一级运算，除在前应先做除，上述错解颠倒了运算顺序，致使结果出现错误.正解：原式三、错在约分例1 当为何值时，分式有意义？[错解]原式.由得.∴时，分式有意义.[解析]上述解法错在约分这一步，由于约去了分子、分母的公因式，扩大了未知数的取值范围，而导致错误.[正解]由得且.∴当且，分式有意义.四、错在以偏概全例2为何值时，分式有意义？[错解]当，得.∴当，原分式有意义.[解析]上述解法中只考虑的分母，没有注意整个分母，犯了以偏概全的错误.[正解]，得，由，得.∴当且时，原分式有意义.五、错在计算去分母例3 计算.[错解]原式=.[解析]上述解法把分式通分与解方程混淆了，分式计算是等值代换，不能去分母，..六、错在只考虑分子没有顾及分母例4 当为何值时，分式的值为零.[错解]由，得.∴当或时，原分式的值为零.[解析]当时，分式的分母，分式无意义，谈不上有值存在，出错的原因是忽视了分母不能为零的条件.，得.由，得且.∴当时，原分式的值为零.七、错在“且”与“或”的用法例7为何值时，分式有意义错解：要使分式有意义，须满足.由得，或由得.当或时原分式有意义.分析：上述解法由得或是错误的.因为与中的一个式子成立并不能保证一定成立，只有与同时成立，才能保证一定成立.故本题的正确答案是且.八、错在忽视特殊情况例8 解关于的方程.错解：方程两边同时乘以，即.当时，，当时，原方程无解.分析：当时，原方程变为取任何值都不能满足这个方程，错解只注意了对的讨论，而忽视了的特殊情况的讨论.正解：方程两边同时乘以，得，即当且时，，当或时，原方程无解.感谢您的阅读，祝您生活愉快。

初二数学分式试题及答案一、选择题（每题3分，共30分）1. 下列分式中，分母不能为0的是（）。

A. \frac{1}{x-1}B. \frac{1}{x+1}C. \frac{1}{x}D.\frac{1}{x^2+1}答案：D2. 计算 \frac{1}{x-1} + \frac{1}{x+1} 的结果是（）。

A. \frac{2}{x^2-1}B. \frac{2}{x^2+1}C. \frac{2x}{x^2-1}D. \frac{2x}{x^2+1}答案：C3. 如果 \frac{a}{b} = \frac{c}{d}，那么 ad = （）。

A. bcB. bdC. acD. cd答案：A4. 下列分式中，最简分式是（）。

A. \frac{2x}{3x}B. \frac{x^2-1}{x-1}C. \frac{x^2+2x+1}{x+1}D. \frac{x^2-4}{x+2}答案：D5. 计算 \frac{1}{x-2} - \frac{1}{x+2} 的结果是（）。

A. \frac{x+2}{x^2-4}B. \frac{x-2}{x^2-4}C. \frac{-4}{x^2-4}D. \frac{4}{x^2-4}答案：C6. 如果 \frac{a}{b} = \frac{c}{d} = \frac{e}{f}，那么\frac{a+c}{b+d} = （）。

A. \frac{e}{f}B. \frac{e+f}{f+d}C. \frac{e+f}{f+b}D.\frac{a+c}{b+d}答案：A7. 下列分式中，可以约分的是（）。

A. \frac{2x^2}{4x}B. \frac{3x^2-3}{3x-3}C. \frac{x^2-4}{x+2}D. \frac{x^2+2x+1}{x+1}答案：B8. 计算 \frac{1}{x-1} \cdot \frac{1}{x+1} 的结果是（）。

初二数学分式试题答案及解析1.下列运算正确的是（）A．B．C．D．【答案】D．【解析】A、，分母的所有项都变号，故A错误；B、分子分母都乘以或除以同一个不为0的数分式的值不变，故B错误；C、分子分母都除以（x-y），故C错误；D、分子分母都除以（x-1），故D正确．故选D．【考点】分式的基本性质．2.若分式的值是0，则x = __________.【答案】 1【解析】由x2-1=0可得x=±1，又x+1≠0，所以x≠-1,所以x=1【考点】分式值为0的条件3.已知【答案】【解析】∵∴x=2y∴原式=【考点】分式的化简求值4.（1）已知计算结果是，求常数m的值；（2）已知计算结果是，求常数A、B的值．【答案】（1）3；（2）.【解析】先把拨给条件进行通分，然后利用恒等式的性质进行计算即可求值. （1）∵=，又∵=，∴（2）∵，又∵=，∴．∴．【考点】1.分式的化简；2.解二元一次方程组.5.若，则x的取值范围是_______．【答案】x＜1．【解析】由绝对值的定义和分式有意义的条件入手求解．试题解析：由题意得x-1≤0且x-1≠0即x≤1，且x≠1所以x＜1．考点: 分式的基本性质．6.如果分式有意义，那么的取值范围是（）A．＞1B．＜1C．≠1D．=1【答案】C【解析】由题,1-x≠0, x≠1,选C.分式有意义的条件是分母不为零,由题,1-x≠0, x≠1,选C.【考点】分式有意义的条件.7.计算：﹣．【答案】【解析】原式利用同分母分式的减法法则计算，约分即可得到结果．解：原式===．点评：此题考查了分式的加减法，分式的加减运算关键是通分，通分的关键是找最简公分母．8.将分式约分时，分子和分母的公因式是．【答案】2a【解析】观察分子分母，提取公共部分即可．解：分式约分时，分子和分母的公因式是：2a．故答案为：2a．点评：此题主要考查了约分，注意：找出分子分母公共因式时，常数项也不能忽略．9.在式子中，分式的个数有（）A．2B．3C．4D．5【答案】B【解析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．解：分式有：，，9x+工3个．故选B．点评：本题主要考查分式的定义，注意π不是字母，是常数，所以不是分式，是整式．10.把分式中的、都扩大3倍，那么分式的值（）.A．扩大3倍B．缩小3倍C．扩大9倍D．不变【答案】A【解析】由题意把、代入原分式，再把化简结果与原分式比较即可作出判断.解：由题意得则分式的值扩大3倍故选A.【考点】分式的基本性质点评：本题属于基础应用题，只需学生熟练掌握分式的基本性质，即可完成.11.已知=，则的值为__________。