五年级奥数平面图形的面积
- 格式:doc
- 大小:56.00 KB
- 文档页数:5
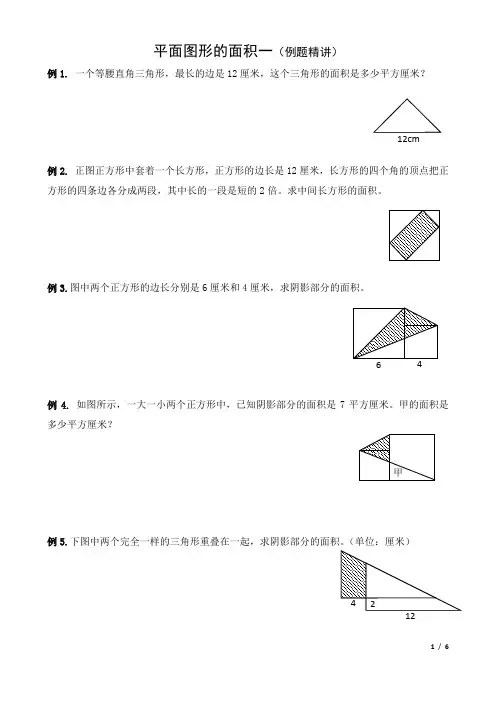
平面图形的面积一(例题精讲)例1. 一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?例2. 正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
例3.图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
例4.如图所示,一大一小两个正方形中,已知阴影部分的面积是7平方厘米。
甲的面积是多少平方厘米?例5.下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)例6. 图中ABCD 是长方形,S 1比S 2的面积大6平方厘米,求EC 的长。
平面图形的面积一(课堂小测)7.求四边形ABCD 的面积。
(单位:厘米)8. 如下图长方形ABCD 的面积是16平方厘米,E 、F 都是所在边的中点,求三角形AEF 的面积。
9.右图中,正方形的边长4厘米,求长方形的面积。
10.如图,平行四边形BCEF 中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比甲的面积小8平方厘米。
平行四边形的高是多少厘米?A BCD 345°CD F CB DS 1A 4 6 S 2EE11.一个正方形的对角线长5厘米,这个正方形的面积是多少平方厘米?12.已知大正方形的边长是12厘米,求中间最小正方形的面积。
13.下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?14.如图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
15.如图所示,长方形的长12厘米,宽8厘米,A 、B 两点是长方形长和宽的中点,那么阴影部分的面积是多少?AB94 3 84 6乙甲5平面图形的面积二(例题精讲)例1. 一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?12×12=144(平方厘米) 144÷4=36(平方厘米)例2. 正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。

平面几何图形的面积1、两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,直角三角形的下面的直角边长为8厘米,求阴影部分的面积.E2、如图,平行四边形ABCD种,BC=Io厘米,直角三角形ECB的边EC=8厘米,已知阴影部分的总面积比三角形EFG的面积大10平方厘米,求平行四边形ABCD的面积・3、在下图中,AB=8厘米,CD=4厘米,BC=6厘米,三角形AFB比三角形EFD 的面积大18平方厘米。
求ED的长。
π Tl4、一块长方形纸片,在长边剪去5厘米,宽边剪去2厘米后(如图),得到的正方形面积比原长方形面积少31平方厘米.求原长方形纸片的面积・5、一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形, 新正方形的面积比原正方形大120平方厘米.求原正方形的面积?6、四边形ABCD 是直角梯形,AD= 12厘米,AB=8厘米,BC= 15厘米,且三角 形ADE,四边形DEBF,三角形CDF 的面积相等,求阴影三角形DEF 的面积是 多少平方厘米?7、如图,直角三角形ABC 套住了一个正方形CDEF, E 恰好在AB 边上,直角 边AC 长20厘米,BC 长12厘米,求正方形的边长是多少?8、如图,有7个小长方形,其中5各小长方形的面积已知,求阴影部分的面积。
6厘来6厘米9、如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是()平方厘米•10、如图,在三角形ABC中,BC二8厘米,高是6厘米,E、F分别为AB和AC的中点,那么三角形EBF的面积是()平方厘米.11、在三角形ABC中,DC二2BD, CE=3AE,三角形ABC的面积是120,则求阴影部分的面积是多少?B D C12、如图,在三角形ABC中,D是BC的中点,AF二EF二EC,三角形ABC的面积是108平方厘米,求三角形CDE的面积是多少?13、如图所示,CA=AB=4厘米,∆ABE比ACDE的面积小2平方厘米,求CD的长为多少厘米?【答案】K阴影部分+右边空白Z=右边空白+下面空白梯形所以阴影部分=下面空白梯形8-3=5 (厘米)(5+8)χ2÷2=13 (平方厘米)2.利用同增同减差不变阴影面积•三角形EFG的面积=10平方厘米同时增加梯形BCGF的面积,则:平行四边形ABCD-三角形BCE=IO三角形BCE的面积=10×8÷2=40 (平方厘米)则平行四边形ABCD的面积=40+10=50 (平方厘米)3.利用同增同减差不变三角形AFB的面积•三角形EFD的面积=18平方厘米同时增加梯形BCDF的面积,贝Ih梯形ABCD∙三角形BCE=I8梯形ABCD面积=(8+4) ×6÷2=36 (平方厘米)则三角形BCE=36-18=18 (平方厘米)EC的长度:18×2÷6=6 (厘米)ED: 6-4=2 (厘米)4. 31-2x5=21 (平方厘米)设剩下的部分正方形的边长为X厘米5x+2x=21X=3原来长方形的长:3+5=8 (厘米〉原来长方形的宽:3+2=5 (厘米)原来长方形的面积:5x8=40 (平方厘米)5、120-6x6=84 (平方厘米)设原来正方形的边长为X厘米6x+6x=84X=7原来正方形的面积:7x7=49 (平方厘米)6.梯形的面积:(12+15) ×8÷2=108 (平方厘米)三角形ADE的面积:108÷3=36 (平方厘米)AE 的长:36×2÷12=6 (厘米)三角形ACF的面积:108÷3=36 (平方厘米)CF 的长:36×2÷8=9 (厘米)BE的长:8-6=2 (厘米)BF的长:15-9=6 (厘米)三角形BEF面积=2×6÷2=6 (平方厘米)阴影面积:36-6=30 (平方厘米)7.连接CE,把大三角形分成两个小三角形,正方形的边长就是这两个三角形的高大三角形ABC的面积是:20×12÷2=120 (平方厘米)设正方形的边长为X厘米20x÷2+12x÷2=12016x=120X=7∙5A 的面积:6×8÷4=12B 的面积:(4+6+8+12) ×10÷20=159. 2510.611、三角形ADC 的面积:120÷ (2+1) ×2=80 阴影面积:80÷ (3+1) =20 12.三角形BEC的面积:108÷3×2=72 (平方厘米)三角形CDE的面积:72÷2=36(平方厘米)三角形CDF的面积:36÷2=18(平方厘米)13、利用同增同减差不变三角形CDE∙三角形ABE的面积=2平方厘米同时增加三角形BCE的面积,则:三角形BCD∙三角形ABC=2三角形ABC的面积=4×4÷2=8 (平方厘米)则三角形BCD的面积=8+2=10 (平方厘米)CD=10×2÷4=5(厘米)。

五年级奥数组合图形的面积Document number:NOCG-YUNOO-BUYTT-UU986-1986UT组合图形的面积1.基本平面图形特征及面积公式特征面积公式正方形①四条边都相等。
②四个角都是直角。
③有四条对称轴。
S=a2长方形①对边相等。
②四个角都是直角。
③有二条对称轴。
S=ab平行四边形①两组对边平行且相等。
②对角相等,相邻的两个角之和为180°③平行四边形容易变形。
S=ah三角形①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
S=ah÷2梯形①只有一组对边平行。
②中位线等于上下底和的一半。
S=(a+b)h÷22.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
1.已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2.右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分别为6厘米、4厘米,DF的长是多少厘米5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分的面积。
6.右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大9.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。

小学五年级数学必须掌握的图形求面积十法!孩子看了不丢分我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
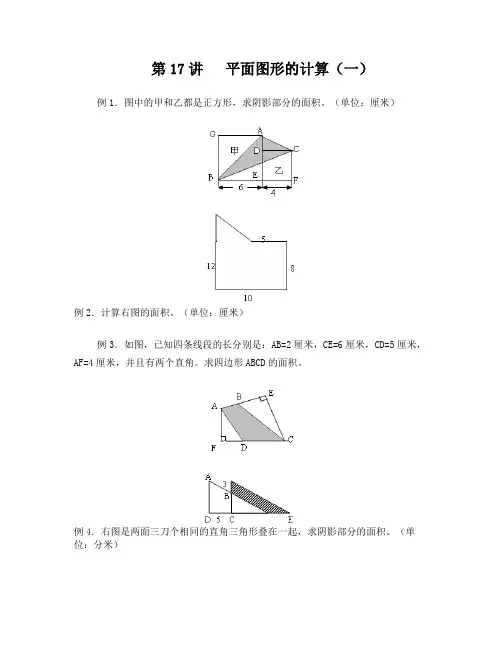
第17讲平面图形的计算(一)例1.图中的甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)例2.计算右图的面积。
(单位:厘米)例3.如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边形ABCD的面积。
例4.右图是两面三刀个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:分米)例5.下页左图是一块长方形草地,长方形的长是16,宽是10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)练习与思考1.求图中阴影部分的面积。
2.求图中阴影部分的面积。
3.下左图的长方形中,三角形ADE与四边形DEBF和三角形CDF的面积分别相等,求三角形DEF的面积。
4.四中平等四边形ABCD的边BC长10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求CF的长。
5.图中三角形的高为4,面积为16;长方形的宽为6,长方形的面积是三角形面积的多少倍?6.如图,长方形的长是8,宽是6,A和B是宽的中点,求长方形内阴影部分的面积。
7.如图,BC长为5,求画斜线的两个三角形的面积之和。
8.上右图是两个一样的直角三角形重叠在一起,按照图上标出的数,计算阴影部分的面积。
9.右图是一块长方形草地,长方形长为16,宽为12,中间有一条宽为2的道路,求草地(阴影部分)的面积。
简便计算作业(12月23日):1.996+19.97+199.82.894.68+4.686.11+4.68 754.7+15.925平均数问题作业(12月23日):1.已知九个数的平均数是72.去掉一个数之后,余下的数的平均数是78。
去掉的数是多少?2.甲、乙、丙三个小组的同学去植树,甲、乙两组平均每组植树18棵,甲、丙两组平均每组植树17棵,乙、丙两组平均每组植树19棵。
三个小组各植树多少棵?3.五一班同学数学考试平均成绩91.5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
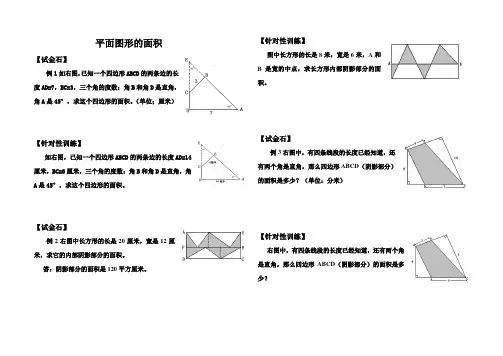
平面图形的面积【试金石】例1如右图,已知一个四边形ABCD的两条边的长度AD=7,BC=3,三个角的度数:角B和角D是直角,角A是45°,求这个四边形的面积。
(单位;厘米)【针对性训练】如右图,已知一个四边形ABCD的两条边的长度AD=14厘米,BC=6厘米,三个角的度数:角B和角D是直角,角A是45°,求这个四边形的面积。
【试金石】例2右图中长方形的长是20厘米,宽是12厘米,求它的内部阴影部分的面积。
答:阴影部分的面积是120平方厘米。
【针对性训练】图中长方形的长是8米,宽是6米,A和B是宽的中点,求长方形内部阴影部分的面积。
【试金石】例3右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?(单位:分米)【针对性训练】右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?【试金石】例4如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积。
【针对性训练】如右图,甲、乙两图形都是正方形,它们的边长分别是6厘米和8厘米,求阴影部分的面积。
【试金石】例5【针对性训练】【试金石】【针对性训练】【智能提速训练营】1、如图,已知BD长是2厘米,DC长是3厘米,E是AD的中点,如果三角形ABD的面积是5平方厘米,那么三角形DEC的面积是多少?2、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?3、如图,在平行四边形ABCD中,AE=ED,BF=FC,CG=GD,平行四边形ABCD的面积是阴影三角形EFG的多少倍?4、如图,BD=6厘米,BC=15厘米,△ABD的面积是24平方厘米,△ADC 的面积是多少平方厘米?5、右图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?(单位:厘米)6、如图,梯形的面积是70平方厘米,上底8厘米,下底12厘米,阴影部分的面积是多少平方厘米?7、如图,四边形ABCD是平行四边形,DC=CE,如果△BCE的面积是15平方厘米,那么梯形ABED的面积是多少平方厘米?8、如图,平行四边形的面积是60平方厘米,阴影三角形的面积是多少平方厘米?9、如图,正方形ABCD的边长是4厘米,CG=3厘米,长方形DEFG的长DG=5厘米,那么它的宽DE是多少厘米?10、如图,四边形ABCD内有一点O,O点到四条边的垂线长都是4厘米,已知四边形的周长是36厘米,四边形ABCD的面积是多少平方厘米?11、如图,已知ABFE是平行四边形,ABCD是长方形,且AD=6厘米,AB=3厘米,CO=2厘米,阴影部分的面积是多少平方厘米?12、一个长方形被两条直线分成四个长方形,其中三个的面积分别是20平方米、25平方米和30平方米,阴影部分的面积是多少平方米?13、如右图,已知正方形ABCD和正方形CEFG,且正方形ABCD每边长为10厘米,求图中阴影(三角形BFD)部分的面积。
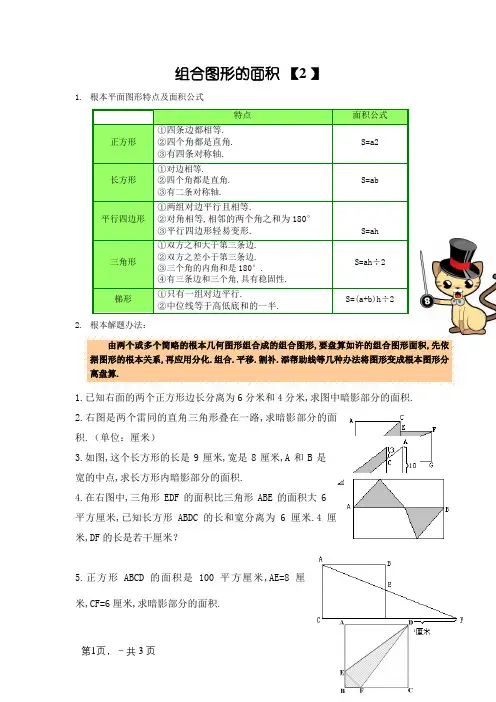
组合图形的面积【2 】1.根本平面图形特点及面积公式特点面积公式正方形①四条边都相等.②四个角都是直角.③有四条对称轴.S=a2长方形①对边相等.②四个角都是直角.③有二条对称轴.S=ab平行四边形①两组对边平行且相等.②对角相等,相邻的两个角之和为180°③平行四边形轻易变形.S=ah三角形①双方之和大于第三条边.②双方之差小于第三条边.③三个角的内角和是180°.④有三条边和三个角,具有稳固性.S=ah÷2梯形①只有一组对边平行.②中位线等于高低底和的一半.S=(a+b)h÷22.根本解题办法:由两个或多个简略的根本几何图形组合成的组合图形,要盘算如许的组合图形面积,先依据图形的根本关系,再应用分化.组合.平移.割补.添帮助线等几种办法将图形变成根本图形分离盘算.1.已知右面的两个正方形边长分离为6分米和4分米,求图中暗影部分的面积.2.右图是两个雷同的直角三角形叠在一路,求暗影部分的面积.(单位:厘米)3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内暗影部分的面积.4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分离为6厘米.4厘米,DF的长是若干厘米?5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求暗影部分的面积.6.右图是一块长方形公园绿地,绿地长24米,宽16米,中央有一条宽为2米的道路,求草地(暗影部分)的面积.7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E.F分离是AF.BC的中点,那么暗影部分的面积是若干?8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中央有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(暗影部分)的面积有多大?9.如图,一个三角形的底长5米,假如底延伸1米,那么面积就增长2平方米.问本来的三角形的面积是若干平方米?1米组合图形的面积功课1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是若干厘米?2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求暗影部分三角形ACE的面积.3.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中暗影部分的面积是若干?4.如图,A.B两点是长方形长和宽的中点,那么暗影部分占长方形的面积是若干?5.如图,在平行四边形ABCD中,E.F分离是AC.BC的三等分点,且平行四边形的.面积为54平方厘米,求S△BEF6.盘算右边图形的面积.(至罕用3种办法)(单位:米)。


完整版)五年级奥数平面图形面积计算五年级奥数第六讲——平面图形面积的计算一、知识要点1.基本平面图形特征及面积公式正方形:特征:四条边相等,四个角都是直角,有四条对称轴。
面积公式:S=边长的平方长方形:特征:对边相等,四个角都是直角,有二条对称轴。
面积公式:S=长×宽平行四边形:特征:两组对边平行且相等,对角相等,相邻的两个角之和为180°,容易变形。
面积公式:S=底边×高三角形:特征:两边之和大于第三条边,两边之差小于第三条边,三个角的内角和是180°,具有稳定性。
面积公式:S=底边×XXX÷2梯形:特征:只有一组对边平行,中位线等于上下底和的一半。
面积公式:S=(上底+下底)×高÷22.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
典型例题】例1】已知平行四边形的面积是28平方厘米,求阴影部分的面积。
例2】求图中阴影部分的面积。
例3】如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE的长度。
例4】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?练与拓展】1.计算下面图形的面积。
2.下面的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
3.正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求三角形DEF的面积和CF的长。
4.平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求CF的长。
5.正方形ABCD的面积是100平方厘米,AE=8厘米,请计算以下图形的面积。
1.在一块长80米、宽30米的长方形地上,修了宽为2米和3米的两条小路,求草地的面积。

巧求表面积教学目标掌握长方体和正方体的特征、表面积和体积计算公式,并能运用公式解决一些实际问题。
教学过程一、例题讲解我们已经学习了长方体和正方体,知道长方体或正方体六个面面积的总和叫做长方体或正方体的表面积。
如果长方体的长用a 表示、宽用b 表示、高用h 表示,那么,长方体的表面积=(ab +ah +bh )×2。
如果正方体的棱长用a 表示,则正方体的表面积=6a 2。
对于由几个长方体或正方体组合而成的几何体,或者是一个长方体或正方体组合而成的几何形体,它们的表面积又如何求呢?涉及立体图形的问题,往往可考查同学们的看图能力和空间想象能力。
小学阶段遇到的立体图形主要是长方体和正方体,这些图形的特点都是可以从六个方向去看,特别是求表面积时,就是上下、左右和前后六个方向(有时只考虑上、左、前三个方向)的平面图形的面积的总和。
有了这个原则,在解决类似问题时就十分方便了。
例1 在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体(下图),求这个立体图形的表面积.( 例1图) (例2图)分析 我们把上面的小正方体想象成是可以向下“压缩"的,“压缩"后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面。
这样这个立体图形有表面积就可以分成这样两部分:上下方向:大正方体的两个底面;侧面: 小正方体的四个侧面 大正方体的四个侧面。
解:上下方向:5×5×2=50(平方分米) 侧面:5×5×4=100(平方分米)4×4×4=64(平方分米) 这个立体图形的表面积为:50+100+64=214(平方分米)答:这个立体图形的表面积为214平方分米。
例2 下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为21厘米的正方体小洞,第三个正方体小洞的挖法与前两个相同,棱长为14厘米.那么最后得到的立体图形的表面积是多少平方厘米?分析 这道题的难点是洞里的表面积不易求.在小洞里,平行于上下表面的所有面的面积和等于边长为1厘米的正方形的面积,这个边长为1厘米的正方形再与图中阴影部分的面积合在一起正好是边长为2厘米的正方体的上表面的面积。

学科培优 数学“直线型面积计算”学生姓名 授课日期 教师姓名授课时长知识定位本讲讲解已经学过的几种基本平面几何图形:正方形、长方形、三角形、平行四边形、梯形等的相关面积计算方法,是几何问题中的常见常考内容。
知识梳理一、 基本平面图形的计算公式【授课批注】在复习学校所学基本面积公式的同时也顺带复习周长的公式,这些知识点在具体题目中都可能用到。
二、 重要模型模型一:同一三角形中,相应面积与底的正比关系:bs 2s 1即:两个三角形高相等,面积之比等于对应底边之比。
S 1︰S 2 =a ︰b ;模型一的拓展: 等分点结论(“鸟头定理”)如图,三角形AED 占三角形ABC 面积的23×14=16模型二:任意四边形中的比例关系 (“蝴蝶定理”) ①S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4②AO ︰OC=(S 1+S 2)︰(S 4+S 3)模型三:梯形中比例关系(“梯形蝴蝶定理”)①S 1︰S 3=a 2︰b 2 ②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为(a+b )2【授课批注】因为四年级还没学过比例,所以在讲用比所表示的模型时可使用份数这个概念,学生更容易理解。
对于部分学有余力的学生可以先讲比例再直接引入上面的关系式。
【重点难点解析】1.等底或等高的三角形的面积关系2.长方形或平行四边形与同底等高三角形的面积关系 3. 三角形内不规则图形部分的面积计算【竞赛考点挖掘】1. 基本几何图形的面积计算2. 三角形中底和高与面积的关系3. 四边形对角线所分成的四个三角形的面积关系S 4S 3s 2s 1ba S 4S 3s 2s 1O DCB A例题精讲【试题来源】【题目】图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍, EF 的长是BF长的3倍.那么三角形AEF的面积是多少平方厘米?【试题来源】【题目】如图,把四边形ABCD的各边都延长2倍,得到一个新四边形EFGH如果ABCD的面积是5平方厘米,则EFGH的面积是多少平方厘米?【试题来源】【题目】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?【试题来源】【题目】如图16-4,已知.AE=15AC,CD=14BC,BF=16AB,那么DEFABC三角形的面积三角形的面积等于多少?【试题来源】【题目】如图,长方形ABCD的面积是2平方厘米,EC=2DE,F是DG的中点.阴影部分的面积是多少平方厘米?【试题来源】【题目】如图,已知D是BC中点,E是CD的中点,F是AC的中点.三角形ABC由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形ABC的面积是多少平方厘米?【试题来源】【题目】左下图是一个各条边分别为5厘米、12厘米、13厘米的直角三角形.如右下图,将它的短直角边对折到斜边上去与斜边相重合,那么右下图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米?习题演练【试题来源】【题目】如图,在一个梯形内有两个三角形的面积分别为10与12,已知梯形的上底长是下底长的23.那么余下阴影部分的面积是多少?【试题来源】【题目】图中ABCD是梯形,三角形ADE面积是1.8,三角形ABF的面积是9,三角形BCF的面积是27.那么阴影部分面积是多少?【试题来源】【题目】如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米,而三角形ABO的面积为12平方厘米.则梯形ABCD的面积为多少平方厘米?【试题来源】【题目】如图,BD,CF将长方形ABCD分成4块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米.问:绿色四边形面积是多少平方厘米?【试题来源】【题目】如图,平行四边形ABCD周长为75厘米.以BC为底时高是14厘米;以CD为底时高是16厘米.求平行四边形ABCD的面积.【试题来源】【题目】如图,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、3 10平方米和25平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【试题来源】【题目】图中外侧的四边形是一边长为10厘米的正方形,求阴影部分的面积.【试题来源】【题目】如图,长方形被其内的一些直线划分成了若干块,已知边上有3块面积分别是13,35,49.那么图中阴影部分的面积是多少?【试题来源】【题目】在右图的△ABC中,CE=2AE,BD=3DC,已知△DEC的面积是4cm2,求△ABC的面积。
第十四讲面积计算在小学阶段学习的各种平面图形之间有着密切的联系.我们把平面图形之间的转化方法及它们的面积、周长公式归纳如下图:计算图形的面积要用面积公式,对于一些复杂的图形有意识地运用运动变化的观点,将平面图形简单地变动位置,可以化繁为简,化难为易,从而获得最佳解法。
例1 已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积?分析利用已给的线段间的比例关系、已给的三角形的面积以及三角形的面积公式,设法把三角形BDE划分成一些与三角形ABC的面积成相应比例的三角形.这样,三角形BDE的面积就能求得了。
解:见上图,连结CE.对于三角形ABC与三角形BEC,分别把AB和BE可知,S△BEC =2S△ABC=2.显然,三角形BEC和三角形CED是两个等底(BC=CD)、等高的三角形,因此S△CED =S△BEC=2。
这样,S△BDE =S△BEC+S△CED=4。
例2 求右图中阴影部分的面积.(大圆直径为2,单位:厘米)。
分析:解题时可以先将图形下半部分翻转拼接为下图.然后将图中的小圆移至中心从图中不难看出求原图中阴影部分的面积就是求一个圆环的面积。
解:大圆半径:2÷2=1(厘米)小圆半径:1÷2=0.5(厘米)阴影面积:3.14×(12-0.52)=2.355(平方厘米)答:阴影部分的面积是2.355平方厘米.例3 如下图.在图中三角形ABE、ADF和四边形AECF的面积相等,求三角形AEF的面积。
分析三角形AEF的面积等于四边形AECF的面积减去三角形ECF的面积.因为长方形ABCD的面积等于三角形ABE、ADF和四边形AECF的面积和,长方形ABCD的长、宽分别为9厘米和6厘米,因此很容易求出它的面积.所以解题关键在于求出三角形ECF的面积。
EC的长度.同理可以求出FC的长度.这样三角形ECF的面积可以求出,使问题得解。
解:长方形ABCD的面积:9×6=54(平方厘米);四边形AECF及三角形ABE、AFD的面积相等,是:EC的长度:9-18×2÷6=3(厘米);FC的长度:6-18×2÷9=2(厘米);三角形AEF的面积:18-3×2÷2=15(平方厘米)。
图形变换求面积问题一、平移:将图形沿着一个方向移动一段距离。
平移变换把图形中的某一个线段或者一个角移动到一个新的位置,使图形中分散的条件 紧密地结合到一起。
一般有2种方法:1. 平移已知条件2. 平移所求问题,把所求问题转化,其实就是逆向证明。
几何题多数都是逆向思考的。
、旋转:将某图形绕着一个固定点转动到另一个位置,以此重新组合图形。
旋转变换把平面图形绕旋转中心,旋转一个定角,使分散的条件集中在一起。
在遇到关于等腰三角形、正三角形、正方形等问题时 ,是经常用到的思维途径 三、对称(也可理解为翻折):某图形对于某条线对称的图形通过作关于某一直线或一点的对称图,把图形中的图形对称到另一个位置上,使分散的 条件集中在一起。
当出现以下两种情况时,经常考虑用此变换:1. 出现了明显的轴对称、中心对称条件时2. 出现了明显的垂线条件时。
【例1】 右图是一块长方形草地,长方形的长是 16,宽是10.中间有两条道路,一条是长方形,一条是如图所眾,将道路平移后的(16-2)x(10-2) = 112【巩固】如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个•请算出阴影部分的面积.【例2】 如图所示,梯形ABCD 中,AB 平行于CD ,又BD 4,AC 3,AB CD 5 .试求梯形ABCD 的面积.平行四边形,它们的宽都是 2,求草地部分的面积(阴影部分)有多大?【巩固】如下图,六边形 ABCDEF 中,AB ED , AF CD , BC EF ,且有 AB 平行于ED , AF 平行于CD , BC 平行于EF ,对角线FD 垂直于BD ,已知FD 24厘米,BD 18厘米,请问六边形ABCDEF 的面积是多少平方厘米?【例3】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4 , 则正六边形 ABCDEF 的面积是 ______________________ 。
平面图形的面积计算例1:已知平行四边形的的面积是28平方厘米,求阴影图形的面积。
模仿练习如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)例2:已知大正方形的边长是5厘米,小正方形的边长是4厘米,求阴影部分的面积。
模仿练习正方形的边长分别是10厘米、6厘米,阴影部分的面积是 平方厘米。
ABC EFD GA B CED G例3:如图,ABCD 是边长为4分米的正方形,长方形DEFG 的长是5分米,求长方形DEFG 的宽。
模仿练习如图,ABCD 是正方形,EDGF 是长方形,CD=6厘米,DG=8厘米,求宽ED=?FA B GCD E 86例4:如图,已知四边形ABCD 被它的两条对角线分成四个三角形,其中甲的面积是1,乙的面积是2,丙的面积是3,求丁的面积。
模仿练习两条对角线把梯形ABCD 分割成四个三角形,已知两个三角形的面积,求另两个三角形的面积。
FA EDCBABC DE 甲丁乙丙A BCDO4812 108铜牌练习(1)右面图形的面积是多少平方厘米。
(单位:厘米)(2)如右图,长方形ABCD 中,BE=4厘米,CE=3厘米,长方形的面积是多少平方厘米。
(3) 一个等腰直角三角形,最长的边是20厘米,这个三角形的面积是多少平方厘米。
(4)一个正方形的对角线长5厘米,这个正方形的面积是 平方厘米C D银牌练习(1)已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
(2)如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大(3)如图,求四边形的面积是是 平方厘米。
(单位:厘米)(4)如图所示,梯形中的两个小三角形的面积为3、9平方厘米,梯形ABCD 的面积是 平方厘米。
金牌练习如右图,在直角三角形ABC 内画一个最大的正方形BEFD , AB=4厘米,BC=6厘米,正方形的面积最大是 平方厘米。
组合图形的面积1.基本平面图形特征及面积公式2.基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先根据图形的基本关系,再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
1.已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
2.右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内阴影部分的面积。
4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分别为6厘米、4厘米,DF的长是多少厘米?5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分的面积。
6.右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的面积是多少?8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?9.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。
问原来的三角形的面积是多少平方米?1米组合图形的面积作业1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是多少厘米?2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE的面积。
3.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中阴影部分的面积是多少?4.如图,A、B两点是长方形长和宽的中点,那么阴影部分占长方形的面积是多少?5.如图,在平行四边形ABCD中,E、F分别是AC、BC的三等分点,且平行四边形的面积为54平方厘米,求S。
学生课程讲义
例题1
在梯形中阴影部分面积是150平方厘米,上底15厘米,下底25厘米,求梯形面积。
随堂练习1
如图,已知平行四边形面积是48平方厘米,求阴影部分面积。
梯形的上底5厘米,高6
厘米。
例题2
如图,将长为9厘米,宽为6厘米的长方形,划分成四个三角形,其面积分别为S1、S2、S3、S4,且S1=S2=S3+S4,求S4。
随堂练习2
如图,四边形ABCD 是直角梯形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADC 、四边形DEBF 及△CDF 的面积相等,求三角形EBF 的面积。
A
B E
D F C
例题3
如图,AE=5厘米,CF=2厘米,AB=6厘米,CD=4厘米,∠B=∠D=90度,求四边形AFCE 的面积。
随堂练习3
如图,四边形ABCD 中,AE=5厘米,AB=10厘米,FC=12厘米,DC=15厘米,∠B=∠D=90度,求四边形AFCE 的面积。
例题4
如图,在大正方形ABCD 里有一个内接长为6厘米,宽为1厘米的长方形,而且长方形的对称轴与正方形的对角线重合,求正方形的面积。
随堂练习4
如图,正方形的面积为18.75平方厘米,在正方形内有两条平行于对角线的线段,将正方形平均分为面积相等的三份,A E B F C
D A
E D B
F C A
H D E C B F G A
求平行线段AB 的长。
例题5
如图,平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的的直角边EC 长8厘米。
已知△BAG 和△FDC 面积的和比三角形FEG 的面积大10平方厘米,求CF 的长。
随堂练习5
如图,正方形ABCD 的边长是12厘米,已知DE 是EC 的长度的2倍。
求 1) △DEF 的面积 2) CF 的长。
例题6
如图,长方形ABCD 与三角形EBC 重叠。
已知三角形EFD 的面积比ABF 的面积大6平方厘米,且CD=4厘米,BC=6厘米。
求ED 的长。
B A D B
C G F E A B C F
D E
E
A F D
随堂练习6
如图,ABCD 是长方形,长是5厘米,宽4厘米。
AE 交CD 于F ,三角形甲的面积比三角形乙的面积大4平方厘米。
求CE 的长。
例题7
如图,长方型EFGH 的长和宽分别是6厘米和4厘米。
阴影的总面积为10平方厘米,求四边形ABCD 的面积。
随堂练习7 如图,三角形ABC 的面积是366平方厘米,是平行四边形CDEF 的面积的3倍。
求三角形BED 的面积。
例题8 如图,在△ABC 中,BD=2DC ,AE=3ED ,FC=7,求AF 。
B
C A
D B
E C 甲
乙 E F H G
A B D E F C A
E
随堂练习8
如图,由面积分别为2、3、5、7的四个三角形拼成一个大三角形ABC 。
问:图中三角形BEF 的面积是多少?
B C D
A 2 C F E
B D 3 5 7。