分式方程学习知识点及典型例题.doc

新人教版初中数学——分式方程知识点归纳及典型题解析1．分式方程的概念分母中含有未知数的方程叫做分式方程．注意：“分母中含有未知数”是分式方程与整式方程的根本区别，也是判定一个方程为分式方程的依据．2．分式方程的解法（1）解分式方程的基本思路是将分式方程化为整式方程，具体做法是去分母，即方程两边同乘以各分式的最简公分母．（2）解分式方程的步骤：①找最简公分母，当分母是多项式时，先分解因式；②去分母，方程两边都乘最简公分母，约去分母，化为整式方程；③解整式方程；④验根．易错提醒：解分式方程过程中，易错点有：①去分母时要把方程两边的式子作为一个整体，记得不要漏乘整式项；②忘记验根，最后的结果还要代回方程的最简公分母中，只有最简公分母不是零的解才是原方程的解．3．增根在方程变形时，有时可能产生不适合原方程的根，这种根叫做方程的增根．由于可能产生增根，所以解分式方程要验根，其方法是将根代入最简公分母中，使最简公分母为零的根是增根，否则是原方程的根．温馨提示：增根虽然不是方程的根，但它是分式方程去分母后变形而成的整式方程的根．若这个整式方程本身无解，当然原分式方程就一定无解．4．分式方程的应用（1）分式方程的应用主要涉及工程问题，有工作量问题、行程问题等．每个问题中涉及到三个量的关系，如：工作时间＝工作量工作效率，时间＝路程速度等．（2）列分式方程解应用题的一般步骤： ①设未知数； ②找等量关系； ③列分式方程； ④解分式方程；⑤检验（一验分式方程，二验实际问题）； ⑥答．考向一 解分式方程分式方程的解法：①能化简的应先化简；②方程两边同乘以最简公分母，化为整式方程； ③解整式方程；④验根．典例1 解分式方程：312242x x x -=--． 【解析】去分母得：6-x =x -2， 解得：x =4，经检验x =4是分式方程的解．【名师点睛】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验． 典例2 方程33122x x x-+=--的解为_______________． 【答案】1x =【解析】方程两边同乘以(2)x -，得(32)3x x -+-=-， 解得1x =，检验：1x =时，20x -≠， 所以1x =是原分式方程的解． 故填1x =．【名师点睛】分式方程的解题步骤：去分母，去括号，移项，合并同类项，系数化为1．同时应注意分式方程必须检验．1．解分式方程13211x x-=--，去分母得 A ．12(1)3x --=-B ．12(1)3x --=C ．1223x --=-D ．1223x -+=2．方程24222x x x x =-+--的解为 A ．2B ．2或4C ．4D ．无解考向二 分式方程的解（1）求出未知数的值后必须验根，因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根.（2）验根时把整式方程的根代入最简公分母，如果最简公分母等于0，这个根就是增根；否则这个根就是原分式方程的根，若解出的根都是增根，则原方程无解. （3）如果分式本身约分了，也要代入进去检验.（4）一般地，解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为零，因此要将整式方程的解代入最简公分母，如果最简公分母的值不为零，则是方程的解.典例3 若关于x 的方程3111ax x x -=++的解为整数解，则满足条件的所有整数a 的和是 A ．6B ．0C ．1D ．9【答案】D【解析】分式方程去分母得：ax -1-x =3， 解得：x =41a -， 由分式方程的解为整数解，得到a -1=±1，a -1=±2，a -1=±4， 解得：a =2，0，3，-1，5，-3（舍去）， 则满足条件的所有整数a 的和是9， 故选D ．【名师点睛】此题考查了分式方程的解，熟练掌握运算法则是解本题的关键．典例4 若关于x 的分式方程121k x -=+的解为负数，则k 的取值范围为_______________． 【答案】3k <且1k ≠【解析】分式方程去分母转化为整式方程，去分母得122k x -=+，解得32x k =-，由分式方程的解为负数，可得203k -<且10x +≠，即213k -≠-，解得3k <且1k ≠．3．若关于x 的方程21111a x x -=++有增根，则a 的值为 A ．－12B ．12C ．2D ．2-4．关于x 的方程2334ax a x +=-的解为1x =，则a =A ．1B ．3C ．-1D ．-3考向三 分式方程的应用分式方程解实际问题的求解步骤：审题、设未知数、列方程、解方程、检验、写出答案，检验时要注意从方程本身和实际问题两个方面进行．典例5 某工厂生产一种零件，计划在20天内完成，若每天多生产4个，则15天完成且还多生产10个．设原计划每天生产x 个，根据题意可列分式方程为A ．2010154x x +=+B ．2010154x x -=+C ．201015x x+=D ．201015x x-= 【答案】A【解析】由题意可知原计划每天生产x 个零件，则实际每天生产了(4)x +个零件，实际15天共生产了(200)1x +个零件，因此根据题意可列分式方程为2010154x x +=+．故选A ．典例6 元旦假期即将来临，某旅游景点超市用700元购进甲、乙两种商品260个，其中甲种商品比乙种商品少用100元，已知甲种商品单价比乙种商品单价高20%，那么乙种商品单价是A ．2元B ．2.5元C ．3元D ．5元【答案】B【解析】设乙种商品单价为x 元，则甲种商品单价为(1)20%x +元，由题易得，甲种商品花费300元，乙种商品花费400元，所以300400260120)%(x x+=+，解得 2.5x =元． 故选B ．5．某单位向一所希望小学赠送1080本课外书，现用A ，B 两种不同的包装箱进行包装，单独使用B 型包装箱比单独使用A 型包装箱可少用6个；已知每个B 型包装箱比每个A 型包装箱可多装15本课外书．若设每个A 型包装箱可以装书x 本，则根据题意列得方程为A ．10801080615x x =+- B ．10801080615x x =-- C ．10801080615x x=-+D ．10801080615x x=++6．在“双十一”购物节中，某儿童品牌玩具淘宝专卖店购进了A 、B 两种玩具，其中A 类玩具的进价比B 玩具的进价每个多3元，经调查发现：用900元购进A 类玩具的数量与用750元购进B 类玩具的数量相同（1）求A 、B 的进价分别是每个多少元？（2）该玩具店共购进了A 、B 两类玩具共100个，若玩具店将每个A 类玩具定价为30元出售，每个B 类玩具定价25元出售，且全部售出后所获得利润不少于1080元，则该淘宝专卖店至少购进A 类玩具多少个？1．下列关于x 的方程： ①153x -=，②121x x =-，③()111x x x -+=，④31x a b =-中，是分式方程的有 A ．4个 B ．3个 C ．2个D ．1个2．方程2131x x 的解为 A ．3x B ．4x C ．5xD ．5x3．解分式方程11222x x x-+=-- A ．2x =是方程的解 B ．3x =是方程的解 C ．4x =是方程的解 D ．无解 4．若关于x 的方程223ax a x =-的解为x =1，则a 等于 A ．0.5B ．-0.5C ．2D ．-25．若代数式12x -和321x +的值相等，则x 的值为 A ．x =-7B ．x =7C ．x =-5D ．x =36．若关于x 的方程3111k x x=---有增根，则k 的值为 A ．3 B ．1 C ．0D ．1-7．若分式方程3211x m x x =+++无解，则m = A ．1- B ．3- C ．0D ．2-8．关于x 的方程2211x a ax x++=--的解不小于0，则a 的取值范围是 A ．2a ≤且1a ≠ B ．2a ≥且3a ≠ C ．2a ≤D ．2a ≥9．一艘船顺流航行90千米与逆流航行60千米所用的时间相等，若水流的速度是2千米/时，求船在静水中的速度．设船在静水中的速度为x 千米/时，则可列出的方程为A ．906022x x =+-B ．906022x x =-+ C ．90602x x += D ．60902x x+=10．若分式方程22111x m x x x x x++-=++有增根，则m 的值是A ．-1或1B ．-1或2C ．1或2D ．1或-211．已知关于x 的分式方程212x ax +=--的解为非负数，则a 的取值范围是 A ．a ≤2B ．a <2C ．a ≤2且a ≠-4D ．a <2且a ≠-412．一项工程，甲队单独做需20天完成，甲、乙合作需12天完成，则乙队单独做需多少天完成？若设乙单独做需x 天完成，则可得方程A ．1112012x += B ．2012x x +=1 C ．111220+=xD ．1112012x +=13．九年级（1）班学生周末从学校出发到某实践基地研学旅行，实践基地距学校150千米，一部分学生乘慢车先行，出发30分钟后，另一部分学生乘快车前往，结果他们同时到达实践基地，已知快车的速度是慢车速度的1.2倍，如果设慢车的速度为x 千米/时，根据题意列方程得A ．1501503012x x -=． B ．1501503012x x +=． C ．1501150212x x-=．D ．1501150212x x+=． 14．整数a 满足下列两个条件，使不等式-2≤352x +<12a +1恰好只有3个整数解，使得分式方程13522ax x x x-----=1的解为整数，则所有满足条件的a 的和为 A ．2B ．3C ．5D ．615．某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道，为尽量减少施工对交通造成的影响，施工时对“……”，设实际每天铺设管道x 米，则可得方程300030001510x x-=-．根据此情景，题中用“……”表示的缺失的条件应补为 A ．每天比原计划多铺设10米，结果延期15天才完成B ．每天比原计划少铺设10米，结果延期15天才完成C ．每天比原计划多铺设10米，结果提前15天才完成D ．每天比原计划少铺设10米，结果提前15天才完成16．某中学为了创建“最美校园图书屋”新购买了一批图书，其中科普类图书平均每本的价格是文学类图书平均每本书价格的1.2倍，已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，那么学校购买文学类图书平均每本书的价格是 A ．20元B ．18元C ．15元D ．10元17．分式方程xx 412=+的解为_______________． 18．若关于x 的分式方程33x ax x+--=2a 无解，则a 的值为__________． 19．关于x 的方程123(2)(3)x x x ax x x x ++-=-+-+的解为非正数，则a 的取值范围为__________． 20．分式72x -与2x x-的和为4，则x 的值为_______________． 21．已知x =3是方程211kx k x x---=2的解，那么k 的值为__________． 22．某物流仓储公司用A ，B 两种型号的机器人搬运物品，已知A 型机器人比B 型机器人每小时多搬运20 kg ，A 型机器人搬运1000 kg 所用时间与B 型机器人搬运800 kg 所用时间相等，设B 型机器人每小时搬运x kg 物品，列出关于x 的方程为_______________．23．解下列方程：（1）1233x x x=+--； （2）2316111x x x +=+--；（3 （4）241111x x x +=---．24．“六一”儿童节前，某玩具商店根据市场调查，用1500元购进一批儿童玩具，上市后很快脱销，接着又用2700元购进第二批，所购数量是第一批数量的1.5倍，但每套进价多了10元，求第二批玩具每套的进价是多少元？25．某服装店购进一批甲、乙两种款型时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6400元．甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元．（1）甲、乙两种款型的T恤衫各购进多少件？（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？26．某商店计划购进甲、乙两种商品，乙种商品的进价是甲种商品进价的九折，用3600元购买乙种商品要比购买甲种商品多买10件．（1）求甲、乙两种商品的进价各是多少元？（2）该商店计划购进甲、乙两种商品共80件，且乙种商品的数量不低于甲种商品数量的3倍．甲种商品的售价定为每件80元，乙种商品的售价定为每件70元，若甲、乙两种商品都能卖完，求该商店能获得的最大利润．A ．x =1B ．x =-1C ．x =2D ．x =-2A ．x =-1B ．x =1C ．x =2D ．x =-23．解分式方程21x x -+212x-=3时，去分母化为一元一次方程，正确的是（ ） A ．x +2=3B ．x -2=3C ．x -2=3（2x -1）D ．x +2=3（2x -1）A ．m ≤3B ．m <3C ．m >-3D ．m ≥-35．甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x 个零件，下列方程正确的是（ ）A ．1201508x x =- B ．1201508x x =+ C ．120150= D ．120150=7．方程1x -+21x -=1的解是__________．8．一艘轮船在静水中的最大航速为30 km /h ，它以最大航速沿江顺流航行120 km 所用时间，与以最大航速逆流航行60 km 所用时间相同，则江水的流速为__________km /h ．9．斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度．如图，某路口的斑马线路段A -B -C 横穿双向行驶车道，其中AB =BC =6米，在绿灯亮时，小明共用11秒通过AC ，其中通过BC 的速度是通过AB 速度的1.2倍，求小明通过AB 时的速度．设小明通过AB 时的速度是x 米/秒，根据题意列方程得：__________．10．解分式方程：21x-=251x-．12．端午节前后，张阿姨两次到超市购买同一种粽子．节前，按标价购买，用了96元；节后，按标价的6折购买，用了72元，两次一共购买了27个．这种粽子的标价是多少？13．列方程解应用题：小明和小刚约定周末到某体育公园打羽毛球．他们两家到体育公园的距离分别是1200米，3000米，小刚骑自行车的速度是小明步行速度的3倍，若二人同时到达，则小明需提前4分钟出发，求小明和小刚两人的速度．14．列方程（组）解应用题：德上高速公路巨野至单县段正在加速建设，预计2019年8月竣工．届时，如果汽车行驶高速公路上的平均速度比在普通公路上的平均速度提高80%，那么行驶81千米的高速公路比行驶同等长度的普通公路所用时间将会缩短36分钟，求该汽车在高速公路上的平均速度．15．为进一步营造扫黑除恶专项斗争的浓厚宣传氛围，推进平安校园建设，甲、乙两所学校各租用一辆大巴车组织部分师生，分别从距目的地240千米和270千米的两地同时出发，前往“研学教育”基地开展扫黑除恶教育活动，已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍，甲校师生比乙校师生晚1小时到达目的地，分别求甲、乙两所学校师生所乘大巴车的平均速度.16．列方程解应用题：小明和小刚约定周末到某体育公园打羽毛球．他们两家到体育公园的距离分别是1200米，3000米，小刚骑自行车的速度是小明步行速度的3倍，若二人同时到达，则小明需提前4分钟出发，求小明和小刚两人的速度．1．【答案】A【解析】方程两边同乘以1x -得到12(1)3x --=-， 故选A ． 2．【答案】C【解析】去分母得：2x =（x -2）2+4，分解因式得：（x -2）[2-（x -2）]=0， 解得：x =2或x =4，经检验x =2是增根，分式方程的解为x =4， 故选C ． 3．【答案】B【解析】方程21111a x x -=++两边同时乘以(1)x +，可得211a x -=+， 因为方程21111a x x -=++有增根，所以最简公分母10x +=，即增根是1x =-， 把1x =-代入整式方程，可得12a =．故选B ． 4．【答案】D【解析】把x =1代入原方程得：23314a a +=-， 去分母得，8a +12=3a -3， 解得a =-3， 故选D ． 5．【答案】C【解析】设每个A 型包装箱可以装书x 本，则每个B 型包装箱可以装书(15)x +本，根据单独使用B 型包装箱比单独使用A 型包装箱可少用6个，列方程得10801080615x x=-+， 故选C ．6．【解析】（1）设B 类玩具的进价为x 元，则A 类玩具的进价是(3)x +元，由题意得：9007503x x=+， 解得：15x =，经检验：15x =是原方程的解． 所以15+3=18（元）．答：A 类玩具的进价是18元，B 类玩具的进价是15元．（2）设购进A 类玩具a 个，则购进B 类玩具(100)a -个，由题意得：1210(100)1080a a +-≥，解得：40a ≥，答：该淘宝专卖店至少购进A 类玩具40个．1．【答案】C【解析】关于x 的方程①153x -=，该方程分母中不含未知数，不是分式方程． 关于x 的方程②121x x =-，该方程分母中含有未知数，是分式方程． 关于x 的方程③()111x x x -+=，该方程分母中含有未知数，是分式方程．关于x 的方程④31x a b =-中，该方程分母中不含未知数，不是分式方程．综上，是分式方程的有②、③，共2个． 故选C ． 2．【答案】C【解析】方程两边同乘()(31)x x +-，可得()213x x -=+，即223x x -=+，即5x =， 检验：当5x =时，1)03()(x x -≠+，所以5x =是原方程的根， 故选C ． 3．【答案】D【解析】方程两边分别乘以x -2得：1-x +2（x -2）=-1， 去括号整理得：x =2， 经检验x =2是方程的增根， 故原方程无解． 故选D ． 4．【答案】B【解析】把x =1代入方程223ax a x =-得：2213a a =-， 解得：a =-0.5，经检验a =-0.5是原方程的解， 故选B ． 5．【答案】B【解析】根据题意得：13221x x =-+， 去分母得：3x -6=2x +1， 解得：x =7，经检验x =7是分式方程的解． 故选B ． 6．【答案】A【解析】将方程的两边同时乘以(1)x -，可得31x k =-+，解得4x k =-，根据方程有增根可得1x =，即41k -=，所以3k =．故选A ． 7．【答案】B【解析】去分母，可得32(1)x m x =++，解得2x m =+， 因为分式方程3211x mx x =+++无解，所以12130x m m +=++=+=，解得3m =-， 故选B ． 8．【答案】A 【解析】2211x a ax x++=-- 方程两边同时乘以（x -1）得：x +a -2a =2（x -1）， 解得：x =2-a ，∵方程的解不小于0，∴2-a ≥0，解得：a ≤2， ∵分式方程分母不为0，∴2-a ≠1，解得：a ≠1， 即a 的取值范围是：a ≤2且a ≠1， 故选A ． 9．【答案】A【解析】因为船在静水中的速度为x 千米/时，所以由题意可得906022x x =+-， 故选A ． 10．【答案】D【解析】方程两边都乘x （x +1），得2x 2-（m +1）=（x +1）2， ∵最简公分母x （x +1）=0， ∴x =0或x =-1． 当x =0时，m =-2；当x =-1时，m =1．故选D ． 11．【答案】C 【解析】212x ax +=--， 去分母可得：22x a x +=-+， 移项可得：22x x a +=- ， 合并同类项可得：32x a =-， 系数化为1可得：23ax -=， 根据分式方程的解为非负数和分式有解可得：203a -≥，且223a-≠，解得：a ≤2且a ≠-4， 故选C ． 12．【答案】D【解析】设乙单独做需x 天完成， 由题意得：1112012x +=，故选D ． 13．【答案】C【解析】设慢车的速度为x 千米/小时，则快车的速度为1.2x 千米/小时， 根据题意可得：1501150212x x-=．． 故选C ． 14．【答案】C【解析】由不等式组-2≤352x +<12a +1，可知-3≤x <33a -， ∵x 有且只有3个整数解，∴-1<33a -≤0，∴0<a ≤3， 由分式方程可知：x =-64a -，将x =-64a -代入x -2≠0，∴a ≠1，∵关于x 的分式方程有整数解，∴6能被a -4整除， ∵a 是整数，∴a =2、3、5、6、7、10、-2； ∵0<a ≤3，∴a =2或3，∴所有满足条件的整数a 之和为5， 故选C ．【解析】题中方程表示原计划每天铺设管道(10)x -米，即实际每天比原计划多铺设10米，结果提前15天完成， 故选C ． 16．【答案】A【解析】设文学类图书平均价格为x 元/本，则科普类图书平均价格为1.2x 元/本， 依题意得：12000120001001.2x x-=， 解得：x =20，经检验，x =20是原方程的解，且符合题意． 故选A ． 17．【答案】2x =【解析】方程x x 412=+两边都乘以x ，可得24x +=，解得2x =，检验：当2x =时，0x ≠，即2x =是原方程的解，故答案为：2x =． 18．【答案】1或12【解析】去分母得：x -a =2a （x -3）， 整理得：（1-2a ）x =-5a ， 当1-2a =0时，方程无解，故a =12； 当1-2a ≠0时，x =521aa -=3时，分式方程无解，则a =3， 则a 的值为：1或12；故答案为：1或12．19．【答案】a ≤3且a ≠-12【解析】去分母，得：（x +1）（x +3）-x （x -2）=x +a ，解得x =35a -， 由题意知35a -≤0且35a -≠-3， 解得：a ≤3且a ≠-12， 故答案为：a ≤3且a ≠-12．【解析】首先根据分式72x -与2xx-的和为4，可得7422x x x +=--，去分母，可得748x x -=-，解得3x =，经检验3x =是原方程的解，故x 的值为3．故答案为：3．21．【答案】2【解析】当x =3时，有321223k k --=， 去分母得：9k -4k +2=12，5k =10， 解得：k =2，故答案为：2． 22．【答案】100080020x x=+ 【解析】设B 型机器人每小时搬运x kg 物品，则A 型机器人每小时搬运（x +20）kg 物品，根据题意可得100080020x x =+，故答案为：100080020x x=+．23．【解析】（1）去分母，可得126x x =--，解得7x =，经检验7x =是分式方程的解， 所以方程1233x x x=+--的解为7x =． （2）去分母，可得3316x x -++=，解得2x =， 经检验2x =是分式方程的解，所以方程2316+=的解为2x =．（3 即5（4）2111x x =---，去分母得2241(1)x x =-++，化简得321x =+，解得1x =， 经检验1x =为方程的增根， 所以方程无解．24．【解析】设第一批玩具每套的进价是x 元，则1500x×1.5=270010x +，解得：x =50．经检验：x =50是原方程的解，则第二批玩具每套的进价是x +10=60（元）． 答：第二批玩具每套的进价为60元．25．【解析】（1）设乙种款型T 恤衫购进x 件，则甲种款型的T 恤衫购进1.5x 件，根据题意：78006400301.5x x+=， 解得40x =，经检验，40x =是原方程的解，且符合题意，1.560x =．答：甲种款型的T 恤衫购进60件，乙种款型的T 恤衫购进40件． （2）6400160x=，16030130-=（元）， 13060%6016060%(402)160[1(160%)0.5](402)⨯⨯+⨯⨯÷-⨯-+⨯⨯÷468019206405960=+-=（元）答：售完这批T 恤衫商店共获利5960元．26．【解析】（1）设甲种商品的进价为x 元/件，则乙种商品的进价为0.9x 元/件，36003600100.9x x+=， 解得，x =40，经检验，x =40是原分式方程的解， ∴0.9x =36，答：甲、乙两种商品的进价各是40元/件、36元/件．（2）设甲种商品购进m 件，则乙种商品购进（80-m ）件，总利润为w 元， w =（80-40）m +（70-36）（80-m ）=6m +2720， ∵80-m ≥3m ， ∴m ≤20，∴当m =20时，w 取得最大值，此时w =2840， 答：该商店获得的最大利润是2840元．经检验x=-1是原方程的根；故选B．2．【答案】A【解析】方程两边同时乘以x（x-1）得，x（x-5）+2（x-1）=x（x-1），解得x=-1，把x=-1代入原方程的分母均不为0，故x=-1是原方程的解．故选A．3．【答案】C【解析】方程两边都乘以（2x-1），得x-2=3（2x-1），故选C．7．【答案】x=-2【解析】2121 1(1)(1)xx x x--=-+-，去分母，得（2x-1）（x+1）-2=（x+1）（x-1），去括号，得2x2+x-3=x2-1，移项并整理，得x2+x-2=0，所以（x+2）（x-1）=0，解得x=-2或x=1，经检验，x=-2是原方程的解．故答案为：x=-2．8．【答案】10【解析】设江水的流速为x km/h，根据题意可得：12030x+=6030x-，解得：x=10，10．【解析】两边都乘以（x+1）（x-1），得：2（x+1）=5，解得：x=32，检验：当x=32时，（x+1）（x-1）=54≠0，∴原分式方程的解为x=32．11．【答案】x=2【解析】方程两边都乘以（x+1）（x-1），去分母得x（x+1）-（x2-1）=3，即x2+x-x2+1=3，解得x=2．检验：当x=2时，（x+1）（x-1）=（2+1）（2-1）=3≠0，∴x=2是原方程的解，故原分式方程的解是x=2．12．【解析】设这种粽子的标价是x元/个，则节后的价格是0.6x元/个，依题意，得：96x+720.6x=27，解得：x=8，经检验，x=8是原方程的解，且符合题意．答：这种粽子的标价是8元/个．经检验得：x=50是原方程的根，故3x=150，答：小明的速度是50米/分钟，则小刚骑自行车的速度是150米/分钟．14．【解析】设汽车行驶在普通公路上的平均速度是x千米/分钟，则汽车行驶在高速公路上的平均15．【解析】设甲校师生所乘大巴车的平均速度为x km/h，则乙校师生所乘大巴车的平均速度为1.5x km/h．根据题意得24027011.5x x-=，解得x=60，经检验，x=60是原分式方程的解，1.5x=90．答：甲、乙两校师生所乘大巴车的平均速度分别为60 km/h和90 km/h．16．【解析】设小明的速度是x米/分钟，则小刚骑自行车的速度是3x米/分钟，根据题意可得：1200x-4=30003x，解得：x=50，经检验得：x=50是原方程的根，故3x=150，答：小明的速度是50米/分钟，则小刚骑自行车的速度是150米/分钟．。

考点4 分式方程的特殊解问题【例7】若关于x 的方程2222=-++-xm x x 的解为正数，求m 的取值范围？【例8】已知关于x 的分式方程21a x ++=1的解是非正数，则a 的取值范围是（ ） A ．a≤-1B ．a≤-1且a≠-2C ．a≤1且a≠-2D ．a≤1【例9】如图，点A ，B 在数轴上，它们所对应的数分别是3-和xx--21，且点A ，B 到原点的距离相等，求x 的值.【课堂练习】 1、分式方程0131-x 2=+-x 的解为（ ）[来源Com] A ．x=3 B ．x=﹣5 C ．x=5 D ．无解2、关于x 的分式方程=1的解为正数，则字母a 的取值范围为（ ）A. a≥﹣1B. a ＞﹣1C. a≤﹣1D. a ＜﹣1 3、若分式方程)2)(1(11+-=--x x m x x 有增根，则m 的值为（ ） A 、0和3 B 、1 C 、1和-2 D 、3 4、关于x 的分式方程1mx +=-1的解是负数，则m 的取值范围是（ ） A ．m ＞-1 B ．m ＞-1且m≠0 C ．m≥-1D ．m≥-1且m≠05、方程201x xx +=+的根是 。

6、分式方程2111x x x +--=3的解是 。

-3xx --21 B ．A ．7、若关于x 的方程15102x mx x-=--无解，则m= 。

8、已知关于x 的分式方程2122=--x a x 的解为非负数，求a 得取值范围。

9、的值求有增根若分式方程m x x m x x ,)2)(1(11+-=--【课后作业】1、解分式方程x x －2＝2＋3x －2，去分母后的结果是( )A ．x ＝2＋3B ．x ＝2(x －2)＋3C ．x(x －2)＝2＋3(x －2)D ．x ＝3(x －2)＋2 2、若分式的值为0，则x 的值是（ ）A. x=3B. x=0C. x=﹣3D. x=﹣43、若3x 与61x -互为相反数，则x 的值为（ ） A.13 B.－13C.1D.－1 4、若方程32x x --=2mx-无解，则m=——————．5、已知x ＝2y ＋33y －2，用x 的代数式表示y ，则y ＝____．6、解方程：（1）x x 332=-； （2）11322x x x -=--- （3）2240x-11x -=-。

八年级分式方程数学知识点一、基本概念分式方程是指未知量中包含分数表达式的方程，可用一组数值解求出未知量的值。

如：\frac{x+1}{2}=3，其中x为未知量。

二、分式方程的解法1. 化简分式，使其成为整式方程。

如：\frac{x+1}{2}=3化简为x+1=6。

2. 通分，消去分母。

如：\frac{3}{x-2}=\frac{1}{x+1}通分后为3(x+1)=x-2。

3. 变形化简后求解。

如：\frac{2}{2x+3}-\frac{3}{x-1}=\frac{4}{x^2-x-3}变形化简后得到x=-1或x=\frac{5}{2}。

三、分式方程的注意事项1. 化简前应检查分母是否有值为0的情况。

如：\frac{x}{x^2-4x+4}=1化简前需考虑x^2-4x+4=0的情况，即x=2。

2. 通分时应注意分母因式分解。

如：\frac{x}{2x-4}-\frac{2}{x+1}=\frac{3x}{x^2-3x+2}通分前需分解(x-1)(x-2)。

3. 将解代回原分式方程检验。

如：\frac{4}{x+3}-\frac{5}{x-1}=\frac{1}{x-2}解得x=5/2，代入原式验证是否成立。

四、分式方程的应用例题1. 甲、乙两地的距离为480km，两地之间有一辆车和一辆自行车相向而行，行至中途时，车停下了，自行车继续前进，最后到达乙地时，车和自行车的距离为40km。

已知车行驶的速度比自行车快20km/h，求车和自行车的速度各是多少。

设自行车的速度为x km/h，车的速度为x+20 km/h，时间为t，车行驶的距离为(x+20)×t，自行车行驶的距离为x×(t+2)。

由题意可得(x+20)t+x(t+2)=480及(x+20)t-x(t+2)=40，解得x=20，车速为40km/h，自行车速度为20km/h。

2. 一条河流的宽度为200m，在河岸的A、B两处浅滩的位置分别离河口12km、18km处。

专题09分式方程（2大考点+4种题型）思维导图核心考点与题型分类聚焦考点一：分式方程及其解法考点二：分式方程应用题题型一：分式方程的解法题型二：根据分式方程解的情况求值题型三：分式方程无解问题题型四：分式方程的实际应用考点一：分式方程及其解法1、分式方程的概念分母中含有未知数的方程叫做分式方程．2、解分式方程的方法通过去分母把分式方程转化为整式方程，再求解．3、增根的概念分式方程在化整式方程求解过程中，整式方程的解如果使得分式方程中的分母为0，那么这个解就是方程的增根．4、解分式方程的一般步骤（1）方程两边都乘以最简公分母，去分母，化成整式方程；（2）解这个整式方程，求出整式方程的根；（3）检验．有两种方法：①将求得的整式方程的根代入最简公分母，如果最简公分母等于0，则这个根为增根，方程无解；如果最简公分母不等于0，则这个根为原方程的根，从而解出原方程的解；②直接代入原方程中，看其是否成立．如果成立，则这个根为原方程的根，从而解出原方程的解；如果不成立，则这个根为增根，方程无解．5、分式方程组的概念由两个或两个以上的分式方程构成的方程组叫做分式方程组．6、解分式方程组的方法找出分式方程组中相同的分式进行换元，将分式方程组转化为整式方程组，解方程组，然后进行检验．考点二：分式方程应用题列方程（组）解应用题时，如何找“相等关系”（1）利用题目中的关键语句寻找相等关系；（2）利用公式、定理寻找相等关系；（3）从生活、生产实际经验中寻找相等关系．题型一：分式方程的解法题型二：根据分式方程解的情况求值题型三：分式方程无解问题值．题型四：分式方程的实际应用【例4】．（2022下·上海·八年级上海市田林第三中学校考期中）5G的速度很快，比4G速度每秒多95MB，一部1000MB的电影，5G比4G要快190秒，求5G的速度．【变式1】．（2022下·上海闵行·八年级上海市民办文绮中学校考阶段练习）若A、B两地相距30千米，甲、乙两人分别从A、B两地相向而行，且甲比乙早出发2小时．如果乙比甲每小时多行2千米，那么两人恰好在AB中点相遇．求甲、乙两人的速度各是每小时多少千米？【变式2】．（2022下·上海普陀·八年级校考期中）一项工程，如果甲、乙两队单独完成，甲队比乙队多用5天，如果甲、乙两队合作，6天可以完成.求两队单独完成此项工程各需多少天？【变式3】．（2023下·上海静安·八年级统考期末）某公司先从甲地用9000元购买了一批商品，后发现乙地同一商品每件比甲地便宜，因此又用12000元从乙地补购了一批同样的商品．公司按每件200元售完这两批商品后，共赚了11000元．(1)设该公司从甲地购进x件商品，请用含字母x的代数式表示从乙地购进的商品件数是______；(2)如果乙地同一商品每件比甲地便宜30元，求该公司分别从甲乙两地购进这种商品各多少件．A．1-B．3C．1-或3D．无法确定22．（2023下·上海黄浦·八年级校考阶段练习）甲乙两人各加工30个零件，甲比乙少用1小时完成任务；乙改进操作方法，使生产效率提高了一倍，结果乙完成30个零件的时间比甲完成24个零件所用的时间少1小时．问甲乙两人原来每小时各加工多少个零件．23．（2022下·上海·八年级期末）学校到学习基地的公路距离为15千米，一部分人骑自行车先走，40分钟后，其余的人乘坐汽车出发，结果他们同时到达，如果汽车的平均速度与自行车的平均速度的比是3:1，问：汽车与自行车的平均速度分别是多少？24．为庆祝“六一”活动,镇活动中心需要600个环保纸袋,原计划由初二(1)班全体同学制作完成、在实际制作时,又有初二(2)班10名同学自愿加入参与制作,这样,实际参加制作的同学人均制作的数量比原计划少5个,那么初二(1)班共有多少名同学?25．（2021下·上海·八年级上海市西南模范中学校考期中）学校开展“书香校园”活动，购买了一批图书．已知购买科普类图书花费了10000元，购买文学类图书花费了9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普类图书的数量比购买文学类图书数量少100本，科普类图书平均每本的价格是多少元？26．（2022下·上海宝山·八年级校考阶段练习）如图反映了甲、乙两名自行车爱好者同时骑车从A 地到B 地进行训练时行驶路程y （千米）和行驶时间x （小时）之间关系的部分图像，根据图像提供的信息，解答下列问题：（1）求乙的行驶路程y 和行驶时间x ()13x ≤≤之间的函数解析式；（2）如果甲的速度一直保持不变，乙在骑行3小时之后又以第1小时的速度骑行，结果两人同时到达B 地，求A 、B 两地之间的距离．。

分式方程及其实际应用是初中阶段数学学习的重点。

据近几年中考对分式方程的考查主要是选择题、填空题，分值一般在3～5分，在计算题和解答题中，其分值一般在5～8分。

知识梳理知识点一：分式方程例1. 解方程：12112-=-x x 。

思路分析：1）题意分析：本题考查解分式方程。

2）解题思路：把分式方程化为整式方程。

解答过程：方程两边同乘以（x 2－1），约去分母，得x ＋1＝2。

解这个整式方程，得x ＝1。

把x ＝1代入x 2－1得0，所以原方程无解。

解题后的思考：解到x ＝1，我们能不能说x ＝1就是原分式方程的解（或根）呢？细心的同学可能会发现，当x ＝1时，原分式方程左边和右边的分母（x －1）与（x 2－1）都是0，方程中出现的两个分式都没有意义，因此，x ＝1不是原分式方程的解，应当舍去。

所以原分式方程无解。

例2. 解方程：（1）730100-=x x ； （2）21212339x x x +=+--； （3）()b a x b b x a a ≠+=+11（未知数为x ）。

思路分析：1）题意分析：本题考查解分式方程。

2）解题思路：（1）首先将分式方程去分母化为整式方程。

（2）注意应先分解因式找到最简公分母。

（3）注意a 、b 为常数，可将其当成已知数去分母解分式方程。

解答过程：（1）方程两边同乘以x （x －7），约去分母，得100（x －7）＝30x 。

解这个整式方程，得x ＝10。

检验：把x ＝10代入x （x －7），得10×（10－7）≠0所以，x＝10是原方程的解。

（2）121233(3)(3) x x x x+=+-+-方程两边同乘以（x＋3）（x－3），得x－3＋2（x＋3）＝12x－3＋2x＋6＝123x＝9x＝3经检验：x＝3是原方程的增根，所以原方程无解。

（3）两边同乘以abx，得bx＋a2b＝ax＋ab2bx－ax＝ab2－a2b（b－a）x＝ab（b－a）abx=（提示：0≠-ba）经检验：x＝ab是原方程的解。

第十六章分式知识点和典型例习题【知识网络】【思想方法】 1．转化思想转化是一种重要的数学思想方法，应用非常广泛，运用转化思想能把复杂的问题转化为简单问题，把生疏的问题转化为熟悉问题，本章很多地方都体现了转化思想，如，分式除法、分式乘法；分式加减运算的基本思想：异分母的分式加减法、同分母的分式加减法；解分式方程的基本思想：把分式方程转化为整式方程，从而得到分式方程的解等． 2．建模思想本章常用的数学方法有：分解因式、通分、约分、去分母等，在运用数学知识解决实际问题时，首先要构建一个简单的数学模型，通过数学模型去解决实际问题，经历“实际问题———分式方程模型———求解———解释解的合理性”的数学化过程，体会分式方程的模型思想，对培养通过数学建模思想解决实际问题具有重要意义． 3．类比法本章突出了类比的方法，从分数的基本性质、约分、通分及分数的运算法则类比引出了分式的基本性质、约分、通分及分式的运算法则，从分数的一些运算技巧类比引出了分式的一些运算技巧，无一不体现了类比思想的重要性，分式方程解法及应用也可以类比一元一次方程．第一讲 分式的运算【知识要点】1.分式的概念以及基本性质;2.与分式运算有关的运算法则3.分式的化简求值(通分与约分)4.幂的运算法则【主要公式】1.同分母加减法则:()0b c b ca a a a±±=≠2.异分母加减法则:()0,0b d bc da bc daa c a c ac ac ac±±=±=≠≠;3.分式的乘法与除法:b d bd ac ac •=,b c b d bda d a c ac÷=•= 4.同底数幂的加减运算法则:实际是合并同类项 5.同底数幂的乘法与除法;am●a n =a m+n ; a m ÷ a n =a m －n6.积的乘方与幂的乘方:(ab)m= a mb n, (a m)n= amn7.负指数幂: a-p=1pa a 0=18.乘法公式与因式分解:平方差与完全平方式(a+b)(a-b)= a2- b 2 ;(a ±b)2= a 2±2ab+b 2（一）、分式定义及有关题型题型一：考查分式的定义（一）分式的概念： 形如AB(A 、B 是整式，且B 中含有字母，B ≠0)的式子，叫做分式.其中 A 叫做分式的分子,B 叫做分式的分母.【例1】下列代数式中：yx yx y x y x b a b a y x x -++-+--1,,,21,22π，是分式的有： .题型二：考查分式有意义的条件：在分式中，分母的值不能是零.如果分母的值是零，则分式没有意义.【例2】当x 有何值时，下列分式有意义（1）44+-x x （2）232+x x （3）122-x （4）3||6--x x（5）xx 11-题型三：考查分式的值为0的条件：1、分母中字母的取值不能使分母值为零，否则分式无意义2、当分子为零且分母不为零时，分式值为零。

分式的知识点及典型例题分析1、分式的定义：例：下列式子中， 152 9a 、 5a b 、 3a 2b 2 2 、 1 、 5xy 1 、xy 、8a b 、-23 2x y 4 、2- m 6 x a1 、 x 221 、 3xy 、 3 、 a 1 中分式的个数为（）2x y m（A ） 2 （B ） 3 （C ） 4(D) 5 练习题：（1）下列式子中，是分式的有.⑴ 2x 7 ； ⑵ x1 ；⑶ 5a 2；⑷ x 2x 2；⑸2 b 2；⑹xyy 2.x 5 2 3a b 2x 2⑵ 下列式子，哪些是分式？a ；x23； y 3； 7 x ； x xy ； 1 b .54y 8 x 2 y 4 52、分式有、无意义 ：（ 1）使分式有意义：令分母≠ 0 按解方程的方法去求解； （ 2）使分式无意义：令分母 =0 按解方程的方法去求解；例 1：当 x 时，分式 1 有意义；x 5例 2：分式 2x1中，当 x ____ 时，分式没有意义；2 x例 3：当 x 时，分式 1 有意义；2 1 x例 4：当 x 时，分式 x 有意义；2 1 x 例 5： x ， y 满足关系时，分式 xy无意义；x y例 6：无论 x 取什么数时，总是有意义的分式是（）A ． 2x B. x C. 3xx 52 2x 13 1 D.x 2 x 1 x x 有意义的 x 的取值范围为（） 例 7：使分式x 2 A ． x 2 B ． x2 C ． x 2 D ． x 2例 8：要是分式x 2没有意义，则 x 的值为（）1)( x(x3)A. 2B.-1 或-3C. -1D.33、分式的值为零：使分式值为零：令分子 =0 且分母≠ 0，注意：当分子等于 0 使，看看是否使分母 =0 了，如果使分母 =0 了，那么要舍去。

例 1：当 x 时，分式1 2a的值为 0； a 12 x1例 2：当 x 时，分式的值为 0例 3：如果分式a2的值为为零 , 则 a 的值为 ( ) a 2A.2 B.2 C.2 D. 以上全不对例 4：能使分式 x2x 的值为零的所有 x 的值是（） x 21A x 0 Bx 1 C x 0 或 x1 D x 0 或 x1例 5：要使分式x 29的值为 0，则 x 的值为（）x 25x 6 A.3 或-3 B.3 C.-3 D 2 例 ：若 a1 0 , 则 a 是 ( ) 6 aA. 正数B. 负数C. 零D. 任意有理数4、分式的基本性质的应用：分式的基本性质： 分式的分子与分母同乘或除以一个不等于 0 的整式，分式的值不变。

分式知识点及典型例题一、分式的定义如果 A、B 表示两个整式，并且 B 中含有字母，那么式子 A/B 就叫做分式。

其中 A 叫做分子，B 叫做分母。

需要注意的是：分式的分母不能为 0，因为分母为 0 时，分式无意义。

例如：1/x ，（x ＋ 1）／（x 2）都是分式，而 1/2 就不是分式，因为它的分母 2 不含字母。

二、分式有意义的条件分式有意义的条件是分母不为 0。

即：对于分式 A/B，B ≠ 0 时，分式有意义。

例如：对于分式 1/（x 1) ，要使其有意义，则x 1 ≠ 0，即x ≠ 1。

三、分式的值为 0 的条件分式的值为 0 时，要同时满足两个条件：1、分子为 0 ，即 A ＝ 0 。

2、分母不为 0 ，即B ≠ 0 。

例如：若分式（x 1）／（x ＋ 2）的值为 0，则 x 1 ＝ 0 且 x ＋2 ≠0 ，解得 x ＝ 1 。

四、分式的基本性质分式的分子和分母同时乘以（或除以）同一个不为 0 的整式，分式的值不变。

即：A/B ＝（A×C）／（B×C）， A/B ＝（A÷C）／（B÷C）（C ≠ 0 ）例如：将分式 2x/3y 的分子分母同时乘以 2 ，得到 4x/6y ，分式的值不变。

五、约分把一个分式的分子和分母的公因式约去，叫做约分。

约分的关键是确定分子和分母的公因式。

确定公因式的方法：1、系数：取分子和分母系数的最大公因数。

2、字母：取相同字母的最低次幂。

例如：对分式（6xy）／（9x²y）进行约分，分子分母的系数 6 和 9 的最大公因数是 3 ，字母部分 x 的最低次幂是 1 ，y 的最低次幂是 1 ，所以公因式是 3xy ，约分后得到 2/（3x) 。

六、通分把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做通分。

通分的关键是确定几个分式的最简公分母。

确定最简公分母的方法：1、取各分母系数的最小公倍数。

2、凡单独出现的字母连同它的指数作为最简公分母的一个因式。

初三数学总复习分式方程及应用一：【课前预习】（一）：【知识梳理】1．分式方程:分母中含有 的方程叫做分式方程．2．分式方程的解法：解分式方程的关键是 （即方程两边都乘以最简公分母）,将分式方程转化为整式方程；3．分式方程的增根问题：⑴ 增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根的增根；⑵ 验根：因为解分式方程可能出现增根，所以解分式方程必须验根。

验根的方法是将所求的根代人 或 ，若 的值为零或 的值为零，则该根就是增根。

4．分式方程的应用：列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解．另外，还要注意从多角度思考、分析、解决问题，注意检验、解释结果的合理性．5．通过解分式方程初步体验“转化”的数学思想方法，并能观察分析所给的各个特殊分式或分式方程，灵活应用不同的解法，特别是技巧性的解法解决问题。

6. 分式方程的解法有 和 。

（二）：【课前练习】1. 把分式方程11122x x x--=--的两边同时乘以(x-2), 约去分母，得（ ） A ．1-(1-x)=1 B ．1+(1-x)=1 C ．1-(1-x)=x-2 D ．1+(1-x)=x-22. 方程2321x x -=+的根是（ ） A.－2 B.12 C.－2，12D.－2，1 3. 当m =_____时，方程212mx m x +=-的根为12 4. 如果25452310A B x x x x x -+=-+--，则 A=____ B ＝________. 5. 若方程1322a x x x -=---有增根，则增根为_____，a=________.二：【经典考题剖析】1. 解下列分式方程：25211111 332552323x x x x x x x x x -+=+==+---++（）；（2）；（）； 2222213(1)1142312211x x x x x x x x x x x x -++⎛⎫⎛⎫+=+=+-+= ⎪ ⎪--++⎝⎭⎝⎭（4）；（5）；（6） 分析：（1）用去分母法；（2）（3）（4）题用化整法；（5）（6）题用换元法；分别设211x y x +=+，1y x x=+，解后勿忘检验。

人教版八年级下册分式全章 知识点和典型例习题 知识点回顾知识点一：分式形如 的式子叫做分式 。

知识点二：分式B A 的值1.当 时,分式有意义;2.当 时,分式无意义;3.当 时,分式的值为0;4.当 时,分式的值为1;5.当 时, 分式的值为正;6.当 时,分式的值为负; 知识点三：分式的基本性质用式子表示 知识点四：分式中的符号法则用式子表示 知识点五： 分式的约分 约去分子、分母的最大公因式，使分式变成最简分式或者整式 1.最大公因式= 。

2.当分式的分子和分母为多项式时， 知识点六：分式的通分把异分母分式变成同分母分式的过程。

1.最简公分母= 。

2.当分式的分子和分母为多项式时，知识点七：分式的乘除法法则（用式子表示）乘法法则：用式子表示 除法法则： 用式子表示 知识点八：回顾因式分解总步骤：一提二套三分组1. 提公因式： 套 平方差公式： 2 . 公 完全平方和：式 完全平方差：知识点九：分式的加减法法则 加法法则：减法法则：知识点十：分式的混合运算先 再 最后再 。

知识点十一：整数指数幂七大公式1.同底数幂的乘法2.同底数幂的乘法3.幂的乘方4.积的乘方5.分式的乘方法则6.0指数幂7.负整数指数幂 知识点十二：科学计数法1.绝对值大于1数都可表示成2. 绝对值小于1数都可表示成 其中101<≤a 。

知识点十三：分式方程 1. 概念 2. 解法:①去分母:② ③知识点十四：分式方程解应用题的步骤 、 、 、 、【例题】下列有理式中是分式的有(1)－3x ；(2)yx ；(3)22732xy y x -；(4)x 81-；(5)35+y ； (6)112--x x ；(7)π12--m ； (8)5.023+m ；【练习】1、在下列各式ma m x xb a x xa,),1()3(,43,2,3222--÷++π中，是分式的有 个2.找出下列有理式中是分式的代号(1)－3x ；(2)yx ；(3)22732xyy x -；(4)－x 81；(5) 35+y ； (6)112--x x ；(7) π-12m ； (8)5.023+m .二．分式的值 【例题】 1.当a 时，分式321+-a a 有意义；2.当_____时,分式4312-+x x 无意义；3.若分式33x x --的值为零，则x = ；4.当_______时,分式534-+x x 的值为1；5.当______时,分式51+-x 的值为正；6.当______时分式142+-x 的值为负.【练习】1．①分式36122--x x 有意义，则x ；②当x_____时，分式1x x x-- 有意义；③当x ____时分式x x 2121-+有意义；④当x_____时,分式11x x +-有意义；⑤使分式9x 1x 2-+有意义的x 的取值范围是 ； 2.当x = 3时，分式bx a x +-无意义，则b ______ 3. ①若分式11x x -+的值为零，则x 的值为 ；②若分式)1x )(3x (1|x |=-+-，则x 的值为_________________； ③分式392--x x 当x __________时分式的值为0；④当ｘ= ＿时，分式22943x x x --+的值为0；⑤当a=______时,分式2232a a a -++ 的值为零；4.当x __ 时，分式x -51的值为正.5.当x=_____时,分式232x x --的值为1.6.若分式231-+x x 的值为负数，则x 的取值范围是__________。

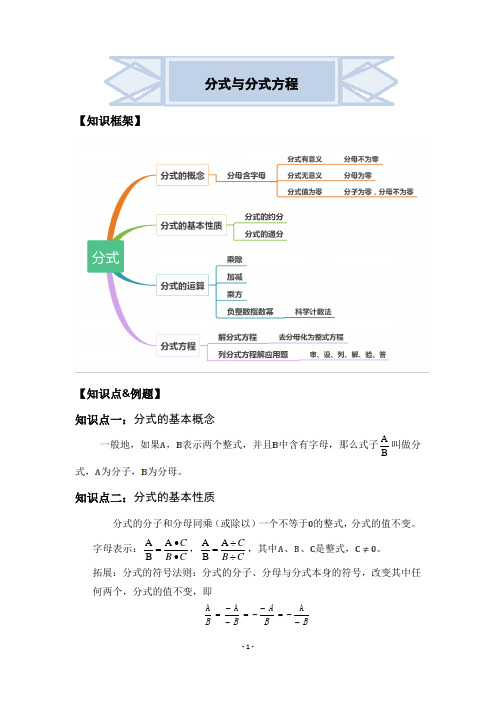
分式与分式方程【知识框架】【知识点&例题】知识点一：分式的基本概念一般地，如果，表示两个整式，并且中含有字母，那么式子B A 叫做分式，为分子，为分母。

知识点二：分式的基本性质 分式的分子和分母同乘（或除以）一个不等于的整式，分式的值不变。

字母表示：C B C••=A B A，C B C÷÷=A B A ，其中、、是整式，。

拓展：分式的符号法则：分式的分子、分母与分式本身的符号，改变其中任何两个，分式的值不变，即B B AB B --=--=--=AAA注意：在应用分式的基本性质时，要注意这个限制条件和隐含条件B ≠0。

知识点三：分式的乘除法法则分式乘分式：用分子的积作为积的分子，分母的积作为积的分母。

式子表示为：db c a d c b a ••=•分式除以分式：把除式的分子、分母颠倒位置后，与被除式相乘。

式子表示为cc ••=•=÷bd a d b a d c b a 分式的乘方：把分子、分母分别乘方。

式子n n nb a b a =⎪⎭⎫ ⎝⎛巩固练习：1.若分式的值为0，则x 的值为 .2.当= 时，分式的值为零.3.计算x xy y xy y xy y x xy y22222222++-÷+-+4.先化简，再求值：其中.242x x --x 26(1)(3)x x x x ----2291333x x x x x ⎛⎫-⋅ ⎪--+⎝⎭13x =5.先化简，再求值：，其中．6、先化简，再求值：，其中7、解下列方程：（1）（2）（3） （4）532224x x x x -⎛⎫--÷ ⎪++⎝⎭3x 22144(1)1a a a a a-+-÷--1a =-3522x x =-223444x x x x =--+22093x x x +=-+35012x x -=+9、在年春运期间，我国南方出现大范围冰雪灾害，导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地千米.抢修车装载着所需材料先从供电局出发，分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的倍，求这两种车的速度。

第二十讲分式方程【要点梳理】要点一、分式方程、根与增根1.分式方程分母中含有未知数的方程叫分式方程.要点诠释：（1）分式方程的重要特征：①是等式；②方程里含有分母；③分母中含有未知数.2.分式方程的根、增根及检验分式方程的解也叫作分式方程的根．在检验时只要把所求出的未知数的值代入最简公分母中，如果它使最简公分母的值不等于O，那么它是原分式方程的一个根；如果它使最简公分母的值为O，那么它不是原分式方程的根，称它是原方程的增根．要点诠释：（1）增根的产生的原因：对于分式方程，当分式中，分母的值为零时，无意义，所以分式方程，不允许未知数取哪些使分母的值为零的值，即分式方程本身就隐含着分母不为零的条件．当把分式方程转化为整式方程以后，这种限制取消了，换言之，方程中未知数的值范围扩大了，如果转化后的整式方程的根恰好是原方程未知数的允许值之外的值，那么就会出现增根．（2）检验增根的方法：把由分式方程化成的整式方程的解代入最简公分母，看最简公分母是否为0，如果为0，则是增根；如果不是0，则是原分式方程的根．要点二、分式方程的解法1.解分式方程的基本思想：将分式方程转化为整式方程.转化方法是方程两边都乘以最简公分母，去掉分母.在去分母这一步变形时，有时可能产生使最简公分母为零的根，这种根叫做原方程的增根.因为解分式方程时可能产生增根，所以解分式方程时必须验根.2.分式方程的一般步骤：（1）方程两边都乘以最简公分母，去掉分母，化成整式方程（注意：当分母是多项式时，先分解因式，再找出最简公分母）；（2）解这个整式方程，求出整式方程的解；（3）检验：将求得的解代入最简公分母，若最简公分母不等于0，则这个解是原分式方程的解，若最简公分母等于0，则这个解不是原分式方程的解，原分式方程无解.要点三、分式方程的应用分式方程的应用主要就是列方程解应用题.列分式方程解应用题按下列步骤进行：（1）审题了解已知数与所求各量所表示的意义，弄清它们之间的数量关系；（2）设未知数；（3）找出能够表示题中全部含义的相等关系，列出分式方程；（4）解这个分式方程；（5）验根，检验是否是增根；（6）写出答案.【典型例题】 类型一、判别分式方程例1、（2016春•闵行区期末）下列方程中，不是分式方程的是（ ）A ．B ．C ．D ．【思路点拨】判断一个方程是否为分式方程主要是看这个方程的分母中是否含有未知数． 【答案】B ；【解析】解：A 、该方程符合分式方程的定义，属于分式方程，故本选项错误； B 、该方程属于无理方程，故本选项正确；C 、该方程符合分式方程的定义，属于分式方程，故本选项错误；D 、该方程符合分式方程的定义，属于分式方程，故本选项错误； 故选：B ．【总结升华】本题考查了分式方程的定义：分母中含有未知数的方程叫做分式方程． 类型二、解分式方程 例2、 解分式方程（1）10522112x x +=--；（2）225103x x x x-=+-． 【答案与解析】 解：（1）10522112x x+=--， 将方程两边同乘(21)x -，得10(5)2(21)x +-=-．解方程，得74x =． 检验：将74x =代入21x -，得52102x -=≠． ∴ 74x =是原方程的根． （2）225103x x x x-=+-， 方程两边同乘以(3)(1)x x x +-，得5(1)(3)0x x --+=．解这个方程，得2x =．检验：把2x =代入最简公分母，得2×5×1＝10≠0． ∴ 原方程的解是2x =．【总结升华】将分式方程化为整式方程时，乘最简公分母时应乘原分式方程的每一项，不要漏乘常数项．特别提醒：解分式方程时，一定要检验方程的根． 举一反三： 【变式】解方程：21233x x x-=---． 【答案】 解：21233x x x-=---， 方程两边都乘3x -，得212(3)x x -=---，解这个方程，得3x =，检验：当3x =时，30x -=， ∴ 3x =是增根， ∴ 原方程无解． 类型三、分式方程的增根【高清课堂405788 分式方程的解法及应用 例3（1）】 例3、（2015春•安岳县期中）若解关于x 的分式方程会产生增根，求m 的值．【思路点拨】增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．把增根代入化为整式方程的方程即可求出m 的值． 【答案与解析】解：方程两边都乘（x+2）（x ﹣2），得2（x+2）+mx=3（x ﹣2）∵最简公分母为（x+2）（x ﹣2）， ∴原方程增根为x=±2，∴把x=2代入整式方程，得m=﹣4． 把x=﹣2代入整式方程，得m=6． 综上，可知m=﹣4或6．【总结升华】增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值． 举一反三： 【变式】如果方程11322xx x-+=--有增根，那么增根是________． 【答案】2x =；提示：因为增根是使分式的分母为零的根，由分母20x -=或20x -=可得2x =．所以增根是2x =．类型四、分式方程的应用例4、甲、乙两班参加绿化校园植树活动，已知乙班每小时比甲班多种2棵树，甲班种 60棵树所用的时间与乙班种66棵树所用的时间相等．求甲、乙两班每小时各种多少棵树? 【思路点拨】本题的等量关系为：甲班种60棵树所用的时间与乙班种66棵树所用的时间相等． 【答案与解析】解：设甲班每小时种x 棵树，则乙班每小时种()2x +棵树．由题意可，得60662x x =+， 解这个方程，得20x =．经检验20x =是原方程的根且符合题意． 所以222x +=(棵)．答：甲班每小时种20棵树，乙班每小时种22棵树．【总结升华】解此题的关键是设出未知数后，用含x 的分式表示甲、乙两班种树所用的时间． 举一反三：【变式】（2015•十堰）在我市开展“五城联创”活动中，某工程队承担了某小区900米长的污水管道改造任务．工程队在改造完360米管道后，引进了新设备，每天的工作效率比原来提高了20%，结果共用27天完成了任务，问引进新设备前工程队每天改造管道多少米？ 【答案】解：设原来每天改造管道x 米，由题意得：+=27，解得：x=30，经检验：x=30是原分式方程的解， 答：引进新设备前工程队每天改造管道30米．【巩固练习】 一.选择题1．下列关于x 的方程中，不是分式方程的是（ ）A ．11=+x xB ．4132=+x xC ．52433=+x xD ．6516-=x x 2．分式方程的解为（ ） A ．x=2 B ．x=﹣2C ．x=﹣D ．x=3．要使54--x x 的值和xx--424的值互为倒数，则x 的值为( )． A.0 B.－1 C.21D.14．已知4321--=+-y y x x ，若用含x 的代数式表示y ，则以下结果正确的是( )． A.310+=x y B.2y x =+ C.310xy -=D.72y x =--5．若关于x 的方程xkx --=-1113有增根，则k 的值为( )． A.3B.1C.0D.－16．一项工程需在规定日期完成，如果甲队独做，就要超规定日期1天，如果乙队单独做，要超过规定日期4天，现在由甲、乙两队共做3天，剩下工程由乙队单独做，刚好在规定日期完成，则规定日期为（ ） A ． 6天 B ． 8天C ． 10天D ．7.5天二.填空题7. 当x ＝______时，分式3x 与26x-的值互为相反数． 8．某市为治理污水，需要铺设一段全长600m 的污水排放管道，铺设120m 后，为加快施工进度，后来每天比原计划增加20m ，结果共用11天完成这一任务，求原计划每天铺设管道的长度．如果设原计划每天铺设xm 管道，那么根据题意，可列方程 ． 9．方程：=1﹣的根是 ．10．当a ＝______时，关于x 的方程4532=-+x a ax 的根是1．11．若方程114112=---+x x x 有增根，则增根是______． 12．关于x 的方程11=+x a的解是负数，则a 的取值范围为____________． 三.解答题13.解分式方程：=﹣．14. 甲、乙两地相距50km，A骑自行车，B乘汽车，同时从甲城出发去乙城．已知汽车的速度是自行车速度的2.5倍，B中途休息了0.5小时还比A早到2小时，求自行车和汽车的速度．15.有一个两位数，它的个位数字比十位数字大1，这个两位数被个位数字除时，商是8，余数是2，求这个两位数．【答案与解析】 一.选择题 1. 【答案】C ；【解析】C 选项中分母不含有未知数，故不是分式方程. 2. 【答案】B ；【解析】解：去分母得：2x=x ﹣2，解得：x=﹣2，经检验x=﹣2是分式方程的解，则分式方程的解为x=﹣2，故选B.3. 【答案】B ； 【解析】由题意442154x x x x --⨯=--，化简得：2415x x -=-解得1x =-. 4. 【答案】C ；【解析】由题意()()()()1423x y x y --=+-，化简得：310y x =-，所以选C. 5. 【答案】A ；【解析】将1x =代入31x k =-+，得3k =. 6. 【答案】B ；【解析】解：设工作总量为1，规定日期为x 天，则若单独做，甲队需x+1天，乙队需x+4天，根据题意列方程得： 3（+）+=1，解方程可得x=8，经检验x=8是分式方程的解， 故选B ．二.填空题 7. 【答案】18； 【解析】3206x x+=-，解得18x =. 8. 【答案】（或）【解析】解：由题意可得，，化简，得.9. 【答案】x=3；【解析】解：去分母得：3﹣x=x ﹣4+1，解得：x=3，经检验x=3是分式方程的解． 故答案为：x=310.【答案】173-； 【解析】将1x =代入原方程，得85512a a +=-，解得173a =-.11.【答案】1x =；【解析】原方程化为：()22141x x +-=-，解得1x =，经检验1x =是增根. 12.【答案】a ＜1且a≠0；【解析】解：方程去分母得，a=x+1，解得，x=a-1， ∵x ＜0，∴a-1＜0即a ＜1，又a≠0则a 的取值范围是a ＜1且a≠0．三.解答题 13. 【解析】 解：原方程可化为：=﹣，两边同时乘以（2x+1）（2x ﹣1）得：x+1=3（2x ﹣1）﹣2（2x+1）， x+1=6x ﹣3﹣4x ﹣2， 解得：x=6．经检验：x=6是原分式方程的解． ∴原方程的解是x=6． 14.【解析】解：设自行车的速度为/xkm h ，汽车的速度为2.5/xkm h ， 由题意，得50500.522.5x x=++， 解方程，得12550 6.25x =+12x =经检验，12x =是原方程的根，2.530x =.所以自行车的速度为12/km h ，汽车的速度是30/km h . 答：自行车的速度为12/km h ，汽车的速度是30/km h . 15.【解析】解：设十位上的数字为x ，则个位上的数字为1x +，得10(1)281x x x ++-=+．解方程，得3x =．经检验：3x =是原方程的根．所以个位上的数字为：1x +＝3＋1＝4． 所以这个两位数是：3×10＋4＝34． 答：这个两位数是34．。

初二数学八上分式和分式方程所有知识点总结和常考题型练习题分式知识点一、分式的定义如果A ，B 表示两个整数，并且B 中含有字母，那么式子B A 叫做分式，A 为分子，B 为分母。

二、与分式有关的条件①分式有意义：分母不为0（0B ≠） ②分式无意义：分母为0（0B =）③分式值为0：分子为0且分母不为0（⎩⎨⎧≠=00B A ） ④分式值为正或大于0：分子分母同号（⎩⎨⎧>>00B A 或⎩⎨⎧<<0B A ） ⑤分式值为负或小于0：分子分母异号（⎩⎨⎧<>00B A 或⎩⎨⎧><0B A ） ⑥分式值为1：分子分母值相等（A=B ）⑦分式值为-1：分子分母值互为相反数（A+B=0） 三、分式的基本性质分式的分子和分母同乘（或除以）一个不等于0的整式，分式的值不变。

字母表示：C B C ∙∙=A B A ，CB C÷÷=A B A ，其中A 、B 、C 是整式，C ≠0。

四、分式的约分定义：把分式的分子与分母的公因式约去，叫做分式的约分。

步骤：把分式分子分母因式分解，然后约去分子与分母的公因。

注意：①分式的分子与分母为单项式时可直接约分，约去分子、分母系数的最大公约数，然后约去分子分母相同因式的最低次幂。

②分子分母若为多项式，约分时先对分子分母进行因式分解，再约分。

最简分式：一个分式的分子与分母没有公因式时，叫做最简分式。

五、分式的通分定义：把几个异分母的分式化成同分母分式，叫做分式的通分。

步骤：分式的通分最主要的步骤是最简公分母的确定。

最简公分母的定义：取各分母所有因式的最高次幂的积作公分母，这样的公分母叫做最简公分母。

确定最简公分母的一般步骤：Ⅰ取各分母系数的最小公倍数；Ⅱ单独出现的字母（或含有字母的式子）的幂的因式连同它的指数作为一个因式；Ⅲ相同字母（或含有字母的式子）的幂的因式取指数最大的。

Ⅳ保证凡出现的字母（或含有字母的式子）为底的幂的因式都要取。

一、基本概念
1.分式：分子和分母都是多项式的数叫做分式。

2.分式方程：含有一个或多个未知数的分式等式叫做分式方程。

二、分式方程的解
1.分式方程的解：使得方程两边分式等价的数叫做分式方程的解。

2.适合分式方程的解：使得分式方程的任意代入都可以使分式方程成立的解叫做适合分式方程的解。

三、分式方程的解的判定
1.分式方程的解的判定方法：将找到的解代入方程，若等式两边可以变成同一个数，则该解为分式方程的解。

2.分式方程的解的验证方法：将方程两边合并，并对两边进行化简，最后验证等式是否成立。

四、分式方程的解的性质
1.分式方程的根的性质：若一个数是分式方程的根，则这个数的相反数也是该方程的根。

2.分式方程的根的性质的应用：利用分式方程的根的性质，可以通过已知根推出其他根。

五、分式方程的解的求解
1.解分式方程的一般步骤：先合并同类项，再化简，最后通过代数运算求解未知数。

2.解分式方程的具体方法：可以通过交叉相乘、通分和消分的方法来解决不同类型的分式方程。

六、分式方程的应用
1.代入法解分式方程：利用推导和分项代入法，将问题转化为分式方程，然后再用分式方程的解来解决问题。

2.混合运算解分式方程：先利用等式性质将分子展开，再通过合并同类项化简，最后求解分式方程得到解。

总结：。

八年级数学下册 分式方程【分式方程的概念】分式的中含有的方程叫做分式方程【分式方程的解法】（1）基本思想：把分式方程转化成为整式方程。

（2）步骤：<1> 去分母：方程两边都乘以最简公分母，化为整式方程。

<2> 解这个整式方程。

<3> 验根：把求出的整式方程的根代入最简公分母。

如果最简公分母为0，则原方程无解，这个未知数的值是原方程的增根；如果最简公分母不为0，则是原方程的解。

产生增根的条件是：①是得到的整式方程的解；②代入最简公分母后值为0。

解分式方程要检验，方法是将求出来的未知数的值代入，看它是不是 ，如果是，说明它是，要舍去。

练习1、分式方程1111112-=+--x x x 去分母时，两边都乘以 2、下列关于x 的方程中，不是分式方程的是（ ）A ．xx ππ= B ．6510-=x x C ．4132=+x x D ．n x m n x =-π 3．如果11-x 与11+x 互为相反数，则x ＝． 4．方程xx 3403440=-的解是． 5．当x=时，分式x x --424的值与45--x x 的值相等． 6．若分式方程52)1()(2-=--x a a x 的解为x=3，则a 的值为． 7．如果方程xx x --=+-21321有增根，那么增根是． 8.某煤厂原计划x 天生产120吨煤，由于采用新的技术，每天增加生产3吨，因此提前2天完成任务，列出方程为（）A ．31202120-=-x xB ．32120120-+=x xC ．31202120-=+xx D ．32120120--=x x 9.若关于x 的方程1011m x x x --=--有增根，则m 的值是 （ ）． A ．3 B ．2 C ．1 D ．－1二、解下列分式方程132+=x x 13132=-+--x x x 21111x x =--43122x x x -=--11322x x x-=---【拓展】1、如果26910x x ++=，那么9x的值是（ ） A 、6 B 、-6 C 、-3 D 、32、已知12x x +=，221x x+的值3、若分式2211111x x x ++--与的值相等，求x 的值列分式方程——基本步骤：① 审—仔细审题，找出等量关系。

第10讲解分式方程知识点1分式方程的解法解分式方程的一般步骤：（1）在方程的两边都乘以最简公分母，约去分母，化成整式方程（2）解这个整式方程（3）验根：把整式方程的根代入最简公分母：如果最简公分母的值不为0，则整式方程的解是原方程的解；如果最简公分母的值为0，则整式方程的解是原方程的增根，即不是原方程的解.【典例】1.解分式方程223124x x x --=+- 【解析】解：223124x x x --=+- ()()231222x x x x --=+-+ 方程两边同乘()()22x x +-，得：()22243x x +=--， 整理得：224443x x x ++=--， 解得：54x =，检验：当54x =时，()()22x x +-≠0，所以原方程的解为54x =. 【方法总结】1、分式方程分母是多项式的要先进行因式分解，再确定最简公分母；不含分母的项也要乘以最简公分母；2、求出整式方程的根后，要注意验根，将整式方程的根代入最简公分母，如果最简公分母的值不为0，则整式方程的根是原分式方程的根；如果最简公分母的值为0，则整式方程的根是原分式方程的增根.2.解分式方程：21421242x x x x x x +-=---+ 【解析】解：方程两边乘以()()22x x +-得：()()()()()2142222x x x x x x x ++=+----去括号：222214244x x x x x x +=+----， 解得：185x = 检验：当185x =时，最简公分母()()181********x x ⎛⎫⎛⎫+=+-≠ ⎪⎪⎝⎭⎝⎭-， 所以，185x =是原方程的解. 【方法总结】1、去分母时，每一项都要乘以()()22x x +-，“-1”项不要漏乘。

2、求出的整式方程的解，不一定是原分式方程的解，所以最后需要验根【随堂练习】1．（2017秋•浠水县期末）解分式方程：﹣=【解答】解：﹣=，去分母，得（2x+2）（x ﹣2）﹣x （x+2）=x 2﹣2，去括号，得﹣4x=2，解得x=﹣，经检验，x=﹣是原分式方程的解．2．（2018春•静安区期末）解方程：﹣1=【解答】解：原方程化为﹣1=， 方程两边都乘以（x+3）（x ﹣1）得：x ﹣1﹣（x+3）（x ﹣1）=﹣2x ，x 2﹣x ﹣2=0，解得：x=2或﹣1，检验：当x=2时，（x+3）（x ﹣1）≠0，所以x=2是原方程的解，当x=﹣1时，（x+3）（x ﹣1）≠0，所以x=﹣1是原方程的解，所以原方程的解为：x 1=2，x 2=﹣1．知识点2 分式方程的解1、类型：给出分式方程的解的限制条件，求分式方程的字母系数，例如：“关于x 的分式方程()()51212x k x x x -=-+-+的解为非负数，求k 的取值范围．” 2、此类问题的步骤（1）解方程：用含字母系数的式子表示分式方程的解；（2）根据“解的限制条件”和“最简公分母不为0”，来列所求系数的关系式；（3）解（2）中的关系式，取公共部分，即为系数的取值范围.【典例】1.关于x 的分式方程()()51212x k x x x -=-+-+的解为非负数，求k 的取值范围． 【解析】解：方程两边同时乘以()()12x x +-得：()()()()5112x x k x x =-+---，去括号，得：22652x x k x x =+----，移项，得：22625x x x x k +++=+-+， 合并同类项，得：7x=7+k ，系数化为1，得：77k x +=， 根据题意得：707k +≥且727k +≠-，717k +≠ 解得k≥-7且k≠-21，k≠0所以k 的取值范围是k≥-7且k≠0.【方法总结】1、“非负数”是大于等于0的数.2、不要漏掉727k +≠-，717k +≠这两个限制条件. 【随堂练习】1．（2018•渝中区校级一模）如果关于x 的不等式组的解集为x ＜2，且关于x 的分式方程：有非负数解．则所有符合条件的整数m 的值之和是（ ）A ．3B ．2C ．﹣1D ．0【解答】解：解不等式≤1，得：x≤m+5， 解不等式x ﹣2＞3（x ﹣2），得：x ＜2，∵不等式组的解为x ＜2，∴m+5≥2，解得：m≥﹣3，解分式方程：得x=，∵分式方程有非负整数解，∴≥0，且≠1，解得m ＜5且m≠1，则﹣3≤m ＜5且m≠1，所以所有符合条件的整数m 的值之和为﹣3﹣2﹣1+0+2+3+4=3，故选：A ．2．（2017春•金堂县期末）若关于x 的方程﹣1=的解为负数，则k 的取值范围是______．【解答】解：去分母得：（x+k ）（x ﹣1）﹣（x+1）（x ﹣1）=k （x+1）， 整理得：x 2+kx ﹣x ﹣k ﹣x 2+1=kx+k ，解得：x=﹣2k+1，由分式方程的解为负数，得到﹣2k+1＜0且﹣2k+1≠﹣1，解得：k ＞且k≠1，故答案为：k ＞且k≠1知识点3分式方程的增根概念：使最简公分母为0的根叫做分式方程的增根【典例】1.若关于x 的方程2151111k k x x x --+=-+-有增根，则k =________.【答案】3或113【解析】解：2151111k k x x x --+=-+- 方程两边都乘()()11x x +-，得()()1511x k x k ++=---，∵分式方程有增根，∴最简公分母()()11x x +-=0，所以增根是1x =或1x =-把1x =代入()()1511x k x k ++=---，整理得3k =把1x =-代入()()1511x k x k ++=---，整理得113k =所以k 的值为3或113 故答案为：3或113． 【方法总结】本题考查了分式方程的增根，解决增根问题的步骤：①去分母，化分式方程为整式方程；②让最简公分母为0，从而确定增根；③把增根代入整式方程即可求得相关字母的值．2.若方程()()6=1111m x x x -+--有增根，则它的增根是（ ） A. x=0 B. x=1C. x=﹣1D. x=1和﹣1 【答案】B.【解析】解：()()6=1111m x x x -+--方程两边都乘()()11x x +-，得()()()6111m x x x +=+--，由最简公分母()()110x x +=-，可知增根可能是1x =或﹣1．把1x =带入()()()6111m x x x +=+--，整理得m=3，把1x =-带入()()()6111m x x x +=+--，整理得6=0，整式方程无解，所以原方程的增根只能是x=1．故选：B【方法总结】此题考查了分式方程的增根的知识，增根是化为整式方程后产生的不适合分式方程的根，可按如下步骤进行：①化分式方程为整式方程；②让最简公分母为0确定可能的增根；③把可能的增根代入整式方程，使整式方程成立的根，是原方程的增根；整式方程不成立，则不是原方程的增根.注意：使最简公分母为0的x 值，不一定是分式方程的增根.【随堂练习】1．（2018春•蓝田县期末）如果关于x 的方程=+1有增根，那么k 的值为 ___ 【解答】解：去分母得：1=k ﹣3+x ﹣2，由分式方程有增根，得到x ﹣2=0，即x=2，把x=2代入整式方程得：k=4，故答案为：42．（2018春•遂宁期末）若分式方程﹣5=有增根，则a 的值为____． 【解答】解：分式方程去分母得：x ﹣5（x ﹣3）=a ，由分式方程有增根，得到x ﹣3=0，即x=3，把x=3代入整式方程得：a=3，故答案为：33．（2018春•姜堰区期末）若关于x 的方程+2=有增根，则增根为____．【解答】解：分式方程的最简公分母为x ﹣4，由分式方程有增根，得到x ﹣4=0，解得：x=4，则增根为x=4，故答案为：x=4知识点4分式方程无解分式方程无解的情况：（1）将分式方程化为整式方程后，整式方程无解.（2）解出的整式方程的根是增根.【典例】1.解分式方程：24163242x x x -=---+ 【解析】解：24163242x x x -=---+ 方程两边同乘()()22x x +-得：()()421632x x +=---，去括号，得：4x+8﹣16=﹣3x+6，移项、合并同类项，得：7x=14，系数化为1，得：x=2，检验：当x=2时，最简公分母()()22x x +-=0，所以x=2是原方程的增根，原方程无解.【方法总结】1、当解出的整式方程的根是增根时，分式方程无解2、注意增根的检验：检验：当x=2时，()()22x x +-=0，所以x=2是原方程的增根，原方程无解。