九年级数学中考复习专题——中点的妙用
- 格式:doc
- 大小:149.00 KB
- 文档页数:6


中点的妙用班别:______姓名:__________学号:_______联想是一种非常重要的数学品质。
善于联想,才能更好地解决问题。
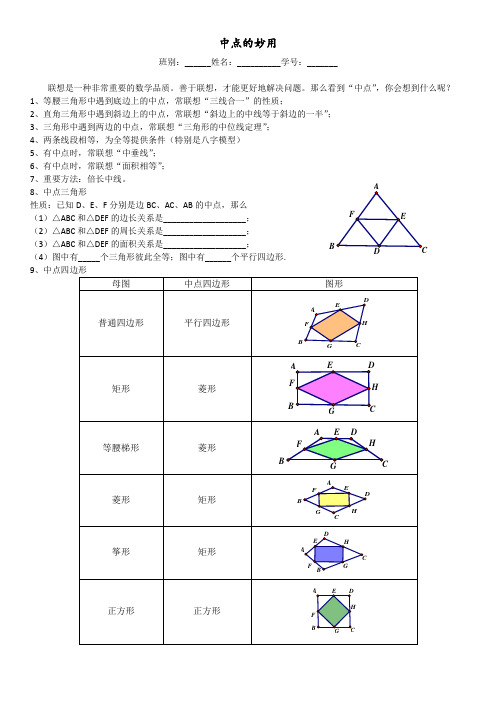
那么看到“中点”,你会想到什么呢? 1、等腰三角形中遇到底边上的中点,常联想“三线合一”的性质;2、直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”;3、三角形中遇到两边的中点,常联想“三角形的中位线定理”;4、两条线段相等,为全等提供条件(特别是八字模型)5、有中点时,常联想“中垂线”;6、有中点时,常联想“面积相等”;7、重要方法:倍长中线。
8、中点三角形性质:已知D 、E 、F 分别是边BC 、AC 、AB 的中点,那么(1)△ABC 和△DEF 的边长关系是___________________;(2)△ABC 和△DEF 的周长关系是___________________; (3)△ABC 和△DEF 的面积关系是___________________; (4)图中有_____个三角形彼此全等;图中有______个平行四边形. 9B例1:如图,在△ABC 中,∠A=90°,AB=AC ,O 是BC 的中点,如果在AB 和AC 上分别有一个动点M 、N 在移动,且在移动时保持AN=BM ,请你判断△OMN 的形状,并说明理由.练习:如图1所示,在△ABC 中,AB=AC=5,BC=6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于( ).A .B .C .D .例2:如图,在四边形ABCD 中,∠DAB=∠DCB=90°,对角线AC 与BD 相交于点O ,M 、N 分别是边BD 、AC 的中点. (1)求证:MN ⊥AC ;(2)当AC=8cm ,BD=10cm 时,求MN 的长.练习:如图,E 是正方形ABCD 边AB 的中点,DF ⊥CE 于点M .说明:AM=AD .例3:已知:△ABC 中,AD 是BC 中线,E 、F 分别是AB 、AC 中点.求证:AD 、EF 互相平分.例4:在四边形ABCD 中,若AB =CD ,E 、F 、G 、H 分别为AD 、BC 、BD 、AC 的中点,求证:四边形EFGH 是菱形.6595125165练习1:如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.练习2:如图,在△ABC中,D、E为边AB、AC上的点,且BD=EC,连接DC、BE,并分别取中点N、M,连接MN并延长交AB、AC于点F、G,求证:AF=AG.例5:如图,四边形ABCD中,AD∥BC,E是AB的中点,DE⊥CE,求证:AD+BC=DC. 练习:△ABC中,D为BC中点,AB=5,AD=6,AC=13。

数学初中中点总结一、中点的定义和性质在数学中,中点是指一条线段的中间点,即将一条线段平均划分为两个相等的部分。
以下是关于中点的定义和性质的总结:1.定义:若线段AB的中点为M,则AM = MB。
2.定理1:如果一个线段的两个端点对换,则线段的中点也对换。
3.定理2:两个线段的中点连线平行于这两个线段。
4.定理3:一个线段的中点将线段平分为两个相等部分。
5.定理4:如果三个点A、B、C在同一条线段上,且B是AC的中点,则AB = BC。
二、中点的求解方法在求解一个线段的中点时,我们可以使用以下方法:1. 使用坐标求解假设线段的两个端点分别是A(x₁, y₁)和B(x₂, y₂),则线段AB的中点M的坐标可以通过以下公式求解:M = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)我们可以将上述公式应用于平面直角坐标系、极坐标系和三维空间中的线段。
2. 使用向量求解我们可以使用向量的加法运算来确定线段的中点。
假设线段的两个端点分别是A和B,则线段AB的中点M可以通过以下公式求解:M = (A + B) / 2其中,A和B是线段的位置向量。
3. 使用尺规作图法求解尺规作图是一种用尺子和圆规来进行几何作图的方法。
我们可以使用尺规作图来求解线段的中点。
方法如下:•步骤1:画出线段AB;•步骤2:以点A为圆心,以线段AB的长度为半径画一个圆;•步骤3:以点B为圆心,以线段BA的长度为半径画一个圆;•步骤4:两个圆的交点即为线段AB的中点M。
三、数学应用中点的概念在数学中有广泛的应用,以下是一些常见的应用场景:1. 几何图形的性质证明在几何证明中,我们常常需要证明线段的性质。
通过使用中点的性质和定理,我们可以更方便地证明某些几何图形的性质。
例如,在证明平行四边形的性质时,我们可以使用中点将对角线平分的性质来简化证明过程。
2. 向量运算在向量运算中,我们经常需要计算两个向量的中点。
通过求解两个向量的位置向量的中点,我们可以方便地计算向量的和、平均值等。

初中数学关于“中点”的综合应用一、遇到两平行线所截得的线段的中点时,常联想“八字型”全等三角形1在□ABCD 中, BC=4cm,F ,G ,分别为BE,CD 的中点为,E 为AD 的中点,求FG 的长.如图,已知AB =12;AB ⊥BC 于B ,AB ⊥AD 于A ,AD =5,BC =10.点E 是CD 的中点,则AE 的长是.二、等腰三角形中遇到底边上的中点,常联想“三线合一”的性质2.如图所示,在△ABC 中,E 为AB 的中点,CD 平分∠ACB,AD⊥CD 于点D .•试说明:(1)DE∥BC.(2)DE=12(BC-AC ).三、直角三角形中遇到斜边上的中点,常联想“斜边上的中线,等于斜边的一半”3:在平行四边形ABCD 中,两对角线交与点O ,E 、F 、P 分别为OB 、OC 、AD 的中点,且AC=2AB 求证:EP=EF四、三角形中遇到两边的中点,常联想“三角形的中位线定理”4.已知如图1,△ABC 中,D 是BC 边的中点,E 是AD 边的中点,连结BE 并延长交AC 于点F. 求证:FC=2AF .图1CBEAC5如图五边形ABCD E 中,∠ A B C= ∠A E D=90度,∠ B A C= ∠E AD,M 是CD 的中点求证:BM=ME6倍长中线:条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求的正的结论集中到同一个三角形中。
阅读理解:课外兴趣小组活动时,老师提出了如下问题:如图, ABC 中,若AB=5,AC=3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E,使DE=AD,再连接BE(或将△ABC 绕点D 旋转180°得到△EBD),把AB 、AC 、2AD 集中在△ABE 中,利用三角形的三边关系可得2<AE<8,则1<AD<4, 感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求的正的结论集中到同一个三角形中。


关于中点的解题技巧嘿,朋友们!今天咱们来聊聊数学里关于中点的那些解题技巧,这就像是在神秘的数学迷宫里找到一把神奇的钥匙,一旦掌握,那可就像超级英雄拥有了超能力一样。
你看啊,中点有时候就像一个平衡大师。
比如说在一条线段上,中点把线段分成了两段相等的部分,这就好比一个大蛋糕被精准地切成了两块一样大小的小蛋糕。
当我们看到中点这个平衡大师的时候,就可以想到很多好玩的东西。
在三角形里,中点可就更有趣了。
三角形的中位线就像是一个低调的小助手。
中位线平行于第三边,而且长度是第三边的一半,这感觉就像是一个小跟班紧紧跟在大佬后面,而且还保持着一种很奇妙的比例关系。
就好像小跟班的身高永远是大佬的一半,还一直亦步亦趋地跟着。
如果遇到平行四边形,对角线的交点是中点的时候,那这个中点就像是一个交通枢纽。
平行四边形的对角线互相平分,这个中点就负责把各种信息(线段关系)合理地分配到各个角落,就像交通枢纽把人流和车流分配到不同的道路一样。
要是在证明题里看到中点,我们可以像侦探一样敏锐。
有时候可以构造中位线,这就像给我们的解题之路搭建了一座便捷的桥梁。
如果没有这座桥,我们可能就像在没有路的森林里乱撞,有了这座桥,那就可以轻松地到达对岸啦。
在圆里,直径的中点也就是圆心,这圆心就像一个强大的引力中心。
圆上的点到圆心的距离都相等,就好像所有的小星星都被这个引力中心牢牢吸引着,规规矩矩地保持着距离。
而且啊,中点常常是隐藏着等量关系的宝库。
我们就像寻宝者一样,一旦发现中点,就要赶紧挖掘它背后的宝藏,那些等量关系可能就是我们解开难题的关键,就像打开宝藏的密码一样。
再比如说,遇到两个中点的时候,我们可以把它们连接起来,这时候这条线就像一条神秘的纽带,把不同的部分联系起来,往往能给我们带来意想不到的解题思路,就像突然发现了一条秘密通道。
总之呢,中点在数学里就像一个充满惊喜的小魔法点,只要我们用心去探索它的奥秘,就能够在数学的世界里玩得转,轻松解决那些看似棘手的问题啦。


ABCD E中点的妙用一、等积转化1、平行四边形转化成等积的矩形: 平行四边形转化成等积的梯形: 平行四边形转化成等积的直角梯形: 平行四边形转化成等积的三角形:2、三角形转化成等积的平行四边形: 三角形转化成等积的矩形: 三角形转化成等积的梯形:3、梯形转化成等积的平行四边形: 梯形转化成等积的平行四边形: 梯形转化成等积的直角梯形: 梯形转化成等积的矩形:4、矩形梯形转化成等积的三角形 矩形梯形转化成等积的梯形5、任意四边形转化成等积的平行四边形:二、辅助线做法1、在△ABC 中,AB =AC ,D 是AB 上一点,E 是AC 延长线上一点,且BD =CE .求证:DM =EM .2、阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E 是BC 的中点,点A 在DE 上,且∠BAE=∠CDE .求证:AB=CD (多种方法)3、如图,在正方形ABCD 中,E 、F 为AB 、BC 的中点,CE 、DF 交于M ,求证:AM=AD 。
EB(2018年杭州市)如图,在菱形ABCD 中,∠A =110°,E ,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P ,则∠FPC =( )A .35°B .45°C .50°D .55°4、(本题满分10分) 已知:线段OA ⊥OB ,点C 为OB 中点,D 为线段OA 上一点。
连结AC , BD 交于点P 。
(1) 如图1,当OA =OB ,且D 为OA 中点时,求PCAP的值; (2) 如图2,当OA =OB ,且AO AD =41时,求tan ∠BPC 的值; (3) 如图3,当AD :AO :OB =1:n :2n 时,直接写出tan ∠BPC 的值。
三、体现的思想和方法 1、 2、A DE P CBFA B D PODO PA BDC OPA B圖1 圖2圖3。
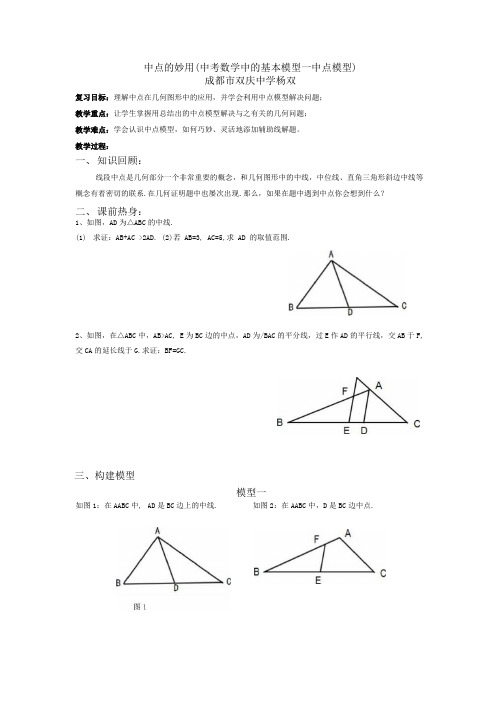
中点的妙用(中考数学中的基本模型一中点模型)成都市双庆中学杨双复习目标:理解中点在几何图形中的应用,并学会利用中点模型解决问题;教学重点:让学生掌握用总结出的中点模型解决与之有关的几何问题;教学难点:学会认识中点模型,如何巧妙、灵活地添加辅助线解题。
教学过程:一、知识回顾:线段中点是几何部分一个非常重要的概念,和几何图形中的中线,中位线、直角三角形斜边中线等概念有着密切的联系.在几何证明题中也屡次出现.那么,如果在题中遇到中点你会想到什么?二、课前热身:1、如图,AD为△ABC的中线.(1)求证:AB+AC >2AD. (2)若 AB=3, AC=5,求 AD 的取值范围.2、如图,在△ABC中,AB>AC, E为BC边的中点,AD为/BAC的平分线,过E作AD的平行线,交AB于F, 交CA的延长线于G.求证:BF=GC.三、构建模型模型一如图1:在AABC中, AD是BC边上的中线. 如图2:在AABC中,D是BC边中点.方法提炼:1. 当题中出现中线时,我们经常根据需要将,使得 与 相等,这种方法叫做""。
2. 当已知条件中出现类中线时,常常将此类中线倍长构造全等三角形解决问题,这种方法叫做 a n四、模型应用例1、(2017成华区八年级下半期检测28题)(1) 在ZXABC 中,若AB=5, AC=8,则BC 边上的中线AD 的取值范围是 .(2) 如图2,在AABC 中,点D 是BC 边上的中点,DE1DF 与点D, DE 交AB 于E, DF 交AC 于点F,连接 EF,求证:BE+CF>EF.变式练习、如图,已知在梯形ABCD 中,AD 〃BC, AB=AD+BC, E 是CD 的中点. 求证:AE_LBE.小结: ________________________________________________________________________模型二如图:AB//CD,点E 是BC 的中点.图1 图2C D当题中出现平行线,且平行线间有中点,我们把这种情况叫做。

精典专题五中点问题一.考情分析二.知识回顾1.与中点有关的内容与中点有关的内容主要包括三角形的中位线、梯形的中位线、直角三角形斜边上的中线等.(1)等腰三角形底边的中线、底边的高与顶角的角平分线“三线合一”。
(2)三角形的中位线平行于第三边,并且等于第三边的一半;.(3)梯形的中位线平行于两底,且等于两底和的一半;(4)直角三角形斜边上的中线等于斜边的一半;(5)弦的中点与垂径定理;2.中点四边形(1)顺次连接四边形四边的中点得到一个平行四边形;(2)顺次连接对角线相等的四边形四边的中点得到一个菱形;(3)顺次连接对角线互相垂直的四边形四边中点得到一个矩形;(4)顺次连接对角线互相垂直且相等的四边形四边中点得到一个正方形;三.重点突破类型一:直角三角形斜边的中线(B)【典型例题1】如图1在△ABC和△ABD中,已知∠=∠=∠,E F分别为边AB和CD的中点,求证:,ACB ADB Rt⊥EF CD.〖搭配练习〗(A )1.如图2,在四边形ABCD 中,,ABC ADC Rt ∠=∠=∠P 为线段AC 的中点,连接,,.BD PB PD 试问:PBD ∠与PDB ∠有何关系?说明理由.(C )2.如图3,在锐角△ABC 中,AD CE 、分别是BC AB 、边上的高,AD CE 、相交于F ,BF 的中点为P ,AC 的中点为Q ,连接PQ 、.DE 求证:直线PQ 是线段DE 的垂直平分线.类型二:中线倍长的用法(A )【典型例题2】如图,在△ABC 中,AD 为BC 边上的中线,求证:()1.2AD AB AC <+(B )【典型例题3】如图6,在△ABC 中,AD 为BC 边上的中线,BF 交AD 于点E ,交AC 于点F ,且满足AF EF =,求证:.BE AC =〖搭配练习〗(A )1.三角形的两边长分别为3和5,试求第三边的中线长x 的取值范围.(B )2. 如图7,在△ABC 中,AD 为BC 边上的中线,DA AC ⊥于点A ,120BAC ∠=︒, 求证:2.AB AC =(C )3.如图8,在△ABC 中,D 为BC 边上的中点,且.ED DF ⊥求证:.BE CF EF +>类型三:三角形的中位线与梯形的中位线(A )【典型例题4】如图9在△ABC 中,AD 平分BAC ∠,BD AD ⊥于点D ,点E 是BC 边上的中点,3,5AB AC ==,试求线段DE 的长.(C )【典型例题5】如图10,梯形ABCD 中,AD ∥BC ,AC BD ⊥于O ,试判断AB CD +与AD BC +的大小,并证明你的结论.〖搭配练习〗(C )1.如图11,在△ABC 中,BE 、CD 分别为ABC ∠与ACB ∠的平分线,AM CD ⊥于点M ,AN BE ⊥于点N ,连接MN ,求证:MN ∥BC .(B )2. 如图12,在等腰梯形ABCD 中,AB ∥CD ,中位线EF 与对角线AC 、BD 交于M 、N 两点,若EF =18 cm ,MN =8 cm ,求AB 的长.(B )3. 如图13,AE 为正方形ABCD 中BAC ∠的平分线,AE 分别交BD 、BC 于点F 、E ,AC 、BD 相交于点O . 求证:1.2OF CE =类型四:四边形的中点(B)【典型例题6】如图14,△ABC与△CDE都是等边三角形,且B、C、D三点共线,分别取AB、BD、DE、EA边的中点M、N、P、Q,连接MN、NP、PQ、QM,试判断四边形MNPQ的形状,说明理由.(B)【典型例题7】如图15,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥C D于点P,则∠FPC= ( )A. 35°B45° C. 50° D. 55°〖搭配练习〗(A)1.如图16,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.7 B.9 C.10 D.11(B)2.如图17,在□ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠DME是()A.150°B.140°C.135°D.130°(B)3.如图18,已知:梯形ABCD中,AB//CD,且BM⊥CM,M是AD的中点,试说明AB+CD=BC.(B )4.已知:如图19,在正方形ABCD 中,Q 在CD 上,且DQ=QC ,P 在BC 上,且AP=CD +CP .求证:AQ 平分∠DAP .类型五:弦的中点与垂径定理(A )【典型例题8】如图20,AB 是⊙O 的直径,CD 是弦,AE ⊥CD 于E ,BF ⊥CD 于F.求证:EC=DF.〖搭配练习〗(A )1.如图21,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C 、D 两点,AB =10cm,CD =6cm ,则AC 的长为( )A .0.5cmB .1cmC .1.5cmD .2cm(A )2.如图22,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦AB CD ⊥,OCD ∠的平分线交⊙O 于点P ,当点C 在上半圆(不包括A 、B 两点)上移动时,点P ( )A .到CD 的距离保持不变B .位置不变C .等分D .随C 点的移动而移动(B )3.如图,已知:在⊙O 中,AB 是直径,CD 是弦,CD CE ⊥交AB 于E ,CD DF ⊥交AB 于F .求证:BF AE =.(B )4.如图,在两个同心圆中,大圆的弦AB ,交小圆于C 、D 两点,设大圆和小圆的半径分别为b a ,.求证:22b a BD AD -=⋅四.复习建议作为几何的基础,中点是解决其他综合问题的必备知识,是几何证明以及几何计算的重要的辅助工具。

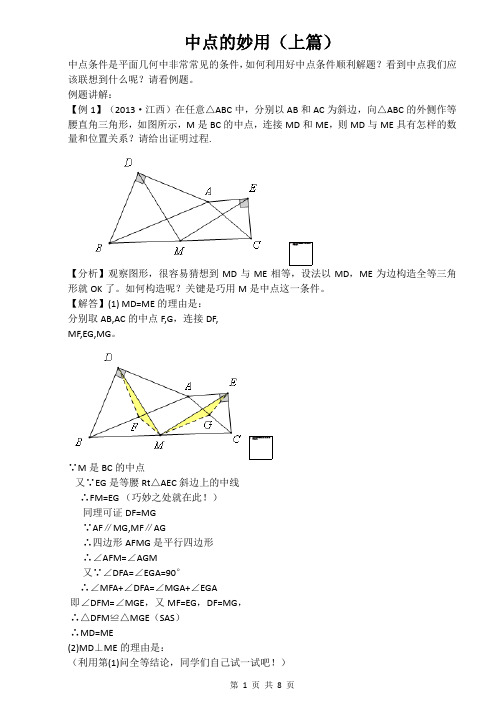
中点的妙用(上篇)中点条件是平面几何中非常常见的条件,如何利用好中点条件顺利解题?看到中点我们应该联想到什么呢?请看例题。
例题讲解:【例1】(2013·江西)在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量和位置关系?请给出证明过程.【分析】观察图形,很容易猜想到MD与ME相等,设法以MD,ME为边构造全等三角形就OK了。
如何构造呢?关键是巧用M是中点这一条件。
【解答】(1) MD=ME的理由是:分别取AB,AC的中点F,G,连接DF,MF,EG,MG。
∵M是BC的中点又∵EG是等腰Rt△AEC斜边上的中线∴FM=EG(巧妙之处就在此!)同理可证DF=MG∵AF∥MG,MF∥AG∴四边形AFMG是平行四边形∴∠AFM=∠AGM又∵∠DFA=∠EGA=90°∴∠MFA+∠DFA=∠MGA+∠EGA即∠DFM=∠MGE,又MF=EG,DF=MG,∴△DFM≌△MGE(SAS)∴MD=ME(2)MD⊥ME的理由是:(利用第(1)问全等结论,同学们自己试一试吧!)方法提炼:我们知道,中学共学习了三个等于线段一半的定理,它们是:①30°所对的直角边等于斜边一半②直角三角形斜边上的中线等于斜边一半③三角形的中位线等于第三边的一半其中定理②,定理③均与中点有关!再加上中点的定义,面对中点条件,我们自然而然采取下列策略:1.倍长中线法2.构造中位线3.构造直角三角形斜边中线变式练习:在任意△ABC中,分别以AB和AC为边向△ABC的外侧作等边三角形,如图所示,I,J,K分别是AD,BC,AE的中点,判断△IJK的形状并证明。
解题感悟:有道是:见到中点有三法一是构造中位线二是构造斜中线三是倍长构全等中点的妙用(中篇)我们学习了中点模型的一道经典例题,介绍了面对中点时可采取的策略,即倍长构造全等(8字型),构造中位线以及构造直角三角形斜边中线。


中点的妙用河南省商水县周口中英文学校刘易宁在几何证明题与求解题中,常会碰到线段或边的中点。
那么,如何利用中点快速的解答题呢?本人就这个问题谈一下中点的妙用。
一、在直角三角形中,如果有斜边的中点,常想斜边上的中线。
例1:如图1,在Rt⊿ABC中,∠A=90°,AC=AB,M、N分别在AC、AB上。
且AN=BM.O为斜边BC的中点.试判断△OMN的形状,并说明理由.分析:O为直角三角形ABC的中点,因为直角三角形斜边上的中1BC=CO.再利用其它条件线等于斜边的一半,所以连接AO,得AO=2证△AOM≌△CON,得MO=ON,且∠MON=90°,从而知道△MON的形状.解:△MON的形状是等腰直角三角形.理由如下:连接AO∵O为BC的中点,∠BAC=90°Array 1BC (直角三角形斜边上∴AO=BO=2的中线等于斜边的一半)∵AB=AC∴∠MAO=∠OAC=45°,AO⊥BC,∠C=45°∵AB=AC,AN=BN∴AM=CN在△AOM和△CON中∵AM=CN∠MOA=∠C=45°AO=CO∴△AOM≌△CON∴OM=ON ∠MOA=∠CON∵∠AON+∠CON=45°∴∠MOA+∠AON=90°即∠MON=90°∴△MON是等腰直角三角形.点拨:在直角三角形中,如果有斜边上的中点,常想构造斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半来解题。
本题还利用了等腰三角形“三线合一”的性质。
二.有中点时常构造垂直平分线。
例2.如图2所示,在△ABC中,AD是BC边上中线,∠C=2∠1BC。
求证:△ADC为等边三角形。
B.AC=2分析:D是BC边的中点,过点D作DE⊥BC交AB于点E.连接CE,1∠ACB,则有△EDC≌△EAC,从而则有EB=EC.有∠ABC=∠ECB=2∠BAC=90°。
故∠ACB=60°,问题得证。

1 / 37
2021中考数学培优练习六------中点妙用
中点妙用
1.两条线段相等,为全等提供条件 。
2.中线平分三角形的面积
3.倍长中线 –全等 4.中位线 --平行且一半
5.斜边上的中线是斜边的一半 6.重心—2:1
7.中点—X 型全等 8.圆中垂径---中点
9.中心对称图形—对称中心 10.反比例函数---中心对称—中点
一.选择题(共5小题)
1.如图,直角△ABC 中,∠B =30°,点O 是△ABC 的重心,连接CO 并延长交AB 于点E ,过点E 作EF ⊥AB 交BC 于点F ,连接AF 交CE 于点M ,则MO MF 的值为( )
A .12
B .√54
C .23
D .√3
3 2.如图,在平行四边形ABCD 中,AC 、BD 相交于点O ,点E 是OA 的中点,连接BE 并延长交AD 于点F ,S △AEF =4,则下列结论:①FD =2AF ;②S △BCE =36;③S △ABE =12;④△AEF ∽△ACD ,其中一定正确的是( )
A .①②③④
B .①②
C .②③④
D .①②③
3.如图,正方形ABCD 的边长为2,将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动.如
果点Q 从点A 出发,沿图中所示方向按A ⇒B ⇒C ⇒D ⇒A 滑动到A 止,同时点R 从点B 出发,沿图中所示方向按B ⇒C ⇒D ⇒A ⇒B 滑动到B 止,在这个过程中,线段QR 的中点M 所经过的路线围成的图形的面积为( )
A .2
B .4﹣π
C .π
D .π﹣1 第 3题 第4 题
第2 题 第5 题 第6 题 第7题。
方法专题:中点的妙用
联想是一种非常重要的数学品质。
善于联想,才能更好的寻求解决问题的方法。
同学们当你遇到中点时,你会产生哪些联想呢?学习完这个专题后,能给你带来一定的启示。
看到中点该想到什么?
1、等腰三角形中遇到底边上的中点,常联想“三线合一”的性质;
2、直角三角形中遇到斜边上的中点,常联想“斜边上的中线,等于斜边的一半”;
3、三角形中遇到两边的中点,常联想“三角形的中位线定理”;
4、两条线段相等,为全等提供条件(遇到两平行线所截得的线段的中点时,常联想“八字型”全等三角形);
5、有中点时常构造垂直平分线;
6、有中点时,常会出现面积的一半(中线平分三角形的面积);
7、倍长中线
8、圆中遇到弦的中点,常联想“垂径定理”
一、等腰三角形中遇到底边上的中点,常联想“三线合一”的性质
1、如图1所示,在△ABC 中,AB=AC=5,BC=6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于( )
A .65
B .95
C .125
D .165
二、直角三角形中遇到斜边上的中点,常联想“斜边上的中线,等于斜边的一半”
2、如图,在Rt⊿ABC 中,∠A=90°,AC=AB,M 、N 分别在AC 、AB 上。
且AN=BM.O 为斜边BC 的中点.试判断△OMN 的形状,并说明理由.
3、如图,正方形ABCD 的边长为2, 将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动.如果点Q 从点A 出发,沿图中所示方向按A D C B A →→→→滑动到点A 为止,同时点F 从点B 出发,沿图中所示方向按B A D C B →→→→滑动到点B 为止,那么在这个过程中,线段QF 的中点M 所经过的路线围成的图形的面积为( ) A. 2 B. 4-π C.π D.1π-
N
M
B
O C
A
B
C Q
M
三、三角形中遇到两边的中点,常联想“三角形的中位线定理” 4、(直接找线段的中点,应用中位线定理) 如图,已知四边形ABCD 的对角线AC 与BD 相交于点O ,且AC=BD ,M 、N 分别是AB 、CD 的中点,MN 分别交BD 、AC 于点E 、F.你能说出OE 与OF 的大小关系并加以证明吗? 5、(利用等腰三角形的三线合一找中点,应用中位线定理)
如图所示,在三角形ABC 中,AD 是三角形ABC ∠BAC 的角平分线,BD ⊥AD ,点D 是垂足,点E 是边BC 的中点,如果AB=6,AC=14,求DE 的长
6、(利用平行四边形对角线的交点找中点,应用中位线定理)
如图所示,AB ∥CD ,BC ∥AD ,DE ⊥BE ,DF=EF ,甲从B 出发,沿着BA 、AD 、DF 的方向运动,乙B 出发,沿着BC 、CE 、EF 的方向运动,如果两人的速度是相同的,且同时从B 出发,则谁先到达F 点?
7、(综合使用斜边中线及中位线性质,证明相等关系问题)
如图,等腰梯形ABCD 中,CD ∥AB ,对角线AC 、BD 相交于点O ,
60ACD ∠=︒,点S 、P 、Q 分别是DO 、AO 、BC 的中点.
求证:△SPQ 是等边三角形。
四、两条线段相等,为全等提供条件(遇到两平行线所截得的线段的中点时,
常联想“八字型”全等三角形)
8、如图:梯形ABCD 中,∠A=90°,AD//BC,AD=1,BC=2,CD=3,
E 为AB 中点,求证:DE ⊥EC
E D C
B A 图2-1
F
E
D
M
N
C
B
A P O A
B
C
D 图6-1S
Q
9、如图甲,在正方形ABCD 和正方形CGEF (CG >BC )中,点B 、C 、G 在同一直线上,M 是AE 的中点,(1)探究线段MD 、MF 的位置及数量关系,并证明;
(2)将图甲中的正方形CGEF 绕点C 顺时针旋转,使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一条直线上,原问题中的其他条件不变。
(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明
五、有中点时常构造垂直平分线
10、如图所示,在△ABC 中,AD 是BC 边上中线,∠C=2∠B.AC=21
BC 。
求证:△ADC 为等边三角形。
六、有中点时,常会出现面积的一半(中线平分三角形的面积) 11、(1)探索:已知ABC ∆的面积为a ,
①如图1,延长ABC ∆的边BC 到点D ,使CD=BC ,连接DA ,若
ACD ∆的面积为1S ,则1S = (用含a 的代数式表示)
②如图2,延长ABC ∆的边BC 到点D ,延长边CA 到点E ,使CD=BC ,AE=CA ,连接DE ,若DEC ∆的面积为2S ,则2S = (用含a 的代数式表示)
③在图2的基础上延长AB 到点F,使BF=AB,连接FD ,FE,得到DEF
∆(如图3),若阴影部分的面积为3S ,3S = (用含a 的代数式表示)
⑵发现:像上面那样,将ABC ∆各边均顺次延长一倍,连接所得端点,得到DEF ∆(如图4),此时,我们称ABC ∆向外扩展了一次。
可以发现,扩展一次后得到的DEF ∆的面积是原来ABC ∆面积的 倍 ⑶应用:如图5,若△ABC 面积为1,第一次操作:分别延长AB ,BC ,CA 至点A 1,B 1,C 1,使得A 1B =AB ,B 1C = BC ,C 1A =CA ,顺次连结A 1,B 1,C 1,得到△A 1B 1C 1. 第二次操作:分别延长A 1B 1,B 1C 1,C 1A 1至点A 2,B 2,C 2,使A 2B 1= A 1B 1,B 2C 1= B 1C 1,C 2A 1= C 1A 1,顺次连结A 2,B 2,C 2,得到△A 2B 2C 2,第三次操作… ,按此规律,要使得到的三角形的面积超过2010,最少要...经过 次操作.
A B C
D F G E
M 图乙
图甲 B A C E D F G M
B
D
C
A
12、如图所示,已知梯形ABCD ,AD ∥BC ,点E 是CD 的中点,连接AE 、 BE , 求证:S △ABE =2
1
S 四边形ABCD 。
13、如图,M 是ABCD 中AB 边的中点。
CM 交BD 于点E,则图中阴影部分面积与ABCD 面积之比为
14、如图所示,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则
ABCD
AGCD S S 矩形四边形等于:A 、65
B 、54
C 、4
3 D 、
3
2
七、倍长中线
15、如图,△ABC 中,D 为BC 中点,AB=5,AD=6,AC=13。
求证:AB ⊥AD
16、如图,点D 、E 三等分△ABC 的BC 边,求证:AB+AC>AD+AE
17、如图,D 为线段AB 的中点,在AB 上取异于D 的点C ,分别以AC 、BC 为斜边在AB 同侧作等腰直角三角形ACE 与BCF ,连结DE 、DF 、EF ,
求证:△DEF 为等腰直角三角形。
八、圆中遇到弦的中点,常联想“垂径定理”
18、半径是 5 cm 的圆中,圆心到 8 cm 长的弦的距离是________
D
C
B
M A E
B A
O
D
C
19、半径为cm 5的圆O 中有一点P ,OP=4,则过P 的最短弦长_________, 最长弦是__________,
20、如图,在圆O 中,AB 、AC 为互相垂直且相等的两条弦,OD ⊥AB ,OE ⊥AC ,垂足分别为D 、E ,若AC=2cm ,则圆O 的半径为____________cm 。
21、如图,在⊙O 中,直径AB 和弦CD 的长分别为10 cm 和8 cm ,则A 、B 两点到直线CD 的距离之和是_____.
22、如图,⊙O 的直径AB 和弦CD 相交于E ,若AE =2cm ,BE =6cm ,∠CEA =300
, 求:CD 的长;
23、某市新建的滴水湖是圆形人工湖。
为测量该湖的半径,小杰和小丽沿湖边选取A 、B 、C 三根木柱,使得A 、B 之间的距离与A 、C 之间的距离相等,并测得BC 长为240米,A 到BC 的距离为5米,如图5所示。
请你帮他们求出滴水湖的半径。
A B
C
倍长中线:
1.)24. 已知:如图①,正方形ABCD中,E为对角线BD上一点,
过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
2.()25.已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为;
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
N
M
D
E
C
A
B
M
E
C
B
A
D
图①图②。