中考数学几何证明题汇编

【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道，每道40分)
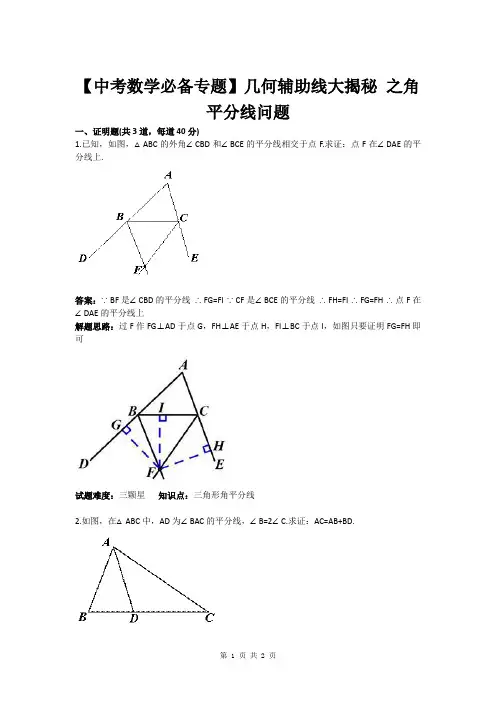
1.已知，如图，△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证：点F在∠DAE的平分线上.
答案：∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路：过F作FG⊥AD于点G，FH⊥AE于点H，FI⊥BC于点I，如图只要证明FG=FH即可
试题难度：三颗星知识点：三角形角平分线
2.如图，在△ABC中，AD为∠BAC的平分线，∠B=2∠C.求证：AC=AB+BD.
答案：∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED（SAS）∴BD=ED，∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路：在AC上截取AE=AB，连接DE，如图只要证明BD=CE即可
试题难度：三颗星知识点：三角形角平分线
3.已知：如图，在△ABC中，BE平分∠ABC，AD⊥BE，垂足为点D.求证：∠BAD=∠DAE+∠C.
答案：∵BE平分∠ABC，AD⊥BE ∴△ABF为等腰三角形（三线合一）∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路：延长AD与BC交于点F，如图只要证明∠BFD=∠BAD即可
试题难度：三颗星知识点：三角形角平分线。

1.（2023.营口24题）在平行四边形ABCD中，∠ADB=90°,点E在CD 上，点G在AB上，点F在BD的延长线上，连接EF，DG, ∠FED=∠ADG，ADBD =DG EF=k.（1）如图1，当k=1时，请用等式表示线段AG与线段DF的数量关系________；（2）如图2，当k=√(3)时，写出线段AD，DE和DF之间的数量关系,并说明理由；（3）在（2）的条件下，当点G是AB的中点时，连接BE，求tan∠EBF的值2.（2023.本溪铁岭辽阳25题）在Rt△ABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上（不与点A，B重合），连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G.（1）如图1，当点D与点O重合时，请直接写出线段AD与线段EF 的数量关系；（2）如图2，当点D在线段AB上时，求证：CG+BD=√2BC；（3）连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。

已知AB=AC，∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折，同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB.”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长.”补足探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC，∠A>90°，△BDE由△ABE翻折得到.（1）如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；（2）如图2，若点E为AC中点，AC=4，CD=3，求BE的长.问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以问题进一步拓展.问题2：如图3，在等腰△ABC中，∠A<90°，AB=AC=BD=4，2∠D=∠ABD.若CD=1，则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中，AE⊥BC，垂足为E，连接DE，将ED绕点E逆时针旋转90°，得到EF，连接BF.（1）当点E在线段BC上，∠ABC=45°时，如图1，求证：AE+EC=BF；（2）当点E在线段BC延长线上，∠ABC=45°时，如图2，当点E在线段CB延长线上，∠ABC=135°时，如图3，请猜想并直接写出线段AE，EC,BF的数量关系；（3）在（1）、（2）的条件下，若BE=3，DE=5，则CE=______.5.（2023.贵州省25题）如图1，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°,过点B作射线BD⊥AB，垂足为B，点P在CB上.（1）【动手操作】如图2，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形，图中∠PBE的度数为______度；（2）【问题探究】根据（1）所画图形，探究线段PA与PE的数量关系，并说明理由；（3）【拓展延伸】如图3，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD将于点E，探究线段BA，BP，BE之间的数量关系，并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中，AB=10，AD=6，∠DAB=60°，点E为BC边上的一点（点E不与点C重合），连接AE，将平行四边形ABCD纸片沿AE所在直线折叠，点C，D的对应点分别为C`，D`，射线C`E与射线AD将于点F.（1）求证：AF=EF；（2）如图2，当EF⊥AF时，DF的长为______;（3）如图3，当CE=2时，过点F作FM⊥AE，垂足为点M，延长FM 交C`D`于点N，连接AN，EN，求△ANE的面积。

2022年中考数学真题汇编圆类几何证明题1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．2.(1)求证：直线PE是⊙O的切线；3.(2)若⊙O的半径为6，∠P=30°，求CE的长．4.(2022·广西壮族自治区贵港市)如图，在△ABC中，∠ACB=90°，点D是AB边的中∠BDC．点，点O在AC边上，⊙O经过点C且与AB边相切于点E，∠FAC=125.(1)求证：AF是⊙O的切线；6.(2)若BC=6，sinB=4，求⊙O的半径及OD的长．57.(2022·山东省烟台市)如图，⊙O是△ABC的外接圆，∠ABC=45°．8.(1)请用尺规作出⊙O的切线AD(保留作图痕迹，不写作法)；9.(2)在(1)的条件下，若AB与切线AD所夹的锐角为75°，⊙O的半径为2，求BC的长．10.(2022·山东省聊城市)如图，点O是△ABC的边AC上一点，以点O为圆心，OA为半径作⊙O，与BC相切于点E，交AB于点D，连接OE，连接OD并延长交CB的延长线于点F，∠AOD=∠EOD．11.(1)连接AF，求证：AF是⊙O的切线；12.(2)若FC=10，AC=6，求FD的长．13.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．14.(1)求证：∠D=∠EBC；15.(2)若CD=2BC，AE=3，求⊙O的半径．16.(2022·湖南省张家界市)如图，四边形ABCD内接于圆O，AB是直径，点C是BD⏜的中点，延长AD交BC的延长线于点E．17.(1)求证：CE=CD；18.(2)若AB=3，BC=√3，求AD的长．19.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．20.(1)求证：CE与⊙O相切；21.(2)若AD=4，∠D=60°，求线段AB，BC的长．22.(2022·贵州省铜仁市)如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F．23.(1)求证：AB=CB；24.(2)若AB=18，sinA=1，求EF的长．325.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．26.(1)求证：BF与⊙O相切；27.(2)若AP=OP，cosA=4，AP=4，求BF的长．528.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD，∠BDC=∠BAD．29.(1)求证：CD是⊙O的切线．30.(2)若tan∠BED=2，AC=9，求⊙O的半径．331.32.(2022·内蒙古自治区呼和浩特市)如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交线段CA的延长线于点E，连接BE．33.(1)求证：BD=CD；34.(2)若tanC=1，BD=4，求AE．235.(2022·北京市)如图，AB是⊙O的直径，CD是⊙O的一条弦，AB⊥CD，连接AC，OD．36.(1)求证：∠BOD=2∠A；37.(2)连接DB，过点C作CE⊥DB，交DB的延长线于点E，延长DO，交AC于点F.若F为AC的中点，求证：直线CE为⊙O的切线．38.(2022·广西壮族自治区百色市)如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点M，作AD⊥MC，垂足为D，已知AC平分∠MAD．39.(1)求证：MC是⊙O的切线；40.(2)若AB=BM=4，求tan∠MAC的值．41.(2022·山东省临沂市)如图，AB是⊙O的切线，B为切点，直线AO交⊙O于C，D两点，连接BC，BD.过圆心O作BC的平行线，分别交AB的延长线、⊙O及BD于点E，F，G．42.(1)求证：∠D=∠E；43.(2)若F是OE的中点，⊙O的半径为3，求阴影部分的面积．44.(2022·辽宁省)如图，在Rt△ABC中，∠ACB=90°，▱ODEF的顶点O，D在斜边AB上，顶点E，F分别在边BC，AC上，以点O为圆心，OA长为半径的⊙O恰好经过点D和点E．45.(1)求证：BC与⊙O相切；46.(2)若sin∠BAC=3，CE=6，求OF的长．547.(2022·湖北省恩施土家族苗族自治州)如图，P为⊙O外一点，PA、PB为⊙O的切线，切点分别为A、B，直线PO交⊙O于点D、E，交AB于点C．48.(1)求证：∠ADE=∠PAE．49.(2)若∠ADE=30°，求证：AE=PE．50.(3)若PE=4，CD=6，求CE的长．51.(2022·内蒙古自治区赤峰市)如图，已知AB为⊙O的直径，点C为⊙O外一点，AC=BC，连接OC，DF是AC的垂直平分线，交OC于点F，垂足为点E，连接AD、CD，且∠DCA=∠OCA．52.(1)求证：AD是⊙O的切线；53.(2)若CD=6，OF=4，求cos∠DAC的值．54.(2022·湖北省潜江市)如图，正方形ABCD内接于⊙O，点E为AB的中点，连接CE交BD于点F，延长CE交⊙O于点G，连接BG．55.(1)求证：FB2=FE⋅FG；56.(2)若AB=6，求FB和EG的长．57.(2022·贵州省毕节市)如图，在△ABC中，∠ACB=90°，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F．58.(1)求证：BF=BD；59.(2)若CF=1，tan∠EDB=2，求⊙O的直径．60.(2022·贵州省黔东南苗族侗族自治州)(1)请在图1中作出△ABC的外接圆⊙O(尺规作图，保留作图痕迹，不写作法)；61.(2)如图2，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE⏜的中点，过点B的切线与AC的延长线交于点D．62.①求证：BD⊥AD；63.②若AC=6，tan∠ABC=3，求⊙O的半径．464.65.(2022·山东省威海市)如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E．66.(1)若AB=AC，求证：∠ADB=∠ADE；67.(2)若BC=3，⊙O的半径为2，求sin∠BAC．68.(2022·江苏省无锡市)如图，边长为6的等边三角形ABC内接于⊙O，点D为AC上的动点(点A、C除外)，BD的延长线交⊙O于点E，连接CE．69.(1)求证：△CED∽△BAD；70.(2)当DC=2AD时，求CE的长．71.(2022·陕西省)如图，AB是⊙O的直径，AM是⊙O的切线，AC、CD是⊙O的弦，且CD⊥AB，垂足为E，连接BD并延长，交AM于点P．72.(1)求证：∠CAB=∠APB；73.(2)若⊙O的半径r=5，AC=8，求线段PD的长．74.(2022·新建生产建设兵团)如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D在⊙O上，AC=CD，连接AD，延长DB交过点C的切线于点E．75.(1)求证：∠ABC=∠CAD；76.(2)求证：BE⊥CE；77.(3)若AC=4，BC=3，求DB的长．78.(2022·江苏省扬州市)如图，AB为⊙O的弦，OC⊥OA交AB于点P，交过点B的直线于点C，且CB=CP．79.(1)试判断直线BC与⊙O的位置关系，并说明理由；80.(2)若sinA=√5，OA=8，求CB的长．5参考答案1.(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，BC=6，在Rt△CDE中，即得CE的长是3．可得BD=CD=12本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(1)作OH⊥FA，垂足为H，连接OE，利用直角三角形斜边上中线的性质得AD=CD，再通过导角得出AC是∠FAB的平分线，再利用角平分线的性质可得OH=OE，从而证明结论；(2)根据BC=6，sinB=4，可得AC=8，AB=10，设⊙O的半径为r，则OC=OE=r，5利用Rt△AOE∽Rt△ABC，可得r的值，再利用勾股定理求出OD的长．本题主要考查了圆的切线的性质和判定，直角三角形的性质，三角函数，相似三角形的判定与性质，勾股定理等知识，熟练掌握切线的判定与性质是解题的关键．3.(1)过点A作AD⊥AO即可；(2)连接OB，OC.证明∠ACB=75°，利用三角形内角和定理求出∠CAB，推出∠BOC=120°，求出CH可得结论．本题考查作图−复杂作图，三角形的外接圆，切线的判定和性质，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．4.(1)根据SAS证△AOF≌△EOF，得出∠OAF=∠OEF=90°，即可得出结论；(2)根据勾股定理求出AF，证△OEC∽△FAC，设圆O的半径为r，根据线段比例关系列方程求出r，利用勾股定理求出OF，最后根据FD=OF−OD求出即可．本题主要考查切线的判定和性质，熟练掌握切线的判定和性质是解题的关键．5.(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．6.(1)连接AC，通过证明△ACE≌△ACB，利用全等三角形的性质分析推理；(2)通过证明△EDC∽△EBA，利用相似三角形的性质分析计算．本题考查相似三角形的判定和性质，全等三角形的判定和性质，圆周角定理，理解相关性质定理，正确添加辅助线是解题关键．7.(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，∠D=60°，即得AB=√3BD=2√3，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=√2AB=√6，又△AOC是等腰直角三角形，OA=OC=2，得AC=2√2，故CF=2√AC2−AF2=√2，从而BC=BF+CF=√6+√2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．8.(1)连接OD，则OD⊥DE，利用BC⊥DE，可得OD//BC，通过证明得出∠A=∠C，结论得证；(2)连接BD，在Rt△ABD中，利用sinA=1求得线段BD的长；在Rt△BDF中，利用3sin∠A=sin∠FDB，解直角三角形可得结论．本题主要考查了圆的切线的性质，垂径定理，圆周角定理，三角形相似的判定与性质，解直角三角形，勾股定理，等腰三角形的判定，平行线的判定与性质．连接过切点的半径和直径所对的圆周角是解决此类问题常添加的辅助线．9.(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，AD，然后利用等腰三角形的进而利用直角三角形三角形斜边上的中线可得BF=EF=12性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE=90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．10.(1)连接OD，由圆周角定理得出∠ADB=90°，证出OD⊥CD，由切线的判定可得出结论；(2)证明△BDC∽△DAC，由相似三角形的性质得出CDAC =BCCD=BDDA=23，由比例线段求出CD和BC的长，可求出AB的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．11.(1)连接AD，利用直径所对的圆周角是直角可得∠ADB=90°，然后利用等腰三角形的三线合一性质即可解答；(2)利用(1)的结论可得BD=DC=4，BC=8，然后在Rt△ADC中，利用锐角三角函数的定义求出AD的长，从而利用勾股定理求出AC的长，最后证明△CDA∽△CEB，利用相似三角形的性质求出CE的长，进行计算即可解答．本题考查了圆周角定理，相似三角形的判定与性质，解直角三角形，等腰三角形的性质，熟练掌握圆周角定理，以及解直角三角形是解题的关键．12.(1)连接AD，首先利用垂径定理得BC⏜=BD⏜，知∠CAB=∠BAD，再利用同弧所对的圆心角等于圆周角的一半可得结论；(2)连接OC，首先由点F为AC的中点，可得AD=CD，则∠ADF=∠CDF，再利用圆的性质，可说明∠CDF=∠OCF，∠CAB=∠CDE，从而得出∠OCD+∠DCE=90°，从而证明结论．本题主要考查了圆周角定理，垂径定理，圆的切线的判定等知识，熟练掌握圆周角定理是解题的关键．13.(1)根据垂直定义可得∠D=90°，然后利用等腰三角形和角平分线的性质可证OC//DA，从而利用平行线的性质可得∠OCM=90°，即可解答；(2)先在Rt△OCM中，利用勾股定理求出MC的长，然后证明A字模型相似三角形△MCO ∽△MDA，从而利用相似三角形的性质可求出AD，CD的长，进而在Rt△ACD中，利用锐角三角函数的定义求出tan∠DAC的值，即可解答．本题考查了切线的判定与性质，相似三角形的判定与性质，勾股定理，解直角三角形，熟练掌握切线的判定与性质，以及相似三角形的判定与性质是解题的关键．14.(1)连接OB，由切线的性质得出∠E+∠BOE=90°，由圆周角定理得出∠D+∠DCB= 90°，证出∠BOE=∠OCB，则可得出结论；(2)求出∠BOG=60°，由三角形面积公式及扇形的面积公式可得出答案．本题考查了切线的性质，直角三角形的性质，等腰三角形的性质，平行线的性质，圆周角定理，扇形的面积公式，熟练掌握切线的性质是解题的关键．15.(1)连接OE，利用平行四边形的性质和圆的性质可得四边形AOEF是平行四边形，则OE//AC，从而得出∠OEB=90°，从而证明结论；(2)过点F作FH⊥OA于点H，根据sin∠CFE=sin∠CAB=35，可得EF的长，由OA=OE，得▱AOEF是菱形，则AF=AO=EF=10，从而得出FH和AH的长，进而求出OF的长．本题主要考查了圆的切线的判定，平行四边形的判定与性质，三角函数的定义，勾股定理等知识，熟练运用相等角的三角函数值相等是解题的关键．16.(1)连接OA，利用切线的性质定理，圆周角定理，同圆的半径相等，等腰三角形的性质和等角的余角相等解答即可；(2)利用(1)的结论，直径所对的圆周角为直角，三角形的外角的性质和等腰三角形的判定定理解答即可；(3)CE=x，则DE=CD+CE=6+x，OA=OE=6+x2，OC=OE−CE=6−x2，OP=OE+PE=14+x2，利用相似三角形的判定与性质得出比例式即可求得结论．本题主要考查了圆的切线的性质，切线长定理，等腰三角形的判定与性质，圆周角定理，垂径定理，相似三角形的判定与性质，连接OA是解决此类问题常添加的辅助线．17.(1)利用等腰三角形的三线合一，平行线的判定与性质和圆的切线的判定定理解答即可；(2)利用全等三角形的判定与性质得到CF=CD=6，利用相似三角形的判定与性质求得线段AC，再利用直角三角形的边角关系定理在Rt△AOC中，求得cos∠OCA，则结论可得．本题主要考查了圆的切线的判定，等腰三角形的性质，平行线的判定与性质，全等三角形的判定与性质，线段垂直平分线的性质，相似三角形的判定与性质，勾股定理，直角三角形的边角关系定理，灵活应用等量代换是解题的关键．18.(1)利用相似三角形的判定与性质解答即可；(2)连接OE，利用平行线分线段成比例定理求得FB；利用相交弦定理求EG即可．本题主要考查了正方形的性质，圆周角定理，垂径定理及其推论，相似三角形的判定与性质，平行线的性质，勾股定理，相交弦定理，灵活运用上述定理及性质是解题的关键．19.(1)连接OE，利用圆的切线的性质定理，平行线的判定与性质，同圆的半径相等和等腰三角形的判定定理解答即可；(2)连接BE，利用直径所对的圆周角为直角，直角三角形的边角关系定理和相似三角形的判定与性质解答即可．本题主要考查了圆的切线的性质定理，平行线的判定与性质，等腰三角形的判定与性质．相似三角形的判定与性质，直角三角形的边角关系定理，连接经过切点的半径和直径所对的圆周角是解决此类问题常添加的辅助线．20.(1)利用尺规作图分别作出AB、AC的垂直平分线交于点O，以O为圆心、OA为半径作圆即可；(2)①连接OB，根据切线的性质得到OB⊥CD，证明OB//AD，根据平行线的性质证明结论；②连接EC，根据圆周角定理得到∠AEC=∠ABC，根据正切的定义求出EC，根据勾股定理求出AE，得到答案．本题考查的是切线的性质、圆周角定理、解直角三角形，掌握圆的切线垂直于经过切点的半径是解题的关键．21.(1)根据圆内接四边形的性质以及等腰三角形的性质即可求证；(2)连接CO并延长交⊙O于点F，连接BF，根据圆周角定理得出∠FBC=90°，∠F=∠BAC，解直角三角形即可得解．此题考查了圆内接四边形的性质、圆周角定理，熟练掌握圆内接四边形的性质、圆周角定理是解题的关键．22.(1)由对顶角的性质，圆周角定理得出∠CDE=∠BDA，∠A=∠E，即可证明△CED∽△BAD；(2)过点D作DF⊥EC于点F，由等边三角形的性质得出∠A=60°，AC=AB=6，由DC=2AD，得出AD=2，DC=4，由相似三角形的性质得ECDE =ABAD=62=3，得出EC=3DE，由含30°角的直角三角形的性质得出DE=2EF，设EF=x，则DE=2x，DF=√3x，EC=6x，进而得出FC=5x，利用勾股定理得出一元二次方程(√3x)2+ (5x)2=42，解方程求出x的值，即可求出EC的长度．本题考查了圆周角定理，等边三角形的性质，相似三角形的判定与性质，熟练掌握圆周角定理，相似三角形的判定与性质，等边三角形的性质，勾股定理，解一元二次方程等知识是解决问题的关键．23.(1)根据平行线的判定和切线的性质解答即可；(2)通过添加辅助线，构造出直角三角形，利用勾股定理和相似三角形的判定和性质解答即可．本题主要考查了切线的性质定理，勾股定理，相似三角形的判定和性质，熟练掌握这些性质定理是解题的关键．24.(1)利用等腰三角形的性质可得∠CAD=∠ADC，再利用同弧所对的圆周角相等可得∠ABC=∠ADC，即可解答；(2)利用切线的性质可得∠OCE=90°，利用圆内接四边形对角互补以及平角定义可得∠CAD=∠CBE，再利用(1)的结论可得∠OCB=∠CBE，然后可证OC//BE，最后利用平行线的性质可得∠E=90°，即可解答；(3)根据直径所对的圆周角是直角可得∠ACB=90°，从而在Rt△ABC中，利用勾股定理求出BA的长，再根据同弧所对的圆周角相等可得∠CAB=∠CDB，进而可证△ACB∽△DEC，然后利用相似三角形的性质可求出DE的长，最后再利用(2)的结论可证△ACB∽△CEB，利用相似三角形的性质可求出BE的长，进行计算即可解答．本题考查了切线的性质，等腰三角形的性质，相似三角形的判定与性质，三角形的外接圆与外心，圆周角定理，熟练掌握相似三角形的判定与性质，以及圆周角定理是解题的关键．25.(1)连接OB，由等腰三角形的性质得出∠A=∠OBA，∠CPB=∠CBP，结合对顶角的性质得出∠APO=∠CBP，由垂直的性质得出∠A+∠APO=90°，进而得出∠OBA+∠CBP=90°，即可得出直线BC与⊙O相切；(2)由sinA=√5，设OP=√5x，则AP=5x，由勾股定理得出方程(√5x)2+82=(5x)2，5=4，再利用勾股定理得出BC2+82=解方程求出x的值，进而得出OP=√5×4√55(BC+4)2，即可求出CB的长．本题考查了切线的判定，勾股定理，锐角三角函数的定义，熟练掌握等腰三角形的性质，切线的判定与性质，勾股定理，锐角三角函数的定义，一元二次方程的解法是解决问题的关键．。

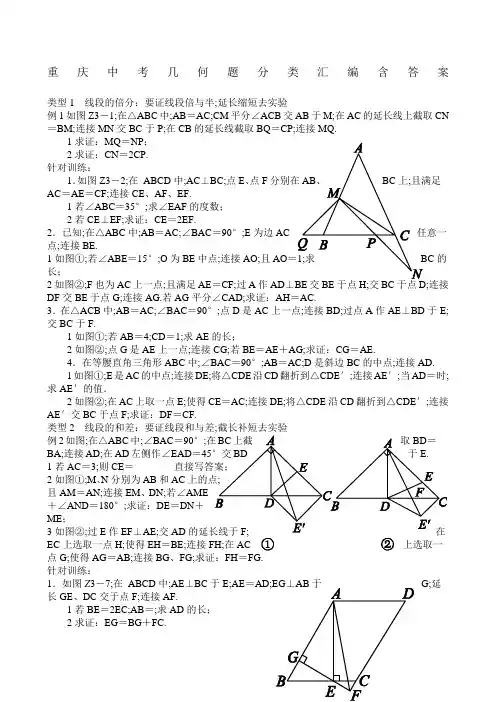
重庆中考几何题分类汇编含答案类型1线段的倍分：要证线段倍与半;延长缩短去实验例1如图Z3－1;在△ABC中;AB＝AC;CM平分∠ACB交AB于M;在AC的延长线上截取CN ＝BM;连接MN交BC于P;在CB的延长线截取BQ＝CP;连接MQ.1求证：MQ＝NP；2求证：CN＝2CP.针对训练：1．如图Z3－2;在ABCD中;AC⊥BC;点E、点FAC＝AE＝CF;连接CE、AF、EF.1若∠ABC＝35°;求∠EAF的度数；2若CE⊥EF;求证：CE＝2EF.2．已知;在△ABC中;AB＝AC;∠BAC＝90°;E为边AC点;连接BE.1如图①;若∠ABE＝15°;O为BE中点;连接AO;且AO的长；2如图②;F也为AC上一点;且满足AE＝CF;过A作AD⊥连接DF交BE于点G;连接AG.若AG平分∠CAD;求证：AH＝AC.3．在△ACB中;AB＝AC;∠BAC＝90°;点D是AC上一点;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点G是AE上一点;连接CG;若BE＝AE＋AG;求证：CG＝AE.4．在等腰直角三角形ABC中;∠BAC＝90°;AB＝AC;D是斜边BC的中点;连接AD.1如图①;E是AC的中点;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′;当AD＝时;求AE′的值．2如图②;在AC上取一点E;使得CE＝AC;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′交BC于点F;求证：DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2如图;在△ABC中;∠BAC＝90°;BA;连接AD;在AD左侧作∠EAD＝451若AC＝3;则CE＝________2如图①;M、N分别为AB和AC且AM＝AN;连接EM、DN;若∠AME＋∠AND＝180°;求证：DE＝DN＋ME；3如图②;过E作EF⊥AE;交ADEC上选取一点H;使得EH＝BE;连接FH;在AC上选取一点G;使得AG＝AB;连接BG、FG;求证：FH＝FG.针对训练：1．如图Z3－7;在ABCD中;AE⊥BC于E;AE＝G;延长GE、DC交于点F;连接AF.1若BE＝2EC;AB＝;求AD的长；2求证：EG＝BG＋FC.2．如图;在正方形ABCD中;点P为AD延长线上一点;连接AC、CP;过点C作CF⊥CP 于点C;交AB于点F;过点B作BM⊥CF于点N;交AC于点M.1若AP＝AC;BC＝4;求S△ACP；2若CP－BM＝2FN;求证：BC＝MC.3．如图;在△ABC中;AB＝BC;以AB为一边向形ABDE;连接DC;EB并延长EB交AC于F;且AE 于G.1若∠EBG＝20°;求∠AFE；2试问线段AE;AF;CF之间的数量关系并证明．类型3倍长中线：三角形中有中线;延长中线等中线例3如图Z3－10①;在Rt△ABC中;∠ABC＝90°;D为斜边AC上两点;且AD＝AB;CE＝CB;连接BD、1求∠EBD的度数；2如图Z3－10②;过点D作FD⊥BD于点D;交BEF;在AB上选取一点H;使得BH＝BC;连接CH;在一点G;使得GD＝CD;连接FH、FG;求证：FH＝FG.针对训练：1．如图;已知在ABCD中;G为BC的中点;点E在AD边上;且∠1＝∠2.1求证：E是AD中点；2若F为CD延长线上一点;连接BF;且满足∠3＝∠2;求证：CD＝BF＋DF.2．如图Z3－12;在菱形ABCD中;点E、F分别是BC、CD上的点;连接AE;AF;DE、EF;∠DAE＝∠BAF.1求证：CE＝CF；2若∠ABC＝120°;点G是线段AF的中点;连接DG;EG.求证：DG⊥GE.3．在Rt△ABC中;∠ACB＝90°;点D与点B在;∠ADC＞∠BAC;且DA＝DC;过点B作BE∥DA交于点E;M为AB的中点;连接MD;ME.1如图①;当∠ADC＝90°时;线段MD与ME________；2如图②;当∠ADC＝60°时;试探究线段MD数量关系;并证明你的结论；3如图③;当∠ADC＝α时;求的值．4．如图①;等边三角形ABC中;CE平分∠ACB;D为BC边上一点;且DE＝CD;连接BE.1若CE＝4;BC＝6;求线段BE的长；2如图②;取BE中点P;连接AP;PD;AD;求证：AP⊥PD且AP＝PD；3如图③;把图Z3－14②中的△CDE绕点C顺时针旋转任意角度;然后连接BE;点P为BE中点;连接AP;PD;AD;问第2问中的结论还成立吗若成立;请证明；若不成立;请说明理由．5．在△ABC中;以AB为斜边;作直角三角形ABD;使点D落在△ABC内;∠ADB＝90°.1如图①;若AB＝AC;∠BAD＝30°;AD＝6;点P、M分别为BC、AB边的中点;连接PM;求线段PM的长；2如图②;若AB＝AC;把△ABD绕点A逆时针旋转一定角度;得到△ACE;连接ED并延长交BC于点P;求证：BP＝CP；3如图③;若AD＝BD;过点D的直线交AC于点E;交BC于点F;EF⊥AC;且AE＝EC;请直接写出线段BF、FC、AD之间的关系不需要证明．类型4中位线：三角形中两中点;连接则成中位线例42017·河南如图①;在Rt△ABC中;∠A＝90°;AB＝AC;点D;E分别在边AB;AC上;AD＝AE;连接DC;点M;P;N分别为DE;DC;BC的中点．1观察猜想：图①中;线段PM与PN的数量关系是__________;位置关系是__________；2探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置;连接MN;BD;CE;判断△PMN 的形状;并说明理由；3拓展延伸：把△ADE绕点A＝10;请直接写出△PMN面积的最大值．针对训练：1．如图①;在任意的三角形ABC以AB和AC为一边作等腰三角形ABE和等腰三角形ACD;AB＝AE;AC＝AD;且∠BAE＋∠CAD＝180°;连接DE;延长CA交DE于F.1求证：∠CAB＝∠AED＋∠ADE；2若∠ACB＝∠BAE＝∠CAD＝90°;如图②;求证：BC＝2AF；3若在△ABC中;如图③所示;作等腰三角形ABE和等腰三角形ACD;AB与DE交于点F;F为DE的中点;请问2中的结论还成立吗若成立;请给出证明;若不成立;请说明理由．2．如图;在△ABC和△ADE中;AB＝AC;AD＝AE;∠BAC＋∠EAD＝180°;△ABC不动;△ADE绕点A旋转;连接BE、CD;F为BE的中点;连接AF.1如图①;当∠BAE＝90°时;求证：CD＝2AF；2当∠BAE≠90°时;1的结论是否成立请结合图②说明理由．3．如图①;在等腰三角形ABC中;AB＝AC;在底边BC上取一点D;在边AC上取一点E;使AE＝AD;连接DE;在∠ABD的内部作∠ABF＝2∠EDC;交AD于点F.1求证：△ABF是等腰三角形；2如图②;BF的延长交AC于点G.若∠DAC＝∠CBG;延长AC至点M;使GM＝AB;连接BM;点N是BG的中点;连接AN;试判断线段AN、BM之间的数量关系;并证明你的结论．类型5角的和差倍分图中有角平分线;关系现．角平分线平行线;;三线合一试试看．例5．如图;把△EFP放置在菱形ABCD中;顶点E;F;P分别在线段AB;AD;AC上;EP＝FP＝6;EF＝6;∠BAD＝60°;且＞6.1求∠EPF的大小；2若AP＝10;求AE＋AF的值．针对训练：1．已知：如图①;AD平分∠BAC;∠B＋∠C＝180°°;易知：DB＝DC.探究：如图②;AD平分∠BAC;∠ABD＋∠ACD;∠ABD＜90°;求证：DB＝DC.2．在△ACB中;AB＝AC;∠BAC＝90°;点D;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点P是AC上一点;连接FP;若AP＝CD;求证：∠ADB＝∠CPF.3．已知;在ABCD中;∠BAD＝45°;AB＝BD;E为BC上一点;连接AE交BD于F;过点D 作DG⊥AE于G;延长DG交BC于H.1如图①;若点E与点C重合;且AF＝;求AD的长；2如图②;连接FH;求证：∠AFB＝∠HFB.4．如图;将正方形纸片ABCD沿EF折叠点E、F分别在边AB、CD上;使点B落在AD边上的点M处;点C落在点N处;MN与CD交于点P;连接EP.当点M在边AD上移动时;连接BM、BP.1求证：BM是∠AMP的平分线；2△PDM的周长是否发生变化证明你的结论．类型6旋转型全等问题：图中若有边相等;可用旋转做例6．△ABC中;∠BAC＝90°;AB＝AC;点D为直线点点D不与B;C重合;以AD为边在AD右侧作正方形ADEF;连接CF.1观察猜想：如图①;当点D在线段BC上时;①BC与CF关系为：________．②BC;CD;CF之间的数量关系为：___________；将结写在横线上2数学思考：如图Z3－25②;当点D在线段CB的延长线上时;结论①;②是否仍然成立若成立;请给予证明；若不成立;请你写出正确结论再给予证明．3拓展延伸：如图Z3－25③;当点D在线段BC的延长线上时;延长BA交CF于点G;连接GE.若已知AB＝2;CD＝BC;请求出GE的长．针对训练：1．在四边形ABCD中;∠B＋∠180°;对角线AC平分∠BAD.1如图①;若∠DAB＝120°;且∠B＝90°;试探究边AD、AB与对角线AC2如图②;若将1中的条件“∠B＝去掉;1中的结论是否成立请说明理由．3如图③;若∠DAB＝90°;探究边AD、AB与对角线AC的数量关系并说明理由．2．如图①;在正方形ABCD中;点E为边BC上一点;将△ABE沿AE翻折得△AHE;延长EH交边CD于F;连接AF.1求证：∠EAF＝45°；2延长AB;AD;如图②;射线AE、AF分别交正方形两个外角的平分线于M、N;连接MN;若以BM、DN、MN为三边围成三角形;试猜想三角形的形状;并证明你的结论．3．如图①;在正方形ABCD内有一点P;PA＝;PB＝;PC＝1;求∠BPC的度数．分析问题根据已知条件比较分散的特点;我们可以通过旋转变换将分散的已知条件集中在一起;于是将△BPC绕点B逆时针旋转90°;得到了△BP′A如图Z3－28②;然后连接PP′.1请你通过计算求出图Z3－28②中∠BPC的度数；2如图③;若在正六边形ABCDEF内有一点P;且PA＝2;PB＝4;PC＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1.证明：1∵AB＝AC;∴∠ABC＝∠ACB.∵∠MBQ＋∠ABC＝180°;∠ACB＋∠PCN＝180°;∴∠MBQ＝∠PCN.在△QBM和△PCN中;∴△QBM≌△PCNSAS．∴MQ＝NP.2过M作MG∥AC交BC于G;∵MG∥AC;∴∠MGB＝∠ACB;∠MGC＝∠PCN;∵由1知;∠ABC＝∠ACB;∴∠ABC＝∠MGB;∴MB＝MG;∵MB＝CN;∴MG＝CN.在△MGP和△NCP中;∴△MGP≌△NCPAAS．∴PG＝CP;∴CG＝CP＋PG;即CG＝2CP.∵CM平分∠ACB;∴∠BCM＝∠MCA;∵MG∥AC;∴∠MCA＝∠GMC;∴∠BCM＝∠GMC;∴MG＝CG;∵MG＝CN;∴CN＝CG;∴CN＝2CP.针对训练1.解：1∵AC⊥BC;∴∠ACB＝90°;又∵AC＝CF;∴∠45°;∵∠ABC＝35°;∴∠EAF＝10°；2证明：方法1：取CF的中点M;连接EM、AM;∵CE⊥EF;∴EM＝CM＝FM＝CF;又∵AC＝AE;∴AM为EC的中垂线;∴∠CAM＋°; 又∵∠ECF＋∠ACE＝90°;∴∠CAM＝∠FCE;又∵∠CEF＝∠ACM＝90°;∴△ACM∽△CEF;∴＝;又∵CF＝AC＝2CM;∴＝＝;即CE＝2EF；方法2：延长FE至M;使EF＝EM;连接CM;∵CE⊥EF;∴△CMF为等腰三角形;又∵AC＝AE＝CF;且∠ACE＝∠CFE易证;∴△CMF≌△CEA;∴FM＝CE＝2EF.2.解：1如图①;在AB上取一点M;使得BM＝ME;连在Rt△ABE中;∵OB＝OE;∴BE＝2OA＝2;∵MB＝ME;∴∠MBE＝∠MEB＝15°;∴∠AME＝∠MBE＋∠MEB＝30°;设AE＝x;则ME＝BM＝2x;AM＝x;∵AB2＋AE2＝BE2;∴2x＋x2＋x2＝22;∴x＝负根舍弃;∴AB＝AC＝2＋·;∴BC＝AB＝＋1.2证明：如图②;作CP⊥AC;交AD的延长线于P;GM⊥AC 于M.∵BE⊥AP;∴∠AHB＝90°;∴∠ABH＋∠BAH＝90°;∵∠BAH＋∠PAC＝90°;∴∠ABE＝∠PAC;又∵AB＝AC;∠BAE＝∠ACP＝90°;∴△ABE≌△CAP;∴AE＝CP＝CF;∠AEB＝∠P;在△DCF和△DCP中;∴△DCF≌△DCP;∴∠DFC＝∠P;∴∠GFE＝∠GEF;∴GE＝GF;∵GM⊥EF;∴FM＝ME;∵AE＝CF;∴AF＝CE;∴AM＝CM;在△GAH和△GAM中;∴△AGH≌△AGM;∴AH＝AM＝CM＝AC.3.解：1∵AB＝4;∴AC＝AB＝4.∵CD＝1;∴AD＝AC－CD＝3.∵在Rt△ABD中;∠BAC＝90°;∴BD＝＝5;∵S＝AB·AD＝AE·BD;∴AE＝2.4.△ABD2证明：如图;在线段EB上截取EH＝AE;并连接∵AE⊥BD;EH＝AE;∴AH＝AE.∵BE＝AE＋AG;∴BH＝BE－HE＝AG.∵∠BAD＝∠BEA＝90°;∴∠ABE＋∠BAE＝∠CAG＋∠BAE＝90°;∴∠ABE＝∠CAG.∵BA＝AC;∴△ABH≌△CAG;∴CG＝AH＝AE.4.解：1∵∠BAC＝90°;AB＝AC;D是斜边BC的中点;∴∠ADC＝90°;∠ACD＝45°.在Rt△ADC中;AC＝AD÷sin45°＝2.∵E是AC的中点;∴CE＝AC＝.∵将△CDE沿CD翻折到△CDE′;∴CE′＝CE＝;∠ACE由勾股定理;得AE′＝＝.2证明：如图;过B作AE′的垂线交AD于点G;交AC于点∵∠ABH＋∠BAF＝90°;∠CAF＋∠BAF＝90°;∴∠ABH＝∠CAF.又∵AB＝AC;∠BAH＝∠ACE′＝90°;∴△ABH≌△CAE′.∴AH＝CE′＝CE;∵CE＝AC;∴AH＝HE＝CE.∵D是BC中点;∴DE∥BH;∴G是AD中点．在△ABG和△CAF中：AB＝AC;∠BAD＝∠ACD＝45°;∠ABH＝∠CAF; ∴△ABG≌△CAF.∴AG＝CF.∵AG＝AD;∴CF＝AD＝CD.∴DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2：解：132证明：延长DN到K;使得NK＝ME;连接AK;如图①;因为∠1＋∠3＝180°;∠1＋∠2＝180°;∴∠2＝∠3.在△AME和△ANK中;∴△AME≌△ANK SAS．∴AE＝AK;∠4＝∠5;∴∠4＋∠EAC＝90°;∴∠5＋∠EAC＝90°;即∠EAK＝∵∠EAD＝45°;∴∠KAD＝∠EAK－∠EAD＝90°－45∴∠EAD＝∠KAD.在△EAD和△KAD中;∴△EAD≌△KAD SAS;∴ED＝KD.∵DK＝DN＋KN;∴ED＝DN＋KN;又NK＝ME;∴ED＝DN＋ME.3证明：延长AE到J;使得EJ＝AE;连接JH;JF.如图②;在△ABE和△JHE中;∴△ABE≌△JHESAS;∴JH＝AB;∠1＝∠2;∵AB＝AG;∴JH＝AG;∵AE＝EJ;EF⊥AJ;∴AF＝JF;∴∠JAF＝∠AJF＝45°;即∠2＋∠3＝45°;∵∠BAC＝90°;∴∠1＋∠EAD＋∠4＝90°;∴∠1＋∠4＝90°－∠EAD;＝90°－45°＝45°;∵∠1＝∠2;∴∠3＝∠4;在△JHF和△AGF中;∴△JHF≌△AGFSAS;∴FH＝FG.针对训练：1.解：1∵四边形ABCD是平行四边形;∴AD＝BC.∵BE＝2EC;设CE＝x;BE＝2x;∴BC＝AD＝AE＝3x.又∵EG⊥AB;∴∠AEB＝90°;∴AB2＝AE2＋BE2;即13＝9x2＋4x2;∴x＝1;∴AD＝3x＝3.2证明：如图;过C作CH⊥AB于H;则四边形CHGF为矩形．∴CF＝HG;∠CHB＝90°;GF＝CH.∵AE⊥BC;EG⊥AB;∴∠AEB＝∠CHB＝90°;∠BCH＋∠B＝90°;∠BAE＋∠B＝90°;∴∠BCH＝∠BAE.又∵AE＝BC;∴△AGE≌△CHB;∴GE＝BH;AG＝GF;∴GE＝BH＝BG＋GH＝BG＋CF.2.解：1∵四边形ABCD是正方形;BC＝4;∴AB＝AD＝CD＝BC＝4;∠ADC＝∠ABC＝90°.∵在Rt△ABC中;AC＝＝4;∴AP＝AC＝;∴S＝AP·CD＝7.△ACP2证明：方法一：如图①;在NC上截取NK＝NF;连接BK.∵四边形ABCD是正方形;∴AB＝BC＝DC;∠ABC＝∠BCD＝∠ADC＝90°.∵∠BCD＝90°;CF⊥CP;∴∠1＋∠DCF＝∠2＋∠DCF＝90°;∴∠1＝∠2;∵在△FBC和△PDC中;∴△FBC≌△PDCASA;∴CF＝CP;∵CP－2FN＝BM;∴CF－FK＝BM;即CK＝BM;∵∠FBC＝90°;BM⊥CF;∴∠1＋∠NBC＝∠4＋∠NBC; ∴∠1＝∠4;∵在△ABM和△BCK中;∴△ABM≌△BCKSAS;∴∠7＝∠6.∵BM⊥CF;NK＝NF;∴BF＝BK;∵BF＝BK;BM⊥CF;∴∠4＝∠∴∠4＋∠7＝∠5＋∠6;∵∠8＝∠4＋∠7;∴∠8＝∠MBC;∴BC＝MC.解：方法二：如图②;延长BM交AD于点G;过A作AE⊥BGE先证△AEB≌△BNCAAS;∴AE＝BN;又证△AEG≌△BNFAAS;∴EG＝NF;再证四边形BCPG为平行四边形;∴BG＝CP;∵CP－BM＝2FN;∴BG－BM＝2EG;∴MG＝2EG;∴点E为MG中点;∵AE⊥MG;EM＝EG;∴AM＝AG;∴∠3＝∠4;∵∠2＝∠3;∠1＝∠4;∴∠1＝∠2;∴BC＝MC.3.解：1∵∠EBG＝20°;CB⊥AE;∴∠BEG＝70o;∠CBF＝∠EBG＝20°;∵四边形ABDE是菱形;∴∠ABE＝∠BEG＝70°;∴∠ABG＝50°;∵AB＝BC;∴∠FCB＝25°;∴∠AFE＝∠CBF＋∠FCB＝45°；2AE;AF;CF之间的数量关系是AF2＋CF2＝2AE2;证明如下：连接DF;∵四边形ABDE是菱形;∴AB＝DB;∠DBE＝∠ABE;∴∠DBF＝∠ABF;∵BF＝BF;∴△DBF≌△ABFSAS;∴DF＝AF;∠BDF＝∠BAF;∵∠BCF＝∠BAF;∴∠BCF＝∠BDF; ∵CB⊥AE;AE∥DB;∴DB⊥CB;∵CB＝AB＝BD;∴△DBC是等腰直角三角形;∴DC＝BD＝AE;∵∠DPB＝∠CPF;∴∠CFP＝∠DBP＝90°;∴DF2＋CF2＝DC2; 即有：AF2＋CF2＝2AE2.类型3倍长中线：三角形中有中线;延长中线等中线例3解：1设∠BEC＝α;∠BDA＝β;则∠C＝180°－2α;∠A＝180°－2β.∵在Rt△ABC中;∠ABC＝90°;∴∠A＋∠C＝90°;即180°－2α＋180°－2β＝90°;∴α＋β＝135°;∴∠EBD＝45°.2证明：法一：如图①;延长BD至点B′;使得DB′＝在△GDB′和△CDB中;∴△GDB′≌△CDB.∴GB′＝BC＝BH;∠GB′D∵FD⊥BD;BD＝DB′;∴FB＝FB′.∵∠FB′G＝45°－∠GB′D;∠HBF＝90°－45°－∠CBD＝45°－∠CBD;∴∠FB′G＝∠HBF.在△FHB和△FGB′中;∴△FHB≌△FGB′;∴HF＝GF.法二：如图②;延长FD至点F′;使得DF′＝DF;先证△DGF≌△DCF′;再证△BHF≌△BCF′;∴HF＝GF.针对训练1.证明：1∵四边形ABCD是平行四边形;∴AB＝CD;AD＝BC;∠A＝∠C.又∵∠1＝∠2;∴△ABE≌△CDG ASA;∴AE＝CG.∵G为BC中点;∴CG＝BC;∴AE＝CG＝BC＝AD;∴E是AD中点．2如图;延长BE;CD交于点H.∵四边形ABCD是平行四边形;∴AB綊CD;∴∠A＝∠ADH;∠1＝∠4;又∵∠1＝∠2;∠3＝∠2;∴∠1＝∠2＝∠3＝∠4;∴FH＝FB.由1;E是AD中点;∴AE＝DE;∴△ABE≌△DHEAAS;∴AB＝DH;∴CD＝AB＝DH＝DF＋FH＝DF＋BF;即CD＝BF＋DF.2.证明：1在菱形ABCD中;AB＝BC＝CD＝AD;∠ADF＝∠ABE; ∵∠DAE＝∠BAF;∴∠DAE－∠EAF＝∠BAF－∠EAF;即∠DAF＝∠BAE.∴△DAF≌△BAE;∴BE＝DF.又∵BC＝CD;∴CE＝CF2如图;延长DG交AB于H;连接EH;∵在菱形ABCD中;AB∥CD;∴∠DFA＝∠GAH.∵G为AF中点;∴AG＝GF.又∵∠DGF＝∠AGH;∴△DGF≌△HGA.∴DG＝又∵AB＝CD;∴BH＝CF.又∵AB∥CD;∠ABC＝120°;∴∠C＝60°.又∵CE＝CF;∴△CEF为等边三角形;∴CF＝EF;∠CFE＝60°;∴EF＝BH;∠DFE＝∠ABC＝120°.又∵BE＝DF;∴△EFD≌△HBE;∴HE＝ED;又∵HG＝DG;∴DG⊥GE.3.解：1MD=ME2MD＝ME.理由如下：如图①;延长EM交DA于点F.∵BE∥DA;∴∠FAM＝∠EBM.又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.∵DA＝DC;∠ADC＝60°;∴∠BED＝∠ADC＝60°;∠ACD＝60°.∵∠ACB＝90°;∴∠ECB＝30°;∴∠EBC＝30°;∴CE＝BE;∴AF＝EC;∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∴∠MDE＝30°.在Rt△MDE中;tan∠MDE＝＝.∴MD＝ME.3如图②;延长EM交DA于点F;∵BE∥DA;∴∠FAM＝∠EBM;又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.延长BE交AC于点N;∴∠BNC＝∠DAC.∵DA＝DC;∴∠DCA＝∠DAC;∴∠BNC＝∠DCA;∵∠ACB＝90°;∴∠ECB＝∠EBC;∴CE＝BE;∴AF＝CE.∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∵∠ADC＝α;∴∠MDE＝.∴在Rt△MDE中;＝tan∠MDE＝tan.4.解：1如图①;作EH⊥BC于点H.∵△ABC是等边三角形;∴∠ACB＝60°.∵CE平分∠ACB;∴∠ECH＝∠ACB＝30°;∵EC＝4;∠ECH＝30°;∴EH＝2;HC＝2.∵BC＝6;∴BH＝6－2＝4.在Rt△BHE中;BE2＝42＋22＝52;∴BE＝2.2如图②;延长DP至M;使DP＝PM;连接BM、AM.在△PDE和△PMB中;∴△PDE≌△PMB SAS．∴BM＝DE;∠1＝∠2.∴BM∥DE.∴∠MBD＋∠BDE＝180°.∵CE平分∠ACB;DE＝CD;∴∠BDE＝30°＋30°＝60∴∠MBD＝120°.∵△ABC是等边三角形;∴∠ABC＝60°;∴∠3＝60°.∵BM＝DE;DE＝CD;∴BM＝CD.在△ABM和△ACD中;∴△ABM≌△ACD SAS．∴AD＝AM;∠4＝∠5.∵PD＝PM;∴AP⊥PD.∵∠4＝∠5;∠BAD＋∠5＝60°;∴∠4＋∠BAD＝60°;即∠MAD＝60°.∴∠PAD＝∠MAD＝30°.∵在Rt△APD中;tan30°＝;∴AP＝PD.3第2问中的结论成立;理由如下：如图③;延长DP至使DP＝PN;连接BN、AN;取BE、AC交于点O.在△PDE∴△PDE≌△PNBSAS．∴BN＝DE;∠1＝∠2.∵DE＝CD;∴BN＝CD.∵∠AOB＝∠EOC;∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO＝60°;∠DEC＝∠DCE＝30°;∴∠1＋∠3∴∠3＝∠4.在△ABN和△ACD中;∴△ABN≌△ACDSAS．∴∠5＝∠6;AN＝AD.∵PD＝PN;∴AP⊥PD.∵∠NAC＋∠5＝60°;∴∠NAC＋∠6＝60°;即∠NAD＝60°.∴∠PAD＝∠NAD＝30°; ∵在Rt△APD中;tan∠PAD＝;∴AP＝PD.5.解：1∵∠ADB＝90°;∠BAD＝30°;AD＝6;∴cos∠BAD＝;∴＝;∴AB＝12.又∵AB＝AC;∴AC＝12;∴PM为△ABC的中位线;∴PM＝AC＝6.2证明：方法一：如图①;在截取ED上截取EQ＝PD;∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4.在△BDP和△CEQ中;PD＝QE;∠1＝∠4;BD＝CE;∴△BDP≌△CEQ.∴BP＝CQ;∠DBP＝∠QCE;又∵∠5＝∠1＋∠DBP;∠6＝∠4＋∠QCE;∴∠5＝∠6;∴PC＝CQ;∴BP＝CP.方法二：如图②;过点B作EP的垂线交EP的延长线于点M;过C EP的垂线交EP于点N.∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4;在△BMD和△CNE中;∠1＝∠4;∠BMD＝∠CNE＝90°;BD＝CE;∴△BMD≌△CNE.∴BM＝CN.在△BMP和△CNP中;∠5＝∠6;∠BMP＝∠CNP;BM＝CN;∴△BMP≌△CNP;∴BP＝CP.方法三：如图③;过点B作BM∥CE交EP略证△BMP≌△CEP;∴BP＝CP.3BF2＋FC2＝2AD2.类型4中位线：三角形中两中点;连接则成中位线例4:解：1PM=PN;PM⊥PN2△PMN为等腰直角三角形;理由如下：由题意知△ABC和△ADE均为等腰直角三角形;∴AB＝AC;AD＝AE;∠BAC＝∠DAE＝90°;∴∠BAD＋∠DAC＝∠CAE＋∠DAC;∴∠BAD＝∠CAE;∴△BAD≌△CAE;∴∠ABD＝∠ACE;BD＝CE.又∵M、P、N分别是DE、CD、BC的中点;∴PM是△CDE的中位线;∴PM∥CE且PM＝CE;∠MPD＝∠ECD＝∠ACD＋∠ACE.同理;PN∥BD且PN＝BD;∠DBC＝∠PNC;又∵BD＝CE;∠ABD＝∠ACE;∴PM＝PN;∴∠MPN＝∠MPD＋∠DPN＝∠ECD＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°;∴PM⊥PN;∴△PMN为等腰直角三角形；3△PMN面积的最大值为.提示：在旋转的过程中;由2中的结论知△PMN为等腰直角三角形;S＝PN2＝BD2;当S△PMN有最大值时;则BD的值最大;由三角形三边关系可推断出当B、A、D三△PMN点共线时;BD的值最大;其最大值为14;此时S△PMN＝PN2＝BD2＝×14×14＝.针对训练：1.解：1证明：延长DA交BE于G点．∵∠BAE＋∠CAD＝180°;即∠EAG＋∠GAB＋∠CAD＝180°;∵∠GAB＋∠BAC＋∠CAD＝180°;∴∠EAG＝∠CAB.∵∠EAG＝∠AED＋∠ADE;∴∠CAB＝∠AED＋∠ADE.2证明：如图①;过E点作DA延长线的垂线;垂足为H.∴∠AHE＝∠ACB＝90°;由1可知;∠EAH＝∠BAC;又∵AE＝AB;∴△AHE≌△ACB;∴EH＝BC;AH＝AC.∵AC＝AD;∴AH＝AD.∵∠EHA＝∠FAD＝90°;∴AF∥EH.∵A为DH中点;∴AF为△DHE中位线;∴EH＝2AF;∴BC＝2AF.3成立．证明如下：如图②;延长DA至M点;使AM＝DA;连接EM;∵∠BAE＋∠CAD＝180°;∠CAD＋∠CAM＝180°;∴∠BAE＝∠CAM;∴∠BAE＋∠CAC＝∠CAM＋∠EAC;即∠BAC＝∠CAM.∵AM＝AD;AD＝AC;∴AM＝AC.又∵AB＝AE;∠BAC＝∠EAM;∴△BAC≌△EAM;∴BC＝EM.∵F、A分别为DE、DM中点;∴AF为△DEM中位线;∴EM＝2AF;∴BC＝2AF.2.解：1证明：∵∠BAC＋∠EAD＝180°;∠BAE＝90°;∴∠DAC＝90°;在△ABE与△ACD中;AE＝AD;∠BAE＝∠CAD＝90°;AB＝AC;∴△ABE≌△ACDSAS;∴CD＝BE;∵在Rt△ABE中;F为BE的中点;∴BE＝2AF;∴CD＝2AF.2成立;证明：如图;延长EA交BC于G;在AG上截取AH＝∵∠BAC＋∠EAD＝180°;∴∠EAB＋∠DAC＝180°;∵∠EAB＋∠BAH＝180°;∴∠DAC＝∠BAH;在△ABH与△ACD中;AH＝AD;∠BAH＝∠CAD;AB＝AC;∴△ABH≌△ACDSAS;∴BH＝DC;∵AD＝AE;AH＝AD;∴AE＝AH;∵EF＝FB;∴BH＝2AF;∴CD＝2AF.3.解：1证明：∵AB＝AC;∴∠ABD＝∠ACD;∵AE＝AD;∴∠ADE＝∠AED;∵∠BAD＋∠ABD＝∠ADE＋∠EDC;∠EDC＋∠ACD∴∠BAD＝2∠EDC;∵∠ABF＝2∠EDC;∴∠BAD＝∠ABF;∴△ABF是等腰三角形；2方法一：如图①;延长CA至点H;使AG＝AH;连接BH;∵点N是BG的中点;∴AN＝BH;∵∠BAD＝∠ABF;∠DAC＝∠CBG;∴∠CAB＝∠CBA;∴△ABC是等边三角形．∴AB＝BC＝AC;∠BAC＝∠BCA＝∵GM＝AB;AB＝AC;∴CM＝AG;∴AH＝CM;在△BAH和△BCM中;∴△BAH≌△BCMSAS;∴BH＝BM;∴AN＝BM;方法二：如图②;延长AN至K;使NK＝AN;连接KB;同方法一;先证△ABC是等边三角形;再证△ANG≌△KNB SAS;所以BK＝AG＝CM;然后可以证得∠ABK＝∠BCN＝120°;最后证△ABK≌△BCN SAS;所以BM＝AK＝2AN.类型5角的和差倍分例5：解：1如图;过点P作PG⊥EF于G.∵PE＝PF＝6;EF＝6;∴FG＝EG＝3;∠FPG＝∠EPG＝∠EPF.在Rt△FPG中;sin∠FPG＝＝＝.∴∠FPG＝60°;∴∠EPF＝2∠FPG＝120°.2如图;作PM⊥AB于M;PN⊥AD于N.∵AC为菱形ABCD的对角线;∴∠DAC＝∠BAC;AM＝AN;PM＝PN.在Rt△PME和Rt△PNF中;PM＝PN;PE＝∴Rt△PME≌Rt△PNF;∴NF＝ME.又∵AP＝10;∠PAM＝∠DAB＝30°;∴AM＝AN＝AP cos30°＝10×＝5.∴AE＋AF＝AM＋ME＋AN－NF＝AM＋AN针对训练：1.证明：如图;过D作DE⊥AB于E;过D作DF⊥AC于F;∵DA平分∠BAC;DE⊥AB;DF⊥AC;∴DE＝DF;∵∠B＋∠ACD＝180°;∠ACD＋∠FCD＝180°∴∠B＝∠FCD;在△DFC和△DEB中;∴△DFC≌△DEB;∴DC＝DB.2.解：1∵AC＝AB＝4;且CD＝1;∴AD＝AC－CD＝3.在Rt△ABD中;∠BAD＝90°;∴BD＝＝5;＝AB·AD＝AE·BD;∵S△ABD∴AE＝2.4.2证明：如图;取BC的中点M;连接AM交BD于点N.∵∠BAC＝90°;AB＝AC;点M为BC的中点;∴AM＝BM＝CM;AM⊥BC;∠NAD＝∠FCP＝45°;∴∠AMF＝∠BMN＝90°.∵AE⊥BD;∴∠MAF＋∠ANE＝∠MBN＋∠BNM＝90°;又∠ANE＝∠BNM;∴∠MAF＝∠MBN;∴△AMF≌△BMN;∴MF＝MN;∴AM－MN＝CM－MF;即AN＝CF.∵AP＝CD;∴AC－CD＝AC－AP;即AD＝CP.∴△ADN≌△CPF;∴∠ADB＝∠CPF.3.解：1∵AB＝BD;∠BAD＝45°;∴∠BDA＝45°;即∠ABD＝90°.∵四边形ABCD是平行四边形;∴当E、C重合时;BF＝BD＝AB.∵在Rt△ABF中;AB2＋BF2＝AF2;∴2BF2＋BF2＝2;∴BF＝1;AB＝2.在Rt△ABD中;AD＝＝＝2.2证明：如图;在AF上截取AK＝HD;连接BK.∵∠AFD＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°; ∴∠2＝∠3.在△ABK与△DBH中;∴△ABK≌△DBH;∴BK＝BH;∠6＝∠5.∵四边形ABCD是平行四边形;∴AD∥BC;∴∠5＝∠4＝45°;∴∠6＝∠5＝45°;∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK与△BFH中;∴△BFK≌△BFH.∴∠BFK＝∠BFH;即∠AFB＝∠HFB.4.解：1证明：由折叠知∠EMN＝∠ABC＝90°∴∠EMB＝∠EBM;∴∠EMN－∠EMB＝∠ABC－∠EBM;即∠BMP＝∠MBC.∵在正方形ABCD中;AD∥BC;∴∠AMB＝∠MBC;∴∠AMB＝∠BMP;∴BM是∠AMP的平分线．2△PDM的周长没有发生变化．证明如下：如图;过B作BQ∵∠A＝90°;且由1知BM是∠AMP的平分线;∴BA＝BQ;∵∠A＝∠MQB＝90°;∠AMB＝∠BMP;MB＝MB;∴△AMB≌△QMB AAS．∴MA＝MQ.∵BA＝BC;∴BQ＝BC;又∵∠BQP＝90°＝∠C;BP＝BP;∴Rt△BPC≌Rt△BPQ HL．∴PC＝PQ;∴△PDM的周长＝MD＋MP＋DP＝MD＋MQ＋QP＋PD＝MD＋MA＋PC＋PD＝AD＋DC＝2AD.∴△PDM的周长没有发生变化．类型6旋转型全等问题：图中若有边相等;可用旋转做实验例6：解：1①∵四边形ADEF是正方形;∴AD＝AF;AB＝AC;∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠B＝∠ACF;∴∠ACB＋∠ACF＝90°;即CF⊥BC；②∵△DAB≌△FAC;∴CF＝BD;∵BC＝BD＋CD;∴BC＝CF＋CD.2结论①成立;结论②不成立．∵四边形ADEF是正方形;∴AD＝AF;AB＝AC.∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠ABD＝∠ACF;CF＝BD;∴∠BCF＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°;即CF⊥BC；∵BC＝CD－BD;∴BC＝CD－CF.3如图;过A作AH⊥BC于H;过E作EM⊥BD于M;EN∵∠BAC＝90°;AB＝AC;∴BC＝AB＝4;AH＝CH＝BC∴CD＝BC＝1;∴DH＝3;同2证得△BAD≌△CAF;∴∠ABD＝∠ACF＝45°;∴∠BCF＝∠ACB＋∠ACF＝∴BC⊥CF;CF＝BD＝5.∵四边形ADEF是正方形;∴AD＝DE;∠ADE＝90°;∵BC⊥CF;EM⊥BD;EN⊥CF;∴四边形CMEN是矩形;∴NE＝CM;EM＝CN;∵∠AHD＝∠ADE＝∠EMD＝90°;∴∠ADH＋∠EDM＝∠EDM＋∠DEM＝90°;∴∠ADH＝∠DEM;∴△ADH≌△DEM;∴EM＝DH＝3;DM＝AH＝2;∴CN＝EM＝3;EN＝CM＝3;∵∠ABC＝45°;∴∠BGC＝45°;∴△BCG是等腰直角三角形;∴CG＝BC＝4;∴GN＝1;∴EG＝＝.针对训练：1.解：1AC＝AD＋AB.证明如下：∵∠B＋∠D＝180°;∠B＝90°;∴∠D＝90°.∵∠DAB＝120°;AC平分∠DAB;∴∠DAC＝∠BAC＝60°;∵∠B＝90°;∴AB＝AC;同理AD＝AC.∴AC＝AD＋AB.21中的结论成立;理由如下：如图①;以C为顶点;AC为一边作∠ACE＝60°;∠ACE的另一边交AB的延长线于点E;∵∠BAC＝60°;∴△AEC为等边三角形;∴AC＝AE＝CE;∠E＝60°;∵∠ABC＋∠D＝180°;∠DAB＝120°;∴∠DCB＝60°;∴∠DCA＝∠ECB.在△DAC和△BEC中;∴△DAC≌△BEC;∴AD＝BE;∴AC＝AE＝AD＋AB.3AD＋AB＝AC.理由如下：如图②;过点C作CE⊥AC交AB的延长于点E;∵∠ABC＋∠D＝180°;∠DAB＝90°;∴∠DCB＝90°;∵∠ACE＝90°;∴∠DCA＝∠BCE;又∵AC平分∠DAB;∴∠CAB＝45°;∴∠E＝45°;∴AC＝CE.∴△CDA≌△CBE;∴AD＝BE;∴AD＋AB＝AE.∵在Rt△ACE中;∠CAB＝45°;∴AE＝＝AC;∴AD＋AB＝AC.2.解：1证明：∵四边形ABCD是正方形;∴∠B＝∠D＝∠BAD＝90°;AB＝AD;∵△ABE沿AE翻折得到△AHE;∴△ABE≌△AHE;∴AH＝AB＝AD;BE＝EH;∠AHE＝∠AHF＝∠B＝∠D＝90°.在Rt△AHF和Rt△ADF中;∴Rt△AHF≌Rt△ADFHL;∴∠HAF＝∠DAF;∴∠EAF＝∠EAH＋∠FAH＝∠BAH＋∠HAD＝∠BAD＝45°;2以BM;DN;MN为三边围成的三角形为直角三角形．证明如下：如图;过点A作AH⊥AN并截取AH＝AN;连接BH、HM;∵∠1＋∠BAN＝90°;∠3＋∠BAN＝90°;∴∠1＝∠3;在△ABH和△ADN中;∴△ABH≌△ADN SAS;∴BH＝DN;∠HBA＝∠NDA＝135°;∵∠HAN＝90°;∠MAN＝45°;∴∠1＋∠2＝∠HAM＝∠MAN＝45°;在△AHM和△ANM中;∴△AHM≌△ANM SAS;∴HM＝NM;∴∠HBP＝180°－∠HBA＝180°－135°＝45°;∴∠HBP＋∠PBM＝45°＋45°＝90°;∴△HBM是直角三角形;∵HB＝DN;HM＝MN;∴以BM;DN;MN为三边围成的三角形为直角三角形．3.解：1如图①;将△PBC绕点B逆时针旋转90°得△P△AP′B≌△CPB;∴P′B＝PB＝;P′A＝PC＝1;∠1＝∠2;∠AP′B＝∠BPC.∵四边形ABCD是正方形;∴AB＝BC;∠ABC＝90°;∴∠2＋∠3＝90°;∴∠1＋∠3＝90°;即∠P′BP＝90°;∴∠BP′P＝45°.在Rt△P′BP中;由勾股定理;得PP′2＝ 4. ∵P′A＝1;AP＝∴P′A2＝1;AP2＝5;∴P′A2＋PP′2＝AP2;∴△P′AP是直角三角形;∴∠AP′P＝90°;∴∠AP′B＝45°＋90°＝135°;∴∠BPC＝135°.2仿照分析中的思路;将△BPC绕点B逆时针旋转120°;得到了△BP′A;连接PP′;如图②.则△PBC≌△P′BA;∴P′B＝PB＝4;P′A＝PC＝2;∠BPC＝∠BP′A;∴△BPP′为等腰三角形;∵∠ABC＝120°;∴∠PBP′＝120°;∴∠BP′P＝30°;过点B作BG⊥PP′于G;则∠P′GB＝90°;∴PP′＝2P′G.∵P′B＝PB＝4;∠BP′P＝30°;∴BG＝2;∴P′G＝2.∴PP′＝4;在△APP′中;∵PA＝2;P′A＝2;PP′＝4;∴P′A2＋P′P2＝PA2;∴△PP′A是直角三角形;∴∠AP′P＝90°;∴∠BPC＝∠BP′A＝∠PP′B＋∠AP′P＝30°＋90°＝120°.。

专题八：几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位．根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低．但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型．热点探究类型一：关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2．1求证：BD=CE；2求证：∠M=∠N．分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可．解答1证明：在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE；2证明：∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得：△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N．点评本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．类型二：关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG．1请判断四边形EBGD的形状;并说明理由；2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值．考点平行四边形的判定与性质；角平分线的性质．分析1结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题．解答解：1四边形EBGD是菱形．理由：∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=．MC=3;∴EC===10．∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10．点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型．同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．类型三：关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证：1四边形EBFD是矩形；2DG=BE．考点正方形的性质；矩形的判定；圆周角定理．分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案；2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG．解答证明：1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形；2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．类型四：关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F．1求证：△ACD∽△BFD；2当tan∠ABD=1;AC=3时;求BF的长．考点相似三角形的判定与性质．分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明．2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题．解答1证明：∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD．2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3．同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=．1试判断△ABC 的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD 的值．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线．1求证：△ADE ≌△CBF ；2若∠ADB 是直角;则四边形BEDF 是什么四边形 证明你的结论．5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上．设∠PCB=α;∠POC=β．求证：tanα tan=．DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．参考答案类型一：关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．考点等腰三角形的性质．分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数；2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论．解答1①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE．∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC．在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE．②解：∵△ACD≌△BCE;∴∠ADC=∠BEC．∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°．∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．2证明：∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°．∵CM⊥DE;∴∠CMD=90°;DM=EM．在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°．在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN．∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM．点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是：1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；2找出线段AD、DE的长．本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键．类型二：关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．考点正方形的性质．分析1根据正方形的性质以及勾股定理即可求得；2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM．解答解：1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1；2CN=CM．证明：∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM．类型三：关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．思路分析：本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点．故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线；对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得；对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得．解题过程：1证明：连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线；2证明：∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD．∴BC2=2CD OE；3解：∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15．又∵AC=2OE;∴OE=12AC=152．规律总结：熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键．要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可．类型四：关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可；2①BP＝5；②71解析1证明：∵∠ACP＝∠B;∠BAC＝∠CAP;∴△ACP∽△ABC;∴AC：AB＝AP：AC;∴AC2＝AP·AB；2①如图;作CQ∥BM交AB延长线于Q;设BP＝x;则P Q＝2x∵∠PBM＝∠ACP;∠PAC＝∠CAQ;∴△APC∽△ACQ;由AC2＝AP·AQ得：22＝3－x35即BP②如图：作CQ⊥AB 于点Q;作CP 0＝CP 交AB 于点P 0;∵AC ＝2;∴AQ＝1;CQ ＝BQ; 设P0Q ＝PQ ＝1－x;BP －1＋x;∵∠BPM＝∠CP 0A ;∠BMP＝∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C ＝2012P C ==AP 0 BP ＝1＋x;解得x ∴BP ＝－11-．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．考点正方形的性质；全等三角形的判定与性质．分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论；2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析．解答解：1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．考点三角形例行;特殊四边形的性质与判定..1证明：∵点E 是AD 的中点;∴AE ＝DE ．∵AF ∥BC;∴∠AFE ＝∠DCE;∠FAE ＝∠CDE ．∴△EAF ≌△EDC ．∴AF ＝DC ．∵AF ＝BD;∴BD ＝DC;即D 是BC 的中点．2四边形AFBD 是矩形．证明如下：∵AF ∥BD;AF ＝BD;∴四边形AFBD 是平行四边形．∵AB ＝AC;又由1可知D 是BC 的中点;∴AD ⊥BC ．DC EF B A图6∴□AFBD是矩形．3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=．1试判断△ABC的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD的值．思路分析：1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形；2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解．解题过程：解：1△ABC为等腰三角形．理由如下：连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形；2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===．规律总结：本题考查了圆周角定理：在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半．推论：半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质和勾股定理．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线．1求证：△ADE≌△CBF；2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．分析：1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF；2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形．解答：1证明：∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS；2若∠ADB是直角;则四边形BEDF是菱形;理由如下：解：由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形．点评：本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键．5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上．设∠PCB=α;∠POC=β．求证：tanα tan=．解析：连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=．解答：证明：连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===．点评：本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=．6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．所有分析： 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE;故可得出结论；2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论．解答： 1证明：∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP；2解：由勾股定理得;BP===4．∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=．由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．考点：切线的判定．分析： 1如图;连接OE．欲证明PE是⊙O的切线;只需推知OE⊥PE即可；2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论；3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长．解答： 1证明：如图;连接OE．∵CD是圆O的直径;∴∠CED=90°．∵OC=OE;∴∠1=∠2．又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线；2证明：∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等．又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP；3解：设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=．点评：本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键．。

矩形24.已知:如图，在△ABC 中，AB=AC ，A D ⊥BC ，垂足为点D ，M 在BA 的延长线上AN 是∠MAC 的平分线，CE ⊥AN ，垂足为E 。

（1）试说明：四边形ADCE 为矩形；（2）当△ABC 满足什么条件时，四边形ADCE 是一个正方形？说明理由。

24．（本小题9分）已知：如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为E ，连接DE 交AC 于F （1）求证：四边形ADCE 为矩形 （2）求证：DF ∥AB ，DF ＝12AB21.如图所示折叠长方形的一边AD ，点D 落在BC 边的点F 处，已知AB ＝12cm ， BC ＝13cm,求EC 的长。

5.如图8，将矩形纸片ABCD 沿对角线AC 折叠，使点B 落在点E 处，求证：EF =DF .BDECF19．如图，把一张矩形的纸ABCD 沿对角线BD 折叠，使点C 落在点E 处，BE 与AD 交于点F ．①求证：ΔABF ≌ΔEDF ；②若将折叠的图形恢复原状，点F 与BC 边上的点M 正好重合，连接DM ，试判断四边形BMDF 的形状，并说明理由．12、如图，矩形ABCD 中，O 是AC 与BD 的交点，过O 点的直线EF 与AB CD ，的延长线分别交于E F ，．（1）求证：BOE DOF △≌△； （2）当EF 与AC 满足什么关系时，以A E C F ，，，为顶点的四边形是菱形？证明你的结论．1.如图，在△ABC 中，D 是BC 边上的一点，E 是AD 的中点，过A 点作BC 的平行线交CE 的延长线于点F ，且AF =BD ，连结BF 。

（1） 求证：BD =CD ； （2） 如果AB =AC ，试判断四边形AFBD 的形状，并证明你的结论。

F D OB E AC D B A M 第22题图F EFED C B A 3.如图，四边形ABCD 是矩形，△PBC 和△QCD 都是等边三角形，且点P 在矩形上方，点Q 在矩形内． 求证：（1）∠PBA =∠PCQ =30°；（2）P A =PQ ．7、已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF=ED,EF ⊥ED. 求证:AE 平分∠BAD.8、如图，矩形ABCD 中，点E 是BC 上一点，AE ＝AD ，DF ⊥AE 于F ，连结DE ，求证：DF ＝DC ．23．（本小题6分）已知如图,在矩形ABCD 中,E 为BC 上的一点,且DE=BC,AF ⊥DE 于点F,求证:EF=BE 14、（本题8分）已知：如图，在矩形ABCD 中，AF=DE,求证：BE=CF（第23题）ACBD PQBDDC BAOE18.在矩形ABCD 中，O 是对角线AC 的中点，EF 是线段AC 的中垂线，交AD 、BC 于E 、F .求证：四边形AECF 是菱形1、如左下图，在矩形ABCD 中，AC 、BD 相交于O ，AE 平分∠BAD ，交BC 于E ，若∠CAE =15°，求∠BOE 的度数.2、如右上图ABCD ，四内角平分线相交于E 、F 、G 、H .求证：四边形EFGH 是矩形6．（2012•聊城）如图，矩形ABCD 的对角线相交于点O ，DE∥AC，CE∥BD． 求证：四边形OCED 是菱形．9．（2010四川眉山）如图，O 为矩形ABCD 对角线的交点，DE ∥AC ，CE ∥BD ．（1）试判断四边形OCED 的形状，并说明理由； （2）若AB =6，BC =8，求四边形OCED 的面积．10．（2012娄底）如图，在矩形ABCD 中，M 、N 分别是AD ．BC 的中点，P 、Q 分别是BM 、DN 的中点．（1）求证：△MBA ≌△NDC ；（2）四边形MPNQ 是什么样的特殊四边形？请说明理由．16．（2012六盘水）如图，已知E 是▱ABCD 中BC 边的中点，连接AE 并延长AE 交DC 的延长线于点F ．（1）求证：△ABE ≌△FCE ．（2）连接AC ．BF ，若∠AEC=2∠ABC ，求证：四边形ABFC 为矩形．5.两个完全相同的矩形纸片ABCD 、BFDE 如图7放置，AB BF ，求证：四边形BNDM 为菱形．19. （2012.云南省）如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M ，与BD 相交于点N ，连接BM ，DN ． （1）求证：四边形BMDN 是菱形； （2）若AB=4，AD=8，求MD 的长．8.如图，矩形ABCD 中，AC 、BD 相交于点O ，AE 平分∠BAD ，若∠EAO=15°，求∠BOE 的度数。

1.三角形的有关概念知识考点：理解三角形三边的关系及三角形的主要线段（中线、高线、角平分线）和三角形的内角和定理。

关键是正确理解有关概念，学会概念和定理的运用。

应用方程知识求解几何题是这部分知识常用的方法。

【例1】已知一个三角形中两条边的长分别是a 、b ，且b a >，那么这个三角形的周长L 的取值范围是（ ） A 、b L a 33>> B 、a L b a 2)(2>>+ C 、a b L b a +>>+262 D 、b a L b a 23+>>- 变式与思考：在△ABC 中，AC ＝5，中线AD ＝7，则AB 边的取值范围是（ ） A 、1＜AB ＜29 B 、4＜AB ＜24 C 、5＜AB ＜19 D 、9＜AB ＜19 【例2】如图，已知△ABC 中，∠ABC ＝450，∠ACB ＝610，延长BC 至E ，使CE ＝AC ，延长CB 至D ，使DB ＝AB ，求∠DAE 的度数。

一、填空题：1、三角形的三边为1，a -1，9，则a 的取值范围是 。

2、已知三角形两边的长分别为1和2，如果第三边的长也是整数，那么第三边的长为 。

3、在△ABC 中，若∠C ＝2（∠A ＋∠B ），则∠C ＝ 度。

4、如果△ABC 的一个外角等于1500，且∠B ＝∠C ，则∠A ＝ 。

5、如果△ABC 中，∠ACB ＝900，CD 是AB 边上的高，则与∠A 相等的角是 。

6、如图，在△ABC 中，∠A ＝800，∠ABC 和∠ACB 的外角平分线相交于点D ，那么∠BDC ＝ 。

7、如图，CE 平分∠ACB ，且CE ⊥DB ，∠DAB ＝∠DBA ，AC ＝18cm ，△CBD 的周长为28 cm ，则DB ＝ 。

8、纸片△ABC 中，∠A ＝650，∠B ＝750，将纸片的一角折叠，使点C 落在△ABC 内（如图），若∠1＝200，则∠2的度数为 。

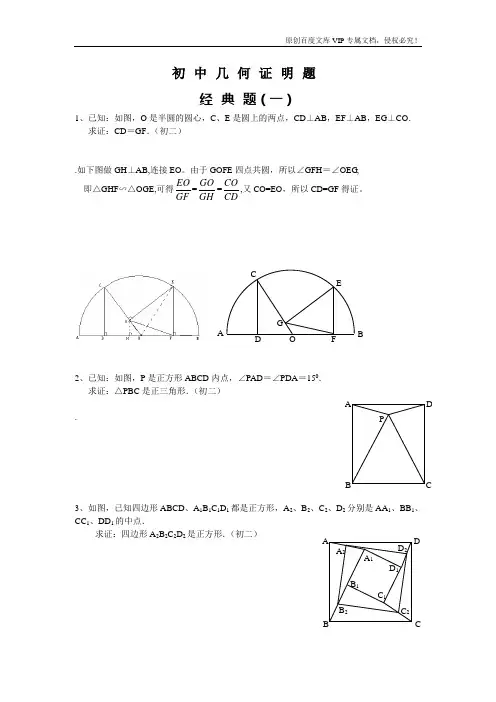
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）.3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．BF求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5． 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ． 求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、 设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值． A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图，正方形ABCD中，对角线AC, BD交于点。

，点E.点OB ,线段AB上，且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点，AE J5,求BF的长：(2)如图2,若AE平分BAC,求证：FG HG;(3)如图3,点E在线段BO (含端点)上运动，连接HE，当线段HE长度取得最大值时，直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图，平行四边形ABCD中，AB=2BC, B 60 . 曲 DC中点，连接AE . F为AD上一点，连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证：EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点，M是BC边上的点.(1)如图1,若点M与点G重合，AH 5, AD 显26 ,求CF的长：2(2)如图2.若AM是BAD的角平分线，连接MH , HMG MAH ,求证：AM 2 .2HM(3)如图3,若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中，E 为边CD 上一点(不与点 C 、D 第4页共34重合)，垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时，若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时，判断线段AN 、MB 、EC 之间的数量关系，并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时，连接 NB,将^ BPN 沿着BN 翻折，点P 落在点P 处，AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中，/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上，且AC=g AF, AF=超时，求CE的长；(2)如图2,当/ AFC = 90°时，求证：E是BC的中点；(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图，在？ABCD中，/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上，且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长；(2)求证：AD+AM= 22DN .(3)如图，连接EF、探究AF、EF、CF之间存在的数量关系，直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图，在平行四边形ABCD中，AC为对角线，过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图，若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图，若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证：DG 立CG22.如图，已知ABCD中，/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证：CD 2DF 版AG .(3)如图，在(2)的条件下，若FG J5,点M、N是线段CF、CD上的动点，DM+MN 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形，CD，AB交AB于M, DBXBC, E是AC上一点，EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图，若EC=-AC , EH=6,求BE 的长. 5(2)如图，连接AF,将AF绕点A顺时针旋转，使F点落在BD边上的G点处，AG交CD 于Q,求证：BG=CF.(3)如图，在(2)的条件下，连接FG,交BE于N,连接MN,若竺勺，4AGF的面QG 3积为49户，求MN的长.3.(万州国本中学初三下期中考试)已知，在0ABCD中，AB BD, AB BD, E为射线BC上一点，连接AE交BD于点F .(1)如图1,若点E与点C重合，且AF 2胫，求AD的长；(2)如图2,当点E在BC边上时，过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证：AF DH FH ；(3)如图3,当点E在射线BC上运动时，过点D作DG AE于G , M为AG的中点，点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .（万州国本中学初三下第一次诊断） 【问题背景】如图1所示，在gABC 中，AB= BC, ABC=90，点D 为直线BC 上的一个动点（不与 B 、C 重合），连结AD,将线段AD 绕点D 按顺时针方向旋转90。

2022年中考数学真题汇编三角形类几何证明题1.(2022·江苏省南通市)如图，AC和BD相交于点O，OA=OC，OB=OD．(1)求证：∠A=∠C；(2)求证：AB//CD．2.(2022·西藏)如图，已知AD平分∠BAC，AB=AC.求证：△ABD≌△ACD．3.(2022·湖南省益阳市)如图，在Rt△ABC中，∠B=90°，CD//AB，DE⊥AC于点E，且CE=AB.求证：△CED≌△ABC．4.(2022·辽宁省大连市)如图，在△ABC中，∠ACB=90°，BC=4，点D在AC上，CD=3，连接DB，AD=DB，点P是边AC上一动点(点P不与点A，D，C重合)，过点P作AC的垂线，与AB相交于点Q，连接DQ，设AP=x，△PDQ与△ABD重叠部分的面积为S．(1)求AC的长；(2)求S关于x的函数解析式，并直接写出自变量x的取值范围．5.(2022·黑龙江省牡丹江市)如图，△ABC和△DEF，点E，F在直线BC上，AB=DF，∠A=∠D，∠B=∠F.如图①，易证：BC+BE=BF.请解答下列问题：(1)如图②，如图③，请猜想BC，BE，BF之间的数量关系，并直接写出猜想结论；(2)请选择(1)中任意一种结论进行证明；(3)若AB=6，CE=2，∠F=60°，S△ABC=12√3，则BC=______，BF=______．6.(2022·广西壮族自治区柳州市)如图，点A，D，C，F在同一条直线上，AB=DE，BC=EF.有下列三个条件：①AC=DF，②∠ABC=∠DEF，③∠ACB=∠DFE．(1)请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为(填写序号)______(只需选一个条件，多选不得分)，你判定△ABC ≌△DEF的依据是______(填“SSS”或“SAS”或“ASA”或“AAS”)；(2)利用(1)的结论△ABC≌△DEF.求证：AB//DE．7.(2022·上海市)如图所示，在等腰三角形ABC中，AB=AC，点E，F在线段BC上，点Q在线段AB上，且CF=BE，AE2=AQ⋅AB．求证：(1)∠CAE=∠BAF；(2)CF⋅FQ=AF⋅BQ．8.(2022·广西壮族自治区河池市)如图，点A，F，C，D在同一直线上，AB=DE，AF=CD，BC=EF．(1)求证：∠ACB=∠DFE；(2)连接BF，CE，直接判断四边形BFEC的形状．9.(2022·吉林省长春市)图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．(1)网格中△ABC的形状是______；(2)在图①中确定一点D，连结DB、DC，使△DBC与△ABC全等；(3)在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA；(4)在图③中△ABC的边AB上确定一点P，在边BC上确定一点Q，连结PQ，使△PBQ∽△ABC，且相似比为1：2．10.(2022·北京市)下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．三角形内角和定理：三角形三个内角的和等于180°．已知：如图，△ABC，求证：∠A+∠B+∠C=180°．方法一证明：如图，过点A作DE//BC．方法二证明：如图，过点C作CD//AB．11.(2022·山东省青岛市)已知：Rt△ABC，∠B=90°．求作：点P，使点P在△ABC内部．且PB=PC，∠PBC=45°．12.(2022·贵州省铜仁市)如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB=CD.求证：△ABC≌△CDE．13.(2022·北京市)在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC，延长DC到点E，使得CE=DC．(1)如图1，延长BC到点F，使得CF=BC，连接AF，EF.若AF⊥EF，求证：BD⊥AF；(2)连接AE，交BD的延长线于点H，连接CH，依题意补全图2.若AB2=AE2+BD2，用等式表示线段CD与CH的数量关系，并证明．14.(2022·吉林省)如图，AB=AC，∠BAD=∠CAD.求证：BD=CD．15.(2022·广东省云浮市)如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E.求证：△OPD≌△OPE．16.(2022·黑龙江省鹤岗市)△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+PC=PB)成立(不需证明)；(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．17.(2022·湖南省长沙市)如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．(1)求证：△ABC≌△ADC；(2)若AB=4，CD=3，求四边形ABCD的面积．18.(2022·内蒙古自治区赤峰市)如图，已知Rt△ABC中，∠ACB=90°，AB=8，BC=5．(1)作BC的垂直平分线，分别交AB、BC于点D、H；(要求：尺规作图，不写作法，保留作图痕迹)(2)在(1)的条件下，连接CD，求△BCD的周长．19.(2022·福建省)如图，点B，F，C，E在同一条直线上，BF=EC，AB=DE，∠B=∠E.求证：∠A=∠D．20.(2022·广西壮族自治区玉林市)问题情境：在数学探究活动中，老师给出了如图的图形及下面三个等式：①AB=AC；②DB=DC；③∠BAD=∠CAD.若以其中两个等式作为已知条件，能否得到余下一个等式成立？解决方案：探究△ABD与△ACD全等．问题解决：(1)当选择①②作为已知条件时，△ABD与△ACD全等吗？______(填“全等”或“不全等”)，理由是______；(2)当任意选择两个等式作为已知条件时，请用画树状图法或列表法求△ABD≌△ACD的概率．21.(2022·四川省宜宾市)已知：如图，点A、D、C、F在同一直线上，AB//DE，∠B=∠E，BC=EF.求证：AD=CF．22.(2022·陕西省)如图，在△ABC中，点D在边BC上，CD=AB，DE//AB，∠DCE=∠A.求证：DE=BC．23.(2022·湖南省衡阳市)如图，在△ABC中，AB=AC，D、E是BC边上的点，且BD=CE.求证：AD=AE．24.(2022·四川省乐山市)如图，B是线段AC的中点，AD//BE，BD//CE.求证：△ABD≌△BCE．25.(2022·浙江省杭州市)如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE.已知∠A=50°，∠ACE=30°．(1)求证：CE=CM．(2)若AB=4，求线段FC的长．参考答案1.证明：(1)在△AOB和△COD中，{OA=OC∠AOB=∠CODOB=OD,∴△AOB≌△COD(SAS)，∴∠A=∠C；(2)由(1)得∠A=∠C，∴AB//CD．2.证明：∵AD平分∠BAC，∴∠BAD=∠CAD，在△ABD和△ACD中，{AB=AC∠BAD=∠CAD AD=AD，∴△ABD≌△ACD(SAS)．3.证明：∵DE⊥AC，∠B=90°，∴∠DEC=∠B=90°，∵CD//AB，∴∠A=∠DCE，在△CED和△ABC中，{∠DCE=∠A CE=AB∠DEC=∠B，∴△CED≌△ABC(ASA)．4.解：(1)在Rt△BCD中，BC=4，CD=3，∴BD=√BC2+CD2=5，又∵AD=BD，∴AC=AD+CD=5+3=8；(2)当点P在点D的左侧时，即0<x<5，如图1，此时阴影部分的面积就是△PQD的面积，∵PQ⊥AC，BC⊥AC，∴PQ//BC，∴△ABC∽△AQP，∴APPQ =ACBC=84=2，设AP=x，则PQ=12x，PD=AD−AP=5−x，∴S阴影部分=S△PQD=12(5−x)×12x=−14x2+54x；当点P在点D的右侧时，即5<x<8，如图2，由(1)得，AP=x，PQ=12x，则PD=x−5，∵PQ//BC，∴△DPE∽△DCB，∴DPEP =DCBC=34，∴PE=43(x−5)，∴S阴影部分=S△PQD−S△DPE=12(x−5)×12x−12(x−5)×43(x−5)=−512x2+2512x−503；答：S关于x的函数解析式为：当0<x<5时，S=−14x2+54x；当5<x<8时，S=−512x2+2512x−503．5.814或186.①SSS7.证明：(1)∵AB=AC，∴∠B=∠C，∵CF=BE，∴CF−EF=BE−EF，即CE=BF，在△ACE和△ABF中，{AC=AB∠C=∠BCE=BF，∴△ACE≌△ABF(SAS)，∴∠CAE=∠BAF；(2)∵△ACE≌△ABF，∴AE=AF，∠CAE=∠BAF，∵AE2=AQ⋅AB，AC=AB，∴AEAQ =ACAF，∴△ACE∽AFQ，∴∠AEC=∠AQF，∴∠AEF=∠BQF，∵AE=AF，∴∠AEF=∠AFE，∴∠BQF=∠AFE，∵∠B=∠C，∴△CAF∽△BFQ，∴CFBQ =AFFQ，即CF⋅FQ=AF⋅BQ．8.(1)证明：∵AF=CD，∴AF+CF=CD+CF，即AC=DF，在△ABC和△DEF中，{AB=DE BC=EF AC=DF，∴△ABC≌△DEF(SSS)，∴∠ACB=∠DFE；(2)解：如图，四边形BFEC是平行四边形，理由如下：由(1)可知，∠ACB=∠DFE，∴BC//EF，又∵BC=EF，∴四边形BFEC是平行四边形．9.直角三角形10.证明：方法一：∵DE//BC，∴∠B=∠BAD，∠C=∠CAE，∵∠BAD+∠BAC+∠CAE=180°，∴∠B+∠BAC+∠C=180°；方法二：延长BC，如图，∵CD//AB，∴∠A=∠ACD，∠B=∠DCE，∵∠ACB+∠ACD+∠DCE=180°，∴∠A+∠ACD+∠B=180°．11.解：①先作出线段BC的垂直平分线EF；②再作出∠ABC的角平分线BM，EF与BM的交点为P；则P即为所求作的点．12.证明：∵AB⊥BD，ED⊥BD，AC⊥CE，∴∠B=∠D=∠ACE=90°，∴∠DCE+∠DEC=90°，∠BCA+∠DCE=90°，∴∠BCA=∠DEC，在△ABC和△CDE中，{∠BCA=∠DEC ∠B=∠DAB=CD，∴△ABC≌△CDE(AAS)．13.(1)证明：在△BCD和△FCE中，{BC=CF∠BCD=∠FCE CD=CE，∴△BCD≌△FCE(SAS)，∴∠DBC=∠EFC，∴BD//EF，∵AF⊥EF，∴BD⊥AF；(2)解：由题意补全图形如下：CD=CH．证明：延长BC到F，使CF=BC，连接AF，EF，∵AC⊥BF，BC=CF，∴AB=AF，由(1)可知BD//EF，BD=EF，∵AB2=AE2+BD2，∴AF2=AE2+EF2，∴∠AEF=90°，∴AE⊥EF，∴BD⊥AE，∴∠DHE=90°，又∵CD=CE，∴CH=CD=CE．14.证明：在△ABD与△ACD中，{AB=AC∠BAD=∠CAD AD=AD，∴△ABD≌△ACD(SAS)，∴BD=CD．15.证明：∵∠AOC=∠BOC，PD⊥OA，PE⊥OB，∴PD=PE，在Rt△OPD和Rt△OPE中，{OP=OPPD=PE，∴Rt△OPD≌Rt△OPE(HL)．16.解：(2)PB=PA+PC，理由如下：如图②，在BP上截取BF=PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠CAD+∠DAE，即∠DAB=∠EAC，∴△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵AB=AC，BF=CP，∴△BAF≌△CAP(SAS)，∴AF=AP，∠BAF=∠CAP，∴∠BAC=∠PAF=90°，∴△AFP是等边三角形，∴PF=PA，∴PB=BF+PF=PC+PA；(3)PC=PA+PB，理由如下：如图③，在PC上截取CM=PB，连接AM，同理得：△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵AB=AC，PB=CM，∴△AMC≌△APB(SAS)，∴AM=AP，∠BAP=∠CAM，∴∠BAC=∠PAM=60°，∴△AMP是等边三角形，∴PM=PA，∴PC=PM+CM=PA+PB．17.(1)证明：∵AC平分∠BAD，∴∠BAC=∠DAC，∵CB⊥AB，CD⊥AD，∴∠B=90°=∠D，在△ABC和△ADC中，{∠B=∠D∠BAC=∠DAC AC=AC，∴△ABC≌△ADC(AAS)；(2)解：由(1)知：△ABC≌△ADC，∴BC=CD=3，S△ABC=S△ADC，∴S△ABC=12AB⋅BC=12×4×3=6，∴S△ADC=6，∴S四边形ABCD=S△ABC+S△ADC=12，答：四边形ABCD的面积是12．18.解：(1)如图，DH为所作；(2)∵DH垂直平分AB，∴DC=DB，∴∠B=∠DCB，∵∠B+∠A=90°，∠DCB+∠DCA=90°，∴∠A=∠DCA，∴DC=DA，∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13．19.证明：∵BF=EC，∴BF+CF=EC+CF，即BC=EF，在△ABC和△DEF中，{AB=DE∠B=∠EBC=EF，∴△ABC≌△DEF(SAS)，∴∠A=∠D．20.全等三边对应相等的两个三角形全等21.证明：∵AB//DE，∴∠A=∠EDF．在△ABC和△DEF中，{∠A=∠EDF ∠B=∠EBC=EF，∴△ABC≌△DEF(AAS)．∴AC=DF，∴AC−DC=DF−DC，即：AD=CF．22.证明：∵DE//AB，∴∠EDC=∠B，在△CDE和△ABC中，{∠EDC=∠B CD=AB∠DCE=∠A，∴△CDE≌△ABC(ASA)，∴DE=BC．23.证明：∵AB=AC，∴∠B=∠C，在△ABD和△ACE中，{AB=AC ∠B=∠C BD=CE，∴△ABD≌△ACE(SAS)，∴AD=AE．24.证明：∵点B为线段AC的中点，∴AB=BC，∵AD//BE，∴∠A=∠EBC，∵BD//CE，∴∠C=∠DBA，在△ABD与△BCE中，{∠A=∠EBC AB=BC∠DBA=∠C，∴△ABD≌△BCE.(ASA)．25.(1)证明：∵∠ACB=90°，点M为边AB的中点，∴MC=MA=MB，∴∠MCA=∠A，∠MCB=∠B，∵∠A=50°，∴∠MCA=50°，∠MCB=∠B=40°，∴∠EMC=∠MCB+∠B=80°，∵∠ACE=30°，∴∠MEC=∠A+∠ACE=50°，∴∠MEC=∠EMC，∴CE=CM；(2)解：∵AB=4，∴CE=CM=1AB=2，2∵EF⊥AC，∠ACE=30°，∴FC=CE⋅cos30°=√3．。

中考数学证明题第一篇：中考数学证明题中考数学证明题o是已知线段ab上的一点，以ob为半径的圆o交ab于点c，以线段ao为直径的半圆圆o于点d，过点b作ab的垂线与ad的延长线交于点e(1)说明ae切圆o于点d(2)当点o位于线段ab何处时，△odc恰好是等边三角形〉说明理由答案：一题：显然三角形doe是等边三角形：理由：首先能确定o为圆心然后在三角形obd中：bo=od，再因角b为60度，所以三角形obd为等边三角形;同理证明三角形oce为等边三角形从而得到：角bod=角eoc=60度，推出角doe=60度再因为od=oe，三角形doe为等腰三角形，结合上面角doe=60度，得出结论：三角形doe为等边三角形第三题没作思考，有事了，改天再解二题：要证明三角形ode为等边三角形，其实还是要证明角doe=60度，因为我们知道三角形ode是等腰三角形。

此时，不妨设角abc=x度，角acb=y度，不难发现，x+y=120度。

此时我们要明确三个等腰三角形：ode;bod;oce此时在我们在三角形bod中，由于角obd=角odb=x度从而得出角bod=180-2x同理在三角形oce中得出角eoc=180-2y则角bod+角eoc=180-2x+180-2y，整理得：360-2(x+y)把x+y=120代入，得120度。

由于角eoc+角bod=120度，所以角doe就为60度。

外加三角形doe本身为等腰三角形，所以三角形doe为等边三角形!图片发不上来，看参考资料里的1如图，ab⊥bc于b，ef⊥ac于g，df⊥ac于d，bc=df。

求证：ac=ef。

2已知ac平分角bad，ce垂直ab于e，cf垂直ad于f，且bc=cd(1)求证：△bce全等△dcf3.如图所示，过三角形abc的顶点a分别作两底角角b和角c的平分线的垂线，ad垂直于bd于d，ae垂直于ce于e，求证：ed||bc.4.已知，如图，pb、pc分别是△abc的外角平分线，且相交于点p。

中考数学经典几何证明题60例一、解答题（共60小题）1．（遵义）在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积．2．（珠海）已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．（1）如图1，连接BD，AF，则BD AF（填“＞”、“＜”或“=”）；（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．3．（镇江）如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．（1）求证：△BAE≌△BCF；（2）若∠ABC=50°，则当∠EBA=°时，四边形BFDE是正方形．4．（漳州）如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．5．（玉林）如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O 的切线CD交AB的延长线于点C，E为的中点，连接DE，EB．（1）求证：四边形BCDE是平行四边形；（2）已知图中阴影部分面积为6π，求⊙O的半径r．6．（永州）如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．7．（营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD=，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．8．（徐州）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE=时，四边形BFCE是菱形．9．（宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．10．（湘西州）如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．（1）求证：△ADE≌△CBF；（2）求证：四边形BFDE为矩形．11．（咸宁）已知关于x的一元二次方程mx2﹣（m+2）x+2=0．（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．12．（咸宁）如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F．（1）若∠B=30°，求证：以A、O、D、E为顶点的四边形是菱形．（2）若AC=6，AB=10，连结AD，求⊙O的半径和AD的长．13．（梧州）如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．（1）求证：HF=AP；（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．14．（威海）如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE=CE；（2）若BD=2，BE=3，求AC的长．15．（铜仁市）已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．16．（通辽）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．17．（铁岭）如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．（1）若DE=BF，求证：四边形AFCE是平行四边形；（2）若四边形AFCE是菱形，求菱形AFCE的周长．18．（天水）如图，AB是⊙O的直径，BC切⊙O于点B，OC平行于弦AD，过点D作DE⊥AB于点E，连结AC，与DE交于点P．求证：（1）AC•PD=AP•BC；（2）PE=PD．19．（泰安）如图，△ABC是直角三角形，且∠ABC=90°，四边形BCDE是平行四边形，E 为AC中点，BD平分∠ABC，点F在AB上，且BF=BC．求证：（1）DF=AE；（2）DF⊥AC．20．（随州）如图，射线PA切⊙O于点A，连接PO．（1）在PO的上方作射线PC，使∠OPC=∠OPA（用尺规在原图中作，保留痕迹，不写作法），并证明：PC是⊙O的切线；（2）在（1）的条件下，若PC切⊙O于点B，AB=AP=4，求的长．21．（绥化）如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．（1）求证：BD+2DE=BM．（2）如图2，连接BN交AD于点F，连接MF交BD于点G．若AF：FD=1：2，且CM=2，则线段DG=．22．（苏州）如图，在△ABC中，AB=AC，分别以B、C为圆心，BC长为半径在BC下方画弧．设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC=50°，求DE、DF的长度之和（结果保留π）．23．（上海）已知，如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，连接DE．（1）求证：DE⊥BE；（2）如果OE⊥CD，求证：BD•CE=CD•DE．24．（厦门）如图，在平面直角坐标系中，点A（2，n），B（m，n）（m＞2），D（p，q）（q＜n），点B，D在直线y=x+1上．四边形ABCD的对角线AC，BD相交于点E，且AB∥CD，CD=4，BE=DE，△AEB的面积是2．求证：四边形ABCD是矩形．25．（庆阳）如图，在正方形ABCD中，点E是边BC的中点，直线EF交正方形外角的平分线于点F，交DC于点G，且AE⊥EF．（1）当AB=2时，求△GEC的面积；（2）求证：AE=EF．26．（青海）如图，梯形ABCD中，AB∥DC，AC平分∠BAD，CE∥DA交AB于点E．求证：四边形ADCE是菱形．27．（钦州）如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．（1）求证：BC是⊙O的切线；（2）连接OC，如果OC恰好经过弦BD的中点E，且tanC=，AD=3，求直径AB的长．28．（黔东南州）如图，已知PC平分∠MPN，点O是PC上任意一点，PM与⊙O相切于点E，交PC于A、B两点．（1）求证：PN与⊙O相切；（2）如果∠MPC=30°，PE=2，求劣弧的长．29．（潜江）如图，AC是⊙O的直径，OB是⊙O的半径，PA切⊙O于点A，PB与AC的延长线交于点M，∠COB=∠APB．（1）求证：PB是⊙O的切线；（2）当OB=3，PA=6时，求MB，MC的长．30．（盘锦）如图1，AB为⊙O的直径，点P是直径AB上任意一点，过点P作弦CD⊥AB，垂足为P，过点B的直线与线段AD的延长线交于点F，且∠F=∠ABC．（1）若CD=2，BP=4，求⊙O的半径；（2）求证：直线BF是⊙O的切线；（3）当点P与点O重合时，过点A作⊙O的切线交线段BC的延长线于点E，在其它条件不变的情况下，判断四边形AEBF是什么特殊的四边形？请在图2中补全图象并证明你的结论．31．（内江）如图，将▱ABCD的边AB延长至点E，使AB=BE，连接DE，EC，DE交BC 于点O．（1）求证：△ABD≌△BEC；（2）连接BD，若∠BOD=2∠A，求证：四边形BECD是矩形．32．（南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．33．（南平）如图，AB是半圆O的直径，C是AB延长线上的一点，CD与半圆O相切于点D，连接AD，BD．（1）求证：∠BAD=∠BDC；（2）若∠BDC=28°，BD=2，求⊙O的半径．（精确到0.01）34．（南京）如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：∠A=∠AEB；（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．35．（南充）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：（1）△AEF≌△CEB；（2）AF=2CD．36．（南昌）（1）如图1，纸片▱ABCD中，AD=5，S▱ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AEE′D 的形状为A．平行四边形B．菱形C．矩形D．正方形（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，将它平移至△DE′F′的位置，拼成四边形AFF′D．①求证：四边形AFF′D是菱形．②求四边形AFF′D的两条对角线的长．37．（梅州）如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连接BD，与AC交于点E，连接AD，CD．（1）求证：△ABC≌△ADC；（2）若∠BAC=30°，∠BCA=45°，AC=4，求BE的长．38．（龙岩）如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．（1）求证：AE=DC；（2）已知DC=，求BE的长．39．（柳州）如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，边CD与⊙O相交于点E，连接AE，BE．（1）求证：AB=AC；（2）若过点A作AH⊥BE于H，求证：BH=CE+EH．40．（辽阳）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，DG⊥AC于点G，交AB的延长线于点F．（1）求证：直线FG是⊙O的切线；（2）若AC=10，cosA=，求CG的长．41．（连云港）如图，将平行四边形ABCD沿对角线BD进行折叠，折叠后点C落在点F 处，DF交AB于点E．（1）求证；∠EDB=∠EBD；（2）判断AF与DB是否平行，并说明理由．42．（莱芜）如图，△ABC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD 交于点F．（1）判断四边形ACGD的形状，并说明理由．（2）求证：BE=CD，BE⊥CD．43．（酒泉）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE=cm时，四边形CEDF是矩形；②当AE=cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）44．（荆门）已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O 于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．（1）求证：BD是⊙O的切线；（2）求证：CE2=EH•EA；（3）若⊙O的半径为5，sinA=，求BH的长．45．（吉林）如图①，半径为R，圆心角为n°的扇形面积是S扇形=，由弧长l=，得S扇形==••R=lR．通过观察，我们发现S扇形=lR类似于S三角形=×底×高．类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．（1）设扇环的面积为S扇环，的长为l1，的长为l2，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=×（上底+下底）×高，用含l1，l2，h的代数式表示S扇环，并证明；（2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？46．（黄石）在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．（1）如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，证明：①AC′=BD′；②AC′⊥BD′；（2）如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．47．（黄冈）已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点M，交BC于点N，连接AN，过点C的切线交AB的延长线于点P．（1）求证：∠BCP=∠BAN（2）求证：=．48．（湖北）如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．（1）求证：BE=CF；（2）当四边形ACDE为菱形时，求BD的长．49．（葫芦岛）如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G、F两点．（1）求证：AB与⊙O相切；（2）若等边三角形ABC的边长是4，求线段BF的长？50．（呼伦贝尔）如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．（1）求证：△ADE≌△CBF；（2）若∠ADB是直角，则四边形BEDF是什么四边形？证明你的结论．51．（呼伦贝尔）如图，已知直线l与⊙O相离．OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．（1）求证：AB=AC；（2）若PC=2，求⊙O的半径．52．（贺州）如图，AB是⊙O的直径，C为⊙O上一点，AC平分∠BAD，AD⊥DC，垂足为D，OE⊥AC，垂足为E．（1）求证：DC是⊙O的切线；（2）若OE=cm，AC=2cm，求DC的长（结果保留根号）．53．（贺州）如图，将矩形ABCD沿对角线BD对折，点C落在E处，BE与AD相交于点F．若DE=4，BD=8．（1）求证：AF=EF；（2）求证：BF平分∠ABD．54．（河南）如图，AB是半圆O的直径，点P是半圆上不与点A、B重合的一个动点，延长BP到点C，使PC=PB，D是AC的中点，连接PD、PO．（1）求证：△CDP≌△POB；（2）填空：①若AB=4，则四边形AOPD的最大面积为；②连接OD，当∠PBA的度数为时，四边形BPDO是菱形．55．（桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．56．（贵港）如图，已知AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，且点E 是OD的中点，⊙O的切线BM与AO的延长线相交于点M，连接AC，CM．（1）若AB=4，求的长；（结果保留π）（2）求证：四边形ABMC是菱形．57．（甘南州）如图1，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB=∠DCE=90°，AB与CE交于F，ED与AB，BC，分别交于M，H．（1）求证：CF=CH；（2）如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM 是什么四边形？并证明你的结论．58．（东莞）如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG．（1）求证：△ABG≌△AFG；（2）求BG的长．59．（大庆）如图，四边形ABCD内接于⊙O，AD∥BC，P为BD上一点，∠APB=∠BAD．（1）证明：AB=CD；（2）证明：DP•BD=AD•BC；（2）证明：BD2=AB2+AD•BC．60．（赤峰）如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO 交PO延长线于点E，连接PB，∠EDB=∠EPB．（1）求证：PB是的切线．（2）若PB=6，DB=8，求⊙O的半径．中考数学经典几何证明题60例参考答案与试题解析一、解答题（共60小题）1．（遵义）在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积．考点：菱形的判定与性质；全等三角形的判定与性质；直角三角形斜边上的中线；三角形中位线定理．专题：证明题．分析：（1）根据AAS证△AFE≌△DBE；（2）利用①中全等三角形的对应边相等得到AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论；（3）由直角三角形ABC与菱形有相同的高，根据等积变形求出这个高，代入菱形面积公式可求出结论．解答：（1）证明：①∵AF∥BC，∴∠AFE=∠DBE，∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD，在△AFE和△DBE中，，∴△AFE≌△DBE（AAS）；（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．∵DB=DC，∴AF=CD．∵AF∥BC，∴四边形ADCF是平行四边形，∵，∠BAC=90°，D是BC的中点，E是AD的中点，∴AD=DC=BC，∴四边形ADCF是菱形；（3）解：设菱形DC边上的高为h，∴RT△ABC斜边BC边上的高也为h，∵BC==，∴DC=BC=，∴h==，菱形ADCF的面积为：DC•h=×=10．点评：本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用，菱形的面积计算，主要考查学生的推理能力．2．（珠海）已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．（1）如图1，连接BD，AF，则BD=AF（填“＞”、“＜”或“=”）；（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．考点：全等三角形的判定与性质；等腰三角形的性质；平移的性质．专题：证明题．分析：（1）根据等腰三角形的性质，可得∠ABC与∠ACB的关系，根据平移的性质，可得AC与DF的关系，根据全等三角形的判定与性质，可得答案；（2）根据相似三角形的判定与性质，可得GM与HN的关系，BM与FN的关系，根据全等三角形的判定与性质，可得答案．解答：（1）解：由AB=AC，得∠ABC=ACB．由△ABC沿BC方向平移得到△DEF，得DF=AC，∠DFE=∠ACB．在△ABF和△DFB中，，△ABF≌△DFB（SAS），BD=AF，故答案为：BD=AF；（2）证明：如图：MN∥BF，△AMG∽△ABC，△DHN∽△DEF，=，=，∴MG=HN，MB=NF．在△BMH和△FNG中，，△BMH≌△FNG（SAS），∴BH=FG．点评：本题考查了全等三角形的判定与性质，利用了平移的性质，相似三角形的判定与性质，全等三角形的判定与性质．3．（镇江）如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．（1）求证：△BAE≌△BCF；（2）若∠ABC=50°，则当∠EBA=20°时，四边形BFDE是正方形．考点：菱形的性质；全等三角形的判定与性质；正方形的判定．专题：证明题．分析：（1）由题意易证∠BAE=∠BCF，又因为BA=BC，AE=CF，于是可证△BAE≌△BCF；（2）由已知可得四边形BFDE对角线互相垂直平分，只要∠EBF=90°即得四边形BFDE 是正方形，由△BAE≌△BCF可知∠EBA=∠FBC，又由∠ABC=50°，可得∠EBA+∠FBC=40°，于是∠EBA=×40°=20°．解答：（1）证明：∵菱形ABCD的对角线AC，BD相交于点O，∴AB=BC，∠BAC=∠BCA，∴∠BAE=∠BCF，在△BAE与△BCF中，∴△BAE≌△BCF（SAS）；（2）∵四边形BFDE对角线互相垂直平分，∴只要∠EBF=90°即得四边形BFDE是正方形，∵△BAE≌△BCF，∴∠EBA=∠FBC，又∵∠ABC=50°，∴∠EBA+∠FBC=40°，∴∠EBA=×40°=20°．故答案为：20．点评：本题考查了菱形的性质，全等三角形的判定与性质以及正方形的判定．本题关键是根据SAS证明△BAE≌△BCF．4．（漳州）如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求的值．考点：翻折变换（折叠问题）；勾股定理；菱形的判定与性质；矩形的性质．专题：证明题．分析：（1）根据折叠的性质，易知DG=FG，ED=EF，∠1=∠2，由FG∥CD，可得∠1=∠3，易证FG=FE，故由四边相等证明四边形DEFG为菱形；（2）在Rt△EFC中，用勾股定理列方程即可CD、CE，从而求出的值．解答：（1）证明：由折叠的性质可知：DG=FG，ED=EF，∠1=∠2，∵FG∥CD，∴∠2=∠3，∴FG=FE，∴DG=GF=EF=DE，∴四边形DEFG为菱形；（2）解：设DE=x，根据折叠的性质，EF=DE=x，EC=8﹣x，在Rt△EFC中，FC2+EC2=EF2，即42+（8﹣x）2=x2，解得：x=5，CE=8﹣x=3，∴=．点评：本题主要考查了折叠的性质、菱形的判定以及勾股定理，熟知折叠的性质和菱形的判定方法是解答此题的关键．5．（玉林）如图，在⊙O中，AB是直径，点D是⊙O上一点且∠BOD=60°，过点D作⊙O 的切线CD交AB的延长线于点C，E为的中点，连接DE，EB．（1）求证：四边形BCDE是平行四边形；（2）已知图中阴影部分面积为6π，求⊙O的半径r．考点：切线的性质；平行四边形的判定；扇形面积的计算．专题：证明题．分析：（1）由∠BOD=60°E为的中点，得到，于是得到DE∥BC，根据CD 是⊙O的切线，得到OD⊥CD，于是得到BE∥CD，即可证得四边形BCDE是平行四边形；（2）连接OE，由（1）知，，得到∠BOE=120°，根据扇形的面积公式列方程即可得到结论．解答：解：（1）∵∠BOD=60°，∴∠AOD=120°，∴=，∵E为的中点，∴，∴DE∥AB，OD⊥BE，即DE∥BC，∵CD是⊙O的切线，∴OD⊥CD，∴BE∥CD，∴四边形BCDE是平行四边形；（2）连接OE，由（1）知，，∴∠BOE=120°，∵阴影部分面积为6π，∴=6π，∴r=6．点评：本题考查了切线的性质，平行四边形的判定，扇形的面积公式，垂径定理，证明是解题的关键．6．（永州）如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．考点：全等三角形的判定与性质．专题：证明题．分析：（1）根据四边形的内角和等于360°求出∠B+∠ADC=180°，再根据邻补角的和等于180°可得∠CDE+∠ADE=180°，从而求出∠B=∠CDE；（2）根据“边角边”证明即可．解答：（1）证明：在四边形ABCD中，∵∠BAD=∠BCD=90°，∴90°+∠B+90°+∠ADC=360°，∴∠B+∠ADC=180°，又∵∠CDE+∠ADC=180°，∴∠ABC=∠CDE，（2）连接AC，由（1）证得∠ABC=∠CDE，在△ABC和△EDC中，，∴△ABC≌△EDC（SAS）．点评：本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，根据四边形的内角和定理以及邻补角的定义，利用同角的补角相等求出夹角相等是证明三角形全等的关键，也是本题的难点．7．（营口）如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．（1）求证：PC是⊙O的切线；（2）若PD=，AC=8，求图中阴影部分的面积；（3）在（2）的条件下，若点E是的中点，连接CE，求CE的长．考点：切线的判定；扇形面积的计算．专题：证明题．分析：（1）连接OC，证明△PAO≌△PCO，得到∠PCO=∠PAO=90°，证明结论；（2）证明△ADP∽△PDA，得到成比例线段求出BC的长，根据S阴=S⊙O﹣S△ABC 求出答案；（3）连接AE、BE，作BM⊥CE于M，分别求出CM和EM的长，求和得到答案．解答：（1）证明：如图1，连接OC，∵PA切⊙O于点A，∴∠PAO=90°，∵BC∥OP，∴∠AOP=∠OBC，∠COP=∠OCB，∵OC=OB，∴∠OBC=∠OCB，∴∠AOP=∠COP，在△PAO和△PCO中，，∴△PAO≌△PCO，∴∠PCO=∠PAO=90°，∴PC是⊙O的切线；（2）解：由（1）得PA，PC都为圆的切线，∴PA=PC，OP平分∠APC，∠ADO=∠PAO=90°，∴∠PAD+∠DAO=∠DAO+∠AOD，∴∠PAD=∠AOD，∴△ADP∽△ODA，∴，∴AD2=PD•DO，∵AC=8，PD=，∴AD=AC=4，OD=3，AO=5，由题意知OD为△的中位线，∴BC=6，OD=6，AB=10．∴S阴=S⊙O﹣S△ABC=﹣24；（3）解：如图2，连接AE、BE，作BM⊥CE于M，∴∠CMB=∠EMB=∠AEB=90°，∵点E是的中点，∴∠ECB=∠CBM=∠ABE=45°，CM=MB=3，BE=AB•cos45°=5，∴EM==4，则CE=CM+EM=7．点评：本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质，灵活运用切线的性质：圆的切线垂直于过切点的半径和切线的判定是解题的关键．8．（徐州）如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE=4时，四边形BFCE是菱形．考点：平行四边形的判定；菱形的判定．专题：证明题．分析：（1）由AE=DF，∠A=∠D，AB=DC，易证得△AEC≌△DFB，即可得BF=EC，∠ACE=∠DBF，且EC∥BF，即可判定四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，根据菱形的性质即可得到结果．解答：（1）证明：∵AB=DC，∴AC=DF，在△AEC和△DFB中，∴△AEC≌△DFB（SAS），∴BF=EC，∠ACE=∠DBF∴EC∥BF，∴四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，∵AD=10，DC=3，AB=CD=3，∴BC=10﹣3﹣3=4，∵∠EBD=60°，∴BE=BC=4，∴当BE=4 时，四边形BFCE是菱形，故答案为：4．点评：此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识．此题综合性较强，难度适中，注意数形结合思想的应用，注意掌握辅助线的作法．9．（宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．考点：平行四边形的判定与性质；等腰三角形的性质．专题：证明题．分析：（1）根据同旁内角互补两直线平行求出BC∥AD，再根据两直线平行，内错角相等可得∠CBE=∠DFE，然后利用“角角边”证明△BEC和△FCD全等，根据全等三角形对应边相等可得BE=EF，然后利用对角线互相平分的四边形是平行四边形证明即可；（2）分①BC=BD时，利用勾股定理列式求出AB，然后利用平行四边形的面积公式列式计算即可得解；②BC=CD时，过点C作CG⊥AF于G，判断出四边形AGCB 是矩形，再根据矩形的对边相等可得AG=BC=3，然后求出DG=2，利用勾股定理列式求出CG，然后利用平行四边形的面积列式计算即可得解；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾．解答：（1）证明：∵∠A=∠ABC=90°，∴BC∥AD，∴∠CBE=∠DFE，在△BEC与△FED中，，∴△BEC≌△FED，∴BE=FE，又∵E是边CD的中点，∴CE=DE，∴四边形BDFC是平行四边形；（2）①BC=BD=3时，由勾股定理得，AB===2，所以，四边形BDFC的面积=3×2=6；②BC=CD=3时，过点C作CG⊥AF于G，则四边形AGCB是矩形，所以，AG=BC=3，所以，DG=AG﹣AD=3﹣1=2，由勾股定理得，CG===，所以，四边形BDFC的面积=3×=3；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾，此时不成立；综上所述，四边形BDFC的面积是6或3．点评：本题考查了平行四边形的判定与性质，等腰三角形的性质，全等三角形的判定与性质，（1）确定出全等三角形是解题的关键，（2）难点在于分情况讨论．10．（湘西州）如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．（1）求证：△ADE≌△CBF；（2）求证：四边形BFDE为矩形．考点：矩形的判定；全等三角形的判定与性质；平行四边形的性质．专题：证明题．分析：（1）由DE与AB垂直，BF与CD垂直，得到一对直角相等，再由ABCD为平行四边形得到AD=BC，对角相等，利用AAS即可的值；（2）由平行四边形的对边平行得到DC与AB平行，得到∠CDE为直角，利用三个角为直角的四边形为矩形即可的值．解答：证明：（1）∵DE⊥AB，BF⊥CD，∴∠AED=∠CFB=90°，∵四边形ABCD为平行四边形，∴AD=BC，∠A=∠C，在△ADE和△CBF中，，∴△ADE≌△CBF（AAS）；（2）∵四边形ABCD为平行四边形，∴CD∥AB，∴∠CDE+∠DEB=180°，∵∠DEB=90°，∴∠CDE=90°，∴∠CDE=∠DEB=∠BFD=90°，则四边形BFDE为矩形．点评：此题考查了矩形的判定，全等三角形的判定与性质，以及平行四边形的性质，熟练掌握矩形的判定方法是解本题的关键．11．（咸宁）已知关于x的一元二次方程mx2﹣（m+2）x+2=0．（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．考点：根的判别式；解一元二次方程-公式法．专题：证明题．分析：（1）求出方程根的判别式，利用配方法进行变形，根据平方的非负性证明即可；（2）利用一元二次方程求根公式求出方程的两个根，根据题意求出m的值．解答：（1）证明：△=（m+2）2﹣8m=m2﹣4m+4=（m﹣2）2，∵不论m为何值时，（m﹣2）2≥0，∴△≥0，∴方程总有实数根；（2）解：解方程得，x=，x1=，x2=1，∵方程有两个不相等的正整数根，∴m=1或2，m=2不合题意，∴m=1．点评：本题考查的是一元二次方程根的判别式和求根公式的应用，掌握一元二次方程根的情况与判别式△的关系：△＞0⇔方程有两个不相等的实数根；△=0⇔方程有两个相等的实数根；△＜0⇔方程没有实数根是解题的关键．12．（咸宁）如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆恰好与BC相切于点D，分别交AC、AB于点E、F．（1）若∠B=30°，求证：以A、O、D、E为顶点的四边形是菱形．（2）若AC=6，AB=10，连结AD，求⊙O的半径和AD的长．考点：切线的性质；菱形的判定与性质；相似三角形的判定与性质．专题：证明题．分析：（1）连接OD、OE、ED．先证明△AOE是等边三角形，得到AE=AO=0D，则四边形AODE是平行四边形，然后由OA=OD证明四边形AODE是菱形；（2）连接OD、DF．先由△OBD∽△ABC，求出⊙O的半径，然后证明△ADC∽△AFD，得出AD2=AC•AF，进而求出AD．解答：（1）证明：如图1，连接OD、OE、ED．∵BC与⊙O相切于一点D，∴OD⊥BC，∴∠ODB=90°=∠C，∴OD∥AC，∵∠B=30°，∴∠A=60°，∵OA=OE，∴△AOE是等边三角形，∴AE=AO=0D，∴四边形AODE是平行四边形，∵OA=OD，∴四边形AODE是菱形．（2）解：设⊙O的半径为r．∵OD∥AC，∴△OBD∽△ABC．∴，即10r=6（10﹣r）．解得r=，∴⊙O的半径为．如图2，连接OD、DF．∵OD∥AC，∴∠DAC=∠ADO，∵OA=OD，∴∠ADO=∠DAO，∴∠DAC=∠DAO，∵AF是⊙O的直径，∴∠ADF=90°=∠C，∴△ADC∽△AFD，∴，∴AD2=AC•AF，∵AC=6，AF=，∴AD2=×6=45，∴AD==3．点评：本题考查了切线的性质、圆周角定理、等边三角形的判定与性质、菱形的判定和性质以及相似三角形的判定和性质，是一个综合题，难度中等．熟练掌握相关图形的性质及判定是解本题的关键．13．（梧州）如图，在正方形ABCD中，点P在AD上，且不与A、D重合，BP的垂直平分线分别交CD、AB于E、F两点，垂足为Q，过E作EH⊥AB于H．（1）求证：HF=AP；（2）若正方形ABCD的边长为12，AP=4，求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．专题：证明题．分析：（1）先根据EQ⊥BO，EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH，故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE，故可得出结论；（2）由勾股定理求出BP的长，根据EF是BP的垂直平分线可知BQ=BP，再根据锐角三角函数的定义得出QF=BQ的长，由（1）知，△APB≌△HFE，故EF=BP=4，再根据EQ=EF﹣QF即可得出结论．解答：（1）证明：∵EQ⊥BO，EH⊥AB，∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH，∴△EMQ∽△BMH，∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中，，∴△APB≌△HFE，∴HF=AP；（2）解：由勾股定理得，BP===4．∵EF是BP的垂直平分线，∴BQ=BP=2，∴QF=BQ•tan∠FBQ=BQ•tan∠ABP=2×=．由（1）知，△APB≌△HFE，∴EF=BP=4，∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质，熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．14．（威海）如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE=CE；（2）若BD=2，BE=3，求AC的长．考点：相似三角形的判定与性质；等腰三角形的性质；圆周角定理．专题：证明题．分析：（1）连结AE，如图，根据圆周角定理，由AC为⊙O的直径得到∠AEC=90°，然后利用等腰三角形的性质即可得到BE=CE；（2）连结DE，如图，证明△BED∽△BAC，然后利用相似比可计算出AB的长，从而得到AC的长．解答：（1）证明：连结AE，如图，∵AC为⊙O的直径，∴∠AEC=90°，∴AE⊥BC，而AB=AC，∴BE=CE；（2）连结DE，如图，∵BE=CE=3，∴BC=6，∵∠BED=∠BAC，而∠DBE=∠CBA，∴△BED∽△BAC，∴=，即=，∴BA=9，∴AC=BA=9．点评：本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．也考查了角平分线的性质和圆周角定理．15．（铜仁市）已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．考点：全等三角形的判定与性质；等边三角形的判定与性质．专题：证明题．分析：作DG∥BC交AC于G，先证明△DFG≌△EFC，得出GD=CE，再证明△ADG是等边三角形，得出AD=GD，即可得出结论．解答：证明：作DG∥BC交AC于G，如图所示：则∠DGF=∠ECF，在△DFG和△EFC中，，∴△DFG≌△EFC（AAS），∴GD=CE，。

P CG FAD E初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ． 经典1、已知：△ABC 中，H 为垂心（各边高线的交点），O （1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 设MN 是圆O 的弦，过MN 的中点A 任作两弦于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二） 经典题（三） 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．AQ P NM · O B D AF D AFGCEBO D求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二） 4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5． 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA DPC ．（初二） 经典难题（五）1、 设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ， 求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数． 经典题（一）1.如下图做GH ⊥AB,连接EO 。

中考数学几何证明题1.（1）如图1所示，在四边形ABCD 中，AC =BD ，AC 与BD 相交于点O ，E F 、分别是AD BC 、的中点，联结EF ，分别交AC 、BD 于点M N 、，试判断OMN △的形状，并加以证明；（2）如图2，在四边形ABCD 中，若AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，分别与BA CD 、的延长线交于点M N 、，请在图2中画图并观察，图中是否有相等的角，若有，请直接写出结论： ；（3）如图3，在ABC △中，AC AB >，点D 在AC 上，AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，与BA 的延长线交于点M ，若45FEC ∠=︒，判断点M 与以AD 为直径的圆的位置关系，并简要说明理由．图 1 图2 图3FBACD EFM NO2．（1）如图1，已知矩形ABCD 中，点E 是BC 上的一动点，过点E 作EF ⊥BD 于点F ，EG ⊥AC 于点G ，CH ⊥BD 于点H ，试证明CH=EF+EG;图1D(2) 若点E 在ＢＣ的延长线上，如图2，过点E 作EF ⊥BD 于点F ，EG ⊥AC 的延长线于点G ，CH ⊥BD 于点H ， 则EF 、EG 、ＣH 三者之间具有怎样的数量关系，直接写出你的猜想；(3) 如图3，BD 是正方形ABCD 的对角线,L 在BD 上，且BL=BC, 连结CL ，点E 是CL 上任一点, EF ⊥BD 于点F ，EG ⊥BC 于点G ，猜想EF 、EG 、BD 之间具有怎样的数量关系，直接写出你的猜想； (4) 观察图1、图2、图3的特性，请你根据这一特性构造一个图形， 使它仍然具有EF 、EG 、ＣH 这样的线段，并满足（1）或（2）的结论，写出相关题设的条件和结论.图3CDBGAFDECH3. 如图，△ABC 是等边三角形，F 是AC 的中点，D 在线段BC 上，连接DF ，以DF 为边在DF 的右侧作等边△DFE ，ED 的延长线交AB 于H ，连接EC ，则以下结论：①∠AHE +∠AFD =180°；②AF =21BC ；③当D 在线段BC 上（不与B ，C 重合）运动，其他条件不变时BD BH 是定值；④当D 在线段BC 上（不与B ，C 重合）运动，其他条件不变时DCECBC 21是定值；（1）其中正确的是-------------------； （2）对于（1）中的结论加以说明；4. 在ABC △中，AC=BC ，90ACB ∠=︒，点D 为AC 的中点．（1）如图1，E 为线段DC 上任意一点，将线段DE 绕点D 逆时针旋转90°得到线段DF ，连结CF ，过点F 作FH FC ⊥，交直线AB 于点H ．判断FH 与FC 的数量关系并加以证明． （2）如图2，若E 为线段DC 的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．5. 如图12，在△ABC 中，D 为BC 的中点，点E 、F 分别在边AC 、AB 上，并且∠ABE =∠ACF ，BE 、CF 交于点O ．过点O 作OP ⊥AC ，OQ ⊥AB ，P 、Q 为垂足．求证：DP=DQ ．H F图2图1HFEB C DAE D BC A6. 如图。

2022中考考点必杀500题专练12（几何证明大题）（30道）三角形1．（2022·上海徐汇·二模）如图，四边形ABCE 中，∠BAC ＝90°，AB ＝AC ，BF ∠CE 于点F ，点D 为BF 上一点，且∠BAD ＝∠CAE ．(1)求证：AD ＝AE ；(2)设BF 交AC 于点G ，若22BC BD BG =⋅，判断四边形ADFE 的形状，并证明．2．（2022·湖北宜昌·一模）如图，在平行四边形ABCD 中，B AFE ∠=∠，EA 是∠BEF 的角平分线，求证：(1)ABE AFE ∆≅∆；(2)FAD CDE ∠=∠．3．（2022·四川广元·一模）如图，在ABC 中，45,75ABC ACB ∠=︒∠=︒，D 是BC 上一点，且60ADC ∠=︒，CF AD ⊥于点F ，AE BC ⊥于点E ，AE 交CF 于点G ．(1)求证：AFG CFD ≌△△；(2)若1,FD AF ==EG 的长．4．（2022·上海嘉定·二模）如图，已知平行四边形ABCD 中，E 是边CD 的中点，连接AE 并延长交BC 的延长线于点F ，连接AC ．(1)求证：AD ＝CF ；(2)若AB ∠AF ，且AB ＝8，BC ＝5，求sin∠ACE 的值．5．（2022·江苏盐城·一模）在四边形ABCD 中，180B D ∠+∠=︒，对角线AC 平分∠BAD ．(1)推理证明：如图1，若120DAB ∠=︒，且90D ∠=︒，求证：AD AB AC +=；(2)问题探究：如图2，若120DAB ∠=︒，试探究AD 、AB 、AC 之间的数量关系；(3)迁移应用：如图3，若90DAB ∠=︒，AD =2，AB =4，求线段AC 的长度．6．（2022·山东泰安·一模）在ABC ∆中，90BAC ∠=︒，AB AC =，AD BC ⊥于点D ．(1)如图1，点E ，F 分别在AB ，AC 上，且90EDF ∠=︒，求证：AE CF =；(2)如图2，点M 在AD 的延长线上，点N 在AC 上，且90BMN ∠=︒，求证：AC AN +=．7．（2022·山东·枣庄市台儿庄区教育局教研室一模）已知AOB 和MON ＜OM ＜OA ），∠AOB ＝∠MON ＝90°．(1)如图1，连接AM ，BN ，求证：AM ＝BN ；(2)将MON 绕点O 顺时针旋转．如图2，当点M 恰好在AB 边上时，求证：AM 2+BM 2＝2OM 2； 8．（2022·湖南·株洲县教学研究室一模）如图，点E ，F 分别在菱形ABCD 的边BC ，CD 上，且BE DF =，连接EF ，交对角线于点G ．求证：(1)BAE DAF ∠=∠(2)AC EF ⊥9．（2022·广东·塘厦初中一模）如图，AD 是ABC 的角平分线，DE 、DF 分别是ABD △和ACD △的高．(1)求证：AD 垂直平分EF ；(2)若10AB AC +=，3DE =，求ABC 的面积ABC S ．10．（2022·湖南·师大附中梅溪湖中学一模）如图，在△ABC 中，AB =AC ，AD ∠BC 于点D ，BE ∠AC 于点E ，AD 、BE 相交于点H ，AE =BE ．(1)求证：△AEH ∠△BEC ．(2)若AH =4，求BD 的长．四边形11．（2022·上海市青浦区教育局二模）如图，已知在梯形ABCD 中，//AD BC ，对角线AC 、BD 交于E ，BD 平分ABC ∠，点G 在底边BC 上，连结DG 交对角线AC 于F ，DGB DAB ∠=∠．(1)求证：四边形ABGD 是菱形；(2)连结EG ，求证：BG EG BC EF ⋅=⋅．12．（2022·广西南宁·一模）如图，在ABCD 中，连接对角线BD ，过点,A C 分别作AE BD CF BD ⊥⊥，，垂足为,E F ．(1)求证：AE CF =；(2)如图2，延长AE 至点G ，使得AE GE =，连接CG ，求证：四边形EGCF 是矩形．13．（2022·山东聊城·一模）如图，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，∠BOC ∠∠CEB ．(1)求证：四边形OBEC 是矩形；(2)若∠ABC =120°，AB =6，求矩形OBEC 的周长．14．（2022·江苏扬州·一模）如图，在ABC 中，90BAC ∠=︒，D 是BC 的中点，E 是AD 的中点，过点A 作AF //BC 交BE 的延长线于点F ．(1)求证：AEF DEB ≌；(2)若3,4AC AB ==，求四边形ADCF 的面积．15．（2022·福建三明·二模）已知：如图，在ABCD 中，E 为BC 的中点，DF ∠AE 于点F ，CG ∠DF 于点G ．求证：(1)∠DAE = ∠BCG ；(2)G 为DF 的中点．16．（2021·四川德阳·二模）如图，在四边形ABCD 中，AD ∠BC ，对角线BD 的垂直平分线与边AD 、BC 分别相交于M 、N ．(1)判断四边形BNDM 的形状，并证明你的结论；(2)若BD＝24，MN＝10，求四边形BNDM的周长．=．17．（2022·新疆乌鲁木齐·一模）如图，四边形ABCD是菱形，点E，F在对角线AC上，且AE CF(1)求证：ADE CBF△△；≌(2)求证：四边形DEBF是菱形．18．（2022·四川绵阳·一模）如图，在四边形ABCD中，AB∠CD，AB≠CD，∠ABC＝90°，点E、F分别在线段BC、AD上，且EF∠CD，AB＝AF，CD＝DF．(1)求证：CF∠FB；(2)求证：以AD为直径的圆与BC相切；(3)若EF＝2，∠DFE＝120°，求∠ADE的面积．19．（2022·宁夏·银川市第十中学二模）如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF．(1)求证：∠ABE∠∠CDF；(2)当AC∠EF时，四边形AECF是菱形吗？请说明理由．20．（2022·北京市燕山教研中心一模）如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作⊥交BC的延长线于点E．DE BD(1)求证：四边形ACED 是平行四边形；(2)若4BD =，3AC =，求sin CDE ∠的值．圆21．（2022·浙江绍兴·一模）如图，AC 为O 的直径，点B 是AC 上方半圆上的一点，作BD 平分ABC ∠交O 于点D ，过点D 作DE //AC 交BC 的延长线于点E ．(1)求证：DE 是O 的切线；(2)若2,3AB BE ==，求BD 的长．22．（2022·陕西·一模）如图，AB 是∠O 的直径，AC 是∠O 的切线，且CA =BA ．连接BC ，OC ．过点A 作AD ∠OC 于点D ，延长AD 交BC 于点E ，交∠O 于点F ，连接BF ．(1)求证：∠F AB =∠ACD ；(2)若BF =4，求DE 的长．23．（2022·陕西西安·三模）如图，AB 是∠O 的直径，点C 为∠O 上一点，∠ABC 的外角平分线BD 交∠O 于点D ，DE 与∠O 相切，交CB 的延长线于点E ，连接AD ．(1)求证：AC ∠DE ；(2)若BD ＝BE ＝2，求CB 的长．24．（2022·新疆乌鲁木齐·一模）如图，已知AC 是O 的直径，点P 是O 外一点，PC 与O 交于点B ，12PAB AOB ∠=∠．(1)求证：P A 是O 的切线；(2)若1tan 3OPC ∠=，求PB OP的值． 25．（2022·山东济南·二模）如图，BE 是∠O 的直径，点A 和点D 是∠O 上的两点，过点A 作∠O 的切线交BE 延长线于点C ．(1)若29ADE ∠=︒，求∠C 的度数；(2)若AC 1CE =，求∠O 半径的长．26．（2022·山东聊城·一模）如图，AB 为∠O 的直径，直线l 与∠O 相切于点C ，AD ∠l ，垂足为D ，AD 交∠O 于点E ，连接CE ．(1)求证：∠CAD＝∠CAB；(2)若EC＝4，sin∠CAD13＝，求∠O的半径．27．（2022·河南商丘·二模）如图，以AB为直径的O中，AC为弦，点P为O上一点，过点A的切线交CP 延长线于点D，PC交AB于点Q，连接AP，PAB PQA∠=∠(1)求证：PA PD=；(2)若3PA=，5AC=，求OA的长．28．（2022·山东·济宁学院附属中学二模）如图，AB是∠O的直径，C是弧AB的中点，∠O的切线BD交AC 的延长线于点D，E是OB的中点，CE的延长线交切线BD于点F，AF交∠O于点H，连接BH．(1)求证：AC=CD(2)若OB=2，求BH的长29．（2022·江苏苏州·模拟预测）如图，AB是∠O的直径，点D在∠O上，且DM是∠O的切线，过点B作DM的平行线交∠O于点C，交AD于点E，连接AC并延长与DM相交于点F．(1)求证：CD＝BD；(2)若CD＝6，AD＝8，求cos∠ABC的值30．（2022·湖北·荆州市教育科学研究院一模）如图，∠O是∠ABC的外接圆，AD是∠O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD．(1)求证：CF是∠O的切线；(2)若cos B＝35，AD＝2，求AC和FD的长．。

几何证明题专题1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H在边BF上，且∠HDF=∠E，连接CH，求证：∠BCH=45°﹣∠EBC．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．7、已知：如图， ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD 为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．30、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．参考答案1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．证明：（1）已知等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，∴AB=DC，∠BAE=∠CDE，AE=DE，∴△BAE≌△CDE，∴BE=CE；（2）延长CD和BE的延长线交于H，∵BF⊥CD，∠HEC=90°，∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH，又∠BEC=∠CEH=90°，BE=CE（已证），∴△BEG≌△CEH，∴EG=EH，BG=CH=DH+CD，∵△BAE≌△CDE（已证），∴∠AEB=∠GED，∠HED=∠AEB，∴∠GED=∠HED，又EG=EH（已证），ED=ED，∴△GED≌△HED，∴DG=DH，∴BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：∵ED平分∠AEF，∠A=∠DFE=90°，∴AD=DF，∵DF=DC﹣FC，∵△EBH≌△GFC，∴FC=BH=1，∴AD=4﹣1=3．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．（2）过E点作EM⊥DB于点M，四边形FDME是矩形，FE=DM，∠BME=∠BCE=90°，∠BEC=∠MBE=60°，△BME≌△ECB，BM=CE，继而可证明BD=DM+BM=EF+CE．（1）解：∵AD=CD，∴∠DAC=∠DCA，∵DC∥AB，∴∠DCA=∠CAB，∴，∵DC∥AB，AD=BC，∴∠DAB=∠CBA=60°，∴∠ACB=180°﹣（∠CAB+∠CBA）=90°，∴∠BCE=180°﹣∠ACB=90°，∵BE⊥AB，∴∠ABE=90°，∴∠CBE=∠ABE﹣∠ABC=30°，在Rt△BCE中，BE=2CE=2，，∴…（5分）（2）证明：过E点作EM⊥DB于点M，∴四边形FDME是矩形，∴FE=DM，∵∠BME=∠BCE=90°，∠BEC=∠MBE=60°，∴△BME≌△ECB，∴BM=CE，∴BD=DM+BM=EF+CE…（10分）4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E作EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．解答：（1）证明：延长EF交AD于G（如图），在平行四边形ABCD中，AD∥BC，AD=BC，∵EF∥CA，EG∥CA，∴四边形ACEG是平行四边形，∴AG=CE，又∵，AD=BC，∴，∵AD∥BC，∴∠ADC=∠ECF，在△CEF和△DGF中，∵∠CFE=∠DFG，∠ADC=∠ECF，CE=DG，∴△CEF≌△DGF（AAS），∴CF=DF，∵四边形ABCD是平行四边形，∴OB=OD，∴OF∥BE．（2）解：如果梯形OBEF是等腰梯形，那么四边形ABCD是矩形．证明：∵OF∥CE，EF∥CO，∴四边形OCEF是平行四边形，∴EF=OC，又∵梯形OBEF是等腰梯形，∴BO=EF，∴OB=OC，∵四边形ABCD是平行四边形，∴AC=2OC，BD=2BO．∴AC=BD，∴平行四边形ABCD是矩形．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H 在边BF 上，且∠HDF=∠E ，连接CH ，求证：∠BCH=45°﹣∠EBC ．（1）解：连接BD ，由∠ABC=90°，AD ∥BC 得∠GAD=90°，又∵BF ⊥CD ，∴∠DFE=90°又∵DG=DE ，∠GDA=∠EDF ，∴△GAD ≌△EFD ，∴DA=DF ，又∵BD=BD ，∴Rt △BAD ≌Rt △BFD （HL ），∴BF=BA=，∠ADB=∠BDF 又∵CF=6，∴BC=，又∵AD ∥BC ，∴∠ADB=∠CBD ，∴∠BDF=∠CBD ，∴CD=CB=8．（2）证明：∵AD ∥BC ，∴∠E=∠CBF ，∵∠HDF=∠E ，∴∠HDF=∠CBF ，由（1）得，∠ADB=∠CBD ，∴∠HDB=∠HBD ，∴HD=HB ，由（1）得CD=CB ，CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ，∴∠DCH=∠BCH ，∴∠BCH=∠BCD==．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．解：（1）连AC，过C作CM⊥AD于M，如图，在Rt△ABC中，AB=6，sin∠ACB==，∴AC=10，∴BC=8，在Rt△CDM中，∠D=45°，∴DM=CM=AB=6，∴AD=6+8=14，∴梯形ABCD的面积=•（8+14）•6=66（cm2）；（2）证明：过G作GN⊥AD，如图，∵∠D=45°，∴△DNG为等腰直角三角形，∴DN=GN，又∵AD∥BC，∴∠BFH=∠FHN，而∠EFH=∠FHG，∴∠BFE=∠GHN，∵EF=GH，∴Rt△BEF≌Rt△NGH，∴BE=GN，BF=HN，∴DA=AN+DN=AN+DG=BF+BE．7、已知：如图，▱ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．（1）证明：如图．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵DF=CD，∴AB∥DF．∵DF=CD，∴AB=DF．∴四边形ABDF是平行四边形，∴AE=DE．（2）解：∵四边形ABCD是平行四边形，且AB=BC，∴四边形ABCD是菱形．∴AC⊥BD．∴∠COD=90°．∵四边形ABDF是平行四边形，∴AF∥BD．∴∠CAF=∠COD=90°．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．（1）证明：在△DAE和△DCE中，∠ADE=∠CDE（正方形的对角线平分对角），ED=DE（公共边），AE=CE（正方形的四条边长相等），∴△DAE≌△DCE（SAS），∴∠DAE=∠DCE（全等三角形的对应角相等）；（2）解：如图，由（1）知，△DAE≌△DCE，∴AE=EC，∴∠EAC=∠ECA（等边对等角）；又∵CG=CE（已知），∴∠G=∠CEG（等边对等角）；而∠CEG=2∠EAC（外角定理），∠ECB=2∠CEG（外角定理），∴4∠EAC﹣∠ECA=∠ACB=45°，∴∠G=∠CEG=30°；过点C作CH⊥AG于点H，∴∠FCH=30°，∴在直角△ECH中，EH=CH，EG=2CH，在直角△FCH中，CH=CF，∴EG=2×CF=3CF．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．（1）证明：连接PC．∵ABCD是正方形，∴∠ABE=∠ADF=90°，AB=AD．∵BE=DF，∴△ABE≌△ADF．（SAS）∴∠BAE=∠DAF，AE=AF．∴∠EAF=∠BAD=90°．∵P是EF的中点，∴PA=EF，PC=EF，∴PA=PC．又AD=CD，PD公共，∴△PAD≌△PCD，（SSS）∴∠ADP=∠CDP，即DP平分∠ADC；（2）作PH⊥CF于H点．∵P是EF的中点，∴PH=EC．设EC=x．由（1）知△EAF是等腰直角三角形，∴∠AEF=45°，∴∠FEC=180°﹣45°﹣75°=60°，∴EF=2x，FC=x，BE=2﹣x．在Rt△ABE中，22+（2﹣x）2=（x）2解得x1=﹣2﹣2（舍去），x2=﹣2+2．∴PH=﹣1+，FD=（﹣2+2）﹣2=﹣2+4．=（﹣2+4）×=3﹣5．∴S△DPF10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．（1）证明：∵AD∥BC，∴∠DAE=∠F，∠ADE=∠FCE．∵E为CD的中点，∴ED=EC．∴△ADE≌△FCE．∴EF=EA．（5分）（2）解：连接GA，∵AD∥BC，∠ABC=90°，∴∠DAB=90°．∵DG⊥BC，∴四边形ABGD是矩形．∴BG=AD，GA=BD．∵BD=BC，∴GA=BC．由（1）得△ADE≌△FCE，∴AD=FC．∴GF=GC+FC=GC+AD=GC+BG=BC=GA．∵由（1）得EF=EA，∴EG⊥AF．（5分）11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD为边在直角梯形ABCD外作等边三角形ADF，点E 是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，∴AF=AD，∠FAD=60°（1分）∵∠DAB=90°，∠EAD=15°，AD=AB（2分）∴∠FAE=∠BAE=75°，AB=AF，（3分）∵AE为公共边∴△FAE≌△BAE（4分）∴EF=EB（5分）（2）解：如图，连接EC．（6分）∵在等边三角形△ADF中，∴FD=FA，∵∠EAD=∠EDA=15°，∴ED=EA，∴EF是AD的垂直平分线，则∠EFA=∠EFD=30°．（7分）由（1）△FAE≌△BAE知∠EBA=∠EFA=30°．∵∠FAE=∠BAE=75°，∴∠BEA=∠BAE=∠FEA=75°，∴BE=BA=6．∵∠FEA+∠BEA+∠GEB=180°，∴∠GEB=30°，∵∠ABC=60°，∴∠GBE=30°∴GE=GB．（8分）∵点G是BC的中点，∴EG=CG∵∠CGE=∠GEB+∠GBE=60°，∴△CEG为等边三角形，∴∠CEG=60°，∴∠CEB=∠CEG+∠GEB=90°（9分）∴在Rt△CEB中，BC=2CE，BC2=CE2+BE2∴CE=，∴BC=（10分）；解法二：过C作CQ⊥AB于Q，∵CQ=AB=AD=6，∵∠ABC=60°，∴BC=6÷=4．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．（1）证明：∵AB=DC，∴梯形ABCD为等腰梯形．∵∠C=60°，∴∠BAD=∠ADC=120°，又∵AB=AD，∴∠ABD=∠ADB=30°．∴∠DBC=∠ADB=30°．∴∠BDC=90°．（1分）由已知AE⊥BD，∴AE∥DC．（2分）又∵AE为等腰三角形ABD的高，∴E是BD的中点，∵F是DC的中点，∴EF∥BC．∴EF∥AD．∴四边形AEFD是平行四边形．（3分）∴AE=DF（4分）∵F是DC的中点，DG是梯形ABCD的高，∴GF=DF，（5分）∴AE=GF．（6分）（2）解：在Rt△AED中，∠ADB=30°，∵AE=1，∴AD=2．在Rt△DGC中∠C=60°，并且DC=AD=2，∴DG=．（8分）由（1）知：在平行四边形AEFD中EF=AD=2，又∵DG⊥BC，∴DG⊥EF，∴四边形DEGF的面积=EF•DG=．（10分）13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．解答：（1）证明：∵∠ABC=90°，DE⊥AC于点F，∴∠ABC=∠AFE．∵AC=AE，∠EAF=∠CAB，∴△ABC≌△AFE，∴AB=AF．∴AE﹣AB=AC﹣AF，即FC=BE；（2）解：∵AD=DC=2，DF⊥AC，∴AF=AC=AE．∴AG=CG，∴∠E=30°．∵∠EAD=90°，∴∠ADE=60°，∴∠FAD=∠E=30°，∴FC=，∵AD∥BC，∴∠ACG=∠FAD=30°，∴CG=2，∴AG=2．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．（1）证明：∵AD∥BC，∴∠BAD+∠ABC=180°，∵∠ABC=90°，∴∠BAD=∠ABC=90°，∵DE⊥EC，∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°，∴∠BEC=∠ADE，∵∠DAE=∠EBC，AE=BC，∴△EAD≌△EBC，∴AD=BE．（2）答：△ABF是等腰直角三角形．理由是：延长AF交BC的延长线于M，∵AD∥BM，∴∠DAF=∠M，∵∠AFD=∠CFM，DF=FC，∴△ADF≌△MFC，∴AD=CM，∵AD=BE，∴BE=CM，∵AE=BC，∴AB=BM，∴△ABM是等腰直角三角形，∵△ADF≌△MFC，∴AF=FM，∴∠ABC=90°，∴BF⊥AM，BF=AM=AF，∴△AFB是等腰直角三角形．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．解答：（1）证明：连接AC，∵AB∥CD，∴∠ACD=∠BAC，∵AB=BC，∴∠ACB=∠BAC，∴∠ACD=∠ACB，∵AD⊥DC，AE⊥BC，∴∠D=∠AEC=90°，∵AC=AC，∴，∴△ADC≌△AEC，（AAS）∴AD=AE；（2）解：由（1）知：AD=AE，DC=EC，设AB=x，则BE=x﹣4，AE=8，在Rt△ABE中∠AEB=90°，由勾股定理得：82+（x﹣4）2=x2，解得：x=10，∴AB=10．说明：依据此评分标准，其它方法如：过点C作CF⊥AB用来证明和计算均可得分．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．（1）证明：∵AD∥CB，∴∠ADB=∠CBD，又BD平分∠ABC，∴∠ABD=∠CBD，∴∠ADB=∠ABD，∴AB=AD，∴△ABD是等腰三角形，已知E是BD的中点，∴AE⊥BD．（2）解：延长AE交BC于G，∵BD平分∠ABC，∴∠ABE=∠GBE，又∵AE⊥BD（已证），∴∠AEB=∠GEB，BE=BE，∴△ABE≌△GBE，∴AE=GE，BG=AB=AD，又F是AC的中点（已知），所以由三角形中位线定理得：EF=CG=（BC﹣BG）=（BC﹣AD）=×（14﹣4）=5．答：EF的长为5．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．（1）证明：∵AD∥BC，∴∠DAC=∠BCE，而BE⊥AC，∴∠D=∠BEC=90°，AC=BC，∴△BCE≌△CAD．∴CD=BE．（2）解：在Rt△ADC中，根据勾股定理得AC==5，∵△BCE≌△CAD，∴CE=AD=3．∴AE=AC﹣CE=2．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．解：如图，过点D作DF∥AB，分别交AC，BC于点E，F．（1分）∵AB⊥AC，∴∠AED=∠BAC=90度．∵AD∥BC，∴∠DAE=180°﹣∠B﹣∠BAC=45度．在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×=2（2分）在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=．∴CE=AC﹣AE=．（4分）在Rt△DEC中，∠CED=90°，∴DC==．（5分）19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．证明：∵FC=F′C，EC=EC，∠ECF'=∠BCF+∠DCE=∠ECF，∴△FCE≌△F′CE，∴EF′=EF=DF′+ED，∴BF=EF﹣ED；（2）解：∵AB=BC，∠B=80°，∴∠ACB=50°，由（1）得∠FEC=∠DEC=70°，∴∠ECB=70°，而∠B=∠BCD=80°，∴∠DCE=10°，∴∠BCF=30°，∴∠ACF=∠BCA﹣∠BCF=20°．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．解：（1）作EM⊥AB，交AB于点M．∵AE=BE，EM⊥AB，∴AM=BM=×6=3；∵∠AME=∠MAF=∠AFE=90°，∴四边形AMEF是矩形，∴EF=AM=3；在Rt△AFE中，AE==5；（2）延长AF、BC交于点N．∵AD∥EN，∴∠DAF=∠N；∵∠AFD=∠NFC，DF=FC，∴△ADF≌△NCF（AAS），∴AD=CN；∵∠B+∠N=90°，∠BAE+∠EAN=90°，又AE=BE，∠B=∠BAE，∴∠N=∠EAN，AE=EN，∴BE=EN=EC+CN=EC+AD，∴CE=BE﹣AD．．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．解：（1）证明：过D作DE∥AC交BC延长线于E，（1分）∵AD∥BC，∴四边形ACED为平行四边形．（2分）∴CE=AD，DE=AC．∵四边形ABCD为等腰梯形，∴BD=AC=DE．∵AC⊥BD，∴DE⊥BD．∴△DBE为等腰直角三角形．（4分）∵DH⊥BC，∴DH=BE=（CE+BC）=（AD+BC）．（5分）（2）∵AD=CE，∴．（7分）∵△DBE为等腰直角三角形BD=DE=6，∴．∴梯形ABCD的面积为18．（8分）注：此题解题方法并不唯一．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．（1）证明：∵△ABC是等边三角形，DG∥BC，∴∠AGD=∠ABC=60°，∠ADG=∠ACB=60°，且∠BAC=60°，∴△AGD是等边三角形，AG=GD=AD，∠AGD=60°．∵DE=DC，∴GE=GD+DE=AD+DC=AC=AB，∵∠AGD=∠BAD，AG=AD，∴△AGE≌△DAB；（2）解：由（1）知AE=BD，∠ABD=∠AEG．∵EF∥DB，DG∥BC，∴四边形BFED是平行四边形．∴EF=BD，∴EF=AE．∵∠DBC=∠DEF，∴∠ABD+∠DBC=∠AEG+∠DEF，即∠AEF=∠ABC=60°．∴△AFE是等边三角形，∠AFE=60°．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．解：（1）证明：∵EF=EC，∴∠EFC=∠ECF，∵EF∥AB，∴∠B=∠EFC，∴∠B=∠ECF，∴梯形ABCD是等腰梯形；（2）△DCF是等腰直角三角形，证明：∵DE=EC，EF=EC，∴EF=CD，∴△CDF是直角三角形（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形），∵梯形ABCD是等腰梯形，∴CF=（BC﹣AD）=1，∵DC=，∴由勾股定理得：DF=1，∴△DCF是等腰直角三角形；（3）共四种情况：∵DF⊥BC，∴当PF=CF时，△PCD是等腰三角形，即PF=1，∴PB=1；当P与F重合时，△PCD是等腰三角形，∴PB=2；当PC=CD=（P在点C的左侧）时，△PCD是等腰三角形，∴PB=3﹣；当PC=CD=（P在点C的右侧）时，△PCD是等腰三角形，∴PB=3+．故共四种情况：PB=1，PB=2，PB=3﹣，PB=3+．（每个1分）24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．解答：（1）证明：∵在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，∴AB=CD，∵AD=DC，∴BA=AD，∠BAE=∠ADF=120°，∵DE=CF，∴AE=DF，在△BAE和△ADF中，，∴△ABE≌△DAF（SAS）．（2）解：∵由（1）△BAE≌△ADF，∴∠ABE=∠DAF．∴∠BPF=∠ABE+∠BAP=∠BAE．而AD∥BC，∠C=∠ABC=60°，∴∠BPF=120°．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？解答：解：（1）∵AD∥BC，∴∠ADB=∠DBC，∵AB=AD，∴∠ADB=∠ABD，∴∠DBC=∠ABD，∵在梯形ABCD中AB=DC，∴∠ABC=∠DCB=2∠DBC，∵BD⊥DC，∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°（2）过点D作DH⊥BC，垂足为H，∵∠DBC=30°，BC=8，∴DC=4，∵CF=CD∴CF=4，∴BF=12，∵∠F+∠FDC=∠DCB=60°，∠F=∠FDC∴∠F=30°，∵∠DBC=30°，∴∠F=∠DBC，∴DB=DF，∴，在直角三角形DBH中，∴，∴，∴，即△DBF的面积为．26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．（1）证明：连接BE，∵梯形ABCD中，AB=DC，∴AC=BD，可证△ABC≌△DCB，∴∠GCB=∠GBC，又∵∠BGC=∠AGD=60°∴△AGD为等边三角形，（2）解：∵BE为△BCG的中线，∴BE⊥AC，在Rt△ABE中，EF为斜边AB上的中线，∴EF=AB=5cm．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．解：（1）∵∠BEC=75°，∠ABC=90°，∴∠ECB=15°，∵∠ECD=45°，∴∠DCF=60°，在Rt△DFC中：∠DCF=60°，FC=3，∴DF=3，DC=6，由题得，四边形ABFD是矩形，∴AB=DF=3，∵AB=BC，∴BC=3，∴BF=BC﹣FC=3﹣3，∴AD=DF=3﹣3，∴C=3×2+6+3﹣3=9+3，梯形ABCD答：梯形ABCD的周长是9+3．（2）过点C作CM垂直AD的延长线于M，再延长DM到N，使MN=BE，∴CN=CE，可证∠NCD=∠DCE，∵CD=CD，∴△DEC≌△DNC，∴ED=EN，∴ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．（1）证明：∵AD∥BC，E是AB的中点，∴AE=BE，∠B=∠EAF，∠BCE=∠F．∴△BCE≌△AFE（AAS）．（2）解：∵AD∥BC，∴∠DAB=∠ABC=90°．∵AE=BE，∠AEF=∠BEC，∴△BCE≌△AFE．∴AF=BC=4．∵EF2=AF2+AE2=9+16=25，∴EF=5．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．（1）∵DC=BC，∠1=∠2，CF=CF，∴△DCF≌△BCF．（2）延长DF交BC于G，∵AD∥BG，AB∥DG，∴四边形ABGD为平行四边形．∴AD=BG．∵△DFC≌△BFC，∴∠EDF=∠GBF，DF=BF．又∵∠3=∠4，∴△DFE≌△BFG．∴DE=BG，EF=GF．∴AD=DE．（3）∵EF=GF，DF=BF，∴EF+BF=GF+DF，即：BE=DG．∵DG=AB，∴BE=AB．∵C=DF+FE+DE=6，△DFE∴BF+FE+DE=6，即：EB+DE=6．∴AB+AD=6．又∵AD=2，∴AB=4．∴DG=AB=4．∵BG=AD=2，∴GC=BC﹣BG=5﹣2=3．又∵DC=BC=5，在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°．=（AD+BC）•DG∴S梯形ABCD=（2+5）×430、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．解答：解：（1）证明：∵AD∥BC，DE2=CD2+CE2=42+32=25，∴∠OAD=∠OEB，∴DE=5又∵AB=AD，AO⊥BD，∴AD=BE=5，=．∴OB=OD，∴S梯形ABCD又∵∠AOD=∠EOB，∴△ADO≌△EBO（AAS），∴AD=EB，又∵AD∥BE，∴四边形ABCD是平行四边形，又∵AB=AD∴四边形ABCD是菱形．（2）∵四边形ABCD是菱形，∴AD=DE=BE，。

AMNEFP几何证明题分类汇编一、证明两线段相等1．如图3，在梯形ABCD 中，AD BC ∥，EA AD ⊥，M 是AE 上一点，BAE MCE =∠∠，45MBE =∠．〔1〕求证：BE ME =．〔2〕假设7AB =，求MC 的长．2、〔8分〕如图11，一张矩形纸片ABCD ，其中AD=8cm ，AB=6cm ，先沿对角线BD 折叠，点C 落在点C ′的位置，BC ′交AD 于点G. 〔1〕求证：AG=C ′G ；〔2〕如图12，再折叠一次，使点D 与点A 重合，的折痕EN ，EN 角AD 于M ，求EM 的长.2、类题演练3如图，分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE ．∠BAC =30º，EF ⊥AB ，垂足为F ，连结DF ． 〔1〕试说明AC =EF ；〔2〕求证：四边形ADFE 是平行四边形．4如图，在△ABC 中，点P 是边AC 上的一个动点，过点P 作直线MN ∥BC ，设MN 交∠BCA 的平分线于点E ，交∠BCA 的外角平分线于点F ． (1)求证：PE ＝PF ；(2)*当点P 在边AC 上运动时，四边形BCFE 可能是菱形吗？说明理由；(3)*假设在AC 边上存在点P ，使四边形AECF 是正方形，且 AP BC ＝32．求此时∠A 的大小．图3A BCDMEA B CD E F第20题图二、证明两角相等、三角形相似及全等1、〔9分〕AB 是⊙O 的直径，点E 是半圆上一动点〔点E 与点A 、B 都不重合〕，点C 是BE 延长线上的一点，且CD ⊥AB ，垂足为D ，CD 与AE 交于点H ，点H 与点A 不重合。

〔1〕〔5分〕求证：△AHD ∽△CBD〔2〕〔4分〕连HB ，假设CD=AB=2，求HD+HO 的值。

2、〔此题8分〕如图9，四边形ABCD 是正方形，BE ⊥BF ，BE=BF ，EF 与BC 交于点G 。

几何证明与计算——作图1. 如图，在△ABC 中，∠ACB =90°．（1）作出经过点B ，圆心O 在斜边AB 上且与边AC 相切于点E 的⊙O ； （要求尺规作图，保留作图痕迹，不写作法和证明）（2）设（1）中所作的⊙O 与边AB 交异于点B 的另外一点D ，若⊙O 的直径为5，BC =4，求DE 的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）CAB2. 如图1，Rt △ACB 中，∠C =90°，点D 在AC 上，∠CBD =∠A ，过A ，D 两点的圆的圆心O 在AB 上．（1）利用直尺和圆规在图1中画出⊙O （不写作法，保留作图痕迹，并用黑色水笔把线条描清楚）；（2）判断BD 所在直线与（1）中所作的⊙O 的位置关系，并证明你的结论； （3）设⊙O 交AB 于点E ，连接DE ，过点E 作EF ⊥BC ，F 为垂足．若点D 是线段AC 的黄金分割点（即DC ADAD AC ），如图2，试说明四边形DEFC 是正方形．图1DCBA图2BA3.已知平行四边形ABCD．（1）尺规作图：作∠BAD的平分线交直线BC于点E，交DC延长线于点F（要求：尺规作图，保留作图痕迹，不写作法）；（2）在（1）的条件下，求证：CE=CF．ADB C4.如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．D CAB5. 如图，在矩形ABCD 中，AB =2，ADP 是BC 边上的一点，且BP =2CP ．（1）用尺规在图1中作出CD 边上的中点E ，连接AE ，BE （保留作图痕迹，不写作法）；（2）如图2，在（1）的条件下，判断EB 是否平分∠AEC ，并说明理由； （3）如图3，在（2）的条件下，连接EP 并延长交AB 的延长线于点F ，连接AP ，不添加辅助线，△PFB 能否由都经过P 点的两次变换与△P AE 组成一个等腰三角形？如果能，说明理由，并写出两种方法（指出对称轴、旋转中心、旋转方向和平移距离）图1图2EF图3ABC DP。