线性规划问题计算机解法

第四章线性规划问题的计算机求解4.1 有以下线性规划数学问题：max Z=2x l+3 x2S.T. x l+ x2≤102x l+ x2≥4x l+3 x2≤242x l+ x2≤16x l 、x2≥01、用EXCEL线性规划求解模板求解该数学模型。

2、本问题的最优解是什么？此时最大目标函数值是多少？3、四个约束条件中，哪些约束条件起到了作用？各约束条件的剩余量或松弛量及对偶价格是多少？4、目标函数中各变量系数在什么范围内变化时，最优解不变？5、确定各给定条件中的常数项的上限和下限。

解：1、2、最优解：（3，7），最优值：273、第一、第三个约束条件起到了约束作用。

松弛量/剩余量对偶价格x l+ x2≤10 0 1.52x l+ x2≥4 9 0x l+3 x2≤24 0 0.52x l+ x2≤16 13 04、目标函数中各变量系数1≤C1≤32≤C1≤65、常数项8≤b1≤9.2无限≤b2≤1318≤b3≤3013≤b4≤无限4.2 有以下线性规划数学问题：min f=8x l+3 x2S.T. 500x l+100 x2≤12000005x l+4 x2≥60000100x l≥300000x l 、x2≥01、用EXCEL线性规划求解模板求解该数学模型。

2、本问题的最优解是什么？此时最大目标函数值是多少？3、各约束条件的剩余量或松弛量及对偶价格是多少？分别解释其含义。

4、目标函数中各变量系数在什么范围内变化时，最优解不变？5、确定各给定条件中的常数项的上限和下限。

解：本问题无解。

4.3 有以下线性规划数学问题：max Z=x l+2 x2+3 x3- x4S.T. x l+2 x2+3 x3≤152x l+ x2+5 x3≤20x l+2 x2+ x3+ x4≤10x l 、x2、x3、x4≥01、用EXCEL线性规划求解模板求解该数学模型。

2、本问题的最优解是什么？此时最大目标函数值是多少？3、分别解释“递减成本”栏中各数据的含义。

第三章思考题、主要概念及内容“管理运筹学”软件的操作方法“管理运筹学”软件的输出信息分析复习题1.见第二章第7题，设x1为产品Ⅰ每天的产量，x2为产品Ⅱ每天的产量，可以建立下面的线性规划模型：max z=500x1+400x2；约束条件：2x1≤300，3x2≤540，2x1+2x2≤440，1.2x1+1.5x2≤300，x1，x2≥0．使用“管理运筹学”软件，得到的计算机解如图1所示图1根据图3-5回答下面的问题：(1) 最优解即最优产品组合是什么?此时最大目标函数值即最大利润为多少?(2) 哪些车间的加工工时数已使用完?哪些车间的加工工时数还没用完?其松弛变量即没用完的加工工时数为多少?(3) 四个车间的加工工时的对偶价格各为多少?请对此对偶价格的含义予以说明．(4) 如果请你在这四个车间中选择一个车间进行加班生产，你会选择哪个车间?为什么?(5) 目标函数中x1的系数c1，即每单位产品Ⅰ的利润值，在什么范围内变化时，最优产品的组合不变?(6) 目标函数中x2的系数c2，即每单位产品Ⅱ的利润值，从400元提高为490元时，最优产品组合变化了没有?为什么?(7) 请解释约束条件中的常数项的上限与下限．(8) 第1车间的加工工时数从300增加到400时，总利润能增加多少?这时最优产品的组合变化了没有?(9) 第3车间的加工工时数从440增加到480时，从图3-5中我们能否求得总利润增加的数量?为什么?(10) 当每单位产品Ⅰ的利润从500元降至475元，而每单位产品Ⅱ的利润从400元升至450元时，其最优产品组合(即最优解)是否发生变化?请用百分之一百法则进行判断．(11) 当第1车间的加工工时数从300增加到350，而第3车间的加工工时数从440降到380时，用百分之一百法则能否判断原来的对偶价格是否发生变化?如不发生变化，请求出其最大利润．2. 见第二章第8题(2)，仍设xA为购买基金A的数量，xB为购买基金B的数量，建立的线性规划模型如下：max z=5xA+4xB；约束条件：50xA+100xB≤1 200 000，100xB≥300 000，xA，xB≥0．使用“管理运筹学”软件，求得计算机解如图2所示．图2根据图2，回答下列问题：(1) 在这个最优解中，购买基金A和基金B的数量各为多少?这时获得的最大利润是多少?这时总的投资风险指数为多少?(2) 图3-7中的松弛/剩余变量的含义是什么?(3) 请对图3-7中的两个对偶价格的含义给予解释．(4) 请对图3-7中的目标函数范围中的上、下限的含义给予具体说明，并阐述如何使用这些信息．(5) 请对图3-7中的常数项范围的上、下限的含义给予具体说明，并阐述如何使用这些信息．(6) 当投资总金额从1 200 000元下降到600 000元，而在基金B上至少投资的金额从300 000元增加到600 000元时，其对偶价格是否发生变化?为什么?3. 考虑下面的线性规划问题：min z=16x1+16x2+17x3；约束条件：x1+x3≤30，　-x2+6x3≥15，05x13x1+4x2-x3≥20，x1，x2，x3≥0．其计算机求解结果如图3所示．图3根据图3，回答下列问题：(1) 第二个约束方程的对偶价格是一个负数(为-3622)　，它的含义是什么?　，它的含义是什么?(2) x2的相差值为0703(3) 当目标函数中x1的系数从16降为15，而x2的系数从16升为18时，最优解是否发生变化?(4) 当第一个约束条件的常数项从30减少到15，而第二个约束条件的常数项从15增加到80时，你能断定其对偶价格是否发生变化吗?为什么?。

线性规划问题的两种求解方式线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。

线性规划所研究的是：在一定条件下，合理安排人力物力等资源，使经济效果达到最好。

一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。

解决线性规划问题常用的方法是图解法和单纯性法，而图解法简单方便，但只适用于二维的线性规划问题，单纯性法的优点是可以适用于所有的线性规划问题，缺点是单纯形法中涉及大量不同的算法，为了针对不同的线性规划问题，计算量大，复杂繁琐。

在这个计算机高速发展的阶段，利用Excel建立电子表格模型，并利用它提供的“规划求解”工具，能轻松快捷地求解线性模型的解。

无论利用哪种方法进行求解线性规划问题，首先都需要对线性规划问题建立数学模型，确定目标函数和相应的约束条件，进而进行求解。

从实际问题中建立数学模型一般有以下三个步骤；1、根据所求目标的影响因素找到决策变量；2、由决策变量和所求目标的函数关系确定目标函数；3、由决策变量所受的限制条件确定决策变量所要满足的约束条件。

以下是分别利用单纯形法和Excel表格中的“规划求解”两种方法对例题进行求解的过程。

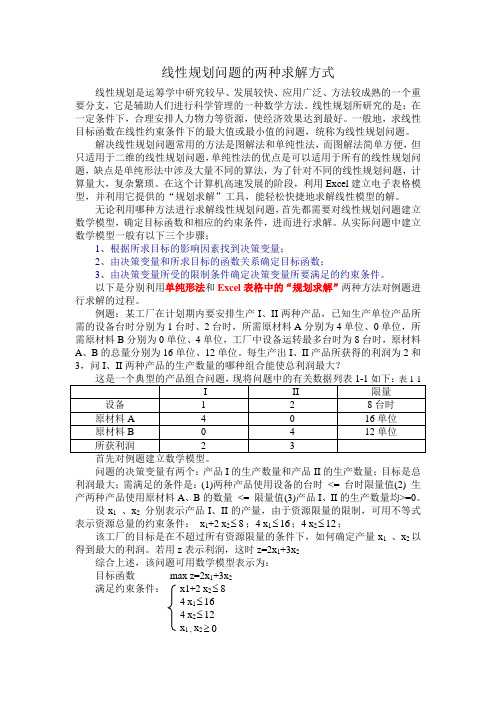
例题：某工厂在计划期内要安排生产I、II两种产品，已知生产单位产品所需的设备台时分别为1台时、2台时，所需原材料A分别为4单位、0单位，所需原材料B分别为0单位、4单位，工厂中设备运转最多台时为8台时，原材料A、B的总量分别为16单位、12单位。

每生产出I、II产品所获得的利润为2和3，问I、II两种产品的生产数量的哪种组合能使总利润最大？问题的决策变量有两个：产品I的生产数量和产品II的生产数量；目标是总利润最大；需满足的条件是：(1)两种产品使用设备的台时<= 台时限量值(2) 生产两种产品使用原材料A、B的数量<= 限量值(3)产品I、II的生产数量均>=0。

线性规划问题计算机解法本节将简要介绍几种软件求解线性规划问题的方法．1.6.1应用EXCEL求解线性规划问题以EXCEL2007为例，首先加载EXCEL规划求解加载项，具体操作步骤为：Office按钮——EXCEL选项——加载项——转到——加载宏——规划求解加载项，此时在“数据”选项卡中出现带有“规划求解”按钮的“分析”组．下面仍然以例１．５为例，说明其求解过程：１设计电子表格将模型中的数据直接输入到工作表中并保存文档．其中，Ａ列为说明性文字，Ａ3为决策变量的初始值，可以任意给定，本例均设为０；在Ｄ4其中键入“=SUMPRODUCT (B$3:C$3,B4:C4)”或者从直接从函数中选择，SUMPRODUCT是EXCEL的一个内置函数，,x x初始其功能是两个向量或者矩阵对应元素乘积的和，因此表示表示目标函数值，由于12值设为０，因而显示０；同理在Ｄ5其中键入“=SUMPRODUCT(B$3:C$3,B5:C5)”，以此类推，其显示值均为０．２设置规划求解参数点击“分析”组中的“规划求解”按钮即可弹出如下对话框：在设计目标目标单元格中键入$D$4，或者直接点击单元格D4，并选择“最大值”选项，如下图所示点击对话框中“添加”，弹出如下对话框在“单元格引用位置”栏中键入“$D$ 5”（或点击单元格D5），选择“<=”(点击出现下拉菜单，可以选择其他约束形式)，在约束值栏中键入“$F$5”（或点击单元格F5），确定后弹出下面对话框：类似于上一步操作，添加所有的约束条件后如下图所示：3 应用规划求解工具：点击“求解”弹出如下对话框，选择“保存规划求解结果”与“运算结果报告”确定后则形成一张新的工作表：如果想得到价值系数、资源向量等条件对最优值的影响，可以在步骤3中选择输出“敏感性报告”．1.6.1应用LINGO求解线性规划问题从上面的介绍中看出，用EXCEL求解线性规划问题时操作简单，而其在输入数据方面有其方便之处．但如果决策变量和约束条件很多的话，其运行速度就不及专业的优化软件了．本节介绍一种专业的优化软件－－LINGO的使用方法．LINDO 是 Linear Interactive Discrete Optimizer的缩写，是一个线性和整数规划的软件系统. LINDO /386 5.3以上版本，最大规模的模型的非零系数可以达到1,000,000个，最大变量个数可以达到100,000个，最大目标函数和约束条件个数可以达到32000个，最大整数变量个数可以达到100,000个。

运筹学实验报告实验课程:运筹学实验日期: 2020年4月4日任课教师:杨小康班级：数学1802 姓名：王超学号：2501180224一、实验名称: 简单线性规划模型的求解与Lingo软件的初步使用二、实验目的：了解Lingo软件的基本功能和简单线性规划模型的求解的输入和输出结果。

熟悉Lingo 软件在运筹学模型求解中的作用，增强自身的动手能力，提高实际应用能力三、实验要求:1、熟悉Lingo软件的用户环境，了解Lingo软件的一般命令2、给出Lingo中的输入，能理解Solution Report中输出的四个部分的结果。

4、能给出最优解和最优值；5、能给出实际问题的数学模型，并利用lingo求出最优解四、报告正文（文挡，数据，模型，程序，图形）:1.在Lingo中求解下面的线性规划数学模型;(1)12132412512345 max2543..28,,,,0z x xx xx xs tx x xx x x x x=++=⎧⎪+=⎪⎨++=⎪⎪≥⎩(2)12121212max2343..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(3)12121212max243..28,0z x xxxs tx xx x=+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩(4)12121212max324 ..3,0z x xx xs t x xx x=+-≤⎧⎪-+≤⎨⎪≥⎩(5)1212121212max102401.530.50,0z x xx xx xs tx xx x=++≤⎧⎪+≤⎪⎨+≥⎪⎪≥⎩2、某工厂利用三种原料生产五种产品，其有关数据如下表。

原料可利用数（千克）每万件产品所用材料数（千克）A B C D E甲10 1 2 1 0 1 乙24 1 0 1 3 2 丙21 1 2 2 2 2 每万件产品的利润（万元）8 20 10 20 21 (l)建立该问题的运筹学模型。

（2）利用lingo 软件求出最优解，得出最优生产计划解：（1）设xi（i=1,2...,5）为所用材料生产的件数则数学模型,,,,21 2222242 3102;212010208max543215 43215431532154321≥≤++++≤+++≤+++++++ =xxxxxx xxxxt xxxx xxxxsxxxxxz （2）结果为220.3：现有15米长的钢管若干，生产某产品需4米、5米、7米长的钢管各为100、150、120根，问如何截取才能使原材料最省？（建立线性规划模型并利用lingo软件求解）解：方案4米5米7米剩余量截取长度1 3 0 0 32 2 1 0 23 2 0 1 04 1 2 0 15 0 3 0 06 0 1 1 37 0 0 2 14人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。

线性规划问题经常出现在高考数学试题中.此类问题通常会要求同学们从实际问题中抽象出二元一次不等式，在了解二元一次不等式的几何意义的基础上，画出二元一次不等式组所表示的平面区域，并求出最优解.但问题中的目标函数经常会有所变化，常见的形式有直线型、分式型、平方型，且解法各不相同.下面结合实例，谈一谈三类线性规划问题的解法.一、直线型目标函数直线型的目标函数一般形如z =ax +by (ab ≠0)，这类问题通常要求根据二元一次不等式组，求目标函数z =ax +by (ab ≠0)的最值.求解此类线性规划问题，一般需将函数z =ax +by 转化为直线的斜截式方程：y =-a b x +z b，根据二元一次不等式组画出可行域后，在可行域内讨论直线的截距zb的最值.通过求直线的截距zb的最值来间接求出z 的最值.例1.设x ，y 满足ìíîïïx -y ≥0,x +y -2≤0,y ≥-2,则z =2x +y 的最大值为.解：画出ìíîïïx -y ≥0,x +y -2≤0,y ≥-2,表示的可行域，如图1中的阴影部分所示，由{x +y -2≤0,y ≥-2,可得{x =4,y =-2,平移直线y =-2x +z ，可知当直线y =-2x +z 经过点()4,-2时，该直线在纵轴上的截距最大，即在()4,-2点处，z 取大值，可得z max =2×4-2=6．由于直线的截距有正有负，所以取最值的情形有所不同.当b >0时，截距zb取最大值，此时z 也取最大值，当截距zb 取最小值时，z 也取最小值；当b <0时，截距z b 取最大值，此时z 取最小值，当截距z b取最小值时，z 取最大值．图1图2例2.某养鸡场有1万只鸡，用动物饲料和谷物饲料混合喂养.每天每只鸡平均吃混合饲料0.5kg ，其中动物饲料不能少于谷物饲料的15.动物饲料每千克0.9元，谷物饲料每千克0.28元，饲料公司每周仅能保证供应谷物饲料50000kg ，问怎样混合饲料，才使成本最低.解:设每周需用谷物饲料x kg,动物饲料y kg,每周总的饲料费用为z 元，由题意可得ìíîïïïïx +y ≥35000，y ≥15x ，0≤x ≤50000，y ≥0，则z =0.28x +0.9y ，作出以上不等式组所表示的平面区域，如图2中阴影部分所示，联立x +y =35000和y =15x ，可得x =875003，y =175003，则A (875003,175003)，作一组平行直线y =-2890+10z9（即图2中虚线），当直线经过可行域内的点A (875003,175003)时，直线的纵截距最小，此时z 最小.故当x =875003，y =175003时，即将谷物饲料和动物饲料按5:1的比例混合时，成本最低.本题是一道实际应用问题.解答此类线性规划问题，需首先仔细读题，根据题意设出变量，建立关于变量的不等关系式以及目标函数.而本题中的目标函数为直线型，所以需将其转化为直线的截距式，在可行域内寻找直线的截距取最小值时的点，即可解题.一般地，线性目标函数的最优解一般会在可行域的顶点或边界处取得，我们可以重点研究可行域的顶点或边界上的点.二、分式型目标函数分式型目标函数一般形如z =y -bx -a.求解此类线性规划问题，需根据目标函数的几何意义：已知点(a ,b )与可行域内的点(x ,y )连线的斜率.当斜率取最大值时，z 取最大值；当斜率取最小值时，z 取最小值.而直线的斜率k =tan a 受倾斜角a 影响：（1）当倾斜角a 为魏上茗43当直线经过点(1,6)时，直线的斜率取得最大值，最大值为6；当直线经过点直线的斜率最小，此时yx取得最小值，最小的取值范围是éëùû95,6，所以本题选A.本题的可行域在第一象限，所以只需讨论直线的范围内的变化情况，可将直线y=zx在可行域内找出直线的倾斜角最大或即斜率取最值时的点，即可解题.图4图5例5.设实数x,y满足ìíîïïx+y-6≥0,x+2y-14≤0,2x+y-10≤0,则x2+y的最小值为____．解：x2+y2表示可行域内的点P(x,y)到原点的距离，作出不等式组表示的平面区域,如图5中的阴影部分所示，过点O作OA垂直于直线x+y-6=0，垂足为A在可行域内），所以原点到直线x+y-6=0的距离，就是点P(x,y)到原点距离的最小值，由点到直线的图3。

线性规划问题本⽂主要内容介绍线性规划问题 (Linear Programming) 及其对偶问题 (Dual Problem)。

Introduction线性规划 (Linear Programming) 就是⾼中数学讲的那个线性规划，不过现在是从计算机的⾓度来谈这个问题的。

给定⼀个⽬标函数 (Objective function) ，和若⼲个不等式约束 (Constraints) ：max x1+6x2x1≤200x2≤300x1+x2≤400x1,x2≥0求出⽬标函数的最⼤值。

常规的做法是令c=x1+6x2，然后可得x2=16(−x1+c) ，通过作图法，找出截距c的最⼤值。

这⾥的可⾏域是⼀个封闭的区域，因此最优解必然存在，最优解不存在的 2 种情况是：可⾏域是空的，⽐如x≤1,x≥2 .可⾏域不是封闭的，⽐如⽬标函数为max x1+x2，约束条件为x1,x2≥0 。

但应当注意的是，即使可⾏域不是封闭的，最优解可能依然存在，⽐如⽬标函数为max x1，⽽约束条件为x1≤1,x2≥0 .SimplexLP 问题是 NP-Hard 的，单纯形法 (Simplex) 是⼀个解决 LP 问题的算法，将在下⼀篇⽂章详细介绍，在这⾥先给出⼀个直观的介绍。

从可⾏域的⼀个有效点出发，若果存在⼀个相邻顶点使得⽬标函数具有更优值，那么令当前顶点为这个邻居顶点，重复这个过程直到不存在这样的更优邻居顶点。

为什么这样的局部测试 (Local Test) 会找到全局最优解呢？In this way it does hill-climbing on the vertices of the polygon, walking from neighbor to neighbor so as to steadily increase profit along the way.By simple geometry - think of the profit line passing through this vertex. Since all the vertex’s neighbors lie below the line, the rest of the feasible polygon must also lie below this line.如果存在 3 个变量，即：那么 Simplex 的过程实际上是在⼀个凸多⾯体的边缘上进⾏ hill-climbing:Standard and slack forms对于⼀个 LP 问题的实例，我们都能把它转换为⼀个标准型 (Standard Form) ：⽬标函数是max类型的。

运筹学实验报告(一)线性规划问题的计算机求解-(1)-CAL-FENGHAI.-(YICAI)-Company One1运筹学实验报告实验课程:运筹学实验日期: 任课教师:王挺第五种方案0 3 0 0第六种方案0 1 1 3第七种方案0 0 2 1设：第i种方案需要的钢管为Xi根（其中i=1，2...6）,可得:minz=X1+X2+X3+X4+X5+X6+X7解：model:min= X1+X2+X3+X4+X5+X6+X7;3*X1+2*X2+2*X3+X4>=100;X2+2*X4+3*X5+X6>=150;X3+X6+2*X7>=120;endObjective value: 135.0000Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX1 0.000000 0.2500000X2 0.000000 0.1666667X3 50.00000 0.000000X4 0.000000 0.8333333E-01X5 50.00000 0.000000X6 0.000000 0.1666667X7 35.00000 0.0000004人力资源分配问题某昼夜服务的公交线路每天各时间段内所需司机和乘务人员人数如表1所示。

班次时间所需人数班次时间所需人数1 6:00~10:00 60 4 18:00~22:00 502 10:00~14:00 70 5 22:00~2:00 203 14:00~18:00 60 6 2:00~6:00 30设司机和乘务人员分别在各时间段开始时上班，并连续工作8小时，问该公交线路应怎样安排司机和乘务人员，既能满足工作需要，又使配备司机和乘务人员的人数最少？5投资计划问题某地区在今后三年内有四种投资机会，第一种是在3年内每年年初投资，年底可获利润20%，并可将本金收回。

第四章 线性规划问题的计算机求解4.1 有以下线性规划数学问题： max Z=2x l +3 x 2 S.T. x l + x 2≤10 2x l + x 2≥4x l +3 x 2≤24 2x l + x 2≤16x l 、 x 2≥01、 用EXCEL 线性规划求解模板求解该数学模型。

2、 本问题的最优解是什么？此时最大目标函数值是多少？3、 四个约束条件中，哪些约束条件起到了作用？各约束条件的剩余量或松弛量及对偶价格是多少？4、 目标函数中各变量系数在什么范围内变化时，最优解不变？5、 确定各给定条件中的常数项的上限和下限。

解： 1、2、最优解：（3，7），最优值：273、 可变单元格约束对于求最大化的问题，对偶价格=阴影价格松弛量/剩余量对偶价格x l+ x2≤10 0 1.52x l+ x2≥4 9 0x l+3 x2≤24 0 0.52x l+ x2≤16 13 0 因第一、第三个约束条件的松弛量/剩余量为0 ，所以这两个约束条件起到了约束作用。

4、目标函数中各变量系数1≤C1≤32≤C1≤65、常数项8≤b1≤9.2无限≤b2≤1318≤b3≤3013≤b4≤无限4.2 有以下线性规划数学问题：min f=8x l+3 x2S.T. 500x l+100 x2≤12000005x l+4 x2≥60000100x l≥300000x l 、x2≥01、用EXCEL线性规划求解模板求解该数学模型。

2、本问题的最优解是什么？此时最大目标函数值是多少？3、各约束条件的剩余量或松弛量及对偶价格是多少？分别解释其含义。

4、目标函数中各变量系数在什么范围内变化时，最优解不变？5、确定各给定条件中的常数项的上限和下限。

解：本问题无解。

4.3 有以下线性规划数学问题：max Z=x l+2 x2+3 x3- x4S.T. x l+2 x2+3 x3≤152x l+ x2+5 x3≤20x l+2 x2+ x3+ x4≤10x l 、x2、x3、x4≥01、用EXCEL线性规划求解模板求解该数学模型。

方法集锦线性规划问题是指在线性约束条件下求线性目标函数的最大值或最小值问题，重点考查同学们的建模、运算、分析能力.本文主要探讨三种不同类型目标函数的线性规划问题及其解法.一、z =ax +by 型若目标函数为z =ax +by 型（直线型），我们一般需先将目标函数变形为：y =-a b x +zb，通过求直线的截距的最值间接求出z 的最值，这样便将求目标函数最值问题转化为求直线的截距的最值.①若b >0，当y =-a b x +z b截距最大时z 最小，当截距最小时z 最大；若b <0，当y =-a b x +zb截距最大时z 最大，当截距最小时z 最小.例1.已知x ,y 满足约束条件ìíîïïïï2x +y ≤40,x +2y ≤50,x ≥0,y ≥0,则z =3x +2y 的最大值为_____.解：将z =3x +2y 变形为y =-32x +z2.作出如图1所示的可行域，由图可知当y =-32x +z 2过点A 时，直线的截距最大，则{2x +y =40，x +2y =50，解得ìíîx =10,y =20，此时z max =70.在画出可行域后，我们通过观察图形便能很快确定当直线经过A 点时y =-32x +z2的截距最大，此时z 最大，解方程组便可求得z 的最值.图1图2图3二、z =y -bx -a型对于目标函数为z =y -bx -a （斜率型）的线性规划问题，我们一般要依据y -bx -a的几何意义来求解.首先，根据线性约束条件画出可行域，将z 看作是可行域内的动点P (x ,y )与定点A (a ,b )连线的斜率，求得斜率的最值便可求出z 的最值.例2.已知x ,y 满足约束条件ìíîïïx -y +1≤0,x >0,x ≤1,求z =yx的最大值.解析：该目标函数为斜率型，可将z 看作是可行域内的动点P (x ,y )与原点连线的斜率，求出斜率的最值即可.解：作出如图2所示的可行域，将z =yx变形为z =y -0x -0，可将z 看作可行域内任意一点P (x ,y )与原点的连线的斜率.由图2可知当直线过交点A 时，PO 的斜率最大，{x -y +1=0,x =1,解得ìíîx =1,y =2，所以z max =2.三、z =(x -a )2+(y -b )2型当遇到目标函数为z =(x -a )2+(y -b )2（距离型）的线性规划问题时，我们可以把z 看作可行域内动点P (x ,y )与定点A (a ,b )的距离的平方，结合可行域找到最值点，利用两点间的距离公式便能求出z 的最值.例3.已知x ,y 满足约束条件ìíîïïx -y +1≤0,2x -y -2≤0,x ≥1,则z =x 2+y 2的最小值为_____.解析：该目标函数为距离型，可将z 看作是可行域内任意一点P (x ,y )到原点的距离的平方，求得PO 两点间距离的最小值，便可求得z 的最小值.解：将z =x 2+y 2变形为z =（x -0）2+(y -0)2，作出如图3所示的可行域，由图可知点A 到原点的距离最小，{x -y +1=0,x =1,解得ìíîx =1,y =2，所以z min =5.可见，解答线性规划类问题的基本思路是，（1）根据线性约束条件画出可行域；（2）将目标函数变形为直线型、斜率型、距离型；（3）在可行域内移动直线、点，找出最值点；（4）联立交点处的直线方程，求出最值点的坐标；（5）将点的坐标代入目标函数中求得最值.（作者单位：中国烟台赫尔曼·格迈纳尔中学）44。