大物习题答案
- 格式:doc
- 大小:70.00 KB
- 文档页数:10

大学物理习题答案 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-一、 单项选择题:1. 北京正负电子对撞机中电子在周长为L 的储存环中作轨道运动。
已知电子的动量是P ,则偏转磁场的磁感应强度为: ( C ) (A)eLP π; (B)eL P π4; (C) eLPπ2; (D) 0。
2. 在磁感应强度为B的均匀磁场中,取一边长为a 的立方形闭合面,则通过该闭合面的磁通量的大小为: ( D )(A) B a 2; (B) B a 22; (C) B a 26; (D) 0。
3.半径为R 的长直圆柱体载流为I ,电流I 均匀分布在横截面上,则圆柱体内(R r 〈)的一点P 的磁感应强度的大小为 ( B ) (A) r I B πμ20=; (B) 202R Ir B πμ=; (C) 202rIB πμ=; (D) 202RIB πμ=。
4.单色光从空气射入水中,下面哪种说法是正确的 ( A ) (A) 频率不变,光速变小; (B) 波长不变,频率变大; (C) 波长变短,光速不变; (D) 波长不变,频率不变.5.如图,在C 点放置点电荷q 1,在A 点放置点电荷q 2,S 是包围点电荷q 1的封闭曲面,P 点是S 曲面上的任意一点.现在把q 2从A 点移到B 点,则 (D )(A) 通过S 面的电通量改变,但P 点的电场强度不变;(B) 通过S 面的电通量和P 点的电场强度都改变; (C) 通过S 面的电通量和P 点的电场强度都不变; (D) 通过S 面的电通量不变,但P 点的电场强度改变。
6.如图所示,两平面玻璃板OA 和OB 构成一空气劈尖,一平面单色光垂直入射到劈尖上,当A 板与B 板的夹角θ增大时,干涉图样将 ( C )(A) 干涉条纹间距增大,并向O 方向移动; (B) 干涉条纹间距减小,并向B 方向移动; (C) 干涉条纹间距减小,并向O 方向移动; (D) 干涉条纹间距增大,并向O 方向移动.7.在均匀磁场中有一电子枪,它可发射出速率分别为v 和2v 的两个电子,这两个电子的速度方向相同,且均与磁感应强度B 垂直,则这两个电子绕行一周所需的时间之比为 ( A )(A) 1:1; (B) 1:2; (C) 2:1; (D) 4:1.8.如图所示,均匀磁场的磁感强度为B ,方向沿y 轴正向,欲要使电量为Q 的正离子沿x 轴正向作匀速直线运动,则必须加一个均匀电场E ,其大小和方向为 ( D )(A) E =νB ,E 沿z 轴正向; (B) E =vB ,E 沿y 轴正向;(C) E =B ν,E 沿z 轴正向; (D) E =B ν,E 沿z 轴负向。

第九章 静电场 (Electrostatic Field)二、计算题9.7 电荷为+q 和-2q 的两个点电荷分别置于x =1 m 和x =-1 m 处.一试验电荷置于x 轴上何处,它受到的合力等于零?解:设试验电荷0q 置于x 处所受合力为零,根据电力叠加原理可得()()()()022220000(2)(2)ˆˆ0041414141q q q q q q i i x x x x εεεε⋅-⋅-+=⇒+=π-π+π-π+即:2610(3x x x m -+=⇒=±。
因23-=x 点处于q 、-2q 两点电荷之间,该处场强不可能为零.故舍去.得()223+=x m9.8 一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如题图9.4所示.试求圆心O 处的电场强度.解:把所有电荷都当作正电荷处理. 在θ 处取微小电荷d q = λd l = 2Q d θ / π它在O 处产生场强θεεd 24d d 20220R QR q E π=π=按θ 角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202R QE E x π==θθεθd cos 2cos d d 202RQE E y π-=-= 对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =02022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以j R Q j E i E E y x202επ-=+=9.9如图9.5所示,一电荷线密度为λ的无限长带电直导线垂直纸面通过A 点;附近有一电量为Q 的均匀带电球体,其球心位于O 点。
AOP ∆是边长为a 的等边三角形。
已知P 处场强方向垂直于OP ,求:λ和Q 间的关系。

习 题 一1—1 一质点在平面xOy 内运动,运动方程为x =2t ,2219t y -= (SI)。
(1)求质点的运动轨道;(2)求t =1s 和t =2s 时刻质点的位置矢量;(3)求t =1s 和t =2s 时刻质点的瞬时速度和瞬时加速度;(4)在什么时刻,质点的位置矢量和速度矢量垂直?这时x 、y 分量各为多少?(5)在什么时刻,质点离原点最近?最近距离为多大?[解] 质点的运动方程:t x 2=,2219t y -= (1)消去参数t ,得轨道方程为: 22119x y -= (2)把t=1s 代入运动方程,得j i j i r 172)219(22+=-+=t t 把t =2s 代入运动方程,可得j i j i r 114)2219(222+=⨯-+⨯= (3)由速度、加速度定义式,有4/,0/4/,2/-====-====dt dv a dt dv a t dt dy v dt dx v y y x x y x所以,t 时刻质点的速度和加速度为 j i j i t v v v y x 42-=+= j j i a 4-=+=y x a a所以,t=1s 时,j i v 42-=,j a 4-= t=2s 时,j i v 82-=,j a 4-= (4)当质点的位置矢量和速度矢量垂直时,有 0=⋅v r即 0]42[])219(2[2=-⋅-+j i j i t t t 整理,得 093=-t t解得 3,3;0321-===t t t (舍去) m 19,0,s 011===y x t 时 m 1,m 6,s 322===y x t 时 (5)任一时刻t 质点离原点的距离 222)219()2()(t t t r -+= 令d r/d t =0 可得 t =3所以,t =3s 时,质点离原点最近 r1—2 一粒子按规律59323+--=t t t x 沿x 轴运动,试分别求出该粒子沿x 轴正向运动;沿x 轴负向运动;加速运动,减速运动的时间间隔。

《大学物理》练习题一. 单选题:1.下列说法正确的是……………………………………() 参看课本P32-36A . 惯性系中,真空中的光速与光源的运动状态无关,与光的频率有关B . 惯性系中,真空中的光速与光源的运动状态无关,与光的频率无关C . 惯性系中,真空中的光速与光源的运动状态有关,与光的频率无关D . 惯性系中,真空中的光速与光源的运动状态有关,与光的频率有关2.下列说法正确的是………………………………… ( ) 参看课本P32-36A . 伽利略变换与洛伦兹变换是等价的B . 所有惯性系对一切物理定律都是不等价的C . 在所有惯性系中,真空的光速具有相同的量值cD . 由相对论时空观知:时钟的快慢和量尺的长短都与物体的运动无关3.下列说法正确的是………………………………… ( )参看课本P58,76,103 A . 动量守恒定律的守恒条件是系统所受的合外力矩为零 B . 角动量守恒定律的守恒条件是系统所受的合外力为零 C . 机械能守恒定律的守恒条件是系统所受的合外力不做功 D . 以上说法都不正确4. 下列关于牛顿运动定律的说法正确的是…………( ) 参看课本P44-45A . 牛顿第一运动定律是描述物体间力的相互作用的规律B . 牛顿第二运动定律是描述力处于平衡时物体的运动规律C . 牛顿第三运动定律是描述物体力和运动的定量关系的规律D . 牛顿三条运动定律是一个整体,是描述宏观物体低速运动的客观规律5.下列关于保守力的说法错误的是…………………( ) 参看课本P71-72 A . 由重力对物体所做的功的特点可知,重力是一种保守力B . 由弹性力对物体所做的功的特点可知,弹性力也是一种保守力C . 由摩擦力对物体所做的功的特点可知,摩擦力也是一种保守力D . 由万有引力对物体所做的功的特点可知,万有引力也是一种保守力6.已知某质点的运动方程的分量式是,,式中R 、ω是常cos x R t ω=sin y R t ω=数.则此质点将做………………………………………………() 参看课本P19A . 匀速圆周运动B . 匀变速直线运动C . 匀速直线运动D . 条件不够,无法确定7.如图所示,三个质量相同、线度相同而形状不同的均质物体,它们对各自的几何对称轴的转动惯量最大的是………( )A . 薄圆筒B . 圆柱体 参看课本P95C . 正方体D . 一样大8.下列关于弹性碰撞的说法正确的是………………() 中学知识在课堂已复习A . 系统只有动量守恒B . 系统只有机械能守恒C . 系统的动量和机械能都守恒D . 系统的动量和机械能都不守恒9.某人张开双臂,手握哑铃,坐在转椅上,让转椅转动起来,若此后无外力矩作用.则当此人收回双臂时,人和转椅这一系统的…………………( ) 参看课本P104A . 转速不变,角动量变大B . 转速变大,角动量保持不变C . 转速和角动量都变大D . 转速和角动量都保持不变10.下列关于卡诺循环的说法正确的是………………( ) 参看课本P144 A . 卡诺循环是由两个平衡的等温过程和两个平衡的绝热过程组成的B . 卡诺循环是由两个平衡的等温过程和两个平衡的等体过程组成的C . 卡诺循环是由两个平衡的等体过程和两个平衡的等压过程组成的D . 卡诺循环是由两个平衡的绝热过程和两个平衡的等压过程组成的11. 如图所示,在场强为E 的匀强电场中,有一个半径为R 的半球面,若场强E 的方向与半球面的对称轴平行,则通过这个半球面的电通量大小为…………………( ) 参看课本P172-173A .B .2E 22R E πC . D . 02R E 12.一点电荷,放在球形高斯面的中心处,下列情况中通过高斯面的电通量会发生变化的…………………………( ) 参看课本P173 A . 将另一点电荷放在高斯面内 B . 将高斯面半径缩小C . 将另一点电荷放在高斯面外D . 将球心处的点电荷移开,但仍在高斯面内13.如图所示,在与均匀磁场垂直的平面内有一长为l 的铜棒B MN ,设棒绕M 点以匀角速度ω转动,转轴与平行,则棒的动B 生电动势大小为……………()参看课本P257A .B . Bl ω2BlωC .D . 12Bl ω212Blω14. 、方均v 、最概然速率为,则这气体分子的三种速率的关系是…………(p v ) A .B 参看课本P125v >p vC .D p v pv =15. 下列关于导体静电平衡的说法错误………………( ) 参看课本P190-191 A . 导体是等势体,其表面是等势面 B . 导体内部场强处处为零 C . 导体表面的场强处处与表面垂直 D . 导体内部处处存在净电荷16. 下列哪种现代厨房电器是利用涡流原理工作的…( ) 参看课本P259A . 微波炉B . 电饭锅17. 下列关于电源电动势的说法正确的是……………() 参看课本P249-250A . 电源电动势等于电源把电荷从正极经内电路移到负极时所作的功B . 电源电动势的大小只取于电源本身的性质,而与外电路无关C . 电动势的指向习惯为自正极经内电路到负极的指向D . 沿着电动势的指向,电源将提高电荷的电势能18. 磁介质有三种,下列用相对磁导率正确表征它们各自特性的是………( r μ)A . 顺磁质,抗磁质,铁磁质 参看课本P39-2400r μ<0r μ<1r μ?B . 顺磁质,抗磁质,铁磁质1r μ>1r μ=1r μ?C . 顺磁质,抗磁质,铁磁质0r μ>0r μ>0r μ> D . 顺磁质,抗磁质,铁磁质1r μ>1r μ<1r μ?19. 在均匀磁场中,一带电粒子在洛伦兹力作用下做匀速率圆周运动,如果磁场的磁感应强度减小,则………………………………………………( ) 参看课本P231 A . 粒子的运动速率减小 B . 粒子的轨道半径减小 C . 粒子的运动频率不变 D . 粒子的运动周期增大20. 两根无限长的载流直导线互相平行,通有大小相等,方向相反的I 1和I 2,在两导线的正中间放一个通有电流I 的矩形线圈abcd ,如图所示. 则线圈受到的合力为…………( ) 参看课本P221-223A . 水平向左B . 水平向右C . 零D . 无法判断21. 下列说法错误的是……………………………………( ) 参看课本P263A . 通过螺线管的电流越大,螺线管的自感系数也越大B . 螺线管的半径越大,螺线管的自感系数也越大C . 螺线管中单位长度的匝数越多,螺线管的自感系数也越大D . 螺线管中充有铁磁质时的自感系数大于真空时的自感系数22. 一电偶极子放在匀强电场中,当电矩的方向与场强的方向不一致时,则它所受的合力F 和合力矩M 分别为…………………………………( ) 参看课本P168-169A . F =0 ,M =0B . F ≠0 ,M ≠0C . F =0 ,M ≠0D . F ≠0 ,M =023. 若一平面载流线圈在磁场中既不受磁力,也不受磁力矩作用,这说明……( )A . 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行 参看课本P223-224B . 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行C . 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直D . 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直24. 下列关于机械振动和机械波的说法正确的是………( ) 参看课本P306A . 质点做机械振动,一定产生机械波B .波是指波源质点在介质的传播过程C . 波的传播速度也就是波源的振动速度D . 波在介质中的传播频率与波源的振动频率相同,而与介质无关25. 在以下矢量场中,属保守力场的是…………………( ) A . 静电场 B . 涡旋电场 参看课本P180,212,258C . 稳恒磁场D . 变化磁场26. 如图所示,一根长为2a 的细金属杆AB 与载流长直导线共面,导线中通过的电流为I ,金属杆A 端距导线距离为a .金属杆AB 以速度v 向上匀速运动时,杆内产生的动生电动势为……( ) 参看课本P261 (8-8)A . ,方向由B →A B .,方向由A →B2ln 20πμεIv i =2ln 20πμεIv i =C . ,方向由B →A D . ,方向由A →B0ln 32i Iv μεπ=3ln 20πμεIv i =27.在驻波中,两个相邻波节间各质点的振动………( ) 参看课本P325A . 振幅相同,相位相同B . 振幅不同,相位相同C . 振幅相同,相位不同D . 振幅不同,相位不同28.两个质点做简谐振动,曲线如图所示,则有( )A . A 振动的相位超前B 振动π/2 参看课本P291B . A 振动的相位落后B 振动π/2C . A 振动的相位超前B 振动πD . A 振动的相位与B 振动同相29.同一点光源发出的两列光波产生相干的必要条件是…() 参看课本P336A . 两光源的频率相同,振动方向相同,相位差恒定B . 两光源的频率相同,振幅相同,相位差恒定C . 两光源发出的光波传播方向相同,振动方向相同,振幅相同D .两光源发出的光波传播方向相同,频率相同,相位差恒定30.如图所示,在一圆形电流I 所在的平面内选取一个同心圆形闭合环路L ,则由安培环路定理可知……………………………………………( ) 参看课本P235A . ,且环路上任一点B =0d 0L B l ⋅=⎰B . ,但环路上任一点B ≠0d 0L B l ⋅=⎰ C . ,且环路上任一点B ≠0d 0 L B l ⋅≠⎰D . ,且环路上任一点B =常量d 0 LB l ⋅≠⎰二. 填空题:31. 平行板电容器充电后与电源断开,然后充满相对电容率为εr 的各向均匀电介质. 则其电容C 将______,两极板间的电势差U 将________. (填减小、增大或不变) 参看课本P195,20032. 某质点沿x 轴运动,其运动方程为: x =10t –5t 2,式中x 、t 分别以m 、s 为单位. 质点任意时刻的速度v =________,加速度a =________. 参看课本P16-1733. 某人相对地面的电容为60pF ,如果他所带电荷为,则他相对地面的电C 100.68-⨯势差为__________,他具有的电势能为_____________. 参看课本P200,20234. 一人从10 m 深的井中提水,起始时,桶中装有10 kg 的水,桶的质量为1 kg ,由于水桶漏水,每升高1m 要漏去0.1 kg 的水,则水桶匀速地从井中提到井口,人所作的功为____________.参看课本P70 (2-14)35.质量为m 、半径为R 、自转运动周期为T 的月球,若月球是密度均匀分布的实球体,则其绕自转轴的转动惯量是__________,做自转运动的转动动能是__________.参看课本P100 (3-4)36. 1mol 氢气,在温度为127℃时,氢气分子的总平均动能是_____________,总转动动能是______________,内能是_____________. 〔已知摩尔气体常量R = 8.31 J/(mol ·K ) 参看课本 P120 (4-8)37. 如图所示,两个平行的无限大均匀带电平面,其面电荷密度分别为+σ和-σ. 则区域Ⅱ的场强大小E Ⅱ=___________ . 参看课本P17738. 用一定波长的单色光进行双缝干涉实验时,要使屏上的干涉条纹间距变宽,可采用的方法是: (1) _________________________;(2) ________________________. 参看课本P34439. 通过磁场中任意闭合曲面的磁通量等于_________. 感生电场是由______________产生的,它的电场线是__________曲线. (填闭合或不闭合) 参看课本P212,25840. 子弹在枪膛中前进时受到的合力与时间关系为,子弹飞出枪口5400410N F t =-⨯的速度为200m /s ,则子弹受到的冲量为_____________. 参看课本P55-5641. 将电荷量为2.0×10-8C 的点电荷,从电场中A 点移到B 点,电场力做功6.0×10-6J . 则A 、B 两点的电势差U AB =____________ . 参看课本P18142. 如图所示,图中O 点的磁感应强度大小B =______________.参看课本P229-23043. 一个螺线管的自感L =10 mH ,通过线圈的电流I =2A ,则它所储存的磁能W =_____________. 参看课本P26744. 理想气体在某热力学过程中内能增加了ΔE =250J ,而气体对外界做功A =50J ,则气体吸收的热量Q = . 参看课本P132-13345. 一平面简谐波沿x 轴的正方向传播,波速为100 m/s ,t =0时的曲线如图所示,则简谐波的波长λ =____________,频率ν =_____________. 参看课本P30946. 两个同心的球面,半径分别为R 1、R 2(R 1R 2),分别<带有总电量为Q 1、Q 2. 设电荷均匀分布在球面上,则两球面间的电势差U 12= ________________________.参看课本P186-187三. 计算题:47. 一正方形线圈由外皮绝缘的细导线绕成,共绕有100匝,每边长为10 cm ,放在B = 5.0T 的磁场中,当导线中通有I =10.0A 的电流时,求: (1) 线圈磁矩m 的大小;(2) 作用在线圈上的磁力矩M 的最大值. 参看课本P225 (7-7)48.如图所示,已知子弹质量为m ,木块质量为M ,弹簧的劲度系数为k,子弹以初速v o射入木块后,弹簧被压缩了L.设木块与平面间的滑动摩擦因数为μ,不计空气阻力.求初速v o.参看课本P80 (2-23)49. 一卡诺热机的效率为40%,其工作的低温热源温度为27℃.若要将其效率提高到50%,求高温热源的温度应提高多少?参看课本P148 (5-14)50. 质量均匀的链条总长为l,放在光滑的桌面上,一端沿桌面边缘下垂,其长度为a,如图所示.设开始时链条静止,求链条刚刚离开桌边时的速度.参看课本P70 (2-18)51.一平面简谐波在t =0时刻的波形如图所示,设波的频率ν=5 Hz,且此时图中P点的运动方向向下,求:(1) 此波的波函数;(2) P点的振动方程和位置坐标.参看课本P318 (10-11)52.如图所示,A和B两飞轮的轴杆可由摩擦啮合器使之连接,A轮的转动惯量J A=10 kg·m2.开始时,B轮静止,A轮以n A= 600 r/min的转速转动.然后使A和B连接,连接后两轮的转速n = 200 r/min.求: (1) B轮的转动惯量J B ;(2) 在啮合过程中损失的机械能ΔE.参看课本P105 (3-9及补充)53.如图所示,载流I的导线处于磁感应强度为B的均匀磁场中,导线上的一段是半径为R、垂直于磁场的半圆,求这段半圆导线所受安培力.参看课本P224-22554.如图所示的截面为矩形的环形均匀密绕的螺绕环,环的内外半径分别a和b,厚度为h,共有N匝,环中通有电流为I .求: (1) 环内外的磁感应强度B;(2) 环的自感L.参看课本P237-238 (7-23及补充)55.如图所示,一长直导线通有电流I,在与其相距d处放在有一矩形线框,线框长为l ,宽为a ,共有N 匝. 当线框以速度v 沿垂直于长导线的方向向右运动时,线框中的动生电动势是多少? 参看课本P255 (8-3)二. 填空题:31. 增大 减小32.33. 1000V 0.03 J1010m/s t -210m/s t -34. 1029 (或1050) J 35. 36. 4986J 3324J 8310 J 225mR 22245mR T π37. 38. (1) 将两缝的距离变小 (2) 将双缝到光屏的距离变大σε39. 零 变化的磁场 闭合 40.41.300V42.0.2N s ⋅0112I R μπ⎛⎫- ⎪⎝⎭43. 0.02 J44. 300 J45. 0.8 m 125 Hz46.1012114Q R R πε⎛⎫- ⎪⎝⎭三. 计算题:47. 线圈磁矩22100100.110A m m NIS ==⨯⨯=⋅线圈最大磁力矩max 10550N mM mB ==⨯=⋅48. 设子弹质量为m ,木块质量为M ,子弹与木块的共同速度v由动量守恒定律得①0()mv m M v =+由功能原理得 ②2211()()22m M gL kL m M v μ-+=-+由①、②式得 0v =49. 卡诺热机效率: 211T T η=-21300500K 110.4T T η⇒===--同理 21300600K 110.5T T η'==='--高温热源应提高的温度 11600500100KT T '-=-=n50. 设桌面为零势面,由机械能守恒定律得21222a a l mg mg mv l -=-+v ⇒=51. 解:(1) 由图中v P <0知此波沿x 轴负向传播,继而知原点此时向y 正向运动原点处0002A y v =->,023ϕπ⇒=-又x = 3m 处3300y v =>,32πϕ⇒=-由 得2x ϕπλ∆∆=2x λπϕ∆=∆30236m 223πππ-=⨯=⎛⎫--- ⎪⎝⎭此波的波函数 02cos 2x y A t ππνϕλ⎛⎫=++ ⎪⎝⎭20.10cos 10m 183t x πππ⎛⎫=+- ⎪⎝⎭(2) P 点处 P P 00y v =,<P 2πϕ⇒=P 点振动方程P P cos(2)y A t πνϕ=+0.10cos 10m 2t ππ⎛⎫=+ ⎪⎝⎭P 点位置坐标 p 363321m22x λ=+=+=52. (1) 由动量矩守恒定律得A A AB ()J J J ωω=+A A AB 2()2J n J J n ππ=+B 60020010(10)6060J ⨯=+⨯2B 20kg m J ⇒=⋅(2) 损失的机械能2222A A A B A A A B 222241111()(2)()(2)222216001200104(1020)4 1.31510J 260260E J J J J n J J n ωωππππ∆=-+=-+⎛⎫⎛⎫=⨯⨯-+⨯=⨯ ⎪ ⎪⎝⎭⎝⎭53. 依题意得 d 0x x F F =∑=d d sin d sin sin d y F F BI l BIR θθθθ===0sin d 2y F F BIR BIRπθθ===⎰54. (1)0d 2B r B r Iπμ⋅=⋅=∑⎰ 环外的磁感应强度 0B =环内的磁感应强度 02B r NIπμ⋅=02NI B rμπ=(2) 0d d d 2NIhBh r r rμΦπ==001d d ln 22b a NIh NIh br r aμμΦΦππ===⎰⎰环的自感 20ln 2N h N b L I I aμψΦπ===55. 线框的动生电动势1212()N B B lvεεε=-=-001122()NIlv NIlav d d a d d a μμππ⎛⎫=-= ⎪++⎝⎭。

《大学物理》各章练习题及答案解析第1章 质点运动学一、选择题:1.以下五种运动中,加速度a保持不变的运动是 ( D ) (A) 单摆的运动。
(B) 匀速率圆周运动。
(C) 行星的椭圆轨道运动。
(D) 抛体运动。
(E) 圆锥摆运动。
2.下面表述正确的是( B )(A)质点作圆周运动,加速度一定与速度垂直; (B) 物体作直线运动,法向加速度必为零; (C)轨道最弯处法向加速度最大; (D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动,则下列说法正确的是( C )(A)质点的速度不变; (B)质点的加速度不变 (C)质点的角速度不变; (D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r , 的端点处,其速度大小为( D )()()(()22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dtrd B dt drA5. 一质点在平面上运动,运动方程为:j t i t r222+=,则该质点作( B )(A)匀速直线运动 (B)匀加速直线运动(C)抛物线运动 (D)一般曲线运动6.一质点做曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,s 表示路程,a t 表示切向加速度,对下列表达式,正确的是( B )(A)dt dr v = (B) dt ds v = (C) dtdv a = (D) dt vd a t=7. 某质点的运动方程为 3723+-=t t X (SI ),则该质点作 [ D ](A)匀加速直线运动,加速度沿 x 轴正方向; (B)匀加速直线运动,加速度沿 x 轴负方向; (C)变加速直线运动.加速度沿 x 轴正方向; (D)变加速直线运动,加速度沿 x 轴负方向8.一质点沿x 轴运动,其运动方程为()SI t t x 3235-=,当t=2s 时,该质点正在( A )(A)加速 (B)减速 (C)匀速 (D)静止1.D2. B3. C4.D5.B ,6B ,7A 8 A二 、填空题1. 一质点的运动方程为x =2t ,y =4t 2-6t ,写出质点的运动方程(位置矢量)j t t i t r)64(22-+=,t =1s 时的速度j i v22+=,加速度j a 8=,轨迹方程为x x y 32-=。

大物实验考试题库及答案1. 题目:请简述牛顿第三定律的内容,并举例说明其在日常生活中的应用。
答案:牛顿第三定律指的是作用力和反作用力的关系,即当一个物体对另一个物体施加力时,另一个物体也会对第一个物体施加一个大小相等、方向相反的力。
例如,在踢足球时,脚对足球施加一个向前的力,足球也会对脚施加一个相等大小、方向相反的力,这就是为什么踢足球时脚会感到疼痛。
2. 题目:解释什么是光的干涉现象,并描述双缝实验中观察到的干涉条纹。
答案:光的干涉现象是指两束或多束相干光波相遇时,由于光波的叠加而产生明暗相间的条纹。
在双缝实验中,当光通过两个紧密排列的缝隙时,从缝隙出来的光波会在屏幕上产生干涉条纹。
这些条纹是由于来自两个缝隙的光波相互叠加,形成构造性干涉(亮条纹)和破坏性干涉(暗条纹)的结果。
3. 题目:描述欧姆定律的数学表达式,并解释其物理意义。
答案:欧姆定律的数学表达式为 \( V = IR \),其中 \( V \) 代表电压,\( I \) 代表电流,\( R \) 代表电阻。
欧姆定律描述了在电路中,通过导体的电流与导体两端的电压成正比,与导体的电阻成反比。
物理意义是,当电阻一定时,电压越高,电流越大;当电压一定时,电阻越大,电流越小。
4. 题目:解释什么是电磁感应,并说明法拉第电磁感应定律的内容。
答案:电磁感应是指在变化的磁场中,导体中会产生电动势的现象。
法拉第电磁感应定律表明,导体中产生的电动势与穿过导体的磁通量变化率成正比。
数学表达式为 \( \mathcal{E} = -\frac{d\Phi_B}{dt} \),其中 \( \mathcal{E} \) 代表电动势,\( \Phi_B \) 代表磁通量,\( t \) 代表时间。
负号表示感应电动势的方向与磁通量变化的方向相反。
5. 题目:描述理想气体状态方程,并解释其各参数的含义。
答案:理想气体状态方程为 \( PV = nRT \),其中 \( P \) 代表气体的压强,\( V \) 代表气体的体积,\( n \) 代表气体的摩尔数,\( R \) 代表理想气体常数,\( T \) 代表气体的绝对温度。

⼤学物理教材习题答案第⼀章质点运动习题解答⼀、分析题1.⼀辆车沿直线⾏驶,习题图1-1给出了汽车车程随时间的变化,请问在图中标出的哪个阶段汽车具有的加速度最⼤。
答: E 。
位移-速度曲线斜率为速率,E 阶段斜率最⼤,速度最⼤。
2.有⼒P 与Q 同时作⽤于⼀个物体,由于摩擦⼒F 的存在⽽使物体处于平衡状态,请分析习题图1-2中哪个可以正确表⽰这三个⼒之间的关系。
答: C 。
三个⼒合⼒为零时,物体才可能处于平衡状态,只有(C )满⾜条件。
3.习题图1-3(a )为⼀个物体运动的速度与时间的关系,请问习题图1-3(b )中哪个图可以正确反映物体的位移与时间的关系。
答:C 。
由v-t 图可知,速度先增加,然后保持不变,再减少,但速度始终为正,位移⼀直在增加,且三段变化中位移增加快慢不同,根据v-t 图推知s-t 图为C 。
三、综合题:1.质量为的kg 50.0的物体在⽔平桌⾯上做直线运动,其速率随时间的变化如习题图1-4所⽰。
问:(1)设s 0=t 时,物体在cm 0.2=x 处,那么s 9=t 时物体在x ⽅向的位移是多少?(2)在某⼀时刻,物体刚好运动到桌⼦边缘,试分析物体之后的运动情况。
解:(1)由v-t 可知,0~9秒内物体作匀减速直线运动,且加速度为:220.8cm/s 0.2cm/s 4a == 由图可得:0 2.0cm s =,00.8cm/s v =, 1.0cm/s t v =-,则由匀减速直线运动的位移与速度关系可得:22002() t a s s v v -=- 2200()/2t s v v a s =-+ 22[0.8( 1.0)]/20.2 2.0cm =--?+1.1c m =(2)当物体运动到桌⼦边缘后,物体将以⼀定的初速度作平抛运动。
2.设计师正在设计⼀种新型的过⼭车,习题图1- 5为过⼭车的模型,车的质量为0.50kg ,它将沿着图⽰轨迹运动,忽略过⼭车与轨道之间的摩擦⼒。

B 班级 学号 姓名第1章 质点运动学1-2 已知质点的运动方程为r i 3j 6k e e tt-=++。
(1)求:自t =0至t =1质点的位移。
(2)求质点的轨迹方程。
解:(1) ()k j i r 630++= ()k j i r 6e 3e 1-1++= 质点的位移为()j i r ⎪⎭⎫⎝⎛-+-=3e 31e ∆(2) 由运动方程有t x e =,t y -=e 3, 6=z 消t 得 轨迹方程为 1=xy 且6=z1-3运动质点在某瞬时位于矢径()y x,r 的端点处,其速度的大小为( D ) (A)dt dr (B)dt d r(C)dt d r (D)22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx1-5某质点的运动方程为k j i r 251510t t ++-=,求:t =0,1时质点的速度和加速度。
^解:由速度和加速度的定义得k j r v t dt d 1015+==, k va 10==dtd 所以 t =0,1时质点的速度和加速度为 015==t j v 11015=+=t kj v1010,ka ==t1-8 一质点在平面上运动,已知质点的运动方程为j i r 2235t t +=,则该质点所作运动为[ B ](A) 匀速直线运动 (B) 匀变速直线运动 (C) 抛体运动 (D) 一般的曲线运动*1-6一质点沿Ox 轴运动,坐标与时间之间的关系为t t x 233-=(SI)。
则质点在4s 末的瞬时速度为 142m·s -1 ,瞬时加速度为 72m·s -2 ;1s 末到4s 末的位移为 183m ,平均速度为 61m·s -1 ,平均加速度为 45m·s -2。
解题提示:瞬时速度计算dt dxv =,瞬时加速度计算22dtx d a =;位移为()()14x x x -=∆,平均速度为()()1414--=x x v ,平均加速度为 ()()1414--=v v a】~1-11 已知质点沿Ox 轴作直线运动,其瞬时加速度的变化规律为t a x 3=2s m -⋅。

练习 十三知识点:理想气体状态方程、温度、压强公式、能量均分原理、理想气体内能一、选择题1. 容器中储有一定量的处于平衡状态的理想气体,温度为T ,分子质量为m ,则分子速度在x 方向的分量平均值为 (根据理想气体分子模型和统计假设讨论) ( )(A )x υ=(B )x υ= (C )m kT x 23=υ; (D )0=x υ。
解:(D)平衡状态下,气体分子在空间的密度分布均匀,沿各个方向运动的平均分子数相等,分子速度在各个方向的分量的各种平均值相等,分子数目愈多,这种假设的准确度愈高.2. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻耳兹曼常量,R 为摩尔气体常量,则该理想气体的分子数为 ( )(A )pV /m ; (B )pV /(kT ); (C )pV /(RT ); (D )pV /(mT )。
解: (B)理想气体状态方程NkT T N R N RT m N Nm RT M M pV AA mol ====3.根据气体动理论,单原子理想气体的温度正比于 ( )(A )气体的体积; (B )气体的压强;(C )气体分子的平均动量;(D )气体分子的平均平动动能。
解: (D)kT v m k 23212==ε (分子的质量为m )4.有两个容器,一个盛氢气,另一个盛氧气,如果两种气体分子的方均根速率相等,那么由此可以得出下列结论,正确的是 ( )(A )氧气的温度比氢气的高; (B )氢气的温度比氧气的高; (C )两种气体的温度相同; (D )两种气体的压强相同。
解:(A) kT v m k 23212==ε,2222H O H O T T m m =(分子的质量为m ) 5.如果在一固定容器内,理想气体分子速率都提高为原来的2倍,那么 ( )(A )温度和压强都升高为原来的2倍;(B )温度升高为原来的2倍,压强升高为原来的4倍; (C )温度升高为原来的4倍,压强升高为原来的2倍; (D )温度与压强都升高为原来的4倍。

一、 选择题1. 对一个作简谐振动的物体,下面哪种说法是正确的? [ C ](A) 物体处在运动正方向的端点时,速度和加速度都达到最大值; (B) 物体位于平衡位置且向负方向运动时,速度和加速度都为零; (C) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零;(D) 物体处在负方向的端点时,速度最大,加速度为零。
2. 一沿X 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为43π,则t=0时,质点的位置在: [ D ](A) 过1x A 2=处,向负方向运动; (B) 过1x A 2=处,向正方向运动;(C) 过1x A 2=-处,向负方向运动;(D) 过1x A 2=-处,向正方向运动。
3. 一质点作简谐振动,振幅为A ,在起始时刻质点的位移为/2A ,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为 [ B ]x o A ϖ x ω(A) A/2 ω (B) (C)(D)o ooxxxA ϖ x ω ωA ϖA ϖxA/2 -A/2 -A/2 (3)题4. 图(a)、(b)、(c)为三个不同的谐振动系统,组成各系统的各弹簧的倔强系数及重物质量如图所示,(a)、(b)、(c)三个振动系统的 (为固有圆频率)值之比为:[ B ](A) 2:1:1; (B) 1:2:4; (C) 4:2:1; (D) 1:1:25. 一弹簧振子,当把它水平放置时,它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上如图,试判断下面哪种情况是正确的: [ C ](A) 竖直放置可作简谐振动,放在光滑斜面上不能作简谐振动;(B) 竖直放置不能作简谐振动,放在光滑斜面上可作简谐振动; (C) 两种情况都可作简谐振动; (D) 两种情况都不能作简谐振动。
6. 一谐振子作振幅为A 的谐振动,它的动能与势能相等时,它的相位和坐标分别为: [ C ]2153(A),or ;A;(B),;332663223(C),or ;(D),;4433ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动,振动方程为 10.04cos(2)3x t ππ=+(SI ),从t = 0时刻起,到质点位置在x = m 处,且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81; (B) s 61; (C) s 41; (D) s 218. 图中所画的是两个简谐振动的振动曲线,这两个简谐振动叠加后合成的余弦振动的初相为[ C ]xtOx 1x 2(8)题(A) π23; (B) π; (C) π21 ; (D) 0二、 填空题9. 一简谐振动用余弦函数表示,振动曲线如图所示,则此简谐振动的三个特征量为: A=10cm ,/6rad /s =ωπ, /3=φπ10. 用40N 的力拉一轻弹簧,可使其伸长20 cm 。
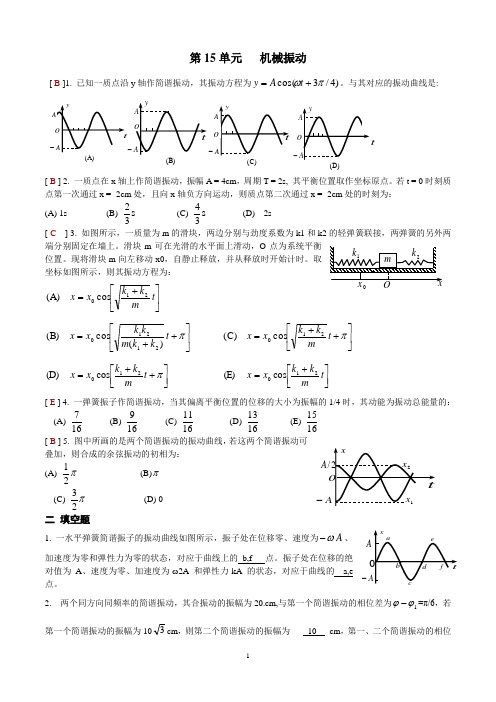
第15单元 机械振动[ B ]1. 已知一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是:[ B ] 2. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
若t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,则质点第二次通过x = -2cm 处的时刻为: (A) 1s (B)s 32 (C) s 34(D) 2s [ C ] 3. 如图所示,一质量为m 的滑块,两边分别与劲度系数为k1和k2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如图所示,则其振动方程为:⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210 ⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D)⎥⎦⎤⎢⎣⎡+=t mk k x x 210cos (E)[ E ] 4. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的: (A)167 (B) 169 (C) 1611 (D) 1613(E) 1615 [ B ] 5. 图中所画的是两个简谐振动的振动曲线,若这两个简谐振动可叠加,则合成的余弦振动的初相为:(A) π21(B)π(C) π23(D) 0二 填空题1. 一水平弹簧简谐振子的振动曲线如图所示,振子处在位移零、速度为A ω-、加速度为零和弹性力为零的状态,对应于曲线上的 b,f 点。
振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力-kA 的状态,对应于曲线的 a,e点。
2两个同方向同频率的简谐振动,其合振动的振幅为20.cm,与第一个简谐振动的相位差为1ϕϕ-=π/6,若第一个简谐振动的振幅为103cm ,则第二个简谐振动的振幅为____10___cm ,第一、二个简谐振动的相位--(C)/A -A-差21ϕϕ-为2π-。


大学物理课后习题答案(共15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1—1 一质点在xOy 平面上运动,运动方程为2135,342x t y t t t s x y m =+=+-式中以计,,以计。
(1)以时间t 为变量,写出质点位置矢量的表示式; (2)计算第1秒内质点的位移;(3)计算0t = s 时刻到4t = s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算4t = s 时质点的速度; (5)计算0t = s 到4t = s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算4t = s 是质点的加速度。
(位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式)解:(1) 质点t 时刻位矢为:j t t i t r⎪⎭⎫ ⎝⎛-+++=4321)53(2(m)(2) 第一秒内位移 j y y i x x r)()(01011-+-=∆)(5.33)101(3)01(21)01(32m j i j i +=⎥⎦⎤⎢⎣⎡-+--=(3) 前4秒内平均速度 )s m (53)2012(411-⋅+=+=∆∆=j i j i t r V(4) 速度)s m ()3(3d d 1-⋅++==j t i tr V ∴ )s m (73)34(314-⋅+=++=j i j i V(5) 前4秒平均加速度)s m (43704204-⋅=-=--=∆∆=j j V V t V a(6) 加速度)s m ()s m (d d 242--⋅=⋅==j a j tV a1—2 质点沿直线运动,速度32132()v t t m s -=++,如果当时t=2 s 时,x=4 m,求:t=3 s 时质点的位置、速度和加速度。
解:23d d 23++==t t txv c t t t c t v x x +++=+==⎰⎰241d d 34 当t =2时x =4代入求证 c =-12 即1224134-++=t t t x tt tv a t t v 63d d 23223+==++= 将t =3s 代入证)s m (45)s m (56)(414123133--⋅=⋅==a v m xP .31 1—9 一个半径R= m 的圆盘,可依绕一个水平轴自由转动,一根轻绳子饶在盘子的边缘,其自由端拴一物体。

习题1选择题(1) 一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为(A)dt dr (B)dtr d(C)dtr d ||(D) 22)()(dt dy dt dx +[答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为 (A)t R t R ππ2,2 (B) tRπ2,0(C) 0,0 (D)0,2tRπ [答案:B]填空题(1) 一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是 ;经过的路程是 。
[答案: 10m ; 5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m ·s -1,则当t 为3s 时,质点的速度v= 。
[答案: 23m ·s -1 ](3) 轮船在水上以相对于水的速度1V 航行,水流速度为2V,一人相对于甲板以速度3V 行走。
如人相对于岸静止,则1V 、2V 和3V的关系是 。
[答案: 0321=++V V V]一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状;(2) 物体的内部结构;(3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
下面几个质点运动学方程,哪个是匀变速直线运动(1)x=4t-3;(2)x=-4t3+3t2+6;(3)x=-2t2+8t+4;(4)x=2/t2-4/t。
给出这个匀变速直线运动在t=3s时的速度和加速度,并说明该时刻运动是加速的还是减速的。
习题六6—1 一轻弹簧在60N得拉力下伸长30cm。
现把质量为4kg物体悬挂在该弹簧得下端,并使之静止,再把物体向下拉10cm,然后释放并开始计时。
求:(1)物体得振动方程;(2)物体在平衡位置上方5cm时弹簧对物体得拉力;(3)物体从第一次越过平衡位置时刻起,到它运动到上方5cm处所需要得最短时间。
[解] (1)取平衡位置为坐标原点,竖直向下为正方向,建立坐标系设振动方程为x=cos(7、07t+φ)t=0时, x=0、1 0、1=0、1cosφφ=0故振动方程为x=0、1cos(7、07t)(m)(2)设此时弹簧对物体作用力为F,则:F=k(Δx)=k(x0 +x)=mg/k=40/200=0、2(m)其中x因而有F= 200(0、2-0、05)=30(N)(3)设第一次越过平衡位置时刻为t1,则:0=0、1cos(7、07t1 ) t1 =0、5π/7、07第一次运动到上方5cm处时刻为t2,则-0、05=0、1cos(7、07t2) t2=2π/(3×7、07)故所需最短时间为:Δt=t2 -t1 =0、074s6—2 一质点在x轴上作谐振动,选取该质点向右运动通过点A时作为计时起点(t=0),经过2s后质点第一次经过点B,再经2s后,质点第二经过点B,若已知该质点在A、B两点具有相同得速率,且AB=10cm,求:(1)质点得振动方程:(1)质点在A点处得速率。
[解] 由旋转矢量图与可知s(1) 以得中点为坐标原点,x轴指向右方。
t=0时,t=2s时,由以上二式得因为在A点质点得速度大于零,所以所以,运动方程为:(2)速度为:当t=2s时6—3 一质量为M得物体在光滑水平面上作谐振动,振幅为12cm,在距平衡位置6cm处,速度为24,求:(1)周期T; (2)速度为12时得位移。
[解] (1) 设振动方程为以、、代入,得:利用则解得(2) 以代入,得:解得: 所以故6—4 一谐振动得振动曲线如图所示,求振动方程。
[解] 设振动方程为:根据振动曲线可画出旋转矢量图由图可得: φ=2π/3ω=Δφ/Δt=(π/3+π/2)/2=5π/12故振动方程为x=10cos(5πt/12+2π/3) (cm)6—5 一质点沿x轴作简谐振动,其角频率,试分别写出以下两种初始状态得振动方程;(1)其初始位移=7、5 cm,初始速度;(2)其初始位移=7、5 cm,初速度。
[解] 设振动方程为x=A cos(10t+φ)(1) 由题意得: 7、5=Acosφ75=-10A sinφ解得: A=10、6cm故振动方程为:x=10、6cos(10t)(cm)(2) 同理可得:x=10、6cos(10t)本题用旋转矢量法更为直观。
另外,同学们在做作业时,不要用“同理可得”。
6—6 一轻弹簧在60 N得拉力作用下可伸长30cm。
现将一物体悬挂在弹簧得下端并在它上面放一小物体,它们得总质量为4kg待其静止后再把物体向下拉10cm,然后释放。
问:(1)此小物体就是停止在推动物体上面还就是离开它?(2)如果使放在振动物体上得小物体与振动物体分离,则振幅A需满足何条件?二者在何位置开始分离?[解] (1)小物体停止在振动物体上不分离。
(2) 设在平衡位置弹簧伸长,则又故当小物体与振动物体分离时,即,故在平衡位置上方0、196m处分离。
6—7 一木板在水平面上作简谐振动,振幅就是12cm,在距平衡位置6cm处,速度就是24。
如果一小物块置于振动木板上,由于静摩擦力得作用,小物块与木板一起运动(振动频率不变),当木板运动到最大位移处时,物块正好开始在木板上滑动,问物块与木板之间得静摩系数就是多大?[解] 设振动方程为x=12cos(ωt+φ)则:v=-12ωsin(ωt+φ)以x=6cm v=24cm/s代入得:6=12cos(ωt+φ)24=-12ωsin(ωt+φ)解得ω=最大位移处:由题意,知6—8 两根倔强系数分别为与得轻弹簧串接后,上端固定,下端与质量为m得物体相连结,组成振动系统。
当物体被拉离平衡位置而释放时,物体就是否作谐振动?若作谐振动,其周期就是多少?若将两弹簧并联,其周期就是多少?[解] (1) 串接:当弹簧、与物体静止时,将串接得两弹簧瞧作一个弹性系数为k得弹簧,由于,得到选平衡位置为坐标原点,正方向朝下。
分析受力,根据牛顿第二定律。
由于,代入得到,符合第二个判据,所以该系统得运动就是简谐振动。
其角频率因此周期(2) 并接:当弹簧、与物体静止时,将并接得两弹簧瞧作一个弹性系数为k得弹簧,由于,得到选平衡位置为坐标原点,,正方向朝下。
分析受力,根据牛顿第二定律。
由于,代入得到,符合第二个判据,所以该系统得运动就是简谐振动。
其角频率因此周期6—9 在竖直平面内半径为R得一段光滑圆弧轨道上放一小物体,使其静上于轨道得最低点,如图所示。
若触动小物体,使其沿圆弧形轨道来回作小幅度运动,试证明:(1)此物体作谐振动;(2)振动周期。
[证明] 取最低点为平衡位置,物体与O点连线偏离得角为。
(1) 物体与O点连线偏离角时,指向平衡位置得力矩,很小,故,所以可见该力矩为指向平衡位置得线形回复力矩,故物体作谐振动。
(2) 因为所以因此所以6—10 如图所示,半径为R得圆环静止于刀口点O上,令其在自身平面内作微小得摆动。
(1)求其振动得周期;(2)求与其振动周期相等得单摆得长度。
[解] (1)设圆环偏离角度为,所作振动为谐振所以(2) 单摆周期为得摆长为。
6—11 如图所示,质量为m、半径为R得半圆柱,可绕圆柱得轴线O在重力作用下作微振动,已知半圆柱得质心在距轴处,求其振动周期。
[解] OC偏离中垂线角时指向中间得力矩根据转动定理其中代入得即所以因此6—12 测量液体阻尼系数得装置如图所示。
若在空气中测得振动频率为,在液体中测得振动频率为,求在液体中物体振动时得阻尼因子。
[解] 在空气中振动方程为在液体中振动方程(为阻尼系数)对应得振动角频率则即所以6—13 一弹簧振子,当位移就是振幅之半时,该振动系统得动能与总能量之比就是多少?位移为多大时,动能与势能各占总能量之半?[解] 设振幅为A,弹簧倔强系数为k,(1) 当位移就是振幅之半时(2) 位移为x时,动能、势能各占总能量得一半则有所以6—14 一弹簧振子,弹簧得倔强系数,当物体以初动能0、2J与初势能0、6J振动时,(1)求谐振动得振幅;(2)位移就是多大时,势能与动能相等?(3)位移就是振幅之半时,势能就是多大?[解] (1) 设振幅为A,由机械能守恒定律,得kA2 /2=0、2+0、6A=(1、2/25)1/2 =0、253 (m)(2) 动能、势能相等时有:kx2 /2=0、4x=±0、179 (m)(3) 位移为振幅一半时,势能为=0、5k(0、5A)2=E/4=0、2 (J)6—15 如图所示,有一水平弹簧振子,弹簧得倔强系数,重物得质量为m=6 kg,重物静止在平衡位置上。
设以一水平恒力F=10 N向左作用于物体(无摩擦),使之由平衡位置向左运动了0、05 m,此时撤去力F。
当重物运动到左方最大位置时开始计时,求物体得振动方程。
[解] 以平衡位置为坐标原点,向右为正方向建立坐标系, 设振幅为A,由动能定理可得: FS=kA2 /2A=(2FS/k)1/2=(2×10×0、05/24)1/2=0、204 (m)ω=(k/m)1/2 =2 (rad/s)又因物体运动到左边最大位移处开始计时,故初相为π故得运动方程为: x=0、204cos(2t+π) (m)本题必须建立坐标系,否则,相位不能确定。
6—16 两谐振动得振动方程分别为(SI)试求其合振动得振幅与初相位。
[解] 由振动合成公式,得:6—17 两个同方向、同频率得谐振动,其合振动得振幅为20cm,合振动与第一个谐振动得相位差为。
若第一个谐振动得振幅为cm,求第二个谐振动得振幅及第一、二两谐振动得相位差。
[解] 由题意可画出两简谐振动合成得矢量图,由图知易证故第一、二两振动得相位差为6—18 质量为0、4kg得质点同时参与两个互相垂直得振动(S1)求:(1)质点得轨迹方程;(2)质点在任一位置所受得作用力。
[解] (1) y方向得振动可化为消去三角函数部分可得质点得轨迹方程为(2) 由可得同理因此6—19 一平面简谐波沿x轴正向传播,振幅A=10cm,圆频率,当t=1、0s时,x=10cm处质点得位移为零,速度沿负方向,此时x=20cm处质点得位移为5、0cm,速度沿正方向。
已知波长>10cm,试写出该波得波函数。
[解] 由已知得A=0、1m, ,波沿x轴正向传播,故可设波函数为:(m)当t=1s 时,x=0、1m处,y=0m 故故有: (1)对t=1、0s ,x=0、2m 处,有故有: (2)对(1)、(2)两式k取相同得值得根据就是>10cm由(1)、(2)得:故所求波函数为6—20 一简谐波得周期T=0、5s,波长=10 m,振幅A=0、1 m。
当t=0时刻,波源振动得位移恰好为正方向得最大值。
若坐标原点与波源重合,且波沿Ox轴正向传播;求:(1)此波得波函数,(2)时刻,处质点得位移;(3)时刻, 处质点得振动速度。
[解] (1)由已知条件,可设波函数为:由已知t=0,x=0时,y=0、1m故由此得因而波函数为(2) ,处:(3) ,处,振动速度为6—21 一平面简谐波沿Ox轴正向传播,其振幅为A,频率为,波速为u。
设时刻得波形曲线如图所示。
求:(1)x=0处质点得振动方程;(2)该波得波函数。
[解] (1) 设x处该质点得振动方程为:所以,得时:,所以x=0处得振动方程为:(2) 该波得波函数为:6—22 根据如图所示得平面简谐波在t=0时刻得波形图,试求:(1)该波得波函数;(2)点P 处得振动方程。
[解] 由已知,得u=0、08m/s,λ=0、4m(1) 设波函数为:当t=0,x=0时因故则波函数为:(2) 将P点坐标代入上式,得6—23 已知一简谐平面波得波函数为。
(1)试求t=4、2s时各波峰位置得坐标表示式,井计算此时离原点最近得一个波峰得位置,该波峰何时通过原点?(2)画出t=4、2 s时得波形曲线。
[解] (1) 波峰位置满足条件所以显然k=0、8时,x=-0、4,离坐标原点最近,设通过原点时刻为t,则所以(2) t=4、2s时得波形曲线6—24 一平面简谐波沿Ox轴正向传播,其振幅与角频率分别为A与,波速为u。
设t=0时得波形曲线如图所示。
(1)写出该波得波函数;(2)求距点O分别为与两处质点得振动方程;(3)求距点O分别为与两处质点在t=0时得振动速度。
[解] (1) 波函数(2) 时,时,(3)6—25 如图所示为一平面简谐波在t=0时刻得波形图,试画出点P处质点与点Q处质点得振动曲线,然后写出相应得振动方程。