第五章Nyquist稳定判据
- 格式:ppt
- 大小:2.35 MB
- 文档页数:71


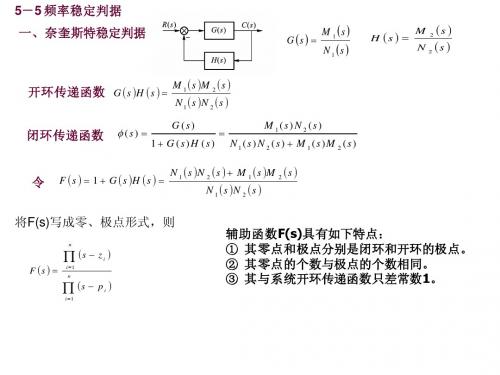







第五节奈奎斯特稳定判据一、幅角定理:对于一个复变函数)())(()())(()(2121n m p s p s p s z s z s z s K s F ++++++=式中-z i (i=1,2,…,m)为F (s )的零点,-p j (j=1,2,…,n)为F (s )的极点。
函数F (s )是复变量s 的单值函数,s 可以在整个S 平面上变化,对于其上的每一点,除有限(n)个极点外,函数F (s )都有唯一的一个值与之对应。
)1,1(j d s -⋅)1,0(j d f -⋅平面s 平面)(s F ⇒⨯1-2-[例]设:,则S 平面上d s 点(-1,j 1),映射到F(s )平面上的点d f 为(0,-j 1),见下图:ss s F 2)(+=jjj F j j F -=+-+=+-=-=+++=+1)1(112)(时,,,当ωσωσωσF (s )的值域构成的复平面称为F (s )平面。
S 平面上的每一点依照所给的函数关系,将映射到F (s )平面上的相应点。
其中S 平面上的全部零点都映射到F (s )平面上的原点;S 平面上的极点映射到F (s )平面上时都变成了无限远点。
除了S 平面上的零、极点之外的普通点,映射到F (s )平面上是除原点之外的有限远点。
注意,虽然函数F (s )从S 平面到F (s )平面的映射是一一对应的,然而逆过程往往并非如此。
例如已知)2)(1()(++=s s s Ks F 这个函数在有限的S 平面上除S =0,-1, -2以外均解析,除此三点外,S 平面上的每一个S 值在F (s )平面只有一个对应点,但是F (s )平面上的每一个点在S 平面上却有三个映射点。
最简单的说明方式就是将方程改写成)()2)(1(s F Ks s s =++当F (s )取一个常数时上式是一个三次方程,应有三个根与之对应。
现考虑S 平面上一点s 1映射到F (s )平面上的点F (s 1)可以用一个向量来表示,即当∏∏=+∠=+∠∠++==nj p s j j mi z s j i s F j j i ep sez s K e s F s F 1)(11)(1)(11111)()(向量的幅值为∑+∠-∑+∠=∠==nj j mi i p s z s s F 11111)()()(⎥⎥⎦⎤⎢⎢⎣⎡+∠-+∠==∑∑++===∏∏n j j m i i p s z s j nj jmi iep sz s K 1111)()(1111∏∏==++=nj j m i i p sz s K s F 11111)()()(∏∏==++=nj jm i ip sz s K s F 11111)(向量的相角为ReIm ReIm S 平面F(s)平面⨯)(s ϕ)(s F⨯⨯∙∙平面)(s F 平面s 1-2-⨯[例]设:,则s 平面上d s 点(-1,j1),映射到F (s )平面上的点d f 为(0,-j1),计算如下:ss s F 2)(+=jjjj F j j j F -=+-+=+-=-=+++=+11)1(112)(时,,,当ωσωσωσωσ⇒)1,1(j d s -⋅⋅)1,0(j d f -⋅⋅向量的相角为︒-=︒-︒=+∠-+∠=∠9013545)()()(111j i p s z s s F 向量的幅值为111)1(=-=+-+=+-j jjj F 若取d s 点为(-1,j0)则在F (s )平面的向量的幅值为1向量的相角为-180°当S 平面上动点s 从s 1经过某曲线C S 到达s 2,映射到F (s )平面上也将是一段曲线C F ,该曲线完全由F (s )表达式和s 平面上的曲线C S 决定。

![[工学]控制工程基础第五章系统的稳定性](https://img.taocdn.com/s1/m/063b2600cfc789eb172dc863.png)



第五章线性系统的频域分析法5.4 线性系统稳定性分析对数幅相图——Nichols图纵坐标为20lg|G(jω)| ,单位为dB,线性分度。
横坐标为∠G(jω),单位为度, 线性分度。
Nichols图的绘制过程:先绘制出Bode图,再由其绘制Nichols图。
多用于控制系统校正。
)1)(10(100)(++=s s s s G )1)(11.0(100)(++=s s s s G 例:已知系统开环传递函数为解:(1) 首先将系统开环传递函数写成典型环节串联的形式,即试绘制该系统的开环对数频率特性曲线。
5.4 Nyquist稳定判据和相对稳定性稳定判据:代数判据—Routh判据判断工程实用的图解法判据—Nyquist稳定性判据和Bode图稳定性判据判别系统的稳定性,实际上就是判别系统在S平面右半平面有否闭环极点。
幅角定理设F(S)是复变量S的单值连续解析函数(除S平面上的有限个奇点外)。
S平面上的某一封闭曲线D的内部包含了F(S)的P个极点和Z个零点(包含重根点),且曲线D不通过F(S)任何一个零点和极点。
当S按顺时针方向沿封闭曲线D连续的变化一周时,曲线F(S)在复平面上也按顺时针方向包围原点N=Z-P圈此处定义N为顺时针圈数,即顺时针圈数为正数,逆时针圈数为负数,总圈数为顺时针圈数与逆时针圈数的代数和。
由于系统闭环稳定性与S 平面右半平面中的闭环特征根的数量有关。
故如果选取a)s 平面封闭曲线D 为顺时针包含整个S 平面右半平面的曲线b)F(S)选为F(S)=1+G(s)H(s)()()11()B s F s G(s)H(s)A s =+=+F (s )的极点为开环系统的极点,F (s )的零点为闭环极点则有:有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)假设S平面右半平面包含了F(S)的P个极点和Z个零点,即封闭曲线D包围了F(S)在S右半平面的P个极点和Z个零点根据幅角定理,系统稳定⇒F(S)在S右半平面的零点数Z=0⇒F(S)顺时针包围原点的次数满足N=Z-P=-P。


