精选2010年中考数学压轴题100题
- 格式:doc
- 大小:3.46 MB
- 文档页数:36


2010年中考数学压轴题100题精选(5160题)答案2010年中考数学压轴题100题精选(51-60题)【051】如图14(1),抛物线与x轴交于A、B两点,与y 轴交于点C(0,).[图14(2)、图14(3)为解答备用图](1),点A的坐标为,点B的坐标为;(2)设抛物线的顶点为M,求四边形ABMC的面积;(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;(4)在抛物线上求点Q,使△BCQ是以BC为直角边的直角三角形.图14(1)图14(2)图14(3)【052】已知二次函数()的图象经过点,,,直线()与轴交于点.(1)求二次函数的解析式;(2)在直线()上有一点(点在第四象限),使得为顶点的三角形与以为顶点的三角形相似,求点坐标(用含的代数式表示);(3)在(2)成立的条件下,抛物线上是否存在一点,使得四边形为平行四边形?若存在,请求出的值及四边形的面积;若不存在,请说明理由.yxO【053】如图所示,在平面直角坐标系中,抛物线()经过,,三点,其顶点为,连接,点是线段上一个动点(不与重合),过点作轴的垂线,垂足为,连接.(1)求抛物线的解析式,并写出顶点的坐标;(2)如果点的坐标为,的面积为,求与的函数关系式,写出自变量的取值范围,并求出的最大值;12331DyCBAP2ExO(3)在(2)的条件下,当取得最大值时,过点作的垂线,垂足为,连接,把沿直线折叠,点的对应点为,请直接写出点坐标,并判断点是否在该抛物线上.【054】如图,在直角坐标系中,矩形ABCD的边AD在y 轴正半轴上,点A、C的坐标分别为(0,1)、(2,4).点P从点A出发,沿A→B→C以每秒1个单位的速度运动,到点C停止;点Q在x轴上,横坐标为点P的横、纵坐标之和.抛物线经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S (平方单位).(1)求抛物线对应的函数关系式.(2)分别求t=1和t=4时,点Q的坐标.(3)当0<≤5时,求S与t之间的函数关系式,并直接写出S的最大值.【055】在平面直角坐标系中,现将一块等腰直角三角板放在第二象限,斜靠在两坐标轴上,且点,点,如图所示:抛物线经过点.(1)求点的坐标;(2)求抛物线的解析式;(3)在抛物线上是否还存在点(点除外),使仍然是以为直角边的等腰直角三角形?若存在,求所有点的坐标;若不存在,请说明理由.BACxy(0,2)(-1,0)(第25题)【056】如图18,抛物线F:的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:,抛物线F′与x轴的另一个交点为C.⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);⑵若a、b、c满足了①求b:b′的值;②探究四边形OABC的形状,并说明理由.图18【057】直线与坐标轴分别交于、两点,、的长分别是方程的两根(),动点从点出发,沿路线→→以每秒1个单位长度的速度运动,到达点时运动停止.(1)直接写出、两点的坐标;(2)设点的运动时间为(秒),的面积为,求与之间的函数关系式(不必写出自变量的取值范围);(3)当时,直接写出点的坐标,此时,在坐标轴上是否存在点,使以、、、为顶点的四边形是梯形?若存在,请直接写出点的坐标;若不存在,请说明理由.【058】如图,已知抛物线与轴交于A、B两点,与轴交于点C.(1)求A、B、C三点的坐标.(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP 的面积.CPByA(3)在轴上方的抛物线上是否存在一点M,过M作MG 轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.【059】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN 的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(4分)(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(4(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.(5分)图(2)MBEACDFG NNMBE CDFG图(1)【060】已知:如图所示,关于的抛物线与轴交于点、点,与轴交于点.(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点,使四边形为等腰梯形,写出点的坐标,并求出直线的解析式;BAOCyx(第26题图)(3)在(2)中的直线交抛物线的对称轴于点,抛物线上有一动点,轴上有一动点.是否存在以为顶点的平行四边形?如果存在,请直接写出点的坐标;如果不存在,请说明理由.2010年中考数学压轴题100题精选(51-60题)答案【051】解:(1),(-1,0),B(3,0). (3)分(2)如图14(1),抛物线的顶点为M(1,-4),连结OM.则△AOC的面积= ,△MOC的面积= ,△MOB的面积=6,∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.···················································6分图14(2)说明:也可过点M作抛物线的对称轴,将四边形ABMC的面积转化为求1个梯形与2个直角三角形面积的和.(3)如图14(2),设D(m,),连结OD.则0<m<3,<0.且△AOC的面积= ,△DOC的面积= ,△DOB的面积=- (),∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积= = .图14(3)图14(4)∴存在点D ,使四边形ABDC的面积最大为.(4)有两种情况:如图14(3),过点B作BQ1⊥BC,交抛物线于点Q1、交y 轴于点E,连接Q1C.∵∠CBO=45°,∴∠EBO=45°,BO=OE=3.∴点E的坐标为(0,3).∴直线BE的解析式为.····················12分由解得∴点Q1的坐标为(-2,5).······13分如图14(4),过点C作CF⊥CB,交抛物线于点Q2、交x 轴于点F,连接BQ2.∵∠CBO=45°,∴∠CFB=45°,OF=OC=3.∴点F的坐标为(-3,0).∴直线CF的解析式为.····················14分由解得∴点Q2的坐标为(1,-4).综上,在抛物线上存在点Q1(-2,5)、Q2(1,-4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形.yxOBADC(x=m)(F2)F1E1 (E2)【052】解:(1)根据题意,得解得..(2分)(2)当时,得或,∵,当时,得,∴,∵点在第四象限,∴.······························(4分)当时,得,∴,∵点在第四象限,∴.···················································(6分)(3)假设抛物线上存在一点,使得四边形为平行四边形,则,点的横坐标为,当点的坐标为时,点的坐标为,∵点在抛物线的图象上,∴,∴,∴,∴(舍去),∴,∴.·······································································(9分)当点的坐标为时,点的坐标为,∵点在抛物线的图象上,∴,∴,∴,∴(舍去),,∴,∴.【053】解:(1)设,把代入,得, (2)分∴抛物线的解析式为:.顶点的坐标为.·························5分(2)设直线解析式为:(),把两点坐标代入,得解得.∴直线解析式为.·················7分,∴············9分.················································10分∴当时,取得最大值,最大值为.·················································11分(E)12331DyCBAP2xOFMH(3)当取得最大值,,,∴.∴四边形是矩形.作点关于直线的对称点,连接.法一:过作轴于,交轴于点.设,则.在中,由勾股定理,.解得.∵,∴.由,可得,.∴.∴坐标.·············································································13分法二:连接,交于点,分别过点作的垂线,垂足为.易证.(E)12331DyCBAP2xOFMHNM∴.设,则.∴,.由三角形中位线定理,.∴,即.∴坐标. (13)分把坐标代入抛物线解析式,不成立,所以不在抛物线上.··············14分【054】(1)由抛物线经过点A(0,1),C(2,4),得解得∴抛物线对应的函数关系式为:.·························(2分)(2)当时,P点坐标为(1,1),∴Q点坐标为(2,0).当时,P点坐标为(2,3),∴Q点坐标为(5,0).·······················(5分)(3)当≤2时,.S .当≤5时,.S .(8分)BADCOMNxyP1P2 当时,S的最大值为2.···················································(10分)【055】(1)过点作轴,垂足为,;又,,点的坐标为; (4)分(2)抛物线经过点,则得到, (5)分解得,所以抛物线的解析式为;····································7分(3)假设存在点,使得仍然是以为直角边的等腰直角三角形:若以点为直角顶点;则延长至点,使得,得到等腰直角三角形,·····················8分过点作轴,;,可求得点;·······11分若以点为直角顶点;则过点作,且使得,得到等腰直角三角形,···········12分过点作轴,同理可证;·····································13分,可求得点;·······································14分经检验,点与点都在抛物线上.······················16分【056】解:(1)C(3,0);(2)①抛物线,令=0,则= ,∴A点坐标(0,c).∵,∴,∴点P的坐标为().∵PD⊥轴于D,∴点D的坐标为().……………………………………5分根据题意,得a=a′,c= c′,∴抛物线F′的解析式为.又∵抛物线F′经过点D(),∴.……………6分∴.又∵,∴.∴b:b′= .②由①得,抛物线F′为.令y=0,则.∴.∵点D的横坐标为∴点C的坐标为().设直线OP的解析式为.∵点P的坐标为(),∴,∴,∴.∵点B是抛物线F与直线OP的交点,∴.∴.∵点P的横坐标为,∴点B的横坐标为.把代入,得.∴点B的坐标为.∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),∴四边形OABC是平行四边形.又∵∠AOC=90°,∴四边形OABC是矩形.【057】(1)(2)∵,,∴当点在上运动时,,;当点在上运动时,作于点,有∵,∴∴(3)当时,,,此时,过各顶点作对边的平行线,与坐标轴无第二个交点,所以点不存在;当时,,,此时,、【058】解:(1)令,得解得,令,得ECB yPA∴A B C ·········3分(2)∵OA=OB=OC= ∴BAC= ACO= BCO=∵AP∥CB,∴PAB= ,过点P作PE 轴于E,则APE为等腰直角三角形令OE= ,则PE= ∴P∵点P在抛物线上∴解得,(不合题意,舍去)∴PE= ·······································4分∴四边形ACBP的面积= AB?OC+AB?PE= ·····················5分(3).假设存在∵PAB= BAC = ∴PA AC∵MG 轴于点G,∴MGA= PAC =在Rt△AOC中,OA=OC= ∴AC= ,在Rt△PAE中,AE=PE= ∴AP= ··6分GM CB yPA设M点的横坐标为,则M①点M在轴左侧时,则(ⅰ) 当AMG PCA时,有= ∵AG= ,MG= 即解得(舍去)(舍去)………7分(ⅱ) 当MAG PCA时有= GM CB yPA即,解得:(舍去)∴M ···············································································8分②点M在轴右侧时,则(ⅰ) 当AMG PCA时有=∵AG= ,MG=∴解得(舍去)∴M(ⅱ) 当MAG PCA时有= 即解得:(舍去)∴M ∴存在点M,使以A、M、G三点为顶点的三角形与PCA相似,M点的坐标为,,MBEACNDFG图(1)H 【059】解:(1)∵四边形ABCD 和四边形AEFG是正方形∴AB=AD,AE=AG,∠BAD=∠EAG=90o∴∠BAE+∠EAD=∠DAG+∠EAD∴∠BAE=∠DAG∴△BAE≌△DAG …………4分(2)∠FCN=45o …………5分理由是:作FH⊥MN于H∵∠AEF=∠ABE=90o∴∠BAE +∠AEB=90o,∠FEH+∠AEB=90o∴∠FEH=∠BAE 又∵AE=EF,∠EHF=∠EBA =90o∴△EFH≌△ABE …………7分∴FH=BE,EH=AB=BC,∴CH=BE=FH∵∠FHC=90o,∴∠FCH=45o …………8分MBEACNDFG图(2)H (3)当点E由B向C运动时,∠FCN的大小总保持不变,…………9分理由是:作FH⊥MN于H由已知可得∠EAG=∠BAD=∠AEF=90o结合(1)(2)得∠FEH=∠BAE=∠DAG又∵G在射线CD上,∠GDA=∠EHF=∠EBA=90o ∴△EFH≌△GAD,△EFH∽△ABE ……11分∴EH=AD=BC=b,∴CH=BE,∴==∴在Rt△FEH中,tan∠FCN===BAOCyx第26题图Q4Q3Q1Q2P3P1P2DCP4∴当点E由B向C运动时,∠FCN 的大小总保持不变,tan∠FCN=【060】解:(1)根据题意,得,解得抛物线的解析式为,顶点坐标是(2,4)(2),设直线的解析式为直线经过点点(3)存在.,,,。

2010全国中考数学经典压轴题100题(三)答案【021】解:(1)21k k −;………………………………3分(2)①EF ∥AB .……………………………………4分证明:如图,由题意可得A (–4,0),B (0,3),2(4,)4k E −−,2(,3)3k F .∴PA=3,PE=234k +,PB=4,PF=243k +.∴223121234PA k PEk ==++,224121243PB k PFk ==++∴∴7分②过轴于点N ,两线交由上知M (0,24−),N (23,0),Q (23,24k −).…8分而S △EFQ=S △PEF ,∴S2=S △PEF -S △OEF =S △EFQ -S △OEF =S △EOM +S △FON +S 矩形OMQN =4321212222kk k k ⋅++=222112k k+=221(6)312k+−.…………………………10分当26k>−时,S2的值随k2的增大而增大,而0<k2<12.……………11分∴0<S2<24,s2没有最小值.………12分说明:1.证明AB∥EF时,还可利用以下三种方法.方法一:分别求出经过A、B两点和经过E、F两点的直线解析式,利用这两个解析式中x的系数相等来证明AB∥EF;方法二:利用tan PAB∠=tan PEF∠来证明AB∥EF;方法三:连接AF、BE,利用S△AEF=S△BFE得到点A、点B到直线EF 的距离相等,再由A、B两点在直线EF同侧可得到AB∥EF.2.求S2的值时,还可进行如下变形:S2=S△PEF-S△OEF=S△PEF-(S四边形PEOF-S△PEF)=2S△PEF-S四边形PEOF,再利用第(1)题中的结论.【022】解:(1)设抛物线的解析式为:y=a(x-m+2)(x-m -2)=a(x-m)2-4a.……2分∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=4,∴C(m,-2)代入得a=12.∴解析式为:y=12(x-m)2-2.………………………5分(亦可求C点,设顶点式)(2)∵m为小于零的常数,∴只需将抛物线向右平移-m个单位,再向上平移2个单位,可以使抛物线y =12(x -m)2-2顶点在坐标原点.……………………………………7分(3)由(1)得D(0,12m2-2),设存在实数m ,使得△BOD 为等腰三角形.∵△BOD 为直角三角形,∴只能OD =OB .……………9分∴12m2-2=|m +2|,当m +2>0时,解得m =4或m =-2(舍).当m +2<0时,解得m =0(舍)或m =-2(舍);当m +2=0时,即m =-2时,B 、O 、D 三点重合(不合题意,舍)综上所述:存在实数m =4,使得△BOD 为等腰三角形.……………………………12分【023】(1)证明:∵MBC △是等边三角形∴60MB MC MBC MCB ===°,∠∠∵M 是AD 中点∴AM MD =∵AD BC∥∴60AMB MBC ==°∠∠,60DMC MCB ==°∠∠∴AMB DMC △≌△∴AB DC =∴梯形ABCD 是等腰梯形.(2)解:在等边MBC △中,4MB MC BC ===,60MBC MCB ==°∠∠,60MPQ =°∠∴120BMP BPM BPM QPC +=+=°∠∠∠∠∴BMP QPC =∠∠∴BMP CQP △∽△∴PC CQBM BP =5分∵PC x MQ y ==,∴44BP x QC y =−=−,6分ADCBPMQ60°∴444x y x−=−∴2144y x x =−+7分(3)解:①当1BP =时,则有BP BP MD ∥∥,则四边形ABPM和四边形MBPD均为平行四边形∴211333444MQ y ==×−+=当3BP =时,则有PC AM PC MD ∥∥,,则四边形MPCD和四边形APCM均为平行四边形∴11311444MQ y ==×−+=∴当1314BP MQ ==,或1334BP MQ ==,时,以P 、M 和A 、B 、C 、D△y 取最小值时,x =∴P°,∴30CPQ =°∠,∴∠【ABC 为等腰直∴3,0m −).(2)∵45ODA OAD ∠=∠=°∴3OD OA m ==−,则点D 的坐标是(0,3m −).又抛物线顶点为(1,0)P ,且过点B 、D ,所以可设抛物线的解析式为:2(1)y a x =−,得:22(31)(01)3a m a m ⎧−=⎪⎨−=−⎪⎩解得14a m =⎧⎨=⎩∴抛物线的解析式为221y x x =−+………7分(3)过点Q 作QM AC ⊥于点M ,过点Q 作QN BC ⊥于点N ,设点Q 的坐标是2(,21)x x x −+,则2(1)QM CN x ==−,3MC QN x ==−.∵//QM CE ∴PQM ∆∽PEC∆∴QM PMEC PC =即2(1)12x x EC −−=,得2(1)EC x =−∵//QN FC∴BQN∆∽BFC∆∴QN BNFC BC=即234(1)4x x FC −−−=,得41FC x =+又∵4AC =∴2(1)8x +=即【M 的纵坐标为-x ∣=x ;∴C x+4+x )=8的周长不发生变(2)根据题意得:S 四边形OCMD =MC ·MD =(-x+4)·x =-x2+4x =-(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x (0<x<4)的二次函数,并且当x =2,即当点M 运动到线段AB 的中点时,四边形OCMD 的面积最大且最大面积为4;(3)如图10(2),当20≤<a时,42121422+−=−=aaS;如图10(3),当42<≤a时,22)4(21)4(21−=−=aaS;∴S与a的函数的图象如下图所示:的))4<≤a【026】解:(1)∵AH∶AC=2∶3,AC=6 ∴AH=23AC=23×ACB………1分 ∴2分 ∴3分 (4分∵′H为平行四边5分又∴当CD=CH=2时,四边形CDH′H为正方形此时可得t=2秒时,四边形CDH′H为正方形………6分 ②(Ⅰ)∵∠DEF=∠ABC,∴EF∥AB∴当t=4秒时,直角梯形的腰EF与BA重合.当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.…………7分 过F 作FM ⊥DE 于M ,F M M E=tan ∠DEF=tan ∠ABC=A CB C=68=34∴ME=43FM=43×2=83,HF=DM=DE-ME=4-83=43∴直角梯形DEFH ′的面积为12(4+43)×2=163∴y=163(Ⅱ)∵当4<t ≤513时,重叠部分的面积为四边形CBGH的面积-矩形CDH ′H 的面积. 而S 边形CBGH=S △ABC-S△AHG=12×8×6-323=403S 矩形CDH ′H =2t ∴y=403-2tAB 于P. BD=8-t∴y=S ,△8-t )2=38t2-6t+24y=40338t2-6t+24(513<t ≤8)【027】解:(1)设抛物线的解析式为:4)1(21+−=x a y ,把A (3,0)代入解析式求得1−=a所以324)1(221++−=+−−=x x x y ,设直线AB 的解析式为:bkx y +=2由3221++−=x x y 求得B 点的坐标为)3,0(把)0,3(A ,)3,0(B 代入b kx y +=2中解得:3,1=−=b k 所以32+−=x y 6分(2)因为C 点坐标为(1,4),所以当x =1时,y1=4,y2=2所以CD =4-2=28分32321=××=∆CAB S (平方单位)(3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PABx x x 3)32+−=+−,由S △389×,化简得:42−x 322++x x 中,解得P【0,3),)根据题意,得⎩⎨=++0339b a ,解得⎩⎨=2b ∴抛物线的解析式为322++−=x x y (5′)(2)(5′)由顶点坐标公式得顶点坐标为(1,4)(2′)设对称轴与x 轴的交点为F∴四边形ABDE 的面积=ABO DFEBOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF⋅++⋅+⋅=11113(34)124222××++×+××=9(5′)(3)(2′)相似如图,BD===;∴====∴2220BDBE +=,220DE =即:222BD BE DE +=,所以BDE ∆是直角三角形∴∠∴∆(2′)【04>所x 轴总有两个交(2a x x −=+21,1•x x 是13,所以|1−x 即:13)(221=−x x 变形为:134)(21221=•−+x x x x ……………………(5分)所以:13)2(4)(2=−−−a a ,整理得:0)1)(5(=+−a a 解方程得:15−=或a ,又因为:a<0,所以:a=-1所以:此二次函数的解析式为32−−=x xy ………………(6分)(3)设点P 的坐标为),(0y x o ,因为函数图象与x 轴的两个交点间的距离等于13,所以:AB=13,所以:S △PAB=213||210=•y AB 所以:2132||130=y 即:3||0=y ,则30±=y 当30=y 时,3320=−−o x x ,即0)2)(3(0=+−o x x 解此方程得:x =-2或3,当30−=y 时,3320−=−−o x x ,即)1(0=−o x x 解此方程得:0x =0或1(-2,3),(3,3),(0,-3)【2分)(2A 到点D 并随⊙有5,垂足为F ,则由∠得CDF EDO △∽△,则3(5)45CF t −−=.解得485t CF −=.由12CF ≤t ,即48152t t −≤,解得163t ≤.∴当C ⊙与射线DE 有公共点时,t 的取值范围为41633t ≤≤.11(5分)②当PA AB =时,过P 作PQ x ⊥轴,垂足为Q ,有222PA PQ AQ =+221633532525t t t ⎛⎞=+−−+⎜⎟⎝⎠.2229184205t t t ∴−+=,即2972800t t −+=.解得1242033t t ==.(7分)当PA PB =时,有PC AB ⊥,3535t t ∴−=−.解得35t =.(9分)当PB AB =时,有2222216132525PB ⎛⎞1320t ∴11分)∴当5t =,或203t =.。

2010年中考数学压轴题100题精选(1-10题)【001】如图,已知抛物线2(1)y a x=-+a≠0)经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB=,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t()s,连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【002】如图16,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).Array(1)当t = 2时,AP = ,点Q到AC的距离是;(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4)当DE经过点C 时,请直接..写出t的值.图16【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D (8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD 向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。

1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D.(1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22)2. 已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经过点T ,折痕TP 与射线AB 交于点P ,设点T 的横坐标为t ,折叠后纸片重叠部分(图中的阴影部分)的面积为S ;(1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式; (2)当纸片重叠部分的图形是四边形时,求t 的取值范围;(3)S 存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由.3. 如图,在R t ABC △中,90A ∠=,6A B =,8A C =,D E ,分别是边A B A C ,的中点,点P 从点D 出发沿D E 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交A C 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到B C 的距离D H 的长;y x OB CA Tyx O BC AT(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.4.在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x . (1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?5、如图1,已知双曲线y=xk (k>0)与直线y=k ′x 交于A ,B 两点,点A 在第一象限.试解答下列问题:(1)若点A 的坐标为(4,2).则点B 的坐标为 ;若点A 的横坐标为m ,则点B 的坐标可表示为 ;(2)如图2,过原点O 作另一条直线l ,交双曲线y=xk (k>0)于P ,Q 两点,点P 在第一象限.①说明四边形APBQ 一定是平行四边形;②设点A.P 的横坐标分别为m ,n ,四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,直接写出mn 应满足的条件;若不可能,请说明理由.ABCMN P图 3OABC MND 图 2 OABCMNP图 1O A BCD ER P H QxyBA O 图1B AOPQ图26. 如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,连结AP ,并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.(1)求直线AB 的解析式;(2)当点P 运动到点(3,0)时,求此时DP 的长及点D 的坐标;(3)是否存在点P ,使ΔOPD 的面积等于43,若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.7.如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系;②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a ,BC=b ,CE=ka , CG=kb (a ≠b ,k >0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结D G 、B E ,且a =3,b =2,k =12,求22BE DG +的值.8. 如图1所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E .(1)将直线l 向右平移,设平移距离CD 为t (t ≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图2所示, OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.①求梯形上底AB 的长及直角梯形OABC 的面积; ②当42<<t 时,求S 关于t 的函数解析式;(2)在第(1)题的条件下,当直线l 向左或向右平移时(包括l 与直线BC 重合),在直线..AB ..上是否存在点P ,使PDE ∆为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标;若不存在,请说明理由.9.如图,菱形ABCD 的边长为2,BD=2,E 、F 分别是边AD ,CD 上的两个动点,且满足AE+CF=2.(1)求证:△BDE ≌△BCF ;(2)判断△BEF 的形状,并说明理由;(3)设△BEF 的面积为S ,求S 的取值范围.10.如图,抛物线21:23L y x x =--+交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ,2L 交x 轴于C 、D 两点. (1)求抛物线2L 对应的函数表达式;(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.11.2008年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A 地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.(1)求A 地经杭州湾跨海大桥到宁波港的路程.(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A 地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用是多少元?(3)A 地准备开辟宁波方向的外运路线,即货物从A 地经杭州湾跨海大桥到宁波港,再从宁波港运到B 地.若有一批货物(不超过10车)从A 地按外运路线运到B 地的运费需8320元,其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B 地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?12.如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸….已知标准纸...的短边长为a . (1)如图2,把这张标准纸对开得到的“16开”张纸按如下步骤折叠:第一步 将矩形的短边AB 与长边A D 对齐折叠,点B 落在A D 上的点B '处,铺平后得折痕AE ; 第二步 将长边A D 与折痕AE 对齐折叠,点D 正好与点E 重合,铺平后得折痕AF .则:A D A B 的值是 ,A D A B ,的长分别是 , .(2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值.(3)如图3,由8个大小相等的小正方形构成“L ”型图案,它的四个顶点E F G H ,,,分别在“16开”纸的边A B B C C D D A ,,,上,求D G 的长.(4)已知梯形M NPQ 中,M N P Q ∥,90M =∠,2MN MQ PQ ==,且四个顶点M N P Q ,,,都在“4开”纸的边上,请直接写出2个符合条件且大小不同的直角梯形的面积.13.如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F .ABCD BCA D EGHF FE B '4开2开8开16开 图1图2 图3a①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸……都是矩形. ②本题中所求边长或面积都用含a 的代数式表示.(1)求梯形ABCD 的面积;(2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能, 求出正方形MEFN 的面积;若不能,请说明理由.14.如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y的图象上.(1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A ,B ,M ,N 为顶点的四边形是平行四边形, 试求直线MN 的函数表达式.(3)选做题:在平面直角坐标系中,点P 的坐标为(5,0),点Q 的坐标为(0,3),把线段PQ 向右平 移4个单位,然后再向上平移2个单位,得到线段P 1Q 1, 则点P 1的坐标为 ,点Q 1的坐标为 .15.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线. 如图12,点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点,已知点D 的坐标为(0,-3),AB 为半圆的直径,半圆圆心M 的坐标为(1,0),半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围; (2)你能求出经过点C 的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D 的“蛋圆”切线的解析式.C D A BE F NMxO yAB 友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分.xOy1 2 31 Q P2 P 1Q 1AOBMDCyx16.将一矩形纸片O A B C 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿O C 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿A O 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t =时,如图1,将O P Q △沿PQ 翻折,点O 恰好落在C B 边上的点D 处,求点D 的坐标;(4) 连结A C ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与A C 能否平行?P E 与A C能否垂直?若能,求出相应的t 值;若不能,说明理由.17.如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标; (2)在抛物线上是否存在点P ,使A B P △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线A C 上是否存在一点M ,使得M B F △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.18.如图所示,在平面直角坐标系中,矩形A B O C 的边B O 在x 轴的负半轴上,边O C 在y 轴的正半轴上,且1AB =,3O B =,矩形A B O C 绕点O 按顺时针方向旋转60 后得到图1OP A xBDC Q y图2OPA x BC QyE A O xyBFC图16矩形E F O D .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形A B O C 面积的2倍,且点P在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由. 19.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .(1)写出直线B C 的解析式.(2)求A B C △的面积.(3)若点M 在线段A B 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线B C 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出M N B △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,M N B △的面积最大,最大面积是多少?20.如图,在平面直角坐标系xOy 中,△OAB 的顶点A的坐标为(10,0),顶点B 在第一象限内,且AB =35,sin ∠OAB=55.(1)若点C 是点B 关于x 轴的对称点,求经过O 、C 、A 三点的抛物线的函数表达式; (2)在(1)中,抛物线上是否存在一点P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若将点O 、点A 分别变换为点Q ( -2k ,0)、点R (5k ,0)(k>1的常数),设过Q 、R 两点,且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ,其顶点为M ,记△y xODECFABQNM 的面积为QMN S ∆,△QNR 的面积QNR S ∆,求QMN S ∆∶QNR S ∆的值.21.(2008年乐山市)在平面直角坐标系中△ABC 的边AB 在x 轴上,且OA>OB,以AB 为直径的圆过点C 若C 的坐标为(0,2),AB=5, A,B 两点的横坐标X A ,X B 是关于X 的方程2(2)10x m x n -++-=的两根:(1) 求m ,n 的值(2) 若∠ACB 的平分线所在的直线l 交x 轴于点D ,试求直线l 对应的一次函数的解析式 (3) 过点D 任作一直线`l 分别交射线CA ,CB (点C 除外)于点M ,N ,则11C MC N+的值是否为定值,若是,求出定值,若不是,请说明理由22.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3)△AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22) ACO BNDML`23.已知抛物线c bx ax y ++=232,(Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标;(Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围; (Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.24.如图①,四边形A E F G 和A B C D 都是正方形,它们的边长分别为a b ,(2b a ≥),且点F 在A D 上(以下问题的结果均可用a b ,的代数式表示). (1)求D BF S △;(2)把正方形A E F G 绕点A 按逆时针方向旋转45°得图②,求图②中的D BF S △; (3)把正方形A E F G 绕点A 旋转一周,在旋转的过程中,D BF S △是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由. .25. 已知24A B A D ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线B C 上的动点(点E 与点B 不重合),M 是线段D E 的中点.(1)设BE x =,A B M △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)如果以线段A B 为直径的圆与以线段D E 为直径的圆外切,求线段B E 的长;(3)联结B D ,交线段A M 于点N ,如果以A N D ,,为顶点的三角形与B M E △相似,求线段B E 的长.DCBAE F GGF EABCD ①②BADMECBADC26. 某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站.由供水站直接铺设管道到另外两处. 如图,甲,乙两村坐落在夹角为30 的两条公路的A B 段和C D 段(村子和公路的宽均不计),点M 表示这所中学.点B 在点M 的北偏西30 的3km 处,点A 在点M 的正西方向,点D 在点M 的南偏西60 的23km 处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点M 处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;方案二:供水站建在乙村(线段C D 某处),甲村要求管道建设到A 处,请你在图①中,画出铺设到点A 和点M 处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段A B 某处),请你在图②中,画出铺设到乙村某处和点M 处的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?27. 已知:如图①,在Rt △ACB 中,∠C =90°,AC =4cm ,BC =3cm ,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为t (s )(0<t <2),解答下列问题: (1)当t 为何值时,PQ ∥BC ?(2)设△AQP 的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使线段PQ 恰好把Rt △ACB 的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把△PQC 沿QC 翻折,得到四边形PQP ′C ,那么是否存在某一时刻t ,使四边形PQP ′C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.MAEC D BF30乙村 甲村 东北图①MAEC D BF30乙村 甲村图②OO28. 已知双曲线k y x=与直线14y x =相交于A 、B 两点.第一象限上的点M (m ,n )(在A点左侧)是双曲线k y x=上的动点.过点B 作BD ∥y 轴于点D.过N(0,-n )作NC ∥x 轴交双曲线ky x=于点E ,交BD 于点C.(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值.(2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA =pMP ,MB =qMQ ,求p -q 的值.29. 一种电讯信号转发装置的发射直径为31km .现要求:在一边长为30km 的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求? (2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求? 答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km 的正方形城区示意图,供解题时选用)P '图②A Q CPB图①AQCPB图1 图2 图 3 图4D BCE NO A Myx。

2010年中考数学压轴题100题精选(51-60题)答案【051】解:(1)3k =-,(-1,0),B (3,0). ······················· 3分 (2)如图14(1),抛物线的顶点为M (1,-4),连结OM .则 △AOC 的面积=23,△MOC 的面积=23,△MOB 的面积=6,∴ 四边形 ABMC 的面积=△AOC 的面积+△MOC 的面积+△MOB 的面积=9. ·································· 6分说明:也可过点M 作抛物线的对称轴,将四边形ABMC 的面积转化为求1个梯形与2个直角三角形面积的和. (3)如图14(2),设D (m ,322--m m ),连结OD . 则 0<m <3,322--m m <0. 且 △AOC 的面积=23,△DOC 的面积=m 23, △DOB 的面积=-23(322--m m ), ∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积=629232++-m m =875)23(232+--m . ∴ 存在点D 315()24-,,使四边形ABDC 的面积最大为875.(4)有两种情况:如图14(3),过点B 作BQ 1⊥BC ,交抛物线于点Q 1、交y 轴于点E ,连接Q 1C . ∵ ∠CBO =45°,∴∠EBO =45°,BO =OE =3. ∴ 点E 的坐标为(0,3). ∴ 直线BE 的解析式为3y x =-+. ···························· 12分由2323y x y x x =-+⎧⎨=--⎩, 解得1125x y ,;2230.x y ,∴ 点Q 1的坐标为(-2,5). ········· 13分如图14(4),过点C 作CF ⊥CB ,交抛物线于点Q 2、交x 轴于点F ,连接BQ 2.∵ ∠CBO =45°,∴∠CFB =45°,OF =OC =3. ∴ 点F 的坐标为(-3,0).∴ 直线CF 的解析式为3y x =--.····························· 14分 由2323y x y x x =--⎧⎨=--⎩, 解得1103x y ,;2214x y ,.∴点Q 2的坐标为(1,-4).综上,在抛物线上存在点Q 1(-2,5)、Q 2(1,-4), 使△BCQ 1、△BCQ 2是以BC 为直角边的直角三角形.【052】解:(1)根据题意,得04202.a b c a b c c ++=⎧⎪++=⎨⎪=-⎩,,图14(2)图14(3) 图14(4)yxOBA DE 1 (E 2)解得132a b c =-==-,,.232y x x ∴=-+-.(2分) (2)当EDB AOC △∽△时,得AO CO ED BD =或AO COBD ED=, ∵122AO CO BD m ===-,,,当AO CO ED BD =时,得122ED m =-, ∴22m ED -=,∵点E 在第四象限,∴122m E m -⎛⎫⎪⎝⎭,. ··········································· (4分) 当AO CO BD ED =时,得122m ED=-,∴24ED m =-, ∵点E 在第四象限,∴2(42)E m m -,. ········································································· (6分)(3)假设抛物线上存在一点F ,使得四边形ABEF 为平行四边形,则 1EF AB ==,点F 的横坐标为1m -, 当点1E 的坐标为22m m -⎛⎫ ⎪⎝⎭,时,点1F 的坐标为212m m -⎛⎫- ⎪⎝⎭,,∵点1F 在抛物线的图象上,∴22(1)3(1)22mm m -=--+--,∴2211140m m -+=, ∴(27)(2)0m m --=,∴722m m ==,(舍去),∴15324F ⎛⎫- ⎪⎝⎭,, ∴33144ABEFS=⨯=. ····································································································· (9分) 当点2E 的坐标为(42)m m -,时,点2F 的坐标为(142)m m --,, ∵点2F 在抛物线的图象上,∴242(1)3(1)2m m m -=--+--,∴27100m m -+=,∴(2)(5)0m m --=,∴2m =(舍去),5m =,∴2(46)F -,,∴166ABEFS =⨯=.【053】解:(1)设(1)(3)y a x x =+-,把(03)C ,代入,得1a =-, ······························ 2分∴抛物线的解析式为:223y x x =-++.顶点D 的坐标为(14),. ··································· 5分 (2)设直线BD 解析式为:y kx b =+(0k ≠),把B D 、两点坐标代入,得304.k b k b +=⎧⎨+=⎩,解得26k b =-=,.∴直线AD 解析式为26y x =-+. ························· 7分2111(26)3222s PE OE xy x x x x ===-+=-+,∴23(13)s x x x =-+<< ·················· 9分 22993934424s x x x ⎛⎫⎛⎫=--++=--+ ⎪ ⎪⎝⎭⎝⎭. ····································································· 10分∴当32x =时,s 取得最大值,最大值为94. ······································································ 11分 (3)当s 取得最大值,32x =,3y =,∴332P ⎛⎫⎪⎝⎭,.∴四边形PEOF 是矩形. 作点P 关于直线EF 的对称点P ',连接P E P F ''、. 法一:过P '作P H y '⊥轴于H ,P F '交y 轴于点M设MC m =,则332MF m P M m P E ''==-=,,.在Rt P MC '△中,由勾股定理,223(3)2m m ⎛⎫+-= ⎪⎝⎭解得158m =.∵CM P H P M PE '''=,∴910P H '=. 由EHP EP M ''△∽△,可得EH EP EP EM '=',65EH =.∴69355OH =-=. ∴P '坐标99105⎛⎫-⎪⎝⎭,. ·············································································································· 13分 法二:连接PP ',交CF 于点H ,分别过点H P '、作PC 的垂线,垂足为M N 、. 易证CMH HMP △∽△.∴12CM MH MH PM ==. 设CM k =,则24MH k PM k ==,.∴5PC =由三角形中位线定理,12845PN k P N k '====,∴12395210CN PN PC =-=-=,即910x =-. 69355y PF P N '=-=-=∴P '坐标99105⎛⎫- ⎪⎝⎭,. ··把P '坐标99105⎛⎫-⎪⎝⎭,代入抛物线解析式,不成立,所以P '不在抛物线上. ····················· 14分 【054】(1)由抛物线经过点A (0,1),C (2,4),得21,122 4.4c b c =⎧⎪⎨-⨯++=⎪⎩解得2,1.b c =⎧⎨=⎩ ∴抛物线对应的函数关系式为:21214y x x =-++. ··································· (2分)(2)当1t =时,P 点坐标为(1,1),∴Q 点坐标为(2,0). 当4t =时,P 点坐标为(2,3),∴Q 点坐标为(5,0). ································ (5分)(3)当0t <≤2时,211(211)124S t t =-++-⨯.S 218t t =-+.当2t <≤5时,1(5)(2212)2S t t =-+-+-.S 215322t t =-+-. (8分)当3t =时,S 的最大值为2. ································【055】(1)过点B 作BD x ⊥轴,垂足为D , 9090BCD ACO ACO CAO ∠+∠=∠+∠=°,°BCD CAO ∴∠=∠;又90BDC COA CB AC ∠=∠==°;, BCD CAO ∴△≌△,12BD OC CD OA ∴====,∴点B 的坐标为(31)-,; ·················································· 4(2)抛物线22y ax ax =+-经过点(31)B -,,则得到1932a a =--, ··························· 5分 解得12a =,所以抛物线的解析式为211222y x x =+-; ···················································· 7分 (3)假设存在点P ,使得ACP △仍然是以AC 为直角边的等腰直角三角形:①若以点C 为直角顶点;则延长BC 至点1P ,使得1PC BC =,得到等腰直角三角形1ACP △, ······························ 8分 过点1P 作1PM x ⊥轴,11190CP BC MCP BCD PMC BDC =∠=∠∠=∠=,,°; 1MPC DBC ∴△≌△121CM CD PM BD ∴====,,可求得点1P (1,-1); ·········· 11分 ②若以点A 为直角顶点;则过点A 作2AP CA ⊥,且使得2AP AC =,得到等腰直角三角形2ACP △, ················ 12分 过点2P 作2P N y ⊥轴,同理可证2AP N CAO △≌△; ····················································· 13分221NP OA AN OC ∴====,,可求得点2(21)P ,; ······················································· 14分 经检验,点1(11)P -,与点2(21)P ,都在抛物线211222y x x =+-上. ································ 16分 【056】解:(1) C (3,0);(2)①抛物线c bx ax y ++=2,令x =0,则y =c , ∴A 点坐标(0,c ).∵ac b 22=,∴ 242424442c a ac a ac ac a b ac ==-=-,∴点P 的坐标为(2,2ca b -). ∵PD ⊥x 轴于D ,∴点D 的坐标为(0,2ab-). ……………………………………5分 根据题意,得a=a ′,c= c ′,∴抛物线F ′的解析式为c x b ax y ++='2.又∵抛物线F ′经过点D (0,2a b-),∴c a b b ab a +-+⨯=)2('4022.……………6分 ∴ac bb b 4'202+-=.又∵ac b 22=,∴'2302bb b -=.∴b :b ′=32. ②由①得,抛物线F ′为c bx ax y ++=232. 令y=0,则0232=++c bx ax . ∴abx a b x -=-=21,2.∵点D 的横坐标为,2a b -∴点C 的坐标为(0,ab-). 设直线OP 的解析式为kx y =.∵点P 的坐标为(2,2ca b -), ∴k a b c 22-=,∴22222b b b b ac b ac k -=-=-=-=,∴x by 2-=. ∵点B 是抛物线F 与直线OP 的交点,∴x b c bx ax 22-=++.∴abx a b x -=-=21,2.∵点P 的横坐标为a b 2-,∴点B 的横坐标为ab-.把a b x -=代入x by 2-=,得c a ac a b a b b y ===--=222)(22.∴点B 的坐标为),(c ab-.∴BC ∥OA ,AB ∥OC .(或BC ∥OA ,BC =OA ),∴四边形OABC 是平行四边形.又∵∠AOC =90°,∴四边形OABC 【057】(1) )6,0(),0,8(B A(2)∵8=OA ,6=OB ,∴AB 当点P 在OB 上运动时,t OP =1t t OP OA S 4821211=⨯⨯=⨯=; 当点P 在BA 上运动时,作D P ⊥2有AB AP BO D P 22=∵t AP -+=1062∴51925125348821212+-=-⨯⨯=⨯⨯=t t D P OA S (3)当124=t 时,3=t ,)3,0(1P ,此时,过AOP ∆各顶点作对边的平行线,与坐标轴无第二个交点,所以点M 不存在; 当125192512=+-t 时,11=t ,)3,4(2P ,此时,)3,0(1M 、)6,0(2-M 【058】解:(1)令0y =,得210x -= 解得1x =±,令0x =,得1y =-∴ A (1,0)- B (1,0) C (0,1)- ·············(2)∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O=45 ∵A P ∥CB ,∴∠P AB =45,过点P 作P E ⊥x 轴于E , 则∆A P E 为等腰直角三角形令O E =a ,则P E =1a + ∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a +=-解得12a =,21a =-(不合题意,舍去) ∴P E =3 · 4分 ∴四边形ACB P 的面积S =12AB •O C +12AB •P E =112123422⨯⨯+⨯⨯= ································ 5分 (3). 假设存在∵∠P AB =∠BAC =45 ∴P A ⊥AC∵MG ⊥x 轴于点G , ∴∠MG A =∠P AC =90在Rt △A O C 中,O A =O C =1 ∴AC ,在Rt △P AE 中,AE =P E =3 ∴A P= ······· 6分设M 点的横坐标为m ,则M 2(,1)m m - ①点M 在y 轴左侧时,则1m <- (ⅰ) 当∆A MG ∽∆P CA 时,有AG PA =MGCA∵A G=1m --MG=21m -2= 解得11m =-(舍去) 223m =(舍去)………7分 (ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即 2=,解得:1m =-(舍去) 22m =-∴M (2,3)- ························································ 8分② 点M 在y 轴右侧时,则1m >(ⅰ) 当∆A MG ∽∆P CA 时有AG PA =MGCA∵A G=1m +,MG=21m -∴2= 解得11m =-(舍去) 243m = ∴M 47(,)39(ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA 即2=解得:11m =-(舍去) 24m = ∴M (4,15) ∴存在点M ,使以A 、M 、G 三点为顶点的三角形与∆P CA 相似,M 点的坐标为(2,3)-,47(,)39,(4,15)【059】解:(1)∵四边形ABCD 和四边形AEFG 是正方形 ∴AB =AD ,AE =AG ,∠BAD =∠EAG =90º∴∠BAE +∠EAD =∠DAG +∠EAD ∴∠BAE =∠DAG∴△ BAE ≌△DAG …………4分(2)∠FCN =45º …………5分 理由是:作FH ⊥MN 于H∵∠AEF =∠ABE =90º∴∠BAE +∠AEB =90º,∠FEH +∠AEB =90º∴∠FEH =∠BAE 又∵AE =EF ,∠EHF =∠EBA =90º∴△EFH ≌△ABE …………7分 ∴FH =BE ,EH =AB =BC ,∴CH =BE =FH∵∠FHC =90º,∴∠FCH =45º …………8分(3)当点E 由B 向C 运动时,∠FCN的大小总保持不变,…………9分理由是:作FH ⊥MN 于H由已知可得∠EAG =∠BAD =∠AEF =90º 结合(1)(2)得∠FEH =∠BAE =∠DAG又∵G 在射线CD 上,∠GDA =∠EHF =∠EBA =90º ∴△EFH ≌△GAD ,△EFH ∽△ABE ……11分 ∴EH =AD =BC =b ,∴CH =BE ,∴EH AB =FH BE =FHCH∴在Rt △FEH 中,tan ∠FCN =FH CH =EH AB =b a∴当点E 由B 向C 运动时,∠FCN =ba【060】解:(1)根据题意,得 4203660a c a c -+=⎧⎨++=⎩,解得143a c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解析式为2134y x x =-++,顶点坐标是(2,4) (2)(43)D ,,设直线AD 的解析式为(0)y kx b k =+≠ 直线经过点(20)A -,、点(43)D ,2043k b k b -+=⎧∴⎨+=⎩121k b ⎧=⎪∴⎨⎪=⎩ 112y x ∴=+(3)存在.120)Q ,,2(2)Q -,0,3(6Q -,4(6Q +M B E AC ND F G 图(2) HM B E A C ND F G图(1)H第26题图。

2010中考数学压轴题精选(一)★★1、(2010北京)在平面直角坐标系xOy 中,抛物线y = -41-m x 2+45mx +m 2-3m +2 与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上。
(1)求点B 的坐标; (2)点P 在线段OA 上,从O 点出发向点运动,过P 点作x 轴的垂线,与直线OB 交于点E 。
延长PE 到点D ,使得ED =PE ,以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动)当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一 点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动)。
过Q 点作x 轴的垂线,与直线AB 交于点F 。
延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点,N 点也随之运动)。
若P 点运动到t 秒时,两个等腰直角三角形分别有一条直角边恰好落在同一条直线上,求此刻t 的值。
★★2、(2010北京)问题:已知△ABC 中,∠BAC =2∠ACB ,点D 是△ABC 内的一点,且AD =CD ,BD =BA 。
探究∠DBC 与∠ABC 度数的比值。
请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。
(1) 当∠BAC =90︒时,依问题中的条件补全右图。
观察图形,AB 与AC 的数量关系为 ; 当推出∠DAC =15︒时,可进一步推出∠DBC 的度数为 ;可得到∠DBC 与∠ABC 度数的比值为 ;(2) 当∠BAC ≠90︒时,请你画出图形,研究∠DBC 与∠ABC 度数的比值是否与(1)中的结论相同,写出你的猜想并加以证明。
★★3、(2010郴州)如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y A C B轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C .(1)求点A 的坐标;(2)当b =0时(如图(2)),ABE 与ACE 的面积大小关系如何?当4b >-时,上述BOC 是以b ;若★★4、(2010滨州)如图,四边形ABCD 是菱形,点D的坐标是(0,3),以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点.(1)求A 、B 、C 三点的坐标;(2)求过A 、B 、C 三点的抛物线的解析式;(3)若将上述抛物线沿其对称轴向上平移后恰好过D 点,求平移后抛物线的解析式,并指出平移了多少个单位?★★5、(2010长沙)已知:二次函数22y ax bx =+-的图象经过点(1,0),一次函数图象经过原点和点(1,-b ),其中0a b >>且a 、b 为实数. (1)求一次函数的表达式(用含b 的式子表示); (2)试说明:这两个函数的图象交于不同的两点;(3)设(2)中的两个交点的横坐标分别为x1、x2,求| x1-x2 |的范围.★★6、(2010长沙)如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA , OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.(1)用t 的式子表示△OPQ 的面积S ;(2)求证:四边形OPBQ 的面积是一个定值,并求出这个定值;(3)当△OPQ 与△PAB 和△QPB 相似时,抛物线214y x bx c =++经过B 、P 两点,过线段BP 上一动点M 作y 轴的平行线交抛物线于N ,当线段MN 的长取最大值时,求直线MN 把四边形OPBQ 分成两部分的面积之比.★★7、(2010常德)如图9,已知抛物线212y x bx c x =++与轴交于点A (-4,0)和B (1,0)两点,与y 轴交于C 点. (1)求此抛物线的解析式;第26题图(2)设E 是线段AB 上的动点,作EF∥AC 交BC 于F ,连接CE ,当C E F 的面积是BEF 面积的2倍时,求E 点的坐标;(3)若P 为抛物线上A 、C 两点间的一个动点,过P 作y 轴的平行线,交AC 于Q ,当P 点运动到什么位置时,线段PQ 的值最大,并求此时P 点的坐标.★★8、(2010常德)如图10,若四边形ABCD 、四边形CFED 都是正方形,显然图中有AG=CE ,AG⊥CE.(1)当正方形GFED 绕D 旋转到如图11的位置时,AG=CE 是否成立?若成立,请给出证明;图9x若不成立,请说明理由.(2)当正方形GFED 绕D 旋转到如图12的位置时,延长CE 交AG 于H ,交AD 于M. ①求证:AG⊥CH;②当AD=4,CH 的长。

2010年各地中考压轴题精选1(北京)问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA。
探究∠DBC与∠ABC度数的比值。
请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。
(1) 当∠BAC=90︒时,依问题中的条件补全右图。
观察图形,AB与AC的数量关系为;可得到∠DBC与∠ABC度数的比值为;(2) 当∠BAC≠90︒时,请你画出图形,研究∠DBC与∠ABC度数的比值是否与(1)中的结论相同,写出你的猜想并加以证明。
2(盐城)已知:函数y=ax2+x+1的图象与x轴只有一个公共点.(1)求这个函数关系式;(2)如图所示,设二次..函数y=ax2+x+1图象的顶点为B,与y轴的交点为A,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;(3)在(2)中,若圆与x轴另一交点关于直线PB的对称点为M,试探索点M是否在抛物线y=ax2+x+1上,若在抛物线上,求出M点的坐标;若不在,请说明理由.3.(广州)如图所示,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),点D是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线y =-12x +b 交折线OAB 于点E .(1)记△ODE 的面积为S ,求S 与b 的函数关系式;(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形OA 1B 1C 1,试探究OA 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.4.(南平)如图1,已知点B (1,3)、C (1,0),直线y=x +k 经过点B ,且与x 轴交于点A ,将△ABC 沿直线AB 折叠得到△ABD. (1)填空:A 点坐标为(____,____),D 点坐标为(____,____); (2)若抛物线y= 13x 2+b x +c 经过C 、D 两点,求抛物线的解析式;(3)将(2)中的抛物线沿y 轴向上平移,设平移后所得抛物线与y 轴交点为E ,点M 是平移后的抛物线与直线AB 的公共点,在抛物线平移过程中是否存在某一位置使得直线EM ∥x 轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.(提示:抛物线y=ax 2+b x +c(a ≠0)的对称轴是x =-b 2a ,顶点坐标是(-b 2a ,4a c -b24a).图1备用图5(大连)如图17,抛物线F :2(0)y ax bx c a =++>与y 轴相交于点C ,直线1L 经过点C 且平行于x 轴,将1L 向上平移t 个单位得到直线2L ,设1L 与抛物线F 的交点为C 、D ,2L 与抛物线F 的交点为A 、B ,连接AC 、BC (1)当12a =,32b =-,1c =,2t =时,探究△ABC 的形状,并说明理由; (2)若△ABC 为直角三角形,求t 的值(用含a 的式子表示);(3)在(2)的条件下,若点A 关于y 轴的对称点A ’恰好在抛物线F 的对称轴上,连接A ’C ,BD ,求四边形A ’CDB 的面积(用含a 的式子表示)6.(宿迁)已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ,交y轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴; (2)连接BC ,过点O 作直线BC OE ⊥交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形;(3)问Q 抛物线上是否存在点Q ,使得△OBQ的面积等于四边形ODBE 的面积的31?若存在,求出点Q 的坐标;若不存在,请说明理由.(第28题)(第28题2)7.(烟台)如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C。
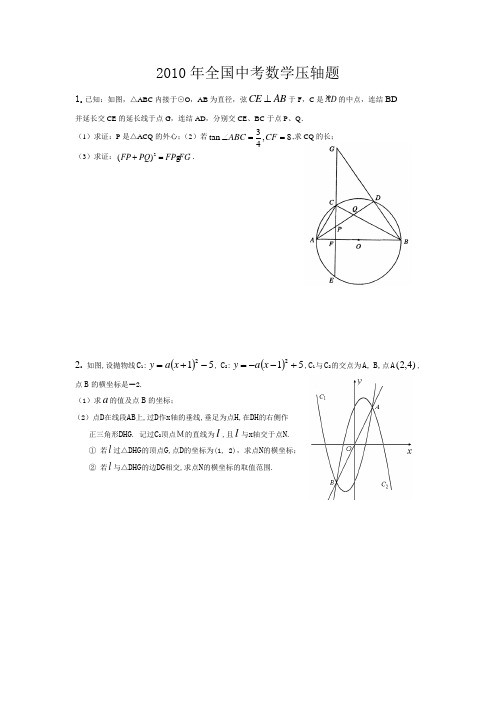
2010年全国中考数学压轴题1.已知:如图,△ABC 内接于⊙O ,AB 为直径,弦CE AB ⊥于F ,C 是 AD 的中点,连结BD并延长交CE 的延长线于点G ,连结AD ,分别交CE 、BC 于点P 、Q . (1)求证:P 是△ACQ 的外心;(2)若3tan ,84ABC CF ∠==,求CQ 的长; (3)求证:2()FP PQ FP FG += .2. 如图,设抛物线C 1:()512-+=x a y , C 2:()512+--=x a y ,C 1与C 2的交点为A, B,点A )4,2(,点B 的横坐标是-2.(1)求a 的值及点B 的坐标;(2)点D 在线段AB 上,过D 作x 轴的垂线,垂足为点H ,在DH 的右侧作 正三角形DHG . 记过C 2顶点M的直线为l ,且l 与x 轴交于点N . ① 若l 过△DHG 的顶点G ,点D 的坐标为(1, 2),求点N 的横坐标; ② 若l 与△DHG 的边DG 相交,求点N 的横坐标的取值范围.3.如图,二次函数k m x y ++=2)(的图象,其顶点坐标为M(1,-4).(1)求出图象与x 轴的交点A,B 的坐标; (2)二次函数的图象上是否存在点P ,使M A B P A BS S ∆∆=45,若存在,求P 点的坐标;若不存在,请说明;(3)将二次函数的图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线)1(<+=b b x y 与此图象有两个公共点时,b 的取值范围.4.已知:函数y=ax 2+x+1的图象与x 轴只有一个公共点.(1)求这个函数关系式;(2)如图所示,设二次..函数y=ax 2+x+1图象的顶点为B ,与y 轴的交点为A ,P 为图象上的一点,若以线段PB 为直径的圆与直线AB 相切于点B ,求P 点的坐标;(3)在(2)中,若圆与x 轴另一交点关于直线PB 的对称点为M ,试探索点M 是否在抛物线y=ax 2+x+1上,若在抛物线上,求出M 点的坐标;若不在,请说明理由.A xyOB5.如图,在平面直角坐标系中,顶点为(4,1-)的抛物线y 轴于A 点,交x 轴于B ,C 两点(点B在点C 的左侧). 已知A 点坐标为(0,3). (1)求此抛物线的解析式; (2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明; (3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积.6.在直角梯形OABC 中,CB//OA ,∠COA=90︒,CB=3,OA=6,BA=3分别以OA 、OC 边所在直线为x 轴、y 轴建立如图所示的平面直角坐标系。

2011年中考数学压轴题100题精选(1-10题)【01】如图,已知抛物线2(1)y a x =-+a ≠0)经过点(20)A ,-,抛物线的顶点为D ,过O 作射线O M A D ∥.过顶点D 平行于x 轴的直线交射线O M 于点C ,B 在x 轴正半轴上,连结B C .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线O M 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形D A O P 分别为平行四边形?直角梯形?等腰梯形?(3)若O C O B =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿O C 和B O 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【02】如图16,在Rt △ABC 中,∠C =90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB -BC -CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与t 的函数关系式;(不必写出t 的取值范围) (3)在点E 从B 向C 运动的过程中,四边形QBED 能否成为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接..写出t 的值.图16【03】如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。

2010年中考数学压轴题100题精选(81-90题)【081】如图,已知抛物线y =34x 2+bx +c 与坐标轴交于A 、B 、C 三点, A 点的坐标为(-1,0),过点C 的直线y =34tx -3与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH ⊥OB 于点H .若PB =5t ,且0<t <1.(1)填空:点C 的坐标是_▲_,b =_▲_,c =_▲_; (2)求线段QH 的长(用含t 的式子表示);(3)依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似?若存在,求出所有t 的值;若不存在,说明理由.【082】(09上海)在直角坐标平面内,O 为原点,点A 的坐标为(10),,点C 的坐标为(04),,直线CM x ∥轴(如图7所示).点B 与点A 关于原点对b=+(b为常数)经过点B,且与直线CM相交于点D,联结OD.称,直线y x b(1)求b的值和点D的坐标;△是等腰三角形,求点P的坐标;(2)设点P在x轴的正半轴上,若POD(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.【083】如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.【084】如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P (0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?BAOyx【085】如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.【086】如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分3,∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=5 AD=12.⑴求证:△ANM≌△ENM;⑵求证:FB是⊙O的切线;⑶证明四边形AMEN是菱形,并求该菱形的面积S.【087】如图,已知抛物线y =x 2+bx +c 经过矩形ABCD 的两个顶点A 、B ,AB 平行于x 轴,对角线BD 与抛物线交于点P ,点A 的坐标为(0,2),AB =4. (1)求抛物线的解析式;(2)若S △APO =23,求矩形ABCD 的面积.【088】如图所示,已知在直角梯形OABC 中,AB OC BC x ∥,⊥轴于点(11)(31)C A B ,,、,.动点P 从O 点出发,沿x 轴正方向以每秒1个单位长度的速度移动.过P 点作PQ 垂直于直线..OA ,垂足为Q .设P 点移动的时间为t 秒(04t <<),OPQ △与直角梯形OABC 重叠部分的面积为S . (1)求经过O A B 、、三点的抛物线解析式; (2)求S 与t 的函数关系式;(3)将OPQ △绕着点P 顺时针旋转90°,是否存在t ,使得OPQ △的顶点O 或Q 在抛物线上?若存在,直接写出t 的值;若不存在,请说明理由.【089】如图,在平面直角坐标系xOy 中,半径为1的圆的圆心O 在坐标原点,且与两坐标轴分别交于A B C D 、、、四点.抛物线2y ax bx c =++与y 轴交于点D ,与直线y x =交于点M N 、,且MA NC 、分别与圆O 相切于点A 和点C . (1)求抛物线的解析式;(2)抛物线的对称轴交x 轴于点E ,连结DE ,并延长DE 交圆O 于F ,求EF 的长. (3)过点B 作圆O 的切线交DC 的延长线于点P ,判断点P 是否在抛物线上,说明理由.【090】如图(9)-1,抛物线23y ax ax b =-+经过A (1-,0),C (3,2-)两点,与y 轴交于点D ,与x 轴交于另一点B . (1)求此抛物线的解析式;(2)若直线)0(1≠+=k kx y 将四边形ABCD 面积二等分,求k 的值;(3)如图(9)-2,过点E (1,1)作EF ⊥x 轴于点F ,将△AEF 绕平面内某点旋转180°得△MNQ (点M 、N 、Q 分别与点A 、E 、F 对应),使点M 、N 在抛物线上,作MG ⊥x 轴于点G ,若线段MG ︰AG =1︰2,求点M ,N 的坐标.y=kx +1图(9)-1图(9)-2。

合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网2010年中考数学压轴题(91-100题)【091】已知二次函数y =x 2-x +c .(1)若点A (-1,a )、B (2,2n -1)在二次函数y =x 2-x +c 的图象上,求此二次函数的最小值; (2)若点D (x 1,y 1)、E (x 2,y 2)、P (m ,n )(m >n )在二次函数y =x 2-x +c 的图象上,且D 、E两点关于坐标原点成中心对称,连接OP .当22≤OP ≤2+2时,试判断直线DE 与抛物线y =x 2-x +c + 38的交点个数,并说明理由.合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【092】已知:直角梯形OABC 的四个顶点是O (0,0),A (32,1), B (s ,t ),C (72,0),抛物线y =x 2+mx -m 的顶点P 是直角梯形OABC 内部或边上的一个动点,m 为常数. (1)求s 与t 的值,并在直角坐标系中画出..直角梯形OABC ; (2)当抛物线y =x 2+mx -m 与直角梯形OABC 的边AB 相交时,求m 的取值范围.(第24题)合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【093】已知在平面直角坐标系中,四边形OABC 是矩形,点A 、C 的坐标分别为()3A 0,、()04C ,,点D 的坐标为()D 5-0,,点P 是直线AC 上的一动点,直线DP 与y 轴交于点M .问: (1)当点P 运动到何位置时,直线DP 平分矩形OABC 的面积,请简要说明理由,并求出此时直线DP 的函数解析式;(2)当点P 沿直线AC 移动时,是否存在使D O M △与A B C △相似的点M ,若存在,请求出点M的坐标;若不存在,请说明理由;(3)当点P 沿直线AC 移动时,以点P 为圆心、半径长为R (R >0)画圆,所得到的圆称为动圆P .若设动圆P 的直径长为AC ,过点D 作动圆P 的两条切线,切点分别为点E 、F .请探求是否存在四边形DEPF 的最小面积S ,若存在,请求出S 的值;若不存在,请说明理由. 注:第(3)问请用备用图解答.备用图合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【094】在平面直角坐标系中,已知(40)A -,,(10)B ,,且以A B 为直径的圆交y 轴的正半轴于点(02)C ,,过点C 作圆的切线交x 轴于点D .(1)求过A B C ,,三点的抛物线的解析式(2)求点D 的坐标(3)设平行于x 轴的直线交抛物线于E F ,两点,问:是否存在以线段E F 为直径的圆,恰好与x合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【095】)如图1,已知:抛物线212y x b x c =++与x 轴交于A B 、两点,与y 轴交于点C ,经过B C 、两点的直线是122y x =-,连结A C .(1)B C 、两点坐标分别为B (_____,_____)、C (_____,_____),抛物线的函数关系式为______________;(2)判断A B C △的形状,并说明理由;(3)若A B C △内部能否截出面积最大的矩形D E F C (顶点D E F 、、、G 在A B C △各边上)?若能,求出在A B 边上的矩形顶点的坐标;若不能,请说明理由.[抛物线2y ax bx c =++的顶点坐标是24,24b a c b a a ⎛⎫-- ⎪⎝⎭]图1图2(备用)(第26题)合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【096】如图12,已知抛物线经过坐标原点O 和x 轴上另一点E ,顶点M 的坐标为 (2,4);矩形ABCD 的顶点A 与点O 重合,AD 、AB 分别在x 轴、y 轴上,且AD=2,AB=3. (1)求该抛物线所对应的函数关系式;(2)将矩形ABCD 以每秒1个单位长度的速度从图12所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度.....从点A 出发向B 匀速移动,设它们运动的时间为t 秒(0≤t ≤3),直线AB 与该抛物线的交点为N (如图13所示). ① 当t=25时,判断点P 是否在直线ME 上,并说明理由;② 设以P 、N 、C 、D 为顶点的多边形面积为S ,试问S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【097】矩形O A B C 在平面直角坐标系中位置如图13所示,A C 、两点的坐标分别为(60)A ,,(03)C -,,直线34y x =-与B C 边相交于D 点.(1)求点D 的坐标; (2)若抛物线294y a x x =-经过点A ,试确定此抛物线的表达式;(3)设(2)中的抛物线的对称轴与直线O D 交于点M ,点P 为对称轴上一动点,以P O M、、为顶点的三角形与O C D △相似,求符合条件的点P 的坐标.合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【098】如图,在平面直角坐标系中,点A (0,6),点B 是x 轴上的一个动点,连结AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90o ,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(t ,0).(1)当t =4时,求直线AB 的解析式;(2)当t >0时,用含t 的代数式表示点C 的坐标及△ABC 的面积;(3)是否存在点B ,使△ABD 为等腰三角形?若存在,请求出所有符合条件的点B 的坐标;若不存在,请说明理由.· yOA x备用图合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【099】我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提................出相关的概念和问题(或者根据问题构造图形),并加以研究............................ 例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).请你用上面的思想和方法对下面关于圆的问题进行研究:(1) 如图1,在圆O 所在平面上,放置一条..直线m (m 和圆O 分别交于点A 、B ),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?(2) 如图2,在圆O 所在平面上,请你放置与圆O 都相交且不同时经过圆心.......的两条..直线m 和n (m 与圆O 分别交于点A 、B ,n 与圆O 分别交于点C 、D ). 请你根据所构造的图形提出一个结论,并证明之. (3) 如图3,其中AB 是圆O 的直径,AC 是弦,D 是的中点,弦DE ⊥AB 于点F . 请找出点C 和点E 重合的条件,并说明理由.ABC 第25题图1第25题图2AB第25题图3合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【100】抛物线)0(2≠++=a c bx axy 的顶点为M ,与x 轴的交点为A 、B (点B 在点A 的右侧),△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。

2010年中考数学压轴题100题精选(1-10题)答案【001】解:(1) ∴二次函数的解析式为:2333y x x =-++(2)D为抛物线的顶点D ∴过D 作DN OB ⊥于N,则DN=3660AN AD DAO =∴=∴∠=,°OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形66(s)OP t ∴=∴= ②当DP OM⊥时,四边形DAOP 是直角梯形过O 作OHAD ⊥于H ,2AO =,则1AH =55(s)OP DH t ∴===③当PD OA =时,四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t=、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.(3)则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,116(62)22BCPQS t ∴=⨯⨯⨯-=2322t ⎫-⎪⎝⎭当32t =时,BCPQ S此时3339332444OQ OP OE QE PE ==∴=-==,=,2PQ ∴===【002】解:(1)1,85; (2)作QF ⊥AC 于点F ,如图3, AQ = CP = t ,∴3AP t =-.由△AQF ∽△ABC,4BC ==, 得45QF t =.∴45QF t =. ∴14(3)25S t t =-⋅, (3)能.①当DE ∥QB 时,如图4.∵DE ⊥PQ ,∴PQ ⊥QB ,四边形QBED 是直角梯形. 由△APQ ∽△ABC . 解得98t =. ②如图5,当PQ ∥BC 时,DE ⊥BC ,四边形QBED 是直角梯形. 由△AQP ∽△ABC ,得AQ AP AB AC =,解得158t =.(4)52t =或4514t =.P图5【注:①点P 由C 向A 运动,DE 经过点C . 方法一、连接QC ,作QG ⊥BC 于点G ,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--.由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =. 方法二、由CQ CP AQ ==,得QAC QCA ∠=∠,进而可得B BCQ ∠=∠,得CQ BQ =,∴52AQ BQ ==.∴52t =. ②点P 由A 向C 运动,DE 经过点C ,如图7.22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】【003】解.(1)点A 的坐标为(4,8) …………………1分 将A (4,8)、C (8,0)两点坐标分别代入y=ax 2+bx 8=16a +4b 得0=64a +8b 得a =-12,b =4 解∴抛物线的解析式为:y =-12x 2+4x …………………3分(2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE =PE AP =BC AB ,即PE AP =48∴PE =12AP =12t .PB=8-t .∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t 2+8. …………………5分∴EG=-18t 2+8-(8-t ) =-18t 2+t .∵-18<0,∴当t =4时,线段EG 最长为2. …………………7分②共有三个时刻. …………………8分t 1=163, t 2=4013,t 3= …………………11分 【004】(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8xB =∴.点坐标为()80,.∴()8412AB =--=.(2分) 由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,.(3分)∴111263622ABCC S AB y ==⨯⨯=△·.(4分) (2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,. ∴D 点坐标为()88,.(5分)又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,.(6分)∴8448OEEF =-==,.(7分)(3)解法一:①当03t<≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CMAB ⊥于M,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =.Rt Rt AFH AMC △∽△,∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.(10分)【005】(1)如图1,过点E 作EG BC ⊥于点G . ································· 1分∵E 为AB 的中点,∴122BE AB ==. 在Rt EBG △中,60B =︒∠,∴30BEG =︒∠. (2)分∴112BG BE EG ====, 即点E 到BC ······························································· 3分 (2)①当点N 在线段AD 上运动时,PMN △的形状不发生改变.∵PM EF EG EF ⊥⊥,,∴PM EG ∥.∵EF BC ∥,∴EP GM =,PM EG == 同理4MNAB ==. ······························································································································· 4分 如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥, ∴6030NMC B PMH ==︒=︒∠∠,∠. ∴12PHPM == ∴3cos302MH PM =︒= .(图3)(图1)(图2)图1AD EBF CG图2ADEBF CPNH则35422NHMN MH =-=-=. 在Rt PNH △中,PN = ∴PMN △的周长=4PMPN MN ++.································································· 6分 ②当点N 在线段DC 上运动时,PMN △的形状发生改变,但MNC △恒为等边三角形.当PMPN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==. ·································································································································· 7分 ∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=. ··························································· 8分当MP MN =时,如图4,这时MC MN MP ===此时,615x EP GM ===-= 当NPNM =时,如图5,30NPM PMN ==︒∠∠. 则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠.因此点P 与F 重合,PMC △为直角三角形.∴tan 301MC PM =︒= .此时,6114x EP GM ===--=.综上所述,当2x=或4或(5时,PMN △为等腰三角形.【006】解:(1)OC=1,所以,q=-1,又由面积知0.5OC ×AB=45,得AB=52,设A (a,0),B(b,0)AB=b -a=52,解得p=32±,但p<0,所以p=32-。

合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网2010年中考数学压轴题100题精选(71-80题)【071】已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标. (3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(第24题图)合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【072】如图1所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E .(1)将直线l 向右平移,设平移距离CD 为t (t ≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图2所示, OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.①求梯形上底AB 的长及直角梯形OABC 的面积; ②当42<<t 时,求S 关于t 的函数解析式;(2)在第(1)题的条件下,当直线l 向左或向右平移时(包括l 与直线BC 重合),在直线..AB ..上是否存在点P ,使PD E ∆为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标;若不存在,请说明理由.【073】)如图,半径为O 内有互相垂直的两条弦AB 、CD 相交于P 点.合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网(1)求证:PA ·PB =PC ·PD ;(2)设BC 的中点为F ,连结FP 并延长交AD 于E ,求证:EF ⊥AD : (3)若AB =8,CD =6,求OP 的长.【074】如图,在平面直角坐标系中,点1O 的坐标为(40) ,,以点1O 为圆心,8为半径的圆与x 轴交于A B ,两点,过A 作直线l 与x 轴负方向相交成60°的角,且交y 轴于C 点,以点2(135)O ,为第23题图合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网圆心的圆与x 轴相切于点D . (1)求直线l 的解析式;(2)将2O ⊙以每秒1个单位的速度沿x 轴向左平移,当2O ⊙第一次与1O ⊙外切时,求2O ⊙平移的时间.【075】如图11,已知抛物线b ax ax y --=22(0>a )与x 轴的一个交点为(10)B -,,与y 轴的负半轴交于点C ,顶点为D .(1)直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点A 的坐标; (2)以AD 为直径的圆经过点C . ①求抛物线的解析式;合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网②点E 在抛物线的对称轴上,点F 在抛物线上,且以E F A B ,,,四点为顶点的四边形为平行四边形,求点F 的坐标.【076】如图,抛物线n mx x y ++=221与x 轴交于A 、B 两点,与y 轴交于C 点,四边形OBHC 为矩形,CH 的延长线交抛物线于点D (5,2),连结BC 、AD . (1)求C 点的坐标及抛物线的解析式;(2)将△BCH 绕点B 按顺时针旋转90°后 再沿x 轴对折得到△BEF (点C 与点E 对应),判断点E 是否落在抛物线上,并说明理由;(3)设过点E 的直线交AB 边于点P ,交CD 边于点Q . 问是否存在点P ,使直线PQ 分梯形ABCD的面积为1∶3两部分?若存在,求出P 点坐标;若不存在,请说明理由.图11合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【077】已知直线m x y +-=43与x 轴y 轴分别交于点A 和点B ,点B 的坐标为(0,6) (1)求的m 值和点A 的坐标;(2)在矩形OACB 中,点P 是线段BC 上的一动点,直线PD ⊥AB 于点D ,与x 轴交于点E ,设BP=a ,梯形PEAC 的面积为s 。

2010年中考数学压轴题(一)1、(2010年北京市)24. 在平面直角坐标系xOy 中,抛物线y = -41-m x 2+45mx +m 2-3m +2与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上。
(1) 求点B 的坐标;(2) 点P 在线段OA 上,从O 点出发向点运动,过P 点作x 轴的 垂线,与直线OB 交于点E 。
延长PE 到点D 。
使得ED =PE 。
以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动 时,C 点、D 点也随之运动)当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;若P 点从O 点出发向A 点作匀速运动,速度为每秒1点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止 运动,P 点也同时停止运动)。
过Q 点作x 轴的垂线,与直线AB 交于点F 。
延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点,N 点也随之运动)。
若P 点运动到t 秒时,两个等腰直角三角形分 别有一条直角边恰好落在同一条直线上,求此刻t 的值。
2、(2010年北京市)25. 问题:已知△ABC 中,∠BAC =2∠ACB ,点D 是△ABC 内的一点,且AD =CD ,BD =BA 。
探究∠DBC 与∠ABC 度数的比值。
请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。
(1) 当∠BAC =90︒时,依问题中的条件补全右图。
观察图形,AB 与AC 的数量关系为 ;当推出∠DAC =15︒时,可进一步推出∠DBC 的度数为 ; 可得到∠DBC 与∠ABC 度数的比值为 ; (2) 当∠BAC ≠90︒时,请你画出图形,研究∠DBC 与∠ABC 度数的比值 3、(2010年安徽省芜湖市)23.(本小题满分12分)如图,BD 是⊙O 的直径,OA ⊥OB ,M 是劣弧AB ⌒上一点,过点M 点作⊙O 的切线MP 交OA 的延长线于P 点,MD 与OA 交于N 点.(1)求证:PM =PN ;(2)若BD =4,PA = 32AO ,过点B 作BC ∥MP 交⊙O 于C 点,求BC 的长.4、(2010年安徽省芜湖市)24.(本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO ,其顶点为A (0,1)、B (-33,1)、C (-33,0)、O (0,0).将此矩形沿着过E (-3,1)、F (-433,0)的直线EF 向右下方翻折,B 、C 的对应点分别为B ′、C ′.(1)求折痕所在直线EF 的解析式;(2)一抛物线经过B 、E 、B ′三点,求此二次函数解析式;(3)能否在直线EF 上求一点P ,使得△PBC 周长最小?如能,求出点P 的坐标;若不能,说明理由.A C B5、(2010年安徽省) 22.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售。
精选2010年中考数学压轴题100题【001】如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【002】如图16,在Rt △ABC 中,∠C =90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB -BC -CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与t 的函数关系式;(不必写出t 的取值范围) (3)在点E 从B 向C 运动的过程中,四边形QBED 能否成为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接..写出t 的值.【003】如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形?请直接写出相应的t 值。
图16【004】如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合. (1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移, 设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关t 的函数关系式,并写出相应的t 的取值范围.【005】如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①当点N 在线段AD 上时(如图2),PMN △的形状是否发生改变?若不变,求出PMN △的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.A DB EO C F xy1l2l(G ) (第26题) A D EFAD E FA D E BF C图1 图2A D E BFCPNM图3A DE BFCPNM(第25题)【006】如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与ΔABC 的外接圆有公共点,求m 的取值范围; (3)在该二次函数的图象上是否存在点D ,使四边形ABCD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
【007】如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(-3,4), 点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H . (1)求直线AC 的解析式;(2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S ≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);(3)在(2)的条件下,当 t 为何值时,∠MPB 与∠BCO 互为余角,并求此时直线OP 与直线AC 所夹锐角的正切值.【008】如图所示,在直角梯形ABCD 中,∠ABC=90°,AD ∥BC ,AB=BC ,E 是AB 的中点,CE ⊥BD 。
(1) 求证:BE=AD ;(2) 求证:AC 是线段ED 的垂直平分线; (3) △DBC 是等腰三角形吗?并说明理由。
【009】一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD . (1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形; ②AN BM =.(2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.【010】如图,抛物线23y ax bx =+-与x 轴交于A B ,两点,与y 轴交于C 点,且经过点(23)a -,,对称轴是直线1x =,顶点是M .(1)求抛物线对应的函数表达式;(2)经过C,M 两点作直线与x 轴交于点N ,在抛物线上是否存在这样的点P ,使以点P A C N ,,,为顶点的四边形为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)设直线3y x =-+与y 轴的交点是D ,在线段BD 上任取一点E (不与B D ,重合),经过A B E ,,三点的圆交直线BC 于点F ,试判断AEF △的形状,并说明理由;(4)当E 是直线3y x =-+上任意一点时,(3)中的结论是否成立?(请直接写出结论).O C F MDE N Ky x11()A x y ,22()B x y ,(图1)OC D KF E N y x11()A x y ,33()x y ,M(图2)O BxyA MC13-【011】已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG .(1)求证:EG =CG ;(2)将图①中△BEF 绕B 点逆时针旋转45º,如图②所示,取DF 中点G ,连接EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)【012】如图,在平面直角坐标系xOy 中,半径为1的圆的圆心O 在坐标原点,且与两坐标轴分别交于A BC D 、、、四点.抛物线2y ax bx c =++与y 轴交于点D ,与直线y x =交于点M N 、,且MA NC 、分别与圆O相切于点A 和点C . (1)求抛物线的解析式;(2)抛物线的对称轴交x 轴于点E ,连结DE ,并延长DE 交圆O 于F ,求EF 的长. (3)过点B 作圆O 的切线交DC 的延长线于点P ,判断点P 是否在抛物线上,说明理由.【013】如图,抛物线经过(40)(10)(02)A B C -,,,,,三点.(1)求出抛物线的解析式;(2)P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标.D ①D E②③【014】在平面直角坐标中,边长为2的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上,点O 在原点.现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线y x =上时停止旋转,旋转过程中,AB 边交直线y x =于点M ,BC 边交x 轴于点N (如图). (1)求边OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 和AC 平行时,求正方形 OABC 旋转的度数;(3)设MBN ∆的周长为p ,在旋转正方形OABC 的过程中,p 值是否有变化?请证明你的结论.【015】如图,二次函数的图象经过点D(0,397),且顶点C 的横坐标为4,该图象在x 轴上截得的线段AB 的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P ,使PA+PD 最小,求出点P 的坐标;⑶在抛物线上是否存在点Q ,使△QAB 与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由.【016】如图9,已知正比例函数和反比例函数的图象都经过点(33)A ,.(1)求正比例函数和反比例函数的解析式;(2)把直线O A 向下平移后与反比例函数的图象交于点(6)B m ,,求m 的值和这个一次函数的解析式; (3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式; (4)在第(3)问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足:123S S =若存在,求点E 的坐标;若不存在,请说明理由.(第26题)OABCMNy x =xyy xOC BA3 36【017】如图,已知抛物线2y x bx c =++经过(10)A ,,(02)B ,两点,顶点为D .(1)求抛物线的解析式;(2)将OAB △绕点A 顺时针旋转90°后,点B 落到点C 的位置,将抛物线沿y 轴平移后经过点C ,求平移后所得图象的函数关系式; (3)设(2)中平移后,所得抛物线与y 轴的交点为1B ,顶点为1D ,若点N 在平移后的抛物线上,且满足1NBB △的面积是1NDD △面积的2倍,求点N 的坐标.【018】如图,抛物线24y ax bx a =+-经过(10)A -,、(04)C ,两点,与x 轴交于另一点B . (1)求抛物线的解析式;(2)已知点(1)D m m +,在第一象限的抛物线上,求点D 关于直线BC 对称的点的坐标; (3)在(2)的条件下,连接BD ,点P 为抛物线上一点,且45DBP ∠=°,求点P 的坐标.【019】如图所示,将矩形OABC 沿AE 折叠,使点O 恰好落在BC 上F 处,以CF 为边作正方形CFGH ,延长BC至M ,使CM =|CF —EO |,再以CM 、CO 为边作矩形CMNO (1)试比较EO 、EC 的大小,并说明理由 (2)令;四边形四边形CNMN CFGHS S m =,请问m 是否为定值?若是,请求出m 的值;若不是,请说明理由(3)在(2)的条件下,若CO =1,CE =31,Q 为AE 上一点且QF =32,抛物线y =mx 2+bx+c 经过C 、Q 两点,请求出此抛物线的解析式.(4)在(3)的条件下,若抛物线y =mx 2+bx+c 与线段AB 交于点P ,试问在直线BC 上是否存在点K ,使得以P 、B 、K 为顶点的三角形与△AEF 相似?若存在,请求直线KP 与y 轴的交点T 的坐标?若不存在,请说明理由。