中级微观经济学(第二讲)PPT课件

格式：ppt
大小：912.50 KB
文档页数：28

下载文档原格式

中级微观经济学 ppt课件

含券预算线
2020/4/1
x1
x1
15
二、消费者偏好
strict preference indifference
weak preference
消费束
X(x1,x2)
对于两个消费束
X(x1,x2) Y(y1,y2)
▪ 严格偏好关系（X 确实比Y 好）
(x 1 ,x 2 ) (y 1 ,y 2 )
x2
原预算线斜率 p 1
p2
征税后的预算线斜率
p1 t
p2
2020/4/1
x1
11
配给对预算集的限制
配给使预算集进一步受到约束，预算空间缩小
p1x1p2x2m
x1 x1
x2
2020/4/1
x1
x1
12
税收与配额的混合使用
x2
2020/4/1
预算线斜率 p 1 p2
含义：对超过既定数量
消费者的预算约束（可以假定所有收入等于消费）
p1x1p2x2m
满足该约束条件的消费束称为消费者的预算集。
预算线
2020/4/1
p1x1p2x2m
x2
m p2
p1 p2
x1
2
对预算约束的理解
理解 1：将 x2 视为除 x1 之外的一切其他商品
p1x1p2x2m
理解 2：将 x2 视为购买一切其他商品的货币支出；也可称其为一种复合商品，价格为 1
x2
消费者有一个最佳的消费束，就其偏好而言，越接近餍足点越好。
x1
x1
分析：曲线斜率的变化特征。
2020/4/1
25
偏好的非饱和性假定
如果两个商品组合的区别仅仅在于其中一种商品的数量的不同，那么，消费者总是偏好于含有这种商品数量较多的那个组合；

中级微观经济学ppt课件

这种预期收入产生的预期效用为: E(u) = 0.5(18) + 0.5(10) = 14
完整版ppt课件
Slide 42
风险溢价图示
效用 18 16
14
10
风险规避者
D
C
F
A
E
由于确定性收入为16 与期望值为20的不确定收入所产生的效用均为14，因此，4就是风险溢价。
0
10
完整版ppt课件
第5章
不确定性与消费者行为
本章讨论的主题
描述风险风险偏好降低风险对风险资产的需求* 行为经济学
完整版ppt课件
Slide 2
5.1 描述风险
为了计量风险，我们必须知道: 1) 所有可能的结果 2) 每一种结果发生的可能性
完整版ppt课件
Slide 3
5.1.1 概率
概率（Probability）
间没有特别的偏好。
收入
0
10
20
30
完整版ppt课件
Slide 37
风险偏好者
如果消费者在期望收入相同的确定性工作与不确定性工作中选择了后者，那么，该消费者就是风险偏好者（risk loving）。
例如：赌博、一些犯罪活动
完整版ppt课件
Slide 38
风险偏好者
风险偏好者
效用
18
该消费者宁可去接受有风险的工作，而不选择确定收入的工作，因此，她是风险爱好型的。
工作1
离差的平方
工作1 工作2
2,100 1510
250,000 100
工作2
离差的平方
收入的期望值
标准差
1,100 510
250,000 980,100

中级微观经济学讲义-2

第二讲消费者理论
四、显示偏好简介
（一）显示偏好弱公理
与古典的从偏好关系到效用函数再到需求函数的逻辑思路不同，求函数的逻辑思路不同，萨缪尔森从行为结果本身推导人的行为准则，抛却了效用理论果本身推导人的行为准则，中的许多主管假定，而仅需要一些隐含的、中的许多主管假定，而仅需要一些隐含的、弱的要求，比如一致性。弱的要求，比如一致性。
第二讲消费者理论
二、效用最大化与支出最小化
（二）效用最大化－续（2）效用最大化－
罗伊恒等式】【罗伊恒等式】构造拉格朗日函数 L( x , λ ) = u( x ) + λ ( y − px )， ∂v ( p, y ) ∂L( x * , λ* ) 根据包络定理，根据包络定理， = = λ*以及 ∂y ∂y ∂v ( p, y ) ∂L( x * , λ* ) = = − λ* x i*，可以得到 ∂ pi ∂p i ∂v ( p , y ) − ∂ pi x i* = x i ( p, y ) = ∂v ( p , y ) ∂y
x 2 f x1 , ∀t ∈ [0,1] ⇒ x t = tx 2 + (1 − t )x1 ~ x1 f ~ 公理 7 : 严格凸性 x 2 ≠ x1 , x 2 f x1 ⇒ x t f x1 ~ (排除了无差异集凹向原点 < 多元化消费 > )
第二讲消费者理论
一、偏好、效用与预算偏好、
第二讲消费者理论
一、偏好、效用与预算偏好、
（一）偏好关系－续（1）偏好关系－
偏好公理：偏好公理：公理 4 : 局部非饱和性公理 5 : 严格单调性公理 6 : 凸性 ∀x 0 ∈ R n , ∃ε > 0 , ∃x ∈ B ε ( x 0 ) I R n ⇒ x f x 0 + + (排除了无差异区域的存在 ) ∀x 0， x1 ∈ R n ， x1 ≥ x 0 ⇒ x1 f x 0 + ~ (排除了无差异集向上弯曲)

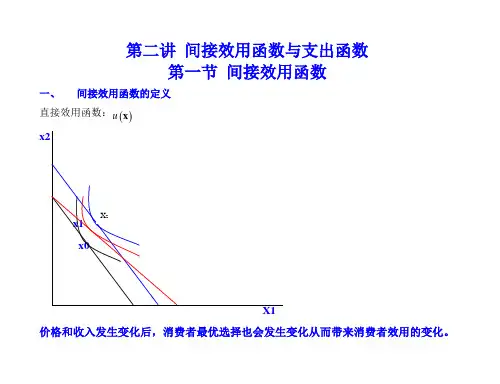
中级微观经济学02

第二讲间接效用函数与支出函数第一节间接效用函数一、间接效用函数的定义直接效用函数：()u x价格和收入发生变化后，消费者最优选择也会发生变化从而带来消费者效用的变化。

也就是说，消费者最大化效用是收入和价格向量的函数。

记这种效用函数为：间接效用函数：()()max ,..v p y u s t y =≤x px x()()()*,,v y u y ==p x x p间接效用函数的政策意义：通过价格政策（p ）和收入政策（y ）可以控制消费者行为。

二、间接效用函数的特征：间接效用函数),(y v p1) 在n+++⨯ 上连续2) 在(),y p 上零次齐次性3) 在y 上严格递增4) 在p 上严格递减5) 在(),y p 上拟凹6) 罗伊恒等式：如果(),v y p 在()00,y p 上可导，并且()00,0v y y δδ≠p ，有：()()()000000,,,1,...,,ii v y p x y i n v y yδδδδ==p p p 间接效用函数()()max ,..v y u s t y =≤p x px x的特征 1、间接效用函数在n+++⨯ 上连续最大值定理：如果目标函数和约束条件在参数上连续，定义域为紧集，则值函数在参数上连续。

含义：当收入和价格有微量变化时，极大化了的效用也会有微量变化。

2、间接效用函数在(),y p 上零次齐次性()()max ,..v y u s t y ==p x px x间接效用函数在(),y p 上零次齐次性：()()()0,,,,0v t ty t v y v y t ==>p p p()()()()()ma max ,,..x ..,u v t u v t ty s ty v t t t y y s yt ===⇒==x p p x px x p xpx3、间接效用函数(),v y p 对于y 严格递增，(),0v y yδδ>p 应用包络定理：构造拉格朗日函数()()(),L x u y λλ=+-x px根据包络定理，()(),,v y L x y yδδλλδδ==p ：λ的符号？ ()() ()?00,,000i i i L u v y p x x y δλδδλλδδδλ>>=-=⇒>⇒=>x x p4.间接效用函数(),v y p 关于价格p 递减设*i x 0,>用与（3）同样的方法可证：****ii iv(p,y)L(x ,)x p p λλ∂∂==-∂∂〈5、间接效用函数(),v y p 在(),y p 上拟凸定义A1.27：一个函数:f D → 是拟凸函数，当且仅当对于所有D ∈21X ,X ，有：)](),(max[)(21t X X X f f f ≤。

中级微观经济学(第二讲)

经济学应用：
y = f(x1, x2) dy = f1 dx1 + f2 dx2 = f11dx12 + 2f12dx1dx2 + f22dx22
d 2y
18
无约束的最优化（1）

一元函数的最优化：
一阶条件：
19
无约束的最优化（2）

一元函数的最优化：

二阶条件：

证明：假设在x*处于最大值，即：对于任意的h，
中级微观经济学
第2讲最优化的数学方法
四川农业大学经济学院
课程安排

集合和函数

微分和求导最优化问题
·无约束的最优化 ·等式约束下的最优化
2

集合与函数（1）

集合（set）：
所有对象组成的全集，集合中的每个对象称为元素；
例子：
X={x/x=(x1, x2), x1≥0, x2≥0}

根据泰勒展开式，

20
无约束的最优化（3）

二元函数的最优化：

函数形式：y = f(x1, x2)
一阶条件：
y/x1 = f1 = 0 y/x2 = f2 = 0
二阶条件
：
d 2y = f11dx12 + 2f12dx1dx2 + f22dx22 <0 f11 < 0 and f11 f22 - f122 > 0

2. 求x1，x2使得下列函数有最值：

26
作业（3）

3. 请分别利用替换法和拉格朗日乘子法，求x1， x2使得函数出现最大值：

MAX f(x1，x2 )= x12 *x23 s.t 2x1+3x2 =10

中级微观经济学第二讲

补贴与税收正好相反
从量补贴:(p1-s)x1 +(p2-s)x2 = m
从价补贴:(1-σ) p1x1 + (1-σ) p2x2 = m
总额税: p1x1＋p2x2 ＝ m-T 总额补贴: p1x1＋p2x2 ＝ m+m'
13
பைடு நூலகம்
配给供应: 某种消费品的数量不能超过某个数量
x2
预算线
x'1 预算集
x2 x z
y
x1
23
x2
I1 x
z
I2
y
I3 x1
24
Indifference Curves Cannot Intersect （无差异曲线不能相交）
x2
I1
I2
x
y
z
x1
25
无差异曲线的斜率（Slopes）
Good 2
Two goods negatively sloped （负斜率）
Good 1
49
效用函数：为每个消费束指派一个数字的方法。
指派给受较多偏好的消费束大于指派给较少偏好的消费束的数字。效用指派的惟一重要特征是：它对消费束的排序，给无差异曲线标明序数的办法。因为只有消费束的排序才有意义，所以不可能只存在一种为消费束指派效用的办法。
50
效用函数与偏好
借助效用函数来描述偏好
47
基数效用理论的难题：
效用是主观心理概念，衡量是个问题
不同人的效用的可比性不科学，依赖于边际效用递减这个先验规律，不能被证明假设条件苛刻
48
序数效用理论和效用函数
序数效用理论：认为效用作为一种心理现象无法计量，也不能加总求和，只能表示出满足程度的高低与顺序，效用只能用序数（第一，第二，第三，……）来表示。序数效用论采用的是无差异曲线分析法

中级微观经济学(全套课件233P) ppt课件

➢ 第二套房子将出租给愿付490美元的人，随着我们沿需求曲线向下移动，依此类推。
价格歧视（差别价格）垄断市场均衡
p p1 =$500 p2 =$490 p3 =$475
pe
123
S
得到住房的人与市场解决的情形正好一样，即这些人都是按超过 pe的价格租赁的人。但人们支付的数量不同。
QD,QS
--- John Maynard Keynes
精品资料
你怎么称呼老师？
如果老师最后没有总结一节课的重点的难点，你是否会认为老师的教学方法需要改进？你所经历的课堂，是讲座式还是讨论式？教师的教鞭
“不怕太阳晒，也不怕那风雨狂，只怕先生骂我笨，没有学问无颜见爹娘 ……” “太阳当空照，花儿对我笑，小鸟说早早早……”
一般垄断市场均衡
❖ 一般垄断者都要限制可能的
p
产量，从而使他的利润最大
化。
❖ 此时均衡价格Pe*高于竞争市
场的均衡价格pe的价格。
空置房 Pe*
pe
S
QD,QS
1.7.2 价格歧视（差别价东，他拥有所有的住房。或者我们把许许多多个别的房东看作是—个整体，把他们的行动看作是—个人的行动。
目的通过假设简化模型评估判断
1.1建立模型
经济模型的目的： ➢ 帮助提供关于经济现象的精确的洞察力 ➢ 因而：
不同的现象需要不同的模型。通过假设简化是必要的。案例：住房市场 ➢ 目的：住房价格由什么决定和谁将得到住房？ ➢ 通过假设简化模型所有的住房除了位置不同之外，在其他任何方面都是相同的外城区住房的价格是外生变量。有大量潜在的住房需求者和供给者，即住房市场是完全竞争的。
➢ 在出租房子时，房东可以决定依次把房子拍卖给愿出最高价的人。

中级微观02PPT课件

用（x1，x2）来表示消费者的消费束（组合）， x1，x2分别表示消费者对商品1和商品2的消费量。用（p1，p2）分别表示商品1和商品2的价格。p1 x1就表示消费者花费在商品1上的货币数，p2 x2就表示消费者花费在商品2上的货币数，消费者花费的货币总数为p1 x1 ＋p2 x2；用m表示消费者的收入
15
经济解释 : 斜率变化表示增加一单位商品1的消费,必须减少商品2
的消费量为p’1/p2 如果商品1的价格上升，p’1> p1 ，则斜率变大，表示增
加一单位商品1的消费,必须减少更多的商品2的消费量。
16
纵截距没有变化表示不管商品1的价格如何变化，消费者用于购买商品2 的最大数量不会发生任何变化。
3
预算约束的概念
消费者花在所有商品上的货币支出不能超过消费者的收入的关系式称为预算约束。
消费者的预算约束（可以假定所有收入等于消费）
p1x1 p2 x2 m
满足该约束条件的消费束称为消费者的预算集。
4
对预算约束的理解
理解 1：将 x2 视为除 x1 之外的一切其他商品
p1x1 p2 x2 m
p1x1 p2 x2 pn xn m
23
税收与补贴
税收有两种形式：从量税，从价税
p1 p1 t p1 (1 ) p1
补贴与税收相反。形式：从量补贴，从价补贴
p1 p1 s p1 (1 ) p1
税收和补贴的另一种形式：总额税，总额补贴
24
• 数量税（从量税）：对每单位商品所征收的税，即消费者每消费一单位商品要支付一定的税。常见的例子是汽油征税。
9
预算线的性质
• 预算线是一条直线，斜率为－p1/p2
• 斜率的经济意义是什么？ • 当商品1的消费增加 x1后，商品2的消费有何变动呢？

中级微观经济学课件.ppt

16
Expectations
▪ Expectations affect consumers’ buying
decisions.
▪ Future income and future prices ▪ Examples:
▪ If people expect their incomes to rise,
their demand for meals at expensive restaurants may increase now.
▪ If people expect the price of gold to rise,
their demand for gold may increase now.
17
$6.00 $5.00 $4.00 $3.00 $2.00 $1.00
Price of chocolate
(USD)
Quantity of
chocolates demanded
$0.00
16
1.00
14
2.00
12
3.00
10
4.00
8
5.00
6
6.00
4
$0.00 0
Quantity of
5
10
15 chocolates
▪ If any of these other factors change, the
demand curve will shift.
9
Demand Curve Shifters
P
An increase in
demand is
represented by a
shift of the demand
curve to the right.

中级微观经济学课件

况
市场均衡及其形成机制
市场均衡定义：市场上的供给和需求相等，价格不再变动的一种状态。
形成机制：在竞争市场中，价格变动会引发供给和需求的调整，最终达到市场均衡。
均衡的稳定性：在短期内，市场均衡是相对稳定的；但在长期中，市场均衡可能会因为外部因素而发生变化。市场均衡的意义：市场均衡是经济学的核心概念之一，对于理解市场经济运行规律和制定经济政策具有重要的意义。
价格歧视和垄断定价
价格歧视定义：对同一商品或服务在不同市场以不同价格销售的行为。目的：增加利润，最大化企业收益。类型：一级、二级和三级价格歧视。垄断定价：在独家垄断市场中，企业通过限制产量和抬高价格来最大化利润。
福利经济学及其主要观点
福利经济学定义：研究如何实现社会福利最大化的经济学分支。
消费者行为及其影响因素
消费者偏好：影响消费者行为的重要因素，决定了消费者的购买决策。收入水平：收入水平的高低直接影响消费者的购买能力，进而影响其消费行为。价格变动：价格变动对消费者行为有显著影响，价格上升或下降会影响消费者的需求量。消费者预期：消费者对未来经济状况的预期会影响其当前的消费行为。
类型：垄断竞争市场、寡头市场、完全垄断市场特点：产品差异、市场壁垒、市场集中度高、价格接受者
寡头市场的形成和竞争策略
寡头市场的定义：少数几家大企业占据了大部分的市场份额，从而影响市场的价格和产量。
寡头市场的形成原因：市场进入壁垒、规模经济、产品差异化和政府政策等因素导致市场结构趋于寡头化。
竞争策略：采用价格战、广告战Байду номын сангаас研发和创新等手段来争夺市场份额，提高自身竞争力。
合作策略：通过达成协议、建立联盟等方式来共同控制市场价格和产量，实现共赢。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

所有对象组成的全集，集合中的每个对象称为元素；
例子： X={x/x=(x1, x2), x1≥0, x2≥0}
凸集（convex set）：
2020年3月27日
NBER CG 2005 B Yeung
3
集合与函数（2）
函数（(Function）：
定义域：X 值域： Y 对应法则：f
MAX f(x1，x2 )= x12 *x23 s.t 2x1+3x2 =10
2020年3月27日
NBER CG 2005 B Yeung
27
参考资料
张树民，《中级微观经济学》第2章，中国财政经济出版社；
E.Roy Weintraub,《经济数学》
2020年3月27日
NBER CG 2005 B Yeung
12
微分和求导（5）
二阶导数（Second derivative）：
例子：
2020年3月27日
NBER CG 2005 B Yeung
13
微分和求导（5）
二阶导数与函数极值：
2020年3月27日
NBER CG 2005 B Yeung
14
微分和求导（6）
二阶导数与函数的极值：
函数存在极大值
直觉：
A function is continuous if “small” changes in x produces “small” changes in f(x)
2020年3月27日
NBER CG 2005 B Yeung
6
集合与函数（5）
函数的连续性（continuous）：
直觉：
2020年3月27日
函数存在极小值
2020年3月27日
NBER CG 2005 B Yeung
15
微分和求导（7）
多元函数的偏导数
let
练习1：练习2：
2020年3月27日
NBER CG 2005 B Yeung
16
微分和求导（8）
多元函数的全微分：
经济学应用：
边际替代率（
边际技术替代率（
2020年3月27日
中级微观经济学
第2讲最优化的数学方法
四川农业大学经济学院
2020年3月27日
NBER CG 2005 B Yeung
1
课程安排
集合和函数
微分和求导
最优化问题
·无约束的最优化 ·等式约束下的最优化
2020年3月27日
NBER CG 2005 B Yeung
2
集合与函数（1）
集合（set）：
NBER CG 2005 B Yeung
））
17
微分和求导（8）
杨氏定理（Young’s Theorem）：
(f / xi ) x j
2 f x j xi
fij
(f / x j ) xi
2 f xi x j
f ji
经济学应用：
y = f(x1, x2) dy = f1 dx1 + f2 dx2
d 2y = f11dx12 + 2f12dx1dx2 + f22dx22 <0
f11 < 0 and f11 f22 - f122 > 0
2020年3月27日
NBER CG 2005 B Yeung
21
无约束的最优化（4）
二元函数的最优化：
2020年3月27日
NBER CG 2005 B Yeung
d 2y = f11dx12 + 2f12dx1dx2 + f22dx22
2020年3月27日
NBER CG 2005 B Yeung
18
无约束的最优化（1）
一元函数的最优化：
一阶条件：
2020年3月27日
NBER CG 2005 B Yeung
19
无约束的最优化（2）
一元函数的最优化：
9
微分和求导（2）
导数（differentiable）：
直觉：
2020年3月27日
NBER CG 2005 B Yeung
10
微分和求导（3）
求导法则
2020年3月27日
NBER CG 2005 B Yeung
11
微分和求导（4）
求导法则
（链式法则）
2020年3月27日
NBER CG 2005 B Yeung
二阶条件：
证明：假设在x*处于最大值，即：对于任意的h，
根据泰勒展开式，
2020年3月27日
NBER CG 2005 B Yeung
20
无约束的最优化（3）
二元函数的最优化：
函数形式：y = f(x1, x2)
一阶条件：
y/x1 = f1 = 0 y/x2 = f2 = 0
二阶条件：
22
等式约束的最优化（1）
最优化问题：
Method 1：替换法 Method 2：拉格朗日乘子法
2020年3月27日
NBER CG 2005 B Yeung
23
等式约束的最优化（2）
最优化问题：
Method 2：拉格朗日乘子法一阶条件:
2020年3月27日

NBER CG 2005 B Yeung
NBER CG 2005 B Yeung
7
集合与函数（6）
函数的连续性（continuous）：
直觉：
2020年3月27日
NBER CG 2005 B Yeung
8
微分和求导（1）
导数（differentiable）：
（一元函数）
练习1：
练习2： 2020年3月27日
NBER CG 2005 B Yeung
24
作业（1）
1. 求下列函数的导数：
2020年3月27日
NBER CG 2005 B Yeung
25
作业（2）
2. 求x1，x2使得下列函数有最值：
2020年3月27日
NBER CG 2005 B Yeung
26
作业（3）
3. 请分别利用替换法和拉格朗日乘子法，求x1， x2使得函数出现最大值：
表示：
例子：y=f（x）=x^2
2020年3月27日
NBER CG 2005 B Yeung
4
集合与函数（3）
极限（ Limits ）：
例子：f(x)=3+2x，当x趋近于3时，f(x)的极限：
2020年3月27日
NBER CG 2005 B Yeung
5
集合与函数（4）
函数的连续性（continuous）：
28