电磁场试题B及答案
- 格式:doc
- 大小:215.00 KB
- 文档页数:7

大学电磁场考试题及答案一、单项选择题(每题2分,共20分)1. 电磁波在真空中的传播速度是:A. 300,000 km/sB. 299,792,458 m/sC. 1,000,000 km/sD. 299,792,458 km/s答案:B2. 麦克斯韦方程组中描述电磁场与电荷和电流关系的方程是:A. 高斯定律B. 法拉第电磁感应定律C. 麦克斯韦-安培定律D. 所有上述方程答案:D3. 以下哪项不是电磁场的基本概念?A. 电场B. 磁场C. 引力场D. 电磁波答案:C4. 根据洛伦兹力定律,一个带电粒子在磁场中的运动受到的力与以下哪个因素无关?A. 粒子的电荷量B. 粒子的速度C. 磁场的强度D. 粒子的质量答案:D5. 电磁波的波长和频率的关系是:A. 波长与频率成正比B. 波长与频率成反比C. 波长与频率无关D. 波长与频率的乘积是常数答案:B6. 以下哪项是电磁波的主要特性?A. 需要介质传播B. 具有粒子性C. 具有波动性D. 以上都是答案:C7. 电磁波在介质中的传播速度比在真空中:A. 快B. 慢C. 相同D. 无法确定答案:B8. 根据电磁波的偏振特性,以下说法正确的是:A. 只有横波可以偏振B. 纵波也可以偏振C. 所有波都可以偏振D. 只有电磁波可以偏振答案:A9. 电磁波的反射和折射遵循的定律是:A. 斯涅尔定律B. 牛顿定律C. 欧姆定律D. 法拉第电磁感应定律答案:A10. 电磁波的干涉现象说明了:A. 电磁波具有粒子性B. 电磁波具有波动性C. 电磁波具有量子性D. 电磁波具有热效应答案:B二、填空题(每空1分,共10分)1. 电磁波的传播不需要________,可以在真空中传播。
答案:介质2. 麦克斯韦方程组由四个基本方程组成,分别是高斯定律、高斯磁定律、法拉第电磁感应定律和________。
答案:麦克斯韦-安培定律3. 根据洛伦兹力定律,一个带电粒子在磁场中受到的力的大小与粒子的电荷量、速度以及磁场强度的乘积成正比,并且与粒子速度和磁场方向的________垂直。
.;.淮 海 工 学 院10 - 11 学年 第 2 学期 电磁场与电磁波期末试卷(B 闭卷)答案及评分标准一、判断题(本大题共10小题,每题1分,共10分)1.导体或介质所受到的静电力可以由能量的空间变化率计算得出。
(√ )2.在恒定电流场中,电流密度通过任一闭合面的通量一定为零。
(√ )3.均匀导体中没有净电荷,在导体面上,也没有电荷分布。
(× )4. 标量场梯度的方向沿其等值面的切线方向。
(× )5.在理想导电体的表面上电场强度的切向分量等于零。
(√ )6.在无限大理想介质中传播的平面电磁波不衰减。
(√ )7.复能流密度矢量的实部代表能量的流动,虚部代表能量交换。
(√ ) 8.平面波的频率是由波源决定的。
(√ )9.用单站雷达可以发现隐形飞机。
(× )10.地面雷达存在低空盲区。
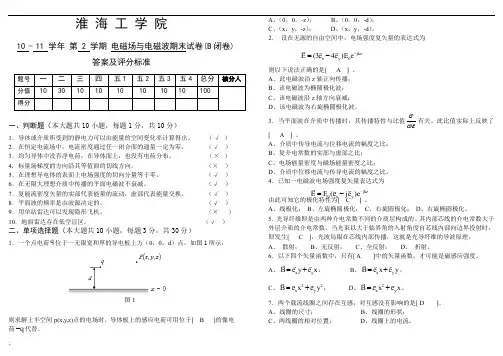
(√ )二、单项选择题(本大题共10小题,每题3分,共30分)1.一个点电荷q 位于一无限宽和厚的导电板上方(0,0,d )点,如图1所示,则求解上半空间p(x,y,z)点的电场时,导体板上的感应电荷可用位于[ B ]的像电荷q -代替。
A 、(0,0,-z );B 、(0,0,-d );C 、(x ,y ,-z );D 、(x ,y ,-d )。
2. 设在无源的自由空间中,电场强度复矢量的表达式为 j 0(34e )e kz x y E e E -=-则以下说法正确的是[ A ] 。
A 、此电磁波沿z 轴正向传播; B 、该电磁波为椭圆极化波; C 、该电磁波沿z 轴方向衰减;D 、该电磁波为右旋椭圆极化波。
3.当平面波在介质中传播时,其传播特性与比值σωε有关。
此比值实际上反映了[ A ] 。
A 、介质中传导电流与位移电流的幅度之比; B 、复介电常数的实部与虚部之比; C 、电场能量密度与磁场能量密度之比; D 、介质中位移电流与传导电流的幅度之比。
4.已知一电磁波电场强度复矢量表达式为 由此可知它的极化特性为[ C ] 。

大学电磁场考试题及答案一、选择题(每题2分,共20分)1. 电磁场中,电场与磁场的相互作用遵循以下哪个定律?A. 高斯定律B. 法拉第电磁感应定律C. 安培环路定律D. 洛伦兹力定律答案:D2. 在真空中,电磁波的传播速度是多少?A. 100,000 km/sB. 300,000 km/sC. 1,000,000 km/sD. 3,000,000 km/s答案:B3. 一个点电荷产生的电场强度与距离的平方成什么关系?A. 正比B. 反比C. 对数关系D. 线性关系答案:B4. 以下哪种介质不能支持电磁波的传播?A. 真空B. 空气C. 玻璃D. 金属答案:D5. 麦克斯韦方程组中描述变化电场产生磁场的方程是?A. 高斯定律B. 高斯磁定律C. 法拉第电磁感应定律D. 安培环路定律答案:C6. 一个均匀带电球壳内部的电场强度是多少?A. 零B. 与球壳内的电荷分布有关C. 与球壳外的电荷分布有关D. 与球壳的总电荷量成正比答案:A7. 电磁波的频率和波长之间有什么关系?A. 频率与波长成正比B. 频率与波长成反比C. 频率与波长无关D. 频率越大,波长越小答案:B8. 根据洛伦兹力公式,一个带电粒子在磁场中运动时,其受到的力的方向与什么因素有关?A. 粒子的速度B. 磁场的方向C. 粒子的电荷D. 所有上述因素答案:D9. 电磁波的偏振现象说明电磁波是横波,这是因为?A. 电磁波的振动方向与传播方向垂直B. 电磁波的振动方向与传播方向平行C. 电磁波的传播不需要介质D. 电磁波在真空中传播速度最快答案:A10. 一个闭合电路中的感应电动势遵循以下哪个定律?A. 欧姆定律B. 基尔霍夫电压定律C. 法拉第电磁感应定律D. 安培环路定律答案:C二、填空题(每题2分,共20分)11. 电磁波的传播不需要______,因此它可以在真空中传播。
答案:介质12. 根据麦克斯韦方程组,电荷守恒定律可以表示为:∇⋅ E =______。

**学院202*-202*学年第*学期级 专业《大学物理及实验B2》期末试卷(B 卷)(电磁学加强类)(闭卷)院(系)____________班级___________姓名_____________学号________题号 一 二 三 总分 分值202060100一、选择题(每小题只有一个正确答案,选对得2分,不选或选错得0分,共20分) 1.一导体球壳半径为 R ,带电量q ,设“无限远”处为电势零点,则在离球心O 为r (R r <)处一点的电势为( ) (A ) 0; (B )Rq 04πε; (C )rq 04πε ; (D )rq 04πε-。
2.库仑定律的适用范围是( )(A )真空中两个带电球体间的相互作用; (B )真空中任意带电体间的相互作用; (C )真空中两个正点电荷间的相互作用;(D )真空中两个带电体的大小远远小于它们之间的距离。
3.磁场的高斯定理⎰⎰=⋅0S d B说明了下面的哪些叙述是正确的( )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )a d ; (B )a c ; (C )c d ; (D )a b 。
4.顺磁物质的磁导率( )(A )比真空的磁导率略小; (B )比真空的磁导率略大; (C )远小于真空的磁导率;(D )远大于真空的磁导率。
5.在均匀磁场中有一电子枪,它可发射出速率分别为v 和2v 的两个电子,这两个电子的速度方向相同,且均与B 垂直,则这两个电子绕行一周所需的时间之比为( ) (A )1:1; (B )1:2; (C )2:1; (D )4:1。
6.假设空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁 场分布( )(A )不能用安培环路定理来计算; (B )可以直接用安培环路定理求出; (C )只能用毕奥-萨伐尔定律求出;(D )可以用安培环路定理和磁感应强度的叠加原理求出。

电磁场考试试题及答案讲课稿电磁场考试试题及答案电磁波考题整理⼀、填空题1. 某⼀⽮量场,其旋度处处为零,则这个⽮量场可以表⽰成某⼀标量函数的(梯度)形式。
2. 电流连续性⽅程的积分形式为(s dSj=-dtdq)3. 两个同性电荷之间的作⽤⼒是(相互排斥的)。
4. 单位⾯积上的电荷多少称为(⾯电荷密度)。
5. 静电场中,导体表⾯的电场强度的边界条件是:(D1n-D2n=ρs)6. ⽮量磁位A和磁感应强度B之间的关系式:(B=▽ x A)7. .E(Z,t)=e x E m sin(wt-kz-)+ e y E m cos(wt-kz+),判断上述均匀平⾯电磁波的极化⽅式为:(圆极化)(应该是90%确定)8. 相速是指均匀平⾯电磁波在理想介质中的传播速度。
9.根据电磁波在波导中的传播特点,波导具有(HP)滤波器的特点。
(HP,LP,BP三选⼀)10.根据电与磁的对偶关系,我们可以由电偶极⼦在远区场的辐射场得到(磁偶极⼦)在远区产⽣的辐射场11. 电位移⽮量D=ε0E+P在真空中 P的值为(0)12.平板电容器的介质电容率ε越⼤,电容量越⼤。
13.恒定电容不会随时间(变化⽽变化)14.恒定电场中沿电源电场强度⽅向的闭合曲线积分在数值上等于电源的(电动势)15. 电源外媒质中电场强度的旋度为0。
16.在给定参考点的情况下,库伦规范保证了⽮量磁位的(散度为零)17.在各向同性媚质中,磁场的辅助⽅程为(D=εE, B=µH, J=σE)18.平⾯电磁波在空间任⼀点的电场强度和磁场强度都是距离和时间的函数。
19. 时变电磁场的频率越⾼,集肤效应越明显。
20. 反映电磁场中能量守恒与转换规律的定理是坡印廷定理。
⼆、名词解释1. ⽮量:既存在⼤⼩⼜有⽅向特性的量2. 反射系数:分界⾯上反射波电场强度与⼊射波电场强度之⽐3. TEM波:电场强度⽮量和磁场强度⽮量均与传播⽅向垂直的均匀平⾯电磁波4.⽆散场:散度为零的电磁场,即·=0。

电磁场考试试题及答案一、选择题1. 下列哪个物理量不是描述电磁场的基本量?A. 电场强度B. 磁感应强度C. 电势D. 磁化强度2. 静电场的本质特征是:A. 磁场产生于电场B. 电场产生于静电荷C. 电场与磁场相互作用D. 电场与静电荷相互作用3. 关于电磁场的能量密度,以下说法正确的是:A. 电磁场的能量密度只与电场强度有关B. 电磁场的能量密度只与磁感应强度有关C. 电磁场的能量密度与电场和磁感应强度都有关D. 电磁场的能量密度与电荷和电流有关4. 电磁波中电场和磁场的相互关系是:A. 电场和磁场以90°的相位差波动B. 电场和磁场以180°的相位差波动C. 电场和磁场处于同相位波动D. 电场和磁场没有固定的相位关系5. 有一根长直导线,通有电流,要使其产生的磁场最强,应将观察点放置在:A. 导线的外侧B. 导线的内侧C. 导线的中央D. 对称轴上二、填空题1. 电荷为2μC的点电荷在距离它10cm处的电场强度大小为______ N/C。
2. 一根长度为50cm的直导线通有5A的电流,它产生的磁感应强度大小为______ T。
三、简答题1. 什么是电磁场?它的基本特征是什么?电磁场是一种通过电荷和电流相互作用而产生的物质场。
它基于电荷和电流的特性,表现为电场和磁场的存在和相互作用。
电磁场的基本特征包括:电场与静电荷相互作用,磁场与电流相互作用,电磁场遵循麦克斯韦方程组等。
2. 电场与磁场有何区别和联系?电场是由电荷产生的一种物质场,描述电荷对其他电荷施加的作用力的特性。
而磁场则是由电流产生的一种物质场,描述电流对其他电流施加的作用力的特性。
电场和磁场之间存在密切的联系,根据麦克斯韦方程组的推导可知,变化的电场会产生磁场,而变化的磁场也会产生电场。
3. 什么是电磁波?其特点是什么?电磁波是由电场和磁场相互耦合在空间中传播的波动现象。
其特点包括:- 电磁波是横波,电场与磁场的振动方向垂直于波传播方向。

初中电磁场考试题及答案
1. 电磁场的基本概念
电磁场是由变化的电场和磁场相互作用而产生的物理现象。
电场是由电荷产生的,而磁场则是由运动的电荷产生的。
电磁场的传播速度等于光速。
2. 电磁感应现象
当导体在磁场中运动时,会在导体中产生电动势,这种现象称为电磁感应。
根据法拉第电磁感应定律,感应电动势的大小与磁通量变化率成正比。
3. 电磁波的传播
电磁波是由变化的电场和磁场相互作用而产生的波动现象。
电磁波可以在真空中传播,其传播速度为光速,即每秒约300,000公里。
4. 电磁波的应用
电磁波在现代通信、广播、雷达等领域有着广泛的应用。
例如,无线电波用于无线通信,微波用于雷达探测,红外线用于遥感探测等。
5. 电磁场的生物效应
电磁场对生物体有一定的影响,如对细胞的生物电活动产生干扰。
长期暴露在高强度电磁场中可能会对人体产生一定的健康风险。
答案:
1. 电磁场是由变化的电场和磁场相互作用而产生的物理现象。
2. 电磁感应现象是指当导体在磁场中运动时,在导体中产生电动势的现象。
3. 电磁波是由变化的电场和磁场相互作用而产生的波动现象,其传播
速度为光速。
4. 电磁波在现代通信、广播、雷达等领域有着广泛的应用。
5. 电磁场对生物体有一定的影响,长期暴露在高强度电磁场中可能会对人体产生一定的健康风险。

电磁场考试试题及答案一、选择题(每题5分,共20分)1. 麦克斯韦方程组描述了电磁场的基本规律,下列哪一项不是麦克斯韦方程组中的方程?A. 高斯定律B. 法拉第电磁感应定律C. 欧姆定律D. 安培环路定律答案:C2. 在电磁波传播过程中,电场和磁场的相位关系是:A. 相位相同B. 相位相反C. 相位相差90度D. 相位相差180度答案:C3. 根据洛伦兹力定律,带电粒子在磁场中运动时受到的力的方向是:A. 与速度方向相同B. 与速度方向相反C. 与速度方向垂直D. 与磁场方向垂直答案:C4. 以下哪种介质的磁导率不是常数?A. 真空B. 铁C. 铜D. 空气答案:B二、填空题(每题5分,共20分)1. 根据高斯定律,通过任何闭合表面的电通量与该闭合表面所包围的总电荷量成正比,比例常数为____。
答案:\(\frac{1}{\varepsilon_0}\)2. 法拉第电磁感应定律表明,闭合回路中的感应电动势等于通过该回路的磁通量变化率的负值,其数学表达式为 \(\mathcal{E} = -\frac{d\Phi_B}{dt}\),其中 \(\Phi_B\) 表示____。
答案:磁通量3. 根据安培环路定律,磁场 \(\vec{B}\) 在闭合回路上的线积分等于该回路所包围的总电流乘以比例常数 \(\mu_0\),其数学表达式为\(\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}}\),其中\(I_{\text{enc}}\) 表示____。
答案:回路所包围的总电流4. 电磁波在真空中的传播速度为 \(c\),其值为 \(3 \times 10^8\) 米/秒,该速度也是光速,其物理意义是____。
答案:电磁波在真空中传播的速度三、简答题(每题15分,共40分)1. 简述电磁波的产生机制。
答案:电磁波是由变化的电场和磁场相互作用产生的。
当电场变化时,会在周围空间产生磁场;同样,变化的磁场也会在周围空间产生电场。

电磁场试卷答案及评分标准一.1.0;02.gradu u =∇;x y z u u u u ee e x y z ∂∂∂∇=++∂∂∂ 3.12012212()4||r l l d d F l l e I I r πμ⨯⨯=⎰⎰;024||r Id l d B e r πμ⨯=4.0s B dS∙=⎰ ;c H dl I ∙=⎰5.D E ε=;介质的本构方程二.×√√√√×√√×√三.1.对于矢量A 与B ,A ∙B=||||cos A B θ ,其中θ为A 与B 向量的夹角; A ⨯B =||||sin n A B e θ,n e 为A 与B 右手法则确定。
若A =xe x A +y ey A +z e z A ,B =x e x B +y e y B +z e z B , A ∙B=x A x B +y A y B +z A z B ; A ⨯B =x e (y A z B -z A y B )+y e (z A x B -x A z B )+z e (x A y B -y A xB ) 2.通量:矢量场A 沿其中有向曲面S 中某一侧面的曲面积分, s I =s A dS ∙⎰ ;矢量A沿场中某一封闭的有向曲线l 的曲线积分为环量,l l A d lI =∙⎰3.0s J dS∙=⎰ ;0J ∇∙=4.s D dSq ∙=⎰ ,D ρ∇∙=;0lE dl ∙=⎰ ,0E∇⨯= 5.12n n J J =即1212n n ϕϕγγ∂∂=∂∂;12t tE E =即12ϕϕ= 6.在无自由电流的空间(J=0)H 是无旋的,0H∇⨯=,因而H 可以用一个标量函数的负梯度表示,令m H ϕ=-∇,式中m ϕ称为标量磁位,单位为安培,其中的负号是为了与电位的定义相对应而人为附加的。
四.由电位分布求解电场强度和电荷分布,一般用关系式0,()E E ϕρε=-∇=∇可得到200()2()2x E ax b axe E a ϕρεε=-∇=-∇+=-=∇=-五.此题不便应用高斯定律求解。

大学电磁场考试题及答案一、单项选择题(每题2分,共20分)1. 电场强度的定义式为E=______。
A. F/qB. q/FC. F*qD. F/q^2答案:A2. 电场中某点的电势为零,该点的电场强度一定为零。
(判断对错)A. 对B. 错答案:B3. 电场线与等势面的关系是______。
A. 垂直B. 平行C. 重合D. 相交答案:A4. 电容器的电容与两极板间的距离成反比,与两极板的面积成正比。
(判断对错)A. 对B. 错答案:B5. 电容器充电后断开电源,其电量Q和电压U将如何变化?A. Q增大,U不变B. Q不变,U增大C. Q不变,U减小D. Q减小,U增大答案:B6. 根据安培环路定理,磁场强度B沿闭合回路的线积分等于该回路所包围的总电流的______倍。
A. μ0B. 1/μ0C. μ0ε0D. 1/μ0ε0答案:A7. 磁感应强度B的方向与电流I的方向的关系是______。
A. 垂直B. 平行C. 重合D. 相反答案:A8. 根据右手定则,当电流I沿正z轴方向时,磁场B的方向是______。
A. 正x轴B. 正y轴C. 负x轴D. 负y轴答案:B9. 磁通量Φ的单位是______。
A. TB. WbC. JD. N答案:B10. 根据法拉第电磁感应定律,感应电动势ε与磁通量变化率dΦ/dt的关系是______。
A. ε=-dΦ/dtB. ε=dΦ/dtC. ε=-μ0dΦ/dtD. ε=μ0dΦ/dt答案:B二、填空题(每题2分,共20分)11. 电场强度的定义式为E=______,其中F是试探电荷所受的电场力,q是试探电荷的电量。
答案:F/q12. 电场强度的方向是______,电势的方向是______。
答案:正电荷受力的方向;电势降低的方向13. 电容器的电容C与两极板间的距离d和两极板的面积A的关系为C=______。
答案:εA/d14. 电容器的储能公式为W=______。

电磁场期末考试试题及答案一、选择题(每题2分,共20分)1. 麦克斯韦方程组包括以下哪四个方程?A. 高斯定律B. 法拉第电磁感应定律C. 安培环路定律D. 所有上述选项答案:D2. 电磁波在真空中传播的速度是多少?A. 299792458 m/sB. 300000000 m/sC. 3×10^8 m/sD. 3×10^5 km/s答案:C3. 以下哪个不是电磁波的类型?A. 无线电波B. 微波C. 光波D. 声波答案:D4. 电磁波的频率和波长之间有什么关系?A. 频率与波长成反比B. 频率与波长相等C. 频率与波长成正比D. 没有关系答案:A5. 什么是电磁感应?A. 电流通过导线产生磁场B. 磁场变化产生电流C. 电流变化产生磁场D. 磁场变化产生电压答案:B6. 以下哪个不是电磁场的基本性质?A. 能量守恒B. 动量守恒C. 电荷守恒D. 质量守恒答案:D7. 什么是洛伦兹力?A. 电荷在电场中受到的力B. 电荷在磁场中受到的力C. 电荷在电场和磁场中受到的合力D. 电荷在磁场中受到的力,与电荷速度成正比答案:C8. 电磁波的偏振是指什么?A. 电磁波的传播方向B. 电磁波的振动方向C. 电磁波的频率D. 电磁波的波长答案:B9. 什么是电磁波的反射?A. 电磁波在不同介质界面上部分能量返回原介质的现象B. 电磁波在不同介质界面上全部能量返回原介质的现象C. 电磁波在不同介质界面上部分能量进入新介质的现象D. 电磁波在不同介质界面上全部能量进入新介质的现象答案:A10. 什么是电磁波的折射?A. 电磁波在不同介质界面上传播方向的改变B. 电磁波在不同介质界面上频率的改变C. 电磁波在不同介质界面上波长的改变D. 电磁波在不同介质界面上振幅的改变答案:A二、填空题(每空2分,共20分)11. 根据法拉第电磁感应定律,当磁通量变化时,会在闭合电路中产生_______。
答案:感应电动势12. 麦克斯韦方程组中,描述电场与电荷关系的方程是_______。
大学物理B2习题(一、电磁学部分1、如图所示,真空中一长为L的均匀带电细直杆,总电荷为q,试求在直杆延长线上距杆的一端距离为d的P点的电场强度和电势.2、一半径为R的均匀带电半圆环,电荷线密度为 ,求换新处O点的电场强度和电势。
3、实验证明,地球表面上方电场不为0,晴天大气电场的平均场强约为120V/m,方向向下,这意味着地球表面上有多少过剩电荷?试以每平方厘米的额外电子数表示。
(526.6410/cm ⨯个)解 设想地球表面为一均匀带电球面,总面积为S ,则它所总电量为00d Sq E S ES εε=⋅=⎰⎰单位面积带电量为 E Sq0εσ==单位面积上的额外电子数为19120106.11201085.8--⨯⨯⨯===e Ee n εσ92526.6410/m 6.6410/cm =⨯=⨯4、地球表面上方电场方向向下,大小可能随高度变化,设在地面上方100m 高处场强为150N/C ,300m 高处场强为100N/C ,试由高斯定理求在这两个高度之间的平均体电荷密度,以多余的或缺少的电子数密度表示。
(缺少,721.3810/m ⨯个)5、如图所示,电量1q 均匀分布在半径为1R 的球面上,电量2q 均匀分布在同心的半径为2R 的球面上,2R >1R 。
(1)利用高斯定理求出r <1R ,1R <r <2R ,r >2R 区域的电场强度 (2)若r >2R 区域的电场强度为零,则?1=qq ,1q 与2q 同号还是异号?6、二个无限长同轴圆筒半径分别为1R 和2R ,单位长度带电量分别为λ+和λ-。
求内筒的内部、两筒间及外筒外部的电场分布。
解 由对称性分析可知,E分布具有轴对称性,即与圆柱轴线距离相等的同轴圆柱面上各点场强大小相等,方向均沿径向。
如解用图,作半径为r ,高度为h 、与两圆柱面同轴的圆柱形高斯面,则穿过圆柱面上下底的电通量为零,穿过整个高斯面的电通量等于穿过圆柱形侧面的电通量。
《电磁场与电磁波》(B 卷)考试试卷答案及评分标准一.填空(20分,每空2分) 1. 12916x y z --+e e e 2.54,1516± 3. =53x y z --R e e e,0=53)x y z R =--R R e e e 4. -2,336x y z ---e e e5. 21()s ρ-=n D D ,21()⨯-0n E E =,21()s ⨯-n H H =J6. ()()()t t t =⨯S E H二、判断题:(每题2分,共16分)1. B2. A3. D4. C5. A6. C7. A8. B 三、证明题(共2题,每题8分,总计16分) 1.证明:(1)=()+()+()=xy zx y z z y x z y xx y z y z z x x y xyz∂∂∂∂∂∂∂∂∂∇⨯---∂∂∂∂∂∂∂∂∂0e e e R =e e e (4分)(2)设常矢A 为=x x y y z z A A A ++A e e e 则=()()=x x y y z z x y z x y z A A A x y z A x A y A z++++++A R e e e e e e (2分)所以()=()()()=xx y x z z x x y y z zA x A y A z x y z A A A ∂∂∂∇++∂∂∂++A R e e e e e e (2分) 2. 根据已知可以得到(1)证明:三个顶点的位置矢量分别为12y z -r =e e ,243x y z -r =e +e e ,3625x y z +r =e +e e (2分)则12214x z-=-R =r r e e ,233228x y z-=++R =r r e e e ,311367x y z -=---R =r r e e e (2分)由此可见,1223(4)(28)=0x z x y z -++R R =e e e e e (2分)所以,123PP P ∆是直角三角形。
前面是答案和后面是题目,大家认真对对. 三、稳恒磁场答案1-5 CADBC 6-8 CBC 三、稳恒磁场习题1. 有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B 1 / B 2为 (A) 0.90. (B) 1.00.(C) 1.11. (D) 1.22. [ ]2.边长为l 的正方形线圈中通有电流I ,此线圈在A 点(见图)产生的磁感强度B 为(A) l I π420μ. (B) l Iπ220μ.(C)l Iπ02μ. (D) 以上均不对. [ ]3.通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为:(A) B P > B Q > B O . (B) B Q > B P > B O .(C) B Q > B O > B P . (D) B O > B Q > B P .[ ]4.无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B ϖ的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示.正确的图是 [ ]5.电流I 由长直导线1沿平行bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框,再由b 点沿垂直ac 边方向流出,经长直导线2返回电源(如图).若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B ϖ、2B ϖ和3Bϖ表示,则O 点的磁感强度大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ϖϖ,B 3 = 0.(C) B ≠ 0,因为虽然B 2 = 0、B 3= 0,但B 1≠ 0.(D) B ≠ 0,因为虽然021≠+B B ϖϖ,但B 3≠ 0. [ ]6.电流由长直导线1沿半径方向经a 点流入一电阻均匀的圆环,再由b 点沿切向从圆环流出,经长导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 与圆心O 三点在同一直线上.设直电流1、2及圆环电流分别在O 点产生的磁感强度为1B ϖ、2B ϖ及3Bϖ,则O 点的磁感强度的大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为021=+B B ϖϖ,B 3= 0.(C) B ≠ 0,因为虽然B 1 = B 3 = 0,但B 2≠ 0. (D) B ≠ 0,因为虽然B 1 = B 2 = 0,但B 3≠ 0.(E) B ≠ 0,因为虽然B 2 = B 3 = 0,但B 1≠ 0. [ ] v7.电流由长直导线1沿切向经a 点流入一个电阻均匀的圆环,再由b 点沿切向从圆环流出,经长直导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 和圆心O 在同一直线上.设长直载流导线1、2和圆环中的电流分别在O 点产生的磁感强度为1B ϖ、2B ϖ、3Bϖ,则圆心处磁感强度的大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ϖϖ,B 3 = 0.(C) B ≠ 0,因为B 1≠ 0、B 2≠ 0,B 3≠ 0.(D) B ≠ 0,因为虽然B 3= 0,但021≠+B B ϖϖ. [ ]8.a R r OO ′I在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a ,如图.今在此导体上通以电流I ,电流在截面上均匀分布,则空心部分轴线上O ′点的磁感强度的大小为(A) 2202R a a I ⋅πμ (B)22202R r a a I -⋅πμ(C) 22202r R a a I-⋅πμ (D) )(222220a r Ra a I -πμ [ ]参考解:导体中电流密度)(/22r R I J -π=.设想在导体的挖空部分同时有电流密度为J 和-J 的流向相反的电流.这样,空心部分轴线上的磁感强度可以看成是电流密度为J 的实心圆柱体在挖空部分轴线上的磁感强度1B ϖ和占据挖空部分的电流密度-J 的实心圆柱在轴线上的磁感强度2B ϖ的矢量和.由安培环路定理可以求得02=B , )(222201r R a Ia B -π=μ 所以挖空部分轴线上一点的磁感强度的大小就等于)(22201r R IaB -π=μ 9. πR 2c3分10.221R B π-3分11. 6.67×10-7 T 3分7.20×10-7 A ·m 2 2分12. 减小 2分在2/R x <区域减小;在2/R x >区域增大.(x 为离圆心的距离) 3分13. 0 1分I 0μ- 2分14. 4×10-6 T 2分 5 A 2分15. I0μ 1分 0 2分2I0μ 2分16. 解:①电子绕原子核运动的向心力是库仑力提供的.即∶ 02202041a m a e v =πε,由此得 002a m e επ=v 2分②电子单位时间绕原子核的周数即频率000142a m a e a ενππ=π=v 2分 由于电子的运动所形成的圆电流00214a m a e e i ενππ== 因为电子带负电,电流i 的流向与 v ϖ方向相反 2分 ③i 在圆心处产生的磁感强度002a i B μ=00202018a m a eεμππ= 其方向垂直纸面向外 2分17.1 234 R ROI a β2解:将导线分成1、2、3、4四部份,各部分在O 点产生的磁感强度设为B 1、B 2、B 3、B 4.根据叠加原理O 点的磁感强度为:4321B B B B B ϖϖϖϖϖ+++= ∵ 1B ϖ、4B ϖ均为0,故32B B B ϖϖϖ+= 2分)2(4102R I B μ= 方向⊗ 2分 242)sin (sin 401203R I a I B π=-π=μββμ)2/(0R I π=μ 方向 ⊗ 2分其中 2/R a =, 2/2)4/sin(sin 2=π=β 2/2)4/sin(sin 1-=π-=β∴ R I R I B π+=2800μμ)141(20π+=R I μ 方向 ⊗ 2分 18. 解:电流元1d l I ϖ在O 点产生1d B ϖ的方向为↓(-z 方向) 电流元2d l I ϖ在O 点产生2d B ϖ的方向为⊗(-x 方向) 电流元3d l I ϖ在O 点产生3d B ϖ的方向为⊗ (-x 方向) 3分kR I i R IB ϖϖϖπ-+ππ-=4)1(400μμ 2分 19. 解:设x 为假想平面里面的一边与对称中心轴线距离,⎰⎰⎰++==Rx RRxrl B r l B S B d d d 21Φ, 2分d S = l d r2012R IrB π=μ (导线内) 2分r I B π=202μ (导线外) 2分)(42220x R R Il -π=μΦR R x Il +π+ln20μ 2分 令 d Φ / d x = 0, 得Φ 最大时 Rx )15(21-= 2分20. 解:洛伦兹力的大小 B q f v = 1分对质子:1211/R m B q v v = 1分 对电子: 2222/R m B q v v = 1分∵ 21q q = 1分 ∴ 2121//m m R R = 1分21.解:电子在磁场中作半径为)/(eB m R v =的圆周运动. 2分连接入射和出射点的线段将是圆周的一条弦,如图所示.所以入射和出射点间的距离为:)/(3360sin 2eB m R R l v ==︒= 3分2解:在任一根导线上(例如导线2)取一线元d l ,该线元距O 点为l .该处的磁感强度为θμsin 20l I B π=2分 方向垂直于纸面向里. 1分电流元I d l 受到的磁力为 B l I F ϖϖϖ⨯=d d 2分其大小θμsin 2d d d 20l lI l IB F π== 2分 方向垂直于导线2,如图所示.该力对O 点的力矩为 1分θμsin 2d d d 20π==lI F l M 2分 任一段单位长度导线所受磁力对O 点的力矩⎰⎰+π==120d sin 2d l l l I M M θμθμsin 220π=I 2分 导线2所受力矩方向垂直图面向上,导线1所受力矩方向与此相反.23. (C) 24. (B)25. 解: ===l NI nI H /200 A/m3分===H H B r μμμ0 1.06 T 2分26. 解: B = Φ /S=2.0×10-2 T 2分===l NI nI H /32 A/m 2分 ==H B /μ 6.25×10-4 T ·m/A 2分=-=1/0μμχm 496 2分9. 一磁场的磁感强度为k c j b i a B ϖϖϖϖ++= (SI),则通过一半径为R ,开口向z 轴正方向的半球壳表面的磁通量的大小为____________Wb .10.任意曲面在匀强磁场B ϖ中,取一半径为R 的圆,圆面的法线n ϖ与B ϖ成60°角,如图所示,则通过以该圆周为边线的如图所示的任意曲面S 的磁通量==⎰⎰⋅Sm S B ϖϖd Φ_______________________.11. 一质点带有电荷q =8.0×10-10 C ,以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m 的圆周上,作匀速圆周运动.该带电质点在轨道中心所产生的磁感强度B =__________________,该带电质点轨道运动的磁矩p m =___________________.(μ0 =4π×10-7 H ·m -1)12. 载有一定电流的圆线圈在周围空间产生的磁场与圆线圈半径R 有关,当圆线圈半径增大时,(1) 圆线圈中心点(即圆心)的磁场__________________________.(2) 圆线圈轴线上各点的磁场________如图,平行的无限长直载流导线A 和B ,电流强度均为I ,垂直纸面向外,两根载流导线之间相距为a ,则(1) AB 中点(P 点)的磁感强度=p B ϖ_____________.(2) 磁感强度B ϖ沿图中环路L 的线积分 =⎰⋅L l B ϖϖd ______________________.14. 一条无限长直导线载有10 A 的电流.在离它 0.5 m 远的地方它产生的磁感强度B 为______________________.一条长直载流导线,在离它 1 cm 处产生的磁感强度是10-4 T ,它所载的电流为__________________________.两根长直导线通有电流I ,图示有三种环路;在每种情况下,⎰⋅lB ϖϖd 等于:____________________________________(对环路a ).____________________________________(对环路b ).____________________________________(对环路c ).设氢原子基态的电子轨道半径为a 0,求由于电子的轨道运动(如图)在原子核处(圆心处)产生的磁感强度的大小和方向.17.一根无限长导线弯成如图形状,设各线段都在同一平面内(纸面内),其中第二段是半径为R 的四分之一圆弧,其余为直线.导线中通有电流I ,求图中O 点处的磁感强度.18.z y xR 1 321d l I ϖ2d l I ϖ3d l I ϖO如图,1、3为半无限长直载流导线,它们与半圆形载流导线2相连.导线1在xOy平面内,导线2、3在Oyz 平面内.试指出电流元1d l I ϖ、2d l I ϖ、3d l I ϖ在O 点产生的Bϖd 的方向,并写出此载流导线在O 点总磁感强度(包括大小与方向).19.一根半径为R 的长直导线载有电流I ,作一宽为R 、长为l 的假想平面S ,如图所示。
莆田学院期末考试参考答案及评分标准2008 — 2009 学年第 一 学期 (B )卷课程名称: 电磁场 适用年级/专业: 06/电信 试卷类别 开卷( )闭卷(√) 学历层次 本科 考试用时 120 分钟 一、填空题(每空3分,共30分) 1. ①z y x 43++- 2. ① 1 ② 03. ① 4.①y 2 5.① 26.① ;② 变化的磁场能够激发电场 (或类似描述)7.①l ρ- ② 位于线电荷与圆柱轴线的连线上,且距轴心距离为d a 2二、简答题(每小题6分,共18分) 1.答:介质恒定磁场的基本方程2.答:介质的极化过程未加电场时,由于分子热运动,不同电偶极子的偶极距的方向不规则,宏观上说,所有分子的等效电偶极距的矢量和为零,对外不成电性;-----2分外加电场作用下,各分子电距发生转向,均沿外加电场方向,对外呈电性;---2分 极化的结果是在电介质的内部和表面形成极化电荷。
---2分 3.答:一般的波动方程为14222=++z y x 或---------2分 ---------2分 ---------2分tE ∂∂=⨯∇J H B μ==⨯∇=⋅∇(有旋)(无源)0⎰⎰⎰=⋅=⋅=⋅SCS Id l d d 02∂E三、计算题1.(8分)解:由题得,方向余弦为{}⎭⎬⎫⎩⎨⎧=21,22,21cos ,cos ,cos γβα再由方向导数的计算公式 得2.(10分)解:球体上电荷分布是球对称的, 仅有径向分量Er ,且具有球对称性质,作一个与带电体同心、半径为r 的球面,应用高斯定理的积分式 得 当r >a 时, 即当r <a 时, 即当r >a 时, 当r <a 时,3.(8分)解:媒质内的漏电电流沿径向从内导体流向外导体, 设沿轴向方向单位长度(L =1)---------3分--------2分 ----2分 0222=∂∂-∇tHμεγβαcos cos cos 0zuy u x u luP ∂∂+∂∂+∂∂=∂∂221)1122(22)21112(21)211(cos )2(cos )2(cos )(22)2,1,1(=⨯-⨯+⨯-⨯⨯+⨯-=-+-+-=∂∂γβαxy z xz xy yz y lu---------2分---------3分 ---------3分⎰=⋅SQd 0ε3002344a r E r περπ=故 )(32030αερ>=r ra E r 3002344r r E rπερπ=)(300αερ<=r rE r )(32030αερ>=r r a a r )(300αερ<=r r a E r -------2分ra dr r a dr E rr r 030203033ερερϕ===⎰⎰∞∞⎪⎪⎭⎫⎝⎛-=+=⎰⎰∞332200r a dr E dr E arar r ερϕ-------2分-------2分从内导体流向外导体的漏电电流为I ,则媒质内任一点的电流密度和电场为内、外导体间的电压为 单位长度的漏电电导为4.(8分)解:取圆柱坐标系的z 轴和磁介质柱的中轴线重合, 磁介质的下底面位于z =0处,上底面位于z =L 处。
电磁场试题及参考答案电磁场试题一、选择题一、选择题:(每小题至少有一个选项是正确的,每小题4分,共48分)1.D2.BCD3.A4.CD5.ABC6.ABC7.D8.B9.B10.D11.B12.A二、填空题(每空3分,共30分,请把答案填写在题中横线上)13、最大、最大、零、零、零14、充电完毕、负电荷15、3:116、1.64106 1.83102三,计算题电磁场试题二、填空题17、(7分)(由法拉第电磁感应现象说明均匀变化的磁场所产生的电场是恒定的18、(7分)某雷达工作时发射的电磁波的波长=20m,每秒脉冲数n=5000个,每个脉冲持续时间t=0.02s,问电磁波的振荡频率为多少?每个光脉冲的长度L 是多少?最大的侦察距离是多少?19.(8分)一个波长范围为150~600m的无线电波段内,为避免邻台干扰,两个相邻电台频率至少应相差10kHz,求在此波段内,最多能容纳Q多少个电台.电磁场试题三、计算题(每空3分,共30分)13、LC振荡电路中,当电容器C放电完毕时,下列各物理量为(最大或零):电流i____,磁场能E磁____,电压UC___,L中电动势自____,C上电量q____。
14、如图中LC振荡电路的周期为T=210-2s。
从电流逆时针最大开始计时,当t=2.510-2s时,电容器正处于_____状态;这时电容器上极板的带电情况为_____。
15.在图所示的电路中,可变电容器的最大电容是270 pF,最小电容为30 pF,若L保持不变,则可变电容器的动片完全旋出与完全旋入时,电路可产生的振荡电流的频率之比为_____. 16.某收音机调谐电路的可变电容器动片完全旋入时,电容是390 PF,这时能接收到520kHz 的无线电电波,动片完全旋出时,电容变为39 PF,这时能收到的无线电电波的频率是______106 Hz,此收音机能收到的无线电电波中,最短的波长为______m.(取三位有效数字)电磁场试题参考答案(每小题至少有一个选项正确,每小题4分,共48分)1.根据麦克斯韦电磁理论,如下说法正确的是 ( )A.变化的电场一定产生变化的磁场B.均匀变化的电场一定产生均匀变化的磁场C.稳定的电场一定产生稳定的磁场D.振荡的电场一定产生同频率的振荡磁场2、关于LC振荡电路在振荡过程中,下列说法正确的是( )A、电流最大的时刻电压也最高B、电流增大的过程是电容器的放电过程C、电流最小的时刻电压却最高D、自感电动势最大时电容器带电量最大3. 要使LC振荡电路的周期增大一倍,可采用的办法是 ( )A.自感系数L和电容C都增大一倍B.自感系数L和电容C都减小一半C.自感系数L增大一倍,而电容C减小一半D.自感系数L减小一半,而电容C增大一倍4.在LC振荡电路的`工作过程中,下列的说法正确的是 ( )A.在一个周期内,电容器充、放电各一次B.电容器两极板间的电压最大时,线圈中的电流也最大C.电容器放电完了时,两极板间的电压为零,电路中的电流达到最大值D.振荡电路的电流变大时,电场能减少,磁场能增加5.LC回路发生电磁振荡时,振荡周期为T.若从电容器开始放电取作t=0,则 ( )A.5T/4和7T/4两个时刻,回路中电流最大,方向相反B.3T/2和2T两个时刻,电容器所带电量最大C.5T/4至3T/2时间内,回路中电流减小,电容器所带电量增加D.3T/2至7T/4时间内,磁场能向电场能转化6、下列说法正确的是 ( )A、摄像机摄像管实际上是一种将光信号转变为电信号的装置B、电视机显像管实际上是一种将电信号转变为光信号的装置C、摄像机在一秒钟内要送出25张画面D、电视机接收的画面是连续的7、由自感系数为L的线圈和可变电容器C构成收音机的调谐电路,为使收音机能接收到f1为550千赫至 f2为1650千赫范围内的所有电台的播音,则可变电容器与f1 对应的电容C1与f2对应的电容C2之比为( )A、1:3B、 3 :1C、1:9D、9:18、如图所示,L是不计电阻的电感器,C是电容器,闭合电键K,待电路达到稳定状态后,再断开电键K,LC电路中将产生电磁振荡。
2010-2011 学年第 1 学期末考试试题(B 卷)
电磁场与电磁波
使用班级: 08050641X-3X
一、简答题(30分,每题10分)
1写出电流连续性方程,并说明其意义。
()()t
t r t r J ∂∂-=⋅∇,,ρ (5分) 电荷守恒定理(5分)
2 根据自己的理解,解释镜像法的基本原理。
用位于场域边界外虚设的较简单的镜像电荷分布来等效替代该边界上未知的较为复杂的电荷分布,在保持边界条件不变的情况下,将边界面移去,从而将原含该边界的非均匀媒质空间变换成无限大单一均匀媒质的空间,使分析计算过程得以明显简化的一种间接求解法。
3 写出麦克斯韦方程组,并说明每个方程的意义。
(6分)
麦克斯韦第一方程,表明传导电流和变化的电场都能产生磁场 麦克斯韦第二方程,表明变化的磁场产生电场
麦克斯韦第三方程表明磁场是无源场,磁感线总是闭合曲线 麦克斯韦第四方程,表明电荷产生电场(4分)
二、计算题(每题10分,共40分)
1 求标量场3
2yz xy u +=在点()1,1,2-M 处的梯度,以及在矢量z y x e e e l -+=22方向的方向导数。
()
22232yz e z xy e y e z u e y u e x u e u z y x z y x +++=∂∂+∂∂+∂∂=∇(2分) 在点M 处的梯度为
z y x e e e u 33--=∇(2分)
⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎨⎧=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇ρD B t B E t D
J H 0
矢量z y x e e e l -+=22的单位矢量为 z y x l e e e e 3
13232-+=(2分) 因此,u 在l 方向的方向导数为
3
1-=⋅=∂∂l M e gradu l u
(4分)
2 在直角坐标系下证明矢量恒等式()0=∇⨯∇ϕ。
3 电荷按体密度()⎪⎪⎭
⎫ ⎝⎛-=2201a r r ρρ分布于一个半径为a 的球形区域内,其中0ρ为常数。
试计算球内外的电场强度。
解:电场明显具有球面对称性, 0D 沿半径方向且大小只是r 的函数。
球的电荷总量为
(2分) 当 a r ≥时,以球心到场点的距离为半径作一球面(高斯面),应用 高斯定律的积分形式,得
(3分) 当 a r ≤ 时,应用高斯定律得
()300242020158d 4d 4a r a r r r r Q a
a ρππρπρ=⎪⎪⎭⎫ ⎝⎛-==⎰⎰Q
S D s
=⋅⎰ d 023
002215
84a D r ρππ=23
002152r
a D ρ=r a r r S D r s d 4d 0242001⎰⎰⎪⎪⎭⎫ ⎝
⎛-=⋅πρ ⎪⎪⎫ ⎛-=553001244r r D r πρπ2
03002152r a E ερ=
(5分)
4 题目同题3,求球内外的电场能量。
0252020202020220158d 421d 21d 21επρπεεεa r r D V D V E W a a a e ====⎰⎰⎰∞∞∞
(5分)
⎥⎦⎤⎢⎣⎡-+====⎰⎰⎰1052225632d 421d 21d 213702020201002010200a a a r r D V D V E W a a a
e επρπεεε(5分)
⎪⎪⎭
⎫ ⎝⎛-=3300153a r r D ρ⎪⎪⎭
⎫ ⎝⎛-=33000153a r r E ερ
三、计算题(30分)
求无限长同轴线单位长度内的磁场能量,如图所示。
解:由安培环路定理,得
(10分)
三个区域单位长度内的磁场能量分别为
2222202π2π2π0rI e r a a I e a r b H r I c r e b r c r c b r c
⎧<<⎪⎪⎪<<⎪=⎨⎪-⎪<<-⎪⎪>⎩φ
φ
φ22220m322()()2πd 22πc b I c r W r r r c b -=-⎰μ200m120()2πd 22π16πa I rI W r r a =
=⎰μμ2200m2()2d ln 22π4πb a I I b W r r r a ==⎰μμπ242203I c c c b μ⎡
⎤-
(15分)
单位长度内总的磁场能量为
(5分) m m1m2m3
222
422000222223ln ln 16π4π
4π()4()W W W W I I I b c c c b a c b b c b μμμ=++⎡⎤-=++-⎢⎥--⎣⎦。