2020-2021备战中考物理易错题专题复习-杠杆平衡练习题及答案解析

一、初中物理杠杆平衡条件的应用问题1．如图所示，在探究杠杆平衡条件的实验中，杠杆处于水平平衡状态，所用钩码完全相同。

下列做法中能使杠杆再次平衡的是A ．分别在两边钩码下再增加一个相同钩码B ．左边减少1个钩码，右边减少2个钩码C ．两边钩码均向支点移动相同的距离D ．左边钩码向左移1.5cm ，右边钩码向右移1cm【答案】D【解析】【详解】设一个钩码的重力为G ，左边钩码到支点的距离为3l ，因为杠杆正处于水平平衡，所以由杠杆平衡条件可得233G l G l ⨯=⨯右，解得2l l =右，即右边钩码到支点的距离为2l ；A ．若分别在两边钩码下再增加一个相同钩码，则3342G l G l ⨯≠⨯，此时杠杆不再平衡，不符合题意；B ．若左边减少1个钩码，右边减少2个钩码，则32G l G l ⨯≠⨯ ，此时杠杆不再平衡，不符合题意；C ．若两边的钩码均向支点移动相同的距离l ，则223G l G l ⨯≠⨯，此时杠杆不再平衡，不符合题意；D ．若左边钩码向左移1.5cm ，右边钩码向右移1cm ，则2(3 1.5)3(21)G l G l ⨯+=⨯+，此时杠杆平衡，符合题意。

2．按如下原理制作一杆可直接测量液体密度的秤，称为密度秤，其外形和普通的杆秤差不多，装秤钩的地方吊着体积为1cm 3的较重的合金块，杆上有表示液体密度数值的刻度，当秤砣放在Q 点处时秤杆恰好平衡，如图所示。

当合金块完全浸没在待测密度的液体中时，移动秤砣的悬挂点，直至秤杆恰好重新平衡，便可直接在杆秤上读出液体的密度，下列说法中错误的是（ ）A．密度秤的零点刻度在Q点B．密度秤的刻度都在Q点的左侧C．密度秤的刻度都在Q点的右侧D．秤杆上密度读数较大的刻度在较小的刻度的左边【答案】C【解析】【分析】【详解】A．合金块没有浸入液体时，液体的密度应为零，所以秤的零刻度应该在Q处；故A正确，不符合题意；BC．若秤砣由Q向右移动，它的力臂变长，则左边合金块拉秤杆的力应增大，但合金块受到的浮力不可能竖直向下，所以零点的右边应该是没有刻度的，其刻度都在Q点的左侧。

一、初中物理杠杆平衡条件的应用问题1．如图所示，杠杆恰好处于水平平衡状态，若在B处下方再挂一个钩码，若要使杠杆在水平位置再次平衡，下列可行的操作是______。

（选填字母）A．减少一个悬挂在A处的钩码B．增加一个悬挂在A处的钩码C．将悬挂在A处的钩码向左移动一格D．将悬挂A处的钩码向右移动一格【答案】C【解析】【分析】【详解】假设一个钩码重力为G，杠杆一格为l，杠杆平衡时⨯=⨯=32236G l G l Gl若在B处下方再挂一个钩码，则右边为339⨯=G l GlA．减少一个悬挂在A处的钩码，则左边为⨯=224G l Gl左边小于右边，杠杆不能平衡，故A项不符合题意；B．增加一个悬挂在A处的钩码，则左边为⨯=G l Gl428左边小于右边，杠杆不能平衡，故B项不符合题意；C．将悬挂在A处的钩码向左移动一格，则左边为⨯=G l Gl339左边等于右边，杠杆能再次平衡，故C项符合题意；D．将悬挂A处的钩码向右移动一格，则左边为⨯=G l Gl313左边小于右边，杠杆能再次平衡，故D项不符合题意。

故选C。

2．如图所示，作用在A点的各个力中，不可能使杠杆平衡的力是A ．F 3和F 4B ．F 1和F 3C ．F 2和F 4D ．F 1和F 2 【答案】A 【解析】 【详解】因为力F 3的作用线所在的直线过支点O ，所以力F 3的力臂为0，又因为0乘以任何数都为0，所以力F 3不能使杠杆平衡；力F 4使杠杆转动方向与重物使杠杆的转动方向相同，所以力F 4不能使杠杆平衡；力F 1和F 2使杠杆转动方向与重物使杠杆转动方向相反，所以力F 1和F 2可以使杠杆平衡；故选A 。

3．AC 硬棒质量忽略不计，在棒的B 、C 两点施加力F 1、F 2，F 2的方向沿OO'线，棒在图所示位置处于静止状态，则（ ）A ．F 1<F 2B ．F 1=221s F s C ．F 1力臂等于s 1 D ．F 2方向沿OO '线向上 【答案】D 【解析】 【详解】AC ．由图知，F 2的方向沿OO ′线，其力臂最长，为s 2；而F 1的方向竖直向下，所以其力臂L 1是从A 点到F 1的垂线段，小于s 1，更小于s 2， 由F 1L 1=F 2L 2知，L 1＜s 2，所以F 1一定大于F 2，故AC 不符合题意； B ．由F 1L 1=F 2L 2知，F 1L 1=F 2s 2，即2211F s F L故B 不符合题意；D ．已知F 1的方向是竖直向下的，为保持杠杆平衡，F 2的方向应该沿OO′向上，故D 符合题意。

一、初中物理杠杆平衡条件的应用问题1．如图所示，杠杆在水平位置处于平衡状态。

下列操作仍能使杠杆在水平位置保持平衡的是（）A．两侧钩码同时向外移一格B．左侧的钩码向左移一格，右侧增加一个钩码C．在两侧钩码下方，同时加挂一个相同的钩码D．在两侧钩码下方，同时减去一个相同的钩码【答案】B【解析】【分析】【详解】设一个钩码的重力为G，横梁上一个格的长度为L，原来杠杆处于平衡状态，则有⨯=⨯G L G L2332A．两边各向外移一格，左边⨯=248G L GL右边⨯=339G L GL由于89<GL GL杠杆右端下沉，故A不符合题意；B．左侧的钩码向左移一格，右侧增加一个钩码，因左边⨯24G L右边⨯42G L因2442⨯=⨯G L G L故B符合题意；C．在两侧钩码下方，同时加挂一个相同的钩码，左边⨯=339G L GL右边⨯=428G L GL因为98GL GL >杠杆左端下沉，故C 不符合题意；D ．在两侧钩码下方，同时减去一个相同的钩码，左边33G L GL ⨯=右边224G L GL ⨯=由于34GL GL <杠杆右端下沉，故D 不符合题意。

故选B 。

2．AC 硬棒质量忽略不计，在棒的B 、C 两点施加力F 1、F 2，F 2的方向沿OO'线，棒在图所示位置处于静止状态，则（ ）A ．F 1<F 2B ．F 1=221s F s C ．F 1力臂等于s 1D ．F 2方向沿OO '线向上【答案】D【解析】【详解】AC ．由图知，F 2的方向沿OO ′线，其力臂最长，为s 2；而F 1的方向竖直向下，所以其力臂L 1是从A 点到F 1的垂线段，小于s 1，更小于s 2， 由F 1L 1=F 2L 2知，L 1＜s 2，所以F 1一定大于F 2，故AC 不符合题意；B ．由F 1L 1=F 2L 2知，F 1L 1=F 2s 2，即2211F s F L =故B 不符合题意；D．已知F1的方向是竖直向下的，为保持杠杆平衡，F2的方向应该沿OO′向上，故D符合题意。

一、初中物理杠杆平衡条件的应用问题1．如图所示，在“探究杠杆的平衡条件”的实验中，已知杠杆上每个小格的长度为2cm ，用弹簧测力计在A 点斜向上（与水平方向成30°角）拉杠杆，使杠杆在水平位置平衡。

下列说法中正确的是（ ）A ．此时杠杆的动力臂为0.08mB ．此时为省力杠杆C ．当弹簧测力计向左移至竖直位置时，其示数为1ND ．图中钩码的总重力为2N【答案】D【解析】【分析】【详解】A ．当弹簧测力计在A 点斜向上拉（与水平方向成30°角）杠杆，所以动力臂11142cm 4cm=0.04m 22l OA ==⨯⨯= 故A 错误；B ．由图知，钩码对杠杆拉力为阻力，阻力臂的大小l 2=3×2cm=6cm ＞l 1杠杆为费力杠杆，故错误；CD ．由图知，弹簧测力计示数为3N ，根据杠杆的平衡条件F 1l 1=Gl 2可得1123N 4cm =2N 6cmF lG l ⨯== 竖直向上拉A 点时，力臂大小等于OA ，由杠杆平衡条有'12F OA Gl ⋅= ，所以测力计的示数212N 6cm =1.5N 2cm 4Gl F OA '⨯==⨯ 故C 错误，D 正确。

故选D 。

2．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A．左右钩码各向支点移一格B．左右各减少一个钩码C．左右各减少一半钩码D．左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L，一个钩码的重为G．原来4G×2L=2G×4L；左、右钩码各向支点移动一格，左边=4G×L=4GL，右边=2G×3L=6GL，左边＜右边，杠杆向右端下沉，A不符合题意；左右各减少一个钩码，左边=3G×2L=6GL，右边=G×4L=4GL，左边＞右边，杠杆向左下沉，B 不符合题意；左、右钩码各减少一半法码，左边=2G×2L=4GL，右边=G×4L=4GL，左边=右边，杠杆平衡；C符合题意；左右各增加两个钩码，左边=6G×2L=12GL，右边=4G×4L=16GL，左边＜右边，杠杆右边下沉，D不符合题意，故选C．3．如图所示，作用在A点的各个力中，不可能使杠杆平衡的力是A．F3和F4B．F1和F3C．F2和F4D．F1和F2【答案】A【解析】【详解】因为力F3的作用线所在的直线过支点O，所以力F3的力臂为0，又因为0乘以任何数都为0，所以力F3不能使杠杆平衡；力F4使杠杆转动方向与重物使杠杆的转动方向相同，所以力F4不能使杠杆平衡；力F1和F2使杠杆转动方向与重物使杠杆转动方向相反，所以力F1和F2可以使杠杆平衡；故选A。

一、初中物理杠杆平衡条件的应用问题1．如图为搬运砖头的独轮车，车箱和砖头所受的总重力G 为1 000 N （车架所受重力忽略不计），独轮车的有关尺寸如图所示，推车时，人手向上的力F 的大小为 （ ）A ．200 NB ．300 NC ．400 ND ．500 N【答案】B 【解析】 【分析】 【详解】 由平衡条件可知12Gl Fl =则121000N 0.3=300N mGl F l ⨯==ｍ１ 故选B 。

2．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A ．左右钩码各向支点移一格B ．左右各减少一个钩码C ．左右各减少一半钩码D ．左右各增加两个钩码【答案】C 【解析】设杠杆的分度值为 L ，一个钩码的重为G ．原来4G ×2L =2G ×4L ；左、右钩码各向支点移动一格，左边=4G ×L =4GL ，右边=2G ×3L =6GL ，左边＜右边，杠杆向右端下沉，A 不符合题意；左右各减少一个钩码，左边=3G ×2L =6GL ，右边=G ×4L =4GL ，左边＞右边，杠杆向左下沉，B不符合题意；左、右钩码各减少一半法码，左边=2G ×2L =4GL ，右边=G ×4L =4GL ，左边=右边，杠杆平衡；C 符合题意；左右各增加两个钩码，左边=6G ×2L =12GL ，右边=4G×4L =16GL ，左边＜右边，杠杆右边下沉，D 不符合题意，故选C ．3．如图所示的轻质杠杆OA 上悬挂着一重物G ，O 为支点，在A 端用力使杠杆平衡。

下列叙述正确的是（ ）A ．此杠杆一定是省力杠杆B ．沿竖直向上方向用力最小C ．沿杆OA 方向用力也可以使杠杆平衡D ．此杠杆可能是省力杠杆，也可能是费力杠杆 【答案】D 【解析】 【分析】 【详解】A ．因为无法确定动力臂的大小，所以无法确定是哪种杠杆，故A 错误；B ．沿垂直杠杆向上的方向用力，动力臂最大，动力最小，最省力，故B 错误；C ．沿OA 方向动力臂是零，杠杆无法平衡，故C 错误。

一、初中物理杠杆平衡条件的应用问题1．在一个长3米的跷跷板（支点在木板中点）的两端分别放置两个木箱，它们的质量分别为m 1=30kg ，m 2=20kg ，为了使跷跷板在水平位置平衡，以下做法可行的是（ ）A ．把m 1向右移动0.5米B ．把m 2向左移动0.5米C ．把m 1向右移动0.2米D ．把m 2向左移动0.3米【答案】A【解析】【分析】【详解】 跷跷板的支点在木板中点，根据图中信息可知，木板左边受到的压力比右边大，为了使跷跷板在水平位置平衡，应该将m 1向右移，则m 2的力臂不变为1.5m ，根据杠杆的平衡条件有1122m gl m gl '=代入数据可得m 1向右移后的力臂 221120kg 1.5m 1m 30kgm gl l m g ⨯'=== m 1的力臂由1.5m 变为1m ，为了使跷跷板在水平位置平衡，把m 1向右移动0.5米，所以BCD 项错误，A 项正确。

故选A 。

2．如图所示，一根均匀木尺放在水平桌面上，它的一端伸出桌面的外面，伸到桌面外面的部分长度是木尺长的14，在木尺末端的B 点加一个作用力F ，当力F =3N 时，木尺的另一端A 开始向上翘起，那么木尺受到的重力为（ ）A ．3NB ．9NC ．1ND ．2N【答案】A【解析】【分析】【详解】设直尺长为l，如图所示：从图示可以看出：杠杆的支点为O，动力F=3N 动力臂OB=1 4 l阻力为直尺的重力G，阻力臂CO=12l-14l=14l由杠杆平衡的条件得F×OB=G×OC3N×14l= G×14l G=3N故选A。

3．如图所示，为提升重物，现选用轻质杠杆，不考虑杠杆支点O点处的摩擦，每次利用杠杆把同一重物匀速提升相同高度，下列说法正确的是A．当重物悬挂在A点，动力作用在C点时，该杠杆一定是省力杠杆B．当重物悬挂在C点，动力作用在B点时一定比作用在A点时要省力C．无论重物挂在A点还是B点时，利用该机械所做的有用功都相等D．如果动力作用在C点且方向始终保持与杆保持垂直，则提升重物过程动力大小不变【答案】C【解析】【分析】灵活运用杠杆平衡公式分析即可；【详解】AB．不论重物悬挂在A点或C点，也不论动力作用在C点还是B点，判断杠杆是省力还是费力，需要根据杠杆平衡公式，不仅与力的作用点有关，还与力的方向有关，因此无法在只知道力的作用点的情况下判断是否省力，故AB错误；C．无论重物挂在A点还是B点时，由于物体质量相同，上升高度相同，则根据W Gh可知，该机械所做的有用功都相等，故C正确；D．动力作用在C点且方向始终保持与杆保持垂直时，可得动力臂大小始终不发生变化，但由于物体上升，重物的阻力臂会逐渐减小，则由杠杆平衡公式可知动力会减小，故D错误。

一、初中物理杠杆平衡条件的应用问题1．如图所示为建筑工地上常用的吊装工具，物体Ｍ是重5000N的配重，杠杆AB的支点为O，已知长度OA∶OB=1∶2，滑轮下面挂有建筑材料P，每个滑轮重100N，工人体重为700N，杠杆与绳的自重、滑轮组摩擦均不计。

当工人用300N的力竖直向下以1m/s的速度匀速拉动绳子时（）A．建筑材料P上升的速度为3m/s B．物体M对地面的压力为5000NC．工人对地面的压力为400N D．建筑材料P的重力为600N【答案】C【解析】【分析】【详解】A．物重由2段绳子承担，建筑材料P上升的速度v=12v绳=12×1m/s=0.5m/s故A错误；B．定滑轮受向下的重力、3段绳子向下的拉力、杠杆对定滑轮向上的拉力，由力的平衡条件可得F A′=3F+G定=3×300N+100N=1000N杠杆对定滑轮的拉力和定滑轮对杠杆的拉力是一对相互作用力，大小相等，即F A= F A′=1000N根据杠杆的平衡条件F A×OA=F B×OB，且OA:OB=1:2，所以F B=F A×OAOB=1000N×2OAOA=500N因为物体间力的作用是相互的，所以杠杆对物体M的拉力等于物体M对杠杆的拉力，即F B′=F B=500N物体M受竖直向下的重力、竖直向上的支持力、竖直向上的拉力，则物体M受到的支持力为F M支持=G M− F B′=5000N−500N=4500N因为物体间力的作用是相互的，所以物体M对地面的压力F M 压=F M 支持=4500N故B 错误；C ．当工人用300N 的力竖直向下拉绳子时，因力的作用是相互的，则绳子对工人会施加竖直向上的拉力，其大小也为300N ，此时人受竖直向下的重力G 、竖直向上的拉力F 、竖直向上的支持力F 支，由力的平衡条件可得F +F 支=G ，则F 支=G−F =700N−300N=400N因为地面对人的支持力和人对地面的压力是一对相互作用力，大小相等，所以工人对地面的压力F 压=F 支=400N故C 正确；D ．由图可知n =2，且滑轮组摩擦均不计，由F =12(G +G 动)可得，建筑材料P 重 G =2F −G 动=2×300N−100N=500N故D 错误。

一、初中物理杠杆平衡条件的应用问题1．如图所示，杠杆恰好处于水平平衡状态，若在B处下方再挂一个钩码，若要使杠杆在水平位置再次平衡，下列可行的操作是______。

（选填字母）A．减少一个悬挂在A处的钩码B．增加一个悬挂在A处的钩码C．将悬挂在A处的钩码向左移动一格D．将悬挂A处的钩码向右移动一格【答案】C【解析】【分析】【详解】假设一个钩码重力为G，杠杆一格为l，杠杆平衡时⨯=⨯=32236G l G l Gl若在B处下方再挂一个钩码，则右边为339⨯=G l GlA．减少一个悬挂在A处的钩码，则左边为⨯=G l Gl224左边小于右边，杠杆不能平衡，故A项不符合题意；B．增加一个悬挂在A处的钩码，则左边为⨯=G l Gl428左边小于右边，杠杆不能平衡，故B项不符合题意；C．将悬挂在A处的钩码向左移动一格，则左边为G l Gl⨯=339左边等于右边，杠杆能再次平衡，故C项符合题意；D．将悬挂A处的钩码向右移动一格，则左边为G l Gl⨯=313左边小于右边，杠杆能再次平衡，故D项不符合题意。

故选C。

2．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A．左右钩码各向支点移一格B．左右各减少一个钩码C．左右各减少一半钩码D．左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L，一个钩码的重为G．原来4G×2L=2G×4L；左、右钩码各向支点移动一格，左边=4G×L=4GL，右边=2G×3L=6GL，左边＜右边，杠杆向右端下沉，A不符合题意；左右各减少一个钩码，左边=3G×2L=6GL，右边=G×4L=4GL，左边＞右边，杠杆向左下沉，B 不符合题意；左、右钩码各减少一半法码，左边=2G×2L=4GL，右边=G×4L=4GL，左边=右边，杠杆平衡；C符合题意；左右各增加两个钩码，左边=6G×2L=12GL，右边=4G×4L=16GL，左边＜右边，杠杆右边下沉，D不符合题意，故选C．3．如图所示，在一个轻质杠杆的中点挂一重物，在杆的另一端施加一个动力F，使杠杆保持平衡，然后向右缓慢转动F至水平方向，这一过程中（）A．F先变小后变大B．F逐渐变大C．动力臂逐渐变小D．动力臂逐渐变大【答案】A【解析】【分析】杠杆平衡条件及应用。

一、初中物理杠杆平衡条件的应用问题1．如图，轻质杠杆可绕O 点转动（不计摩擦）．A 处挂着一重为80N 、底面积为500cm 2的物体G ．在B 点施加一个垂直于杆的动力F 使杠杆水平平衡，且物体G 对地面的压强为1000Pa ，OB =3OA ．则B 点的拉力F 的大小为A ．50NB ．30NC ．10ND ．90N【答案】C 【解析】 【分析】 【详解】地面对物体G 的支持力21000Pa 0.05m 50N F F ps ===⨯=压支物体G 对杠杆的拉力A 80N 50N 30N F G F =-=-=支已知OB =3OA ，由杠杆平衡的条件A F F OB OA ⨯=⨯可得：A 1=30N =10N 3F OA F OB ⨯=⨯． 故选C ．2．如图所示的轻质杠杆OA 上悬挂着一重物G ，O 为支点，在A 端用力使杠杆平衡。

下列叙述正确的是（ ）A ．此杠杆一定是省力杠杆B ．沿竖直向上方向用力最小C ．沿杆OA 方向用力也可以使杠杆平衡D ．此杠杆可能是省力杠杆，也可能是费力杠杆 【答案】D【解析】【分析】【详解】A．因为无法确定动力臂的大小，所以无法确定是哪种杠杆，故A错误；B．沿垂直杠杆向上的方向用力，动力臂最大，动力最小，最省力，故B错误；C．沿OA方向动力臂是零，杠杆无法平衡，故C错误。

D．因为杠杆的动力臂无法确定，所以它可能是省力杠杆，也可能是费力杠杆，故D正确。

故选D。

3．如图所示，杠杆在水平状态保持静止，要使弹簧测力计的示数变为原来的12，下列措施中可行的是A．去掉三个钩码B．把钩码向左移动2小格C．把钩码向右移动2小格D．把弹簧秤测力计向左移动2小格【答案】B【解析】【分析】【详解】根据杠杆平衡条件F1L1＝F2L2得，4G×4L＝F2×8L，解得F2＝2G，要使弹簧测力计的示数变为原来的12，即F2＝G。

A．去掉三个钩码，根据杠杆平衡条件F1L1＝F2L2得，G×4L＝F'2×8L，所以F'2＝12G，不符合题意；B．把钩码向左移动2小格，根据杠杆平衡条件F1L1＝F2L2得，4G ×2L ＝F '2×8L ，所以F '2＝G ，故B 符合题意；C ．把钩码向右移动2小格，根据杠杆平衡条件F 1L 1＝F 2L 2得，4G ×6L ＝F '2×8L ，所以F '2＝3G ，故C 不符合题意；D ．把弹簧秤测力计向左移动2小格，根据杠杆平衡条件F 1L 1＝F 2L 2得，4G ×4L ＝F '2×6L ，所以F '2＝83G ，故D 不符合题意。

一、初中物理杠杆平衡条件的应用问题1．如图，轻质杠杆可绕O 点转动（不计摩擦）．A 处挂着一重为80N 、底面积为500cm 2的物体G ．在B 点施加一个垂直于杆的动力F 使杠杆水平平衡，且物体G 对地面的压强为1000Pa ，OB =3OA ．则B 点的拉力F 的大小为A ．50NB ．30NC ．10ND ．90N【答案】C【解析】【分析】【详解】 地面对物体G 的支持力21000Pa 0.05m 50N F F ps ===⨯=压支物体G 对杠杆的拉力A 80N 50N 30N F G F =-=-=支已知OB =3OA ，由杠杆平衡的条件A F F OB OA ⨯=⨯可得： A 1=30N =10N 3F OA F OB ⨯=⨯． 故选C ．2．如图所示，轻质杠杆OA 的B 点挂着一个重物，A 端用细绳吊在圆环M 下，此时OA 恰成水平且A 点与圆弧形架PQ 的圆心重合，那么当环M 从P 点逐渐滑至Q 点的过程中，绳对A 端的拉力大小将（ ）A ．保持不变B ．逐渐增大C ．逐渐减小D ．先变小再变大【答案】D【解析】【详解】作出当环M位于P点、圆弧中点、Q点时拉力的力臂l1、l2、l3如下由图可知，动力臂先增大，再减小，阻力与阻力臂不变，则由杠杆平衡公式F1l1=F2l2可知，拉力先变小后变大，故选D。

3．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A．左右钩码各向支点移一格B．左右各减少一个钩码C．左右各减少一半钩码D．左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L，一个钩码的重为G．原来4G×2L=2G×4L；左、右钩码各向支点移动一格，左边=4G×L=4GL，右边=2G×3L=6GL，左边＜右边，杠杆向右端下沉，A不符合题意；左右各减少一个钩码，左边=3G×2L=6GL，右边=G×4L=4GL，左边＞右边，杠杆向左下沉，B 不符合题意；左、右钩码各减少一半法码，左边=2G×2L=4GL，右边=G×4L=4GL，左边=右边，杠杆平衡；C符合题意；左右各增加两个钩码，左边=6G×2L=12GL，右边=4G×4L=16GL，左边＜右边，杠杆右边下沉，D不符合题意，故选C．4．如图所示，在一个轻质杠杆的中点挂一重物，在杆的另一端施加一个动力F，使杠杆保持平衡，然后向右缓慢转动F至水平方向，这一过程中（）A．F先变小后变大B．F逐渐变大C．动力臂逐渐变小D．动力臂逐渐变大【答案】A【解析】【分析】杠杆平衡条件及应用。

一、初中物理杠杆平衡条件的应用问题1．用如图所示的杠杆提升重物，设作用在A端的力F始终与杆垂直，那么，在将重物提升到最高处的过程中，力F的大小将 ( )A．逐渐变小B．先变小，后变大C．逐渐变大D．先变大，后变小【答案】D【解析】【分析】【详解】由题知，当慢慢提升重物时，重力(阻力)不变，阻力臂增大(水平时最大)，动力臂不变，即：G不变、L1不变,，L2增大∵FL1＝GL2∴力F逐渐变大；故选C.2．如图所示，作用在A点的各个力中，不可能使杠杆平衡的力是A．F3和F4B．F1和F3C．F2和F4D．F1和F2【答案】A【解析】【详解】因为力F3的作用线所在的直线过支点O，所以力F3的力臂为0，又因为0乘以任何数都为0，所以力F3不能使杠杆平衡；力F4使杠杆转动方向与重物使杠杆的转动方向相同，所以力F4不能使杠杆平衡；力F1和F2使杠杆转动方向与重物使杠杆转动方向相反，所以力F1和F2可以使杠杆平衡；故选A。

3．如图所示，一根均匀木尺放在水平桌面上，它的一端伸出桌面的外面，伸到桌面外面的部分长度是木尺长的14，在木尺末端的B点加一个作用力F，当力F=3N时，木尺的另一端A开始向上翘起，那么木尺受到的重力为（）A．3N B．9N C．1N D．2N 【答案】A【解析】【分析】【详解】设直尺长为l，如图所示：从图示可以看出：杠杆的支点为O，动力F=3N动力臂OB=1 4 l阻力为直尺的重力G，阻力臂CO=12l-14l=14l由杠杆平衡的条件得F×OB=G×OC3N×14l= G×14l G=3N故选A。

4．用图示装置探究杠杆平衡条件，保持左侧的钩码个数和位置不变，使右侧弹簧测力计的作用点A 固定，改变测力计与水平方向的夹角θ，动力臂l 也随之改变，所作出的“F-θ”图象和“F-l”图象中，正确的是A ．B ．C ．D ．【答案】C【解析】【详解】A ．动力F 和θ的关系，当F 从沿杆方向（水平向左）→垂直于杆方向（与水平方向成90°）→沿杆方向（水平向右），由图可知，F 对应的动力臂l =OA ×sinθ，动力臂l 先变大后变小，则动力F 先变小后变大，所以A 错误；B ．当θ等于90°时，动力臂最大，动力最小但不为零，所以B 错误；CD ．根据杠杆平衡条件Fl =F 2l 2可得：F =22F l l，由于F 2、l 2不变，则F 和l 成反比，故C 正确，D 错误。

一、初中物理杠杆平衡条件的应用问题1．如图所示，在探究杠杆平衡条件的实验中，杠杆处于水平平衡状态，所用钩码完全相同。

下列做法中能使杠杆再次平衡的是A ．分别在两边钩码下再增加一个相同钩码B ．左边减少1个钩码，右边减少2个钩码C ．两边钩码均向支点移动相同的距离D ．左边钩码向左移1.5cm ，右边钩码向右移1cm 【答案】D 【解析】 【详解】设一个钩码的重力为G ，左边钩码到支点的距离为3l ，因为杠杆正处于水平平衡，所以由杠杆平衡条件可得233G l G l ⨯=⨯右，解得2l l =右，即右边钩码到支点的距离为2l ； A ．若分别在两边钩码下再增加一个相同钩码，则3342G l G l ⨯≠⨯，此时杠杆不再平衡，不符合题意；B ．若左边减少1个钩码，右边减少2个钩码，则32G l G l ⨯≠⨯ ，此时杠杆不再平衡，不符合题意；C ．若两边的钩码均向支点移动相同的距离l ，则223G l G l ⨯≠⨯，此时杠杆不再平衡，不符合题意；D ．若左边钩码向左移1.5cm ，右边钩码向右移1cm ，则2(3 1.5)3(21)G l G l ⨯+=⨯+，此时杠杆平衡，符合题意。

2．按如下原理制作一杆可直接测量液体密度的秤，称为密度秤，其外形和普通的杆秤差不多，装秤钩的地方吊着体积为1cm 3的较重的合金块，杆上有表示液体密度数值的刻度，当秤砣放在Q 点处时秤杆恰好平衡，如图所示。

当合金块完全浸没在待测密度的液体中时，移动秤砣的悬挂点，直至秤杆恰好重新平衡，便可直接在杆秤上读出液体的密度，下列说法中错误的是（ ）A．密度秤的零点刻度在Q点B．密度秤的刻度都在Q点的左侧C．密度秤的刻度都在Q点的右侧D．秤杆上密度读数较大的刻度在较小的刻度的左边【答案】C【解析】【分析】【详解】A．合金块没有浸入液体时，液体的密度应为零，所以秤的零刻度应该在Q处；故A正确，不符合题意；BC．若秤砣由Q向右移动，它的力臂变长，则左边合金块拉秤杆的力应增大，但合金块受到的浮力不可能竖直向下，所以零点的右边应该是没有刻度的，其刻度都在Q点的左侧。

一、初中物理杠杆平衡条件的应用问题1．如图所示，轻质杠杆AOB 的支点是O ，AO=BO 。

若在A 端和B 端分别悬挂重力相等的两个重物，则杠杆（ ）A ．保持平衡B ．A 端下沉C ．B 端下沉D ．以上均可能【答案】B【解析】【分析】【详解】轻质杠杆AOB 的重力可不计，杠杆的示意图如下所示：动力和阻力大小均等于物体的重力，两个重物的重力相等，则F 1=F 2；动力臂为OA ，阻力臂为OC ，满足OC OB OA <=所以可知12F OA F OC ⨯>⨯根据杠杆的平衡条件可知，A 端下沉。

故选B 。

2．如图所示，在一个轻质杠杆的中点挂一重物，在杆的另一端施加一个动力F ，使杠杆保持平衡，然后向右缓慢转动F 至水平方向，这一过程中（ ）A ．F 先变小后变大B ．F 逐渐变大C ．动力臂逐渐变小D ．动力臂逐渐变大【答案】A【解析】【分析】杠杆平衡条件及应用。

【详解】杠杆在图中所示位置平衡，阻力（重物对杠杆的拉力）及阻力臂大小不变；动力F由图中所示位置转动至水平方向的过程中，当动力F的方向与杠杆垂直时，动力F的力臂最长，因此动力F的力臂先增大后减小，由杠杆平衡条件F1l1=F2l2可知，动力Ｆ先变小后变大。

故选A。

【点睛】中等题.失分的原因是：①不知道动力F方向变化的过程中阻力和阻力臂的大小不变；②不会画动力F在不同位置时的动力臂；③不会利用杠杆平衡条件通过动力臂的变化分析出动力的变化；④不知道当动力F与杠杆垂直时，动力臂最大，动力F最小。

3．如图所示，杠杆在水平状态保持静止，要使弹簧测力计的示数变为原来的12，下列措施中可行的是A．去掉三个钩码B．把钩码向左移动2小格C．把钩码向右移动2小格D．把弹簧秤测力计向左移动2小格【答案】B【解析】【分析】【详解】根据杠杆平衡条件F1L1＝F2L2得，4G×4L＝F2×8L，解得F2＝2G，要使弹簧测力计的示数变为原来的12，即F2＝G。

一、初中物理杠杆平衡条件的应用问题1．如图所示，直杆OA的下端挂一重物G且可绕O点转动。

现用一个始终与直杆垂直的力F将直杆由竖直位置缓慢转动到水平位置，不计杆的重力，则拉力F大小的变化情况是（）A．一直变小B．一直不变C．一直变大D．先变小后变大【答案】C【解析】【分析】【详解】由图可知，由于力F始终与杠杆垂直，则力F所对应的力臂始终不变，大小为力F的作用点到O点的距离，设为l1，在逐渐提升的过程中，重力大小不变，方向竖直向下，则对应力臂逐渐变大，设为l2，由于缓慢转动，视为受力平衡，则由杠杆平衡公式可得Fl1=Gl2由于等式右端重力G不变，l2逐渐变大，则乘积逐渐变大，等式左端l1不变，则可得F逐渐变大，故选C。

2．按如下原理制作一杆可直接测量液体密度的秤，称为密度秤，其外形和普通的杆秤差不多，装秤钩的地方吊着体积为1cm3的较重的合金块，杆上有表示液体密度数值的刻度，当秤砣放在Q点处时秤杆恰好平衡，如图所示。

当合金块完全浸没在待测密度的液体中时，移动秤砣的悬挂点，直至秤杆恰好重新平衡，便可直接在杆秤上读出液体的密度，下列说法中错误的是（）A．密度秤的零点刻度在Q点B．密度秤的刻度都在Q点的左侧C．密度秤的刻度都在Q点的右侧D．秤杆上密度读数较大的刻度在较小的刻度的左边【答案】C【解析】【分析】【详解】A．合金块没有浸入液体时，液体的密度应为零，所以秤的零刻度应该在Q处；故A正确，不符合题意；BC．若秤砣由Q向右移动，它的力臂变长，则左边合金块拉秤杆的力应增大，但合金块受到的浮力不可能竖直向下，所以零点的右边应该是没有刻度的，其刻度都在Q点的左侧。

故B正确，不符合题意，C错误，符合题意；D．秤砣的质量不变，由Q向左移动时，它的力臂变短，则左边合金块拉秤杆的力减小，说明合金块受到的浮力增大，而合金块排开液体的体积不变，说明液体的密度变大，所以刻度应逐渐变大，即秤杆上较大的刻度在较小的刻度的左边；故D正确，不符合题意。

一、初中物理杠杆平衡条件的应用问题1．如图所示，杠杆在水平位置平衡．下列操作仍能让杠杆在水平位置保持平衡的是（）A．两侧钩码同时向外移一格B．两侧钩码同时向内移一格C．在两侧钩码下方，同时加挂一个相同的钩码D．左侧增加一个钩码，右侧钩码向外移一格【答案】D【解析】【分析】【详解】设一个钩码的重力为G，横梁上一个格的长度为l，原来杠杆处于平衡状态，则有2332⨯=⨯G l G lA．两侧钩码同时向外移一格,左边为⨯=G l Gl248右边为⨯=339G l GlGl Gl<89杠杆右端下沉，故A项不符合题意；B．两侧钩码同时向内移一格，左边为⨯=G l Gl224右边为313⨯=G l Gl<34Gl Gl杠杆左端下沉，故B项不符合题意；C．同时加挂一个相同的钩码，左边为⨯=G l Gl339右边为⨯=G l Gl428<Gl Gl89杠杆左端下沉，故C项不符合题意；D．左侧增加一个钩码，右侧钩码向外移一格，左边为⨯=G l Gl339右边为⨯=G l Gl339=99Gl Gl杠杆平衡，故D项符合题意。

故选D。

2．如图所示的轻质杠杆OA上悬挂着一重物G，O为支点，在A端用力使杠杆平衡。

下列叙述正确的是（）A．此杠杆一定是省力杠杆B．沿竖直向上方向用力最小C．沿杆OA方向用力也可以使杠杆平衡D．此杠杆可能是省力杠杆，也可能是费力杠杆【答案】D【解析】【分析】【详解】A．因为无法确定动力臂的大小，所以无法确定是哪种杠杆，故A错误；B．沿垂直杠杆向上的方向用力，动力臂最大，动力最小，最省力，故B错误；C．沿OA方向动力臂是零，杠杆无法平衡，故C错误。

D．因为杠杆的动力臂无法确定，所以它可能是省力杠杆，也可能是费力杠杆，故D正确。

故选D。

3．如图甲是制作面团的情景，把竹竿的一端固定在绳扣中，人骑在另一端施加一个向下的大小为F的力，面团被不断挤压后变得更有韧性，图乙为压面团原理图．关于压面团过程的叙述正确的是（）A．面团对杆的作用力方向向下B．面团对杆的作用力大小等于FC．面团被压扁说明力能使物体发生形变D．A点向下移动的距离小于B点向下移动的距离【答案】C【解析】【分析】【详解】A．杆对面团的作用力向下，面团对杆的作用力向上，故A错误；B．由于面团B点到支点C的距离小于A点到C的距离，根据杠杆定律F1L1=F2L2，可知面团对杆的作用力大于F，故B错误；C．面团被压扁说明力能使物体发生形变，故C正确；D．C为支点，A点向下移动的距离大于B点向下移动的距离，故D错误；故选C。

一、初中物理杠杆平衡条件的应用问题1．如图，轻质杠杆可绕O 点转动（不计摩擦）．A 处挂着一重为80N 、底面积为500cm 2的物体G ．在B 点施加一个垂直于杆的动力F 使杠杆水平平衡，且物体G 对地面的压强为1000Pa ，OB =3OA ．则B 点的拉力F 的大小为A ．50NB ．30NC ．10ND ．90N【答案】C【解析】【分析】【详解】 地面对物体G 的支持力21000Pa 0.05m 50N F F ps ===⨯=压支物体G 对杠杆的拉力A 80N 50N 30N F G F =-=-=支已知OB =3OA ，由杠杆平衡的条件A F F OB OA ⨯=⨯可得： A 1=30N =10N 3F OA F OB ⨯=⨯． 故选C ．2．如图所示，在一个轻质杠杆的中点挂一重物，在杆的另一端施加一个动力F ，使杠杆保持平衡，然后向右缓慢转动F 至水平方向，这一过程中（ ）A ．F 先变小后变大B ．F 逐渐变大C ．动力臂逐渐变小D ．动力臂逐渐变大【解析】【分析】杠杆平衡条件及应用。

【详解】杠杆在图中所示位置平衡，阻力（重物对杠杆的拉力）及阻力臂大小不变；动力F 由图中所示位置转动至水平方向的过程中，当动力F 的方向与杠杆垂直时，动力F 的力臂最长，因此动力F 的力臂先增大后减小，由杠杆平衡条件F 1l 1=F 2l 2可知，动力Ｆ先变小后变大。

故选A 。

【点睛】中等题.失分的原因是：①不知道动力F 方向变化的过程中阻力和阻力臂的大小不变；②不会画动力F 在不同位置时的动力臂；③不会利用杠杆平衡条件通过动力臂的变化分析出动力的变化；④不知道当动力F 与杠杆垂直时，动力臂最大，动力F 最小。

3．如图所示，将重150N 的甲物体用细绳挂在轻质杠杆的A 端，杠杆的B 端悬挂乙物体，杠杆在水平位置平衡，已知：乙物体所受重力为30N ，:1:3AO OB =，甲物体的底面积为0.2m 2，g 取10N/kg 。

一、初中物理杠杆平衡条件的应用问题1．将打足气的篮球和套扎在气针上的未充气的气球，一起悬挂在杠杆右端，左端挂适量钩码使杠杆水平平衡。

将气针插入篮球气孔中，篮球中的部分空气充入气球后，杠杆左端下降，如图所示。

这个现象说明（）A．大气压的存在B．钩码重大于篮球与气球总重C．空气充入气球后，钩码对杠杆的拉力与其力臂的乘积变大D．空气充入气球后，篮球和气球受到总的空气浮力变大【答案】D【解析】【分析】【详解】开始杠杆平衡，由杠杆平衡条件得G钩码×L左=F绳拉力×L右篮球与气球受到竖直向下的重力G、竖直向上的绳子拉力F、空气的浮力F浮作用而静止，处于平衡状态，由平衡条件得G=F+F浮则F=G-F浮将气针插入篮球的孔中，篮球中的部分空气就充入气球后，篮球与气球受到的浮力F浮变大，而重力G不变，绳子的拉力F变小，因为球对杠杆的拉力F绳拉力等于球受到的拉力F，所以杠杆右端受到的拉力F绳拉力变小，而G钩码、L左、L右不变，因此G钩码×L左>F绳拉力×L右杠杆左端下沉。

故A、B、C不符合题意，D符合题意。

故选D。

2．如图所示为等刻度轻质杠杆，A处挂4牛的物体，若使杠杆在水平位置平衡，则在B处施加的力（）A．可能为0.5牛B．一定为2牛C．一定为3牛D．可能是4牛【答案】D 【解析】 【分析】 【详解】设杠杆每小格的长度为L ，若在B 点用垂直OB 竖直向下的力使杠杆在水平位置平衡，此时所用的力最小，根据杠杆平衡条件1122Fl F l =可得min 42F L G L ⋅=⋅则有min 24N 22N 44G L F L ⋅⨯=== 若在B 点斜拉使杠杆在水平位置平衡，由杠杆平衡条件1122Fl F l =可知2211F l F l =则此时杠杆左边的阻力与阻力臂的乘积不变，动力臂减小，故动力将增大，故若使杠杆在水平位置平衡，在B 点施加的力2N F ≥故选D 。

3．用图示装置探究杠杆平衡条件，保持左侧的钩码个数和位置不变，使右侧弹簧测力计的作用点 A 固定，改变测力计与水平方向的夹角 θ，动力臂l 也随之改变，所作出的“F -θ”图象和“F -l ” 图象中，正确的是A ．B ．C ．D ．【答案】C 【解析】 【详解】A ．动力F 和θ的关系，当F 从沿杆方向（水平向左）→垂直于杆方向（与水平方向成90°）→沿杆方向（水平向右），由图可知，F 对应的动力臂l =OA ×sinθ，动力臂l 先变大后变小，则动力F 先变小后变大，所以A 错误；B ．当θ等于90°时，动力臂最大，动力最小但不为零，所以B 错误； CD ．根据杠杆平衡条件Fl =F 2l 2可得：F =22F l l，由于F 2、l 2不变，则F 和l 成反比，故C 正确，D 错误。

一、初中物理杠杆平衡条件的应用问题1．如图所示，小明利用一根长为L 的扁担挑水，他在扁担的左端挂上质量为m 1的水桶，在右端挂上质量为m 2的水桶，右手扶着扁担右侧。

已知m 1> m 2 ，不计扁担自重，下列说法正确的是（ ）A ．若要右手不使力，小明的肩应靠近扁担左端B ．若要右手不使力，小明的肩应靠近扁担右端C ．小明的肩位于扁担中点时，右手需要给扁担施加向上的力D ．扁担与肩的接触面积越小，肩受到的压强越小【答案】A【解析】【分析】【详解】AB ．扁担在左端挂了m 1的水桶，右端挂了m 2的水桶，左端的重力大于右端的重力，根据杠杆的平衡条件1122F L F L =可知，若要扁担平衡右手不使力，人的肩膀应靠近扁担左端，故A 正确，B 错误；C ．小明的肩位于扁担中点时，左端的重力大于右端的重力，根据杠杆的平衡条件1122F L F L =可知，左端下沉，为了使扁担在水平位置平衡，右手需要给扁担施加向下的力，故C 错误；D ．根据压强的公式F p S=可知，压力一定时，扁担与肩的接触面积越小，肩受到的压强越大，故D 错误。

故选A 。

2．如图所示的轻质杠杆OA 上悬挂着一重物G ，O 为支点，在A 端用力使杠杆平衡。

下列叙述正确的是（ ）A．此杠杆一定是省力杠杆B．沿竖直向上方向用力最小C．沿杆OA方向用力也可以使杠杆平衡D．此杠杆可能是省力杠杆，也可能是费力杠杆【答案】D【解析】【分析】【详解】A．因为无法确定动力臂的大小，所以无法确定是哪种杠杆，故A错误；B．沿垂直杠杆向上的方向用力，动力臂最大，动力最小，最省力，故B错误；C．沿OA方向动力臂是零，杠杆无法平衡，故C错误。

D．因为杠杆的动力臂无法确定，所以它可能是省力杠杆，也可能是费力杠杆，故D正确。

故选D。

3．如图所示，在一个轻质杠杆的中点挂一重物，在杆的另一端施加一个动力F，使杠杆保持平衡，然后向右缓慢转动F至水平方向，这一过程中（）A．F先变小后变大B．F逐渐变大C．动力臂逐渐变小D．动力臂逐渐变大【答案】A【解析】【分析】杠杆平衡条件及应用。

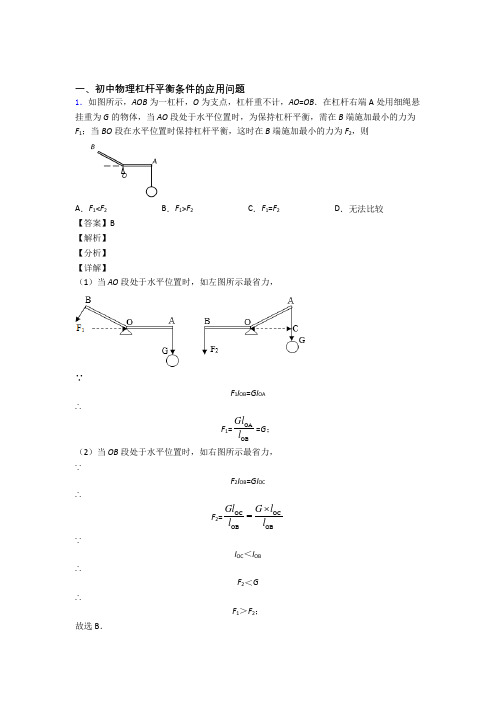
一、初中物理杠杆平衡条件的应用问题1．如图所示，AOB 为一杠杆，O 为支点，杠杆重不计，AO =OB ．在杠杆右端A 处用细绳悬挂重为G 的物体，当AO 段处于水平位置时，为保持杠杆平衡，需在B 端施加最小的力为F 1；当BO 段在水平位置时保持杠杆平衡，这时在B 端施加最小的力为F 2，则A ．F 1<F 2B ．F 1>F 2C ．F 1=F 2D ．无法比较【答案】B 【解析】 【分析】 【详解】（1）当AO 段处于水平位置时，如左图所示最省力，∵F 1l OB =Gl OA∴F 1=OAOBGl l =G ； （2）当OB 段处于水平位置时，如右图所示最省力， ∵F 2l OB =Gl OC∴F 2=OC OCOB OBGl G l l l ⨯= ∵l OC ＜l OB∴F 2＜G∴F 1＞F 2；故选B ．2．AC 硬棒质量忽略不计，在棒的B 、C 两点施加力F 1、F 2，F 2的方向沿OO'线，棒在图所示位置处于静止状态，则（ ）A ．F 1<F 2B ．F 1=221s F s C ．F 1力臂等于s 1 D ．F 2方向沿OO '线向上 【答案】D 【解析】 【详解】AC ．由图知，F 2的方向沿OO ′线，其力臂最长，为s 2；而F 1的方向竖直向下，所以其力臂L 1是从A 点到F 1的垂线段，小于s 1，更小于s 2， 由F 1L 1=F 2L 2知，L 1＜s 2，所以F 1一定大于F 2，故AC 不符合题意； B ．由F 1L 1=F 2L 2知，F 1L 1=F 2s 2，即2211F s F L故B 不符合题意；D ．已知F 1的方向是竖直向下的，为保持杠杆平衡，F 2的方向应该沿OO′向上，故D 符合题意。

3．如图甲是制作面团的情景，把竹竿的一端固定在绳扣中，人骑在另一端施加一个向下的大小为F 的力，面团被不断挤压后变得更有韧性，图乙为压面团原理图．关于压面团过程的叙述正确的是（ ）A．面团对杆的作用力方向向下B．面团对杆的作用力大小等于FC．面团被压扁说明力能使物体发生形变D．A点向下移动的距离小于B点向下移动的距离【答案】C【解析】【分析】【详解】A．杆对面团的作用力向下，面团对杆的作用力向上，故A错误；B．由于面团B点到支点C的距离小于A点到C的距离，根据杠杆定律F1L1=F2L2，可知面团对杆的作用力大于F，故B错误；C．面团被压扁说明力能使物体发生形变，故C正确；D．C为支点，A点向下移动的距离大于B点向下移动的距离，故D错误；故选C。

一、初中物理杠杆平衡条件的应用问题1．如图，一块厚度、密度均匀的长方形水泥板放在水平地面上，用一竖直向上的力，欲使其一端抬离地面，则（）A．F1＞F2，因为甲方法的动力臂长B．F1=F2，因为动力臂都是阻力臂的2倍C．F1＞F2，因为乙方法的阻力臂短D．F1＜F2，因为乙方法的动力臂长【答案】B【解析】【分析】【详解】由图示可知，无论用哪种方法来抬，动力臂总是阻力臂的二倍，所用的力总等于阻力的二分之一，由于阻力就是重力，大小是不变的，所以动力的大小也是不变的，故应选B。

2．工人师傅利用如图所示的两种方式，将重均为 400N 的货物从图示位置向上缓慢提升一段距离．F1、F2始终沿竖直方向；图甲中BO=2AO，图乙中动滑轮重为 50N，重物上升速度为 0.02m/s．不计杠杆重、绳重和摩擦,则下列说法正确的是( )A．甲方式F1由 150N 逐渐变大B．乙方式F2的功率为 3WC．甲乙两种方式都省一半的力D．乙方式中滑轮组的机械效率约为 88.9%【答案】D【解析】【详解】A．由图知道，重力即阻力的方向是竖直向下的，动力F1的方向也是竖直向下的，在提升重物的过程中，动力臂和阻力臂的比值是：1 22 1L OB L OA==所以，动力F1的大小始终不变，故A错误；BC．由于在甲图中，OB=2OA，即动力臂为阻力臂的2倍，由于不计摩擦及杠杆自重，所以，由杠杆平衡条件知道，动力为阻力的一半，即111400N200N22F G==⨯=由图乙知道，承担物重是绳子的段数是n=3，不计绳重和摩擦，则()()211500N+50N150N22F G G=+=⨯=动，即乙中不是省力一半；所以，绳子的自由端的速度是：v绳 =0.02m/s×3=0.06m/s，故乙方式F2的功率是：P=F2v绳 =150N×0.06m/s=9W，故BC错误；D．不计绳重和摩擦，乙方式中滑轮组的机械效率是：400N100%=100%=100%88.9%400N50NW GhW Gh G hη=⨯⨯⨯≈++有用总轮故D正确．3．如图所示，杠杆挂上钩码后刚好平衡，每个钩码的质量相同，在下列情况中，杠杆还能平衡的是A．左右钩码各向支点移一格B．左右各减少一个钩码C．左右各减少一半钩码D．左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L，一个钩码的重为G．原来4G×2L=2G×4L；左、右钩码各向支点移动一格，左边=4G×L=4GL，右边=2G×3L=6GL，左边＜右边，杠杆向右端下沉，A不符合题意；左右各减少一个钩码，左边=3G×2L=6GL，右边=G×4L=4GL，左边＞右边，杠杆向左下沉，B 不符合题意；左、右钩码各减少一半法码，左边=2G×2L=4GL，右边=G×4L=4GL，左边=右边，杠杆平衡；C符合题意；左右各增加两个钩码，左边=6G×2L=12GL，右边=4G×4L=16GL，左边＜右边，杠杆右边下沉，D不符合题意，故选C．4．生活中，小华发现有如图甲所示的水龙头，很难徒手拧开，但用如图乙所示的钥匙，安装并旋转钥匙就能正常出水（如图丙所示）．下列有关这把钥匙的分析中正确的是A．在使用过程中可以减小阻力臂B．在使用过程中可以减小阻力C．在使用过程中可以减小动力臂D．在使用过程中可以减小动力【答案】D【解析】【详解】由图可知，安装并旋转钥匙，阻力臂不变，阻力不变，动力臂变大，根据杠杆平衡的条件F1L1=F2L2可知，动力变小，故选D。