2018年吉林省中考数学试卷解析版

word 文档可编写——2018 年吉林省中考数学试卷一、选择题 (共 6 小题，每题 2 分，满分12 分)1．(2 分)计算 (﹣1)×(﹣2)的结果是 ()A ．2B ．1C．﹣ 2D．﹣ 32． (2 分 )如图是由4 个同样的小正方体构成的立体图形，它的主视图是()A ．B ．C．D．3． (2 分 )以下计算结果为a6的是 ()A ．a2?a3B ．a12÷a2C． (a2 )3D． (﹣ a2) 34． (2 分 )如图，将木条a，b 与 c 钉在一同，∠1=70°，∠2=50°，要使木条 a 与 b 平行，木条 a 旋转的度数起码是()A．10°B．20°C． 50°D． 70°5． (2 分 )如图，将△ABC 折叠，使点 A 与 BC 边中点 D 重合，折痕为MN，若 AB=9，BC=6，则△DNB 的周长为 ()A．12B．13C． 14D． 156． (2 分 )我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡 x 只，兔 y 只，可列方程组为 ()A ．B ．C．D．二、填空题 (共 8 小题，每题 3 分，满分24 分)7．(3 分)计算：=．8． (3 分 )买单价 3 元的圆珠笔 m 支，对付元．9． (3 分 )若 a+b=4，ab=1，则 a2b+ab2=．10． (3 分 )若对于 x 的一元二次方程 x2+2x﹣m=0 有两个相等的实数根，则m 的值为．word 文档可编写——11． (3 分 )如图，在平面直角坐标系中，A(4，0)， B(0，3)，以点 A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C，则点C坐标为．12． (3 分 )如图是丈量河宽的表示图，AE 与 BC 订交于点 D ，∠ B= ∠C=90°，测得 BD=120m，DC=60m，EC=50m，求得河宽AB =m．13． (3 分 )如图， A，B，C， D 是⊙ O 上的四个点，=，若∠AOB=58°，则∠ BDC=度．14． (3 分 )我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特点值”，记作k，若k=，则该等腰三角形的顶角为度．三、解答题 (共 12 小题，满分84 分 )15． (5 分 )某同学化简a(a+2b)﹣ (a+b)(a﹣b)出现了错误，解答过程以下：原式 =a2+2ab﹣ (a2﹣ b2) ( 第一步 )=a2+2ab﹣ a2﹣b2(第二步 )=2ab﹣ b2 (第三步 )(1)该同学解答过程从第步开始犯错，错误原由是；(2)写出本题正确的解答过程．16． (5 分 )如图，在正方形ABCD 中，点 E，F 分别在 BC， CD 上，且 BE=CF ，求证：△ABE≌△ BCF ．17．(5 分 )一个不透明的口袋中有三个小球，上边分别标有字母 A ，B，C，除所标字母不一样外，其余完整同样，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图( 或列表 )的方法，求该同学两次摸出的小球所标字母相同的概率．18． (5 分 )在平面直角坐标系中，反比率函数y= ( k≠0)图象与一次函数y=x+2 图象的一个交点为P，且点 P 的横坐标为1，求该反比率函数的分析式．19． (7 分 )如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．依据以上信息，解答以下问题．(1)冰冰同学所列方程中的x 表示，庆庆同学所列方程中的y 表示；(2)两个方程中任选一个，并写出它的等量关系；(3)解 (2)中你所选择的方程，并回答老师提出的问题．20．(7 分 )如图是由边长为 1 的小正方形构成的 8×4 网格，每个小正方形的极点叫做格点，点A，B，C，D 均在格点上，在网格中将点 D 按以下步骤挪动：第一步：点 D 绕点 A 顺时针旋转180 °获得点 D1；第二步：点 D 1绕点 B 顺时针旋转90°获得点 D2；第三步：点 D 2绕点 C 顺时针旋转90°回到点 D．(1)请用圆规画出点D→D1→D2→ D 经过的路径；(2)所绘图形是对称图形；(3)求所绘图形的周长( 结果保存π)．21．(7 分 )数学活动小组的同学为丈量旗杆高度，先拟订了以下丈量方案，使用工具是测角仪和皮尺，请帮助组长林平达成方案内容，用含a，b，α的代数式表示旗杆AB 的高度．数学活动方案活动时间： 2018 年 4 月 2 日活动地址：学校操场填表人：林平活动目的运用所学数学知识及方法解决实质问题方案表示图丈量步骤(1)用测得∠ADE =α；(2)用测得BC=a 米，CD =b米．计算过程22． (7 分 )为了检查甲、乙两台包装机分装标准质量为400g 奶粉的状况，质检员进行了抽样检查，过程以下，请补全表一、表二中的空白，并回答提出的问题．采集数据：从甲、乙包装机分装的奶粉中各自随机抽取10 袋，测得实质质量( 单位： g) 以下：甲： 400 ，400，408， 406， 410，409，400， 393， 394，395乙： 403 ，404，396， 399， 402，402，405， 397， 402，398整理数据：表一质量 ( g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜ 408408≤x＜411频数种类甲30013乙0150剖析数据：表二种类均匀数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装状况比较好的是(填甲或乙 )，说明你的原由．23．(8 分 )小玲和弟弟小东分别从家和图书室同时出发，沿同一条路相向而行，小玲开始跑步半途改为步行，抵达图书室恰巧用 30min．小东骑自行车以300m/min 的速度直接回家，两人离家的行程y(m)与各自走开出发地的时间x(min)之间的函数图象以下图(1)家与图书室之间的行程为m，小玲步行的速度为m/min；(2)求小东离家的行程y 对于 x 的函数分析式，并写出自变量的取值范围；(3)求两人相遇的时间．24．(8 分 )如图①，在△ABC 中， AB=AC，过 AB 上一点 D 作 DE ∥ AC 交 BC 于点 E，以 E 为极点， ED 为一边，作∠DEF =∠A，另一边 EF 交 AC 于点 F．(1)求证：四边形 ADEF 为平行四边形；(2)当点 D 为 AB 中点时， ? ADEF 的形状为；(3)延伸图①中的 DE 到点 G，使 EG=DE ，连结 AE，AG， FG ，获得图②，若 AD=AG，判断四边形AEGF 的形状，并说明理由．25． (10 分 )如图，在矩形ABCD 中， AB=2cm，∠ ADB=30°．P ，Q 两点分别从A， B 同时出发，点P 沿折线 AB﹣BC 运动，在 AB 上的速度是2cm/s，在 BC 上的速度是 2 cm/s；点 Q 在 BD 上以 2cm/s 的速度向终点 D 运动，过点P 作 PN⊥ AD ，垂足为点 N．连结 PQ，以 PQ，PN 为邻边作 ?PQMN ．设运动的时间为x(s) ，? PQMN 与矩形 ABCD 重叠部分的图形面积为y(cm2)(1)当 PQ⊥ AB 时， x=；(2)求 y 对于 x 的函数分析式，并写出x 的取值范围；(3)直线 AM 将矩形 ABCD 的面积分红1：3 两部分时，直接写出x 的值．word 文档可编写——26．(10分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜ 0)与 x 轴订交于A，B 两点，与 y 轴订交于点C，极点为 D ，直线DC 与 x 轴订交于点E．(1)当a= ﹣1 时，抛物线极点 D 的坐标为，OE=；(2)O E 的长能否与 a 值相关，说明你的原由；(3)设∠DEO =β， 45°≤β≤，60求°a 的取值范围；(4)以 DE 为斜边，在直线 DE 的左下方作等腰直角三角形 PDE．设 P(m，n) ，直接写出 n 对于 m 的函数分析式及自变量 m 的取值范围．2018 年吉林省中考数学试卷参照答案与试题分析一、选择题(共 6 小题，每题 2 分，满分12 分)1． (2 分 )计算 ( ﹣1) ×(﹣2)的结果是 ()A．2 B．1 C．﹣ 2D．﹣ 3【剖析】依据“两数相乘，同号得正”即可求出结论．【解答】解： ( ﹣1) ×(﹣2)=2 ．应选： A．2． (2 分 )如图是由4 个同样的小正方体构成的立体图形，它的主视图是()A．B．C．D．【剖析】找到从正面看所获得的图形即可，注意全部的看到的棱都应表此刻主视图中．【解答】解：从正面看易得第一层有 3 个正方形，第二层最右侧有一个正方形．应选： B．3． (2 分 )以下计算结果为a6的是 ()A ．a2?a3B ．a12÷a2 C． (a2)3D ． (﹣ a2)3【剖析】分别依据同底数幂相乘、同底数幂相除、幂的乘方的运算法例逐个计算可得．【解答】解： A 、a2?a3=a5，此选项不切合题意；B、a12÷a2=a10，此选项不切合题意；C、 (a2)3 =a6，此选项切合题意；D 、 (﹣ a2)3 =﹣ a6，此选项不切合题意；应选： C．4． (2 分 )如图，将木条a，b 与 c 钉在一同，∠1=70°，∠ 2=50°，要使木条a 与 b 平行，木条 a 旋转的度数起码是()A．10°B．20°C． 50°D． 70°【剖析】依据同位角相等两直线平行，求出旋转后∠ 2 的同位角的度数，而后用∠1减去即可获得木条 a 旋转的度数．【解答】解：如图．∵∠ AOC= ∠2=50°时， OA∥b，∴要使木条 a 与 b 平行，木条 a 旋转的度数起码是70°﹣50°=20°．应选： B．5． (2 分 )如图，将△ABC 折叠，使点 A 与 BC 边中点 D 重合，折痕为MN，若 AB=9，BC=6，则△DNB 的周长为 ()A．12B．13C． 14D． 15【剖析】由 D 为 BC 中点知 BD =3，再由折叠性质得ND=NA，进而依据△DNB 的周长=ND +NB+BD=NA+NB+BD =AB +BD可得答案．【解答】解：∵ D 为 BC 的中点，且BC=6，∴BD = BC=3，由折叠性质知 NA=ND，则△DNB 的周长 =ND+NB+BD =NA+NB+BD=AB+BD=3+9=12 ，应选： A．6． (2 分 )我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为()A ．B ．C．D．【剖析】依据题意能够列出相应的方程组，进而能够解答本题．【解答】解：由题意可得，，应选： D．二、填空题 (共 8小题，每题 3 分，满分24 分)7． (3 分 )计算：= 4 ．【剖析】依据算术平方根的观点去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵ 42=16，∴=4，故答案为 4．8． (3 分 )买单价 3 元的圆珠笔m 支，对付3m元．【剖析】依据总价= 单价×数目列出代数式．【解答】解：依题意得：3m．故答案是： 3m．9． (3 分 )若 a+b=4，ab=1，则 a2b+ab2= 4．【剖析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵ a+b=4， ab=1，∴a2b+ab2=ab(a+b) =1×4=4．故答案为： 4．10． (3 分 )若对于【剖析】因为对于x 的一元二次方程x 的一元二次方程x2+2x﹣m=0 有两个相等的实数根，则m 的值为2x +2x﹣m=0 有两个相等的实数根，可知其鉴别式为﹣ 1．0，据此列出对于m 的不等式，解答即可．【解答】解：∵ 对于x 的一元二次方程x2+2x﹣ m=0 有两个相等的实数根，∴△ =b2﹣ 4ac=0，2解得： m=﹣ 1，应选答案为﹣ 1．11． (3 分 )如图，在平面直角坐标系中，A(4，0)， B(0，3)，以点 A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C，则点C 坐标为(﹣ 1，0)．【剖析】求出OA、OB，依据勾股定理求出AB，即可得出AC，求出 OC 长即可．【解答】解：∵点 A， B 的坐标分别为 (4， 0)， (0，3) ，∴OA=4， OB=3，在 Rt△AOB 中，由勾股定理得： AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点 C 的坐标为 ( ﹣1， 0)，故答案为： (﹣ 1，0) ，12． (3 分 )如图是丈量河宽的表示图， AE 与 BC 订交于点 D ，∠ B= ∠C=90°，测得 BD=120m，DC=60m，EC=50m，求得河宽 AB = 100 m．【剖析】由两角对应相等可得△BAD∽△ CED ，利用对应边成比率可得两岸间的大概距离AB．【解答】解：∵∠ ADB =∠ EDC ，∠ ABC= ∠ECD=90 °，∴△ ABD ∽△ ECD ，∴，，解得： AB=(米 )．故答案为： 100．13． (3 分 )如图， A，B，C， D 是⊙ O 上的四个点，= ，若∠AOB=58°，则∠ BDC=29 度．【剖析】依据∠ BDC= ∠BOC 求解即可；【解答】解：连结OC．∵= ，∴∠ AOB=∠ BOC=58°，∴∠ BDC= ∠ BOC=29°，故答案为29．14． (3分 )我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特点值”，记作k，若k=，则该等腰三角形的顶角为36度．【剖析】依据等腰三角形的性质得出∠ B=∠C，依据三角形内角和定理和已知得出5∠A=180，°求出即可．【解答】解：∵△ ABC 中， AB =AC，∴∠ B=∠ C，“特点值”，记作k，若k=，∵ 等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的∴∠ A：∠ B=1： 2，即 5∠ A=180 ，°∴∠ A=36°，故答案为： 36．三、解答题 (共 12 小题，满分84 分 )15． (5 分 )某同学化简a(a+2b)﹣ (a+b)(a﹣b)出现了错误，解答过程以下：222=a2+2ab﹣ a2﹣b2(第二步 )=2ab﹣ b2 (第三步 )(1)该同学解答过程从第二步开始犯错，错误原由是去括号时没有变号；(2)写出本题正确的解答过程．【剖析】先计算乘法，而后计算减法．【解答】解： (1)该同学解答过程从第二步开始犯错，错误原由是去括号时没有变号；故答案是：二；去括号时没有变号；(2)原式 =a2+2ab﹣(a2﹣ b2 )=a2+2ab﹣ a2 +b2=2ab+b2．16． (5 分 )如图，在正方形ABCD 中，点 E，F 分别在 BC， CD 上，且 BE=CF ，求证：△ABE≌△ BCF ．【剖析】依据正方形的性质，利用SAS 即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE= ∠BCF =90°，在△ABE 和△BCF 中，，∴△ ABE≌△ BCF ．17．(5 分 )一个不透明的口袋中有三个小球，上边分别标有字母A ，B，C，除所标字母不一样外，其余完整同样，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图 ( 或列表 )的方法，求该同学两次摸出的小球所标字母相同的概率．【剖析】列表得出全部等可能的状况数，再找出两次摸出的小球所标字母同样的状况数，即可求出其概率．【解答】解：列表得：A B CA(A，A)(B，A)(C，A)B(A，B)(B，B)(C，B)C(A，C)(B， C)( C，C)由列表可知可能出现的结果共9 种，此中两次摸出的小球所标字母同样的状况数有 3 种，因此该同学两次摸出的小球所标字母同样的概率= = ．18． (5 分 )在平面直角坐标系中，反比率函数y= ( k≠0)图象与一次函数y=x+2 图象的一个交点为P，且点 P 的横坐标为1，求该反比率函数的分析式．【剖析】先求出P 点的坐标，再把P 点的坐标代入反比率函数的分析式，即可求出答案．【解答】解：∵把 x=1 代入 y=x+2 得： y=3，即 P 点的坐标是 (1，3)，把 P 点的坐标代入 y= 得： k=3 ，即反比率函数的分析式是 y= ．19． (7 分 )如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．依据以上信息，解答以下问题．(1)冰冰同学所列方程中的x 表示甲队每日修路的长度，庆庆同学所列方程中的y 表示甲队修路400 米所需时间或乙队修路600 米所需时间；(2)两个方程中任选一个，并写出它的等量关系；(3)解 (2)中你所选择的方程，并回答老师提出的问题．【剖析】 (1)依据两人的方程思路，可得出： x 表示甲队每日修路的长度； y 表示甲队修路 400 米所需时间或乙队修路 600 米所需时间；(2)依据题意，可找出：(冰冰 )甲队修路 400 米所用时间 =乙队修路600 米所用时间； ( 庆庆 )乙队每日修路的长度﹣甲队每日修路的长度 =20 米；(3)选择两个方程中的一个，解之即可得出结论．【解答】解： (1)∵冰冰是依据时间相等列出的分式方程，∴ x 表示甲队每日修路的长度；∵ 庆庆是依据乙队每日比甲队多修20 米列出的分式方程，∴ y 表示甲队修路400 米所需时间或乙队修路600 米所需时间．故答案为：甲队每日修路的长度；甲队修路400 米所需时间或乙队修路600 米所需时间．(2)冰冰用的等量关系是：甲队修路400 米所用时间=乙队修路600 米所用时间；庆庆用的等量关系是：乙队每日修路的长度﹣甲队每日修路的长度=20 米(选择一个即可)．(3)选冰冰的方程：=，去分母，得： 400x+8000=600x，移项， x 的系数化为1，得： x=40 ，查验：当x=40 时， x、 x+20 均不为零，∴x=40．答：甲队每日修路的长度为 40 米．选庆庆的方程：﹣=20，去分母，得： 600 ﹣400=20y，将 y 的系数化为1，得：y=10，经验：当0，y=10 时，分母 y 不为∴ y=10，∴=40．答：甲队每日修路的长度为40 米．20．(7 分 )如图是由边长为 1 的小正方形构成的8×4 网格，每个小正方形的极点叫做格点，点A，B，C，D 均在格点上，在网格中将点 D 按以下步骤挪动：第一步：点 D 绕点 A 顺时针旋转180 °获得点 D1；第二步：点 D 1绕点 B 顺时针旋转90 °获得点 D2；第三步：点 D 2绕点 C 顺时针旋转90 °回到点 D．(1)请用圆规画出点D→D 1→D 2→ D 经过的路径；(2)所绘图形是轴对称对称图形；(3)求所绘图形的周长( 结果保存π)．【剖析】 (1)利用旋转变换的性质画出图象即可；(2)依据轴对称图形的定义即可判断；(3)利用弧长公式计算即可；【解答】解： (1)点 D→D 1→D 2→ D 经过的路径以下图：(2)察看图象可知图象是轴对称图形，故答案为轴对称．(3)周长 =4×=8π．21．(7 分 )数学活动小组的同学为丈量旗杆高度，先拟订了以下丈量方案，使用工具是测角仪和皮尺，请帮助组长林平达成方案内容，用含a，b，α的代数式表示旗杆AB 的高度．数学活动方案活动时间： 2018 年 4 月 2 日活动地址：学校操场填表人：林平课题丈量学校旗杆的高度活动目的运用所学数学知识及方法解决实质问题方案表示图测 (1)用测角量仪测得∠步ADE=α；骤(2)用皮尺测得BC=a 米，CD=b 米．计算过程【剖析】在Rt△ADE 中，求出 AE ，再利用 AB=AE+BE 计算即可；【解答】解： (1)用测角仪测得∠ADE =α；(2)用皮尺测得BC=a 米， CD=b 米．(3)计算过程：∵四边形 BCDE 是矩形，∴DE =BC=a， BE=CD=b，在 Rt△ADE 中， AE=ED?tanα=a?tanα，∴ AB=AE+EB=a?tanα+b．22． (7 分 )为了检查甲、乙两台包装机分装标准质量为400g 奶粉的状况，质检员进行了抽样检查，过程以下，请补全表一、表二中的空白，并回答提出的问题．采集数据：从甲、乙包装机分装的奶粉中各自随机抽取10 袋，测得实质质量( 单位： g) 以下：甲： 400 ，400，408， 406， 410，409，400， 393， 394，395乙： 403 ，404，396， 399， 402，402，405， 397， 402，398整理数据：表一质量 ( g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜ 408408≤x＜411频数种类甲303013乙031510剖析数据：表二种类均匀数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：包装机分装状况比较好的是乙(填甲或乙 ) ，说明你的原由．【剖析】整理数据：由题干中的数据联合表中范围确立个数即可得；剖析数据：依据众数和中位数的定义求解可得；得出结论：依据方差的意义，方差小分装质量较为稳固即可得．【解答】解：整理数据：表一质量 ( g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜ 408408≤x＜411频数种类甲303013乙031510剖析数据：将甲组数据从头摆列为：393、 394、 395、400、400、 400、 406、408 、409、410，∴甲组数据的中位数为400；乙组数据中402 出现次数最多，有 3 次，∴乙组数据的众数为402 ；表二种类均匀数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳固，因此包装机分装状况比较好的是乙．故答案为：乙．23．(8 分 )小玲和弟弟小东分别从家和图书室同时出发，沿同一条路相向而行，小玲开始跑步半途改为步行，抵达图书室恰巧用 30min．小东骑自行车以300m/min 的速度直接回家，两人离家的行程y(m)与各自走开出发地的时间x(min)之间的函数图象以下图(1)家与图书室之间的行程为4000 m，小玲步行的速度为100 m/min；(2)求小东离家的行程 y 对于 x 的函数分析式，并写出自变量的取值范围；(3)求两人相遇的时间．【剖析】 (1)仔细剖析图象获得行程与速度数据；(2)采纳方程思想列出小东离家行程y 与时间 x 之间的函数关系式；(3)两人相遇其实是函数图象求交点．【解答】解： (1)联合题意和图象可知，线段CD 为小东行程与时间函数图象，折线O﹣ A﹣ B 为小玲行程与时间图象则家与图书室之间行程为4000m，小玲步行速度为 2000 ÷20=100m/s故答案为： 4000， 100(2)∵小东从离家 4000m 处以 300m/min 的速度返回家，则xmin 时，∴他离家的行程 y=4000﹣300x自变量 x 的范围为 0 ≤x≤(3)由图象可知，两人相遇是在小玲改变速度以前∴4000﹣ 300x=200x解得 x=8∴两人相遇时间为第8 分钟．24．(8 分 )如图①，在△ABC 中， AB=AC，过 AB 上一点 D 作 DE ∥ AC 交 BC 于点 E，以 E 为极点， ED 为一边，作∠DEF =∠ A，另一边 EF 交 AC 于点 F．(1)求证：四边形 ADEF 为平行四边形；(2)当点 D 为 AB 中点时， ? ADEF 的形状为菱形；(3)延伸图①中的 DE 到点 G，使 EG=DE ，连结 AE，AG， FG ，获得图②，若 AD=AG，判断四边形AEGF 的形状，并说明理由．【剖析】 (1)依据平行线的性质获得∠BDE =∠ A，依据题意获得∠ DEF =∠BDE，依据平行线的判断定理获得AD ∥ EF，依据平行四边形的判断定理证明；(2)依据三角形中位线定理获得DE= AC，获得AD =DE，依据菱形的判断定理证明；(3)依据等腰三角形的性质获得AE⊥ EG，依占有一个角是直角的平行四边形是矩形证明．【解答】 (1)证明：∵DE ∥ AC，∴∠ BDE =∠ A，∵∠ DEF =∠ A，∴∠ DEF =∠ BDE，∴AD ∥EF，又∵DE∥ AC，∴四边形 ADEF 为平行四边形；(2)解： ? ADEF 的形状为菱形，原由以下：∵点 D 为 AB 中点，∴AD = AB，∵DE ∥AC，点 D 为 AB 中点，∴DE = AC，∵ AB=AC，∴AD =DE，∴平行四边形 ADEF 为菱形，故答案为：菱形；(3)四边形 AEGF 是矩形，原由以下：由 (1)得，四边形ADEF 为平行四边形，∴AF∥ DE，AF=DE，∵ EG=DE，∴AF∥ DE，AF=GE，∴四边形 AEGF 是平行四边形，∵ AD =AG， EG=DE ，∴AE⊥ EG，∴四边形 AEGF 是矩形．25． (10 分 )如图，在矩形ABCD 中， AB=2cm，∠ ADB=30°．P ，Q 两点分别从A， B 同时出发，点P 沿折线 AB﹣BC 运动，在 AB 上的速度是2cm/s，在 BC 上的速度是 2 cm/s；点 Q 在 BD 上以 2cm/s 的速度向终点 D 运动，过点P 作 PN⊥ AD ，垂足为点 N．连结 PQ，以 PQ，PN 为邻边作 ?PQMN ．设运动的时间为x(s) ，? PQMN 与矩形 ABCD 重叠部分的图形面积为y(cm2)(1)当 PQ⊥ AB 时， x=s ；(2)求 y 对于 x 的函数分析式，并写出x 的取值范围；(3)直线 AM 将矩形 ABCD 的面积分红1：3 两部分时，直接写出x 的值．【剖析】 (1)当 PQ⊥ AB 时， BQ=2PB，由此建立方程即可解决问题；(2)分三种情况分别求解即可解决问题；(3)分两种情况分别求解即可解决问题；【解答】解： (1)当 PQ⊥ AB 时， BQ=2PB，∴2x=2(2﹣ 2x)，∴x= s．故答案为 s．(2)①如图 1 中，当 0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y= (2﹣x+2tx×x= x2+ x③如图 3 中，当 1＜ x＜2 时，重叠部分是四边形PNEQ．y= (2﹣x+2) ×[ x﹣2 ( x﹣1)]= x2﹣ 3 x+4；综上所述， y=．(3)①如图 4 中，当直线AM 经过 BC 中点 E 时，知足条件．则有： tan∠ EAB=tan∠ QPB，∴=，解得 x= ．②如图 5 中，当直线AM 经过 CD 的中点 E 时，知足条件．此时tan∠ DEA=tan ∠QPB，∴=，解得x=，综上所述，当x=或时，直线AM 将矩形ABCD的面积分红1： 3 两部分．26．(10 分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x轴订交于A，B 两点，与 y 轴订交于点C，极点为 D ，直线 DC 与 x 轴订交于点E．(1)当 a= ﹣1 时，抛物线极点 D 的坐标为(﹣ 1， 4)，OE=3；(2)O E 的长能否与 a 值相关，说明你的原由；(3)设∠DEO =β， 45°≤β≤，60求°a 的取值范围；(4)以 DE 为斜边，在直线 DE 的左下方作等腰直角三角形 PDE．设 P(m，n) ，直接写出 n 对于 m 的函数分析式及自变量 m 的取值范围．【剖析】 (1)求出直线CD 的分析式即可解决问题；(2)利用参数a，求出直线CD 的分析式求出点 E 坐标即可判断；(3)求出落在特别情况下的 a 的值即可判断；(4)如图，作PM⊥对称轴于 M， PN⊥AB 于 N．两条全等三角形的性质即可解决问题；y=﹣x2﹣2x+3，【解答】解： (1)当 a= ﹣1 时，抛物线的分析式为∴极点 D(﹣ 1，4)，C(0， 3)，∴直线 CD 的分析式为y=﹣x+3，∴ E(3， 0)，∴ OE=3，故答案为 ( ﹣1， 4)， 3．(2)结论： OE 的长与 a 值没关．原由：∵y=ax2+2ax﹣ 3a，∴C(0，﹣ 3a)， D(﹣1，﹣ 4a)，∴直线 CD 的分析式为 y=ax﹣3a，当 y=0 时， x=3，∴ E(3， 0)，∴ OE=3，∴ OE 的长与 a 值没关．(3)当β =45时°， OC=OE=3，∴ ﹣3a=3，∴ a=﹣ 1，OE=3，当β =60时°，在 Rt△OCE 中， OC=∴ ﹣3a=3，∴a=﹣，∴45°≤β≤，60a°的取值范围为﹣≤a≤﹣1．(4)如图，作PM⊥对称轴于 M， PN⊥AB 于 N．word 文档可编写——∵PD =PE，∠ PMD = ∠PNE=90°，∠DPE =∠MPN=90°，∴∠ DPM =∠ EPN，∴△ DPM ≌△ EPN，∴ PM=PN， DM =EN，∵D(﹣ 1，﹣ 4a)，E(3 ，0)，∴EN=4+n=3﹣ m，∴n=﹣ m﹣ 1，当极点 D 在 x 轴上时， P(1，﹣ 2)，此时 m 的值 1，∵ 抛物线的极点在第二象限，∴m＜1．∴n=﹣ m﹣ 1(m＜ 1)．。

2018年吉林省中考数学试卷参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：（﹣1）×（﹣2）=2．故选：A．【点评】本题考查了有理数的乘法，牢记“两数相乘，同号得正，异号得负，并把绝对值相乘”是解题的关键．2．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（2.00分）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．【点评】本题主要考查幂的运算，解题的关键是掌握同底数幂相乘、同底数幂相除、幂的乘方的运算法则．4．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a 与b平行，木条a旋转的度数至少是（）A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．【点评】本题考查了旋转的性质，平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【分析】由D为BC中点知BD=3，再由折叠性质得ND=NA，从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案．【解答】解：∵D为BC的中点，且BC=6，∴BD=BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12，故选：A．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．【分析】根据题意可以列出相应的方程组，从而可以解答本题．【解答】解：由题意可得，，故选：D．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：=4．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16，∴=4，故答案为4．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．8．（3.00分）买单价3元的圆珠笔m支，应付3m元．【分析】根据总价=单价×数量列出代数式．【解答】解：依题意得：3m．故答案是：3m．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．9．（3.00分）若a+b=4，ab=1，则a2b+ab2=4．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m 的值为﹣1．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．【点评】本题考查了根的判别式，解题的关键是了解根的判别式如何决定一元二次方程根的情况．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），【点评】本题考查了勾股定理和坐标与图形性质的应用，解此题的关键是求出OC的长，注意：在直角三角形中，两直角边的平方和等于斜边的平方．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴，，解得：AB=（米）．故答案为：100．【点评】此题主要考查了相似三角形的应用；用到的知识点为：两角对应相等的两三角形相似；相似三角形的对应边成比例．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC=29度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接OC．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=∠BOC=29°，故答案为29．【点评】本题考查圆周角定理，圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为36度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC中，AB=AC，∴∠B=∠C，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．【点评】本题考查了三角形内角和定理和等腰三角形的性质，能根据等腰三角形性质、三角形内角和定理和已知得出5∠A=180°是解此题的关键．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a2+2ab﹣（a2﹣b2）=a2+2ab﹣a2+b2=2ab+b2．【点评】考查了平方差公式和实数的运算，去括号规律：①a+（b+c）=a+b+c，括号前是“+”号，去括号时连同它前面的“+”号一起去掉，括号内各项不变号；②a﹣（b﹣c）=a﹣b+c，括号前是“﹣”号，去括号时连同它前面的“﹣”号一起去掉，括号内各项都要变号．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．【分析】根据正方形的性质，利用SAS即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，在△ABE和△BCF中，，∴△ABE≌△BCF．【点评】本题考查正方形的性质全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．【解答】解：列表得：由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率==．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【分析】先求出P点的坐标，再把P点的坐标代入反比例函数的解析式，即可求出答案．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=．【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征，能求出P点的坐标是解此题的关键．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【分析】（1）根据两人的方程思路，可得出：x表示甲队每天修路的长度；y表示甲队修路400米所需时间；（2）根据题意，可找出：（冰冰）甲队修路400米所用时间=乙队修路600米所用时间；（庆庆）乙队每天修路的长度﹣甲队每天修路的长度=20米；（3）选择两个方程中的一个，解之即可得出结论．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：=，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．选庆庆的方程：﹣=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，∴=40．答：甲队每天修路的长度为40米．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【分析】（1）利用旋转变换的性质画出图象即可；（2）根据轴对称图形的定义即可判断；（3）利用弧长公式计算即可；【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×=8π．【点评】本题考查作图﹣旋转变换，弧长公式、轴对称图形等知识，解题的关键是理解题意，正确画出图形，属于中考常考题型．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平【分析】在Rt△ADE中，求出AE，再利用AB=AE+BE计算即可；【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．（3）计算过程：∵四边形BCDE是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一分析数据：表二得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．【点评】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义及数据的整理是解题的关键．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x （min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000m，小玲步行的速度为200m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【分析】（1）认真分析图象得到路程与速度数据；（2）采用方程思想列出小东离家路程y与时间x之间的函数关系式；（3）两人相遇实际上是函数图象求交点．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷10=200m/s故答案为：4000，200（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．【点评】本题是一次函数实际应用问题，考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC 于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【分析】（1）根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到DE=AC，得到AD=DE，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．【点评】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=s；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．【分析】（1）当PQ⊥AB时，BQ=2PB，由此构建方程即可解决问题；（2）分三种情形分别求解即可解决问题；（3）分两种情形分别求解即可解决问题；【解答】解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=s或时，直线AM将矩形ABCD的面积分成1：3两部分．【点评】本题考查四边形综合题、矩形的性质平行四边形的性质、锐角三角函数、解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，学会用方程的思想解决问题，属于中考压轴题．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为（﹣1，4），OE=3；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n关于m的函数解析式及自变量m的取值范围．【分析】（1）求出直线CD的解析式即可解决问题；（2）利用参数a，求出直线CD的解析式求出点E坐标即可判断；（3）求出落在特殊情形下的a的值即可判断；（4）如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D（﹣1，4），C（0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=OE=3，∴﹣3a=3，∴a=﹣，∴45°≤β≤60°，a的取值范围为﹣≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，PM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．【点评】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

2018年吉林省初中毕业、升学考试数学（满分120分，考试时间120分钟）一．单项选择题（每小题2分，共12分）1．（2018吉林省，1, 2分）计算（﹣1）×（﹣2）的结果是（ ） A ．2B ．1C ．﹣2D ．﹣3【答案】A【解析】根据“两数相乘，同号得正”即可求出（﹣1）×（﹣2）=2．故选A ． 【知识点】有理数的乘法2．（2018吉林省，2, 2分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（ ）A ．B ．C ．D ．【答案】B【解析】从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B ． 【知识点】三视图3．（2018吉林省，3, 2分）下列计算结果为6a 的是（ ）A. 23a a •B. 122a a ÷ C. 23()a D. 23()a -【答案】C【解析】分别根据同底数幂相乘, 同底数幂相除,幂的乘方逐一计算即可判断．23236()a aa ⨯==,故选C.【知识点】幂的乘方、同底数幂乘除．4. （2018吉林省，4, 2分）如图，将木条a,b 与c 钉在一起，∠1=70°，∠2=50°. 要使木条a 与b 平行，木条a 旋转的度数至少是（ ）A. 10°B. 20°C. 50°D. 70°【答案】B【解析】由两直线平行，同位角相等，旋转变化后为∠1=50°，所以木条a旋转的度数为70°-50°=20°，故选B.【知识点】平行线的性质5．（2018吉林省，5, 2分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【答案】A【解析】∵D为BC的中点，且BC=6，∴BD=12BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12．【知识点】翻折变换的性质：6．（2018吉林省，6, 2分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．352294x yx y+=⎧⎨+=⎩B．354294x yx y+=⎧⎨+=⎩C．354494x yx y+=⎧⎨+=⎩D．352494x yx y+=⎧⎨+=⎩【答案】D【解析】根据题意可以列出相应的方程组，从而可以解答本题,故选：D．【知识点】由实际问题抽象出二元一次方程组．二．填空题（每小题3分，共24分）7．（2018吉林省，7, 216=4．【答案】4【解析】161616故答案为4．【知识点】算术平方根】8. （2018吉林省，8, 2分）买单价3元的圆珠笔m 支，应付______元 【答案】3m【解析】金额=单价×数量这一数量关系容易得出应付3m 元 【知识点】列代数式9．（2018吉林省，9, 2分）若a +b=4，ab=1，则22a b ab += 4 ． 【答案】4【解析】：∵a +b=4，ab=1， ∴22a b ab +2=ab （a +b ）=1×4=4． 【知识点】提取公因式法分解因式．10．（2018吉林省，10, 2分）若关于x 的一元二次方程220x x m +-=有两个相等的实数根，则m 的值为 ﹣1 ． 【答案】B 【解析】方程有两个相等的实数根，可知其判别式为0，据此列出关于m 的不等式，所以∆=0，即2²-4×1×（-m ）=0，解得m=-1.【知识点】根的判别式11. （2018吉林省，11, 2分）如图，在平面直角坐标系中，A(4，0),B(0，3),以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C ，则点C 坐标为__________【答案】（-1,0）【解析】由题意知，OA=4,OB=3,∴AC=AB=5，则OC=1. 则点C 坐标为（-1,0） 【知识点】尺规作图，实数与数轴的一一对应关系12．（2018吉林省，12, 2分）如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B=∠C=90°，测得BD=120m ，DC=60m ，EC=50m ，求得河宽AB= 100 m ．【答案】100【解析】两角对应相等可得△BAD ∽△CED ，利用对应边成比例可得两岸间的大致距离AB ．易证△ABD∽△ECD，∴AB BDEC CD=，即1205060AB=，∴AB=100.【知识点】相似三角形的应用13．（2018吉林省，13, 2分）如图，A，B，C，D是⊙O上的四个点，=⌒BC，，若∠AOB=58°，则∠BDC=___度．【答案】29【解析】连接CO，根据同圆中，等弧所对圆心角相等，则∠COB=∠AOB=58°，∴∠BDC=29°【知识点】圆周角定理，圆心角、弧、弦之间的关系14．（2018吉林省，14, 2分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=12，则该等腰三角形的顶角为度．【答案】36【解析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．设顶角为α，则其底角为1-2α︒（180），由k=12，可得1-2α︒（180）=2α，解出α=36°。

2018年吉林省中考数学试卷—-选择题（共6小题，每小题2分，满分12分）1 . （2分）计算（-1） X （ - 2）的结果是（）A. 2B. 1C. - 2D. - 32 . （2分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A. B- C- D3. （2分）下列计算结果为a6的是（）A . a ?aB • a * aC < a ）D- （ - a）4 . （2分）如图，将木条a, b与c钉在一起，/仁70。

,/ 2=50。

,要使木条a与b平行，木条a旋转的度数至少是（）A . 10°B • 20° C. 50° D 70°5 . （2分）如图，将△ ABC折叠，使点A与BC边中点D重合，折痕为MN若AB=9，BC=6，则△ DNB勺周长为（）A . 12B • 13C 14D 156 . （2分）我国古代数学著作《孙子算经》中有"鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何.”设鸡x只「兔y只-可列方程组为（）x + y = 35 1 3(4v = 35 f J + y = 35[J < y = 35YA.[: + 2y - 94 B .4JC f 2y - 41 C.H K + 4y - 94 D.[2x + 4y・ 91二、填空题（共8小题•每小题3分•满分24分）7 . （3 分）计算：，$= _____ .8 . （3分）买单价3元的圆珠笔m支，应付__元.9 . （3 分）若a+b=4 - ab=1，则a2b+ab2=_ ,10 . （3分）若关于x的一元二次方程X2+2X- m=0有芮个相等的实数根•则m的值为 _________13.的四个点，眞，若/ AO 序（3分）我们规定：等腰&若心，则该等腰11. （3分）如图，在平面直角坐标系中，A （4 , 0） , B （0 , 3），以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C,则 点C 坐标为12 . （3分）如图是测量河宽的示意图，AE 与BC 相交于点D / B=Z C=90°，测得Bt=120m DC=60m EC=50m 求得河宽AB= m（3分）如图，A, B ，CD 是。

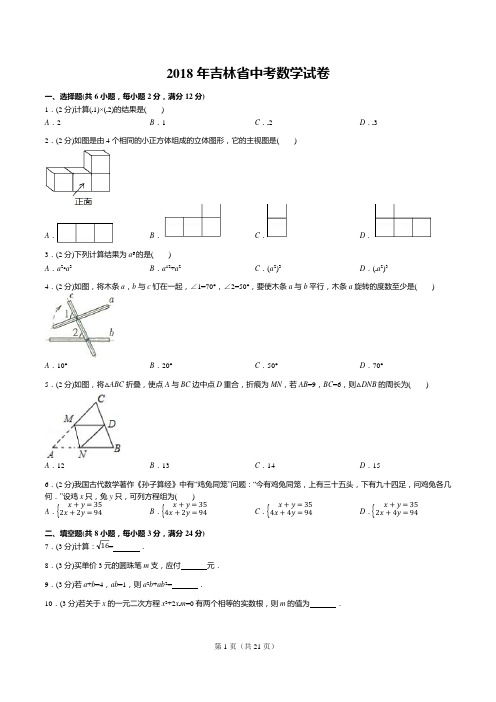
A ．{B ．{C ．{D ．{2018 年吉林省中考数学试卷一、选择题(共 6 小题，每小题 2 分，满分 12 分) 1．(2 分)计算(﹣1)×(﹣2)的结果是( ) A ．2B ．1C ．﹣2D ．﹣32．(2 分)如图是由 4 个相同的小正方体组成的立体图形，它的主视图是()A ．B ．C ．D ．3．(2 分)下列计算结果为 a 6 的是( )A ．a 2•a 3B ．a 12÷a 2C ．(a 2)3D ．(﹣a 2)34．(2 分)如图，将木条 a ，b 与 c 钉在一起，∠1=70°，∠2=50°，要使木条 a 与 b 平行，木条 a 旋转的度数至少是()A ．10°B ．20°C ．50°D ．70°5．(2 分)如图，将△ABC 折叠，使点 A 与 BC 边中点 D 重合，折痕为 MN ，若 AB =9，BC =6，则△DNB 的周长为()A ．12B ．13C ．14D ．156．(2 分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡 x 只，兔 y 只，可列方程组为( )x + y = 35 2x + 2y = 94 x + y = 354x + 2y = 94x + y = 354x + 4y = 94x + y = 352x + 4y = 94二、填空题(共 8 小题，每小题3 分，满分 24 分) 7．(3 分)计算： 16=．8．(3 分)买单价 3 元的圆珠笔 m 支，应付 元． 9．(3 分)若 a +b =4，ab =1，则 a 2b +ab 2=．10．(3 分)若关于 x 的一元二次方程 x 2+2x ﹣m =0 有两个相等的实数根，则 m 的值为．11．(3 分)如图，在平面直角坐标系中，A(4，0)，B(0，3)，以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C，则点C 坐标为．12．(3 分)如图是测量河宽的示意图，AE 与BC 相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB= m．13．(3 分)如图，A，B，C，D 是⊙O 上的四个点，AB=BC，若∠AOB=58°，则∠BDC= 度．114．(3 分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=2，则该等腰三角形的顶角为度．三、解答题(共12 小题，满分84 分)15．(5 分)某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误，解答过程如下：原式=a2+2ab﹣(a2﹣b2) (第一步)=a2+2ab﹣a2﹣b2(第二步)=2ab﹣b2 (第三步)(1)该同学解答过程从第步开始出错，错误原因是；(2)写出此题正确的解答过程．16．(5 分)如图，在正方形ABCD 中，点E，F 分别在BC，CD 上，且BE=CF，求证：△ABE≌△BCF．17．(5 分)一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．k18．(5 分)在平面直角坐标系中，反比例函数y=x(k≠0)图象与一次函数y=x+2 图象的一个交点为P，且点P 的横坐标为1，求该反比例函数的解析式．19．(7 分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示，庆庆同学所列方程中的y 表示；(2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．20．(7 分)如图是由边长为1 的小正方形组成的8×4 网格，每个小正方形的顶点叫做格点，点A，B，C，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D1；第二步：点D1绕点B 顺时针旋转90°得到点D2；第三步：点D2绕点C 顺时针旋转90°回到点D．(1)请用圆规画出点D→D1→D2→D 经过的路径；(2)所画图形是对称图形；(3)求所画图形的周长(结果保留π)．21．(7 分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α 的代数式表示旗杆AB 的高度．数学活动方案22．(7 分)为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10 袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：得出结论：包装机分装情况比较好的是(填甲或乙)，说明你的理由．23．(8 分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min 的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为m，小玲步行的速度为m/min；(2)求小东离家的路程y 关于x 的函数解析式，并写出自变量的取值范围；(3)求两人相遇的时间．24．(8 分)如图①，在△ABC 中，AB=AC，过AB 上一点D 作DE∥AC 交BC 于点E，以E 为顶点，ED 为一边，作∠DEF=∠A，另一边EF 交AC 于点F．(1)求证：四边形ADEF 为平行四边形；(2)当点D 为AB 中点时，▱ADEF 的形状为；(3)延长图①中的DE 到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF 的形状，并说明理由．25．(10 分)如图，在矩形ABCD 中，AB=2cm，∠ADB=30°．P，Q 两点分别从A，B 同时出发，点P 沿折线AB﹣BC 运动，在AB 上的速度是2cm/s，在BC 上的速度是2 3cm/s；点Q 在BD 上以2cm/s 的速度向终点D 运动，过点P 作PN⊥AD，垂足为点N．连接PQ，以PQ，PN 为邻边作▱PQMN．设运动的时间为x(s)，▱PQMN 与矩形ABCD 重叠部分的图形面积为y(cm2)(1)当PQ⊥AB 时，x= ；(2)求y 关于x 的函数解析式，并写出x 的取值范围；(3)直线AM 将矩形ABCD 的面积分成1：3 两部分时，直接写出x 的值．26．(10 分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x 轴相交于A，B 两点，与y 轴相交于点C，顶点为D，直线DC 与x 轴相交于点E．(1)当a=﹣1 时，抛物线顶点D 的坐标为，OE= ；(2)OE 的长是否与a 值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a 的取值范围；(4)以DE 为斜边，在直线DE 的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n 关于m 的函数解析式及自变量m 的取值范围．2018 年吉林省中考数学试卷参考答案与试题解析一、选择题(共6 小题，每小题2 分，满分12 分)1．(2 分)计算(﹣1)×(﹣2)的结果是( )A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：(﹣1)×(﹣2)=2．故选：A．2．(2 分)如图是由4 个相同的小正方体组成的立体图形，它的主视图是( )A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3 个正方形，第二层最右边有一个正方形．故选：B．3．(2 分)下列计算结果为a6 的是( )A．a2•a3 B．a12÷a2 C．(a2)3 D．(﹣a2)3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、(a2)3=a6，此选项符合题意；D、(﹣a2)3=﹣a6，此选项不符合题意；故选：C．4．(2 分)如图，将木条a，b 与c 钉在一起，∠1=70°，∠2=50°，要使木条a 与b 平行，木条a 旋转的度数至少是( )A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2 的同位角的度数，然后用∠1 减去即可得到木条a 旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a 与b 平行，木条a 旋转的度数至少是70°﹣50°=20°．故选：B．A ．{B ．{ {，5．(2 分)如图，将△ABC 折叠，使点 A 与 BC 边中点 D 重合，折痕为 MN ，若 AB =9，BC =6，则△DNB 的周长为()A ．12B ．13C ．14D ．15【分析】由 D 为 BC 中点知 BD =3，再由折叠性质得 ND =NA ，从而根据△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD 可得答案．【解答】解：∵D 为 BC 的中点，且 BC =6，1∴BD =2BC =3， 由折叠性质知 NA =ND ，则△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD =3+9=12， 故选：A ．6．(2 分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡 x 只，兔 y 只，可列方程组为()x + y = 35 2x + 2y = 94 x + y = 35 4x + 4y = 94 x + y = 354x + 2y = 94x + y = 352x + 4y = 94【分析】根据题意可以列出相应的方程组，从而可以解答本题． 【解答】解：由题意可得， x + y = 352x + 4y = 94故选：D ．二、填空题(共 8 小题，每小题 3 分，满分 24 分) 7．(3 分)计算： 16= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果． 【解答】解：∵42=16，故答案为 4．8．(3 分)买单价 3 元的圆珠笔 m 支，应付 3m 元． 【分析】根据总价=单价×数量列出代数式． 【解答】解：依题意得：3m ． 故答案是：3m ．9．(3 分)若 a +b =4，ab =1，则 a 2b +ab 2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．∴ 16=4， C ．{ D ．{【解答】解：∵a +b =4，ab =1， ∴a 2b +ab 2=ab (a +b ) =1×4 =4．故答案为：4．10．(3 分)若关于 x 的一元二次方程 x 2+2x ﹣m =0 有两个相等的实数根，则 m 的值为 ﹣1 ．【分析】由于关于 x 的一元二次方程 x 2+2x ﹣m =0 有两个相等的实数根，可知其判别式为 0，据此列出关于 m 的不等式，解答即可．【解答】解：∵关于 x 的一元二次方程 x 2+2x ﹣m =0 有两个相等的实数根， ∴△=b 2﹣4ac =0， 即：22﹣4(﹣m )=0， 解 得 ：m =﹣1， 故选答案为﹣1．11．(3 分)如图，在平面直角坐标系中，A (4，0)，B (0，3)，以点 A 为圆心，AB 长为半径画弧，交 x 轴的负半轴于点 C ，则点 C 坐 标 为 (﹣1，0) ．【分析】求出 OA 、OB ，根据勾股定理求出 AB ，即可得出 AC ，求出 OC 长即可． 【解答】解：∵点 A ，B 的坐标分别为(4，0)，(0，3)， ∴OA =4，OB =3，在 Rt △AOB 中，由勾股定理得：AB = 32 + 42=5， ∴AC =AB =5， ∴OC =5﹣4=1，∴点 C 的坐标为(﹣1，0)， 故答案为：(﹣1，0)，12．(3 分)如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B =∠C =90°，测得BD =120m ，DC =60m ，EC =50m ，求得河宽AB = 100 m ．【分析】由两角对应相等可得△BAD ∽△CED ，利用对应边成比例可得两岸间的大致距离 AB ． 【解答】解：∵∠ADB =∠EDC ，∠ABC =∠ECD =90°， ∴△ABD ∽△ECD ，ABBD∴E C = CD ，AB =BD × E C CD ，120 × 50解得：AB= 60 = 100(米)．故答案为：100．13．(3 分)如图，A，B，C，D 是⊙O 上的四个点，AB=BC，若∠AOB=58°，则∠BDC= 29 度．1【分析】根据∠BDC=2∠BOC 求解即可；【解答】解：连接OC．∵AB=BC，∴∠AOB=∠BOC=58°，1∴∠BDC=2∠BOC=29°，故答案为29．114．(3 分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=2，则该等腰三角形的顶角为 36 度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC 中，AB=AC，∴∠B=∠C，1∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=2，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．三、解答题(共12 小题，满分84 分)15．(5 分)某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误，解答过程如下：原式=a2+2ab﹣(a2﹣b2) (第一步)=a2+2ab﹣a2﹣b2(第二步)=2ab﹣b2 (第三步)(1)该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；{(2) 写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：(1)该同学解答过程从第 二步开始出错，错误原因是 去括号时没有变号； 故答案是：二；去括号时没有变号； (2)原式=a 2+2ab ﹣(a 2﹣b 2) =a 2+2ab ﹣a 2+b 2 =2ab +b 2．16．(5 分)如图，在正方形 ABCD 中，点 E ，F 分别在 BC ，CD 上，且 BE =CF ，求证：△ABE ≌△BCF ．【分析】根据正方形的性质，利用 SAS 即可证明； 【解答】证明：∵四边形 ABCD 是正方形， ∴AB =BC ，∠ABE =∠BCF =90°， 在△ABE 和△BCF 中，AB = BC ∠ABE = ∠BCF ，B E = CF∴△ABE ≌△BCF ．17．(5 分)一个不透明的口袋中有三个小球，上面分别标有字母 A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．AB C A (A ，A ) (B ，A ) (C ，A ) B (A ，B ) (B ，B ) (C ，B ) C(A ，C )(B ，C )(C ，C )由列表可知可能出现的结果共 9 种，其中两次摸出的小球所标字母相同的情况数有 3 种， 3 1所以该同学两次摸出的小球所标字母相同的概率=9=3．k18．(5 分)在平面直角坐标系中，反比例函数 y =x (k ≠0)图象与一次函数 y =x +2 图象的一个交点为 P ，且点 P 的横坐标为 1，求 该反比例函数的解析式．【分析】先求出 P 点的坐标，再把 P 点的坐标代入反比例函数的解析式，即可求出答案． 【解答】解：∵把 x =1 代入 y =x +2 得：y =3， 即 P 点的坐标是(1，3)，k把 P 点的坐标代入 y =x 得：k =3，3即反比例函数的解析式是 y =x ．19．(7 分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示甲队每天修路的长度，庆庆同学所列方程中的y 表示甲队修路400 米所需时间或乙队修路600 米所需时间；(2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．【分析】(1)根据两人的方程思路，可得出：x 表示甲队每天修路的长度；y 表示甲队修路400 米所需时间或乙队修路600 米所需时间；(2)根据题意，可找出：(冰冰)甲队修路400 米所用时间=乙队修路600 米所用时间；(庆庆)乙队每天修路的长度﹣甲队每天修路的长度=20 米；(3)选择两个方程中的一个，解之即可得出结论．【解答】解：(1)∵冰冰是根据时间相等列出的分式方程，∴x 表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20 米列出的分式方程，∴y 表示甲队修路400 米所需时间或乙队修路600 米所需时间．故答案为：甲队每天修路的长度；甲队修路400 米所需时间或乙队修路600 米所需时间．(2)冰冰用的等量关系是：甲队修路400 米所用时间=乙队修路600 米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20 米(选择一个即可)．400 600(3)选冰冰的方程：x=x + 20，去分母，得：400x+8000=600x，移项，x 的系数化为1，得：x=40，检验：当x=40 时，x、x+20 均不为零，∴x=40．答：甲队每天修路的长度为40 米．600 400选庆庆的方程：y﹣y=20，去分母，得：600﹣400=20y，将y 的系数化为1，得：y=10，经验：当y=10 时，分母y 不为0，∴y=10，400∴y=40．答：甲队每天修路的长度为40 米．20．(7 分)如图是由边长为1 的小正方形组成的8×4 网格，每个小正方形的顶点叫做格点，点A，B，C，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D1；第二步：点D1绕点B 顺时针旋转90°得到点D2；第三步：点D2绕点C 顺时针旋转90°回到点D．(1)请用圆规画出点D→D1→D2→D 经过的路径；(2)所画图形是轴对称对称图形；(3)求所画图形的周长(结果保留π)．【分析】(1)利用旋转变换的性质画出图象即可；(2)根据轴对称图形的定义即可判断；(3)利用弧长公式计算即可；【解答】解：(1)点D→D1→D2→D 经过的路径如图所示：(2)观察图象可知图象是轴对称图形，故答案为轴对称．90 ⋅ π⋅ 4(3)周长=4×180=8π．21．(7 分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α 的代数式表示旗杆AB 的高度．数学活动方案课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测(1) 用测角量仪测得∠步ADE=α；骤(2) 用皮尺测得BC=a 米，CD=b 米．计算过程【解答】解：(1)用测角仪测得∠ADE=α；(2)用皮尺测得BC=a 米，CD=b 米．(3)计算过程：∵四边形BCDE 是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE 中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．22．(7 分)为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10 袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：包装机分装情况比较好的是乙(填甲或乙)，说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402 出现次数最多，有3 次，∴乙组数据的众数为402；得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．23．(8 分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min 的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为 4000 m，小玲步行的速度为 100 m/min；(2)求小东离家的路程y 关于x 的函数解析式，并写出自变量的取值范围；(3)求两人相遇的时间．【分析】(1)认真分析图象得到路程与速度数据；(2)采用方程思想列出小东离家路程y 与时间x 之间的函数关系式；(3)两人相遇实际上是函数图象求交点．【解答】解：(1)结合题意和图象可知，线段CD 为小东路程与时间函数图象，折线O﹣A﹣B 为小玲路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷20=100m/s故答案为：4000，100(2)∵小东从离家4000m 处以300m/min 的速度返回家，则xmin 时，∴他离家的路程y=4000﹣300x40自变量x 的范围为0≤x≤ 3(3)由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8 分钟．24．(8 分)如图①，在△ABC 中，AB=AC，过AB 上一点D 作DE∥AC 交BC 于点E，以E 为顶点，ED 为一边，作∠DEF=∠A，另一边EF 交AC 于点F．(1)求证：四边形ADEF 为平行四边形；(2)当点D 为AB 中点时，▱ADEF 的形状为菱形；(3)延长图①中的DE 到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF 的形状，并说明理由．【分析】(1)根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；1(2)根据三角形中位线定理得到DE=2AC，得到AD=DE，根据菱形的判定定理证明；(3)根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】(1)证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF 为平行四边形；(2)解：▱ADEF 的形状为菱形，理由如下：∵点D 为AB 中点，1∴AD=2AB，∵DE∥AC，点D 为AB 中点，1∴DE=2AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF 为菱形，故答案为：菱形；(3)四边形AEGF 是矩形，理由如下：由(1)得，四边形ADEF 为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF 是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF 是矩形．25．(10 分)如图，在矩形ABCD 中，AB=2cm，∠ADB=30°．P，Q 两点分别从A，B 同时出发，点P 沿折线AB﹣BC 运动，在AB 上的速度是2cm/s，在BC 上的速度是2 3cm/s；点Q 在BD 上以2cm/s 的速度向终点D 运动，过点P 作PN⊥AD，垂足为点N．连接PQ，以PQ，PN 为邻边作▱PQMN．设运动的时间为x(s)，▱PQMN 与矩形ABCD 重叠部分的图形面积为y(cm2) 2(1)当PQ⊥AB 时，= 3s ；(2)求y 关于x 的函数解析式，并写出x 的取值范围；(3)直线AM 将矩形ABCD 的面积分成1：3 两部分时，直接写出x 的值．【分析】(1)当PQ⊥AB 时，BQ=2PB，由此构建方程即可解决问题；(2)分三种情形分别求解即可解决问题；(3)分两种情形分别求解即可解决问题；【解答】解：(1)当PQ⊥AB 时，BQ=2PB，∴2x=2(2﹣2x)，2∴x=3s．2故答案为3s．2(2)①如图1 中，当0＜x≤3时，重叠部分是四边形PQMN．3 2y =2(2﹣x +2tx × 3x = 2 x 2+ 3x1 3y =2x × 3x =2 3x 2．2②如图②中，当3＜x ≤1 时，重叠部分是四边形 PQEN ．③如图 3 中，当 1＜x ＜2 时，重叠部分是四边形 PNEQ ．13y =2(2﹣x +2)×[ 3x ﹣2 3(x ﹣1)]= 2 x 2﹣3 3x +4 3； 2(0＜x ≤ 3) 综上所述，y ={3x 2 + 3x(2＜x ≤ 1)．33x 2 ‒ 3 3x + 4 (1＜x ＜2)(3) ①如图 4 中，当直线 AM 经过 BC 中点 E 时，满足条件．2 3x 22 31则有：tan∠EAB=tan∠QPB，3 3x∴2 =2 ‒ 2x‒ x，2解得x=5．②如图5 中，当直线AM 经过CD 的中点E 时，满足条件．此时tan∠DEA=tan∠QPB，3x∴=2 ‒ 2x‒x，4解得x=7，2 4综上所述，当x=5或7时，直线AM 将矩形ABCD 的面积分成1：3 两部分．26．(10 分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x 轴相交于A，B 两点，与y 轴相交于点C，顶点为D，直线DC 与x 轴相交于点E．(1)当a=﹣1 时，抛物线顶点D 的坐标为 (﹣1，4) ，OE= 3 ；(2)OE 的长是否与a 值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a 的取值范围；(4)以DE 为斜边，在直线DE 的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n 关于m 的函数解析式及自变量m 的取值范围．【分析】(1)求出直线CD 的解析式即可解决问题；(2)利用参数a，求出直线CD 的解析式求出点E 坐标即可判断；(3)求出落在特殊情形下的a 的值即可判断；(4)如图，作PM⊥对称轴于M，PN⊥AB 于N．两条全等三角形的性质即可解决问题；【解答】解：(1)当a=﹣1 时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D(﹣1，4)，C(0，3)，∴直线CD 的解析式为y=﹣x+3，∴E(3，0)，∴OE=3，故答案为(﹣1，4)，3．(2)结论：OE 的长与a 值无关．理由：∵y=ax2+2ax﹣3a，∴C(0，﹣3a)，D(﹣1，﹣4a)，∴直线CD 的解析式为y=ax﹣3a，当y=0 时，x=3，∴E(3，0)，∴OE=3，∴OE 的长与a 值无关．(3)当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE 中，OC= 3OE=3 3，∴﹣3a=3 3，∴a=﹣3，∴45°≤β≤60°，a 的取值范围为﹣3≤a≤﹣1．(4)如图，作PM⊥对称轴于M，PN⊥AB 于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D(﹣1，﹣4a)，E(3，0)，∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D 在x 轴上时，P(1，﹣2)，此时m 的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1(m＜1)．第21 页（共21 页）。

吉林省2018年中考数学真题试题一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣32．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A． B． C． D．3．（2.00分）下列计算结果为a6的是（）A．a2•a3 B．a12÷a2C．（a2）3D．（﹣a2）34．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10° B．20° C．50° D．70°5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．156．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A． B．C． D．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：= ．8．（3.00分）买单价3元的圆珠笔m支，应付元．9．（3.00分）若a+b=4，ab=1，则a2b+ab2= ．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB= m．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC= 度．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为度．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第步开始出错，错误原因是；（2）写出此题正确的解答过程．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE ≌△BCF．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动： 第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． （1）请用圆规画出点D→D 1→D 2→D 经过的路径； （2）所画图形是 对称图形； （3）求所画图形的周长（结果保留π）．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题． 收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g ）如下： 甲：400，400，408，406，410，409，400，393，394，395 乙：403，404，396，399，402，402，405，397，402，398 整理数据： 表一分析数据：表二得出结论：包装机分装情况比较好的是（填甲或乙），说明你的理由．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为m，小玲步行的速度为m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E 为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q 在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN 为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x= ；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为，OE= ；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n 关于m的函数解析式及自变量m的取值范围．参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：（﹣1）×（﹣2）=2．故选：A．【点评】本题考查了有理数的乘法，牢记“两数相乘，同号得正，异号得负，并把绝对值相乘”是解题的关键．2．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A． B． C． D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（2.00分）下列计算结果为a6的是（）A．a2•a3 B．a12÷a2C．（a2）3D．（﹣a2）3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．【点评】本题主要考查幂的运算，解题的关键是掌握同底数幂相乘、同底数幂相除、幂的乘方的运算法则．4．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10° B．20° C．50° D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．【点评】本题考查了旋转的性质，平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【分析】由D为BC中点知BD=3，再由折叠性质得ND=NA，从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案．【解答】解：∵D为BC的中点，且BC=6，∴BD=BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12，故选：A．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A． B．C． D．【分析】根据题意可以列出相应的方程组，从而可以解答本题．【解答】解：由题意可得，，故选：D．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16，∴=4，故答案为4．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．8．（3.00分）买单价3元的圆珠笔m支，应付3m 元．【分析】根据总价=单价×数量列出代数式．【解答】解：依题意得：3m．故答案是：3m．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．9．（3.00分）若a+b=4，ab=1，则a2b+ab2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为﹣1 ．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．【点评】本题考查了根的判别式，解题的关键是了解根的判别式如何决定一元二次方程根的情况．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），【点评】本题考查了勾股定理和坐标与图形性质的应用，解此题的关键是求出OC的长，注意：在直角三角形中，两直角边的平方和等于斜边的平方．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB= 100 m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴，，解得：AB=（米）．故答案为：100．【点评】此题主要考查了相似三角形的应用；用到的知识点为：两角对应相等的两三角形相似；相似三角形的对应边成比例．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC= 29 度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接OC．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=∠BOC=29°，故答案为29．【点评】本题考查圆周角定理，圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为36 度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC中，AB=AC，∴∠B=∠C，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．【点评】本题考查了三角形内角和定理和等腰三角形的性质，能根据等腰三角形性质、三角形内角和定理和已知得出5∠A=180°是解此题的关键．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a2+2ab﹣（a2﹣b2）=a2+2ab﹣a2+b2=2ab+b2．【点评】考查了平方差公式和实数的运算，去括号规律：①a+（b+c）=a+b+c，括号前是“+”号，去括号时连同它前面的“+”号一起去掉，括号内各项不变号；②a﹣（b﹣c）=a﹣b+c，括号前是“﹣”号，去括号时连同它前面的“﹣”号一起去掉，括号内各项都要变号．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE ≌△BCF．【分析】根据正方形的性质，利用SAS即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，在△ABE和△BCF中，，∴△ABE≌△BCF．【点评】本题考查正方形的性质全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．【解答】解：列表得：由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率==．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【分析】先求出P点的坐标，再把P点的坐标代入反比例函数的解析式，即可求出答案．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=．【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征，能求出P点的坐标是解此题的关键．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【分析】（1）根据两人的方程思路，可得出：x表示甲队每天修路的长度；y表示甲队修路400米所需时间；（2）根据题意，可找出：（冰冰）甲队修路400米所用时间=乙队修路600米所用时间；（庆庆）乙队每天修路的长度﹣甲队每天修路的长度=20米；（3）选择两个方程中的一个，解之即可得出结论．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：=，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．选庆庆的方程：﹣=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，∴=40．答：甲队每天修路的长度为40米．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【分析】（1）利用旋转变换的性质画出图象即可；（2）根据轴对称图形的定义即可判断；（3）利用弧长公式计算即可；【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×=8π．【点评】本题考查作图﹣旋转变换，弧长公式、轴对称图形等知识，解题的关键是理解题意，正确画出图形，属于中考常考题型．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平【分析】在Rt△ADE中，求出AE，再利用AB=AE+BE计算即可；【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．（3）计算过程：∵四边形BCDE是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一分析数据：表二得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．【点评】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义及数据的整理是解题的关键．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000 m，小玲步行的速度为200 m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【分析】（1）认真分析图象得到路程与速度数据；（2）采用方程思想列出小东离家路程y与时间x之间的函数关系式；（3）两人相遇实际上是函数图象求交点．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷10=200m/s故答案为：4000，200（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．【点评】本题是一次函数实际应用问题，考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E 为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【分析】（1）根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到DE=AC，得到AD=DE，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．【点评】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q 在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN 为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x= s ；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．【分析】（1）当PQ⊥AB时，BQ=2PB，由此构建方程即可解决问题；（2）分三种情形分别求解即可解决问题；（3）分两种情形分别求解即可解决问题；【解答】解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=s或时，直线AM将矩形ABCD的面积分成1：3两部分．【点评】本题考查四边形综合题、矩形的性质平行四边形的性质、锐角三角函数、解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，学会用方程的思想解决问题，属于中考压轴题．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为（﹣1，4），OE= 3 ；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n 关于m的函数解析式及自变量m的取值范围．【分析】（1）求出直线CD的解析式即可解决问题；（2）利用参数a，求出直线CD的解析式求出点E坐标即可判断；（3）求出落在特殊情形下的a的值即可判断；（4）如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D（﹣1，4），C（0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=OE=3，∴﹣3a=3，∴a=﹣，∴45°≤β≤60°，a的取值范围为﹣≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，PM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．【点评】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．21。

2018年吉林省中考数学试卷一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣32．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．3．（2.00分）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）34．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a 与b平行，木条a旋转的度数至少是（）A．10°B．20°C．50°D．70°5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．156．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：=．8．（3.00分）买单价3元的圆珠笔m支，应付元．9．（3.00分）若a+b=4，ab=1，则a2b+ab2=．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m 的值为．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=m．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC=度．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为度．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第步开始出错，错误原因是；（2）写出此题正确的解答过程．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是对称图形；（3）求所画图形的周长（结果保留π）．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测量步骤（1）用测得∠ADE=α；（2）用测得BC=a米，CD=b米．计算过程22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲30013乙0150分析数据：表二种类平均数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装情况比较好的是（填甲或乙），说明你的理由．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x （min）之间的函数图象如图所示（1）家与图书馆之间的路程为m，小玲步行的速度为m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC 于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC 上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为，OE=；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n关于m的函数解析式及自变量m的取值范围．2018年吉林省中考数学试卷参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：（﹣1）×（﹣2）=2．故选：A．【点评】本题考查了有理数的乘法，牢记“两数相乘，同号得正，异号得负，并把绝对值相乘”是解题的关键．2．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（2.00分）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．【点评】本题主要考查幂的运算，解题的关键是掌握同底数幂相乘、同底数幂相除、幂的乘方的运算法则．4．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a 与b平行，木条a旋转的度数至少是（）A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．【点评】本题考查了旋转的性质，平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【分析】由D为BC中点知BD=3，再由折叠性质得ND=NA，从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案．【解答】解：∵D为BC的中点，且BC=6，∴BD=BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12，故选：A．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．【分析】根据题意可以列出相应的方程组，从而可以解答本题．【解答】解：由题意可得，，故选：D．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：=4．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16，∴=4，故答案为4．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．8．（3.00分）买单价3元的圆珠笔m支，应付3m元．【分析】根据总价=单价×数量列出代数式．【解答】解：依题意得：3m．故答案是：3m．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．9．（3.00分）若a+b=4，ab=1，则a2b+ab2=4．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m 的值为﹣1．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．【点评】本题考查了根的判别式，解题的关键是了解根的判别式如何决定一元二次方程根的情况．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），【点评】本题考查了勾股定理和坐标与图形性质的应用，解此题的关键是求出OC的长，注意：在直角三角形中，两直角边的平方和等于斜边的平方．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴，，解得：AB=（米）．故答案为：100．【点评】此题主要考查了相似三角形的应用；用到的知识点为：两角对应相等的两三角形相似；相似三角形的对应边成比例．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC=29度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接OC．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=∠BOC=29°，故答案为29．【点评】本题考查圆周角定理，圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为36度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC中，AB=AC，∴∠B=∠C，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．【点评】本题考查了三角形内角和定理和等腰三角形的性质，能根据等腰三角形性质、三角形内角和定理和已知得出5∠A=180°是解此题的关键．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a2+2ab﹣（a2﹣b2）=a2+2ab﹣a2+b2=2ab+b2．【点评】考查了平方差公式和实数的运算，去括号规律：①a+（b+c）=a+b+c，括号前是“+”号，去括号时连同它前面的“+”号一起去掉，括号内各项不变号；②a﹣（b﹣c）=a﹣b+c，括号前是“﹣”号，去括号时连同它前面的“﹣”号一起去掉，括号内各项都要变号．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．【分析】根据正方形的性质，利用SAS即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，在△ABE和△BCF中，，∴△ABE≌△BCF．【点评】本题考查正方形的性质全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．【解答】解：列表得：A B CA（A，A）（B，A）（C，A）B（A，B）（B，B）（C，B）C（A，C）（B，C）（C，C）由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率==．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【分析】先求出P点的坐标，再把P点的坐标代入反比例函数的解析式，即可求出答案．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=．【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征，能求出P点的坐标是解此题的关键．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【分析】（1）根据两人的方程思路，可得出：x表示甲队每天修路的长度；y表示甲队修路400米所需时间；（2）根据题意，可找出：（冰冰）甲队修路400米所用时间=乙队修路600米所用时间；（庆庆）乙队每天修路的长度﹣甲队每天修路的长度=20米；（3）选择两个方程中的一个，解之即可得出结论．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：=，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．选庆庆的方程：﹣=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，∴=40．答：甲队每天修路的长度为40米．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【分析】（1）利用旋转变换的性质画出图象即可；（2）根据轴对称图形的定义即可判断；（3）利用弧长公式计算即可；【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×=8π．【点评】本题考查作图﹣旋转变换，弧长公式、轴对称图形等知识，解题的关键是理解题意，正确画出图形，属于中考常考题型．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测量步骤（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．计算过程【分析】在Rt△ADE中，求出AE，再利用AB=AE+BE计算即可；【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．（3）计算过程：∵四边形BCDE是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．【点评】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义及数据的整理是解题的关键．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x （min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000m，小玲步行的速度为200m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【分析】（1）认真分析图象得到路程与速度数据；（2）采用方程思想列出小东离家路程y与时间x之间的函数关系式；（3）两人相遇实际上是函数图象求交点．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷10=200m/s故答案为：4000，200（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．【点评】本题是一次函数实际应用问题，考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC 于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【分析】（1）根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到DE=AC，得到AD=DE，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．【点评】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC 上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=s；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．【分析】（1）当PQ⊥AB时，BQ=2PB，由此构建方程即可解决问题；（2）分三种情形分别求解即可解决问题；（3）分两种情形分别求解即可解决问题；【解答】解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=s或时，直线AM将矩形ABCD的面积分成1：3两部分．【点评】本题考查四边形综合题、矩形的性质平行四边形的性质、锐角三角函数、解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，学会用方程的思想解决问题，属于中考压轴题．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为（﹣1，4），OE=3；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n关于m的函数解析式及自变量m的取值范围．【分析】（1）求出直线CD的解析式即可解决问题；（2）利用参数a，求出直线CD的解析式求出点E坐标即可判断；（3）求出落在特殊情形下的a的值即可判断；（4）如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D（﹣1，4），C（0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=OE=3，∴﹣3a=3，∴a=﹣，∴45°≤β≤60°，a的取值范围为﹣≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，PM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．【点评】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

吉林省2018年中考数学真题试题一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣32．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．3．（2.00分）下列计算结果为a6的是（）A．a2•a3 B．a12÷a2C．（a2）3D．（﹣a2）34．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10° B．20° C．50° D．70°5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．156．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：= ．8．（3.00分）买单价3元的圆珠笔m支，应付元．9．（3.00分）若a+b=4，ab=1，则a2b+ab2= ．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB= m．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC= 度．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为度．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第步开始出错，错误原因是；（2）写出此题正确的解答过程．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE ≌△BCF．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是对称图形；（3）求所画图形的周长（结果保留π）．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一分析数据：表二得出结论：包装机分装情况比较好的是（填甲或乙），说明你的理由．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为m，小玲步行的速度为m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E 为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x= ；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为，OE= ；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n 关于m的函数解析式及自变量m的取值范围．参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：（﹣1）×（﹣2）=2．故选：A．【点评】本题考查了有理数的乘法，牢记“两数相乘，同号得正，异号得负，并把绝对值相乘”是解题的关键．2．（2.00分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（2.00分）下列计算结果为a6的是（）A．a2•a3 B．a12÷a2C．（a2）3D．（﹣a2）3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．【点评】本题主要考查幂的运算，解题的关键是掌握同底数幂相乘、同底数幂相除、幂的乘方的运算法则．4．（2.00分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10° B．20° C．50° D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．【点评】本题考查了旋转的性质，平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．5．（2.00分）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【分析】由D为BC中点知BD=3，再由折叠性质得ND=NA，从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案．【解答】解：∵D为BC的中点，且BC=6，∴BD=BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12，故选：A．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．（2.00分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．【分析】根据题意可以列出相应的方程组，从而可以解答本题．【解答】解：由题意可得，，故选：D．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）计算：= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16，∴=4，故答案为4．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．8．（3.00分）买单价3元的圆珠笔m支，应付3m 元．【分析】根据总价=单价×数量列出代数式．【解答】解：依题意得：3m．故答案是：3m．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．9．（3.00分）若a+b=4，ab=1，则a2b+ab2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．10．（3.00分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为﹣1 ．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．【点评】本题考查了根的判别式，解题的关键是了解根的判别式如何决定一元二次方程根的情况．11．（3.00分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），【点评】本题考查了勾股定理和坐标与图形性质的应用，解此题的关键是求出OC的长，注意：在直角三角形中，两直角边的平方和等于斜边的平方．12．（3.00分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB= 100 m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴，，解得：AB=（米）．故答案为：100．【点评】此题主要考查了相似三角形的应用；用到的知识点为：两角对应相等的两三角形相似；相似三角形的对应边成比例．13．（3.00分）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC= 29 度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接OC．∵=，∴∠AOB=∠B OC=58°，∴∠BDC=∠BOC=29°，故答案为29．【点评】本题考查圆周角定理，圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（3.00分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为36 度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC中，AB=AC，∴∠B=∠C，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．【点评】本题考查了三角形内角和定理和等腰三角形的性质，能根据等腰三角形性质、三角形内角和定理和已知得出5∠A=180°是解此题的关键．三、解答题（共12小题，满分84分）15．（5.00分）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a2+2ab﹣（a2﹣b2）=a2+2ab﹣a2+b2=2ab+b2．【点评】考查了平方差公式和实数的运算，去括号规律：①a+（b+c）=a+b+c，括号前是“+”号，去括号时连同它前面的“+”号一起去掉，括号内各项不变号；②a﹣（b﹣c）=a﹣b+c，括号前是“﹣”号，去括号时连同它前面的“﹣”号一起去掉，括号内各项都要变号．16．（5.00分）如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE ≌△BCF．【分析】根据正方形的性质，利用SAS即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，在△ABE和△BCF中，，∴△ABE≌△BCF．【点评】本题考查正方形的性质全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（5.00分）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．【解答】解：列表得：由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率==．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．18．（5.00分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【分析】先求出P点的坐标，再把P点的坐标代入反比例函数的解析式，即可求出答案．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=．【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征，能求出P点的坐标是解此题的关键．19．（7.00分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【分析】（1）根据两人的方程思路，可得出：x表示甲队每天修路的长度；y表示甲队修路400米所需时间；（2）根据题意，可找出：（冰冰）甲队修路400米所用时间=乙队修路600米所用时间；（庆庆）乙队每天修路的长度﹣甲队每天修路的长度=20米；（3）选择两个方程中的一个，解之即可得出结论．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：=，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．选庆庆的方程：﹣=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，∴=40．答：甲队每天修路的长度为40米．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．20．（7.00分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【分析】（1）利用旋转变换的性质画出图象即可；（2）根据轴对称图形的定义即可判断；（3）利用弧长公式计算即可；【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×=8π．【点评】本题考查作图﹣旋转变换，弧长公式、轴对称图形等知识，解题的关键是理解题意，正确画出图形，属于中考常考题型．21．（7.00分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平【分析】在Rt△ADE中，求出AE，再利用AB=AE+BE计算即可；【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．（3）计算过程：∵四边形BCDE是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（7.00分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一分析数据：表二得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．【点评】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义及数据的整理是解题的关键．23．（8.00分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000 m，小玲步行的速度为200 m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【分析】（1）认真分析图象得到路程与速度数据；（2）采用方程思想列出小东离家路程y与时间x之间的函数关系式；（3）两人相遇实际上是函数图象求交点．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷10=200m/s故答案为：4000，200（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．【点评】本题是一次函数实际应用问题，考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题．24．（8.00分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E 为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【分析】（1）根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到DE=AC，得到AD=DE，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．【点评】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．25．（10.00分）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x= s ；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．【分析】（1）当PQ⊥AB时，BQ=2PB，由此构建方程即可解决问题；（2）分三种情形分别求解即可解决问题；（3）分两种情形分别求解即可解决问题；【解答】解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=s或时，直线AM将矩形ABCD的面积分成1：3两部分．【点评】本题考查四边形综合题、矩形的性质平行四边形的性质、锐角三角函数、解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，学会用方程的思想解决问题，属于中考压轴题．26．（10.00分）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为（﹣1，4），OE= 3 ；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n 关于m的函数解析式及自变量m的取值范围．【分析】（1）求出直线CD的解析式即可解决问题；（2）利用参数a，求出直线CD的解析式求出点E坐标即可判断；（3）求出落在特殊情形下的a的值即可判断；（4）如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D（﹣1，4），C（0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=OE=3，∴﹣3a=3，∴a=﹣，∴45°≤β≤60°，a的取值范围为﹣≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，PM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．【点评】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

2018年吉林省中考数学试卷一、选择题(共6小题，每小题2分，满分12分) 1．(2分)计算(﹣1)×(﹣2)的结果是( ) A ．2B ．1C ．﹣2D ．﹣32．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是( )A ．B ．C ．D ．3．(2分)下列计算结果为a 6的是( )A ．a 2•a 3B ．a 12÷a 2C ．(a 2)3D ．(﹣a 2)34．(2分)如图，将木条a ，b 与c 钉在一起，∠1=70°，∠2=50°，要使木条a 与b 平行，木条a 旋转的度数至少是( )A ．10°B ．20°C ．50°D ．70°5．(2分)如图，将△ABC 折叠，使点A 与BC 边中点D 重合，折痕为MN ，若AB =9，BC =6，则△DNB 的周长为( )A ．12B ．13C ．14D ．156．(2分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为( )A ．{x +y =352x +2y =94B ．{x +y =354x +2y =94C ．{x +y =354x +4y =94D ．{x +y =352x +4y =94二、填空题(共8小题，每小题3分，满分24分) 7．(3分)计算：√16= ．8．(3分)买单价3元的圆珠笔m 支，应付 元．9．(3分)若a +b =4，ab =1，则a 2b +ab 2= ．10．(3分)若关于x 的一元二次方程x 2+2x ﹣m =0有两个相等的实数根，则m 的值为 ．11．(3分)如图，在平面直角坐标系中，A (4，0)，B (0，3)，以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C ，则点C 坐标为 ．12．(3分)如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B =∠C =90°，测得BD =120m ，DC =60m ，EC =50m ，求得河宽AB = m ．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，AB ̂=BC ̂，若∠AOB =58°，则∠BDC = 度．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 度．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下： 原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步) =2ab ﹣b 2 (第三步)(1)该同学解答过程从第 步开始出错，错误原因是 ； (2)写出此题正确的解答过程．16．(5分)如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．18．(5分)在平面直角坐标系中，反比例函数y=kx(k≠0)图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；(2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 对称图形； (3)求所画图形的周长(结果保留π)．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题 方案示意图测量步骤(1)用 测得∠ADE =α；(2)用 测得BC =a 米，CD =b 米．计算过程22．(7分)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量(g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411频数种类甲30013乙0150分析数据：表二种类平均数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装情况比较好的是(填甲或乙)，说明你的理由．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为m，小玲步行的速度为m/min；(2)求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；(3)求两人相遇的时间．24．(8分)如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．(1)求证：四边形ADEF为平行四边形；(2)当点D为AB中点时，▱ADEF的形状为；(3)延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．(10分)如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2√3cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x(s)，▱PQMN与矩形ABCD重叠部分的图形面积为y(cm2)(1)当PQ⊥AB时，x=；(2)求y关于x的函数解析式，并写出x的取值范围；(3)直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．(10分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．(1)当a=﹣1时，抛物线顶点D的坐标为，OE=；(2)OE的长是否与a值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a的取值范围；(4)以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n关于m的函数解析式及自变量m的取值范围．2018年吉林省中考数学试卷参考答案与试题解析一、选择题(共6小题，每小题2分，满分12分)1．(2分)计算(﹣1)×(﹣2)的结果是()A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：(﹣1)×(﹣2)=2．故选：A．2．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是()A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．3．(2分)下列计算结果为a6的是()A．a2•a3B．a12÷a2C．(a2)3D．(﹣a2)3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、(a2)3=a6，此选项符合题意；D、(﹣a2)3=﹣a6，此选项不符合题意；故选：C．4．(2分)如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是()A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．5．(2分)如图，将△ABC 折叠，使点A 与BC 边中点D 重合，折痕为MN ，若AB =9，BC =6，则△DNB 的周长为( )A ．12B ．13C ．14D ．15【分析】由D 为BC 中点知BD =3，再由折叠性质得ND =NA ，从而根据△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD 可得答案．【解答】解：∵D 为BC 的中点，且BC =6， ∴BD =12BC =3，由折叠性质知NA =ND ，则△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD =3+9=12，故选：A ．6．(2分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为( )A ．{x +y =352x +2y =94B ．{x +y =354x +2y =94C ．{x +y =354x +4y =94D ．{x +y =352x +4y =94【分析】根据题意可以列出相应的方程组，从而可以解答本题． 【解答】解：由题意可得， {x +y =352x +4y =94， 故选：D ．二、填空题(共8小题，每小题3分，满分24分) 7．(3分)计算：√16= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16， ∴√16=4，故答案为4．8．(3分)买单价3元的圆珠笔m 支，应付 3m 元． 【分析】根据总价=单价×数量列出代数式． 【解答】解：依题意得：3m ．故答案是：3m ．9．(3分)若a +b =4，ab =1，则a 2b +ab 2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab(a+b)=1×4=4．故答案为：4．10．(3分)若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为﹣1．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4(﹣m)=0，解得：m=﹣1，故选答案为﹣1．11．(3分)如图，在平面直角坐标系中，A(4，0)，B(0，3)，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为(﹣1，0)．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为(4，0)，(0，3)，∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB=√32+42=5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为(﹣1，0)，故答案为：(﹣1，0)，12．(3分)如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴ABEC=BDCD，AB=BD×ECCD，解得：AB =120×5060=100(米)．故答案为：100．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，AB ̂=BC ̂，若∠AOB =58°，则∠BDC = 29 度．【分析】根据∠BDC =12∠BOC 求解即可；【解答】解：连接OC ．∵AB̂=BC ̂， ∴∠AOB =∠BOC =58°， ∴∠BDC =12∠BOC =29°，故答案为29．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 36 度．【分析】根据等腰三角形的性质得出∠B =∠C ，根据三角形内角和定理和已知得出5∠A =180°，求出即可．【解答】解：∵△ABC 中，AB =AC ， ∴∠B =∠C ，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，∴∠A ：∠B =1：2， 即5∠A =180°， ∴∠A =36°，故答案为：36．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下： 原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步) =2ab ﹣b 2 (第三步)(1)该同学解答过程从第 二 步开始出错，错误原因是 去括号时没有变号 ；(2)写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：(1)该同学解答过程从第 二步开始出错，错误原因是 去括号时没有变号； 故答案是：二；去括号时没有变号；(2)原式=a 2+2ab ﹣(a 2﹣b 2) =a 2+2ab ﹣a 2+b 2=2ab +b 2．16．(5分)如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，且BE =CF ，求证：△ABE ≌△BCF ．【分析】根据正方形的性质，利用SAS 即可证明； 【解答】证明：∵四边形ABCD 是正方形， ∴AB =BC ，∠ABE =∠BCF =90°，在△ABE 和△BCF 中， {AB =BC∠ABE =∠BCF BE =CF， ∴△ABE ≌△BCF ．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率． 【解答】解：列表得：A B C A (A ，A ) (B ，A ) (C ，A ) B (A ，B ) (B ，B ) (C ，B ) C(A ，C )(B ，C )(C ，C )由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种， 所以该同学两次摸出的小球所标字母相同的概率=39=13．18．(5分)在平面直角坐标系中，反比例函数y =kx (k ≠0)图象与一次函数y =x +2图象的一个交点为P ，且点P 的横坐标为1，求该反比例函数的解析式．【分析】先求出P 点的坐标，再把P 点的坐标代入反比例函数的解析式，即可求出答案． 【解答】解：∵把x =1代入y =x +2得：y =3， 即P 点的坐标是(1，3)，把P 点的坐标代入y =kx 得：k =3，即反比例函数的解析式是y =3x．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示 甲队每天修路的长度 ，庆庆同学所列方程中的y 表示 甲队修路400米所需时间或乙队修路600米所需时间 ；(2)两个方程中任选一个，并写出它的等量关系； (3)解(2)中你所选择的方程，并回答老师提出的问题．【分析】(1)根据两人的方程思路，可得出：x 表示甲队每天修路的长度；y 表示甲队修路400米所需时间或乙队修路600米所需时间；(2)根据题意，可找出：(冰冰)甲队修路400米所用时间=乙队修路600米所用时间；(庆庆)乙队每天修路的长度﹣甲队每天修路的长度=20米；(3)选择两个方程中的一个，解之即可得出结论．【解答】解：(1)∵冰冰是根据时间相等列出的分式方程， ∴x 表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程， ∴y 表示甲队修路400米所需时间或乙队修路600米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间或乙队修路600米所需时间． (2)冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米(选择一个即可)． (3)选冰冰的方程：400x=600x+20，去分母，得：400x +8000=600x ， 移项，x 的系数化为1，得：x =40， 检验：当x =40时，x 、x +20均不为零， ∴x =40．答：甲队每天修路的长度为40米． 选庆庆的方程：600y﹣400y=20，去分母，得：600﹣400=20y ， 将y 的系数化为1，得：y =10， 经验：当y =10时，分母y 不为0， ∴y =10， ∴400y=40．答：甲队每天修路的长度为40米．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 轴对称 对称图形； (3)求所画图形的周长(结果保留π)．【分析】(1)利用旋转变换的性质画出图象即可； (2)根据轴对称图形的定义即可判断； (3)利用弧长公式计算即可；【解答】解：(1)点D →D 1→D 2→D 经过的路径如图所示：(2)观察图象可知图象是轴对称图形， 故答案为轴对称．(3)周长=4×90⋅π⋅4180=8π．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题方案示意图测量步骤 (1)用 测角仪 测得∠ADE =α； (2)用 皮尺 测得BC =a 米，CD =b 米．计算过程【分析】在Rt △ADE 中，求出AE ，再利用AB =AE +BE 计算即可； 【解答】解：(1)用 测角仪测得∠ADE =α； (2)用 皮尺测得BC =a 米，CD =b 米． (3)计算过程：∵四边形BCDE 是矩形， ∴DE =BC =a ，BE =CD =b ，在Rt △ADE 中，AE =ED •tan α=a •tan α，∴AB =AE +EB =a •tan α+b ．22．(7分)为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题． 收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量(g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411频数种类甲303013乙031510分析数据：表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：包装机分装情况比较好的是乙(填甲或乙)，说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一质量(g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411频数种类甲303013乙031510分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为 4000 m ，小玲步行的速度为 100 m /min ； (2)求小东离家的路程y 关于x 的函数解析式，并写出自变量的取值范围； (3)求两人相遇的时间．【分析】(1)认真分析图象得到路程与速度数据；(2)采用方程思想列出小东离家路程y 与时间x 之间的函数关系式； (3)两人相遇实际上是函数图象求交点．【解答】解：(1)结合题意和图象可知，线段CD 为小东路程与时间函数图象，折线O ﹣A ﹣B 为小玲路程与时间图象 则家与图书馆之间路程为4000m ，小玲步行速度为2000÷20=100m /s 故答案为：4000，100(2)∵小东从离家4000m 处以300m /min 的速度返回家，则xmin 时， ∴他离家的路程y =4000﹣300x 自变量x 的范围为0≤x ≤403(3)由图象可知，两人相遇是在小玲改变速度之前 ∴4000﹣300x =200x 解得x =8∴两人相遇时间为第8分钟．24．(8分)如图①，在△ABC 中，AB =AC ，过AB 上一点D 作DE ∥AC 交BC 于点E ，以E 为顶点，ED 为一边，作∠DEF =∠A ，另一边EF 交AC 于点F ．(1)求证：四边形ADEF 为平行四边形；(2)当点D 为AB 中点时，▱ADEF 的形状为 菱形 ；(3)延长图①中的DE 到点G ，使EG =DE ，连接AE ，AG ，FG ，得到图②，若AD =AG ，判断四边形AEGF 的形状，并说明理由．【分析】(1)根据平行线的性质得到∠BDE =∠A ，根据题意得到∠DEF =∠BDE ，根据平行线的判定定理得到AD ∥EF ，根据平行四边形的判定定理证明；(2)根据三角形中位线定理得到DE =12AC ，得到AD =DE ，根据菱形的判定定理证明；(3)根据等腰三角形的性质得到AE ⊥EG ，根据有一个角是直角的平行四边形是矩形证明． 【解答】(1)证明：∵DE ∥AC ， ∴∠BDE =∠A ， ∵∠DEF =∠A ， ∴∠DEF =∠BDE ，∴AD ∥EF ，又∵DE ∥AC ， ∴四边形ADEF 为平行四边形；(2)解：▱ADEF 的形状为菱形， 理由如下：∵点D 为AB 中点， ∴AD =12AB ，∵DE ∥AC ，点D 为AB 中点， ∴DE =12AC ， ∵AB =AC ， ∴AD =DE ，∴平行四边形ADEF 为菱形， 故答案为：菱形； (3)四边形AEGF 是矩形，理由如下：由(1)得，四边形ADEF 为平行四边形， ∴AF ∥DE ，AF =DE ， ∵EG =DE ，∴AF ∥DE ，AF =GE ，∴四边形AEGF 是平行四边形， ∵AD =AG ，EG =DE ， ∴AE ⊥EG ，∴四边形AEGF 是矩形．25．(10分)如图，在矩形ABCD 中，AB =2cm ，∠ADB =30°．P ，Q 两点分别从A ，B 同时出发，点P 沿折线AB ﹣BC 运动，在AB 上的速度是2cm /s ，在BC 上的速度是2√3cm /s ；点Q 在BD 上以2cm /s 的速度向终点D 运动，过点P 作PN ⊥AD ，垂足为点N ．连接PQ ，以PQ ，PN 为邻边作▱PQMN ．设运动的时间为x (s )，▱PQMN 与矩形ABCD 重叠部分的图形面积为y (cm 2) (1)当PQ ⊥AB 时，x =23s ；(2)求y 关于x 的函数解析式，并写出x 的取值范围；(3)直线AM 将矩形ABCD 的面积分成1：3两部分时，直接写出x 的值．【分析】(1)当PQ ⊥AB 时，BQ =2PB ，由此构建方程即可解决问题； (2)分三种情形分别求解即可解决问题； (3)分两种情形分别求解即可解决问题； 【解答】解：(1)当PQ ⊥AB 时，BQ =2PB ， ∴2x =2(2﹣2x )， ∴x =23s ．故答案为23s ．(2)①如图1中，当0＜x ≤23时，重叠部分是四边形PQMN ．y =2x ×√3x =2√3x 2． ②如图②中，当23＜x ≤1时，重叠部分是四边形PQEN ．y =12(2﹣x +2tx ×√3x =√32x 2+√3x ③如图3中，当1＜x ＜2时，重叠部分是四边形PNEQ ．y =12(2﹣x +2)×[√3x ﹣2√3(x ﹣1)]=√32x 2﹣3√3x +4√3； 综上所述，y ={2√3x 2(0＜x ≤23)√32x 2+√3x(23＜x ≤1)√32x 2−3√3x +4√3(1＜x ＜2)．(3)①如图4中，当直线AM 经过BC 中点E 时，满足条件．则有：tan ∠EAB =tan ∠QPB ，∴√32=√3x 2−2x−x， 解得x =25．②如图5中，当直线AM 经过CD 的中点E 时，满足条件．此时tan ∠DEA =tan ∠QPB ，∴2√31=√3x2−2x−x， 解得x =47，综上所述，当x =25或47时，直线AM 将矩形ABCD 的面积分成1：3两部分．26．(10分)如图，在平面直角坐标系中，抛物线y =ax 2+2ax ﹣3a (a ＜0)与x 轴相交于A ，B 两点，与y 轴相交于点C ，顶点为D ，直线DC 与x 轴相交于点E ．(1)当a =﹣1时，抛物线顶点D 的坐标为 (﹣1，4) ，OE = 3 ； (2)OE 的长是否与a 值有关，说明你的理由； (3)设∠DEO =β，45°≤β≤60°，求a 的取值范围；(4)以DE 为斜边，在直线DE 的左下方作等腰直角三角形PDE ．设P (m ，n )，直接写出n 关于m 的函数解析式及自变量m 的取值范围．【分析】(1)求出直线CD 的解析式即可解决问题；(2)利用参数a，求出直线CD的解析式求出点E坐标即可判断；(3)求出落在特殊情形下的a的值即可判断；(4)如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：(1)当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D(﹣1，4)，C(0，3)，∴直线CD的解析式为y=﹣x+3，∴E(3，0)，∴OE=3，故答案为(﹣1，4)，3．(2)结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C(0，﹣3a)，D(﹣1，﹣4a)，∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E(3，0)，∴OE=3，∴OE的长与a值无关．(3)当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=√3OE=3√3，∴﹣3a=3√3，∴a=﹣√3，∴45°≤β≤60°，a的取值范围为﹣√3≤a≤﹣1．(4)如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D(﹣1，﹣4a)，E(3，0)，∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P(1，﹣2)，此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1(m＜1)．第21页（共21页）。

2018年吉林省中考数学试卷参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2分）计算（﹣1）×（﹣2）的结果是（）A．2B．1C．﹣2D．﹣3【解答】解：（﹣1）×（﹣2）=2．故选：A．2．（2分）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．3．（2分）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）3【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．4．（2分）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a 与b平行，木条a旋转的度数至少是（）A ．10°B ．20°C ．50°D ．70°【解答】解：如图．∵∠AOC=∠2=50°时，OA ∥b ，∴要使木条a 与b 平行，木条a 旋转的度数至少是70°﹣50°=20°．故选：B ．5．（2分）如图，将△ABC 折叠，使点A 与BC 边中点D 重合，折痕为MN ，若AB=9，BC=6，则△DNB 的周长为（）A ．12B ．13C ．14D ．15【解答】解：∵D 为BC 的中点，且BC=6，∴BD=12BC=3，由折叠性质知NA=ND ，则△DNB 的周长=ND +NB +BD=NA +NB +BD=AB +BD=3+9=12，故选：A ．6．（2分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为（）A．+=352+2=94B．+=354+2=94C．+=354+4=94D．+=352+4=94【解答】解：由题意可得，+=352+4=94，故选：D．二、填空题（共8小题，每小题3分，满分24分）7．（3分）计算：16=4．【解答】解：∵42=16，∴16=4，故答案为4．8．（3分）买单价3元的圆珠笔m支，应付3m元．【解答】解：依题意得：3m．故答案是：3m．9．（3分）若a+b=4，ab=1，则a2b+ab2=4．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．10．（3分）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m 的值为﹣1．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．11．（3分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB=32+42=5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），12．（3分）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【解答】解：∵∠ADB=∠EDC ，∠ABC=∠ECD=90°，∴△ABD ∽△ECD ，=，=×，解得：AB=120×5060=100（米）．故答案为：100．13．（3分）如图，A ，B ，C ，D 是⊙O 上的四个点，=，若∠AOB=58°，则∠BDC=29度．【解答】解：连接OC ．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=12∠BOC=29°，故答案为29．14．（3分）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k=12，则该等腰三角形的顶角为36度．【解答】解：∵△ABC 中，AB=AC ，∴∠B=∠C ，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k=12，∴∠A ：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．三、解答题（共12小题，满分84分）15．（5分）某同学化简a （a +2b ）﹣（a +b ）（a ﹣b ）出现了错误，解答过程如下：原式=a 2+2ab ﹣（a 2﹣b 2）（第一步）=a 2+2ab ﹣a 2﹣b 2（第二步）=2ab ﹣b 2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a 2+2ab ﹣（a 2﹣b 2）=a 2+2ab ﹣a 2+b 2=2ab +b 2．16．（5分）如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，且BE=CF ，求证：△ABE ≌△BCF ．【解答】证明：∵四边形ABCD 是正方形，∴AB=BC ，∠ABE=∠BCF=90°，在△ABE 和△BCF 中，=∠=∠=，∴△ABE ≌△BCF ．17．（5分）一个不透明的口袋中有三个小球，上面分别标有字母A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【解答】解：列表得：AB C A （A ，A ）（B ，A ）（C ，A ）B （A ，B ）（B ，B ）（C ，B ）C（A ，C ）（B ，C ）（C ，C ）由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率=39=13．18．（5分）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=3．19．（7分）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：400=600+20，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．600﹣400=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，400=40．答：甲队每天修路的长度为40米．20．（7分）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×90⋅⋅4180=8π．21．（7分）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测量步骤（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a 米，CD=b 米．计算过程【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a 米，CD=b 米．（3）计算过程：∵四边形BCDE 是矩形，∴DE=BC=a ，BE=CD=b ，在Rt △ADE 中，AE=ED•tan α=a•tan α，∴AB=AE+EB=a•tanα+b．22．（7分）为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【解答】解：整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．23．（8分）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000m，小玲步行的速度为100m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷20=200m/s 故答案为：4000，100（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤40 3（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．24．（8分）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D 为AB 中点，∴AD=12AB ，∵DE ∥AC ，点D 为AB 中点，∴DE=12AC ，∵AB=AC ，∴AD=DE ，∴平行四边形ADEF 为菱形，故答案为：菱形；（3）四边形AEGF 是矩形，理由如下：由（1）得，四边形ADEF 为平行四边形，∴AF ∥DE ，AF=DE ，∵EG=DE ，∴AF ∥DE ，AF=GE ，∴四边形AEGF 是平行四边形，∵AD=AG ，EG=DE ，∴AE ⊥EG ，∴四边形AEGF 是矩形．25．（10分）如图，在矩形ABCD 中，AB=2cm ，∠ADB=30°．P ，Q 两点分别从A ，B 同时出发，点P 沿折线AB ﹣BC 运动，在AB 上的速度是2cm/s ，在BC 上的速度是23cm/s ；点Q 在BD 上以2cm/s 的速度向终点D 运动，过点P 作PN ⊥AD ，垂足为点N ．连接PQ ，以PQ ，PN 为邻边作▱PQMN ．设运动的时间为x （s ），▱PQMN 与矩形ABCD 重叠部分的图形面积为y （cm 2）（1）当PQ ⊥AB 时，x=23s ；（2）求y 关于x 的函数解析式，并写出x 的取值范围；（3）直线AM 将矩形ABCD 的面积分成1：3两部分时，直接写出x 的值．【解答】解：（1）当PQ ⊥AB 时，BQ=2PB ，∴2x=2（2﹣2x ），∴x=23s ．23s ．（2）①如图1中，当0＜x ≤23时，重叠部分是四边形PQMN ．y=2x ×3x=23x 2．23＜x ≤1时，重叠部分是四边形PQEN ．y=12（2﹣x +2tx ×3x=32x 2+3x③如图3中，当1＜x ＜2时，重叠部分是四边形PNEQ．y=12（2﹣x +2）×[3x ﹣23（x ﹣1）]=32x 2﹣33x +43；综上所述，y={232(0＜≤23)322+3(23＜≤1)322−33+43(1＜＜2)．（3）①如图4中，当直线AM 经过BC中点E 时，满足条件．则有：tan ∠EAB=tan ∠QPB ，∴32=32−2−，解得x=25．②如图5中，当直线AM 经过CD 的中点E 时，满足条件．此时tan ∠DEA=tan ∠QPB ，231=32−2−，解得x=47，综上所述，当x=25或47时，直线AM 将矩形ABCD 的面积分成1：3两部分．26．（10分）如图，在平面直角坐标系中，抛物线y=ax 2+2ax ﹣3a （a ＜0）与x 轴相交于A ，B 两点，与y 轴相交于点C ，顶点为D ，直线DC 与x 轴相交于点E ．（1）当a=﹣1时，抛物线顶点D 的坐标为（﹣1，4），OE=3；（2）OE 的长是否与a 值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a 的取值范围；（4）以DE 为斜边，在直线DE 的左下方作等腰直角三角形PDE ．设P （m ，n ），直接写出n 关于m 的函数解析式及自变量m 的取值范围．【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x 2﹣2x +3，∴顶点D （﹣1，4），C （0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=3OE=33，∴﹣3a=33，∴a=﹣3，∴45°≤β≤60°，a的取值范围为﹣3≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．。

2018年省中考数学试卷一、选择题(共6小题，每小题2分，满分12分)1．(2分)计算(﹣1)×(﹣2)的结果是( )A．2 B．1 C．﹣2 D．﹣32．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是( )A．B．C．D．3．(2分)下列计算结果为a6的是( )A．a2•a3B．a12÷a2C．(a2)3D．(﹣a2)34．(2分)如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是( )A．10°B．20°C．50°D．70°5．(2分)如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为( )A．12 B．13 C．14 D．156．(2分)我国古代数学著作《子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为( )A．{x+x=352x+2x=94B．{x+x=354x+2x=94C．{x+x=354x+4x=94D．{x+x=352x+4x=94二、填空题(共8小题，每小题3分，满分24分)7．(3分)计算：√16= ．8．(3分)买单价3元的圆珠笔m支，应付元．9．(3分)若a+b=4，ab=1，则a2b+ab2= ．10．(3分)若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为．11．(3分)如图，在平面直角坐标系中，A (4，0)，B (0，3)，以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C ，则点C 坐标为 ．12．(3分)如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B =∠C =90°，测得BD =120m ，DC =60m ，EC =50m ，求得河宽AB = m ．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，xx̂=xx ̂，若∠AOB =58°，则∠BDC = 度．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 度．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下：原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步)=2ab ﹣b 2(第三步)(1)该同学解答过程从第 步开始出错，错误原因是 ； (2)写出此题正确的解答过程．16．(5分)如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，且BE =CF ，求证：△ABE ≌△BCF ．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．18．(5分)在平面直角坐标系中，反比例函数y =x x(k ≠0)图象与一次函数y =x +2图象的一个交点为P ，且点P 的横坐标为1，求该反比例函数的解析式．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示 ，庆庆同学所列方程中的y 表示 ； (2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 对称图形；(3)求所画图形的周长(结果保留π)．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题 方案示意图测量步骤(1)用 测得∠ADE =α；(2)用 测得BC =a 米，CD =b 米．计算过程22．(7分)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量(g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411频数种类甲30013乙0150分析数据：表二种类平均数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装情况比较好的是(填甲或乙)，说明你的理由．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为m，小玲步行的速度为m/min；(2)求小东离家的路程y关于x的函数解析式，并写出自变量的取值围；(3)求两人相遇的时间．24．(8分)如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．(1)求证：四边形ADEF为平行四边形；(2)当点D为AB中点时，▱ADEF的形状为；(3)延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．(10分)如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB 上的速度是2cm/s，在BC上的速度是2√3cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x(s)，▱PQMN与矩形ABCD重叠部分的图形面积为y(cm2)(1)当PQ⊥AB时，x= ；(2)求y关于x的函数解析式，并写出x的取值围；(3)直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．(10分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．(1)当a=﹣1时，抛物线顶点D的坐标为，OE= ；(2)OE的长是否与a值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a的取值围；(4)以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n关于m的函数解析式及自变量m的取值围．2018年省中考数学试卷参考答案与试题解析一、选择题(共6小题，每小题2分，满分12分)1．(2分)计算(﹣1)×(﹣2)的结果是( )A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：(﹣1)×(﹣2)=2．故选：A．2．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是( )A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．3．(2分)下列计算结果为a6的是( )A．a2•a3B．a12÷a2C．(a2)3D．(﹣a2)3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、(a2)3=a6，此选项符合题意；D、(﹣a2)3=﹣a6，此选项不符合题意；故选：C．4．(2分)如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是( )A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．5．(2分)如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为( )A ．12B ．13C ．14D ．15【分析】由D 为BC 中点知BD =3，再由折叠性质得ND =NA ，从而根据△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD 可得答案． 【解答】解：∵D 为BC 的中点，且BC =6，∴BD =12BC =3，由折叠性质知NA =ND ，则△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD =3+9=12， 故选：A ．6．(2分)我国古代数学著作《子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为( ) A ．{x +x =352x +2x =94 B ．{x +x =354x +2x =94C ．{x +x =354x +4x =94D ．{x +x =352x +4x =94【分析】根据题意可以列出相应的方程组，从而可以解答本题． 【解答】解：由题意可得， {x +x =352x +4x =94， 故选：D ．二、填空题(共8小题，每小题3分，满分24分) 7．(3分)计算：√16= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16， ∴√16=4， 故答案为4．8．(3分)买单价3元的圆珠笔m 支，应付 3m 元． 【分析】根据总价=单价×数量列出代数式． 【解答】解：依题意得：3m ． 故答案是：3m ．9．(3分)若a +b =4，ab =1，则a 2b +ab 2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案． 【解答】解：∵a +b =4，ab =1，∴a 2b +ab 2=ab (a +b ) =1×4 =4．故答案为：4．10．(3分)若关于x 的一元二次方程x 2+2x ﹣m =0有两个相等的实数根，则m 的值为 ﹣1 ．【分析】由于关于x 的一元二次方程x 2+2x ﹣m =0有两个相等的实数根，可知其判别式为0，据此列出关于m 的不等式，解答即可．【解答】解：∵关于x 的一元二次方程x 2+2x ﹣m =0有两个相等的实数根，∴△=b 2﹣4ac =0，即：22﹣4(﹣m )=0， 解得：m =﹣1， 故选答案为﹣1．11．(3分)如图，在平面直角坐标系中，A (4，0)，B (0，3)，以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C ，则点C 坐标为 (﹣1，0) ．【分析】求出OA 、OB ，根据勾股定理求出AB ，即可得出AC ，求出OC 长即可． 【解答】解：∵点A ，B 的坐标分别为(4，0)，(0，3)， ∴OA =4，OB =3，在Rt △AOB 中，由勾股定理得：AB =√32+42=5， ∴AC =AB =5， ∴OC =5﹣4=1，∴点C 的坐标为(﹣1，0)， 故答案为：(﹣1，0)，12．(3分)如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B =∠C =90°，测得BD =120m ，DC =60m ，EC =50m ，求得河宽AB = 100 m ．【分析】由两角对应相等可得△BAD ∽△CED ，利用对应边成比例可得两岸间的大致距离AB ． 【解答】解：∵∠ADB =∠EDC ，∠ABC =∠ECD =90°， ∴△ABD ∽△ECD ，∴xx xx =xx xx，xx =xx ×xxxx ，解得：AB =120×5060=100(米)．故答案为：100．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，xx̂=xx ̂，若∠AOB =58°，则∠BDC = 29 度．【分析】根据∠BDC =12∠BOC 求解即可； 【解答】解：连接OC ．∵xx̂=xx ̂， ∴∠AOB =∠BOC =58°， ∴∠BDC =12∠BOC =29°， 故答案为29．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 36 度．【分析】根据等腰三角形的性质得出∠B =∠C ，根据三角形角和定理和已知得出5∠A =180°，求出即可．【解答】解：∵△ABC 中，AB =AC ， ∴∠B =∠C ，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12， ∴∠A ：∠B =1：2， 即5∠A =180°， ∴∠A =36°， 故答案为：36．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下：原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步)=2ab ﹣b 2(第三步)(1)该同学解答过程从第 二 步开始出错，错误原因是 去括号时没有变号 ； (2)写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：(1)该同学解答过程从第 二步开始出错，错误原因是 去括号时没有变号； 故答案是：二；去括号时没有变号；(2)原式=a 2+2ab ﹣(a 2﹣b 2) =a 2+2ab ﹣a 2+b 2=2ab +b 2．16．(5分)如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，且BE =CF ，求证：△ABE ≌△BCF ．【分析】根据正方形的性质，利用SAS 即可证明； 【解答】证明：∵四边形ABCD 是正方形， ∴AB =BC ，∠ABE =∠BCF =90°， 在△ABE 和△BCF 中， {xx =xx∠xxx =∠xxx xx =xx， ∴△ABE ≌△BCF ．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率． 【解答】解：列表得：A B CA (A ，A ) (B ，A ) (C ，A ) B (A ，B )(B ，B )(C ，B )C(A ，C ) (B ，C ) (C ，C )由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种， 所以该同学两次摸出的小球所标字母相同的概率=39=13．18．(5分)在平面直角坐标系中，反比例函数y =x x (k ≠0)图象与一次函数y =x +2图象的一个交点为P ，且点P 的横坐标为1，求该反比例函数的解析式．【分析】先求出P 点的坐标，再把P 点的坐标代入反比例函数的解析式，即可求出答案． 【解答】解：∵把x =1代入y =x +2得：y =3， 即P 点的坐标是(1，3)，把P 点的坐标代入y =x x得：k =3，即反比例函数的解析式是y =3x．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示 甲队每天修路的长度 ，庆庆同学所列方程中的y 表示 甲队修路400米所需时间或乙队修路600米所需时间 ；(2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．【分析】(1)根据两人的方程思路，可得出：x 表示甲队每天修路的长度；y 表示甲队修路400米所需时间或乙队修路600米所需时间；(2)根据题意，可找出：(冰冰)甲队修路400米所用时间=乙队修路600米所用时间；(庆庆)乙队每天修路的长度﹣甲队每天修路的长度=20米；(3)选择两个方程中的一个，解之即可得出结论．【解答】解：(1)∵冰冰是根据时间相等列出的分式方程， ∴x 表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y 表示甲队修路400米所需时间或乙队修路600米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间或乙队修路600米所需时间． (2)冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米(选择一个即可)． (3)选冰冰的方程：400x =600x +20， 去分母，得：400x +8000=600x ， 移项，x 的系数化为1，得：x =40，检验：当x =40时，x 、x +20均不为零， ∴x =40．答：甲队每天修路的长度为40米． 选庆庆的方程：600x ﹣400x=20， 去分母，得：600﹣400=20y ，将y 的系数化为1，得：y =10， 经验：当y =10时，分母y 不为0， ∴y =10， ∴400x=40． 答：甲队每天修路的长度为40米．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1；第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 轴对称 对称图形； (3)求所画图形的周长(结果保留π)．【分析】(1)利用旋转变换的性质画出图象即可； (2)根据轴对称图形的定义即可判断； (3)利用弧长公式计算即可；【解答】解：(1)点D →D 1→D 2→D 经过的路径如图所示：(2)观察图象可知图象是轴对称图形， 故答案为轴对称．(3)周长=4×90⋅x ⋅4180=8π．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题方案示意图测量步骤 (1)用 测角仪 测得∠ADE =α； (2)用 皮尺 测得BC =a 米，CD =b 米．计算过程【分析】在Rt △ADE 中，求出AE ，再利用AB =AE +BE 计算即可； 【解答】解：(1)用 测角仪测得∠ADE =α； (2)用 皮尺测得BC =a 米，CD =b 米． (3)计算过程：∵四边形BCDE 是矩形， ∴DE =BC =a ，BE =CD =b ，在Rt △ADE 中，AE =ED •tan α=a •tan α， ∴AB =AE +EB =a •tan α+b ．22．(7分)为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题． 收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g )如下： 甲：400，400，408，406，410，409，400，393，394，395 乙：403，404，396，399，402，402，405，397，402，398整理数据：表一393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411质量(g)频数种类甲30 3 013乙0 3 15 1 0分析数据：表二种类平均数中位数众数方差甲401.5400 40036.85乙400.8402402 8.56得出结论：包装机分装情况比较好的是乙(填甲或乙)，说明你的理由．【分析】整理数据：由题干中的数据结合表中围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411质量(g)频数种类甲303013乙031510分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为4000 m，小玲步行的速度为100 m/min；(2)求小东离家的路程y关于x的函数解析式，并写出自变量的取值围；(3)求两人相遇的时间．【分析】(1)认真分析图象得到路程与速度数据；(2)采用方程思想列出小东离家路程y与时间x之间的函数关系式；(3)两人相遇实际上是函数图象求交点．【解答】解：(1)结合题意和图象可知，线段CD为小东路程与时间函数图象，折线O﹣A﹣B为小玲路程与时间图象则家与图书馆之间路程为4000m ，小玲步行速度为2000÷20=100m /s 故答案为：4000，100(2)∵小东从离家4000m 处以300m /min 的速度返回家，则xmin 时， ∴他离家的路程y =4000﹣300x 自变量x 的围为0≤x ≤403(3)由图象可知，两人相遇是在小玲改变速度之前 ∴4000﹣300x =200x 解得x =8∴两人相遇时间为第8分钟．24．(8分)如图①，在△ABC 中，AB =AC ，过AB 上一点D 作DE ∥AC 交BC 于点E ，以E 为顶点，ED 为一边，作∠DEF =∠A ，另一边EF 交AC 于点F ．(1)求证：四边形ADEF 为平行四边形；(2)当点D 为AB 中点时，▱ADEF 的形状为 菱形 ；(3)延长图①中的DE 到点G ，使EG =DE ，连接AE ，AG ，FG ，得到图②，若AD =AG ，判断四边形AEGF 的形状，并说明理由．【分析】(1)根据平行线的性质得到∠BDE =∠A ，根据题意得到∠DEF =∠BDE ，根据平行线的判定定理得到AD ∥EF ，根据平行四边形的判定定理证明；(2)根据三角形中位线定理得到DE =12AC ，得到AD =DE ，根据菱形的判定定理证明； (3)根据等腰三角形的性质得到AE ⊥EG ，根据有一个角是直角的平行四边形是矩形证明． 【解答】(1)证明：∵DE ∥AC ， ∴∠BDE =∠A ， ∵∠DEF =∠A ， ∴∠DEF =∠BDE ，∴AD ∥EF ，又∵DE ∥AC ，∴四边形ADEF 为平行四边形； (2)解：▱ADEF 的形状为菱形， 理由如下：∵点D 为AB 中点， ∴AD =12AB ，∵DE ∥AC ，点D 为AB 中点， ∴DE =12AC ，∵AB =AC ， ∴AD =DE ，∴平行四边形ADEF 为菱形， 故答案为：菱形；(3)四边形AEGF 是矩形，理由如下：由(1)得，四边形ADEF 为平行四边形， ∴AF ∥DE ，AF =DE ， ∵EG =DE ，∴AF ∥DE ，AF =GE ，∴四边形AEGF 是平行四边形， ∵AD =AG ，EG =DE ， ∴AE ⊥EG ，∴四边形AEGF 是矩形．25．(10分)如图，在矩形ABCD 中，AB =2cm ，∠ADB =30°．P ，Q 两点分别从A ，B 同时出发，点P 沿折线AB ﹣BC 运动，在AB 上的速度是2cm /s ，在BC 上的速度是2√3cm /s ；点Q 在BD 上以2cm /s 的速度向终点D 运动，过点P 作PN ⊥AD ，垂足为点N ．连接PQ ，以PQ ，PN 为邻边作▱PQMN ．设运动的时间为x (s )，▱PQMN 与矩形ABCD 重叠部分的图形面积为y (cm 2) (1)当PQ ⊥AB 时，x = 23s ；(2)求y 关于x 的函数解析式，并写出x 的取值围；(3)直线AM 将矩形ABCD 的面积分成1：3两部分时，直接写出x 的值．【分析】(1)当PQ ⊥AB 时，BQ =2PB ，由此构建方程即可解决问题； (2)分三种情形分别求解即可解决问题； (3)分两种情形分别求解即可解决问题； 【解答】解：(1)当PQ ⊥AB 时，BQ =2PB ， ∴2x =2(2﹣2x )， ∴x =23s ． 故答案为23s ．(2)①如图1中，当0＜x ≤23时，重叠部分是四边形PQMN ．y =2x ×√3x =2√3x 2．②如图②中，当23＜x ≤1时，重叠部分是四边形PQEN ．y =12(2﹣x +2tx ×√3x =√32x 2+√3x ③如图3中，当1＜x ＜2时，重叠部分是四边形PNEQ ．y =12(2﹣x +2)×[√3x ﹣2√3(x ﹣1)]=√32x 2﹣3√3x +4√3；综上所述，y ={2√3x2(0＜x ≤23)√32x 2+√3x (23＜x ≤1)√32x 2−3√3x +4√3(1＜x＜2)．(3)①如图4中，当直线AM 经过BC 中点E 时，满足条件．则有：tan ∠EAB =tan ∠QPB ， ∴√32=√3x2−2x −x，解得x =25．②如图5中，当直线AM 经过CD 的中点E 时，满足条件．此时tan ∠DEA =tan ∠QPB ，∴2√31=√3x2−2x −x， 解得x =47，综上所述，当x =25或47时，直线AM 将矩形ABCD 的面积分成1：3两部分．26．(10分)如图，在平面直角坐标系中，抛物线y =ax 2+2ax ﹣3a (a ＜0)与x 轴相交于A ，B 两点，与y 轴相交于点C ，顶点为D ，直线DC 与x 轴相交于点E ．(1)当a=﹣1时，抛物线顶点D的坐标为(﹣1，4) ，OE= 3 ；(2)OE的长是否与a值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a的取值围；(4)以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n关于m的函数解析式及自变量m的取值围．【分析】(1)求出直线CD的解析式即可解决问题；(2)利用参数a，求出直线CD的解析式求出点E坐标即可判断；(3)求出落在特殊情形下的a的值即可判断；(4)如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：(1)当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D(﹣1，4)，C(0，3)，∴直线CD的解析式为y=﹣x+3，∴E(3，0)，∴OE=3，故答案为(﹣1，4)，3．(2)结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C(0，﹣3a)，D(﹣1，﹣4a)，∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E(3，0)，∴OE=3，∴OE的长与a值无关．(3)当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=√3OE=3√3，∴﹣3a=3√3，∴a=﹣√3，∴45°≤β≤60°，a的取值围为﹣√3≤a≤﹣1．(4)如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D(﹣1，﹣4a)，E(3，0)，∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P(1，﹣2)，此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1(m＜1)．。

2018年吉林省中考数学试卷一、选择题(共6小题，每小题2分，满分12分) 1．(2分)计算(﹣1)×(﹣2)的结果是( ) A ．2B ．1C ．﹣2D ．﹣32．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是( )A ．B ．C ．D ．3．(2分)下列计算结果为a 6的是( )A ．a 2•a 3B ．a 12÷a 2C ．(a 2)3D ．(﹣a 2)34．(2分)如图，将木条a ，b 与c 钉在一起，∠1=70°，∠2=50°，要使木条a 与b 平行，木条a 旋转的度数至少是( )A ．10°B ．20°C ．50°D ．70°5．(2分)如图，将△ABC 折叠，使点A 与BC 边中点D 重合，折痕为MN ，若AB =9，BC =6，则△DNB 的周长为( )A ．12B ．13C ．14D ．156．(2分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为( )A ．{x +y =352x +2y =94B ．{x +y =354x +2y =94C ．{x +y =354x +4y =94D ．{x +y =352x +4y =94二、填空题(共8小题，每小题3分，满分24分) 7．(3分)计算：√16= ．8．(3分)买单价3元的圆珠笔m 支，应付 元．9．(3分)若a +b =4，ab =1，则a 2b +ab 2= ．10．(3分)若关于x 的一元二次方程x 2+2x ﹣m =0有两个相等的实数根，则m 的值为 ．11．(3分)如图，在平面直角坐标系中，A (4，0)，B (0，3)，以点A 为圆心，AB 长为半径画弧，交x 轴的负半轴于点C ，则点C 坐标为 ．12．(3分)如图是测量河宽的示意图，AE 与BC 相交于点D ，∠B =∠C =90°，测得BD =120m ，DC =60m ，EC =50m ，求得河宽AB = m ．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，AB̂=BC ̂，若∠AOB =58°，则∠BDC = 度．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 度．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下： 原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步) =2ab ﹣b 2 (第三步)(1)该同学解答过程从第 步开始出错，错误原因是 ； (2)写出此题正确的解答过程．16．(5分)如图，在正方形ABCD中，点E，F分别在BC，CD上，且BE=CF，求证：△ABE≌△BCF．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．18．(5分)在平面直角坐标系中，反比例函数y=kx(k≠0)图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；(2)两个方程中任选一个，并写出它的等量关系；(3)解(2)中你所选择的方程，并回答老师提出的问题．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 对称图形； (3)求所画图形的周长(结果保留π)．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题 方案示意图测量步骤(1)用 测得∠ADE =α；(2)用 测得BC =a 米，CD =b 米．计算过程22．(7分)为了调查甲、乙两台包装机分装标准质量为400g奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量(g)393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411频数种类甲30013乙0150分析数据：表二种类平均数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装情况比较好的是(填甲或乙)，说明你的理由．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示(1)家与图书馆之间的路程为m，小玲步行的速度为m/min；(2)求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；(3)求两人相遇的时间．24．(8分)如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．(1)求证：四边形ADEF为平行四边形；(2)当点D为AB中点时，▱ADEF的形状为；(3)延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．(10分)如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2√3cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x(s)，▱PQMN与矩形ABCD重叠部分的图形面积为y(cm2)(1)当PQ⊥AB时，x=；(2)求y关于x的函数解析式，并写出x的取值范围；(3)直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．(10分)如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a(a＜0)与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．(1)当a=﹣1时，抛物线顶点D的坐标为，OE=；(2)OE的长是否与a值有关，说明你的理由；(3)设∠DEO=β，45°≤β≤60°，求a的取值范围；(4)以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P(m，n)，直接写出n关于m的函数解析式及自变量m的取值范围．2018年吉林省中考数学试卷参考答案与试题解析一、选择题(共6小题，每小题2分，满分12分)1．(2分)计算(﹣1)×(﹣2)的结果是()A．2B．1C．﹣2D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：(﹣1)×(﹣2)=2．故选：A．2．(2分)如图是由4个相同的小正方体组成的立体图形，它的主视图是()A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．3．(2分)下列计算结果为a6的是()A．a2•a3B．a12÷a2C．(a2)3D．(﹣a2)3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、(a2)3=a6，此选项符合题意；D、(﹣a2)3=﹣a6，此选项不符合题意；故选：C．4．(2分)如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是()A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．5．(2分)如图，将△ABC 折叠，使点A 与BC 边中点D 重合，折痕为MN ，若AB =9，BC =6，则△DNB 的周长为( )A ．12B ．13C ．14D ．15【分析】由D 为BC 中点知BD =3，再由折叠性质得ND =NA ，从而根据△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD 可得答案．【解答】解：∵D 为BC 的中点，且BC =6， ∴BD =12BC =3，由折叠性质知NA =ND ，则△DNB 的周长=ND +NB +BD =NA +NB +BD =AB +BD =3+9=12，故选：A ．6．(2分)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x 只，兔y 只，可列方程组为( )A ．{x +y =352x +2y =94B ．{x +y =354x +2y =94C ．{x +y =354x +4y =94D ．{x +y =352x +4y =94【分析】根据题意可以列出相应的方程组，从而可以解答本题． 【解答】解：由题意可得， {x +y =352x +4y =94， 故选：D ．二、填空题(共8小题，每小题3分，满分24分) 7．(3分)计算：√16= 4 ．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16， ∴√16=4，故答案为4．8．(3分)买单价3元的圆珠笔m 支，应付 3m 元． 【分析】根据总价=单价×数量列出代数式． 【解答】解：依题意得：3m ．故答案是：3m ．9．(3分)若a +b =4，ab =1，则a 2b +ab 2= 4 ．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab(a+b)=1×4=4．故答案为：4．10．(3分)若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为﹣1．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4(﹣m)=0，解得：m=﹣1，故选答案为﹣1．11．(3分)如图，在平面直角坐标系中，A(4，0)，B(0，3)，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为(﹣1，0)．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为(4，0)，(0，3)，∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB=√32+42=5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为(﹣1，0)，故答案为：(﹣1，0)，12．(3分)如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴ABEC=BDCD，AB=BD×ECCD，解得：AB =120×5060=100(米)．故答案为：100．13．(3分)如图，A ，B ，C ，D 是⊙O 上的四个点，AB̂=BC ̂，若∠AOB =58°，则∠BDC = 29 度．【分析】根据∠BDC =12∠BOC 求解即可；【解答】解：连接OC ．∵AB̂=BC ̂， ∴∠AOB =∠BOC =58°， ∴∠BDC =12∠BOC =29°，故答案为29．14．(3分)我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，则该等腰三角形的顶角为 36 度．【分析】根据等腰三角形的性质得出∠B =∠C ，根据三角形内角和定理和已知得出5∠A =180°，求出即可．【解答】解：∵△ABC 中，AB =AC ， ∴∠B =∠C ，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k ，若k =12，∴∠A ：∠B =1：2， 即5∠A =180°， ∴∠A =36°，故答案为：36．三、解答题(共12小题，满分84分)15．(5分)某同学化简a (a +2b )﹣(a +b )(a ﹣b )出现了错误，解答过程如下： 原式=a 2+2ab ﹣(a 2﹣b 2) (第一步) =a 2+2ab ﹣a 2﹣b 2(第二步) =2ab ﹣b 2 (第三步)(1)该同学解答过程从第 二 步开始出错，错误原因是 去括号时没有变号 ；(2)写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：(1)该同学解答过程从第 二步开始出错，错误原因是 去括号时没有变号； 故答案是：二；去括号时没有变号；(2)原式=a 2+2ab ﹣(a 2﹣b 2) =a 2+2ab ﹣a 2+b 2=2ab +b 2．16．(5分)如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，且BE =CF ，求证：△ABE ≌△BCF ．【分析】根据正方形的性质，利用SAS 即可证明； 【解答】证明：∵四边形ABCD 是正方形， ∴AB =BC ，∠ABE =∠BCF =90°，在△ABE 和△BCF 中， {AB =BC∠ABE =∠BCF BE =CF， ∴△ABE ≌△BCF ．17．(5分)一个不透明的口袋中有三个小球，上面分别标有字母A ，B ，C ，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图(或列表)的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率． 【解答】解：列表得：A B C A (A ，A ) (B ，A ) (C ，A ) B (A ，B ) (B ，B ) (C ，B ) C(A ，C )(B ，C )(C ，C )由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种， 所以该同学两次摸出的小球所标字母相同的概率=39=13．18．(5分)在平面直角坐标系中，反比例函数y =kx (k ≠0)图象与一次函数y =x +2图象的一个交点为P ，且点P 的横坐标为1，求该反比例函数的解析式．【分析】先求出P 点的坐标，再把P 点的坐标代入反比例函数的解析式，即可求出答案． 【解答】解：∵把x =1代入y =x +2得：y =3， 即P 点的坐标是(1，3)，把P 点的坐标代入y =kx 得：k =3，即反比例函数的解析式是y =3x．19．(7分)如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．(1)冰冰同学所列方程中的x 表示 甲队每天修路的长度 ，庆庆同学所列方程中的y 表示 甲队修路400米所需时间或乙队修路600米所需时间 ；(2)两个方程中任选一个，并写出它的等量关系； (3)解(2)中你所选择的方程，并回答老师提出的问题．【分析】(1)根据两人的方程思路，可得出：x 表示甲队每天修路的长度；y 表示甲队修路400米所需时间或乙队修路600米所需时间；(2)根据题意，可找出：(冰冰)甲队修路400米所用时间=乙队修路600米所用时间；(庆庆)乙队每天修路的长度﹣甲队每天修路的长度=20米；(3)选择两个方程中的一个，解之即可得出结论．【解答】解：(1)∵冰冰是根据时间相等列出的分式方程， ∴x 表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程， ∴y 表示甲队修路400米所需时间或乙队修路600米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间或乙队修路600米所需时间． (2)冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米(选择一个即可)． (3)选冰冰的方程：400x=600x+20，去分母，得：400x +8000=600x ， 移项，x 的系数化为1，得：x =40， 检验：当x =40时，x 、x +20均不为零， ∴x =40．答：甲队每天修路的长度为40米． 选庆庆的方程：600y﹣400y=20，去分母，得：600﹣400=20y ， 将y 的系数化为1，得：y =10， 经验：当y =10时，分母y 不为0， ∴y =10， ∴400y=40．答：甲队每天修路的长度为40米．20．(7分)如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A ，B ，C ，D 均在格点上，在网格中将点D 按下列步骤移动：第一步：点D 绕点A 顺时针旋转180°得到点D 1； 第二步：点D 1绕点B 顺时针旋转90°得到点D 2； 第三步：点D 2绕点C 顺时针旋转90°回到点D ． (1)请用圆规画出点D →D 1→D 2→D 经过的路径； (2)所画图形是 轴对称 对称图形； (3)求所画图形的周长(结果保留π)．【分析】(1)利用旋转变换的性质画出图象即可； (2)根据轴对称图形的定义即可判断； (3)利用弧长公式计算即可；【解答】解：(1)点D →D 1→D 2→D 经过的路径如图所示：(2)观察图象可知图象是轴对称图形， 故答案为轴对称．(3)周长=4×90⋅π⋅4180=8π．21．(7分)数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a ，b ，α的代数式表示旗杆AB 的高度． 数学活动方案活动时间：2018年4月2日 活动地点：学校操场 填表人：林平课题 测量学校旗杆的高度活动目的 运用所学数学知识及方法解决实际问题方案示意图测量步骤 (1)用 测角仪 测得∠ADE =α； (2)用 皮尺 测得BC =a 米，CD =b 米．计算过程【分析】在Rt △ADE 中，求出AE ，再利用AB =AE +BE 计算即可； 【解答】解：(1)用 测角仪测得∠ADE =α； (2)用 皮尺测得BC =a 米，CD =b 米． (3)计算过程：∵四边形BCDE 是矩形， ∴DE =BC =a ，BE =CD =b ，在Rt △ADE 中，AE =ED •tan α=a •tan α，∴AB =AE +EB =a •tan α+b ．22．(7分)为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题． 收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量(单位：g)如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量(g)频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：包装机分装情况比较好的是乙(填甲或乙)，说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一质量(g)频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013乙031510分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二种类平均数中位数众数方差甲401.540040036.85乙400.84024028.56得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．23．(8分)小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min ．小东骑自行车以300m /min 的速度直接回家，两人离家的路程y (m )与各自离开出发地的时间x (min )之间的函数图象如图所示(1)家与图书馆之间的路程为 4000 m ，小玲步行的速度为 100 m /min ； (2)求小东离家的路程y 关于x 的函数解析式，并写出自变量的取值范围； (3)求两人相遇的时间．【分析】(1)认真分析图象得到路程与速度数据；(2)采用方程思想列出小东离家路程y 与时间x 之间的函数关系式； (3)两人相遇实际上是函数图象求交点．【解答】解：(1)结合题意和图象可知，线段CD 为小东路程与时间函数图象，折线O ﹣A ﹣B 为小玲路程与时间图象 则家与图书馆之间路程为4000m ，小玲步行速度为2000÷20=100m /s 故答案为：4000，100(2)∵小东从离家4000m 处以300m /min 的速度返回家，则xmin 时， ∴他离家的路程y =4000﹣300x 自变量x 的范围为0≤x ≤403(3)由图象可知，两人相遇是在小玲改变速度之前 ∴4000﹣300x =200x 解得x =8∴两人相遇时间为第8分钟．24．(8分)如图①，在△ABC 中，AB =AC ，过AB 上一点D 作DE ∥AC 交BC 于点E ，以E 为顶点，ED 为一边，作∠DEF =∠A ，另一边EF 交AC 于点F ．(1)求证：四边形ADEF 为平行四边形；(2)当点D 为AB 中点时，▱ADEF 的形状为 菱形 ；(3)延长图①中的DE 到点G ，使EG =DE ，连接AE ，AG ，FG ，得到图②，若AD =AG ，判断四边形AEGF 的形状，并说明理由．【分析】(1)根据平行线的性质得到∠BDE =∠A ，根据题意得到∠DEF =∠BDE ，根据平行线的判定定理得到AD ∥EF ，根据平行四边形的判定定理证明；(2)根据三角形中位线定理得到DE =12AC ，得到AD =DE ，根据菱形的判定定理证明；(3)根据等腰三角形的性质得到AE ⊥EG ，根据有一个角是直角的平行四边形是矩形证明． 【解答】(1)证明：∵DE ∥AC ， ∴∠BDE =∠A ， ∵∠DEF =∠A ，∴∠DEF =∠BDE ，∴AD ∥EF ，又∵DE ∥AC ， ∴四边形ADEF 为平行四边形； (2)解：▱ADEF 的形状为菱形， 理由如下：∵点D 为AB 中点， ∴AD =12AB ，∵DE ∥AC ，点D 为AB 中点， ∴DE =12AC ， ∵AB =AC ， ∴AD =DE ，∴平行四边形ADEF 为菱形， 故答案为：菱形； (3)四边形AEGF 是矩形，理由如下：由(1)得，四边形ADEF 为平行四边形， ∴AF ∥DE ，AF =DE ， ∵EG =DE ，∴AF ∥DE ，AF =GE ，∴四边形AEGF 是平行四边形， ∵AD =AG ，EG =DE ， ∴AE ⊥EG ，∴四边形AEGF 是矩形．25．(10分)如图，在矩形ABCD 中，AB =2cm ，∠ADB =30°．P ，Q 两点分别从A ，B 同时出发，点P 沿折线AB ﹣BC 运动，在AB 上的速度是2cm /s ，在BC 上的速度是2√3cm /s ；点Q 在BD 上以2cm /s 的速度向终点D 运动，过点P 作PN ⊥AD ，垂足为点N ．连接PQ ，以PQ ，PN 为邻边作▱PQMN ．设运动的时间为x (s )，▱PQMN 与矩形ABCD 重叠部分的图形面积为y (cm 2) (1)当PQ ⊥AB 时，x =23s ；(2)求y 关于x 的函数解析式，并写出x 的取值范围；(3)直线AM 将矩形ABCD 的面积分成1：3两部分时，直接写出x 的值．【分析】(1)当PQ ⊥AB 时，BQ =2PB ，由此构建方程即可解决问题； (2)分三种情形分别求解即可解决问题； (3)分两种情形分别求解即可解决问题； 【解答】解：(1)当PQ ⊥AB 时，BQ =2PB ， ∴2x =2(2﹣2x )， ∴x =23s ．故答案为23s ．(2)①如图1中，当0＜x ≤23时，重叠部分是四边形PQMN ．y =2x ×√3x =2√3x 2．②如图②中，当23＜x ≤1时，重叠部分是四边形PQEN ．y =12(2﹣x +2tx ×√3x =√32x 2+√3x ③如图3中，当1＜x ＜2时，重叠部分是四边形PNEQ ．y =12(2﹣x +2)×[√3x ﹣2√3(x ﹣1)]=√32x 2﹣3√3x +4√3； 综上所述，y ={2√3x 2(0＜x ≤23)√32x 2+√3x(23＜x ≤1)√32x 2−3√3x +4√3(1＜x ＜2)．(3)①如图4中，当直线AM 经过BC 中点E 时，满足条件．则有：tan ∠EAB =tan ∠QPB ，∴√32=√3x 2−2x−x， 解得x =25．②如图5中，当直线AM 经过CD 的中点E 时，满足条件．此时tan ∠DEA =tan ∠QPB ，∴2√31=√3x2−2x−x， 解得x =47，综上所述，当x =25或47时，直线AM 将矩形ABCD 的面积分成1：3两部分．26．(10分)如图，在平面直角坐标系中，抛物线y =ax 2+2ax ﹣3a (a ＜0)与x 轴相交于A ，B 两点，与y 轴相交于点C ，顶点为D ，直线DC 与x 轴相交于点E ．(1)当a =﹣1时，抛物线顶点D 的坐标为 (﹣1，4) ，OE = 3 ； (2)OE 的长是否与a 值有关，说明你的理由； (3)设∠DEO =β，45°≤β≤60°，求a 的取值范围；(4)以DE 为斜边，在直线DE 的左下方作等腰直角三角形PDE ．设P (m ，n )，直接写出n 关于m 的函数解析式及自变量m 的取值范围．【分析】(1)求出直线CD 的解析式即可解决问题；(2)利用参数a，求出直线CD的解析式求出点E坐标即可判断；(3)求出落在特殊情形下的a的值即可判断；(4)如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：(1)当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D(﹣1，4)，C(0，3)，∴直线CD的解析式为y=﹣x+3，∴E(3，0)，∴OE=3，故答案为(﹣1，4)，3．(2)结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C(0，﹣3a)，D(﹣1，﹣4a)，∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E(3，0)，∴OE=3，∴OE的长与a值无关．(3)当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=√3OE=3√3，∴﹣3a=3√3，∴a=﹣√3，∴45°≤β≤60°，a的取值范围为﹣√3≤a≤﹣1．(4)如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D(﹣1，﹣4a)，E(3，0)，∴EN=4+n=3﹣m，资料收集于网络，如有侵权请联系网站删除∴n=﹣m﹣1，当顶点D在x轴上时，P(1，﹣2)，此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1(m＜1)．只供学习与交流。

2018年吉林省中考数学试卷一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）（2018•吉林）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣32．（2.00分）（2018•吉林）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．3．（2.00分）（2018•吉林）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）34．（2.00分）（2018•吉林）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10°B．20°C．50°D．70°5．（2.00分）（2018•吉林）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．156．（2.00分）（2018•吉林）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）（2018•吉林）计算：=．8．（3.00分）（2018•吉林）买单价3元的圆珠笔m支，应付元．9．（3.00分）（2018•吉林）若a+b=4，ab=1，则a2b+ab2=．10．（3.00分）（2018•吉林）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为．11．（3.00分）（2018•吉林）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为．12．（3.00分）（2018•吉林）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=m．13．（3.00分）（2018•吉林）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC=度．14．（3.00分）（2018•吉林）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为度．三、解答题（共12小题，满分84分）15．（5.00分）（2018•吉林）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第步开始出错，错误原因是；（2）写出此题正确的解答过程．16．（5.00分）（2018•吉林）如图，在正方形ABCD中，点E，F分别在BC，CD 上，且BE=CF，求证：△ABE≌△BCF．17．（5.00分）（2018•吉林）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．18．（5.00分）（2018•吉林）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．19．（7.00分）（2018•吉林）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示，庆庆同学所列方程中的y表示；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．20．（7.00分）（2018•吉林）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是对称图形；（3）求所画图形的周长（结果保留π）．21．（7.00分）（2018•吉林）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测量步骤（1）用测得∠ADE=α；（2）用测得BC=a米，CD=b米．计算过程22．（7.00分）（2018•吉林）为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲30013乙0150分析数据：表二种类平均数中位数众数方差甲401.540036.85乙400.84028.56得出结论：包装机分装情况比较好的是（填甲或乙），说明你的理由．23．（8.00分）（2018•吉林）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为m，小玲步行的速度为m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．24．（8.00分）（2018•吉林）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC 于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．25．（10.00分）（2018•吉林）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．26．（10.00分）（2018•吉林）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为，OE=；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n关于m的函数解析式及自变量m的取值范围．2018年吉林省中考数学试卷参考答案与试题解析一、选择题（共6小题，每小题2分，满分12分）1．（2.00分）（2018•吉林）计算（﹣1）×（﹣2）的结果是（）A．2 B．1 C．﹣2 D．﹣3【分析】根据“两数相乘，同号得正”即可求出结论．【解答】解：（﹣1）×（﹣2）=2．故选：A．【点评】本题考查了有理数的乘法，牢记“两数相乘，同号得正，异号得负，并把绝对值相乘”是解题的关键．2．（2.00分）（2018•吉林）如图是由4个相同的小正方体组成的立体图形，它的主视图是（）A．B．C．D．【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看易得第一层有3个正方形，第二层最右边有一个正方形．故选：B．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（2.00分）（2018•吉林）下列计算结果为a6的是（）A．a2•a3B．a12÷a2C．（a2）3D．（﹣a2）3【分析】分别根据同底数幂相乘、同底数幂相除、幂的乘方的运算法则逐一计算可得．【解答】解：A、a2•a3=a5，此选项不符合题意；B、a12÷a2=a10，此选项不符合题意；C、（a2）3=a6，此选项符合题意；D、（﹣a2）3=﹣a6，此选项不符合题意；故选：C．【点评】本题主要考查幂的运算，解题的关键是掌握同底数幂相乘、同底数幂相除、幂的乘方的运算法则．4．（2.00分）（2018•吉林）如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（）A．10°B．20°C．50°D．70°【分析】根据同位角相等两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．【解答】解：如图．∵∠AOC=∠2=50°时，OA∥b，∴要使木条a与b平行，木条a旋转的度数至少是70°﹣50°=20°．故选：B．【点评】本题考查了旋转的性质，平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．5．（2.00分）（2018•吉林）如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）A．12 B．13 C．14 D．15【分析】由D为BC中点知BD=3，再由折叠性质得ND=NA，从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案．【解答】解：∵D为BC的中点，且BC=6，∴BD=BC=3，由折叠性质知NA=ND，则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12，故选：A．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．（2.00分）（2018•吉林）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组为（）A．B．C．D．【分析】根据题意可以列出相应的方程组，从而可以解答本题．【解答】解：由题意可得，，故选：D．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．二、填空题（共8小题，每小题3分，满分24分）7．（3.00分）（2018•吉林）计算：=4．【分析】根据算术平方根的概念去解即可．算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根，由此即可求出结果．【解答】解：∵42=16，∴=4，故答案为4．【点评】此题主要考查了算术平方根的定义，算术平方根的概念易与平方根的概念混淆而导致错误．8．（3.00分）（2018•吉林）买单价3元的圆珠笔m支，应付3m元．【分析】根据总价=单价×数量列出代数式．【解答】解：依题意得：3m．故答案是：3m．【点评】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．9．（3.00分）（2018•吉林）若a+b=4，ab=1，则a2b+ab2=4．【分析】直接利用提取公因式法分解因式，再把已知代入求出答案．【解答】解：∵a+b=4，ab=1，∴a2b+ab2=ab（a+b）=1×4=4．故答案为：4．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．10．（3.00分）（2018•吉林）若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，则m的值为﹣1．【分析】由于关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，可知其判别式为0，据此列出关于m的不等式，解答即可．【解答】解：∵关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根，∴△=b2﹣4ac=0，即：22﹣4（﹣m）=0，解得：m=﹣1，故选答案为﹣1．【点评】本题考查了根的判别式，解题的关键是了解根的判别式如何决定一元二次方程根的情况．11．（3.00分）（2018•吉林）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为（﹣1，0）．【分析】求出OA、OB，根据勾股定理求出AB，即可得出AC，求出OC长即可．【解答】解：∵点A，B的坐标分别为（4，0），（0，3），∴OA=4，OB=3，在Rt△AOB中，由勾股定理得：AB==5，∴AC=AB=5，∴OC=5﹣4=1，∴点C的坐标为（﹣1，0），故答案为：（﹣1，0），【点评】本题考查了勾股定理和坐标与图形性质的应用，解此题的关键是求出OC的长，注意：在直角三角形中，两直角边的平方和等于斜边的平方．12．（3.00分）（2018•吉林）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=100m．【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，∴△ABD∽△ECD，∴，，解得：AB=（米）．故答案为：100．【点评】此题主要考查了相似三角形的应用；用到的知识点为：两角对应相等的两三角形相似；相似三角形的对应边成比例．13．（3.00分）（2018•吉林）如图，A，B，C，D是⊙O上的四个点，=，若∠AOB=58°，则∠BDC=29度．【分析】根据∠BDC=∠BOC求解即可；【解答】解：连接OC．∵=，∴∠AOB=∠BOC=58°，∴∠BDC=∠BOC=29°，故答案为29．【点评】本题考查圆周角定理，圆心角、弧、弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．14．（3.00分）（2018•吉林）我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为36度．【分析】根据等腰三角形的性质得出∠B=∠C，根据三角形内角和定理和已知得出5∠A=180°，求出即可．【解答】解：∵△ABC中，AB=AC，∴∠B=∠C，∵等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，∴∠A：∠B=1：2，即5∠A=180°，∴∠A=36°，故答案为：36．【点评】本题考查了三角形内角和定理和等腰三角形的性质，能根据等腰三角形性质、三角形内角和定理和已知得出5∠A=180°是解此题的关键．三、解答题（共12小题，满分84分）15．（5.00分）（2018•吉林）某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了错误，解答过程如下：原式=a2+2ab﹣（a2﹣b2）（第一步）=a2+2ab﹣a2﹣b2（第二步）=2ab﹣b2（第三步）（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；（2）写出此题正确的解答过程．【分析】先计算乘法，然后计算减法．【解答】解：（1）该同学解答过程从第二步开始出错，错误原因是去括号时没有变号；故答案是：二；去括号时没有变号；（2）原式=a2+2ab﹣（a2﹣b2）=a2+2ab﹣a2+b2=2ab+b2．【点评】考查了平方差公式和实数的运算，去括号规律：①a+（b+c）=a+b+c，括号前是“+”号，去括号时连同它前面的“+”号一起去掉，括号内各项不变号；②a﹣（b﹣c）=a﹣b+c，括号前是“﹣”号，去括号时连同它前面的“﹣”号一起去掉，括号内各项都要变号．16．（5.00分）（2018•吉林）如图，在正方形ABCD中，点E，F分别在BC，CD 上，且BE=CF，求证：△ABE≌△BCF．【分析】根据正方形的性质，利用SAS即可证明；【解答】证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，在△ABE和△BCF中，，∴△ABE≌△BCF．【点评】本题考查正方形的性质全等三角形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（5.00分）（2018•吉林）一个不透明的口袋中有三个小球，上面分别标有字母A，B，C，除所标字母不同外，其它完全相同，从中随机摸出一个小球，记下字母后放回并搅匀，再随机摸出一个小球，用画树状图（或列表）的方法，求该同学两次摸出的小球所标字母相同的概率．【分析】列表得出所有等可能的情况数，再找出两次摸出的小球所标字母相同的情况数，即可求出其概率．【解答】解：列表得：A B CA（A，A）（B，A）（C，A）B（A，B）（B，B）（C，B）C（A，C）（B，C）（C，C）由列表可知可能出现的结果共9种，其中两次摸出的小球所标字母相同的情况数有3种，所以该同学两次摸出的小球所标字母相同的概率==．【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．18．（5.00分）（2018•吉林）在平面直角坐标系中，反比例函数y=（k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．【分析】先求出P点的坐标，再把P点的坐标代入反比例函数的解析式，即可求出答案．【解答】解：∵把x=1代入y=x+2得：y=3，即P点的坐标是（1，3），把P点的坐标代入y=得：k=3，即反比例函数的解析式是y=．【点评】本题考查了用待定系数法求反比例函数的解析式和函数图象上点的坐标特征，能求出P点的坐标是解此题的关键．19．（7.00分）（2018•吉林）如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．根据以上信息，解答下列问题．（1）冰冰同学所列方程中的x表示甲队每天修路的长度，庆庆同学所列方程中的y表示甲队修路400米所需时间；（2）两个方程中任选一个，并写出它的等量关系；（3）解（2）中你所选择的方程，并回答老师提出的问题．【分析】（1）根据两人的方程思路，可得出：x表示甲队每天修路的长度；y表示甲队修路400米所需时间；（2）根据题意，可找出：（冰冰）甲队修路400米所用时间=乙队修路600米所用时间；（庆庆）乙队每天修路的长度﹣甲队每天修路的长度=20米；（3）选择两个方程中的一个，解之即可得出结论．【解答】解：（1）∵冰冰是根据时间相等列出的分式方程，∴x表示甲队每天修路的长度；∵庆庆是根据乙队每天比甲队多修20米列出的分式方程，∴y表示甲队修路400米所需时间．故答案为：甲队每天修路的长度；甲队修路400米所需时间．（2）冰冰用的等量关系是：甲队修路400米所用时间=乙队修路600米所用时间；庆庆用的等量关系是：乙队每天修路的长度﹣甲队每天修路的长度=20米（选择一个即可）．（3）选冰冰的方程：=，去分母，得：400x+8000=600x，移项，x的系数化为1，得：x=40，检验：当x=40时，x、x+20均不为零，∴x=40．答：甲队每天修路的长度为40米．选庆庆的方程：﹣=20，去分母，得：600﹣400=20y，将y的系数化为1，得：y=10，经验：当y=10时，分母y不为0，∴y=10，∴=40．答：甲队每天修路的长度为40米．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．20．（7.00分）（2018•吉林）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是轴对称对称图形；（3）求所画图形的周长（结果保留π）．【分析】（1）利用旋转变换的性质画出图象即可；（2）根据轴对称图形的定义即可判断；（3）利用弧长公式计算即可；【解答】解：（1）点D→D1→D2→D经过的路径如图所示：（2）观察图象可知图象是轴对称图形，故答案为轴对称．（3）周长=4×=8π．【点评】本题考查作图﹣旋转变换，弧长公式、轴对称图形等知识，解题的关键是理解题意，正确画出图形，属于中考常考题型．21．（7.00分）（2018•吉林）数学活动小组的同学为测量旗杆高度，先制定了如下测量方案，使用工具是测角仪和皮尺，请帮助组长林平完成方案内容，用含a，b，α的代数式表示旗杆AB的高度．数学活动方案活动时间：2018年4月2日活动地点：学校操场填表人：林平课题测量学校旗杆的高度活动目的运用所学数学知识及方法解决实际问题方案示意图测量步骤（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．计算过程【分析】在Rt△ADE中，求出AE，再利用AB=AE+BE计算即可；【解答】解：（1）用测角仪测得∠ADE=α；（2）用皮尺测得BC=a米，CD=b米．（3）计算过程：∵四边形BCDE是矩形，∴DE=BC=a，BE=CD=b，在Rt△ADE中，AE=ED•tanα=a•tanα，∴AB=AE+EB=a•tanα+b．【点评】本题考查解直角三角形的应用﹣仰角俯角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（7.00分）（2018•吉林）为了调查甲、乙两台包装机分装标准质量为400g 奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．收集数据：从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：g）如下：甲：400，400，408，406，410，409，400，393，394，395乙：403，404，396，399，402，402，405，397，402，398整理数据：表一质量（g）频数种类393≤x＜396396≤x＜399399≤x＜402402≤x＜405405≤x＜408408≤x＜411甲303013分析数据：表二得出结论：包装机分装情况比较好的是乙（填甲或乙），说明你的理由．【分析】整理数据：由题干中的数据结合表中范围确定个数即可得；分析数据：根据众数和中位数的定义求解可得；得出结论：根据方差的意义，方差小分装质量较为稳定即可得．【解答】解：整理数据：表一分析数据：将甲组数据重新排列为：393、394、395、400、400、400、406、408、409、410，∴甲组数据的中位数为400；乙组数据中402出现次数最多，有3次，∴乙组数据的众数为402；表二得出结论：表二知，乙包装机分装的奶粉质量的方差小，分装质量比较稳定，所以包装机分装情况比较好的是乙．故答案为：乙．【点评】本题考查了众数、中位数以及方差，掌握众数、中位数以及方差的定义及数据的整理是解题的关键．23．（8.00分）（2018•吉林）小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min．小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示（1）家与图书馆之间的路程为4000m，小玲步行的速度为100m/min；（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；（3）求两人相遇的时间．【分析】（1）认真分析图象得到路程与速度数据；（2）采用方程思想列出小东离家路程y与时间x之间的函数关系式；（3）两人相遇实际上是函数图象求交点．【解答】解：（1）结合题意和图象可知，线段CD为小玲路程与时间函数图象，折现O﹣A﹣B为为小东路程与时间图象则家与图书馆之间路程为4000m，小玲步行速度为2000÷20=200m/s故答案为：4000，100（2）∵小东从离家4000m处以300m/min的速度返回家，则xmin时，∴他离家的路程y=4000﹣300x自变量x的范围为0≤x≤（3）由图象可知，两人相遇是在小玲改变速度之前∴4000﹣300x=200x解得x=8∴两人相遇时间为第8分钟．【点评】本题是一次函数实际应用问题，考查了对一次函数图象代表意义的分析和从方程角度解决一次函数问题．24．（8.00分）（2018•吉林）如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC 于点F．（1）求证：四边形ADEF为平行四边形；（2）当点D为AB中点时，▱ADEF的形状为菱形；（3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．【分析】（1）根据平行线的性质得到∠BDE=∠A，根据题意得到∠DEF=∠BDE，根据平行线的判定定理得到AD∥EF，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到DE=AC，得到AD=DE，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE⊥EG，根据有一个角是直角的平行四边形是矩形证明．【解答】（1）证明：∵DE∥AC，∴∠BDE=∠A，∵∠DEF=∠A，∴∠DEF=∠BDE，∴AD∥EF，又∵DE∥AC，∴四边形ADEF为平行四边形；（2）解：▱ADEF的形状为菱形，理由如下：∵点D为AB中点，∴AD=AB，∵DE∥AC，点D为AB中点，∴DE=AC，∵AB=AC，∴AD=DE，∴平行四边形ADEF为菱形，故答案为：菱形；（3）四边形AEGF是矩形，理由如下：由（1）得，四边形ADEF为平行四边形，∴AF∥DE，AF=DE，∵EG=DE，∴AF∥DE，AF=GE，∴四边形AEGF是平行四边形，∵AD=AG，EG=DE，∴AE⊥EG，∴四边形AEGF是矩形．【点评】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．25．（10.00分）（2018•吉林）如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）（1）当PQ⊥AB时，x=s；（2）求y关于x的函数解析式，并写出x的取值范围；（3）直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．【分析】（1）当PQ⊥AB时，BQ=2PB，由此构建方程即可解决问题；（2）分三种情形分别求解即可解决问题；（3）分两种情形分别求解即可解决问题；【解答】解：（1）当PQ⊥AB时，BQ=2PB，∴2x=2（2﹣2x），∴x=s．故答案为s．（2）①如图1中，当0＜x≤时，重叠部分是四边形PQMN．y=2x×x=2x2．②如图②中，当＜x≤1时，重叠部分是四边形PQEN．y=（2﹣x+2tx×x=x2+x③如图3中，当1＜x＜2时，重叠部分是四边形PNEQ．y=（2﹣x+2）×[x﹣2（x﹣1）]=x2﹣3x+4；综上所述，y=．（3）①如图4中，当直线AM经过BC中点E时，满足条件．则有：tan∠EAB=tan∠QPB，∴=，解得x=．②如图5中，当直线AM经过CD的中点E时，满足条件．此时tan∠DEA=tan∠QPB，∴=，解得x=，综上所述，当x=s或时，直线AM将矩形ABCD的面积分成1：3两部分．【点评】本题考查四边形综合题、矩形的性质平行四边形的性质、锐角三角函数、解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，学会用方程的思想解决问题，属于中考压轴题．26．（10.00分）（2018•吉林）如图，在平面直角坐标系中，抛物线y=ax2+2ax﹣3a（a＜0）与x轴相交于A，B两点，与y轴相交于点C，顶点为D，直线DC与x轴相交于点E．（1）当a=﹣1时，抛物线顶点D的坐标为（﹣1，4），OE=3；（2）OE的长是否与a值有关，说明你的理由；（3）设∠DEO=β，45°≤β≤60°，求a的取值范围；（4）以DE为斜边，在直线DE的左下方作等腰直角三角形PDE．设P（m，n），直接写出n关于m的函数解析式及自变量m的取值范围．【分析】（1）求出直线CD的解析式即可解决问题；（2）利用参数a，求出直线CD的解析式求出点E坐标即可判断；（3）求出落在特殊情形下的a的值即可判断；（4）如图，作PM⊥对称轴于M，PN⊥AB于N．两条全等三角形的性质即可解决问题；【解答】解：（1）当a=﹣1时，抛物线的解析式为y=﹣x2﹣2x+3，∴顶点D（﹣1，4），C（0，3），∴直线CD的解析式为y=﹣x+3，∴E（3，0），∴OE=3，故答案为（﹣1，4），3．（2）结论：OE的长与a值无关．理由：∵y=ax2+2ax﹣3a，∴C（0，﹣3a），D（﹣1，﹣4a），∴直线CD的解析式为y=ax﹣3a，当y=0时，x=3，∴E（3，0），∴OE=3，∴OE的长与a值无关．（3）当β=45°时，OC=OE=3，∴﹣3a=3，∴a=﹣1，当β=60°时，在Rt△OCE中，OC=OE=3，∴﹣3a=3，∴a=﹣，∴45°≤β≤60°，a的取值范围为﹣≤a≤﹣1．（4）如图，作PM⊥对称轴于M，PN⊥AB于N．∵PD=PE，∠PMD=∠PNE=90°，∠DPE=∠MPN=90°，∴∠DPM=∠EPN，∴△DPM≌△EPN，∴PM=PN，DM=EN，∵D（﹣1，﹣4a），E（3，0），∴EN=4+n=3﹣m，∴n=﹣m﹣1，当顶点D在x轴上时，P（1，﹣2），此时m的值1，∵抛物线的顶点在第二象限，∴m＜1．∴n=﹣m﹣1（m＜1）．【点评】本题考查二次函数综合题、一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。