锁相放大器原理
- 格式:pdf
- 大小:333.75 KB
- 文档页数:12

锁相放大器正弦波调制因子【原创实用版】目录1.锁相放大器的概念与原理2.正弦波的基本特性3.调制因子的定义与作用4.锁相放大器在正弦波调制中的应用5.锁相放大器的优缺点及发展前景正文锁相放大器是一种频率调制技术,主要用于信号处理、通信和雷达系统等领域。
其基本原理是通过锁相环路,将输入信号与本振信号进行混频,得到一个具有本振信号频率和输入信号幅度的输出信号。
这种技术可以有效地放大输入信号,提高系统的灵敏度和性能。
正弦波是一种常见的信号波形,具有周期性、振幅不变和频率单一等基本特性。
在通信和信号处理领域,正弦波被广泛应用于信号调制和解调。
通过对正弦波的幅度、频率或相位进行调整,可以实现不同类型的调制信号,以适应不同的传输环境和系统需求。
调制因子是指调制过程中信号参数的变化程度,通常用一个无量纲的数值来表示。
调制因子的大小决定了调制信号与原始信号之间的相似程度,以及调制过程中信号能量的分布情况。
在实际应用中,通过调整调制因子,可以实现对信号的优化和增强,提高系统的传输效率和性能。
锁相放大器在正弦波调制中的应用主要体现在信号放大和解调两个方面。
首先,锁相放大器可以对输入信号进行放大,提高系统的灵敏度和性能。
其次,锁相放大器可以通过混频过程,将输入信号与本振信号混合,得到一个具有本振信号频率和输入信号幅度的输出信号。
这个输出信号可以用于后续的信号处理和解调,实现对原始信号的恢复和提取。
锁相放大器具有许多优点,例如放大倍数高、频率响应宽、抗干扰能力强等。
然而,它也存在一定的局限性,如对本振信号的稳定性要求较高,以及可能引入的噪声和失真等。
在实际应用中,需要根据具体的系统和需求,综合考虑锁相放大器的优缺点,选择合适的技术方案。
随着科技的发展和技术的创新,锁相放大器在通信和信号处理领域的应用前景十分广阔。
未来,锁相放大器将不断优化和升级,以满足不断提高的系统性能和传输速率需求。

锁相放大器基本原理锁相放大器(lock-in amplifier)是一种高精度的电子测量设备,是利用同步检测技术对弱信号进行放大的一种方法。
它可以通过抑制噪声,增加测量信号的信噪比,从而提高测量精度。
锁相放大器广泛应用于科学研究、精密测量、信号处理等领域。
锁相放大器的基本原理是通过与输入信号进行相位锁定,以获得信号的正弦成分,并通过放大和滤波等处理,最终得到一个精确测量值。
下面将详细介绍锁相放大器的工作原理。
1. 相位锁定锁相放大器需要获取一个参考信号,通常通过输入到参考输入端口上,这个参考信号可以是一个外部信号源产生的参考信号,也可以是输入信号中的某一部分。
锁相放大器将参考信号分成两个信号,一个是正弦波(reference signal),另一个是余弦波(quadrature signal)。
锁相放大器接收到待测信号后,将待测信号与正弦波相乘,经过低通滤波器后输出相干检测信号(in-phase signal),再将待测信号与余弦波相乘,经过低通滤波器后输出正交检测信号(quadrature signal)。
这两个信号的相位差就是输入信号的相位。
将相干检测信号和正交检测信号分别输入到两个输入通道后,通过比例放大器放大信号的幅度,使待测信号和参考信号的相位锁定。
2. 信号放大锁相放大器通过放大信号的幅度来提高测量的灵敏度。
通常情况下,锁相放大器的放大倍数可达到几百万倍。
锁相放大器的放大倍数和滤波器的带宽有密切的关系。
放大倍数越大,需要的滤波器带宽越小。
3. 滤波处理锁相放大器采用低通滤波器对输入信号进行滤波处理。
滤波器的带宽可以通过滤波器控制电路进行调节。
对于较宽的带宽,锁相放大器可以对高频噪声信号进行有效抑制,提高信号的信噪比。
对于较小的带宽,锁相放大器可以提高信号的时域和频域分辨率。
4. 数据输出锁相放大器最终输出的是经过放大和滤波处理后的幅度和相位信息。
通过这些信息,可以得到一个精确的测量值。

锁相放大器原理锁相放大器是一种高灵敏度、高稳定性的测量仪器,主要用于测量高精度的弱信号,如光信号和电信号。
其原理是利用参考信号和待测信号的相位差,进行频率选择和信号增益放大。
锁相放大器基本原理是通过一个正弦参考信号和待测信号在相位上的比较来测量待测信号的幅度和相位差。
在锁相放大器中,参考信号经过参考信号发生器产生,同时作为激励信号送入模拟电路,待测信号则在探测器中测量得到,然后送入锁相放大器。
在锁相放大器中,待测信号与参考信号混频,同时将混频信号分为正弦和余弦两路。
正弦和余弦两路信号分别经过相移器和低通滤波器,得到相位和幅度信息,最终输出通过运算放大器得到的结果。
锁相放大器最大特点是可以通过不同相位角的乘法器来进行相位选择,使得信号在不同相角的幅度值得到不同的权重,从而提高锁相放大器的灵敏度和稳定性。
锁相放大器主要有四个部分组成:参考信号发生器、混频器、相位选择器和低通滤波器。
参考信号发生器用于产生基准信号以及参考信号,基准信号一般是一定频率和幅度的正弦波。
混频器用于将待测信号与参考信号进行混频,在混频时需要注意保证混频信号在频率范围内。
相位选择器一般包括相移器、乘法器、运算放大器等,用于对混频信号进行相位角的选择,从而提高锁相放大器的灵敏度和稳定性。
低通滤波器主要用于滤除混频信号中的高频噪声,提高测量精度。
锁相放大器具有很多优点。
首先,相比于其他测量仪器,锁相放大器具有较高的灵敏度和低的噪声;其次,相位选择器可以实现对混频信号相位的选取,提高了系统的稳定性;最后,锁相放大器具备强抗干扰性,能够有效地抑制外部干扰信号,提高测量精度。
锁相放大器广泛应用于生物医学、光学、物理、电学等领域。
其中,在光学领域,锁相放大器主要用于实现光学检测和光学成像;在电学领域,锁相放大器主要用于检测直流信号和交流信号的分量,同时也可以用于测量电容、电感和电阻等电学元件的参数。
在物理领域,锁相放大器主要用于精密时间测量和振动测量等领域。

实验2-2微弱信号检测技术随着科学技术的发展,使测量技术得到日趋完善的发展,同时也提出更高要求。
尤其是一些极端条件下的测量已成为现代认识自然的主要手段,由于微弱信号检测(weak signal detection)能测量传统观念认为不能测量的微弱量,所以才获得迅速的发展和普遍的重视,微弱信号检测已逐渐形成一门边缘学科学。
锁相放大器(lock-in. Amplifier 简称LIA)就是检测淹没在噪声中的微弱信号的仪器,它可用于测量交流信号的幅度和相位,有极强的抑制干扰和噪声的能力,有极高的灵敏度,可测量毫微伏量级的微弱信号,自1962年美国PARC第一个相干检测的锁相放大器问世以来,锁相放大器有了迅速的发展,性能指标有了很大的提高,现已被广泛应用于科学技术的很多领域,本实验使用128A用电容电压法测量P-N结的杂质浓度分布和PN结电容,即是一个很好的应用实例。
一实验原理(一)PN结电容及杂质浓度分布在半导体的设计和制造过程中,如何控制半导体内部的杂质浓度分布,从而达到对器件电学性能的要求,是半导体材料和器件的基本测量之一,本实验是用电容—电压法测量P-N结的杂质浓度分布,具有简单快捷,又不破坏样品的特点,是较常用的测量方法之一。
它仅能反映P-N结轻掺杂一边的杂质分布。
P-N结是由P型和N半导体“接触”形成的,交界之处的杂质浓度可以是突变的,或是缓慢的,在结的界面处形成势垒区,也称空间电荷区,如(图2-2—1 a、b)所示。
P-N结外加电压时,势垒区的空间电荷数量将随外加电压变化,与电容器的作用相同,这种由势垒区电荷变化引起的电容称为势垒电容另外,P-N结加正向偏压时,P区和N区的空穴和电子各自对各自向对方发散,并能在对方(扩散区)形成一定的电荷积累,积累电荷的多少也随外加电压而变化,称为扩散电容图2-2—1 突变结(a)和缓变结(b)所以,P-N结的电容与一般电容不同,不是恒定不变的,要随外加电压的变化而变化。
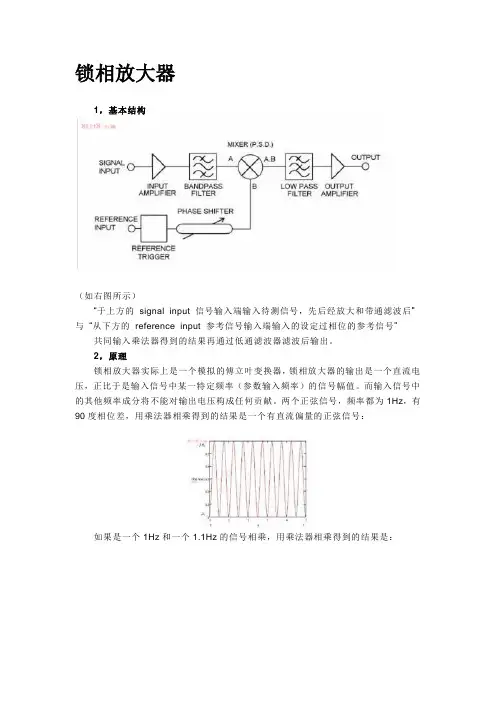
锁相放大器1,基本结构(如右图所示)“于上方的signal input 信号输入端输入待测信号,先后经放大和带通滤波后” 与“从下方的reference input 参考信号输入端输入的设定过相位的参考信号”共同输入乘法器得到的结果再通过低通滤波器滤波后输出。
2,原理锁相放大器实际上是一个模拟的傅立叶变换器,锁相放大器的输出是一个直流电压,正比于是输入信号中某一特定频率(参数输入频率)的信号幅值。
而输入信号中的其他频率成分将不能对输出电压构成任何贡献。
两个正弦信号,频率都为1H z,有90度相位差,用乘法器相乘得到的结果是一个有直流偏量的正弦信号:如果是一个1Hz和一个1.1Hz的信号相乘,用乘法器相乘得到的结果是:从上面的分析看来,只有与参考信号频率完全一致的信号才能在乘法器输出端得到直流偏量,其他信号在输出端都是交流信号。
如果在乘法器的输出端加一个低通滤波器,那么所有的交流信号分量全部被滤掉,剩下的直流分量就只是正比于输入信号中的特定频率的信号分量的幅值。
3.用途即使有用的信号被淹没在噪声信号里面,即使噪声信号比有用的信号大很多,只要知道有用的信号的频率值,就能准确地测量出这个信号的幅值。
锁相放大器原理锁相放大器是以相干检测技术为基础,利用参考信号频率与输入输入信号频率相关,与噪声信号不相关,从而从较强的噪声中提取出有用信号,使得测量精度大大提高,而它的核心部件为相敏检测器(phase sensitive detector ,简称PSD ,又称相关器),图1所示为锁相放大器的原理框图。
图1锁相放大器原理图相敏检测器是由乘法器和积分器组成,其中乘法器一般采用开关乘法器,积分器通常由低通滤波器组成,图2给出相敏检测器的构成原理图。
图2相敏检测器原理图设待测信号()()()()()t n t cos V t n t V t V s s s s1s ++=+=ϕω,其中)t (V s1为待测信号中的有效信号,n ()t 为噪声。

锁相放大器原理
锁相放大器原理是一种在测量系统中应用的电子技术,用于提取和放大输入信号中特定频率的成分。
该原理基于相位锁定环路的工作原理,通过与参考信号进行比较和处理,从而实现对输入信号的精确测量。
锁相放大器由几个主要部分组成,包括参考信号源、混频器、低通滤波器、放大器和相位锁定环路。
首先,参考信号源产生一个稳定的频率和相位的信号,作为参考信号输入到混频器中。
混频器将输入信号与参考信号进行乘积运算,产生一个包含频率和相位差的交流信号。
接下来,低通滤波器过滤掉高频成分,只保留所需的频率成分。
通过放大器对滤波后的信号进行放大,以增强信号的强度。
最后,信号被送回相位锁定环路,与参考信号进行比较并进行反馈调节。
相位锁定环路通过控制输入信号的相位,使其与参考信号同步,从而实现对输入信号的精确测量。
锁相放大器的工作原理基于负反馈控制,通过持续的相位比较和调节,使输入信号的相位与参考信号保持一致。
通过这种方式,锁相放大器可以提取和放大输入信号中特定频率的成分,从而提高信号的测量精度和灵敏度。
总之,锁相放大器利用相位锁定环路的原理,通过与参考信号的比较和调节,实现对输入信号的精确测量。
它在科学研究、精密测量、信号处理等领域具有广泛的应用。

锁相放大器原理锁相放大器(Lock-inAmplifier,简称LIA)是一种信号处理仪器,用于放大小幅度和短暂变化信号。
它主要应用于测量电性能,实时监测与采集信号,仪器仪表制造以及工业控制等。
锁相放大器的原理是将被测信号与一个正弦波(称为参考信号)相比较,输出信号与输入信号的波形几乎相同,只是信号的幅度大大放大。
因此,即使是一些微弱的短时信号,也可以在锁相放大器中捕获,进而被测量和解析。
锁相放大器的运作原理非常简单,它包括一个锁相电路,一个放大器以及一个相位环节。
首先,被测信号会首先进入锁相电路,在锁相电路中,被测信号和参考信号会分别被放大,并以复数形式传递到相位环节,在相位环节做处理后,将被测信号与参考信号相比较,以确定被测信号与参考信号之间的相位差,最后,被测信号会被反馈到放大器中,放大器会只放大被测信号和参考信号的相位差的部分,因而得到信号的放大。
一般来说,锁相放大器的时域精度高,可以用来测量短时间或小幅度信号,它运行的频率范围很宽,可以从低于10 Hz到1000 MHz,也可以应用于极其复杂的系统,这些方面都使得锁相放大器极大地拓展了测量应用的范围。
进步仪器推出了一系列优质的锁相放大器,它们采用先进科技,有着更高的分辨率,更高的精度,能够支持多种协同测量,具有更完善的噪声抑制功能,还具有多种扩展模块,使用起来方便快捷,更适合使用于高端科学研究中。
从上面可以看出,锁相放大器是一种极其重要的仪器,采用它可以放大小幅度信号,使这些信号能够被精确测量和检测,用于多种复杂的环境中,这种仪器无疑是研究者极其宝贵的工具,进步仪器贴心地为研究者提供优质的锁相放大器,以满足所有科研需求。
综上所述,锁相放大器是一种重要的信号处理仪器,它的原理是将被测信号与参考信号进行比较,从而放大被测信号,具有时域精度高,频率范围宽,容易扩展等优点,进步仪器凭借先进的技术,提供了一系列优质的锁相放大器,满足科学研究者的多种需求。

锁相放大器正弦波调制因子(原创版)目录1.锁相放大器的概念与原理2.正弦波的概念与特性3.调制因子的定义与作用4.锁相放大器在正弦波调制中的应用5.锁相放大器在实际工程中的重要性正文锁相放大器是一种信号处理电路,它的主要作用是放大输入信号的相位,并将其与本地振荡信号进行同步。
这种放大器广泛应用于通信、雷达和测量仪器等领域。
锁相放大器的工作原理是基于相位敏感检测器和电压放大器,通过调整放大器的增益和带宽,可以实现对特定频率信号的相位放大。
正弦波是一种周期性的波动信号,其波形呈正弦函数。
正弦波具有很多特性,如振幅、频率、相位等。
在通信和信号处理领域,正弦波常用于调制其他信号,以实现信号的传输和变换。
正弦波的调制因子是指正弦波的振幅、频率或相位与被调制信号之间的关系。
调制因子的大小决定了调制后信号的性能,如信噪比、传输距离等。
锁相放大器在正弦波调制中具有重要应用。
通过对正弦波的调制因子进行调整,可以实现对信号的相位、频率和振幅的控制。
这种控制可以使信号在传输过程中具有更好的抗干扰性能,提高信号传输的可靠性。
锁相放大器还可以用于正弦波的解调,通过检测正弦波的调制因子,可以还原出原始信号。
在实际工程中,锁相放大器具有很高的实用价值。
例如,在通信系统中,锁相放大器可以用于信号的调制和解调,提高信号传输的质量和效率。
在雷达系统中,锁相放大器可以用于信号的处理和分析,提高雷达的探测能力和抗干扰能力。
在测量仪器中,锁相放大器可以用于信号的放大和滤波,提高测量的精度和可靠性。
总之,锁相放大器是一种重要的信号处理电路,其原理和应用涉及多个领域。

锁相放大器的工作原理一.什么是锁相放大器锁相放大器是一种对交变信号进行相敏检波的放大器。
它利用和被测信号有相同频率和相位关系的参考信号作为比较基准,只对被测信号本身和那些与参考信号同频(或者倍频)、同相的噪声分量有响应。
因此,能大幅度抑制无用噪声,改善检测信噪比。
此外,锁相放大器有很高的检测灵敏度,信号处理比较简单,是弱光信号检测的一种有效方法。
锁相放大器实物图二.锁相放大器的构成锁相放大器采用在无线电电路中已经非常成熟的外差式振荡技术,把被测量的信号通过频率变换的方式转变成为直流。
在外差式振荡技术中被称为本地振荡(Local Oscillation)的、用于做乘法运算的信号,锁相放大器中被称为参照信号,是从外面输入的。
锁相放大器能够(从被测量信号中)检测出与这个参照信号频率相同的分量。
在被测量的信号里所包含的各种信号分量中,只有与参照信号频率相同的那个分量才会被转换成为直流,因而才能够通过低通滤波器(LPF)。
其他频率的分量因为被转换成为频率不等于零的交流信号,所以被低通滤波器(LPF)滤除。
在频率域中,如下图所示。
锁相放大器的基本组成三.锁相放大器的应用锁相放大器可用于检测到在杂噪信号中被埋没的微弱的信号。
采用选频放大技术,使放大器的中心频率f 0与待测信号频率相同,从而对噪声进行抑制,但此法存在中心频度不稳、带宽不能太窄及对等测信号缺点。
后来发展了锁相放大技术。
它利用等测信号和参与信号的相互关检测原理实现对信号的窄带化处理,能有效的抑制噪声,实现对信号的检测和跟踪。
目前,锁相放大技术已广泛地用于物理、化学、生物、电讯、医学等领域。
应用一:用于测量现场尘粒浓度。
尘粒浓度测量仪采用光电收发对称式探测头,能够对温度、振动、器件老化等因素进行抑制。
光信号在烟道中的衰减与烟道中尘粒浓度关系遵从朗伯-比尔定律。
当烟道内尘粒浓度增大到一定程度,使得光信号大幅衰减,环境杂散光等成为不可忽视的噪声信号。
应用二:用于红外线温度传感器的低温范围拓展。


题目:锁相放大器的原理及应用姓名:单位:学号:联系方式:摘要锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
本文主要介绍了锁相放大器原理,发展过程,基本组成,重要参数和在各方面的应用。
关键词:锁相放大器,噪声,傅立叶变换一、锁相放大器的定义锁相放大器是一种对交变信号进行相敏检波的放大器。
它利用和被测信号有相同频率和相位关系的参考信号作为比较基准,只对被测信号本身和那些与参考信号同频(或者倍频)、同相的噪声分量有响应。
因此,能大幅度抑制无用噪声,改善检测信噪比。
此外,锁相放大器有很高的检测灵敏度,信号处理比较简单,是弱光信号检测的一种有效方法。
锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
二、锁相放大器的历史上世纪六十年代美国公司研制出第一台利用模拟电路实现微弱正弦信号测量的锁相放大器,使微弱信号检测技术突破性飞越,为解决大量电子测量做出贡献,在物质表面组份分析以及表面电子能态研宄方面有重大意义。
自上世纪后期开始,国内外越来越多的人开始研宄锁相放大器,随着科技的发展,越来越多性能优良的锁相放大器被研发出来,在各个领域应用广泛,极大程度上推动了各个学科的发展,目前,从提高系统的灵敏度、减小噪声带宽、提高检测精度、改善信噪比上都有了很大的进步。
近年来,数字电子技术飞速发展,锁相放大器也在这一契机下,出现了模数混合的锁相放大器与数字锁相放大器,这在一定程度上弥补了由于物理器件造成的模拟锁相放大器的缺点,极大改善了性能,提升了研究层次与扩大了应用范围。
题目:锁相放大器的原理及应用姓名:单位:学号:联系方式:摘要锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
本文主要介绍了锁相放大器原理,发展过程,基本组成,重要参数和在各方面的应用。
关键词:锁相放大器,噪声,傅立叶变换一、锁相放大器的定义锁相放大器是一种对交变信号进行相敏检波的放大器。
它利用和被测信号有相同频率和相位关系的参考信号作为比较基准,只对被测信号本身和那些与参考信号同频(或者倍频)、同相的噪声分量有响应。
因此,能大幅度抑制无用噪声,改善检测信噪比。
此外,锁相放大器有很高的检测灵敏度,信号处理比较简单,是弱光信号检测的一种有效方法。
锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
二、锁相放大器的历史上世纪六十年代美国公司研制出第一台利用模拟电路实现微弱正弦信号测量的锁相放大器,使微弱信号检测技术突破性飞越,为解决大量电子测量做出贡献,在物质表面组份分析以及表面电子能态研宄方面有重大意义。
自上世纪后期开始,国外越来越多的人开始研宄锁相放大器,随着科技的发展,越来越多性能优良的锁相放大器被研发出来,在各个领域应用广泛,极大程度上推动了各个学科的发展,目前,从提高系统的灵敏度、减小噪声带宽、提高检测精度、改善信噪比上都有了很大的进步。
近年来,数字电子技术飞速发展,锁相放大器也在这一契机下,出现了模数混合的锁相放大器与数字锁相放大器,这在一定程度上弥补了由于物理器件造成的模拟锁相放大器的缺点,极大改善了性能,提升了研究层次与扩大了应用围。
锁相放大器原理
锁相放大器是一种电子测量仪器,用于测量信号的幅度和相位。
其工作原理基于相位比较和反馈控制。
锁相放大器通过与参考信号比较输入信号的相位差,以获得输入信号的幅度和相位信息。
为了实现相位比较,锁相放大器内部产生了与参考信号频率相同的参考信号。
该参考信号与输入信号进行乘法运算后,得到两者的乘积信号。
乘积信号经过低通滤波器,滤除高频成分,得到直流分量。
该直流分量与参考信号的相位差决定了乘积信号的幅度。
通过控制参考信号的相位,可以改变乘积信号的幅度。
为了实现相位和幅度的测量,锁相放大器引入了反馈控制。
反馈控制通过调整参考信号的相位,使得乘积信号的幅度最大化。
通过不断优化相位调整,锁相放大器可以获取输入信号的精确幅度和相位信息。
通过锁相放大器,可以对微弱或者嵌入在噪声中的信号进行精确的测量。
其广泛应用于光学、电子学、生物医学和材料科学等领域。
题目:锁相放大器的原理及应用姓名:单位:学号:联系方式:摘要锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
本文主要介绍了锁相放大器原理,发展过程,基本组成,重要参数和在各方面的应用。
关键词:锁相放大器,噪声,傅立叶变换一、锁相放大器的定义锁相放大器是一种对交变信号进行相敏检波的放大器。
它利用和被测信号有相同频率和相位关系的参考信号作为比较基准,只对被测信号本身和那些与参考信号同频(或者倍频)、同相的噪声分量有响应。
因此,能大幅度抑制无用噪声,改善检测信噪比。
此外,锁相放大器有很高的检测灵敏度,信号处理比较简单,是弱光信号检测的一种有效方法。
锁相放大器又称锁定放大器是对正弦信号(含具有窄带特点的调幅信号)进行相敏检波的放大器,它实际上是一个模拟的傅立叶变换器,在强噪声下,利用有用信号的频率值准确测出有用信号的幅值。
应用在科学研究的各个领域中:如通讯、工业、国防、生物、海洋等。
二、锁相放大器的历史上世纪六十年代美国公司研制出第一台利用模拟电路实现微弱正弦信号测量的锁相放大器,使微弱信号检测技术突破性飞越,为解决大量电子测量做出贡献,在物质表面组份分析以及表面电子能态研宄方面有重大意义。
自上世纪后期开始,国内外越来越多的人开始研宄锁相放大器,随着科技的发展,越来越多性能优良的锁相放大器被研发出来,在各个领域应用广泛,极大程度上推动了各个学科的发展,目前,从提高系统的灵敏度、减小噪声带宽、提高检测精度、改善信噪比上都有了很大的进步。
近年来,数字电子技术飞速发展,锁相放大器也在这一契机下,出现了模数混合的锁相放大器与数字锁相放大器,这在一定程度上弥补了由于物理器件造成的模拟锁相放大器的缺点,极大改善了性能,提升了研究层次与扩大了应用范围。
锁相放大器正弦波调制因子
摘要:
一、锁相放大器简介
1.锁相放大器的概念
2.锁相放大器的工作原理
二、正弦波在锁相放大器中的应用
1.正弦波的基本特性
2.锁相放大器对正弦波的放大作用
3.锁相放大器对正弦波的调制作用
三、调制因子在锁相放大器中的作用
1.调制因子的定义
2.调制因子对锁相放大器性能的影响
3.调制因子与正弦波的关系
正文:
锁相放大器是一种广泛应用于通信、雷达和测量领域的放大器,它的主要作用是对输入信号进行放大和调制。
锁相放大器的工作原理是利用锁定正弦波的相位,从而实现对输入信号的放大。
正弦波是锁相放大器中的重要应用对象,它是一种频率单一、振幅随时间呈正弦变化的波形。
在锁相放大器中,正弦波作为基准信号,用于调整放大器的输出信号,使其具有与输入信号相同的频率和相位。
正弦波在锁相放大器中的放大作用,可以使得信号在传输过程中更加稳定,减小信号衰减。
调制因子是衡量锁相放大器性能的一个重要参数,它表示输出信号与输入信号之间的相位差。
调制因子对锁相放大器性能的影响主要表现在放大器的稳定性和灵敏度方面。
调制因子与正弦波的关系是相互影响的,调制因子可以改变正弦波的形状,从而影响锁相放大器的性能。
总之,锁相放大器、正弦波和调制因子三者之间存在着密切的联系。
鎖相放大器(Lock-in-Amplifier)的原理:在真實情況中,進入鎖相放大器的信號在放大後除了待測信號Vsig外,同時包含雜訊信號。
而PSD 與低通濾波器將僅輸出與參考信號頻率極為接近的信號,而雜訊信號的頻率ωnoise在通過PSD 後,不論和頻ωnoise+ωref或差頻ωnoise–ωref都將被低通濾波器濾除。
當然,與參考頻率極接近的雜訊信號仍會通過低通濾波器,使輸出中包含緩慢的雜訊變化,頻寬較窄的低通濾波器可改善此問題,使得只有與參考信號同頻率的信號不受低通濾波器影響而被輸出。
由前面結果可知,我們需要一個與待測信號頻率相同的參考信號,此外,兩者間的相位必須不隨時間改變,否則輸出信號將因Cos(δsig−δref)隨時間變化而不為一個DC 信號。
換句話說,參考信號必須被待測信號鎖相(phase-locked) 。
鎖相放大器使用鎖相回路(phase-locked-loop,PLL)以產生參考信號。
當然,其需要一個由外部提供的參考信號(以上面的例子,其為一個方波,但事實上其亦可為其他種波形)。
PLL 會使鎖相放大器中內含的內部參考震盪器(internaleference oscillator)與外來的參考信號鎖相,並產生一頻率為ωref,,相位為δref的參考信號。
由於PLL 是動態追蹤(actively tracks)外部參考信號的頻率,因此當參考信號隨時間變動時,鎖相放大器的輸出結果仍不受影響。
除了使用來自外部的參考信號(external reference source),許多鎖相放大器亦提供波形產生器的功能,同時作為實驗系統的調制電壓源以及內部參考信號。
由於PSD的輸出正比於VsigCos(δ) ,其中δ=δsig−δref為待測信號與參考信號間的相位差,因此藉由改變δref可使δ等於0,因此可得量得Vsig。
但相對的,若調整δref使δ等於90度,則輸出信號將為0。
如果鎖相放大器中具有兩個PSD,且使參考信號進入此二者時相差90度相位,則兩者的輸出將分別為VsigCos(δ) 與Vsig Sin (δ) 。
锁相放大器原理锁相放大器是一种用于检测和放大微弱信号的电子设备,利用频率相位差锁定的原理进行信号处理和增强。
本文将介绍锁相放大器的原理和工作方式,以及其在科学研究和工程应用中的重要性。
一、锁相放大器概述锁相放大器是一种特殊的放大器,其主要功能是将微弱信号转化为可观测的输出信号,并降低噪声和干扰的影响。
锁相放大器通常由参考信号发生器、输入信号放大器、相敏检测器和低通滤波器等组成。
二、锁相放大器原理锁相放大器的工作原理基于频率相位差锁定。
首先,参考信号发生器产生一个稳定的高精度时钟信号,并将其作为参考信号。
然后,输入信号经过放大器放大后,与参考信号进行相位比较。
相敏检测器会检测输入信号和参考信号之间的相位差,并产生一个电压信号。
最后,通过低通滤波器将输出信号滤波,得到最终的输出结果。
三、锁相放大器应用锁相放大器在各个领域都有广泛的应用,特别是在实验物理学、光学和电子工程等领域。
以下是锁相放大器的一些应用示例:1. 光学干涉测量:锁相放大器可以用于测量光学干涉信号中的微弱位移或形变,从而实现高精度的测量和检测。
2. 生物医学研究:锁相放大器在生物医学研究中的应用十分重要,可以用于检测生物体内微弱的电生理信号,如脑电图和心电图等。
3. 光谱分析:锁相放大器可以用于光学光谱分析,通过检测和放大光谱信号,提高信号的检测灵敏度和分辨率。
4. 信号恢复:锁相放大器可以提取被噪声和干扰掩盖的信号,对于解析控制系统中的微弱信号具有重要意义。
5. 工业检测:锁相放大器可以应用于工业测试和检测领域,对于检测和分析微弱信号,提高系统的信噪比和性能具有重要意义。
四、锁相放大器的优势与局限锁相放大器作为一种高精度的信号处理设备,具有以下优势:- 高增益:锁相放大器可以将微弱信号放大到可以观测和测量的范围,提高信号的检测灵敏度。
- 低噪声:锁相放大器能够有效降低噪声和干扰的影响,从而提高信号的质量和准确性。
然而,锁相放大器也有一些局限性:- 系统复杂性:锁相放大器的设计和调试过程相对复杂,需要专业的知识和经验。
如何测量被噪声埋没了的信号?在测量各种物理量(温度、加速度等)时,用传感器将其变换成为电信号,然后输入到分析仪器(测量仪器)中去。
但是,仅想获得必要的信号是很难做到的。
通常是连不必要的信号(也就是噪声)也一起被测量了。
在各种情况下,噪声都有可能混进来。
噪声并不仅限于电信号,也有包含在被测量的物理量中的情况。
另外,根据不同场合,也出现噪声强度远远高出所需要的目的信号电平的情况。
想要测量的信号越微弱,那么噪声就相对地越大。
在这里,让我们来看一下用交流电压表来测量不同电平的1kHz 的正弦波信号的结果。
在信号上叠加了0.1Vmrs 的白噪声。
“毫伏计”是一般的交流电压表,“锁相放大器”是一种专门测量微小信号的(特殊的)交流电压表。
信号电平 (正弦波信号)波 形(叠加了噪声的波形)毫伏计的 测量结果锁相放大器的 测量结果1Vrms1Vrms 0.999Vrms100mVrms140mVrms 99mVrms1mVrms105mVrms 1.01mVrms0.1mVrms105mVrms 0.107mVrms毫伏计也同时测量噪声。
即使用数字万用表(DMM )来测量,也会得到与毫伏计相同的测量结果。
但锁相放大器,能在比目的信号(1kHz 正弦波)强1000倍的噪声中把目的信号几乎准确无误地检测出来。
在测量埋没在噪声中的信号时,使用锁相放大器最为合适。
为什么锁相放大器具有那么强的抗噪声能力?锁相放大器不容易受到噪声影响的原因,是因为很好地利用了噪声(白噪声)与目的信号(正弦波)之间在性质上的差别。
在这里,我们一方面整理白噪声的性质和正弦波的性质,一方面解说为什么锁相放大器会具有很强的噪声抑制能力。
噪声的性质 ■平坦的频谱在宽阔的频率范围内,该信号具有几乎相同的频谱。
信号的瞬时电平成为预测不到的随机的值。
■随着频带宽度不同测量电压会改变在用毫伏计测量白噪声时,得到的测量值和白噪声所具有的频谱带宽(BandWidth: B.W.)的平方根以及电平成比例。
测量得到的电压值,与下图中的浅蓝色部分的面积成比例。
即使对于同样的噪声,如果用带通滤波器(BPF)来限制所通过的频带,那么测量所得的电压值就会不同。
把测量所得的噪声电压(Vrms),除以频带宽度的平方根,就得到用表示噪声大小的单位、也即称作噪声电压密度(V/√Hz)来衡量的值。
频道宽度如果缩小到1/100,那么测量所得的噪声电压就缩小到1/10。
下面,让我们来看一看正弦波的性质正弦波的性质■频谱非常集中1kHz正弦波信号的频谱,只存在于1kHz的位置,其他地方的频谱的电平都为零。
■与频带宽度无关,测量所得电压保持一定的值。
因为频谱是集中分布的,所以不受频带宽度的影响,测量所得的电压保持一定的值。
但是,必须要使信号频率存在于所取的频带之内。
用交流电压表所测量的电压值,与频带宽度无关,是上图中的V。
那么,在正弦波上叠加了白噪声以后会怎么样呢?白噪声与正弦波合成的信号即使白噪声与正弦波进行加法运算所得的信号,测量所得的电压对于频带宽度所具有的各种性质也不会有变化。
所以,当带通滤波器的频带宽度变狭窄时,就会有以下结果:1.想要测量的信号的电平不变;2.白噪声的强度减小;3.交流声等频率不同的成分也当然被削弱。
从以上这些结果可知,为了测量被噪声所掩埋的信号,应该将带通滤波器的频带宽度变窄。
如果将频带宽度缩小到1/N,那么噪声就减小到1/√N,而信号却不改变,其结果SN比(信噪比)改善为1/√N。
但是,这样的带通滤波器也是有一个限度的。
为了说明「锁相放大器利用了噪声与目的信号所具有的不同性质,所以不容易受到噪声的影响」,前面已解说了以下几个要点:∙噪声(白噪声)的性质;∙正弦波的性质;∙从白噪声与正弦波合成的信号中,使用带通滤波器可以使目的信号(正弦波)从噪声中浮现出来。
带通滤波器的限制■使通带变狭窄的限度使用带通滤波器只让想要测量的频率信号通过,可以抑制噪声,让目的信号浮现出来。
但是,使带通滤波器的通带宽度变窄,这也是有限度的。
在带通滤波器中,中心频率与通带宽度的比值称作Q值,作为衡量带通滤波器的滤波尖锐程度的一项指标来使用。
Q值越大,通带宽度就越窄,抑制噪声的能力就越强。
但是,一般的滤波器所能够实现的Q值,大约在100左右。
对于1kHz的中心频率,相应的通带宽度的限界大约在10Hz左右。
Q值不能任意增大的原因,在于组成滤波器的零部件的精确度和时间/温度的稳定性是有限的。
把带通滤波器与锁相放大器做一个比较。
Q(中心频率/通带宽度)中心频率带通滤波器100左右 (10Hz@1kHz)固定(不容易改变)锁相放大器~107左右 (0.1mHz@1kHz)追随测量信号锁相放大器用特殊的方法,使Q提高到约为107(通常的带通滤波器约为100左右),而且实现了一种特殊的带通滤波器,能够自动地将中心频率跟踪和保持在测量频率上。
请看介绍锁相放大器的构成!锁相放大器的构成锁相放大器采用在无线电电路中已经非常成熟的外差式振荡技术,把被测量的信号通过频率变换的方式转变成为直流。
在外差式振荡技术中被称为本地振荡(Local Oscillation)的、用于做乘法运算的信号,在锁相放大器中被称为参照信号,是从外面输入的。
锁相放大器能够(从被测量信号中)检测出与这个参照信号频率相同的分量。
在被测量的信号里所包含的各种信号分量中,只有与参照信号频率相同的那个分量才会被转换成为直流,因而才能够通过低通滤波器(LPF)。
其他频率的分量因为被转换成为频率不等于零的交流信号,所以被低通滤波器(LPF)滤除。
在频率域中,如下图所示。
锁相放大器对于噪声的抑制能力,是由上图中低通滤波器(LPF)的截止频率来确定的。
例如,在测量10kHz的信号时,如果使用1mHz的低通滤波器(LPF),那么就等效于在使用10kHz±1mHz的带通滤波器时的噪声抑制能力。
如果换算成为Q值,就相当于5×106。
要想真正制造这样高的Q值的带通滤波器,那是不可能的。
但是,使用锁相放大器,这就很容易实现了。
如同前面所解说的那样,在使用通频带非常狭窄的带通滤波器(BPF)时,如果其中心频率与被测量信号的频率有所偏离,那么就会产生测量误差,最糟糕的情况下可能会把被测量信号也滤除了。
与这种情况相比较,对于锁相放大器来说,即使低通滤波器的截止频率多少有些偏离,只要还能够让直流通过,那么对测量结果也不会有大的影响。
与带通滤波器相比较,锁相放大器更容易实现通频带非常狭窄的低通滤波器,不管通频带多么狭窄都能实现。
由此可见,锁相放大器具有强大的能力从噪声中检测出被掩埋的信号。
那么,实际的锁相放大器又是什么样的呢?■使用PSD(相敏检波器)作为乘法器。
如前面所解说的那样,频率变换是通过乘法运算来进行的。
一般的乘法运算模拟电路,其线性程度和温度稳定性都存在问题。
所以,在实际的锁相放大器中,采用开关元件进行同步检波,由此实现频率变换。
由开关元件所进行的同步检波电路,称作 PSD(相敏检波器,Phase Sensitive Detector),这是组成锁相放大器的心脏部分。
采用方波作为参照信号,与参照信号同步使被测量信号的极性翻转,也就是在×1/×(-1)这两者之间进行切换。
■需要进行相位调节。
如下图所示,PSD的输出信号会由于被测量信号与参照信号之间的相位差,而产生很大的变化。
由此,低通滤波器(LPF)的输出信号(也就是锁相放大器测量所得到的值)也会产生变化。
除了相位差为0°之外,在其他状态下不能很好地测量被测信号的大小。
这样,就需要把参照信号与被测量信号之间的相位差调节到0°,然后再输入到PSD。
这个相位调节的电路,称作移相电路(Phase Shifter),是锁相放大器中必不可少的电路。
上述的锁相放大器,称作「单相位锁相放大器」。
为了能够正确地测量振幅和相位,需要有能够调节移相电路的「相位调节」部分。
另外,如果将参照信号的相位移动90°,使用两个PSD,那么也可以组成不需要调节相位的「双相位锁相放大器」。
最后,让我们来说明锁相放大器的一个重要参数——“动态保留”。
动态保留是什么对于通常的电压表,是有测量量程的。
在10V量程,能测量的最大电压为10V。
如果超过了10V电压,那么就需要增大量程,例如,用20V的量程进行测量。
锁相放大器也是一种电压表,当然也有测量的量程。
但是,锁相放大器是用来测量被掩埋在噪声中的微弱信号的,所以除了通常的测量量程之外,还具有被称作为“动态保留”的一个参数。
该参数表示可以容忍测量量程的最大多少倍的噪声,由下面的公式来定义。
对于几乎所有的锁相放大器,与被测量的信号在一起,“动态保留”是有若干个档级可以变更的。
例如,在一开始介绍的「在要测量的0.1mVrms的目的信号上,叠加了0.1Vrms(≈0.8Vp-p)的噪声电压」的那一个例子中,如果把测量量程设定为0.1mV量程,那么就需要有78dB以上的动态保留。
「用微小电流来测量接插件的接触电阻」~是否用大电流来测量接插件的接触电阻?~接插件的接触电阻,是通过电流流过接触点时所产生的电压降来进行测量的。
在JIS 等标准中,规定了测量电流为10~20mA。
但是,除了电源线以外,实际上真正使用这样大的电流的接插件几乎是没有的,这是实情。
用于传递信号的接插件,在实际使用情况下的电流接近于0,所以,用大电流测量所得的值很可能与实际的使用状态不同。
如果使用锁相放大器,那么即使是用以往在事实上不可能的1μA左右的微小电流,也能够稳定地测量接触电阻。
零部件名称电阻值印刷电路板插头座9.2mΩ用于设备内部连接的插头座 3.9mΩ用于设备之间连接的插头座 1.8mΩ用于设备之间的金属插头座 1.1mΩ小型拨动开关 1.2mΩ集成电路插座 3.9mΩ∙能够用1μA左右的微小电流来测量接触电阻。
∙因为采用交流法进行测量,所以不会受到接触电位、温差电动势的影响。
「测量光源的方向特性」~有干扰光的影响,不会降低测量精度吗?~在进行光的测量时,为了避免外来光线的干扰,需要在暗室里进行测量,这是一般的常识。
但是,不管设置多么好的暗室,也不可能使外来的干扰光线化为零。
另外,在用红外光谱仪测量时,周围的温度本身就成为外来的干扰光线。
被外来干扰光线所掩埋的微弱光信号,如果使用锁相放大器,就能够「将外来干扰光线除去」、也就是「将噪声除去」,而仅将目的信号检测出来。
下面所示的是一个测量光源的发光强度分布状况(方向特性)。
光源向着正面方向发射最大的光通量。
越偏离正面方向,光通量就越少。
在处理传感器检测出来的信号时,除了有上图所示的锁相放大器之外,也有使用下图所示的●交流电压表●带通滤波器+交流电压表来进行测量的例子。