当前位置：文档之家 › 线性代数课件(完整版)

线性代数课件(完整版)

  • 格式：ppt
  • 大小：6.03 MB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

线性代数课本课件

线性代数课本课件

最小二乘法的计算实例
直线拟合的计算实例
通过最小二乘法拟合一组数据点，得到最佳 直线方程。
多项式拟合的计算实例
通过最小二乘法拟合一组数据点，得到最佳 多项式方程。
非线性拟合的计算实例
通过最小二乘法结合适当的变换，拟合非线 性模型。
THANKS FOR WATCHING
感谢您的观看
04 特征值与特征向量
特征值与特征向量的概念
特征值
设A是n阶方阵，如果存在数λ和 非零n维列向量x，使得Ax=λx成
立，则称λ是A的特征值。
特征向量
对应于特征值λ的满足Ax=λx的非 零向量x称为A的对应于特征值λ的 特征向量。
特征空间
对应于同一特征值的所有特征向量 （包括零向量）的集合，加上零向 量后构成的线性子空间称为特征空 间。
线性方程组的应用举例
线性规划问题
图像处理
线性方程组可用于描述和解决线性规划问 题，如资源分配、生产计划等。
在计算机图像处理中，线性方程组可用于 图像滤波、图像恢复等任务。
机器学习
电路分析
在机器学习领域，线性方程组常用于线性 回归、逻辑回归等模型的参数求解。
在电路分析中，线性方程组可用于描述电路 中的电流、电压等物理量之间的关系，从而 进行电路分析和设计。
向量的线性组合关系不变。
线性变换的性质
02
线性变换具有保持线性组合、保持线性相关等性质，同时线性
变换的核与像也是重要的概念。
线性变换的运算
03
线性变换之间可以进行加法和数量乘法运算，同时线性变换的
逆变换和复合变换也是常见的运算。
线性空间的基与维数
基的概念
线性空间中的一组线性无关的向量，可以表示该空间中的任意向 量，称为该线性空间的基。

线性代数课件(完整版)

线性代数课件(完整版)

二、三阶行列式
定义 设有9个数排成3行3列的数表
a11 a12 a13
a 21 a 22 a 23
引进记号
a 31 a 32 a 33
原则：横行竖列
主对角线 a 1 1 a 1 2 a 1 3
a 2 1 a 2 2 a 2 3
a11a22a33a12a23a31a13a21a32
副对角线 a 3 1 a 3 2 a 3 3
2021/3/11
18
3个不同的元素一共有3! =6种不同的排法 123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前.
b1 b2
由消元法，得
( a a a a ) x b a a b 12 12 12 21 1 1 22 12 2
( a a a a ) x a b b a 12 12 12 21 2 12 11 21
当 a 1a 1 2 2a 1a 时2 2，1 该0 方程组有唯一解
x b1a22a12b2
行列式的性质及计算.
§6 行列式按行（列）展开
§7 克拉默法则 —— 线性方程组的求解.
2021/3/11
4
§1 二阶与三阶行列式
我们从最简单的二元线性方程组出发，探 求其求解公式，并设法化简此公式.
一、二元线性方程组与二阶行列式
二元线性方程组
aa1211xx11
a12 x2 a22 x2
aa1211xx11
a12 x2 a22 x2
b1 b2
若令
D a11 a12 a21 a22
(方程组的系数行列式)

线性代数ppt

线性代数ppt
A 其中A是A的伴随阵.
推论 设A、B 都是n阶方阵，若AB E(或
BA E) , 则B A1.
3. 可逆矩阵的性质
1 若A可逆,则A1也可逆,且 A1 1 A.
2 若A可逆,数 0,则A可逆,且 A1 1 A1.
3 若A, B为同阶可逆矩阵,则AB也可逆,且 1
1 1
4 若A可逆,则AT也可逆 ,且 A A .
线性代数总复习
第一章 行列式
第一节 n阶行列式的定义
二阶行列式的计算方法
a11 a21
a12 a22
a11a22
a12a21.
三阶行列式的计算方法——沙路法
一些常用的行列式结果：
a11 a12 a1n
1.
0 a22 a2n
a11a22
ann
0 0 ann
1
2.
2
12 n
1
n
3.
（其中 为数）;
3 AB C AB AC, B C A BA CA;
方阵的幂运算： （1） Ak Al Akl （2） ( Ak )l Akl
注意：ABk AkBk .
转置运算：
1 AT T A;
2 A BT AT BT ; 3 AT AT ; 4 ABT BT AT .
M
M
M
an1
an2
ann
则D等于下列两个行列式之和：
a11 a12 a1n
a11 a12 a1n
MMM
bi 2 bin ci1
M
M
M
ci 2 cin
M
M
an1 an2 ann
an1 an2 ann
性质1.6 把行列式的某一行（列）的各元素乘以 同一数然后加到另一行(列)对应的元素上去，行列 式不变． (倍加运算)

线性代数课件ppt

线性代数课件ppt
aij bij i 1,2,,m; j 1,2,,n,
则称矩阵A与B相等,记作A B.
第12页/共90页
例3: 设 A 1 2 3, 3 1 2
B 1 x 3, y 1 z
已知 A B,求 x, y, z. 解: A B,
x 2, y 3, z 2.
第13页/共90页
0 0 1 a31 a32 a33 a31 a32 a33
a11 x1 a12 x2 a1n xn a21 x1 a22 x2 a2n xn
b1
b2
,
am1 x1 am2 x2 amn xn bm
所以方程组可以用矩阵的乘法来表示．方程组中 系数组成的矩阵A称为系数矩阵，
第28页/共90页
方程组中系数与常数组成的矩阵
3 3 6 2 8 1 6 8 9
第16页/共90页
2、 矩阵加法的运算规律
1 A B B A;
2 A B C A B C .
a11
3
A
a21
a12
a22
am1 am1
称为矩阵A的负矩阵.
a1n a2n amn
aij ,
4 A A 0, A B A B.
主对角线 a11 a12
A
a21
a22
副对角线 am1 am2
a1n
a2n
amn
矩阵A的
m, n元
简记为
A Amn
aij
mn
aij
.
这m n个数称为A的元素,简称为元.
元素是实数的矩阵称为实矩阵,
元素是复数的矩阵称为复矩阵.
第5页/共90页
例1:线性方程组
a11 x1 a12 x2

(完整版)自考线性代数全套课件

(完整版)自考线性代数全套课件
f x12 2 x22 5 x32 2 x1 x2 2 x1 x3 6 x2 x3 为标 准形, 并求 所用的 变换矩 阵.
解
含有平方项
含有 x1的项配方
f x12 2x22 5x32 2x1 x2 2x1 x3 6x2 x3
x12 2x1 x2 2x1 x3 2x22 5x32 6x2 x3
15
4．将正交向量组单位化，得正交矩阵 P
令
i
i i
,
i 1,2,3,
1 3
2 5
2 45
得 1 2 3, 2 1 5 , 3 4 45 .
2 3
0
5
45
所以
1 3
P 2 3
2
3
2 5 15
0
2 45
4 45 .
5
45
16
于是所求正交变换为
解 1．写出对应的二次型矩阵，并求其特征值
17 2 2 A 2 14 4
2 4 14
17 2 A E 2 14
2 4
182
9
2 4 14
14
从而得特征值 1 9, 2 3 18.
2．求特征向量
将1 9代入A E x 0,得基础解系
1 (1 2,1,1)T .
x Cy
9
将其代入 f xT Ax,有
f xT Ax CyT ACy yT CT AC y.
定理1 任给可逆矩阵C ,令B C T AC ,如果A为对称
矩阵,则B也为对称矩阵,且RB RA.
证明 A为对称矩阵,即有A AT ,于是
BT C T AC T C T AT C C T AC B,
将2 3 18代入A E x 0,得基础解系

线性代数完整版ppt课件

线性代数完整版ppt课件
a11x1 a12x2 b1 a21x1 a22x2 b2
求解公式为
x1
x
2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12a 21 b1a 21 a12a 21
请观察，此公式有何特点？ Ø分母相同，由方程组的四个系数确定. Ø分子、分母都是四个数分成两对相乘再
a11 a12 a13 D a21 a22 a23
a31 a32 a33
实线上的三个元素的乘积冠正号， 虚线上的三个元素的乘积冠负号.
a11a22a33 a12a23a31 a13a21a32 a13a22a31a12a21a33 a11a23a32
注意：对角线法则只适用于二阶与三阶行列式.
.
13
(方程组的系数行列式)
D1
b1 b2
a12 a22
D2
a11 a 21
b1 b2
则上述二元线性方程组的解可表示为
x1
b1a22 a11a22
a12b2 a12a21
D1 D
x2
a11b2b1a21 a11a22a12a21.
D2 D
10
例1
求解二元线性方程组
32x1x1 2xx22
12 1
3 2
显然 P n n ( n 1 ) ( n 2 )3 2 1 n !
即n 个不同的元素一共有n! 种不同的排法.
.
18
3个不同的元素一共有3! =6种不同的排法 123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前.
线性代数（第五版）

同济大学出版社线性代数课件(完整版)

同济大学出版社线性代数课件(完整版)

0 0
0 0 0 a44
0 0 0 a14
0 D2 0
0 a23 a32 0
0 0
a41 0 0 0
a11 a12 a13 a14
0 D3 0
a22 a23 a24 0 a33 a34
0 0 0 a44
a11 0 0 0
D4

a21 a32
a22 a32
0 a33
0 0
a41 a42 a43 a44
引进记号
a21 a22 a23
原则：行列式
主对角线 a11 a12 a13
a21 a22 a23 a11a22a33 a12a23a31 a13a21a32
副对角线 a31 a32 a33
a13a22a31 a12a21a33 a11a23a32
a11 a12
a1n
D a21 a22
a2n
(1) a a t( p1 p2 pn ) 1 p1 2 p2
p1 p2 pn
anpn
an1 an2 二、annn 阶行简列记式作的det定(a，ij 义)
1. n 阶行列式共有 n! 项．
其中a为ij 行列式D的(i, j)元
2. 每一项都是位于不同行不同列的 n 个元素的乘积．

b1 b2
求解公式为
请观察，此公式有何特点？

x1


x2

b1a22 a11a22 a11b2 a11a22
a12b2 a12a21 b1a21 a12a21
分母相同，由方程组的四个系数确定. 分子、分母都是四个数分成两对相乘再
相减而得.
二元线性方程组

线性代数全套课件

线性代数全套课件
2
它们的和
j1 jn
J 1 a1 j a2 j
1
2
anjn
称为n阶行列式。
a11 a12 a1n
记为
a21 a22 a2 n an1 an 2 ann a11 a12 a1n a21 a22 a2 n an1 an 2 ann
aij 称为行列式的元素
行列式中，除对角线上的元素以外，其他元素全为 零（即i≠j时元素aij＝0）的行列式称为对角行列式， 它等于对角线上元素的乘积。
例 证明
a a n 1 ,1 a n1 a a n 1, 2 an 1
n ( n 1 ) 2
a1n a2,n1 an1, 2 an1
i1 i p i q i n 与 i1 iq i p in 只经过一次对换
a11 a12 a13 a 23 0 0 a 21 a 22 D a 31 a 32 a41 0
n n 1 2
a1na2,n1 an1, 2an1
a14 0 a14a 23a 32a41 0 0
§3 对 换
定义5 排列中，将某两个数对调，其余的数不动， 这种对排列的变换叫对换，将相邻两数对换，叫做 相邻对换（邻换）。 定理1 一个排列中的任意两数对换， 排列改变奇偶性。
此式称为n阶行列式的 展开式或行列式的值
D

j1 jn
1
J
a1 j1 a2 j2 anjn
例
计算4阶行列式
a11 D
0
0 0 a 33 a43
0 0 0 a44
a 21 a 22 a 31 a 32 a41 a42
解： 根据定义，D是4！＝24项的代数和，但每一 项的乘积 a1 j1 a2 j 2 a3 j3 a4 j中只要有一个元素为 0，乘积 n 就等于0，所以只需展开式中不明显为0 的项。

线性代数_课件

线性代数_课件

2020/3/1
22
五、关于等价定义的说明
对于行列式中的任一项
(1) a1p1...aipi ...a jpj ...anpn
(1)
其中 1...i... j...n为自然排列， 为列下标排
列 p1...pi...p j... pn 的逆序数。对换 (1) 中元
素a
与
ip i
a jp
j
成：
(1) a1p1...a jpj ...aipi ...anpn
解：∵ 排列p1 p2 p3…pn与排列 pn…p3 p2 p1的逆序
数之和等于1～ n 这 n 个数中任取两个数的组合
数即 ：

(
p1 p2... pn )

(
pn
pn1... p1)

Cn2

n(n 1) 2

(
pn
pn1... p1)

n(n 1) 2

k
2020/3/1
9
例4 求排列(2k)1(2k 1)2(2k 2)...(k 1)k
a22 ...
... a2n ... ...
a11a22...ann
0 0 ... ann
2020/3/1
16
3) 次上三角行列式
a1,1 ... a1,n1 a1,n
a2,1 ... a2,n1 ... ... ...
0 ...
n ( n 1)
(1) 2 a1,na2,n1...an,n
例6 若 a13a2ia32a4k , a11a22a3ia4k , ai2a31a43ak 4 为四阶行列式的项，试确定i与k，使前两项带正号， 后一项带负号。

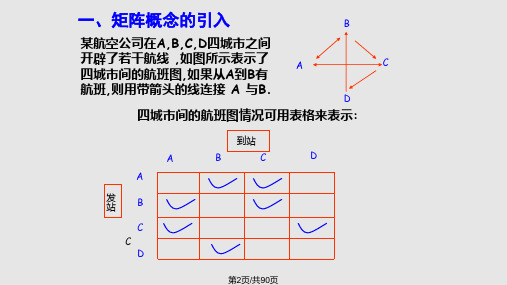
线性代数-课件ppt

线性代数-课件ppt

a11
A
A
a21
a12
a22
a1n
a2n
.
am1 am1 amn
2、数乘矩阵的运算规律
（设 A、B为 m n 矩阵， ,为数）
1 A A; 2 A A A;
3 A B A B.
矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算.
3 2 7 5
例1：已知
A
1 6
线性代数
• 矩阵的概念 • 矩阵的基本运算 • 矩阵的初等变换与矩阵的秩 • 逆矩阵 • 线性方程组解的判定
矩阵的概念
• 一、矩阵概念的引入 • 二、矩阵的定义 • 三、几种特殊的矩阵 • 四、同型矩阵和矩阵相等
一、矩阵概念的引入
B
某航空公司在A,B,C,D四城市之间
开辟了若干航线 ,如图所示表示了 四城市间的航班图,如果从A到B有
13 6 19 7
7 10
2 28
2 2
21 24
三、矩阵的乘法
引例：某校明后两年计划建筑教学楼和宿舍楼。建筑面积及材料耗用量如表：
建筑面积（单位：100平方米）
教学楼 宿舍楼
材料（每100平方米耗用量，单位：吨）
钢材 水泥 铝材
明年 20
10
教学楼
2
18
0.4
后年 30
20
宿舍楼 1.5
1 2 3 4
解：设A
4 3 2
1 4 3
2 1 4
123 ,
x1
X
x x x
2 3 4
,
1
B
2 2 1
,
所以方程组可表示为 ：
1 2 3 4 x1 1

线性代数ppt课件

线性代数ppt课件

VS
线性代数的特点
线性代数具有抽象性、实用性、广泛性等 特点，是数学中重要的分支之一。
线性代数的历史背景
线性代数的起源
线性代数起源于17世纪，主要目的 是为了解决线性方程组的问题。
线性代数的发展
随着数学的发展，线性代数逐渐成为 一门独立的数学分支，并在20世纪得 到了广泛的应用和发展。
线性代数的应用领域
转置矩阵
一个矩阵A的转置矩阵是满足$A^T_{ij}=A_{ ji}$的矩阵
行列式与高斯消元
03
法
行列式的定义及性质
总结词
行列式是线性代数中重要的工具之一，它具有特殊的性质和计算规则。
详细描述
行列式是由一组方阵中的元素按照一定规则组成的，它是一个方阵是否可逆的判断标准，同时也有一 些重要的性质和计算规则，如交换两行或两列、对角线上的元素相乘等。了解行列式的定义和性质是 学习线性代数的基础。
矩阵的运算规则
加法
两个相同大小的矩阵，对应位置的元素相加
数乘
用一个数乘以矩阵的每一个元素
减法
两个相同大小的矩阵，对应位置的元素相减
乘法
要求两个矩阵满足乘法运算的规则，即第一 个矩阵的列数等于第二个矩阵的行数
矩阵的逆与转置
逆矩阵
一个矩阵A的逆矩阵是满足$AA^{-1}=I$的矩阵，其中$I$是单位矩阵
高斯消元法的原理
总结词
高斯消元法是一种解线性方程组的直接方法 ，其原理是将方程组转化为阶梯形矩阵。
详细描述
高斯消元法的基本思想是通过一系列的行变 换将线性方程组转化为阶梯形矩阵，这样就 可以直接求解方程组。高斯消元法包括三种 基本的行变换：将两行互换、将一行乘以非 零常数、将一行加上另一行的若干倍。通过 这些行变换，我们可以将矩阵转化为阶梯形 矩阵，从而求解方程组。

(完整版)《大学线性代数》PPT课件

(完整版)《大学线性代数》PPT课件

下特页点
结束
a11 a12 … a1n
a21
…
a22 … a2n … ……
=
(-1) N ( j1 j2 jn ) a1 j1 a2 j2 anjn 。
an1 an2 … ann
n阶行列式共有n!项，且冠以正号的项和冠以负号的 项各占一半。
在行列式中，a1 j1 a2 j2 anjn 是取自不同行不同列
结束
例2．计算 n 阶下三角形行列式D的值： a11 0 0 … 0 a21 a22 0 … 0
D = a31 a32 a33 … 0 … … … …… an1 an2 an3 … ann
其中aii0(i=1, 2, , n)。
解：为使取自不同行不同列的元素的乘积不为零，
第一行只能取a11，第二行只能取a22，第三行只能取a33， ， 第 n 行只能取ann。 这样不为零的乘积项只有
结束
对换：
在一个排列i1isitin中，将两个数码 is与it对调， 就得到另一个排列 i1 it is in ，这样的变换称为一个 对换，记为对换(is , it)。
例如，排列 21354 经对换(1, 4)，得到排列24351。 提问：
排列 21354 经对换 (1, 4)，得到的排列是 24351， 排列的奇偶性有无变化？ 提示：
的 n 个元素的乘积。
a1 j1 a2 j2 anjn 之前的符号是 (-1) N(j1 j2 jn) 。
行列式有时简记为| a ij |。一阶行列式|a|就是a。
首页
上页
四阶行列式
a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44

线性代数课件

线性代数课件
a11 a21 a31 a12 a22 a32 a13 a23 a33
偶排列
奇排列
1
N ( j1 j2 j3 )
a1 j1 a2 j2 a3 j3
线性代数 第一章 行列式
11
定义 设有 n 2 个数，排成 n 行 n 列的数表
a11 a12 n 称为n 阶行列式. 简记为 a ij
it 这种变换称为对换，记作（ i s ，）
定理1.1 任一 排列经过一次对换后奇偶性发生改变。
定理1.2
n! n级排列共有 n! 个，其中奇、偶排列相等，各为 2
线性代数 第一章 行列式
10
2
a11 a21 a31
n 阶行列式的定义
a12 a22 a32 a13 a23 a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32 a33
主讲
田立芳
统计与数学学院
目录 线性代数 第一章 行列式 退出
1
目
录
行列式 矩阵 线性空间 线性方程组 矩阵的特征值 二次型
线性代数 第一章 主页 行列式 线性代数
退出
2
第一章 行列式
§1 n 阶行列式的定义
§2 行列式的性质 §3 行列式的计算 §4 克莱姆法则
线性代数 第一章 行列式
3
§1.1
线性代数 第一章 行列式
18
性质1 对任何行列式D，有D=DT（行列式与其转置行列式相等） 证
D
T
将DT记为
于是有 bij a ji ( i , j 1,2, , n) 按行列式的定义

j1 j2 jn

线性代数-行列式(完整版)ppt课件

线性代数-行列式(完整版)ppt课件
设 D
,
31
(1)当为何值时， D 0,
(2)当为何值时 D0.
解 230 0，或 3
2
D
2
31
.
例3 求二阶行列式
a 1 b2
.
(2)三阶行列式
记号
a 11 a 12 a 13 a 21 a 22 a 23 称为三阶行列式. a 31 a 32 a 33
它表示数
a 1a 1 2a 2 3 3a 1a 2 2a 3 3 1a 1a 3 2a 1 32 a 1a 3 2a 2 3 1a 1a 2 2a 1 3 3a 1a 1 2a 3 32
27下三角行列式的值等于其主对角线上. 各元素的乘积 .
同理可得 上三角形行列式
a 11 a 12 a 13 a 1n
0
D 0
a 22 a 23 a 2n
0 a 33 a 3 n a11a22ann
0 0 0 a nn
其中 aii 0 (i1,2,n)
特殊情况 : 对角形行列式
a1n
a21 a22 a2n1 0
0 0 a2n1 a2n
an11 an12 0 an1 0 0
0
0 an12 an1n1 an1n
0 an1 an2 ann1 ann
( 1 ) aaa a N (j1 j2 jn 1 jn ) 1 j12 j2
和式中仅当 j1n ,j2n 1 , ,jn 12 ,jn1时，
a1j1a2j2annj0
D ( 1 ) nN (n (n ( 1n ) 1 ) 3) 2 a 1 n 1 a 2 ,n 1 a n 1
29
(1) 2 12n .
注：
类似可得
a11 a12 a1n1 a1n 0 0 0

《线性代数》PPT课件幻灯片PPT

《线性代数》PPT课件幻灯片PPT

特别当矩阵A与对角阵=diag(1, 2,···, n )相似时,
那么
Am = PmP-1; (A)= P()P-1.
而对于对角阵, 有
1k
k =
k2
;
kn
()=
(1)
(2)
(n).
利用上述结论可以很方便地计算矩阵A的多项式
(A). 结论: 假设f( )为矩阵A的特征多项式, 那么矩阵
A的多项式 f(A)=O. 此结论的一般性证明较困难, 但当矩阵A与对角
因此, 当a = –1时矩阵A能对角化.
三、小 结
1. 相似矩阵 相似是矩阵之间的一种关系, 它具有很多良好的 性质, 除了课堂内介绍的以外, 还有: (1) 假设A与B相似, 那么det(A)=det(B); (2) 假设A与B相似, f(x)为多项式, 那么f(A)与f(B) 相似; (3) 假设A与B相似, 且A可逆, 那么B也可逆, 且A1与B2-1. 相相似似.变换与相似变换矩阵 相似变换是对方阵进展的一种运算, 它把A变成 P-1AP, 可逆矩阵P称为进展这一变换的相似变换矩阵.
-2
P1AP
1 1.
矩阵P的列向量和对角矩阵中特征值的位置要相
互对应.
例3:设A= 110
0 1 0
a10,当a为何值时, 矩阵A能对角化?
0 1 解: | A –E | = 1 1 a = –(–1)2(+1).
1 0
得矩阵A的特征值 1 = –1, 2 = 3 = 1. 对应单根1 = –1, 恰好可求得一个线性无关的特
阵 相似时很容易证明即.
f(A)=Pf()P=POP-1=O.
二、利用相似变换将方阵对角化
n阶方阵A是否与对角阵 =diag( 1, 2,···, n ) 相似, 那么我们需要解决如下两个问题:

线性代数课件(完整版)同济大学

线性代数课件(完整版)同济大学

二元线性方程组
aa1211
x1 x1

a12 x2 a22 x2

b1 b2
求解公式为

x1


x2

b1a22 a11a22 a11b2 a11a22
a12b2 a12a21 b1a21 a12a21
请观察，此公式有何特点？ ➢分母相同，由方程组的四个系数确定. ➢分子、分母都是四个数分成两对相乘再
a31 a32 a33 a13a22a31 a12a21a33 a11a23a32
规律：
1. 三阶行列式共有6项，即3!项．
2. 每一项都是位于不同行不同列的三个元素的乘积．
3. 每一项可以写成 a1p1a2 p（2 a3正p3负号除外），其中
是1、2、3的某个排列.
p1 p2 p3
4. 当 p1 p2是p3偶排列时，对应的项取正号； 当 p1 p是2 p奇3 排列时，对应的项取负号.
注意：对角线法则只适用于二阶与三阶行列式.
例2 计算行列式
1 2 -4 D -2 2 1
-3 4 -2
解 按对角线法则，有
D 1 2 (2) 2 1 (3) (4) (2) 4 11 4 2 (2) (2) (4) 2 (3)
p1 p2 p3
其中 表示对1、2、3的所有排列求和. p1 p2 p3
二阶行列式有类似规律.下面将行列式推广到一般的情形.
二、n 阶行列式的定义
a11 a12 L a1n
D a21 a22 L MM
a2n
M (1) a a L a p1 p2L pn
t ( p1 p2L pn )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

因此大部分的排列都不是“顺序”，
而是“逆序”.
-
19
对于n 个不同的元素，可规定各元素之间的标准次序. n 个不同的自然数，规定从小到大为标准次序.
-3 4 -2
解 按对角线法则，有
D1 2 ( 2 ) 2 1 ( 3 ) ( 4 ) ( 2 ) 4
1 1 4 2 ( 2 ) ( 2 ) ( 4 ) 2 ( 3 )
4 6 3 4 2 8 24
1.4
-
14
例3 求解方程 1 1 1
( a 1 a 2 1 2 a 1 a 2 2 ) x 1 2 a 1 b 2 1 b 1 a 21
当 a 1a 1 2 2a 1a 时2 2，1 该0 方程组有唯一解
x b1a22a12b2
1 a a a a
11 22
12 21
x2
a11b2 b1a21 a11a22a12a21
-
6
二元线性方程组
aa1211xx11
a12 x2 a22 x2
b1 b2求解公式为x来自1x2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12 a 21 b1a 21 a12 a 21
请观察，此公式有何特点？ ➢分母相同，由方程组的四个系数确定. ➢分子、分母都是四个数分成两对相乘再
线性代数（第五版）
2013.12.14修改汇总
修改人：xiaobei93521
在以往的学习中，我们接触过二 元、三元等简单的线性方程组.
但是，从许多实践或理论问题里 导出的线性方程组常常含有相当 多的未知量，并且未知量的个数 与方程的个数也不一定相等.
-
2
我们先讨论未知量的个数与方程 的个数相等的特殊情形.
§6 行列式按行（列）展开
§7 克拉默法则 —— 线性方程组的求解.
-
4
§1 二阶与三阶行列式
我们从最简单的二元线性方程组出发，探 求其求解公式，并设法化简此公式.
一、二元线性方程组与二阶行列式
二元线性方程组
aa1211xx11
a12 x2 a22 x2
b1 b2
由消元法，得
( a a a a ) x b a a b 12 12 12 21 1 1 22 12 2
a 11 a 12 数表 a 2 1 a 2 2
a 11 a12 记号 a 2 1 a 2 2
表达式 a11a22称a12为a2由1 该
数表所确定的二阶行列式，即
Da11 a21
a12 a22
a11a22a12a21
其中，aij(i1,2;j1,2)称为元素.
i 为行标，表明元素位于第i 行；
j-
为列标，表明元素位于第j
a31 a32 a33
实线上的三个元素的乘积冠正号， 虚线上的三个元素的乘积冠负号.
a11a22a33 a12a23a31 a13a21a32 a13a22a31a12a21a33 a11a23a32
注意：对角线法则只适用于二阶与三阶行列式.
-
13
1 2 -4
例2 计算行列式 D - 2 2 1
D1
b1 b2
a12 a22
D2
a11 a 21
b1 b2
则上述二元线性方程组的解可表示为
x1
b1a22 a11a22
a12b2 a12a21
D1 D
x2
a11b2b1a21 a11a22a12a21-
D2 D
10
例1
求解二元线性方程组
32x1x1 2xx22
12 1
3 2
解 因为 D
3 ( 4 ) 7 0
列. 8
二阶行列式的计算 ——对角线法则
主对角线 a 1 1 副对角线 a 2 1
a 12 a 22
a11a22a12a21
即：主对角线上两元素之积－副对角线上两元素之积
-
9
二元线性方程组
aa1211xx11
a12 x2 a22 x2
b1 b2
若令
D a11 a12 a21 a22
(方程组的系数行列式)
21
122
D11
12 (2)14 1
3 12
D2 2
32421 1
所以
x1
D1 D
14 7
2,
x2
D2 D
213 7
-
11
二、三阶行列式
定义 设有9个数排成3行3列的数表
引进记号
a11 a12 a13 a 21 a 22 a 23 a 31 a 32 a 33
原则：横行竖列
主对角线 a 1 1 a 1 2 a 1 3
a 2 1 a 2 2 a 2 3
a11a22a33a12a23a31a13a21a32
副对角线 a 3 1 a 3 2 a 3 3
a13a22a31a12a21a33a11a23a32
称为三阶行列式.
二阶行列式的对角线法则
并不适用！
-
12
三阶行列式的计算 ——对角线法则
a11 a12 a13 D a21 a22 a23
相减而得.
-
7
二元线性方程组
aa1211xx11
a12 x2 a22 x2
b1 b2
其求解公式为
x
1
x
2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12 a 21 b1a 21 a12 a 21
原则：横行竖列
我们引进新的符号来表示“四个 数分成两对相乘再相减”.
在讨论这一类线性方程组时，我 们引入行列式这个计算工具.
-
3
第一章
• 内容提要
行列式 •行列式是线性代 数的一种工具！ •学习行列式主要 就是要能计算行列 式的值.
§1 二阶与三阶行列式
§2 全排列及其逆序数 行列式的概念.
§3 n 阶行列式的定义
§4 对换 （选学内容）
§5 行列式的性质
行列式的性质及计算.
显然 P n n ( n 1 ) ( n 2 ) L 3 2 1 n !
即n 个不同的元素一共有n! 种不同的排法.
-
18
3个不同的元素一共有3! =6种不同的排法 123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前.
2 3 x 0. 4 9 x2
解 方程左端 D 3 x 2 4 x 1 9 x 8 2 x 2 12 x25x6,
由 x25x60得
x2或 x3.
-
15
§2 全排列及其逆序数
问题 把 n 个不同的元素排成一列，共有多少种不同的 排法？
定义 把 n 个不同的元素排成一列，叫做这 n 个元素 的全排列. n 个不同元素的所有排列的种数，通常用Pn 表示.

相关主题