当前位置：文档之家 › 清华大学微积分高等数学课件第19讲定积分的应用一演示课件

清华大学微积分高等数学课件第19讲定积分的应用一演示课件

  • 格式：ppt
  • 大小：423.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

《定积分进一步应》课件

《定积分进一步应》课件
《定积分进一步应用》 PPT课件
• 定积分的几何应用 • 定积分的物理应用 • 定积分的经济应用 • 定积分的数值计算方法
01
定积分的几何应用
平面图形的面积
矩形面积
01
定积分可用于计算矩形区域的面积，即对长度函数在区间上的
积分。
圆形面积
02
通过定积分计算圆的面积，利用圆的半径和面积之间的关系。
详细描述
万有引力定律是指任何两个物体之间都存在相互吸引的力，这个力的大小与两 个物体的质量成正比，与它们之间的距离的平方成反比。在引力问题中，我们 可以通过定积分来计算两个物体之间的引力。
引力问题
公式
F = G∫dm1 dm2 / r^2
解释
F表示两个物体之间的引力，G表示万有引力常数，∫dm1和∫dm2分别表示两个 物体的质量积分，r表示它们之间的距离。
梯形法
将积分区间分成若干个小区间，每个 小区间上取一个梯形，然后求这些梯 形的面积之和。
辛普森法则
辛普森法则是定积分近似计算的一种 方法，它利用了梯形法的思想，将积 分区间分成若干个小区间，然后在每 个小区间上取一个梯形，最后将这些 梯形的面积之和作为定积分的近似值 。
VS
辛普森法则是基于梯形法的改进，它 通过选取不同的权重因子来提高近似 值的精度。
曲线的弧长
直线段长度
定积分可用于计算直线段的长度，即对一元函数在区间上的积分 。
圆弧长度
通过定积分计算圆弧的长度，利用圆的半径和弧长之间的关系。
复杂曲线弧长
对于不规则的曲线，可以通过分割成若干个简单曲线段，再分别计 算弧长后求和。
02
定积分的物理应用
变力沿直线运动所做的功
总结词：变力做功 公式：W = ∫F(x)dx

《定积分的应》课件

《定积分的应》课件
区间可加性：定积分具有区间可加性，即对于函数在区间[a,b]上的定积分，可以将该区间分成若干个子区 间，并对每个子区间上的函数进行定积分，然后将这些定积分的和作为整个区间[a,b]上的定积分的值。
积分常数倍性质：定积分具有积分常数倍性质，即对于函数f(x)在区间[a,b]上的定积分，有∫k f(x) dx = k ∫ f(x) dx，其中k为常数。
定义：直接计算法是指通过直接计算定积分来求解的方法 适用范围：适用于被积函数简单、积分区间已知的情况 计算步骤：首先确定积分区间，然后根据定积分的定义进行计算 注意事项：在计算过程中需要注意积分的上下限和被积函数的取值范围
适用范围：当被积函数较复 杂或难以直接计算时
定义：将定积分中的被积函数 进行适当的变量替换，以便简 化计算
定义：特殊函数是指具有特殊性质 的函数，如三角函数、指数函数等。
注意事项：在计算特殊函数的定积 分时，需要注意函数的性质和计算 公式的适用范围。
添加标题
添加标题
添加标题
添加标题
计算方法：对于特殊函数的定积分， 我们可以利用已知的定积分的计算 公式进行计算。
应用：特殊函数的定积分在数学、 物理等领域有着广泛的应用。
添加文档副标题
目录
01.
02.
03.
04.
05.
06.
定义：定积分是函数在区间[a,b]上与直线x=a,x=b及x轴围成的曲边梯形的面积 几何意义：定积分表示曲边梯形的面积 性质：定积分具有线性性质、可加性、可减性、可积性、积分区间上的可加性 计算方法：利用微积分基本原理计算定积分的值
线性性质：定积分具有线性性质，即对于两个函数的和或差的定积分，可以分别对每个函数进行定积分后 再相加或相减。

定积分的应用课件

定积分的应用课件

液体静压力计算步骤
详细阐述液体静压力计算的步骤，包 括确定计算区域、选择坐标系、列出 被积函数等。
其他物理问题中定积分应用
引力计算
通过定积分求解质点系或连续体 之间的引力问题。
波动问题
将波动问题转化为定积分问题， 进而求解波动过程中的各种物理 量。
01
02
电场强度计算
利用定积分求解电荷分布连续体 所产生的电场强度。
消费者剩余和生产者剩余计算
消费者剩余计算
消费者剩余是消费者愿意支付的价格与实际支付价格之间的差额。在需求曲线和价格线之间的面积表示消费者 剩余，可以通过定积分计算。
生产者剩余计算
生产者剩余是生产者实际得到的价格与愿意接受的最低价格之间的差额。在供给曲线和价格线之间的面积表示 生产者剩余，同样可以通过定积分计算。
01
通过定积分求解绕x轴或y轴旋转一周所得旋转体的体积。
平行截面面积为已知的立体体积计算
02
利用定积分将立体划分为无数个平行截面，通过截面面积和高
度求解体积。
参数方程表示立体体积计算
03
将参数方程转化为普通函数形式，再利用定积分求解体积。
曲线弧长求解方法
1 2
直角坐标下曲线弧长计算
通过定积分求解曲线在直角坐标系下的弧长。
参数方程表示曲线弧长计算
将参数方程转化为普通函数形式，再利用定积分 求解弧长。
3
极坐标下曲线弧长计算
通过定积分求解曲线在极坐标系下的弧长。
03
定积分在物理学中应用
变力做功问题求解方法
微元法求解变力做功
通过将变力做功的过程划分为无数个微小的 元过程，每个元过程中力可视为恒力，从而 利用定积分求解变力做功。

定积分的应用通用课件

定积分的应用通用课件

计算需求弹性
总结词
定积分在计算需求弹性方面具有重要应用，帮助企业了解市场需求并制定相应的营销策 略。
详细描述
需求弹性是衡量市场需求对价格变动敏感度的指标，对于企业的定价和营销策略具有指 导意义。通过定积分，可以将需求函数转化为弹性函数，从而帮助企业了解市场需求并
制定相应的营销策略。
预测市场趋势和销售量
详细描述
分部积分法的关键是选择合适的函数对，使得其中一个函数的导数容易计算， 而另一个函数的原函数容易找到。通过分部积分法，可以将复杂的定积分转化 为简单的定积分，从而简化计算过程。
03
定积分在几何学中的应用
计算平面图形的面积
01 矩形面积
对于任意长度a和宽度b的矩形，其面积A=a×b。
02 圆形面积
06
定积分在其他领域的应用
在信号处理中的应用
信号的强度变化
定积分可以用来计算信号的强度 变化，例如声音信号的振幅变化
。
信号的平滑处理
通过定积分，可以对信号进行平滑 处理，消除噪声和干扰，提高信号 质量。
信号的滤波
定积分可以用于信号的滤波，例如 低通滤波器和高通滤波器的设计。
在控制系统中的应用
控制系统的稳定性分析
定积分的应用通用课 件
目录
• 定积分的概念与性质 • 定积分的基本计算方法 • 定积分在几何学中的应用 • 定积分在物理学中的应用 • 定积分在经济学中的应用 • 定积分在其他领域的应用
01
定积分的概念与性质
定积分的定义
定积分是积分的一种，是函数在某个区间上的积分和的 极限。定积分常用于计算平面图形的面积、体积、平面 曲线的长度等。
控制系统的误差分析
定积分可以用来分析控制系统的稳定 性，例如判断系统的收敛性和稳定性 。

定积分的几何应用课件

定积分的几何应用课件

电场中的电势
总结词
定积分可计算电场中的电势
详细描述
在静电场中，电势差与电场强度成正比。通过定积分可以计算出 某一点处的电势，即对电场强度进行积分。
公式表示
电势 = ∫E·dl
05
定积分的近似计算
方法
矩形法
总结词
矩形法是一种简单直观的定积分近似计算方法，通过将积分 区间划分为若干个小的矩形，然后求和来逼近定积分。
详细描述
辛普森法则是梯形法的一种改进，它考虑了函数在积分区间的整体变化趋势，将 积分区间分成若干个小的子区间，然后在每个子区间上应用梯形法来逼近定积分 。辛普森法则的精度比矩形法和梯形法更高，但计算量也相对较大。
THANKS
感谢您的观看
3
曲边三角形面积的近似计算
在无法直接计算定积分的情况下，可以使用近似 方法计算曲边三角形的面积，如矩形法、梯形法 等。
任意图形的面积
任意图形面积的计算
01
通过定积分计算任意图形的面积，首先需要找到图形的边界曲
线表达式，然后确定上下限，最后计算定积分。
任意图形面积的几何意义
02
任意图形面积表示的是边界曲线围成的平面区域面积。
详细描述
矩形法的基本思想是将积分区间分成若干个小的矩形，每个 矩形的宽度为小区间的宽度，高度为函数在相应小区间的平 均值。然后，将这些矩形的面积加起来，得到的就是定积分 的近似值。
梯形法
总结词
梯形法是一种基于几何直观的定积分近似计算方法，通过将积分区间划分为若干个小的梯形，然后求 和来逼近定积分。
围绕旋转轴旋转的平面图形被称为 旋转面。
旋转体的体积公式
圆柱的体积公式
V = πr²h，其中r是底面半径，h是高。

《数学定积分的应用》课件

《数学定积分的应用》课件

线性性质
定积分具有线性性质，即对于两个函数的和或差 的积分，可以分别对每个函数进行积分后再求和 或求差。
区间可加性
定积分具有区间可加性，即对于任意两个不重叠 的区间[a, b]和[b, c]，有 ∫(a,c)f(x)dx=∫(a,b)f(x)dx+∫(b,c)f(x)dx。
积分中值定理
如果函数f(x)在区间[a, b]上连续，那么至少存在 一个点ξ∈[a, b]，使得∫(a,b)f(x)dx=f(ξ)(b-a)。
电路中的电流和电压
要点一
总结词
定积分在电路分析中用于计算电流和电压，通过求解电路 中的微分方程，可以得到电流和电压的分布。
要点二
详细描述
在电路分析中，电流和电压的变化规律通常由微分方程描 述。通过应用定积分，可以将电路中的电压和电流表示为 时间的函数。然后通过求解这个微分方程，可以得到电流 和电压在整个电路中的分布情况。
详细描述
对于曲线形构件，其质量可以通过定积分计算。首先，确定构件的材料密度分 布，然后对密度函数在构件的体积上进行积分，得到构件的总质量。
引力场的强度
总结词
通过定积分计算引力场的强度
详细描述
在引力场中，物体受到的引力大小与物体质 量成正比，与物体之间的距离的平方成反比 。通过定积分计算在某一空间区域内的引力 场强度，即在该区域内所有物体产生的引力 对该点的合力。具体地，将引力函数在空间 区域上进行积分，得到该区域内的引力场强 度。
dx进行计算。
功和压力
总结词
定积分可以用于计算变力做功和压力。
详细描述
对于一个质点在力F(x)=f(x)*dx的作用下沿直线运动 ，力F所做的功可以通过计算定积分得出，公式为 ∫(b a) f(x) dx。

定积分的应用课件

定积分的应用课件

2 信号处理
定积分可以计算信号的功 率、频谱和通量。
3 流体力学
通过定积分可以计算流体 的压力、速度和流率。
定积分在地理学中的应用
地形测量
通过定积分可以计算地球表面和 地质构造的高程。
气象学
定积分可以计算气象参数在空气 层中的分布和变化。
人口地理学
通过定积分可以计算人口密度和 城市发展的空间格局。
将面积概念应用于实际场 景，如教室布置和园艺规 划。
3 面积游戏
通过面积游戏和竞赛激发 学生学习兴趣和动力。
和混合效果。
3
创意表达
定积分可以用于艺术家和设计师的创意 表达和构思。
定积分在社会科学中的应用
社会学
定积分可以用于计算人口统计数 据和社会发展指标。
心理学
通过定积分可以建模心理过程和 行为变化。
经济学
定积分可以用于经济模型和政策 的评估和预测。
小学生学习面积时的应用
1 绘图和标注
2 实际场景
通过绘制图形和标注边长， 引导学生进行面积计算。
3
经济增长
通过计算国民收入的定积分，可以评估经济的增长率。
定积分在生物学中的应用
种群动态
定积分可以计算物种数量和 种群生长率。
生态系统
通过定积分可以计算能量流 量和物质循环。
药物浓度
定积分可以计算药物在体内 的浓度和释放速率。
定积分在工程学中的应用
1 结构分析
定积分可以计算结构的强 度、刚度和变形。
定积分在计算机科学中的应用
1 图像处理
定积分可以计算图像的亮 度、对比度和边缘检测。
2 数据挖掘
通过计算定积分，可以评 估数据的分布和模式。

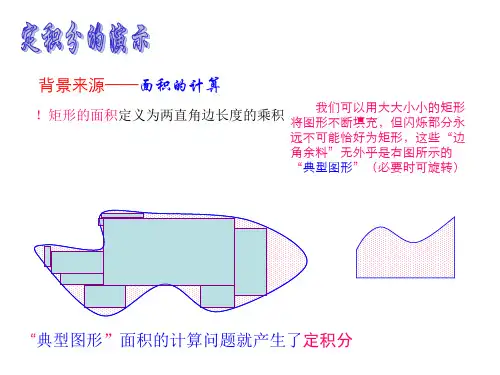
高等数学-定积分及其应用ppt课件.ppt

高等数学-定积分及其应用ppt课件.ppt
一、引例
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K，则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点，则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?

《定积分及其应用》课件

《定积分及其应用》课件
在经济学中，供需关系决定了市场的价格。供需曲线的面积表示市场上供应和需求的关系。通过计算这个面积， 我们可以了解市场的均衡点，也就是市场上的价格。同时，通过观察供需曲线面积的变化，我们可以了解市场的 价格变动趋势。
感谢您的观看
THANKS
在曲线上的积分。
曲线的转动惯量
总结词
通过定积分计算曲线的转动惯量
详细描述
转动惯量是描述物体转动难易程度的物理量。对于一个 均匀细长的物体，其转动惯量可以通过定积分来计算。 转动惯量等于质量分布相对于某一轴的转动惯量，等于 质量密度函数在物体质量分布上的积分。
05
定积分的经济应用
收益流的现值
总结词
收益流的现值是定积分在经济中的一个重要应用，它 可以帮助我们计算未来的现金流在当前的价值。
详细描述
在金融和经济学中，我们经常需要考虑未来的收益流 ，也就是未来的现金流。由于货币的时间价值，我们 需要将未来的现金流折现到现在的价值。定积分可以 用来计算这种折现的值。
投资决策问题
总结词
投资决策问题涉及到如何分配有限的资源以获得最大 的回报。定积分可以用来解决这类问题。
定积分的几何意义
总结词
定积分的值等于函数图像与x轴所夹的面积。
详细描述
定积分的值可以通过几何意义来解释，即定积分的值等于函数图像与x轴所夹的 面积。这个面积可以是正的、负的或零，取决于函数图像在给定区间上的上下 位置。
定积分的性质
总结词
定积分具有线性性质、可加性、可减性和区间可加性等性质。
详细描述
体积的计算
总结词
定积分在计算三维空间中物体体积的问 题中起到关键作用，特别是对于旋转体 和薄片绕旋转轴旋转形成的体积。
VS

定积分及其应用高数(共68张PPT)

定积分及其应用高数(共68张PPT)
例2 计算广义积分
例1 计算广义积分
例(2)4参数计方算程以所下(表定2示积)的分函. 数(t)在 [, ]或 ([,]上 )具有连续导数,
〔2〕无界函数的广义积分
R[a,b], 且其值域 奇、偶函数在对称区间上的定积分性质
变上限的定积分函数的性质
〔1〕无穷限的广义积分
那么有 〔2〕定积分的分部积分法
0
0
1
1(xx3)dx2(x3x)dx5
0
1
2
例3 计算 si3n xsi5n xd.x 0 3
解 f(x)si3x n si5x ncoxssinx2
si3nxsi5n xdx
coxssin x2 3dx
0
0
3
2coxssinx2dx
0
coxssinx23dx
3
2 sinx2dsinx
A1 A2
A3 A4
a bf(x )d x A 1 A 2A 3 A 4
2.定积分的性质
b
b
b
性质1 a [f(x ) g (x )d ] x af(x ) d x a g (x ) dx
性质2
b
b
a kf ( x)dx ka f ( x)dx
( k 为常数)
性质3 〔区间可加性〕
b
c
b
af(x)d x af(x)d x cf(x)dx
0
这个公式就是说： 周期函数在任何长为一周期的
区间上的定积分都相等.
例1 设
f(x)52x
0x1, 求 1x2
2
0 f (x)d.x
解2
1
2
0f(x )d x 0f(x )d x 1f(x )dx

定积分的应用ppt课件共37页PPT

定积分的应用ppt课件共37页PPT

例 连接坐标原点O 及点 P(h, r )的直线、直线
x h及 x轴围成一个直角三角形．将它绕 x轴旋
转构成一个底半径为r 、高为h的圆锥体，计算
圆锥体的体积．
y
P
解 直线 OP方程为
y r x
o
h
r
h
x
取积分变量为x，x[0,h]
在 [ 0 ,h ] 上 任 取 小 区 间 [ x ,x d ] ， x
以 d为 底 x 的 窄 边 梯 形 绕 x 轴 旋 转 而 成 的 薄 片 的
体 积 为
y
dVhr x2dx o
P
r
h
x
圆 锥 体 的 体 积
V
0hhr x2dx
r 2 h2
x3 h 3 0
hr 3
2
.
三、定积分在医学中的应用举例
如果函数 f ( x)在闭区间[a, b]上连续，
则在积分区间[a, b]上至少存在一个点 ，
y2 2x y x4
(2 , 2 )(,8 ,4 ).
选 y为积分变量 y[2,4]
yx4
y2 2x
dAy4y2dy
4
A dA18.
2
2
特别地,当曲边梯形的曲边由参数方程
x(t) y(t), (T1 t T2)
给出时,则此曲边梯形的面积为:
A T2(t)(t)dt T1
其中T1和T2是对应于曲线的起点及终点的 参数值.
x (y)、直线y c、y d及y轴所围
成的曲边梯形绕y轴旋转一周而成的立体，
体积为
y
V d [(y)]2dy c
d
x(y)
cox源自例 4 证 明 底 半 径 为 r , 高 为 h 的 圆 锥 的 体 积 公 式 .

《定积分及其应用》课件

《定积分及其应用》课件

性质
1 线性性质
定积分的线性性质使得我们能够对函数的和、差、乘以常数进行积分。
2 区间可加性
在一个区间上的积分等于在多个子区间上的积分之和。
3 保号性质
当函数在一个区间上不改变符号时，其定积分保持正负性质。
计算方法
换元法
通过变量代换，将原本复杂的积分转化为简单 的积分。
分部积分法
将原本难以求解的函数积分转换成两个易于求 解的函数之积分。
定积分的应用
通过物理、经济学相关实例展示定积分在实际中 的应用价值。
总结与回顾
在本课件中，我们深入学习了定积分的定义、性质、计算方法以及应用。希 望这些知识能够帮助你更好地理解和应用定积分，在解决实际问题中发挥重 要作用。
《定积分及其应用》PPT 课件
欢迎大家来到本次关于《定积分及其应用》的PPT课件，本课件将带领你深 入探索定积分的世界，揭示其定义、性质、计算方法以及广泛的应用。让我 们开始这个精彩的学习之旅吧！
定义
定积分代表曲线和x轴之间的面积，可以看作是无穷多个微小的面积的累加。
区别。
应用
几何意义
定积分可以计算曲线和x轴之间的面积，可以应用于计算图形的面积、弧长、体积等。
物理应用
定积分可以应用于物理学中的速度、加速度、质量等问题的求解。
经济学应用
定积分可以应用于经济学中的边际效应、总收益、总成本等的分析和计算。
综合实例展示
曲线的定积分
通过实际例子展示如何计算曲线和x轴之间的定 积分。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

oa
xxx b
x
f(x)C[a, b]
x
A(x) f(t)dt A (x)f(x) a
AdAf(x)dxdAf(x)dx
09.10.2020 A f( x ) d o x (x )(x 0 )4
微元分析法
第一步：分割 [a,区b],间 取具有代表
的小区[x间 , xx]“ , 不变代,写 变出 ”
a
13
[解] 利用对称性
a
A4A1 4 0 ydx
40asi3n t3aco2t(ssitn )dt
2
122a2s i4n t(1s i2n t)dx 0
1a 2 2(31531)
422 6422 3 a2
8
09.10.2020
14
（二）空间立体的体积 1. 已知平行截面面积立体的体积
分x的 变 化 区[0间 ,2] 体积微元是什麽？
dV2xydx
o
2
xxdx
V2
2
xxBiblioteka x0| 22x52 2162
思考： 5 0 5
薄壁圆桶
09.10.2020
何 时 选 择x为 积 分 变 量 ？ 何 时 选 择y为 积 分 变 量20？
（三）平面曲线的弧长 何谓曲线的长 ？ —内接折线长的极限
由Lagrang中 e 值定理得到
| 2
12(14y2)dy2(y4y3)
1 2
2
0
3 03
09.10.2020
10
2. 极坐标系下平面图形面积的计算
求曲线 ( )
及射线 ,
所围成的面积.
d
面积微元
()
o
面积微元：小圆扇形
dA 12()d
2
09.10.2020
A1 2()d
2
11
[例 3] 求 心脏 a(线 1cos)所 围
(1)由 直 线 xa, xb及x轴 和 连 续 曲 线y f (x)所 围 曲 边 梯 形 的 A 面
根据定积分的定义和几何意义知
b
Aa f(x) dx
09.10.2020
6
(2)由曲y线 f(x),yg(x)和直线
xa,xb所围成的 A 面积
先 , g (x 看 ) f(x )x [ a ,b ]
x(y) x(y)
c
面积公式：
o
x
09.10.2020
d
A [ (y) (y)]dy
c
9
[例 2]求 由x曲 5y2线 ,x1y2所 围
的 面 A. 积 1 y
[解] 解 方 程 组
2
x 5y2
x x
5y2
1 y2
y1 y 2
1 2
12
o
A 1 x1 y2
x
1
A2A1202(1y25y2)dy
y y f(x)
面积微元
d A [f(x)g(x)d ] x
b
yg(x)
A [f(x)g(x)]dx
oa
xxdx b x a
b
Aa f(x)g(x)dx
09.10.2020
7
[例 1]求 由x曲 y1及 线直 yx 线 ,x2 所围成 A . 的面积
[解] 解 方 程 组
y xy1 yx
x y 1
y
x
x1
x
2
1 1
(1, 1) x2
2
1
A
1
(x
)d x
x
o
| x2
23
( lnx) ln2
2
12
09.10.2020
2
1
x
8
设连续 (函 y) , (数 y)满足
0 (y )(y )y [ c ,d ]
求由曲 x线 (y),x(y),和直线
yc, yd所围成的 A 面积
y
d
y dyy
作业
P201 习题7.1 P210 习题7.2 P218 综合题 P113 习题4.3
1(5) 2. 8(2). 11(1). 15(1) 5. 15(2).
预习: P211—218
09.10.2020
1
第十九讲 定积分的应用（一）
一、微元分析法
二、几何应用
09.10.2020
2
一、微元分析法
可以应用定积分计算的量有如下特点:
(1)不 均 匀 变化 的 整 A依体赖量于
自 变 量 x的 某 个 区[a,间b].
n
(2)具 有 可 .即 , 加 A 性 Ai
i1
(3)部分量 Ai可“以不变代变”
求得近似值 Ai f (i )xi
09.10.2020
3
y
关键是 部分量 的近似
y
f(x)
b
a
f(t)dtA(b)
A
A( x)
y
Mi M i1
M1
A M0
o
xi
09.10.2020
xi xi
m 1inaM xi1Mi
B M n
n
l lim Mi1Mi
0 i1
x
21
(1) 设曲线段方程为 yf(x ) (axb )
曲线是 ,即 光 f(x)滑 在 [a,的 b]上连
M i 1 M i(x i) 2 (y i) 2( i 1 ,2 , ,n )
局部量的近似值 Af(x)x
微分近似
要 A 求 f ( x ) x ( ： x )
第 二 步 ： x令 0,微 元 在 区 [a, b间 ]上
无 限 积,得累定 积 分 就 是 整 体
b
09.10.2020
Aa f (x)dx
5
二、几何应用
（一）平面图形的面积
1. 直角坐标系下平面图形面积的计算
的 面 A. 积
[解] 利用对称性
A2A1
21 2
2()d
0
[a(1c
os)]2d
0
o
4a2
c
o4s
d
0
2
8a2 2co4stdt 0
09.10.2020
3 a2
2
12
3.参数方程下求图形面积
[例 4] 求 星 形 xy线 aasc： io3n 3tst t[0, 2]
所围面积。
09.10.2020
3
18
[例6]怎 样 求 由 曲 y线x, 直 线x2
和x轴 所 围 图 ,绕形y轴 旋 转 所
旋转体的体积？
[解法一]
y+dy
取y为 积 分 变 .即量 y
分y的 变 化 区 [0, 间2] o
2
V22 2 2x2dy4 2 2 y4dy
0
0
4 24 2162
09.10.2020
5
5
19
[解法二] 取x为积分变.即 量
17
[例5]
求
椭ax圆 22 by22
1绕x轴
y
旋
转
所
旋 转 体 的V.体 积
[解] 上半椭圆方程为
o
y b a2 x2 (axa)
a
x
a
利 用 对 称,性得 到
V2V1 2 0ay2dx2ab22
a(a2 x2)dx
0
| 2
09.10.2020
b2 a2
(a2xx3) 3
a 0
4 ab 2
A(x)
a
体积
09.10.2020
x xdx
b
V a A(x)dx
x
b
15
2. 旋转体的体积 y
A(x)y2
y f(x)
x
oa
xxdx b
V by2dx bf2(x)dx
a
a
09.10.2020
16
y
d
x(y)
y+dy y
c
x
o
A(y)x2
Vdx2dy d2(y)dy
c
c
09.10.2020

相关主题